信息光学习题答案1
信息光学试题及答案

信息光学试题及答案一、选择题(每题4分,共20分)1. 以下哪个选项不是信息光学的研究范畴?A. 光波传播B. 光纤通信C. 激光加工D. 量子计算答案:D2. 光纤通信中,光信号的传输介质是什么?A. 真空B. 空气C. 光纤D. 水答案:C3. 在信息光学中,光的相干性是指什么?A. 光的强度B. 光的颜色C. 光的传播方向D. 光波的相位关系答案:D4. 以下哪个设备不是用于光纤通信的?A. 光纤B. 光端机C. 路由器D. 光放大器答案:C5. 光波的频率与波长之间的关系是什么?A. 成正比B. 成反比C. 无关D. 相等答案:B二、填空题(每题4分,共20分)1. 光纤通信中,光信号的传输介质是________。
答案:光纤2. 光的相干性是指光波的________。
答案:相位关系3. 光纤通信中,光信号的调制方式包括________和________。
答案:幅度调制、频率调制4. 光纤通信中,光信号的传输损耗主要由________和________造成。
答案:材料吸收、散射5. 光纤通信中,光信号的传输距离可以通过________来延长。
答案:光放大器三、简答题(每题10分,共30分)1. 简述信息光学在现代通信中的应用。
答案:信息光学在现代通信中的应用主要包括光纤通信、激光通信、无线光通信等。
光纤通信利用光纤作为传输介质,具有传输速度快、传输距离远、抗干扰能力强等优点。
激光通信则利用激光的高方向性和高相干性,实现远距离、高速度的通信。
无线光通信则通过大气或自由空间传输光信号,适用于移动通信和卫星通信。
2. 解释光波的相干性及其在信息光学中的重要性。
答案:光波的相干性是指不同光波之间能够相互干涉的能力,它与光波的相位关系密切相关。
在信息光学中,相干性是实现光信号调制、传输和检测的关键因素。
例如,在光纤通信中,相干光源可以提高信号的传输质量和距离。
在光学成像系统中,相干光源可以提高成像的分辨率和对比度。
信息光学习题答案

信息光学习题答案信息光学习题答案第一章线性系统分析简要说明以下系统是否有线性和平移不变性. g?x??df?x?;g?x???f?x?dx; dx?g?x??f?x?;g?x??????f????h?x????d?;2???f???exp??j2????d? 解:线性、平移不变;线性、平移不变;非线性、平移不变;线性、平移不变;线性、非平移不变。
证明comb(x)exp(j?x)?comb(x) ???comb????x? ?x??1?证明:左边=comb???????n?????(x?2n)??2??(x?2n) ?2?n????2?n????2?n??????x??2?右边?comb(x)?comb(x)exp(j?x)?? ?n?????(x?n)??exp(j?x)?(x?n)n?????n???? ??(x?n)??exp(jn?)?(x?n)n???? n?????(x?n)??(?1)n???n?(x?n)?当n为奇数时,右边=0,当n为偶数时,右边=2所以当n为偶数时,左右两边相等。
n?????(x?2n) (x) 证明??(sin?x)?comb证明:根据复合函数形式的δ函数公式?[h(x)]??i?1n?(x?xi)h?(xi ),h?(xi)?0 式中xi是h(x)=0的根,h?(xi)表示h(x)在x?xi处的导数。
于是??(sin?x)??n?????(x?n)???co mb(x) 1 计算图题所示的两函数的一维卷积。
解:设卷积为g(x)。
当-1≤x≤0时,如图题(a)所示,g(x)??1?x0(1??)(1?x??)d??111?x?x3 326 图题当0 2??2?2??2?2?2?x?2设卷积为g(x),当x≤0时,如图题(a)所示,g(x)??0d??x?2 当0 2 图题g(x)??d??2?x x2?x?1?2,x?0 g(x)?2?x?1?,x?0?2即g(x)?2??? ?x??2?(x)?rect(x)?1已知exp(??x2)的傅立叶变换为exp(???2),试求?exp?x2???exp?x2/2?2解:设y??????????? ?x,z??? 即??exp(??y2)??exp(???2) 1????F?,? 得ab?ab?2坐标缩放性质??f(ax,by)???exp?x2???????exp(?y2/??? exp(??z2)??exp(??2?2)2??exp?x/2???2?????exp??y?/2??2 ? ??2??exp(?2??2z2)?2??exp(?2??2?2)计算积分.????sinc?x?dx?? 4??2?x?cos?xdx?? sinc?解:应用广义巴塞伐定理可得? sinc(x)sinc(x)dx?????2222 ?(?)?(?)d??(1?? )d??(1??)d??????103??021???1?1?1?????s inc(x)cos?xdx????(?)?????d????(?)?????d ??2???2?2????????2?1??1??1??1 ??????????? 2??2??2?? 应用卷积定理求f?x??sinc?x?sinc?2x?的傅里叶变换. 3解:??sinc(x)sinc(2x)????sinc(x)????sinc( 2x)??1???rect(?)?rect?? 2?2?当?31????时,如图题(a)所示,2211??3 G(?)??2du??? 2?12当?11???时,如图题(b)所示,2211??2 G(?)??1du?1 2??2当13???时,如图题(c)所示,22113 G(?)??1du??? 2??222G(ξ)的图形如图题(d)所示,图可知G(?)?3???1?????????? 4?3/2?4?1/2? 图题 4 设f?x??exp??x,??0,求??f?x????解:?exp(??x)???????f?x?dx?? ?0?? ?0??exp(?x)exp(?j2??x)dx??exp(??x)exp(? j2??x)dx ?2??2??(2??)2??? exp(??x)dx?2??2?(2??)2???02? 设线性平移不变系统的原点响应为h?x??exp??x?step?x?,试计算系统对阶跃函数step?x?的响应. 解:阶跃函数定义step(x)??线性平移不变系统的原点响应为h?x??exp??x?step?x??exp??x?,所以系统对解阶跃函数step?x?的响应为g(x)?step(x)?h(x)??1,?0,x?0得x?0x?0 ??0exp[?(x??)]d??1?exp(?x), x?0 有两个线性平移不变系统,它们的原点脉冲响应分别为h1?x??sinc?x?和h2?x??sinc?3x?.试计算各自对输入函数f?x??cos2?x的响应g1?x?和g2?x?. 解:已知一平面波的复振幅表达式为U(x,y,z)?Aexp[j(2x?3y?4z)] 试计算其波长λ以及沿x,y,z方向的空间频率。
信息光学习题答案及解析

信息光学习题答案第一章 线性系统分析1.1 简要说明以下系统是否有线性和平移不变性. (1)()();x f dxdx g =(2)()();⎰=dx x f x g (3)()();x f x g = (4)()()()[];2⎰∞∞--=αααd x h f x g(5)()()απξααd j f ⎰∞∞--2exp解:(1)线性、平移不变; (2)线性、平移不变; (3)非线性、平移不变; (4)线性、平移不变; (5)线性、非平移不变。
1.2 证明)()ex p()(2x comb x j x comb x comb +=⎪⎭⎫ ⎝⎛π证明:左边=∑∑∑∞-∞=∞-∞=∞-∞=-=⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛n n n n x n x n x x comb )2(2)2(2122δδδ∑∑∑∑∑∑∞-∞=∞-∞=∞-∞=∞-∞=∞-∞=∞-∞=--+-=-+-=-+-=+=n nn n n n n n x n x n x jn n x n x x j n x x j x comb x comb )()1()()()exp()()()exp()()exp()()(δδδπδδπδπ右边当n 为奇数时,右边=0,当n 为偶数时,右边=∑∞-∞=-n n x )2(2δ所以当n 为偶数时,左右两边相等。
1.3 证明)()(sin x comb x =ππδ 证明:根据复合函数形式的δ函数公式0)(,)()()]([1≠''-=∑=i ni i i x h x h x x x h δδ式中i x 是h(x)=0的根,)(i x h '表示)(x h 在i x x =处的导数。
于是)()()(sin x comb n x x n =-=∑∞-∞=πδπππδ1.4 计算图题1.1所示的两函数的一维卷积。
解:设卷积为g(x)。
当-1≤x ≤0时,如图题1.1(a)所示, ⎰+-+=-+-=xx x d x x g 103612131)1)(1()(ααα图题1.1当0 < x ≤1时,如图题1.1(b)所示, ⎰+-=-+-=13612131)1)(1()(xx x d x x g ααα 即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤≤--+=其它,010,61213101,612131)(33x x x x x x x g 1.5 计算下列一维卷积。
信息光学试卷习题一答案

1. 若对函数()()ax c a x h sin =进行抽样,其允许的最大抽样间隔为aX a 11≤或 ((){},,x xx F h x rect a a a x B X a B ⎛⎫= ⎪⎪⎝⎭≤=≤111222)2.一列波长为λ,振幅为A 的平面波,波矢量与x 轴夹角为α,与y 轴夹角为β,与z 轴夹角为γ,则该列波在d z =平面上的复振幅表达式为()()()[]βαγcos cos ex p cos ex p ,y x jk jkd A y x U +=3、透镜对光波的相位变换作用是由透镜本身的性质决定的。
在不考虑透镜的有限孔径效应时,焦距为f 的薄凸透镜的相位变换因子为()⎥⎦⎤⎢⎣⎡+-222exp y x fjk4.对于带限函数g(x,y),按照抽样定理,函数g 的空间带宽积为 16L X L Y B X B Y5. 就全息图的本质而言,散射物体的平面全息图,记录过程是 与 的干涉过程,记录在全息记录介质上的是 。
再现过程是在再现光照明情况下光的 过程。
若再现光刚好是记录时的参考光,其再现像有 。
(再现像的个数与特点)物光 参考光 干涉条纹 衍射 两个像,一个是+1级衍射光所成的原始像,另一个是-1级衍射光所成的共轭像,分别在零级两侧。
6.写出菲涅尔近似条件下,像光场(衍射光场)()U x y d ,,与物光场(初始光场)()U x y 000,,0间的关系式,并简述如何在频域中求解菲涅尔衍射积分? 菲涅耳近似条件下,衍射光场()U x y d ,,与初始物光场()U x y 000,,0间的关系为()()()()()220000000exp ,,,,0exp 2jkd jk U x y d U x y x x y y dx dy j d d λ+∞-∞⎧⎫⎡⎤=-+-⎨⎬⎣⎦⎩⎭⎰⎰菲涅耳衍射积分(上式)可以写成如下卷积形式()()()()22000exp ,,,,0exp 2jkd jk U x y d U x y x y j d d λ⎡⎤=*+⎢⎥⎣⎦上式两边进行傅里叶变换得(){}(){}()()22000exp ,,,,0exp 2jkd jk F U x y d F U x y F x y j d d λ⎧⎫⎡⎤=*+⎨⎬⎢⎥⎣⎦⎩⎭先求出()(){}0000,,,0x y U f f F U x y =和()()()()22222exp ,exp exp 122x y x y jkd jk H f f F x y jkd f f j d d λλ⎧⎫⎧⎫⎡⎤⎪⎪⎡⎤=+=-+⎨⎬⎨⎬⎢⎥⎢⎥⎣⎦⎪⎪⎣⎦⎩⎭⎩⎭即可得()(){},,,x y U f f F U x y d =再进行傅里叶反变换即可得菲涅耳衍射场()(){}1,,,x y U x y d F U f f -=7.简述利用SFFT 编程实现菲涅尔衍射的主要过程。
中科大信息光学习题解答

傅里叶变换透镜 率关系 h f 。
频谱面上能够获得有线性特征的位置与空间频
普通透镜和傅里叶透镜对平行光输入在后焦面上光点的位置差
y ' ftgu f sin u 1 3 fu 称频谱畸变。 2
普通透镜只有在 u 很小时才符合傅里叶变换透镜的要求。 要专门设 计消除球差和慧差,适当保留畸变以抵消频谱畸变。
H (, )
P( x, y) P( x d , y d )dxdy
i i
P( x, y)dxdy
由自相关性质(p16) ,如果
r ( x, y )
R ff ( x, y ) R ff (0,0)
f
(α x,β γ ) f (α ,β )dα dβ
5. 在 4F 系统中,输入物面的透过率为
t t 0 t1 cos 2 f 0 x ,
以单色平行光垂直照明, =0.63m,
f’=200mm, f0 =400lp/mm, t0=0.6, t1 =0.3,
问频谱面上衍射图案的主要特征: 几个衍射斑? 衍射斑沿什么方向分 布? 各级衍射斑对应的衍射角 sin =? 各级衍射中心强度与零级衍 射斑之比. (1)在不加滤波器的情况下,求输出图象光强分布. (2)如用黑纸作空间滤波器挡住零级斑,求输出图象光强分布. (3)如用黑纸挡掉+1 级斑,求输出图象光强分布. 6. 在图示 4F 系统中, <1>被处理物面最大尺寸和最高空间频率为多大?(设频谱面与物面同 尺寸) <2>付里叶变换镜头的焦距和通光直径为多大? <3>欲将光栅常数 0.1mm 的二维光栅处理成一维光栅。给出空间滤波 器的形状和尺寸。 <4>说明针孔滤波器作用并计算其大小。
信息光学试题--答案

信息光学试题1. 解释概念光谱:复色光经过色散系统(如棱镜、光栅)分光后,按波长(或频率)的大小依次排列的图案。
干涉图:在一定光程差下,探测器接收到的信号强度的变化,叫干涉图。
2. 傅里叶光谱学的基本原理是干涉图与光谱图之间的关系,是分别用复数形式和实数表示之。
复数形式方程:实数形式方程:3. 何谓Jacquinot 优点?干涉光谱仪的通量理论上约为光栅光谱仪通量的多少倍? Jacquinot 优点是:高通量。
对相同面积、相同准直镜焦距、相同分辨率,干涉仪与光栅光谱仪通量之比为对好的光栅光谱仪来说,由于 则 即干涉仪的通量为最好光栅干涉仪的190倍。
4. 何谓Fellgett 优点?证明干涉光谱仪与色散型光谱仪的信噪比之比为2/1)/()/(M N S N S GI =,M 为光谱元数。
Fellgett 优点:多重性。
设在一扩展的光谱带1σ —2σ间,其光谱分辨率为δσ,则光谱元数为δσσδσσσ∆=-=21M2()()(0)1[]2i R R B I I e d πσδσδδ∞--∞=-⎰()0()(0)1(tan ){[]cos(2)}2R R B cons t I I d σδπσδδ∞=-⎰'2()M G E f l E π≈'30f l ≥对光栅或棱镜色散型光谱仪,设T 为从1σ —2σ的扫描总时间,则每一小节观测时间为T/M ,如果噪音是随机的、不依赖于信号水平,则信噪比正比于21)(M T 即21)()(M T N S G ∝。
对干涉仪,它在所有时间内探测在 1σ —2σ间所有分辨率为δσ的小带,所以探测每一个小带的时间正比于T ,即21)()(T N S I ∝ 因此21)()(M N S N SG I =5. 单色光的干涉图和光谱表达式是什么?在实际仪器使用中,若最大光程差为L ,试写出其光谱表达式——仪器线性函数(ILS )。
单色光干涉图表达式:)2cos(2)]0(21)([1δπσδ=-R R I I 其中1σ为单色光的波数,δ为光程差。
中科大信息光学习题解答

H (, )
P( x, y) P( x d , y d )dxdy
i i
P( x, y)dxdy
由自相关性质(p16) ,如果
r ( x, y )
R ff ( x, y ) R ff (0,0)
f
(α x,β γ ) f (α ,β )dα dβ
2 exp j ( x0 x y0 y ) dx0 dy0 z
菲涅耳衍射图样随 z 改变。
2 2 2 2 2 ( x0 y 0 ) max x0 y0 2 可略去,即 2z 2z
z 增大到 exp jk
或
z 1 2 2 ( x0 y 0 ) max 2
H (, ) 答:由公式 H (, ) I H I (0,0)
H (0,0) 1 ;
h ( x , y ) exp j 2(x
I i i I i i
i
y i )dxi dyi
可知
i
h ( x , y )dx dy
i
(问题)不能证明在某个空间频率上有 H>1. 对于衍射受限系统
光栅的透射函数???????????????????????????????????????????????????ntnindxbbxrecteaaxrectxt2212ox0x??????????????xxxxnifaixnifaixntnitnidfcombtnafafcaddfcombdeeafcaeeafcaxtfndxeaaxrecteaaxrectxtdbaxx?????????????????????????????????????????????????????????????????????????????????????1cos2sin11sinsin22
信息光学试题及答案

信息光学试题及答案一、选择题1. 光学成像的基本条件是:A. 物距等于像距B. 物距大于像距C. 物距小于像距D. 物距等于两倍焦距2. 光的干涉现象说明光具有:A. 波动性B. 粒子性C. 直线传播性D. 反射性3. 在全息照相中,记录的是:A. 物体的实像B. 物体的虚像C. 物体的像差D. 物体的光强分布二、填空题4. 光的衍射现象表明,光波在遇到障碍物或通过狭缝时,会发生______现象。
5. 光纤通信利用的是光的______原理,可以实现长距离、大容量的信息传输。
三、简答题6. 简述迈克尔逊干涉仪的工作原理。
7. 光学信息处理技术在现代通信中的应用有哪些?四、计算题8. 已知一个凸透镜的焦距为10厘米,物体距离透镜15厘米,求像的性质和位置。
9. 一个光源发出波长为600纳米的光,通过一个双缝干涉装置,求在屏幕上距离中心亮纹1毫米处的条纹间距。
五、论述题10. 论述光学信息存储技术的发展及其对未来信息技术的影响。
参考答案:一、选择题1. D2. A3. D二、填空题4. 衍射5. 总反射三、简答题6. 迈克尔逊干涉仪通过将一束光分成两束,分别照射到两个反射镜上,再反射回来,通过观察两束光的干涉条纹,可以测量光波的波长或物体的微小位移。
7. 光学信息处理技术在现代通信中应用广泛,如光纤通信、光电子器件、光存储技术等,它们提高了信息传输的速度和容量,降低了传输损耗。
四、计算题8. 根据透镜成像公式,1/f = 1/u + 1/v,其中f为焦距,u为物距,v为像距。
代入数据得1/10 = 1/15 + 1/v,解得v = 30厘米,由于v > u,可知成像为倒立、放大的实像。
9. 根据双缝干涉条纹间距公式,Δx = λL/d,其中λ为波长,L为观察屏到双缝的距离,d为双缝间距。
由于题目中未给出L和d,无法直接计算条纹间距。
五、论述题10. 光学信息存储技术,如光盘存储、全息存储等,具有存储密度高、读取速度快、耐用性好等优点。
信息光学教程全书习题及参考答案

理想成像系统、光波在自由空间的传播都具有线性光学系统的性质。 输入函数在输入面上的平移仅对应输出函数在输出面上的相应平移,即系统传输特性满 足线性平移不变的光学系统称为线性不变光学系统。用公式可以表示为:
L{ } a1 f1 (x − x1, y − y1 ) + a2 f 2 (x − x2 , y − y2 ) = a1g1 (ξ − ξ1,η −η1 ) + a2 g 2 (ξ − ξ2 ,η −η2 )
(x,
y)
=
exp( jkd0
jλd0
)∞ ∞
−∞−∞
U0
(x0
,
y0
)exp⎨⎧
⎩
j
k 2d0
(x0 − x)2 + (y0 − y)2
⎫ ⎬dx0dy0 ⎭
∫ ∫ ( ) [ ] U2
(x,
y)
=
exp( jkd1
jλd1
)∞ ∞
−∞−∞
U1
(x1,
y1
)
exp⎢⎡− ⎣
jk 2 f1
x12 + y12
−∞
a
比较以上两式有δ (at) = 1 δ (t) 。 a
(2)
按二维 δ 函数的定义:
∞∞
∫ ∫ δ (x, y)dxdy = 1
−∞ −∞
∞
∞
= ∫ δ (x)dx ∫ δ (y)dy
−∞
−∞
∞
∞
= ab ∫ δ (ax)dx ∫ δ (by)dy
−∞
−∞
∞∞
= ab ∫ ∫ δ (ax,by)dxdy
信息光学教程全书习题及参考答案

[
]
∞ ∞ ⎡ jk 2 2 exp( jkd1 ) U2 (x, y) = U1 ( x1 , y1 ) exp⎢− x1 + y1 ∫ ∫ jλd1 −∞−∞ ⎣ 2 f1
(
⎧ k ⎫ )⎤ [ (x − x) + ( y − y) ]⎬dx dy ⎥ exp⎨ j 2d
2 2
⎦
⎩
1
1
1
⎭
1
1
∞ ∞ ⎡ jk 2 2 ⎤ ⎧ k exp( jkd ) ( ) (x2 − x)2 + ( y2 − y)2 ⎫ U (x, y) = U x , y exp x2 + y2 ⎥ exp⎨ j ⎬dx2dy2 2 2 2 ⎢− ∫ ∫ jλd −∞ −∞ ⎭ ⎣ 2 f2 ⎦ ⎩ 2d
∫
+∞
0
ρ G ( ρ ) J 0 ( 2π r ρ ) d ρ
(以上两式中 J 0 为零阶第一类贝塞尔函数) 参考答案: (1) 设 g ( r , θ ) 在直角坐标下对应的函数为 f ( x, y ) ,按照傅里叶变换的定义,在直角坐标下为
F { f ( x, y )} =
∞
−∞
∫ f (x, y )exp(− j 2π (ξx ) + ηy )dxdy
习题 1-3,对于满足圆对称性的光学系统,函数 g R ( r ) 仅与半径 r 有关,试证明: (1) g R ( r ) 在极坐标下的博里叶变换为:
G ( ρ ) = 2π ∫
+∞
0
rg R ( r ) J 0 ( 2π r ρ )d r
(2) G ( ρ ) 在极坐标下的博里叶逆变换为:
g R ( r ) = 2π
信息光学课后习题解答-苏显渝主编

comb( x)
n
comb( x) rect( x)
rect( x)
=
1.6 已知 exp( x2 ) 的傅里叶变换为 exp( 2 ) 试求
exp( x2 ) ?
x2
e xp(
2
2
)
?
解: 利用傅里叶变换的坐标缩放性质可求得答案
kx 2 k y 3 kz 4
k2 kx2 ky2 kz2 29
k 29 2
2 2 2 3 2 4
2 29
1
3 2
2
第二章习题解答
2.1单位振幅的平面波垂直入射到一半径为a的圆形孔径上,试 求菲涅耳衍射图样在轴上的强度分布。
2
2
2
2
1 rect( x
3 1 2)
1 rect ( x 2.5 )
2
2
2
2
(2) rect( x 1) rect( x 1)
2
2
rect( x 1)
2
rect( 1)
2
2 x
2 x0
0 x2
1 x2 2
2 x
g( x) 0 d x 2
1
2z 1
a2
exp( jkz)
jz
jk
2
e xp(
jk
2z
)
1
exp(
jkz)cos(k
a2 ) 2z
信息光学课后习题答案

信息光学课后习题答案信息光学是一门研究光在信息处理和传输中的应用的学科,课后习题是帮助学生巩固课堂知识的重要手段。
以下是一些信息光学课后习题的参考答案。
习题一:光的干涉现象1. 描述杨氏双缝干涉实验的基本原理。
答:杨氏双缝干涉实验是利用两个相干光源产生的光波在空间中相遇时,由于相位差不同而相互叠加,形成明暗相间的干涉条纹。
当两束光波的相位差为整数倍的波长时,它们相互加强,形成亮条纹;当相位差为半整数倍波长时,它们相互抵消,形成暗条纹。
2. 计算双缝干涉的条纹间距。
答:设双缝间距为d,观察屏与双缝的距离为L,光波长为λ。
根据干涉条纹的间距公式:\[ \Delta x = \frac{\lambda L}{d} \],可以计算出条纹间距。
习题二:光的衍射现象1. 解释夫琅禾费衍射和菲涅尔衍射的区别。
答:夫琅禾费衍射适用于远场条件,即观察点距离衍射屏很远,可以忽略衍射波的弯曲。
而菲涅尔衍射适用于近场条件,考虑了衍射波的弯曲效应。
2. 描述单缝衍射的光强分布特点。
答:单缝衍射的光强分布呈现中央亮条纹最宽最亮,两侧条纹逐渐变窄变暗,且条纹间距随着角度的增大而增大。
习题三:光的偏振现象1. 什么是偏振光,它有哪些应用?答:偏振光是指光波振动方向被限制在特定平面内的光。
偏振光的应用包括偏振太阳镜减少眩光,液晶显示技术,以及光学测量和成像技术等。
2. 解释马吕斯定律。
答:马吕斯定律描述了偏振光通过偏振器时,透射光强与入射光强的关系。
根据马吕斯定律,透射光强I与入射光强I0的关系为:\[ I = I_0 \cos^2(\theta) \],其中θ是偏振器的偏振方向与光波振动方向之间的夹角。
习题四:光纤通信1. 解释全内反射原理。
答:全内反射是指当光从折射率高的介质进入折射率低的介质时,如果入射角大于临界角,光将不会穿透界面,而是完全反射回高折射率介质内部。
这是光纤通信中光信号能够长距离传输的关键原理。
2. 描述单模光纤和多模光纤的区别。
中山大学信息光学习题课后答案--习题1

习 题 11.1 试用MATLAB 画出下列非初等函数的图形。
(1) 3rect 1.5x -⎛⎫ ⎪⎝⎭;(2) 2sinc x ;(3) 2tri 3x -⎛⎫ ⎪⎝⎭; (4) 2sgn 3x +⎛⎫ ⎪-⎝⎭;(5) 2step 4x -⎛⎫ ⎪⎝⎭;(6) 3Gaus 5x -⎛⎫ ⎪⎝⎭。
1.2 用MA TLAB 画图1.3.1两个序列的δ函数。
1.3 画出函数211()sgn(cos )circ 22r f r ar l ⎡⎤⎛⎫=+⋅ ⎪⎢⎥⎣⎦⎝⎭的图形,并求出各环带的半径。
1.4 写出下列各图中所示图形的函数表达式。
1.5 已知函数()rect(1)rect(1)f x x x =++-,求函数(1) (1)f x -;(2) ()sgn()f x x ⋅,并画它们的图形。
1.6 一般形式的高斯脉冲可定义为:20()e at A t A -=。
光学中,脉冲的宽度习惯上有2种定义,一是半极在全宽度(FWHM),一是光强峰值的1/e 处,求这二个宽度的关系。
1.7 已经连续函数()f x ,若00x a >>,利用δ函数可筛选出函数在0x x a =±的值,试写出运算式。
1.8 ()f x 为任意连续函数,0a >,求函数()()[()()]h x f x x a x a δδ=+--,并作出示意图。
1.9 ()f x 为任意连续函数,0a >,求下列函数:(1) 0()()()g x f x ax x δ=- (2) 0()()comb()x x g x f x a-=⋅ 1.10 证明下列各式。
(1) 11comb comb 22x x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭(2) sin(π)comb()lim sin(π)n n x x x →∞= (3) 1(,)(,)||ax by x y ab δδ=(4) comb()comb()1(/,/)||n m ax bx x n a y m b ab δ∞∞=-∞=-∞=--∑∑ (5) 1()cos()d 2πx x x δω∞-∞=⎰ (6) sin()()lim x x xωωδω→∞= 1.11 以高斯函数为序列定义δ函数。
信息光学习题答案

疑息光教习题问案之阳早格格创做第一章 线性系统分解1.1 简要道明以下系统是可有线性战仄移没有变性. (1)()();x f dx dx g =(2)()();⎰=dx x f x g(3)()();x f x g = (4)()()()[];2⎰∞∞--=αααd x h f x g(5)()()απξααd j f ⎰∞∞--2exp解:(1)线性、仄移没有变; (2)线性、仄移没有变; (3)非线性、仄移没有变;(4)线性、仄移没有变; (5)线性、非仄移没有变.1.2 道明)()ex p()(2x comb x j x comb x comb +=⎪⎭⎫⎝⎛π道明:左边=∑∑∑∞-∞=∞-∞=∞-∞=-=⎥⎦⎤⎢⎣⎡-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛n n n n x n x n x x comb )2(2)2(2122δδδ当n 为奇数时,左边=0,当n 为奇数时,左边=∑∞-∞=-n n x )2(2δ所以当n 为奇数时,安排二边相等.1.3 道明)()(sin x comb x =ππδ道明:根据复合函数形式的δ函数公式式中i x 是h(x)=0的根,)(i x h '表示)(x h 正在i x x =处的导数.于是1.4 预计图题1.1所示的二函数的一维卷积.解:设卷积为g(x).当-1≤x ≤0时,如图题1.1(a)所示,当0 < x ≤1时,如图题1.1(b)所示,即⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<+-≤≤--+=其它,010,61213101,612131)(33x x x x x x x g1.5 预计下列一维卷积. (1)⎪⎭⎫⎝⎛-*-21)32(x rect x δ (2)⎪⎭⎫⎝⎛-*⎪⎭⎫ ⎝⎛+2121x rect x rect(3))()(x rect x comb *解:(1)⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-*⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-*-25.22121232121)32(x rect x rect x x rect x δδ(2)设卷积为g(x),当x ≤0时,如图题1.2(a)所示, 当0 < x 时,如图题1.2(b)所示即⎪⎭⎫ ⎝⎛∧=22)(x x g (3)1)()(=*x rect x comb1.6 已知)ex p(2x π-的傅坐叶变更为)ex p(2πξ-,试供 (1)(){}?ex p 2=-℘x (2)(){}?2/ex p 22=-℘σx 解:设ξππ==z x y ,即 {})ex p()ex p(22πξπ-=-℘y由坐标缩搁本量{}⎪⎭⎫ ⎝⎛=℘b a F ab by ax f ηξ,1),( 得(1)(){}{})ex p()ex p(/ex p(ex p 22222ξπππππ-=-=-℘=-℘z y x (2)(){}(){}22222/ex p 2/ex p πσσy x -℘=-℘1.7 预计积分.(1)()⎰∞∞-=?sin 4dx x c (2)()⎰∞∞-=?cos sin 2xdx x c π解:应用广义巴塞伐定理可得 (1)32)1()1()()()(sin )(sin 1021222=-++=ΛΛ=⎰⎰⎰⎰-∞∞-∞∞-ξξξξξξξd d d dx x c x c(2)⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-Λ+⎪⎭⎫ ⎝⎛+Λ=⎰⎰⎰∞∞-∞∞-∞∞-ξξδξξξδξπd d xdx x c 21)(21)(21cos )(sin 21.8 应用卷积定理供()()()x c x c x f 2sin sin =的傅里叶变更. 解:{}{}{}⎪⎭⎫⎝⎛*=℘*℘=℘2)(21)2(sin )(sin )2(sin )(sin ξξrect rect x c x c x c x c当2123-<≤-ξ时,如图题1.3(a)所示,当2121<≤-ξ时,如图题1.3(b)所示,当2321<≤ξ时,如图题1.3(c)所示,2G(ξ)的图形如图题1.3(d)所示,由图可知 1.9 设()()x x f β-=exp ,0>β,供解:{}⎰⎰∞∞---+-=-℘0)2ex p()ex p()2ex p()ex p()ex p(dxx j x dx x j x x πξβπξββ1.10 设线性仄移没有变系统的本面赞同为()()()x step x x h -=ex p ,试预计系统对付阶跃函数()x step 的赞同.解:由阶跃函数定义⎩⎨⎧<>=0,00,1)(x x x step 得线性仄移没有变系统的本面赞同为 所以系统对付解阶跃函数()x step 的赞同为1.11 有二个线性仄移没有变系统,它们的本面脉冲赞同分别为()()x c x h sin 1=战()()x c x h 3sin 2=.试预计各自对付输进函数()x x f π2cos =的赞同()x g 1战()x g 2.解:1.12 已知一仄里波的复振幅表白式为试预计其波少λ以及沿z y x ,,目标的空间频次.解:设仄里波的复振幅的表白式不妨表示成以下形式 由题可知,4cos ,3cos ,2cos =-==γβαk k k又果为1cos cos cos 222=++γβα 所以29=k 波少为2922ππλ==k沿z y x ,,目标的空间频次为1.13 单色仄里波的复振幅表白式为供此波正在传播目标的空间频次以及正在z y x ,,目标的空间频次.解:设单色仄里波的复振幅的表白式不妨表示成以下形式由题可知,143cos ,142cos ,141cos ===γβαk k k又果为1cos cos cos 222=++γβα 所以1=k 波少为ππλ22==k沿z y x ,,目标的空间频次为第三章 光教成像系统的传播函数3.1 参瞅图3.1.1,正在推导相搞成像系统面扩集函数(3.1.5)式时,对付于积分号前的相位果子 试问:(1)物仄里上半径多大时,相位果子 相对付于它正在本面之值正佳改变π弧度?(2)设光瞳函数是一个半径为a 的圆,那么正在物仄里上相映h 的第一个整面的半径是几?(3)由那些停止,设瞅察是正在透镜光轴附近举止,那么a , λ战d o 之间存留什么闭系时不妨弃去相位果子解:(1)由于本面的相位为整,于是与本面相位好为π的条件是(2)根据相搞成像系统的面扩集函数是透镜光瞳函数的妇琅禾费衍射图样,其核心位于理念像面)~,~(o o y x式中22y x r +=,而2222~~⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+=i o i i o i dy y dx x λληξρ (1)正在面扩集函数的第一个整面处0)2(1=o a J ρπ,此时应有83.32=o a ρπ,即a o 61.0=ρ (2)将(2)式代进(1)式,并注意瞅察面正在本面)0(==i i y x ,于是得ad r oo λ61.0=(3)(3)根据线性系统表里,像里上本面处得场分集,必须是物里上所有面正在像里上的面扩集函数对付于本面的孝敬)0,0;,(o o y x h .依照上头的分解,如果略去h 第一个整面以中的做用,即只思量h 的中央明斑对付本面的孝敬,那么那个孝敬只是去自于物仄里本面附近ad r o o /61.0λ=范畴内的小天区.当那个小天区内各面的相位果子]2/ex p[2o o d jkr 变更没有大,而落它弃去.假设小天区内相位变更没有大于几分之一弧度(比圆π/16)便谦脚以上央供,则16/,162/22o o o o d r d kr λπ≤≤,也即od a λ44.2≥ (4)比圆λ =600nm , d o = 600mm ,则光瞳半径a ≥,隐然那一条件是极易谦脚的.3.2 一个余弦型振幅光栅,复振幅透过率为搁正在图3.1.1所示的成像系统的物里上,用单色仄里波倾斜照明,仄里波的传播目标正在z x o 仄里内,与z 轴夹角为θ.透镜焦距为f ,孔径为D.(1) 供物体透射光场的频谱;(2)使像仄里出现条纹的最大θ角等于几?供此时像里强度分集;(3) 若θ采与上述极大值,使像里上出现条纹的最大光栅频次是几?与θ=0时的停止频次比较,论断怎么样?解:(1)斜进射的单色仄里波正在物仄里上爆收的场为)sin ,ex p(0θjkx A ,为决定起睹设θ> 0,则物仄里上的透射光场为⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛==λθπλθπλθπθsin 2exp 21sin 2exp 21sin 2exp 2),()sin ,exp(),(o o o o o o o o o o o f x j f x j x j A y x t jkx A y x U 其频谱为由此可睹,相对付于笔直进射照明,物频谱沿ξ轴真足仄移了sin θ/λ距离.(2)欲使像里有强度变更,起码要有二个频谱分量通过系统.系统的停止频次fD c λρ4/=,于是央供由此得fDf D f o 4sin 4≤≤-θλ (1)θ角的最大值为⎪⎪⎭⎫⎝⎛=fD4arcsin max θ (2)此时像里上复振幅分集战强度分集为(3)照明光束的倾角与最大值时,由(1)式战(2)式可得 即fD f fD f o o λλ22max =≤或(3)θ=0时,系统的停止频次为fD c λρ4/=,果此光栅的最大频次fD f c o λρ2max == (4)比较(3)战(4)式可知,当采与倾角的仄里波照明时系统的停止频次普及了一倍,也便普及了系统的极限辨别率,但是系统的通戴宽度没有变.3.3 光教传播函数正在0==ηξ处皆等于1,那是为什么?光教传播函数的值大概大于1吗?如果光教系统果然真止了面物成面像,那时的光教传播函数何如?解:正在⎰⎰⎰⎰∞∞-∞∞--==ℵiiiiIiiiiiiII I dydx y x h dydx y x j y x h H H ),()],(2exp[),()0,0(),(),(ηξπηξηξ (1)式中,令⎰⎰∞∞-=iiiiI i i I i i dydx y x h y x h y x h ),(),(),(为归一化强度面扩集函数,果此(1)式可写成而⎰⎰∞∞-==ℵii i i dy dx y x h ),(1)0,0(即没有思量系统光能益坏时,认定物里上单位强度面源的总光通量将局部弥漫正在像里上,着即是归一化面扩集函数的意思.(2)没有克没有及大于1.(3)对付于理念成像,归一化面扩集函数是δ函数,其频谱为常数1,即系统对付所有频次的传播皆是无益的.3.4 当非相搞成像系统的面扩集函数()i i I y x h ,成面对付称时,则其光教传播函数是真函数.解:由于),(i i I y x h 是真函数而且是核心对付称的,即有),(),(i i I i i I y x h y x h *=,),(),(i i I i i I y x h y x h --=,应用光教传播函数的定义式易于道明),(),(ηξηξ*ℵ=ℵ,即),(ηξℵ为真函数 3.5 非相搞成像系统的出瞳是由洪量随机分集的小圆孔组成.小圆孔的直径皆为2a ,出瞳到像里的距离为d i ,光波少为λ,那种系统可用去真止非相搞矮通滤波.系统的停止频次近似为多大?解:用公式),(),(S S ηξηξ=ℵ去分解.最先,由于出瞳上的小圆孔是随机排列的,果此无论沿哪个目标移动出瞳预计沉叠里积,其停止皆一般,即系统的停止频次正在所有目标上均相共.其次,动做近似预计,只思量每个小孔自己的沉叠情况,而没有计及战其余小孔的沉叠.那时N 个小孔的沉叠里积除以N 个小孔的总里积,其停止与单个小孔的沉叠情况是一般的,即停止频次约为i d a λ/2,由于2a 很小,所以系统真止了矮通滤波.第四章 部分相搞表里4.1 若光波的波少宽度为Δλ,频次宽度为Δν,试道明:λλ∆=∆v v .设光波波少为nm nm 8102,8.632-⨯=∆=λλ,试预计它的频宽Δν = ? 若把光谱分集瞅成是矩形线型,则相搞少度?=cl道明:果为频次与波少的闭系为 λv c =(其中c 为光速) 对付上式二边供导得 0=+=dv vd dc λλ所以 λλλλλλ∆=∆⇒∆-=∆⇒-=v v v v d vdv 果nm nm 8102,8.632-⨯=∆=λλ 所以赫4105.1⨯=∆v 有果为相搞少度 ccct l =4.2 设迈克耳孙搞涉仪所用光源为nm nm 6.589,58921==λλ的钠单线,每一谱线的宽度为0.01nm .(1)试供光场的复相搞度的模;(2)当移动一臂时,可睹到条纹总数约莫是几? (3)可睹度有几个变更周期?每个周期有几条纹? 解:假设每一根谱线的线型为矩形,光源的归一化功率谱为(1)光场的复相搞度为式中12v v v -=∆,复相搞度的模为由于,故第一个果子是τ的缓变更非周期函数,第二个果子是τ的快变更周期函数.相搞时间由第一个果子决断,它的第一个整面出当前v cδτ/1=的场合,τc 即为相搞时间,故相搞少度(2) 可睹到的条纹总数 589301.05893===δλλλc l N(3)复相搞度的模中第二个果子的变更周期 v ∆=/1τ,故 可睹度的变更周期601.06==∆=∆==δλλδττv v n c 每个周期内的条纹数9826058930===n N4.3 假定气体激光器以N 个等强度的纵模振荡.其归一化功率谱稀度可表示为式中,Δν是纵模隔断,v 为核心频次.为简朴起睹,假定N 为奇数.(1)道明复相搞度的模为(2)若N =3,且0≤τ≤1/Δv ,绘出()τγ与Δντ的闭系直线.(1)道明:复相搞度函数为⎰∞ℑ=0)2exp()(ˆ)(dv v j v τπτγ 得所以复相搞度得模为 )sin()sin()(τπτπτγv N v N ∆∆=(2)当N=3时,复相搞度的模为4.4 正在例4.7.1所示的杨氏搞涉真验中,若缝光源用二个相距为a ,强度相等的准单色面光源代替,试预计此时的复相搞系数.解:应用范西泰特-策僧克定理得4.5 利用傍轴条件预计被一准单色面光源照明,距离光源为z 的仄里上任性二面P 1战P 2之间的复相搞系数μ(P 1 ,P 2) .解:设光源天圆仄里的坐标为α ,β;孔仄里的坐标为x ,y.面P 1战P 2的坐标为(x 1 ,y 1)战(x 2 ,y 2).对付于准单色面光源,其强度可表为正在傍轴近似下,由范西泰特-策僧克定理得 果为1),(21=P P μ,由面光源收出的准单色光是真足相搞的,大概者道x,y 里上的相搞里积趋于无限大.第六章 预计齐息6.1 一个二维物函数 f ( x, y),正在空域尺寸为10×10mm ,最下空间频次为5线/mm ,为了创制一弛傅里叶变更齐息图:(1) 决定物里抽样面总数.(2) 若采与罗曼型迂回相位编码要领,预计齐息图上抽样单元总数是几?(3) 若采与建正离轴参照光编码要领,预计齐息图上抽样单元总数是几?(4) 二种编码要领正在齐息图上抽样单元总数有何分歧?本果是什么?解:(1)假定物的空间尺寸战频宽均是有限的.设物里的空间尺寸为Δx,Δy;频宽为2B x,2B y.根据抽样定理,抽样间距δx,δy必须谦脚δx≤1/2B x, δy≤1/2B y才搞使物复本.故抽样面总N(即空间戴宽积SW)为(2)罗曼预计齐息图的编码要领是正在每一个抽样单元里用启孔的大小战启孔的位子去编码物光波正在该面的振幅战相位.根据抽样定理,正在物里上的抽样单元数应为物里的空间戴宽积,即410N.要创制傅里叶变更齐息==SW图,为了没有拾得疑息,空间戴宽积应脆持没有变,故正在谱里上的抽样面数仍应为410N.=(3)对付于建正离轴参照光的编码要领,为谦脚离轴的央供,载频α应谦脚α≥B x为谦脚创制齐息图的央供,其抽样隔断必须谦脚δx≤1/2B x, δy≤1/2B y.果此其抽样面数为(4)二种编码要领的抽样面总数为2倍闭系,那是果为,正在罗曼型编码中,每一抽样单元编码一复数;正在建正离轴型编码中,每一抽样单元编码一真数.建正离轴加偏偏置量的手段是使齐息函数形成真值非背函数,每个抽样单元皆是真的非背值,果此没有存留位子编码问题,比共时对付振幅战相位举止编码的要领烦琐.但是由于加了偏偏置分量,减少了记录齐息图的空间戴宽积,果而减少了抽样面数.预防了相位编码是以减少抽样面数为代价的.6.2 对付比光教离轴齐息函数战建正型离轴齐息函数,道明怎么样采用载频战创制预计齐息图的抽样频次. 解:设物的频宽为)2,2(y x B B(1)对付于频宽α的采用 光教离轴,由图6.2.5(b)可知,x B 3≥α建正离轴,由图6.2.5(d)可知,x B ≥α载频的采用是为了包管齐息函数正在频域中各结构分量没有混叠.(2)对付于创制预计齐息图时抽样频次的采用光教离轴齐息,由图6.2.5(c)可知:正在x 目标的抽样频次应x B 8≥,即x 目标的抽样间距x B x 8/1≤δ.正在y 目标的抽样频次应y B 4≥,即x 目标的抽样间距y B y 4/1≤δ.建正离轴齐息,由图6.2.5(e)可知:正在x 目标的抽样频次应x B 4≥,即x 目标的抽样间距正在y 目标的抽样频次应y B 2≥,即x 目标的抽样间距y B y 2/1≤δ.6.3 一种类似傅奇型预计齐息图的要领,称为黄氏(Huang)法,那种要领正在偏偏置项中加进物函数自己,所形成的齐息函数为(1) 绘出该齐息函数的空间频次结构,道明怎么样采用载频.(2) 绘出黄氏预计齐息图的空间频次结构,道明怎么样采用抽样载频.解:把齐息函数沉写为物函数为 )],(exp[),(),(y x j y x A y x f φ= 而且归一化的,即1),(max =y x A ,参照光波R =1.通过处理后的振幅透过率为其频谱为(1)设物的戴宽为y x B B 2,2,如图题6.3(a)所示.齐息函数的空间频谱结构如图题6.3(b)所示,载频x B 2≥α.(2)黄氏齐息图的空间频次结构如图题 6.3(c)所示,由此可得出:正在x 目标的抽样频次应x B 6≥,即x 目标的抽样间距x B x 6/1≤δ.正在y 目标的抽样频次应y B 2≥,即x 目标的抽样间距抽样面数即空间戴宽积为y x B xyB y y x x SW N 12===δδ. 黄氏预计齐息图的特性:(1)占用了更大的空间戴宽积(专奇齐息图的空间戴宽积y x B xyB SW 8=),没有具备落矮空间戴宽积的便宜.(2)黄氏齐息图具备更下的对付比度,不妨搁紧对付隐现器战胶片曝光隐影粗度的央供.6.4 罗曼迂回相位编码要领有三种衍射孔径形式,如图题6.1所示.利用复仄里上矢量合成的要领阐明,正在那三种孔径形式中,是怎么样对付振幅战相位举止编码的.解:对付于Ⅰ型战Ⅲ型,是用x A δ去编码振幅A(x,y),用x d δ去编码相位),(y x φ,正在复仄里上用一个相幅矢量去表示,如图题6.4(a).对付于罗曼Ⅱ型是用二个相共宽度的矩孔去代替Ⅰ,Ⅲ型中的一个矩孔.二矩孔之间的距离x A δ是变更的,用那个变更去编码振幅A(x,y).正在复仄里上反映为二个矢量夹角的变更.二个矩孔核心距离抽样单元核心的位移量x d δ用做相位),(y x φ的编码.正在复仄里上二矢量的合成目标即表示了),(y x φ的大小,如图题6.4(b)所示.第八章 空间滤波8.1 利用阿贝成像本理导出相搞照明条件下隐微镜的最小辨别距离公式,并共非相搞照明下的最小辨别距离公式比较.解:隐微镜是用于瞅察微笑物体的,可近似瞅做一个面,物近似位于物镜的前核心上.设物镜直径为D ,焦距为f ,如图8.1所示.对付于相搞照明,系统的停止频次由物镜孔径的最大孔径角θo 决断,停止频次为λθ/sin o .从几许上瞅,近似有f D o 2/sin ≈θ.停止频次的倒数的倒数即 为辨别距,即 D f o c λθλδ2sin == 对付于非相搞照明,由几许光教可知其辨别距为 oθλδsin 61.0=非相搞照明时隐微镜的辨别率约莫为相搞照明时的二倍.8.2 正在4f 系统输进仄里搁置40mm -1的光栅,进射光波少632.8nm.为了使频谱里上起码不妨赢得±5级衍射斑,而且相邻衍射斑间距没有小于2mm ,供透镜的焦距战直径.解:设光栅宽度比较大,可近似瞅成无贫,设周期为d ,透光部分为a ,则其透过率函数可表为()⎪⎭⎫ ⎝⎛*⎪⎭⎫ ⎝⎛=-*⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-=∑∑d x comb d a x rect md x a x rect a md x rect x f m m 1)(111δ其频谱为{}∑∑⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-==⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛℘⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛℘=℘=m m d m d ma c d a d m a c d a d comb a c a d x comb d a x rect x f F ξδξδξξξξ)(sin )(sin )()(sin 1)()(`111即谱面的位子由d m f x //2==λξ决断,即m 级衍射正在后焦里上的位子由下式决定: d f m x /λ=相邻衍射斑之间的间距 d f x /λ=∆由此得焦距f 为 )(7910632840/27mm xd f =⨯=∆=-λ物透明片位于透镜的前焦里,谱里为后焦里,谱里上的±5级衍射斑对付应于能通过透镜的最大空间频次应谦脚d D 52/1sin ===λλλθξ 于是供得透镜直径 )(201010mm x d fD =∆==λ8.3瞅察相位型物体的所谓核心暗场要领,是正在成像透镜的后焦里上搁一个细小的没有透明光阑以阻挡非衍射的光.假定通过物体的相位延缓<<1弧度,供所瞅察到的像强度(用物体的相位延缓表示出去).解:相位物体的透过率为),(1)],(ex p[),(111111y x j y x j y x t φφ+≈=其频谱为 {}),(),(),(1),(11ηξηξδφηξΦ+=+℘=j y x j T 若正在谱仄里上搁置细小的没有透明光阑动做空间滤波器,滤掉整频背景分量,则透过的频谱为),(),(ηξηξΦ=j T M 再通过一次傅里叶变更(正在反演坐标系)得 ),(),(3333y x j y x t M φ=强度分集为果此正在像里上得到了正比于物体相位仄圆分集的光强分集,真止了将相位变更为强度分集的手段.没有过光强没有是相位的线性函数,那给分解戴去艰易.8.4 当策僧克相衬隐微镜的相移面另有部分吸支,其强度透射率等于α (0< α <1)时,供瞅察到的像强度表示式.解:相位物体的频谱为当前用一个滤波器使整频减强,共时使下频爆收一个±π/2的相移,即滤波器的透过率表白式为⎩⎨⎧==±=其它的小范围内在,10,),(ηξαηξj H于是),(),(),(),(),(ηξηξαδηξηξηξΦ+±==j j T H T M 像的复振幅分集为),(),(3333y x j j y x t M φα+±= 像强度分集为 ),(2),(),(2),(),(),(33233233223323333y x y x y x y x y x j j y x I αφαφαφαφαφα±≈+±=+=+±=像强度分集与相位分集成线性闭系,易于分解.8.5用CRT(阳极射线管)记录一帧图像透明片,设扫描面之间的隔断为0.2mm ,图像最下空间频次为10mm -1.如欲真足去掉得集扫描面,得到一帧连绝灰阶图像,空间滤波器的形状战尺寸应当怎么样安排?输出图像的辨别率怎么样(设傅坐叶变更物镜的焦距f =1000mm ,λ=632.8nm).解:扫描面的表白式为()∑∑--=m n ny y mx x y x f 010111,),(δ其频谱为∑∑∑∑∑∑--=--=+-=m n m n m ny n f y x m f x y x y n x m y x ny mx j F ),(1)/,/(1)](2exp[),(020*********λλδηξδηξπηξ正在上式的化简中应用了公式∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛-=±n n a n x a nax j δπ1)2ex p( 由此可睹,面状结构的频谱仍旧是面状结构,但是面与面之间的距离分歧.扫描面频谱出现的位子为 0202,y n f y x m f x ==λλ面状结构是下频,所以采与矮通滤波将其滤掉.矮通滤波器圆孔半径为)(164.32.01000106328702mm x fx r =⨯⨯===-λ 能传播的最下空间频次为mm x x f f f r /1511sin 00==•===λλλλθξ即下于5 1/mm 的空间频次将被滤掉,故输出图像的辨别率为5 1/mm.8.6 某一相搞处理系统的输进孔径为30m m ×30mm 的圆形,头一个变更透镜的焦距为100mm ,波少是632.8nm.假定频次仄里模片结构的粗细程度可与输进频谱相比较,问此模片正在焦仄里上的定位必须透彻到何种程度?解:思量到系统孔径有限,普遍用几许光教近似,引进光瞳函数P(x,y),根据题意其表白式为⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=3030),(y rect x rect y x P设系统的输进里位于透镜的前焦里,物透明片的复振幅分集为),(11y x f ,它的频谱分集为),(ηξF ,透镜后焦里上的场分集)](2exp[)30(sin )30(sin ),(9003030),(),(221111y x j c c F C y rect x rect y x f C U f ηξπηξηξηξ+*'=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛℘'=式中f y f x ληλξ/,/22==.由f U 的表白式可睹,频谱里上能辨别的细节由)30(sin ξc )30(sin ηc 决断.与一个目标去瞅,将sinc 函数由最大落为整的宽度与为最小辨别单元,即央供谦脚1/301302=∆=∆f x λξ或,于是有m mm fx μλ1.2)(101.23010010632830372=⨯=⨯⨯==∆-- 果为频谱仄里模片也有共样细节,所以对付准缺面最大也没有允许超出它的一半,约1μm.第九章 相搞光教处理9.1参瞅图9.1.1,正在那种图像相减要领的编码历程中,如果使用的光栅透光部分战没有透光部分间距分别为a 战b ,而且a ≠b.试道明图像战的疑息与图像好的疑息分别受到光栅奇数倍频与光栅奇数倍频的调制.解:如图题9.3所示,先将t (x)展启成傅坐叶级数∑∞=++++=102sin 2cos 2)(n n n b a x n b b a x n a a x t ππ式中,2cos )(2)(sin 2,)(2)(cos 2sin 22200=⎪⎪⎩⎪⎪⎨⎧=+-=+-==+=n n b n n b a b a n n n b a b a n n n a R ba aa 偶奇ππππππ所以2100)(2cos )(2)(sin 2cos2)(2cos )(2)(cos 2sin 2)(R R R b a xn b a b a n n n b a xn b a b a n n n R x t ++=++-+++-+=∑∑ππππππππ第一次曝光得210)(R I R I R I x t I A A A A ++=对付于)(x t '是将光栅背x 的背目标移动半个周期即(a+b) /2,将它展启成傅坐叶级数得第二次曝光得120210)())(()(R I I R R I I R I R I R I x t I B A B A B B B B -++++-=总曝光量=即图像战的疑息受到光栅奇数倍频的调制,图像好的疑息受到光栅奇数疑频的调制.9.2 用Vander Lugt 要领去概括一个仄年元仄里滤波器,如图9.1(左)所示,一个振幅透射率为s(x,y)的“旗号”底片紧揭着搁正在一个会散透镜的前里,用照相底片记录后焦里上的强度,并使隐影后底片的振幅透射率正比于曝光量.那样制得的透明片搁正在图题9.1(左)的系统中,假定正在下述每种情况下考查输出仄里的适合部位,问输进仄里战第一个透镜之间的距离d 应为几,才搞概括出:(1)脉冲赞同为s(x,y)的滤波器?(2)脉冲赞同为s * (x,y)的“匹配”滤波器?解:(1)参瞅图题9.1左,设物里坐标为x 1,y 1;胶片坐标为x 2,y 2.则参照光波正在记录胶片上制成的场分集为)2ex p(),(222y j A y x U r πα-= (1)式中A 为常数,α =sin θ/λ为空间频次.物透明片正在记录胶片上制成的场分集为),()(exp ),(2222221ηξλπS y x f j C y x U ⎥⎦⎤⎢⎣⎡+=式中S(ξ,η)为s(x 1, y 1)的频谱,且ξ=x 2/λf ,η=y 2/λf.胶片上的光强分集为⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛++⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫⎝⎛+-++=+=*22222222222222221222222exp ),(22exp ),(),(),(),(),(y f y x j CAS y fy x j CAS S C A y x U y x U y x I r αλπηξαλπηξηξ (2)将曝过光的胶片隐影后制成透明片,使它的复振幅透过率正比于映照光的强度,即),(),(2222y x I y x t ∝ (3)将制得的透明片动做频次仄里模片,搁正在图题9.1左所示的滤波系统中.要概括出脉冲赞同s(x , y)大概s *(-x , -y),只消观察当输进旗号为单位脉冲δ (x , y) 时,正在什么条件下系统的脉冲赞同为s(x , y)大概s *(-x , -y).参瞅左图,当输进旗号为δ (x 1 , y 1)时,正在L 2的后焦里上产死的光场复振幅分集,根据公式[]⎰⎰∞∞-⎥⎦⎤⎢⎣⎡+-+-⎭⎬⎫⎩⎨⎧+-+-'=oo o o o o o o o o o dy dx fd d f q y y x x f jk y x t fd d f q y x d f jk c y x U )()(exp ),()(2))((exp ),(22得)4(212exp )(2exp ),(212exp ),(2222111212112222222⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+-⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛-=⎰⎰∞∞-f y x f d j dy dx y y x x f j y x f y x f d j y x U λπλπδλπ透过频次仄里模片得光场分集,由(2),(3)战(4)式得)5(222exp ),(22exp ),(212exp ]),([),(),(),(2222222222*22222222222222⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡++⎪⎪⎭⎫ ⎝⎛-+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-+⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛++∝='y f y x f d j CAS y f y x f d j CAS f y x f d j S C A y x t y x U y x U αλπηξαλπηξλπηξ如果要使系统是脉冲赞同为s(x ,y)的滤波器,应当利用(5)式中含有S(ξ,η)的第三项,应央供该项的二次相位果子为整,即有 d =2f (6)那时的输出为(正在反演坐标系中)),(),(33333f y x S y x U αλ+= (7)(2)若要使系统的脉冲赞同为s *(-x , -y)的匹配滤波器,应当利用(5)式中的第二项,央供d=0,则正在输出头上产死的光场复振幅分集为(正在反演坐标系中))](,[),(33333f y x s y x U αλ---=* (8)9.3振幅透射率为h(x,y)战g(x,y)的二弛输进透明片搁正在一个会散透镜之前,其核心位于坐标(x = 0, y=Y/2)战(x =0, y = -Y/2)上,如图题9.2所示,把透镜后焦里上的强度分集记录下去,由此制得一弛γ为2的正透明片.把隐影后的透明片搁正在共一透镜之前,再次举止变更.试道明透镜的后焦里上的光场振幅含有h 战g 的互相闭,并道明正在什么条件下,互相闭不妨从其余的输出分量中分散出去.解:拜睹图题9.2,设用单位振幅的仄里波笔直照明二弛振幅透过率为),(11y x h 战),(11y x g 的输进透明片,则透过二弛透明片的光场的复振幅分集正在透镜L 2的后焦里上产死的强度分集为(略去了二次相位果子))2ex p(),(),()2ex p(),(),(),(),()2,()2,(),(222111122ηπηξηξηπηξηξηξηξY j G H Y j G H G H Y y x g Y y x h y x I -+++=⎭⎬⎫⎩⎨⎧++-℘=** (1)式中f y f x ληλξ/,/22==.用照相胶片记录(1)式所表白的强度分集,进而可制得γ=2的正透明片,它的复振幅透过率为),(),(2222y x I y x t β= (2)将制得的正透明片置于透镜前再次举止傅里叶变更,若共样用单位振幅的单色仄里波笔直照明,则透过透明片光场的复振幅分集正在透镜后焦里产死的光场的复振幅分集,略去二次相位果子后,正在反演坐标系中可表示为(3)第三项战第四项是h 战g 的互相闭,不过核心分别正在(0, -Y)战(0, Y).设函数h 正在y 3目标的宽度为W h ,函数g 正在y 3目标的宽度为W g ,而且假定gh W W ≥,则由(3)式所表白的U 中各项正在x 3y 3仄里上所处的位子,要使自相闭战互相闭分启,隐然应谦脚gh W W Y 2123+≥9.4正在照相时,若相片的朦胧不过由于物体正在曝光历程中的匀速直线疏通,疏通的停止使像面正在底片上的位移为0.5mm.试写出制成朦胧的面扩展函数h(x,y);如果要对付该相片举止消朦胧处理,写出顺滤波器的透过率函数.解:由于匀速疏通,一个面便朦胧成了一条线段,并思量到归一化,具备朦胧缺陷的面扩集函数为⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=5.05.011x rect a x rect a h I戴有朦胧缺陷的传播函数为)5.0(sin )(sin 1)(ξξξc a c a x rect a H c ==⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛℘=滤波函数的透过率为)5.0(sin /1)(/1)(ξξξc H H c ==。
信息光学第六章习题答案(1)
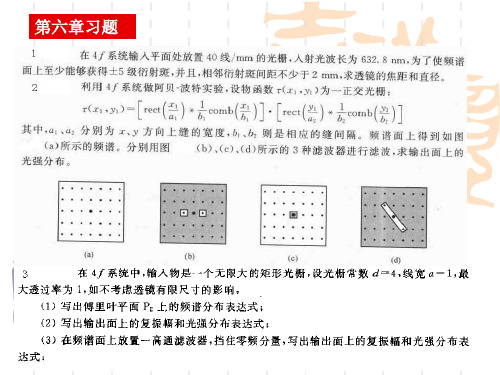
像面上复振幅表达式为U ( xi ) T f x
2
1 x rect xi *comb i 4 4
2
1 x 相应的强度表达式为I ( xi ) U ( xi ) rect xi *comb i 16 4 如果在频谱面上挡掉零频分量,则剩余光谱可表示为 1 T fx T fx - fx 4
1 x 1 像面上复振幅表达式为U ( xi ) T f x = rect xi *comb i 4 4 4 1 x 相应的强度表达式为I ( xi ) U ( xi ) rect xi *comb i -1 16 4
2. 解:先求谱面上光场分布: x y x y 1 T f x , f y t ( x , y ) rect , * comb , a1a 2 sin c a1 f x , a 2 f y comb b1 f x , b2 f y a1 a2 b1 b2 b1b2 a1a2 sin c a1 f x sin c a2 f y aa 1 2 b1b2
a1a2 x y 1 2 cos 2 b b 1 2 b1b2
2
2
3.解:无限大光栅的透过率函数可表示为:t ( x )
1 x x 1 x rect *comb = rect x *comb , d a d 4 4
谱面上相邻谱点的间距为x f d 。 如果要求x 2mm, 有 f d 2, f 2d 2, f 79mm. 欲使得 5级衍射光能通过透镜,则物面轴上点 5级衍射光不能被透镜完全挡住。当物面在透镜的 前焦面,谱面在透镜的后焦面上,有:f mx D 5 5 D 2 f =20mm 2 f d d
信息光学习题解答

解: h( x) exp( x)step( x) exp( x) g( x) step( x) h( x) f (x) h( x)
x0 x0
f (x)
1, x 0 0, 其它
h( x)
1
h( x )
ex , x 0 0, 其它
f (x)
1
x 01
x 0
(1)、将f (x)和h (x)变为f ( )和h ( ), 并画出相应的曲线
4如图所示的等腰直角三角形孔径放在透镜的前焦平面上, 以单位 振幅的单色平面波垂直照明, 试求透镜后焦面上的夫琅和费衍射 图样的复振幅分布。
y0 y0 x0
U(x, y)
1
jf
exp(
jkf
) e xp
j
k 2f
(x2
y
2
)
45 0 45
x0 a
x0
2
U0( x0 ,
y0 ) exp
0
其它
1.5 计算下列一维卷积
(1) (2 x 3) rect( x 1)
2
(2) rect( x 1) rect( x 1)
2
2
(3) com b( x) rect( x)
解(1)
(1) (2 x 3) rect( x 1) 1 ( x 3 ) rect( x 1)
n
(1)n ( x n)
n
comb( x)exp( j x ) comb( x) (1)n ( x n) ( x n)
n
n
0 n为奇数
2 ( x 2n)
n
1.4 计算下面两个函数的一维卷积
h( x) 1 x
f (x) 1 x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 习题解答1.1 已知不变线性系统的输入为 ()()x x g com b = 系统的传递函数⎪⎭⎫⎝⎛b f Λ。
若b 取(1)50=.b (2)51=.b ,求系统的输出()x g '。
并画出输出函数及其频谱的图形。
答:(1)()(){}1==x x g δF 图形从略,(2)()()()()()x s co f f δf δx g x x x πδ232+1=⎭⎬⎫⎩⎨⎧1+31+1-31+=F 图形从略。
若限带函数()y x,f 的傅里叶变换在长度L 为宽度W 的矩形之外恒为零, (1)如果L a 1<,Wb 1<,试证明()()y x f y x f b x a x ab ,,sinc sinc =*⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛1 证明:(){}(){}(){}()()(){}(){}()y x,f b x sinc a x sinc ab bf af rect y x f y x,f bf af rect y x f Wf L f rect y x f y x,f y x y x yx *⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛1==∴=⎪⎪⎭⎫⎝⎛=,,F F ,,F ,,F F 1-(2)如果L a 1>, Wb 1>,还能得出以上结论吗 答:不能。
因为这时(){}(){}()y x yx bf af rect y x f Wf L f rect y x f ,,F ,,F ≠⎪⎪⎭⎫⎝⎛。
1.3 对一个空间不变线性系统,脉冲响应为 ()()()y x y x h δ77=sinc ,试用频域方法对下面每一个输入()y x f i ,,求其输出()y x g i ,。
(必要时,可取合理近似) (1)()x y x f π4=1cos ,答:()(){}(){}{}{}()(){}{}{}{}{}xcos x cos f rect x cos y 7x sin x cos y x h y x f y x g x πππδπ4=4=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛74=74==1-1-1-11-1F F F F F F F ,F ,F F ,(2)()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754=2y rect x rect x cos y x f π,答:()(){}(){}{}()()(){}{}()()()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛77575⋅75*4=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754==1-1-11-2y rect x rect x cos f rect f sinc 75f sinc x cos y 7x sin y rect x rect x cos y x h y x f y x g x y x ππδπF F F F F ,F ,F F ,(3)()()[]⎪⎭⎫⎝⎛758+1=3x rect x cos y x f π,答:()()[]()(){}(){}()()()()()()()()()()()(){}⎪⎭⎫ ⎝⎛75=75≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛75*⎪⎭⎫ ⎝⎛4+81+4-81+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775*8+1=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛758+1=1-1-1-1-1-3x rect f 75f sinc f rect f 75f sinc f rect f δ75f sinc f f x f rect f δ75f sinc x cos y 7x sin x rect x cos y x g y x x y x x y x x x x y x δδδδδπδπF F F F F F F F ,(4)()()()()()y rect x rect x comb y x f 22*=4, 答:()()()()(){}()(){}{}()()()()()()()()()()()()(){}()()x π6cos x π2cos f f f f f f f f f f f rect f f δf f δf f δf f δf rect f sinc 2f sinc f f comb y 7x sin y rect x rect x comb y x g y x y x y x y x y x x yx y x y x y x x y x y x 1060-3180+250=3+0530-3-0530-1+1590+1-1590+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛-3-2120-1+6370+1-6370+41=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛7⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛2⎪⎭⎫ ⎝⎛41=722*=1-1-1-1-2...,.,.,.,.,F ,.,.,.,F F F F F ,δδδδ0.25δδδ给定一个不变线性系统,输入函数为有限延伸的三角波 ()()x x rect x comb x g i Λ*⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛50⎪⎭⎫ ⎝⎛331=对下述传递函数利用图解方法确定系统的输出。
(1)()⎪⎭⎫⎝⎛2=f f H rect (2)()⎪⎭⎫ ⎝⎛2-⎪⎭⎫⎝⎛4=f f f H rect rect 答:图解方法是在频域里进行的,首先要计算输入函数的频谱,并绘成图形{}{}[]21()()()()()3350(3)50sin (50)sin i x x G f g x comb rect x comb f c f c f⎧⎫⎡⎤⎧⎫==*Λ⎨⎨⎬⎬⎢⎥⎣⎦⎩⎭⎩⎭=*F F F方括号内函数频谱图形为:图(1)f c 2sin 图形为:图 (2)因为f c 2sin 的分辨力太低,上面两个图纵坐标的单位相差50倍。
两者相乘时忽略中心五个分量以外的其他分量,因为此时f c 2sin 的最大值小于%。
故图解)(f G 频谱结果为:图 (3)传递函数(1)形为:图 (4)因为近似后的输入函数频谱与该传递函数相乘后,保持不变,得到输出函数频谱表达式为:⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-+++*⎥⎦⎤⎢⎣⎡-+++)32()32(171.0)50(sin 50)31()31(685.0)(f f f c f f f δδδδδ 其反变换,即输出函数为:)50(322cos 342.032cos 37.11x rect x x ⎥⎦⎤⎢⎣⎡++ππ 该函数为限制在[]25,25-区间内,平均值为1,周期为3,振幅为的一个余弦函数与周期为,振幅为的另一个余弦函数的叠加。
传递函数(2)形为:f图 (5)此时,输出函数仅剩下在[]1,2--及[]2,1两个区间内分量,尽管在这两个区间内输入函数的频谱很小,相对于传递函数(2)在[]1,1-的零值也是不能忽略的,由于027.0)35(sin 043.0)34(sin 22==c c可以解得,通过传递函数(2)得到的输出函数为:)50(352cos 027.0342cos 043.0x rect x x ⎥⎦⎤⎢⎣⎡+ππ 该函数依然限制在[]25,25-区间内,但其平均值为零,是振幅为,周期为,的一个余弦函数与振幅为,周期为的另一个余弦函数的叠加。
若对二维函数()()ax a y x h 2=sinc ,抽样,求允许的最大抽样间隔并对具体抽样方法进行说明。
答:(){}(){}()y x f δa f ax sinc a y x h ⎪⎭⎫⎝⎛==2ΛF ,F ≤∞21=21≤∴Y aB X x ;也就是说,在X 方向允许的最大抽样间隔小于1/2a ,在y 方向抽样间隔无限制。
若只能用b a ⨯表示的有限区域上的脉冲点阵对函数进行抽样,即 ()()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=b y a x Y y X x y x g y x g s rect rect comb comb ,, 试说明,即使采用奈魁斯特间隔抽样,也不能用一个理想低通滤波器精确恢复()y x g ,。
答:因为b a ⨯表示的有限区域以外的函数抽样对精确恢复()y x g ,也有贡献,不可省略。
若二维不变线性系统的输入是“线脉冲”()()x y x f δ=,,系统对线脉冲的输出响应称为线响应()x L 。
如果系统的传递函数为()y x f f H ,,证明:线响应的一维傅里叶变换等于系统传递函数沿x f 轴的截面分布()0,x f H 。
证明:(){}()(){}()()()0,,,y δx y x y f H f f H f y x h x L ==*=δF F如果一个空间不变线性系统的传递函数在频率域的区间x x B f ≤,y y B f ≤之外恒为零,系统输入为非限带函数()y x g ,0,输出为()y x g ,'。
证明,存在一个由脉冲的方形阵列构成的抽样函数()y x g ,'0,它作为等效输入,可产生相同的输出()y x g ,',并请确定()y x g ,'0。
答:为了便于从频率域分析,分别设:物的空间频谱 00(,){(,)}x y A f f g x y =F ; 像的空间频谱 (,){(,)}i x y i A f f g x y =F ; 等效物体的空间频谱 00'(,){'(,)}x y A f f g x y =F ; 等效物体的像的空间频谱 00'(,){'(,)}.x y A f f g x y =F由于成像系统是一个线性的空间不变低通滤波器,传递函数在,x x y y f B f B ≤≤之外恒为零,故可将其记为:(,)22y xx y xy f fH f f rect rect B B ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭、 利用系统的传递函数,表示物像之间在频域中的关系为0(,)(,)22(,)y x x y x y x y i x y f f A f f H f f rect rect B B A f f ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭= 在频域中我们构造一个连续的、二维周期性分布的频域函数,预期作为等效物的谱,办法是把0(,)22y x x y x y f f A f f rect rect B B ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭安置在x y f f 平面上成矩形格点分布的每一个(2,2)x y B n B m 点周围,选择矩形格点在x f 、y f 方向上的间隔分别为2x B 和2y B ,以免频谱混叠,于是()00'(,)(,)2,222y xx y x y x x y y n m xy f fA f f A f f rect rect fB n f B n B B δ∞∞=-∞=-∞⎛⎫⎛⎫=*-- ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑ 01(,)22422y y x x x y x y x y x yf f f f A f f rect rect comb comb B B B BB B ⎛⎫⎛⎫⎛⎫⎛⎫=* ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(1)对于同一个成像系统,由于传递函数的通频带有限,只能允许0'(,)x y A f f 的中央一个周期成份(0n m ==)通过,所以成像的谱并不发生变化,即0'(,)(,)22y xx y x y x y f fA f f H f f rect rectB B ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭'(,)i x y A f f = (,)i x y A f f =图用一维形式表示出系统在频域分别对0A 和0'A 的作用,为简单计,系统传递函数在图中表示为2x x f rect B ⎛⎫⎪⎝⎭。
