两表法测量三相电路功率
用二瓦特计法测量三相三线制电路平

容易看出,当一个瓦特计的电流线圈通过 的电流为iB,电压线圈通过的电流为uBA,另一 个瓦特计的电流线圈通过的电流为iC,电压线圈 通过的电压为uCA时,两个瓦特计侧得的平均功 率的代数和仍是三相负载的平均功率;或者, 当一个瓦特计的电流线圈通过的电流为iC,电压 线圈接入的电压为uBA时,两个瓦特计测得的平 均功率的代数和也是三相负载的平均功率。
A
*
W1
*
B
*
C
W2
*
三相 负载
图 用二瓦特计法测量三相三线制电路的平均功率
P I ] U AC cos 1 1 Re[U
* AC A
P2 Re[U I ] U BC cos 2
* BC A
式中,1为 U AC与 I A 之间的相为差, 2为 UBC与 I A 之间的相为差。 现在证明三相负载的平均功率
* * * * P P Re[ U I ] Re[ U I ] Re[ U I U I 1 2 AC A BC B AC A BC B ] * Re[(U AN ' U CN ' ) I * ( U U ) I A BN ' CN ' B] * * * Re[U AN ' I * U I U ( I I A BN ' B CN ' A B )] * * Re[U AN ' I * U I U I A BN ' B CN ' C ]
二瓦特计法测量三相平均功率
在三相电路中,根据电路是否对称,电路是三相四 线制还是三相三线制等不同情况,可以用一个、两个或 三个瓦特计测量三相平均功率。一瓦表法、二瓦表法相 对来说容易理解,用二瓦特计法测量三相三线制电路 平 均功率的方法则相对较难理解。下面予以讨论
三相四线制电路中两功率表法计量误差分析

的, 决定 一 R[
6 ]正负 主要 由 j 。决定 。。为 A、 j
B C三 相 电流 之 和 ,。的 幅值 和 相 位 不 但 决 定 于 、 j 负 载 的平 衡情 况 , 且 决 定 于 电路 的功 率 因 数 。 而 当
超前 j 。在 0 ~ 9 。 围 内, R [,j 为 负 , 。 0范 ~ (B ]
差 , 电力 企业 、 计单 位 、 对 设 施工 单位 都有 着极 为 重
要 的意 义 。
1 两 表 法 测 量 有 功 功 率 误 差 理 论 分 析
1 1 测 量 电路及 功 率计 算 . 两 功 率 表法 测 量 三 相 四线 电路 和三 相 三 线 电 路有 功 功率 的接 线 图如 图 1 示 。 所
i a a y e O s a d r iem e s r me t cr u t n e u e t e e r r fg t n r y me e s i a u e n , s n l z d t t n a d z a u e n ic i a d r d c h r o s o a e e e g t r n me s r me t s
少计 量 。 目前我们 国家 西南 地 区很 多地 方小 型火力
电量 测试 的人员 所认识 。 但 在实 际 测量 中 , 相 _ l 1 三
发 电厂仍 然采用 两 功率 表 法 测 量 三相 四线 电路 有
收稿 日期 :0 9 1— 9修 回 日期 :0 91 —5 2 0— 0 2 ; 2 0— 1 2
R[ j 古]为正 , 测量将 产 生正 误差 。
一
() a 两功率 表法 测量三 相三 线电路 功率
般 电路 中都 存在 着正 序 、 负序 和零序 组 电压
三相电路功率测量实验小结

三相电路功率测量实验小结
一、实验目的
1、掌握用二瓦特表的方法测量三相电路有功功率与无功功率的方法。
2、进一步熟悉掌握功率表的接线和使用方法。
二、实验设备和器材
交流电压表 0~500 V
交流电流表 0~5 A
单相功率表
万用表 MF-500型
三相自耦调压器 0~430 V
三相灯组负载 220 V,40 W白炽灯
三相电容负载 1uF,2.2 uF,4.7 uF/500V
三、实验原理与说明
1、对于三相四线制供电的三相星形连接的负载,可用一只功率表测量各相的有功功率PA、PB、PC,则三相负载的总有功功率∑P = PA+PB+PC。
这就是一瓦特表法,如实验图7-1所示。
若三相负载是对称的,则只需测量一相的功率,再乘以3即得三相总的有功功率。
2、三相三线制供电系统中,不论三相负载是否对称,也不论负载是Y形接法还是△形接法,都可用二瓦特表法测量三相负载的总有功功率,测量线路如实验图7-2所示。
若负载为感性或容性,且当相位差φ>60o时,线路中的一只功率表指针将反偏(数字式功率表
将出现负读数),这时应将功率表中电流线圈的两个端子调换(不能调换电压线圈端子),其读数应记为负值。
而三相总功率∑P = P1+P2(P1、P2本身不含任何意义)。
两表法测量三相电路功率

两表法测量三相电路功率
三相电路的功率测量有三种方法:
1.两表法
在三相三线制电路中,不论负载接成Y形或Δ形,也不论负载对称或不对称,都可使用功率表测量三相功率。
测量功率
P=P1+P2。
其中P1、P2分别为两边的读数。
2.三表法
该法适用于三相四线制电路。
负载不对称时,用三只单相功率表测量出三相各自功率值,测量功率P=P1+P2+P3。
其中P1、P2、P3分别为三表的读数。
3.一表法
该法适用于对称三相电路。
单表读数的3倍即为三相电路的功率。
二表法可以接三相三线,因为当负载不是三相对称负载时中性线上会有电流流过,这样的话就少测了一个功率消耗。
三相电路功率测量主要有三表法和两表法。
也称三瓦计法和二瓦计法。
三表法直接测量每一相的功率,三相功率之和等于总功率。
两表法运用了基尔霍夫电流定律,每块表测量的功率本身并无物理意义,但是,两块表的功率之和等于三相功率之和。
详细情况参阅参考资料“浅谈变频电机的功率测试”。
三角形负载时,不能同时测量到相电压和相电流,所以不能采用三表法。
而两表法完全能够满足需要。
实验二 三相电路相序及功率的测量
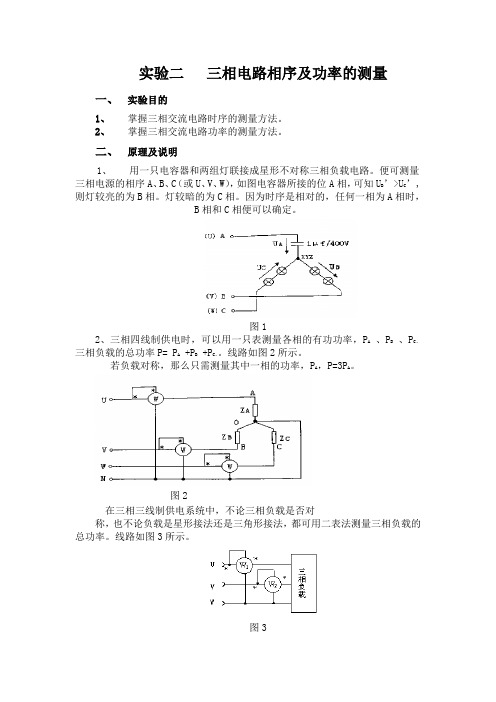
实验二三相电路相序及功率的测量一、实验目的1、掌握三相交流电路时序的测量方法。
2、掌握三相交流电路功率的测量方法。
二、原理及说明1、用一只电容器和两组灯联接成星形不对称三相负载电路。
便可测量三相电源的相序A、B、C(或U、V、W),如图电容器所接的位A相,可知UB ’>UC’,则灯较亮的为B相。
灯较暗的为C相。
因为时序是相对的,任何一相为A相时,B相和C相便可以确定。
图12、三相四线制供电时,可以用一只表测量各相的有功功率,PA 、PB、PC。
三相负载的总功率P= PA +PB+PC。
线路如图2所示。
若负载对称,那么只需测量其中一相的功率,PA ,P=3PA。
图2在三相三线制供电系统中,不论三相负载是否对称,也不论负载是星形接法还是三角形接法,都可用二表法测量三相负载的总功率。
线路如图3所示。
图3三、仪器设备电工实验装置:DG032T、DG04T、DY11T、DG053T四、实验内容实验注意:1、实验线路须经指导教师检查无误后再通电。
2 、更改线路,拆、接线时要断开电源。
1、判断三相电路的相序相序测量如图1所示,白炽灯可选三相电路实验板两相对称灯。
接通三相电源,观察两组灯的明暗状态,则灯较亮的为B相,灯较暗的为C相。
2、三相功率的测量●负载星接,参考图2、3,分别用三表法和二表法测三相电路功率,所测数据填入表1中。
●作不对陈负载实验时,在A相并入一组白炽灯。
所测数据填表1中。
●负载角接,用分别用三表法和二表法测三相电路功率,所测数据填入表2中。
●作不对称负载实验时,在A相并入一组白炽灯。
所测数据填表2中。
、五、报告要求1、比较测量结果,并进行分析。
2、总结三相电路功率测量的方法。
两表法测量三相电路功率

三相电路功率的测量方法 三相电路功率的测量是三相电路分析的重要内容,本文按三相三线制和三相四线制分类,较详细地讨论了三相电路功率测量的接线问题,总结了两表法和三表法各自的适用范围及功率表读数在不同接线方式下的物理意义,指出了它们的联系与区别。
关键词:三相电路,功率测量本文将围绕测量三相电路功率的两表法和三表法的原理和接线方法进行讨论,指出它们之间的联系与区别,希望对能对同学的理解以及总结归纳有所帮助。
1 对称三相电路功率的测量1.1 对称三相电路功率的测量对称三相电路即三相电源对称、三相负载均衡的三相电路。
以下分别从三相四线制和三相三线制两种情况讨论。
对三相四线制系统,测三相平均功率的接线如图1 所示。
它的接线特点是每个功率表所接的电压均是以中线N 为参考点,三个功率表WAN,WBN 和WCN 的读数分别为PAN,PBN 和PCN,可用式(1)表示。
PAN=UAN IA cosϕ<uAN , iA>PBN=UBN IB cosϕ<uBN , iB> (1)PCN=UCN IC cosϕ<uCN , iC>图1 三表法测三相四线制三相负载平均功率的接线示意图三相的总功率为P = P CN + P BN +P AN 。
三个表的读数均有明确的物理意义,即PAN,PBN 和PCN 分别表示A 相、B 相和C 相负载各自吸收的平均功率。
这就是三表法。
这种接线方法是最容易理解的。
实际上,三表法测三相功率不止图1 所示的一种接线方式,另外还有三种接线方式,如图2 所示,分别称作共A,共B 和共C 接法(与此相对应,图1 中的接法可称作共中线N 接法)。
对应每一种接线中的三个表的读数的代数和均表示三相负载吸收的总功率(后面将给出证明)。
实际上,因为是对称三相电路,有i N =0 ,所以图2(a),(b)和(c)中的W NA , W NBW NC的读数必为零,在测量时可不接,此时的三表法便简化为两表法。
两表法和三表法测量三相电路功率

φφPNC=UNCINcosφ6
(2)
其中,φ4为线电压uAC与相电流iA的相位差角,φ5为线电压uBC与相
电流iB的相位差角,φ6为相电压uNC与相电流iC之间的相位差角。
三相瞬时功率:
pAC+pBC+pNC=uACiA+uBCiB+uNCiN
=(uAN-uCN)iA+(uBN-uCN)iB+(-uCN)iN
学术交流◆Xues hu J iaoliu
两表法和三表法测量三相电路功率
张明霞
(南京航空航天大学金城学院,江苏 南京 211156)
摘 要:三相电路功率的测量是三相电路分析的重要内容。详细讨论三表法和两表法测量三相电路功率的问题。在三相三线制中,依 据二表法测量三相电路有功功率的原理,分析和讨论了在采用二表法测量三相三线制有功功率时,电路中各线电压和线电流之间的关系。 分析三相三线制供电的三相对称负载,一表法测三相负载的总无功功率接线方法。总结了两表法和三表法各自的适用范围及功率表读数 在不同接线方式下的物理意义,指出了它们的联系与区别。
当负载阻抗角φ=-60°(容性)时,PAC=0; 当负载阻抗角 φ Φ60°时,当负载为感性时,PBC读数为 负值,当负载为容性时,PAC读数为负值。 如果三相三线制电路是对称三相电路,且假设负载为感 性负载,其阻抗角为φ,采用正弦稳态电路的相量分析法,将 图 3 共 C 接 法 电 路 中 的 电 量(iA,iB,uA,uB等)表 示 为 其 对 应 的 相量(I觶 A,I觶 B,U觶 A,U觶 B)则可画出反映各电量关系的相量图如图 4所示。
机电信息 2009 年第 36 期总第 246 期 167
关键词:两表法;三表法;三相电路;功率测量
1 三相四线制供电系统中三相电路功率的测量
三相电路功率的测量实验原理

三相电路功率的测量实验原理1.对于三相四线制供电的三相星形连接的负载(即Y0 接法),可用一个功率表测量各相的有功功率PU,PV,PW,则三相负载的总有功功率∑P=PU+PV+PW。
这就是一瓦特表法,如图1 所示。
若三相负载是对称的,则只要测量一相的功率,再乘以3 即可得到三相总的有功功率。
2.三相三线制供电系统中,不论三相负载是否对称,也不论负载是星形接法还是三角形接法,都可以用二瓦特表法测量三相负载的总有功功率。
测量线路如图2 所示。
若负载为感性或容性,且当相位差Φ=60°时,线路中的一只功率表的指针将反偏(数字式功率表将出现负读数),这时应将功率表电流线圈的两个接线端子调换(不可调换电压线圈接线端子),其读数记为负值。
而三相总的有功功率∑P=P1+P2(此处是代数和)。
在图2 中,功率表W1 的电流线圈串联接入U 线,通过线电流IA,加在功率表w1 电压线圈的电压为Uuw;功率表W2 的电流线圈串联接入V 线,通过线电流IV,加在功率表w2 电压线圈的电压为UVW;在这样的连接方式下,我们来证明两个功率表的读数之代数和就是三相负载的总有功功率。
图1 一瓦特表法测量三相功率示意图图2 二瓦特表法测量三相功率示意图在三相电路中,若三相负载是星形连接,则各相负载的相电压在此用UU,UV,UW 表示。
若三相负载是三角形连接,可用一个等效的星形连接的负载来代替,则UU,UV,UW 表示代替以后二相电路的负载的相电压。
因为UUW=UU-UW,UVW=UV-UW所以IUUUW+IVUVW=IU(UU-UW)+IV(UV-UW)=IUUU+IVUV-(IU+IV)UW由于在这里讨论的是三相二线制电路,故有。
三相电路的功率测量

三相电路的功率测量一、实验目的1.学习并验证用“二瓦计“法测量三相电路的有功功率2.学习并应用“三表跨相”法测量三相电路的无功功率二、实验原理与说明1.三相电路的有功功率的测量(1)三瓦计法:三相负载所吸收的有功功率等于各相负载有功功率之和。
在对称三相电路中,因各相负载所吸收有功功率相等,所以可以只用一只单相功率表测出一相负载的有功功率,再乘以3即可;在不对称三相电路中,因各相负载所吸收的有功功率不等,就必须测出三相各自的有功功率,再相加即可。
三瓦计法适用于三相四线制电路。
三瓦计法是将三只功率表的电流回路分别串入三条线中(A、B、C线),电压回路的“*”端接在电路回路的“*”端,非“*”端共同接在中线上。
三只功率表读数相加就等于待测的三相功率。
(2)二瓦计法:对于对称电路中的三线三相制电路,或者不对称三相电路中,因均是三相三线制电路,所以可以采用两只单相功率表来测量三相电路的总的有功功率。
接法如图13-1所示。
两只功率表的电路回路分别串入任意两条线中(图示为A、B线),电压回路的“*”端接在电路回路的“*”端,非“*”端共同接在第三相线上(图示为C线)。
两只功率表读数的代数和等于待测的三相功率。
图13-1 二表法测有功功率2.三相电路无功功率的测量(1)对称三相电路无功功率的测量(a )一表跨相法:即将功率表的电流回路串入任一相线中(如A 线),电压回路的“*”端接在按正相序的下一相上(B 相),非“*”端接在下一相上(C 相),将功率表读数乘以3即得对称三相电路的无功功率Q 。
(b )二表跨相法:接法同一表跨相法,只是接完一只表,另一只表的电流回路要接在另外两条中任一条相线中,其电压回路接法同一表跨想法。
将两只功率表的读数之和乘以3/2即得三相电路的无功功率Q 。
(c )用测量有功功率的二瓦计法计算三相无功功率:按式子213()Q P P =-算出。
(2)不对称三相电路的无功功率测量三表跨相法:三只功率表的电流回路分别串入三个相线中(A 、B 、C 线),电压回路接法同一表跨相法。
三相电路功率的测量要点

实验九
三相电路功率的测量
(综合性实验)
北方民族大学电工电子实验中心
一、实验目的
• 1. 掌握用一瓦特表法、二瓦特表法测量 三相电路有功功率与无功功率的方法。
• 2. 进一步熟练掌握功率表的接线和使用方 法。
二、原理说明
1.对于三相四线制供电的三相星形联接的负载( 即Yo接法),可用一只功率表测量各相的有功功率PA
有另外两种连接法,即接成(
IV、UUW)或(IW、UUV)。
三、仪器设备和选用组件箱
序号 1 2 3 4 5 6 7 名称 电源控制屏(调压器)、 日光灯 数量 1 1 1 1 1 1 1 备注 DG01或GDS-01
交流电压表
交流电流表 功率、功率因数表 荧光灯、可变电容 三相灯组负载 万用表
D36或GDS-11
开灯盏数 负载情况 A相 B相 C相 P1(W) P2(W) Σ P (W ) 测量数据 计算值
Y接平衡负载
3பைடு நூலகம்
3
3
Y接不平衡负载
1
2
3
△接不平衡负载
1
2
3
△接平衡负载
3
3
3
四、实验内容
• 3. 用一瓦特表法测定三相对称星形负载的无功功率,按图9-6 所示的电路接线。
图 9-6
用一瓦特表法测定三相对称星形负载的无功功率
• (1)每相负载由白炽灯和电容器并联而成,并由开关控制其 接入。检查接线无误后,接通三相电源,将调压器的输出线电压 调到 220V,读取三表的读数,并计算无功功率Σ Q,记入表9-4。 • (2)分别按IV、UUW和IW、UUV接法,重复(1)的测量,并比较 各自的Σ Q值。
实验三相电路功率测量全解

二瓦计法
P1 / W
P2 / W
41.93
42.03
52.97
55.31
0
45.54
-60.6 95.55 -116 64.6
41.93 94.03 245.9 63.16
七、实验结果分析
Y-Y(对称) Y-Y (A=4uf) Y-Y (A相开路) Y-Yo( A=4uf) Y- ∆ (对称) Y- ∆(A相电容 ) Y- ∆(A相开路)
2. 三相四线制不对称连接时,三瓦计法测量所得 的总功率与二瓦计法测量所得的总功率不等。 因为此时中线有电流通过,不能用二瓦计法测 量电路的总功率。
3. 三相三线制不对称负载星形或三角形连接时, 三瓦计法测量所得的总功率与二瓦计法测量所 得的总功率基本。
实验结果分析
1.
三瓦计法测量功率会不会出现负值?为什么?
预习知识及要求 相关知识点 注意事项
实验相关知识
预习知识及要求
1. 预习三瓦计、二瓦计法测量功率的工作原理及其所含的物理意义。 2. 预习三瓦计、二瓦计法的测量方法和适用电路。
对称三相电路中的功率 三相电路功率的测量
相关知识点
注意事项
1. 测量时,严禁用身体的任何部位接触带电的金属裸露部分。 2. 严禁带电改接线路,改接线中时应断开电源,如电路中有电容负载,应在断开电源后,将电
三瓦法 PA + PB + PC / W
84.27 109.14 45.25 57.36 189.88 128.27 126.84
二瓦法 P1 + P2 / W
83.96 108.28 45.54 -18.67 189.58 129.9 127.76
八、实验结果分析 实验数据表明:在三相四线制不对称联接不能
两表法测三相功率原理-概述说明以及解释

两表法测三相功率原理-概述说明以及解释1.引言1.1 概述概述部分是文章引言的一部分,旨在对整篇文章的主题进行简单介绍和总结。
在撰写概述部分时,可以提及两表法测三相功率原理的基本概念和重要性,为读者提供一个整体的认知框架。
以下是概述部分的一个参考写作内容:概述:在现代电力系统中,三相功率的测量是非常重要的一个任务。
而测量三相功率的方法有很多,其中两表法测三相功率作为一种常用而有效的方法备受关注。
本文旨在探讨两表法测三相功率的原理及其在实际应用中的价值。
首先,我们将介绍两表法测量原理的基本概念和理论基础。
随后,我们将深入探讨三相功率的计算方法,包括有功功率、无功功率和视在功率的计算方式。
最后,我们将通过一些实际的应用场景,展示两表法测三相功率在电力系统中的实际应用。
通过本文的阅读,读者将能够全面了解两表法测三相功率的原理和方法,并认识到其在电力系统中的重要性和实际应用价值。
同时,本文也将对未来该领域的发展方向进行展望,以期为相关研究和实际工程应用提供参考和指导。
通过深入研究和理解两表法测三相功率原理,我们可以更好地应对电力系统中的功率测量问题,提高电力系统的可靠性和稳定性。
因此,掌握两表法测三相功率原理对于电力工程技术人员和研究人员来说具有重要意义。
本文将为读者提供一个系统而全面的介绍,帮助读者更好地理解和应用该原理,并为相关的研究和实践工作提供有益的参考。
文章结构部分的内容可以包括以下几个方面:1.2 文章结构本文分为三个部分进行论述。
第一部分是引言,主要包括概述、文章结构和目的的介绍。
第二部分是正文,主要涵盖了两表法测量原理、三相功率计算方法以及实际应用场景的详细讨论。
最后一部分是结论,对两表法测三相功率原理进行总结,并重点强调其应用价值,同时对未来发展方向进行展望。
在引言部分,我们将首先简要概述两表法测三相功率的背景和意义,介绍其在实际应用中的重要性。
然后,我们将详细阐述本文的文章结构,即正文部分所涉及的内容和顺序。
两表法测三相功率原理

两表法测三相功率原理在电力系统中,三相电能是最常见的电能形式之一。
而对于三相电能的测量,两表法是一种常用的方法。
本文将介绍两表法测三相功率的原理及其应用。
首先,我们需要了解一些基本概念。
在三相电路中,通常会有三个电压和三个电流进行测量。
在两表法中,我们使用两个电能表来测量三相功率。
具体原理如下:假设我们有一个三相负载,分别为A、B、C相,对应的电流为Ia、Ib、Ic,电压为Uab、Ubc、Uca。
我们可以使用两个电能表,分别连接到A、B两相上,测量功率Pab;以及连接到B、C两相上,测量功率Pbc。
那么三相总功率P可以通过以下公式计算得出:P = Pab + Pbc。
这就是两表法测量三相功率的基本原理。
通过测量两个相之间的功率,然后相加得到总功率。
在实际应用中,两表法具有一定的优势。
首先,它可以通过两个电能表来完成三相功率的测量,相对于使用三个电能表来说,成本更低。
其次,两表法可以更好地适应不同的三相电路结构,不需要对电路进行改动。
然而,两表法也存在一些局限性。
首先,由于只测量了两个相之间的功率,可能会忽略掉一些潜在的问题。
其次,如果电路中存在不平衡负载,两表法可能无法准确测量总功率。
因此,在实际应用中,我们需要根据具体情况选择合适的功率测量方法。
在一些要求严格的场合,可能需要使用三个电能表同时进行测量,以确保测量结果的准确性。
总之,两表法是一种常用的测量三相功率的方法,它通过测量两个相之间的功率来得到总功率。
在实际应用中,我们需要根据具体情况选择合适的方法,以确保测量结果的准确性和可靠性。
三相电路功率的测量方法

三相电路功率的测量方法摘要:本文主要论述三相功率的测量方法,包括有功功率和无功功率。
较详细地讨论了三相电路功率测量的接线问题,总结了两表法和三表法测量有功功率时各自的适用范围及功率表读数在不同接线方式下的物理意义,指出了它们的联系与区别。
关键词:三相电路,功率测量本文阐述三相电路功率的测量方法,包括有功功率和无功功率的测量方法。
说明它们各自的接线方式,阐述它们的测量原理,并且围绕测量有功功率的两表法和三表法的原理和接线方法进行讨论。
总结了两表法和三表法各自的适用范围及功率表读数在不同接线方式下的物理意义,指出了它们的联系与区别。
1.功率的定义在直流电路里,电压乘电流就是有功功率。
但在交流电路里,电压乘电流是视在功率,而能起到作功的一部分功率(即有功功率)将小于视在功率。
有功功率与视在功率之比叫做功率因数,以cosΦ表示。
在实际电路中由于有电机设备(如鼓风机、抽水机、压缩机等)等感性负载,便产生了无功功率.无功功率使得电能没有全部转化为人们所用(即有功功率)。
2.有功功率的测量有功功率是保持用电设备正常运行所需的电功率,也就是将电能转换为其他形式能量(机械能、光能、热能)的电功率,称为有功功率。
下面分别以对称三相电路和非对称三相电路进行说明。
对称三相电路是指三相电源对称、三相负载均衡的三相电路。
以下为三相电路原理图,图中所示的是YY型对称电路。
图1 三相电路原理图图1中电源相电压的相角差为120度,阻抗Z A=Z B=Z C,在实际应用中这种电路称为三相四线制电路。
电源相电压向量形式如下:由于电压源是三相对称电源,负载为对称三相负载,因此A,B,C相的相电流的数值相等。
他们的矢量和为零,就没有电流从N流到N’。
计算三相电路的功率可以转化为计算一相的功率。
所以当计算他们三相功率时,只需计算一相的功率,它的数值再乘3,就可以得到电路的总功率。
功率一般讲瞬时功率和平均功率。
对称三相电路的瞬时功率是一个常量,其值等于平均功率,这是对称三相电路的一个优越性能。
二表法测量三相电路有功功率

讨论二表法测量三相电路有功功率, 是从功率计算公式 P = UI cos 出发, 围绕有功功率表的电压线 圈所测电压为线电压、所测电流是流经电流线圈的线电流进行计算, 正确计算的关键是如何利用各电量的相 量关系确定两者之间的相位差角这个重点来展开。文中思想旨在依据二表法的测量原理, 借助于相量图反 映各电量间的相位关系, 确定所测端口线电压与线电流的相位差角, 从而得出在不同接线情况下均适用的分 析计算方法。
Vol. 29 No. 8 Aug. 2007
二表法测量三相电路有功功率
谢榕
( 华中科技大学电气与电子工程学院, 武汉 430074)
摘 要: 依据二表法测量三相电路有功功率的原理, 分析和讨论了在 采用二表 法测量三相 三线制有 功功率 时, 电路中 各线电压和线电流之间的关系。围绕有功功率表的 读数等于该功率表 电压线圈 所接电压的 有效值、电流 线圈所 通过的
UBC = 380 ! - 90 V
UCB = 380 ! 90 V
= cos- 10. 866 = 30
IA = 4. 386 ! - 30 A
( 3) 线电流、相电 压及线电压的 相量关系如图 9 所示。得到 I A 和 UAB间的相位 差角:
UABI Acos 1= 833. 3, 即功率表 W1 读数为 833. 3 W。
两个功率表的一种连接方式见图 1, 两个功率表的电流线圈分别串入 A、B 两火线, 它们的电压线圈的* 端分别接至电流线圈的* 端, 其非* 端共同接到火线 C( 非电流线圈所在的第 3 条火线上) 。这种测量方法
收稿日期: 2007 05 10. 作者简介: 谢 榕( 1960 ) , 女 , 副教授. E mail: rong - x ie- mm@ yahoo . com. cn
变电运行与检修专业电测仪表工中级工理论知识复习题

变电运行与检修专业电测仪表工中级工理论知识复习题一、判断题(正确的请在括号内打“√”,错误的请在括号内打“×”,每题2分,共420分)1.为减小频率误差,高准确度的电磁系仪表在线路上常采用频率补偿措施,常见的补偿方法是在辅助线圈上串接电容和电阻。
( )答案:√2.交直流两用仪表既可用于直流电路,又可用于交流电路,所以检验时,只要在直流或交流一种情况下检验一次就可以了。
( )答案:×3.已知电压表100V刻度点的误差为0.15V,所以当电压表指示在100V时,其实际值为100.15V。
( )4.当用“两表法”测量三相三线电路的有功功率时,三相电路完全对称和简单不对称,才能正确测量。
( )5.如果不对铁磁电动系功率表进行角误差补偿,当负载为感性时,角误差为正值,仪表读数偏快。
( )6.补偿电动系功率表角误差的方法,一般是设法增大动圈电流与外加电压的夹角。
( )7.在检验角误差未经补偿的单相电动系功率表时,当负载为感性时,角误差使仪表读数偏快;当负载为容性时,角误差使仪表读数偏慢。
( )8.检定电流表或电压表时,在电流表电路中串联一个电阻或在电压表两端并联一个电阻,对仪表本身的误差无影响,对测量电路可能有影响。
( )9.将两元件跨相90°的无功率表改为有功功率表的方法是:将原无功功率表电压回路A相、C相接线端子互换一下位置,把电流回路A相两个端子互换一下位置,将各相电阻减小到原电阻的就可以了。
( )10.测量中改变万用表的电阻量程时,必须相应调节零欧姆调整旋钮,使指针指向零欧姆处。
( )11.外附分流器具有两对端钮,与测量仪表连接的端钮是电位端钮。
( )12.使用无定位结构的电磁系仪表时应水平放置。
( )13.当用万用表的交流档测量非正弦交流电压时,将产生波形误差。
( )14.若铁磁电动系三相功率表角误差未得到补偿,单、三相检验结果将有差别。
越低,差别越大;时,差别最小。
两表法测三相功率原理及前提条件

两表法测三相功率原理及前提条件示例文章篇一:哎呀呀,同学们,今天我要跟大家讲讲两表法测三相功率的原理和前提条件,这可有趣啦!你们想啊,三相电就好像三个小伙伴一起干活,它们的力量有大有小,我们怎么知道它们一起出了多少力呢?这就得靠两表法啦!那两表法到底是怎么测的呢?就好像我们要数清楚一群小蚂蚁搬了多少东西。
我们把三相电想象成三条不同的道路,电流和电压就像是在这三条路上跑的车和路的高低起伏。
两个表呢,就像是两个超级聪明的小助手,一个盯着一条路和另一条路,另一个盯着另外两条路。
通过这两个小助手的观察,我们就能算出这三相电到底出了多少力,也就是功率啦!那用两表法测量三相功率有啥前提条件呢?这就好比我们要参加一个比赛,得先满足一些规则一样。
首先呀,三相电路得是对称的,这就好像三个人的力气得差不多大,要是有一个人特别强或者特别弱,那可就不行啦!为啥呢?你想想,如果有一个人太厉害或者太弱,那两个小助手不就被搞糊涂了,算出来的结果能准吗?还有哦,负载得是感性或者容性的,这就好比我们走路得有个方向,不能乱走,不然怎么能走到目的地呢?同学们,你们说这两表法是不是很神奇呀?我们通过这么巧妙的方法就能知道三相电的功率啦!总之,两表法测三相功率,原理就是靠两个聪明的小助手来帮忙,前提条件就是三相电路要对称,负载要有特定的性质。
这样我们就能准确地知道三相电的功率啦!示例文章篇二:哇塞!今天老师给我们讲了两表法测三相功率,这可真是个神奇又复杂的知识呀!我一开始听到这个名字的时候,脑袋里充满了问号:啥是两表法?怎么就能测三相功率啦?同学们也都和我一样,一脸懵圈。
老师看我们这副迷茫的样子,笑着说:“同学们,别着急,听我慢慢给你们讲。
”老师在黑板上画了个图,开始给我们解释。
她说:“想象一下,三相电路就像三条不同的道路,电流和电压在这三条路上跑来跑去。
而我们要用两表法来测量它们产生的功率。
”两表法呀,简单来说,就是用两个功率表来测量三相功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三相电路功率的测量方法 三相电路功率的测量是三相电路分析的重要内容,本文按三相三线制和三相四线制分类,较详细地讨论了三相电路功率测量的接线问题,总结了两表法和三表法各自的适用范围及功率表读数在不同接线方式下的物理意义,指出了它们的联系与区别。
关键词:三相电路,功率测量
本文将围绕测量三相电路功率的两表法和三表法的原理和接线方法进行讨论,指出它们之间的联系与区别,希望对能对同学的理解以及总结归纳有所帮助。
1 对称三相电路功率的测量
1.1 对称三相电路功率的测量
对称三相电路即三相电源对称、三相负载均衡的三相电路。
以下分别从三相四线制和三相三线制两种情况讨论。
对三相四线制系统,测三相平均功率的接线如图1 所示。
它的接线特点是每个功率表所接的电压均是以中线N 为参考点,三个功率表WAN,WBN 和WCN 的读数分别为PAN,PBN 和PCN,可用式(1)表示。
PAN=UAN IA cosϕ<uAN , iA>
PBN=UBN IB cosϕ<uBN , iB> (1)
PCN=UCN IC cosϕ<uCN , iC>
图1 三表法测三相四线制三相负载平均功率的接线示意图
三相的总功率为P = P CN + P BN +P AN 。
三个表的读数均有明确的物理意义,即PAN,PBN 和PCN 分别表示A 相、B 相和C 相负载各自吸收的平均功率。
这就是三表法。
这种接线方法是最容易理解的。
实际上,三表法测三相功率不止图1 所示的一种接线方式,另外还有三种接线方式,如图2 所示,分别称作共A,共B 和共C 接法(与此相对应,图1 中的接法可称作共中线N 接法)。
对应每一种接线中的三个表的读数的代数和均表示三相负载吸收的总功率(后面将给出证明)。
实际上,因为是对称三相电路,有i N =0 ,所以图2(a),(b)和(c)中的W NA , W NBW NC的读数必为零,在测量时可不接,此时的三表法便简化为两表法。
可见,此时的两表法是三表法的特例。
当然,这里单个表的读数没有明确的物理意义。
上述四种三表法的接线的特点是每组接线中的三个表所接电压均以同一根线为参考点,即分别是共A, B, C 或N,而电流则分别是非参考线中的电流。
功率表接线的极性端如图中所示。
图2 三表法测三相四线制三相负载平均功率的另三种接线图 对于三相三线制系统(Y 接或Δ接),由于没有中线,故图1 所示的接法便不存在,图2中接在中线上的功率表也不存在。
此时的接线方法将只有图3 所示的共A, 共B 和共C 三种接线方式。
可见,此时功率的测量只能用两表法测量,每组接线中单个功率表的读数没有
物理意义,两个表读数的代数和表示三相负载吸收的总平均功率。
以图3(c)共c 接法为例,两个表W AC WBC 和的读数分别为
PAC=UAC IA cosϕ<uAC , iA>
PBC=UBC IB cosϕ<uBC , iB> (2)
如果是对称三相电路,式(2)可进一步简化为
PAC=UL IL cos(30 °-ϕ)
PBC=UL IL cos(30 °+ϕ)(3)式(3)中UL,IL 分别为线电压和线电流; ϕ为负载的阻抗角。
图3 二表法测量三相三线制三相负载平均功率的测量接线图
图3(a)和(b)中的两个表的读数类似得到。
三相三线制系统中的例外情况是Y 接时中点可以引出的情况。
此时可以将功率表的公共点接在N 点,即仍可以用三表法测三相功率。
三个表的读数仍分别表示对应相的负载功率。
但此时实际上是相当于从负载中点引出一中线,对负载端而言,可将其归于三相四线制。
1.2 不对称三相电路的功率测量
不对称三相电路又可分为三相电源对称、负载不对称和电源、负载均不对称等情况。
在本文的功率测量方法讨论中,它们并无差别。
讨论仍分别从三相四线制和三相三线制两种情况讨论。
(1)不对称三相四线制系统。
其测量接线图仍分别有图1 和图2 四种接线方式。
与对称三相电路不同的是,此时中电流 i N ≠0 ,所以,图2 中电流线圈接在中线上的功率表读数一般不为零。
就是说,此时两表法不再成立,而必须用三表法测得三相负载的总功率。
以图2(c)共C 接线为例,三个功率表W AC ,W BC,W NC 的读数分别为
PAC=UACIA cosϕ<uAC , iA>
PBC=UBC IB cosϕ<uBC , iB> (4)
PNC=UNC IC cosϕ<uNC , iC>
式(4)中的三个功率P AC , P BC,P NC 和的代数和即表示三相负载吸收的平均功率。
证明如下。
瞬时功率
p AC+p BC+ pNC = u AC i A+ u BC i B+ u NC i N = ( u AN□ u CN ) i A+ (u BN□ uCN) i B+ u NC i N= u AN i A+ u BN i B+ u CN (- i A- i B- i N) (5)
电流关系为
i A + i B + i C +i N =0 (6)
将式(6)代入式(5),得
pAC+p BC+ p NC = u AN i A+ u BN i B+ u CN i C (7)
式(7)两边在一个周期内取平均值,得
PAC + PBC+ PNC =UANIA cosϕ<uAN , iA>+UBN IB cosϕ<uBN , iB>+UCN IB cosϕ<uCN , iC> (8)
可见,用图2(c)的共C 接法的三表法同样可测出三相电路的总平均功率。
同样可以证明图2(a)和(b)中的三个功率表读数的代数和是不对称三相电路的总平均功率。
但图2 所示的三种接线中,单个表的读数无明确物理意义。
(2)不对称三相三线制(Y 接和Δ接)系统。
其功率测量接线将只有图3 所示的三种两表法的接线方式。
其读数的表达式仍如式(2)所示(共C 接法)。
对称和不对称两种情况的不同之处是,在对称三相电路中,两表的读数表达式有式(3)所示的简单结果,而不对称时无此结果。
不对称三相三线制系统的例外情况依然是Y 接时中点可以引出的情况。
此时可以将功率表的公共点接在N 点,即仍可以用三表法测三相功率。
2 总结
本文按三相三线制和三相四线制分类,讨论了三相电路的功率分析和测量接线问题,并将其与一般三端网络和四端网络相联系。
概括地讲,两表法和三表法的相同点是它们都可以测量三相电路的总功率。
但它们的适用范围和意义有所不同。
两表法适用于三相三线制对称与不对称三相电路,特例是可用于对称的三相四线制三相电路(共A、共B 和共C 接法);三表法则适用对称与不对称三相四线制三相电路,特例是可用于Y 接时中点N 可引出的三相三线制三相电路(共N 接法)。
三表法在共N 接法时,每个表的读数为对应相负载的功率,有明确的物理意义,它们分别表示对应各相负载的功率;而三表法的共A、共B 和共C 接法及两表法接线时,单个表的读数无直接的物理意义,只有各功率表的代数和才表示三相平均功率。
