物理化学第四章
合集下载
物理化学第四章-化学平衡
平衡 正向自发
ii (产物) ii (反应物) 逆向自发
自发变化的方向：反应总是从化学势较高的一边流向化 学势较低的一边。
1. 化学反应的限度
所有的化学反应既可以正向进行亦可以逆向进行， 且反应正向进行和逆向进行均有一定的程度，反应 物不会完全转化为产物。
典型例子：
H2(g)+I2(g)↔2HI C2H5OH(l)+CH3COOH(l)↔CH3COOC2H5+H2O
任意化学反应： rGm rGm RT ln Qa
rGm ii (产物) jj (反应物)
(化学反应的吉布斯自由能改变量)
rGm
i
i
(产物)
jj (反应物)
(化学反应的标准吉布斯自由能改变量)
1.rGm 是任意反应系统的吉布斯自由能变化
rGm 是任意反应系统的标准摩尔吉布斯自由能变化
rGm 指产物和反应物都处于标准态时，产物的吉布
斯函数与反应物的吉布斯函数总和之差，称为化学
反应的“标准摩尔Gibbs 自由能变化值”，只是温
度的函数。
平衡时Leabharlann gGhHa
A
b
B
r Gm
若上述反应在定温定压下进行，其中各分压是任意的而 不是平衡时的分压，此时反应的吉布斯函数变化为：
非平衡时
rGm gG hH (aA bB )
B
B
RT
ln( PB
/
P )
g[G
RT
ln(
pG
/
p
)]
h[
H
RT
ln(
pH
/
p
)]
a[
A
RT
ln(
物理化学 第4章化学平衡
当 B 0 时 K Kc Kn K y
1/31/2020
祝大家学习愉快，天天进步！
17/114
§４.2-3.有纯态凝聚相参加的理气反应 K
ΔrGm RTln K
J p
B (g)
pB p
(g)
νB(g)
K
B(g)
peq B(g) p
结论：化学反应方程中计量系数呈倍数关系，Δ r Gm
的值也呈倍数关系，而 K 值则呈指数的关系。
1/31/2020
祝大家学习愉快，天天进步！
15/114
§４.2-2.理想气体反应的 K K c K y Kn
气体的组成可用分压力，摩尔分数，浓度表 示，故平衡常数也有不同的表示方法．
K
B
2
(g)
CO
2
(g)
Δ G r m,2 RT lnK 2
(3) CO 2 (g) C(s) 2CO(g) Δ G r m,3 RT lnK3 例 4.5.1
因为： (3) = (1) 2(2)
pB p
B
e
pB yB p
K
B
pB p
B
e
B
yB p
p
B
e
B
y B B
e
B
p
p
B
Ky
p p
B
1/31/2020
祝大家学习愉快，天天进步！
16/114
§４.2—2.理想气体反应的 K K c K y Kn
物理化学：第4章_多组分系统热力学_
Vm*,B Vm*,C Vm*,B xC
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
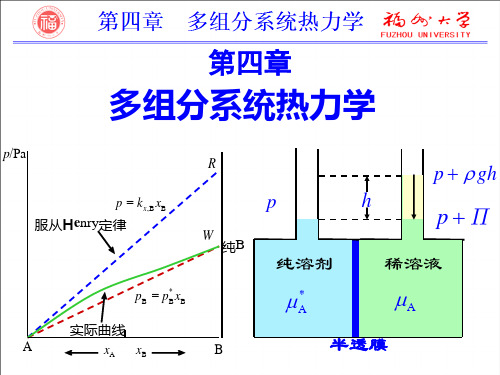
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
大学物理化学--第四章
由两种或两种以上物质以分子，原子或离子为 基本单元相互均匀混合而成的均匀系统。
混合物（mixture）：对系统中的各组分采用同样 的标准态和研究方法，系统中的各组分是平等的。
溶液（solution）： 各组分区分为溶剂（solvent） 和溶质（solute ），并对二者采用不同的标准态和研 究方法；系统中的各组分是不平等的。
偏摩尔量
XB
(
X nB
)T
,
p
,
，下标必须是
nC
T
,
p。, nC
只有广度量才有偏摩尔量（质量除外）。
偏摩尔量是强度量。
偏摩尔量随温度、压力、组成（浓度）变化而变， 与系统的总量无关。
上一内容 下一内容 回主目录
返回
2020/8/23
§4.1 偏摩尔量
偏摩尔量的加和公式
X nB X B
B
它的含义是：在一定温度、压力下，一定组成混合
物理化学电子教案—第四章
多组分系统热力学
上一内容 下一内容 回主目录
返回
2020/8/23
第四章 多组分系统热力学
目录
§4.1 偏摩尔量 §4.2 化学势 §4.3 气体组分的化学势 §4.4 逸度及逸度因子 §4.5 拉乌尔定律和亨利定律 §4.6 理想液态混合物 §4.7 理想稀溶液
§4.8 活度及活度因子 §4.9 稀溶液的依数性
标准态 kb,B ( p p )
实际溶液 pB - bB 关系曲线
pB
O
b
上一内容 下一内容 回主目录
bB
返回
2020/8/23
4.7 理想稀溶液
理想稀溶液中溶质的化学势
B(溶 质)
0 B(溶 质)
混合物（mixture）：对系统中的各组分采用同样 的标准态和研究方法，系统中的各组分是平等的。
溶液（solution）： 各组分区分为溶剂（solvent） 和溶质（solute ），并对二者采用不同的标准态和研 究方法；系统中的各组分是不平等的。
偏摩尔量
XB
(
X nB
)T
,
p
,
，下标必须是
nC
T
,
p。, nC
只有广度量才有偏摩尔量（质量除外）。
偏摩尔量是强度量。
偏摩尔量随温度、压力、组成（浓度）变化而变， 与系统的总量无关。
上一内容 下一内容 回主目录
返回
2020/8/23
§4.1 偏摩尔量
偏摩尔量的加和公式
X nB X B
B
它的含义是：在一定温度、压力下，一定组成混合
物理化学电子教案—第四章
多组分系统热力学
上一内容 下一内容 回主目录
返回
2020/8/23
第四章 多组分系统热力学
目录
§4.1 偏摩尔量 §4.2 化学势 §4.3 气体组分的化学势 §4.4 逸度及逸度因子 §4.5 拉乌尔定律和亨利定律 §4.6 理想液态混合物 §4.7 理想稀溶液
§4.8 活度及活度因子 §4.9 稀溶液的依数性
标准态 kb,B ( p p )
实际溶液 pB - bB 关系曲线
pB
O
b
上一内容 下一内容 回主目录
bB
返回
2020/8/23
4.7 理想稀溶液
理想稀溶液中溶质的化学势
B(溶 质)
0 B(溶 质)
物理化学 第四章 多组分系统热力学
Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B，C形成真实液态混合物： 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时，两组分的偏摩尔体积可用下法表示： 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线，此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB，VC。
B
系统中各广度量的偏摩尔量： 对于多组分系统中的组分B，有： 偏摩尔体积： VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能： UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓： HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵： SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数：AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数： GB=(ƽG/ƽnB)T,p,n
C
几点说明： (1)偏摩尔量为两个广度性质之比，所以为强度 性质； (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下，偏导数式的下标为T，p 时才是偏摩尔量； (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中，偏摩尔量不同； (4)若系统为单组分系统，则该组分的偏摩尔量 与该组分的摩尔量相等，即： XB=X*B，m
C
=VB (数学知识：二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势，用符号μB表示：
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质，其化学势等于它的摩尔吉布斯函 数。
物理化学 4第四章 化学平衡
第四章 化学平衡内容提要1、反应进度反应进度描述了化学反应体系的状态，反应进度的变化表示为： Δξ=B∨∆Bn （4-1）当ξ =1时，就表示按给定的反应式进行了一个完整反应，也称发生了一个单位反应。
对于同一反应方程式，可以用任一反应物或任一产物表示反应进度ξ，与物质的选择没有关系；当化学反应方程式的写法不同时，反应进度ξ的数值不同。
2、吉布斯自由能变在等温等压、W ＇＝0时，一定组成、无限大量的体系中，体系的吉布斯自由能随反应进度而改变的变化率表示为：Δr G m =P T ∂∂,)(ξG=∑νB μB （4-2） Δr G m 是反应系统在任意情况下的吉布斯自由能变化，是强度性质，与体系物质的量无关，单位为 J/mol 或kJ/mol 。
对同一反应来讲，Δr G m 的具体数值与化学方程式的写法有关。
Δr G m 值可以表明反应的自发方向和进行趋势的大小，具有化学反应推动力的含义。
当Δr G m ＜0时，反应物化学势高，反应能自发地由左向右进行； 当Δr G m ＞0时，产物化学势高，反应不能自发地由左向右进行； 当Δr G m ＝0时，产物和反应物的化学势相等，反应体系处于平衡状态。
在温度T 时，把物质的化学势µ B=OB μ + RTlna B代入式（4-2），得：Δr G m =∑νB OB μ + RTlnQa（4-3）3、化学平衡的条件化学平衡的条件为：等T 、等P 、W ＇＝0 时， Δr G m ＝p T G,)(ξ∂∂＝∑νB μB ＝0 （4-4） 4、化学平衡常数在一定条件下，当化学反应达到平衡时，产物活度的计量系数次方幂的乘积与反应物活度的计量系数次方幂的乘积的商为一常数，称为化学平衡常数(equilibrium constant)。
标准平衡常数(standard equilibrium constant) 表示反应所能达到的最大限度，单位是1，用OK(上角标“Ө”表示处于标准态)表示，也称为热力学平衡常数，表达式为：OK = (Q a )eq = (d Da A r Rg G a a a a ⋅⋅)eq （4-5）O K 越大，则反应进行的程度越大。
物理化学第四章课后答案完整版
第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B，质量摩尔浓度为b B，此溶液的密度为。
以M A，M B分别代表溶剂和溶质的摩尔质量，若溶液的组成用B的摩尔分数x B表示时，试导出x B与c B，x B与b B之间的关系。
解：根据各组成表示的定义4.2D-果糖溶于水（A）中形成的某溶液，质量分数，此溶液在20℃时的密度。
求：此溶液中D-果糖的（1）摩尔分数；（2）浓度；（3）质量摩尔浓度。
解：质量分数的定义为4.3在25℃，1 kg水（A）中溶有醋酸（B），当醋酸的质量摩尔浓度b B介于和之间时，溶液的总体积求：（1） 把水（A ）和醋酸（B ）的偏摩尔体积分别表示成b B 的函数关系。
（2）时水和醋酸的偏摩尔体积。
解：根据定义当时4.4 60℃时甲醇的饱和蒸气压是84.4 kPa ，乙醇的饱和蒸气压是47.0 kPa 。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %，求60℃时此混合物的平衡蒸气组成，以摩尔分数表示。
解：甲醇的摩尔分数为58980049465004232500423250....x B =+=4.5 80℃时纯苯的蒸气压为100 kPa ，纯甲苯的蒸气压为38.7 kPa 。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物，80℃时气相中苯的摩尔分数，求液相的组成。
解：4.6在18℃，气体压力101.352 kPa下，1 dm3的水中能溶解O2 0.045 g，能溶解N2 0.02 g。
现将1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾，赶出所溶解的O2和N2，并干燥之，求此干燥气体在101.325 kPa，18℃下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为：，解：显然问题的关键是求出O2和N2的亨利常数。
4.7 20℃下HCl 溶于苯中达平衡，气相中HCl 的分压为101.325 kPa 时，溶液中HCl 的摩尔分数为0.0425。
物理化学第四章 多组分系统(72)
pg：理想气体
• 3.2 理想气体混合物中任一组分的化学势
B ( pg ) B ( g ) RT ln( pB / p )
★不同系统中各组分的化学势表达式是本章的一个重要 内容，要注意区分不同的表达式，特别是明确其中标准 态的不同
§4.5 拉乌尔定律与亨利定律
• 5.1 液态混合物的气液平衡
B (l ) B ( g) B ( g) RT ln( pB / p )
将拉乌尔定律代入： (l ) ( g ) RT ln( p x / p ) B B B B 该式可以看成 是理想液态混 合物的定义式
B
B ( g ) RT ln( pB / p ) RT ln xB
★在恒温、恒压条件下，在大量系统中，除了B 组分以外， 保持其它组分的数量不变，加入1mol 组分B 引起的系统广度 量X 的变化 ★或：在等温等压下，系统广度性质X 随着组分B的量的变 化率就是XB。
（3）说明
1) X 代表体系的任一广度性质
V VB nB T , p ,n C U UB nB T , p ,n C
§4.1 偏摩尔量
• 1.1 问题的提出
而对多组分系统， 如水与无水乙醇的混合： V n水Vm,水 n乙醇Vm,乙醇
对纯物质而言： nVm V
由此可见：由纯组分混合形成混合物时不仅体积发生变化， 而且体积变化多少与形成混合物的组成有关
广度性质 X (如 V，G，S，U 等)除与温度、压力有关外， 还与系统中各组分的量n1、n2、n3、…、nk有关。
X B X nB T , p ,n
C
G S GB SB nB T , p ,n nB T , p ,n C C
物理化学第四章
• 但碳的相图中最多只能三相共存,不可能四相共存.
一.克-克方程(Clausius-Clapeyron equation)
• 当单组分体系两相共存时,自由度f=3－2=1， 体系只有一个自由度。 • 单组分的相变温度与压力之间存在一定的关 系, 此关系即为克-克方程. • 设一纯物质在T,p下达两相平衡：
相图：表示体系状态变化的图形
•
• 相(phase): 体系内物理性质和化学性质
完全均匀的部分. • 均匀的要求： •
均匀到分子水平
• 一个体系中可以含有多个相,这些相与相 之间一般存在明显的界面,界面处体系的 热力学性质是间断的.
气体：凡气体成一相.
气体体系无论有多少种气体,一般都达到分子水 平的混合，故为一相。
• (3)式称为克拉贝龙方程. • 克拉贝龙方程适用于纯物质任何平衡相变过 程,应用范围很广.
• 1. 气-液,气-固两相平衡:
• 纯物质的两相平衡中有一相为气相,另一相必为 凝聚相. 以气-液平衡为例,有: • dp/dT=Hm/TVm= Hm/T(Vm,g－Vm,l) (4) • ∵ Vm,g>>Vm,l • ∴ Vm,g－Vm,l≈ Vm,g=RT/p • 代入(4)式: • dp/dT= Hm/[T(RT/p)] •
• 体系的独立变量数f(即自由度)应该等于总变量 数减去关系式总数: • 总变量数：S+2 • 关系式数：＋S(－1) • •
f = S+2－－S+S
f = S－ + 2
(1)
• (1)式就是相律的数学表达式. • 相律的物理含义是:
体系的自由度等于体系的物种数S减去相 数再加上环境变量数2(温度和压力).
物理化学课件-相平衡
水的相图
E p B 冰 水
A C D T 气
水的相图
dp/dT=∆fusHm/∆fusVm ∆ ∆ E p
-20oC, 2.×108Pa × 临界点 374oC, × B 2.23×107Pa
冰
水
A C D T1 0.0098oC T 气
水的相图
AB 是气 液两相平衡线，即水的蒸气压曲线。它不能任意 是气-液两相平衡线 即水的蒸气压曲线。 液两相平衡线， 延长，终止于临界点 临界点p=2.2×107Pa，T=647K，这时 临界点。 延长，终止于临界点。临界点 × ， ， 液界面消失。 气-液界面消失。高于临界温度，不能用加压的方法使气体 液界面消失 高于临界温度， 液化。 液化。
f=K-Φ +2
相律是由吉布斯(Gibbs)１８７６年得到 １８７６年得到 相律是由吉布斯 １８７６ 是自然界的普遍规律之一. 的，是自然界的普遍规律之一
相律推导
个组分, 个相.每个相中每种物质都存在 并没有化学反应. 每个相中每种物质都存在,并没有化学反应 设平衡系统中有Ｋ个组分 Φ 个相 每个相中每种物质都存在 并没有化学反应
µB(β) =µB θ(β)+ห้องสมุดไป่ตู้Tlna B(β) β β β
f=Φ(K-1)+2-K(Φ-１) １ = KΦ-Φ+2-KΦ+K=K-Φ+2 Φ Φ
相律
如果指定了温度或压力: 如果指定了温度或压力 f*=K- Φ +１ １ f*称为条件自由度 如果考虑到 个因素的影响 则相 称为条件自由度,如果考虑到 个因素的影响,则相 如果考虑到n个因素的影响 律应写为: 律应写为 f*=K- Φ +n 在上述推导中假设每个组分在每个相中都有分配,如 在上述推导中假设每个组分在每个相中都有分配 如 中不含Ｂ 总变量中应减去一个变量,相 果某一相( 中不含 物质,总变量中应减去一个变量 果某一相 α)中不含Ｂ物质 总变量中应减去一个变量 相 应的化学势相等的等式中也减少一个,因此 因此,不影响相律的 应的化学势相等的等式中也减少一个 因此 不影响相律的 表达式. 表达式
《物理化学第4版》第四章4-1 多组分系统组成表示法ppt课件
第四章 液态混合物和溶液
1. 混合物及溶液的分类
多组分系统
非均相(多相) 均相(单相)
混合物 溶液
1
(i) 对混合物中的各组分不区分为溶 剂及溶质，对各组分均选用同样 的标准态；
(ii) 对溶液中的各组分区分为溶剂 及溶质，并选用不同的标准态加 以研究。
2
按聚集状态不同，
气态混合物如空气；
混合物液态混合物如苯和甲苯；
固态混合物如粘土和沙石。 液态溶液如Mn Fe液态合金；
溶液 固态溶液（固溶体黄铜 青铜等）；
3
液态溶液— 简称溶液电非解电质解溶质液溶如 液食 （盐 分水 子溶 溶液液; 如高分子溶液）
非电解质溶液：蔗糖水溶液； 氧O2溶于水； 乙醇水溶液 H2O（l）—— C6H5NH3（l）溶液；
金属溶液： Fe（l）—— Mn（l）溶液； Cu（l）——Zn（l）溶液。
MA
bB
MA
17
def cB nB /V
SI单位:moldm-3
8
五、溶质B的质量摩尔浓度 溶质B的物质的量与溶剂的质量之比。
bB 或mB def nB / mA
用于液态或固态溶液的溶质，也可 以用下式定义：
bB 或mB def nB /(nAM A )
SI 单位：molkg-1 9
由于溶质B的质量摩尔浓度与温度无 关，在热力学处理中比较方便。在电 化学中也主要采用该浓度表示电解质 的浓度。
12
x1 = n1 / (n1 + n2 )= 0.321 mol / (0.321 mol+0.652 mol) = 0.329 b1= n1 /m2 = 0.321 mol / 30.0 10-3 kg = 10.7 molkg-1 w1 = m1 / ( m1+ m2 ) = 25.0 g / (25.0+30.0) g = 0.455
1. 混合物及溶液的分类
多组分系统
非均相(多相) 均相(单相)
混合物 溶液
1
(i) 对混合物中的各组分不区分为溶 剂及溶质，对各组分均选用同样 的标准态；
(ii) 对溶液中的各组分区分为溶剂 及溶质，并选用不同的标准态加 以研究。
2
按聚集状态不同，
气态混合物如空气；
混合物液态混合物如苯和甲苯；
固态混合物如粘土和沙石。 液态溶液如Mn Fe液态合金；
溶液 固态溶液（固溶体黄铜 青铜等）；
3
液态溶液— 简称溶液电非解电质解溶质液溶如 液食 （盐 分水 子溶 溶液液; 如高分子溶液）
非电解质溶液：蔗糖水溶液； 氧O2溶于水； 乙醇水溶液 H2O（l）—— C6H5NH3（l）溶液；
金属溶液： Fe（l）—— Mn（l）溶液； Cu（l）——Zn（l）溶液。
MA
bB
MA
17
def cB nB /V
SI单位:moldm-3
8
五、溶质B的质量摩尔浓度 溶质B的物质的量与溶剂的质量之比。
bB 或mB def nB / mA
用于液态或固态溶液的溶质，也可 以用下式定义：
bB 或mB def nB /(nAM A )
SI 单位：molkg-1 9
由于溶质B的质量摩尔浓度与温度无 关，在热力学处理中比较方便。在电 化学中也主要采用该浓度表示电解质 的浓度。
12
x1 = n1 / (n1 + n2 )= 0.321 mol / (0.321 mol+0.652 mol) = 0.329 b1= n1 /m2 = 0.321 mol / 30.0 10-3 kg = 10.7 molkg-1 w1 = m1 / ( m1+ m2 ) = 25.0 g / (25.0+30.0) g = 0.455
物理化学第四章 相图(材料版)
d T TΔ Vm
Δ Hm - 摩尔相变热； Δ Vm - 相变时摩尔体积变化量
用于任何纯物质的两相平衡系统
对气-液或气-固两相平衡， DVm Vm ( g ) ,
并假定气体为理想气体:
d ln p = DHm dT RT 2
若 DHm可近似看作常数，则：
ln p = - DHm 1 + I RT
4.3 相 律
相律（phase rule）：讨论平衡系统中相数、独立组分数与描述该平 衡系统的变数之间的关系。 相(phase)：系统中，物理及化学性质完全均一的部分。相与相之间有 明显界面，界面两边的性质有突变。
相数(number of phases)：系统中所包含相的总数，以符号 表示
气体: 一个系统中无论含有多少种气体，只能有一个气相； 液体:一个系统中可有一个或两个，一般不超过三个液相； 固体:系统中所含的不同种固体达到了分子程度的均匀混合，就形成了固溶
Φ =3
f = 1 单变量系统 f = 0 无变量系统
水的相图 水的相图是根据实验绘制的。以压力为纵坐标，温度为横坐标。
三个单相区 三条两相平衡线 一个三相点
三个单相区:温度和压力独立地有限度地变化不会引起相的改变。
三条两相平衡线：压力与温度只能改变一个，指定了压力，则温度由系统自定。
OA: 是气-液两相平衡线，即水的蒸气压曲线。它不能任意延长，终止于临 界点。临界点T=647K, p=2.2×107Pa，这时气-液界面消失。
独立组分数C = S - R = 2，相数Ф = 1，自由度 f = 2 - 1 + 2 = 3
(2) N2(g)、H2(g)和NH3(g)，其中N2和H2均由NH3分解而来 解：物种数S = 3，独立反应数 R = 1,R' = 1
Δ Hm - 摩尔相变热； Δ Vm - 相变时摩尔体积变化量
用于任何纯物质的两相平衡系统
对气-液或气-固两相平衡， DVm Vm ( g ) ,
并假定气体为理想气体:
d ln p = DHm dT RT 2
若 DHm可近似看作常数，则：
ln p = - DHm 1 + I RT
4.3 相 律
相律（phase rule）：讨论平衡系统中相数、独立组分数与描述该平 衡系统的变数之间的关系。 相(phase)：系统中，物理及化学性质完全均一的部分。相与相之间有 明显界面，界面两边的性质有突变。
相数(number of phases)：系统中所包含相的总数，以符号 表示
气体: 一个系统中无论含有多少种气体，只能有一个气相； 液体:一个系统中可有一个或两个，一般不超过三个液相； 固体:系统中所含的不同种固体达到了分子程度的均匀混合，就形成了固溶
Φ =3
f = 1 单变量系统 f = 0 无变量系统
水的相图 水的相图是根据实验绘制的。以压力为纵坐标，温度为横坐标。
三个单相区 三条两相平衡线 一个三相点
三个单相区:温度和压力独立地有限度地变化不会引起相的改变。
三条两相平衡线：压力与温度只能改变一个，指定了压力，则温度由系统自定。
OA: 是气-液两相平衡线，即水的蒸气压曲线。它不能任意延长，终止于临 界点。临界点T=647K, p=2.2×107Pa，这时气-液界面消失。
独立组分数C = S - R = 2，相数Ф = 1，自由度 f = 2 - 1 + 2 = 3
(2) N2(g)、H2(g)和NH3(g)，其中N2和H2均由NH3分解而来 解：物种数S = 3，独立反应数 R = 1,R' = 1
物理化学 第四章 多组分系统热力学
AB
( nB
)T , p ,nC
G
GB
( nB
)T , p ,nC
注意：偏摩尔量的下脚标为：T，P，C（C≠ B)
使用偏摩尔量时应注意： 1.偏摩尔量的含义是：在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下，广度性 质X的随组分B的物质的量的变化率。
2.只有广度性质才有偏摩尔量，而偏摩尔量是强度 性质。
六、偏摩尔量之间的函数关系
对于组分B：VB、UB、HB、SB、AB、GB之间的关系：
HB= UB +PVB ，
AB= UB －ＴSB
GB = HB －ＴSB＝ UB +PVB －ＴSB UB ＝AB+PVB
(
GB P
)T
,nA
VB
(
GB T
)
P,nA
SB
( GB )
[T T
]P,nB
3.纯物质的偏摩尔量就是它的摩尔量。
4.任何偏摩尔量都是T，p和组成的函数。
偏摩尔量的集合公式
设一个均相体系由1、2、 、k个组分组成，则体 系任一广度量Z应是T，p及各组分物质的量的函数，即：
X X (T , p, n1, n2,, nk )
在等温、等压条件下：
X
X
dX
( n1
···········
dG= dG(α) ＋ dG(β) +·········
恒T，p时 dG SdT Vdp
B
dnB
B
同理，有
dU TdS pdV B ( )dnB ( ) B
dH TdS Vdp B ( )dnB ( ) B
物理化学-第四章相平衡
所以 C＝1 单组分系统
例2. 碳在氧气中燃烧，有如下方程：
(1) C(s)+O2 (g)=CO2 (g)
(2)
C(s)+
1 2
O2
(g)=CO(g)
因为(3)＝(1) - (2) 所以 R＝2
1 (3) CO(g)+ 2 O2 (g)=CO2 (g)
S = 4， R’＝0， 则 C＝4－2＝2 二组分系统
面
两相平衡： P＝2 f=1 一个独立变量
线
三相平衡： P＝3 f=0 无变量
点
p
B
冰
水A
①三条线：OA, OB, OC
D
O气
C
水的局部相图示意
三个区：单相区
三相点(triple point)：
T O点：三相共存，f = 0,
0.0099℃, 610.6 Pa 与冰点不同
OA：g-l共存，水的饱和蒸汽压曲线
S = 3, R = 1, R’ = 0，则 C＝3 -1＝2
注意：对于浓度限制条件，是固定不变的浓度关系。
2. 自由度和自由度数（f） (the number of freedom degree)
如何描述一个相平衡系统的状态(平衡性质)?
p1
p2
H2O(l) T1
H2O(g)
H2O(l) T2
相平衡的一个重要性质是它与各相中物质的量无关。 一个多相系统的相平衡状态是由体系的强度性质决定 的。例如 pv , Tb , Tf , 溶解度等。
d
ln p /[ p] dT
gc d H m RT 2
(1) 条件：纯物质g-l（s) 平衡，
（近似：忽略Vm (cd)，理想气体） (2) 若近似gcdHm不随T变化，则
《物理化学》第四章(相平衡)知识点汇总
《物理化学》重要 知识点
第四章：相平衡
第四章 相平衡 相律
温度或压力都没有指定时，相律表达式为：
f K 2
如果指定了温度或压力，则相律表达式为：
f K 1
55
克劳修斯－克拉珀龙方程 液－气平衡
ln p Vap H m RT K
p2 Vap H m 1 1 ln ( ) p1 R T1 T2
60
最大负偏差非理想完全互溶双液系统体系
在p-x图上，p与拉乌 等温 尔计算值相比为负， 且在某一组成范围内， p < pA*， p有最小值。
液
p
气
在T-x图,与压力最
小值相对应，出现 了具有最高恒沸点 的最高恒沸物。
Aa
xBbΒιβλιοθήκη B气左侧：yB<xB 右侧：yB>xB
A
T
液
xB
B
A
a x B
b
B
完全不互溶的双液系统
y
z R
冰+(NH4)2SO4
E
H2O
m B%
(NH4)2SO4
二、生成化合物的相图
1.生成稳定化合物的相图 C6H5OH与C6H5NH2 化合物C C6H5OH∙C6H5NH2
C C+L
L(熔化物)
T/k
能生成具有固定熔点
A+L E1
C+L B+L B+C E2 B
C6H5NH2
A+C
A
C6H5OH
最大正偏差非理想完全互溶双液系统体系
在p-x图上，p与拉乌 尔计算值相比为正， 且在某一组成范围内， p >pB*， p有最大值。
第四章：相平衡
第四章 相平衡 相律
温度或压力都没有指定时，相律表达式为：
f K 2
如果指定了温度或压力，则相律表达式为：
f K 1
55
克劳修斯－克拉珀龙方程 液－气平衡
ln p Vap H m RT K
p2 Vap H m 1 1 ln ( ) p1 R T1 T2
60
最大负偏差非理想完全互溶双液系统体系
在p-x图上，p与拉乌 等温 尔计算值相比为负， 且在某一组成范围内， p < pA*， p有最小值。
液
p
气
在T-x图,与压力最
小值相对应，出现 了具有最高恒沸点 的最高恒沸物。
Aa
xBbΒιβλιοθήκη B气左侧：yB<xB 右侧：yB>xB
A
T
液
xB
B
A
a x B
b
B
完全不互溶的双液系统
y
z R
冰+(NH4)2SO4
E
H2O
m B%
(NH4)2SO4
二、生成化合物的相图
1.生成稳定化合物的相图 C6H5OH与C6H5NH2 化合物C C6H5OH∙C6H5NH2
C C+L
L(熔化物)
T/k
能生成具有固定熔点
A+L E1
C+L B+L B+C E2 B
C6H5NH2
A+C
A
C6H5OH
最大正偏差非理想完全互溶双液系统体系
在p-x图上，p与拉乌 尔计算值相比为正， 且在某一组成范围内， p >pB*， p有最大值。
物理化学04多组分系统热力学
dG＝dG( ) +dG()
当恒温恒压，W’=0 时
β相
dG() ()dn()
dG( ) ( )dn( )
dn( ) dn()
dX
X T
p,nB ,nc ,nD
X
dT
p
T ,nB ,nc ,nD
X
dp
nB
T , p,nc ,nD
dnB
X
X
nC
T , p,nB p,nB ,nc
dnD
2021/1/6
偏摩尔量XB的定义为： X B def
X ( nB )T , p,nc
2021/1/6
解：取1kg溶液
nH2O
mH2O M H2O
(1 0.12)1 18.015 103
mol
48.85mol
nAgNO3
mAgNO3 M AgNO3
0.12 1 169.89 103
mol
0.7064mol
xAgNO3
nAgNO3
n n AgNO3
H2O
0.01425
cAgNO3
2021/1/6
由题意：
VA 17.35cm3 / mol
VB 39.01cm3 / mol
由集合公式，混合后：
V nAVA nBVB {0.617.35 0.4 39.01}cm3 26.01cm3
混合前：
VA '
nAM A A
10.84cm3
VB'
nB M B B
16.19cm3
dA SdT pdV BdnB
dA
B
BdnB 0
自发 ＝平衡
B
(dT 0，dV 0, W ' 0)
液态混合物和溶液-物理化学
如果组成溶液的物质有不同的状态，通常将液态 物质称为溶剂，气态或固态物质称为溶质。
如果都是液态，则把含量多的一种称为溶剂，含 量少的称为溶质。
以物态分
气态溶液（如空气）、 固态溶液（如金属固熔体） 液态溶液。
以溶质的导电性分 ）
多组分均匀体系中，溶剂和溶质不加区分，各组 分均可选用相同的标准态，使用相同的经验定律， （一视同仁）这种体系称为混合物，也可分为气态 混合物（如空气）、液态混合物（如石油）和固态 混合物（如合金）。
单位：mol·kg-3
37 B的摩尔比：
rB
nB nA
.
6
§4.2 拉乌尔定律和享利定律
一：拉乌尔定律－溶剂的气液平衡规律
在一定的温度下 PA< PA*
A（g） PA*
A（L）
PA A+B
❖ 在一定温度下,稀溶液中溶剂的蒸汽压PA等于纯溶剂 的 蒸 汽 压 PA* 与 其 溶 液 中 纯 溶 剂 的 摩 尔 分 数 xA 的 乘 积 用数学式可表示为：
第四章 液态混合物和溶液
溶液（solution）(混合物）
广义地说，两种或两种以上物质彼此以分子或离子 状态均匀混合所形成的体系称为溶液(混合物） 。
溶液和混合物的区别：
溶液有溶剂和溶质之分而混合物没有；对溶液中 的溶剂和溶质采用不同的研究方法，而对混合物 则采用同一的研究方法。
.
1
溶剂（solvent）和溶质（solute）
PA*- PA=ΔPA= PA*xB
(4-2)
溶剂的蒸汽压下降与溶质的摩尔分数成比例。
2.若溶质不止一种，则
pA p*A xB B .
(4-3)
9
二、亨利定律－溶质的气液平衡规律
物理化学第4章-2 化学平衡
1化学反应速率与化学平衡34.3.1 可逆反应与化学平衡（一）化学反应的可逆性和可逆反应绝大多数化学反应都有一定可逆性：例如：N 2 (g) + 3 H 2 (g) 2 NH 3 (g)只有极少数反应是不可逆的：例如： 2 KClO 3(s) =2 KCl (s) + 3 O 2 (g)可逆反应：在同一条件下，能同时向两个相反方向进行的反应。
4（二）化学平衡化学平衡的特征：（1）系统的组成不随时间而改变;（2）化学平衡是动态平衡。
（3）平衡状态与达到平衡的途径无关;定义：可逆反应在一定条件下，正反应速率等于逆反应速率时，反应体系所处的状态。
4.3.1 可逆反应与化学平衡5在373 K 恒温槽中反应一段时间后，达到平衡，测得平衡时N 2O 4和NO 2 浓度。
0.1600.100NO 2开始0.370.0700.100N 2O 4从反应混合物0.0720.100NO 2开始0.370.0140N 2O 4从产物0.1200NO 2开始0.360.0400.100N 2O 4从反应物c 2(NO 2)/c (N 2O 4)平衡浓度起始浓度N 2O 4-NO 2体系的平衡浓度（mol/L ）（373K ）化学平衡的实例N 2O 4 (g) 2 NO 2(g)无色红棕色64.3.2 平衡常数1. 定义：在一定温度下，可逆反应达到平衡时，产物浓度的方程式计量系数次方的乘积与反应物浓度的方程式计量系数次方的乘积之比，为一常数，称为“平衡常数”。
用K 表示。
2. 意义：表示在一定条件下，可逆反应能进行的极限。
K 越大，正反应进行得越彻底。
7有关化学平衡常数的说明①化学平衡常数K 只是温度的函数。
②平衡常数不涉及时间概念，不涉及反应速率。
例如：N 2O 4(g) 2 NO 2(g)T /K 273 323 373K 5×10-4 2.2×10-2 3.7×10-12SO 2(g) + O 2(g) 2SO 3(g) K =3.6 ×1024(298K)K 很大，但常温下反应速率很小。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dA = d (G－pV)
dG Sd T Vd p Bd nB
B
dU TdS pdV B dnB dH TdS Vdp B dnB dA SdT pdV B dnB
B
上一内容 下一内容 回主目录
B
B
返回
2015-5-19
—— 溶液热力学基础
上一内容 下一内容 回主目录
返. 偏摩尔量之间的关系
全部广延量 纯组分系统 适用于 热力学函数式 用偏摩尔量代替 多组分系统
H U PV A U TS
G H TS
H B U B PVB AB U B TS B
B
——Gibbs-Duhem方程
返回
2015-5-19
上一内容
下一内容
回主目录
§4.1 偏摩尔量
应用
G-D方程给出各组分XB变化间
必须服从的制约关系 判断所测不同组成x下各组分XB数据质量： 符合Gibbs-Duhem方程 —— 数据可靠
不符合 Gibbs-Duhem方程—— 数据不可靠
—— 热力学一致性的校验
xAdVA xBdVB 0
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
x A dV A x B dV B 0
分析： 若dVA > 0 → dVB < 0； 由VA变化求VB变化
→ VA、VB变化非独立, 相互制约 扩展：多组分、其它性质（恒T、p）
通式： x BdX B 0
X X X X dX dnB dnC ... dp dT T p ,nB p T ,nB nB T , p ,nc nC T , p ,nD
上一内容 下一内容 回主目录
溶液—气体、液体或固体溶于液体溶剂中即形成溶液
上一内容
返回
2015-5-19
第四章
溶液
溶剂（A） 溶质（B）
3 混合物和溶液的区别
混合物—各组分均选用同样的标准态和同样的研究 方法。 溶液—对组分溶剂和溶质选用不同的标准态和不同 的研究方法。
上一内容
下一内容
回主目录
返回
2015-5-19
G mB n B T , p ,n C
上一内容 下一内容 回主目录
返回
2015-5-19
§4.2 化学势
2. 多组分系统的热力学基本方程 G = G (T, p, nB, nC, nD,)
G G G dG dnB ... dT dp T p , n p T , n nB T , p ,n
U UB n B T ,V ,nC
返回
2015-5-19
§4.1 偏摩尔量
* 4) 偏摩尔量与组成有关
V VB n B T , p ,nc
VB
dV dn B
下一内容 回主目录
上一内容
返回
例3： 恒T、p下，1molA (l)和2molB (l)混合， 混合物的体积为140cm3。现混合物中加入 0.0001mol(极少量) A (l)后，测得混合物 体积增加0.002cm3，求该T、p下A (l)和 B (l)的偏摩尔体积。
解： VA 0.002 20cm3 m ol1
B B C
（1）单相：
SdT Vdp BdnB CdnC ... SdT Vdp
上一内容 下一内容 回主目录
dn
B B
B
返回
2015-5-19
§4.2 化学势
结合函数定义式：
dU = d (G－pV +T S)
d H = d ( G +T S )
S nB p T , n B
S p nB T , p , n C S B p T , nB
上一内容
下一内容
回主目录
返回
2015-5-19
§4.1 偏摩尔量
§4.1 偏摩尔量
1. 问题的提出
200 C
101 .325 kPa
物质的量：nA 体积：
nB nA nB — 不变
* B m,B
nV
* A m,A
nV
V
— 变化
nAVA nBVB
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
说明
同是1mol物质：
GB H B TS B
GB VB P T GB S B T P
返回
2015-5-19
G V P T G S T P
上一内容 下一内容 回主目录
§4.1 偏摩尔量
0.0001
VA 2VB 140cm3
VB
上一内容
140 20 cm 3 mol 1 60cm 3 mol 1 2
回主目录
下一内容
返回
2015-5-19
§4.2 化学势
在各偏摩尔量中，偏摩尔吉布斯函数GB应用最广， 最重要。因而特别地把偏摩尔吉布斯函数定义为化 学势,用符号 μB 表示。 1. 定义：
可看出：
U H A G B nB S ,V ,nC nB S , p ,nC nB T ,V ,nC nB T , p ,nC
G 其中只有 n B
2015-5-19
§4.1 偏摩尔量
5) 偏摩尔量可正、可负还可为0
VB
上一内容 下一内容 回主目录
dV d n B
返回
2015-5-19
§4.1 偏摩尔量
VB V
* m, B
（1）分子大小(结构）
（2）分子间相互作用力
理想液态 混合物
(1)分子大小(结构) ——相同
V＝V（T、p、nB、nC、nD ）
V V V V dV dT dp dnB dnC ... T p ,nB p T ,nB nB T , p ,nc nC T , p ,nD
(2)分子间相互作用力——相等
ΔmixV 0
上一内容 下一内容
V
B
V
* m, B
2015-5-19
回主目录
返回
§4.1 偏摩尔量
物 理 意 义
V VB n B T , p ,n c 恒T、p及其
它组分都不 变下： 有限量系统 中加入dnB →dV →折合 成加入1mol 增加体积 无限大量系 统中加入 1mol组分B 增加的体积
§4.2 化学势
dU TdS pdV B dnB CdnC ... dH TdS Vdp B dnB CdnC ... dA SdT pdV B dnB CdnC ... dG SdT Vdp B dnB CdnC ...
积分可得
X
0
dX X B dnB X C dnC
0 0
nB
nc
X nB X B nC X C nB X B
B
即,在一定T、P下，混合系统的任一广度性质等于各组分在该组成 时的偏摩尔量XB与其摩尔数nB的乘积之和。
上一内容
下一内容
回主目录
返回
2015-5-19
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
3. Gibbs-Duhem方程 XB随组成变化 系统中不同组分XB变化有无规律？ ——Gibbs-Duhem方程
上一内容
下一内容
回主目录
返回
2015-5-19
§4.1 偏摩尔量
推导:
恒T、p下二组分系统
V V nA , nB
Maxwell 关系式
p , nB
V 证：
B
T
V T nB T , p , n p , nB C V nB T p , nB
T , p , nC T , p , nC T , nB
证明例1：
G B p VB T ,nB
G G 证： B p nB T , p ,n p T , nB C G nB p T , nB
T ,nB
返回
2015-5-19
§4.1 偏摩尔量
X G GB n B T , p ,n c nB T , p ,n
U UB n B T , p ,nC
定义: X B
C
S SB n B T , p ,nC
§4.1 偏摩尔量
注意几点： 1) ——研究混合物时提出 纯组分系统——只有 X
* m, B
2) 只有广度性质才有偏摩尔量，但偏摩尔量 本身为强度量 3) 必须强调恒T、p条件——偏摩尔量；
U UB n B T , p ,nC
上一内容 下一内容 回主目录
—— 混合物总体积随B组分物质的量的变化率
——m3/mol ——偏导
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
dG Sd T Vd p Bd nB
B
dU TdS pdV B dnB dH TdS Vdp B dnB dA SdT pdV B dnB
B
上一内容 下一内容 回主目录
B
B
返回
2015-5-19
—— 溶液热力学基础
上一内容 下一内容 回主目录
返. 偏摩尔量之间的关系
全部广延量 纯组分系统 适用于 热力学函数式 用偏摩尔量代替 多组分系统
H U PV A U TS
G H TS
H B U B PVB AB U B TS B
B
——Gibbs-Duhem方程
返回
2015-5-19
上一内容
下一内容
回主目录
§4.1 偏摩尔量
应用
G-D方程给出各组分XB变化间
必须服从的制约关系 判断所测不同组成x下各组分XB数据质量： 符合Gibbs-Duhem方程 —— 数据可靠
不符合 Gibbs-Duhem方程—— 数据不可靠
—— 热力学一致性的校验
xAdVA xBdVB 0
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
x A dV A x B dV B 0
分析： 若dVA > 0 → dVB < 0； 由VA变化求VB变化
→ VA、VB变化非独立, 相互制约 扩展：多组分、其它性质（恒T、p）
通式： x BdX B 0
X X X X dX dnB dnC ... dp dT T p ,nB p T ,nB nB T , p ,nc nC T , p ,nD
上一内容 下一内容 回主目录
溶液—气体、液体或固体溶于液体溶剂中即形成溶液
上一内容
返回
2015-5-19
第四章
溶液
溶剂（A） 溶质（B）
3 混合物和溶液的区别
混合物—各组分均选用同样的标准态和同样的研究 方法。 溶液—对组分溶剂和溶质选用不同的标准态和不同 的研究方法。
上一内容
下一内容
回主目录
返回
2015-5-19
G mB n B T , p ,n C
上一内容 下一内容 回主目录
返回
2015-5-19
§4.2 化学势
2. 多组分系统的热力学基本方程 G = G (T, p, nB, nC, nD,)
G G G dG dnB ... dT dp T p , n p T , n nB T , p ,n
U UB n B T ,V ,nC
返回
2015-5-19
§4.1 偏摩尔量
* 4) 偏摩尔量与组成有关
V VB n B T , p ,nc
VB
dV dn B
下一内容 回主目录
上一内容
返回
例3： 恒T、p下，1molA (l)和2molB (l)混合， 混合物的体积为140cm3。现混合物中加入 0.0001mol(极少量) A (l)后，测得混合物 体积增加0.002cm3，求该T、p下A (l)和 B (l)的偏摩尔体积。
解： VA 0.002 20cm3 m ol1
B B C
（1）单相：
SdT Vdp BdnB CdnC ... SdT Vdp
上一内容 下一内容 回主目录
dn
B B
B
返回
2015-5-19
§4.2 化学势
结合函数定义式：
dU = d (G－pV +T S)
d H = d ( G +T S )
S nB p T , n B
S p nB T , p , n C S B p T , nB
上一内容
下一内容
回主目录
返回
2015-5-19
§4.1 偏摩尔量
§4.1 偏摩尔量
1. 问题的提出
200 C
101 .325 kPa
物质的量：nA 体积：
nB nA nB — 不变
* B m,B
nV
* A m,A
nV
V
— 变化
nAVA nBVB
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
说明
同是1mol物质：
GB H B TS B
GB VB P T GB S B T P
返回
2015-5-19
G V P T G S T P
上一内容 下一内容 回主目录
§4.1 偏摩尔量
0.0001
VA 2VB 140cm3
VB
上一内容
140 20 cm 3 mol 1 60cm 3 mol 1 2
回主目录
下一内容
返回
2015-5-19
§4.2 化学势
在各偏摩尔量中，偏摩尔吉布斯函数GB应用最广， 最重要。因而特别地把偏摩尔吉布斯函数定义为化 学势,用符号 μB 表示。 1. 定义：
可看出：
U H A G B nB S ,V ,nC nB S , p ,nC nB T ,V ,nC nB T , p ,nC
G 其中只有 n B
2015-5-19
§4.1 偏摩尔量
5) 偏摩尔量可正、可负还可为0
VB
上一内容 下一内容 回主目录
dV d n B
返回
2015-5-19
§4.1 偏摩尔量
VB V
* m, B
（1）分子大小(结构）
（2）分子间相互作用力
理想液态 混合物
(1)分子大小(结构) ——相同
V＝V（T、p、nB、nC、nD ）
V V V V dV dT dp dnB dnC ... T p ,nB p T ,nB nB T , p ,nc nC T , p ,nD
(2)分子间相互作用力——相等
ΔmixV 0
上一内容 下一内容
V
B
V
* m, B
2015-5-19
回主目录
返回
§4.1 偏摩尔量
物 理 意 义
V VB n B T , p ,n c 恒T、p及其
它组分都不 变下： 有限量系统 中加入dnB →dV →折合 成加入1mol 增加体积 无限大量系 统中加入 1mol组分B 增加的体积
§4.2 化学势
dU TdS pdV B dnB CdnC ... dH TdS Vdp B dnB CdnC ... dA SdT pdV B dnB CdnC ... dG SdT Vdp B dnB CdnC ...
积分可得
X
0
dX X B dnB X C dnC
0 0
nB
nc
X nB X B nC X C nB X B
B
即,在一定T、P下，混合系统的任一广度性质等于各组分在该组成 时的偏摩尔量XB与其摩尔数nB的乘积之和。
上一内容
下一内容
回主目录
返回
2015-5-19
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量
3. Gibbs-Duhem方程 XB随组成变化 系统中不同组分XB变化有无规律？ ——Gibbs-Duhem方程
上一内容
下一内容
回主目录
返回
2015-5-19
§4.1 偏摩尔量
推导:
恒T、p下二组分系统
V V nA , nB
Maxwell 关系式
p , nB
V 证：
B
T
V T nB T , p , n p , nB C V nB T p , nB
T , p , nC T , p , nC T , nB
证明例1：
G B p VB T ,nB
G G 证： B p nB T , p ,n p T , nB C G nB p T , nB
T ,nB
返回
2015-5-19
§4.1 偏摩尔量
X G GB n B T , p ,n c nB T , p ,n
U UB n B T , p ,nC
定义: X B
C
S SB n B T , p ,nC
§4.1 偏摩尔量
注意几点： 1) ——研究混合物时提出 纯组分系统——只有 X
* m, B
2) 只有广度性质才有偏摩尔量，但偏摩尔量 本身为强度量 3) 必须强调恒T、p条件——偏摩尔量；
U UB n B T , p ,nC
上一内容 下一内容 回主目录
—— 混合物总体积随B组分物质的量的变化率
——m3/mol ——偏导
上一内容 下一内容 回主目录
返回
2015-5-19
§4.1 偏摩尔量