气体扩散.ppt分解
合集下载
第04章大气污染扩散模型环境保护概论ppt课件

平衡浓度为:
第六节 区域大气环境质量模型
多源大气环境质量模型 区域内大气中某一点的污染物浓度等于背景浓度和各
污染源对该点浓度的贡献值之和:
《制定地方大气污染物排放标准的技术方法》中排放总量 限值的计算方法
第七节 厂址的选择和烟囱的设计
如果用y0表示烟流半宽度,z0表 示烟流半高度,则有:
封闭型扩散模式
计算简化:
熏烟型扩散模式
假设: D 换成hf(垂向均匀分布);q只包括进入混合层部分,
则仍可用上面公式
熏烟型扩散模式
第五节 城市及山区扩散模式
城市大气扩散模式
1.线源扩散模式
风向与线源垂直时
边缘效应
城市大气扩散模式
2.面源扩散模式
城市大气扩散模式
2. 面源扩散模式(续)
简化为点源的面源扩散模式(续) 形心上风向距x0处有一虚拟点源,其烟流在形心处宽度正好
与正方形宽度相等
烟流宽度:中心线到浓度为中心处距离的两倍
(正态分布:
)
确定 、 之后即可按点源计算面源浓度
城市大气扩散模式
2. 面源扩散模式(续)
窄烟流模式
某点的污染物浓度主要取决于上风向面单元的源强,上风向 两侧单元对其影响很小
定状态,σ较大,即σ与稳定度密切相关。
扩散参数的确定
P-G曲线法
P-G曲线:Pasquill常规气象资料估算;Gifford制成图表
方法要点
将大气稳定度分为6个等级: A — 极不稳定,B —不稳定,C — 弱不稳定, D — 中性,E — 弱稳定,F —稳定。
太阳辐射
稳定级别 下风距离
P-G曲线图 P-G 表
Eutrophication)
Acid Rain
第六节 区域大气环境质量模型
多源大气环境质量模型 区域内大气中某一点的污染物浓度等于背景浓度和各
污染源对该点浓度的贡献值之和:
《制定地方大气污染物排放标准的技术方法》中排放总量 限值的计算方法
第七节 厂址的选择和烟囱的设计
如果用y0表示烟流半宽度,z0表 示烟流半高度,则有:
封闭型扩散模式
计算简化:
熏烟型扩散模式
假设: D 换成hf(垂向均匀分布);q只包括进入混合层部分,
则仍可用上面公式
熏烟型扩散模式
第五节 城市及山区扩散模式
城市大气扩散模式
1.线源扩散模式
风向与线源垂直时
边缘效应
城市大气扩散模式
2.面源扩散模式
城市大气扩散模式
2. 面源扩散模式(续)
简化为点源的面源扩散模式(续) 形心上风向距x0处有一虚拟点源,其烟流在形心处宽度正好
与正方形宽度相等
烟流宽度:中心线到浓度为中心处距离的两倍
(正态分布:
)
确定 、 之后即可按点源计算面源浓度
城市大气扩散模式
2. 面源扩散模式(续)
窄烟流模式
某点的污染物浓度主要取决于上风向面单元的源强,上风向 两侧单元对其影响很小
定状态,σ较大,即σ与稳定度密切相关。
扩散参数的确定
P-G曲线法
P-G曲线:Pasquill常规气象资料估算;Gifford制成图表
方法要点
将大气稳定度分为6个等级: A — 极不稳定,B —不稳定,C — 弱不稳定, D — 中性,E — 弱稳定,F —稳定。
太阳辐射
稳定级别 下风距离
P-G曲线图 P-G 表
Eutrophication)
Acid Rain
气体的扩散原理PPT课件

肺气肿、肺不张、肺叶切除→ 呼吸膜面积↓ → 气体交换↓
第8页/共17页
3.通气/血流比值
(ventilation/perfusion ratio)
概念: 指每分肺泡通气量(VA)和每分肺血流量 (Q)之间的比值(VA/Q) 正常值:
(4.2L/min)/(5L/min )=0.84
第9页/共17页
第14页/共17页
肺气体交换的影响因素
第15页/共17页
三、组织换气
换气驱动力: 血液与组织液间气体分压差
换气结果: 动脉血
静脉血
换气影响因素:
1、距离毛细血管远的细胞获得的O2少 2、组织的血流量减少时组织换气量降低 3、组织代谢率高时气体的扩散速率增大
第16页/共17页
感谢您的观看。
第17页/共17页
人体直立时肺局部的VA/Q 肺上区 肺下区
VA(L/min)0.24 Q(L/min)0.07
0.82 1.29
VA/Q
3.3 0.63
第12页/共17页
(三)肺扩散容量(DL)——自学 概 念:指气体在单位分压差作用下每分钟通过呼
吸膜扩散的体积。
意 义:肺扩散容量是测定呼吸气通过呼
吸膜的能力的一种指标。
∵CO2的扩散系数是O2的20倍,在同等条件下,CO2
的扩散速率是O2的20倍;但在肺中,由于肺泡气和V
血间分压差的不同,CO2的扩散速率实际约为O2的2
倍。
∴肺功能衰竭患者往往第缺6页O/共1显7页著,CO 潴留不明显。
2.呼吸膜
正常呼吸膜非常薄,通透性与面积极大(70-80m2)。
①血液流经肺毛细血管 全长约需0.7s,而完成 气体交换的时间仅需 0.3s(≈前1/3段) ,有气 体交换的时间储备;
第8页/共17页
3.通气/血流比值
(ventilation/perfusion ratio)
概念: 指每分肺泡通气量(VA)和每分肺血流量 (Q)之间的比值(VA/Q) 正常值:
(4.2L/min)/(5L/min )=0.84
第9页/共17页
第14页/共17页
肺气体交换的影响因素
第15页/共17页
三、组织换气
换气驱动力: 血液与组织液间气体分压差
换气结果: 动脉血
静脉血
换气影响因素:
1、距离毛细血管远的细胞获得的O2少 2、组织的血流量减少时组织换气量降低 3、组织代谢率高时气体的扩散速率增大
第16页/共17页
感谢您的观看。
第17页/共17页
人体直立时肺局部的VA/Q 肺上区 肺下区
VA(L/min)0.24 Q(L/min)0.07
0.82 1.29
VA/Q
3.3 0.63
第12页/共17页
(三)肺扩散容量(DL)——自学 概 念:指气体在单位分压差作用下每分钟通过呼
吸膜扩散的体积。
意 义:肺扩散容量是测定呼吸气通过呼
吸膜的能力的一种指标。
∵CO2的扩散系数是O2的20倍,在同等条件下,CO2
的扩散速率是O2的20倍;但在肺中,由于肺泡气和V
血间分压差的不同,CO2的扩散速率实际约为O2的2
倍。
∴肺功能衰竭患者往往第缺6页O/共1显7页著,CO 潴留不明显。
2.呼吸膜
正常呼吸膜非常薄,通透性与面积极大(70-80m2)。
①血液流经肺毛细血管 全长约需0.7s,而完成 气体交换的时间仅需 0.3s(≈前1/3段) ,有气 体交换的时间储备;
《燃气安全技术(第3版)》教学课件第2章燃气的泄露与扩散

泄漏燃气的扩散模型与泄漏燃气物理性质、 泄漏管道系统的周边环境和气候条件有极 大的关系。
泄漏燃气温度、密度与大气温度、密度的 差异及风速和泄漏现场各类障碍物的存在, 使泄漏燃气扩散模拟变得十分复杂。
2.2.1泄漏液体的蒸发
1)闪蒸 液体燃气(如液化天然气、液化石油气)的
沸点通常低于环境温度,当液态燃气从压力 容器中泄漏出来时,由于压力突减,液态燃 气会突然蒸发,称为闪蒸。 闪蒸的蒸发速度由下式计算:
κ-气体的绝热指数,双原子气体取1.4,多原子气体取
1.29,单原子取1.66;
M-燃气的分子量kg/mol;
R-气体常数,8.3144J/(mol.k);
T-气体的温度,K。
当
p0 (
2
k
) k 1
p k 1
时,气体流动属于亚音
速流动,燃气泄漏的质量流量为:
qmG Cdg AP
kM RT
(
k
当Fv<<1时,可认为泄漏的液体不会发生闪蒸, 此时泄漏量按液体泄漏量公式(2.1)计算;泄漏出 来的液体会在地面上蔓延,遇到防液堤而聚集形 成液池;
当 Fv <1时,泄漏量按两相流模型(2.4)计算;
当 Fv =1时,泄漏出来的液体发生完全闪蒸,此 时应按气体泄漏(2.3)处理。
当 Fv >0.2时,可以认为不形成液池。
k
)( 1
p p0
)
2 k
1
(
p p0
)
k 1 k
(2.3)
3)两相流泄漏
在过热液体发生泄漏时,有时会出现液、气两相流 动。均匀两相流的质量泄漏速度可按下式计算:
qm Cd A 2m ( pm pC )
泄漏燃气温度、密度与大气温度、密度的 差异及风速和泄漏现场各类障碍物的存在, 使泄漏燃气扩散模拟变得十分复杂。
2.2.1泄漏液体的蒸发
1)闪蒸 液体燃气(如液化天然气、液化石油气)的
沸点通常低于环境温度,当液态燃气从压力 容器中泄漏出来时,由于压力突减,液态燃 气会突然蒸发,称为闪蒸。 闪蒸的蒸发速度由下式计算:
κ-气体的绝热指数,双原子气体取1.4,多原子气体取
1.29,单原子取1.66;
M-燃气的分子量kg/mol;
R-气体常数,8.3144J/(mol.k);
T-气体的温度,K。
当
p0 (
2
k
) k 1
p k 1
时,气体流动属于亚音
速流动,燃气泄漏的质量流量为:
qmG Cdg AP
kM RT
(
k
当Fv<<1时,可认为泄漏的液体不会发生闪蒸, 此时泄漏量按液体泄漏量公式(2.1)计算;泄漏出 来的液体会在地面上蔓延,遇到防液堤而聚集形 成液池;
当 Fv <1时,泄漏量按两相流模型(2.4)计算;
当 Fv =1时,泄漏出来的液体发生完全闪蒸,此 时应按气体泄漏(2.3)处理。
当 Fv >0.2时,可以认为不形成液池。
k
)( 1
p p0
)
2 k
1
(
p p0
)
k 1 k
(2.3)
3)两相流泄漏
在过热液体发生泄漏时,有时会出现液、气两相流 动。均匀两相流的质量泄漏速度可按下式计算:
qm Cd A 2m ( pm pC )
第八章-扩散

合金中的扩散也是一样,原子总是从化学位高的地方向化 学位低的地方扩散,当各相中同一组元的化学位相等(多 相合金),则达到平衡状态,宏观扩散停止。原子扩散的 真正驱动力是化学位梯度。
F ui x
当化学位降低的方向与浓度降低的方向相反,如溶质原子 的偏聚、调幅分解等,扩散表现为向浓度高的方向进行, 称为上坡扩散。
1.弹性应力作用下的扩散 金属晶体中存在弹性应力梯度时,将造成原子的扩散。 2.晶界的内吸附 如果溶质原子位于晶界上可使体系总能量降低,它们就会
扩散而聚集在晶界上,使得晶界上浓度比晶内高。 3.电场作用下的扩散
第二节 扩散机制
§8.2.1 间隙扩散(Interstitial diffusion)
间隙扩散是小的间隙原子, 扩散时由一个间隙位置跃 迁到另一个间隙位置。间 隙原子换位时,必须从基 体原子之间挤过去,这就 要求间隙原子具有足够的 激活能来克服基体原子造
成的势垒。
图 间隙扩散机制示意图
图 面心立方结构的八面体间隙及(100)间隙
§8.2.2 置换扩散
1.柯肯达尔效应 柯肯达尔(Kirkendall)于1947年首先用实验验证了置换
将伴随有相变过程的扩散,或者有新相产生的扩散称为反 应扩散或者相变扩散。
图 反应扩散时的相图(a)与对应的浓度分布(b)和相分布(c)
图 纯铁的表面氮化 (a)Fe-N相图 (b)相分布 (c)氮浓度分布
第三节 影响扩散的因素
§8.3.1温度
由扩散系数的表达式 D=D0exp(-Q/RT) ,可以看 出,温度对扩散的影响是 很大的。
D0和Q是随成分和晶体结 构变化而变化的,与温度 基本无关,常看作常数。 扩散系数与温度的变化就 是指数关系。
图 Na+在NaCl中的扩散系数
F ui x
当化学位降低的方向与浓度降低的方向相反,如溶质原子 的偏聚、调幅分解等,扩散表现为向浓度高的方向进行, 称为上坡扩散。
1.弹性应力作用下的扩散 金属晶体中存在弹性应力梯度时,将造成原子的扩散。 2.晶界的内吸附 如果溶质原子位于晶界上可使体系总能量降低,它们就会
扩散而聚集在晶界上,使得晶界上浓度比晶内高。 3.电场作用下的扩散
第二节 扩散机制
§8.2.1 间隙扩散(Interstitial diffusion)
间隙扩散是小的间隙原子, 扩散时由一个间隙位置跃 迁到另一个间隙位置。间 隙原子换位时,必须从基 体原子之间挤过去,这就 要求间隙原子具有足够的 激活能来克服基体原子造
成的势垒。
图 间隙扩散机制示意图
图 面心立方结构的八面体间隙及(100)间隙
§8.2.2 置换扩散
1.柯肯达尔效应 柯肯达尔(Kirkendall)于1947年首先用实验验证了置换
将伴随有相变过程的扩散,或者有新相产生的扩散称为反 应扩散或者相变扩散。
图 反应扩散时的相图(a)与对应的浓度分布(b)和相分布(c)
图 纯铁的表面氮化 (a)Fe-N相图 (b)相分布 (c)氮浓度分布
第三节 影响扩散的因素
§8.3.1温度
由扩散系数的表达式 D=D0exp(-Q/RT) ,可以看 出,温度对扩散的影响是 很大的。
D0和Q是随成分和晶体结 构变化而变化的,与温度 基本无关,常看作常数。 扩散系数与温度的变化就 是指数关系。
图 Na+在NaCl中的扩散系数
热传导方程(扩散方程)ppt课件

( x ,t0) ( x )
波方程的Cauchy问题
由泛定方程和相应边界条件构成的定解问题称为 边值问题。
u0, (x,y),
u f (x, y).
Laplace方程的边值问题
由偏微分方程和相应的初始条件及边界条件构成 的定解问题称为混合问题。
uutt0a2(u(xxx,y,uzy)yuzz)0
kn|x0k(x) qnq0
u x
|xl
q0 k
u x |x0
q0 k
xl
若端点是绝热的,则
u u x|xl x x0 0
三、定解问题
定义1 在区域 G[0,) 上,由偏微分方程、初 始条件和边界条件中的其中之一组成的定解问题称为 初边值问题或混合问题。
u ut x,a 02 u xx (x 0),,
注 1、热传导方程不仅仅描述热传导现象,也可以
刻画分子、气体的扩散等,也称扩散方程;
2、上述边界条件形式上与波动方程的边界条件 一样,但表示的物理意义不一样;
3、热传导方程的初始条件只有一个,而波动方 程有两个初始条件。
4、除了三维热传导方程外,物理上,温度的分 布在同一个界面上是相同的,可得一维热传导方
gk1 k
u1.
注意第三边界条件的推导:
研究物体与周围介质在物体表面上的热交换问题
把一个温度变化规律为 u(x, y, z, t)的物体放入 空
气介质中,已知与物体表面接触处的空气介质温度
为 u1(x, y, z, t),它与物体表面的温度u(x, y, z, t)并不
相同。这给出了第三边界条件的提法。
或
u knk1(uu1).
即得到(1.10): ( u nu)|(x,y,z) g(x,y,z,t).
气体扩散.ppt分解共59页

40、学而不思则罔,思而不学则殆。——孔子
气体扩散.ppt分解
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
谢谢!Leabharlann 36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
气体在多孔气体中的扩散
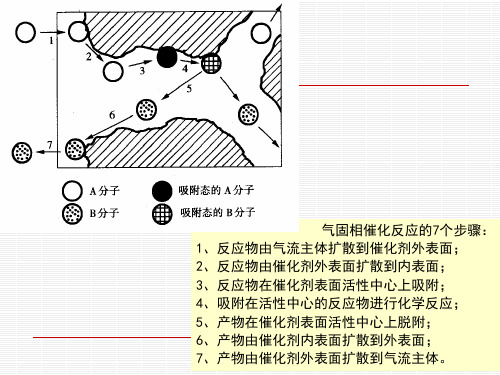
内外扩散都有影响时的有效因子
内外扩散都有影响的 内外扩散均有影响时的 反应速率 o 有效因子 扩散无影响时的反应速 率
A kGam cAG cAS kwcAS okwcAG
c AS c AG k 1 w k G am
A kwcAS
r R p , c A c AS dcA r 0, 0 dr
比较薄片催化剂
L
kp De
R p sinh 3r R p cA c AS r sinh3
1 1 1 tanh3 3
6.4.2
内扩散有效因子
d 2c A dr 2 1 dcA k p cA r dr De
圆柱催化剂
Vp ap
kp De
r R p , c A c AS dcA r 0, 0 dr
I 0 2 r R p cA c AS I 0 2
I1 2 I 0 2
特别注意:
< 0.4, 1 > 3.0,
1
6.4.4
2、平行反应
P A
k1
S A
k2
主反应 副反应
n 1 AS
n rA 1 k1cA m rA 2 k2cB
无内扩散影响时,催化剂内浓度就是表面浓度 :
S′
P
kc 1 n m k1cAS k2 cAS 1 k2 c m n AS k1
6.5 内扩散与复合反应选择性的影响 1、两个独立并行的反应
k1 A P C k2 B S W
主反应 副反应
k1 > k2
第六章 扩散

直接应用菲克第二定律解决实际扩散问题,往往很复杂。 但是有两条由菲克第二定律推导出来的结论却十分简单、 有用:
推论 (1)对于同一扩散系统、扩散系数D与 扩散时间t的乘积为一常数。
已知Cu在Al中的扩散系数D, 在500℃和600℃时分别为 4.8×10-14 m2/s和5.3×10-13 m2/s。假如一个工件在600℃ 需要处理10小时,如果在500℃处理,要达到同样的效果 则需要多少小时? (Dt)500 = (Dt)600
三、扩散的热力学分析
1.扩散驱动力 浓度梯度有关的扩散:顺扩散(高浓度→低浓度),逆扩散 (低浓度→高浓度) 热力学:决定组元扩散流向的是化学位 浓度梯度与化学位梯度一致,顺扩散,成分趋于均匀,如铸 锭均匀化 浓度梯度与化学位梯度不一致,逆扩散,成分区域性不均匀, 如共析分解 i, j 两组元系统,组元的体积浓度为 Ci , ni 为组元 i 的摩尔 数,M:组元i的摩尔质量。 C i c M n 则Ci=Mni, i i ,则 n i
渗碳层按齿廓分布的渗碳齿轮
1. 概述
实际上,金属的真空冶炼、材料的提纯、 铸件的凝固和成分均匀化、变形金属的回 复再结晶、相变、化学热处理、粉末冶金 或陶瓷材料的烧结等都受扩散影响 原子或分子的迁移现象称为扩散。扩散的 本质是原子依靠热运动从一个位置迁移到 另一个位置。扩散是固体中原子迁移的唯 一方式。 扩散过程是传质过程。它是一个不可逆过 程,也是体系熵增过程。
§2.2 菲克第二定律
考虑如图所示的扩散系统, 扩散物质沿x方向通过横截面 积为A(=ΔyΔz)、长度为Δx的 微元体,假设流入微元体(x 处)和流出微元体(x+Δx处) 的扩散通量分别为Jx和Jx+Δx, 则在Δt时间内微元体中累积 的扩散物质量为
化学教学:气体的扩散

tO2 t
=4 1
, tO2
= 4t
32 = 4 2.0 1
学习成果评量
1. 同温、同压下的氧气与氢气,两气体的逸散速率比
为何?
rH2 = MO2 = 32 = 4
rO2
MH2
21
2. 已知 500 毫升的氢气通过多孔素烧圆筒需时 10.0
分钟,试计算在同状态下 200 毫升的氧气通过该素
烧圆筒需时多少分钟?
3. 1 atm=76 cmHg=760 mmHg=760 托 =1.013×105 帕=1.013 巴
4. 气体的通性:
(123465) 气可定体充 以压粒满 无快完时子任 限速全,撞何 地移互定击形膨动溶量器状胀,。气壁流与;体产体具动的生积有性体压的很极积力佳容好随,。器的温当。可度温压之度缩上愈性升高,而,体增运积加动愈,速 率小随会,温愈压度快力之,愈下撞大降击。而器缩壁小的。频率增加,使得压力愈大。
彼此碰撞而混合的过程,称为扩散。气体分 子经由小孔,进入真空之过程,则称为通孔 扩散或逸散。 18. 温度愈高,气体分子的平均运动速率愈快。
将铀和氟反应成为具有挥发性的六氟化铀,因
为 235UF6 和 238UF6 的分子量不同,将六氟化 铀通过数千层多孔性的障壁扩散,最后即可达
到浓缩的目的。
范例 1-12
已知在同温、同压下,某气体的扩散速率为氧
气的 1,则此气体的分子量为何?(分子量: 2
O2=32.0)
解答 设此气体的分子量为 M
9. 气体的莫耳体积:在 STP 下,1 莫耳气体的体积为 22.414 升。
CH1
本章摘要
1-3 理想气体 10. 理想气体方程式:PV=nRT。 11. 气体常数
气体的扩散

氢分子的有效直径为210-10m。
解:按气体分子算术平均速率公式 算得
v 8RT
v
8RT =
8 8.31 273 3.14 2 103
m
/
s
1.70
103
m
/
s
按公式 p=nkT 可知单位体积中分子数为
n
p = 1.013105 kT 1.38 1023 273
第4章 气体内的输运过程
本章内容 4.1 气体分子的平均自由程 4.2 输运过程的宏观规律 4.3 输运过程的微观解释
基本要求 ☆掌握刚球模型下的平均自由程和碰撞频率的概念,深刻
理解其物理意义。
☆理解和掌握三种输运过程的微观机制、原因和结果,掌
握相应的宏观规律。
☆理解描述三种输运过程的系数的统计含义和统计方法,
u = u (z)
B
x
牛顿粘滞定律 :f du S
dz z0
称为粘滞系数,代表单位截面积单位速度梯度的粘滞力。
4.2.2 热传导现象
1. 热传导现象
物体内各部分温度不均匀时,将有热量由温度较高处传
递到温度较低处,这种现象叫做热传导现象。
2. 傅里叶热传导定律
设沿 z 方向温度梯度最大,实验 指出,单位时间内,通过垂直于z 轴
4.1.1 平均碰撞频率与平均自由程
单位时间内一个气体分子与其它分子碰撞的平均次数叫
做分子的平均碰撞频率,用表示 。分子在相继两次碰
撞之间能自由通过的路程自由程,分子在两次碰撞之间
自由运动的平均路程叫做分子的平均自由程 Z.
vt v
Z t Z
线度 ~ 10-8m
解:按气体分子算术平均速率公式 算得
v 8RT
v
8RT =
8 8.31 273 3.14 2 103
m
/
s
1.70
103
m
/
s
按公式 p=nkT 可知单位体积中分子数为
n
p = 1.013105 kT 1.38 1023 273
第4章 气体内的输运过程
本章内容 4.1 气体分子的平均自由程 4.2 输运过程的宏观规律 4.3 输运过程的微观解释
基本要求 ☆掌握刚球模型下的平均自由程和碰撞频率的概念,深刻
理解其物理意义。
☆理解和掌握三种输运过程的微观机制、原因和结果,掌
握相应的宏观规律。
☆理解描述三种输运过程的系数的统计含义和统计方法,
u = u (z)
B
x
牛顿粘滞定律 :f du S
dz z0
称为粘滞系数,代表单位截面积单位速度梯度的粘滞力。
4.2.2 热传导现象
1. 热传导现象
物体内各部分温度不均匀时,将有热量由温度较高处传
递到温度较低处,这种现象叫做热传导现象。
2. 傅里叶热传导定律
设沿 z 方向温度梯度最大,实验 指出,单位时间内,通过垂直于z 轴
4.1.1 平均碰撞频率与平均自由程
单位时间内一个气体分子与其它分子碰撞的平均次数叫
做分子的平均碰撞频率,用表示 。分子在相继两次碰
撞之间能自由通过的路程自由程,分子在两次碰撞之间
自由运动的平均路程叫做分子的平均自由程 Z.
vt v
Z t Z
线度 ~ 10-8m
气体的扩散

2 n
及分子数密度有关。
p nkT
1
2 d 2n
在标准状态下,多数气体平均
自由程 ~10-8m,只有氢气约 为10-7m。一般d~10-10m,故 d。可求得 Z ~109/秒。 每秒钟一个分子竟发生几十亿
kT
2 d 2 p
次碰撞!
例题 求氢在标准状态下,在1s 内分子的平均碰撞次数。已知
解:因为
1 v 1
3
3
4kmT 1
d 2
而 m 28 10 3 kg 4.610 26 kg 6.02 10 23
代入数值得:=1.1×10-5N·s·m-2
实验测得在15°C时氮气的粘滞系数为1.73×10-5N·s·m-2
4.3.5 低压下的热传导和粘滞现象
4.3 输运过程的微观解释
4.3.1 三种输运过程的实质
1. 输运过程的宏观规律
dY
( dX
dz
)z0
dSdt
该式适用于粘滞现象、热传导现象和扩散现象,这里
的不均匀性X指速度u、温度 T和密度,输运的量Y指动 量dK、热量和质量。
2. 输运过程的实质
这三种输运过程可以说是输运的共性反映在三个具体过 程之中,所以这三种过程的宏观规律的形式完全相似,意 义也相似。粘滞现象是因为宏观速度的不均匀性造成动量 的定向转移。热传导现象是因为宏观温度的不均匀性造成 热量的定向转移。扩散现象是因为宏观密度的不均匀性造 成质量的定向转移。
z
zu
B
dS
z0 A
o
o
y
x →u
y
x
流速不均匀,沿 z 变化(或有梯度),速度梯度 du dz
及分子数密度有关。
p nkT
1
2 d 2n
在标准状态下,多数气体平均
自由程 ~10-8m,只有氢气约 为10-7m。一般d~10-10m,故 d。可求得 Z ~109/秒。 每秒钟一个分子竟发生几十亿
kT
2 d 2 p
次碰撞!
例题 求氢在标准状态下,在1s 内分子的平均碰撞次数。已知
解:因为
1 v 1
3
3
4kmT 1
d 2
而 m 28 10 3 kg 4.610 26 kg 6.02 10 23
代入数值得:=1.1×10-5N·s·m-2
实验测得在15°C时氮气的粘滞系数为1.73×10-5N·s·m-2
4.3.5 低压下的热传导和粘滞现象
4.3 输运过程的微观解释
4.3.1 三种输运过程的实质
1. 输运过程的宏观规律
dY
( dX
dz
)z0
dSdt
该式适用于粘滞现象、热传导现象和扩散现象,这里
的不均匀性X指速度u、温度 T和密度,输运的量Y指动 量dK、热量和质量。
2. 输运过程的实质
这三种输运过程可以说是输运的共性反映在三个具体过 程之中,所以这三种过程的宏观规律的形式完全相似,意 义也相似。粘滞现象是因为宏观速度的不均匀性造成动量 的定向转移。热传导现象是因为宏观温度的不均匀性造成 热量的定向转移。扩散现象是因为宏观密度的不均匀性造 成质量的定向转移。
z
zu
B
dS
z0 A
o
o
y
x →u
y
x
流速不均匀,沿 z 变化(或有梯度),速度梯度 du dz
金属学与热处理第八章扩散ppt课件.ppt

场和磁场等。 (二)温度足够高。
固态扩散是依靠原子热激活能进行的过程,必须在足 够高的温度才能进行。当温度低于某一温度时,原子被激 活的几率很低,扩散几乎不能进行即被“冻结”。C被冻 结的温度为100℃ ,Fe被冻结的温度为500℃。
(三)时间足够长。 扩散原子在晶体中每跃迁一次最多也只能移动0.3~
不同的金属或合金,其扩散机制是不同的。目前,被 大家所公认的扩散机制由如下几种:间隙扩散机制;换位 扩散机制;空位扩散机制等。
(一)间隙扩散 1)在间隙固溶体中,溶质原子由一个间隙位置跳到其
相邻的另一间隙位置,即为间隙扩散。
这种方式进行扩散的可能性很大,因为在间隙固溶体 中,溶质原子只占据少量间隙位置,即每个间隙原子周围 都有较多的间隙位置是空着的,故供其跃迁的位置很多。
在微小体积Adx内的物资积存速率为:
(CAdx) C Adx (2)
t
t
式(1)与式(2)相等,则可得
C Adx J Adx
t
x
即: C J (3)
t
x
将扩散第一定律代入(3)有:
C C
(D ) t x x
(4)
式(4)即为菲克第二定律,如果扩散系数 是 D与浓度无 关的常数,则式(4)可写为:
0.5nm的距离,经过相当长的时间才能造成物质的宏观定 向迁移。
由这一原理人们设计了固溶处理,如:铝合 金的固溶处理,不锈钢的固溶处理等。
此外,在热加工刚完成时迅速将金属材料冷却到室温, 抑制扩散过程,避免发生静态再结晶,可把动态回复或动 态再结晶的组织保留下来,以达到提高金属材料性能的目 的。
(四)扩散原子要有固溶。 扩散原子在基体金属中必须有一定的固溶度,能够溶入
C t
固态扩散是依靠原子热激活能进行的过程,必须在足 够高的温度才能进行。当温度低于某一温度时,原子被激 活的几率很低,扩散几乎不能进行即被“冻结”。C被冻 结的温度为100℃ ,Fe被冻结的温度为500℃。
(三)时间足够长。 扩散原子在晶体中每跃迁一次最多也只能移动0.3~
不同的金属或合金,其扩散机制是不同的。目前,被 大家所公认的扩散机制由如下几种:间隙扩散机制;换位 扩散机制;空位扩散机制等。
(一)间隙扩散 1)在间隙固溶体中,溶质原子由一个间隙位置跳到其
相邻的另一间隙位置,即为间隙扩散。
这种方式进行扩散的可能性很大,因为在间隙固溶体 中,溶质原子只占据少量间隙位置,即每个间隙原子周围 都有较多的间隙位置是空着的,故供其跃迁的位置很多。
在微小体积Adx内的物资积存速率为:
(CAdx) C Adx (2)
t
t
式(1)与式(2)相等,则可得
C Adx J Adx
t
x
即: C J (3)
t
x
将扩散第一定律代入(3)有:
C C
(D ) t x x
(4)
式(4)即为菲克第二定律,如果扩散系数 是 D与浓度无 关的常数,则式(4)可写为:
0.5nm的距离,经过相当长的时间才能造成物质的宏观定 向迁移。
由这一原理人们设计了固溶处理,如:铝合 金的固溶处理,不锈钢的固溶处理等。
此外,在热加工刚完成时迅速将金属材料冷却到室温, 抑制扩散过程,避免发生静态再结晶,可把动态回复或动 态再结晶的组织保留下来,以达到提高金属材料性能的目 的。
(四)扩散原子要有固溶。 扩散原子在基体金属中必须有一定的固溶度,能够溶入
C t
第六章 可燃气体扩散燃烧

6.4.2 扩散火焰与动力火焰
图6 - 8 动力火焰逐渐转化为扩散火焰的过程
6.4.2 扩散火焰与动力火焰
表6 - 2 空气中各种火焰的临界雷诺数
6.4.2 扩散火焰与动力火焰
图6 - 9 火焰的形状及高度随射流速度增加时的变化
6.5 湍流扩散火焰
(1)初始射流动量通量与作用在火焰上方的力之比,即火焰的傅鲁特(Froude) 数。 (2)喷管内流体密度与环境气体密度之比。 (3)初始射流直径。 (4)成分组成为化学当量比时,燃料的质量分数。
6.5 湍流扩散火焰
火焰的傅鲁特数定义如下:
(6-67)
6.2.1 层流射流模型
6.2.2 层流射流求解
图6 - 3 层流射流 a)原始轴向速度分布 b)自相似轴向速度分布 c)自相似径向速度分布
6.2.2 层流射流求解
6.2.2 层流射流求解
(6-9) (6-10)
(6-11)
(6-12)
(6-13)
6.2.2 层流射流求解
(6-14) (6-15)
(6-16)
(6-17)
(6-18)
6.2.2 层流射流求解
(6-19) (6-20)
(6-21)
(6-22)
(6-23)
6.2.2 层流射流求解
(6-24) (6-25)
(6-26)
(6-27)
(6-28)
6.2.2 层流射流求解
(6-29) (6-30)
(6-31)
(6-32)
(6-33)
6.2.3 射流参数
1.中心轴线速度 2.扩张率和扩张角 3.卷吸量
1.中心轴线速度
(6-34) (6-35)
(6-36a)
气体的扩散和压强

在地球表面,压强通常用大气压来表示,即一个 03 标准大气压为101325帕斯卡。
压强的测量
测量压强的仪器称为压力计或压力表 ,根据测量原理的不同,可以分为液
柱式、弹性式和电测式等类型。
弹性式压力计利用弹性元件的变形来 测量压强,其优点是测量范围广、稳
定性好,但精度较低。
液柱式压力计通过液柱产生的压力来 测量气体或液体的压强,其优点是结 构简单、准确度高,但受温度影响较 大。
02 观察气体扩散
在一定时间内观察气体在管道中的扩散情况,记 录扩散速度和扩散距离。
03 测量压强
使用压力计测量容器内气体的压强,记录数据。
实验设备
密封玻璃容器
用于装气体,保持容器内 气体浓度稳定。
压力计
用于测量容器内气体的压 强。
管道
连接两个容器,使气体能 够从一个容器扩散到另一 个容器。
实验结果分析
扩散与压强的关系
扩散是指物质从高浓度区域向低浓度区域的传递过程,扩散速率与浓度差成正比,扩散系数是 描述扩散速率的物理量。
在一定温度下,扩散系数与压强有一定的关系。一般来说,随着压强的增加,气体分子的平均 自由程减小,分子之间的碰撞频率增加,扩散系数减小。
扩散系数与压强的关系
扩散系数与压强的关系取决于气体分子的性质和温度。在一定温度下,对于一定种类的气体,扩散系数随压强的变化而变化 。
通过压缩气体提高压力,利用管道将气体输送到 目的地,如天然气、煤气等管道输送。
03 燃烧与爆炸
气体燃烧和爆炸过程中,扩散和压强的变化对于 燃烧反应的速率和爆炸威力具有重要影响。
生物学上的应用
呼吸作用
生物体内的气体交换依赖于气体的扩散作用,氧气和二氧化碳通过呼吸道的扩散进入和排出肺 部。
压强的测量
测量压强的仪器称为压力计或压力表 ,根据测量原理的不同,可以分为液
柱式、弹性式和电测式等类型。
弹性式压力计利用弹性元件的变形来 测量压强,其优点是测量范围广、稳
定性好,但精度较低。
液柱式压力计通过液柱产生的压力来 测量气体或液体的压强,其优点是结 构简单、准确度高,但受温度影响较 大。
02 观察气体扩散
在一定时间内观察气体在管道中的扩散情况,记 录扩散速度和扩散距离。
03 测量压强
使用压力计测量容器内气体的压强,记录数据。
实验设备
密封玻璃容器
用于装气体,保持容器内 气体浓度稳定。
压力计
用于测量容器内气体的压 强。
管道
连接两个容器,使气体能 够从一个容器扩散到另一 个容器。
实验结果分析
扩散与压强的关系
扩散是指物质从高浓度区域向低浓度区域的传递过程,扩散速率与浓度差成正比,扩散系数是 描述扩散速率的物理量。
在一定温度下,扩散系数与压强有一定的关系。一般来说,随着压强的增加,气体分子的平均 自由程减小,分子之间的碰撞频率增加,扩散系数减小。
扩散系数与压强的关系
扩散系数与压强的关系取决于气体分子的性质和温度。在一定温度下,对于一定种类的气体,扩散系数随压强的变化而变化 。
通过压缩气体提高压力,利用管道将气体输送到 目的地,如天然气、煤气等管道输送。
03 燃烧与爆炸
气体燃烧和爆炸过程中,扩散和压强的变化对于 燃烧反应的速率和爆炸威力具有重要影响。
生物学上的应用
呼吸作用
生物体内的气体交换依赖于气体的扩散作用,氧气和二氧化碳通过呼吸道的扩散进入和排出肺 部。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体动理论
6-1 物质的微观模型 统计规律性
物质结构的微观模型 :
1 、宏观物体是由大量微观粒子 — 分子(或原子 )组成的,分子之间有空隙;
2、分子在不停地作无规则的运动,其剧烈程度与 温度有关; 3、分子之间存在相互作用力。 这些观点就是气体动理论的基本出发点。统计物 理学的任务就是从上述物质分子运动论的基本观点 出发,研究和说明宏观物体的各种现象和性质。
. . . . . . . . . . . . . . . .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . .. .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 i ix 2 ix i
压强P为
dI 1 2 2 P mn vix mn v dSdt 3
理想气体压强公式的简易推导
1 2 引入气体分子平均平动动能 : k mv 2
则又有
2 1 2 2 P n ( mv ) n k 3 2 3
vx v y vz 0
1 2 v v v v 3
2 x 2 y 2 z
二、理想气体压强公式 容器内的气体施加在器壁上的压强,从微观看 是大量气体分子不断与器壁碰撞的结果。每个分子 每次碰撞都给器壁一微小的冲量,大量分子不断碰 撞,表现为一个恒定、均匀、持续的压力。
设贮有理想气体的容器的容积为V,气体分子 的质量为m,分子总数为N,则单位体积内的分子数 为n=N/V。为了便于讨论,将分子分成若干个“等 速组”,即每组内分子具有大小相等、方向相同的 速度vi。将单位体积内速度分别为v1、v2…vi…的分 子数表示为n1、n2 …ni …于是有
四、统计规律
统计规律,是指大量偶然事件整体所遵循的规 律。虽然每个事件都是偶然、无规律的,但总体上 却存在着确定的规律性。伽尔顿板是说明统计规律 的演示实验。 单个小球下落时与哪些铁 钉碰撞,最后落入哪个狭槽完 全是无法预测的偶然事件(随机 事件)。大量小球总体上的分布 有确定的规律性:落入中央狭槽 的小球较多,而落入两端狭槽 的小球较少。重复几次同样实 验,得到的结果都近似相同。
2mvix ni vix dtdS 2ni mv dtdS
2 ix
对于所有可能的速度,全部分子施于dS的总冲量为
dI
vix 0
2n mv dSdt
iห้องสมุดไป่ตู้2 ix
式中限制了vix>0,这是因为vix<0的分子是不可 能与dS相碰的。只要除以2即可去掉vix>0 的限制。 于是有
dI m n v dSdt mnv dSdt
n ni
如图,在器壁上任取一小块面 积dS,设某一分子以速度vi与dS 相碰,碰撞是完全弹性的,所以 Y、Z两个方向的速度分量viy变为 -vix。所以,碰撞一次,分子的 动量变化为
mvix mvix 2mvix
分子施于面元dS的冲量为2mvix。在速度为vi的 分子中,dt时间内能够与dS相碰的分子只是位于以 dS为底、vixdt为高、vi为轴的斜柱体内的那部分。分 子数可表示为ni vixdtdS。因此,速度为vi的“等速组 ”分子施于dS的总冲量为
一、分子的线度与间隙 在标准状态下,气体分子间的距离约为分子直径 的10倍,于是每个分子所占有的体积约为分子本身 的体积的1000倍。因而气体分子可看成是大小可以 忽略不计的质点。 气体分子的间距很大,因而很容易压缩;液体 和固体分子间也有空隙,如:50升水+50升酒精= 97升溶液;在2万个大气压下,液体也会从钢管壁 上渗出等等。 二、分子热运动
6-2 理想气体的压强公式 温度的微观实质
一、理想气体分子的微观模型和统计假设 1.理想气体分子的微观模型 (1)由于气体分子间距较大,分子的大小可以忽 略不计,即可把分子视为质点。
( 2 )气体分子间的相互作用力很弱,可忽略不计 。即认为除碰撞的瞬间外,分子之间以及分子与容 器壁之间都没有相互作用力。
(3)分子之间以及分子与器壁之间的碰撞可视为 完全弹性碰撞。
2.统计假设
(1)容器中各处的分子数密度相同。
(2)分子沿任一方向的运动不比其他方向的运动占 优势,即分子向各个方向运动的几率均等。在任一 时刻,朝着直角坐标系的x、-x、y、-y、z和-z 轴各个方向运动的分子数应相等,并且都等于总分 子数的1/6。 (3)分子速度在各个方向上的分量的各种统计平均 值相等。如:
描述单个分子运动情况的物理量,称为微观量 。例如分子的坐标、速度、动量、能量等,都是微 观量。由于大量气体分子间频繁的碰撞,许多微观 量都是随机量,个别分子的运动规律是无法把握的 。但在平衡态下用于描述系统整体性质的各宏观物 理量(P、T等)均有确定、稳定的值,这说明由大 量分子所组成的系统要遵从确定的统计规律。 本章将要研究的理想气体的压强公式和温度公 式、能量均分定律、麦克斯韦速率分布律等都是统 计规律。从个别分子的力学规律入手,通过对大量 分子求算术平均,建立微观量的统计平均值与宏观 量的联系,从而揭示出宏观量的微观实质,这种方 法称为统计方法。
分子热运动的基本特征是分子的永恒运动和频 繁的相互碰撞。分子热运动具有混乱性和无序性。 分子无规则运动的剧烈程度与温度有关。
三、分子力 分子之间同时存在吸引力 和排斥力。实验证明当分子间 距较大时,存在的引力很小, 随着间距的减小,引力逐渐加 强,当r=r0时,分子力为零, 称r0为平衡位置。r<r0分子力 表现在排斥力,r>r0分子力表 现在吸引力,当r>10r0时,分 子力可以忽略不计。 分子间彼此趋近到分子的直径d时,分子将在强 大的斥力作用下被排斥开,类似小球间“弹性碰撞 ”过程。d的平均值称为分子有效直径,数量级约为 10-10m。
6-1 物质的微观模型 统计规律性
物质结构的微观模型 :
1 、宏观物体是由大量微观粒子 — 分子(或原子 )组成的,分子之间有空隙;
2、分子在不停地作无规则的运动,其剧烈程度与 温度有关; 3、分子之间存在相互作用力。 这些观点就是气体动理论的基本出发点。统计物 理学的任务就是从上述物质分子运动论的基本观点 出发,研究和说明宏观物体的各种现象和性质。
. . . . . . . . . . . . . . . .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . .. .. .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 i ix 2 ix i
压强P为
dI 1 2 2 P mn vix mn v dSdt 3
理想气体压强公式的简易推导
1 2 引入气体分子平均平动动能 : k mv 2
则又有
2 1 2 2 P n ( mv ) n k 3 2 3
vx v y vz 0
1 2 v v v v 3
2 x 2 y 2 z
二、理想气体压强公式 容器内的气体施加在器壁上的压强,从微观看 是大量气体分子不断与器壁碰撞的结果。每个分子 每次碰撞都给器壁一微小的冲量,大量分子不断碰 撞,表现为一个恒定、均匀、持续的压力。
设贮有理想气体的容器的容积为V,气体分子 的质量为m,分子总数为N,则单位体积内的分子数 为n=N/V。为了便于讨论,将分子分成若干个“等 速组”,即每组内分子具有大小相等、方向相同的 速度vi。将单位体积内速度分别为v1、v2…vi…的分 子数表示为n1、n2 …ni …于是有
四、统计规律
统计规律,是指大量偶然事件整体所遵循的规 律。虽然每个事件都是偶然、无规律的,但总体上 却存在着确定的规律性。伽尔顿板是说明统计规律 的演示实验。 单个小球下落时与哪些铁 钉碰撞,最后落入哪个狭槽完 全是无法预测的偶然事件(随机 事件)。大量小球总体上的分布 有确定的规律性:落入中央狭槽 的小球较多,而落入两端狭槽 的小球较少。重复几次同样实 验,得到的结果都近似相同。
2mvix ni vix dtdS 2ni mv dtdS
2 ix
对于所有可能的速度,全部分子施于dS的总冲量为
dI
vix 0
2n mv dSdt
iห้องสมุดไป่ตู้2 ix
式中限制了vix>0,这是因为vix<0的分子是不可 能与dS相碰的。只要除以2即可去掉vix>0 的限制。 于是有
dI m n v dSdt mnv dSdt
n ni
如图,在器壁上任取一小块面 积dS,设某一分子以速度vi与dS 相碰,碰撞是完全弹性的,所以 Y、Z两个方向的速度分量viy变为 -vix。所以,碰撞一次,分子的 动量变化为
mvix mvix 2mvix
分子施于面元dS的冲量为2mvix。在速度为vi的 分子中,dt时间内能够与dS相碰的分子只是位于以 dS为底、vixdt为高、vi为轴的斜柱体内的那部分。分 子数可表示为ni vixdtdS。因此,速度为vi的“等速组 ”分子施于dS的总冲量为
一、分子的线度与间隙 在标准状态下,气体分子间的距离约为分子直径 的10倍,于是每个分子所占有的体积约为分子本身 的体积的1000倍。因而气体分子可看成是大小可以 忽略不计的质点。 气体分子的间距很大,因而很容易压缩;液体 和固体分子间也有空隙,如:50升水+50升酒精= 97升溶液;在2万个大气压下,液体也会从钢管壁 上渗出等等。 二、分子热运动
6-2 理想气体的压强公式 温度的微观实质
一、理想气体分子的微观模型和统计假设 1.理想气体分子的微观模型 (1)由于气体分子间距较大,分子的大小可以忽 略不计,即可把分子视为质点。
( 2 )气体分子间的相互作用力很弱,可忽略不计 。即认为除碰撞的瞬间外,分子之间以及分子与容 器壁之间都没有相互作用力。
(3)分子之间以及分子与器壁之间的碰撞可视为 完全弹性碰撞。
2.统计假设
(1)容器中各处的分子数密度相同。
(2)分子沿任一方向的运动不比其他方向的运动占 优势,即分子向各个方向运动的几率均等。在任一 时刻,朝着直角坐标系的x、-x、y、-y、z和-z 轴各个方向运动的分子数应相等,并且都等于总分 子数的1/6。 (3)分子速度在各个方向上的分量的各种统计平均 值相等。如:
描述单个分子运动情况的物理量,称为微观量 。例如分子的坐标、速度、动量、能量等,都是微 观量。由于大量气体分子间频繁的碰撞,许多微观 量都是随机量,个别分子的运动规律是无法把握的 。但在平衡态下用于描述系统整体性质的各宏观物 理量(P、T等)均有确定、稳定的值,这说明由大 量分子所组成的系统要遵从确定的统计规律。 本章将要研究的理想气体的压强公式和温度公 式、能量均分定律、麦克斯韦速率分布律等都是统 计规律。从个别分子的力学规律入手,通过对大量 分子求算术平均,建立微观量的统计平均值与宏观 量的联系,从而揭示出宏观量的微观实质,这种方 法称为统计方法。
分子热运动的基本特征是分子的永恒运动和频 繁的相互碰撞。分子热运动具有混乱性和无序性。 分子无规则运动的剧烈程度与温度有关。
三、分子力 分子之间同时存在吸引力 和排斥力。实验证明当分子间 距较大时,存在的引力很小, 随着间距的减小,引力逐渐加 强,当r=r0时,分子力为零, 称r0为平衡位置。r<r0分子力 表现在排斥力,r>r0分子力表 现在吸引力,当r>10r0时,分 子力可以忽略不计。 分子间彼此趋近到分子的直径d时,分子将在强 大的斥力作用下被排斥开,类似小球间“弹性碰撞 ”过程。d的平均值称为分子有效直径,数量级约为 10-10m。
