计算物理课后部分习题答案
大学物理学(第三版上) 课后习题3答案详解
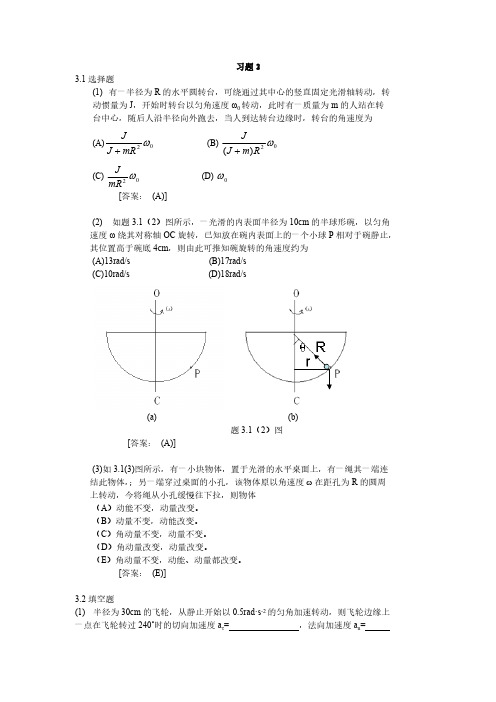
习题33.1选择题(1) 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A) (B) 02ωmRJ J+02)(ωR m J J +(C) (D) 02ωmRJ0ω[答案: (A)](2) 如题3.1(2)图所示,一光滑的内表面半径为10cm 的半球形碗,以匀角速度ω绕其对称轴OC 旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm ,则由此可推知碗旋转的角速度约为(A)13rad/s (B)17rad/s (C)10rad/s (D)18rad/s (a)(b)题3.1(2)图[答案: (A)](3)如3.1(3)图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A )动能不变,动量改变。
(B )动量不变,动能改变。
(C )角动量不变,动量不变。
(D )角动量改变,动量改变。
(E )角动量不变,动能、动量都改变。
[答案: (E)]3.2填空题(1) 半径为30cm 的飞轮,从静止开始以0.5rad·s -2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度a τ= ,法向加速度a n = 。
0.15; 1.256[答案:](2) 如题3.2(2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的 守恒,原因是 。
木球被击中后棒和球升高的过程中,对木球、子弹、细棒、地球系统的 守恒。
题3.2(2)图[答案:对o轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对o轴的合外力矩为零,机械能守恒](3) 两个质量分布均匀的圆盘A和B的密度分别为ρA和ρB (ρA>ρB),且两圆盘的总质量和厚度均相同。
大物书后习题答案整理(杨晓峰版)-习题13

习题 13-9 解答: 两个圆环形导体垂直放置,a 导体产生的磁场与 b 导体所在线圈的法线相互
垂直,即 b 中的磁通量为零,同理 a 中的磁通量也为零,两个线圈中不会产生互 感电动势,因此没有互感。但是由于自身电流的变化,在每个线圈中产生自感电 流。
习题 13-10 解答: 电流和电压的均方根值等于它们瞬时值的平方在一个周期内的积分的平均
0 2π (x + d )
负号表示棒上动生电动势的方向与 dx 的方向相反,即由 B 到 A 。
习题 13-13 解答: 金属线框平面的法线和磁场方向相互垂直,因此金属框在旋转过程中通过它
的磁通量没有变化,因此回路中的感应电动势为零。a、c 两点间的电势差只要 通过求解 ac 棒中的感应电动势即可得到。
习题 13-5 解答: 感应电场电场线是闭合的,感生电场是非保守力场,且在闭合曲线上 EK 不
一定相等,故(A)、(B)、(C)排除,又由于电势的概念是根据静电场力是保守力而 引入,故答案为(D)。
习题 13-6 解答: 联结 OA 、OB ,构成闭合回路 OBAO(三角型)或 OBCAO(扇型),由于 OA
t2 t1
Iidt
1 R
2 d
1
1 R
(2
1 )
可知,线圈中通过的电荷与时
间无关,又2
1
BS
cos 60
BS
1 2
BS
,则电荷与线圈面积成正比。
习题 13-3 解答:
当 aOc 以速度v 沿 x 轴正向运动时, 选定 aoc 为正方向,根据动生电动势的
定义 i
b (v
a
B) dl
,可得 co
得到金属棒上产生的动生电动势。
人教版八年级物理课后习题及答案

人教版八年级物理课后习题及答案TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-第一章机械运动第一节长度时间及测量1、许多石英电子手表具有听表的功能,通过反复尝试学会使用这个功能。
2、在一条长绳的一端系一个小铁块就做成了一个来回摆。
测出它摆动一个来回所用的时间。
怎样能测得更准确你能做一个周期为1s的摆吗答:测出小铁块摆动若干次所用的时间,然后除以摆动次数,这样测量的结果更准确。
对于后一个问题,可让学生通过不断尝试,认识到小铁块的摆动周期只与绳的长度有关。
3、各组同学之间比一比,怎样才能更精确地测量硬币的直径、硬币的周长、一页纸的厚度、铜丝直径你能想出多少种测量硬币周长的方法答:略4、用宽约2cm的牛皮纸条,自制量程为2m、分度值为1cm的卷尺。
用这个卷尺测量家里某个人的身高。
起床后和临睡前各测一次,你会发现什么?答:由于白天人们多处于站立姿势,自身的重使得骨骼间缝隙变小,因此临睡前的身高要低于起床后的身高。
5、联系电流表、温度计等测量工具的用法,总结一下,使用刻度尺时容易出现哪些错误哪些做法会引起较大的误差答:使用刻度尺常出现的错误有:(1)不注意起始刻度;(2)读数时视线与尺面不垂直测量结果不写单位;(3)刻度尺没有与被测物体重合;第二节运动的描述1.以火车头、车厢的座椅、乘客、路边的树木、房屋为参照物填空:在平稳行驶的列车中,放在行李架上的物品相对于___________是静止的,相对于___________是运动的。
答:火车;树木、房屋等。
2.坐在逆水行驶的船中的乘客,我们说他静止是以下列哪个物体为参照物的?B A.河岸上的树B.船舱 C.迎面驶来的船 D.河水3.看电视转播的百米赛跑时,我们常常感觉运动员跑的很快,但实际上他们始终处于屏幕上。
这是为什么?答:运动员和屏幕之间相对静止,而跑道在不断运动。
4.我国自1984年4月8日第一颗地球同步通信卫星以来,已经陆续发射了多颗这类通信卫星。
大学物理课后习题答案

第九章 静电场 (Electrostatic Field)二、计算题9.7 电荷为+q 和-2q 的两个点电荷分别置于x =1 m 和x =-1 m 处.一试验电荷置于x 轴上何处,它受到的合力等于零?解:设试验电荷0q 置于x 处所受合力为零,根据电力叠加原理可得()()()()022220000(2)(2)ˆˆ0041414141q q q q q q i i x x x x εεεε⋅-⋅-+=⇒+=π-π+π-π+即:2610(3x x x m -+=⇒=±。
因23-=x 点处于q 、-2q 两点电荷之间,该处场强不可能为零.故舍去.得()223+=x m9.8 一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如题图9.4所示.试求圆心O 处的电场强度.解:把所有电荷都当作正电荷处理. 在θ 处取微小电荷d q = λd l = 2Q d θ / π它在O 处产生场强θεεd 24d d 20220R QR q E π=π=按θ 角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202R QE E x π==θθεθd cos 2cos d d 202RQE E y π-=-= 对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =02022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以j R Q j E i E E y x202επ-=+=9.9如图9.5所示,一电荷线密度为λ的无限长带电直导线垂直纸面通过A 点;附近有一电量为Q 的均匀带电球体,其球心位于O 点。
AOP ∆是边长为a 的等边三角形。
已知P 处场强方向垂直于OP ,求:λ和Q 间的关系。
《计算物理》第四章习题参考答案

i 1, j B sin
i , j 1 B sin
i h ( j 1) h sin L L i h j h h j h h B sin sin cos cos sin , L L L L L i h ( j 1) h i , j 1 B sin sin L L i h j h h j h h B sin sin cos cos sin . L L L L L
4. 证:依题,中子扩散方程的形式为 2 f ( x, y ) q( x, y ).
其中, f ( x, y) a 2 , q( x, y ) sin
y sin . L L
x
则依“五点差分”格式(正方形网格划分) ,
ij
引入层向量,
1, j 1 , j , j 1, , N 1; N 1 N 1, j g 0, j 0 b1 1 B , b j , j 2, , N ; 4 b N 1 0 g N, j
=ij( k )
当
4
) (k ) (k ) (k ) (k ) (i(k1, j i , j 1 i 1, j i , j 1 4ij )
(k )
(k )
时,stop ! 其中,移位矢量 ( k ) { i( k ) } {i( k ) i( k 1) }.
] , L
大学物理课后习题答案(上下册全)武汉大学出版社 习题3详解

3-1 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为 [ ] A.2ωmR J J + B. 02)(ωR m J J+ C.02ωmR JD. 0ω 答案:A3-2 如题3-2图所示,圆盘绕O 轴转动。
若同时射来两颗质量相同,速度大小相同,方向相反并在一直线上运动的子弹,子弹射入圆盘后均留在盘内,则子弹射入后圆盘的角速度ω将:[ ]A. 增大.B. 不变.C. 减小.D. 无法判断. 题3-2 图 答案: C3-3 芭蕾舞演员可绕过脚尖的铅直轴旋转,当她伸长两手时的转动惯量为J 0,角速度为ω0,当她突然收臂使转动惯量减小为J 0 / 2时,其角速度应为:[ ] A. 2ω0 . B. ω0 . C. 4ω0 . D. ω 0/2. 答案:A3-4 如题3-4图所示,一个小物体,位于光滑的水平桌面上,与一绳的一端相连结,绳的另一端穿过桌面中心的小孔O . 该物体原以角速度ω 在半径为R 的圆周上绕O 旋转,今将绳从小孔缓慢往下拉.则物体:[ ]A. 动量不变,动能改变; 题3-4图B. 角动量不变,动量不变;C. 角动量改变,动量改变;D. 角动量不变,动能、动量都改变。
答案:D3-5 在XOY 平面内的三个质点,质量分别为m 1 = 1kg, m 2 = 2kg,和 m 3 = 3kg,位置坐标(以米为单位)分别为m 1 (-3,-2)、m 2 (-2,1)和m 3 (1,2),则这三个质点构成的质点组对Z 轴的转动惯量J z = .答案: 38kg ·m 23-6 如题3-6图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O 转动,今有一子弹沿着与水平面成一角度的方向击中木球并嵌于其中,则在此击中过程中,木球、子弹、细棒系统对o 轴的 守恒。
计算物理学课后答案(第一章、第二章)

第1章:绪论【1.2】设准确值为* 3.78694x =,*10y =,取它们的近似值分【1.1】按有效数字的定义,从两个方面说出1.0,1.00,1.000的不同含义【解】1.0,1.00,1.000的有效数字分别是两位,三位和四位;绝对误差限分别是0.05,0.005和0.0005别为123.7869, 3.780x x ==及129.9999, 10.1y y ==,试分析1212,,,x x y y 分别具有几位有效数字。
【解】*10.000040.00005x x -=<,1x 有5位有效数字;*20.006940.005x x -=>,2x 有2位有效数字;*10.000010.0005y y -=<,1y 有4位有效数字*2||0.10.5y y -=<,2y 有2位有效数字【1.3】(1)设p 的近似数有4位有效数字,求其相对误差限。
(2)用22/7和355/113作为 3.14159265p =L 的近似值,问它们各有几位有效数字?【解】(1)其绝对误差限是0.0005,则相对误差限为0.0005/3.1420.01591%r E ==(2)22/7 3.142857...=,有3位有效数字;355/113 3.14159292...=,有7位有效数字。
【1.4】试给出一种算法计算多项式32216180x a x a x a ++的函数值,使得运算次数尽可能少。
【解】24816328163281632012012,,,,x x x x x a x a x a x a x a x a x Þ++=++,总共8次乘法,两次加法【1.5】测量一木条长为542cm ,若其绝对误差不超过0.5cm ,问测量的相对误差是多少?【解】相对误差为0.5/5420.09%Î==【1.6】已知 2.71828e =L ,试问其近似值1232.7, 2.71, 2.718x x x ===各有几位有效数字?并给出他们的相对误差限。
大学物理(下册)课后部分习题答案

2
j
11畅13( a)
11畅13( b)
(2) 设该异线应放在 y = - d 处 ,显然 ,该异线在轴线处产生的磁成应强度应
与原来的半圆柱面产生的磁感应强度相同 ,即
μ0 I 2π d
=
μ0 I π2 R
所以
d=
πR 2
因面 ,另一导线应放在 y = - π2R处 .
12唱7 均匀磁场 B 被限制在半径 R = 0 .10 m 的无限长圆柱空间内 ,方向垂
同理 ,空腔轴线上的磁感应强度
因 R2 = 0 ,B0′2 = 0 ,故
B0′ = B0′1 + B0′2
B0′1
=
μ0 Ia 2π( R21 - R22 )
=
2 × 10 -4 T
11畅13 如图11畅13( a)所示 ,一半径为 R 的无限长半圆柱面导体 ,其上电流与其
轴线上一无限长直导线的电流等值反向 ,电流 I 在半圆柱面上均匀分布 .试求 :
当 r < R1 时 ,有
促 E · d S = E · 4π r2 = 0
S
E =0
当 R1 < r < R2 时 ,有
促S
E · d S = E · 4π r2 =
1 ε0
q
E
=
1 4π ε0
q r2
当 r > R2 时 ,有
促S
E · d S = E · 4π r2 =
1 ε0
ab · h
= 1600π - 4 3 × 10 -2 V 式中 h 为由 O 到ab的垂直距离 ,感应电流沿顺时针方向 .
∮ 此题也可用 Ei = Ev · d l 公式直接积分求解 .
图 12 唱7
高中物理二轮总复习课后习题 计算题专项练(四)

计算题专项练(四)(满分:46分时间:45分钟)1.(7分)趣味运动“充气碰碰球”如图所示。
用完全封闭的PVC薄膜充气膨胀成型,人钻入洞中,进行碰撞游戏。
充气之后碰碰球内气体体积为0.8 m3,压强为1.5×105 Pa。
碰撞时气体最大压缩量是0.08 m3,不考虑压缩时气体的温度变化。
(1)求压缩量最大时,球内气体的压强。
(结果保留3位有效数字)(2)为保障游戏安全,球内气体压强不能超过1.75×105 Pa,那么,在早晨17 ℃环境下充完气的碰碰球,球内气体压强为1.5×105 Pa,若升温引起的球内容积变化可忽略,请通过计算判断是否可以安全地在中午37 ℃的环境下进行碰撞游戏。
2.(9分)如图所示,在竖直平面内建立、电荷量为q的质子,自原点O以初速度v0沿x轴正方向运动。
若在以O为圆心的圆形区域内分布着垂直于xOy平面的匀强磁场,一段时间后质子沿与y轴夹角为30°方向经P点射入第二象限。
若撤去磁场,在第一象限内加一与x轴正方向夹角为150°的匀强电场(电场、磁场均未画出),该质子恰能经过y轴上的P点。
已知点P到O的距离为l,求:(1)磁场的磁感强度B的大小;(2)匀强电场的电场强度E的大小。
3.(14分)如图所示,水平面上固定两条光滑金属轨道,两导轨PQ、PR关于x轴对称放置且与x轴夹角均为θ=37°,在的金属杆CD置于y轴上时,杆两端点CD恰好与导轨和y轴的两交点重合。
整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B=0.5 T。
现给杆的中点施加外力,使杆以速度v0=4 m/s沿x轴正方向匀速运动,运动过程中杆始终与y轴平行。
已知导轨和杆电阻与长度的比值均为λ=0.5 Ω/m,杆与导轨始终接触良好,接触电阻不计,sin 37°=0.6。
(提示:可以用F-x图像下的“面积”代表力F所做的功)求:(1)杆在O位置时,杆上通过的电流大小;(2)杆从O位置运动到P位置过程中,杆两端点CD间的电势差U CD与杆所在处的横坐标x的关系式;(3)杆从O位置运动到P位置,杆产生的焦耳热。
计算物理学(刘金远)第 3 章 函数近似方法(课后习题及答案)

第3章函数近似方法(习题及答案)§3.1插值法【3.1.1】已知sin()x 在030,45,60的值分别为1/2,分别用一次插值和二次插值求0sin(50)近似值。
【3.1.2】误差函数的数据表:x 0.460.470.480.49…f(x)0.48465550.49374520.50274980.5116683…利用二次插值计算:(1)(0.472)f ;(2)()0.5,?f x x ==【3.1.3】【3.1.4】已知列表函数x -101y-15-5-3给出二次插值函数【解】0(0)(1)1()(1)(10)(11)2x x l x x x --==-----;1(1)(1)()(1)(1)(01)(01)x x l x x x +-==--++-2(1)(0)1()(1)(11)(10)2x x l x x x +-==++-2153()(1)5(1)(1)(1)22L x x x x x x x =--+-+--【3.1.5】已知,3)9(,2)4(==f f 用线性插值计算)5(f ,并估计误差。
【解】取插值节点014, 9x x ==,两个插值基函数分别为)9(51)(1010--=--=x x x x x x l )4(51)(0101-=--=x x x x x x l 故有565)4(53)9(52)()()(11001+=-+--=+=x x x y x l y x l x L 2.25655)5()5(1=+=»L f 误差为)(2)95)(45(!2)()5(2x x f f R ¢¢-=--¢¢=【3.1.6】已知(1)2,(1)1,(2)1f f f -===,求()f x 的二次拉格郎日插值多项式【解】22(1)(2)(1)(2)(1)(1)()21(11)(12)(11)(12)(21)(21)1(38)6x x x x x x L x x x --+-+-=++----+-+-=-+【3.1.7】求经过(0,1),(1,2),(2,3)A B C 三点的二次拉格郎日插值多项式【解】22(1)(2)(0)(2)(0)(1)()123(01)(02)(10)(12)(20)(21)1(343)2x x x x x x L x x x ------=++------=-+【3.1.8】编写拉格朗日三点插值程序,绘出)cos(x y =在[p ,0]区间的插值曲线,将[p ,0]区间8等份(9个插值点),由插值函数取25个点绘出插值曲线。
2024-2025学年人教版八年级物理上学期课后习题答案

第一章机械运动第1节 长度和时间的测量练习与应用(P18) 1.身高约是脚长的7倍。
(1)硬币直径的测量方法:2.①把硬币沿直线密排在桌面上,用刻度尺测出排列的长度L ;数出所排硬币的个数n ,用d =dd 计算直径; ②用直尺和三角尺组合测出硬币的直径,如图所示:③在硬币的边缘做一个标记,沿纸上的一条直线转动一周,测出其长度后再除以π,就可以得到硬币的直径; ④以硬币边缘的一个点为圆心,让刻度尺在硬币上转动,测出的最长的距离就是硬币的直径。
(2)硬币周长的测量方法:①在硬币边缘做一个标记,沿纸上的一条直线转动一周,用刻度尺测出其长度即周长; ②用不可伸长的棉线在硬币边缘绕一圈,用刻度尺测出此段棉线的长度即周长; ③用直尺和三角尺测量出硬币的直径,乘π得到周长。
3. 8 760h 86 400s4.测量摆动多个周期的总时间,再除以周期的个数,就得到摆动一个周期所用的时间;调整摆长可以做出周期为1s 的摆,摆长约为0.248m 。
5.刻度尺的零刻度线没有对准被测物体的一端;读数时,视线没有正对刻度线。
改正了错误的测量方法只能避免错误,不能避免误差,也不能减小误差。
因为在测量长度时,受所用仪器和测量方法的限制,测量值和真实值之间总会有差别。
第2节 运动的描述练习与应用(P21)1.火车头、车厢的座椅 树木、房屋2.船3.运动 静止 运动4.以电梯外的建筑物底端为参照物,若距离越来越远.观光电梯上行;若距离越来越近,观光电柳下行。
第3节 运动的快慢练习与应用(P25)6km/h 1.67m/s 2.60 km/h 10 min 3.40m L.(1)284.46km /h (2)列车在由济南西站驶往南京南站路段运行得最快,在由北京南站驶往天津南站路段运行得号慢 1. 6km/h 1.67m/s 2. 60km/h 10min 3. 40m4. (1)284.46km/h (2)列车在由济南西站驶向南京南站路段运行的最快,在由北京南站驶往天津南站路段运行的最慢。
计算物理学(刘金远)第5章:微分方程(课后习题及答案)

5.1 计算物理学第5章:微分方程课后习题答案初值问题【5.1.1】采用euler 方法求初值问题'2/, 01(0)1y y x y x y =-££ìí=î【解】取0.1h =,1(,)(2/)n n n n n n n n y y hf x y y h y x y +=+=+-x0.00.10.20.3y 1.000 1.1000 1.1918 1.2774【5.1.2】用euler 预测-校正公式求初值问题22', (0)1y x y y ì=-í=î【解】取0.1h =,1(,)n n n n y y hf x y +=+111(,)n n n n y y hf x y +++=+1000(,)0.9y y hf x y =+=221011(,)10.1(0.10.9)0.92y y hf x y =+=+´-=【5.1.3】用euler 公式和梯形公式建立的预测-校正公式求初值问题'23, 0(0)1y x y x y =+£ìí=î取0.1h =,(1)求(0.1)y ;(2)编程计算0:0.01:2x =【解】1111(,)1[(,)(,)]2n n n n n n n n n n y y hf x y y y h f x y f x y ++++=+=++10001000110.1(23) 1.30.05[(23)(23)]1.355y y x y y y x y x y =++==++++=【5.1.4】用显式Euler 方法,梯形方法和预估-校正Euler 方法给出求初值问题1,01(0)1d y y x x dx y ì=-++<<ïíï=î的迭代公式(取步长0.1h =)【解】取0.1h =,,0,1,k x kh k ==L ,(1)显式Euler 方法12(,)(1)(1)k k k k k k k y y hf x y y h y kh y h kh h+=+=+-++=-++1911010010k k k y y +=++(2)梯形方法为1121()2(2)(21)2219112110510k k k k k k k h y y f f h y k h h y hy k +++=++-+++=+=++(3)预估-校正Euler 方法为1111(,)[(,)(,)],20,1,,1x k k k k k k k k k k k y y h f x y h y y f x y f x y k n ++++=+ìïï=++íï=-ïîL 221(1/2)(/2)0.9050.00950.1k k k y y h h kh h h hy k +=-++-+=++【5.1.5】考虑下面初值问题2'''(0)1;'(0)2y y y t y y ì=-++í==î使用中点RK2,取步长0.1h =,求出()y h 的近似值【解】00,0.1t h =='y u y æö=ç÷èø,012u æö=ç÷èø,2''(,)'y u f t u y y t æö==ç÷-++èø,1002(,)1k f t u æö==ç÷èø,2001212 1.111(,)(0.05,0.05)(0.05,)21 2.0522 2.05 2.050.891.1 2.050.05k f t h u hk f f æöæöæö=++=+=ç÷ç÷ç÷èøèøèøæöæö==ç÷ç÷-++èøèø102 1.2052.089u u hk æö=+=ç÷èø,1(0.1) 1.205y y ==【5.1.6】考虑下面初值问题2'''2''(0)1;'(0)0,''(0)2y y y t y y y ì=++í===-î使用中点RK2,取步长0.2h =,求出()y h 的近似值【解】00,0.2t h ==取表示符号'''y u y y æöç÷=ç÷ç÷èø,2''(,)''2''y u f t u y y y t æöç÷==ç÷ç÷++èø,0102u æöç÷=ç÷ç÷-èø,010002000'()0(,)''()262()''()y t k f t u y t y t y t t æöæöç÷ç÷===-ç÷ç÷ç÷ç÷++èøèø200121011(,)(0.1,00.12)2226 10.20.2(0.1,0.2) 1.4 1.41.4 3.9721( 1.4)0.1k f t h u hk f f æöæöç÷ç÷=++=+-ç÷ç÷ç÷ç÷-èøèøæö--æöæöç÷ç÷ç÷=-=-=-ç÷ç÷ç÷ç÷ç÷ç÷-´+-èøèøèø1020.960.281.206u u hk æöç÷=+=-ç÷ç÷-èø,(0.2)0.96y =【5.1.7】采用Rk4编程求下列微分方程的初值问题:(1)23'1, (0)0y y x y =++=(2)2'2(1), (1)2y y x y =+--=(3)'', ()0,'()3y y y y p p =-==【5.1.8】求下面微分方程组的数值解2323'2'4(0)1,(0)0x x y t t t y x y t tx y ì=-+--ï=+-+íï==î补充题【5.1.1】对微分方程'(,)y f x y =用Sinpson 求积公式推出数值微分公式【解】{}111111111'(,)4(,)(,)3n n x n n n n n n n n x y dx y y h f x y f x y f x y +-+---++=-=++ò【5.1.2】用标准的4阶龙格库塔方法求初值问题',(0)1y x y y =+ìí=î,取0.1h =,计算出(0.2)y 【解】()1123422/6i i y y h k k k k +=++++1213243(,)(/2,/2)(/2,/2)(,)i i i i i i i i k f x y k f x h y hk k f x h y hk k f x h y hk ==++=++=++'(,)y f x y x y ==+,00(,)(0,1)x y =100200130024003(,)1(/2,/2) 1.1(/2,/2) 1.105(,) 1.2105k f x y k f x h y hk k f x h y hk k f x h y hk ===++==++==++=()10123422/6 1.1103y y h k k k k =++++=,11(,)(0.1,1.1103)x y =111211*********(,) 1.2103(/2,/2) 1.3208(/2,/2) 1.3263(,) 1.4429k f x y k f x h y hk k f x h y hk k f x h y hk ===++==++==++=()2112342(0.2)22/6 1.2428y y y h k k k k y ==++++==然后由22(,)(0.2,1.2428)x y =计算3(0.3)y y =,。
大学物理教程上课后习题答案

物理部分课后习题答案标有红色记号的为老师让看的题27页 1-2 1-4 1-121-2 质点的运动方程为22,(1)x t y t ==-,,x y 都以米为单位,t 以秒为单位,求:(1) 质点的运动轨迹;(2) 从1t s =到2t s =质点的位移的大小; (3) 2t s =时,质点的速度和加速度;解:1由运动方程消去时间t 可得轨迹方程,将t =,有21)y =或 1=2将1t s =和2t s =代入,有11r i =, 241r i j =+213r r r i j =-=-位移的大小 231r =+=3 2x dxv t dt== 2(1)y dy v t dt==-22(1)v ti t j =+-2xx dv a dt==, 2y y dv a dt == 22a i j =+当2t s =时,速度和加速度分别为42/v i j m s =+22a i j =+ m/s 21-4 设质点的运动方程为cos sin ()r R ti R t j SI ωω=+,式中的R 、ω均为常量;求1质点的速度;2速率的变化率;解 1质点的速度为sin cos d rv R ti R t j dtωωωω==-+ 2质点的速率为v R ω==速率的变化率为0dvdt= 1-12 质点沿半径为R 的圆周运动,其运动规律为232()t SI θ=+;求质点在t 时刻的法向加速度n a 的大小和角加速度β的大小;解 由于 4d t dtθω== 质点在t 时刻的法向加速度n a 的大小为2216n a R Rt ω==角加速度β的大小为 24/d rad s dtωβ==77页2-15, 2-30, 2-34,2-15 设作用于质量1m kg =的物体上的力63()F t SI =+,如果物体在这一力作用下,由静止开始沿直线运动,求在0到2.0s 的时间内力F 对物体的冲量;解 由冲量的定义,有2.02.02.02(63)(33)18I Fdt t dt t t N s ==+=+=⎰⎰2-21 飞机着陆后在跑道上滑行,若撤除牵引力后,飞机受到与速度成正比的阻力空气阻力和摩擦力f kv =-k 为常数作用;设撤除牵引力时为0t =,初速度为0v ,求1滑行中速度v 与时间t 的关系;20到t 时间内飞机所滑行的路程;3飞机停止前所滑行的路程;解 1飞机在运动过程中只受到阻力作用,根据牛顿第二定律,有dvf mkv dt ==- 即 dv k dt v m=- 两边积分,速度v 与时间t 的关系为2-31 一质量为m 的人造地球卫星沿一圆形轨道运动,离开地面的高度等于地球半径的2倍即2R ,试以,m R 和引力恒量G 及地球的质量M 表示出:(1) 卫星的动能;(2) 卫星在地球引力场中的引力势能.解 1 人造卫星绕地球做圆周运动,地球引力作为向心力,有22(3)3Mm v G m R R= 卫星的动能为 2126k GMmE mv R ==2卫星的引力势能为3p GMmE R=-00v t v dv k dt v m =-⎰⎰2-37 一木块质量为1M kg =,置于水平面上,一质量为2m g =的子弹以500/m s的速度水平击穿木块,速度减为100/m s ,木块在水平方向滑行了20cm 后停止;求:(1) 木块与水平面之间的摩擦系数; (2) 子弹的动能减少了多少;解 子弹与木块组成的系统沿水平方向动量守恒12mv mv Mu =+对木块用动能定理2102Mgs Mu μ-=-得 1 2212()2m v v Mgsμ-==322(210)(500100)0.16219.80.2-⨯⨯-=⨯⨯⨯ 2 子弹动能减少2212121()2402k k E E m v v J -=-= 114页3-11,3-9,例3-2 如图所示,已知物体A 、B 的质量分别为A m 、B m ,滑轮C 的质量为C m ,半径为R ,不计摩擦力,物体B 由静止下落,求1物体A 、B 的加速度; 2绳的张力;3物体B 下落距离L 后的速度; 分析: 1本题测试的是刚体与质点的综合运动,由于滑轮有质量,在运动时就变成含有刚体的运动了;滑轮在作定轴转动,视为圆盘,转动惯量为例3-2图212J mR =; 2角量与线量的关系:物体A 、B 的加速度就是滑轮边沿的切向加速度,有t a R β=; 3由于滑轮有质量,在作加速转动时滑轮两边绳子拉力12T T ≠; 分析三个物体,列出三个物体的运动方程:物体A 1A T m a = 物体B 2B B m g T m a -= 物体C ''22111()22C C T T R J m R m Ra ββ-=== 解 112B A B Cm g a m m m =++;2112A B A B C m m g T m m m =++, 21()212A C AB Cm m g T m m m +=++;3对B 来说有,2202v v aLv -===例3-4 有一半径为R 的圆形平板平放在水平桌面上,平板与水平桌面的摩擦系数为μ,若平板绕通过其中心且垂直板面的固定轴以角速度ω0开始旋转,它将在旋转几圈后停止 已知圆形平板的转动惯量221mR J =,其中m 为圆形平板的质量 分析: 利用积分求圆形平板受桌面的摩擦力矩,运用转动定律求出平板的角加速度,再用运动学公式求转动的圈数.解:在距圆形平板中心r 处取宽度为dr 的环带面积,环带受桌面的摩擦力矩为r r r RmgM d 2d 2⋅π⋅π=μ总摩擦力矩为mgR M M Rμ32d 0==⎰ 故平板的角加速度为M Jβ=222 可见圆形平板在作匀减速转动,又末角速度0ω=,因此有2022M Jθωβθ==设平板停止前转数为n,则转角2n θπ=,可得22003416J R n M ωωμ==πgπ3-2:如题3-2图所示,两个圆柱形轮子内外半径分别为R 1和R 2,质量分别为M 1和M 2;二者同轴固结在一起组成定滑轮,可绕一水平轴自由转动;今在两轮上各绕以细绳,细绳分别挂上质量为m 1和m 2的两个物体;求在重力作用下,定滑轮的角加速度;解: m 1:1111a m g m T=-m 2:2222a m T g m=-转动定律:βJ T R T R =-1122其中:2222112121R M R M J += 运动学关系:2211R a R a ==β 解得:222221111122)2/()2/()(R m M R m M gR m R m +++-=β3-6 一质量为m 的质点位于11,y x 处,速度为j v i v v y x+=, 质点受到一个沿x 负方向的力f 的作用,求相对于坐标原点的角动量以及作用于质点上的力的力矩.解: 由题知,质点的位矢为j y i x r11+=作用在质点上的力为i f f -=所以,质点对原点的角动量为v m r L⨯=0)()(11j v i v m i y i x y x +⨯+=k mv y mv x x y )(11-=作用在质点上的力的力矩为k f y i f j y i x f r M1110)()(=-⨯+=⨯=3-11 如题3-11图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆于水平位置由静止开始摆下.求:1初始时刻的角加速度; 2杆转过θ角时的角速度. 解: 1由转动定律,有2123()=l mgml β 则 lg23=β 2由机械能守恒定律,有22110232()-=lml ωmg sin θ题3-11图所以有 lg θωsin 3=3-13 一个质量为M 、半径为R 并以角速度ω转动着的飞轮 可看作匀质圆盘,在某一瞬时突然有一片质量为m 的碎片从轮的边缘上飞出,见题3-13图.假定碎片脱离飞轮时的瞬时速度方向正好竖直向上. 1问它能升高多少2求余下部分的角速度、角动量和转动动能.解: 1碎片离盘瞬时的线速度即是它上升的初速度ωR v =0设碎片上升高度h 时的速度为v ,则有 题3-13图gh v v 2202-=令0=v ,可求出上升最大高度为2220212ωR gg v H ==2圆盘的转动惯量212=J MR ,碎片抛出后圆盘的转动惯量2212'=-J MR mR ,碎片脱离前,盘的角动量为J ω,碎片刚脱离后,碎片与破盘之间的内力变为零,但内力不影响系统的总角动量,碎片与破盘的总角动量应守恒,即'=+'0J ωJ ωmv R式中ω'为破盘的角速度.于是R mv mR MR MR 0222)21(21+'-=ωωωω'-=-)21()21(2222mR MR mR MR 得ωω=' 角速度不变圆盘余下部分的角动量为ω)21(22mR MR - 转动动能为222)21(21ωmR MR E k -=258页8-2,8-12,8-178-7 试计算半径为R 、带电量为q 的均匀带电细圆环的轴线过环心垂直于圆环所在平面的直线上任一点P 处的场强P 点到圆环中心的距离取为x .解 在圆环上任取一电荷元dq ,其在P 点产生的场强为 ()2204Rx dqdE +=πε方向沿dq 与P 点的连线.将其分解为平行于轴线的分量和垂直于轴线的分量,由电荷分布的对称性可知,各dq 在P 点产生的垂直于轴线的场强分量相互抵消,而平行于轴线的分量相互加强,所以合场强平行于轴线, 大小为:E =E ∥=()()()23220212222044cos R x qxR x x R x dq dE q +=+⋅+=⎰⎰πεπεθ 方向:q >0时,自环心沿轴线向外;q <0时,指向环心.8-12 两个均匀带电的同心球面半径分别为R 1和R 2R 2>R 1,带电量分别为q 1和q 2,求以下三种情况下距离球心为r 的点的场强:1r <R 1;2R 1<r <R 23r >R 2.并定性地画出场强随r 的变化曲线解 过所求场点作与两带电球面同心的球面为高斯面,则由高斯定理可知: (1) 当r <R 1时,0,04cos 2=∴=⋅==Φ⎰E r E dS E e πθ(2) 当R 1<r <R 2时,2010124,4cos rq E q r E dS E e πεπθ=∴=⋅==Φ⎰(3) 当r >R 2 时,()()2021021244cos rq q E q q r E dS E e πεεπθ+=∴+=⋅==Φ⎰8-13 均匀带电的无限长圆柱面半径为R ,每单位长度的电量即电荷线密度为λ. 求解8-7图E12解8-12图 场强随r 的变化曲线圆柱面内外的场强.解 过所求场点作与无限长带电圆柱面同轴的、长为l 的封闭圆柱面,使所求场点在封闭圆柱面的侧面上.由电荷分布的对称性可知,在电场不为零的地方,场强的方向垂直轴线向外设λ>0,且离轴线的距离相等的各点场强的大小相等. 所以封闭圆柱面两个底面的电通量为零,侧面上各点场强的大小相等,方向与侧面垂直与侧面任一面积元的法线方向平行.设所求场点到圆柱面轴线的距离为r ,当r <R 即所求场点在带电圆柱面内时,因为0,02000cos cos =∴=⋅=++==Φ⎰⎰E rl E dS E dS E e πθ;当r >R 即所求场点在带电圆柱面外时,rE l rl E e 002,2πελελπ=∴=⋅=Φ . 8-15 将q=×10-8C 的点电荷从电场中的A 点移到B 点,外力作功×10-6J .问电势能的增量是多少 A 、B 两点间的电势差是多少哪一点的电势较高若设B 点的电势为零,则A 点的电势是多少解 电势能的增量:J 100.56-⨯==-=∆外A W W W A B ;A 、B 两点间的电势差:V 100.2105.2100.5286⨯-=⨯⨯-=-=-=---q W W q W q W U U B A B A B A <0, ∴ B 点的电势较高;若设B 点的电势为零,则 V 100.22⨯-=A U .8-17 求习题8-12中空间各点的电势.解 已知均匀带电球面内任一点的电势等于球面上的电势Rq 04πε,其中R 是球面的半径;均匀带电球面外任一点的电势等于球面上的电荷全部集中在球心上时的电势.所以,由电势的叠加原理得:(1) 当r <R 1即所求场点在两个球面内时:20210144R q R q U πεπε+=;(2) 当R 1<r <R 2即所求场点在小球面外、大球面内时:2020144R q rq U πεπε+=;当r >R 2即所求场点在两个球面外时:r q q r q r q U 0210201444πεπεπε+=+=当r >R 2即所求场点在两个球面外时:rq q rq rq U 0210201444πεπεπε+=+=285页9-3,9-49-3.如图,在半径为R 的导体球外与球心O 相距为a 的一点A 处放置一点电荷+Q ,在球内有一点B 位于AO 的延长线上,OB = r ,求:1导体上的感应电荷在B 点产生的场强的大小和方向;2B 点的电势.解:1由静电平衡条件和场强叠加原理可知,B 点的电场强度为点电荷q 和球面感应电荷在该处产生的矢量和,且为零,即04130=+'=r rE E p B πε r r a E B30)(41+-=πε 2由电势叠加原理可知,B 点的电势为点电荷q 和球面感应电荷在该处产生的电势的标量和,即rq V V BB 04πε+'=由于球体是一个等势体,球内任一点的电势和球心o 点的电势相等aq V V V B 0004πε+'==因球面上的感应电荷与球心o 的距离均为球的半径R,且感应电荷的总电贺量为零,所以感应电荷在o 点产生的电势为零,且00V V =',因此aq V V B 004πε==所以, B 点的电势 aq V B 04πε=9-4.如图所示,在一半径为R 1 = cm 的金属球A 外面罩有一个同心的金属球壳B.已知球壳B 的内、外半径分别为R 2 = cm,R 3 = cm,A 球带有总电量Q A = ×10-8 C,球壳B 带有总电量Q B = ×10-8 C.求:1球壳B 内、外表面上所带的电量以及球A 和球壳B 的电势;2将球壳B 接地后再断开,再把金属球A 接地,求金属球A 和球壳B 的内、外表面上所带的电量,以及球A 和球壳B 的电势.习题图解:1在导体到达静电平衡后,A Q 分布在导体球A的表面上.由于静电感应,在B 球壳的内表面上感应出负电荷A Q ,外表面上感应出正电荷A Q ,则B 球壳外表面上的总电荷B A Q Q +;由场的分布具有对称性,可用高斯定理求得各区域的场强分布)(4),(02120211R r R r Q E R r E A<<=<=πε)(4),(03204323R r rQ Q E R r R E BA >+=<<=πε E 的方向眼径向外.导体为有限带电体,选无限远处为电势零点;由电势的定义可计算两球的电势B A V V 和. A 球内任一场点的电势A V 为)(4144321020204321321332211R Q Q R Q R Q rd r Q Q r d r Q rd E r d E r d E r d E V BA A A RB A R R A R R R R R R rA ++-=++=⋅+⋅+⋅+⋅=⎰⎰⎰⎰⎰⎰∞∞πεπεπεB 球壳内任一点的电势B V 为30204344333R Q Q dr r Q Q rd E r d E V B A R B A R R rB πεπε+=+=⋅+⋅=⎰⎰⎰∞∞9-5.两块无限大带电平板导体如图排列,试证明:1相向的两面上图中的2和3,其电荷面密度大小相等而符号相反;2背向的两面上图中的1和4,其电荷面密度大小相等且符号相同. 解:因两块导体板靠得很近,可将四个导体表面视为四个无限大带点平面;导体表面上的电荷分布可认为是均匀的,且其间的场强方向垂直导体表面;作如图所示的圆柱形高斯面,因导体在到达静电平衡后内部场强为零,导体外的场强方向与高斯面的侧面平行,由高斯定理可得习题图320320σσεσσ-=∴+=; 再由导体板内的场强为零,可知P 点合场强0)2()2()2(204030201=-++-+εσεσεσεσ 由 32σσ-= 得41σσ-=9-7. 一平行板电容器,充电后极板上的电荷面密度为σ = ×10-5 C . m -2,现将两极板与电源断开,然后再把相对电容率为εr = 的电介质充满两极板之间.求此时电介质中的D 、E 和P . 解:当平行板电容器的两板与电源断开前后,两极板上所带的电荷量没有发生变化,所以自由电荷面密度也没有发生变化,由 1-'=r r εσεσ ∴极化电荷面密度rr )(εεσσ1-='对于平行板电容器σ'=P 0r E εεσ)1(-'=∴1-'=r r D εσε 且E D P ,,的方向均沿径向.9-11.圆柱形电容器由半径为R 1的导线和与它同轴的导体圆筒构成,其间充满相对电容率为εr 的电介质.圆筒内半径为R 2.电容器长为L,沿轴线单位长度上的电荷为± λ,略去边缘效应,试求:1两极的电势差;2电介质中的电场强度、电位移、极化强度; 3电介质表面的极化电荷面密度.解:1 设导线上的电荷均匀地分布在导线的表面上,圆筒上的电荷均匀的分布在圆筒的内表面上,可由高斯定理求得各区域的场强110R ,rE <=习题图10-6ByOlllzx12022R r ,R rE r >>=επελ23,0R r E >= ∴两极的电位差1201202ln 2ln 221R R R R r l d E u r r R R επελεπελ==⋅=⎰2 由第1问知,电介质中的电场强度 rE r επελ02=电位移rr r E D πλεε20== 极化强度 0)1(εε-=r P rr r πελε2)1(-=329页10-9,10-1010-6 一边长为0.15l =m 的立方体如图放置,有一均匀磁场(63 1.5)B i j k =++T 通过立方体所在区域.计算:1通过立方体上阴影面积的磁通量; 2通过立方体六面的总磁通量. 解:1立方体一边的面积2S l =2(63 1.5)(0.15)0.135B S i j k i Wb Φ==++=(2)总通量0B ds Φ=•=⎰⎰10-11 如图所示,已知相距为d 的两平行长直导线载有相同电流,求1两导线所在平面与此两导线等距一点处的磁感应强度; 2通过图中矩形面积的磁通量 ()31r r =解 在两导线所在平面内,两导线之间的任一点P 处,两导线所产生的磁感应强度B 1和B 2方向相同,都垂直纸面向外;故P P P B B B 21+= 设P 点离导线1的距离为r ,则 RIB P πμ21=,()r d I B P -=πμ22代入上式得()r d Ir I B P -+=πμπμ22 (1) 在导线等距的点有 2d r =, dI B πμ2= (2) 取面积元ldr dS =,则通过矩形面积的磁通量为⎰=ΦSm B d S ()ldr r d I r I r r r ⎰+⎥⎦⎤⎢⎣⎡-+=21122πμπμ πμ2Il =㏑121r r r ++πμ2Il ㏑211r r d r d ---πμIl =㏑11r r d -10-10 如图,载流导线弯成a 、b 、c 所示的形状,求三图中P 点的磁感应强度B 的大小和方习题图10-10习题图10-6By Olllzx向.解:a 水平方向的载流导线对P 电磁感应强度的贡献为0;竖直部分对P 点磁感应强度10-6 一边长为0.15l =m 的立方体如图放置,有一均匀磁场(63 1.5)B i j k =++T 通过立方体所在区域.计算:1通过立方体上阴影面积的磁通量; 2通过立方体六面的总磁通量. 解:1立方体一边的面积2S l =2(63 1.5)(0.15)0.135B S i j k i Wb Φ==++=(3)总通量0B ds Φ=•=⎰⎰ 10-11 如图所示,已知相距为d 的两平行长直导线载有相同电流,求1两导线所在平面与此两导线等距一点处的磁感应强度;通过图中矩形面积的磁通量 ()31r r =2解 在两导线所在平面内,两导线之间的任一点P 处,两导线所产生的磁感应强度B 1和B 2方向相同,都垂直纸面向外;故P P P B B B 21+= 设P 点离导线1的距离为r ,则 RIB P πμ21=,()r d I B P -=πμ22代入上式得()rd Ir I B P -+=πμπμ22(3) 在导线等距的点有002100(cos cos )(cos90cos180)44[0(1)]44o o I IB r aI a I a μμθθππμπμπ=-=-=--=2d r =, dI B πμ2= (4) 取面积元ldr dS =,则通过矩形面积的磁通量为⎰=ΦSm B d S ()ldr r d I r I r r r ⎰+⎥⎦⎤⎢⎣⎡-+=21122πμπμ πμ2Il =㏑121r r r ++πμ2Il ㏑211r r d r d ---πμIl =㏑11r r d - 10-10 如图,载流导线弯成a 、b 、c 所示的形状,求三图中P 点的磁感应强度B 的大小和方向.解:a 水平方向的载流导线对P 电磁感应强度的贡献为0;竖直部分对P 点磁感应强度方向垂直纸面向外.bP 点处的磁感应强度为三部分载流导线所产生的磁感应强度的叠加,则00123132*********22(cos cos )422;90;108;2[0(1)]42224I I B B B B B B r r r a I I I IB a r a rμμθθθππθθθπμμμμππππ=++=+=-+====∴=--+=+方向垂直纸面向里.cB 为三边磁感应强度叠加,由对称性习题图10-10002100(cos cos )(cos90cos180)44[0(1)]44o o I IB r aIa I aμμθθππμπμπ=-=-=--=习题图10-1401231210033(cos cos )41393.42IB B B B B rr h IB I h aμθθπμμππ=++==-=∴==方向垂直纸面向里.10-14 一根很长的铜导线,载有电流10 A,在导线内部通过中心线作一平面S ,如图所示.试计算通过导线1m 长的S 平面内的磁通量铜材料本身对磁场分布无影响.解:设距轴线为r 处的磁感应强度为B .则0222200022002000000220076,;22224410101 1.0104R Rs I IB dl I r R r r I I B r I R R I B rRI I l I l B d s r ld r rdr R R Wbμπππμμπμμμπππππ--⋅==∴=⋅=∴=Φ====⨯⨯⨯==⨯⎰⎰⎰⎰⎰即S 平面内的磁通量为61.010Wb -⨯.方向垂直纸面向外.bP 点处的磁感应强度为三部分载流导线所产生的磁感应强度的叠加,则习题图10-1400123132*********22(cos cos )422;90;108;2[0(1)]42224I I B B B B B B r r r a I I I IB a r a rμμθθθππθθθπμμμμππππ=++=+=-+====∴=--+=+方向垂直纸面向里.cB 为三边磁感应强度叠加,由对称性01231210033(cos cos )41393.42IB B B B B rr h IB I h aμθθπμμππ=++==-=∴==方向垂直纸面向里.10-14 一根很长的铜导线,载有电流10 A,在导线内部通过中心线作一平面S ,如图所示.试计算通过导线1m 长的S 平面内的磁通量铜材料本身对磁场分布无影响.解:设距轴线为r 处的磁感应强度为B .则0222200022002000000220076,;22224410101 1.0104R Rs I IB dl I r R r r I I B r I R R I B rRI I l I l B d s r ld r rdr R R Wbμπππμμπμμμπππππ--⋅==∴=⋅=∴=Φ====⨯⨯⨯==⨯⎰⎰⎰⎰⎰即S 平面内的磁通量为61.010Wb -⨯. 367页11-1,11-511-1 一载流I 的无限长直导线,与一N 匝矩形线圈ABCD 共面;已知AB 长为L ,与导线间距为a ;CD 边与导线间距为bb ›a;线圈以 v 的速度离开直导线,求线圈内感应电动势的方向和大小;解 由于I 为稳恒电流,所以它在空间各点产生的磁场为稳恒磁场;当矩形线圈ABCD 运动时,不同时刻通过线圈的磁通量发生变化,故有感应电动势产生;取坐标系如图a 所示;设矩形线圈以速度 v 以图示位置开始运动,则经过时间t 之后,线圈位置如图b 所示;取面积元ldx dS =,距长直导线的距离为x ,按无限长直载流导线的磁感应强度公式知,该面积元处B 的大小为 B =xπμ20I 通过该面积元的磁通量为 ldx xIBdS d πμ20==Φ 于是通过线圈的磁通量为 ()⎰⎰⎰++++==Φ=Φvt b vt a vtb vt a xldxI ldx x I d t πμπμ2200 =πμ20Il ㏑vta vtb ++ 由法拉第电磁感应定律可知,N 匝线圈内的感应电动势为()()()⎥⎦⎤⎢⎣⎡++-+++-=Φ-=202vt a v vt b v vt a vt b vt a lIN dt d N E πμ ()()()()vt a vt b vvt b v vt a lIN +++-+-=πμ20令t = 0,并代入数据,则得线圈刚离开直导线时的感应电动势()ab a b NlIv b a lIvN dtd NE t πμπμ2112000-=⎪⎭⎫ ⎝⎛-=Φ-== 按楞次定律可知,E 感应电动势的方向沿顺时针方向;11-5 在无限长螺线管中,均匀分布着与螺线管轴线平行的磁场B t;设B 以速率dtdB=К变化К为大于零的常量;现在其中放置一直角形导线 abc;若已知螺线管截面半径为R,l ab =,求:1螺线管中的感生电场EV;2bc ab ,两段导线中的感生电动势;解 1由于系统具有轴对称性,如图所示,可求出感生电场;在磁场中取圆心为O ,半径为()R r r <的圆周,根据感生电场与变化磁场之间的关系m V LS d BE dl d S dtt Φ∂=-=-∂⎰⎰可得222V dBE r r r dtπππκ=-=- 有2V rE κ=-()R r < 由楞次定律可以判断感生电场为逆时针方向;2解法一 用法拉第电磁感应定律求解;连接Ob Oa ,和Oc ,在回路OabO 中,穿过回路所围面积的磁通量为1222124l BS Bl R ⎛⎫Φ=-=-- ⎪⎝⎭则11222221112424d l dB l E l R l R dt dt κ⎛⎫⎛⎫Φ=-=--=- ⎪ ⎪⎝⎭⎝⎭而ab oa bo ab E E E E E =++=1 所以12221124ab l E E lk R ⎛⎫==- ⎪⎝⎭方向由a 指向b同理可得 1222124bc l E lk R ⎛⎫=- ⎪⎝⎭方向由b 指向c解法二 也可由感生电场力做功求解;由于1中已求出EV;则122224bab V ak l E E dl l R ⎛⎫=⋅=- ⎪⎝⎭⎰122224cbc V bk l E E dl l R ⎛⎫=⋅=- ⎪⎝⎭⎰11-1.解: 1由电磁感应定律812)1(--=Φ-t dtd i ε2)2(102.3-⨯-=i ε2 2106.1-⨯==RI iε由于磁通量是增加的,所以线圈中产生的感应电动势使R 中产生感应电流的方向是由左向右11-4解:由题意可知金属棒沿杆下滑的速度为重力加速度所引起t BgL L Bgt l d B V )cos sin (cos sin )(θθθθε==⋅⨯=⎰11-5解:由于I 为稳定电流,所以它在空间各点产生的磁场为稳恒磁场.当矩形线圈ABCD 运动时,不同时刻通过线圈的磁通量回发生变化,故有感应电动势产生.取坐标系如图;设矩形线圈以速度V 从图示位置开始运动,经过时间t 之后,线圈位置如图b 所示,取面积元ds=ldx,距长直导线的距离为x,按无限长直载流导体的磁感应强度公式知,该面积元外B的大小为x I B πμ20= 通过该面积元的磁通量为ldx x I Bds d ⋅==Φπμ20 于是通过线圈的磁通量为⎰⎰⎰++++⋅=⋅=Φ=Φvt b vt a vt b vt a xldx x I ldx x I d t πμπμ22)(00 va vtb IL ++=ln 20πμ 由法拉第电磁感应定律可知,N 匝线圈中的感应电动势为])()()([220vt a v vt b v vt a vt b vt a ILN dt d N E ++-+++-=Φ-=πμ -=))(()()(20vt b vt a v vt b v vt a IN +++-+πμ 令t=0,代入数据,得到线圈,刚离开直导线时的感应电动势)11(200ba LIVN dt d N E t -=Φ-==πμ )(100.32.01.02)1.02.0(0.30.52.010104737V --⨯=⨯⨯-⨯⨯⨯⨯⨯⨯=ππ 按楞次定律E 的方向为图b 中的顺时针方向1、 一质点作匀速率圆周运动,其质量为m,线速度为v,半径为R;求它对圆心的角动 量;它相对于圆周上某一点的角动量是否为常量,为什么答:它对圆心的角动量Rmv ,是常量;它相对于圆周上某一点的角动量不是常量;4、彗星绕太阳作椭圆轨道运动,太阳位于椭圆轨道的一个焦点上,问系统的角动量是否 守恒 近日点与远日点的速度哪个大答:在彗星绕太阳轨道运转过程中,只受万有引力作用,万有引力对太阳不产生力矩,系统角动量守恒;近日点 r 小 v 大,远日点 r 大 v 小;这就是为什么彗星运转周期为几十年,而经过太阳时只有很短的几周时间;彗星接近太阳时势能转换成动能,而远离太阳时,动能转换成势能;8.利用角动量守恒定律简要分析花样滑冰、跳水运动过程;答:对这一力学现象可根据角动量守衡定律来解释;例如旋转着的芭蕾舞演员要加快旋转时,总是将双手收回身边,这时演员质量分布靠近转轴,转动惯量变小,转动速度加快,转动动能增加;3-5题图。
计算物理课后部分习题答案2

1.1 Show that the error in the n th-order Lagrange interpolation scheme isbounded bywhere γn = max[| f (n +1)(x )|], for x ∈ [x 0, xn ])()(1n x f 10n x x x x x x ---+=∆ )()!()(γ设γn=max[|f(n+1)|]当x 在区间[x 0,x n ],h 是h i =x i+1-x i 中的最大的一个,Eq (2.9)中的γ可以用γn 代替 要证明()hn x f n14)(+≤∆γn+1须证)1(4)!1()())((110+≤+---+n h n x x x x x x n n(1)首先我们考虑该式子前项,我们假设x 在x k 与x k+1之间 则)!1()())(())(()!1()())((11010+-----=+---+n x x x x x x x x x x n x x x x x x n k k n (2)又因为式子中的4))((21h x x x x k k ≤--+运用“缩放法”可得(2)式[])1(4!)!1(4)!()!1(11+≤+-+≤++n h n n h k n k n n )1(41+=+n h n既得证(1)式成立∴1)1(4)(++≤∆nn hnxfγ2.2Write a program that implements the Lagrange interpolation scheme directly. Test it by evaluating f (0.3) and f (0.5) from the data taken from theerror function with f (0.0) = 0, f (0.4) =0.428 392, f (0.8) = 0.742 101, f (1.2) = 0.910 314, and f (1.6) = 0.970 348. Examine the accuracy of the interpolation by comparing the results obtained from the interpolation with the exact values f (0.3) = 0.328 627 and f (0.5) = 0.520 500public class a {public static void main(String[] args) {double xi[]={0,0.4,0.8,1.2,1.6};double fi[]={0,0.428392,0.742101,0.910314,0.970348};double x1=0.3;double f1=aitken(x1,xi,fi);double x2=0.5;double f2=aitken(x2,xi,fi);System.out.println("interpolated value:"+f1);System.out.println("interpolated value:"+f2);}//Methed to carry out the Aitken recursions.public static double aitken(double x,double xi[],double fi[]){int n =xi.length-1;double ft[]=(double[]) fi.clone();for (int i=0; i<n; ++i) {for(int j=0; j<n-i; ++j) {ft[j]=(x-xi[j])/(xi[i+j+1]-xi[j])*ft[j+1]+(x-xi[i+j+1])/(xi[j]-xi[i+ j+1])*ft[j];}}return ft[0];}}运行结果:interpolated value:0.32934490136718747interpolated value:0.5199387451171875与the exact values f(0.3)=0.328627 and f(0.5)=0.520500对比2.3The Newton interpolation is another popular interpolation scheme thatadopts the polynomialShow that this polynomial is equivalent to that of the Lagrange interpolation and the coefficients c j here are recursivelygiven byWrite a subprogram that creates all c j with given xi and fi/*** 输入各个x和f的值及检验值xi;* 定义系数ci和牛顿插值结果p;* 引入函数aitken1和aitken2;* 输出所求系数ci在给出x和f值下的各个数值;* 根据所求牛顿插值与拉格朗日插值比较并输出比较结果;* *定义函数aitken1* *引入定义ci,t,T,y;* *for循环求出各个系数ci的值;* *返回ci值;* *定义函数aitken2* *引入定义p,g;* *for循环求出牛顿插值结果P;* *返回p[j]值;*/public class sun3 {public static void main (String argv[]){double x[]={0,0.5,1.0,1.5,2.0};//输入x的各个值;double f[]={1.000000,0.938470,0.765198,0.511828,0.223891};//输入f的各个值;double xi=0.9;//输入所需求的x值;double[] h = new double[5];double[] ci = aitken1 (x,f);double pi = aitken2 (xi,x,ci);double fi=0.807473;for(int i=0;i<5;i++)System.out.println("All c with given x and f:c"+i+"="+ci[i]);//输出ci 的各个值;System.out.println("Lagrange interpolation:"+fi);//输出fi的值;System.out.println("Newton interpolation:"+pi);//输出p近似值;System.out.println("We can see that the Lagrange interpolation"+fi +" is equivalent to the Newton interpolation"+pi);}//Method to carry out the aitken1 recursions.--引入 aitken1 函数;public static double[] aitken1(double x[],double f[]){int n=x.length-1;int i,j;double[] h = new double[n+1];double[] t = new double[n+1];double[] T = new double[n+1];double[] y = new double[n+1];//引入 h t T ;for( i=0;i<n+1;i++){for( j=1;j<i+1;j++){h[0]=f[0];t[0]=1;T[0]=0;y[0]=1;T[j]=T[j-1]-t[j-1]*h[j-1];t[j]=t[j-1]*(x[i]-x[j-1]);y[j]=y[j-1]*(x[i]-x[j-1]);}h[i]=(f[i]+T[i])/y[i];}//求 h 的各个值;return h;//返回各个 h 的值;}//Method to carry out the ba recursions.--引入aitken2 函数;public static double aitken2 (double xi,double x[],double ci[]){ int n=x.length-1;double[] p = new double[n+1];double[] g = new double[n+1];double[] v = new double[n+1];int i,j;p[0]=ci[0];v[0]=0;for( j=1;j<n+1;j++){for( i=1;i<j+1;i++){g[0]=1;g[i]=g[i-1]*(xi-x[i-1]);}v[j]=ci[i-1]*g[i-1];p[j]=p[j-1]+v[j];}return p[4];}}输出结果:All c with given x and f:c0=1.0All c with given x and f:c1=-0.12305999999999995All c with given x and f:c2=-0.22348400000000002All c with given x and f:c3=0.04219199999999986All c with given x and f:c4=0.009258000000000247Lagrange interpolation:0.807473Newton interpolation:0.8074728208000002We can see that the Lagrange interpolation0.807473 is equivalent to the Newton interpolation0.80747282080000022.4Show that the coefficients in the Newton interpolation, defined in Exercise 2.3, can be cast into divided differences recursively aswhere ai = fi are the discrete data and a0...i = ci are the coefficients inthe Newton interpolation. Write a subprogram that creates ci in this way.Apply this subprogram to create another subprogram that evaluates theinterpolated value from the nested expression of the polynomialUse the values of the Bessel function in Section 2.1 to test the program/*第四题 pn=c0+c1*(x-x0)+c2*(x-x0)*(x-x1)+.........public class Newton4 {public static void main(String[] args) {double pn;pn=0;double xi[]={0,0.5,1,1.5,2};double fi[]={1,0.938470,0.765198,0.511828,0.223891};double x=0.9;int n=xi.length-1;double dx=1;double ft[]={1,0.938470,0.765198,0.511828,0.223891};System.out.println("value of c0: "+1.0);for(int i=0;i<n;i++){for(int j=0;j<n-i;j++){ft[j]=(ft[j+1]-fi[0])/(xi[j+i+1]-xi[i]);}fi=ft;System.out.println("value of ci :"+fi[0]);for(int k=0;k<=i;k++){dx *= (x-xi[k]);}pn+=(fi[0]*dx);}pn=pn+1;System.out.println("value of pn: "+pn);}}输出结果如下:value of c0: 1.0value of ci :-0.12305999999999995value of ci :-0.22348400000000002value of ci :0.24304000000000003value of ci :-1.1915873333333336value of pn: 0.8143025768125697结果和书上的 Aitken 数值相近。
大学物理学第三版课后习题答案修订版

大学物理学第三版课后习题答案Document number:PBGCG-0857-BTDO-0089-PTT19981-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得tss t l ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的,∴ tsv v t l v d d ,d d 0-==-=船绳 即 θcos d d d d 00v v s l t l s l t s v ==-=-=船或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m ,v =0,求该质点在t =10s 时的速度和位置.解:∵ t tva 34d d +==分离变量,得 t t v d )34(d +=积分,得 12234c t t v ++= 由题知,0=t ,00=v ,∴01=c故 2234t t v +=又因为 2234d d t t t x v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++= 由题知 0=t ,50=x ,∴52=c故 521232++=t t x所以s 10=t 时1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R . (提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示. 题1-10图 (1)在最高点,又∵ 1211ρv a n =∴ m1010)60cos 20(22111=︒⨯==n a v ρ (2)在落地点,2002==v v 1s m -⋅,而 o 60cos 2⨯=g a n∴ m 8060cos 10)20(22222=︒⨯==n a v ρ1-13 一船以速率1v =30km ·h -1沿直线向东行驶,另一小艇在其前方以速率2v =40km ·h -1 沿直线向北行驶,问在船上看小艇的速度为何在艇上看船的速度又为何解:(1)大船看小艇,则有1221v v v-=,依题意作速度矢量图如题1-13图(a)题1-13图由图可知 1222121h km 50-⋅=+=v v v方向北偏西 ︒===87.3643arctan arctan21v v θ (2)小船看大船,则有2112v v v-=,依题意作出速度矢量图如题1-13图(b),同上法,得2-2 一个质量为P 的质点,在光滑的固定斜面(倾角为α)上以初速度0v 运动,0v 的方向与斜面底边的水平线AB 平行,如图所示,求这质点的运动轨道.解: 物体置于斜面上受到重力mg ,斜面支持力N .建立坐标:取0v方向为X 轴,平行斜面与X 轴垂直方向为Y 轴.如图2-2.题2-2图X 方向: 0=x F t v x 0= ①Y 方向: y y ma mg F ==αsin ②0=t 时 0=y 0=y v由①、②式消去t ,得2-4 质点在流体中作直线运动,受与速度成正比的阻力kv (k 为常数)作用,t =0时质点的速度为0v ,证明(1) t 时刻的速度为v =t mke v )(0-;(2) 由0到t 的时间内经过的距离为x =(k mv 0)[1-t m ke )(-];(3)停止运动前经过的距离为)(0kmv ;(4)证明当k m t =时速度减至0v 的e1,式中m 为质点的质量.答: (1)∵ tvm kv a d d =-=分离变量,得即 ⎰⎰-=vv t m t k v v00d d ∴ tm kev v -=0(2) ⎰⎰---===tttm k m ke kmv t ev t v x 000)1(d d (3)质点停止运动时速度为零,即t →∞,故有 ⎰∞-=='00d kmv t ev x tm k (4)当t=km时,其速度为 即速度减至0v 的e1.2-10 一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量.解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量将bat =代入,得 (3)由动量定理可求得子弹的质量2-13 以铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉进入木板内的深度成正比,在铁锤击第一次时,能将小钉击入木板内1 cm ,问击第二次时能击入多深,假定铁锤两次打击铁钉时的速度相同.解: 以木板上界面为坐标原点,向内为y 坐标正向,如题2-13图,则铁钉所受阻力为题2-13图第一锤外力的功为1A⎰⎰⎰==-='=ssky ky y f y f A 1012d d d ①式中f '是铁锤作用于钉上的力,f 是木板作用于钉上的力,在0d →t 时,f 'f -=.设第二锤外力的功为2A ,则同理,有⎰-==21222221d y kky y ky A ② 由题意,有2)21(212kmv A A =∆== ③即 222122k k ky =-所以, 22=y 于是钉子第二次能进入的深度为2-15 一根劲度系数为1k 的轻弹簧A 的下端,挂一根劲度系数为2k 的轻弹簧B ,B 的下端一重物C ,C 的质量为M ,如题2-15图.求这一系统静止时两弹簧的伸长量之比和弹性势 能之比.解: 弹簧B A 、及重物C 受力如题2-15图所示平衡时,有题2-15图又 11x k F A ∆= 所以静止时两弹簧伸长量之比为 弹性势能之比为2-17 由水平桌面、光滑铅直杆、不可伸长的轻绳、轻弹簧、理想滑轮以及质量为1m 和2m 的滑块组成如题2-17图所示装置,弹簧的劲度系数为k ,自然长度等于水平距离BC ,2m 与桌面间的摩擦系数为μ,最初1m 静止于A 点,AB =BC =h ,绳已拉直,现令滑块落下1m ,求它下落到B 处时的速率.解: 取B 点为重力势能零点,弹簧原长为弹性势能零点,则由功能原理,有式中l ∆为弹簧在A 点时比原长的伸长量,则联立上述两式,得题2-17图2-19 质量为M 的大木块具有半径为R 的四分之一弧形槽,如题2-19图所示.质量为m 的小立方体从曲面的顶端滑下,大木块放在光滑水平面上,二者都作无摩擦的运动,而且都从静止开始,求小木块脱离大木块时的速度.解: m 从M 上下滑的过程中,机械能守恒,以m ,M ,地球为系统,以最低点为重力势能零点,则有又下滑过程,动量守恒,以m ,M 为系统则在m 脱离M 瞬间,水平方向有联立,以上两式,得习题八8-1 电量都是q 的三个点电荷,分别放在正三角形的三个顶点.试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)(2)这种平衡与三角形的边长有无关系解: 如题8-1图示(1) 以A 处点电荷为研究对象,由力平衡知:q '为负电荷 解得 q q 33-=' (2)与三角形边长无关.题8-1图 题8-2图8-2 两小球的质量都是m ,都用长为l 的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如题8-2图所示.设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量.解: 如题8-2图示 解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204rq E πε=,当被考察的场点距源点电荷很近(r →0)时,则场强→∞,这是没有物理意义的,对此应如何理解解: 020π4r r q Eε=仅对点电荷成立,当0→r 时,带电体不能再视为点电荷,再用上式求场强是错误的,实际带电体有一定形状大小,考虑电荷在带电体上的分布求出的场强不会是无限大. 8-4 在真空中有A ,B 两平行板,相对距离为d ,板面积为S ,其带电量分别为+q 和-q .则这两板之间有相互作用力f ,有人说f=2024d q πε,又有人说,因为f =qE ,SqE 0ε=,所以f =Sq 02ε.试问这两种说法对吗为什么 f 到底应等于多少解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不对的,第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的.正确解答应为一个板的电场为Sq E 02ε=,另一板受它的作用力Sq S qq f 02022εε==,这是两板间相互作用的电场力.8-5 一电偶极子的电矩为l q p=,场点到偶极子中心O 点的距离为r ,矢量r 与l的夹角为θ,(见题8-5图),且l r >>.试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示,将p 分解为与r 平行的分量θsin p 和垂直于r的分量θsin p .∵ l r >>∴ 场点P 在r 方向场强分量 垂直于r 方向,即θ方向场强分量题8-5图 题8-6图 8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=-9C ·m-1的正电荷.试求:(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强;(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强.解: 如题8-6图所示(1)在带电直线上取线元x d ,其上电量q d 在P 点产生场强为 用15=l cm ,9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理 2220d d π41d +=x x E Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ,即Q E只有y 分量,∵ 22222220dd d d π41d ++=x x x E Qyλε以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅,方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环,电荷线密度为λ,求环心处O 点的场强.解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==,它在O 点产生场强大小为20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==积分RR E x 000π2d sin π4ελϕϕελπ==⎰ ∴ RE E x0π2ελ==,方向沿x 轴正向. 8-8 均匀带电的细线弯成正方形,边长为l ,总电量为q .(1)求这正方形轴线上离中心为r 处的场强E ;(2)证明:在l r >>处,它相当于点电荷q 产生的场强E . 解: 如8-8图示,正方形一条边上电荷4q在P 点产生物强P E d 方向如图,大小为∵ 22cos 221l r l +=θ∴ 24π4d 22220l r l l r E P++=ελP Ed 在垂直于平面上的分量βcos d d P E E =⊥∴ 424π4d 2222220l r rl r l r lE +++=⊥ελ题8-8图由于对称性,P 点场强沿OP 方向,大小为 ∵ lq 4=λ∴ 2)4(π422220l r l r qrE P++=ε 方向沿OP8-9 (1)点电荷q 位于一边长为a 的立方体中心,试求在该点电荷电场中穿过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的电通量是多少*(3)如题8-9(3)图所示,在点电荷q 的电场中取半径为R 的圆平面.q 在该平面轴线上的A 点处,求:通过圆平面的电通量.(xR arctan =α)解: (1)由高斯定理0d εqS E s ⎰=⋅立方体六个面,当q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量06εq e=Φ.(2)电荷在顶点时,将立方体延伸为边长a 2的立方体,使q 处于边长a 2的立方体中心,则边长a 2的正方形上电通量06εq e=Φ对于边长a 的正方形,如果它不包含q 所在的顶点,则024εq e =Φ,如果它包含q 所在顶点则0=Φe.如题8-9(a)图所示.题8-9(3)图题8-9(a)图 题8-9(b)图 题8-9(c)图 (3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量,球冠面积* ∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算:见题8-9(c)图8-10 均匀带电球壳内半径6cm ,外半径10cm ,电荷体密度为2×510-C ·m-3求距球心5cm ,8cm ,12cm 各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s,02π4ε∑=q r E当5=r cm 时,0=∑q ,0=E8=r cm 时,∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅, 方向沿半径向外. 12=r cm时,3π4∑=ρq -3(外r )内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R >1R )的两无限长同轴圆柱面,单位长度上分别带有电量λ和-λ,试求:(1)r <1R ;(2) 1R <r <2R ;(3) r >2R 处各点的场强.解: 高斯定理0d ε∑⎰=⋅qS E s取同轴圆柱形高斯面,侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰对(1) 1R r < 0,0==∑E q(2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为1σ和2σ,试求空间各处场强.解: 如题8-12图示,两带电平面均匀带电,电荷面密度分别为1σ与2σ,两面间, n E)(21210σσε-=1σ面外, n E)(21210σσε+-= 2σ面外, n E)(21210σσε+= n:垂直于两平面由1σ面指为2σ面.8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r <R 的小球体,如题8-13图所示.试求:两球心O 与O '点的场强,并证明小球空腔内的电场是均匀的.解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合,见题8-13图(a).(1) ρ+球在O 点产生电场010=E,ρ-球在O 点产生电场'dπ4π3430320OO r E ερ= ∴ O 点电场'd 33030OO r E ερ= ;(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ρ-球在O '产生电场002='E∴ O ' 点电场 003ερ='E'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为r',相对O 点位矢为r (如题8-13(b)图)则 03ερrE PO =,3ερr E O P '-=' ,∴ 0003'3)(3ερερερd OO r r E E E O P PO P=='-=+='∴腔内场强是均匀的. 8-14 一电偶极子由q =×10-6C的两个异号点电荷组成,两电荷距离d=0.2cm ,把这电偶极子放在×105N ·C -1的外电场中,求外电场作用于电偶极子上的最大力矩.解: ∵ 电偶极子p在外场E中受力矩∴ qlE pE M ==max 代入数字8-15 两点电荷1q =×10-8C ,2q =×10-8C ,相距1r =42cm ,要把它们之间的距离变为2r =25cm ,需作多少功解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εε )11(21r r - 外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示,在A ,B 两点处放有电量分别为+q ,-q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点,求移动过程中电场力作的功.解: 如题8-16图示∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强和电势.解: (1)由于电荷均匀分布与对称性,AB 和CD 段电荷在O 点产生的场强互相抵消,取θd d R l =则θλd d R q =产生O 点Ed 如图,由于对称性,O 点场强沿y 轴负方向题8-17图R 0π4ελ=[)2sin(π-2sin π-] (2) AB 电荷在O 点产生电势,以0=∞U同理CD 产生 2ln π402ελ=U半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动.求带电直线上的线电荷密度.(电子质量0m =×10-31kg ,电子电量e =×10-19C)解: 设均匀带电直线电荷密度为λ,在电子轨道处场强 电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1,超过这个数值时空气要发生火花放电.今有一高压平行板电容器,极板间距离为d =0.5cm ,求此电容器可承受的最高电压.解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E与电势U 的关系UE -∇= ,求下列电场的场强:(1)点电荷q 的电场;(2)总电量为q ,半径为R 的均匀带电圆环轴上一点;*(3)偶极子ql p =的l r >>处(见题8-20图).解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ε=∂∂-= 0r为r 方向单位矢量. (2)总电量q ,半径为R 的均匀带电圆环轴上一点电势 ∴ ()i x R qx ix U E2/3220π4+=∂∂-=ε(3)偶极子l q p=在l r >>处的一点电势∴ 30π2cos r p r U E rεθ=∂∂-=8-21 证明:对于两个无限大的平行平面带电导体板(题8-21图)来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同.证: 如题8-21图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时,有∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反;(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等,符号相同. 8-22 三个平行金属板A ,B 和C 的面积都是200cm 2,A 和B 相距4.0mm ,A 与C 相距2.0 mm .B ,C 都接地,如题8-22图所示.如果使A 板带正电×10-7C ,略去边缘效应,问B 板和C 板上的感应电荷各是多少以地的电势为零,则A 板的电势是多少解: 如题8-22图示,令A 板左侧面电荷面密度为1σ,右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =,即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC ACAC A E U εσV8-23 两个半径分别为1R 和2R (1R <2R )的同心薄金属球壳,现给内球壳带电+q ,试计算:(1)外球壳上的电荷分布及电势大小;(2)先把外球壳接地,然后断开接地线重新绝缘,此时外球壳的电荷分布及电势;*(3)再使内球壳接地,此时内球壳上的电荷以及外球壳上的电势的改变量.解: (1)内球带电q +;球壳内表面带电则为q -,外表面带电为q +,且均匀分布,其电势题8-23图(2)外壳接地时,外表面电荷q +入地,外表面不带电,内表面电荷仍为q -.所以球壳电势由内球q +与内表面q -产生: (3)设此时内球壳带电量为q ';则外壳内表面带电量为q '-,外壳外表面带电量为+-q q ' (电荷守恒),此时内球壳电势为零,且 得 q R R q 21=' 外球壳上电势8-24 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量.解: 如题8-24图所示,设金属球感应电荷为q ',则球接地时电势0=O U8-24图由电势叠加原理有:得 -='q 3q8-25 有三个大小相同的金属小球,小球1,2带有等量同号电荷,相距甚远,其间的库仑力为0F .试求:(1)用带绝缘柄的不带电小球3先后分别接触1,2后移去,小球1,2之间的库仑力;(2)小球3依次交替接触小球1,2很多次后移去,小球1,2之间的库仑力.解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后,小球3和小球1均带电 2q q =', 小球3再与小球2接触后,小球2与小球3均带电 q q 43=''∴ 此时小球1与小球2间相互作用力 00220183π483π4"'2F r qr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后,每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r qq F ==ε*8-26 如题8-26图所示,一平行板电容器两极板面积都是S ,相距为d ,分别维持电势A U =U ,B U =0不变.现把一块带有电量q 的导体薄片平行地放在两极板正中间,片的面积也是S ,片的厚度略去不计.求导体薄片的电势.解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ,2σ,3σ,4σ,5σ,6σ如图所示.由静电平衡条件,电荷守恒定律及维持U U AB =可得以下6个方程题8-26图解得 Sq 261==σσ 所以CB 间电场 S qd U E 00422εεσ+==注意:因为C 片带电,所以2U U C≠,若C 片不带电,显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳,介质相对介电常数为r ε,金属球带电Q .试求: (1)电介质内、外的场强; (2)电介质层内、外的电势; (3)金属球的电势.解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强 303π4,π4r rQ E r r Q D r εε ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D ε ==外(2)介质外)(2R r >电势 rQ E U 0r π4r d ε=⋅=⎰∞外介质内)(21R r R <<电势(3)金属球的电势 r d r d 221 ⋅+⋅=⎰⎰∞R R R E E U 外内r d r d ⋅+⋅=⎰⎰∞∞rrE E U 外内8-28 如题8-28图所示,在平行板电容器的一半容积内充入相对介电常数为r ε的电介质.试求:在有电介质部分和无电介质部分极板上自由电荷面密度的比值.解: 如题8-28图所示,充满电介质部分场强为2E,真空部分场强为1E,自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D得 11σ=D ,22σ=D而 101E D ε=,202E D r εε= ∴r D D εσσ==1212 题8-28图 题8-29图8-29 两个同轴的圆柱面,长度均为l ,半径分别为1R 和2R (2R >1R ),且l >>2R -1R ,两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时,求:(1)在半径r 处(1R <r <2R =,厚度为dr ,长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量; (2)电介质中的总电场能量; (3)圆柱形电容器的电容. 解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时,Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82lr Q D w εε==薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容:∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ,A 和B 原来都不带电.现在A 的中心放一点电荷1q ,在B 的中心放一点电荷2q ,如题8-30图所示.试求:(1) 1q 对2q 作用的库仑力,2q 有无加速度;(2)去掉金属壳B ,求1q 作用在2q 上的库仑力,此时2q 有无加速度.解: (1)1q 作用在2q 的库仑力仍满足库仑定律,即 但2q 处于金属球壳中心,它受合力..为零,没有加速度. (2)去掉金属壳B ,1q 作用在2q 上的库仑力仍是2210π41r q q F ε=,但此时2q 受合力不为零,有加速度.题8-30图 题8-31图8-31 如题8-31图所示,1C =0.25μF ,2C =0.15μF ,3C =0.20μF .1C 上电压为50V .求:AB U .解: 电容1C 上电量电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”,把它们串联起来后等值电容是多少如果两端加上1000 V 的电压,是否会击穿解: (1) 1C 与2C 串联后电容 (2)串联后电压比231221==C C U U ,而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿,然后2C 也击穿.8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源,再将每一电容器的正极板与另一电容器的负极板相联.试求: (1)每个电容器的最终电荷; (2)电场能量的损失.解: 如题8-33图所示,设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U C q q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失8-34 半径为1R =2.0cm 的导体球,外套有一同心的导体球壳,壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ,当内球带电荷Q =×10-8C时,求:(1)整个电场储存的能量;(2)如果将导体壳接地,计算储存的能量; (3)此电容器的电容值.解: 如图,内球带电Q ,外球壳内表面带电Q -,外表面带电Q题8-34图(1)在1R r <和32R r R <<区域在21R r R <<时 301π4r r Q E ε=3R r >时 302π4r r Q E ε=∴在21R r R <<区域 在3R r >区域∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε(2)导体壳接地时,只有21R r R <<时30π4r r Q E ε=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε习题九9-1 在同一磁感应线上,各点B的数值是否都相等为何不把作用于运动电荷的磁力方向定义为磁感应强度B的方向解: 在同一磁感应线上,各点B 的数值一般不相等.因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B的方向有关,而且与电荷速度方向有关,即磁力方向并不是唯一由磁场决定的,所以不把磁力方向定义为B的方向.9-2 (1)在没有电流的空间区域里,如果磁感应线是平行直线,磁感应强度B的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)(2)若存在电流,上述结论是否还对解: (1)不可能变化,即磁场一定是均匀的.如图作闭合回路abcd 可证明21B B=∴ 21B B=(2)若存在电流,上述结论不对.如无限大均匀带电平面两侧之磁力线是平行直线,但B方向相反,即21B B ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场答: 不能,因为有限长载流直导线周围磁场虽然有轴对称性,但不是稳恒电流,安培环路定理并不适用.9-4 在载流长螺线管的情况下,我们导出其内部nI B 0μ=,外面B =0,所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L ·d l =0但从安培环路定理来看,环路L 中有电流I 穿过,环路积分应为⎰外B L·d l =I 0μ这是为什么解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提,即每匝电流均垂直于螺线管轴线.这时图中环路L 上就一定没有电流通过,即也是⎰∑==⋅LI l B 0d 0μ 外,与⎰⎰=⋅=⋅Ll l B 0d 0d外是不矛盾的.但这是导线横截面积为零,螺距为零的理想模型.实际上以上假设并不真实存在,所以使得穿过L 的电流为I ,因此实际螺线管若是无限长时,只是外B的轴向分量为零,而垂直于轴的圆周方向分量rIB πμ20=⊥,r 为管外一点到螺线管轴的距离. 题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转,能否肯定这个区域中没有磁场如果它发生偏转能否肯定那个区域中存在着磁场解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存在互相垂直的电场和磁场,电子受的电场力与磁场力抵消所致.如果它发生偏转也不能肯定那个区域存在着磁场,因为仅有电场也可以使电子偏转. 9-6 已知磁感应强度0.2=B Wb ·m-2的均匀磁场,方向沿x 轴正方向,如题9-6图所示.试求:(1)通过图中abcd 面的磁通量;(2)通过图中befc 面的磁通量;(3)通过图中aefd 面的磁通量.解: 如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是 (2)通过befc 面积2S 的磁通量 (3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ΦWb (或曰24.0-Wb )题9-7图9-7 如题9-7图所示,AB 、CD 为长直导线,C B为圆心在O 点的一段圆弧形导线,其半径为R .若通以电流I ,求O 点的磁感应强度.解:如题9-7图所示,O 点磁场由AB 、C B、CD 三部分电流产生.其中AB 产生 01=BCD产生RIB 1202μ=,方向垂直向里CD 段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ,方向⊥向里. 9-8 在真空中,有两根互相平行的无限长直导线1L 和2L ,相距0.1m ,通有方向相反的电流,1I =20A,2I =10A ,如题9-8图所示.A ,B 两点与导线在同一平面内.这两点与导线2L 的距离均为5.0cm .试求A ,B 两点处的磁感应强度,以及磁感应强度为零的点的位置.题9-8图解:如题9-8图所示,A B方向垂直纸面向里(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示,两根导线沿半径方向引向铁环上的A ,B 两点,并在很远处与电源相连.已知圆环的粗细均匀,求环中心O 的磁感应强度.解: 如题9-9图所示,圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生,但∞A 和∞B 在O 点产生的磁场为零。
大学物理课后习题答案第五章

第五章机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示. [解答](1)与标准波动方程比较得:2π/λ= 0.6, 因此波长为:λ = 10.47(m);圆频率为:ω = 10π, 频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv = 52.36(m·s -1).且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为(m).试求:(1)简谐波的波动方程;(2)x= -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:; 即= 0.03cos[4π(t – 5x ) + π/2]. (2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2]= 0.03cos(4πt - π/2).5.3已知平面波波源的振动表达式为(m).求距波源5m 处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为:, 位相差为 Δφ = 5π/4(rad).5.4有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少? [解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m .由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π. 当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2. 原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.5.5一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求: (1)P 点的振动表达式;2cos()xy A t πωλ=-0.03cos(4)2A y t ππ=-cos[()]Ax x y A t uωϕ-=-+0.050.03cos[4()]0.22x y t ππ-=--20 6.010sin2y t π-=⨯26.010sin()2xy t u π-=⨯-50.06sin()24t ππ=-0.03cos[50()]2x y t u ππ=-+(2)波动方程; (3)画出O 点的振动曲线.[解答](1)设P 点的振动方程为y P = A cos(ωt + φ), 其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m),所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程;(2)画出x = λ/2处质点的振动曲线;(3)图中波线上a 和b 两点的位相差φa – φb 为多少?[解答](1)设此波的波动方程为: ,当t = T /4时的波形方程为:. 在x = 0处y = 0,因此得sin φ = 0,解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0. 因此波动方程为:. (2)在x = λ/2处质点的振动方程为:, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为; x b = λ处的质点的振动方程为.波线上a 和b 两点的位相差φa – φb = -3π/2.0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+cos[2()]t xy A T πϕλ=++cos(2)2xy A ππϕλ=++sin(2)xA πϕλ=-+cos 2()t x y A T πλ=+cos(2)cos 2t t y A A T Tπππ=+=-cos(2)2a t y A T ππ=+cos(22)b ty A Tππ=+图5.55.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点?(2)画出t = 4.2s 时的波形曲线.[解答]波的波动方程可化为:y = A cos2π(2t – x ),与标准方程比较,可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1. (1)当t = 4.2s 时的波形方程为 y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…), 各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示. (1)写出时x = 0处质点的振动方程;(2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1).(1)设x = 0处的质点的振动方程为y = A cos(ωt + φ), 其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3).(2)波的表达式为:.(3)t = 1s 时刻的波形方程为,波形曲线如图所示.5.9在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.cos[2()]t x y A T πϕλ=-+cos[2()]t xy A T πϕλ=-+cos[()]23t x ππ=-+5cos()26y x ππ=-图5.8[解答]设波动方程为:, 那么A 和B 两点的振动方程分别为:, . 两点之间的位相差为:,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1). 5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程;(2)如以距A 点5m 处的B 点为坐标原点,写出波动方程; (3)写出传播方向上B ,C ,D 点的振动方程. [解答](1)以A 点为坐标原点,波动方程为 .(2)以B 点为坐标原点,波动方程为. (3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为, ,.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量. [解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1), 波的平均能量密度为:= 158(J·m -3), 平均能流密度为:= 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5.12一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强?此时声强相当于多少分贝?已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1), 声波的平均能量密度为:= 6.37×10-6(J·m -3), cos[2()]t xy A T πϕλ=-+cos[2()]AA x ty A T πϕλ=-+cos[2()]BB x ty A Tπϕλ=-+2(2)6BAx x πππλλ---=-3cos 4()3cos(4)5x x y t t u πππ=+=+3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-3cos 4()3cos(4)BB x y t t u πππ=+=-33cos 4()3cos(4)5C C x y t t u πππ=+=-93cos 4()3cos(4)5D D x y t t u πππ=+=+2212w A ρω=I wu =2212w A ρω=图5.10平均能流密度为:= 2.16×10-3(W·m -2), 标准声强为:I 0 = 1×10-12(W·m -2), 此声强的分贝数为:= 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为, 其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 660(Hz). 火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 550(Hz). (2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 680(Hz). 当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 533(Hz). [注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m); 在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m); 在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).(2)反射面接收到的频率为 = 1421(Hz).将反射面作为波源,其频率为ν1,反射声音的频率为= 1768(Hz).I wu =010lgIL I =BB S Su u u u νν-=-33060033030B S S u u u νν==--33060033030B S S u u u νν==-+3301060033030B B S S u u u u νν-+==--3301060033030B B S S u u u u νν--==-+1033165108033130B Su u u u νν++==⨯--`11331142133165B u u u νν==⨯--反射声音的波长为=0.1872(m).或者= 0.1872(m). [注意]如果用下式计算波长=0.2330(m), 结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为,那么S 2在S 1左侧产生的波的波动方程为,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为,那么S 2在其右侧产生的波的波动方程为,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16两相干波源S 1与S 2相距5m ,其振幅相等,频率都是100Hz ,位相差为π;波在媒质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为 ,那么S 2在其左侧产生的波的波动方程为. 两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).5.17设入射波的表达式为,`1111331651421BBu u u uλννν--=-==`1`13311768uλν==`111650.27871768Bu λλν=-=-1cos[2()]t xy A T πϕλ=++2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-1cos[2()]t xy A T πϕλ=-+2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+1/2cos[2()]x l y A t u πνϕ+=-+5cos(2)24A t x πππνϕ=-+-2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-1cos 2()t xy A T πλ=+S 1 S 2S 12在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为.(2)合成波为y = y 1 + y 2,将三角函数展开得,这是驻波的方程.5.18两波在一很长的弦线上传播,设其表达式为:,,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:,, 可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).2cos 2()t xy A T πλ=-222coscosy A x t Tππλ=1 6.0cos(0.028.0)2y x t π=-2 6.0cos(0.028.0)2y x t π=+1 6.0cos 2()0.5200t x y π=-2 6.0cos 2()0.5200t x y π=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五题/*计算物理作业 3.5题*学号:20092200129*/程序:public class sun {public static void main(String argv[]){double del=1e-6;int n=10,m=10;double h=Math.PI/(2*n);//Evaluate the derivative and output the resultint k=0;for(int i=0;i<=n;++i){double x=h*i;double d=(f(x+h)-2*f(x)+f(x-h))/(h*h);double f2=firstOrderDerivative3(x,h,d,del,k,m);double df2=f2-O(x,f2);System.out.println("x="+x);System.out.println(" f"(x)="+f2);System.out.println("Error in f"(x):"+df2);System.out.println();System.out.println();}}//Method to carry out 2st-order derivative throuth the adaptive scheme.public static double firstOrderDerivative3(double x,double h,doubled,double del,int step,int maxstep){step++;h=h/2;double d2=(f(x+h)-2*f(x)+f(x-h))/(h*h);if(step>=maxstep){System.out.println("Not converged after"+step+"recursions");return d2;}else{if((h*h*Math.abs(d-d2))<del)return(4*d2-d)/3;else return firstOrderDerivative3(x,h,d2,del,step,maxstep);}}public static double f(double x){return Math.exp(-x)*Math.log(x);}public static double O(double x,double f2){returnMath.exp(-x)*Math.log(x)-(2*Math.exp(-x))/x-Math.exp(-x)/(x*x);}}运行结果:Not converged after10recursionsx=0.0f"(x)=NaNError in f"(x):NaNx=0.15707963267948966f"(x)=-47.10058585750553Error in f"(x):3.329329885559673E-6x=0.3141592653589793f"(x)=-12.896114166464196Error in f"(x):8.610592701074893E-7x=0.47123889803846897f"(x)=-5.929972627646059Error in f"(x):1.254731920141694E-6x=0.6283185307179586f"(x)=-3.2974024228908525Error in f"(x):2.3189374909193816E-7x=0.7853981633974483f"(x)=-2.010313400857776Error in f"(x):1.0145469402367269E-6x=0.9424777960769379f"(x)=-1.2886478977422928Error in f"(x):3.5448832647055895E-7x=1.0995574287564276f"(x)=-0.8495690372991292Error in f"(x):1.4696104200240256E-7x=1.2566370614359172f"(x)=-0.568185223209793Error in f"(x):6.901975246886849E-8x=1.413716694115407f"(x)=-0.38160076561659223Error in f"(x):3.562357669961713E-8x=1.5707963267948966f"(x)=-0.25505577758216Error in f"(x):3.170312274369813E-7第六题解题思路:首先定义主函数,计算出x[i],f[i],然后调用两个子函数,两个子函数分别计算泰勒展开式求最后一项的结果和辛普森方法求得last slice的结果。
对于两个子函数来书直接用last=h*(5*y[n]+8*y[n-1]-y[n-2])/12即可求得辛普森算法的最后一个的结果而泰勒方法中最后一项等于=h*h*f(x0)的一阶导数/2+h*f[n-1]+h*h*h*f(x0)的二阶导数/二的阶乘。
对于f(x0)的一阶和二阶导数则由另外两个子程序分别计算一阶导数=c[i]=(y[i+1]-y[i-1])/(2*h);二阶导数c[i]=(y[i+1]-2*y[i]+y[i-1])/(h*h);将所得值比较即可。
源程序:import ng.*;public class n2 {static final int n=9;public static void main (String argv[]){double f[]= new double[n+1];double h=Math.PI/(2.0*n);//定义均匀间隔for(int i=0;i<=n;i++){double x=h*i;f[i]=Math.sin(x);//为f[i]赋值}double l=lastlice(f,h);double t=taylor(f,h);System.out.println("lastlice is "+l);System.out.println("taylor is "+t);if(l == t)System.out.println("they are equal");elseSystem.out.println("they are not equal");}//辛普森方法的last slicepublic static double lastlice(double f[],double h){d ouble y[]= new double [n+1];f or(int i=0;i<=n;i++){y[i]=f[i];}d ouble l=h*(5*y[n]+8*y[n-1]-y[n-2])/12;r eturn l;}public static double taylor(double f[],double h){//泰勒展开式求最后一项d ouble y[]= new double [n+1];f or(int i=0;i<=n;++i){y[i]=f[i];}d ouble fl=first(n,y,h);d ouble s=second(n,y,h);d ouble t=h*h*fl/2+h*f[n-1]+h*h*h*s/6;return t;}public static double first(int n,double y[],double h){ //定义first orderd ouble c[]=new double [n+1];f or(int i=1;i<n;i++){c[i]=(y[i+1]-y[i-1])/(2*h);}r eturn c[n-1];}p ublic static double second(int n,double y[],double h){ //定义second orderdouble c[]=new double [n+1];for(int i=1;i<n;i++){c[i]=(y[i+1]-2*y[i]+y[i-1])/(h*h);}return c[n-1];}}运行结果:lastlice is 0.1736423622701241taylor is 0.1736423622701241they are equal事实证明结果一样。
第十一题// An example of searching for a root via the secant method // for f(x)=exp(x)*ln(x)-x*x=0.import ng.*;public class Root {public static void main(String argv[]) {double del = 1e-6, a = 0, b =2;double dx = (b-a)/10, x = (a+b)/2;int n = 6;x = secant(n, del, x, dx);System.out.println("Root obtained: " + x);}// Method to carry out the secant search.public static double secant(int n, double del,double x, double dx) {int k = 0;double x1 = x+dx;while ((Math.abs(dx)>del) && (k<n)) {double d = f(x1)-f(x);double x2 = x1-f(x1)*(x1-x)/d;x = x1;x1 = x2;dx = x1-x;k++;}if (k==n) System.out.println("Convergence not" + " found after " + n + " iterations");return x1;}public static double f(double x) {return Math.exp(x*x)*Math.log(x*x)-x;}}解题思路:f(x)=ⅇx2∗Log[ⅇ,x2]−x的大致图像如图由于正割法对初始值有依赖,只能逼近较近的根,所以我们可以通过改变初始点来求解函数的多个根;容易观察到函数在[-1,2]区间上有两个根,所以调整初值求解如下:运行结果:a=-1,b=2时:Root obtained: 1.1624063469159338a=-1,b=0时:Root obtained: -0.8105015386160186第十三题// An example of searching for a minimum of a multivariable// function through the steepest-descent method.import ng.*;public class minimum13 {static double c=-1;//区间static double d=2;//区间public static void main(String argv[]) {double del = 1e-6, a = 0.1;double x =0.2;x=steepestDescent(x, a, del);//compare the functions at the points of x=c,x=ddouble min=0;double mx=0;if(g(c)>g(d)){min=g(d);mx=d;}else{min=g(c);mx=c;}//ensure the x isamong [c,d]if(x>c&&x<d){if(g(x)<min) {min=g(x);mx=x;}}System.out.println("The minimum is at"+ " x= " + mx+" "+"minimum=" +min);}// Method to carry out the steepest-descent search.public static double steepestDescent(double x,double a, double del) {double h = 1e-6;double g0 = g(x);double fi = f(x, h);double dg = 0;dg += fi*fi;dg = Math.sqrt(dg);double b = a/dg;while (dg > del) {x-= b*fi;h /= 2;fi = f(x, h);dg = 0;dg += fi*fi;dg = Math.sqrt(dg);b = a/dg;double g1 = g(x);if (g1 > g0) a/= 2;else g0 = g1;}return x;}// Method to provide the gradient of g(x).public static double f(double x, double h) {double z;double y = x;y+=h;double g0 = g(x);z = (g(y)-g0)/h;return z;}// Method to provide function g(x).public static double g(double x) {return x*x;}}运行结果:在区间[-1,2]:The minimum is at x= 0.0 minimum=0.0在区间[3,5]: The minimum is at x= 3.0 minimum=9.0第十五题程序://第十五题任时坤//let ∑=sigma=E=m=1;//so V=4(pow((1/r),12)-pow((1/r),6))//using the exp(theta) and log(ruth) to plot the relations between theta and cross section;public class Lennard15 {static final int n = 1000, m = 100;static double b;public static void main(String argv[]) {int nc = 100, ne = 2;double del = 1e-6, db = 0.5, b0 = 0.01, h = 0.01;double g1, g2;double theta[] = new double[n+1];double fi[] = new double[n+1];double sig[] = new double[m+1];for (int i=0; i<=m; ++i) {b = b0+i*db;// Calculate the first term of thetafor (int j=0; j<=n; ++j) {double r = b+h*(j+1);fi[j] = 1/(r*r*Math.sqrt(fb(r)));}g1 = simpson(fi, h);// Find r_m from 1-b*b/(r*r)-U/E = 0double rm = secant(nc, del, b, h);// Calculate the second term of thetafor (int j=0; j<=n; ++j) {double r = rm+h*(j+1);fi[j] = 1/(r*r*Math.sqrt(f(r)));}g2 = simpson(fi, h);theta[i] = 2*b*(g1-g2);}// Calculate d theta/d bsig = firstOrderDerivative(db, theta, ne);// Put the cross section in log form with the exact// result of the Coulomb scattering (ruth)//theta = abs(theta)for (int i=m; i>=0; --i) {b = b0+i*db;sig[i] = b/(Math.abs(sig[i])*Math.sin(Math.abs(theta[i])));theta[i] = Math.abs(theta[i]);double ruth = 1/Math.pow(Math.sin(theta[i]/2),4);ruth /= 16;// because of sig and ruth are always very big numbersdouble si = Math.log(sig[i]);double ru = Math.log(ruth);//useing the exp(theta)---log(ruth)://System.out.println(Math.exp(theta[i])+" "+ru);System.out.println("theta = " + theta[i]);System.out.println("ln sigma(theta) = " + si);System.out.println("ln sigma_r(theta) = " + ru);System.out.println();}}// Method to achieve the evenly spaced Simpson rule.public static double simpson(double y[], double h) { int n = y.length-1;double s0 = 0, s1 = 0, s2 = 0;for (int i=1; i<n; i+=2) {s0 += y[i];s1 += y[i-1];s2 += y[i+1];}double s = (s1+4*s0+s2)/3;// Add the last slice separately for an even n+1if ((n+1)%2 == 0)return h*(s+(5*y[n]+8*y[n-1]-y[n-2])/12);elsereturn h*s;}// Method to carry out the secant search.public static double secant(int n, double del,double x, double dx) {int k = 0;double x1 = x+dx;while ((Math.abs(dx)>del) && (k<n)) {double d = f(x1)-f(x);double x2 = x1-f(x1)*(x1-x)/d;x = x1;x1 = x2;dx = x1-x;k++;}if (k==n) System.out.println("Convergence not" +" found after " + n + " iterations");return x1;}// Method for the 1st-order derivative with the 3-point // formula. Extrapolations are made at the boundaries.public static double[] firstOrderDerivative(double h,double f[], int m) {int n = f.length-1;double[] y = new double[n+1];double[] xl = new double[m+1];double[] fl = new double[m+1];double[] fr = new double[m+1];for (int i=1; i<n; ++i)y[i] = (f[i+1]-f[i-1])/(2*h);// Lagrange-extrapolate the boundary pointsfor (int i=1; i<=(m+1); ++i) {xl[i-1] = h*i;fl[i-1] = y[i];fr[i-1] = y[n-i];}y[0] = aitken(0, xl, fl);y[n] = aitken(0, xl, fr);return y;}// The Aitken method for the Lagrange interpolation.public static double aitken(double x, double xi[],double fi[]) {int n = xi.length-1;double ft[] = (double[]) fi.clone();for (int i=0; i<n; ++i) {for (int j=0; j<n-i; ++j) {ft[j] = (x-xi[j])/(xi[i+j+1]-xi[j])*ft[j+1]+(x-xi[i+j+1])/(xi[j]-xi[i+j+1])*ft[j];}}return ft[0];}// Method to provide function f(x) for the root search.public static double f(double x) {return 1-b*b/(x*x)-4*0.01*(Math.pow(4/x, 12)-Math.pow(4/x, 6));}// Method to provide function 1-b*b/(x*x).public static double fb(double x) {return 1-b*b/(x*x);}}结果:theta = 1.846559973157913E-8ln sigma(theta) = 39.46332190354649ln sigma_r(theta) = 71.2294252391947theta = 1.9678432294709114E-8ln sigma(theta) = 41.44547859635677ln sigma_r(theta) = 70.97497043326803theta = 2.0984203072983707E-8ln sigma(theta) = 41.29685975650948ln sigma_r(theta) = 70.71798366765296theta = 2.23910832153687E-8ln sigma(theta) = 41.146741657981565ln sigma_r(theta) = 70.45841211231631theta = 2.390804116802342E-8ln sigma(theta) = 40.99510503114457ln sigma_r(theta) = 70.1962039362033theta = 2.554492433300831E-8ln sigma(theta) = 40.84190815616484ln sigma_r(theta) = 69.9313087850952theta = 2.731263311225862E-8ln sigma(theta) = 40.68710838170971ln sigma_r(theta) = 69.66366596170842theta = 2.9223164015913793E-8ln sigma(theta) = 40.530684636823345ln sigma_r(theta) = 69.39321661577095ln sigma(theta) = 40.37260354657837 ln sigma_r(theta) = 69.11990334355792theta = 3.3526957719659523E-8ln sigma(theta) = 40.21283100549856 ln sigma_r(theta) = 68.84366405467912theta = 3.595097888327986E-8ln sigma(theta) = 40.0513********ln sigma_r(theta) = 68.56443809651903theta = 3.857973084525623E-8ln sigma(theta) = 39.888040827526325 ln sigma_r(theta) = 68.28215522411509theta = 4.143302109810981E-8ln sigma(theta) = 39.72294822235678 ln sigma_r(theta) = 67.99675065188941theta = 4.453289077006872E-8ln sigma(theta) = 39.55599779288899 ln sigma_r(theta) = 67.70815120943685theta = 4.790380100420932E-8ln sigma(theta) = 39.387160641391176 ln sigma_r(theta) = 67.41628393108627theta = 5.157289538093579E-8ln sigma(theta) = 39.216384308703816 ln sigma_r(theta) = 67.12107834313481theta = 5.5570533061197186E-8ln sigma(theta) = 39.043619581398794 ln sigma_r(theta) = 66.82245102837247theta = 5.99304568799086E-8ln sigma(theta) = 38.86882832471159 ln sigma_r(theta) = 66.52032399578432theta = 6.46903786532399E-8ln sigma(theta) = 38.691957273192436 ln sigma_r(theta) = 66.21461341422884ln sigma(theta) = 38.51295815805794ln sigma_r(theta) = 65.90523242502154theta = 7.558386080179501E-8ln sigma(theta) = 38.3317748114848ln sigma_r(theta) = 65.5920922320363theta = 8.181753405028802E-8ln sigma(theta) = 38.14835589090251ln sigma_r(theta) = 65.27509705445983theta = 8.865279546306503E-8ln sigma(theta) = 37.96264830487491ln sigma_r(theta) = 64.95415308486821theta = 9.615640111509949E-8ln sigma(theta) = 37.77458657724528ln sigma_r(theta) = 64.62915917147035theta = 1.0440352998339342E-7ln sigma(theta) = 37.58411412087224ln sigma_r(theta) = 64.30000939987208theta = 1.1347885113151267E-7ln sigma(theta) = 37.39116871455187ln sigma_r(theta) = 63.96659740412114theta = 1.2347806189527687E-7ln sigma(theta) = 37.195682818068484 ln sigma_r(theta) = 63.62880933253239theta = 1.345093455251689E-7ln sigma(theta) = 36.997588804528476 ln sigma_r(theta) = 63.28652862743951theta = 1.4669530836800004E-7ln sigma(theta) = 36.796815908764096 ln sigma_r(theta) = 62.939632533761774theta = 1.6017502676726746E-7ln sigma(theta) = 36.593289325848964 ln sigma_r(theta) = 62.58799480923479ln sigma(theta) = 36.38693222724815ln sigma_r(theta) = 62.23148173935577theta = 1.9167030948119556E-7ln sigma(theta) = 36.17766504484714ln sigma_r(theta) = 61.86995631603575theta = 2.1007138338434426E-7ln sigma(theta) = 35.96540241655411ln sigma_r(theta) = 61.50327377244451theta = 2.3054472993791484E-7ln sigma(theta) = 35.750057714899796 ln sigma_r(theta) = 61.13128374882553theta = 2.5335927519312685E-7ln sigma(theta) = 35.531539119699225 ln sigma_r(theta) = 60.753829181994995theta = 2.7882362735029416E-7ln sigma(theta) = 35.30975100457115ln sigma_r(theta) = 60.37074566022896theta = 3.07292622861513E-7ln sigma(theta) = 35.08459242279057ln sigma_r(theta) = 59.98186149762503theta = 3.3917520823927016E-7ln sigma(theta) = 34.855959129143315 ln sigma_r(theta) = 59.586996098468155theta = 3.7494352488370854E-7ln sigma(theta) = 34.623741482142805 ln sigma_r(theta) = 59.18596169050993theta = 4.151441435293335E-7ln sigma(theta) = 34.38782385725622ln sigma_r(theta) = 58.77856017286608theta = 4.604110535080114E-7ln sigma(theta) = 34.14808583292972ln sigma_r(theta) = 58.36458460759438ln sigma(theta) = 33.904400024954256 ln sigma_r(theta) = 57.94381718855084theta = 5.692151840329396E-7ln sigma(theta) = 33.65663315821511ln sigma_r(theta) = 57.51602917996846theta = 6.346164715751585E-7ln sigma(theta) = 33.40464498182495ln sigma_r(theta) = 57.080980009182426theta = 7.08862596056209E-7ln sigma(theta) = 33.148287972084795 ln sigma_r(theta) = 56.63841651533806theta = 7.933367794020485E-7ln sigma(theta) = 32.8874063658783ln sigma_r(theta) = 56.188072060697465theta = 8.896690350412157E-7ln sigma(theta) = 32.62183592432788ln sigma_r(theta) = 55.72966525648614theta = 9.997857765142727E-7ln sigma(theta) = 32.351403415585345 ln sigma_r(theta) = 55.26289921759669theta = 1.1259707037666184E-6ln sigma(theta) = 32.07592576636889ln sigma_r(theta) = 54.787460186218226theta = 1.2709395789602812E-6ln sigma(theta) = 31.795209114472588 ln sigma_r(theta) = 54.30301642030872theta = 1.4379326957132678E-6ln sigma(theta) = 31.50904830915759ln sigma_r(theta) = 53.809216415418184theta = 1.6308292001151331E-6ln sigma(theta) = 31.21722588807881ln sigma_r(theta) = 53.30568784307433ln sigma(theta) = 30.919510821416043 ln sigma_r(theta) = 52.79203535679371theta = 2.1139343178147585E-6ln sigma(theta) = 30.61565773149832ln sigma_r(theta) = 52.267838964384744theta = 2.416566206005638E-6ln sigma(theta) = 30.305405437773395 ln sigma_r(theta) = 51.732651794235196theta = 2.770453722952815E-6ln sigma(theta) = 29.988475657942747 ln sigma_r(theta) = 51.18599780911595theta = 3.1856879611830147E-6ln sigma(theta) = 29.664571469016604 ln sigma_r(theta) = 50.62736916757544theta = 3.6746383340544035E-6ln sigma(theta) = 29.333375610469282 ln sigma_r(theta) = 50.05622337058027theta = 4.252536203071811E-6ln sigma(theta) = 28.99454854777367ln sigma_r(theta) = 49.47197999740563theta = 4.93822662616647E-6ln sigma(theta) = 28.647726366980937 ln sigma_r(theta) = 48.87401709509007theta = 5.755142357569132E-6ln sigma(theta) = 28.292518410731745 ln sigma_r(theta) = 48.26166711907795theta = 6.732573461354642E-6ln sigma(theta) = 27.928504575092518 ln sigma_r(theta) = 47.634212403477896theta = 7.907333024784469E-6ln sigma(theta) = 27.555232254078774 ln sigma_r(theta) = 46.99087999219401ln sigma(theta) = 27.17221300370534ln sigma_r(theta) = 46.330835826113045theta = 1.1047630828540518E-5ln sigma(theta) = 26.778918618778874 ln sigma_r(theta) = 45.653178*********theta = 1.3148109286668792E-5ln sigma(theta) = 26.374776732486097 ln sigma_r(theta) = 44.95693036066628theta = 1.5725012876565414E-5ln sigma(theta) = 25.959165866061433 ln sigma_r(theta) = 44.24103174611569theta = 1.8905037492587125E-5ln sigma(theta) = 25.531409680376637 ln sigma_r(theta) = 43.504328549712504theta = 2.2853858185053202E-5ln sigma(theta) = 25.090770478433576 ln sigma_r(theta) = 42.74556242615165theta = 2.778985758680505E-5ln sigma(theta) = 24.636441723209035 ln sigma_r(theta) = 41.96335775550143theta = 3.4003342543032086E-5ln sigma(theta) = 24.167539454931855 ln sigma_r(theta) = 41.15620691255692theta = 4.18837209046552E-5ln sigma(theta) = 23.683092446964054 ln sigma_r(theta) = 40.322453316662596theta = 5.195835833631451E-5ln sigma(theta) = 23.18203088644655ln sigma_r(theta) = 39.46027184613055theta = 6.4948782643445E-5ln sigma(theta) = 22.66317341440529ln sigma_r(theta) = 38.56764623271658ln sigma(theta) = 22.12521233161425ln sigma_r(theta) = 37.642342997328385theta = 1.0406754740503121E-4ln sigma(theta) = 21.566696875806777 ln sigma_r(theta) = 36.68188150330053theta = 1.3357132418628624E-4ln sigma(theta) = 20.98601462403819ln sigma_r(theta) = 35.68349983987055theta = 1.7320596395968308E-4ln sigma(theta) = 20.381371414537902 ln sigma_r(theta) = 34.6441165189257theta = 2.2711088897784586E-4ln sigma(theta) = 19.75077092040879ln sigma_r(theta) = 33.560288656833634theta = 3.01409068290954E-4ln sigma(theta) = 19.09194311482954ln sigma_r(theta) = 32.42816875512143theta = 4.053162908582683E-4ln sigma(theta) = 18.40251914958873ln sigma_r(theta) = 31.243371349660784theta = 5.529029996976504E-4ln sigma(theta) = 17.679849592743274 ln sigma_r(theta) = 30.001311967934182theta = 7.661195683031765E-4ln sigma(theta) = 16.921021997658006 ln sigma_r(theta) = 28.696689321881497theta = 0.0010797952324843956ln sigma(theta) = 16.12320163486973ln sigma_r(theta) = 27.323935615821338theta = 0.0015502182762195764ln sigma(theta) = 15.283874246657785 ln sigma_r(theta) = 25.87743853892223theta = 0.002269769554237988ln sigma(theta) = 14.401745878318513ln sigma_r(theta) = 24.352308741038165theta = 0.0033912436700995877ln sigma(theta) = 13.478901248373013ln sigma_r(theta) = 22.74623615888332theta = 0.005164095381224361ln sigma(theta) = 12.526616258062047ln sigma_r(theta) = 21.0641057876601theta = 0.007965793323853805ln sigma(theta) = 11.583767293951484ln sigma_r(theta) = 19.330405533020915theta = 0.012192937936150904ln sigma(theta) = 10.797226474868692ln sigma_r(theta) = 17.6276181881397theta = 0.017210180336480897ln sigma(theta) = 11.564602732336702ln sigma_r(theta) = 16.249066126079722theta = 0.014957527039389101ln sigma(theta) = 8.58553644926581ln sigma_r(theta) = 16.81019978782069theta = 0.039112308192289655ln sigma(theta) = 5.9394958026453475ln sigma_r(theta) = 12.965527261356753theta = 0.2550969665562406ln sigma(theta) = 3.1561366006712133ln sigma_r(theta) = 5.475297811713763theta = 0.6315321811346928ln sigma(theta) = 1.8701683740161505ln sigma_r(theta) = 1.9051200004245903theta = 1.040747665790346ln sigma(theta) = 1.2952272070259088ln sigma_r(theta) = 0.02242657177744099theta = 1.428172678843424ln sigma(theta) = 1.0021476205032662ln sigma_r(theta) = -1.079664214060937theta = 1.7861676543974974ln sigma(theta) = 0.8169839653186198ln sigma_r(theta) = -1.773658246046629theta = 2.1110088158201457ln sigma(theta) = 0.7031431382362978ln sigma_r(theta) = -2.2162250149887663theta = 2.369163840140268ln sigma(theta) = -0.3748970500196441ln sigma_r(theta) = -2.466540159639649theta = 1.0478280744015163ln sigma(theta) = -5.90995091993309ln sigma_r(theta) = -0.002183401622834268第十六题//using the simpson methodpublic class pendulum_16 {static final int n = 100000;static final double pi=Math.PI;static final double l=1,g=9.8;public static void main(String argv[]) {double f[] = new double[n+2];double space[] ={pi/128,pi/64,pi/32,pi/16,pi/8,pi/4,pi/2};for(int k=space.length-1;k>=0;k--){double sp=space[k];double h=sp/n;for (int i=0; i<n; i++) {double theta = h*i;f[i] = 4*Math.sqrt(l/(2*g))/Math.sqrt(Math.cos(theta)-Math.cos(sp));}double s = simpson(f, h);System.out.println("While the theta0 = "+space[k]+" The integral is: " + s); }System.out.println("The T = 2pi*sqrt(l/g) = "+2*pi*Math.sqrt(l/g));}//Method to achieve the evenly spaced Simpson rule.public static double simpson(double y[], double h) {int n = y.length-1;double s0 = 0, s1 = 0, s2 = 0;for (int i=1; i<n; i+=2) {s0 += y[i];s1 += y[i-1];s2 += y[i+1];}double s = (s1+4*s0+s2)/3;// Add the last slice separately for an even n+1if ((n+1)%2 == 0)return h*(s+(5*y[n]+8*y[n-1]-y[n-2])/12);elsereturn h*s;}}运行结果:While the theta0 = 1.5707963267948966 The integral is: 2.364243960873343 While the theta0 = 0.7853981633974483 The integral is: 2.0832788690555177 While the theta0 = 0.39269908169872414 The integral is: 2.022723192575113 While the theta0 = 0.19634954084936207 The integral is: 2.00809006000594 While the theta0 = 0.09817477042468103 The integral is: 2.0044621218895236 While the theta0 = 0.04908738521234052 The integral is: 2.003557015039689 While the theta0 = 0.02454369260617026 The integral is: 2.003330855409693 The T = 2pi*sqrt(l/g) = 2.007089923154493第十七题://用simpson方法解决此积分问题;public class problem_17 {static final double l=1,g=9.8;static final double thit=0;static final int n = 1000;static final double pi=Math.PI;public static void main(String argv[]) { double f[] = new double[n+1];double space[] ={pi/8,pi/4,pi/2};for(int k=0;k<space.length;k++){double sp=space[k];double h=sp/n;for (int i=0; i<n; i++) {double theta = h*i;f[i] = 0.5*Math.sqrt(l/(3*g))*Math.sqrt((1+3*Math.cos(theta)*Math.cos(theta))/(Math.sin(sp)-Math.sin(theta)));}double s = simpson(f, h);System.out.println("theta0 = "+space[k]+" The integral of t is: " + s); }}//Method to achieve the evenly spaced Simpson rule.public static double simpson(double y[], double h) {int n = y.length-1;double s0 = 0, s1 = 0, s2 = 0;for (int i=1; i<n; i+=2) {s0 += y[i];s1 += y[i-1];s2 += y[i+1];}double s = (s1+4*s0+s2)/3;// Add the last slice separately for an even n+1if ((n+1)%2 == 0)return h*(s+(5*y[n]+8*y[n-1]-y[n-2])/12);elsereturn h*s;}}运行结果:theta0 = 0.39269908169872414 The integral of t is: 0.22615514392751754 theta0 = 0.7853981633974483 The integral of t is: 0.3206139187126751 theta0 = 1.5707963267948966 The integral of t is: 1.1404447118395957第十八题// set : T0= 2*pi,E0=1.6,// w = T0*Math.sqrt(E0)/(2*pi*Math.sqrt(2*m))=1;// u = 10//so x(u) = ∫ (1+alfa[k]*Math.exp(-e/E0))/Math.sqrt(u-e) dxpublic class problem_18 {static final int n = 10000;static final double pi=Math.PI,u=10;static final double T0=2*pi,E0=1.6,w=1;public static void main(String argv[]) {double f[] = new double[n+1];double alfa[] = {0,0.1,1,10};for(int k=0;k<alfa.length;k++){double h=u/n;for (int i=0; i<n; i++) {double e = h*i;f[i] = (1+alfa[k]*Math.exp(-e/E0))/Math.sqrt(u-e);}double s = simpson(f, h);System.out.println("alfa = "+alfa[k]+" The integral is: " + s); }}//Method to achieve the evenly spaced Simpson rule.public static double simpson(double y[], double h) {int n = y.length-1;double s0 = 0, s1 = 0, s2 = 0;for (int i=1; i<n; i+=2) {s0 += y[i];s1 += y[i-1];s2 += y[i+1];}double s = (s1+4*s0+s2)/3;// Add the last slice separately for an even n+1if ((n+1)%2 == 0)return h*(s+(5*y[n]+8*y[n-1]-y[n-2])/12);elsereturn h*s;}}运行结果:alfa = 0.0 The integral is: 6.284751047501293 alfa = 0.1 The integral is: 6.341179576835809 alfa = 1.0 The integral is: 6.849036340846619 alfa = 10.0 The integral is: 11.927603980954794。
