材料力学规范练习冯立富主编西安交通大学出版社
西安交通大学 材料力学总复习与习题课

第二章轴向拉伸与压缩
• 基本概念: • 轴向拉伸与压缩的特点:杆件所受外力或 其合力作用线沿杆的轴线,杆件的主要变 形为轴向伸长或缩短。 • 拉压杆的内力——轴力(轴力是横截面位 置x的函数) • 截面法:利用假想平面将杆截成两端,对 每一段进行分析,求解杆的轴力(内力) • 截面法求轴力绘制轴力图
• 应力集中现象:由于截面急剧变化所引 起的局部应力聚增的现象 • 安全系数、许用应力、强度条件 • 极限应力:材料丧失正常工作的能力时 的应力。 [σ]= σu /n • n-安全系数, [σ]-许用应力 • σ<= [σ]-强度条件 • 计算三类强度计算问题: • 1、强度校核;2、设计截面尺寸;3、确 定许可载荷
y Z y1 τmax h
第五章 弯曲变形
• 挠度和转角的概念:横截面形心在垂直于 轴线(x轴)方向的线位移称为挠度y;横 截面的角位移称为转角θ 。 • 挠曲线方程:y=y(x);y“=M (x) /EI; EI称为抗 弯刚度 • 利用积分法求挠曲线: • θ =y´= ∫ M (x) /EI+C1; • y= ∫ ∫ M (x) /EI+C1x+C2 • 利用边界条件确定常系数C1 、C2
• • • • • • • • • •
圆轴扭转时的切应力计算公式: 距离圆心任意距离ρ处的切应力: τ ρ= T ρ/I ρ =MT ρ/I p ,I p极惯性矩 在距离圆心同位置处切应力大小相等, 方向与半径垂直。当ρ=R处切应力最大: τmax= T R/I p = T /W ρ W ρ = I p /R 。 W ρ为抗扭截面模量 实心圆轴I p = πD4 /32; W ρ = πD3 /16 空心圆轴I p = πD4 /32(1-α4) W ρ = πD3 /16(1-α4) 薄壁圆轴: I p =2 πR30t; W p =2 πR20t
材料力学习题册答案

练习1 绪论及基本概念1-1 是非题(1)材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是 )(3)构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4)应力是内力分布集度。
(是 )(5)材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6)若物体产生位移,则必定同时产生变形。
(非 ) (7)各向同性假设认为,材料沿各个方向具有相同的变形。
(F )(8)均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1)根据材料的主要性质对材料作如下三个基本假设:连续性假设 、均匀性假设 、 各向同性假设 。
(2)工程中的 强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3)保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性 三个方面。
(4)图示构件中,杆1发生 拉伸 变形,杆2发生 压缩 变形, 杆3发生 弯曲 变形。
(5)认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设 。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6)图示结构中,杆1发生 弯曲 变形,构件2发生 剪切 变形,杆件3发生 弯曲与轴向压缩组合。
变形。
(7)解除外力后,能完全消失的变形称为 弹性变形 ,不能消失而残余的的那部分变形称为 塑性变形 。
(8)根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
交大材料力学复习题五套答案

材料力学复习题(一)一、1. B 2. B 3. A 、C 4. D5. A 、B 、D 6. C 7. A 、B 8. A 、B 、D 二、3.43-=xy τMPa ,3.43-''y x τMPa ,50='y σMPa三、3.254=BC Cr FkN ,45][=F kN四、略, 五、1.14-=Hx σMPa ,6.0=Hxz τ MPa ,2.143=r σMPa六、EIQl Ql EIh v Cd 94)41811(33++=材料力学复习题(二)一、选择题1、D ;2、B ;3、D ;4、C ;5、D 。
二、填空1、3段;位移边界条件 0,0,0===D A A w w θ;光滑连续条件CD C BC C w w ,,=,CD C BC C ,,θθ=,BC B AB B w w ,,=。
2、h y c 32=3、连续性假设;均匀性假设;各向同性假设;线弹性;小变形。
4、< ;= 。
5、0.003;0.002;47.12kN 。
三、计算题1、图示为由五根直径50d mm =的圆形钢杆组成边长 为1a m =的正方形结构,材料为235Q 钢,比例极限aABC FaDF 题 3-1 图200p MPa σ=,屈服应力235s MPa σ=,弹性模量200E GPa =,中柔度杆的临界应力公式为304 1.12()cr MPa σλ=-。
试求该结构的许用载荷[]F 。
解:(1)求AB 、BD 和AD 杆的内力绘制节点A 和B 的受力图如图所示。
FF BAF DAA45ºF ABF BCF BDBAB 杆和AD 杆为受压杆,BD 杆受拉。
其内力分别为:2F F F AD AB ==,F F BD =(2)根据杆AB 和AD 的压杆稳定确定许可载荷圆杆4504mm d i ==,杆AB 和AD 的柔度均为805041000=⨯==mm i a μλ。
材料力学刘德华版课后习题问题详解word版
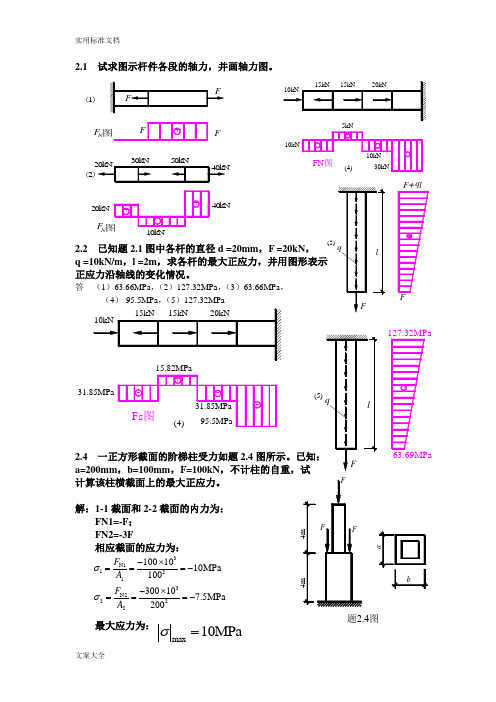
2.1 试求图示杆件各段的轴力,并画轴力图。
2.2 已知题2.1图中各杆的直径d =20mm ,F =20kN ,q =10kN/m ,l =2m ,求各杆的最大正应力,并用图形表示 正应力沿轴线的变化情况。
答 (1)63.66MPa ,(2)127.32MPa ,(3)63.66MPa ,(4)-95.5MPa ,(5)127.32MPa2.4 一正方形截面的阶梯柱受力如题2.4图所示。
已知:a=200mm ,b=100mm ,F=100kN ,不计柱的自重,试 计算该柱横截面上的最大正应力。
解:1-1截面和2-2截面的内力为: FN1=-F ;FN2=-3F相应截面的应力为:最大应力为:15kN15kN20kN10kN(4)10kN5kN10kN 30kN+---FN 图-+++FF FF 20kN 30kN 50kN 40kN40kN10kN 20kN (2)(1)F N 图图N F l(5)q FFF q ll(5)qF+127.32MPa63.69MPa15kN 15kN 20kN 10kN (4)31.85MPa 15.82MPa +---Fs 图31.85MPa95.5MPa 4m4mabF题2.4图FF3N11213N22221001010MPa 100300107.5MPa200F A F A σσ-⨯===--⨯===-max 10MPaσ=2.6 钢杆受轴向外力如图所示,横截面面积为500mm2,试求 ab 斜截面上的应力。
解: FN=20kN2.8 图示钢杆的横截面积 A=1000mm2,材料的弹性模量E=200GPa ,试求:(1)各段的轴向变形;(2)各段的轴向线应变;(3)杆的总伸长。
解:轴力图如图所示2.10 图示结构中,五根杆的抗拉刚度均为EA ,杆AB 长为l ,ABCD 是正方形。
在小变形条件下,试求两种加载情况下,AB 杆的伸长。
解 (a )受力分析如图,由C 点平衡可知:3020kNob aa b a b p αs αατF N o N N 0cos30==F F p A A ααo 2oN 03cos30cos 302010330MPa 5004F p A σ==⨯=⨯=αα3o o o N020103sin30cos30sin3017.32MPa 5004F p A ⨯===⨯=αατ-+20kN20kN 20kN ⅠⅡⅢ20kN20kN1m 1m 2m12320N 0N 20N N N N F k F k F k ===-41119624333962011020010100010020221020010100010N N F l L m EA L m F l L m EA ----⨯∆===⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L m l mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-实用标准文档F ’AC=F ’CB=0;由D 点平衡可知: F ’AD=F ’BD=0; 再由A 点的平衡:因此(b )受力分析如图,由C 点平衡可知:再由A 点的平衡:因此2.12 图示结构中,水平刚杆AB 不变形,杆①为钢杆,直径d1=20mm ,弹性模量E1=200GPa ;杆②为铜杆,直径d2=25mm ,弹性模量E2=100GPa 。
材料力学练习册

工程力学练习册
(材料力学部分)
姓名:
学号:
年级、专业、班级:
土木与建筑工程学院力学教研室
第一章材料力学的基本概念和拉伸、压缩与剪切
一.是非题:(正确的在括号中打“√”、错误的打“×”)(6小题)
1.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。( )
8.如图1.12所示螺钉在拉力作用下,已知材料的剪切许用应力 和拉伸许用应力 之间的关系为 。试求螺钉直径d与钉头高度h的合理比值。
第二章 扭转
一.是非题:(正确的在括号中打“√”、错误的打“×”)(3小题)
1.圆轴扭转时,各横截面绕其轴线发生相对转动。( )
2.薄壁圆筒扭转时,其横截面上剪应力均匀分布,方向垂直半径。( )
5.应力变化不大,而应变显著增加的现象,称为。
6.当应力不超过比例极限时,横向应变与纵向应变之比的绝对值,称为。
7.三根试件的尺寸相同,但材料不同,其 - 曲线如图1.1所示。第根试件材料强度高,第根试件材料的弹性模量大,第根试件材料的塑性好。
图14.1
8.约束反力和轴力都能通过静力平衡方程求出,称这类问题为;反之则称为;未知力多于平衡方程的数目称为。
5.当剪应力不超过材料的时,剪应力与剪应变成正比例关系,这就是。
6.称为材料的截面抗扭刚度。
三.单项选择题:(5小题)
1.扭转切应力公式 不适用的杆件范围是()。
(A)等截面直杆(B)实心圆截面杆
(C)实心或空心圆截面杆(D)矩形截面杆
2.空心园轴扭转时横截面上的剪应力分布如下图所示,其中正确的分布图是()。
6.杆件在拉伸或压缩时,任意截面上的剪应力均为零。( )
西安交大 2010年材料力学期末考试试卷及答案

强度足够
μ= 1 , i
2E I d 99.3 20 mm , p p A 4
l
i
1 4000 200 > p , 细长杆 20
2 EI 2 200 109 804 1012 Fcr 248kN ( l )2 (1 4 ) 2 64
q
a a
D
a
题4图
第 2 页
西 安 交 通 大 学 考 试 题
5.图示结构中,q = 20 kN/m,梁 AB 的截面为矩形,b1=100mm,h1=150mm;柱 BC 的截 面为圆形,d =80mm。梁和柱均为低碳钢,E = 200 GPa, s= 240 MPa, p= 200 MPa,a = 304 MPa,b = 1.12 MPa。若[ ] = 180 MPa,规定稳定安全因数[nst ] = 3。试校核结构的安 全性。 (15 分) q B A 5m b1 h1
bs
F 62.5MPa [ ] (b d )t
第 1 页
7. (共 15 分)解: Dj 2Bj 2(Bj Cj ) 0.96mm
Kd 1 1
2h 7.53 Dj
M A QL 80 Nm
Mn QL 通大学考试题
课
学
成绩
年 月 日
程
院
材 料 力 学 A
考 试 日 期
专业班号 姓 名 学 号 期中 期末
1
2
3
4
5
6
7
8
9
10
卷面
平时
总分
一、简答题(共 3 小题,15 分) 1. 没有明显屈服阶段的塑性材料,用名义屈服极限0.2 作为
材料力学第版课后习题答案轴向拉压与伸缩
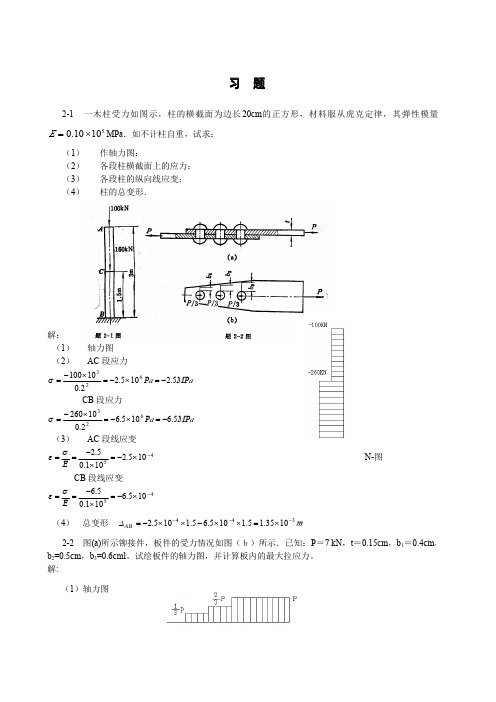
40 100
×10
=
4cm 2
Α = ab = 2a 2
a ≥ Α 2 = 1.414cm
b ≥ 2.828cm
2-7 大功率低速柴油机的气缸盖螺栓如图示,螺栓承受预紧力 P=390 kN,材料的弹性模量E= 210Gpa,求螺栓的伸长变形。
解:
∆l = Ρl1 + Ρl2 =
390
⎛ ⎜
90
+
802
arctan(0.2) = 11�20′ 。杠杆长度OA=lm,OB=5cm,拉杆BC的直径dl=1.0cm,CE杆与CD杆的直径相
同d2=2.0cm。试求(1)此时拉杆BC,以及杆CD与CE内的应力;(2)木材的弹性模量E=10GPa,计算 被压试件的缩短变形。
解:
(1)
Ν BC
= 400 ×1 = 8000Ν 0.05
2
[σ ] ≥ 4R
πd 2
d≤
4R
π [σ ] =
2 × 6000 ×10 = 7.98cm π × 600
2-15 木材试件(立方体 2 × 2 × 2 cm)在手压机内进行压缩。作用力 P=400N,其方向垂直于杠
杆OA,此杠杆可绕固定心轴 o转动,在某一时刻,拉杆 BC垂直于 OB且平分 ECD角,∠CED=
= 63.66 × sin 30°
= 55.13ΜΡa
2-4 图示结构中ABC与CD均为刚性梁,C与D均为铰接,铅垂力P=20kN作用在C铰,若(1)杆的
直径d1=1cm,(2)杆的直径d2=2cm,两杆的材料相同,E=200Gpa,其他尺寸如图示,试求(1)两杆 的应力;(2)C点的位移。
解 (1) 1 杆的应力
解
材料力学A80学时练习册

1、AB、BC 两段都产生位移。
2、AB、BC 两段都产生变形。
正确答案是
。
2
材料力学 练习册 80 学时
昆明理工大学
专业
学号
姓名
日期
评分
P
A
B
C
B’
C’
E
D
选题 1.1 图
1.2 选题 1.2 图所示等截面直杆在两端作用有力偶,数值为 M,力偶作用面与杆的对称面
一致。关于杆中点处截面 A—A 在杆变形后的位置(对于左端,由 A’ —A’表示;对
拉伸与剪切等强度设计,螺栓杆直径 d 与螺栓头高度 h 的比值应取 d/ h =
。
2.13 木榫接头尺寸如图示,受轴向拉力 F 作用。接头的剪切面积 A=
,切应力
τ=
;挤压面积 Abs=
,挤压应力 σbs=
。
2.14 两矩形截面木杆通过钢连接器连接(如图示),在轴向力 F 作用下,木杆上下两侧的剪切
(
)
2.6 空心圆杆受轴向拉伸时,在弹性范围内,其外径与壁厚的变形关系是外径增大且壁厚也
同时增大。
(
)
2.7 已知低碳钢的 σp=200MPa,E=200GPa,现测得试件上的应变 ε=0.002,则其应力能用
胡克定律计算为:σ=Eε=200×103×0.002=400MPa。
(
)
2.9 图示三种情况下的轴力图是不相同的。
学号
姓名
日期
评分
第一章 绪论
一、是非判断题
1.1 材料力学的研究方法与理论力学的研究方法完全相同。
(
)
1.2 内力只作用在杆件截面的形心处。
(
)
1.3 杆件某截面上的内力是该截面上应力的代数和。
材料力学习题及参考答案

工程上规定 0.2 作为名义屈服极限,此时相对应的
应变量为 0.2%。
()
答案:
四、计算
1.矿井起重机钢绳如图(a)所示,AB段截面积 A1 300mm2, BC段截面积 A2 400mm2,钢绳的单位体积重量 28kN / m3, 长度l 50m,起吊重物的重量 P 12kN,求:1)钢绳内的最大 应力;2)作轴力图。
C
l2 2
B
l1 1
A P
a
解:1)在可能危险的1段B面,2段C面截开(图b),有
NB P A1l 12 28 3104 50 12.42kN
B
NB A1
12.42 103 3104
41.4MPa
NC P A1l A2l 12.42 28 4104 50 12.98kN
A B
C
o
答案: A,B,C,C
3.两端固定的阶梯杆如图所示,横截面面积A2 2 A1 , 受轴向载荷P后,其轴力图是( )。
A2
A1 B
AP
x
ll
N
P
N
2
P
x
2
x
P
A
B
N
P
3
2P
x
3
C
答案: C
N
P
x
D
三、判断题
1.两端固定的等截面直杆受轴向载荷P作用,则图示AC、
CB段分别受压缩
NAC 和P拉 伸
y
II
x Iz
答案: B
(A)
cQ1
P,M1
1 2
Pa;
弯曲
2 P,M2 Pa; 拉伸+弯曲
弯曲
d Q1 P,M1 PR BD段:弯曲;
西安交通大学材料力学试题与答案2008~2010

n
1
K
a
3、在稳定性计算中,对于中长杆,若误用欧拉公式计算其临界力,则压杆是否安全? 对于细长杆,若误用经验公式计算其临界力,能否判断压杆的安全性?并简述理由。 (5分) 否 计算临界应力大于压杆真实临界应力
4、作梁的剪力图和弯矩图。并求出
q
A a
Q
max
和 M
max
(15分)
2qa qa2 B A C D a q
a
5 4
a 题4图
Ra
qa
Rc
5 4
7 4
qa
Q
M
5 4 qa
2
max
5 4
qa ,
M
max
5 4
qa
2
Q
qa
2
qa
1 4
qa
2
3 4
qa
1 2
qa
2
5.图示结构中,q = 20 kN/m,梁AB的截面为矩形,b1=100mm, h1=150mm;柱BC的截面为圆形,d =80mm。梁和柱均为低碳钢,E = 200 GPa, s= 240 MPa, p= 200 MPa,a = 304 MPa,b = 1.12 MPa。若[ ] = 180 MPa,规定稳定安全因数[nst ] = 3。试校核结构的安全性。(15分)
F F e b 题8图 h
1)、轴线(轴向)+温度补偿 2)、 E A F 3)、图
9、重量不计的刚性梁悬挂在三根杆上,两侧1、3杆为铜制,其弹性模量为Ec, 线膨胀因数为αc,中间2杆为钢制,其其弹性模量为Es,线膨胀因数为αs,横截 面面积A2 = 2A1 = 2A3,试求当温度升高时候各杆的内力。 (12 分)
解析法求解平面汇交力系

工程技术 DOI:10.16660/ki.1674-098X.2019.31.047
科技创新导报 2019 NO.31
Science and Technology Innovation Herald
解析法求解平面汇交力系①
韩福娥 (西安工程大学城市规划与市政工程学院 陕西西安 710048)
摘 要:几何法和解析法均可以求解平面汇交力系,几何法在求解平面汇交力系过程中有优势,然而几何法在求解过程中
的劣势也凸显出来。本文笔者在日常的教学工作中经过总结归纳,详细介绍了解析法对平面汇交力系的简化和平衡条件的
推导过程。
关键词:解析法 求解 平面汇交力系
中图分类号:O316
文献标识码:A
文章编号:1674-098X(2019)11(a)-0047-02
1.4 平面汇交力系的简化
根 据 合Байду номын сангаас投 影定理和力在 直 角坐标系中的分 解可以得
出以下式子
n
n
∑ ∑ FR = FR2x + FR2y = ( Fix )2 + ( Fiy )2
=i 1=i 1
n
tg=β
F= Ry FRx
∑ Fiy
i =1
n
∑ Fix
i =1
由此可见,n 个力组成的平面汇交力系可以简化成一个
合力F R,合力的大小可以根据组成合力的各个分力在两个
图1 力下的分解
图2 力下在y轴上的投影Fy
材料力学练习1-推荐下载

答案 答疑
正确选择:a、c 只有 a、c 的外力的合力作用线与杆件轴线重合。
3、杆件受力如图,由于 1、2 截面上的轴力为 N1=N2=P,截面面积 A1=2A2,所以正应力分别为 σ1=N1/A1=P/2A2,σ2=N2/A2=P/A2。即: σ2=2σ1,对吗?如果不对,在什么情况下可以得到上述结果?
2、轴向拉压时横截面上的内力称为
。
5、“只根据轴力图就可以判断出轴向拉压变形时杆件的危险面”
答案 此说法错误 答疑 判断危险面的位置应综合考 虑轴力的大小,横截面面积的大小;轴力大,横截面面积也大,不 一定是危险面。
答案
轴力答疑 简述
内力的合力作用线与杆件的轴线重合 轴向拉压时横截面上的内力
合的外力系使杆件产生轴向拉压
合力作用线与杆件的轴线重 A:a; B:b;
C:c;
D:d;
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术0艺料不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试22下卷,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看2度并22工且22作尽22下可22都能2可地护1以缩关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编5试要写、卷求重电保技要气护术设设装交备备4置底高调、动。中试电作管资高气,线料中课并3敷试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
材料力学内部习题集及答案

第二章 轴向拉伸和压缩2-1 一圆截面直杆,其直径d =20mm, 长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3, 杆的上端固定,下端作用有拉力F =4KN ,试求此杆的:⑴最大正应力; ⑵最大线应变; ⑶最大切应力;⑷下端处横截面的位移∆。
题 2 - 1 图+5004.8N4000N解:首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 故最大正应力为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Ad d σππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α(α为杆内斜截面与横截面的夹角)为45︒时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2 试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ,长度为L,材料的容重为γ。
AB题 2-2 图A B解:距离A 为x 处的轴力为N ()F x Ax γ=⋅ 所以总伸长 2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3 图示结构,已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其方位角θ的大小。
《材料力学》课程教学(自学)基本要求
(1)确定 AB 段直径 d1 和 BC 段直径 d2 。
(2)若全轴选用同一直径,应为多少。 (3)主动轮,从动轮如何安排较合理。
第五章 弯曲内力 习题:5-7b、5-16
1.设 P、q、M0、L、a、b 均为已知,试用下列方法作剪力图与弯矩图,并求 Q max 及 上交作业 M ,并将这三种方法加以比较。见下图所示。
3.弯拐 ABC 如题 9-17 图 所示,AB 段截面为圆形,其直径为 d=5cm,试求 F 截面 的最大正应力、最大剪应 力、危险点的主应 力,以及该点按第 四强度理论计算 的相
4
当应力 xd4 。
第十章 压杆稳定 习题:10-11、10-20 1.题 10-11 图示细长立柱,L=6m,由两根 10 号槽钢组成,立柱上端为球铰支座,下 端为固定端。试问当 a 为多大时,立柱的临界载荷值最大?相应的 PLj=?已知材料 为 A3 钢, σ p=200MPa,E=200GPa。
5
2.题 2-10 图示刚架,已知 AC 和 CD 两部分的 I=3×103cm4,E=200GPa。试求截面 D 的水平位移和转角,若 P=10kN,L=1m。
3.重量为 Q 的重物自高度 H 下落冲击于梁的 C 点,设梁的 E、I 及抗弯截面模量 W 皆为已知量。试求梁内最大正压力及梁跨度中点的挠度,见题 2-31 图所示。
第二章 拉伸与压缩
习题:2-19、2-26 1.油缸盖与缸体采用 6 个螺栓联接。已知油缸内径 D=350mm,油压 p=1MN/m2,若 螺栓材料的许用应力为[σ ]=40 MN/m2,如题 2-19 图所示,求螺栓的内径。
2.某拉伸试验机的结构示意图如题 2-26 图所示。设试验机的 CD 杆与试件 AB 材料
材料力学附加习题.docx

第一章绪论1- 1求图示构件在a-a 和b-b 截面上的内力,并指出构件AB 发生何种基本变形。
1- 2四边形平板变形后为如图1-2所示的平行四边形,水平轴线在四边形AC 边保持不变,求1) 沿AB 边的平均线应变;2)平板A 点的剪应变。
第二章拉伸压缩与剪切图2-22- 2图示试件宽50mm,厚13mm,求和力-b 截面内的拉应力和剪应力,并求试件内的最大拉 应力和最大剪应力。
2- 3已知图示杆的许用应力为[<7](拉压许用应力的绝对值相同),截面面积为A,试求许用载荷[P ]。
2-1.试绘制如下各杆轴力图。
图2-1 图1-2p=3P/L‘4448N图2-3 图2-42-4图示桁架。
已知杆①的直径di=30mm,杆②的直径d2=20mm,材料的许用应力[cr]=160MPa,试求此桁架的许用载荷[P]等于多少?2-5受轴向拉力P作用的铭镒硅钢管,内外径尺寸为Z)xd = 30x27”泊,出现裂纹后需加套管修理。
若套管材料为20号钢,已知铭镒硅钢管的许用应力[crJ=500MPa,套管的许用应力为[cy2] = 100MPa。
求套管的外径D。
2-6对于图示对称的汇交杆系,已知各杆许用应力[可、材料比重「、距离D与载荷P。
试确定使结构重量w为最小时的杆件方向角a,并给出相应的横截面面积A。
a iaL图2-62-7若一拉伸试件的标距由50.000mm增加到50.030mm,直径由12.000mm减小到11.998mm, 对应的载荷为4.68kN,试确定材料的弹性模量及泊松比。
假设应力低于比例极限。
2-8图示阶梯形杆,已知载荷P=5kN,长L=400mm,截面面积A I=2A2=1 00mm2,^$性模量E=200GPa, 试求此杆的轴向变形。
O.5P --------------------------< --------- L ----------- ------------ L ---------- ►图2-82-9图示桁架,P=50kN,杆①为钢杆,杆②为木质杆,已知Ei=200GPa, E2=10GPa, Ai=400mm2, A2=8000mm2, L=1.5m,试用Willot作图法求节点A的水平位移,并用卡氏定理求节点A的垂直位移和水平位移。
材料力学学习 鹿山

,横 向 线 应 变 ε’ 为
,弹性模量
E为
GPa,泊松比 v 为
。
二、选择
1. 单位面积上的内力称为( )。 (A)正应力 ; (B)拉应力;
(C)应力; (D)压应力。
2. 与截面垂直的应力称为( )。 (A)正应力 ; (B)拉应力;
(C)压应力; (D)切应力。
3. 内力和应力的关系是( ) (A)内力大于应力 (C)内力是矢量,应力是标量
力称为
;构件抵抗变形的能力称为
;构件保持原有平衡状态的能力称为
。
5. 构件的承载能力,主要从
、
和
等三方面衡量。
6. 杆件变形的四种基本形式有
、
、
和
。
二、选择
1. 下列结论中,正确的是 (
)
(A) 材料力学主要研究各种材料的力学问题
(B) 材料力学主要研究各种材料的力学性质
(C) 材料力学主要研究杆件受力后变形与破坏的规律
图 10
三、作图(轴力图)
第 4页
共 50 页
应用本科《材料力学》同步练习册
四、计算
1.一木桩柱受力如图所示。柱的横截面为边长 200mm 的正方形,材料可认为符合胡克定律,其弹性 模量 E=10 GPa。如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的 纵向线应变;(4)柱端 A 的位移。
应用本科《材料力学》同步练习册
第 1 章 绪论
一、填空
1. 材料力学是对可变形固体作
、
、
局限于弹性变形范围内及 小变形假设 而研究的。
的三个基本假设后,再
2. 可变形固体的变形可分为
和 塑性变形 。
