土力学-土渗透性及渗流
合集下载
土力学 第2章 土的渗透性
n Vv Av 1 Av V A1 A
A > Av
v
vs
v n
Vs=q/Av V=q/A
(3)适用条件
v
层流(线性流):大部分砂土，粉土；
疏松的粘土及砂性较重的粘性土。
o
v=k i
v
v ki (a) 层流 i
(4)两种特例
密实粘性土：近似适用： v=k(i - i0 ) ( i >i0 ) i0：起始水力梯度
选取几组不同的h1和h2及对应的时间t=t2-t1，利用式(2-11)计算出相 应的渗透系数k，然后取其平均值作为该土样的渗透系数。
2. 现场井孔抽水试验
(1)室内试验的优缺点 优点：设备简单、操作方便、费用低廉。 缺点：取样和制样对土扰动、试样不一定是现场的代表性土，导致室内
测定的渗透系数难以反映现场土的实际渗透性。
☆水工建筑物防渗
一般采用“上堵下疏”原则。即上游截渗，延长渗径；下 游通畅渗透水流，减小渗透压力，防止渗透变形。
☆基坑开挖防渗
工程实例：
2003年7月1日，上海市轨道交通4号线发生一起管涌坍 塌事故，防汛墙塌陷、隧道结构损坏、周边地面沉降、造成 三幢建筑物严重倾斜。直接经济损失高达1.5亿人民币。
(2-34)
式中Fs为流土安全系数，通常取1.5~2.0。
பைடு நூலகம்
流土
(2)管涌(潜蚀) 定义：在渗流作用下土体的细土粒在粗土粒形成的孔隙通道中
发生移动并被带出的现象。 长期管涌破坏土的结构，最终导致土体内形成贯通的渗流 管道，造成土体坍陷。
管涌(土体内部细颗粒被带走)
管涌破坏(土体坍塌)
◆判别
①土类条件
2 土力学 第二章 土的渗透性及水的渗流
作用方向与渗流方向一致！
二、临界水力梯度及渗透破坏 当土中水向上渗流时，渗透力垂直向上而与土样重力方向相反，若渗透力 等于土样浮度，即
j = iγ w = γ , 得临界水力梯度： i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此，若土中水向上渗流： ⑴若i>icr，会发生流土破坏，即“管涌”； ⑵若i=icr，流土处于临界状态，即“悬浮”； ⑶若i<icr，不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小，hv≈0，因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为：
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差：
作业题：P54： 2-7，2-9 补题1：什么是渗透力、临界水力梯度？
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性：由于土中孔隙是相互连同 的，土体孔隙中的自由水会由于总水头 差而产生流动，这种土体被水透过的性 质，称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成：势水头 z、静水头hw和动水头hv，即：
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得，只能通过试验确定。 测定k值室内方法：定水头法、变水头法。 （1）定水头法 保持总水头差Δh不变，在t时间内，量得透过土样的水量为Q，求k： 根据达西定律
二、临界水力梯度及渗透破坏 当土中水向上渗流时，渗透力垂直向上而与土样重力方向相反，若渗透力 等于土样浮度，即
j = iγ w = γ , 得临界水力梯度： i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此，若土中水向上渗流： ⑴若i>icr，会发生流土破坏，即“管涌”； ⑵若i=icr，流土处于临界状态，即“悬浮”； ⑶若i<icr，不会发生流土破坏。
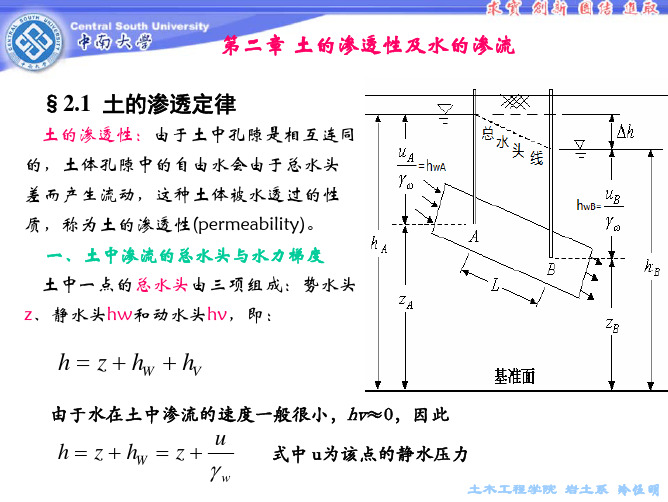
h = z + hW + hV
由于水在土中渗流的速度一般很小，hv≈0，因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为：
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差：
作业题：P54： 2-7，2-9 补题1：什么是渗透力、临界水力梯度？
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性：由于土中孔隙是相互连同 的，土体孔隙中的自由水会由于总水头 差而产生流动，这种土体被水透过的性 质，称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成：势水头 z、静水头hw和动水头hv，即：
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得，只能通过试验确定。 测定k值室内方法：定水头法、变水头法。 （1）定水头法 保持总水头差Δh不变，在t时间内，量得透过土样的水量为Q，求k： 根据达西定律
土力学：土的渗透性及渗流
13
3.3.2 流网特征及绘制
等势线表示测压管水头齐平的线，流线表示水质点的运动路线。
1、流网的特征
（1）等势线与流线正交；
（2）流线与等势线构成的各网格长宽比为常数，通常 b / L 1 ；
（3）相邻等势线之间的水头损失相等； （4）各流槽的渗流量相等。
即正交、等比、等水位差、等流量。
2、流网的绘制
土的渗透性及渗流
基本要求：
掌握土的层流渗透定律及渗透性指标；
熟悉渗透性指标的测试方法及影响因素，渗流时渗水量
的计算，渗透破坏与渗流控制问题； 了解二维渗流及流网的概念和应用。
1
本章内容
3.1 概述 3.2 土的渗透性 3.3 土中二维渗流及流网 3.4 渗透破坏与控制
2018/10/22
hi
Hi qy k iy
n
总水头差为： 用等效渗透系数
h hi q y
i 1 i 1
n
Hi k iy
k y表示
H h q y ky
ky H
因此：
k x 由 ki max 控制， k y 由 ki min 控制。
2018/10/22
H
i 1
n
i
/ kiy
12
t
2018/10/22
8
2、现场试验
在现场设置一个抽水井（直径15cm以上）和两个以上的观测井。边抽 水边观察水位情况，当单位时间从抽水井中抽出的水量 q 稳定，并且 抽水井及观测井中的水位稳定之后，测定抽水井和观测井的水位。
qk
dh 2rh dr
q
r2
r1
h2 dr 2k hdh h1 r
土力学-第3章土的渗透性及渗流
v k i
§3 土的渗透性及渗流
二. 土的层流渗透定律 适用条件：
层流（线性流）
§3.2土的渗透性 2. 达西定律
岩土工程中的绝大多数渗流问 题，包括砂土或一般粘土，均 属层流范围 在粗粒土孔隙中，水流形态可 能会随流速增大呈紊流状态， 渗流不再服从达西定律。 可用雷诺数Re进行判断：
• 室内试验方法1—常水头试验 法 试验装置：如图 试验条件: Δh，A，L=const 量测变量: Q，t 结果整理 Q=qt=vAt v=ki
三. 渗透试验及渗透系数
§3.2土的渗透性 1. 测定方法
h
土样
L Q
Q
i=Δh/L
QL k Ath
A
适用土类：透水性较大的砂性土
透水性较小的粘性土?
mgz
mg u w
u w
动能：
1 mv 2 2
E mgz mg u 1 mv 2 w 2
总能量：
质量 m 压力 u 流速 v 0 基准面
z
0
单位重量水流的能量：
u v2 h z w 2g
称为总水头，是水流动 的驱动力
水流动的驱动力 - 水头
16
§3 土的渗透性及渗流
§3.2土的渗透性
一．渗流基本概念
板桩墙
基坑
A B L
透水层
不透水层
渗流中的水头与水力坡降
17
§3 土的渗透性及渗流
§3.2土的渗透性
一．渗流基本概念 总水头－单位重量水体所具有的能量
u v2 h z w 2g
z：位置水 头 ：压力水 u/γ
w
uA w
Δh A
uB w
土质学与土力学土的渗透性与土中渗流
级配良好的土和 级配不良的土哪 一种土易发生管涌?
第22页/共35页
有效应力原理
（K.Terzaghi,1936) 1. 饱和土中的两种应力形态
饱和土是由固体颗粒构成的骨架和充满其间的水组成的两相体，当外力 作用于土体后一部分由土骨架承担，并通过颗粒之间的接触面进行应力的传 递．称之为粒间应力；另一部分则由孔隙中的水来承担，水虽然不能承担剪 应力，但却能承受法向应力．并且可以通过连通的孔隙水传递，这部分水压 力称为孔隙水压力。
第8页/共35页
土的渗透系数范围
土的类型
渗透系数 k(cm/s)
砾石、粗砂
a×10-1 ~ a×10-2
中砂
a×10-2 ~ a×10-3
细砂、粉砂
a×10-3 ~ a×10-4
粉土
a×10-4 ~ a×10-6
粉质粘土
a×10-6 ~ a×10-7
粘土
a×10-7 ~ a×10-10
第9页/共35页
n
h h1 h2 h3 hi i 1
将达西定律代入上式可得沿竖直方向的等效
渗透系数kz：
kz
H n hi k i 1 i
第12页/共35页
渗透力和渗透变形
(一)渗透力实验验证 当h1＝h2时，土中水处于静止状态，无渗流发生， 贮水器向上提升，使h1＞h2，由于存在水头差．土中产生向上的渗流。水 头差h是土体中渗流所损失的能量。能量损失说明土粒对水流给以阻力；反 之．渗流必然对每个土颗粒有推动、摩擦和拖曳的作用力，称之为渗透力，可 定义为每单位土体内土颗粒所受的渗流作用力，用 j表示。
第4页/共35页
达西定律的适用范围
达西定律是描述层流状态下渗透流速与水头损失关系的规律， 即渗流速度v与水力坡降i成线性关系只适用于层流范围。在土木 工程中，绝大多数渗流，无论是发生砂土中或一般的粘性土中， 均介于层流范围，故达西定律均可适用。
第22页/共35页
有效应力原理
（K.Terzaghi,1936) 1. 饱和土中的两种应力形态
饱和土是由固体颗粒构成的骨架和充满其间的水组成的两相体，当外力 作用于土体后一部分由土骨架承担，并通过颗粒之间的接触面进行应力的传 递．称之为粒间应力；另一部分则由孔隙中的水来承担，水虽然不能承担剪 应力，但却能承受法向应力．并且可以通过连通的孔隙水传递，这部分水压 力称为孔隙水压力。
第8页/共35页
土的渗透系数范围
土的类型
渗透系数 k(cm/s)
砾石、粗砂
a×10-1 ~ a×10-2
中砂
a×10-2 ~ a×10-3
细砂、粉砂
a×10-3 ~ a×10-4
粉土
a×10-4 ~ a×10-6
粉质粘土
a×10-6 ~ a×10-7
粘土
a×10-7 ~ a×10-10
第9页/共35页
n
h h1 h2 h3 hi i 1
将达西定律代入上式可得沿竖直方向的等效
渗透系数kz：
kz
H n hi k i 1 i
第12页/共35页
渗透力和渗透变形
(一)渗透力实验验证 当h1＝h2时，土中水处于静止状态，无渗流发生， 贮水器向上提升，使h1＞h2，由于存在水头差．土中产生向上的渗流。水 头差h是土体中渗流所损失的能量。能量损失说明土粒对水流给以阻力；反 之．渗流必然对每个土颗粒有推动、摩擦和拖曳的作用力，称之为渗透力，可 定义为每单位土体内土颗粒所受的渗流作用力，用 j表示。
第4页/共35页
达西定律的适用范围
达西定律是描述层流状态下渗透流速与水头损失关系的规律， 即渗流速度v与水力坡降i成线性关系只适用于层流范围。在土木 工程中，绝大多数渗流，无论是发生砂土中或一般的粘性土中， 均介于层流范围，故达西定律均可适用。
土力学土的渗透性和渗流
水平方向的h>垂直方向v
整理课件
4、渗透系数k的经验确定方法 ➢ 洁净不含细粒土的松砂 k=1.0-1.5(d10)2 ➢ 较密实、击实砂土
k=0.35(d15)2
➢ 黏性土 k=C3(en/1+e)
整理课件
5、成层土的等效渗透系数
（1）与层面平行的渗流的情况(水平渗透系数)
q1x k1
H1
qx q2x
kx
1 H
n
ki Hi
i1
整理课件
(2)垂直渗透系数
根据水流连续定理，通过整个 土层的渗流量等于通过各土层
k1
qy H1
q1y
k2
H2 H
k3
q2y H3
q3y
总水头损失等于各
的渗流量
qyq1yq2y qny
各土层的相应的水力坡降为i1、 i2、…、in，总的水力坡降为i
kyiA k1 i1A k2i2A kninA
2.管涌——在渗流作用下，土中的细小颗粒在粗颗粒形成的孔隙 中移动，随着土孔隙不断扩大，发生移动并被带出的现象， 渗透 速度不断增加，较粗的颗粒也相继被水流带走，最终导致土体内 形成贯通的渗流管道，造成土体塌陷。
土体在渗透水流作用下，细小颗粒被带出，孔隙逐渐增大，形成 能穿越地基的细管状渗流通道，掏空地基或坝体，使其变形或失 稳。管涌既可以发生在土体内部，也可以发生在渗流出口处，发 展一般有个时间过程，是一种整理渐课件进性的破坏
第3章 土的渗透性和渗流
整理课件
整理课件
土的渗透性及渗流
土的渗透性与土的强度、变形特性一起，是土力 学中的几个重要课题
土的渗透性研究的三个主要方面问题及其与工程 的关系
研究土的渗透性规律及其与工程的关系具有重要 意义，土的渗透性是反映土的孔隙性规律基本内 容之一
土力学-第三章土的渗透性及渗流
天津城市建设学院土木系岩土教研室
3.4.2 流砂或流土现象
土力学
在向上的渗流力的作用下，粒间的有效应力为零时，颗粒群 发生悬浮、移动的现象称为流砂现象或流土现象。
说明：流砂现象的产生不仅取决于渗流力的大小，同时与土的 颗粒级配、密度及透水性等条件有关
使土开始发生流砂现象时的水力梯度称为临界水力梯度icr
常用的有现场井孔抽水试验或井孔注水试验。 对于均质粗粒土层，现场测出的k值比室内试验得出的值要准确
观测孔 r2
Q
r r1
r处过水断面积为A=2πrh,假设该处
水力梯度i为常数，且等于地下水位
在该处的坡度时，i=dh/则dr
q=kAi=2πrhkdh/dr
dr
qdr/r=2πkhdh
d
分离变量积分
h
h h1
k3
q3y H3
总水头损失等于各层水头损失之和 Hi H1i1 H 2i2 H ni n
代入
垂直渗 透系数
ky
1 H
(i1H1
i2H2
inHn )
k1i1
k2i2
knin
整个土层与层面垂 直的平均渗透系数
k y
H1
H H2
Hn
H n ( Hi )
k1 k2
kn
k i1 iy
天津城市建设学院土木系岩土教研室
土力学
渗透系数k既是反映土的渗透能力的定量指标，也是渗流计算 时必须用到的一个基本参数。测定方法有：室内和现场
1.室内渗透试验测定渗透系数 （1）常水头试验————整个试 验过程中水头保持不变
适用于透水性大（k>10-3cm/s） 的土，例如砂土。
时间t内流出的水量 Q qt kiAt k h At L
土力学-第二章土的渗透性及渗流
1.达西渗透试验
试验前提：层流 试验装置：如图 试验条件: h1，A，L=const 量测变量: h2，V，t 试验结果 Δh=h1-h2 q=V/t
Δh↑，q↑ A↑，q↑ L↑， q↓
h q A L
q 断面平均流速 v A
h 水力梯度 i L
vi
23
2.达西定律
渗透定律
适用于粗颗粒土
水力梯度
h i L
渗流速度
由Darcy定律
v ki
L 平均流速 v nv v t nvL k h
39
三、成层土的平均渗透系数
天然土层多呈层状
确立各层的k
考虑渗流方向
等效渗透系数
40
水平渗流
将土层简化为均质土，便于计算
总流量等于各土层流量之和 （各层的水力梯度相等） 条件: im i h
库水位升降引发滑坡
17
第一节 土的渗透定律
一、水头 二、水力梯度 三、达西渗透定律
四、达西定律的适用范围
18
水流动的驱动力
水往低处流
位置：使水流从位置势能 高处流向位置势能低处
速度v
水往高处“跑”
压力u
流速：水具有的动能 压力：水所具有的压力势能
19
一、水头
水头 hydraulic head：单位重量的水所具有的能量。
渗流 渗透性 渗透特性 强度特性 变形特性
3
为什么要学习土的渗透性和水的渗流？
土的渗透性和水的渗流 直接影响 工程活动
（1） 渗透变形（破坏）问题 （2） 渗流量的计算问题
（3） 渗流变形控制问题
4
1、渗透变形（破坏）问题
因渗流造成土体变形甚至破坏
试验前提：层流 试验装置：如图 试验条件: h1，A，L=const 量测变量: h2，V，t 试验结果 Δh=h1-h2 q=V/t
Δh↑，q↑ A↑，q↑ L↑， q↓
h q A L
q 断面平均流速 v A
h 水力梯度 i L
vi
23
2.达西定律
渗透定律
适用于粗颗粒土
水力梯度
h i L
渗流速度
由Darcy定律
v ki
L 平均流速 v nv v t nvL k h
39
三、成层土的平均渗透系数
天然土层多呈层状
确立各层的k
考虑渗流方向
等效渗透系数
40
水平渗流
将土层简化为均质土，便于计算
总流量等于各土层流量之和 （各层的水力梯度相等） 条件: im i h
库水位升降引发滑坡
17
第一节 土的渗透定律
一、水头 二、水力梯度 三、达西渗透定律
四、达西定律的适用范围
18
水流动的驱动力
水往低处流
位置：使水流从位置势能 高处流向位置势能低处
速度v
水往高处“跑”
压力u
流速：水具有的动能 压力：水所具有的压力势能
19
一、水头
水头 hydraulic head：单位重量的水所具有的能量。
渗流 渗透性 渗透特性 强度特性 变形特性
3
为什么要学习土的渗透性和水的渗流？
土的渗透性和水的渗流 直接影响 工程活动
（1） 渗透变形（破坏）问题 （2） 渗流量的计算问题
（3） 渗流变形控制问题
4
1、渗透变形（破坏）问题
因渗流造成土体变形甚至破坏
土力学-土渗透和渗流
土 样 内 对 水 流 的 阻 力 : J ' = j ' L A = - J
（3）渗透力的计算 考虑下图的平衡条件得：
w h w A L A w j'L A w h 1 A
j' w(h1hwL)
L
w
h L
wi
j j' wi
由上式可知：渗透力是一种体积力（而不是面 力），其量纲与rw相同 渗透力的大小和水力梯度成正比，其方向与渗流 方向一致。 （4）临界水力梯度
Bernoulli’s Equation
z位能水头;u静水压力;w水重度;h-总水头
不 计 流 速 的 影 响 : h z u w
hA HAZA
HA uA /w
hB HBZB
HB uB /w
hhA hB
水力梯度i:
单位长度总水头 的变化
i h L
二、达西渗流定律：
1856年法国学者Darcy根据试验结果建立下式
v ki
v—渗流速度（宏观平均值）
k—渗透系数 q v A
q—单位时间流过截面A的水量（平均流量） A—垂直于渗流方向土的截面面积
Q—总流量（通过确定面积A） t —渗流时间
Q qt
渗透系数k的确定方法
实
验
方
法
室内试验方法定水头试验-适用于中.粗砂
变 水 头 试 验 - 适 用 于 粘 土 . 细 粒 土
2、土骨架与孔隙水分开考虑（见图3.8等号右端）
（1）土骨架反力 土 粒 有 效 重 量 ：
w’=r’·L·A 向下的总渗透力：
J=j·L·A 滤网向上的支承力：
P
（2）孔隙水的受力 ● 孔隙水重量+土
（3）渗透力的计算 考虑下图的平衡条件得：
w h w A L A w j'L A w h 1 A
j' w(h1hwL)
L
w
h L
wi
j j' wi
由上式可知：渗透力是一种体积力（而不是面 力），其量纲与rw相同 渗透力的大小和水力梯度成正比，其方向与渗流 方向一致。 （4）临界水力梯度
Bernoulli’s Equation
z位能水头;u静水压力;w水重度;h-总水头
不 计 流 速 的 影 响 : h z u w
hA HAZA
HA uA /w
hB HBZB
HB uB /w
hhA hB
水力梯度i:
单位长度总水头 的变化
i h L
二、达西渗流定律：
1856年法国学者Darcy根据试验结果建立下式
v ki
v—渗流速度（宏观平均值）
k—渗透系数 q v A
q—单位时间流过截面A的水量（平均流量） A—垂直于渗流方向土的截面面积
Q—总流量（通过确定面积A） t —渗流时间
Q qt
渗透系数k的确定方法
实
验
方
法
室内试验方法定水头试验-适用于中.粗砂
变 水 头 试 验 - 适 用 于 粘 土 . 细 粒 土
2、土骨架与孔隙水分开考虑（见图3.8等号右端）
（1）土骨架反力 土 粒 有 效 重 量 ：
w’=r’·L·A 向下的总渗透力：
J=j·L·A 滤网向上的支承力：
P
（2）孔隙水的受力 ● 孔隙水重量+土
土的渗透性和渗流问题
第二篇 土力学第四章 土的渗透性和渗流问题第一节 概述土是由固体相的颗粒、孔隙中的液体和气体三相组成的，而土中的孔隙具有连续的性质，当土作为水土建筑物的地基或直接把它用作水土建筑物的材料时，水就会在水头差作用下从水位较高的一侧透过土体的孔隙流向水位较低的一侧。
渗透：在水头差作用下，水透过土体孔隙的现象渗透性：土允许水透过的性能称为土的渗透性。
水在土体中渗透，一方面会造成水量损失，影响工程效益；另一方面将引起土体内部应力状态的变化，从而改变水土建筑物或地基的稳定条件，甚者还会酿成破坏事故。
此外，土的渗透性的强弱，对土体的固结、强度以及工程施工都有非常重要的影响。
本章将主要讨论水在土体中的渗透性及渗透规律，以及渗透力渗透变形等问题。
第二节 土的渗透性一、土的渗透规律——达西定律(一)渗流中的总水头与水力坡降液体流动的连续性原理：（方程式）dw v dw v w w ⎰⎰=2211 2211v w v w =1221w w v v = 表明：通过稳定总流任意过水断面的流量是相等的；或者说是稳定总流的过水断面的 平均流速与过水断面的面积成反比。
前提：流体是连续介质流体是不可压缩的；流体是稳定流，且流体不能通过流面流进或流出该元流。
理想重力的能量方程式（伯努利方程式1738年瑞士数学家应用动能定理推导出来的。
）c gv r p Z =++22饱和土体空隙中的渗透水流，也遵从伯努利方程，并用水头的概念来研究水体流动中 的位能和动能。
水头：实际上就是单位重量水体所具有的能量。
按照伯努利方程，液流中一点的总水头h ，可以用位置水头Z ，压力水头U/r w 和流速水 头V 2/2g 之和表示，即gv r u Z h w 22++= 4-1 此方程式中各项的物理意义均代表单位重量液体所具有的各种机械能，而其量纲都是 长度。
教材P37图22表示渗流在水中流经A ，B 两点时，各种水头的相互关系。
按照公式（4－1），A,B 两点的总水头可分别表示为：gv r u Z h A w A A A 22++= gv r u Z h B w B B B 22++= h h h B A ∆+=式中：Z A ，Z B ：为A ，B ，两点相对于任意选定的基准面的高度，代表单位重量液体 所具有的位能（位置高度）故称Z 为位置水头。
土力学-第三章土的渗透性及渗流
aL
At2
t1 lg
h1 h2
－adh=kAh/Ldt
分离变量 积分
k＝
aL
At2
t1 ln
h1 h2
天津城市建设学院土木系岩土教研系数
常用的有现场井孔抽水试验或井孔注水试验。 对于均质粗粒土层，现场测出的k值比室内试验得出的值要准确
第3章 土的渗透性及渗流
3.1 概述 3.2 土的渗透性 3.3 土中二维渗流及流网（了解） 3.4 渗透破坏与控制
土力学
天津城市建设学院土木系岩土教研室
第3章 土的渗透性及渗流
3.1 概述 3.2 土的渗透性 3.3 土中二维渗流及流网（了解） 3.4 渗透破坏与控制
土力学
天津城市建设学院土木系岩土教研室
渗流作用于单位土体的力
j
J AL
whA
AL
i
w
说明：渗透力j是渗流对单位土体的作用力，是一种体积力，其大 小与水力坡降成正比，作用方向与渗流方向一致，单位为kN/m3
天津城市建设学院土木系岩土教研室
3.4.2 流砂或流土现象
土力学
渗透力的存在，将使土体内部受力发生变化，这种变化对 土体稳定性有显著的影响
（3）土的饱和度
土中封闭气体阻塞渗流通道，使土的渗透系数降低。封闭气体含量愈多， 土的渗透性愈小。
（4）土的结构
细粒土在天然状态下具有复杂的结构，一旦扰动，原有的过水通道的形态、 大小及其分布都改变，k值就不同。扰动与击实土样的k值比原始的要小
（5）水的温度
粘滞系数随水温发生明显的变化。水温愈高，水的粘滞系数愈小，土的渗 透系数则愈大。
h v2 p z
土的渗透性和渗流
一、平面渗流的连续性分析
对于一个稳定的渗流来说，渗流场中各点的测管水头h 及流速v等仅是位置的函数而与时间无关，即： h = f (x, z)，v = g(x, z)。
z
vz+
v z z
dz
dz vx
图2-9 二维稳定 渗流场中
vz
的某微元
dx
vx+
vx x
dx
x
单位时间流入微元的水量为：
(b) 等效图
图2-8 层状土的垂直渗流情况
其特点有：
（1）通过各层土的流量与等效土层的流量均相 同，即：
qz = q1z = q2z = q3z = ∙∙∙∙∙，v = v1 = v2 = v3 = ∙∙∙∙∙∙ （2）流经等效土层的水头损失等于各土层的水
头损失之和，即：
Δh = Δh1 + Δh2 + Δh3 + ∙∙∙∙∙ = Σhi
分布规律，结合一定的边界条件后，求解该方
程即可得到此条件下的渗流场。
以上就是教材P50-51三个式子的由来。
求解拉普拉斯方程有以下四种方法：
（1）解析法 — 边界条件复杂时，难以求解；
（2）数值解法 — 差分法和有限元方法已应用越 来越广；
（3）实验法 — 用一定比尺的模型实验来模拟渗 流场，应用较广的是电比拟法等；
有
vx
kx
h x
，vz
kz
h z
，将这两式代入连续
方程(2-12)可得：
kx
2h x 2
kz
2h z 2
0
(2-13)
对于各向同性的均质土kx = kz，(2-13)还可变为：
土力学-土的渗透性及渗流
• 防止发生流土破坏的设计要求
所需入土深度
水力梯度 i h h 2h
临界水力梯度 i c r
w
所需入土深度 h Fs w h 2
地下连续墙
h
坑底
渗
透
h
力
向
上
地表
渗 透 力 向 下
• 管涌 piping 在渗流作用下，土中的细粒在粗粒形成的孔隙中移动以至流失→孔
z
（1）连续方程的建立
流入微单元的水量（厚度为1）
dqxvxdz1vxdz dqz vzdx dqxdqzvxdzvzdx
vx
dz
流出微单元的水量
(vz v zzdz)dx(vx v xxdx)dz
vz
vz z
dz
vx
vx x
dx
vz
dx
x
对稳定流，流入量＝流出量（忽略土体的变形） z
v x d z v z d x ( v z v z zd z )d x ( v x v x xd x )d z dz vx vx vz 0 x z
（2）水力梯度 水头 hydraulic head：单位重量的水所具有的能量。（故量纲为长度）
测压管水头
总水头 hzhwhv zu/wv2/2g hzu/w
势静 动
孔
渗
水水 水
隙
流
土中渗流速度通常较小，可忽略
头头 头
水
速
头位头压 头速
压
度
置力 度
水水 水
• 水力梯度
uA w
hA zA
测压管 piezometer tube
隙增大，渗流速度增加→粗粒流走→贯通的水流通道→土体塌陷。
管涌
土力学第二章土的渗透性和渗透问题
三．渗透系数的测定及影响因素
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
A
B
L
h1
h2
zA
zB
Δh
0
0
基准面
水力坡降线
总水头－单位质量水体所具有的能量
流速水头≈0
A点总水头：
B点总水头：
总水头：
水力坡降：
一．渗流中的水头与水力坡降
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
概述
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
概述
Teton坝
渗流量
渗透变形
渗水压力
渗流滑坡
土的渗透性及渗透规律
二维渗流及流网
渗透力与渗透变形
扬压力
土坡稳定分析
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 边坡渗流
§2.3 渗透力与渗透变形 Seepage force and seepage deformaton
学习目标
学习基本要求
参考学习进度
学习指导
学习目标
掌握土的渗透定律与渗透力计算方法，具备对地基渗透变形进行正确分析的能力。
掌握土的渗透定律
01
掌握二维渗流及流网绘制
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
A
B
L
h1
h2
zA
zB
Δh
0
0
基准面
水力坡降线
总水头－单位质量水体所具有的能量
流速水头≈0
A点总水头：
B点总水头：
总水头：
水力坡降：
一．渗流中的水头与水力坡降
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
概述
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
概述
Teton坝
渗流量
渗透变形
渗水压力
渗流滑坡
土的渗透性及渗透规律
二维渗流及流网
渗透力与渗透变形
扬压力
土坡稳定分析
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 边坡渗流
§2.3 渗透力与渗透变形 Seepage force and seepage deformaton
学习目标
学习基本要求
参考学习进度
学习指导
学习目标
掌握土的渗透定律与渗透力计算方法，具备对地基渗透变形进行正确分析的能力。
掌握土的渗透定律
01
掌握二维渗流及流网绘制
土力学 第3章 土的渗透性与渗流
（课本第42-43页）
假如： 总应力为σ，截面面积为A
有效应力为σs 土颗粒接触面积之和为As 孔隙水压力为uw 孔隙水截面面积之和为Aw 孔隙气压力为ua 气体截面面积之和为Aa
则：
u ' u ' u 'u u ' u
a
a
A s As uw Aw ua Aa
总 固 液 气
（课本第41页） 基坑降水和预防流砂发生的措施
1、井点降水：在基坑 周边打抽水井，把地 下水位降低到基坑下 0.5～1.0m。
注意：抽水泵不能停 电，否则水位恢复， 基坑浸水、地下室浮 起。
基坑
透水层 不透水层
基坑降水井点计算将在《基础工程》中学习
（课本第41页） 基坑降水和预防流砂发生的措施
h 渗透速度：v k L ki
或
渗流量为： q vA kiA
q——单位渗流量，cm3/s； v——渗透速度，cm/s； k——渗透系数，cm/s； i——水头梯度（△h/L） ； A——过水面积，cm2。 v——渗透速度是假想的平均渗流速度，不是地下水的实际流速，是土体 断面包括了土颗粒所占的面积的平均渗透速度，但水仅仅通过土体中的 孔隙流动。
2、设置地下连续墙或 钢板桩：在基坑周边 施工地下连续墙或打 钢板桩，隔断地下水，
基坑
同时在基坑内设置集 中井，把地下水位降 低到基坑下0.5～1.0m。
不透水层
透水层
流砂导致工程破坏示例 （课本第41-42页）
(a)基坑因流砂破坏；(b)河堤外覆盖层流砂涌出；(c)流 砂涌向基坑引起房屋不均匀沉降
渗流：指土中水在重力作用下穿过土中孔隙流动的现象。
渗透性：指土具有被水透过的性质。 引起工程 问题 渗漏问题——水库大坝、河流堤岸等水量损 失，甚至造成溃坝、决堤。 渗透稳定问题——引起土体应力、强度、变形 等变化，出现流砂、管涌问题， 造成滑坡、基坑或挡土墙失稳。
土力学 第3章 土的渗流
三、在稳定渗流作用作用下发生由上向下的渗流情况。此时在 土层表面b-b上的孔隙水应力与静水情况相同，仍等于γwh1，面aa平面上的孔隙水应力将因水头损失而减小，其值为
第三章 土的渗透性
a-a平面上的总应力仍保持不变，等于
于是，根据有效应力原理，a-a平面上的有效应力为
地下水按埋藏条件可分上层滞水、潜水、承压水3类。 上层滞水：存在于地面以下 局部隔水层上面的积水。分 布范围有限，是季节性或临 时性的水源。 潜水：埋藏在地面以下第一 个连续稳定的隔水层以上， 具有自由水面的地下水。潜 水的水面标高称为地下水位。 潜水水位往往低于上层滞水。 承压水：充满在两个稳定的 隔水层问的承受一定静水压 力的地下水。承压水上下都有 隔水层存在，它的埋藏区与补 给区不一致。 因此，承压水的动态变化， 受局部气候的影响不明显。
5
3-2
土的渗透性
一、达西渗透定律 由于土体中的孔隙一般非常微小，水在土体中流动时的粘滞阻力很大 、流速缓慢，因此，其流动状态大多属于层流，即相邻2个水分子运 动的轨迹相互平行而不混流。 著名的达西(Darcy)渗透定律：
渗透速度：
h v k ki L
或 渗流量为：
q vA kiA
qx q1x q2 x qnx qix
i 1
n
整个土层与层面平行的平均渗流系数为：
kx
1 H
k H
i 1 i
n
i
第三章 土的渗透性
如图3－6 (b) 所示与层面垂直的渗流情况。通过整个土层的总 渗流量qy应为各土层渗流量之总和，即
qy q1y q2 y qny
第三章 土的渗透性
a-a平面上的总应力仍保持不变，等于
于是，根据有效应力原理，a-a平面上的有效应力为
地下水按埋藏条件可分上层滞水、潜水、承压水3类。 上层滞水：存在于地面以下 局部隔水层上面的积水。分 布范围有限，是季节性或临 时性的水源。 潜水：埋藏在地面以下第一 个连续稳定的隔水层以上， 具有自由水面的地下水。潜 水的水面标高称为地下水位。 潜水水位往往低于上层滞水。 承压水：充满在两个稳定的 隔水层问的承受一定静水压 力的地下水。承压水上下都有 隔水层存在，它的埋藏区与补 给区不一致。 因此，承压水的动态变化， 受局部气候的影响不明显。
5
3-2
土的渗透性
一、达西渗透定律 由于土体中的孔隙一般非常微小，水在土体中流动时的粘滞阻力很大 、流速缓慢，因此，其流动状态大多属于层流，即相邻2个水分子运 动的轨迹相互平行而不混流。 著名的达西(Darcy)渗透定律：
渗透速度：
h v k ki L
或 渗流量为：
q vA kiA
qx q1x q2 x qnx qix
i 1
n
整个土层与层面平行的平均渗流系数为：
kx
1 H
k H
i 1 i
n
i
第三章 土的渗透性
如图3－6 (b) 所示与层面垂直的渗流情况。通过整个土层的总 渗流量qy应为各土层渗流量之总和，即
qy q1y q2 y qny
相关主题