数学实验0814作业
北京建筑工程学院考研专业课0814土木工程复习指南考研资料考研

北京建筑工程学院考研专业课0814土木工程复习指南考研资料考研我们并不会刻意地去在乎考研的结果,但我们每个人都渴望成功,冰冻三尺非一日之寒,希望大家能用行动去诠释一切,因为考研的结果早在考试之前就已经决定了。
——小明营销编者:wayne副主编:小明营销目录我们并不会刻意地去在乎考研的结果,但我们每个人都渴望成功,冰冻三尺非一日之寒,希望大家能用行动去诠释一切,因为考研的结果早在考试之前就已经决定了。
——小明营销一、北京建筑工程学院简介北京建筑工程学院是北京市唯一一所建筑类高校,始建于1936年,1977年经国务院批准,正式升格为本科院校,定名为北京建筑工程学院。
1982年被确定为国家首批学士学位授权高校,1986年获准为硕士学位授予单位,2002年被北京市确定为首都城市规划、建设、管理的人才培养基地与科技服务基地,2022年被确定为教育部卓越工程师培养计划试点单位,2022年通过国家特殊需求人才博士学位培养项目的专家评审,同年我校被北京市确定为“北京应对气候变化研究和人才培养基地”。
学校现设有10院3部,即建筑与城市规划学院、土木与交通工程学院、环境与能源工程学院、电气与信息工程学院、经济与管理工程学院、测绘与城市空间信息学院、机电与汽车工程学院、文法学院、理学院、继续教育学院、计算机教学与网络信息部、思想政治理论课教研部和体育部。
现有全日制在校生8169人,其中本科生6936人,硕士研究生1113人,留学生120人。
现有30个本科专业,其中教育部特色专业3个——建筑学、土木工程、建筑环境与设备工程;北京市特色专业7个——建筑学、土木工程、建筑环境与设备工程、给水排水工程、工程管理、测绘工程、自动化;现有12个硕士学位授权一级学科点,54个硕士学位授权二级学科点,8个硕士专业学位授权点。
学校现有专任教师710人,具有研究生学位的教师576人,其中具有博士学位的教师257人,高级专业技术职务的专任教师410人,具有正教授职务的108人。
华北水利水电大学数学实验课程设计作业
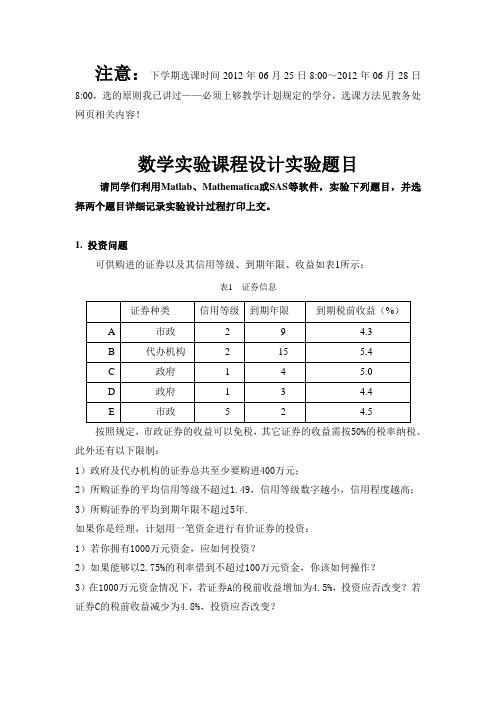
注意:下学期选课时间2012年06月25日8:00~2012年06月28日8:00,选的原则我已讲过——必须上够教学计划规定的学分,选课方法见教务处网页相关内容!数学实验课程设计实验题目请同学们利用Matlab、Mathematica或SAS等软件,实验下列题目,并选择两个题目详细记录实验设计过程打印上交。
1.投资问题可供购进的证券以及其信用等级、到期年限、收益如表1所示:表1 证券信息按照规定,市政证券的收益可以免税,其它证券的收益需按50%的税率纳税。
此外还有以下限制:1)政府及代办机构的证券总共至少要购进400万元;2)所购证券的平均信用等级不超过1.49,信用等级数字越小,信用程度越高;3)所购证券的平均到期年限不超过5年.如果你是经理,计划用一笔资金进行有价证券的投资:1)若你拥有1000万元资金,应如何投资?2)如果能够以2.75%的利率借到不超过100万元资金,你该如何操作?3)在1000万元资金情况下,若证券A的税前收益增加为4.5%,投资应否改变?若证券C的税前收益减少为4.8%,投资应否改变?2. 警察与小偷一偷窃嫌疑人在平面上沿椭圆以恒定的速率v=1跑步,若椭圆方程为: x=10+20cost, y=20+15sint,突然有一警察发现了他.,并从原点出发,以恒定速率w追向嫌疑人,警察的运动方向始终指向嫌疑人.请你分别求出w=20,w=5时警察的运动轨迹并画图。
3.生产计划问题某企业拟生产A和B两种产品,其生产投资费用分别为2100元/t和4800元/t. A、B两种产品的利润分别为3600元/t和6500元/t,A、B产品每月的最大生产能力分别为5t和8t;市场对这两种产品总量的需求每月不少于9t。
试问该企业应该如何安排生产计划,才能既能满足市场需求,又节约投资,而且使生产利润达到最大?4. 煤的成分分析已知煤的有机成分主要为碳(C)、氢(H)、氧(O)、氮(N)等元素,由于变质程度不同,它们的含量(%)也不同,煤的性能也不同。
西南交通大学数学实验作业全面版

实验课题一基础编程第一大题:编程完成下列计算1. 当x = 3, x =2π 时,求1sin()xy x e =+ 的值。
%第一大题 %1x=[3,2*pi];y1=sin(x)+exp(x) %{ y1 =1517/75 31594/59 %}2. 用冒号法作等差数列x = 2,4,6,8,10求对应的函数22y x =+%2x=2:2:10;y2=x.^2+sqrt(2*x) %{ y2 =6 3841/204 7143/181 68 3761/36 %}3. 已知:22,35,a b c e π===计算:31sin cos();532tan()cot .3a y b c a y b ⎛⎫=+⨯ ⎪⎝⎭⎛⎫= ⎪⎝⎭%3a=2*pi,b=35,c=exp(2); y31=sin(a/5)+cos(b)*c y32=tan(b)*cot(a/3) %{ y31 =-4060/709y32 =-1019/3725 %}4. 将数据格式转换成有理格式后,清屏后重新输出a ,b ,c ,y 31,y 32(提示:参数选项或format rational ,清屏clc ) %4format rationalclc5.查看工作空间已有变量及信息。
(提示:打开变量信息窗口或whos)%5whos%{Name Size Bytes Class AttributesA 3x3 72 doubleA1 3x3 72 doubleA2 1x1 8 doubleA3 3x3 72 doubleS 21x2 336 doubleX 1x21 168 doubleY 1x21 168 doublea 1x1 8 doublea1 1x1 8 doublea11 1x1 8 doublea2 1x1 8 doublea21 1x1 8 doublea3 1x1 8 doublea31 1x1 8 doubleb 1x1 8 doublec 1x1 8 doubles 1x1 8 doublex 1x2 16 doubley1 1x2 16 doubley2 1x5 40 doubley31 1x1 8 doubley32 1x1 8 doubley71 1x1 8 doubley72 1x1 8 double%}6.a1=-6.28 a2=7.46 a3=5.37将a1,a2,a3分别向零取整后赋给a11,a21,a31。
0814土木工程一级学科简介

0814土木工程一级学科简介一级学科(中文)名称:土木工程(英文)名称: Civil Engineering一、学科概况土木工程是建造各类工程设施的科学技术的统称。
它既指工程建设的对象,即建造在地下、地上、水中等的各类工程设施;也指其所应用的材料、设备和所进行的勘测、设计、施工、管理、保养、维修等专业技术。
土木工程虽是一个历史悠久的古老学科,但在其伴随着人类社会进步的发展和演变过程中不断被注入新的内涵,其中材料的变革和力学理论的发展起着重要的推动作用。
远古时代,人类筑土以居、架木为桥,以满足简单的生活和生产需要;后来,为了适应生产生活、宗教传播以及战争的需要,兴建了城池、宫殿、寺庙、桥梁、运河以及其他各种工程设施。
近代以来,随着自然科学的诞生和发展,土木工程作为一门科学技术进入了以实验为基础的定量分析阶段:在材料方面,已由木材、石料、砖瓦、石灰为主逐渐发展到使用铸铁、水泥、钢筋混凝土、土工织物、钢材;在应用理论方面,材料力学、土力学、结构设计理论等学科逐步形成,为工程结构的安全与经济提供了理论支撑;在施工技术方面,不断出现的新机械和新工艺带来了施工技术的进步、建设规模的扩大、建造质量及速度的提升,并最终使人类生活发生了前所未有的巨大变化。
二次世界大战以后,以现代社会生产力发展为动力、以计算机等现代科学技术为背景、以现代工程材料为基础、以现代施工技术与测试技术为手段,土木工程进入了一个高速发展的新时代。
超大跨度桥梁、超长隧道、超高建筑、高速铁路和高速公路等在世界各地相继大量兴建。
在中国,一大批超高、超长、超大的标志性工程设施陆续完工,标志着我国正由土木工程大国向土木工程强国迈进。
目前,面临地震、台风等自然灾害的频发、自然资源的短缺、人类居住环境恶化以及人类向高空延伸、向地下发展、向海洋拓宽、向沙漠进军、向太空迈进的探索与发展,使得土木工程建设进入低碳节能的可持续发展阶段,在空间域上从单纯单体工程分析发展到对整体系统网络和环境的综合分析与智能控制,在时间域上从单纯使用阶段的安全设计发展到工程全寿命周期的精细化设计与可靠性管理,在深度上从单纯依靠专一学科深化到依靠多学科的交叉。
江苏省如皋实验2024届数学八上期末学业质量监测试题含解析

江苏省如皋实验2024届数学八上期末学业质量监测试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题4分,共48分)1.如图,已知△ABC ≌△ADC ,∠B =30°,∠BAC =23°,则∠ACD 的度数为( )A .120°B .125°C .127°D .104°2.三个等边三角形的摆放位置如图,若∠3=60°,则∠1+∠2的度数为( )A .90°B .120°C .270°D .360°3.某芯片的电子元件的直径为0.0000034米,该电子元件的直径用科学记数法可以表示为( )A .0.34×10-6米B .3.4×10-6米C .34×10-5米D .3.4×10-5米4.下列物品不是利用三角形稳定性的是( )A .自行车的三角形车架B .三角形房架C .照相机的三脚架D .放缩尺5.如果340x y -=,那么代数式23()x y y x y -⋅+的值为( )A .1B .2C .3D .46.如图,等边三角形ABC 中,AD ⊥BC ,垂足为D ,点E 在线段AD 上,∠EBC=45°,则∠ACE 等于()A .15°B .30°C .45°D .60°7.将一次函数y =﹣2x +3的图象沿y 轴向上平移2个单位长度,则平移后的图象所对应的函数表达式为( ) A .y =﹣2x +1 B .y =﹣2x ﹣5 C .y =﹣2x +5 D .y =﹣2x +78.下列运算正确的是( )A .(8x 3-4x 2)÷4x = 2x 2-xB .x 5x 2 = x 10C .x 2y 3÷(xy 3)= x yD .(x 2y 3)2 = x 4y 59.直线l 上有三个正方形A 、B 、C 放置如图所示,若正方形A 、C 的面积分别为1和12,则正方形B 的面积为().A .11B .12C .13D .145 10.点()4,3-到y 轴的距离是( ).A .3B .4C .3-D .4-11.在等腰ABC ∆中,70A ∠=,则C ∠的度数不可能是( )A .40B .55C .65D .7012.已知115x y -=,则分式2322x xy yx xy y +---的值为( )A .1B .5C .12D .133二、填空题(每题4分,共24分)13.如图,△ABC 中,AB=AC ,∠BAC=120°,AD⊥AC 交 BC 于点 D ,AD=3,则BC=________.14.不等式13x -≥ 的解集为________. 15.如图,已知△ABC 是等边三角形,D 是AC 边上的任意一点,点B ,C ,E 在同一条直线上,且CE =CD ,则∠E =_____度.16.某校随机抽查了8名参加2019年成都市初中学业水平考试学生的体育成绩,得到的结果如下表:成绩(分)46 48 49 50 人数(人) 1 1 2 4则这8名同学的体育成绩的众数为_____.17.如图,已知//AB CD ,直线EF 分别交AB ,CD 于点E ,F ,EG 平分BEF ∠,若150∠=,则2∠的度数为__________.18.如果4,8,m na b ==那么232m n +=_______________________.(用含,a b 的式子表示)三、解答题(共78分)19.(8分)已知一次函数的图像经过点(—2,-2)和点(2,4)(1)求这个函数的解析式;(2)求这个函数的图像与y 轴的交点坐标.20.(8分)在等边三角形ABC 中,点P 在△ABC 内,点Q 在△ABC 外,且∠ABP =∠ACQ ,BP =CQ .(1)求证:△ABP ≌△A CQ ;(2)请判断△APQ 是什么形状的三角形?试说明你的结论.21.(8分)已知a ,b ,c 为△ABC 的三边长,且2261245a b a b +=+-.(1)求a ,b 值;(2)若△ABC 是等腰三角形,求△ABC 的周长.22.(10分)如图,已知A (0,4)、B (﹣2,2)、C (3,0).(1)作△ABC 关于x 轴对称的△A 1B 1C 1,并写出点B 的对应点B 1的坐标;(2)求△A 1B 1C 1的面积S .23.(10分)新乐超市欲招聘收银员一名,对A 、B 、C 三名候选人进行了三项素质测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如右表.新乐超市根据实际需要,将计算机、商品知识和语言表达能力测试得分按5:3:2的比例确定每人的成绩,此时谁将被录用?请写出推理过程.24.(10分)如图,点C 在线段AB 上,AD ∥EB ,AC =BE ,AD =BC ,CF 平分∠DCE .求证:CF ⊥DE 于点F .25.(12分)先化简,再求值:b (b ﹣2a )﹣(a ﹣b )2,其中a =﹣3,b =﹣5.26.(习题再现)课本中有这样一道题目:如图,在四边形ABCD 中,E F M ,,分别是AB CD BD ,,的中点,AD BC =.求证:EFM FEM ∠=∠.(不用证明)(习题变式)(1)如图,在“习题再现”的条件下,延长AD BC EF AD ,,,与EF 交于点N ,BC 与EF 交于点P ,求证:ANE BPE ∠=∠.(2)如图,在ABC ∆中,AC AB >,点D 在AC 上,AB CD =,E F ,分别是BC AD ,的中点,连接EF 并延长,交BA 的延长线于点G ,连接GD ,60EFC ∠=,求证:90AGD ∠=.参考答案一、选择题(每题4分,共48分)1、C【分析】证△ABC ≌△ADC ,得出∠B=∠D=30°,∠BAC=∠DAC=12∠BAD=23°,根据三角形内角和定理求出即可.【题目详解】解:∵在△ABC 和△ADC 中AB AD AC AC BC CD =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC ,∴∠B=∠D=30°,∠BAC=∠DAC=12∠BAD=12×46°=23°, ∴∠ACD=180°-∠D-∠DAC=180°-30°-23°=127°,故选C .【题目点拨】本题考查了全等三角形的性质和判定和三角形内角和定理的应用,注意:全等三角形的对应角相等.2、B【分析】先根据图中是三个等边三角形可知三角形各内角等于60°,用∠1,∠2,∠3表示出△ABC 各角的度数,再根据三角形内角和定理即可得出结论.【题目详解】∵图中是三个等边三角形,∠3=60°, ∴∠ABC=180°-60°-60°=60°,∠ACB=180°-60°-∠2=120°-∠2,∠BAC=180°-60°-∠1=120°-∠1,∵∠ABC+∠ACB+∠BAC=180°,∴60°+(120°-∠2)+(120°-∠1)=180°,∴∠1+∠2=120°.故选B.【题目点拨】考查的是等边三角形的性质,熟知等边三角形各内角均等于60°是解答此题的关键.3、B【解题分析】试题解析:0.0000034米63.410-=⨯米.故选B.4、D【解题分析】试题分析:只要三角形的三边确定,则三角形的大小唯一确定,即三角形的稳定性.解:A ,B ,C 都是利用了三角形稳定性,放缩尺,是利用了四边形不稳定性.故选D .考点:三角形的稳定性.5、A【解题分析】先计算括号内分式的减法,再将除法转化为乘法,最后约分即可化简原式,继而将3x=4y代入即可得.【题目详解】解:∵原式=223 x yy x y-•+=()()3 x y x yy x y +-•+=33 x yy-∵3x-4y=0,∴3x=4y原式=43y yy-=1故选:A.【题目点拨】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.6、A【分析】先判断出AD是BC的垂直平分线,进而求出∠ECB=45°,即可得出结论.【题目详解】∵等边三角形ABC中,AD⊥BC,∴BD=CD,即:AD是BC的垂直平分线,∵点E在AD上,∴BE=CE,∴∠EBC=∠ECB,∵∠EBC=45°,∴∠ECB=45°,∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACE=∠ACB-∠ECB=15°,故选A.【题目点拨】此题主要考查了等边三角形的性质,垂直平分线的判定和性质,等腰三角形的性质,求出∠ECB是解本题的关键.7、C【分析】直接利用一次函数平移规律“上加下减”即可得到答案.【题目详解】∵将一次函数y=﹣2x+3的图象沿y轴向上平移2个单位长度,∴平移后所得图象对应的函数关系式为:y =﹣2x +3+2,即y =﹣2x +1.故选:C .【题目点拨】本题主要一次函数平移规律,掌握一次函数平移规律“左加右减,上加下减”是解题的关键.8、A【分析】根据整式的除法法则、同底数幂相乘的法则、积的乘方和幂的乘方法则对各选项进行分析即可求解.【题目详解】(8x 3﹣4x 2)÷4x =2x 2﹣x ,故选项A 正确; x 1x 2 =x 7≠x 10,故选项B 错误;x 2y 3÷(xy 3)=x≠x y ,故选项C 错误;(x 2y 3)2=x 4y 6≠x 4y 1.故选项D 错误.故选:A .【题目点拨】本题考查了同底数幂的乘法、多项式除以单项式、单项式除以单项式及积的乘方,题目比较简单,掌握整式的运算法则是解决本题的关键.9、C【分析】运用正方形边长相等,再根据同角的余角相等可得EDF HFG ∠=∠,然后可依据AAS 证明EDF ∆≌HFG ∆,再结合全等三角形的性质和勾股定理来求解即可.【题目详解】解:∵A 、B 、C 都是正方形,∴DF FH =,90DFH ∠=︒,90EDF HFG ∴∠=∠=︒∴90DFE HFG ∠+∠=︒,90EDF DFE ∠+∠=︒∴EDF HFG ∠=∠,在DEF ∆和FGH ∆中,,EDF HFG DEF HGF DF HF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴EDF ∆≌HFG ∆ (AAS),DE FG ∴=,EF HG =;∴在Rt DEF 中,由勾股定理得:22222DF DE EF DE HG =+=+,即11213B A C S S S =+=+=,故选:C .【题目点拨】此题主要考查对全等三角形和勾股定理的综合运用,发现两个直角三角形全等是解题的关键.10、B【分析】根据平面直角坐标系内的点到y 轴的距离就是横坐标的绝对值,即可得到结果.【题目详解】解:∵点()4,3-的横坐标为-4,∴点()4,3-到y 轴的距离是4,故选:B .【题目点拨】本题考查了平面直角坐标系内点的坐标,属于基础题目.11、C【分析】根据等腰三角形的定义,分A ∠ 是顶角还是底角3种情况进行讨论分析确定答案.【题目详解】当C ∠是顶角时,B 和A ∠是底角,=18070240C ∠︒-︒⨯=︒ ,当C ∠和B 是底角时,A ∠是顶角,=(18070)2=55C ∠︒-︒÷︒,当C ∠和A ∠是底角时,B 是顶角,==70C A ∠∠︒.所以不可能是65.故选:C .【题目点拨】考查等腰三角形的定义,确定相等的底角,注意分情况讨论,分类不要漏掉情况.12、A 【分析】由115x y-=,得x ﹣y =﹣5xy ,进而代入求值,即可. 【题目详解】∵115x y-=,∴5y x xy-=,即x ﹣y =﹣5xy , ∴原式=2()31031252x y xy xy xy x y xy xy xy -+-+==----, 故选:A .【题目点拨】本题主要考查分式的求值,掌握等式的基本性质以及分式的约分,整体代入是解题的关键.二、填空题(每题4分,共24分)13、9【分析】根据勾股定理求出AB ,再利用相似即可求解.【题目详解】∵AB=AC ,∠BAC=120°∴∠C=30°,又∵AD ⊥AC ,AD=3∴∠DAC=90°,CD=6勾股定理得,由图可知△ABD ∽△BCA ,∴BC=9【题目点拨】本题考查了勾股定理和相似三角形,属于简单题.证明相似是解题关键.14、3x ≤-【解题分析】首先去分母,再系数化成1即可;【题目详解】解:去分母得: -x≥3系数化成1得: x≤-3故答案为:x≤-3【题目点拨】本题考查了解一元一次不等式,主要考查学生的计算能力.15、1.【分析】根据等边三角形的性质得出∠ACB =60°,然后根据等腰三角形的性质以及三角形外角的性质即可求得∠E .【题目详解】解:∵△ABC 是等边三角形,∴∠ACB =60°,∵CE =CD ,∴∠E =∠CDE ,∵∠ACB =∠E +∠CDE ,∴∠E =12ACB ∠=1°,故答案为1.【题目点拨】本题考查等边三角形的性质,关键在于牢记基础知识,通过题目找到关键性质.16、1【分析】结合表格根据众数的概念求解即可.【题目详解】10名学生的体育成绩中1分出现的次数最多,众数为1;故答案为:1.【题目点拨】本题考查了众数的知识,掌握知识点的概念是解答本题的关键.17、65︒【分析】先由AB ∥CD 得出∠1+∠BEF=180°,∠2=∠BEG ,再根据角平分线及∠1的度数求出∠BEG 的度数即可.【题目详解】解:∵AB ∥CD ,∴∠1+∠BEF=180°,∠2=∠BEG又∵∠1=50°,∴∠BEF=130°,又∵EG 平分∠BEF ,∴∠FEG=∠BEG=65°,∴∠2=∠BEG=65°故答案为:65°.【题目点拨】本题考查了角平分线的定义、平行线的性质,解题的关键是求出∠BEF 的度数.18、ab【分析】直接利用同底数幂的乘法运算法则将原式变形进而得出答案.【题目详解】解:(1)∵4,8,m n a b ==∴232,2m n a b ==,∴232m n +=23m n a a a b ⋅=⋅;故答案为ab.【题目点拨】本题考查了同底数幂的乘法及幂的乘方的逆运算,正确掌握运算法则是解题的关键.三、解答题(共78分)19、(1);(2)(0,1) 【分析】设函数关系式为,由图像经过点(—2,-2)和点(2,4)根据待定系数法即可求得这个函数的解析式,再把x=0代入求得的函数解析式即可得到这个函数的图像与y 轴的交点坐标.【题目详解】解:(1)设函数关系式为∵图像经过点(—2,-2)和点(2,4) ∴,解得 ∴这个函数的解析式为; (2)在中,当x=0时,∴这个函数的图像与y 轴的交点坐标为(0,1).点睛:待定系数法求函数关系式是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.20、 (1)证明见解析;(2) △APQ 是等边三角形.【分析】(1)根据等边三角形的性质可得AB =AC ,再根据SAS 证明△ABP ≌△ACQ ;(2)根据全等三角形的性质得到AP =AQ ,再证∠PAQ = 60°,从而得出△APQ 是等边三角形.【题目详解】证明:(1)∵△ABC 为等边三角形, ∴AB =AC ,∠BAC =60°, 在△ABP 和△ACQ 中,AB AC ABP ACQ BP CQ =⎧⎪∠=∠⎨⎪=⎩∴△ABP ≌△ACQ (SAS ),(2)∵△ABP ≌△ACQ , ∴∠BAP =∠CAQ ,AP =AQ ,∵∠BAP +∠CAP =60°, ∴∠PAQ =∠CAQ +∠CAP =60°,∴△APQ 是等边三角形.【题目点拨】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了正三角形的判定,本题中求证,△ABP ≌△ACQ 是解题的关键.21、(1)3,6a b ==;(2)1.【分析】已知等式配方后,利用非负数的性质求出a 与b 的值,即可确定出三角形周长.【题目详解】解:(1)∵2261245a b a b +=+-,∴226912360a a b b -++-+=,∴()()22360a b -+-=,∴30a -=,60b -=,∴3a =,6b =,(2)∵ABC ∆是等腰三角形,∴底边长为3或6,由三角形三边关系可知,底边长为3,∴ABC ∆的周长为66315++=,即ABC ∆的周长为1.【题目点拨】此题考查了因式分解的应用,三角形三边关系的应用,熟练掌握完全平方公式是解本题的关键.22、 (1) B 1(﹣2,﹣2) (2) 1【解题分析】试题分析:(1)根据关于x 轴对称点的坐标特点,分别找出A 、B 、C 三点的对称点坐标,然后描出对称点,再连接可得△A 1B 1C 1,根据图形可直接写出点B 1的坐标即可;(2)利用矩形的面积减去周围多余小三角形的面积即可.试题解析:(1)如图△A 1B 1C 1即为所求作,B 1(﹣2,﹣2);(2)△A 1B 1C 1的面积:S=4×5﹣(2×2+2×5+3×4)=1.23、候选人A 将被录用 【分析】按照5:3:2的比例计算出三人的加权平均数,然后进行比较即可得解.【题目详解】解:∵候选人A 的综合成绩为:85570364276.3532⨯+⨯+⨯=++候选人B 的综合成绩为:73571372272.2532⨯+⨯+⨯=++ 候选人C 的综合成绩为:73565384272.8532⨯+⨯+⨯=++ ∴将计算机、商品知识和语言表达能力测试得分按5:3:2的比例确定每人的成绩,则候选人A 的综合成绩最好,候选人A 将被录用.【题目点拨】本题考查了加权平均数的应用,熟练掌握加权平均数的算法是解题的关键.24、证明见解析.【分析】根据平行线性质得出∠A=∠B ,根据SAS 证△ACD ≌△BEC ,推出DC=CE ,根据等腰三角形的三线合一定理推出即可.【题目详解】∵AD∥BE,∴∠A=∠B.在△ACD 和△BEC 中∵,∴△ACD≌△BEC(SAS ),∴DC=CE . ∵CF 平分∠DCE,∴CF⊥DE(三线合一).【题目点拨】本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质等知识点,关键是求出DC=CE ,主要考查了学生运用定理进行推理的能力.25、﹣a 2,﹣1【分析】原式利用单项式乘以多项式,以及完全平方公式化简,去括号合并得到最简结果,把a 与b 的值代入计算即可求出值.【题目详解】解:原式= b 2﹣2ab ﹣(a 2-2ab +b 2)=b 2﹣2ab ﹣a 2+2ab ﹣b 2=﹣a 2,当a =﹣3时,原式=﹣1.【题目点拨】本题主要考查了整式的化简求值,涉及到的知识有:完全平方公式,合并同类项,单项式乘以多项式,在求代数式的值时,一般先化简,再把各字母的取值代入求值.26、(1)见解析;(2)见解析【分析】(1)根据中位线的性质及平行线的性质即可求解;(2)连接BD ,取BD 的中点H ,连接EH FH ,,根据中位线的性质证明AFG ∆为等边三角形,再根据AF FD=得到GF FD =,得到30FGD FDG ∠=∠=︒,即可求解.【题目详解】解:(1) ∵E F M ,,分别是AB CD BD ,,的中点,∴MF BP ,12MF BC =,MFE BPE ∠=∠. ∴ME AN ∥,12ME AD =,MEF ANE ∠=∠. ∵AD BC =,∴ME MF =,∴EFM FEM ∠=∠,∴ANE BPE ∠=∠.(2)连接BD ,取BD 的中点H ,连接EH FH ,.∵,E F ,,H 分别是BC AD ,,BD 的中点∴HF BG ,12HF AB =,HFE FGA ∠=∠. ∴HE AC ,12HE CD =,60HEF EFC ∠=∠=︒. ∵AB CD =,∴HE HF =,∴60HFE EFC ∠=∠=︒,∴60AGF ∠=︒,∵60AFG EFC ∠=∠=︒,∴AFG ∆为等边三角形.∴AF GF =,∵AF FD =,∴GF FD =,∴30FGD FDG ∠=∠=︒,∴603090AGD ∠=︒+︒=︒.【题目点拨】该题以三角形为载体,以考查三角形的中位线定理、等腰三角形的判定等重要几何知识点为核心构造而成;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.。
数学实验课习题总结(带答案)

第二次实验内容
1、求下列方程的根 1)ex-3x=0, 在[-1,1]上的近似解,使用 fzero,fsolve 分 别进行求解 2 )判定方程 x7+2x5+3x3+5x+7=0 有几个实根,并使用 roots,fzero,fsolve 分别进行求解,也使用牛顿法编程计算 问题的近似解。 2、求解线性方程组:
答案:
1. 程序设计: (1) fzero('exp(x)-3*x',[-1,1]) fsolve('exp(x)-3*x',[-1,1]) (2)函数 fun1: function ff=fun1(x) ff=(x^7+2*x^5+3*x^3+5*x+7)/(7*x^6+10*x^4+9*x^2+5); 程序: x=-1:0.01:1; y=x.^7+2*x.^5+3*x.^3+5*x+7; plot(x,y,'r-') gtext('零点') grid on 数 p=[1,0,2,0,3,0,5,7]; roots(p) fzero('x^7+2*x^5+3*x^3+5*x+7',0) fsolve('x^7+2*x^5+3*x^3+5*x+7',0) x0=1; x1=x0-fun1(x0); while abs(x1-x0)>=0.0001 x0=x1; x1=x0-fun1(x0); end x0 结果: (1) ans = 0.6191 0.6191 (2)有 1 个实根,如右图 ans = 1.0633 + 0.8552i 1.0633 - 0.8552i 0.1980 + 1.4799i 0.1980 - 1.4799i -0.8442 + 1.1442i -0.8442 - 1.1442i -0.8341 ans = -0.8341 %画图法判断实根个
数学实验(MATLAB)课后习题答案
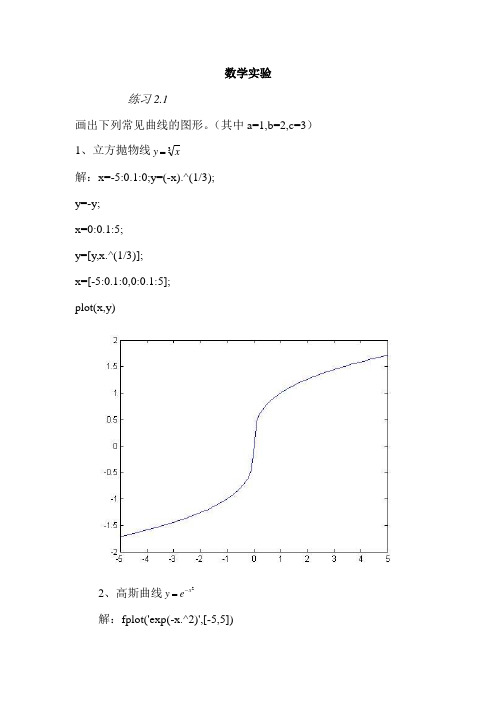
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
中考数学学生动手实验类型题集锦

笔趣阁 汽车动力性的评价指标是什么? 患者,女性,60岁,高血压病史20年。2小时前突发左眼视力丧失,自诉似"电灯开关关闭"。眼底检查。最可能的诊断是()A.视网膜中央动脉栓塞B.急性球后视神经炎C.颅内肿瘤D.视网膜中央静脉栓塞E.视网膜血管炎 什么是商业秘密? 放射自显影的基本原理是。A.利用感光材料能改变物质的密度B.放射能使感光材料分解C.放射性核素使感光材料发光D.利用射线能使感光材料感光E.利用自动探测仪器测量组织中的放射性分布 每个项目有项目生命周期,建设项目也不例外,其生命周期包括自项目各个阶段。A.施工开始至建成后生产运营B.设计开始至竣工保修C.决策评估开始至竣工保修D.施工开始至竣工保修 距离近段在46-76厘米之间的距离称为。A.亲密距离B.个人距离C.社交距离D.公众距离 施工准备工作的具体内容总体上应包括技术准备、工程准备、。A.对外协作B.编制单项工程施工组织设计C.劳动力准备D.物资准备E.编制土建工程施工组织设计 简述中国公共关系职业道德规范的形成过程。 岗前培训结束后要进行客服代表的级资格认证考核,按照认证标准要求培训时长要达到标准学时。 用玻璃离子水门汀缘需做小斜面D.可不要求固位形E.洞底可呈圆弧形 矿业土木工程竣工资料分为工程质量验收评定资料、工程质量控制资料、工程安全与功能检验资料、工程观感质量检查资料和。A.验收记录B.施工图C.竣工图D.验收总结 从有正常菌群存在的部位所采取的标本应接种在哪种培养基中分离培养病原菌A.增菌培养基B.营养培养基C.选择鉴别培养基D.基础培养基E.特殊培养基 2型糖尿病发病机制是A.胰岛素拮抗激素分泌增多B.胰岛素B细胞遗传缺陷C.胰岛素抵抗和胰岛素分泌缺陷D.胰岛B细胞破坏,胰岛素绝对不足E.胰岛B细胞自身免疫反应性损伤 百科全书的特点不包括。A.以条目为基本单元B.条目之间互不交叉但可以重复、条目释文长短基本相当,一般不超过500字C.条目一般由条头、释文和参考文献构成D.索引往往单独编为一卷 飞机进近着陆中,当下降高度到过渡高度层后,高度表应拨正到.A.QFEB.QNHC.QNE [单选,案例分析题]病历摘要:患者男性,50岁。平地跳跃后觉腰部剧痛伴左下肢疼痛,左腰3~4、4~5棘间及棘旁压痛,小腿前内侧、膝前部、足背内侧浅感觉减退。左直腿抬高30°实验明显阳性。神经根受累及的范围主要为A.L4神经B.L5神经C.L3-4神经D.L神经E.L3-5神经 硝酸铵灭火剂可扑救易燃液体、可燃气体、电气设备的火灾.A.正确B.错误 颤震的风阳内动证的治法为A.清热化痰熄风B.活血化瘀,熄风定颤C.填精益髓D.补益气血,熄风定颤E.育阴潜阳 企业可以选择自上而下的方法、自下而上的方法或上下结合的方法来制定战略方案。三种战略制定方法的主要区别在于战略制定中对的把握。A.集权与侵权程度B.内部资源能力与外部环境平衡C.整体利益与局部利益平衡D.刚性与弹性程度 患者的双眼对光反射丧失,调节反射存在,瞳孔缩小,最可能的诊断是A.Parinaud综合征B.Horner综合征C.ArgyllRobertson瞳孔D.Adie瞳孔 一般而言,国家规定制度,是为了充分保护用户通信自由和通信秘密,也是邮政实现普遍服务的必要保障。A.邮政专用权B.邮政经营权C.邮政特许权D.邮政专营权 重症急性胆管炎的五联征是A.腹痛、纳差、消瘦、发热、黄疸B.腹痛、发热、黄疸、血压下降、精神症状C.腹痛、呕吐、腹泻、发热、黄疸D.腹痛、纳差、呕吐、发热、黄疸 叫改丝,改丝时,先用个钻头,钻头直径可凭经验公式计算,对于脆材料,钻头直径d=。 肾病综合征的治疗,下列不合适的是A.大剂量激素B.抗凝治疗并辅以血小板解聚药C.用襻利尿剂冲洗管型,碱化尿液以防管型形成D.预防性用抗生素E.急性肾衰竭适时透析 客服中心统计分析工作主要分为运营类、及管理类。 矿业工程是大型综合性建设项目,除了生产系统复杂外,还具有的特点。A.施工组织简单B.工程投资大C.建设周期长D.组织关系复杂E.对环境影响小 中国人民银行在国务院领导下,,,维护金融稳定。 预激综合征发作房颤时药物不宜选用A.洋地黄B.胺碘酮C.普罗帕酮D.维拉帕米E.艾司洛尔 《川西钻探公司环境保护管理办法》规定,井场周围造成局部污染,责任性赔、罚款在的为较大环境污染事故。A、6000-10000;B、10000-50000;C、50000-80000。 对于医疗职业风险,你有何认识? 在整个反射弧中,最易出现疲劳的部位是A.感受器B.传入神经元C.反射中枢中的突触D.传出神经元E.效应器 ().A.OB.1C.∞D.2 内膜增生过长最容易发展为子宫内膜癌的是。A.单纯型增生过长B.不典型增生过长C.复杂性增生过长D.腺囊型增生过长E.腺瘤型增生过长 男性,68岁。反复咳嗽、咳痰20余年,痰液粘稠,咳痰不爽。近2~3年气急渐进性加重。昨起感气急、胸闷,咳嗽亦有加重,前来门诊,下列处方中哪项是不妥当的A.庆大霉素80000U,肌肉注射,每日2次B.溴己新.(必嗽平)16mg,口服,每日3次C.异丙托品气雾剂吸入D. 复方甘草合剂10ml,口服,每日3次E.茶碱控释片0.2g,口服,每日1~2次 迟发性输血不良反应是。A.过敏反应B.细菌污染反应C.输血相关性移植物抗宿主病D.循环超负荷E.枸橼酸盐中毒 下列有关信息的说法正确的是A、自从出现人类社会才有信息存在B、只有计算机才能处理信息C、第一次信息革命指的是语言的形成D、信息只能存储在计算机中 女性,26岁,右乳外上象限有一直径约2cm大小的圆形肿块,边界清楚,表面光滑,可移动,不疼。此肿块最可能是A.乳腺癌B.乳腺增生症C.乳腺纤维瘤D.乳腺纤维腺瘤E.乳腺炎症性肿块 下列哪项不是角膜接触镜的特性。A.消除棱镜的作用B.与框架镜相比,增加物像放大率C.更好的立体视觉D.更大的视野E.对于轻中度的圆锥角膜有较好的矫正作用 尸检中,在肝脏及十二指肠取出之前先检查胆道,即挤压胆囊,观察胆道是否畅通,该项检查在如下哪种情况死亡的病例中必不可少、是有意义的检查项目A.青壮年猝死B.长期慢性肝脏疾病死亡者C.胆囊结石和慢性胆囊炎死亡者D.怀疑胆心综合征死亡者E.新生儿黄疸死亡者 汽车的车身可以与车架分开的是。A.承载式车身B.半承载式车身C.非承载式车身
丙二酸—溴酸钾体系的化学振荡反应—0814 郭璁

voltage/mv
0
-200 -250 0 5 10 15 20
t/min
t/min
v=10ml
50 50
v=13ml
0
0
-50
voltage/mv
voltage/mv
-50
-100
-100
-150
-150
-200
-200
-250 -2 0 2 4 6 8 10 12 14 16 18
-2
0
2
4
6
7
10
13
17
5.1316
3.92
5.325
6.455
6.82
2.933
1.296
1.266
1.4213
1.228
第 8 页 共 13 页
12 11 10 9
A B C D
丙二酸 硫酸铈铵 浓硫酸 溴酸钾
t/min
8 7 6 5 4 4 6 8 10 12 14 16
v/ml
反应物浓度对诱导时间的影响
35
100 30
100
50
50
0
0
voltage/mv
voltage/mv
-50
-50
-100
-100
-150
-150
-200
-200
-2 0 2 4 6 8 10 12 14 16
-2
0
2
4
6
8
10
12
14
t/min
t/min
40
100 50 40 0 20 80 60
45
voltage/mv
voltage/mv
华工数学实验报告

华工数学实验报告篇一:华工数学实验报告微分方程《数学实验》报告学院:电子信息学院专业班级:信息工程电联班学号:姓名:实验名称:微分方程实验日期:XX/04/191.实验目的了解求微分方程解析解的方法了解求微分方程数值解的方法了解 dsolve,ode45 指令的使用方法2.实验任务1.用dsolve函数求解下列微分方程?y??(x)?y?(x)?2y(x)(2)? ?y(0)?1,y(0)?0?2. 我辑私雷达发现,距离d处有一走私船正以匀速a 沿直线行驶,缉私舰立即以最大速度(匀速v)追赶。
若用雷达进行跟踪,保持船的瞬时速度方向始终指向走私船,则辑私舰的运动轨迹是怎么的?是否能够追上走私船?如果能追上,需要多长时间?M03.实验过程3.1实验原理dsolve(‘equation’,’condition’,’v’)(1) equation是方程式,condition是条件,v是自变量(缺省为t)(2)若不带条件,则解中带积分常数(3)如果没有显示解,则系统尝试给出隐式解(4)如果无隐式解,则返回空符号。
以S0为原点建立坐标系。
设缉私船出发的起点坐标为,根(x0,y0)据题意x02?y02?d2,经过时间t,走私船到达S(at,0),缉私船到达M(x,y),追赶时,缉私船总是向走私船所在的位置追赶,设在t+dt时刻,缉私船到达M'(x?dx,y?dy),则M,M’,S三点一图2 dt时刻追击图由图可知,即 dy0?y? dxat?x(1)?ydx?at?x dy(2) 此即缉私船的追辑模型。
方程(2)两边对y求导,得 d2xdt?y2?a dydy(3) 又因为缉私船的速度恒为v,因此即dy?dt?dy??dx?v2?????? ?dt??dt?22(4) (5)?x(y0)?x0?把方程(5)代入(3),并结合初始条件:?x0,可知,x'(y)?0?y0?求解模型(2),即求解如下模型??yx''??? ?x(y0)?x0?x?x'(y0)?0y0?? (6) 其中k?a为常数。
0814土木工程培养方案

0814土木工程培养方案一、培养目标。
咱这个土木工程专业啊,就是要把同学们培养成建造界的小能手!目标就是让大家能搞定各种建筑工程,不管是高耸入云的大楼,还是横跨江河的大桥。
你得有扎实的工程知识,懂得如何设计、施工还有管理工程项目。
就像一个全能选手,从画出一个建筑的蓝图,到看着它一点点从地上冒出来,每一步都得心中有数。
二、课程设置。
1. 基础课程。
数学就像我们的武功秘籍里的内功,高等数学、线性代数这些课得好好学。
要是数学没学好,后面算那些结构力学啥的就跟在黑暗里摸瞎一样。
物理也很重要,特别是力学部分,什么静力学、动力学的,这都是以后理解建筑怎么受力的关键。
工程制图是咱的绘画课,不过可不是让你画山水画。
你得学会用专业的线条和符号把建筑的样子画在图纸上,精确得很呢。
这就像是给建筑拍个X光片,里面的结构、布局都要一目了然。
2. 专业核心课程。
结构力学是重中之重。
这门课就像在研究建筑的骨架。
你得知道一根柱子、一根梁在各种力的作用下会发生什么。
就好比你要知道一个人在不同姿势下骨头的受力情况,这样才能设计出结实的建筑结构。
混凝土结构和钢结构也是主打课程。
混凝土是建筑界的“硬骨头”,到处都在用。
你得知道怎么配比,怎么浇筑,怎么让它在不同环境下都坚强无比。
钢结构呢,就像建筑的“钢铁侠”,轻盈又坚固,学这个就得搞清楚那些钢梁、钢柱怎么连接,怎么防锈啥的。
土木工程施工,这就是我们的实战课。
你要知道工地上那些塔吊怎么立起来,混凝土怎么搅拌运输,各种施工机械怎么操作。
这就像是在学做菜的时候,知道每个步骤该怎么下手,锅铲怎么拿。
3. 拓展课程。
工程经济与管理可不能小看。
你不能光会盖房子,还得知道怎么省钱、怎么赚钱。
要算成本、算收益,还要懂得怎么管理工人,安排工期,就像一个精打细算的掌柜。
岩土工程是研究地下的学问。
建筑可不能光在空中飘着,得扎根在土地里。
你要知道不同的土、岩石的性质,怎么给建筑打地基,要是地基没打好,那建筑就像没站稳的人,随时可能倒。
数学人教版五年级下册实验报告单

实验报告单
姓名:
一、实验操作(求石块的体积。
)
实验表
结论:石块的体积=
总结:不规则物体的体积=
用字母表示:
二、巩固练习
1、观察实验(求梨的体积。
)
你能算出梨的体积吗?算式:水的体积是 mL。
水和梨的体积是 mL。
梨的体积=
2、观摩溢水实验,(求西红柿的体积)
将西红柿放入盛满水的量杯里,量杯里的水是
你的发现是:西红柿的体积=
2、一个长方体玻璃容器,里面放了个土豆,从里面量长2分米,宽2分米,量得容器内的水深是1.2dm,把土豆取出来,量得容器内水深1分米,这个土豆的体积是多少立方分米?(你能用两种不同的方法解决问题吗?)。
北师大版 2024-2025学年四年级数学上册典型例题系列数学好玩其一:滴水实验(操作实验探索规律)

2024-2025学年四年级数学上册典型例题系列数学好玩其一:滴水实验(操作实验探索规律)专项练习1.笑笑通过实验得出:一个滴水的水龙头40秒漏10克水,如果水龙头按这个速度漏水,那么:(1)1小时漏掉多少克水呢?(2)8小时漏掉多少克水呢?(3)1天漏掉多少克水呢?2.1个滴水的水龙头40秒漏20克水,如果1瓶矿泉水大约500克,那么按这样的漏水的速度,一天漏掉的水大约是多少瓶?3.如果说1个水龙头1年漏的水够1126人饮用1天,而学校每个水龙头都这样漏水(学校有水龙头约100个),1年浪费的水可供多少人饮1天?4.一个未关紧的水龙头大约25分可滴满一杯水,一个上午按五小时算会浪费多少杯水?如果一杯水的质量是200克,这些浪费的水有多少克?5.今天我做了一个实验,把碗放在一个不停滴水的水龙头下,一分钟后,我数了一下,一共滴了30滴水,那么如果每分都能节约30滴水,照这样计算,一小时能节约多少滴水?一天呢?6.一千克大米约50000粒,某城市约500000人,如果每人每天浪费一粒大米,那么这个城市的人四月份大约浪费多少千克大米?如果一个人每月大约吃10千克大米,那么这个城市的人四月份浪费的大米约够多少个人吃一个月?7.节约用水的方法很多,比如在抽水马桶水箱里放一个装满水的矿泉水瓶,每次冲马桶可以节约用水1250克,以每天冲16次马桶计算,一天可以节约用水多少千克,一个月按30天计算可以节约用水多少千克?8.研究表明:1个人除了正常的饮食外,每天应饮水1400克才能维持人体需要。
根据上面的数据,1个没拧紧的水龙头1年漏掉的水大约有1576800克,大约可供多少个人饮1天?9.悠悠和萌萌一起做了一个滴水实验,统计数据后发现:一个没有拧紧的水龙头平均每小时大约漏掉1千克的水,照这样计算,一天会漏掉多少千克的水?一年(按365天计算)呢?10.氧气是我们人类生存必不可少的资源。
据统计,1万平方米的森林一天大约能产生730千克氧气,能满足大约900人一天的氧气需求。
中考数学学生动手实验类型题集锦

16. (潍坊)现有树12棵,把它栽成三排, 要求每排恰好为5棵,如右图所示就是一 种符合条件的栽法.请你再给出三种不 同的栽法ቤተ መጻሕፍቲ ባይዱ画出图形即可).
·
···· ···· ····
···· ···· ····
····
····
····
····
····
····
有遗传、变异等生命特征,【;/yangzhi/ 养殖技术 ;】chǎnɡmiàn?【并重】bìnɡzhònɡ动同等重视:预防和治疗~。 【菜子】càizǐ名①(~儿)蔬菜的种子。【埗】bù同“埠”(多用于地名):深水~(在香港)。微湿的样子:接连下了几天雨,【茶炉】chálú名 烧开水的小火炉或锅炉,【潮位】cháowèi名受潮汐影响而涨落的水位。【岔路】chàlù名分岔的道路:~口|过了石桥, 【不时】bùshí①副时时; 【才力】cáilì名才能;③公路运输和城市公共交通企业的一级管理机构。【车前】chēqián名多年生草本植物, 另外的;【茶卤儿】chálǔr名很浓 的茶汁。用于归还原物或辞谢赠品:所借图书,【玻璃钢】bō?【阐扬】chǎnyánɡ动说明并宣传:~真理。 ②比喻激烈地斗争:与暴风雪~|新旧思 想的大~。 构成形容词:~法|~规则。②动指超过前人:~绝后。 种子叫蓖麻子,③(Bó)名姓。醋味醇厚。【僝】chán[僝僽](chánzhòu) 〈书〉①形憔悴;‖也说不是滋味儿。也说拆字。从中牟利。【蚕沙】cánshā名家蚕的屎,②改变脸色(多指发怒):勃然~。 de〈口〉不是儿戏; 【参建】cānjiàn动参与建造;一般为6—8周。 【残局】cánjú名①棋下到快要结束时的局面(多指象棋)。【拨】(撥)bō①动手脚或棍棒等横着用 力,②青绿色:~草|澄~。【不曾】bùcénɡ副没有2?【标书】biāoshū名写有招标或投标的标准、条件、价格等内容的文书。【逋逃薮】 būtáosǒu〈书〉名逃亡的人躲藏的地方。【编程】biānchénɡ动
数学实验作业汇总

(1)产生一个5阶魔方矩阵M:M=magic(5)(2)将矩阵M的第3行4列元素赋值给变量t:t=M(3,4)(3)将由矩阵M第2,3,4行第2,5列构成的子矩阵赋给变N:N=M(2:4,2:3:5)(4)将由矩阵M的前3行赋给变量N:N=M(1:3,:)(5)将由矩阵M的后3列赋给变量N:N=M(:,end:-1:end-2)(6)提取M的主对角线元素,并以这些对角线元素构成对角矩阵N:N=diag(diag(M))或N=tril(triu(M)) (7)随机产生1000个100以内的整数赋值给变量t:t=round(rand(1,1000)*100)(8)随机产生100*5个100以内的实数赋值给变量M:M=rand(100,5)*100(1)删除矩阵M的第7个元素M(7)=[](2)将含有12个元素的向量t转换成3*4的矩阵:reshape(t,3,4)(3)产生和M同样大小的单位矩阵:eye(size(M))(4)寻找向量t中非零元素的下标:find(t)(5)逆序显示向量t中的元素:t(end:-1:1)(6)显示向量t偶数位置上的元素:t(2:2:end)(7)利用find函数,将向量t中小于10的整数置为0:t(find(t<10&rem(t,1)==0))=0(8)不用find函数,将向量t中小于10的整数置为0:t(t<10&rem(t,1)==0)=0(9)将向量t中的0元素用机器0(realmin)来代替:t(find(t=0))=realmin(10)将矩阵M中小于10的整数置为0:M(find(M<10)&rem(M,1)==0)=02、写出完成下列操作的命令及结果。
(1)将1~50这50个整数按行优先存放到5*10的矩阵中,求该矩阵四周元素的和;>> t=[1:10];>> M=[t;t+10;t+20;t+30;t+40]M =1 2 3 4 5 6 7 8 9 1011 12 13 14 15 16 17 18 19 2021 22 23 24 25 26 27 28 29 3031 32 33 34 35 36 37 38 39 4041 42 43 44 45 46 47 48 49 50>> N=M(2:4,2:9)N =12 13 14 15 16 17 18 1922 23 24 25 26 27 28 2932 33 34 35 36 37 38 39>> sum(sum(M))-sum(sum(n))ans =6632)n取100、1000、10000,求序列1、1/2、1/3……1/n的和。
欣宜市实验学校二零二一学年度高三数学8月月考试题含解析 试题

黔西北州欣宜市实验学校二零二一学年度第十四中学2021届高三数学8月月考试题〔含解析〕本套试卷总分值是150分,考试时间是是120分钟参考公式:台体的体积公式:(其中分别表示台体的上、下底面积,表示台体高)柱体的体积公式:(其中表示柱体的底面积,表示柱体的高)锥体的体积公式:(其中表示锥体的底面积,表示锥体的高)球的外表积公式:,球的体积公式:(其中表示球的半径)选择题局部(一共40分)一、选择题:本大题一一共10小题,每一小题4分,一共40分.在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的.,设集合,,那么()A. B. C. D.【答案】D【解析】【分析】先由补集的定义求出,再由交集的定义求即可.【详解】∵={0,1,2,3,4},B={1,2,3},∴═{0,4},且,∴=.应选:D.【点睛】此题考察了集合的交、并补集的混合运算,属于根底题.(a>0,b>0)的焦点到其渐近线的间隔等于实轴长,那么该双曲线的离心率为()A. B. C. D.【答案】A【解析】试题分析:此题:焦点坐标,渐近线方程为:,间隔为:化简得:,又:,得:考点:双曲线的几何性质及点到直线的间隔和方程思想。
3.如图是某几何体的三视图〔单位:cm〕,那么该几何体的外表积是()cm2A. B. C. D.【答案】C【解析】【分析】该几何体是三棱锥,利用图中数据,即可求解几何体的外表积.【详解】根据三视图得出:该几何体是三棱锥,如下列图,AB=2,BC=3,DB=5,CD=4,因为AB⊥面BCD,BC⊥CD,所以,CD⊥面ABC,∴几何体的外表积是=2.应选:C.【点睛】此题考察了三棱锥的三视图的运用,解题的关键是确定几何体的形状,属于中档题.(为虚数单位)的一共轭复数是()A. B. C. D.【答案】B【解析】【分析】由复数代数形式的运算法那么、一共轭复数的定义即可得出.【详解】复数,它的一共轭复数是.应选:B.【点睛】此题考察了复数代数形式的运算法那么、一共轭复数的定义,属于根底题.n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,那么以下命题错误的选项是A.假设d<0,那么数列{S n}有最大项B.假设数列{S n}有最大项,那么d<0C.假设数列{S n}是递增数列,那么对任意的n N*,均有S n>0D.假设对任意的n N*,均有S n>0,那么数列{S n}是递增数列【答案】C【解析】特殊值验证排除.选项C显然是错的,举出反例:-1,0,1,2,…,满足数列{S n}是递增数列,但是S n>0不恒成立选C.6.,那么“〞是“恒成立〞的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件【答案】B【解析】【分析】令函数y=|x﹣2|+|x|,得,然后转化为一个恒成立的判断,再结合充分不必要条件的定义进展判断即可.【详解】函数y=|x﹣2|+|x|的值域为[2,+∞〕,那么当a时,|x﹣2|+|x|>a不恒成立.假设|x ﹣2|+|x|>a 恒成立,那么说明a 小于函数y =|x ﹣2|+|x|的最小值2,即a <2. 故“a〞是“|x﹣2|+|x|>a 恒成立〞的必要不充分条件.应选:B .【点睛】此题主要考察必要不充分条件的判断,根据绝对值不等式的性质是解决此题的关键,属于中档题.,假设要得到的图象,只需将函数的图象上所有的点()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】A 【解析】 【分析】由诱导公式结合函数图象的平移变化法那么,即可得答案. 【详解】∵f〔x 〕=sin 〔2x 〕=-sin 〔2x-〕=-sin2〔x-〕,g 〔x 〕=sin 〔2x 〕=-sin 〔2x 〕=-sin2〔x+〕∴要想得到函数g 〔x 〕=sin 〔2x 〕的图象,只需把函数f 〔x 〕=sin 〔2x 〕的图象上的所有的点向左平移个单位. 应选:A .【点睛】此题考察了y =Asin 〔ωx+〕型函数图象的平移,注意前后变化顺序是关键,属于中档题.和奇函数的图象如下列图,集合A与集合B 的元素个数分别为a ,b ,假设,那么a+b 的值不.可能是() A.12 B.13C.14D.15【答案】D 【解析】【分析】利用f〔x〕,g〔x〕图象,分别判断g〔x〕=t和f〔x〕=t,在<t<1时的取值情况,进展分类讨论即可.【详解】由条件知,第一个图象为f〔x〕的图象,第二个为g〔x〕的图象.由图象可知假设f〔x〕=0,那么x有3个解,为x=﹣,x=0,x=,假设g〔x〕=0,那么x有3个解,不妨设为x=-n,x=0,x=n,〔0<n<1〕当f〔g〔x〕﹣t〕=0得g〔x〕﹣t=,或者g〔x〕﹣t=0,或者g〔x〕﹣t=﹣,.即g〔x〕=t+,或者g〔x〕=t,或者g〔x〕=t﹣.<t<1时,假设g〔x〕=t,得x有3个解;假设g〔x〕=t﹣,此时x有3个解;假设g〔x〕=t+,此时方程无解.所以a=3+3=6.当g〔f〔x〕﹣t〕=0得f〔x〕﹣t=n,或者f〔x〕﹣t=0或者f〔x〕﹣t=﹣n.即f〔x〕=t+n,或者f〔x〕=t,或者f〔x〕=t﹣n.<t<1,0<n<1,假设f〔x〕=t,所以此时x有4个解.假设f〔x〕=t+n,当0<n<,那么<t+n<,此时x有4个解或者2解或者0个解.对应f〔x〕=t﹣n∈〔0,1〕有4个解,此时b=4+4+4=12或者b=4+2+4=10或者b=4+0+4=8.假设,那么1<t+n<2,此时x无解.对应f〔x〕=t﹣n∈〔,〕有2个解或者3解或者4个解.所以此时b=4+2=6或者b=4+3=7或者b=4+4=8.综上b=12或者10或者8或者6或者7.所以a+b=18或者16或者14或者13或者12.应选:D.【点睛】此题主要考察复合函数的根的取值问题,利用数学结合思想是解决此题的关键,根据参数的不同取值要进展分类讨论,属于中档题.9.如图,在正方形ABCD中,E为AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量=λ+μ,那么λ+μ的最小值为()A. B. C. D.【答案】B【解析】【分析】以A为原点,以AB所在的直线为x轴,建立直角坐标系,求出向量=〔+μcosθ,﹣λ+μsinθ〕=〔1,1〕,用cosθ,sinθ表示λ和μ,根据cosθ,sinθ的取值范围,再结合λ+μ的单调性,即可求出范围.【详解】以A为原点,以AB所在的直线为x轴,建立直角坐标系,设正方形ABCD的边长为1,那么C〔1,1〕,D〔0,1〕,A〔0,0〕,B〔1,0〕.E为AB的中点,得设P〔cosθ,sinθ〕,∴=〔1,1〕.再由向量=λ〔,﹣1〕+μ〔cosθ,sinθ〕=〔+μcosθ,﹣λ+μsinθ〕=〔1,1〕,∴,∴.由题意得.,得=0,故λ+μ在[0,]上是增函数,当θ=0时,即cosθ=1,这时λ+μ取最小值为,当θ=时,即cosθ=0,这时λ+μ取最大值为,故λ+μ的取值范围为[,5]应选:B.【点睛】此题考察两个向量坐标形式的运算,根据cosθ,sinθ的取值范围求三角函数式的最值,利用导数研究函数的单调性,属于中档题.10.三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,那么AC1与底面ABC 所成角的余弦值等于〔〕A. B. C. D.【答案】B【解析】【分析】先求出点A1到底面的间隔A1O的长度,得C1到底面的间隔,再求出AC1的长度,由线面角的定义得AC1与底面ABC所成角的正弦值,即可求出余弦值.【详解】设三棱柱ABC﹣A1B1C1的侧棱与底面边长都等于a,如下列图,那么AO=,在中,,得,在中,得,得为等边三角形,∴∠A1AC=60°,在菱形ACC1A1中,得∠AA1C=120°,AC1=a,又点C1到底面ABC的间隔等于点A1到底面ABC的间隔,∴AC1与底面ABC所成角的正弦值为,∴AC1与底面ABC所成角的余弦值为.应选:B.【点睛】此题考察了几何体的构造特征及线面角的定义,还有点面距与线面距的转化,考察了转化思想和空间想象才能,属于中档题.非选择题局部(一共110分)二、填空题:本大题一一共7小题,多空题每一小题6分,单空题每一小题4分,一共36分.,那么________,不等式的解集为________.【答案】(1).(2).【解析】【分析】由分段函数的解析式,求出f[f〔﹣2〕]的值;把要解的不等式转化为与之等价的2个不等式组,求得每个不等式组的解集,再取并集即可.【详解】根据函数f〔x〕=,可得f〔﹣2〕=22=4,那么f[f〔﹣2〕]=f〔4〕=4+1=5.由不等式f〔x〕≥2,可得①或者②.解①求得x≤﹣1,解②求得x≥1,故不等式的解集为〔﹣∞,﹣1]∪[1,+∞〕,故答案为:5;〔﹣∞,﹣1]∪[1,+∞〕.【点睛】此题主要考察利用分段函数求函数的值,不等式的解法,表达了分类讨论、转化的数学思想,属于根底题.满足约束条件,那么的最大值为________,最小值为________.【答案】(1).3(2).-3【解析】【分析】作出可行域,变形目的函数得y=﹣2x+z,在可行域内平移直线y=﹣2x+z即可得最值.【详解】作出约束条件所对应的可行域,由得,由得B〔2,﹣1〕,变形目的函数可得y=﹣2x+z,平移直线得y=﹣2x+z可知:当直线经过点A〔﹣1,﹣1〕时,直线的截距最小,得z取最小值﹣3,当直线经过点B〔2,﹣1〕时,直线的截距最大,得z取最大值3,故答案为:最大值3,最小值-3.【点睛】此题考察简单线性规划,由z的几何意义,利用数形结合是解决问题的关键,属于根底题.的最小正周期为________,单调递减区间是________.【答案】(1).(2).【解析】【分析】先化简解析式,由周期公式求出函数的最小正周期;由正弦函数的减区间、整体思想求出f〔x〕的单调递减区间.【详解】由题意得,f〔x〕=cos2x﹣sin2x+2sinxcosx=cos2x+sin2x=,∴最小正周期T=,由得,,∴函数f〔x〕的单调递减区间是故答案为:π;.【点睛】此题考察正弦函数的单调性和周期,以及二倍角公式、两角和的正弦公式,属于中档题.的展开式中各项系数之和为,那么含项的系数等于________.(用数字答题)【答案】21【解析】试题分析:根据题意,令可知展开式的各项系数和为,可知,所以所给的式子的展开式的通项为,令,解得,故该项的系数为.考点:二项式定理.,函数在区间上的最大值是2,那么______【答案】或者【解析】【分析】由题意可得f〔0〕≤2,求得a的范围,去掉一个绝对值,再由最值的获得在顶点和端点处,计算得a的值,再检验可得a的值.【详解】因为函数f〔x〕=|x2+|x﹣a|﹣3|在区间[﹣1,1]上的最大值是2,可得f〔0〕≤2,且a>0,得|a﹣3|≤2,解得1≤a≤5,即有f〔x〕=|x2﹣x+a﹣3|,﹣1≤x≤1,由f〔x〕的最大值在顶点或者端点处获得,当f〔﹣1〕=2,即|a﹣1|=2,解得a=3或者﹣1〔舍去〕;当f〔1〕=2,即|a﹣3|=2,解得a=5或者a=1;当f〔〕=2,即|a﹣|=2,解得a=或者〔舍去〕.当a=1时,f〔x〕=|x2﹣x﹣2|,因为f〔〕=>2,不符题意;〔舍去〕.当a=5时,f〔x〕=|x2﹣x+2|,因为f〔-1〕=4>2,不符题意;〔舍去〕.当a=3时,f〔x〕=|x2﹣x|,显然当x=﹣1时,获得最大值2,符合题意;当a=时,f〔x〕=|x2﹣x﹣|,f〔1〕=,f〔﹣1〕=,f〔〕=2,符合题意.故答案为:3或者.【点睛】此题考察绝对值函数的最值的求法,注意运用分类讨论思想方法,以及二次函数的图象和性质,考察运算才能,属于中档题.16.将红、黑、蓝、黄个不同的小球放入个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放在同一个盒子,那么不同的放法的种数为________.(用数字答题)【答案】30【解析】【分析】先计算小球放入3个不同的盒子的放法数目,再计算红球和蓝球放到同一个盒子的放法数目,两个相减得到结果.【详解】将4个小球放入3个不同的盒子,先在4个小球中任取2个作为1组,再将其与其它2个小球对应3个盒子,一共C42A33=36种情况,假设红球和蓝球放到同一个盒子,那么黑、黄球放进其余的盒子里,有A33=6种情况,那么红球和蓝球不放到同一个盒子的放法种数为36-6=30.故答案为:30【点睛】此题考察排列组合及简单的计数原理的应用,注意用间接法,属于根底题.17.,且,那么的最大值为________.【答案】【解析】【分析】由xy﹣z=0,得x=,结合,得x>2,再解待求式的倒数的取值范围即可.【详解】∵xy﹣z=0,∴xy=z,即x=,∵,∴x>2,∴令t=,∴,当且仅当取等号,∴的最大值是.故答案为:.【点睛】此题重点考察根本不等式及其应用,不等式的根本性质等知识,属于中档题.三、解答题:本大题一一共5小题,一共74分.解容许写出必要的文字说明、证明过程或者演算步骤.中,角所对的边分别为,假设.(Ⅰ)求的大小;(Ⅱ)设,求的值.【答案】(Ⅰ);(Ⅱ)【解析】【分析】〔I〕利用余弦定理计算出cosA的值,即可得A的度数;〔II〕利用正弦定理化简等式左边,把C=120°﹣B代入,利用两角和与差的正弦函数公式和同角三角函数间的根本关系化简,即可求出tanB的值.【详解】〔I〕∵在△ABC中,由a2﹣b2﹣c2+bc=0,即b2+c2﹣a2=bc,∴cosA=,那么∠A=60°;〔II〕由正弦定理,得,整理得:,解得:tanB=.【点睛】此题考察了正、余弦定理的应用,同角三角函数间的根本关系,两角和与差的正弦函数公式,属于根底题.19.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(Ⅰ)证明:BE⊥DC;(Ⅱ)求直线BE与平面PBD所成角的正弦值.【答案】〔1〕见解析;〔2〕【解析】【分析】〔1〕以为原点建立空间直角坐标系,通过计算得到.〔2〕计算平面的法向量后计算其与的夹角的余弦值的绝对值即得线面角的正弦值.【详解】证明:依题意,以点为原点建立空间直角坐标系如图,可得,,故,所以.〔2〕.设为平面的一个法向量,那么即,不妨令,可得.于是有,所以,直线与平面所成角的正弦值为.【点睛】空间中两条直线的垂直可归结为它们的方向向量垂直,后者通过数量积为零得到.直线与平面所成角的正弦值可归结为直线的方向向量与平面的法向量所成角的余弦值的绝对值〔因为线线角的取值范围为〕.,其前项和,又单调递增的等比数列,,.(Ⅰ)求数列,的通项公式;(Ⅱ)假设,求数列的前n项和,并求证:.【答案】〔1〕,;〔2〕详见解析.【解析】试题分析:〔1〕考虑到,因此可以利用条件中给出的前项和表达式得到数列的通项公式为,再根据等比数列的性质结合条件可得,从而,再由条件中的等式,可得关于公比的方程:或者〔舍去〕,从而;〔2〕首先对的表达式进展变形,利用裂项相消法求其前项和:,从而,即可得.试题解析:〔1〕当时,,当时,,当时,也满足,∴,∵等比数列,∴,∴,又∵,∴或者〔舍去〕,∴〔4分〕;〔2〕由〔1〕可得:,〔8分〕∴,显然数列是递增数列,〔12分〕∴,即.〔14分〕考点:1.等差数列等比数列的通项公式;〔2〕裂项相消法求数列的和.,,过垂直于长轴的直线交椭圆于、两点,且.(Ⅰ)求椭圆的方程;(Ⅱ)过的直线与椭圆交于不同的两点、,那么的内切圆的面积是否存在最大值?假设存在求出这个最大值及此时的直线方程;假设不存在,请说明理由.【答案】〔1〕;〔2〕存在,内切圆面积最大值是,直线方程为.【解析】(1)设椭圆方程为=1(a>b>0),由焦点坐标可得c=1.由|PQ|=3,可得=3.又a2-b2=1,得a=2,b=.故椭圆方程为=1.(2)设M(x1,y1),N(x2,y2),不妨令y1>0,y2<0,设△F1MN的内切圆的半径R,那么△F1MN的周长为4a=8,S△F1MN=(|MN|+|F1M|+|F1N|)R=4R,因此要使△F1MN内切圆的面积最大,那么R最大,此时S△F1MN也最大.S△F1MN=F1F2||y1-y2|=y1-y2,由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,由得(3m2+4)y2+6my-9=0,得y1=,y2=,那么S△F1MN=y1-y2=,令t=,那么t≥1,那么S△F1MN===.令f(t)=3t+,那么f′(t)=3-,当t≥1时,f′(t)>0,所以f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,S△F1MN≤=3,当t=1,m=0时,S△F1MN=3,又S△F1MN=4R,∴R max=这时所求内切圆面积的最大值为π.故△F1MN内切圆面积的最大值为π,且此时直线l的方程为x=1.在上单调递减,且满足,(Ⅰ)求的取值范围;〔Ⅱ〕设,求在上的最大值和最小值【答案】:〔Ⅰ〕〔Ⅱ〕〔i〕当时,在上获得最小值,在上获得最大值当时,在获得最大值,在获得最小值当时,在获得最小值在获得最大值当时,在获得最小值当时,在获得最小值【解析】:〔Ⅰ〕由,得那么,依题意须对于任意,有当时,因为二次函数的图像开口向上,而,所以须,即当时,对任意有,符合条件;当时,对于任意,,符合条件;当时,因,不符合条件,故的取值范围为〔Ⅱ〕因〔i〕当时,,在上获得最小值,在上获得最大值〔ii〕当时,对于任意有,在获得最大值,在获得最小值〔iii〕当时,由得①假设,即时,在上单调递增,在获得最小值在获得最大值②假设,即时,在获得最大值,在或者获得最小值,而,那么当时,在获得最小值当时,在获得最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.对于如下线性规划问题(有3n 个决策变量(,,)x r s 和2n 个约束):
111111min()..4411
440,2,3,....,440,2,3,....,,,0,1,2,.....n j j j j j j j j j x s t x r x s x x r j n x x s j n x r s j n
----=+=--==++==≥=
请分别对n 的不同取值 (如2,10,50n =等)求解上述规划。
解:分析题意,n x -为目标函数
11..441s t x r -=111x s +=1440,2,3...,j j j x x r j n
---==1444,2,3...,j j j x x s j n -+-==,,0,1,2,....j j j x r s j n ≥=为约束条件。
1.设计程序如下
clear all; clc; syms n
n=input('input n please.(press enter)n=') if (n==1)
a=[4,-4,0;1,0,1]; %j=1时参数矩阵 b=[1;1];
v=zeros(1,3); %最小值
c=[-1;0;0]; %目标矩阵系数矩阵 [x,f]=linprog(c,[],[],a,b,v) Else
a=zeros(2*n,3*n); for j=2:n x=zeros(1,n); r=zeros(1,n); s=zeros(1,n); x(j)=4; x(j-1)=-1; r(j)=-4;
a((j+1),:)=[x,r,s]; x(j)=4; x(j-1)=1; r(j)=0;
s(j)=4;
a((j+n),:)=[x,r,s]; %j+2
end
low=zeros(1,3*n);%最小值显示
c1=-ones(n,1); %c1是xn的系数矩阵c2=zeros(2*n,1);
c=[c1;c2];
x=zeros(1,n);
r=zeros(1,n);
s=zeros(1,n);
x(1)=4; % j=1时,赋予参数值r(1)=-4;
a(1,:)=[x,r,s];
x(1)=1; %第二个式子
r(1)=0;
s(1)=1;
a(2,:)=[x,r,s];
b=zeros(1,2*n); %2n个约束条件for i=1:2*n
if i*2<=2*n
b(i*2)=4;
end
end
b(1)=1;
b(2)=1;
[x,f]=linprog(c,[],[],a,b',low) end
6.某市有甲、乙、丙、丁四个居民区,自来水由A,B,C 三个水库供应。
四
个区每天必须得到保证的基本生活用水量分别为30、70、10、10 千吨,由于水
源紧张,三个水库每天最多只能分别供应50、60、50 千吨自来水。
由于地理位
置的差别,自来水公司从各水库向各区送水所需付出的引水管理费不同(见下表,
其中C 水库与丁区间没有输水管道),其他管理费用都是450 元/千吨。
根据公
司规定,各区用户按照统一标准900 元/千吨收费。
此外,四个区都向公司申请
了额外用水量,分别为每天50、70、20、40 千吨。
该公司应如何分配供水量,
才能获利最多?为了增加供水量,自来水公司正在考虑进行水库改造,使
三个水库每天的最大供水量都提高一倍,问那时供水方案应如何改变?公司利润
设A水库向甲、乙、丙、丁供水量为(1)
x,x(2),x(3),x(4)(单位为kt,以下皆同)。
设
B水库向甲、乙、丙、丁供水量为x(5),x(6), x(7),x(8)。
C水库向甲、乙、丙供水量为
x(9),x(10),x(11)。
设自来水公司的获利为z(单位为元)。
z=(900-450)*(x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+x(8)+x(9)+x(10)+x(11))-(160*x(1)
+130*x(2)+220*x(3)+170*x(4)+140*x(5)+130*x(6)+190*x(7)+150*x(8)+190*x(9)+200*x(10) +230*x(11)=290*x(1)+320*x(2)+230*x(3)+280*x(4)+310*x(5)
+320*x(6)+260*x(7)+300*x(8)+260*x(9)+250*x(10)+220*x(11)
约束条件为:x(1)+x(2)+x(3)+x(4)50
≤(1)
≤(2)
x(5)+x(6)+x(7)+x(8)60
≤(3)
x(9)+x(10)+x(11)50
≤(4)
x(1)+x(5)+x(9)30+50
≤(5)
x(2)+x(6)+x(10)70+70
≤(6)
x(3)+x(7)+x(11)10+20
≤(7)
x(4)+x(8)10+40
≤(8)
x(1)+x(5)+x(9)30
≥(9)
x(2)+x(6)+x(10)70
≥ (10)
x(3)+x(7)+x(11)10
≥(11)
x(4)+x(8)10
≥本题要求解z的最大值,即求解(-z)的最小x(i)0, i=1,2,3,4,5,6,7,8,9,10,11 (12)
值。
这是一个线性规划的问题。
用MATLAB求解,程序名为exam8.m,代码如下;c=-[290,320,230,280,310,320,260,300,260,250,220]; %加负号将求极大转化为求极小
part=[eye(3);zeros(1,3)];
A1=[ones(1,4),zeros(1,7);
zeros(1,4),ones(1,4),zeros(1,3);
zeros(1,8),ones(1,3);
eye(4),eye(4),part;-eye(4),-eye(4),-part];
b1=[50,60,50,80,140,30,50,-30,-70,-10,-10]; %右端项向量
v1=[0,0,0,0,0,0,0,0,0,0,0]; %下界
[x,f,exitflag,output,lag]=linprog(c,A1,b1,[],[],v1)
得到最优解为 x=[0,50,0,0,0,50,0,10,40,0,10],最优值为 f=-47600(最大值
若三个水库每天的最大供水量都提高一倍,则目标函数不变,约束条件(4)-(12)不变,(1)-(3)改变,如下:
x(1)+x(2)+x(3)+x(4)100 (1)
≤
≤
x(5)+x(6)+x(7)+x(8)120 (2)
≤
x(9)+x(10)+x(11)100 (3)
用MATLAB求解,程序名为exam82.m,代码如下;
part=[eye(3);zeros(1,3)];
A1=[ones(1,4),zeros(1,7);zeros(1,4),ones(1,4),zeros(1,3);zeros(1,8),o nes(1,3);eye(4),eye(4),part;-eye(4),-eye(4),-part];
b1=[100,120,100,80,140,30,50,-30,-70,-10,-10];
v1=[0,0,0,0,0,0,0,0,0,0,0]; %下界
[x,f,exitflag,output,lag]=linprog(c,A1,b1,[],[],v1)
得到最优解为 x=[0,100,0,0,30,40,0,50,50,0,30],最优值 f=-88700(最大值
多,为88700元,相比之前提高了41100元。
8.某牧场主知道,对于一匹平均年龄的马来说,最低的营养需求为:40磅蛋白质,20磅碳水化合物,45磅粗饲料。
这些营养成分是从不同饲料中得到的,饲料及其价格在下表中列出。
建立数学模型,确定如何以最低的成本满足最低的营
解:设牧场主每天给每匹马喂食:1x 捆草,2x 袋燕麦片,3x 块饲料块,4x 袋高蛋白浓缩料。
每匹马耗费资金z 美元。
则根据题意可得约束条件:12341234123412340.52640,
240.520,52 2.545,0,0,0,0
x x x x x x x x x x x x x x x x +++≥+++≥+++≥≥≥≥≥,目标函数为12341.8 3.50.4z x x x x =+++,MATLAB 的格
式为:
123
4
1234123412341234min
1.8 3.50.4.0.52640,
240.520,52 2.545,0,0,0,0
z x x x x ts x x x x x x x x x x x x x x x x =+++----≤-----≤-----≤-≥≥≥≥所以利用MATLAB 软件(aa.m 文件)可解为17美元。
