高考数学经典错题深度剖析及针对训练专题27古典概型和几何概型(new)
高考数学经典错题深度剖析及针对训练专题27古典概型和几何概型

专题27 古典概型和几何概型【标题01】忽略了对数函数中底数的范围【习题01】先后抛掷两枚骰子,出现的点数分别记为,a b ,则事件log 12a b= 发生的概率为 . 【经典错解】log 1222ab ba b a =∴=∴=,根据题意得试验的全部结果有6636⨯=个基本事件,事件log 12ab=包含的基本事件有1,22,436a b a b a b ======或或, ,共3个.由古典概型的概率公式得31()3612P A ==,故填112.【详细正解】log 1222a b ba b a =∴=∴=,根据题意得试验的全部结果有6636⨯=个基本事件,01a a >≠且 所以事件log 12a b=包含的基本事件有2,4a b ==和3a =,6b = 共2个.由古典概型的概率公式得21()3618P A ==,故填118.【习题01针对训练】先后抛掷两枚骰子,出现的点数分别记为,a b ,则事件log 12a b≥发生的概率为 .【标题02】事件A 构成的区域找错了【习题02】在半径为1的圆周上有一定点A ,以A 为端点连一弦,另外一端点在圆周上等可能的选取,则弦长超过1的概率为 .【经典错解】如图所示,13AB OA OB AOB π===∴∠=,当点B 在优弧AB 上时,弦长超过1,根据几何概型的概率公式得3301136012P ==.故填1112.【详细正解】如图所示,13AB OA OB OC AC AOB AOC π=====∴∠=∠=,当点B 在优弧BC 上时,弦长超过1,根据几何概型的概率公式得24023603P==.故填23.【深度剖析】(1)经典错解错在事件A构成的区域找错了. (2)错解错在寻找事件A构成的区域时,只顾及了一边,忽略了另外一边.所以在寻找事件A的全部结果构成的区域时,要考虑周全,不能受习惯思维的影响.【习题02针对训练】有一长、宽分别为m50、m30的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出m215,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是()A.43B.83C.163πD.32312π+【标题03】对组合数实际意义理解不清【习题03】甲、乙两人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙依次各抽一题.求甲抽到选择题,乙抽到判断题的概率是多少?【经典错解】甲从选择题抽到一题的结果为16C,乙从判断题中抽到一题的结果为14C,而甲、乙依次抽到一题的结果为210C∴所求概率为1582101416=CCC【详细正解】甲从选择题抽到一题的结果为16C,乙从判断题中抽到一题的结果为14C,而甲、乙依次抽到一题的结果为11109C C∴所求概率为154191101416=CCCC.【习题03针对训练】一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个. (1)从中同时摸出两个球,求两球颜色恰好相同的概率;(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.【标题04】“事件的全部结果”和“事件A的全部结果”对应的区域找错了【习题04】在ABC∆中,6ABCπ∠=,AB=3,BC=3,若在线段BC上任取一点D ,则BAD∠为锐角的概率是 .【经典错解】在ABC∆中,由余弦定理得AC=3. 又由余弦定理得0120BAC∠=,所以BAD∠为锐角的概率是9031204=.【详细正解】当0=90BAD∠时,2BD=,所以BAD∠为锐角的概率是23BDBC=.【习题04针对训练】在Rt ABC∆中,030A∠=,过直角顶点C作射线CM交线段AB于M,使||||AM AC>的概率是.【标题05】“试验的全部结果构成的区域”和“事件A的全部结果构成的区域”理解错误【习题05】在面积为S的ABC∆的边AB上任取一点P,则PBC∆的面积大于4S的概率为 .【经典错解】由题得试验的全部结果构成的区域是如图所示的ABC∆,事件“PBC∆的面积大于4S”的全部结果构成的区域是如图所示的ADE∆,根据几何概型概率的公式得991616SPS== ,故填916.【详细正解】由题得试验的全部结果构成的区域是如图所示的线段AB,事件“PBC∆的面积大于4S”的全部结果构成的区域是如图所示的线段AD ,根据几何概型概率的公式得33414P == ,故填34 .【深度剖析】(1)经典错解错在“试验的全部结果构成的区域”和“事件A 的全部结果构成的区域”理解错误. (2)在做概率题时,一定要认真审题,弄清“试验的全部结果构成的区域”和“事件A 的全部结果构成的区域”.【习题05针对训练】设不等式组⎩⎨⎧≤≤≤≤20,20y x ,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A .4π B .22π- C .6π D .44π-【标题06】考虑问题不周全没有分类讨论【习题06】在ABC ∆中,060,2,6ABC AB BC ∠===,在BC 上任取一点D ,则使ABD ∆为钝角三角形的概率为( ) A .16 B .13 C .12 D .23【经典错解】由题意得,过A 作AF AB ⊥,则24BF AB ==,642CF =-= ,若使得ABD ∆为钝角三角形,则D 在线段FC 上,所以对应的概率为13FC P BC ==,故选B .【详细正解】(1)当BAD ∠为钝角时,由题意得,过A 作AF AB ⊥,则24BF AB ==,642CF =-= ,若使得ABD ∆为钝角三角形,则D 在线段FC 上;(2)当BDA ∠为钝角时,过点A 作AE BC ⊥,则112BE AB ==,若使得ABD ∆为钝角三角形,则D 在线段BE 上.故由几何概型的概率公式得21162FC BE P BC ++=== .故选C .【习题06针对训练】向顶角为0120的等腰三角形ABC (其中BC AC =)内任意投一点M , 则AM 小于AC 的概率为( ) A .33π B .93π C .21 D .3π【标题07】审题错误导致把几何概型看成了古典概型 【习题07】设关于x 的一元二次方程2220x ax b -+=.(1)若,a b 都是从集合{1,2,3,4}中任取的数字,求方程无实根的概率;(2)若a 是从区间[0,4]中任取的数字,b 是从区间[1,4]中任取的数字,求方程有实根的概率.【经典错解】(1)设事件A 为“方程无实根”,记(,)a b 为取到的一种组合,则所有的情况有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).一共16种且每种情况被取到的可能性相同.∵关于x 的一元二次方程2220x ax b -+=无实根,∴22440a b ∆=-<0,0a b >> ∴a b <.∴事件A 包含的基本事件有:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).共6种 ∴6()16P A ==83∴方程无实根的概率83. (2)∵关于x 的一元二次方程2220x ax b -+=有实根,∴22440a b ∆=-≥,0,0a b >> ∴a b ≥.设事件B 为“方程有实根”,记(,)a b 为取到的一种组合,则其包含的基本事件有:(1,1),(2,1),(2,2)(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4).一共10种且每种情况被取到的可能性相同. 105()168P A ∴== 所以方程有实根的概率是58. 【详细正解】(1)同上(2)设事件B =“方程有实根”,记(,)a b 为取到的一种组合. ∵a 是从区间[0,4]中任取的数字,b 是从区间[1,4]中任取的数字, ∴点(,)a b 所在区域是长为4,宽为3的矩形区域.又∵满足a b≥的点的区域是如图所示的阴影部分∴13332()348P B⨯⨯==⨯. ∴方程有实根的概率是38.【习题07针对训练】已知关于x的二次函数2()4 1.f x ax bx=-+(1)设集合}5,4,3,2,1,1{-=A和}4,3,2,1,1,2{--=B,分别从集合A,B中随机取一个数作为a和b,求函数)(xfy=在区间),1[+∞上是增函数的概率.(2)设点),(ba是区域⎪⎩⎪⎨⎧>>≤-+,,8yxyx内的随机点,求函数()f x在区间),1[+∞上是增函数的概率.【标题08】审题不清把总事件没有理解清楚【习题08】有一个半径为4的圆,现在将一枚半径为1的硬币向圆投去,如果不考虑硬币完全落在圆外的情况,则硬币完全落入圆内的概率为 .【经典错解】由题得此概型为几何概型,所有结果组成的区域是以原点为圆心,以4为半径的圆,事件A 的所有结果构成的区域是以原点为圆心,以3为半径的圆,所以由几何概型的定义得991616Pππ==. 【详细正解】由题得此概型为几何概型,所有结果组成的区域是以原点为圆心,以5为半径的圆,当硬币和圆外切时,也是满足题意的,它不是完全落在圆外,因为此时两圆有公共点),事件A的所有结果构成的区域是以原点为圆心,以3为半径的圆,所以由几何概型的定义得992525Pππ==.【深度剖析】(1)经典错解错在审题不清,把总事件没有理解清楚. (2)学习数学,必须养成严谨认真细心的学习习惯,审题必须认真,错解就是审题不清,导致的错误.【习题08针对训练】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.【标题09】对随机模拟求近似值原理理解不清 【习题09】从区间[0,1]上随机抽取2n 个数1212,,,,,,,n n x x x y y y ,构成n 个数对11(,)x y ,22(,)x y ,,(,)n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为__________.A .4n m B .2n m C.4m n D .mn【经典错解】由题得圆周率π的近似值为mn.所以选择D .【详细正解】由题得数学试验的全部结果表示为0101x y ≤≤⎧⎨≤≤⎩,它们构成的是边长为1的正方形,事件A 的全部结果表示为2201011x y x y ⎧≤≤⎪≤≤⎨⎪+<⎩,它们构成的是14个单位圆,它是分布在第一象限的扇形. 根据古典概型和几何概型的概率公式得=S m S n扇形正方形221141m n π== 4mn π∴=. 所以选择C .【习题09针对训练】某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计....出的圆周率π的值为 .(精确到0.01)高中数学经典错题深度剖析及针对训练第27讲:古典概型和几何概型参考答案【习题01针对训练答案】19【习题02针对训练答案】B【习题02针对训练解析】这是一个几何概型问题,所有可能结果用周长160表示,事件发生的结果可用两条线段的长度和60表示,所以8316060==P.【习题03针对训练答案】(1)52;(2)2512.【习题03针对训练解析】(1)摸出两球颜色恰好相同,即两个黑球或两个白球,共有2223C C+=4(种)可能情况.故所求概率为P=222325C CC+=410=25.(2)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑”.故所求概率为P=•+••111123321155CC C C CC=6625+=1225.【习题04针对训练答案】16【习题04针对训练解析】如图,不妨设1BC=,则2AB=,3AC=图中点M恰好使得3AM AC==BM段时,满足||||AM AC>,由三角形的知识易得015BCM∠=∴使||||AM AC>的概率151906P==. 故填16.【习题05针对训练答案】D【习题06针对训练答案】B【习题06针对训练解析】由题可得示意图,试验的全部结果构成的区域是ABC ∆,事件“AM 小于AC ”的全部结果构成的区域是扇形ACD ,由题可知为几何概型:则AM 小于AC 的概率为:0113261911sin1202ABC S p S ππ∆⨯⨯===⨯⨯⨯扇形 ,故选B .所以区域内满足0>a 且a b ≤2的面积为33238821=⨯⨯. 所以,所求概率3132332==p .【习题08针对训练答案】10131152【习题08针对训练解析】这是一个几何概型问题.设甲、乙两艘船到达码头的时刻分别为x 与y ,A 为“甲、乙两船都不需要等待码头空出”,则024x ≤≤ , 024y ≤≤, 且基本事件所构成的区域为{(,)|024,0y 24}x y x Ω=≤≤≤≤要使两船都不需要等待码头空出,当且仅当甲比乙早到达1 小时以上或乙比甲早到达2 小时以上,即12y x x y -≥-≥或,故{(,)|12,0x 24,024}A x y y x x y y =-≥-≥≤≤≤≤或.文档从网络中收集,已重新整理排版.word 版本可编辑.欢迎下载支持.11文档来源为:从网络收集整理.word 版本可编辑.【习题09针对训练答案】3.12【习题09针对训练解析】设正方形的边长为2a ,则内切圆的半径为a ,由题意2239504a aπ=,∴439 3.1250π⨯=≈.。
202X年高考数学一轮复习讲义——古典概型与几何概型

千里之行,始于足下。
202X年高考数学一轮复习讲义——古典概型与几何概型古典概型与几何概型是数学中常用的概率计算方法,对于高考数学复习格外重要。
下面我们来具体介绍一下古典概型与几何概型。
古典概型是指试验样本空间中每一个基本大事发生的概率相等的情形。
这种情形下,我们可以通过计数的方法来确定概率。
常见的例子有扔硬币和掷骰子。
以扔硬币为例,假设试验为连续扔一枚硬币,硬币只有正面和反面两个可能的结果。
将正面定义为大事A,反面定义为大事B。
依据古典概型,硬币正反面消灭的概率相等,即P(A) = P(B) = 1/2。
同理,对于掷骰子的状况,我们可以将掷骰子消灭的点数定义为不同的大事,依据古典概型,掷骰子消灭的每个点数的概率相等,为1/6。
古典概型在实际问题中也有很多应用,比如抽样问题。
假如一个罐子中有红球、白球、蓝球三种颜色的球,从中随机抽取一个球,求抽到红球的概率。
依据古典概型,红球、白球、蓝球的概率相等,为1/3。
几何概型是指试验样本空间可以用几何图形来表示,并且每个大事的概率可以用几何概率来计算。
常见的例子有投点问题和长方形求面积问题。
以投点问题为例,假设将一个点随机地投掷到一个正方形区域中,点落在某个子区域内的概率可以用子区域的面积与正方形区域的面积之比来计算。
例如,正方形区域边长为a,投点落在一个边长为x的小正方形内的概率为P = x^2 / a^2。
第1页/共2页锲而不舍,金石可镂。
对于长方形求面积问题,假设有一块土地的外形为长方形,现在要在上面随机地选取一个点,求这个点在土地上落的概率。
依据几何概型,这个点落在土地上任何一个子区域内的概率等于子区域的面积与整个土地的面积之比。
正由于几何概型的面积比例关系,我们可以将计算概率问题转化为计算几何问题,从而简化计算步骤。
在高考数学中,古典概型与几何概型是常考的学问点,把握这两个概率计算方法对于正确解题格外重要。
在复习时,需要娴熟把握古典概型和几何概型的定义和计算方法,并通过大量的练习题来巩固学习。
古典概型问题常见错解剖析

古典概型问题常见错解剖析
古典概型问题是用来考验和检测学生学习能力的一种常见的题目形式,但学生
在解答的过程中也会出现一些错误。
要想让学生正确解答古典概型问题,就必须剖析常见的错误解题思路,并结合实例加以解释。
首先,不少学生倾向于以过于简单的方法来解答不容易解答的问题。
例如有一
道题是关于如何最大限度地利用电能的,而有些学生则只是完全照搬此类问题中提出的建议,而未能深入思考以及创造出更多可能性。
在推理问题中,此类答案仅能赢得分值较低的评价。
其次,有些学生可能会出现对历史背景或者解题过程中涉及的基本知识的缺乏,从而导致他们无法根据题目暗示的信息来解答古典概型问题。
例如有一道问题是关于文艺复兴时期的经济历史,但某位学生的回答竟然完全无视文艺复兴时期有关的内容,而是给出了近代经济发展的简单解答。
最后,当学生以此学习任务为主导思维方式时,他们可能会忽视学习内容本身,并仅仅当作完成学习任务来看待古典概型问题。
这种做法可能会导致学生缺乏理解,缺少对概型的全面洞察,最终得出的结论可能毫无意义或者不正确。
因此,应该尽可能将学习任务与学习内容结合起来,从而获得更加客观全面的
理解,才能在解答古典概型问题时获得良好的效果。
在此过程之中,教师们也应当给学生在错误解答上以适当的指导,以提高学生解题能力。
高考数学最新真题专题解析—古典概型与几何概型(理科)

高考数学最新真题专题解析—古典概型与几何概型考向一 古典概型【母题来源】2022年高考全国甲卷(理科)【母题题文】 从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为________. 【答案】635. 【试题解析】从正方体的8个顶点中任取4个,有48C 70n ==个结果,这4个点在同一个平面的有6612m =+=个,故所求概率1267035m P n ===.故答案为:635. 【命题意图】本题主要考查古典概型的的概率计算公式,属于基础题.【命题方向】这类试题在考查题型上主要以选择填空形式出现,试题难度不大,多为抵挡题目,是历年高考的热点. 常见的命题角度有:(1)列举法求古典概型的概率;(2)树状图法求古典概型的概率. 【得分要点】(1)理解古典概型及其概率计算公式.(2)会计算一些随机事件所含的基本事件数及事件发生的概率. 考向二 几何概型【母题来源】2021年高考全国卷(理科)【母题题文】在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于74的概率为( )A .79B .2332C .932D .29【答案】B【试题解析】设从区间()()0,1,1,2中随机取出的数分别为,x y ,则实验的所有结果构成区域为(){},01,12x y x y Ω=<<<<,设事件A 表示两数之和大于74,则构成的区域为()7,01,12,4A x y x y x y⎧⎫=<<<+⎨⎬⎩⎭,分别求出,A Ω对应的区域面积,根据几何概型的的概率公式即可解出. 【详解】 如图所示:设从区间()()0,1,1,2中随机取出的数分别为,x y ,则实验的所有结果构成区域为(){},01,12x y x y Ω=<<<<,其面积为111S Ω=⨯=.设事件A 表示两数之和大于74,则构成的区域为()7,01,12,4A x y x y x y ⎧⎫=<<<+⎨⎬⎩⎭,即图中的阴影部分,其面积为133********A S =-⨯⨯=,所以()2332A S P A S Ω== 【命题意图】本题主要考查几何概型的的概率计算公式,属于基础题.【命题方向】这类试题在考查题型上主要以选择填空形式出现,试题难度不大,多为抵挡题目,是历年高考的热点. 常见的命题角度有:(1)由长度比求几何概型的概率;(2)由面积比求几何概型的概率;(3)由体积比求几何概型的概率; (4)由角度比求几何概型的概率. 【得分要点】(1)能运用模拟方法估计概率. (2)了解几何概型的意义.真题汇总及解析 一、单选题1.(2022·河南许昌·高二期末(理))若分配甲、乙、丙、丁四个人到三个不同的社区做志愿者,每个社区至少分配一人,每人只能去一个社区.若甲分配的社区已经确定,则乙与甲分配到不同社区的概率是( ) A .14B .56C .13D .512【答案】B 【解析】 【分析】计算出甲单独去分配的社区,甲和乙,丙,丁三人的一人去分配的社区,从而得到总的分配方法,再计算出甲乙分配到同一舍去的方法,得到乙与甲分配到不同社区的方法,根据古典概型求概率公式进行计算. 【详解】甲单独去分配的社区,有将乙,丙,丁三人分为两组,再和另外两个社区进行全排列,有212312C C A 6 种方法;甲和乙,丙,丁三人的一人去分配的社区,其余两人和另外两个社区进行全排列,有1232C A 6=种方法;其中甲乙分配到同一社区的方法有22A 2=种,则乙与甲分配到不同社区的方法有66210+-=种, 所以乙与甲分配到不同社区的概率是105666=+ 故选:B2.(2022·广东茂名·二模)甲、乙、丙三人是某商场的安保人员,根据值班需要甲连续工作2天后休息一天,乙连续工作3天后休息一天,丙连续工作4天后休息一天,已知3月31日这一天三人均休息,则4月份三人在同一天工作的概率为( ) A .13B .25C .1130D .310【答案】B 【解析】 【分析】列举出三人所有工作日,由古典概型公式可得. 【详解】解:甲工作的日期为1,2,4,5,7,8,10,...,29. 乙工作的日期为1,2,3,5,6,7,9,10,...,30. 丙工作的日期为1,2,3,4,6,7,8,9, (29)在同一天工作的日期为1,2,7,11,13,14,17,19,22,23,26,29 ∴三人同一天工作的概率为122305P ==. 故选:B .3.(2022·辽宁实验中学模拟预测)某国计划采购疫苗,现在成熟的疫苗中,三种来自中国,一种来自美国,一种来自英国,一种由美国和德国共同研发,从这6种疫苗中随机采购三种,若采购每种疫苗都是等可能的,则买到中国疫苗的概率为( ) A .16B .12C .910D .1920【答案】D 【解析】 【分析】由对立事件的概率公式计算. 【详解】没有买到中国疫苗的概率为13611C 20P ==,所以买到中国疫苗的概率为119120P P =-=. 故选:D .4.(2022·河南安阳·模拟预测(文))为推动就业与培养有机联动、人才供需有效对接,促进高校毕业生更加充分更高质量就业,教育部今年首次实施供需对接就业育人项目.现安排甲、乙两所高校与3家用人单位开展项目对接,若每所高校至少对接两家用人单位,则两所高校的选择涉及到全部3家用人单位的概率为( ) A .12 B .23C .34D .1316【答案】D 【解析】【分析】由古典概型与对立事件的概率公式求解即可【详解】因为每所高校至少对接两家用人单位,所以每所高校共有2333314C C+=+=种选择,所以甲、乙两所高校共有4416⨯=种选择,其中甲、乙两所高校的选择涉及两家用人单位的情况有233C=种,所以甲、乙两所高校的选择涉及到全部3家用人单位的概率为31311616P=-=,故选:D5.(2022·全国·模拟预测(理))2022年2月4日,北京冬季奥林匹克运动会开幕式于当晩20点整在国家体育场隆重举行.在开幕式入场环节,91个国家(地区)按顺序入场.入场顺序除奥林匹克发祥地希腊(首先入场)、东道主中国(最后入场)、下届2026年冬季奥运会主办国意大利(倒数第二位入场)外,其余代表团根据简体中文的笔划顺序入场,诠释了中文之美.现若以抽签的方式决定入场顺序(希腊、中国、意大利按照传统出场顺序,不参与抽签),已知前83位出场的国家(地区)均已确定,仅剩乌兹别克斯坦、北马其顿、圣马力诺、安道尔、阿根廷、泰国末抽签,求乌兹别克斯坦、安道尔能紧挨出场的概率()A.25B.13C.16D.14【答案】B【解析】【分析】先求出这六个国家的所有可能出场的顺序的排列数,再求出乌兹别克斯坦、安道尔能紧挨出场的排列数,将即乌兹别克斯坦、安道尔看作一个国家,利用捆绑法,根据古典概型的概率公式求得答案.【详解】由题意得,乌兹别克斯坦、北马其顿、圣马力诺、安道尔、阿根廷、泰国所有可能的出场顺序有66A种,其中乌兹别克斯坦、安道尔能紧挨出场的顺序有2525A A种,故乌兹别克斯坦、安道尔能紧挨出场的概率为252566A A1A3=,故选:B6.(2022·北京·北大附中三模)有一副去掉了大小王的扑克牌(每副扑克牌有4种花色,每种花色13张牌),充分洗牌后,从中随机抽取一张,则抽到的牌为“红桃”或“A”的概率为()A.152B.827C.413D.1752【答案】C【解析】【分析】直接根据古典概型概率计算公式即可得结果.【详解】依题意,样本空间包含样本点为52,抽到的牌为“红桃”或“A”包含的样本点为16,所以抽到的牌为“红桃”或“A”的概率为1645213=,故选:C.7.(2022·湖北省仙桃中学模拟预测)定义:10000100010010,(,,,,)abcde a b c d e a b c d e Z=++++∈,当a b c d e><><时,称这个数为波动数,由1,2,3,4,5组成的没有重复数字的五位数中,波动数的概率为()A .115B .215C .760D .112【答案】B 【解析】 【分析】先判断出由1,2,3,4,5组成的没有重复数字的五位数有120种,列举出波动数有 个,即可求出波动数的概率. 【详解】由1,2,3,4,5组成的没有重复数字的五位数一共有55A 120=种.而构成波动数,需满足a b c d e ><><,有:31425,31524,41325,41523,51324,51423,32415,32514,42315,42513,52314,52413,21435,21534,53412,43512一共16个. 所以波动数的概率为16212015=. 故选:B.8.(2022·河南省杞县高中模拟预测(理))在区间[]0,1上随机取两个数,则这两个数差的绝对值大于12的概率为( ) A .34B .12C .14D .18【答案】C 【解析】 【分析】设在[]0,1上取的两数为x ,y ,满足12x y ->,画出不等式表示的平面区域,结合面积比的几何概型,即可求解.设在[]0,1上取的两数为x ,y ,则12x y ->,即12x y ->,或12x y -<-.画出可行域,如图所示,则12x y ->,或12x y -<-所表示的区域为图中阴影部分,易求阴影部分的面积为14,故所求概率11414P ==; 故选:C.9.(2022·全国·哈师大附中模拟预测)若在区间[]1,1-内随机取一个实数t ,则直线y tx =与双曲线2214xy -=的左、右两支各有一个交点的概率为( )A .14B .12C .18D .34【答案】B 【解析】 【分析】求出双曲线渐近线的斜率,根据已知条件可得出t 的取值范围,结合几何概型的概率公式可求得所求事件的概率. 【详解】双曲线的渐近线斜率为12±,则12t <,即1122t -<<,故所求概率为12P =,10.(2022·陕西·西北工业大学附属中学模拟预测(理))甲、乙两人约定某日上午在M 地见面,若甲是7点到8点开始随机到达,乙是7点30分到8点30分随机到达,约定,先到者没有见到对方时等候10分钟,则甲、乙两人能见面的概率为( ). A .13B .16C .59D .38【答案】B 【解析】 【分析】从早上7点开始计时,设甲经过x 十分钟到达,乙经过y 十分钟到达,可得x 、y 满足的不等式线组对应的平面区域为如图的正方形ABCD ,而甲乙能够见面,x 、y 满足的平面区域是图中的四边形EFGH .分别算出图中正方形和四边形的面积,根据面积型几何概型的概率公式计算可得. 【详解】解:从早上7点开始计时,设甲经过x 十分钟到达,乙经过y 十分钟到达, 则x 、y 满足0639x y ≤≤⎧⎨≤≤⎩,作出不等式组对应的平面区域,得到图中的正方形ABCD ,若甲乙能够见面,则x 、y 满足||1x y -≤, 该不等式对应的平面区域是图中的四边形EFGH ,6636ABCD S =⨯=,114422622EFGH BEHBFGS SS=-=⨯⨯-⨯⨯= 因此,甲乙能见面的概率61366EFGH ABCD S P S ===故选:B .二、填空题11.(2022·上海青浦·二模)受疫情防控需求,现有四位志愿者可自主选择到三个不同的核酸检测点进行服务,则三个核酸检测点都有志愿者到位的概率是_________.(结果用最简分数表示) 【答案】49【解析】【分析】先计算总共的选择数,再计算三个核酸检测点都有志愿者到位的数量,即可得答案.【详解】解:四个志愿者总的选择共333381N =⨯⨯⨯=种,要满足三个核酸检测点都有志愿者到位,则必有2个人到同一核酸检测点,故从4人中选择2人出来,共有24C 6=种,再将这2人看成整体1人和其他2人共3人,选择三个核酸检测点,共33A 6=种,所以6636n =⨯=,所以364819n P N ===.故答案为:49.12.(2022·黑龙江·哈尔滨三中一模(理))关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请120名同学,每人随机写下一个x 、y都小于1的正实数对(),x y ,再统计x 、y 两数能与1构成钝角三角形时的数对(),x y 的个数m ,最后再根据m 来估计π的值.假如统计结果是36m =,那么π的估计值为______.【答案】3.2【解析】【分析】(,)x y 表示的点构成一个正方形区域,x 、y 两数能与1构成钝角三角形时的数对(),x y 表示的点构成图中阴影部分,分别求出其面积,由几何概型概率公式求得其概率后可得.【详解】(,)x y 表示的点构成一个正方形区域,如图正方形OABC (不含边界),x 、y 两数能与1构成钝角三角形满足条件2211x y x y +>⎧⎨+<⎩,(,)x y 表示的点构成的区域是图中阴影部分(不含边界), 因此所求概率为1136********P ππ-==-=,估计 3.2π≈.故答案为:3.213.(2022·河南·模拟预测)现有四张正面分别标有数字-1,0,-2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张记作m 不放回,再从余下的卡片中取一张记作n .则点(),P m n 在第二象限的概率为______. 【答案】16【解析】【分析】列出所有可能的情况,根据古典概型的方法求解即可【详解】由题,点(),P m n 所有可能的情况为()1,0-,()1,2--,()1,3-,()0,1-,()0,2-,()0,3,()2,1--,()2,0-,()2,3-,()3,1-,()3,0,()3,2-共12种情况,其中在第二象限的为()2,3-,()1,3-,故点(),P m n 在第二象限的概率为21126= 故答案为:1614.(2021·江西·新余市第一中学模拟预测(理))寒假即将来临,小明和小强计划去图书馆看书,约定上午8:00~8:30之间的任何一个时间在图书馆门口会合.两人商量好提前到达图书馆的人最多等待对方10分钟,如果对方10分钟内没到,那么等待的人先进去.则两人能够在图书馆门口会合的概率是_________________. 【答案】59【解析】先把两人能够会合转化为几何概型,利用几何概型的概率公式直接求解.【详解】设小明到达的时刻为8时x 分,小强到达的时刻为8时y 分,其中030,030x y ≤≤≤≤, 则当|x-y |≤10时,两人能够在图书馆门口会合.如图示:两人到达时刻(x ,y )构成正方形区域,记面积为S ,而事件A :两人能够在图书馆门口会合构成阴影区域,记其面积为S 1 所以1900-22005()=9009S P A S ⨯==. 故答案为:59.【点睛】(1)几何概型的两个特征——无限性和等可能性,只有同时具备这两个特点的概型才是几何概型;(2)几何概型通常转化为长度比、面积比、体积比。
高考数学热点问题专题练习——古典概型知识归纳及例题讲解

古典概型一、基础知识:1、基本事件:一次试验中可能出现的每一个不可再分的结果称为一个基本事件。
例如:在扔骰子的试验中,向上的点数1点,2点,……,6点分别构成一个基本事件2、基本事件空间:一次试验,将所有基本事件组成一个集合,称这个集合为该试验的基本事件空间,用Ω表示。
3、基本事件特点:设一次试验中的基本事件为12,,,n A A A(1)基本事件两两互斥(2)此项试验所产生的事件必由基本事件构成,例如在扔骰子的试验中,设i A 为“出现i 点”,事件A 为“点数大于3”,则事件456A A A A =(3)所有基本事件的并事件为必然事件 由加法公式可得:()()()()()1212n n P P A A A P A P A P A Ω==+++因为()1P Ω=,所以()()()121n P A P A P A +++=4、等可能事件:如果一项试验由n 个基本事件组成,而且每个基本事件出现的可能性都是相等的,那么每一个基本事件互为等可能事件。
5、等可能事件的概率:如果一项试验由n 个基本事件组成,且基本事件为等可证明:设基本事件为12,,,n A A A ,可知()()()12n P A P A P A ===()()()121n P A P A P A +++= 6、古典概型的适用条件:(1)试验的所有可能出现的基本事件只有有限多个 (2)每个基本事件出现的可能性相等当满足这两个条件时,事件A 发生的概率就可以用事件A 所包含的基本事件个7、运用古典概型解题的步骤:① 确定基本事件,一般要选择试验中不可再分的结果作为基本事件,一般来说,试验中的具体结果可作为基本事件,例如扔骰子,就以每个具体点数作为基本事件;在排队时就以每种排队情况作为基本事件等,以保证基本事件为等可能事件 ② ()(),n A n Ω可通过计数原理(排列,组合)进行计算③ 要保证A 中所含的基本事件,均在Ω之中,即A 事件应在Ω所包含的基本事件中选择符合条件的 二、典型例题:例1:从16-这6个自然数中随机取三个数,则其中一个数是另外两个数的和的概率为________思路:事件Ω为“6个自然数中取三个”,所以()3620n C Ω==,事件A 为“一个数是另外两个数的和”,不妨设a b c =+,则可根据a 的取值进行分类讨论,列举出可能的情况:{}{}{}{}{}{}3,2,1,4,3,1,5,4,1,5,3,2,6,5,1,6,4,2,所以()6n A =。
高考数学冲刺复习几何概型考点深度剖析

高考数学冲刺复习几何概型考点深度剖析在高考数学的复习冲刺阶段,几何概型是一个重要的考点,也是许多同学感到困惑和容易出错的部分。
为了帮助同学们在高考中更好地应对这一考点,我们将对几何概型进行深度剖析。
一、几何概型的概念几何概型是概率论中的一个重要概念,与古典概型相对应。
在古典概型中,试验的结果是有限个等可能的基本事件;而在几何概型中,试验的结果是无限个的,且每个结果出现的可能性相等,通常借助几何图形的长度、面积或体积来计算概率。
例如,在一个边长为 1 的正方形区域内随机取一点,求该点到正方形某个顶点的距离小于 1/2 的概率。
这就是一个典型的几何概型问题。
二、几何概型的特点1、无限性几何概型的基本事件有无限多个。
2、等可能性每个基本事件发生的可能性相等。
3、几何度量通过计算几何图形的长度、面积或体积等几何度量来确定概率。
三、几何概型的计算公式若几何概型中的随机事件 A 对应的区域长度(面积或体积)为 m,全部结果构成的区域长度(面积或体积)为 n,则事件 A 发生的概率为 P(A) = m / n 。
四、常见的几何概型类型1、长度型几何概型例如,在一条线段上取一点,求该点落在某一区间内的概率。
2、面积型几何概型比如,在一个平面区域内随机投点,求点落在某个特定区域内的概率。
3、体积型几何概型像在一个立体空间内随机取点,求点落在某个体积内的概率。
五、解题步骤1、理解题意明确题目中所描述的随机试验和所求概率的事件。
2、确定几何区域找出与随机试验对应的几何图形,并确定其度量(长度、面积或体积)。
3、计算概率根据几何概型的计算公式,计算出所求事件的概率。
六、经典例题解析例 1:在区间0, 5上随机取一个数 x ,求 x 满足 2 < x < 4 的概率。
解:区间0, 5的长度为 5,满足 2 < x < 4 的区间长度为 2,所以概率 P = 2 / 5 。
例 2:在半径为 1 的圆内随机取一点,求该点到圆心的距离小于 1/2 的概率。
高考数学冲刺古典概型考点全面解析

高考数学冲刺古典概型考点全面解析高考对于每一位学子来说,都是人生中的一次重要挑战。
而数学作为其中的关键学科,更是备受关注。
在数学的众多考点中,古典概型是一个不容忽视的重要部分。
在高考冲刺阶段,对古典概型进行全面且深入的复习,对于提高数学成绩具有重要意义。
一、古典概型的基本概念古典概型是一种概率模型,具有两个重要特征:有限性和等可能性。
有限性指的是试验中所有可能出现的基本事件只有有限个;等可能性则表示每个基本事件出现的可能性相等。
例如,掷一枚质地均匀的骰子,出现的点数就是一个古典概型问题。
因为骰子的点数只有 1、2、3、4、5、6 这六种可能,且每种点数出现的可能性相同。
二、古典概型的概率计算公式在古典概型中,事件 A 的概率可以通过以下公式计算:P(A) =事件 A 包含的基本事件个数/试验中所有可能的基本事件个数例如,从装有 3 个红球和 2 个白球的口袋中随机取出一个球,求取出红球的概率。
这里试验中所有可能的基本事件个数为 5(3 个红球和2 个白球),取出红球的基本事件个数为 3,所以取出红球的概率为3/5。
三、古典概型的常见题型1、摸球问题这是古典概型中常见的一类问题。
例如,一个袋子里装有 5 个红球和 3 个白球,从中随机摸出 2 个球,求摸出一红一白的概率。
解决这类问题时,首先要确定总的基本事件个数,即从 8 个球中选2 个的组合数。
然后计算摸出一红一白的基本事件个数,可以分两步考虑,先选一个红球,再选一个白球,两者相乘即为摸出一红一白的基本事件个数。
2、掷骰子问题掷骰子问题常常会与其他条件相结合。
比如,同时掷两枚质地均匀的骰子,求点数之和大于 8 的概率。
对于这种问题,需要列出所有可能的基本事件,然后找出点数之和大于 8 的基本事件个数,最后计算概率。
3、抽样问题抽样问题可以分为有放回抽样和无放回抽样。
例如,从 10 件产品中抽取 3 件,有放回抽样和无放回抽样时,抽到特定产品的概率是不同的。
高中数学总结归纳点拨 古典概型创新题赏析

古典概型创新题赏析古典概型是一种重要的概率模型,也是高考命题的重点.近年来,在高考或各地模拟考试中出现了一些以古典概型为背景的创新题,考查了同学们的探究能力和创新能力.下面撷取几例,与同学们共赏析.一、信息迁移创新信息迁移题是近年高考命题改革的一个新的亮点.此类试题通过给出一个新概念,或定义一种新运算,或给出几个新模型等来创设新的问题情境,要求同学们在阅读理解的基础上,应用所学的知识和方法,实现信息的迁移,以达到灵活解题的目的.例1“渐升数”是指每个数字比其左边的数字大的自然数(如2578),在两位的“渐升数”中任取一个数比37大的概率是_____.解析:十位是1的“渐升数”有8个;十位是2的“渐升数”有7个;…;十位是8的“渐升数”有1个,所以两位的“渐升数”共有8+7+6+5+4+3+2+1=36个;以3为十位比37大的“渐升数”有2个,分别以4,5,6,7,8为十位数的“渐升数”均比37大,且共有5+4+3+2+1=15个,所以比37大的两位“渐升数”共有2+15=17个.故在两位的“渐升数”中任取一个比37大的概率是17 36.二、图表解读创新给出图表,要求同学们对图表进行观察,分析,并提炼,挖掘出图表所给予的有用信息,排除有关数据的干扰,进而抓住问题的实质,达到求解的目的.例2下表为某班英语及数学的成绩分布,全班共有学生50人,成绩分为1~5五个档次.例如表中所示英语成绩为4分,数学成绩为2分的学生共5人(设x,y分别表示英语成绩和数学成绩).(1)4x =的概率是多少?4x =且3y =的概率是多少?3x ≥的概率是多少?(2)2x =的概率是多少?a b +的值是多少?解析:(1)15717(4)5025P x +++===;7(43)50P x y ===,; 7(3)(3)(4)(5)10P x P x P x P x ==+=+==≥; (2)571(2)1(1)(3)150105P x P x P x ==-=-=--=≥; 又1601(2)505b a P x ++++===,则3a b +=.三、知识交汇创新 这类问题从学科知识的内在联系出发,在知识交汇点上做文章,一个题目往往包含多个知识点.例3 先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1,2,3,4,5,6),骰子朝上的面的点数分别为X Y ,,则2log 1X Y =的概率为( )A.16 B.536 C.112 D.12解析:本题是古典概型与对数知识的交汇,可先根据对数性质得到Y与X的关系,进而求解.由题设知,骰子朝上的点数X ,Y 满足2Y X =,就是说朝上的面的点数只能是1,2;2,4;3,6,即所求概率为313612=.故选(C) 例4 设l 为平面上过点(01),的直线,l 的斜率等可能的取0-,则原点到l 的距离小于1的概率是 . 解析:本题是古典概型与解析几何知识的交汇,运用点到直线的距离公式分别求距离得解.原点到过点(01),且斜率分别为0-的直线的距离分别为1122111323323,,,,,,.故原点到l的距离小于1的概率为67.。
高考数学 黄金考点精析精训 考点27 随机事件的概率、古典概型和几何概型 理-人教版高三全册数学试题

考点27 随机事件的概率、古典概型和几何概型【考点剖析】1.最新考试说明:1.事件与概率(1)了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别.(2)了解两个互斥事件的概率加法公式.2.古典概型(1)理解古典概型及其概率计算公式.(2)会计算一些随机事件所含的基本事件数及事件发生的概率.3.随机数与几何概型(1)了解随机数的意义,能运用模拟方法估计概率.(2)了解几何概型的意义.2.命题方向预测:1.随机事件的概率在高考中多以选择题、填空题的形式考查,也时常在解答题中出现,应用题也是常考题型,并且常与统计知识放在一块考查.2.借助古典概型考查互斥事件、对立事件的概率求法.考查古典概型概率公式的应用,尤其是古典概型与互斥、对立事件的综合问题更是高考的热点.在解答题中古典概型常与统计相结合进行综合考查,考查学生分析和解决问题的能力,难度以中档题为主.3.以选择题或填空题的形式考查与长度或面积有关的几何概型的求法是高考对本内容的热点考法,特别是与平面几何、函数等结合的几何概型是高考的重点内容.新课标高考对几何概型的要求较低,因此高考试卷中此类试题以低、中档题为主.3.名师二级结论:一条规律互斥事件与对立事件都是两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求二者之一必须有一个发生,因此,对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件.两种方法求复杂的互斥事件的概率一般有两种方法:(1)直接法:将所求事件的概率分解为一些彼此互斥的事件的概率的和,运用互斥事件的求和公式计算;(2)间接法:先求此事件的对立事件的概率,再用公式())1(A A P P =-,即运用逆向思维(正难则反),特别是“至多”、“至少”型题目,用间接法就显得比较简便. 一条规律从集合的角度去看待概率,在一次试验中,等可能出现的全部结果组成一个集合I ,基本事件的个数n 就是集合I 的元素个数,事件A 是集合I 的一个包含m 个元素的子集.故().cardA mP A cardI n== 两种方法(1)列举法:适合于较简单的试验.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.另外在确定基本事件时,(x ,y )可以看成是有序的,如(1,2)与(2,1)不同;有时也可以看成是无序的,如(1,2)与(2,1)相同. 一条规律对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法. 两种类型(1)线型几何概型:当基本事件只受一个连续的变量控制时.(2)面型几何概型:当基本事件受两个连续的变量控制时,一般是把两个变量分别作为一个点的横坐标和纵坐标,这样基本事件就构成了平面上的一个区域,即可借助平面区域解决. 4.考点交汇展示: (1)与函数相结合【2017某某,7】 记函数2()6f x x x =+-的定义域为D .在区间[4,5]-上随机取一个数x ,则x D ∈的概率是. 【答案】59(2)与线性规划、定积分相结合【2017届某某省某某市第八中学高三春季模拟】若从区间()0,(e e 为自然对数的底数,2.71828...e =)内随机选取两个数,则这两个数之积小于e 的概率为 ( )A.2e B. 1e C. 21e - D. 11e- 【答案】A【解析】可行域为0{0 x ey e xy e<<<<<,画出图像如下图所示,故概率为1212eee dxxe e⋅+=⎰.【考点分类】热点一 随机事件的概率1.【2016年高考理数】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则() A.乙盒中黑球不多于丙盒中黑球 B.乙盒中红球与丙盒中黑球一样多 C.乙盒中红球不多于丙盒中红球 D.乙盒中黑球与丙盒中红球一样多 【答案】C2.【2018届某某省名校高三模拟一】在,,A B C 三个盒子中各有编号分别为1,2,3的3个乒乓球,现分别从每个盒子中随机地各取出1个乒乓球,那么至少有一个编号是奇数的概率为__________. 【答案】2627【解析】从1是个盒子取出的乒乓球的编号是偶数的概率为13,则从3个盒子取出的乒乓球的编号都是偶数的概率为()111133327P A =⨯⨯=,所以至少有一个编号是奇数的概率概率为()12612727P A =-=3.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为________.【答案】5.6【解析】从4只球中一次随机摸出2只,共有6种摸法,其中两只球颜色相同的只有1种,不同的共有5种,所以其概率为5.6【方法总结】求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和;二是先求其对立事件的概率,然后再应用公式求解.如果采用方法一,一定要将事件拆分成若干个互斥事件,不能重复和遗漏;如果采用方法二,一定要找准其对立事件,否则容易出现错误. 热点二 古典概型1.【2018届某某省某某航天高级中学高三9月模拟】设{},0,1,2,3,4m n ∈,向量()1,2a =--,(),b m n =,则//a b 的概率为( )A.225 B. 325 C. 320 D. 15【答案】B【解析】//a b 22m n m n ⇒-=-⇒= ,所以012{,{ ,{ ,024m m m n n n ======因此概率为335525=⨯ ,选B. 2.【2017届某某省红河州高三毕业生复习统一检测】袋中有五X 卡片,其中红色卡片三X ,标号分别为1,2,3;蓝色卡片两X ,标号分别为1,2;从以上五X 卡片中任取两X ,这两X 卡片颜色不同且标号之和小于4的概率为( ) A.13 B. 110 C. 310 D. 23【答案】C【解析】从五X 卡片中任取两X 的所有可能情况有如下10种: 红1红2,红1红3,红1蓝1,红1蓝2,红2红3, 红2蓝1,红2蓝2,红3蓝1,红3蓝2,,蓝1蓝2其中两X 卡片的颜色不同且标号之和小于4的有3种情况,红1蓝1,,红1蓝2,红2蓝1, 故所求的概率为310P = 故答案选C3.【2016高考某某卷】将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是.【答案】5.6【解析】点数小于10的基本事件共有30种,所以所求概率为305.366= 【方法总结】1.计算古典概型事件的概率可分三步:①算出基本事件的总个数n ;②求出事件A 所包含的基本事件个数m ;③代入公式求出概率P . 2.古典概型中基本事件数的探求方法 (1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目. 热点三 几何概型1.【2017课标1,理】如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A .14 B .π8 C .12D .π4【答案】B 【解析】2.【2018届某某省揭阳市惠来县第一中学高三上第一次月考】在[]4,4-上随机地取一个数m ,则事件“直线20x y m -+=与22220x y x ++-=有公共点”发生的概率为( ) A.16 B. 13 C. 23 D. 34【答案】D【解析】由直线20x y m -+=与圆()2222220,13x y x x y ++-=++=有公共点得:13243m m -+≤⇒-≤≤ ,所以概率为()()423444--=-- ,选D. 3.【2016高考某某理数】在[1,1]上随机地取一个数k ,则事件“直线y =kx 与圆22(5)9x y 相交”发生的概率为 . 【答案】34【解析】直线y =kx 与圆22(5)9xy 相交,需要满足圆心到直线的距离小于半径,即2|5k |d 31k =<+,解得33k 44-<<,而[1,1]k,所以所求概率P =33224=.4.【2018届某某省某某中学高三9月大联考】2017年8月1日是中国人民解放军建军90周年,中国人民银行为此发行了以此为主题的金银纪念币.如图所示是一枚8克圆形金质纪念币,直径22mm ,面额100元.为了测算图中军旗部分的面积,现用1粒芝麻向硬币内投掷100次,其中恰有30次落在军旗内,据此可估计军旗的面积大约是( )A.27265mm π B. 236310mm π C. 23635mm π D. 236320mm π【答案】B【解析】利用古典概型近似几何概型可得,芝麻落在军旗内的概率为30310010p ==, 设军旗的面积为S ,由题意可得:()22233363,1111101010S S mm πππ=∴=⨯⨯=⨯. 本题选择B 选项. 【方法总结】(1)当试验的结果构成的区域为长度、面积、体积等时,应考虑使用几何概型求解. (2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域.(3)几何概型有两个特点:一是无限性,二是等可能性.基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的区域都是有限的,因此可用“比例解法”求解几何概型的概率. 应用公式()P A =()()A 构成事件的区域长度面积或体积试验的全部结果所构成的区域长度面积或体积.【热点预测】1.从正五边形的五个顶点中,随机选择三个顶点连成三角形,对于事件A :“这个三角形是等腰三角形”,下列推断正确的是( ) A .事件A 发生的概率等于15 B .事件A 发生的概率等于25C .事件A 是不可能事件D .事件A 是必然事件 【答案】D【解析】因为任意三个顶点连成三角形都是等腰三角形,所以事件A 是必然事件.2.【2016高考新课标1卷】某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( )(A )13 (B )12 (C )23 (D )34【答案】B【解析】如图所示,画出时间轴:8:208:107:507:408:308:007:30小明到达的时间会随机的落在图中线段AB 中,而当他的到达时间落在线段AC 或DB 时,才能保证他等车的时间不超过10分钟根据几何概型,所求概率10101402P +==.故选B . 3.在区间[]0,2上随机地取一个数x ,则事件“121-1log 2x ≤+≤()1”发生的概率为( ) (A )34(B )23(C )13(D )14【解析】由121-1log 2x ≤+≤()1得,11122211113log 2log log ,2,022222x x x ≤+≤≤+≤≤≤(),所以,由几何概型概率的计算公式得,332204P -==-,故选A .4.已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为( )A .0.4B .0.6C .0.8D .1 【答案】B5.【2017届某某某某中学高三摸底】已知4X 卡片上分别写着数字1,2,3,4,甲、乙两人等可能地从这4X 卡片中选择1X ,则他们选择同一X 卡片的概率为( ) A .1 B .116 C .14 D .12【答案】C【解析】甲、乙两人选择卡片的所有基本事件为(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个基本事件,选择同一X 卡片的有4个,所以他们选择同一X 卡片的概率为41164P ==,故选C. 6.【2018届某某省某某昌黎实验学校高三第二次段考】 五个人围坐在一X 圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来;若硬币正面朝下, 则这个人继续坐着. 那么,没有相邻的两个人站起来的概率为 A.12 B. 1532 C. 1132 D. 516【解析】五个人的编号为12345,,,,由题意,所有事件共有5232=种,没有相邻的两个人站起来的基本事件有()()()()()()()()12345131424,,,,,,,,,,,再加上()()2535,,, 没有人站起来的可能有1种,共11种情况, 所以没有相邻的两个人站起来的概率为1132故答案选C .7.【2018届某某市耀华中学高三上学期第一次月考】在6盒酸奶中,有2盒已经过了保质期,从中任取2盒,取到的酸奶中有已过保质期的概率为 ( ) A.13 B. 23 C. 35 D. 115【答案】C【解析】所求概率为24266311155C C -=-= ,选C.8.【2016高考新课标2理数】从区间[]0,1随机抽取2n 个数1x ,2x ,…,n x ,1y ,2y ,…,n y ,构成n 个数对()11,x y ,()22,x y ,…,(),n n x y ,其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为(A )4n m (B )2n m (C )4m n (D )2mn【答案】C【解析】利用几何概型,圆形的面积和正方形的面积比为224S R mS R nπ==圆正方形,所以4m n π=.选C.9.投掷两颗骰子,其向上的点数分别为m 和n ,则复数2)(ni m +为纯虚数的概率为( )A .13B .14C .16D .112【答案】C【解析】∵复数2)(ni m +为纯虚数∴m n =∴61666p ==⨯ 10.【2018届某某省株洲市醴陵第二中学、醴陵第四中学高三上期中】在区间[]0,π上随机地取一个数x ,则事件“1sin 2x ≤”发生的概率为( ) A. 23 B. 12 C. 13 D. 16【答案】C【解析】根据三角函数的图像和特殊角的三角函数值,得到1sin 2x ≤5|066x x x πππ⎧⎫⇒≤≤≤≤⎨⎬⎩⎭或,根据几何概型判断,概率为:13.3ππ=故答案选C 。
高考数学一轮复习专题训练—古典概型与几何概型

古典概型与几何概型考纲要求1.理解古典概型及其概率计算公式;2.会计算一些随机事件所包含的基本事件数及事件发生的概率;3.了解随机数的意义,能运用模拟方法估计概率;4.了解几何概型的意义.知识梳理1.古典概型 (1)基本事件的特点①任何两个基本事件是互斥的.②任何事件(除不可能事件)都可以表示成基本事件的和. (2)古典概型的定义具有以下两个特点的概率模型称为古典概率模型,简称古典概型.(3)古典概型的概率公式 P (A )=A 包含的基本事件的个数基本事件的总数.2.几何概型 (1)几何概型的定义如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,那么称这样的概率模型为几何概率模型,简称几何概型. (2)几何概型的两个基本特点(3)几何概型的概率公式P(A)=构成事件A的区域长度面积或体积试验的全部结果所构成的区域长度面积或体积.1.古典概型中的基本事件都是互斥的,确定基本事件的方法主要有列举法、列表法与树状图法.2.概率的一般加法公式P(A∪B)=P(A)+P(B)-P(A∩B)中,易忽视只有当A∩B=∅,即A,B互斥时,P(A∪B)=P(A)+P(B),此时P(A∩B)=0.3.几何概型的基本事件的个数是无限的,古典概型中基本事件的个数是有限的.诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)“在适宜条件下,种下一粒种子观察它是否发芽”属于古典概型,其基本事件是“发芽与不发芽”.()(2)掷一枚硬币两次,出现“两个正面”“一正一反”“两个反面”,这三个结果是等可能事件.()(3)随机模拟方法是以事件发生的频率估计概率.()(4)概率为0的事件一定是不可能事件.()答案(1)×(2)×(3)√(4)×解析对于(1),发芽与不发芽不一定是等可能,所以(1)不正确;对于(2),三个事件不是等可能,其中“一正一反”应包括正反与反正两个基本事件,所以(2)不正确;对于(4),概率为0的事件有可能发生,所以(4)不正确.2.袋中装有6个白球,5个黄球,4个红球,从中任取一球抽到白球的概率为( ) A.25 B .415C .35D .非以上答案答案 A解析 从袋中任取一球,有15种取法,其中抽到白球的取法有6种,则所求概率为p =615=25. 3.如图,正方形的边长为2,向正方形ABCD 内随机投掷200个点,有30个点落入图形M 中,则图形M 的面积的估计值为____________.答案 0.6解析 由题意可得正方形面积为4,设不规则图形的面积为S ,由几何概型概率公式可得S4≈30200,∴S ≈0.6.4.(2020·全国Ⅰ卷)设O 为正方形ABCD 的中心,在O ,A ,B ,C ,D 中任取3点,则取到的3点共线的概率为( ) A.15 B .25C .12D .45答案 A解析 从O ,A ,B ,C ,D 这5个点中任取3点,取法有{O ,A ,B },{O ,A ,C },{O ,A ,D },{O ,B ,C },{O ,B ,D },{O ,C ,D },{A ,B ,C },{A ,B ,D },{A ,C ,D },{B ,C ,D },共10种,其中取到的3点共线的只有{O ,A ,C },{O ,B ,D }这2种取法,所以所求概率为210=15.故选A.5.(2019·全国Ⅲ卷)两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是( ) A.16 B .14C.13 D .12答案 D解析 设两位男同学分别为A ,B ,两位女同学分别为a ,b ,则用“树形图”表示四位同学排成一列所有可能的结果如图所示.由图知,共有24种等可能的结果,其中两位女同学相邻的结果(画“√”的情况)共有12种,故所求概率为1224=12.6. (2021·郑州模拟)公元前5世纪下半叶,希波克拉底解决了与化圆为方有关的化月牙形为方.如图,以O 为圆心的大圆直径为4,以AB 为直径的半圆面积等于AO 与BO 所夹四分之一大圆的面积,由此可知,月牙形区域的面积与△AOB 的面积相等.现在在两个圆所覆盖的区域内随机取一点,则该点来自阴影部分的概率是________.答案π+68π+4解析 上方阴影部分的面积等于△AOB 的面积,S △AOB =12×2×2=2,下方阴影部分面积等于14×π×22-⎣⎡⎦⎤14×π×22-12×2×2=π2+1,所以根据几何概型概率公式得所求概率P =2+π2+14π+2=π+68π+4.考点一 古典概型的简单计算1.生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( ) A.23 B .35C .25D .15答案 B解析 设5只兔子中测量过某项指标的3只为a 1,a 2,a 3,未测量过这项指标的2只为b 1,b 2,则从5只兔子中随机取出3只的所有可能情况为(a 1,a 2,a 3),(a 1,a 2,b 1),(a 1,a 2,b 2),(a 1,a 3,b 1),(a 1,a 3,b 2),(a 1,b 1,b 2),(a 2,a 3,b 1),(a 2,a 3,b 2),(a 2,b 1,b 2),(a 3,b 1,b 2),共10种可能.其中恰有2只测量过该指标的情况为(a 1,a 2,b 1),(a 1,a 2,b 2),(a 1,a 3,b 1),(a 1,a 3,b 2),(a 2,a 3,b 1),(a 2,a 3,b 2),共6种可能.故恰有2只测量过该指标的概率为610=35.2.(2021·安徽江南十校质量检测)“哥德巴赫猜想”是近代三大数学难题之一,其内容是:一个大于2的偶数都可以写成两个质数(素数)之和,也就是我们所谓的“1+1”问题.它是1742年由数学家哥德巴赫提出的,我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中做出相当好的成绩.若将6拆成两个正整数的和,则拆成的和式中,加数全部为质数的概率为( ) A.15 B .13C .35D .23答案 A解析 6拆成两个正整数的和的所有基本事件有(1,5),(2,4),(3,3),(4,2),(5,1),而加数全为质数的为(3,3),所以所求概率为15,故选A.3.(2020·江苏卷)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是________. 答案 19解析 列表如下:1 2 3 4 5 61 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6789101112点数的和共有点数和为5的概率P =436=19.感悟升华 古典概型中基本事件个数的探求方法:(1)枚举法:适合于给定的基本事件个数较少且易一一列举出的问题.(2)树状图法:适合于较为复杂的问题,注意在确定基本事件时(x ,y )可看成是有序的,如(1,2)与(2,1)不同,有时也可看成是无序的,如(1,2)与(2,1)相同. 考点二 古典概型与其他知识的简单交汇【例1】 (1)(2020·郑州一模)已知集合A =⎩⎨⎧⎭⎬⎫-2,-1,-12,13,12,1,2,3,任取k ∈A ,则幂函数f (x )=x k 为偶函数的概率为________(结果用数值表示).(2)(2021·河北七校联考)若m 是集合{1,3,5,7,9,11}中任意选取的一个元素,则椭圆x 2m +y 22=1的焦距为整数的概率为________. 答案 (1)14 (2)12解析 (1)集合A =⎩⎨⎧⎭⎬⎫-2,-1,-12,13,12,1,2,3,任意k ∈A 的基本事件总数为8,当k =±2时,幂函数f (x )=x k 为偶函数,从而幂函数f (x )=x k 为偶函数包含的基本事件个数为2,∴幂函数f (x )=x k 为偶函数的概率p =14.(2)∵m 是集合{1,3,5,7,9,11}中任意选取的一个元素,∴基本事件总数为6,又满足椭圆x 2m +y 22=1的焦距为整数的m 的取值有1,3,11,共有3个,∴椭圆x 2m +y 22=1的焦距为整数的概率p=36=12. 感悟升华 求解古典概型的交汇问题,关键是把相关的知识转化为事件,然后利用古典概型的有关知识解决,一般步骤为:(1)将题目条件中的相关知识转化为事件; (2)判断事件是否为古典概型; (3)选用合适的方法确定基本事件个数; (4)代入古典概型的概率公式求解.【训练1】 设平面向量a =(m,1),b =(2,n ),其中m ,n ∈{1,2,3,4},记“a ⊥(a -b )”为事件A ,则事件A 发生的概率为( ) A.18 B .14C .13D .12答案 A解析 有序数对(m ,n )的所有可能情况为4×4=16个,由a ⊥(a -b )得m 2-2m +1-n =0,即n =(m -1)2.由于m ,n ∈{1,2,3,4},故事件A 包含的基本事件为(2,1)和(3,4),共2个,所以P (A )=216=18.考点三 古典概型与统计的综合应用【例2】 某城市100户居民的月平均用电量(单位:千瓦时)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.(1)求直方图中x 的值;(2)求月平均用电量的众数和中位数;(3)在月平均用电量为[240,260),[260,280),[280,300]的三组用户中,用分层抽样的方法抽取6户居民,并从抽取的6户中任选2户参加一个访谈节目,求参加节目的2户来自不同组的概率.解 (1)由(0.002 0+0.009 5+0.011 0+0.012 5+x +0.005 0+0.002 5)×20=1得x =0.007 5, 所以直方图中x 的值是0.007 5.(2)月平均用电量的众数是220+2402=230.因为(0.002 0+0.009 5+0.011 0)×20=0.45<0.5, 且(0.002 0+0.009 5+0.011 0+0.012 5)×20=0.7>0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a ,由(0.002 0+0.009 5+0.011 0)×20+0.012 5×(a -220)=0.5,解得a =224, 所以月平均用电量的中位数是224.(3)月平均用电量为[240,260)的用户有0.007 5×20×100=15(户), 月平均用电量为[260,280)的用户有0.005×20×100=10(户), 月平均用电量在[280,300]的用户有0.002 5×20×100=5(户).抽样方法为分层抽样,在[240,260),[260,280),[280,300]中的用户比为3∶2∶1, 所以在[240,260),[260,280),[280,300]中分别抽取3户、2户和1户.设参加节目的2户来自不同组为事件A ,将来自[240,260)的用户记为a 1,a 2,a 3,来自[260,280)的用户记为b 1,b 2,来自[280,300]的用户记为c 1,在6户中随机抽取2户有(a 1,a 2),(a 1,a 3),(a 1,b 1),(a 1,b 2),(a 1,c 1),(a 2,a 3),(a 2,b 1),(a 2,b 2),(a 2,c 1),(a 3,b 1),(a 3,b 2),(a3,c1),(b1,b2),(b1,c1),(b2,c1),共15种取法,其中满足条件的有(a1,b1),(a1,b2),(a1,c1),(a2,b1),(a2,b2),(a2,c1),(a3,b1),(a3,b2),(a3,c1),(b1,c1),(b2,c1),共11种,故参加节目的2户来自不同组的概率P(A)=1115.感悟升华有关古典概型与统计结合的题型是高考考查概率的一个重要题型.概率与统计的结合题,无论是直接描述还是利用频率分布表、频率分布直方图、茎叶图等给出的信息,准确从题中提炼信息是解题的关键.【训练2】海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.(1)求这6件样品中来自A,B(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.解(1)A,B,C三个地区商品的总数量为50+150+100=300,抽样比为6300=1 50,所以样本中包含三个地区的个体数量分别是50×150=1,150×150=3,100×150=2.所以A,B,C三个地区的商品被选取的件数分别是1,3,2.(2)设6件来自A,B,C三个地区的样品分别为:A;B1,B2,B3;C1,C2.则从6件样品中抽取的这2件商品构成的所有基本事件为:{A,B1},{A,B2},{A,B3},{A,C1},{A,C2},{B1,B2},{B1,B3},{B1,C1},{B1,C2},{B2,B3},{B2,C1},{B2,C2},{B3,C1},{B3,C2},{C1,C2},共15个.每个样品被抽到的机会均等,因此这些基本事件的出现是等可能的.记事件D:“抽取的这2件商品来自相同地区”,则事件D包含的基本事件有:{B1,B2},{B1,B 3},{B 2,B 3},{C 1,C 2},共4个. 所以P (D )=415.即这2件商品来自相同地区的概率为415.考点四 几何概型角度1 与长度(角度)有关的几何概型【例3】 (1)在[-6,9]内任取一个实数m ,设f (x )=-x 2+mx +m ,则函数f (x )的图象与x 轴有公共点的概率等于( ) A.215B .715C .35D .1115(2)如图所示,在等腰直角三角形ABC 中,过直角顶点C 在∠ACB 内部任作一条射线CM ,与AB 交于点M ,则AM <AC 的概率为________.答案 (1)D (2)34解析 (1)因为f (x )=-x 2+mx +m 的图象与x 轴有公共点,所以Δ=m 2+4m ≥0,所以m ≤-4或m ≥0,所以在[-6,9]内取一个实数m ,函数f (x )的图象与x 轴有公共点的概率p =[-4--6]+9-09--6=1115. (2)过点C 作CN 交AB 于点N ,使AN =AC ,如图所示.显然当射线CM 处在∠ACN 内时,AM <AC ,又∠A =45°,所以∠ACN =67.5°,故所求概率为p =67.5°90°=34.感悟升华 1.解答几何概型问题的关键在于弄清题中的考查对象和对象的活动范围,当考查对象为点,且点的活动范围在线段上时,用“线段长度”为测度计算概率,求解的核心是确定点的边界位置.2.当涉及射线的转动,扇形中有关落点区域问题时,应以角对应的弧长的大小作为区域度量来计算概率.事实上,当半径一定时,曲线弧长之比等于其所对应的圆心角的弧度数之比. 角度2 与面积有关的几何概型【例4】 在区间(0,1)上任取两个数,则两个数之和小于65的概率是( )A.1225 B .1625C .1725D .1825答案 C解析 设这两个数是x ,y ,则试验所有的基本事件构成的区域即⎩⎪⎨⎪⎧0<x <1,0<y <1确定的平面区域,满足条件的事件包含的基本事件构成的区域即⎩⎪⎨⎪⎧0<x <1,0<y <1,x +y <65确定的平面区域,如图所示,阴影部分的面积是1-12×⎝⎛⎭⎫452=1725,所以这两个数之和小于65的概率是1725.感悟升华 几何概型与平面几何的交汇问题:要利用平面几何的相关知识,先确定基本事件对应区域的形状,再选择恰当的方法和公式,计算出其面积,进而代入公式求概率. 角度3 与体积有关的几何概型【例5】 有一个底面半径为1、高为2的圆柱,点O 为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P ,则点P 到点O 的距离大于1的概率为________. 答案 23解析 由题意得该圆柱的体积V =π×12×2=2π.圆柱内满足点P 到点O 的距离小于等于1的几何体为以圆柱底面圆心为球心的半球,且此半球的体积V 1=12×43π×13=23π,所以所求概率p =V -V 1V =23.感悟升华 对于与体积有关的几何概型问题,关键是计算问题的总体积(总空间)以及事件的体积(事件空间),对于某些较复杂的也可利用其对立事件去求.【训练3】 (1)(2021·西安一模)在区间[-1,1]上随机取一个数k ,使直线y =k (x +3)与圆x 2+y 2=1相交的概率为( ) A.12B .13C .24D .23(2) (2020·新疆一模)剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受.剪纸艺术通过一把剪刀、一张纸就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )A.π64B .π32C .π16D .π8答案 (1)C (2)D解析 (1)圆x 2+y 2=1的圆心为(0,0), 圆心到直线y =k (x +3)的距离为|3k |k 2+1, 要使直线y =k (x +3)与圆x 2+y 2=1相交,则|3k |k 2+1<1,解得-24<k <24. ∴在区间[-1,1]上随机取一个数k ,使直线y =k (x +3)与圆x 2+y 2=1相交的概率为24-⎝⎛⎭⎫-242=24. (2)设黑色小圆的半径为r .由题意得2r +2r +2×2r =1,解得r =18,所以白色区域的面积为π·⎝⎛⎭⎫122-4×π·⎝⎛⎭⎫182-π·⎝⎛⎭⎫142=π8.所以在正方形图案上随机取一点,该点取自白色区域的概率为π81×1=π8.故选D. 基础巩固一、选择题1.一枚硬币连掷2次,恰好出现1次正面的概率是( ) A.12 B .14C .34D .0答案 A解析 列举出所有基本事件,找出“只有1次正面”包含的结果.一枚硬币连掷2次,基本事件有(正,正),(正,反),(反,正),(反,反)共4个,而只有1次出现正面的包括(正,反),(反,正)2个,故其概率为24=12.故选A.2.袋子中有大小、形状完全相同的四个小球,分别写有“和”“谐”“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率.利用电脑随机产生1到4之间(含1和4)取整数值的随机数,分别用1,2,3,4代表“和”“谐”“校”“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下18组随机数: 343 432 341 342 234 142 243 331 112 342 241 244 431 233 214 344 142 134 由此可以估计,恰好第三次就停止摸球的概率为( ) A.19 B .16C .29D .518答案 C解析 由18组随机数得,恰好在第三次停止摸球的随机数是142,112,241,142,共4组,所以恰好第三次就停止摸球的概率约为418=29.故选C.3. (2021·河北六校联考)《周髀算经》中提出了“方属地,圆属天”,也就是人们常说的“天圆地方”.我国古代铜钱的铸造也蕴含了这种“外圆内方”“天地合一”的哲学思想.现将铜钱抽象成如图所示的图形,其中圆的半径为r ,正方形的边长为a (0<a <r ),若在圆内随机取点,得到点取自阴影部分的概率是p ,则圆周率π的值为( )A.a 21-p r 2B .a 21+p r 2C.a1-p rD .a1+p r答案 A解析 由几何概型的概率计算公式,得πr 2-a 2πr 2=p ,化简得π=a 21-p r 2.故选A.4.在集合A ={2,3}中随机取一个元素m ,在集合B ={1,2,3}中随机取一个元素n ,得到点P (m ,n ),则点P 在圆x 2+y 2=9内部的概率为( ) A.12 B .13C .34D .25答案 B解析 点P (m ,n )共有(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),6种情况,只有(2,1),(2,2)这2个点在圆x 2+y 2=9的内部,所求概率为26=13.5.某单位试行上班刷卡制度,规定每天8:30上班,有15分钟的有效刷卡时间(即8:15—8:30),一名职工在7:50到8:30之间到达单位且到达单位的时刻是随机的,则他能有效刷卡上班的概率是( )A.23 B .58C .13D .38答案 D解析 该职工在7:50至8:30之间到达单位且到达单位的时刻是随机的,设其构成的区域为线段AB ,且AB =40,职工的有效刷卡时间是8:15到8:30之间,设其构成的区域为线段CB ,且CB =15,如图,所以该职工有效刷卡上班的概率p =1540=38.故选D.6.(2021·合肥质检)已知三棱锥S -ABC ,在该三棱锥内任取一点P ,则使V P -ABC ≤13V S -ABC的概率为( ) A.13 B .49C .827D .1927答案 D解析 作出S 在底面△ABC 的射影为O ,若V P -ABC =13V S -ABC ,则三棱锥P -ABC 的高等于13SO ,P 点落在平面EFD 上,且SE SA =SD SB =SF SC =23,所以S △EFD S △ABC =49,故V S -EFD =827V S -ABC, ∴V P -ABC ≤13V S -ABC 的概率p =1-827=1927.二、填空题7.(2020·太原模拟)下课以后,教室里还剩下2位男同学和1位女同学,若他们依次随机走出教室,则第2位走出的是女同学的概率是________.答案 13解析 2位男同学记为男1,男2,则三位同学依次走出教室包含的基本事件有:男1男2女,男1女男2,女男1男2,男2男1女,男2女男1,女男2男1,共6种,其中第2位走出的是女同学包含的基本事件有2种.故第2位走出的是女同学的概率是p =26=13.8.在等腰Rt △ABC 中,∠C =90°,在直角边BC 上任取一点M ,则∠CAM <30°的概率是________. 答案33解析 ∵点M 在直角边BC 上是等可能出现的, ∴“测度”是长度.设直角边长为a , 则所求概率为33a a =33.9.(2021·郑州质量预测改编)从2,3,8,9中任取两个不同的数字,分别记为a ,b ,则log a b 为整数的概率是________. 答案 16解析 从2,3,8,9中任取两个不同的数字,分别记为a ,b ,则有(2,3),(2,8),(2,9),(3,8),(3,9),(8,9),(3,2),(8,2),(9,2),(8,3),(9,3),(9,8),共12种取法,其中log a b 为整数的有(2,8),(3,9)两种,故p =212=16.三、解答题10.(2020·成都诊断)某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.(1)求图中实数a的值;(2)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.解(1)由已知,得10×(0.005+0.010+0.020+a+0.025+0.010)=1,解得a=0.030.(2)易知成绩在[40,50)分数段内的人数为40×0.05=2,这2人分别记为A,B;成绩在[90,100]分数段内的人数为40×0.1=4,这4人分别记为C,D,E,F.若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,则所有的基本事件有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个.如果2名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定不大于10.如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定大于10.记“这2名学生的数学成绩之差的绝对值不大于10”为事件M,则事件M包含的基本事件有(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,故所求概率P(M)=715.11.(2019·天津卷)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.(1)应从老、中、青员工中分别抽取多少人?(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.解(1)由已知得老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人、9人、10人.(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.②由表格知,符合题意的所有结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种.所以事件M发生的概率P(M)=1115.能力提升12.(2021·长春质检)我国古人认为宇宙万物是由金、木、水、火、土这五种元素构成的,历史文献《尚书·洪范》提出了五行的说法,到战国晚期,五行相生相克的思想被正式提出.这五种物质属性的相生相克关系如图所示,若从这五种物质中随机选取三种,则取出的三种物质中,彼此间恰好有一个相生关系和两个相克关系的概率为()A.35 B .12C .25D .13答案 B解析 (列举法)依题意,三种物质间相生相克关系如下表,金木水 金木火 金木土 金水火 金水土 金火土 木水火 木水土 木火土 水火土 × √√√×××√×√所以彼此间恰好有一个相生关系和两个相克关系的概率p =510=12,故选B.13.由不等式组⎩⎪⎨⎪⎧x ≤0,y ≥0,y -x -2≤0确定的平面区域记为Ω1,由不等式组⎩⎪⎨⎪⎧x +y ≤1,x +y ≥-2确定的平面区域记为Ω2,若在Ω1中随机取一点,则该点恰好在Ω2内的概率为________. 答案 78解析 如图,平面区域Ω1就是三角形区域OAB ,平面区域Ω2与平面区域Ω1的重叠部分就是区域OACD ,易知C ⎝⎛⎭⎫-12,32.由几何概型的概率公式,所求概率p =S 四边形OACDS △OAB =2-142=78.14.如图所示的茎叶图记录了甲、乙两组各四名同学的植树棵数,其中有一个数据模糊,无法确认,在图中以X 表示.(1)如果X =8,求乙组同学植树棵数的平均数和方差;(2)如果X =9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.解 (1)当X =8时,由茎叶图可知,乙组四名同学的植树棵数分别是8,8,9,10,故x =8+8+9+104=354,s 2=14×⎣⎡⎦⎤⎝⎛⎭⎫8-3542×2+⎝⎛⎭⎫9-3542+⎝⎛⎭⎫10-3542=1116. (2)当X =9时,记甲组四名同学分别为A 1,A 2,A 3,A 4,他们植树的棵数依次为9,9,11,11;乙组四名同学分别为B 1,B 2,B 3,B 4,他们植树的棵数依次为9,8,9,10.分别从甲、乙两组中随机选取一名同学,其包含的基本事件为{A 1,B 1},{A 1,B 2},{A 1,B 3},{A 1,B 4},{A 2,B 1},{A 2,B 2},{A 2,B 3},{A 2,B 4},{A 3,B 1},{A 3,B 2},{A 3,B 3},{A 3,B 4},{A 4,B 1},{A 4,B 2},{A 4,B 3},{A 4,B 4},共16个.设“选出的两名同学的植树总棵数为19”为事件C ,则事件C 中包含的基本事件为{A 1,B 4},{A 2,B 4},{A 3,B 2},{A 4,B 2},共4个.故P (C )=416=14.。
考点27+随机事件的概率、古典概型和几何概型-高考数学(理)提分必备30个黄金考点+Word版含解析

【考点剖析】1.命题方向预测:1.随机事件的概率在高考中多以选择题、填空题的形式考查,也时常在解答题中出现,应用题也是常考题型,并且常与统计知识放在一块考查.2.借助古典概型考查互斥事件、对立事件的概率求法.考查古典概型概率公式的应用,尤其是古典概型与互斥、对立事件的综合问题更是高考的热点.在解答题中古典概型常与统计相结合进行综合考查,考查学生分析和解决问题的能力,难度以中档题为主.3.以选择题或填空题的形式考查与长度或面积有关的几何概型的求法是高考对本内容的热点考法,特别是与平面几何、函数等结合的几何概型是高考的重点内容.新课标高考对几何概型的要求较低,因此高考试卷中此类试题以低、中档题为主. 2.名师二级结论: 一条规律互斥事件与对立事件都是两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求二者之一必须有一个发生,因此,对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件. 两种方法求复杂的互斥事件的概率一般有两种方法:(1)直接法:将所求事件的概率分解为一些彼此互斥的事件的概率的和,运用互斥事件的求和公式计算;(2)间接法:先求此事件的对立事件的概率,再用公式,即运用逆向思维(正难则反),特别是“至多”、“至少”型题目,用间接法就显得比较简便. 一条规律从集合的角度去看待概率,在一次试验中,等可能出现的全部结果组成一个集合I ,基本事件的个数n 就是集合I 的元素个数,事件A 是集合I 的一个包含m 个元素的子集.故 两种方法(1)列举法:适合于较简单的试验.())1(A A P P =-().cardA mP A cardI n==(2)树状图法:适合于较为复杂的问题中的基本事件的探求.另外在确定基本事件时,(x ,y )可以看成是有序的,如(1,2)与(2,1)不同;有时也可以看成是无序的,如(1,2)与(2,1)相同. 一条规律对于几何概型的概率公式中的“测度”要有正确的认识,它只与大小有关,而与形状和位置无关,在解题时,要掌握“测度”为长度、面积、体积、角度等常见的几何概型的求解方法. 两种类型(1)线型几何概型:当基本事件只受一个连续的变量控制时.(2)面型几何概型:当基本事件受两个连续的变量控制时,一般是把两个变量分别作为一个点的横坐标和纵坐标,这样基本事件就构成了平面上的一个区域,即可借助平面区域解决. 3.考点交汇展示:【2017江苏,7】 记函数()f x D .在区间[4,5]-上随机取一个数x ,则x D ∈的概率是 .【答案】591.【2018届东北师范大学附属中学五模】在区间[0,1]上随机取两个数x,y ,记P 为事件"x +y ≤23"的概率,则P =( )A . 23B . 12C . 49D . 29 【答案】D 【解析】如图所示,0≤x ≤1,0≤y ≤1表示的平面区域为ABCD ,平面区域内满足x +y ≤23的部分为阴影部分的区域APQ ,其中P (23,0),Q (0,23), 结合几何概型计算公式可得满足题意的概率值为p =12×23×231×1=29.本题选择D选项.2.【2018届江西省南昌市二轮复习测试四】如图所示,在椭圆x 24+y2=1内任取一个点P,则P恰好取自椭圆的两个端点连线与椭圆围成阴影部分的概率为()A.14−12πB.14−14πC.18D.18−18π【答案】A 【解析】故选:A.【考点分类】考向一随机事件的概率1.【2018年全国卷Ⅲ文】若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A.0.3 B.0.4 C.0.6 D.0.7【答案】B【解析】2.【2018届山西省名校高三模拟一】在三个盒子中各有编号分别为1,2,3的3个乒乓球,现分别从每个盒子中随机地各取出1个乒乓球,那么至少有一个编号是奇数的概率为__________.【答案】【解析】从1是个盒子取出的乒乓球的编号是偶数的概率为,则从3个盒子取出的乒乓球的编号都是偶数的概率为,所以至少有一个编号是奇数的概率概率为3.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为________.【答案】【解析】从4只球中一次随机摸出2只,共有6种摸法,其中两只球颜色相同的只有1种,不同的共有5种,所以其概率为【方法总结】,,A B C262713()111133327P A=⨯⨯=()12612727P A=-=5.65.6求复杂事件的概率通常有两种方法:一是将所求事件转化成彼此互斥的事件的和;二是先求其对立事件的概率,然后再应用公式求解.如果采用方法一,一定要将事件拆分成若干个互斥事件,不能重复和遗漏;如果采用方法二,一定要找准其对立事件,否则容易出现错误.考向二 古典概型1.【2018年理数全国卷II 】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 A. 112 B. 114 C. 115 D. 118 【答案】C 【解析】2.【2018届贵州省遵义航天高级中学高三9月模拟】设,向量,,则的概率为( ) A.B. C. D. 【答案】B【解析】 ,所以 因此概率为 ,选B.3.【2018年江苏卷】某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为________. 【答案】310 【解析】从5名学生中抽取2名学生,共有10种方法,其中恰好选中2名女生的方法有3种,因此所求概率为310.{},0,1,2,3,4m n ∈()1,2a =--(),b m n =//a b 22532532015//a b 22m n m n ⇒-=-⇒=012{ ,{ ,{ ,024m m m n n n ======335525=⨯【方法总结】1.计算古典概型事件的概率可分三步:①算出基本事件的总个数n;②求出事件A所包含的基本事件个数m;③代入公式求出概率P.2.古典概型中基本事件数的探求方法(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.考向三几何概型1.【2018年理新课标I卷】下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为II,其余部分记为III.在整个图形中随机取一点,此点取自I,II,III 的概率分别记为p1,p2,p3,则A. p1=p2B. p1=p3C. p2=p3D. p1=p2+p3【答案】A【解析】2.【2017课标1,理】如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A .B .C .D .【答案】B 【解析】3.【2018届广东省揭阳市惠来县第一中学高三上第一次月考】在上随机地取一个数,则事件“直线与有公共点”发生的概率为( ) A.B. C. D. 【答案】D【解析】由直线与圆有公共点得:,所以概率为,选D. 【方法总结】(1)当试验的结果构成的区域为长度、面积、体积等时,应考虑使用几何概型求解.(2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域.14π812π4[]4,4-m 20x m +=22220x y x ++-=161323340x m +=()2222220,13x y x x y ++-=++=24m ≤⇒-≤≤()()423444--=--(3)几何概型有两个特点:一是无限性,二是等可能性.基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的区域都是有限的,因此可用“比例解法”求解几何概型的概率. 应用公式.【热点预测】1.从正五边形的五个顶点中,随机选择三个顶点连成三角形,对于事件A :“这个三角形是等腰三角形”,下列推断正确的是( )A .事件A 发生的概率等于B .事件A 发生的概率等于C .事件A 是不可能事件D .事件A 是必然事件 【答案】D【解析】因为任意三个顶点连成三角形都是等腰三角形,所以事件A 是必然事件.2.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论哪个是正确的( )A . A,C 互斥B . B,C 互斥 C . 任何两个都互斥D . 任何两个都不互斥 【答案】B 【解析】3. 【2018届四川省成都市双流中学考前模拟】某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为( )A . 110 B . 16 C . 15 D . 56 【答案】B 【解析】()P A =()()A 构成事件的区域长度面积或体积试验的全部结果所构成的区域长度面积或体积1525由题意,此人在50分到整点之间的10分钟内到达,等待时间不多于10分钟,所以概率P =1060=16.故选B .4.【2018届山东省济南省二模】某商场举行有奖促销活动,抽奖规则如下:从装有形状、大小完全相同的2个红球、3个蓝球的箱子中,任意取出两球,若取出的两球颜色相同则中奖,否则不中奖.则中奖的概率为( )A . 15 B . 310 C . 25 D . 35 【答案】C 【解析】从装有形状、大小完全相同的2个红球、3个蓝球的箱子中,任意取出两球共C 52=10种取法,取出的两球颜色相同共C 22+C 32=4种取法,∴中奖的概率为410= 25 故选:C5.【2018届福建省百校临考冲刺】现有大小形状完全相同的4个小球,其中红球有2个,白球与蓝球各1个,将这4个小球排成一排,则中间2个小球不都是红球的概率为( ) A . 16B . 13C . 56D . 23【答案】C 【解析】6.【2018届江西省宜春昌黎实验学校第二次段考】 五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币. 若硬币正面朝上, 则这个人站起来; 若硬币正面朝下, 则这个人继续坐着. 那么, 没有相邻的两个人站起来的概率为 A.B. C. D. 【答案】C1215321132516【解析】五个人的编号为由题意,所有事件共有种,没有相邻的两个人站起来的基本事件有,再加上没有人站起来的可能有种,共种情况,所以没有相邻的两个人站起来的概率为故答案选.7.【2018届江西省南昌市二轮复习测试】将一颗质地均匀的骰子(它是一种各面上分别标有点数1、2、3、4、5、6的正方体玩具)先后抛掷2次,记第一次出现的点数为m,记第二次出现的点数为n,向量a⃑=(m−2,2−m),b⃑⃑=(1,1)则a⃑和b⃑⃑共线的概率为()A.118B.112C.19D.512【答案】B【解析】根据题意,列表表示两次出现的点数情况:共36种情况,若a⃑和b⃑⃑共线,则有m﹣2=2﹣n,即m+n=4,有3种情况,则a⃑和b⃑⃑共线的概率为336=112.;故选:B.12345,,,,5232=()()()()()()()()12345131424,,,,,,,,,,()()2535,,,1111132C8.【2018届宁夏银川一中四模】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为30%,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生0−9之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:402978191925273842812479569683 231357394027506588730113537779则这三天中至少有两天有强浓雾的概率近似为()A.14B.25C.710D.15【答案】D【解析】9.【2019届广东省深圳外国语学校高三初】某学校10位同学组成的志愿者组织分别由李老师和张老师负责,每次献爱心活动均需该组织4位同学参加.假设李老师和张老师分别将各自活动通知的信息独立,随机地发给4位同学,且所发信息都能收到.则甲同学收到李老师或张老师所发活动通知的信息的概率为()A.25B.1225C.1625D.45【答案】C【解析】设甲同学收到李老师的信息为事件A,收到张老师的信息为事件B,A、B相互独立,P(A)=P(B)=4 10=25,则甲同学收到李老师或张老师所发活动通知的信息的概率为1−=1−(1−P(A))(1−P(B))=1−35×35=1625.故选C .10.【2018届安徽省六安市舒城中学仿真(三)】甲乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停泊位时必须等待的概率( )A . 14B . 13C . 34D . 716【答案】D【解析】设甲船到达的时间为x ,乙船到达的时间为y ,则所有基本事件构成的区域Ω满足{0≤x ≤240≤y ≤24这两艘船中至少有一艘在停泊位时必须等待包含的基本事件构成的区域A 满足{0≤x ≤240≤y ≤24|x −y |≤6 ,作出对应的平面区域如图所示这两艘船中至少有一艘在停泊位时必须等待的概率为P (A )=S 阴S Ω=18×1824×24=716 故选D11.【2018届甘肃省兰州第一中学9月月考】《九章算术》是我国古代数学名著,也是古代东方数学的代表作,书中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内投豆子,则落在其内切圆内的概率是( )A. B. C. D. 【答案】B310π320π20π10π12.【江西省南昌市2018届二模】在《周易》中,长横“ ”表示阳爻,两个短横“ ”表示阴爻,有放回地取阳爻和阴爻三次合成一卦,共有23=8种组合方法,这便是《系辞传》所说:“太极生两仪,两仪生四象,四象生八卦”,有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有四种不同的情况,有放回地取阳爻和阴爻三次有八种不同的情况,即为八卦,在一次卜卦中,恰好出现两个阳爻一个阴爻的概率是( )A. 18B. 14C. 38D. 12【答案】C13.【2018年上海卷】有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是_____.【答案】15【解析】编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,3个数中含有1个2;2个2,没有2,3种情况,所有的事件总数为:C 53=10, 这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两个,所以:这三个砝码的总质量为9克的概率是:210=15,故答案为:15.14.袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为a,第二次取出的小球标号为b.(1)记事件A表示“a+b=2”,求事件A的概率;(2)在区间[0,2]内任取两个实数x,y,求“事件x2+y2>(a−b)2恒成立”的概率.【答案】(1) P(A)=412=13;(2)P(B)=1−π4.【解析】试题分析:(1)从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率.(2)记“x2+y2>(a﹣b)2恒成立”为事件B,则事件B 等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型可求得结论.(1)两次不放回抽取小球的所有基本事件为(0,1),(0,21),(0,22),(1,0),(1,21),(1,22),(21,0),(21,1),(21,22),(22,0),(22,1),(22,21),共12个,事件A包含的基本事件为(0,21),(0,22),(21,0),(22,0),共4个.所以P(A)=412=13.。
高考数学经典错题深度剖析及针对训练专题27古典概型和几何概型

专题27 古典概型和几何概型【标题01】忽略了对数函数中底数的范围【习题01】先后抛掷两枚骰子,出现的点数分别记为,a b ,则事件log 12a b= 发生的概率为 . 【经典错解】log 1222ab ba b a =∴=∴=,根据题意得试验的全部结果有6636⨯=个基本事件,事件log 12ab=包含的基本事件有1,22,436a b a b a b ======或或, ,共3个.由古典概型的概率公式得31()3612P A ==,故填112.【详细正解】log 1222a b ba b a =∴=∴=,根据题意得试验的全部结果有6636⨯=个基本事件,01a a >≠且 所以事件log 12a b=包含的基本事件有2,4a b ==和3a =,6b = 共2个.由古典概型的概率公式得21()3618P A ==,故填118.【习题01针对训练】先后抛掷两枚骰子,出现的点数分别记为,a b ,则事件log 12a b≥发生的概率为 .【标题02】事件A 构成的区域找错了【习题02】在半径为1的圆周上有一定点A ,以A 为端点连一弦,另外一端点在圆周上等可能的选取,则弦长超过1的概率为 .【经典错解】如图所示,13AB OA OB AOB π===∴∠=,当点B 在优弧AB 上时,弦长超过1,根据几何概型的概率公式得3301136012P ==.故填1112.【详细正解】如图所示,13AB OA OB OC AC AOB AOC π=====∴∠=∠=,当点B 在优弧BC 上时,弦长超过1,根据几何概型的概率公式得24023603P==.故填23.【深度剖析】(1)经典错解错在事件A构成的区域找错了. (2)错解错在寻找事件A构成的区域时,只顾及了一边,忽略了另外一边.所以在寻找事件A的全部结果构成的区域时,要考虑周全,不能受习惯思维的影响.【习题02针对训练】有一长、宽分别为m50、m30的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出m215,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是()A.43B.83C.163πD.32312π+【标题03】对组合数实际意义理解不清【习题03】甲、乙两人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙依次各抽一题.求甲抽到选择题,乙抽到判断题的概率是多少?【经典错解】甲从选择题抽到一题的结果为16C,乙从判断题中抽到一题的结果为14C,而甲、乙依次抽到一题的结果为210C∴所求概率为1582101416=CCC【详细正解】甲从选择题抽到一题的结果为16C,乙从判断题中抽到一题的结果为14C,而甲、乙依次抽到一题的结果为11109C C∴所求概率为154191101416=CCCC.【习题03针对训练】一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个. (1)从中同时摸出两个球,求两球颜色恰好相同的概率;(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.【标题04】“事件的全部结果”和“事件A的全部结果”对应的区域找错了【习题04】在ABC∆中,6ABCπ∠=,AB=3,BC=3,若在线段BC上任取一点D ,则BAD∠为锐角的概率是 .【经典错解】在ABC∆中,由余弦定理得AC=3. 又由余弦定理得0120BAC∠=,所以BAD∠为锐角的概率是9031204=.【详细正解】当0=90BAD∠时,2BD=,所以BAD∠为锐角的概率是23BDBC=.【习题04针对训练】在Rt ABC∆中,030A∠=,过直角顶点C作射线CM交线段AB于M,使||||AM AC>的概率是.【标题05】“试验的全部结果构成的区域”和“事件A的全部结果构成的区域”理解错误【习题05】在面积为S的ABC∆的边AB上任取一点P,则PBC∆的面积大于4S的概率为 .【经典错解】由题得试验的全部结果构成的区域是如图所示的ABC∆,事件“PBC∆的面积大于4S”的全部结果构成的区域是如图所示的ADE∆,根据几何概型概率的公式得991616SPS== ,故填916.【详细正解】由题得试验的全部结果构成的区域是如图所示的线段AB,事件“PBC∆的面积大于4S”的全部结果构成的区域是如图所示的线段AD ,根据几何概型概率的公式得33414P == ,故填34 .【深度剖析】(1)经典错解错在“试验的全部结果构成的区域”和“事件A 的全部结果构成的区域”理解错误. (2)在做概率题时,一定要认真审题,弄清“试验的全部结果构成的区域”和“事件A 的全部结果构成的区域”.【习题05针对训练】设不等式组⎩⎨⎧≤≤≤≤20,20y x ,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A .4π B .22π- C .6π D .44π-【标题06】考虑问题不周全没有分类讨论【习题06】在ABC ∆中,060,2,6ABC AB BC ∠===,在BC 上任取一点D ,则使ABD ∆为钝角三角形的概率为( ) A .16 B .13 C .12 D .23【经典错解】由题意得,过A 作AF AB ⊥,则24BF AB ==,642CF =-= ,若使得ABD ∆为钝角三角形,则D 在线段FC 上,所以对应的概率为13FC P BC ==,故选B .【详细正解】(1)当BAD ∠为钝角时,由题意得,过A 作AF AB ⊥,则24BF AB ==,642CF =-= ,若使得ABD ∆为钝角三角形,则D 在线段FC 上;(2)当BDA ∠为钝角时,过点A 作AE BC ⊥,则112BE AB ==,若使得ABD ∆为钝角三角形,则D 在线段BE 上.故由几何概型的概率公式得21162FC BE P BC ++=== .故选C .【习题06针对训练】向顶角为0120的等腰三角形ABC (其中BC AC =)内任意投一点M , 则AM 小于AC 的概率为( ) A .33π B .93π C .21 D .3π【标题07】审题错误导致把几何概型看成了古典概型 【习题07】设关于x 的一元二次方程2220x ax b -+=.(1)若,a b 都是从集合{1,2,3,4}中任取的数字,求方程无实根的概率;(2)若a 是从区间[0,4]中任取的数字,b 是从区间[1,4]中任取的数字,求方程有实根的概率.【经典错解】(1)设事件A 为“方程无实根”,记(,)a b 为取到的一种组合,则所有的情况有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).一共16种且每种情况被取到的可能性相同.∵关于x 的一元二次方程2220x ax b -+=无实根,∴22440a b ∆=-<0,0a b >> ∴a b <.∴事件A 包含的基本事件有:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).共6种 ∴6()16P A ==83∴方程无实根的概率83. (2)∵关于x 的一元二次方程2220x ax b -+=有实根,∴22440a b ∆=-≥,0,0a b >> ∴a b ≥.设事件B 为“方程有实根”,记(,)a b 为取到的一种组合,则其包含的基本事件有:(1,1),(2,1),(2,2)(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4).一共10种且每种情况被取到的可能性相同. 105()168P A ∴== 所以方程有实根的概率是58. 【详细正解】(1)同上(2)设事件B =“方程有实根”,记(,)a b 为取到的一种组合. ∵a 是从区间[0,4]中任取的数字,b 是从区间[1,4]中任取的数字, ∴点(,)a b 所在区域是长为4,宽为3的矩形区域.又∵满足a b≥的点的区域是如图所示的阴影部分∴13332()348P B⨯⨯==⨯. ∴方程有实根的概率是38.【习题07针对训练】已知关于x的二次函数2()4 1.f x ax bx=-+(1)设集合}5,4,3,2,1,1{-=A和}4,3,2,1,1,2{--=B,分别从集合A,B中随机取一个数作为a和b,求函数)(xfy=在区间),1[+∞上是增函数的概率.(2)设点),(ba是区域⎪⎩⎪⎨⎧>>≤-+,,8yxyx内的随机点,求函数()f x在区间),1[+∞上是增函数的概率.【标题08】审题不清把总事件没有理解清楚【习题08】有一个半径为4的圆,现在将一枚半径为1的硬币向圆投去,如果不考虑硬币完全落在圆外的情况,则硬币完全落入圆内的概率为 .【经典错解】由题得此概型为几何概型,所有结果组成的区域是以原点为圆心,以4为半径的圆,事件A 的所有结果构成的区域是以原点为圆心,以3为半径的圆,所以由几何概型的定义得991616Pππ==. 【详细正解】由题得此概型为几何概型,所有结果组成的区域是以原点为圆心,以5为半径的圆,当硬币和圆外切时,也是满足题意的,它不是完全落在圆外,因为此时两圆有公共点),事件A的所有结果构成的区域是以原点为圆心,以3为半径的圆,所以由几何概型的定义得992525Pππ==.【深度剖析】(1)经典错解错在审题不清,把总事件没有理解清楚. (2)学习数学,必须养成严谨认真细心的学习习惯,审题必须认真,错解就是审题不清,导致的错误.【习题08针对训练】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.【标题09】对随机模拟求近似值原理理解不清 【习题09】从区间[0,1]上随机抽取2n 个数1212,,,,,,,n n x x x y y y ,构成n 个数对11(,)x y ,22(,)x y ,,(,)n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为__________.A .4n m B .2n m C.4m n D .mn【经典错解】由题得圆周率π的近似值为mn.所以选择D .【详细正解】由题得数学试验的全部结果表示为0101x y ≤≤⎧⎨≤≤⎩,它们构成的是边长为1的正方形,事件A 的全部结果表示为2201011x y x y ⎧≤≤⎪≤≤⎨⎪+<⎩,它们构成的是14个单位圆,它是分布在第一象限的扇形. 根据古典概型和几何概型的概率公式得=S m S n扇形正方形221141m n π== 4mn π∴=. 所以选择C .【习题09针对训练】某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒50粒统计得到落在圆内的豆子数为39粒,则由此估计....出的圆周率π的值为 .(精确到0.01)高中数学经典错题深度剖析及针对训练第27讲:古典概型和几何概型参考答案【习题01针对训练答案】19【习题02针对训练答案】B【习题02针对训练解析】这是一个几何概型问题,所有可能结果用周长160表示,事件发生的结果可用两条线段的长度和60表示,所以8316060==P.【习题03针对训练答案】(1)52;(2)2512.【习题03针对训练解析】(1)摸出两球颜色恰好相同,即两个黑球或两个白球,共有2223C C+=4(种)可能情况.故所求概率为P=222325C CC+=410=25.(2)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑”.故所求概率为P=•+••111123321155CC C C CC=6625+=1225.【习题04针对训练答案】16【习题04针对训练解析】如图,不妨设1BC=,则2AB=,3AC=图中点M恰好使得3AM AC==BM段时,满足||||AM AC>,由三角形的知识易得015BCM∠=∴使||||AM AC>的概率151906P==. 故填16.【习题05针对训练答案】D【习题06针对训练答案】B【习题06针对训练解析】由题可得示意图,试验的全部结果构成的区域是ABC ∆,事件“AM 小于AC ”的全部结果构成的区域是扇形ACD ,由题可知为几何概型:则AM 小于AC 的概率为:0113261911sin1202ABC S p S ππ∆⨯⨯===⨯⨯⨯扇形 ,故选B .所以区域内满足0>a 且a b ≤2的面积为33238821=⨯⨯. 所以,所求概率3132332==p .【习题08针对训练答案】10131152【习题08针对训练解析】这是一个几何概型问题.设甲、乙两艘船到达码头的时刻分别为x 与y ,A 为“甲、乙两船都不需要等待码头空出”,则024x ≤≤ , 024y ≤≤, 且基本事件所构成的区域为{(,)|024,0y 24}x y x Ω=≤≤≤≤要使两船都不需要等待码头空出,当且仅当甲比乙早到达1 小时以上或乙比甲早到达2 小时以上,即12y x x y -≥-≥或,故{(,)|12,0x 24,024}A x y y x x y y =-≥-≥≤≤≤≤或.高考数学经典错题深度剖析及针对训练专题27古典概型和几何概型11 /11【习题09针对训练答案】3.12【习题09针对训练解析】设正方形的边长为2a ,则内切圆的半径为a ,由题意2239504a aπ=,∴439 3.1250π⨯=≈.。
高中数学经典错题深度剖析及针对训练 独立事件、独立重复试验的概率和条件概率
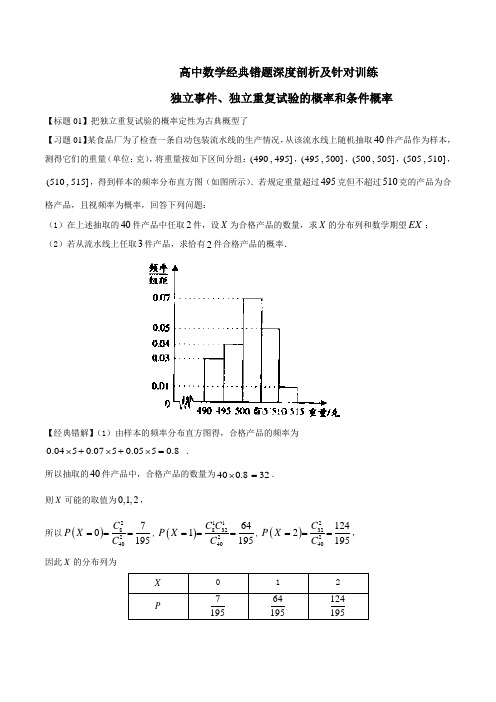
高中数学经典错题深度剖析及针对训练 独立事件、独立重复试验的概率和条件概率【标题01】把独立重复试验的概率定性为古典概型了【习题01】某食品厂为了检查一条自动包装流水线的生产情况,从该流水线上随机抽取40件产品作为样本,测得它们的重量(单位:克),将重量按如下区间分组:(490,495],(495,500],(500,505],(505,510],(510,515],得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:(1)在上述抽取的40件产品中任取2件,设X 为合格产品的数量,求X 的分布列和数学期望EX ; (2)若从流水线上任取3件产品,求恰有2件合格产品的概率.【经典错解】(1)由样本的频率分布直方图得,合格产品的频率为0.0450.0750.0550.8⨯+⨯+⨯=.所以抽取的40件产品中,合格产品的数量为400.832⨯=. 则X 可能的取值为0,1,2,所以()2824070195C P X C ===,()11832240641195C C P X C ===,()2322401242195C P X C ===, 因此X 的分布列为故X 数学期望76412431280121951951951955EX =⨯+⨯+⨯==. (2)由题得从流水线上任取3件产品,求恰有2件合格产品的概率213283404961235C C P C == 【详细正解】(1)同上;(2)因为从流水线上任取1件产品合格的概率为40.85=, 所以从流水线上任取3件产品,恰有2件合格产品的概率为223144855125P C ⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭.【习题01针对训练】某工厂在试验阶段大量生产一种零件,这种零件有A 、B 两项技术指标需要检测,设各项技术指标达标与否互不影响.若仅有A ,A 、B 两项技术指标都不达标的(1)求一个零件经过检测为合格品的概率;(2)若任意抽取该种零件4个,设ξ表示其中合格品的个数,求ξ的分布列及数学期望E ξ.【标题02】把独立重复试验的概率定性为独立事件的概率了【习题02】某次数学考试中有三道选做题,分别为选做题1,2,3.规定每位考生必须且只须在其中选做一 题.甲、乙、丙三名考生选做这一题中任意一题的可能性均为13,每位学生对每题的选择是相互独立的,各 学生的选择相互之间没有影响.求这三个人选做的是同一道题的概率.【经典错解】由题得设这三个人选做的是同一道题为事件A ,则1111()33327P A =鬃=【详细正解】由题得设这三个人选做的是同一道题为事件A ,则131111()3339P A C =鬃?.【深度剖析】(1)经典错解错在把独立重复试验的概率定性为独立事件的概率了.(2)这三个人选做的是同一道题为事件A ,则A 实际上是三个互斥事件和和事件,因为甲乙丙可能同时选做第一题或第二题或第三题,而每一个互斥事件的概率又是三个独立事件同时发生的概率.错解把事件A 直接定性为独立事件同时发生的概率了,是错的.(3)解答概率题时,要先定性(六大概型:古典概型、几何概型、互斥事件的概率、独立事件同时发生的概率、独立重复试验的概率和条件概率),后定量.在定性时,要仔细分析,不要把事件定性错了.【习题02针对训练】某市公租房的房源位于A 、B 、C 三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的任4位申请人中: (1)恰有2人申请A 片区房源的概率;(2)申请的房源所在片区的个数的ξ分布列与期望.【标题03】对事件)4,3,2,1(0=≥i S i 且28=S 理解错误【习题03】某人抛掷一枚均匀骰子,构造数列}{n a ,使⎩⎨⎧-=)(,1)(,1次掷出奇数当第次掷出偶数当第n n a n ,记n n a a a S +++= 21 求)4,3,2,1(0=≥i S i 且28=S 的概率.【经典错解】记事件A :28=S ,即前8项中,5项取值1,另3项取值-1,∴28=S 的概率858)21()(⋅=C A P记事件B :)4,3,2,1(0=≥i S i ,将)4,3,2,1(0=≥i S i 分为两种情形: (1)若第1、2项取值为1,则3,4项的取值在1和-1中任意取值;(2)若第1项为1,第2项为-1,则第3项必为1,第四项在1和-1中任意取值. ∴()P B =83)21()21(32=+ ∴所求事件的概率为()()P P A P B =⋅ =858)21(83⋅⋅C 【详细正解】∵)4,3,2,1(0=≥i S i ∴前4项的取值分为两种情形①若1、3项为1;则余下6项中3项为1,另3项为-1即可.即8361)21(⋅=C P ;②若1、2项为正,为避免与第①类重复,则第3项必为-1,则后5项中只须3项为1,余下2项为-1,即8352)21(⋅=C P ,∴所求事件的概率为783536215)21()(=⋅+=C C P【习题03针对训练】一种电脑屏幕保护画面,只有符号""""X O 和随机地反复出现,每秒钟变化一次,每次变化只出现""""X O 和之一,其中出现""O 的概率为p ,出现""X 的概率为q ,若第k 次出现""O ,则记1=k a ;出现""X ,则记1-=k a ,令n n a a a S +⋅⋅⋅++=21. (1)时,求3S 的分布列及数学期望. (2)时,求),,,且4321(028=≥=i S S i 的概率.【标题04】对事件“A B 、两组中有一组恰有两支弱队”没有理解清楚【习题04】已知8支球队中有3支弱队,以抽签方式将这8支球队分为A B 、两组,每组4支,求A B 、两组中有一组恰有两支弱队的概率.【经典错解】将8支球队均分为A B 、两组,共有4448C C 种方法:A B 、两组中有一组恰有两支弱队的分法为:先从3支弱队取2支弱队,又从5支强队取2支强队,组成这一组共有2325C C 种方法,其它球队分在另一组,只有一种分法.∴所求事件的概率为:7344482225=C C C C . 【详细正解】将8支球队均分为A B 、两组,共有4448C C 种方法:A B 、两组中有一组恰有两支弱队的分法为:先从3支弱队取2支弱队,又从5支强队取2支强队,组成这一组共有2325C C 种方法.再把这这组队伍分给A 组或B 组,有12C种方法,所以所求事件的概率P=76244482225=C C C C .【习题04针对训练】某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同. (1)求恰有2门选修课这3个学生都没有选择的概率;(2)设随机变量ξ为甲、乙、丙这三个学生选修数学史这门课的人数,求ξ的分布列及期望、方差.【标题05】概型判断错误【习题05】某人有5把不同的钥匙,逐把地试开某房门锁,试问他恰在第3次打开房门的概率.【经典错解】由于此人第一次不能开房门的概率为45,若第一次未开,第2次不能打开房门的概率应为34;所以此人第3次打开房门的概率为31. 【详细正解】第1次未打开房门的概率为54;第2次未开房门的概率为43;第3次打开房门的概率为31,所求概率为:51314354=⨯⨯=P .【习题05针对训练】某种项目的射击比赛,开始时在距目标100米处射击,如果命中记3分,且停止射击,若第一次射击未命中,可以进行第二次射击,但目标已经在150米处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200米处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分,已知射手甲在100m 处击中目标的概率为,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.(1)求这名射手在三次射击中命中目标的概率;(2)求这名射手比赛中得分的均值.【标题06】没有注意事件的先后顺序导致遗漏了一些情况 【习题06】某运动员射击一次所得环数x 的分布列如下:现进行两次射击,以该运动员两次射击中最高的环数作为他的成绩记为ξ,求ξ的分布列.【经典错解】ξ的取值为8,9,10.ξ=7,两次环数为7,7;ξ=8,两次成绩为7,8或8,8;ξ=9,两次成绩7,9或8,9或9,9;ξ=10,两次队数为7,10或8,10或9,10或10,10. ∴04.02.02.0)7(=⨯==ξP 15.03.03.02.0)8(2=+⨯==ξP23.03.03.03.03.02.0)9(2=+⨯+⨯==ξP 2.02.03.03.02.03.02.0)10(2=+⋅+⋅⨯==ξP (分布列略)【详细正解】8=ξ,即两次成绩应为7,8或8,7或8,8实际为三种情形,21.03.03.02.02)8(2=+⨯⨯==ξP 9=ξ两次环数分别为7,9(或9,7);8,9(或9,8),9.9∴39.03.03.03.023.02.02)9(2=+⨯⨯+⨯⨯==ξP ,同理36.02.042.03.0212.0)10(22=+⨯⨯+⨯==ξP 【深度剖析】(1)经典错解错在没有注意事件的先后顺序导致遗漏了一些情况.(2)8=ξ,即两次成绩应为7,8或8,7或8,8实际为三种情形,21.03.03.02.02)8(2=+⨯⨯==ξP9=ξ两次环数分别为7,9(或9,7);8,9(或9,8),9.9 ∴39.03.03.03.023.02.02)9(2=+⨯⨯+⨯⨯==ξP ,同理36.02.042.03.0212.0)10(22=+⨯⨯+⨯==ξP .【习题06针对训练】学校要用三辆校车从南校区把教职工接到校本部,已知从南校区到校本部有两条公路,校车走公路①堵车的概率为14,不堵车的概率为34;校车走公路②堵车的概率为p ,不堵车的概率为1p -.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.(Ⅰ)若三辆校车中恰有一辆校车被堵的概率为716,求走公路②堵车的概率;(Ⅱ)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.【标题07】把独立事件的概率定性为互斥事件的概率了【习题07】甲投篮命中概率为0.8,乙投篮命中概率为0.7,每人投3次,两人恰好都命中2次的概率是多少?【经典错解】设“甲恰好投中2次”为事件A ,“乙恰好投中2次”为事件B ,则两人恰好投中2次为A B +.所以()()()P A B P A P B +=+ =825.03.07.02.08.0223223=⨯+⨯C C .【详细正解】设“甲恰好投中2次”为事件A ,“乙恰好投中2次”为事件B ,则两人恰好都投中2次为AB .所以()()()P AB P A P B =⋅ =2222330.80.20.70.3C C ⨯⨯⨯0.169=【习题07针对训练】地为绿化环境,移栽了银杏树2棵,梧桐树3棵.它们移栽后的成活率分别为23、12,每棵树是否存活互不影响,在移栽的5棵树中:(1)求银杏树都成活且梧桐树成活2棵的概率;(2)求成活的棵树ξ的分布列与期望.【标题08】把独立事件同时发生的概率定性为独立重复试验了【习题08】某射手射击一次,击中目标的概率是0.5,现该射手连射4次,(1)求恰好前3次击中的概率;(2)恰好第3次击中的概率.【经典错解】(1)由题得334111()()224P C ==;(2P =(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625= 【详细正解】(1)由题得3111()2216P ==;(2)P =(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【习题08针对训练】甲、乙两人进行乒乓球比赛,采用“五局三胜制”,即五局中先胜三局为赢,若每场比赛甲获胜的概率是23,乙获胜的概率是13,则比赛以甲三胜一负而结束的概率为________.【标题09】把古典概型定性为独立重复试验了【习题09】某产品100件,其中恰有5件次品,现从中任意抽取5件,求恰有一件次品的概率. 【经典错解】由题得145595(A)()()100100P C = 【详细正解】由题得145955100()0.2144C C P A C == 【深度剖析】(1)经典错解错在把古典概型定性为独立重复试验了.(2)所求事件的概型应该是一个古典概型,而错解把它当作是独立重复试验了.因为已知中的抽取,是一次性地从100件产品中抽取5件,所以没有抽多次,所以根本上不是独立重复试验.如果有的同学分5次来抽,每次抽取一件,也不是独立重复.因为第一次抽取时,抽到次品的概率是5100,第二次抽取时,只有99件产品,此时抽到次品的概率肯定不是5100,由于概率不同,所以也不是独立重复试验.【习题09针对训练】现有一批产品共有10件,其中8件为正品,2件为次品. (1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率; (2)如果从中一次取3件,求3件都是正品的概率. 【标题10】把条件概率定性为古典概型了【习题10】一盒中放有大小相同的10个小球,其中8个黑球、2个红球,现甲、乙二人先后各自从盒子中无放回地任意抽取2个小球,已知甲取到了2个黑球,则乙也取到2个黑球的概率是________.【经典错解】由题得228622108151()453C C P A C C ===【详细正解】记事件“甲取到2个黑球”为A ,“乙取到2个黑球”为B ,则有(|)P B A =()()P AB P A =22862288C C C C ⋅⋅=1528,即事件“甲取到2个黑球,乙也取到2个黑球”的概率是1528.【习题10针对训练】某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:设该险种一续保人一年内出险次数与相应概率如下:(1)求一续保人本年度的保费高于基本保费的概率;(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率; (3)求续保人本年度的平均保费与基本保费的比值.【标题11】审题不清忽略了“有放回地取”这个关键词【习题11】一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取1个.求连续取两次都是白球的概率;【经典错解】由题得22241()6A P A A ==.【详细正解】记事件A 为“连续取两次都是白球”,所以()P A 14.【深度剖析】(1)经典错解错在审题不清,忽略了“有放回地取”这个关键词.(2)抽样常用的有“有放回抽样”和“不放回抽样”两种,所以在解题时一定要注意抽样的方法.【习题11针对训练】一个袋中装有形状大小完全相同的球9个,其中红球3个,白球6个,每次随机取1个,直到取出....3.次红球即停止........(1)从袋中不放回地取球,求恰好取4次停止的概率1P ; (2)从袋中有放回地取球;①求恰好取5次停止的概率2P ;②记5次之内(含5次)取到红球的个数为ξ,求随机变量ξ的分布列及数学期望.【标题12】对事件“某位顾客返券的金额为30元”没有理解透彻【习题12】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A 区域返券60元;停在B 区域返券30元;停在C 区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.求某位顾客返券的金额为30元的概率.【经典错解】设A =某位顾客返券的金额为30元,则111()236P A ==.【详细正解】设A =某位顾客返券的金额为30元,则11111()23323P A =+= .【习题12针对训练】某运动员射击一次所得环数x 的分布列如下:现进行两次射击,以该运动员两次射击中最高的环数作为他的成绩记为ξ,求(8)P x =.【标题13】把此种条件概率和“丢开法”条件概率混淆了【习题13】10名同学中,有7个人获得了全国数学联赛一等奖,3人没有获得.现在从中任选2名同学,已知其中1名同学获得全国一等奖,求另外一名同学也获得全国一等奖的概率. 【经典错解】由题得6293P ==. 【详细正解】设A =2名同学中有1人获得全国一等奖,B =2名同学中另外一个同学也获得全国一等奖,由题得27112737()211(|)(A)422C n AB P B A n C C C ====+,所以另外一名同学也获得全国一等奖的概率为12.【习题13针对训练】抛掷红、蓝两颗骰子,设事件A 为“蓝色骰子的点数为3或6”,事件B 为“两颗骰子的点数之和大于8”.当已知蓝色骰子的点数为3或6时,则两颗骰子的点数之和大于8的概率为________.【标题14】把古典概型定性为独立重复试验概率了【习题14】某产品100件,其中恰有5件次品,现从中任意抽取5件,求恰有一件次品的概率. 【经典错解】由题得145595(A)()()100100P C = 【详细正解】由题得145955100()0.2144C C P A C == 【深度剖析】(1)经典错解错在把古典概型定性为独立重复试验概率了.(2)所求事件的概型应该是一个古典概型,而错解把它当作是独立重复试验了.因为已知中的抽取,是一次性地从100件产品中抽取5件,所以没有抽多次,所以根本上不是独立重复试验.如果有的同学分5次来抽,每次抽取一件,也不是独立重复.因为第一次抽取时,抽到次品的概率是5100,第二次抽取时,只有99件产品,此时抽到次品的概率肯定不是5100,由于概率不同,所以也不是独立重复试验. 【习题14针对训练】现有一批产品共有10件,其中8件为正品,2件为次品. (1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率. (2)如果从中一次取3件,求3件都是正品的概率.【标题15】概率定性定错了【习题15】某射手射击一次,击中目标的概率是0.5,现该射手连射4次,(1)求恰好前3次击中的概率;(2)恰好第3次击中的概率.【经典错解】(1)由题得334111()()224P C ==;(2)P= (10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【详细正解】(1)由题得3111()2216P ==;(2)P=(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【习题15针对训练】甲、乙两人进行乒乓球比赛,采用“五局三胜制”,即五局中先胜三局为赢,若每场比赛甲获胜的概率是23,乙获胜的概率是13,则比赛以甲三胜一负而结束的概率为________.高中数学经典错解深度剖析及针对训练第29讲: 独立事件的概率、独立重复试验的概率和条件概率参考答案【习题01针对训练答案】(1(2满足条件的事件是恰有2人申请A 片区房源,共有2242C C ∴根据等可能事件的概率公式得到224248327C C P == (2)由题意知ξ的可能取值是1,2,3.431(1)327P ξ=== 231222341423414(2)327A C C C C C P ξ+=== 234344(3)39C A P ξ=== ∴ξ的分布列是:∴1144651232727927E ξ=⨯+⨯+⨯= 【习题03针对训练答案】(1)详见解析;(2)218780. 【习题03针对训练解析】(1)3,1,1,33--=S()()0318183=⨯+⨯+⨯-+⨯-=EX(2)前4次有2次出现""O 的概率是前4次有3次出现""O 的概率是前4次有4次出现""O 的概率是P (ξ= 0 ) =P (ξ= 1) =P (ξ= 2 ) =P (ξ= 3 ) =∴ξ的分布列为:E np ξ=34416D npq ξ==⨯⨯=【习题05针对训练答案】(1)95144;(2)8548.【习题05针对训练解析】记第一、二、三次射击命中目标分别为事件,,A B C三次均未命中目标的事件为D.依题意1 ()2P A=.(Ⅱ)依题意,设射手甲得分为ξ,则1121(3)(2)2299P Pξξ====⨯=171749(1)(0)298144144P Pξξ==⨯⨯===∴ξ的分布列为∴32102914414448Eξ=⨯+⨯+⨯+⨯=.【习题06针对训练答案】(Ⅰ; (Ⅱ【习题06针对训练解析】(1)由已知条件得即31p=,则所以p的值为(2)解:ξ可能的取值为0,1,2,3所以ξ的分布列为:,【习题7针对训练答案】(1)6;(2)详见解析.ξ∴的分布列为6E ξ∴=. 【习题08针对训练答案】827【习题08针对训练解析】甲三胜一负即前3次中有2次胜1次负,而第4次胜,∴P=C3223⎛⎫⎪⎝⎭2·13⎛⎫⎪⎝⎭·23=827,∴甲三胜一负而结束的概率为827.【习题09针对训练答案】(1)0.512;(2)7 15.【习题10针对训练答案】(1)0.55 ; (2)311;(3)1.23.【习题10针对训练解析】(1)记A为事件:“一续保人本年度的保费不高于基本保费”.则()0.200.200.100.050.55P A=+++=(2)记B为事件:“一续保人本年度的保费比基本保费60%”.()0.100.050.15P B=+=所以()()0.153 (|A)()()0.5511P AB P BP BP A P A====,所以一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率为3 11.(3)续保人本年度的平均保费估计值为0.850.300.15 1.250.20 1.50.20 1.750.1020.05 1.23 EX a a a a a a a =⨯+⨯+⨯+⨯+⨯+⨯=所以续保人本年度的平均保费与基本保费的比值为1.23.【习题11针对训练答案】(1)128;(2) ①881②13181.【习题11针对训练解析】(1)113363149128C C APA==(2)①22224121833381 P C⎛⎫⎛⎫=⨯⨯⨯=⎪ ⎪⎝⎭⎝⎭②随机变量ξ的取值为0,1,2,3; 由n 次独立重复试验概率公式()()1n kk kn n P k C p p -=-,得()505132013243P C ξ⎛⎫==⨯-= ⎪⎝⎭ ()41511801133243P C ξ⎛⎫==⨯⨯-=⎪⎝⎭ ()231511802133243P C ξ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭()328080173124381P ξ++==-=随机变量ξ的分布列是ξ的数学期望是 3280801713101232432432438181E ξ=⨯+⨯+⨯+⨯=∴()P B =1036=518. 当蓝色骰子的点数为3或6时,两颗骰子的点数之和大于8的结果有5个,故()P AB =536.∴(|)P B A =()()P AB P A =53613=512.【习题14针对训练答案】(1)0.512;(2)715. 【习题14针对训练解析】(1)有放回地抽取3次,按抽取顺序(,,)x y z 记录结果,则,,x y z 都有10种可能,所以基本事件总数为10×10×10=103(种);设事件A 为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此338()0.51210P A ==.(2)可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(,,)x y z ,。
几何概型与古典概型的区别

与长度有关的几何概型 [例 1] (2012·辽宁高考)在长为 12 cm 的线段 AB 上任取
一点 C.现作一矩形,邻边长分别等于线段 AC,CB 的长,则
该矩形面积大于 20 cm2 的概率为
1
1
A.6
B.3
()
2
4
C.3
D.5
1.在区间-π2,π2上随机取一个数 x,则 cos x 的值介于 0 到12之 间的概率为________.
求解与长度有关的几何概型的两点注意 (1)求解几何概型问题,解题的突破口为弄清是长度 之比、面积之比还是体积之比; (2)求与长度有关的几何概型的概率的方法,是把题 中所表示的几何模型转化为线段的长度,然后求解,应 特别注意准确表示所确定的线段的长度.
与面积(体积)有关的几何概型
[例 2] (1)已知平面区域 U={(x,y)|x+y≤6,x≥0,
2.已知集合 A={x|-1<x<5},B=xx3- -2x>0 ,在集合 A 中 任取一个元素 x,则事件“x∈A∩B”的概率是_______.
在长为 12 cm 的线段 AB 上任取一点 C,并以线段 AC 为边作正方形,则这个正方形的面积介于 36 cm2 与 81 cm2 之间的概率是多少?
y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域 U 内
随机投一点 P,则点 P 落入区域 A 的概率为________. (2)(2012·湖北高考)如图所示,在圆心角
为直角的扇形 OAB 中,分别以 OA,OB 为
直径作两个半圆,在扇形 OAB 内随机取一
点,则此点取自阴影部分的概率是 ( )
B.9
1
1
4.点CA.4为周长等于 3 的圆周上一个D.定2 点,若在该圆周上随
(完整版)古典概念与几何概型(带答案).docx

古典概型与几何概型1.【 2018 年理新课标 I 卷】下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形的三边所围成的区域记为I ,黑色部分记为IIABC的斜边,其余部分记为BC,直角边AB, AC.△ ABCIII.在整个图形中随机取一点,此点取自I , II, III的概率分别记为p1, p2, p3,则A. p 1=p2B. p1=p3C. p 2=p3D. p1=p2+p3【答案】 A【解析】分析:首先设出直角三角形三条边的长度,根据其为直角三角形,从而得到三边的关系,之后应用相应的面积公式求得各个区域的面积,根据其数值大小,确定其关系,再利用面积型几何概型的概率公式确定出p1,p2, p3的关系,从而求得结果 .详解:设,则有,从而可以求得的面积为,黑色部分的面积为,其余部分的面积为,所以有,根据面积型几何概型的概率公式,可以得到,故选 A.点睛:该题考查的是面积型几何概型的有关问题,题中需要解决的是概率的大小,根据面积型几何概型的概率公式,将比较概率的大小问题转化为比较区域的面积的大小,利用相关图形的面积公式求得结果 .2.【 2018 年理新课标 I卷】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】 A详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为 0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以 A 项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以 B 项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;故选 A.3.【 2018 年理数全国卷II 】我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过 30 的素数中,随机选取两个不同的数,其和等于30 的概率是A. B. C. D.【答案】C【解析】分析:先确定不超过30 的素数,再确定两个不同的数的和等于30 的取法,最后根据古典概型概率公式求概率.详解:不超过30 的素数有2,3, 5, 7, 11, 13, 17, 19, 23, 29,共10 个,随机选取两个不同的数,共有种方法,因为 ,所以随机选取两个不同的数,其和等于 30 的有 3 种方法,故概率为 ,选 C.4.【2017 课标 1,理】 如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称 .在正方形内随机取一点, 则此点取自黑色部分的概率是1π A .B .48 C .1π D .24【答案】 B【解析】【考点】几何概型5. 【 2017 山东,理8】从分别标有 1, 2 , , 9 的 9 张卡片中不放回地随机抽取2 次,每次抽取 1 张.则抽到的 2 张卡片上的数奇偶性不同 的概率是(A )5( B )4(C )5(D )18997 9【答案】 C【考点】古典概型6.【2017 江, 7】函数 f ( x)6 x x2的定域 D .在区[ 4,5]上随机取一个数x ,x D 的概率是▲.【答案】59【考点】几何概型概率7.( 2016 年全国 I 高考)某公司的班在7:30, 8:00, 8:30 ,小明在7:50至 8:30 之到达站乘坐班,且到达站的刻是随机的,他等不超10 分的概率是( A )1123 3(B)2( C)3( D)4【答案】 B8、( 2016 年全国 II 高考)从区0,1随机抽取2n 个数x1,x2,⋯,x n,y1,y2,⋯,y n,构成 n 个数x1 , y1, x2 , y2,⋯, x n , y n,其中两数的平方和小于 1 的数共有m个,用随机模的方法得到的周率的近似( A)4n( B)2n(C)4m( D)2m m m n n【答案】 C9.( 2016 年山高考)在[-1,1]上随机的取一个数k,事件“直y = kx 与( x-5)2 + y2 = 9 相交” 生的概率3【答案】.410.【2015 高考广东,理 4】袋中共有 15 个除了颜色外完全相同的球,其中有 10 个白球, 5个红球。
古典概型与几何概型课后习题解答汇总

游戏3:取两球同色的概率为:
32 1 43 2
取两球异色的概率为: 3113 1 43 43 2
规则公平
2、在所有首位不为0的八位数电话号码中,任取一个电话 号码,求: (1)头两位数码都是8的概率; (2)头两位数码至少有一个不超过8的概率; (3)头两位数码不相同的概率。
解: (1) 1 1 1 9 10 90
(3) 3 2 2 15 5
(4) 3 2 2 15 5
一、课本疑难习题解析
P142 B组 1、甲、乙两艘轮船都要在某个泊位停靠6小 时,假定它们在一昼夜的时间段中随机地到达,试求这 两艘船中至少有一艘在停靠泊位时必须等待的概率。
解:设甲到达的时间为x,乙到达的时间为y,则:
0 x, y 24
(1)A在边上,可以在左边和右边的两个位置中选 一个来站。所以概率为: 1
2
(2)分A在左B在右以及A在右B在左两种情形:2
4
21 3 2
1
1 6
(3)A或B在边上,即为A和B至少有一人在边上,这一事件的
对立事件是:A和B都不在边上,则概率为:
1 21 21 1 1 5 43 21 6 6
(2)分析:如果试过的钥匙不扔掉,概率应为:
22 1 44 4
2、假设有5个条件很类似的女孩,把她们分别记为A,C,
J,K,S。她们应聘秘书工作,但只有3个秘书职位,因
此5人中仅有三人被录用,如果5个人被录用的机会相等,
分别计算下列事件的概率:
3 (1)女孩K得到一个职位; 5 (2)女孩K和S各自得到一个职位;
9:3:3:1
yy
yy
RR
Rr
辨得清方能解得对——例析几何概型的常见错误

学生的错误解答:误看了取的是整数?还是数? 而导 致将这两题的几何概型、古典概型的概念混淆.
正 解 :由|x+1|-|x-2|≥1,解得x≥1.用A表示使|x+1||x-2|≥1成立的事件.
(1)在区间[-3,3]上随机地取一个数,结果不可数, 试验的结果与区间的长度有关, 总区间长度为3-(-3)= 6.事件A为取值在区间[1,3]上,区间长度为3-1=2,故 P(A)= 2 = 1 .
生1: 这个问题研 姨 2
究的是x、y的取值范围
1
问题, 因为有两个变
量,所以这个问题是面
积 比 , 易 知 0 ≤x ≤
O
姨2 x
1
1,0≤y≤1,满足x+y≥
图2
1 ·[1-(姨摇 2 -1)]2
摇
姨
2
的x、y如图2所示,所求概率为
2
12
=3-2
摇
姨
2
.
生2:这个问题研究的是x+y的取值范围问题,这个
解法探究
教学 参谋
学生的错误解答: 由于
C
∠ACB内部的任一射线与边AB的
交点是一一对应的,如图6,当交 点P处于D位置时,AP=AC,故问题 A
可转化为点P在边AB上随机选取
PD B 图6
时,AP<AC的概率.
由于
AC
=
摇
姨
2
,
所以所求概率为
AB 2
摇
姨
2
.
2
事实上,由题意,射线CP在∠ACB内部等可能地选
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【习题02针对训练答案】
【习题02针对训练解析】这是一个几何概型问题, 所有可能结果用周长
表示,事件发生的结果可用两条线段的长度和 表示,所以 .
【习题03针对训练答案】(1) ;(2) .
【习题03针对训练解析】(1)摸出两球颜色恰好相同,即两个黑球或两个白球,共有 =4(种)可能情况.故所求概率为 = = = 。
【习题08针对训练】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
【标题09】对随机模拟求近似值原理理解不清
【习题09】从区间 上随机抽取 个数 ,构成 个数对 , ,
【详细正解】(1)同上
(2)设事件 =“方程有实根",记 为取到的一种组合.
∵ 是从区间 中任取的数字, 是从区间 中任取的数字,
∴点 所在区域是长为4,宽为3的矩形区域.
又∵满足 的点的区域是如图所示的阴影部分
∴ .∴方程有实根的概率是 .
【习题07针对训练】已知关于 的二次函数
(1)设集合 和 ,分别从集合 , 中随机取一个数作为 和 ,求函数 在区间 上是增函数的概率.
【详细正解】由题得此概型为几何概型,所有结果组成的区域是以原点为圆心,以5为半径的圆,当硬币和圆外切时,也是满足题意的,它不是完全落在圆外,因为此时两圆有公共点),事件A的所有结果构成的区域是以原点为圆心,以3为半径的圆,所以由几何概型的定义得 .
【深度剖析】(1)经典错解错在审题不清,把总事件没有理解清楚. (2)学习数学,必须养成严谨认真细心的学习习惯,审题必须认真,错解就是审题不清,导致的错误.
A. B. C. D.
【标题07】审题错误导致把几何概型看成了古典概型
【习题07】设关于 的一元二次方程 .
(1)若 都是从集合 中任取的数字,求方程无实根的概率;
(2)若 是从区间 中任取的数字, 是从区间 中任取的数字,求方程有实根的概率.
【经典错解】(1)设事件 为“方程无实根”,记 为取到的一种组合,则所有的情况有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
【详细正解】如图所示, ,当点 在优弧 上时,弦长超过1,根据几何概型的概率公式得 。故填 。
【深度剖析】(1)经典错解错在事件 构成的区域找错了. (2)错解错在寻找事件 构成的区域时,只顾及了一边,忽略了另外一边.所以在寻找事件 的全部结果构成的区域时,要考虑周全,不能受习惯思维的影响。
【习题02针对训练】有一长、宽分别为 、 的游泳池,一名工作人员在池边巡视,某时刻出现在池边任一位置的可能性相同.一人在池中心(对角线交点)处呼唤工作人员,其声音可传出 ,则工作人员能及时听到呼唤(出现在声音可传到区域)的概率是( )
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.
(2)∵关于 的一元二次方程 有实根,∴ ,
∴ .
设事件 为“方程有实根”,记 为取到的一种组合,则其包含的基本事件有:(1,1),(2,1),(2,2)(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4).一共10种且每种情况被取到的可能性相同. 所以方程有实根的概率是 。
【标题05】“试验的全部结果构成的区域”和“事件A的全部结果构成的区域”理解错误
【习题05】在面积为 的 的边 上任取一点 ,则 的面积大于 的概率为。
【经典错解】由题得试验的全部结果构成的区域是如图所示的 ,事件“ 的面积大于 "的全部结果构成的区域是如图所示的 ,根据几何概型概率的公式得 ,故填 。
【详细正解】(1)当 为钝角时,由题意得,过 作 ,则 ,
,若使得 为钝角三角形,则 在线段 上;(2)当 为钝角时,过点 作 ,则 ,若使得 为钝角三角形,则 在线段 上。故由几何概型的概率公式得 .故选 .
【习题06针对训练】向顶角为 的等腰三角形 (其中 )内任意投一点 , 则 小于 的概率为( )
【详细正解】由题得试验的全部结果构成的区域是如图所示的线段 ,事件“ 的面积大于 ”的全部结果构成的区域是如图所示的线段 ,根据几何概型概率的公式得 ,故填 。
【深度剖析】(1)经典错解错在“试验的全部结果构成的区域"和“事件A的全部结果构成的区域”理解错误. (2)在做概率题时,一定要认真审题,弄清“试验的全部结果构成的区域”和“事件A的全部结果构成的区域”.
专题27 古典概型和几何概型
【标题1】忽略了对数函数中底数的范围
【习题01】先后抛掷两枚骰子,出现的点数分别记为 ,则事件 发生的概率为.
【经典错解】 ,根据题意得试验的全部结果有 个基本事件,事件 包含的基本事件有 ,共3个.由古典概型的概率公式得 ,故填 .
【详细正解】 ,根据题意得试验的全部结果有 个基本事件, 所以事件 包含的基本事件有 和 , 共2个。由古典概型的概率公式得 ,故填 。
(2)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑".故所求概率为 = = = .
【习题04针对训练答案】
【习题04针对训练解析】如图,不妨设 ,则 , ,
图中点 恰好使得 ,∴当点位于 段时,满足 ,
由三角形的知识易得 ∴使 的概率 .故填 .
【习题05针对训练答案】
【习题06针对训练答案】
【详细正解】甲从选择题抽到一题的结果为 ,乙从判断题中抽到一题的结果为 ,而甲、乙依次抽到一题的结果为 ∴所求概率为 .
【习题03针对训练】一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(1)从中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
【习题05针对训练】设不等式组 ,表示平面区域为 ,在区域 内随机取一个点,则此点到坐标原点的距离大于 的概率是( )
A. B. C. D.
【标题06】考虑问题不周全没有分类讨论
【习题06】在 中, ,在 上任取一点 ,则使 为钝角三角形的概率为( )
A. B. C. D.
【经典错解】由题意得,过 作 ,则 , ,若使得 为钝角三角形,则 在线段 上,所以对应的概率为 ,故选 。
A. B. C. D.
【标题03】对组合数实际意义理解不清
【习题03】甲、乙两人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙依次各抽一题.求甲抽到选择题,乙抽到判断题的概率是多少?
【经典错解】甲从选择题抽到一题的结果为 ,乙从判断题中抽到一题的结果为 ,而甲、乙依次抽到一题的结果为 ∴所求概率为
【习题01针对训练】先后抛掷两枚骰子,出现的点数分别记为 ,则事件 发生的概率为。
【标题02】事件 构成的区域找错了
【习题02】在半径为1的圆周上有一定点 ,以 为端点连一弦,另外一端点在圆周上等可能的选取,则弦长超过1的概率为.
【经典错解】如图所示, ,当点 在优弧 上时,弦长超过1,根据几何概型的概率公式得 .故填 。
且基本事件所构成的区域为
要使两船都不需要等待码头空出,当且仅当甲比乙早到达 小时以上或乙比甲早到达 小时以上,即 ,故 .
【习题09针对训练答案】
【习题09针对训练解析】设正方形的边长为 ,则内切圆的半径为 ,由题意 ,∴ 。
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
【标题04】“事件的全部结果"和“事件 的全部结果”对应的区域找错了
【习题04】在 中, , = , =3,若在线段 上任取一点 ,则 为锐角的概率是.
【经典错解】在 中,由余弦定理得 = . 又由余弦定理得 ,所以 为锐角的概率是 。
【详细正解】当 时, ,所以 为锐角的概率是 .
【习题04针对训练】在 中, ,过直角顶点 作射线 交线段 于 ,使 的概率是.
【习题09针对训练】某同学动手做实验:《用随机模拟的方法估计圆周率的值》,在左下图的正方形中随机撒豆子,每个豆子落在正方形内任何一点是等可能的,若他随机地撒 粒统计得到落在圆内的豆子数为 粒,则由此估计出的圆周率 的值为.(精确到 )
高中数学经典错题深度剖析及针对训练
第27讲:古典概型和几何概型参考答案
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).一共16种且每种情况被取到的可能性相同.
∵关于 的一元二次方程 无实根,∴ ∴ .
∴事件 包含的基本事件有:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).共6种∴ = ∴方程无实根的概率 .
