信息论与编码第三版答案
信息论与编码(第3版)第3章部分习题答案

3.1设信源()12345670.20.190.180.170.150.10.01X a a a a a a a P X ⎛⎫⎧⎫=⎨⎬ ⎪⎩⎭⎝⎭ (1) 求信源熵()H X (2) 编二进制香农码(3) 计算平均码长及编码效率。
答:(1)根据信源熵公式()()()()21log 2.6087bit/symbol i i i H X p a p a ==−=∑(2)利用到3个关键公式:①根据()()()100,0i a i k k p a p a p a −===∑计算累加概率;②根据()()*22log 1log ,i i i i p a k p a k N −≤<−∈计算码长;③根据()a i p a 不断地乘m 取整(m 表示编码的进制),依次得到的i k 个整数就是i a 对应的码字根据①②③可得香农编码为(3)平均码长公式为()13.14i i i K p a k ===∑单符号信源L =1,以及二进制m =2, 根据信息率公式()2log bit/symbol m KR K L==编码效率()83.08%H X Rη==3.2对习题3.1的信源编二进制费诺码,计算其编码效率答:将概率从大到小排列,且进制m=2,因此,分成2组(每一组概率必须满足最接近相等)。
根据平均码长公式为()12.74i iiK p a k===∑单符号信源L=1,以及二进制m=2, 根据信息率公式()2log bit/symbolmKR KL==编码效率(信源熵看题3.1)()95.21%H XRη==3.3对习题3.1的信源编二进制赫夫曼码,计算平均码长和编码效率答:将n个信源符号的概率从大到小排列,且进制m=2。
从m个最小概率的“0”各自分配一个“0”和“1”,将其合成1个新的符号,与其余剩余的符号组成具有n-1个符号的新信源。
排列规则和继续分配码元的规则如上,直到分配完所有信源符号。
必须保证两点:(1)当合成后的信源符号与剩余的信源符号概率相等时,将合并后的新符号放在靠前的位置来分配码元【注:“0”位表示在前,“1”表示在后】,这样码长方差更小;(2)读取码字时是从后向前读取,确保码字是即时码。
信息论与编码第3版第3章习题解答

第3章 无失真离散信源编码习题3.1 设信源1234567()0.20.190.180.170.150.10.01X a a a a a a a P X(1) 求信源熵H (X ); (2) 编二进制香农码;(3) 计算其平均码长及编码效率。
解: (1)()()log ()(.log ..log ..log ..log ..log ..log ..log .).7212222222=-020201901901801801701701501501010010012609 i i i H X p a p a bit symbol(2)a i p (a i ) p a (a i ) k i 码字 a 1 0.2 0 3 000 a 2 0.19 0.2 3 001 a 3 0.18 0.39 3 011 a 4 0.17 0.57 3 100 a 5 0.15 0.74 3 101 a 6 0.1 0.89 4 1110 a 70.010.9971111110(3)()3(0.2+0.19+0.18+0.17+0.15)+40.1+70.01=3.1471i i i K k p a()() 2.609=83.1%3.14H X H X R K3.2 对习题3.1的信源编二进制费诺码,计算其编码效率。
解:a i p (a i ) 编 码 码字 k i a 1 0.2 000 2 a 2 0.19 1 0 010 3 a 3 0.18 1 011 3 a 4 0.17 110 2 a 5 0.15 10 110 3 a 6 0.1 10 1110 4 a 70.011 11114()2(0.2+0.17)+3(0.19+0.18+0.15)+4(0.1+0.01)=2.7471i i i K k p a()() 2.609=95.2%2.74H X H X R K3.3 对习题3.1的信源分别编二进制和三进制赫夫曼码,计算各自的平均码长及编码效率。
第三版信息论答案

【】设有 12 枚同值硬币,其中有一枚为假币。
只知道假币的重量与真币的重量不同,但不知究竟是重还是轻。
现用比较天平左右两边轻重的方法来测量。
为了在天平上称出哪一枚是假币,试问至少必须称多少次?解:从信息论的角度看,“12 枚硬币中,某一枚为假币”该事件发生的概率为P 1;12“假币的重量比真的轻,或重”该事件发生的概率为P 1;2为确定哪一枚是假币,即要消除上述两事件的联合不确定性,由于二者是独立的,因此有I log12log2log 24 比特而用天平称时,有三种可能性:重、轻、相等,三者是等概率的,均为P 1 ,因此天3平每一次消除的不确定性为Ilog 3 比特因此,必须称的次数为I1log24I2log3次因此,至少需称 3 次。
【延伸】如何测量?分 3 堆,每堆 4 枚,经过 3 次测量能否测出哪一枚为假币。
【】同时扔一对均匀的骰子,当得知“两骰子面朝上点数之和为 2”或“面朝上点数之和为 8”或“两骰子面朝上点数是 3 和 4”时,试问这三种情况分别获得多少信息量?解:“两骰子总点数之和为 2”有一种可能,即两骰子的点数各为 1,由于二者是独立的,因此该种情况发生的概率为P1 16 61,该事件的信息量为:36I log 36比特“两骰子总点数之和为 8”共有如下可能:2 和 6、3 和 5、4 和 4、5 和 3、6 和2,概率为P 1 1 56 65,因此该事件的信息量为:36I log365比特“两骰子面朝上点数是 3 和 4”的可能性有两种:3 和 4、4 和 3,概率为P因此该事件的信息量为:1 121,6 6 18I log18比特【】如果你在不知道今天是星期几的情况下问你的朋友“明天星期几?”则答案中含有多少信息量?如果你在已知今天是星期四的情况下提出同样的问题,则答案中你能获得多少信息量(假设已知星期一至星期日的顺序)?解:如果不知今天星期几时问的话,答案可能有七种可能性,每一种都是等概率的,均为P 1,因此此时从答案中获得的信息量为7I log 7比特而当已知今天星期几时问同样的问题,其可能性只有一种,即发生的概率为1,此时获得的信息量为0 比特。
信息论与编码习题答案

信息论与编码习题答案1.在无失真的信源中,信源输出由H(X) 来度量;在有失真的信源中,信源输出由R(D) 来度量。
2.要使通信系统做到传输信息有效、可靠和保密,必须首先信源编码,然后_____加密____编码,再______信道_____编码,最后送入信道。
3.带限AWGN波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)=+;当归一化信道容量C/W趋C W SNR近于零时,也即信道完全丧失了通信能力,此时E b/N0为-1.6 dB,我们将它称作香农限,是一切编码方式所能达到的理论极限。
4.保密系统的密钥量越小,密钥熵H(K)就越小,其密文中含有的关于明文的信息量I(M;C)就越大。
5.已知n=7的循环码42=+++,则信息位长g x x x x()1度k为 3 ,校验多项式《信息论与编码A》试卷第 2 页共 10 页《信息论与编码A 》试卷 第 3 页 共 10 页h(x)=31x x ++ 。
6. 设输入符号表为X ={0,1},输出符号表为Y ={0,1}。
输入信号的概率分布为p =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =2,d (1,0) = 1,则D min = 0 ,R (D min )= 1bit/symbol ,相应的编码器转移概率矩阵[p(y/x )]=1001⎡⎤⎢⎥⎣⎦;D max = 0.5 ,R (D max )= 0 ,相应的编码器转移概率矩阵[p(y/x )]=1010⎡⎤⎢⎥⎣⎦。
7. 已知用户A 的RSA 公开密钥(e,n )=(3,55),5,11p q ==,则()φn = 40 ,他的秘密密钥(d,n )=(27,55) 。
若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 。
二、判断题1. 可以用克劳夫特不等式作为唯一可译码存在的判据。
(√ )2. 线性码一定包含全零码。
信息论与编码习题参考答案(全)
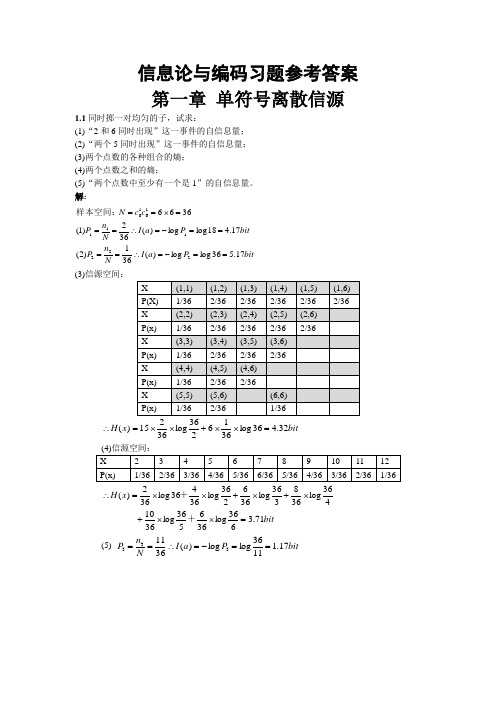
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
第三版信息论答案

【2.1】设有12 枚同值硬币,其中有一枚为假币。
只知道假币的重量与真币的重量不同,但不知究竟是重还是轻。
现用比较天平左右两边轻重的方法来测量。
为了在天平上称出哪一枚是假币,试问至少必须称多少次?解:从信息论的角度看,“12 枚硬币中,某一枚为假币”该事件发生的概率为P 1 ;12“假币的重量比真的轻,或重”该事件发生的概率为P 1 ;2为确定哪一枚是假币,即要消除上述两事件的联合不确定性,由于二者是独立的,因此有I log12 log 2 log 24 比特而用天平称时,有三种可能性:重、轻、相等,三者是等概率的,均为P 1 ,因此天3平每一次消除的不确定性为I log 3 比特因此,必须称的次数为I1log 24I 2 log 32.9 次因此,至少需称3 次。
【延伸】如何测量?分3 堆,每堆4 枚,经过3 次测量能否测出哪一枚为假币。
【2.2】同时扔一对均匀的骰子,当得知“两骰子面朝上点数之和为2”或“面朝上点数之和为8”或“两骰子面朝上点数是3 和4”时,试问这三种情况分别获得多少信息量?解:“两骰子总点数之和为2”有一种可能,即两骰子的点数各为1,由于二者是独立的,因此该种情况发生的概率为P 1 16 61 ,该事件的信息量为:36I log 36 5.17 比特“两骰子总点数之和为8”共有如下可能:2 和6、3 和5、4 和4、5 和3、6 和2,概率为P 1 1 56 6 5 ,因此该事件的信息量为:36I log3652.85 比特“两骰子面朝上点数是3 和4”的可能性有两种:3 和4、4 和3,概率为P 因此该事件的信息量为:1 121 ,6 6 18I log18 4.17 比特【2.3】如果你在不知道今天是星期几的情况下问你的朋友“明天星期几?”则答案中含有多少信息量?如果你在已知今天是星期四的情况下提出同样的问题,则答案中你能获得多少信息量(假设已知星期一至星期日的顺序)?解:如果不知今天星期几时问的话,答案可能有七种可能性,每一种都是等概率的,均为P 1 ,因此此时从答案中获得的信息量为7I log 7 2.807 比特而当已知今天星期几时问同样的问题,其可能性只有一种,即发生的概率为1,此时获得的信息量为0 比特。
信息论与编码习题参考答案(全)

信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
《信息论与编码》第三章部分习题参考答案

第三章习题参考答案3-1解:(1)判断唯一可译码的方法:①先用克劳夫特不等式判定是否满足该不等式;②若满足再利用码树,看码字是否都位于叶子结点上。
如果在叶节点上则一定是唯一可译码,如果不在叶节点上则只能用唯一可译码的定义来判断是不是。
其中C1,C2,C3,C6都是唯一可译码。
对于码C2和C4都满足craft 不等式。
但是不满足码树的条件。
就只能举例来判断。
对C5:61319225218ki i ---==+⨯=>∑,不满足该不等式。
所以C5不是唯一可译码。
(2)判断即时码方法:定义:即时码接收端收到一个完整的码字后,就能立即译码。
特点:码集任何一个码不能是其他码的前缀,即时码必定是唯一可译码, 唯一可译码不一定是即时码。
其中C1,C3,C6都是即时码。
对C2:“0”是“01”的前缀,……,所以C2不是即时码。
(1) 由平均码长61()i i i K p x k ==∑得1236 3 1111712(3456) 241681111712(3456) 2416811152334 24162K bitK bitK bitK bit==⨯+⨯+⨯+++==⨯+⨯+⨯+++==⨯+⨯+⨯⨯=62111223366()()log () 2 /()266.7%3()294.1%178()294.1%178()280.0%52i i i H U p u p u H U K H U K H U K H U K ηηηη==-=============∑比特符号3-7解:(1)信源消息的概率分布呈等比级数,按香农编码方法,其码长集合为自然数数列1, 2, 3, ···, i, ···;对应的编码分别为:0, 10, 110, ···, 111…110 ( i – 1个1), ···。
(2) 先求熵和平均码长,二者的比值即信息传输速率2()()log () 2 /()...2/()1 bit/i i Ii i IH p x p x bit k p x k H R k=-======∑∑X X 符号码元符号码元时间(3)编码效率:η = 1 =100%3-11解:(1)621()()log () 2.355/i i i H X p x p x ==-=∑比特符号(2)香农编码如下表所示:61()0.322(0.220.180.16)30.0840.0452.84/i i i k p x k ===⨯+++⨯+⨯+⨯=∑码元符号() 2.3550.82982.9%2.84H X kη==== (3)费诺编成二进变长制码,%1.984.2355.2)(4.24*04.04*08.03*16.02*18.02*22.02*032)(61====+++++==∑=k x H k x p K ii iη(4)huffman 编码%1.984.2355.2)(4.21=====k x H ii iη(5)huffman 三进制%7.7511.3355.2)(11.33log *)3*04.03*08.03*16.02*18.02*22.01*032(3log *)(2261====+++++==∑=k x H k x p K ii iη(6)log 26=2.58 采用定长码则必须使得K=3才能完成编码 效率%5.783355.2)(===k x H η(7)046.0%1.98355.2355.2)()(==+=+=εεεηx H x HL ≧23865810*046.0505.0*3222==-δεσ3-12解:(1) 821()()log () 2.56/i i i H X p x p x ==-=∑比特符号R=H(X)=2.56 bit/s{}505.0355.2)04.0(log *04.0)08.0(log *08.0)16.0(log *16.0)18.0(log *18.0)22.0(log *22.0)32.0(log *32.0)]([)]()[log ()]()([2222222221222=-+++++=-=-=∑=X H x p x p X H x I E ni iiiσ。
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
信息论与编码姜丹第三版答案
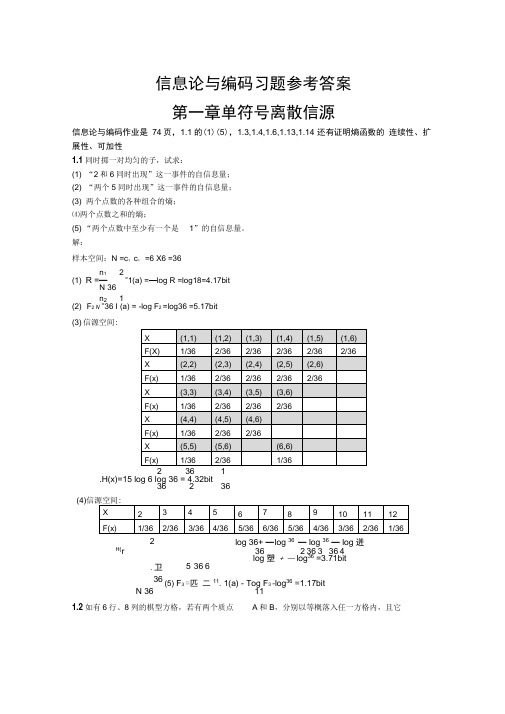
信息论与编码习题参考答案 第一章单符号离散信源信息论与编码作业是 74页,1.1的(1)(5),1.3,1.4,1.6,1.13,1.14 还有证明熵函数的 连续性、扩展性、可加性1.1同时掷一对均匀的子,试求:(1) “2和6同时出现”这一事件的自信息量; (2) “两个5同时出现”这一事件的自信息量; (3) 两个点数的各种组合的熵; ⑷两个点数之和的熵;(5) “两个点数中至少有一个是 1”的自信息量。
解:样本空间:N =c ;c ; =6 X6 =36n 12(1) R =—”1(a) =—log R =log18=4.17bitN 36 n 2 1(2) F 2 N =36 I (a) = -log F 2 =log36 =5.17bit (3) 信源空间:2 36 1.H(x)=15 log 6 log 36 = 4.32bit36 2 36(4)log 36+ — l og 36 — log 36 — log 迸36 2 36 3 36 4 log 塑 + — log 36 =3.71bit5 36 6 (5) F 3 =匹 二11. 1(a) - Tog F 3 -log 36 =1.17bit N 36 111.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它2H(r.卫36们的坐标分别为(Xa,Ya) , (Xb,Yb),但A,B不能同时落入同一方格内。
(1)若仅有质点A,求A落入任一方格的平均信息量;(2)若已知A已落入,求B落入的平均信息量;(3)若A,B是可辨认的,求A,B落入的平均信息量。
解:1(1) 幕A落入任一格的概率:P(a i) I (aj =-log P(aJ = log 484848.H(a) - P(a j)log P(aJ = log 48 =5.58biti 41(2) ;在已知A落入任一格的情况下,B落入任一格的概率是:P(bJ = —47.I(b) - -logP(b i) =log4748.H(b) = -' P(b i)log P(b i) =log47 =5.55biti -11 1(3) AB同时落入某两格的概率是P(ABJ二一一48 47.I(ABJ =-log P(AB i)48 47H(AB」-八P(ABJIog P(ABJ =log(48 47)=11.14biti 二1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
《信息论与编码》课后习题答案

《信息论与编码》课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码习题参考答案(全)
111
(1)在W4=011中,接到第一个码字“0”后获得关于a4的信息量I(a4;0);
(2)在收到“0”的前提下,从第二个码字符号“1”中获取关于a4的信息量I(a4;1/0);
(3)在收到“01”的前提下,从第三个码字符号“1”中获取关于a4的信息量I(a4;1/01);
(4)从码字W4=011中获取关于a4的信息量I(a4;011)。
其中N=2FT,б2X是信号的方差(均值为零),б2N是噪声的方差(均值为零).
再证:单位时间的最大信息传输速率
信息单位/秒
(证明详见p293-p297)
5.12设加性高斯白噪声信道中,信道带宽3kHz,又设{(信号功率+噪声功率)/噪声功率}=10dB.试计算改信道的最大信息传输速率Ct.
解:
5.13在图片传输中,每帧约有2.25×106个像素,为了能很好的重现图像,需分16个量度电平,并假设量度电平等概率分布,试计算每分钟传输一帧图片所需信道的带宽(信噪功率比为30dB).
(2)求信源的极限熵H∞;
(3)求当p=0,p=1时的信息熵,并作出解释。
解:
3.10设某马尔柯夫信源的状态集合S:{S1S2S3},符号集X:{α1α2α3}。在某状态Si(i=1,2,3)下发发符号αk(k=1,2,3)的概率p(αk/Si) (i=1,2,3; k=1,2,3)标在相应的线段旁,如下图所示.
证明:
3.5试证明:对于有限齐次马氏链,如果存在一个正整数n0≥1,对于一切i,j=1,2,…,r,都有pij(n0)>0,则对每个j=1,2,…,r都存在状态极限概率:
(证明详见:p171~175)
3.6设某齐次马氏链的第一步转移概率矩阵为:
信息论与编码姜丹第三版答案精编版

信息论与编码习题参考答案 第一章 单符号离散信源信息论与编码作业是74页,1.1的(1)(5),1.3,1.4,1.6,1.13,1.14还有证明熵函数的连续性、扩展性、可加性1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
信息论与编码曹雪虹第三版第五章

信息论与编码曹雪虹第三版第五章1、在Windows 的"资源管理器" 窗口中,如果想一次选定多个分散的文件或文件夹,正确的操作是()。
[单选题] *A.按住Ctrl 键,用鼠标右键逐个选取B.按住Ctrl 键,用鼠标左键逐个选取(正确答案)C.按住Alt键,用鼠标右键逐个选取D.按住Alt键,用鼠标左键逐个选取2、72.在下列关于字符大小关系的说法中,正确的是()。
[单选题] *A.空格>a>AB.空格>A>aC.a>A>空格(正确答案)D.A>a>空格3、40.下列选项属于面向对象的程序设计语言是()。
[单选题] *A.Java和CB.Java和C++(正确答案)C.VB和CD.VB和Word4、76.计算机病毒的危害表现为()[单选题] *A.能造成计算机芯片的永久性失效B.使磁盘霉变C.影响程序运行,破坏计算机系统的数据与程序(正确答案)D.切断计算机系统电源5、在WPS表格中,关于筛选数据的说法正确的是()。
[单选题] *A.删除不符合设定条件的其它内容B.筛选后仅显示符合我们设定筛选条件的某一值或符合一组条件的行(正确答案)C.将改变不符合条件的其它行的内容6、执行删除操作时,()中的文件不能被送入回收站,而是直接删除。
[单选题] *A. C盘B. D盘C.U盘(正确答案)7、能够实现电子邮件服务器之间传输邮件的协议是()。
易[单选题] *A.DNSB.SNMPC.HTTPD.SMTP(正确答案)8、计算机硬件能直接识别和执行的只有()。
[单选题] *A.高级语言B.符号语言C.汇编语言D.机器语言(正确答案)9、把计算机网络看成是自治的计算机系统的集合,其中“自治的计算机”主要指()易[单选题] *A.可以独立运行的计算机(正确答案)B. 网络计算机C.裸机D. 网络终端10、在Internet 上,政府机构类别的域名中一般包括()。
信息论第三版课后答案

信息论第三版课后答案【篇一:西电邓家先版信息论与编码第3章课后习题解答】6x11/6y13/41/4x2图3.1 二元信道y2?x??x1x2???=?0.60.4?通过一干扰信道,接收符号y=?y1y2?,信道传递概率如p(x)????图3.33所示。
求:(1)信源x中事件x1,和x2分别含有的自信息。
(2)收到消息yj(j=1,2)后,获得的关于xi(i=1,2)的信息量。
(3)信源x和信源y的信息熵。
(4)信道疑义度h(x|y)和噪声熵h(y|x)。
(5)接收到消息y后获得的平均互信息。
解:(1)由定义得:i(x1)= -log0.6=0.74biti(x2)= -log0.4=1.32biti(xi;xj)= i(xi)-i(xi|yj)=log[p(xi|yj)/p(xi)]= log[p(yj|xi)/p(yj)]则 i(x1;y1)= log[p(y1|x1)/p(y1)]=log5/6/0.8=0.059bit i (x1;y2)= log[p(y2|x2)/p(y2)]=log1/6/0.2=-0.263biti(x2;y1)= log[p(y1|x2)/p(y1)]=log3/4/0.8=-0.093bit i(x2;y2)= log[p(y2|x2)/p(y2)]=log1/4/0.2=0.322bit(3)由定义显然 h(x)=0.97095bit/符号h(y)=0.72193bit/符号(4)h(y|x)=?22p(xy)log[1/p(y|x)]=??i?1j?1p(xi)p(yj|xi)log[1/p(yj|xi)]h(x|y)= h(x)+h(y|x)-h(y)=0.9635bit/符号(5) i(x;y)= h(x)-h(x|y)=0.00745 bit/符号3.2设8个等概率分布的消息通过传递概率为p的bsc进行传送。
八个消息相应编成下述码字:m1=0000, m2=0101, m3=0110, m4=0011, m5=1001, m6=1010, m7=1100, m8=1111, 试问 (1) 接受到第一个数字0与m之间的互信息。
最新信息论与编码(第三版)

信息论与编码(第三版)
简介
是一门应用概率论、随机过程、数理统计和近 代代数的方法,来研究信息传输、提取和处理 中一般规律的学科。
信源编码器的主要指标
是它的编码效率。一般来说,效率越高,编译码 器的代价也将越大。
信源译码器
把信道译码器的输出变换成信宿所需的消息形式,
相当于信源编码器的逆过程。
14
信道编码器与译码器
信道编码 主要作用是提高信息传送的可靠性。
信道编码器的作用 在信源编码器输出的代码组上有目的地增加一些监督 码元,使之具有检错或纠错的能力。
1)离散信源
特点:输出单符号消息。符号集的取值A:{a1,a2,…,aq}是 有限的或可数的,可用离散型随机变量X描述。
数学模型:设每个信源符号ai出现的(先验)概率p(ai)
(i=1,2,…,q) 满足:
q
p(ai ) 1
i 1
则 : P X (x ) P ( a a 1 1 )
I(ak)lorP g(1 ak)lorP g(ak)
28
2.1.1 自信息
设离散信源X的概率空间为:
P X (x ) P ( a a 1 1 )
a 2 P (a 2)
a 3 ......a q P (a 3) .....P .(a q)
q
i 1
P(ai )
1
自信息量:事件ai发生所含有的信息量
信宿:信息归宿之意,亦即收信者或用户, 是信息传送的终点或目的地。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息论与编码第三版答案
《信息论与编码》是一本非常经典的书籍,已经成为了信息科
学领域中的经典教材。
本书的第三版已经出版,相比于前两版,
第三版的变化不小,主要是增加了一些新内容,同时也对一些旧
内容做了修改和完善。
作为一本教材,上面的题目和习题都是非常重要的,它们可以
帮助读者更好地理解书中的相关概念和知识点,同时也可以帮助
读者更好地掌握理论和技术。
因此,本文将介绍《信息论与编码》第三版中部分习题的答案,方便读者快速查阅和学习。
第一章:信息量和熵
1.1 习题1.1
Q:两个随机变量的独立性和无关性有什么区别?
A:独立性和无关性是两个不同的概念。
两个随机变量是独立的,当且仅当它们的联合概率分布等于乘积形式的边缘概率分布。
两个随机变量是无关的,当且仅当它们的协方差等于0。
1.2 习题1.7
Q:什么样的随机变量的熵等于0?
A:当随机变量的概率分布是确定的(即只有一个概率为1,其余全为0),其熵等于0。
第二章:数据压缩
2.5 习题2.9
Q:为什么霍夫曼编码比熵编码更加高效?
A:霍夫曼编码能够更好地利用信源的统计特征,将出现频率高的符号用较短的二进制编码表示,出现频率低的符号用较长的二进制编码表示。
这样一来,在编码过程中出现频率高的符号会占用较少的比特数,从而能够更加高效地表示信息。
而熵编码则是针对每个符号分别进行编码,没有考虑符号之间的相关性,因此相比于霍夫曼编码更加低效。
第四章:信道编码
4.2 习题4.5
Q:在线性块码中,什么是生成矩阵?
A:在线性块码中,生成矩阵是一个包含所有二元线性组合系
数的矩阵。
它可以用来生成码字,即任意输入信息序列可以通过
生成矩阵与编码器进行矩阵乘法得到相应的编码输出序列。
4.3 习题4.12
Q:简述CRC校验的原理。
A:CRC校验是一种基于循环冗余校验的方法,用于检测在数
字通信中的数据传输错误。
其基本思想是将发送数据看作多项式
系数,通过对这个多项式进行除法运算,得到余数,将余数添加
到数据尾部,发送给接收方。
接收方将收到的带有余数的数据看
做多项式,使用同样的多项式除以一个预先定义好的生成多项式,
计算出余数,若余数等于0,则认为数据传输成功;否则认为数据传输出错,并进行相应的纠错处理。
以上是对部分《信息论与编码》第三版习题的答案介绍,希望能对读者们有所帮助。
当然,除了这些习题,本书中还有更多的内容等待读者去探索和学习。
