信息论与编码第四章课后习题答案
《信息论与编码》习题解答-第四章(新)

《信息论与编码》习题解答第四章 信息率失真函数-习题答案4.1解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0110d ,转移概率⎥⎦⎤⎢⎣⎡--=εεεε11)|(i j a b p 平均失真:εεεεε=⨯-⨯+⨯⨯+⨯⨯+⨯-⨯==∑∑==0)1(2/112/112/10)1(2/1),()|()(2121j i i j i j i b a d a b p a p D4.2解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0210d , 0min =D ,∑=⨯+⨯=⨯+⨯===ij i i j j y x d x p D D )102/122/1(2/112/102/1),()(min min max 舍去当0min =D ,bit X H R D R 12log )()0()(min ====因为没有失真,此时的转移概率为⎥⎦⎤⎢⎣⎡=1001P当2/1max =D ,0)(max =D R因为取的是第二列的max D 值,所以输出符号概率:,1)(,0)(21==b p b p ,,2221b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=1010P 4.3解:0min =D0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 当0min =D ,bit X H R D R 24log )()0()(min ==== 因为没有失真,此时的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P 当4/3max =D ,0)(max =D R因为任何一列的max D 值均为3/4,所以取输出符号概率:0)(,0)(,0)(,1)(4321====b p b p b p b p ,即14131211,,,b a b a b a b a →→→→因此编码器的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P 4.4解: 依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=4/1014/110d , 0min =D∑=⨯+⨯===ij i i j j y x d x p D D )2/12(4/1)4/12/14/12/1min(),()(min min max 个均为其它当0min =D ,bit X H R D R 12log )()0()(min ====因为没有失真,此时的转移概率为⎥⎦⎤⎢⎣⎡=010001P 当4/1max =D ,0)(max =D R因为取的是第三列的max D 值为1/4,所以取输出符号概率:1)(,0)(,0)(321===b p b p b p ,即3231,b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=100100P 4.5解:(1)依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0110d ,转移概率为:⎥⎦⎤⎢⎣⎡-=q q P 101 )1(0)1()1(1)1(1001),()|()(11p q q p q p p p y x d x y p x p D n i mj j i i j i -⨯=⨯-⨯-+⨯⨯-+⨯⨯+⨯⨯==∑∑==(2) 0min =D因为)(D R 是D 的递减函数,所以)1log()1(log )()()())(m ax (min min p p p p D H p H D R D R ----=-==当0=q 时可达到))(max(D R ,此时0=D(3) ∑-=⨯+⨯===iji i j j ,p p p p y x d x p D D )1(10),()(min min max 舍去更大另一个 因为)(D R 是D 的递减函数,所以0)()()())(m in(max max =-==D H p H D R D R当1=q 时可达到))(min(D R ,此时p D -=1(图略,见课堂展示)4.6解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡∞∞=1010d ,信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/12/110)(u p u 0min =D ,∑⨯+⨯⨯+∞⨯∞⨯+⨯===iji i j j y x d x p D D )12/112/1,02/12/1,2/102/1min(),()(min min max )(1]1,,m in[舍去另二个,∞=∞∞=10≤≤D因为二元等概信源率失真函数:⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中1,2==a n ,所以率失真函数为:D D R -=1)(4.7解:失真矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110d ,按照P81页方法求解。
《信息论与编码》部分课后习题参考答案

若知道是星期几,则从别人的答案中获得的信息量为 0。 2.3 每帧电视图像可以认为是 3*10^5 个像素构成,所有像素均独立变化,且每一像素又取 128 个不同的亮度电平,并设亮度电平等概率出现。问每帧图像喊多少信息量?如果一个广 播员在约 10000 个汉字的字汇中选取 1000 个字来口述此电视图像,试问广播员描述此图像 所广播的信息量是多少(假设汉字字汇是等概率分布,并且彼此独立)?若要恰当地描述此 图像,广播员在口述中至少需用多少汉字? 答:由于每一象素取 128 个不同的亮度电平,各个亮度电平等概率出现。因此每个亮度电平 包含的信息量为 I(X) = – lb(1/128)=lb128=7 bit/像素 每帧图像中像素均是独立变化的, 因此每帧图像信源就是离散亮度电平信源的无记忆 N 次扩展。由此,每帧图像包含的信息量为 I(XN) = NI(X)= 3×105×7 =2.1×106 bit/帧 广播员在约 10000 个汉字中选取字汇来口述此电视图像, 各个汉字等概分布, 因此每个 汉字包含的信息量为 I(Y) = – lb(1/10000)=lb1000=13.29 bit/ 字 广播员述电视图像是从这个汉字字汇信源中独立地选取 1000 个字进行描述,因此广播 员描述此图像所广播的信息量是 I(YN) = NI(Y)= 1000×13.29 =1.329 ×104 bit/字 由于口述一个汉字所包含的信息量为 I(Y),而一帧电视图像包含的信息量是 I(XN),因此 广播员要恰当地描述此图像,需要的汉字数量为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
信息论第四章习题解答

e( x)
1 x x2 x3 x4 x5 x6
0
校验子
s0( x) = 1 s1 ( x) = x s2 ( x) = x2 s3 ( x) = x2 ? 1 s4( x) = x2 ? x ? 1 s5( x) = x ? 1 s6( x) = x2 ? x
s无 (x) = 0
20
习题解答
第 4.13 已知 (7, 4) 循环码的生成多项式为 g( x) = x3 ? x2 ? 1,
注:实际上,正反码仅仅用作纠错码 。
8
习题解答
第 4.6 试分析用于电报系统的纠错码 正反码的检错和纠错
四
能力。若已知信道的误码率 Pe = 10- 4 , 求系统的正确接
章
收概率和漏检概率。
抗解 干 扰 二 元 编 码
(2) 当收到的码字无错或者一位错时, 能够正确接收, 因此正确接收的概率为: P正 = (1 - Pe)10 ? C110 Pe (1 - Pe)9 = 0.9999995502 4;
扰 二解 元 编
汉明码序列。
(1) 生成矩阵 [G] =
1000 101 0100 111 0010 110 0001 011
码
(2) 编码序列 1 1 0 1 1 1 0 1 0 0 1
0110 0110001
1010 1010011
14
习题解答
第 4.10 已知 (7, 3) 汉明码的监督矩阵为:
习题解答
第 四 章
抗 干
第四章 习题解答
扰
二
元
编
码
1
习题解答
第 4.1 写出与 10011 的汉明距离为 3 的码字。
四 章
信息论与编码技术第四章课后习题答案

解:(1) D =
∑ P(u,υ )d (u,υ ) = (1 − p)q
UV
(2)根据题4.5,可知R(D)的最大值为H(p),此时q=0,平均失真D=0; (3)R(D)的最大值为0,此时q=1,平均失真D=(1-p); 4.7 设连续信源 X ,其概率密度分布为
p ( x) =
a − a | x| e 2
达到
D
min
的信道为
⎡1 ⎡1 0 ⎤ ⎡1 0 ⎤ ⎢ ⎥ ⎢ ⎥ ⎢1 [ P (υ j | u i )] = ⎢ ⎢ 0 1 ⎥ , ⎢1 0 ⎥ 或 ⎢ 2 ⎢ ⎣0 1 ⎥ ⎦ ⎢ ⎣0 1⎥ ⎦ ⎢0 ⎣
4.2 已知二元信源 ⎢
0⎤ 1⎥ ⎥ 2⎥ 1⎥ ⎦
1 ⎤ ⎡ X ⎤ ⎡ 0, ⎡0 1⎤ =⎢ =⎢ 以及失真矩阵 ⎡ dij ⎤ ⎥ ⎥ ⎥ ,试求: ⎣ ⎦ ⎣ p ( x ) ⎦ ⎣ p, 1 − p ⎦ ⎣1 0 ⎦
g (θ ) 的傅立叶变换
G s(w) = ∫
+∞ −∞
g
s
(θ )e
− jwθ
dθ =
s
2
s
2 2
+w
, (3)
得: Q( w) = P ( w) + w2 P( w), (4)
2
s
求式(4)的傅立叶反变换,又根据式(2)得
p( y ) = p( x = y) − D 所以 p( y ) =
2
p ( x = y), (5)
⎡0 ⎢1 定义为 D = ⎢ ⎢1 ⎢ ⎣1
解:
1 0 1 1
1 1 0 1
1⎤ 1⎥ ⎥ ,求 Dmax , Dmin 及信源的 R ( D ) 函数,并作出率失真函数曲线(取4到5个点)。 1⎥ ⎥ 0⎦
信息论与编码第四章课后习题答案

∫ =
− log λe−λx
∞ 0
+ log e
ln e−λx de−λx
∫ =
− log
λ
+
log
et
ln
t
0 1
−
log
e
dt
= −log λ + log e
= log e λ
(2)
h( X )
= −∫ p(x)log p(x)dx
∫ = − ∞ 1 λe−λ x log 1 λe−λ x dx
−∞ 2
2
∫ = − ∞ λe−λx log 1 λe−λxdx
0
2
∫ ∫ = − ∞ λe−λx log 1 dx − ∞ λe−λx log λe−λxdx
0
2
0
= log 2 + log e λ
= log 2e λ
注:(2)题直接借用了(1)的结论。
【4.3】设有一连续随机变量,其概率密度函数为:
sin
x
=
1 2
log
e∫
ln(1
+
sin
x)d
sin
x
+
1 2
log
e∫
ln(1
−
sin
x)d
sin
x
∫ ∫ ln(1+ sin x)d sin x
π
= (1 + sin
x) ln(1+ sin
x)
2 −π
−
2
1 + sin x d sin x 1 + sin x
= 2ln 2 − 2
∫ ln(1− sin x)d sin x
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
《信息论、编码与密码学》课后习题问题详解

《信息论、编码与密码学》课后习题答案第1章 信源编码1.1考虑一个信源概率为{0.30,0.25,0.20,0.15,0.10}的DMS 。
求信源熵H (X )。
解: 信源熵 ∑=-=512)(log )(k k k p p X HH(X)=-[0.30*(-1.737)+0.25*(-2)+0.2*(-2.322)+0.15*(-2.737)+0.1*(-3.322)]=[0.521+0.5+0.464+0.411+0.332] =2.228(bit)故得其信源熵H(X)为2.228bit1.2 证明一个离散信源在它的输出符号等概率的情况下其熵达到最大值。
解: 若二元离散信源的统计特性为P+Q=1 H(X)=-[P*log(P)+(1-P)*log(1-P)] 对H(X)求导求极值,由dH(X)/d(P)=0可得211101log ==-=-p ppp p可知当概率P=Q=1/2时,有信源熵)(1)(max bit X H =对于三元离散信源,当概率3/1321===P P P 时,信源熵)(585.1)(max bit X H =, 此结论可以推广到N 元的离散信源。
1.3 证明不等式ln 1x x ≤-。
画出曲线1ln y x =和21y x =-的平面图以表明上述不等式的正确性。
证明:max ()ln 1(0)1()()01001()0()0ln 11ln 1ln 1f x x x x f x xf x x x x f x f x f x x x x x x x =-+>'=''==>∴<≤>≤=≤-≥≤-≤-令,又有时此时也即当时同理可得此时综上可得证毕绘制图形说明如下 可以很明确说明上述 不等式的正确性。
1.4 证明(;)0I X Y ≥。
在什么条件下等号成立?1111(,)(,)(,)(,)log()()n mi j i j i j n mi j i j i j i j I P x y I x y P x y P x y P x P y =====∑∑∑∑(X ;Y )=当和相互独立时等号成立。
信息论编码部分课后习题习题

7
第3章习题 章习题
8
第3章习题 章习题
9
第3章习题 章习题
10
第3章习题 章习题
11
第4章习题 章习题
12
第4章习题 章习题
13
第6章习题 章习题
14
第6章习题 章习题
15
第8章习题 章习题
16
第8章习题 章习题
17
第8章习题 章习题
18
第8章习题 章习题
19
第8章习题 章习题
20
第8章习题 章习题
21
第9章习题 章习题
某线性分组码的生成矩阵为
0 0 G= 1 1 1 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 1 0 0 1 0 1 0 1
求: (1)用系统码的形式表示G; (2)计算系统码的校验矩阵H; (3)若接收到的码字为R1=0010100,检验它是否为码字?
解:(1)对G作行运算,得到系统化后的生成矩阵为
1 0 G= 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 1 0 1 1 1 1 0 0 1 1 1
(3)计算
1 1 0 1 1 0 0 T R1 H = [ 0 0 1 0 1 0 0] 1 1 1 0 0 1 0 0 1 1 1 0 0 1 = [1 0 1] ≠ 0
T
(2)由系统化后的生成矩阵得系统码的校验矩阵H为
1 1 0 1 1 0 0 H = 1 1 1 0 0 1 0 0 1 1 1 0 0 1
因此可断言R1不是码字。
22
信息论课后习题答案信息论基础课后答案信息论导引习题答案信息论与编码信息论与编码论文信息论基础习题解答信息论基础习题信息论与编码试卷信息论与编码试题信息论与编码答案第2章 Nhomakorabea题 章习题
信息论与编码原理-第4、5章课后习题-20140604-23点-自己整理

H (S ) R L 0.839 Rmax log r
s2 s3 s4 s5 s6 4.3 某信源概率空间为 S s1 P(s) 0.3 0.25 0.2 0.15 0.06 0.04 进行二元编码,5种不同的编码方案如表4.20所示。
5.1 设二进制对称信道的传递矩阵为
0.8 0.2 0.2 0.8
(1)若信道输入符号 P(0) 3/ 4, P(1) 1/ 4 ,求 H ( X ) 、 H ( X | Y )、
H (Y | X ) 和 I ( X ; Y ) 。
(2)求该信道的信道容量及达到信道容量的最佳输入概率分布。 (3)如果信道输入符号 P(0) 3/ 4, P(1) 1/ 4 时,计算信道剩余度。
5.4 设某信道的转移矩阵为
p 1 p q q P p q 1 p q
求其信道容量。
1 p q1 p q
p 1 p q P1 p 1 p q q P2 q
(1) H ( x) H ( 3 4 , 1 4) 0.811 bit/符号
X Y 的联合分布概率为:
X
Y
0 1
0 3 5 1 20
1
3 20 1 5
H ( XY ) H ( 3 , 3 , 1 , 1 ) 1.533 bit/符号 5 20 20 5
H (Y ) H (13 20 ,7 ) 0.934 bit/符号 20
5.3 设某对称离散信道的信道矩阵为
0 0.5 0.5 0 0 0 0.5 0.5 P 0.5 0 0 0.5 0 0.5 0.5 0 (1)求其信道容量。
信息论与编码第4章习题解答

《信息论与编码》第四章习题解答4.1 计算如下所示离散无记忆信道的容量: 习题4.1图[解] (a )信道概率转移矩阵为−−−−=δεδεεδδε11P , 信道是准对称信道,因此在输入为等概分布时达到信道容量,即5.0)1()0(====X P X P 时达到信道容量。
这时δ5.05.0)0(−==Y P δ==)1(Y Pδ5.05.0)2(−==Y P相应的信道容量为);1();0(Y X I Y X I C ====∑==2)()0|(log)0|(j j p j p j p 0111-ε1-δε δ 00 121-ε-δ εδδ 1-ε-δ1ε0 221 0.5 δ 110.250.25 0.50.50 2 21-ε ε ε 1-ε1ε 11-ε 0 0 223/41/4 111/3 1/31/3 1/43/40 2 311/3 211/31/3 1/31/31/3 1/3 1/31/3 (c)(a)(b) (e)(f)(d)δεεδδδδδεδε5.05.0log log 5.05.01log)1(−++−−−−−=)5.05.0log()1(log )1log()1(δδεεδεδε−−−+−−−−= (b )信道概率转移矩阵为=5.05.0025.025.05.0001P当5.0)2()0(====X P X P ,0)(=X P 时,5.0)0(==Y P ,25.0)1(==Y P ,25.0)2(==Y P1)()0|(log )0|();0(2===∑=j j p j p j p Y X I bit∑===2)()2|(log)2|();2(j j p j p j p Y X I 125.05.0log 5.025.05.0log 5.0=+= bit10);1(≤==Y X I ; 所以满足定理4.2.2条件,由达到信道容量充要条件可知,信道容量C =1 bit/次(c )信道转移概率矩阵为−−−=εεεεεε101001P ,信道是对称信道,当输入为均匀分布时,即31)2()1()0(======X P X P X P 时,达到信道容量。
信息论与编码第四章课后习题答案

−∫
1 − sin x d sin x 1 − sin x
因此有
h( X ) = −2 A log A −
A log e(2 ln 2 − 2 + 2 ln 2 − 2) 2Байду номын сангаас= −2 A log A + 2 A log e − 2 A log e ln 2 = −2 A log A + 2 A log e − 2 A 1 ,因此 2
试计算 h( X ) , h(Y ) , h( XY ) 和 I ( X ; Y ) 。 解: p( x) = ∫ p ( x, y )dy 1 =∫ dy (a 2 − a1 )(b2 − b1 ) = 1 a2 − a1
同理, p( y ) = 因此
1 。 b2 − b1
h( X ) = − ∫ p ( x ) log p ( x)dx = log(a 2 − a1 ) h(Y ) = − ∫ p( y ) log p( y )dy = log(b2 − b1 ) h( XY ) = − ∫ p ( x, y ) log p ( x, y )dxdy = log( a2 − a1 ) + log(b2 − b1 ) I ( X ; Y ) = h( X ) + h(Y ) − h( XY ) = 0 【4.7】在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1) h( X | Y ) ≤ h( X ) ,当且仅当 X 和 Y 统计独立时等号成立; (2)h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) ,当且仅当 X 1 X 2 L X N 彼此统计 独立时等式成立。 证明: (1) h( XY ) = − ∫ p( y )dy ∫ p( x | y ) log p ( x | y )dx ≤ − ∫ p ( y )dy ∫ p( x | y ) log p ( x )dx = − ∫ p( x, y ) log p ( x )dxdy = h( X ) 等号成立当且仅当 p( x | y ) = p ( x ) ,即 p( x, y ) = p( x ) p ( y ) ,因此仅当 X 和 Y 统计 独立时等号成立。 (2)根据条件概率密度的相关公式,有 h( X 1 X 2 X N ) = h( X 1 ) + h( X 2 | X 1 ) + h( X 3 | X 1 X 2 ) + L + h( X N | X 1 X 2 X N −1 ) 根据(1)的结论,条件差熵小于差熵,因此有 h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) 等号成立当且仅当
信息论与编码第4章习题解答

P[ Z N
= 1|
X
= 0] =
P
Z
'
N
>
1 2
|
X
= 0
=
PZ 'N
−p
>
1 2
−
p|
X
=
0
≤
P|
Z
' N
−
p
|>
1 2
−
p|
X
=
0
≤
σ2 Z 'N |X =0
1 2
−
p 2
= p(1 − p) N (1 − p)2 2
当 p < 1 ,以及 N 充分大时 2
求该级联信道的容量 C N
,并证明
lim
N →∞
C
N
=0
X0
BSC X1
BSC X2 ……
BSC XN
习题 4.4(1)图 级联信道
(2)并联输入信道,把输入 X 并联接到各信道,输出是矢量,当 N → ∞ 时并联输
入信道容量趋于 1。
X
BSC Y1
BSC Y2
BSC YN
习题 4.4(2)图 并联输入信道
所以
C = 6 ⋅ 1 log 1/ 3 + 3 ⋅ 1 log 1/ 3 9 2/9 9 1/3
= 2 log 3 bit/次 32
(f)信道转移概率矩阵
P
=
1
− δ
ε
1
ε −
δ
利用方程求逆方法计算信道容量。设
p( X = 0) = q , p( X = 1) = 1 − q , 0 < q < 1
王育民信息论与编码理论第四章答案2

4.5若将N 个相同的BSC 级联如题图4.5所示,各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11。
令Q t =P{X t =0},t=0,1,…,N,且Q 0为已知。
题图 4.5(a)求Q t 的表达式。
(b)证明N →∞时有Q N →1/2,且与Q 0取值无关,从而证明N →∞级联信道的信道容量C N →0,P>0。
解:(a)对于满足X N 为马氏链的串联信道,他们总的信道转移概率矩阵为各个串联信道矩阵的乘积,即P(X N |X 0)= P(X 1|X 0) P(X 2|X 1)……P(X N |X N-1)由已知得,但各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11 则两个信道级联的转移概率矩阵为: P 2=⎥⎦⎤⎢⎣⎡--p p p p 11⎥⎦⎤⎢⎣⎡--p p p p 11=()()()()⎥⎦⎤⎢⎣⎡-+---+2222112p 12p 1p p p p p p 三个信道级联的转移概率矩阵为: P 3=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+33331221211221211221211-2p 2121p p p 四个信道级联的转移概率矩阵为: P 4=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+44441221211221211221211-2p 2121p p p 以此类推:可得N 个信道级联的转移概率矩阵为:P N =()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+N N N N p p p 1221211221211221211-2p 2121 则Q t =P{X t =0}=()()()()()000121221211122121122121Q p p Q p Q p t t t t -+--=-⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+即Q t 的表达式为:Q t =()()012122121Q p p t t -+-- t=0,1,……,N (b) 由(a)可得到:Q N =()()012122121Q p p t t -+-- 由0<p<1,则0<2p<2,-1<2p-1<1,即|2p-1|<1 则21lim =∞→N N Q ,与Q 0取值无关。
信息论与编码理论-第4章无失真信源编码-习题解答-20071202

信息论与编码理论-第4章无失真信源编码-习题解答-20071202信息论与编码理论第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长。
?X??s14-2 设信源????p(s)P(X)???1s6?p(s2)?p(s6)???s2?p(s)?1。
对此次能源进行m元唯一ii?16可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)?s?X??14-3设信源为??1??p(X)???2?(1)信源的符号熵;(2)这种码的编码效率;s214s3s411816s5132s6s7s8?,编成这样的码:(000,001,111???64128128?010,011,100,101,110,111)。
求(3)相应的仙农码和费诺码。
4-4求概率分布为(,11122信)源的二元霍夫曼编码。
讨论此码对于概率分布为355151511111(,,,,)的信源也是最佳二元码。
555554-5有两个信源X和Y如下:1信息论与编码理论s2s3s4s5s6s7??X??s1??p(X)??0.200.190.180.170.150.100.01?????s2s3s4s5s6s7s8s9??Y??s1??p(Y)??0.490.140.140.070.070.040.020.02 0.01?????(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X和Y进行编码,并计算其平均码长和编码效率;(2)从X,Y两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样霍夫曼码的信源的所有概率分布。
4-7设信源为?码。
信息论编码第四章答案

解:
唯一可译码是A,B,C,E 唯 可译码是A,B,C,E,非延长码为A,C,E A的平均码长:n = p( si )ni
i =1 6
= 3(1 / 2 + 1 / 4 + 1 / 16 + 1 / 16 + 1 / 16 + 1 / 16)
= 3码符号 / 信源符号
编码效率:
η=
H (s) 2 = * 100% = 66.67% n log r 3
2. 有一个信源X如下:
x2 x3 x4 x5 x6 X x1 p ( x) = 0.32 0.22 0.18 0.16 0.08 0.04
(1)、求信源熵; (2)、用Shannon编码法编成二进制变长码,并计算其编码效 率; (3)、用 用Fano编码法编成二进制变长码,并计算其编码效率; 编码法编成二进制变长码 并计算其编码效率 (4)、用Huffman码编码成二进制变长码,并计算其编码效率; (5)、用Huffman码编码成三进制变长码,并计算其编码效率; (6)、比较三种编码方法的优缺点。
H ( X ) 2.3522 = × 100% = 98% n log l r 2.4 log l 2
三进制Huffman编码 ? 首先, 判断q − (r − 1)α = r 6 − (3 − 1) × 2 = 2 < 3
选择m = r − [q − (r − 1)α ] = 3 − 2 = 1个虚假符号
0.40 0.60 0 0.37 0 0.40 1 0 0.23 1 1
L = P( si )li = 2.63
i =1
二元符号/灰度级
通过哈夫曼最佳二元编码后,每个像素平均需要用 2.63个二元符号,则此图象平均共需要用263个二元符 号来表示。因此,需2.63秒才能传送完这幅图象。 (3)在(2)题中计算时没有考虑图象的像素之间的依赖 关系,但实际此图象的像素之间是有依赖的。例如,若 考虑像素前后之间灰度的依赖关系,就有灰度“1”后 面只可能出现灰度“1”或 “2”;灰度“2”后只可能 出现“2” 或“3” ,等等。这时,此图象灰度值信源 S可以看成一阶马尔可夫信源。还可以进一步看成为m 阶马尔可夫信源。因此,在考虑了这些依赖关系后,像 素的灰度值信源S的实际信息熵 H ∞ < H ( S ) 。根据香农第 一理,总可以找到一种编码,使每个灰度级的平均码 长L → H ∞ (极限熵)。所以,这幅图象还可以进一步压缩, 平均每个像素(灰度)所需要的二元码符号数 L < H ( S ) 。
信息论第四章习题解答

抗
故需构造 (10, 6 ) 码。
干
(2) 可以构造出多种 (10, 6 ) 码,下面仅给出其中的一种。
扰
100000 1001
二
010000 1100
元 编
生成阵 [G] =
001000 000100
1110 1111
= [I6 P T ]
000010 0111
码
000001 0011
[ [ ] ] 生成码字 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 = x1 x2 x3 x4 x5 x6 G].
注:实际上,正反码仅仅用作纠错码 。
8
习题解答
第 4.6 试分析用于电报系统的纠错码 正反码的检错和纠错
四
能力。若已知信道的误码率 Pe = 10- 4 , 求系统的正确接
章
收概率和漏检概率。
抗解 干 扰 二 元 编 码
(2) 当收到的码字无错或者一位错时, 能够正确接收, 因此正确接收的概率为: P正 = (1 - Pe)10 ? C110 Pe (1 - Pe)9 = 0.9999995502 4;
8
5
习题解答
第 4.5 已知信道的误码率 Pe = 10- 4 , 若采用五三定比码和 ARQ
四
系统纠错方式,问这时系统的等效 (实际)误码率为多少?
章 解 (1) 五三定比码不能发现的错误为:
抗
偶数位错,且一半为 0 出错,一半为 1 出错。
干
故其漏检概率为:
扰
二
P1
=
C
21C
1 3
Pe
2
(1
-
习题解答
第 四 章
抗 干
信息论与编码理论-第4章无失真信源编码-习题解答-20071202
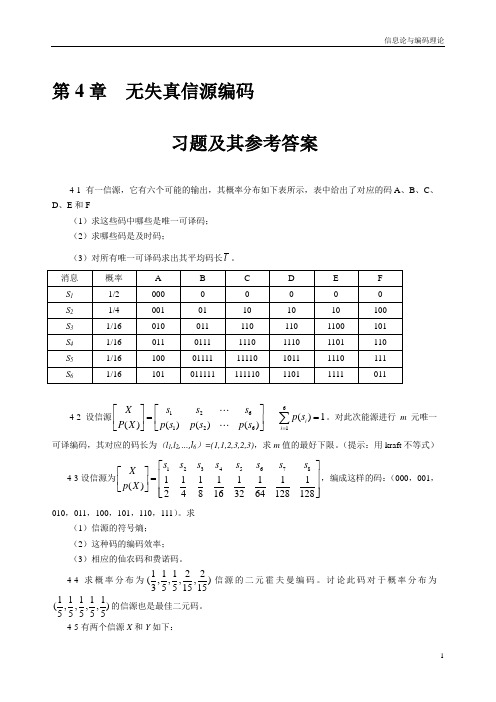
第4章无失真信源编码习题及其参考答案4-1 有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A、B、C、D、E和F(1)求这些码中哪些是唯一可译码;(2)求哪些码是及时码;(3)对所有唯一可译码求出其平均码长l。
4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。
对此次能源进行m元唯一可译编码,其对应的码长为(l1,l2,…,l6)=(1,1,2,3,2,3),求m值的最好下限。
(提示:用kraft不等式)4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,编成这样的码:(000,001,010,011,100,101,110,111)。
求(1)信源的符号熵;(2)这种码的编码效率;(3)相应的仙农码和费诺码。
4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。
讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。
4-5有两个信源X和Y如下:121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码,并计算其平均码长和编码效率;(2)从X ,Y 两种不同信源来比较三种编码方法的优缺点。
4-6设二元霍夫曼码为(00,01,10,11)和(0,10,110,111),求出可以编得这样 霍夫曼码的信源的所有概率分布。
4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,求其三元霍夫曼编码。
信息论与编码理论习题答案

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载信息论与编码理论习题答案地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第二章信息量和熵2.2 八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率。
解:同步信息均相同,不含信息,因此每个码字的信息量为 2=23=6 bit因此,信息速率为 61000=6000 bit/s2.3 掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。
问各得到多少信息量。
解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1} ==得到的信息量 ===2.585 bit(2) 可能的唯一,为 {6,6}=得到的信息量===5.17 bit2.4 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a) =信息量===225.58 bit(b)==信息量==13.208 bit2.9 随机掷3颗骰子,X表示第一颗骰子的结果,Y表示第一和第二颗骰子的点数之和,Z表示3颗骰子的点数之和,试求、、、、。
解:令第一第二第三颗骰子的结果分别为,,,相互独立,则,,==6=2.585 bit===2(36+18+12+9+)+6=3.2744 bit=-=-[-]而=,所以= 2-=1.8955 bit或=-=+-而= ,所以=2-=1.8955 bit===2.585 bit=+=1.8955+2.585=4.4805 bit2.10 设一个系统传送10个数字,0,1,…,9。
奇数在传送过程中以0.5的概率错成另外一个奇数,其余正确接收,求收到一个数字平均得到的信息量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p( x2 | x1 ) = p ( x 2 ) p( x3 | x1 x 2 ) = p ( x3 ) …… p( x N | x1 x2 L x N −1 ) = p( x N ) 即 p( x1 x 2 ) = p ( x1 ) p( x 2 ) p( x1 x 2 x3 ) = p ( x1 ) p( x 2 ) p ( x3 ) …… p( x1 x 2 L x N ) = p ( x1 ) p( x2 )L p( x N ) 【4.8】设连续随机变量 X ,已知 X ≥ 0 ,其平均值受限,即数学期望为 A ,试求 在此条件下获得的最大熵的最佳分布,并求出最大熵。 解: 给定条件如下:
2 2 x1 + x2 2
− ∞ < x1 , x2 < ∞
求随机变量 Y1 = X 1 + X 2 的概率密度函数,并计算变量 Y 的熵 h(Y ) 。 解: 1 − p( x1 x 2 ) = e 2π
2 2 x1 + x2 2
1 − 21 = e 2π
x2
1 − 22 e = p( x1 ) p ( x 2 ) 2π
0 = − log λ + log et ln t 1 − log e ∫ dt
= − log λ + log e = log (2) e λ
h( X ) = − ∫ p ( x ) log p ( x)dx ∞ 1 1 −λ x −λ x = −∫ λe log λe dx −∞ 2 2 ∞ 1 = − ∫ λe −λx log λe −λx dx 0 2 ∞ ∞ 1 = − ∫ λe −λx log dx − ∫ λe −λx log λe −λx dx 0 0 2 e = log 2 + log λ 2e = log λ 注: (2)题直接借用了(1)的结论。
2 h(Y1 ) = h( X ) − E[log1] = h( X ) = log e + log a − log 3 3 当 Y2 = 2 X 时, ∂X 1 = ,因此 ∂Y1 2
1 2 3 h(Y1 ) = h( X ) − E[log ] = h( X ) = log e + log a log 2 3 2 【4.4】设给定两随机变量 X 1 和 X 2 ,它们的联合概率密度为 1 − p( x1 x 2 ) = e 2π
欲使
根据 ∫ p ( x)dx = 1 , ∫ xp( x )dx = A ,可得
∫2
x
λ + µx − log e
dx = 1 ⇒ µ = −2 λ −log e 1
2
∫ xp( x)dx = A ⇒ µ = − A (log e)
2 1 2 − (log e ) 因此 p( x) = (log e ) 2 A ,此时 A
【4.3】设有一连续随机变量,其概率密度函数为: bx 2 p( x) = 0 0≤ x≤a 其他值
试求这随机变量的熵。又若 Y1 = X + K ( K > 0) , Y2 = 2 X ,试分别求出 Y1 和 Y2 的
熵 h(Y1 ) 和 h(Y2 ) 。 解:
h( X ) = − ∫ p( x) log p ( x )dx = − ∫ bx 2 log bx 2 dx
而 ∫ 2π p( x)dx = 1 ,即 A =
− 2
π
1 h( X ) = − log + log e − 1 = 1 + log e − 1 = log e 2 【4.2】计算连续随机变量 X 的差熵 (1) 指数概率密度函数 p( x) = λe − λx , x ≥ 0, λ > 0 1 −λ x (2) 拉普拉斯概率密度函数, p( x) = λe , − ∞ < x < ∞, λ > 0 2
π 2 π − 2
−∫
1 − sin x d sin x 1 − sin x
因此有
h( X ) = −2 A log A −
A log e(2 ln 2 − 2 + 2 ln 2 − 2) 2 = −2 A log A + 2 A log e − 2 A log e ln 2 = −2 A log A + 2 A log e − 2 A 1 ,因此 2
h( X ) = − ∫ p ( x) log p( x )dx 1 2 2 = − log (log e ) + (log e ) A 【 4.9 】 N 维 连 续 型 随 机 序 列 X 1 X 2 L X N , 有 概 率 密 度 p( X 1 X 2 L X N ) 以 及 E[( X i = mi )] = σ i2 。证明:当随机序列的分量各自达到正态分布并彼此统计独立 时熵最大。最大熵为 N 2 2 1/ N log 2πe(σ 12σ 2 ) Lσ N 2 证明: h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) 等号成立当且仅当各分量统计独立。 而对于任何一个分量而言,当 E[( X i = mi )] = σ i2 时,高斯分布的差熵最大,为 h( X i ) = 因此原序列差熵的最大值为: h( X 1 X 2 L X N ) = 1 1 1 2 2 log 2πeσ 12 + log 2πeσ 2 + L + log 2πeσ N 2 2 2 1 N 2 2 N = log 2πe σ 12σ 2 Lσ N 2 1 log 2πeσ i2 2
x2
因此 Y1 = X 1 + X 2 也是一个高斯分布的随机变量,其均值为 0,方差为 2,即
p( x1 x 2 ) = 因此其差熵为
1 −4 e 2π
y2
1 1 2 h(Y ) = log 2πeσ y = log 4πe 2 2 【4.5】设一连续消息通过某放大器,该放大器输出的最大瞬时电压 b ,最小瞬时 电压为 a 。若消息从放大器中输出,问放大器输出消息在每个自由度上的最大熵 是多少?又放大器的带宽为 F ,问单位时间内输出最大信息量是多少? 解: 该问题等价于取值受限的随机变量的最大熵,根据差熵的极值性,当等概率 分布时其差熵最大,即 h(Y ) = log(b − a ) 如果放大器的带宽为 F ,则取样率为 2 F ,单位时间内输出的最大信息量为 2 F log(b − a) 比特/秒 【4.6】有一信源发出恒定宽度,但不同幅度的脉冲,幅度值处在 a1 和 a2 之间, 此信源连至某信道, 信道接收端接收脉冲的幅度 y 处在 b1 和 b2 之间。已知随机变 量 X 和 Y 的联合概率密度函数 p( xy ) = 1 (a2 − a1 )(b2 − b1 )
= − ∫ A cos x log Adx − ∫ A cos x log cos xdx = − A log A sin x − ∫ A cos x log cos xdx
= −2 A log A − ∫ A cos x log cos xdx 而
∫ cos x log cos xdx
= log e ∫ ln 1 − sin 2 x d sin x 1 = log e ∫ ln(1 + sin x ) + ln(1 − sin x )d sin x 2 1 1 = log e ∫ ln(1 + sin x )d sin x + log e ∫ ln(1 − sin x)d sin x 2 2 = (1 + sin x) ln(1 + sin x) = 2 ln 2 − 2
解: (1)
h( X ) = − ∫ p ( x) log p( x )dx
= − ∫ λe −λx log λ e −λx dx = − ∫ λe −λx log λ dx − ∫ λe −λx log e −λx dx = − log λe −λx
∞ 0
+ log e ∫ ln e −λx de −λx
第四章课后习题
【4.1】 设有一连续随机变量,其概率密度函数为 π A cos x x ≤ p( x) = 2 其他值 0 又有 ∫ p( x)dx = 1 ,试求这随机变量的熵。 解: h( X ) = − ∫ p( x) log p ( x )dx
π 2 π − 2 π 2 π − 2
π 2 π − 2
∫ ln(1 + sin x)d sin x ∫ ln(1 − sin x)d sin x
−∫
1 + sin x d sin x 1 + sin x
= − ∫ ln(1 − sin x)d (1 − sin x ) = −(1 − sin x ) ln(1 − sin x ) = 2 ln 2 − 2
试计算 h( X ) , h(Y ) , h( XY ) 和 I ( X ; Y ) 。 解: p( x) = ∫ p ( x, y )dy 1 =∫ dy (a 2 − a1 )(b2 − b1 ) = 1 a2 − a1
同理, p( y ) = 因此
1 。 b2 − b1
h( X ) = − ∫ p ( x ) log p ( x)dx = log(a 2 − a1 ) h(Y ) = − ∫ p( y ) log p( y )dy = log(b2 − b1 ) h( XY ) = − ∫ p ( x, y ) log p ( x, y )dxdy = log( a2 − a1 ) + log(b2 − b1 ) I ( X ; Y ) = h( X ) + h(Y ) − h( XY ) = 0 【4.7】在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1) h( X | Y ) ≤ h( X ) ,当且仅当 X 和 Y 统计独立时等号成立; (2)h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) ,当且仅当 X 1 X 2 L X N 彼此统计 独立时等式成立。 证明: (1) h( XY ) = − ∫ p( y )dy ∫ p( x | y ) log p ( x | y )dx ≤ − ∫ p ( y )dy ∫ p( x | y ) log p ( x )dx = − ∫ p( x, y ) log p ( x )dxdy = h( X ) 等号成立当且仅当 p( x | y ) = p ( x ) ,即 p( x, y ) = p( x ) p ( y ) ,因此仅当 X 和 Y 统计 独立时等号成立。 (2)根据条件概率密度的相关公式,有 h( X 1 X 2 X N ) = h( X 1 ) + h( X 2 | X 1 ) + h( X 3 | X 1 X 2 ) + L + h( X N | X 1 X 2 X N −1 ) 根据(1)的结论,条件差熵小于差熵,因此有 h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) 等号成立当且仅当
