第四章课后习题参考答案
《大学物理教程》郭振平主编第四章光的衍射课后习题答案

第四章 光的衍射一、基本知识点光的衍射:当光遇到小孔、狭缝或其他的很小障碍物时,传播方向将发生偏转,而绕过障碍物继续前行,并在光屏上形成明暗相间的圆环或条纹。
光波的这种现象称为光的衍射。
菲涅耳衍射:光源、观察屏(或者是两者之一)到衍射屏的距离是有限的,这类衍射又称为近场衍射。
夫琅禾费衍射:光源、观察屏到衍射屏的距离均为无限远,这类衍射也称为远场衍射。
惠更斯-菲涅耳原理:光波在空间传播到的各点,都可以看作一个子波源,发出新的子波,在传播到空间某一点时,各个子波之间可以相互叠加。
这称为惠更斯-菲涅耳原理。
菲涅耳半波带法:将宽度为a 的缝AB 沿着与狭缝平行方向分成一系列宽度相等的窄条,1AA ,12A A ,…,k A B ,对于衍射角为θ的各条光线,相邻窄条对应点发出的光线到达观察屏的光程差为半个波长,这样等宽的窄条称为半波带。
这种分析方法称为菲涅耳半波带法。
单缝夫琅禾费衍射明纹条件:sin (21)(1,2,...)2a k k λθ=±+=单缝夫琅禾费衍射暗纹条件:sin (1,2,...)a k k θλ=±=在近轴条件下,θ很小,sin θθ≈, 则第一级暗纹的衍射角为 1aλθ±=±第一级暗纹离开中心轴的距离为 11x f faλθ±±==±, 式中f 为透镜的焦距。
中央明纹的角宽度为 112aλθθθ-∆=-=中央明纹的线宽度为 002tan 2l f f faλθθ=≈∆=衍射图样的特征:① 中央明纹的宽度是各级明纹的宽度的两倍,且绝大部分光能都落在中央明纹上。
② 暗条纹是等间隔的。
③ 当入射光为白光时,除中央明区为白色条纹外,两侧为由紫到红排列的彩色的衍射光谱。
④ 当波长一定时,狭缝的宽度愈小,衍射愈显著。
光栅: 具有周期性空间结构或光学性能(透射率,反射率和折射率等)的衍射屏,统称为光栅。
光栅常数: 每两条狭缝间距离d a b =+称为光栅常数。
《传热学》课后习题答案-第四章
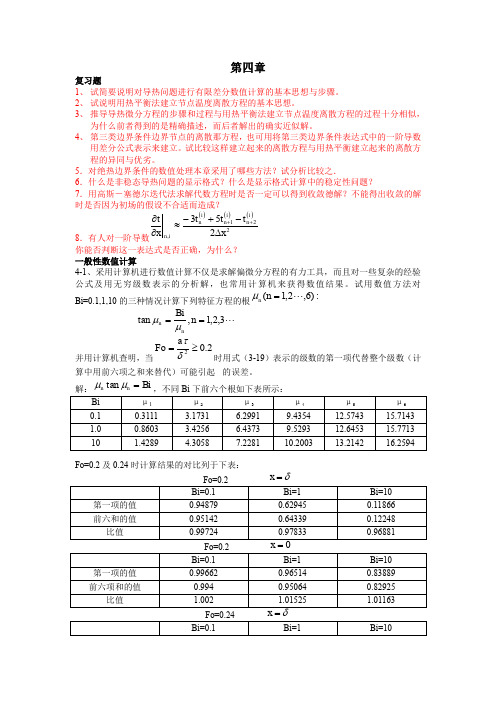
t k i,j 1 t k i,j t k i,j 1 t k i , j r r rj rj r 2 r 2 rj r
并简化,可以得出与上式完全一样相同的结果。
4-7、 一金属短圆柱在炉内受热厚被竖直地移植到空气中冷却, 底面可以认为是绝热的。为用数值法确定冷却过程中柱体温 度的变化, 取中心角为 1rad 的区域来研究 (如本题附图所示) 。 已知柱体表面发射率,自然对流表面传热系数,环境温度, 金属的热扩散率,试列出图中节点(1,1) , (M,1)(M,n)及 (M,N) 的离散方程式。 在 r 及 z 方向上网格是各自均分的。 解:应用热平衡法来建立四个节点点离散方程。 节点(1,1) :
, 离散方程的建立 4-5、试将直角坐标中的常物性无内热源的二维稳态导热微分方程化为显式差分格式,并指 出其稳定性条件( x y) 。 解:常物性无内热源二维非稳态方程微分方程为
4.3636t 2 2.53t1 1.8336t f
t2
2.53t f 1.8336t f
2t 2t t a x 2 y 2
Bi=0.1,1,10 的三种情况计算下列特征方程的根
n (n 1,2,6) :
n a Fo 2 0.2 并用计算机查明,当 时用式(3-19)表示的级数的第一项代替整个级数(计
算中用前六项之和来替代)可能引起 的误差。 解: n Bi 0.1 1.0 10
tan n
第四章
复习题 1、 试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。 2、 试说明用热平衡法建立节点温度离散方程的基本思想。 3、 推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似, 为什么前者得到的是精确描述,而后者解出的确实近似解。 4、 第三类边界条件边界节点的离散那方程,也可用将第三类边界条件表达式中的一阶导数 用差分公式表示来建立。试比较这样建立起来的离散方程与用热平衡建立起来的离散方 程的异同与优劣。 5.对绝热边界条件的数值处理本章采用了哪些方法?试分析比较之. 6.什么是非稳态导热问题的显示格式?什么是显示格式计算中的稳定性问题? 7.用高斯-塞德尔迭代法求解代数方程时是否一定可以得到收敛德解?不能得出收敛的解 时是否因为初场的假设不合适而造成?
形式逻辑(第5版)课后练习参考答案第4章

《形式逻辑》课后习题参考答案第四章简单命题及其推理(下)一、指出下列三段论的格和式,并指出其中的大项、中项和小项,以及大前提、小前提和结论。
1.第一格AAA式。
大项:一定要胜利的;中项:正义的事业;小项:我们的事业。
大前提:一切正义的事业都是一定要胜利的;小前提:我们的事业是正义的事业;结论:我们的事业是一定要胜利的。
2.第三格AAI式。
大项:能导电;中项:石墨;小项:非金属。
大前提:石墨能导电;小前提:石墨是非金属;结论:有的非金属能导电。
3.第二格AEE式。
大项:文学作品;中项:需要创造艺术形象;小项:学术论文。
大前提:一切文学作品都需要创造艺术形象;小前提:学术论文不需要创造艺术形象;结论:学术论文不是文学作品。
4.第二格AEE式。
大项:鱼;中项:用鳃呼吸;小项:鲸。
大前提:鱼都是用鳃呼吸的;小前提:鲸不是用鳃呼吸的;结论:鲸不是鱼。
二、下列三段论是否正确?如果不正确,违反了什么规则?1.不正确。
大项扩张(大项“青年”在前提中不周延,但在结论中周延。
注:按照对当关系,并非所有的青年工人都是共青团员=有的青年不是共青团员)。
2.不正确。
中项两次不周延。
3.不正确。
四概念错误(大小前提中的两个“物质”不是一个概念)4.不正确。
两前提都是特称命题,或者中项两次不周延。
5.不正确。
中项两次不周延(不是快车是不带邮件的=带邮件的是快车)带邮件的是快车)6.不正确。
中项两次不周延。
不正确。
中项两次不周延。
三、在下列括号内填入适当的符号,构成一个正确的三段论,并写出解题过程。
1.它的限制条件少,很多三段论都满足要求,第一格的有AAA, AAI, AII,,第四格的有AAI, 第二格的有AEE, AEO, AOO,第三格的有AAI, AII,第四格的有AEE。
例如,对于第一格的AAA式,即MAP, SAM/SAP,假设结论为SAP,那么S在结论中是周延的。
根据三段论规则3,S在前提中也必须周延。
按照规则4,前提不能出现否定。
计导 课后习题参考答案(第4章

第4章位运算一、复习题1.逻辑运算和算术运算有什么区别?答:逻辑运算是把二进制位看成逻辑值(真或假)进行的运算,包括或运算、与运算、非运算和异或运算。
算术运算是把二进制位看成数值(整数、浮点数)进行的运算,包括加、减、乘、除运算。
2.乘法与加法有什么关系?请举例说明。
答:乘法相当于连加。
例如:3*2=2+2+2。
3.在最后的相加中,最左边一列是怎样进位的?答:如果最左边的列相加后还有进位,则舍弃进位。
4.N(位分配单位)可以等于1吗?为什么?答:不可以,因为在N位分配单位中,最左边的数用来表示正负。
当N=1时,不能表示任何数。
5.解释“溢出”这个词。
答:是指试图把一个数存储在超出指定分配单元所允许的范围时发生的错误。
6.在浮点数的加法运算中,怎么样调整指数不同的数的表示?答:移动小数点,使两者指数相同。
一般调整小指数为大指数。
7.一元运算和二元运算有何不同?答:一元运算输入一个位模式输出一个位模式。
二元运算输入二个位模式输出一个位模式。
8.二元逻辑有哪些?答:或运算、与运算和异或运算。
9.什么是真值表?答:所有输入组合与相应的输出值的对照表。
10.非运算符的作用是什么?答:有1个输入操作数,对输入的位模式逐位取反,即将0变为1,将1变为0。
11.与运算符的结果何时为真?答:当两个操作数同时为真时,与运算的结果为真。
12.或运算符的结果何时为真?答:当两个操作数不全为假时,或运算的结果为真。
13.异或运算符的结果何时为真?答:当两个操作数不相同时,异或运算符的结果为真。
14.何谓与运算符的固有规则?答:任何数与0进行与运算的结果为0。
15.何谓或运算符的固有规则?答:任何数与1进行或运算的结果为1。
16.何谓异或运算符的固有规则?答:如果一个输入位为1,则运算结果就是另一个输入的相对应位取反。
17.何种二元运算可以用来置位?掩码应该用什么位模式?答:或运算。
对于目标位模式中需要置1的位,掩码的相应位设为1。
有机化学课后习题答案第四章

4章思考题4.1 付-克烷基化反应的特点是什么?4.2 解释什么叫定位基,并说明有哪三类定位基。
4.3 解释定位效应。
4.4 共振论对于共振结构式有何规定?4.5 试说明芳香亲电取代反应的机理。
4.6 甲苯和对二甲苯相比哪个对游离基卤代反应更活泼?试说明理由。
4.7 用KMnO4或K2CrO7+H+使PhCH3氧化成PhCOOH的反应产率很差,而由p-O2N-C6H4CH3氧化成p-O2NC6H4COOH,同样的氧化反应却有较好的产率。
如何解释。
4.8 回答下列问题。
(1)(1)环丁二烯只在较低温度下才能存在,高于35K即(如分子间发生双烯合成)转变为二聚体,已知它的衍生物二苯基环丁二烯有三种异构体。
上述现象说明什么?写出二苯基环丁二烯三种异构体的构造式。
(2)(2)1,3,5,7-环辛四烯能使冷的高锰酸钾水溶液迅速褪色,和溴的四氯化碳溶液作用得到C8H8Br8a 、它应具有什么样的结构?b、b、金属钾和环辛四烯作用即得到一个稳定的化合物2K+C8H82-(环辛四烯二负离子)。
这种盐的形成说明了什么?预期环辛四烯二负离子将有怎样的结构?解答4.1 答:(1)因烷基正离子容易重排,易形成烷基异构化产物;(2)烷基可活化苯环,易使烷基化反应产物为多元取代产物;(3)烷基化反应是可逆反应,使得产物可能复杂化。
4.2 答:苯环上已有一个取代基后,再进行亲电取代反应时,新进入的基团进入苯环的位置由环上原有取代基的性质决定,这个原有的取代基叫定位基。
定位基可分为三类,即(1)邻、对位定位基,如—OH、—NH2、—NHCOCH3、—CH3等,这类基团使苯环活化,并且使新引入的取代基在定位基的邻位和对位。
(2)间位定位基,如—NO2、—CN、—COCH3、—COOH、—SO3H等,这类基团使苯环钝化,并使新引入的取代基在它的间位。
(3)卤素是一类特殊的定位基,它使苯环钝化,但都是邻、对定位基。
4.3 答:邻、对位定位基的推电子作用是苯环活化的原因,这又可分为两种情况:①在与苯环成键的原子上有一对未共享电子,这对电子可以通过大π键离域到苯环上;②虽无未共享电子对,但能通过诱导效应或超共轭效应起推电子作用的基团,如甲基或其他烷基。
化工原理课后习题答案详解第四章.doc

第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B,质量摩尔浓度为b B,此溶液的密度为。
以M A,M B分别代表溶剂和溶质的摩尔质量,若溶液的组成用B的摩尔分数x B表示时,试导出x B与c B,x B与b B之间的关系。
解:根据各组成表示的定义4.2D-果糖溶于水(A)中形成的某溶液,质量分数,此溶液在20 C时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3在25 C,1 kg水(A)中溶有醋酸(B),当醋酸的质量摩尔浓度b B介于和之间时,溶液的总体积。
求:(1)把水(A)和醋酸(B)的偏摩尔体积分别表示成b B的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.460 ︒C时甲醇的饱和蒸气压是84.4 kPa,乙醇的饱和蒸气压是47.0 kPa。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %,求60 ︒C 时此混合物的平衡蒸气组成,以摩尔分数表示。
解:质量分数与摩尔分数的关系为求得甲醇的摩尔分数为根据Raoult定律4.580 ︒C是纯苯的蒸气压为100 kPa,纯甲苯的蒸气压为38.7 kPa。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80 ︒C时气相中苯的摩尔分数,求液相的组成。
解:根据Raoult定律4.6在18 ︒C,气体压力101.352 kPa下,1 dm3的水中能溶解O2 0.045 g,能溶解N2 0.02 g。
现将 1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325 kPa,18 ︒C下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为:,解:显然问题的关键是求出O2和N2的Henry常数。
18 C,气体压力101.352 kPa下,O2和N2的质量摩尔浓度分别为这里假定了溶有气体的水的密度为(无限稀溶液)。
有机化学课后第四章习题答案
一、写出下列化合物的构造式或命名:
1、对二乙烯苯 2、对叔丁基甲苯 3、3-氯-4-硝基甲苯
CH2CH CH2
4、
5、
NO2CH2Br 6、 NhomakorabeaCH2CH CH2
O CH3
Cl
二、完成下列反应
CH2CH2 CH3
H3C CH CH3
1、
+
;
COOH
2、Cl2/光照; AlCl3 +
3、H2SO4/0~80℃; 165℃
CH3 Cl
NO2
CH3
Br2
CH3
3、
FeBr3
Br
Br
Br
4、
Br2
ClCOCH3
FeBr3
AlCl3
COCH3
CH3 KMnO4
7、
H+,△
COOH
HNO3 H2SO4 O2N
COOH NO2
八、指出下列化合物硝化时,导入的硝基在环上的位置:
CH3 CH3
CH3 OCH3
CH3
OH
SO3H
Cl
1、
>
NO2
NO2
>
>
NO2
OH
2、
>
COCH3 NO2
>
>
五、由苯或甲苯开始合成下列化合物:
CH3 HNO3
2、
H2SO4
CH3
Cl2
FeCl3
NO2
CH3 Cl
NO2
或:
CH3 浓H2SO4 100℃
CH3
Cl2
FeCl3
SO3H
CH3 Cl
H3O+ 150℃
《传感器与检测技术》课后习题:第四章(含答案)

第四章习题答案1.某电容传感器(平行极板电容器)的圆形极板半径)(4mm r =,工作初始极板间距离)(3.00mm =δ,介质为空气。
问:(1)如果极板间距离变化量)(1m μδ±=∆,电容的变化量C ∆是多少?(2)如果测量电路的灵敏度)(1001pF mV k =,读数仪表的灵敏度52=k (格/mV )在)(1m μδ±=∆时,读数仪表的变化量为多少?解:(1)根据公式SSSd C d d d d d dεεε∆∆=-=⋅-∆-∆ ,其中S=2r π (2)根据公式112k k δδ∆=∆ ,可得到112k k δδ⋅∆∆==31001100.025-⨯⨯= 2.寄生电容与电容传感器相关联影响传感器的灵敏度,它的变化为虚假信号影响传感器的精度。
试阐述消除和减小寄生电容影响的几种方法和原理。
解:电容式传感器内极板与其周围导体构成的“寄生电容”却较大,不仅降低了传感器的灵敏度,而且这些电容(如电缆电容)常常是随机变化的,将使仪器工作很不稳定,影响测量精度。
因此对电缆的选择、安装、接法都有要求。
若考虑电容传感器在高温、高湿及高频激励的条件下工作而不可忽视其附加损耗和电效应影响时,其等效电路如图4-8所示。
图中L 包括引线电缆电感和电容式传感器本身的电感;C 0为传感器本身的电容;C p 为引线电缆、所接测量电路及极板与外界所形成的总寄生电容,克服其影响,是提高电容传感器实用性能的关键之一;R g 为低频损耗并联电阻,它包含极板间漏电和介质损耗;R s 为高湿、高温、高频激励工作时的串联损耗电组,它包含导线、极板间和金属支座等损耗电阻。
此时电容传感器的等效灵敏度为2200220/(1)(1)g e e k C C LC k d d LC ωω∆∆-===∆∆- (4-28)当电容式传感器的供电电源频率较高时,传感器的灵敏度由k g 变为k e ,k e 与传感器的固有电感(包括电缆电感)有关,且随ω变化而变化。
大学化学课后习题答案第四章.

当pH=5.00,其他有关物质均处于标准条件时:
=1.033V
11.由镍电极和标准氢电极组成原电池。若c(Ni 2+=0.0100mol·dm -3时,原电池的电动势为0.315V ,其中镍为负极,计算镍电极的标准电极电势。
12.由两个氢电极H 2(101.325kPa|H +(0.10mol · dm -3|Pt和
(4计算c(I -=1.0×10-2mol·dm -3以及c(Fe 3+=c(Fe 2+/10时,原电池的电动势。
解:(1查阅教材附录10可知:32(Fe /Fe θφ++=0.771V ,
-
2(I /I θ
φ=0.5355 V
E θ=_θθφφ+-=32(Fe /Fe θφ++–-
2
(I
/I θφ=0.771 V – 0.5355 V=0.236 V
第四章电化学与金属腐蚀
1.是非题(对的在括号内填“+”,错的填“-”号
(1取两根铜棒,将一根插入盛有0.1mol·dm-3CuSO4溶液的烧杯中,另一根插入盛有1mol·dm-3CuSO4溶液的烧杯中,并用盐桥将两只烧杯中的溶液连结起来,可以组成一个浓差原电池。(
计算机网络课后习题参考答案第四章

{第四章网络层1.网络层向上提供的服务有哪两种是比较其优缺点。
网络层向运输层提供“面向连接”虚电路(Virtual Circuit)服务或“无连接”数据报服务前者预约了双方通信所需的一切网络资源。
优点是能提供服务质量的承诺。
即所传送的分组不出错、丢失、重复和失序(不按序列到达终点),也保证分组传送的时限,缺点是路由器复杂,网络成本高;后者无网络资源障碍,尽力而为,优缺点与前者互易2.网络互连有何实际意义进行网络互连时,有哪些共同的问题需要解决网络互联可扩大用户共享资源范围和更大的通信区域[进行网络互连时,需要解决共同的问题有:不同的寻址方案不同的最大分组长度不同的网络接入机制不同的超时控制不同的差错恢复方法不同的状态报告方法不同的路由选择技术,不同的用户接入控制不同的服务(面向连接服务和无连接服务)不同的管理与控制方式3.作为中间设备,转发器、网桥、路由器和网关有何区别中间设备又称为中间系统或中继(relay)系统。
物理层中继系统:转发器(repeater)。
数据链路层中继系统:网桥或桥接器(bridge)。
、网络层中继系统:路由器(router)。
网桥和路由器的混合物:桥路器(brouter)。
网络层以上的中继系统:网关(gateway)。
4.试简单说明下列协议的作用:IP、ARP、RARP和ICMP。
IP协议:实现网络互连。
使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。
网际协议IP是TCP/IP体系中两个最主要的协议之一,与IP协议配套使用的还有四个协议。
ARP协议:是解决同一个局域网上的主机或路由器的IP地址和硬件地址的映射问题。
RARP:是解决同一个局域网上的主机或路由器的硬件地址和IP地址的映射问题。
(ICMP:提供差错报告和询问报文,以提高IP数据交付成功的机会因特网组管理协议IGMP:用于探寻、转发本局域网内的组成员关系。
地址分为几类各如何表示IP地址的主要特点是什么分为ABCDE 5类;每一类地址都由两个固定长度的字段组成,其中一个字段是网络号 net-id,它标志主机(或路由器)所连接到的网络,而另一个字段则是主机号 host-id,它标志该主机(或路由器)。
大学电路分析第四章课后习题答案

4-2.5μF 电容的端电压如图示。
(1)绘出电流波形图。
(2)确定2μs t =和10μs t =时电容的储能。
解:(1)由电压波形图写出电容端电压的表达式:10 0μs 1μs10 1μs 3μs ()1040 3μs 4μs 0 4μs t t t u t t t t≤≤⎧⎪≤≤⎪=⎨-+≤≤⎪⎪≤⎩式中时间t 的单位为微秒;电压的单位为毫伏。
电容伏安关系的微分形式:50 0μs 1μs 0 1μs 3μs()()50 3μs 4μs 0 4μs t t du t i t C t dt t<<⎧⎪<<⎪==⎨-<<⎪⎪<⎩上式中时间的单位为微秒;电压的单位为毫伏;电容的单位为微法拉;电流的单位为毫安。
电容电流的波形如右图所示。
(2)电容的储能21()()2w t Cu t =,即电容储能与电容端电压的平方成正比。
当2μs t =时,电容端电压为10毫伏,故:()()22631010μs 11()5101010 2.510J 22t w t Cu ---===⨯⨯⨯⨯=⨯当10μs t =时,电容的端电压为0,故当10μs t =时电容的储能为0。
4-3.定值电流4A 从t=0开始对2F 电容充电,问:(1)10秒后电容的储能是多少100秒后电容的储能是多少设电容初始电压为0。
解:电容端电压:()()()00110422t tC C u t u i d d t C τττ+++=+==⎰⎰;()1021020V C u =⨯=; ()1002100200V C u =⨯=()()211010400J 2C w Cu ==; ()()2110010040000J 2C w Cu ==4-6.通过3mH 电感的电流波形如图示。
(1)试求电感端电压()L u t ,并绘出波形图;(2)试求电感功率()L p t ,并绘出波形图;(3)试求电感储能()L w t ,并绘出波形图。
概率论与数理统计(茆诗松)第二版课后第四章习题参考答案

第四章 大数定律与中心极限定理习题4.11. 如果X X Pn →,且Y X Pn →.试证:P {X = Y } = 1.证:因 | X − Y | = | −(X n − X ) + (X n − Y )| ≤ | X n − X | + | X n − Y |,对任意的ε > 0,有⎭⎬⎫⎩⎨⎧≥−+⎭⎬⎫⎩⎨⎧≥−≤≥−≤2||2||}|{|0εεεY X P X X P Y X P n n ,又因X X Pn →,且Y X Pn →,有02||lim =⎭⎬⎫⎩⎨⎧≥−+∞→εX X P n n ,02||lim =⎭⎫⎩⎨⎧≥−+∞→εY X P n n ,则P {| X − Y | ≥ ε} = 0,取k 1=ε,有01||=⎭⎬⎫⎩⎨⎧≥−k Y X P ,即11||=⎭⎬⎫⎩⎨⎧<−k Y X P , 故11||lim1||}{1=⎭⎬⎫⎩⎨⎧<−=⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧<−==+∞→+∞=k Y X P k Y X P Y X P k k I . 2. 如果X X Pn →,Y Y Pn →.试证:(1)Y X Y X Pn n +→+; (2)XY Y X Pn n →.证:(1)因 | (X n + Y n ) − (X + Y ) | = | (X n − X ) + (Y n − Y )| ≤ | X n − X | + | Y n − Y |,对任意的ε > 0,有⎭⎫⎩⎨⎧≥−+⎭⎬⎫⎩⎨⎧≥−≤≥+−+≤2||2||}|)()({|0εεεY Y P X X P Y X Y X P n n n n ,又因X X P n →,Y Y P n →,有02||lim =⎭⎫⎩⎨⎧≥−+∞→εX X P n n ,02||lim =⎭⎬⎫⎩⎨⎧≥−+∞→εY Y P n n ,故0}|)()({|lim =≥+−++∞→εY X Y X P n n n ,即Y X Y X Pn n +→+;(2)因 | X n Y n − XY | = | (X n − X )Y n + X (Y n − Y ) | ≤ | X n − X | ⋅ | Y n | + | X | ⋅ | Y n − Y |,对任意的ε > 0,有⎭⎬⎫⎩⎨⎧≥−⋅+⎭⎬⎫⎩⎨⎧≥⋅−≤≥−≤2||||2||||}|{|0εεεY Y X P Y X X P XY Y X P n n n n n ,对任意的h > 0,存在M 1 > 0,使得4}|{|1h M X P <≥,存在M 2 > 0,使得8}|{|2hM Y P <≥, 存在N 1 > 0,当n > N 1时,8}1|{|h Y Y P n <≥−, 因| Y n | = | (Y n − Y ) + Y | ≤ | Y n − Y | + | Y |,有4}|{|}1|{|}1|{|22h M Y Y Y P M Y P n n <≥+≥−≤+≥, 存在N 2 > 0,当n > N 2时,4)1(2||2h M X X P n <⎭⎬⎫⎩⎨⎧+≥−ε,当n > max{N 1, N 2}时,有244}1|{|)1(2||2||||22h h h M Y P M X X P Y X X P n n n n =+<+≥+⎭⎬⎫⎩⎨⎧+≥−≤⎭⎬⎫⎩⎨⎧≥⋅−εε,存在N 3 > 0,当n > N 3时,42||1hM Y Y P n <⎭⎬⎫⎩⎨⎧≥−ε,有244}|{|2||2||||11h h h M X P M Y Y P X Y Y P n n =+<≥+⎭⎬⎫⎩⎨⎧≥−≤⎭⎬⎫⎩⎨⎧≥⋅−εε,则对任意的h > 0,当n > max{N 1, N 2, N 3} 时,有h h h Y Y X P Y X X P XY Y X P n n n n n =+<⎭⎬⎫⎩⎨⎧≥−⋅+⎭⎬⎫⎩⎨⎧≥⋅−≤≥−≤222||||2||||}|{|0εεε,故0}|{|lim =≥−+∞→εXY Y X P n n n ,即XY Y X Pn n →.3. 如果X X Pn →,g (x )是直线上的连续函数,试证:)()(X g X g Pn →. 证:对任意的h > 0,存在M > 0,使得4}|{|h M X P <≥, 存在N 1 > 0,当n > N 1时,4}1|{|h X X P n <≥−, 因| X n | = | (X n − X ) + X | ≤ | X n − X | + | X |,则244}|{|}1|{|}1|{|h h h M X P X X P M X P n n =+<≥+≥−≤+≥, 因g (x ) 是直线上的连续函数,有g (x ) 在闭区间 [− (M + 1), M + 1] 上连续,必一致连续, 对任意的ε > 0,存在δ > 0,当 | x − y | < δ 时,有 | g (x ) − g ( y ) | < ε ,存在N 2 > 0,当n > N 2时,4}|{|hX X P n <≥−δ,则对任意的h > 0,当n > max{N 1, N 2} 时,有{}}|{|}1|{|}|{|}|)()({|0M X M X X X P X g X g P n n n ≥+≥≥−≤≥−≤U U δεh hh h M X P M X P X X P n n =++<≥++≥+≥−≤424}|{|}1|{|}|{|δ, 故0}|)()({|lim =≥−+∞→εX g X g P n n ,即)()(X g X g Pn →.4. 如果a X P n →,则对任意常数c ,有ca cX Pn →. 证:当c = 0时,有c X n = 0,ca = 0,显然ca cX Pn →;当c ≠ 0时,对任意的ε > 0,有0||||lim =⎭⎬⎫⎩⎨⎧≥−+∞→c a X P n n ε, 故0}|{|lim =≥−+∞→εca cX P n n ,即ca cX Pn →.5. 试证:X X P n →的充要条件为:n → +∞ 时,有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n .证:以连续随机变量为例进行证明,设X n − X 的密度函数为p ( y ),必要性:设X X Pn →,对任意的ε > 0,都有0}|{|lim =≥−+∞→εX X P n n ,对012>+εε,存在N > 0,当n > N 时,εεε+<≥−1}|{|2X X P n , 则∫∫∫≥<∞+∞−+++=+=⎟⎟⎠⎞⎜⎜⎝⎛−+−εε||||)(||1||)(||1||)(||1||||1||y y n n dy y p y y dy y p y y dy y p y y XX X X E εεεεεεεεεεεεε=+++<≥−+<−+=++≤∫∫≥<11}|{|}|{|1)()(12||||X X P X X P dy y p dy y p n n y y ,故n → +∞ 时,有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n ; 充分性:设n → +∞ 时,有0||1||→⎟⎟⎠⎞⎜⎜⎝⎛−+−XX X X E n n , 因∫∫∫≥≥≥++≤++==≥−εεεεεεεεεε||||||)(||1||1)(11)(}|{|y y y n dy y p y y dy y p dy y p X X P ⎟⎟⎠⎞⎜⎜⎝⎛−+−+=++≤∫∞+∞−||1||1)(||1||1X X X X E dy y p y y n n εεεε, 故0}|{|lim =≥−+∞→εX X P n n ,即X X Pn →.6. 设D (x )为退化分布:⎩⎨⎧≥<=.0,1;0,0)(x x x D试问下列分布函数列的极限函数是否仍是分布函数?(其中n = 1, 2, ….)(1){D (x + n )}; (2){D (x + 1/n )}; (3){D (x − 1/n )}.解:(1)对任意实数x ,当n > −x 时,有x + n > 0,D (x + n ) = 1,即1)(lim =++∞→n x D n ,则 {D (x + n )} 的极限函数是常量函数f (x ) = 1,有f (−∞) = 1 ≠ 0,故 {D (x + n )} 的极限函数不是分布函数; (2)若x ≥ 0,有01>+n x ,11=⎟⎠⎞⎜⎝⎛+n x D ,即11lim =⎟⎠⎞⎜⎝⎛++∞→n x D n ,若x < 0,当x n 1−>时,有01<+n x ,01=⎟⎠⎞⎜⎝⎛+n x D ,即01lim =⎟⎠⎞⎜⎝⎛++∞→n x D n ,则⎩⎨⎧≥<=⎟⎠⎞⎜⎝⎛++∞→.0,1;0,01lim x x n x D n 这是在0点处单点分布的分布函数,满足分布函数的基本性质,故⎭⎬⎫⎩⎨⎧⎟⎠⎞⎜⎝⎛+n x D 1的极限函数是分布函数;(3)若x ≤ 0,有01<−n x ,01=⎟⎠⎞⎜⎝⎛−n x D ,即01lim =⎟⎠⎞⎜⎝⎛−+∞→n x D n ,若x > 0,当x n 1>时,有01>−n x ,11=⎟⎠⎞⎜⎝⎛−n x D ,即11lim =⎟⎠⎞⎜⎝⎛−+∞→n x D n ,则⎩⎨⎧>≤=⎟⎠⎞⎜⎝⎛−+∞→.0,1;0,01lim x x n x D n 在x = 0处不是右连续,故⎭⎬⎫⎩⎨⎧⎟⎠⎞⎜⎝⎛−n x D 1的极限函数不是分布函数.7. 设分布函数列 {F n (x )} 弱收敛于连续的分布函数F (x ),试证:{F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x ). 证:因F (x ) 为连续的分布函数,有F (−∞) = 0,F (+∞) = 1,对任意的ε > 0,取正整数ε2>k ,则存在分点x 1 < x 2 < … < x k −1,使得1,,2,1,)(−==k i kix F i L ,并取x 0 = −∞,x k = +∞, 可得k k i k x F x F i i ,1,,2,1,21)()(1−=<=−−L ε, 因 {F n (x )} 弱收敛于F (x ),且F (x ) 连续,有 {F n (x )} 在每一点处都收敛于F (x ),则存在N > 0,当n > N 时,1,,2,1,2|)()(|−=<−k i x F x F i i n L ε,且显然有20|)()(|00ε<=−x F x F n ,20|)()(|ε<=−k k n x F x F ,对任意实数x ,必存在j ,1 ≤ j ≤ k ,有x j −1 ≤ x < x j ,因2)()()()(2)(11εε+<≤≤<−−−j j n n j n j x F x F x F x F x F ,则εεεε−=−−>−−>−−222)()()()(1x F x F x F x F j n ,且εεεε=+<+−<−222)()()()(x F x F x F x F j n ,即对任意的ε > 0和任意实数x ,总存在N > 0,当n > N 时,都有 | F n (x ) − F (x ) | < ε , 故 {F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x ).8. 如果X X Ln →,且数列a n → a ,b n → b .试证:b aX b X a Ln n n +→+. 证:设y 0是F aX + b ( y ) 的任一连续点,则对任意的ε > 0,存在h > 0,当 | y − y 0 | < h 时,4|)()(|0ε<−++y F y F b aX b aX ,又设y 是满足 | y − y 0 | < h 的F aX + b ( y ) 的任一连续点,因⎟⎠⎞⎜⎝⎛−=⎭⎬⎫⎩⎨⎧−≤=≤+=+a b y F a b y X P y b aX P y F X b aX }{)(,有a b y x −=是F X (x )的连续点,且X X L n→, 有)()(lim x F x F X X n n =+∞→,存在N 1,当n > N 1时,4|)()(|ε<−x F x F X X n ,即4|)()(|ε<−++y F y F b aX b aX n ,则当n > N 1且 | y − y 0 | < h 时,2|)()(||)()(||)()(|00ε<−+−≤−++++++y F y F y F y F y F y F b aX b aX b aX b aX b aX b aX n n , 因X 的分布函数F X (x ) 满足F X (−∞) = 0,F X (+∞) = 1,F X (x ) 单调不减且几乎处处连续, 存在M ,使得F X (x ) 在x = ± M 处连续,且41)(ε−>M F X ,4)(ε<−M F X ,因X X Ln →,有41)()(lim ε−>=+∞→M F M F X X n n ,4)()(lim ε<−=−+∞→M F M F X X n n ,则存在N 2,当n > N 2时,41)(ε−>M F n X ,4)(ε<−M F n X ,可得2)(1)(}|{|ε<−+−=>M F M F M X P n n X X n ,因数列a n → a ,b n → b ,存在N 3,当n > N 3时,M h a a n 4||<−,4||h b b n <−, 可得当n > max{N 2, N 3}时,⎭⎫⎩⎨⎧>−+−=⎭⎬⎫⎩⎨⎧>+−+2|)()(|2|)()(|h b b X a a P h b aX b X a P n n n n n n n2}|{|24||42||||||ε<>=⎭⎬⎫⎩⎨⎧>+⋅≤⎭⎬⎫⎩⎨⎧>−+⋅−≤M X P h h X M hP h b b X a a P nn n n n , 则⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>+−+⎭⎬⎫⎩⎨⎧+≤+≤≤+=+2|)()(|2}{)(000h b aX b X a h y b aX P y b X a P y F n n n n n n n n b X a n n n U222|)()(|200ε+⎟⎠⎞⎜⎝⎛+<⎭⎬⎫⎩⎨⎧>+−++⎭⎬⎫⎩⎨⎧+≤+≤+h y F h b aX b X a P h y b aX P b aX n n n n n n , 且⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>+−+≤+≤⎭⎬⎫⎩⎨⎧−≤+=⎟⎠⎞⎜⎝⎛−+2|)()(|}{22000h b aX b X a y b X a P h y b aX P h y F n n n n n n n n b aX n U2)(2|)()(|}{00ε+<⎭⎬⎫⎩⎨⎧>+−++≤+≤+y F h b aX b X a P y b X a P n n n b X a n n n n n n n , 即22)(22000εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−+++h y F y F h y F b aX b X a b aX n n n n n ,因当n > N 1且 | y − y 0 | < h 时,2)()(2)(00εε+<<−+++y F y F y F b aX b aX b aX n ,在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F aX + b ( y ) 的任一连续点y 1,满足 | y 1 − y 0 | < h ,当n > max{N 1, N 2, N 3}时,εεε+<+≤+⎟⎠⎞⎜⎝⎛+<++++)(2)(22)(0100y F y F h y F y F b aX b aX b aX b X a n n n n n ,在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F aX + b ( y ) 的任一连续点y 2,满足 | y 2 − y 0 | < h ,当n > max{N 1, N 2, N 3}时,εεε−>−≥−⎟⎠⎞⎜⎝⎛−>++++)(2)(22)(0200y F y F h y F y F b aX b aX b aX b X a n n n n n ,即对于F aX + b ( y ) 的任一连续点y 0,当n > max{N 1, N 2, N 3}时,ε<−++|)()(|00y F y F b aX b X a n n n , 故)()(y F y F b aX Wb X a n n n ++→,b aX b X a Ln n n +→+. 9. 如果X X Ln →,a Y Pn →,试证:a X Y X Ln n +→+. 证:设y 0是F X + a ( y ) 的任一连续点,则对任意的ε > 0,存在h > 0,当 | y − y 0 | < h 时,4|)()(|0ε<−++y F y F a X a X ,又设y 是满足 | y − y 0 | < h 的F X + a ( y )的任一连续点,因F X + a ( y ) = P {X + a ≤ y } = P {X ≤ y − a } = F X ( y − a ),有x = y − a 是F X (x )的连续点,且X X Ln →, 有)()(lim x F x F X X n n =+∞→,存在N 1,当n > N 1时,4|)()(|ε<−x F x F X X n ,即4|)()(|ε<−++y F y F a X a X n , 则当n > N 1且 | y − y 0 | < h 时,2|)()(||)()(||)()(|00ε<−+−≤−++++++y F y F y F y F y F y F a X a X a X a X a X a X n n ,因a Y Pn →,有02||lim =⎭⎫⎩⎨⎧>−+∞→h a Y P n n ,存在N 2,当n > N 2时,22||ε<⎭⎬⎫⎩⎨⎧>−h a Y P n , 则⎭⎬⎫⎩⎨⎧⎭⎫⎩⎨⎧>−⎭⎬⎫⎩⎨⎧+≤+≤≤+=+2||2}{)(000h a Y h y a X P y Y X P y F n n n n Y X n n U222||200ε+⎟⎠⎞⎜⎝⎛+<⎭⎬⎫⎩⎨⎧>−+⎭⎬⎫⎩⎨⎧+≤+≤+h y F h a Y P h y a X P a X n n n , 且⎭⎬⎫⎩⎨⎧⎭⎫⎩⎨⎧>−≤+≤⎭⎬⎫⎩⎨⎧−≤+=⎟⎠⎞⎜⎝⎛−+2||}{22000h a Y y Y X P h y a X P h y F n n n n a X n U2)(2||}{00ε+<⎭⎬⎫⎩⎨⎧>−+≤+≤+y F h a Y P y Y X P n n Y X n n n , 即22)(22000εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−+++h y F y F h y F a X Y X a X n n n n ,因当n > N 1且 | y − y 0 | < h 时,2)()(2)(00εε+<<−+++y F y F y F a X a X a X n ,在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F X + a ( y ) 的任一连续点y 1,满足 | y 1 − y 0 | < h ,当n > max{N 1, N 2}时,εεε+<+≤+⎟⎠⎞⎜⎝⎛+<++++)(2)(22)(0100y F y F h y F y F a X a X a X Y X n n n n ,在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F X + a ( y ) 的任一连续点y 2,满足 | y 2 − y 0 | < h ,当n > max{N 1, N 2}时,εεε−>−≥−⎟⎠⎞⎜⎝⎛−>++++)(2)(22)(0200y F y F h y F y F a X a X a X Y X n n n n ,即对于F X + a ( y ) 的任一连续点y 0,当n > max{N 1, N 2}时,ε<−++|)()(|00y F y F a X Y X n n , 故)()(y F y F a X WY X n n ++→,a X Y X Ln n +→+. 10.如果X X Ln →,0Pn Y →,试证:0Pn n Y X →.证:因X 的分布函数F X (x ) 满足F X (−∞) = 0,F X (+∞) = 1,F X (x ) 单调不减且几乎处处连续,则对任意的h > 0,存在M ,使得F X (x ) 在x = ± M 处连续,且41)(h M F X −>,4)(hM F X <−, 因X X L n →,有41)()(lim h M F M F X X n n −>=+∞→,4)()(lim h M F M F X X n n <−=−+∞→,则存在N 1,当n > N 1时,41)(h M F n X −>,4)(hM F n X <−,可得2)(1)(}|{|hM F M F M X P n n X X n <−+−=>,因0Pn Y →,对任意的ε > 0,有0||lim =⎭⎬⎫⎩⎨⎧>+∞→M Y P n n ε,存在N 2,当n > N 2时,2||h M Y P n <⎭⎬⎫⎩⎨⎧>ε, 则当n > max{N 1, N 2}时,有h M Y P M X P M Y M X P Y X P n n n n n n <⎭⎬⎫⎩⎨⎧>+>≤⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧>>≤>εεε||}|{|||}|{|}|{|U ,故0}|{|lim =>+∞→εn n n Y X P ,即0Pn n Y X →.11.如果X X Ln →,a Y Pn →,且Y n ≠ 0,常数a ≠ 0,试证:aXY X L n n →. 证:设y 0是F X / a ( y ) 的任一连续点,则对任意的ε > 0,存在h > 0,当 | y − y 0 | < h 时,4|)()(|0//ε<−y F y F a X a X ,又设y 是满足 | y − y 0 | < h 的F X / a ( y ) 的任一连续点,因)(}{)(/ay F ay X P y a X P y F X a X =≤=⎭⎬⎫⎩⎨⎧≤=,有x = ay 是F X (x )的连续点,且X X Ln →,有)()(lim x F x F X X n n =+∞→,存在N 1,当n > N 1时,4|)()(|ε<−x F x F X X n ,即4|)()(|//ε<−y F y F a X a X n ,则当n > N 1且 | y − y 0 | < h 时,2|)()(||)()(||)()(|0////0//ε<−+−≤−y F y F y F y F y F y F a X a X a X a X a X a X n n ,因X 的分布函数F X (x )满足F X (−∞) = 0,F X (+∞) = 1,F X (x )单调不减且几乎处处连续,存在M ,使得F X (x ) 在x = ± M 处连续,且121)(ε−>M F X ,12)(ε<−M F X ,因X X Ln →,有121)()(lim ε−>=+∞→M F M F X X n n ,12)()(lim ε<−=−+∞→M F M F X X n n ,则存在N 2,当n > N 2时,121)(ε−>M F n X ,12)(ε<−M F n X ,可得6)(1)(}|{|ε<−+−=>M F M F M X P n n X X n ,因0≠→a Y Pn ,有02||lim =⎭⎬⎫⎩⎨⎧>−+∞→h a Y P n n ,存在N 3 > 0,当n > N 3时,62||||ε<⎭⎬⎫⎩⎨⎧>−a a Y P n ,有62||||ε<⎭⎬⎫⎩⎨⎧<a Y P n ,且64||2ε<⎭⎬⎫⎩⎨⎧>−M h a a Y P n , 可得当n > max{N 1, N 2, N 3}时,⎭⎬⎫⎩⎨⎧>⋅−⋅=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−2||||||||2)(2h Y a a Y X P h aY Y a X P h a X Y X P n n n n n n n n n ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎭⎬⎫⎩⎨⎧<⎭⎬⎫⎩⎨⎧>−>≤2||||4||}|{|2a Y M h a a Y M X P n n n U U22||||4||}|{|2ε<⎭⎬⎫⎩⎨⎧<+⎭⎬⎫⎩⎨⎧>−+>≤a Y P M h a a Y P M X P n n n ,则⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎫⎪⎩⎪⎨⎧>−⎭⎬⎫⎩⎨⎧+≤≤⎭⎬⎫⎩⎨⎧≤=22)(000/h a X Y X h y a XP y Y X P y F n n n n n n Y X n n U22220/0ε+⎟⎠⎞⎜⎝⎛+<⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−+⎭⎬⎫⎩⎨⎧+≤≤h y F h a X Y X P h y a X P a X n n n n n ,且⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−⎭⎬⎫⎩⎨⎧≤≤⎭⎬⎫⎩⎨⎧−≤=⎟⎠⎞⎜⎝⎛−222000/h a X Y X y Y X P h y a X P h y F n n n nn n a X n U2)(20/0ε+<⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧>−+⎭⎬⎫⎩⎨⎧≤≤y F h a X Y X P y Y X P n n Y X n n n n n ,即22)(220/0/0/εε+⎟⎠⎞⎜⎝⎛+<<−⎟⎠⎞⎜⎝⎛−h y F y F h y F a X Y X a X n n n n ,因当n > N 1且 | y − y 0 | < h 时,2)()(2)(0//0/εε+<<−y F y F y F a X a X a X n ,在区间⎟⎠⎞⎜⎝⎛++h y h y 00,2取F X / a ( y ) 的任一连续点y 1,满足 | y 1 − y 0 | < h ,当n > max{N 1, N 2, N 3}时,εεε+<+≤+⎟⎠⎞⎜⎝⎛+<)(2)(22)(0/1/0/0/y F y F h y F y F a X a X a X Y X n n n n ,在区间⎟⎠⎞⎜⎝⎛−−2,00h y h y 取F X / a ( y ) 的任一连续点y 2,满足 | y 2 − y 0 | < h ,当n > max{N 1, N 2, N 3}时,εεε−>−≥−⎟⎠⎞⎜⎝⎛−>)(2)(22)(0/2/0/0/y F y F h y F y F a X a X a X Y X n n n n ,即对于F X / a ( y ) 的任一连续点y 0,当n > max{N 1, N 2, N 3}时,ε<−|)()(|0/0/y F y F a X Y X n n ,故)()(//y F y F a X WY X n n →,aX Y X L n n →. 12.设随机变量X n 服从柯西分布,其密度函数为+∞<<∞−+=x x n nx p n ,)1π()(22.试证:0Pn X →.证:对任意的ε > 0,)arctan(π2)arctan(π1)1π(}|{|22εεεεεεn nx dx x n n X P n ==+=<−−∫, 则12ππ2)arctan(lim π2}|0{|lim =⋅==<−+∞→+∞→εεn X P n n n , 故0Pn X →.13.设随机变量序列{X n }独立同分布,其密度函数为⎪⎩⎪⎨⎧<<=.,0;0,1)(其他ββx x p其中常数β > 0,令Y n = max{X 1, X 2, …, X n },试证:βPn Y →.证:对任意的ε > 0,P {| Y n − β | < ε} = P {β − ε < Y n < β + ε} = P {max{X 1, X 2, …, X n } > β − ε}= 1 − P {max{X 1, X 2, …, X n } ≤ β − ε} = 1 − P {X 1 ≤ β − ε} P {X 2 ≤ β − ε} … P {X n ≤ β − ε}n⎟⎟⎠⎞⎜⎜⎝⎛−−=βεβ1, 则11lim }|{|lim =⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−=<−+∞→+∞→nn n n Y P βεβεβ, 故βPn Y →.14.设随机变量序列{X n }独立同分布,其密度函数为⎩⎨⎧<≥=−−.,0;,e )()(a x a x x p a x 其中Y n = min{X 1, X 2, …, X n },试证:a Y Pn →.证:对任意的ε > 0,P {| Y n − a | < ε} = P {a − ε < Y n < a + ε} = P {min{X 1, X 2, …, X n } < a + ε}= 1 − P {min{X 1, X 2, …, X n } ≥ a + ε} = 1 − P {X 1 ≥ a + ε} P {X 2 ≥ a + ε} … P {X n ≥ a + ε}εεεn na a x n a a x dx −∞++−−∞++−−−=⎟⎠⎞⎜⎝⎛−−=⎟⎠⎞⎜⎝⎛−=∫e 1e 1e 1)()(, 则1)e 1(lim }|{|lim =−=<−−+∞→+∞→εεn n n n a Y P ,故a Y Pn →.15.设随机变量序列{X n }独立同分布,且X i ~ U(0, 1).令nni i n X Y 11⎟⎟⎠⎞⎜⎜⎝⎛=∏=,试证明:c Y P n →,其中c 为常数,并求出c .证:设∑∏===⎟⎟⎠⎞⎜⎜⎝⎛==n i i n i i n n X n X n Y Z 11ln 1ln 1ln ,因X i ~ U (0, 1), 则1)ln (ln )(ln 101−=−==∫x x x xdx X E i ,2)2ln 2ln (ln )(ln 12122=+−==∫x x x x x xdx X E i ,1)](ln [)(ln )Var(ln 22=−=i i i X E X E X , 可得1)(ln 1)(1−==∑=n i i n X E n Z E ,n X nZ ni in 1)Var(ln 1)Var(12==∑=,由切比雪夫不等式,可得对任意的ε > 0,221)Var(}|)({|εεεn Z Z E Z P n n n =≤≥−,则01lim }|)({|lim 02=≤≥−≤+∞→+∞→εεn Z E Z P n n n n ,即0}|)({|lim =≥−+∞→εn n n Z E Z P ,1)(−=→n P n Z E Z ,因n Z n Y e =,且函数e x 是直线上的连续函数,根据本节第3题的结论,可得1e e −→=PZ n n Y , 故c Y Pn →,其中1e −=c 为常数.16.设分布函数列{F n (x )}弱收敛于分布函数F (x ),且F n (x ) 和F (x ) 都是连续、严格单调函数,又设 ξ 服从(0, 1)上的均匀分布,试证:)()(11ξξ−−→F F Pn. 证:因F (x ) 为连续的分布函数,有F (−∞) = 0,F (+∞) = 1,则对任意的h > 0,存在M > 0,使得21)(h M F −>,2)(h M F <−, 因F (x ) 是连续、严格单调函数,有F −1( y ) 也是连续、严格单调函数, 可得F −1( y ) 在区间 [F (− M − 1), F (M + 1)] 上一致连续, 对任意的ε > 0,存在δ > 0,当y , y * ∈ [F (− M − 1), F (M + 1)] 且 | y − y * | < δ 时,| F −1( y ) − F −1( y *) | < ε, 设y * 是 [F (−M ), F (M )] 中任一点,记x * = F −1( y *),有x * ∈ [−M , M ],不妨设0 < ε < 1, 则对任意的x 若满足 ε≥−|*|x x ,就有 δ≥−|*)(|y x F ,根据本节第7题的结论知,{F n (x )} 在 (−∞, +∞) 上一致收敛于分布函数F (x ), 则对δ > 0和任意实数x ,总存在N > 0,当n > N 时,都有 | F n (x ) − F (x ) | < δ, 因当n > N 时,δ<−|)()(|x F x F n 且δ≥−|*(|y x F ,有*)(y x F n ≠,即*)(1y F x n −≠, 则对任意的0 < ε < 1,当n > N 时,*)(1y F n −满足ε<−=−−−−|*)(*)(||**)(|111y F y F x y F n n , 可得对任意的0 < ε < 1,当n > N 时,h M F M F P F F P n −>−∈≥<−−−1)]}(),([{}|)()({|11ξεξξ由h 的任意性可知1}|)()({|lim 11=<−−−+∞→εξξF F P n n ,故)()(11ξξ−−→F F Pn.17.设随机变量序列{X n }独立同分布,数学期望、方差均存在,且E (X n ) = µ,试证:µP n k k X k n n →⋅+∑=1)1(2.证:令∑=⋅+=nk k n X k n n Y 1)1(2,并设Var (X n ) = σ 2, 因µµµ=+⋅+=+=∑=)1(21)1(2)1(2)(1n n n n k n n Y E nk n , 且222212222)1(324)12)(1(61)1(4)1(4)Var(σσσ++=++⋅+=+=∑=n n n n n n n n k n n Y nk n , 则由切比雪夫不等式可得,对任意的ε > 0,222)1(3241)Var(1}|{|1σεεεµ++−=−≥<−≥n n n Y Y P n n , 因1)1(3241lim 22=⎥⎦⎤⎢⎣⎡++−+∞→σεn n n n ,由夹逼准则可得1}|{|lim =<−+∞→εµn n Y P , 故µP n k kn X k n n Y →⋅+=∑=1)1(2. 18.设随机变量序列{X n }独立同分布,数学期望、方差均存在,且E (X n ) = 0,Var (X n ) = σ 2.试证:E (X n ) = 0,Var (X n ) = σ 2.试证:2121σP n k k X n →∑=. 注:此题与第19题应放在习题4.3中,需用到4.3节介绍的辛钦大数定律.证:因随机变量序列}{2n X 独立同分布,且222)]([)Var()(σ=+=n n n X E X X E 存在,故}{2nX 满足辛钦大数定律条件,}{2nX 服从大数定律,即2121σP n k k X n →∑=.19.设随机变量序列{X n }独立同分布,且Var (X n ) = σ 2存在,令∑==n i i X n X 11,∑=−=n i i n X X n S 122)(1.试证:22σPnS →.证:2122112122122121)2(1)(1X X n X n X X X n X X X X n X X n S n i i ni i n i i n i i i n i i n−=⎟⎟⎠⎞⎜⎜⎝⎛+−=+−=−=∑∑∑∑∑=====,设E(X n ) = µ,{X n }满足辛钦大数定律条件,{X n }服从大数定律,即µP nk k X n X →=∑=11,则根据本节第2题第(2)小问的结论知,22µPX →,因随机变量序列}{2n X 独立同分布,且2222)]([)Var()(µσ+=+=n n n X E X X E 存在,则}{2nX 满足辛钦大数定律条件,}{2nX 服从大数定律,即22121µσ+→∑=P n k k X n ,故根据本节第2题第(1)小问的结论知,22222122)(1σµµσ=−+→−=∑=P n i i nX X n S .20.将n 个编号为1至n 的球放入n 个编号为1至n 的盒子中,每个盒子只能放一个球,记⎩⎨⎧=.,0;,1反之的盒子的球放入编号为编号为i i X i 且∑==ni i n X S 1,试证明:0)(Pn n n S E S →−. 证:因n X P i 1}1{==,nX P i 11}0{−==,且i ≠ j 时,)1(1}1{−==n n X X P j i ,)1(11}0{−−==n n X X P j i , 则n X E i 1)(=,⎟⎠⎞⎜⎝⎛−=n n X i 111)Var(, 且i ≠ j 时,)1(1)(−=n n X X E j i ,)1(11)1(1)()()(),Cov(22−=−−=−=n n n n n X E X E X X E X X j i j i j i , 有1)()(1==∑=ni i n X E S E ,1)1(1)1(11),Cov(2)Var()Var(211=−⋅−+−=+=∑∑≤<≤=n n n n n X X X S nj i j i ni i n , 可得0)]()([1)(=−=⎥⎦⎤⎢⎣⎡−n n n n S E S E n n S E S E ,221)Var(1)(Var n S n n S E S n n n ==⎥⎦⎤⎢⎣⎡−, 由切比雪夫不等式,可得对任意的ε > 0,2221)(Var 1)()(εεεn n S E S n S E S E n S E S P n n n n n n =⎥⎦⎤⎢⎣⎡−≤⎭⎬⎫⎩⎨⎧≥⎥⎦⎤⎢⎣⎡−−−, 则01lim )()(lim 022=≤⎭⎬⎫⎩⎨⎧≥⎥⎦⎤⎢⎣⎡−−−≤+∞→+∞→εεn n S E S E n S E S P n n n n n n , 故0)(Pn n nS E S →−.习题4.21. 设离散随机变量X 的分布列如下,试求X 的特征函数.1.02.03.04.03210PX解:特征函数ϕ (t ) = e it ⋅ 0 × 0.4 + e it ⋅ 1 × 0.3 + e it ⋅ 2 × 0.2 + e it ⋅ 3 × 0.1 = 0.4 + 0.3 e it + 0.2 e 2it + 0.1 e 3it .2. 设离散随机变量X 服从几何分布P {X = k } = (1 − p ) k − 1 p , k = 1, 2, … .试求X 的特征函数.并以此求E (X ) 和Var (X ). 解:特征函数ititk k ititk k itk p p p p p p t e)1(1e )]1([ee)1(e )(1111−−=−=−⋅=∑∑+∞=−+∞=−ϕ; 因22]e )1(1[e ]e )1(1[]e )1([e ]e )1(1[e )(it it it it it it it p ip p i p p p i p t −−=−−⋅−−⋅−−−⋅⋅=′ϕ,有)()0(2X iE pip ip ===′ϕ,故pX E 1)(=; 因332]e )1(1[]e )1(1[e ]e )1([]e )1(1[e 2]e )1(1[e )(it it it itit itit itp p p i p p ip p i ip t −−−+−=⋅−−⋅−−−−−⋅⋅=′′−−ϕ, 有)(2)2()0(2223X E i pp p p p =−−=−−=′′ϕ,可得222)(p p X E −=, 故222112)Var(p pp p p X −=⎟⎟⎠⎞⎜⎜⎝⎛−−=. 3. 设离散随机变量X 服从巴斯卡分布rk r p p r k k X P −−⎟⎟⎠⎞⎜⎜⎝⎛−−==)1(11}{,k = r , r + 1, …试求X 的特征函数.解:特征函数∑∑+∞=−−+∞=−−+−−−=−⎟⎟⎠⎞⎜⎜⎝⎛−−⋅=r k r k it r k itr r r k r k r itkp r k k r p p p r k t )(e)1)(1()1()!1(e )1(11e )(L ϕ ∑∑+∞=−=−−−+∞=−=−−=+−−−=r k p x r k r r it rk p x r k r it ititdx x d r p x r k k r p e )1(111e )1()()!1()e ()1()1()!1()e (L itit it p x r r it p x r r r it p x k k r r r it x r r p x dx d r p x dx d r p e )1(e )1(11e )1(1111)1()!1()!1()e (11)!1()e ()!1()e (−=−=−−−=+∞=−−−−−⋅−=⎟⎠⎞⎜⎝⎛−⋅−=⎟⎟⎠⎞⎜⎜⎝⎛⋅−=∑rit itr it r it p p p p ⎥⎦⎤⎢⎣⎡−−=−−=e )1(1e ]e )1(1[)e (. 4. 求下列分布函数的特征函数,并由特征函数求其数学期望和方差.(1))0(,e 2)(||1>=∫∞−−a dt a x F x t a ; (2))0(,1π)(222>+=∫∞−a dt at a x F x . 解:(1)因密度函数||11e 2)()(x a ax F x p −=′=,故⎥⎥⎦⎤⎢⎢⎣⎡−++=⎥⎦⎤⎢⎣⎡+=⋅=+∞−∞−+∞+−∞−+∞+∞−−∫∫∫0)(0)(0)(0)(||1e e 2e e 2ee 2)(ait a it a dx dx a dx a t x a it x a it x a it x a it x a itx ϕ 222112at a a it a it a +=⎟⎠⎞⎜⎝⎛−−+=; 因222222221)(22)()(a t ta t a t a t +−=⋅+−=′ϕ,有)(0)0(1X iE ==′ϕ, 故E (X ) = 0;因32242242222222221)(26)(2)(22)(2)(a t a t a a t t a t t a a t a t +−=+⋅+⋅−+⋅−=′′ϕ, 有)(22)0(222641X E i a a a =−=−=′′ϕ,可得222)(a X E =, 故222202)Var(aa X =−=;(2)因密度函数22221π)()(ax a x F x p +⋅=′=, 则∫+∞∞−+⋅=dx a x a t itx 2221e π)(ϕ, 由第(1)小题的结论知∫∞+∞−=+=dx x p a t a t itx )(e )(12221ϕ,根据逆转公式,可得∫∫∞+∞−−∞+∞−−−+⋅===dt at a dt t a x p itx itx x a 2221||1e π21)(e π21e 2)(ϕ, 可得||||222e πe 2π21e y a y a itya a a dt a t −−−+∞∞−=⋅=+⋅∫, 故||||222e e ππ1e π)(t a t a itx a a dx ax a t −−+∞∞−=⋅=+⋅=∫ϕ; 因⎩⎨⎧>−<=′−,0,e ,0,e )(2t a t a t atat ϕ 有a a −=+′≠=−′)00()00(22ϕϕ,即)0(2ϕ′不存在, 故E (X ) 不存在,Var (X ) 也不存在.5. 设X ~ N (µ, σ 2),试用特征函数的方法求X 的3阶及4阶中心矩. 解:因X ~ N (µ, σ 2),有X 的特征函数是222e)(t t i t σµϕ−=,则)(e)(2222t i t t t i σµϕσµ−⋅=′−,)(e)(e )(222222222σσµϕσµσµ−⋅+−⋅=′′−−t t i t t i t i t ,因)()(3e)(e)(2223222222σσµσµϕσµσµ−⋅−⋅+−⋅=′′′−−t i t i t t t i t t i ,有ϕ″′(0) = e 0 ⋅ (i µ )3 + e 0 ⋅ 3i µ ⋅ (−σ 2) = − i µ 3 − 3i µσ 2 = i 3E (X 3) = − i E (X 3), 故E (X 3) = µ 3 + 3µσ 2; 又因2222222422)4()(3e)()(6e)(e)(222222σσσµσµϕσµσµσµ−⋅+−⋅−⋅+−⋅=−−−t t i t t i t t i t i t i t ,有ϕ (4)(0) = e 0 ⋅ (i µ )4 + e 0 ⋅ 6(i µ)2 ⋅ (−σ 2) + e 0 ⋅ 3σ 4 = µ 4 + 6µ 2σ 2 + 3σ 4 = i 4E (X 4) = E (X 4), 故E (X 4) = µ 4 + 6µ 2σ 2 + 3σ 4.6. 试用特征函数的方法证明二项分布的可加性:若X ~ b (n , p ),Y ~ b (m , p ),且X 与Y 独立,则X + Y ~ b (n + m , p ).证:因X ~ b (n , p ),Y ~ b (m , p ),且X 与Y 独立,有X 与Y 的特征函数分别为ϕ X (t ) = ( p e it + 1 − p ) n ,ϕ Y (t ) = ( p e it + 1 − p ) m , 则X + Y 的特征函数为ϕ X + Y (t ) = ϕ X (t ) ⋅ϕ Y (t ) = ( p e it + 1 − p ) n + m ,这是二项分布b (n + m , p )的特征函数, 故根据特征函数的唯一性定理知X + Y ~ b (n + m , p ).7. 试用特征函数的方法证明泊松分布的可加性:若X ~ P (λ1),Y ~ P (λ2),且X 与Y 独立,则X + Y ~ P (λ1 + λ2).证:因X ~ P (λ1),Y ~ P (λ2),且X 与Y 独立,有X 与Y 的特征函数分别为)1(e1e )(−=itt X λϕ,)1(e2e )(−=itt Y λϕ,则X + Y 的特征函数为)1)(e(21e )()()(−++==itt t t Y X Y X λλϕϕϕ,这是泊松分布P (λ1 + λ2)的特征函数,故根据特征函数的唯一性定理知X + Y ~ P (λ1 + λ2).8. 试用特征函数的方法证明伽马分布的可加性:若X ~ Ga (α1, λ),Y ~ Ga (α2, λ),且X 与Y 独立,则X + Y ~ Ga (α1 + α2 , λ).证:因X ~ Ga (α1, λ),Y ~ Ga (α2, λ),且X 与Y 独立,有X 与Y 的特征函数分别为11)(αλϕ−⎟⎠⎞⎜⎝⎛−=it t X ,21)(αλϕ−⎟⎠⎞⎜⎝⎛−=it t Y ,则X + Y 的特征函数为)(211)()()(ααλϕϕϕ+−+⎟⎠⎞⎜⎝⎛−==it t t t Y X Y X ,这是伽马分布Ga (α1 + α2 , λ)的特征函数,故根据特征函数的唯一性定理知X + Y ~ Ga (α1 + α2 , λ).9. 试用特征函数的方法证明χ 2分布的可加性:若X ~ χ 2 (n ),Y ~ χ 2 (m ),且X 与Y 独立,则X + Y ~ χ 2 (n + m ).证:因X ~ χ 2 (n ),Y ~ χ 2 (m ),且X 与Y 独立,有X 与Y 的特征函数分别为2)21()(n X it t −−=ϕ,2)21()(m Y it t −−=ϕ,则X + Y 的特征函数为2)21()()()(m n Y X Y X it t t t +−+−==ϕϕϕ,这是χ 2分布χ 2 (n + m )的特征函数,故根据特征函数的唯一性定理知X + Y ~ χ 2 (n + m ).10.设X i 独立同分布,且X i ~ Exp(λ),i = 1, 2, …, n .试用特征函数的方法证明:),(~1λn Ga X Y ni i n ∑==.证:因X i ~ Exp (λ),i = 1, 2, …, n ,且X i 相互独立,有X i 的特征函数为11)(−⎟⎠⎞⎜⎝⎛−=−=λλλϕit it t i X ,则∑==ni i n X Y 1的特征函数为nni X Y it t t i n −=⎟⎠⎞⎜⎝⎛−==∏λϕϕ1)()(1,这是伽马分布Ga (n , λ)的特征函数,故根据特征函数的唯一性定理知Y n ~ Ga (n , λ).11.设连续随机变量X 的密度函数如下:+∞<<∞−−+⋅=x x x p ,)(π1)(22µλλ, 其中参数λ > 0, −∞ < µ < +∞,常记为X ~ Ch (λ, µ ).(1)试证X 的特征函数为exp{i µ t − λ | t |},且利用此结果证明柯西分布的可加性; (2)当µ = 0, λ = 1时,记Y = X ,试证ϕ X + Y (t ) = ϕ X (t ) ⋅ϕ Y (t ),但是X 与Y 不独立;(3)若X 1, X 2, …, X n 相互独立,且服从同一柯西分布,试证:)(121n X X X n+++L 与X 1同分布. 证:(1)根据第4题第(2)小题的结论知:若X *的密度函数为22π1)(*xx p +⋅=λλ,即X * ~ Ch (λ, 0), 则X *的特征函数为ϕ * (t ) = e −λ | t |,且X = X * + µ 的密度函数为22)(π1)(µλλ−+⋅=x x p , 故X 的特征函数为ϕ X (t ) = e i µ t ϕ * (t ) = e i µ t ⋅ e −λ | t | = e i µ t −λ | t |; 若X 1 ~ Ch (λ1, µ1),X 2 ~ Ch (λ2, µ2),且相互独立,有X 1与X 2的特征函数分别为||111e )(t t i X t λµϕ−=,||222e )(t t i X t λµϕ−=, 则X 1 + X 2的特征函数为||)()(21212121e )()()(t t i X X X X t t t λλµµϕϕϕ+−++==,这是柯西分布Ch (λ1 + λ2, µ1 + µ2)的特征函数,故根据特征函数的唯一性定理知X 1 + X 2 ~ Ch (λ1 + λ2, µ1 + µ2); (2)当µ = 0, λ = 1时,X ~ Ch (1, 0),有X 的特征函数为ϕ X (t ) = e −| t |,又因Y = X ,有Y 的特征函数为ϕ Y (t ) = e −| t |,且X + Y = 2X ,故X + Y 的特征函数为ϕ X + Y (t ) = ϕ 2X (t ) = ϕ X (2t ) = e −| 2t | = e −| t | ⋅ e −| t | =ϕ X (t ) ⋅ϕ Y (t ); 但Y = X ,显然有X 与Y 不独立;(3)因X i ~ Ch (λ, µ ),i = 1, 2, …, n ,且X i 相互独立,有X i 的特征函数为||e )(t t i X t i λµϕ−=, 则)(121n n X X X nY +++=L 的特征函数为 )(e e )()(1||111t n t t t X t t i n t n ti n ni X ni X nY i in ϕϕϕϕλµλµ===⎟⎠⎞⎜⎝⎛==−⎟⎟⎠⎞⎜⎜⎝⎛⋅−⋅==∏∏,故根据特征函数的唯一性定理知)(121n X X X n+++L 与X 1同分布. 12.设连续随机变量X 的密度函数为p (x ),试证:p (x ) 关于原点对称的充要条件是它的特征函数是实的偶函数.证:方法一:根据随机变量X 与−X 的关系充分性:设X 的特征函数ϕ X (t )是实的偶函数,有ϕ X (t ) = ϕ X (−t ),则−X 的特征函数ϕ −X (t ) = ϕ X (−t ) = ϕ X (t ),根据特征函数的唯一性定理知−X 与X 同分布,因X 的密度函数为p (x ),有−X 的密度函数为p (−x ),故由−X 与X 同分布可知p (−x ) = p (x ),即p (x ) 关于原点对称; 必要性:设X 的密度函数p (x ) 关于原点对称,有p (−x ) = p (x ), 因−X 的密度函数为p (−x ),即−X 与X 同分布,则−X 的特征函数ϕ −X (t ) = ϕ X (−t ) = ϕ X (t ),且)(][e ][e ][e )()()(t E E E t t X itX itX X it X X ϕϕϕ=====−−−, 故X 的特征函数ϕ X (t )是实的偶函数. 方法二:根据密度函数与特征函数的关系充分性:设连续随机变量X 的特征函数ϕ X (t )是实的偶函数,有ϕ X (t ) = ϕ X (−t ),因∫+∞∞−−=dt t x p itx )(e π21)(ϕ,有∫∫+∞∞−+∞∞−−−==−dt t dt t x p itxx it )(e π21)(e π21)()(ϕϕ, 令t = −u ,有dt = −du ,且当t → −∞时,u → +∞;当t → +∞时,u → −∞,则)()(e π21)(e π21))((e π21)()(x p du u du u du u x p iuxiux x u i ==−=−−=−∫∫∫+∞∞−−+∞∞−−−∞∞+−ϕϕϕ, 故p (x ) 关于原点对称;必要性:设X 的密度函数p (x ) 关于原点对称,有p (−x ) = p (x ),因∫+∞∞−−==dx x p E t itxitX)(e )(e)(ϕ,有∫∫+∞∞−−+∞∞−−==−dx x p dx x p t itx xt i )(e )(e)()(ϕ,令x = −y ,有dx = −dy ,且当x → −∞时,y → +∞;当x → +∞时,y → −∞, 则)()(e )(e ))((e )()(t dy y p dy y p dy y p t X ity ity y it X ϕϕ==−=−−=−∫∫∫+∞∞−+∞∞−−∞∞+−−,且)(][e ][e ][e )()()(t E E E t t X itX itX X t i X X ϕϕϕ====−=−−, 故X 的特征函数ϕ X (t )是实的偶函数.13.设X 1, X 2, …, X n 独立同分布,且都服从N(µ , σ 2)分布,试求∑==ni i X n X 11的分布.证:因X i ~ N (µ , σ 2),i = 1, 2, …, n ,且X i 相互独立,有X i 的特征函数为222e)(t t i X t i σµϕ−=,则∑==n i i X n X 11的特征函数为nt t i n t n t i n ni X n i X n X n t t t i i 2211112222ee)()(σµσµϕϕϕ−⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛−⋅====⎟⎠⎞⎜⎝⎛==∏∏,这是正态分布⎟⎟⎠⎞⎜⎜⎝⎛n N 2,σµ的特征函数,故根据特征函数的唯一性定理知⎟⎟⎠⎞⎜⎜⎝⎛=∑=n N X n X ni i 21,~1σµ. 14.利用特征函数方法证明如下的泊松定理:设有一列二项分布{b (k , n , p n )},若λ=→∞n n np lim ,则L ,2,1,0,e !),,(lim ==−∞→k k p n k b kn n λλ.证:二项分布b (n , p n )的特征函数为ϕ n (t ) = ( p n e it + 1 − p n ) n = [1 + p n (e it − 1)] n ,且n → ∞时,p n → 0,因)1(e)1(e )1(e 1e )]1(e 1[lim )]1(e 1[lim )(lim −−⋅−→→∞→∞=−+=−+=itit n it n n np p itn p n it n n n n p p t λϕ,。
第四章 课后习题及答案

第四章中学生学习心理课后习题及答案一、理论测试题(一)单项选择题1.当人从黑暗走入亮处后,视网膜的光感受阈限会迅速提高,这个过程是()。
A.适应B.对比C. 明适应D.暗适应2.人的视觉、听觉、味觉等都属于( )。
A.外部感觉B.内部感觉C.本体感觉D.机体感觉3.在热闹的聚会上或逛自由市场时,如果你与朋友聊天,朋友说话时的某个字可能被周围的噪音覆盖,但你还是知道你的朋友在说什么,这是知觉的()在起作用。
A、选择性B、整体性C、恒常性D、理解性4. 知觉的条件在一定范围改变时,知觉映像却保持相对稳定,这是知觉的()。
A.选择性B.整体性C.恒常性D.理解性5.大教室上课,教师借用扩音设备让全体学生清晰感知,这依据感知规律的()。
A.差异率B.强度率C.活动率D.组合率6.“万绿丛中一点红”容易引起人们的无意注意,这主要是由于刺激物具有()。
A.强度的特点B.新异性的特点C.变化的特点D.对比的特点7.小学低年级学生注意了写字的间架结构,就忽略了字的笔画,注意了写字而忘了正确的坐姿,原因是这个年龄阶段的学生()发展水平较低。
A.注意的广度B.注意的稳定性C.注意的分配D.注意的转移8.“视而不见,听而不闻”的现象,典型地表现了()。
A.注意的指向性B.注意的集中性C.注意的稳定性D.注意的分配性9.一种记忆特点是信息的保存是形象的,保存的时间短、保存量大,编码是以事物的物理特性直接编码,这种记忆是()。
A.短时记忆B.感觉记忆C.长时记忆D.动作记忆10.我们常常有这样的经验,明明知道对方的名字,但想不起来,这印证了遗忘的()。
A.干扰说B.消退说C.提取失败说D.压抑说11.学习后立即睡觉,保持的效果往往比学习后继续活动保持的效果要好,这是由于()。
A.过度学习B.记忆的恢复现象C.无倒摄抑制的影响D.无前摄抑制的影响12.遇见小时候的同伴,虽然叫不出他(她)的姓名,但确定是认识的,此时的心理活动是()。
《宏观经济学》课后练习题参考答案4
第四章货币与通货膨胀一、选择题二、名词解释1、M1与M2:都是美联储计算货币存量的指标,M1是指通货加活期存款、旅行支票和其它支票性存款,被称为狭义的货币;M2是指加货币市场基金余额、储蓄存款以及小额定期存款,被称为广义的货币。
M1具有完全的流动性,但没有利息。
M2有利息但不具有完全的流动性。
M1与经济关联性强,而M2与货币政策关联性强。
2、货币需求函数:(1)货币需求函数是为了分析货币需求量的决定因素及其变动规律而建立的一种函数关系。
通常将决定和影响货币需求的各种因素作为自变量,而将货币需求本身作为因变量。
(2)比较典型的货币需求函数有:①传统货币数量论的交易方程式:PV=MY,其中M为货币数量,V为货币流通速度,P为一般物价水平,Y为实际国民收入;②剑桥方程式:M= kPY,其中M为货币数量,k为以货币形式持有的国民收入的比例,P为一般物价水平,Y为实际国民收入;③凯恩斯的货币需求函数:L=L1(Y)+L2(i)。
其中由交易动机和预防动机而产生的货币需求用L1表示,是收入Y的递增函数,即L1=L1(Y);投机性货币需求L2则与利率有关,是利率的递减函数,即L2=L2(i);④弗里德曼的货币需求函数:M=f{P,r b,r c,1/P·dP/dt,w,y,u},其中,M表示名义货币量,P表示价格水平,r b表示债券的预期收益率,r c表示股票的预期收益率,1/P·dP/dt表示物价的预期变动率,w表示人力财富与非人力财富的比率,y表示货币收入,u为其他随机因素。
3、数量方程式:数量方程式是用来表示交易量与货币之间的关系的方程。
它有以下表示形式:MV=PT式中,M为流通中的货币数量,V为货币的流通速度,P为一般物价水平,T为社会总交易额。
交易方程式直观地表示了流通中的货币数量与一般物价水平之间的关系。
如果用Y代表实际GDP,P是GDP平减指数,而PY是名义GDP,数量方程式变为MV=PY。
大学物理学课后习题4第四章答案
x 轴正方向运动,代表此简谐振动的旋转矢量图为
()
[答案:B]
(2)两个同周期简谐振动曲线如图所示,振动曲线 1 的相位比振动曲线 2
的相位 (
)
(A)落后
2
(B)超前
2
(C)落后
(D)超前
[答案: B]
习题 4.1(2)图
(3)一质点作简谐振动的周期是 T,当由平衡位置向 x 轴正方向运动时,从
E
1 2
mvm2
3.16 102 J
E p E k 1 E 1.58102 J 2
当 Ek E p 时,有 E 2E p ,
即
1 kx 2 1 ( 1 kA2 )
2
22
∴
x 2 A 2m
2
20
(3)
(t2 t1 ) 8 (5 1) 32
4.4 一个沿 x 轴作简谐振动的弹簧振子,振幅为 A ,周期为T ,其振动 方程用余弦函数表示.如果 t 0 时质点的状态分别是:
的单位是 s,则 (A)波长为 5m
向传播 [答案:C]
(B)波速为 10ms-1
(C)周期为 1 s 3
(D)波沿 x 正方
(8)如图所示,两列波长为 的相干波在 p 点相遇。波在 S1 点的振动初相是 1 ,点 S1 到点 p 的距离是 r1。波在 S2 点的振动初相是2 ,点 S2 到点 p 的距离是
(A)它的动能转化为势能. (B)它的势能转化为动能. (C)它从相邻的一段质元获得能量其能量逐渐增大. (D)它把自己的能量传给相邻的一段质元,其能量逐渐减小.
[答案:D]
4.2 填空题 (1)一质点在 X 轴上作简谐振动,振幅 A=4cm,周期 T=2s,其平衡位置
分析化学 第四章 酸碱滴定法(课后习题答案)

KW Ka
c sp
1.0 10-14 1.7 10-5
0.05
5.4 10-6
mol
/
L
pOH 5.27
pH=8.73
②林邦误差公式
H 6.31010mol / L, OH 1.6105mol / L, csp 0.05mol / L
2
pH 9.20 8.73 0.47
TE% 10pH 10-pH 100%
第二计量点时,酚羟基被中和,消耗标准溶液:5.19-3.58=1.61(ml)
0.1790 5.19 3.58 188.0
1-羟基-α-萘酸%=
1000 100% 38.64%
0.1402
0.1790 3.58 1.61 172.0
α-萘酸%=
1000 100% 43.26%
0.1402
9. 解:
pH 2.00
pOH 14.00 2.00 12.00
HClO4 在乙醇中:
C2
H5OH
2
0.0100mol
/
L
pC2H5OH2 2.00
pC2H5O 19.10 2.00 17.10 5. 解: ①
W
c V NaOH NaOH
M HA 1000
M HA
W 1000 c V NaOH NaOH
3
第四章 酸碱滴定法(答案) 1. 答: ①滴定强酸,可以完全反应,对结果没有影响。 ②滴定弱酸,NaOH 能中和弱酸,Na2CO3 不能中和弱酸,需要消耗更多的标准 溶液,将带来正误差,导致分析结果偏高。 2. 答:硼砂(Na2B4O7·10H2O)为 H3BO3 和 H2BO3 的混合物,硼酸的 pKa1 9.27 ,
数据结构课后习题答案第四章

第四章串一、单项选择题1.B2. B3.B4.C5. C二、填空题1.空、字符2.由空格字符(ASCII值32)所组成的字符串空格个数3.长度、相等、子、主4.55.011223126.(1)char s[ ] (2) j++ (3) i >= j7.[题目分析]本题算法采用顺序存储结构求串s和串t的最大公共子串。
串s用i指针(1<=i<=s.len)。
t串用j指针(1<=j<=t.len)。
算法思想是对每个i(1<=i<=s.len,即程序中第一个WHILE循环),来求从i开始的连续字符串与从j(1<=j<=t.len,即程序中第二个WHILE循环)开始的连续字符串的最大匹配。
程序中第三个(即最内层)的WHILE循环,是当s中某字符(s[i])与t中某字符(t[j])相等时,求出局部公共子串。
若该子串长度大于已求出的最长公共子串(初始为0),则最长公共子串的长度要修改。
(1) i+k<=s.len && j+k<=t.len && s[i+k]==t[j+k] //所有注释同上(a)(2) con=0 (3) j+=k (4) j++ (5) i++三、应用题1.空格是一个字符,其ASCII码值是32。
空格串是由空格组成的串,其长度等于空格的个数。
空串是不含任何字符的串,即空串的长度是零。
2.(a)A+B “ mule”(b)B+A “mule ”(c)D+C+B “myoldmule”(d)SUBSTR(B,3,2) “le”(e)SUBSTR(C,1,0) “”(f)LENGTH(A) 2(g)LENGTH(D) 2(h)INDEX(B,D) 0(i)INDEX(C,”d”) 3(j)INSERT(D,2,C) “myold”(k)INSERT(B,1,A) “m ule”(l)DELETE(B,2,2) “me”(m)DELETE(B,2,0) “mule”3.朴素的模式匹配(Brute-Force)时间复杂度是O(m*n),KMP算法有一定改进,时间复杂度达到O(m+n)。
高等数学课后习题及参考答案(第四章)

高等数学课后习题及参考答案(第四章)习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231. (3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx xx 21;解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x m n m C x mn dx x dx x mn m m nm nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx xx 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224.(15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx xe e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532; 解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ;解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解 设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|C =2C ,C =3-2=1. 于是所求曲线的方程为 y =ln|x | 1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少? (2)物体走完360m 需要多少时间?解 设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e x ch x 都是x x e xsh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x e x ch x =e x (sh x ch x )x xx x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x e x sh x =e x (ch x sh x )x xx x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x xe d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332xdx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d xdx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2. (11)⎰-+dx e e xx 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ; 解 )sin cos (cos sin 1cos sin cos sin 33x x d x x dx x x x x +--=-+⎰⎰ C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx xx 239; 解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1.(23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a xa x a C t a t a +--=+-=222222arcsin 22sin 421. (35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+xdx 21;解C x x C t t dt t tdt t t x xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan . (40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解 因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解 因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x 23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d xx x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x x x x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解 因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233 ⎰⎰+-+-=dx x dx x x 3127)93(2 C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458; 解 ⎰⎰⎰--++++=--+dx xx x x dx x x dx x x x x 3223458)1(8 ⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解 ⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C xx dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222.8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u xu dx x221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u xu dx x221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17.⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dx x x )122(221111111令 C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4xx dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解 令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxxx x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx .解 令u x x =-+311, 则1133-+=u u x , 232)1(6--=u udx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662.4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解 C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln .6.⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9.⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解 因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax ax axax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e ba ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e edx xx)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x x dx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12.16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a++=tan 1tan 31434C xa x ax a x a+-+-⋅=224322341)(31.17.⎰+241xxdx;解tdt t t tx x xdx 2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx . 24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444.25.⎰-416x dx;解⎰⎰⎰++-=+-=-dx x x dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx xxx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x e x23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x ex x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dx x x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x x C t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C ee x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xd e d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x xxxde e ee x )111(1 C e e e xx x x ++-++-=)1ln(ln 1C e e xe x x x++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ;解 因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t t x dx x 2232/321sin cos sec sec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx x x xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章网络基础知识与Internet应用一、单项选择题二、填空题1.局域网、城域网、广域网或LAN、MAN、WAN2. C、A、C3. 127.0.0.1(本机)、255.255.255.255(限制广播)、0.0.0.0(广播)4. Electronic Commerce, EC5.B2B、B2C6. Instrumented:物联化Interconnected:互联化Intelligent:智能化7.感知层、网络层、应用层8.接入(网络层)、应用(业务层)9.硬件系统、软件系统10.不可否任性三、简答题1. 计算机网络发展包括四个阶段:第一,面向终端的计算机网络;第二,计算机-计算机网络;第三,开放标准网络阶段;第四,因特网与高速计算机网络阶段。
各阶段的特点:第一,面向终端的计算机网络:以单个计算机为中心的远程联机系统,构成面向终端的计算机网络。
第二,计算机-计算机网络:由若干个计算机互联的系统,组成了“计算机-计算机”的通信时代,呈现出多处理中心的特点。
第三,开放标准网络阶段:由于第二阶段出现的计算机网络都各自独立,不相互兼容。
为了使不同体系结构的计算机网络都能互联,国际标准化组织ISO提出了一个能使各种计算机在世界范围内互联成网的标准框架―开放系统互连基本参考模型OSI。
第四,因特网与高速计算机网络阶段:采用高速网络技术,综合业务数字网的实现,多媒体和智能型网络的兴起。
2.TCP/IP网络使用32位长度的地址以标识一台计算机和同它相连的网络,它的格式为:IP 地址=网络地址+ 主机地址。
标准IP地址是通过它的格式分类的,它有四种格式:A类、B类、C类、D类。
3. 电子商务所涵盖的业务范围包括:信息传递与交流;售前及售后服务;网上交易;网上支付或电子支付;运输;组建虚拟企业。
4. 包括banner(网幅广告)、button广告、文字链接广告、弹出式广告(pop up window)及其它形式(如移动logo、网上分类广告等)。
其中banner广告是主流形式,也被认为是最有效的。
5. 国际电信联盟( ITU)对物联网做了如下定义:通过二维码识读设备、射频识别(RFID) 装置、红外感应器、全球定位系统和激光扫描器等信息传感设备,按约定的协议,把任何物品与互联网相连接,进行信息交换和通信,以实现智能化识别、定位、跟踪、监控和管理的一种网络。
这里的“物”要满足以下条件才能够被纳入“物联网”的范围:1、要有相应信息的接收器;2、要有数据传输通路;3、要有一定的存储功能;4、要有CPU;5、要有操作系统;6、要有专门的应用程序;7、要有数据发送器;8、遵循物联网的通信协议;9、在世界网络中有可被识别的唯一编号。
四、操作题当当网购物流程图1、搜索商品当当网为您提供了方便快捷的商品搜索功能:(1)您可以通过在首页输入关键字的方法来搜索您想要购买的商品(2)您还可以通过当当的分类导航栏来找到您想要购买的商品分类,根据分类找到您的商品(3)观看搜索商品演示2、放入购物车在您想要购买的商品的详情页点击“购买”,商品会添加到您的购物车中;您还可以继续挑选商品放入购物车,一起结算。
(1)在购物车中,系统默认每件商品的订购数量为一件,如果您想购买多件商品,可修改购买数量(2)在购物车中,您可以将商品移至收藏,或是选择删除(3)在购物车中,您可以直接查看到商品的优惠折和参加促销活动的商品名称、促销主题(4)购物车页面下方的商品是当当网根据您挑选的商品为您作出的推荐,若有您喜爱的商品,点击“放入购物车”即可温馨提示:(1)商品价格会不定期调整,最终价格以您提交订单后订单中的价格为准(2)优惠政策、配送时间、运费收取标准等都有可能进行调整,最终成交信息以您提交订单时网站公布的最新信息为准3、选择订单(1)当当网和商家的商品需要分别提交订单订购(2)不同商家的商品需要分别提交订单订购4、注册登陆(1)老顾客:请在“登陆”页面输入Email地址或昵称、注册密码进行登陆(2)新顾客:请在“新用户注册”页面按照提示完成注册5、填写收货人信息(1)请填写正确完整的收货人姓名、收货人联系方式、详细的收货地址和邮编,否则将会影响您订单的处理或配送(2)您可以进入“我的当当—帐户管理—收货地址簿”编辑常用收货地址,保存成功后,再订购时,可以直接选择使用6、选择收货方式当当网提供多种收货方式:(1)普通快递送货上门(2)加急快递送货上门(3)普通邮递(4)邮政特快专递(EMS)配送范围、时间及运费7、选择支付方式当当网提供多种支付方式,订购过程中您可以选择:(1)货到付款(2)网上支付(3)银行转帐(4)邮局汇款点击查看各种支付方式订单的支付期限8、索取发票请点击“索取发票”,填写正确的发票抬头、选择正确的发票内容,发票选择成功后,将于订单货物一起送达点击查看发票制度9、提交订单(1)以上信息核实无误后,请点击“提交订单”,系统生成一个订单号,就说明您已经成功提交订单(2)订单提交成功后,您可以登陆“我的当当”查看订单信息或为订单进行网上支付第5章多媒体技术基础一、单项选择题二、填空题1. 多媒体2.表示、传输媒体3. 多样性、交互性4.WAV、MP3、MID、APE5.视频、动画6. 16HZ~16KHZ7. 单轨录、多轨录音8. 视频播放、视频剪辑9. Adobe After Effects、会声会影10. 前期制作、后期制作三、简答题1.媒体的类型有哪些?各自具有什么特点?1、媒体有下列几类:感觉媒体、表示媒体、表现媒体、存储媒体、传输媒体;多媒体技术中的媒体指的是感觉媒体。
2.列举几种常见的静态图像文件格式,它们具有什么特点?答:1、BMP格式BMP是英文Bitmap(位图)的简写,它是Windows操作系统中的标准图像文件格式,能够被多种Windows应用程序所支持.随着Windows操作系统的流行与丰富的Windows应用程序的开发,BMP位图格式理所当然地被广泛应用.这种格式的特点是包含的图像信息较丰富,几乎不进行压缩,但由此导致了它与生俱生来的缺点--占用磁盘空间过大.所以,目前BMP 在单机上比较流行.2、JPEG格式JPEG也是常见的一种图像格式,它由联合照片专家组(Joint Photographic Experts Group)开发并以命名为"ISO 10918-1",JPEG仅仅是一种俗称而已.JPEG文件的扩展名为.jpg 或.jpeg,其压缩技术十分先进,它用有损压缩方式去除冗余的图像和彩色数据,获取得极高的压缩率的同时能展现十分丰富生动的图像,换句话说,就是可以用最少的磁盘空间得到较好的图像质量.同时JPEG还是一种很灵活的格式,具有调节图像质量的功能,允许你用不同的压缩比例对这种文件压缩,比如我们最高可以把1.37MB的BMP位图文件压缩至20.3KB.当然我们完全可以在图像质量和文件尺寸之间找到平衡点.由于JPEG优异的品质和杰出的表现,它的应用也非常广泛,特别是在网络和光盘读物上,肯定都能找到它的影子.目前各类浏览器均支持JPEG这种图像格式,因为JPEG格式的文件尺寸较小,下载速度快,使得Web页有可能以较短的下载时间提供大量美观的图像,JPEG同时也就顺理成章地成为网络上最受欢迎的图像格式.3、TIFF格式TIFF(Tag Image File Format)是Mac中广泛使用的图像格式,它由Aldus和微软联合开发,最初是出于跨平台存储扫描图像的需要而设计的.它的特点是图像格式复杂、存贮信息多.正因为它存储的图像细微层次的信息非常多,图像的质量也得以提高,故而非常有利于原稿的复制.该格式有压缩和非压缩二种形式,其中压缩可采用LZW无损压缩方案存储.不过,由于TIFF格式结构较为复杂,兼容性较差,因此有时你的软件可能不能正确识别TIFF文件(现在绝大部分软件都已解决了这个问题).目前在Mac和PC机上移植TIFF文件也十分便捷,因而TIFF现在也是微机上使用最广泛的图像文件格式之一.4、PSD格式这是著名的Adobe公司的图像处理软件Photoshop的专用格式Photoshop Document (PSD).PSD其实是Photoshop进行平面设计的一张"草稿图",它里面包含有各种图层、通道、遮罩等多种设计的样稿,以便于下次打开文件时可以修改上一次的设计.在Photoshop 所支持的各种图像格式中,PSD的存取速度比其它格式快很多,功能也很强大.由于Photoshop越来越被广泛地应用,所以我们有理由相信,这种格式也会逐步流行起来.5、PNG格式PNG(Portable Network Graphics)是一种新兴的网络图像格式.在1994年底,由于Unysis 公司宣布GIF拥有专利的压缩方法,要求开发GIF软件的作者须缴交一定费用,由此促使免费的png图像格式的诞生.PNG一开始便结合GIF及JPG两家之长,打算一举取代这两种格式.1996年10月1日由PNG向国际网络联盟提出并得到推荐认可标准,并且大部分绘图软件和浏览器开始支持PNG图像浏览,从此PNG图像格式生机焕发.PNG是目前保证最不失真的格式,它汲取了GIF和JPG二者的优点,存贮形式丰富,兼有GIF 和JPG的色彩模式;它的另一个特点能把图像文件压缩到极限以利于网络传输,但又能保留所有与图像品质有关的信息,因为PNG是采用无损压缩方式来减少文件的大小,这一点与牺牲图像品质以换取高压缩率的JPG有所不同;它的第三个特点是显示速度很快,只需下载1/64的图像信息就可以显示出低分辨率的预览图像;第四,PNG同样支持透明图像的制作,透明图像在制作网页图像的时候很有用,我们可以把图象背景设为透明,用网页本身的颜色信息来代替设为透明的色彩,这样可让图像和网页背景很和谐地融合在一起.PNG的缺点是不支持动画应用效果,如果在这方面能有所加强,简直就可以完全替代GIF和JPEG了.Macromedia公司的Fireworks软件的默认格式就是PNG.现在,越来越多的软件开始支持这一格式,而且在网络上也越来截止流行.3.图形和图像有何区别?答:图形是指由外部轮廓线条构成的向量图,有时还要使用实心或有等级变化和色彩填充的区域,如corel draw 产生的cdr 还有象autocad 产生的dwg,dxf,以及很常用的plt(特指hpgl)文件.它们的特点是:通常文件量较小,描述的对象可以任意缩放而不会失真,从本质上讲,它是由数学的坐标和公式来描述的,但一般只能描述轮廓不是非常复杂,色彩不是很丰富的对象,如几何图形,工程图纸等,否则文件量将变得很大,而效果却不理想.图像则是指由许多点阵构成的点位图,在特定的领域有时也称光栅图.如windows 画笔所产生的bmp,其他如gif,tiff,jpg等等.它的特点是:通常文件量较大,所描述得对象会因为缩放而损失细节或产生“锯齿”.它本质上是将对象以一定的分辨率分解后,再将每一个点的色彩信息进行数字化描述,它主要用来描述轮廓和色彩非常丰富的对象,如照片,绘画.它的重要参数是分辨率和色彩深度,根据每点的色彩深度可分位二值,灰度,256色,真彩等格式.图形和图像在一定的条件下是可以转化的.这种转化可以从两个方面来说明,第一是对象和输入输出设备之间的硬转化;第二是对象文件格式之间的软转化。
