二进制ASK调制matlab仿真代码

合集下载

ASK调制与解调的仿真

实验四ASK 调制与解调的仿真一．实验目的1．掌握幅度键控的原理，经过对仿真的过程和结果剖析，加深对其理解。

2.运用 MATLAB对 ASK的调制与解调过程进行仿真。

二．实验内容运用 MATLAB编程实现ASK调制解调过程，并且输出其调制后的波形，画出频谱、功率谱密度图，并比较各样调制的误码率状况，议论其调制成效。

三．软件纲要设计说明，功能模块及流程和工作原理ASK信号调制器的设计：产生二进制振幅键控信号的方法主要有两种：法 1：采纳相乘电路，用基带信号 A t 和载波 cos t 相乘就获得已调信号输出；法 2：采纳开关电路，这里的开关由输入基带信号 A t 控制，用这类方法能够获得相同的输出波形。

ASK 信号解调器的设计：ASK信号的解调方法有两种，即包络检波法和相关解调法，前者属于非相关解调。

此中解调的原理框图以下图。

依据 ASK调制的表达式可知：S2 ASK (t ) a n A cos c t综合式令A＝1，则ASK信号的一般时域表达式为：S 2ASK (t ) a n g(t nT s ) cos c tnS(t ) cos c t式中， T s 为码元间隔， g(t ) 为连续时间 Ts 2,Ts 2 内随意波形形状的脉冲（剖析时一般设为归一化矩形脉冲），而 S(t) 就是代表二进制信息的随机单极性脉冲序列。

依据 ASK 相关解调的表达式：z(t ) y(t) ?cos( c t) m(t ) ? cos 2 ( c t ) m(t) ? 1 [1 cos(2 c t)] 1 m(t) 1 m(t ) cos(2c t) 2 2 2此中第 1 项是基带信号，第 2 项是频次为 2 c 的高频信号，利用低通滤波器可检出基带信号，再经过抽样裁决，可恢复出原始信号序列。

四．软件详尽设计、重点技术与难点、测试数据用 MATLAB 编程以下：t=0::8; % 定义时间采样值y=sin(2*pi*t); % 定义未调信号的表达式x=[ones(1,100),zeros(1,100),ones(1,100),ones(1,100),zeros(1,100),zeros(1,100) ,ones(1,100),zeros(1,101)]; % 定义载波 X 的取值z=x.*y; % 定义已调信号的表达式subplot(3,1,1) % 画第一个图plot(t,x) % 画出载波图axis([0,8,,]) % 定义范围xlabel(' 时间 ') % 定义坐标轴的名字title(' 未调信号 '); % 定义图的名字subplot(3,1,2); % 画第二个图plot(t,y) % 画出调制信号图axis([0,8,,]) % 定义范围xlabel(' 时间 ') % 定义坐标轴的名字title('载波 ')%定义图的名字subplot(3,1,3)%画出第三个图plot(t,z)%画出解调后的图axis([0,8,,]) %定义范围xlabel('时间 ')%定义坐标轴的名字title('已调信号 ');%定义图的名字仿真结果：软件中主要包括有二进制信号的产生，调制信号的产生，调制信号的解调解画图部分。

2ASK调制与解调的MATALAB仿真

数字调制与解调2ASK的仿真概述：数字调制技术在通信系统中占有非常重要的地位，数字通信技术与MA TALAB的结合是现代通信系统发展的一个必然把局势。

本文主要介绍了2ASK调制解调的原理，2ASK调制主要采用OOK 开关监控的方法，2ASK解调主要采用相干解调的方法。

文中还会介绍用MA TALAB如何实现调制解调的系统，采用MA TALAB脚本编写程序，结果表明了设计的正确性。

第一部分原理介绍2ASK信号的调制2ASK技术是通过改变载波信号的幅值变化来表示二进制0或1的。

载波0 ，1信息只改变其振幅，而频率和相位保持不变。

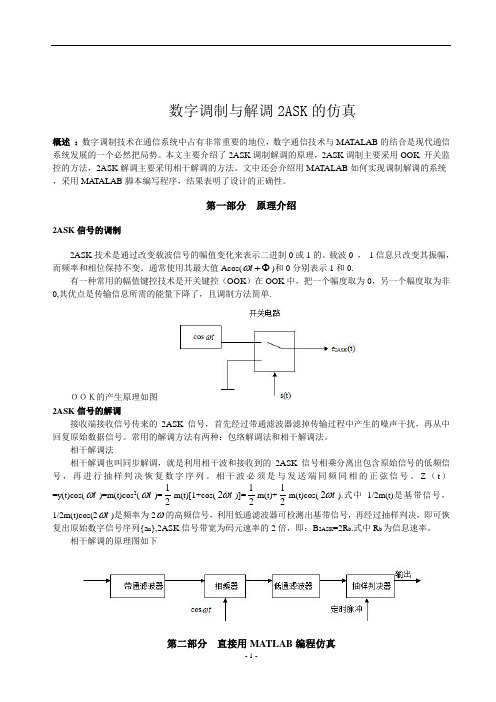
通常使用其最大值Acos(tω+Φ)和0分别表示1和0.有一种常用的幅值键控技术是开关键控（OOK）在OOK中，把一个幅度取为0，另一个幅度取为非0,其优点是传输信息所需的能量下降了，且调制方法简单.ＯＯＫ的产生原理如图2ASK信号的解调接收端接收信号传来的2ASK信号，首先经过带通滤波器滤掉传输过程中产生的噪声干扰，再从中回复原始数据信号。

常用的解调方法有两种：包络解调法和相干解调法。

相干解调法相干解调也叫同步解调，就是利用相干波和接收到的2ASK信号相乘分离出包含原始信号的低频信号，再进行抽样判决恢复数字序列。

相干波必须是与发送端同频同相的正弦信号。

Z（t）=y(t)cos(tω)=m(t)cos2(tω)=12m(t)[1+cos(2tω)]=12m(t)+12m(t)cos(2tω).式中1/2m(t)是基带信号，1/2m(t)cos(2tω)是频率为2ω的高频信号，利用低通滤波器可检测出基带信号，再经过抽样判决，即可恢复出原始数字信号序列{a n},2ASK信号带宽为码元速率的2倍，即：B2ASK=2R b.式中R b为信息速率。

相干解调的原理图如下第二部分直接用MATLAB编程仿真利用MATLAB进行调制与解调的仿真的程序，以下是建立的M文件：编写M脚本文件对数字信号序列1101001101011001进行2ASK调制与解调进行仿真，数字信号的码元速率Rb=1000Band,载波频率为f=4kHZ.以下是仿真程序及注释。

基于MATLAB的ASK调制解调实验

基于MATLAB的ASK调制解调实验基于MATLAB 的ASK 调制解调实验1.实验⽬的(1) 熟悉MATLAB 中M ⽂件的使⽤⽅法，并在掌握ASK 调制解调原理的基础上，编写出ASK 调制解调程序。

(2) 绘制出ASK 信号解调前后在时域和频域中的波形，并观察解调前后频谱有何变化以加深对ASK 信号解调原理的理解。

(3) 对信号叠加噪声，并进⾏解调，绘制出解调前后信号的时频波形，改变噪声功率进⾏解调，分析噪声对信号传输造成的影响。

2.实验原理（1）ASK 调制原理ASK 指的是振幅键控⽅式。

这种调制⽅式是根据信号的不同，调节正弦波的幅度。

幅度键控可以通过乘法器和开关电路来实现。

载波在数字信号1或0的控制下通或断，在信号为1的状态载波接通，此时传输信道上有载波出现；在信号为0的状态下，载波被关断，此时传输信道上⽆载波传送。

那么在接收端我们就可以根据载波的有⽆还原出数字信号的1和0。

对于⼆进制幅度键控信号的频带宽度为⼆进制基带信号宽度的两倍。

幅移键控法(ASK )的载波幅度是随着调制信号⽽变化的，其最简单的形式是，载波在⼆进制调制信号控制下通断，此时⼜可称作开关键控法(OOK )。

⼆进制幅度键控记作2ASK 。

2ASK 是利⽤代表数字信息“0”或“1”的基带矩形脉冲去键控⼀个连续的载波，使载波时断时续地输出。

有载波输出时表⽰发送“1”，⽆载波输出时表⽰发送“0”。

2ASK 信号可表⽰为tw t s t e c cos )()(0=式中，cw 为载波⾓频率，s(t)为单极性NRZ 矩形脉冲序列)()(b nn nT t g a t s -=∑其中，g(t)是持续时间b T 、⾼度为1的矩形脉冲，常称为门函数；n a 为⼆进制数字-=P P a n 101，出现概率为，出现概率为2ASK/OOK 信号的产⽣⽅法通常有两种：模拟调制（相乘器法）和键控法。

本模拟幅度调制的⽅法⽤乘法器实现。

相应的调制如图5-1和图5-2：图5-1模拟相乘法图5-2键控/开关法（2）ASK 解调原理2ASK/OOK 信号有两种基本的解调⽅法：⾮相⼲解调（包络检波法）和相⼲解调（同步检测法）。

2DPSK信号处理仿真（含代码）

2DPSK信号处理仿真（含代码）按照2DPSK产生模型和解调模型分别产生2DPSK信号和高斯白噪声，经过信道传输后进行解调。

对调制解调过程中的波形进行时域和频域观察，并且对解调结果进行误码率测量。

2DPSK信号的解调可以选用非相干解调或者相干解调法。

仿真流程首先通过随机函数产生一列随机的基带信号，这里设定一共有10个码元。

然后对这10个码元进行差分变换，设定起始参考电平为0电平。

则差分序列可以由如下的公式产生：在完成差分序列的产生之后要产生对应的载波，载波采用正弦波，相位设定如下：使用载波与对应的差分序列相乘，首先生成两个ASK波形，叠加这两个ASK波形就得到DPSK调制的已调波形。

完成波形调制之后，直接在波形上叠加高斯白噪声，完成信道传输的模拟。

同时在接收端，首先进行带通滤波，滤除信道中叠加上的噪声，然后通过相干解调的方式进行解调。

让解调后的波形通过低通滤波器，对波形进行平滑处理，最后通过抽样判决判断出接收到的序列码。

对序列码采用公式进行码反变化就可以得到解调后的绝对码序列，对比发送的绝对码序列和接收到的绝对码序列就可以得到误码率。

仿真结果1）码序列：首先可以通过该仿真程序产生输入的绝对码序列和输入的相对码序列。

2）载波信号：产生两个正弦信号作为载波，一个初相为0 ，另一个初相为π。

3）调制后的波形与频谱：为了实现DPSK调制，在完成绝对码向相对码的转换之后，根据这些相对码分别生成对应的ASK调制波形，将两个ASK波形叠加就得到了DPSK的调制波形。

4）通过信道：模拟通过信道，在输入信号上增加均值为0，方差为2的高斯白噪声，得到对应的信号和频谱。

5）通过带通滤波：将接受到的通过信道的波形进行带通滤波，得到滤波后的波形和对应的频谱。

6）相干解调：对经过带通滤波之后的信号再进行相干解调，得到解调后的波形和频谱。

7）通过低通滤波：将上面解调后的信号通过低通滤波可以得到滤波后对应的波形及频谱。

8）得到解调波形及误码率：通过抽样判决得到解调出来的相对码的码序列，然后利用码反变换得到输入的绝对码序列。

matlab2ask信号调制与解调原理

matlab2ask信号调制与解调原理
MATLAB中2ASK（二进制振幅键控）信号的调制与解调原理如下：
1. 调制原理：基带码元d(t)和高频载波相乘实现2ASK信号的调制。

具体来说，如果基带码元为二进制信号，那么其幅度变化将控制载波信号的通断，从而实现数字信息的传递。

在MATLAB中，可以使用信号处理工具箱中的函数来生成2ASK信号。

2. 解调原理：2ASK信号经过信道传输之后，再和载波相乘，然后经过低通滤波后抽样判决恢复出原始基带码元信号。

解调过程中，使用一个同频同相的本地载波与要解调的信号相乘，去掉高频部分即可恢复出原始的基带码元信号。

在MATLAB中，可以使用信号处理工具箱中的函数来实现2ASK信号的解调。

需要注意的是，以上只是一种简化的2ASK调制和解调过程的描述，实际的通信系统中可能还会包括其他的信号处理过程，如信道编码、调制解调、信号同步等。

在MATLAB中进行仿真时，需要根据实际需求进行相应的设计和调整。

二进制ASK调制matlab仿真代码

function ber = sim_ASK2(snrIndB,N,flag)% 二进制ASK调制解调仿真程序% 输入% snr: 信噪比% N: 仿真比特数% flag:绘制调制解调波形标志位% 输出% y: 误码率x = round(rand(1,N));% 产生信号比特fc = 200; % 载波频率fs = 2000;% 采样频率fb = 50; % 比特频率nSamples = fs/fb;% 每比特采样数signal_in_one_bit = cos(2*pi*fc*(0:nSamples-1)/fs);% 传号space_in_one_bit = zeros(1,nSamples); % 空号limitation = sum(signal_in_one_bit.^2)/2; % 判决门限sig_ori = reshape(repmat(x,nSamples,1),1,N*nSamples); % 原始信号%% ASK调制y=zeros(1,nSamples*N);for i=1:length(x)if(x(i)==1)y((i-1)*nSamples+1:i*nSamples) = signal_in_one_bit;elsey((i-1)*nSamples+1:i*nSamples) = space_in_one_bit;endendmod_sig = y;% 调制信号%% 高斯信号传输% rec_sig = awgn(mod_sig,snr,0); % 通过高斯信道后的接收信号snr = 10^(0.1*snrIndB)/(fb/4);sigma = 1/sqrt(snr);rec_sig = awgn_gauss(mod_sig,sigma);%% ASK解调bits_judged = zeros(1,N);for i = 1:N % 逐比特处理rec_seg = rec_sig((i-1)*nSamples+1:(i*nSamples));sum_rec = rec_seg*signal_in_one_bit'; % 相关累积if(sum_rec>=limitation) % 判决bits_judged(i) = 1;elsebits_judged(i) = 0;endendx_pie = bits_judged;% 接收信号判决值ber = length(find(x~=x_pie))/N;% 误码率% 绘制调制解调结果图if(1==flag)bits_display = 30;% 绘图显示的比特数figure;subplot(411);stem(x(1:bits_display));title('原始数据比特'),xlabel('t')subplot(412);plot(mod_sig(1:bits_display*nSamples));title('调制信号'),xlabel('t')subplot(413);plot(rec_sig(1:bits_display*nSamples));title('经过信道后的接收信号'),xlabel('t')subplot(414);stem(x_pie(1:bits_display));title('解调以后的数据比特'),xlabel('t')%% 计算和绘制信号频谱[f1,powerIndB1] = getFre(sig_ori,fs);[f2,powerIndB2] = getFre(mod_sig,fs);[f3,powerIndB3] = getFre(rec_sig,fs);figuresubplot(311);plot(f1,powerIndB1); xlim([0 fs/2]);ylim([-80 10]);title('原始数据的功率谱密度');xlabel('频率(Hz)');ylabel('功率谱密度（w/Hz）');subplot(312);plot(f2,powerIndB2); xlim([0 fs/2]);ylim([-80 10]);title('调制信号的功率谱密度');xlabel('频率(Hz)');ylabel('功率谱密度(w/Hz)');subplot(313);plot(f3,powerIndB3); xlim([0 fs/2]);ylim([-80 10]);title('经过信道接收信号的功率谱密度');xlabel('频率(Hz)');ylabel('功率谱密度(w/Hz)');end。

matlabask调制解调

MATLAB中实现ASK（振幅键控）调制解调的步骤如下：
生成随机比特流：使用MATLAB的随机数生成函数生成二进制比特流。

映射比特流到振幅：将二进制比特流映射到相应的振幅值，通常使用高电平和低电平表示二进制比特流的1和0。

调制信号：使用生成的振幅信号调制高频载波信号。

通常可以使用MATLAB的信号处理函数进行调制，如modulate函数。

传输信号：将调制后的信号通过信道传输。

解调信号：在接收端，使用适当的解调方法将调制信号解调为原始比特流。

常用的解调方法包括相干解调和非相干解调。

在MATLAB中，可以使用相关函数进行相干解调，如demodulate函数。

比特流同步：在解调过程中，需要确保解调器与发送端保持同步，以便正确解调出原始比特流。

可以使用适当的同步算法实现比特流的同步。

误码率分析：最后，可以使用MATLAB的误码率分析工具计算解调后的比特流的误码率，以评估调制解调性能。

以上是MATLAB实现ASK调制解调的大致步骤。

matlab2ask调制

matlab2ask调制
MATLAB2ASK调制是一种将数字信号转化为模拟信号的调制方式。

ASK调制的基本原理是将数字信号转换为二进制数，再将二进制数映
射到不同的振幅上。

当输入数字信号为1时，输出信号的振幅为正值；当输入数字信号为0时，输出信号的振幅为零。

MATLAB2ASK调制具体实现步骤如下：
1. 生成二进制数据：首先需要生成二进制数据，可以使用MATLAB中的randi函数生成指定长度的随机整数序列。

2. 将二进制数据转换成ASK调制波形：使用MATLAB中的if语句和for循环结构将二进制数据映射到不同的振幅上，并利用plot函数绘
图显示出ASK波形。

3. 添加噪声：在实际应用中，通常会存在噪声干扰。

因此，可以使用MATLAB中的awgn函数添加高斯白噪声。

4. 解调ASK波形：解调ASK波形需要使用检测电路。

在MATLAB中可以使用envelope函数对ASK波形进行包络检测，并通过阈值判断
得到解调后的二进制数据。

5. 绘图并比较结果：最后可以通过plot函数分别绘图显示出原始数据、ASK波形、添加噪声后的ASK波形以及解调后的二进制数据，并进行比较。

总结来说，MATLAB2ASK调制是一种简单、易实现的数字信号调制方式。

通过MATLAB中提供的函数和工具箱，可以轻松地实现ASK调制，并进行相应的仿真和分析。

基于MATLAB的2ASK数字调制与解调的系统仿真

基于MATLAB的2ASK数字调制与解调的系统仿真一、本文概述随着信息技术的飞速发展，数字通信在现代社会中扮演着日益重要的角色。

作为数字通信中的关键技术之一，数字调制技术对于提高信号传输的可靠性和效率至关重要。

在众多的数字调制方式中，2ASK （二进制振幅键控）因其实现简单、抗干扰能力强等优点而备受关注。

本文旨在通过MATLAB软件平台，对2ASK数字调制与解调系统进行仿真研究，以深入理解和掌握其基本原理和性能特点。

本文首先介绍了数字调制技术的基本概念，包括数字调制的基本原理、分类和特点。

在此基础上，重点阐述了2ASK调制与解调的基本原理和实现方法。

通过MATLAB编程，本文实现了2ASK调制与解调系统的仿真模型，并进行了性能分析和优化。

在仿真研究中，本文首先生成了随机二进制信息序列，然后利用2ASK调制原理对信息序列进行调制，得到已调信号。

接着，对已调信号进行信道传输，模拟了实际通信系统中的噪声和干扰。

在接收端，通过2ASK解调原理对接收到的信号进行解调，恢复出原始信息序列。

通过对比分析原始信息序列和解调后的信息序列，本文评估了2ASK 调制与解调系统的性能，并讨论了不同参数对系统性能的影响。

本文的仿真研究对于深入理解2ASK数字调制与解调原理、优化系统性能以及指导实际通信系统设计具有重要意义。

通过MATLAB仿真平台的运用，本文为相关领域的研究人员和实践工作者提供了一种有效的分析和优化工具。

二、2ASK数字调制技术原理2ASK（二进制振幅键控）是一种数字调制技术，主要用于数字信号的传输。

它的基本思想是将数字信号（通常是二进制信号，即0和1）转换为模拟信号，以便在模拟信道上进行传输。

2ASK调制的关键在于根据数字信号的不同状态（0或1）来控制载波信号的振幅。

在2ASK调制过程中，当数字信号为“1”时，载波信号的振幅保持在一个较高的水平；而当数字信号为“0”时，载波信号的振幅降低到一个较低的水平或者为零。

ask在matlab中的调制解调

ask在matlab中的调制解调在MATLAB中，调制和解调是数字通信中非常重要的部分。

通过调制和解调技术，我们可以将数字信号转换为模拟信号，或者将模拟信号转换为数字信号。

这篇文章将介绍MATLAB中的调制解调方法以及其在互联网技术中的应用。

一、调制调制是将数字信号转换为模拟信号的过程。

MATLAB中提供了多种调制技术，包括频移键控调制（FSK）、相移键控调制（PSK）、正交振幅调制（QAM）等。

1. 频移键控调制（FSK）频移键控调制是一种基于频率的调制方法，可以将不同的数字信号映射到不同的频率上。

MATLAB中可以使用comm.FSKModulator和comm.FSKDemodulator函数实现FSK调制解调。

2. 相移键控调制（PSK）相移键控调制是一种基于相位的调制方法，可以将不同的数字信号映射到不同的相位上。

MATLAB中可以使用comm.PSKModulator和comm.PSKDemodulator函数实现PSK调制解调。

3. 正交振幅调制（QAM）正交振幅调制是一种结合了频移键控调制和相移键控调制的调制方法，可以将数字信号映射到不同的频率和相位上。

MATLAB中可以使用comm.RectangularQAMModulator和comm.RectangularQAMDemodulator函数实现QAM调制解调。

二、解调解调是将模拟信号转换为数字信号的过程。

在MATLAB中，可以使用相应的解调器函数对调制后的信号进行解调。

1. FSK解调使用comm.FSKDemodulator函数可以对FSK调制后的信号进行解调，将其转换为数字信号。

2. PSK解调使用comm.PSKDemodulator函数可以对PSK调制后的信号进行解调，将其转换为数字信号。

3. QAM解调使用comm.RectangularQAMDemodulator函数可以对QAM调制后的信号进行解调，将其转换为数字信号。

ASK调制与解调系统的MATLAB实现及性能分析

MATLAB第二次实验2ASK调制与解调系统的MATLAB实现及性能分析指导老师：汤建龙作者：余颖智学号：02123021摘要：现代通信系统要求通信距离远、通信容量大、传输质量好。

作为其关键技术之一的调制解调技术一直是人们研究的一个重要方向。

从最早的模拟调幅调频技术的日臻完善，到现在数字调制技术的广泛运用，使得信息的传输更为有效和可靠。

二进制数字振幅键控是一种古老的调制方式，也是各种数字调制的基础。

本课程设计主要是利用MATLAB集成环境下的Simulink仿真平台,设计一个2ASK调制与解调系统.用示波器观察调制前后的信号波形;用频谱分析模块观察调制前后信号频谱的变化;加上各种噪声源,用误码测试模块测量误码率;最后根据运行结果和波形来分析该系统性能。

通过Simulink的仿真功能摸拟到了实际中的2ASK调制与解调情况。

1 引言本课程设计主要是深入理解和掌握振幅通信系统的各个关键环节，包括调制、解调、滤波、传输、噪声对通信质量的影响等。

在数字信号处理实验课的基础上更加深入的掌握数字滤波器的设计原理及实现方法。

使我对系统各关键点的信号波形及频谱有深刻的认识。

1.1 实验目的通过本次设计，巩固并扩展通信课程的基本概念、基本理论、分析方法和仿真实现方法，掌握2ASK 解调原理及其实现方法，了解线性调制时信号的频谱变化。

理解2ASK 的调制和解调原理并用Simulink软件仿真其实现过程，用Simulink 分析二进制振幅键控信号频谱的变化。

认识和理解通信系统，掌握信号是如何经过发端处理被送入信道然后在接收端还原。

会画出数字通信过程的基本框图，掌握数字通信的2ASK调制方式，学会运用MATLAB 来进行通信系统的仿真；实现将理论只是和软件设计紧密结合。

学会2ASK传输系统的二级调制解调结构，测试2ASK传输信号加入噪声后的误码率，分析2ASK传输系统的抗噪声性能。

1.2 实验内容利用MATLAB集成环境下的Simulink仿真平台,设计一个2ASK调制与解调系统.用示波器观察调制前后的信号波形;用频谱分析模块观察调制前后信号频谱的变化;加上各种噪声源,用误码测试模块测量误码率;最后根据运行结果和波形来分析该系统性能。

2ask调制解调 matlab代码仿真

2ask调制解调matlab代码仿真2ASK（2级幅度调制）是一种基本的数字调制方式，其原理是将数字信号转换为一串二进制代码，并在每一位二进制代码上加上不同的幅度。

在MATLAB中，可以利用通信工具箱进行2ASK调制与解调的仿真。

以下是2ASK调制与解调的基本步骤：1. 导入所需库：```matlabclear;clc;import .通信工具箱.*;```2. 定义参数：```matlab符号速率= 1000; // 符号速率（bps）载波频率= 1000; // 载波频率（Hz）采样频率= 10000; // 采样频率（Hz）噪声功率= 10^-5; // 噪声功率（dB）3. 生成随机二进制序列：```matlabnum_bits = 4;bit_sequence = randi([0, 1], 1, num_bits);```4. 2ASK调制：```matlabmodulator = qasymmod(bit_sequence, '2ASK', symbol_rate, 'carrier_frequency', carrier_frequency, 'sampling_frequency', sampling_frequency);```5. 添加高斯白噪声：```matlabnoise = awgn(modulator, snr);```6. 2ASK解调：```matlabdemodulator = qasymdemod(noise, '2ASK', symbol_rate, 'carrier_frequency', carrier_frequency, 'sampling_frequency', sampling_frequency);```7. 解调后的二进制序列：```matlabdemodulated_bits = bitrecovery(demodulator);```8. 绘制波形图：```matlabfigure;subplot(2, 1, 1);plot(modulator);title('调制波');xlabel('时间');ylabel('幅度');subplot(2, 1, 2);plot(noise);title('含噪声的调制波');xlabel('时间');ylabel('幅度');```9. 绘制误码率曲线：```matlabber = biterr(bit_sequence, demodulated_bits);figure;plot(ber);title('误码率');xlabel('迭代次数');ylabel('误码率');```以上代码即可实现2ASK调制与解调的MATLAB仿真。

Matlab的ASK和FSK信号调制解调仿真

马克和空间频率。在另一方面，在相干频移键控或二进制的FSK ，是没有间断期在输出信号。 ✤ 在数字化时代，电脑通信在数据线路（电话线、网络电缆、光纤或者无线媒介）上进行传输，就是用FSK调制信号进
行的，即把二进制数据转换成FSK信号传输，反过来又将接收到的FSK信号解调成二进制数据，并将其转换为用高，低电平所表示的二进制语言，这是计算机能够直接识别的语言。
ASK和FSK信号调制解调仿真
ASK原理
✤ ASK指的是振幅键控方式。这种调制方式是利用载波的幅度变化来传递数字信息，其频率和初始相位保持不变。最基本的ASK是2ASK。
✤ 幅度键控可以通过乘法器和开关电路来实现。载波在数字信号1或0的控制下通或断，在信号为1的状态载波接通，此时传输信道上有载波出现；在信号为0的状态下，载波被关断，此时传输信道上无载波传送。那么在接收端我们就可以根据载波的有无还原出数字信号的1和0。对于二进制幅度键控信号的频带宽度为二进制基带信号宽度的两倍。
✤ 幅移键控法(ASK)的载波幅度是随着调制信号而变化的，其最简单的形式是，载波在二进制调制信号控制下通断，此时又可称作开关键控法 (OOK)。多电平MASK调制方式是一种比较高效的传输方式，但由于它的抗噪声能力较差，尤其是抗衰落的能力不强，因而一般只适宜在恒✤ FSK（Frequency-shift keying）频移键控是信息传输中使用得较早的一种调制方式,它的主要优点是: 实现起来较容易, 抗噪声与抗衰减的性能较好。在中低速数据传输中得到了广泛的应用。
✤ 最常见的是用两个频率承载二进制1和0的双频FSK系统。 ✤ 技术上的FSK有两个分类，非相干和相干的FSK 。在非相干的FSK ，瞬时频率之间的转移是两个分立的价值观命名为
FSK原理

调制解调的MATLAB实现

调制解调的MATLAB实现摘要：数字调制是通信系统中的重要环节之一，数字调制技术的改进对于通信系统性能的提高具有重要的作用。

现代通信系统要求传输的质量好，通信的距离远、通信的容量大，调制技术是其中的关键技术，因此人们正努力的研究调制解调技术，使得调制解调技术更好的服务于现代通信系统。

本文首先分析几种数字解调系统的几种基本调制解调方法，然后用MATLAB实现调制与解调的基本功能，并且进行仿真的验证。

本文通过介绍2ASK，2FSK，2PSK的基本原理和调制解调的实现，对其进行分析，然后设计运用Simulink这个仿真软件对二进制调制解调系统进行模型的构建、系统的设计、仿真的演示、结果的显示、误差的分析和综合性能的分析，本文重点对2ASK，2FSK，2PSK进行性能比较和误差分析。

通过分析可以在实际运用中，根据情况而选择最佳的调制方式。

本文以MATLAB为软件平台，充分利用其提供的通信工具箱和信号处理工具箱中的模块，对数字调制解调系统进行设计仿真，并且进行误差分析。

关键词：MATLAB；调制解调；ASK；FSK；PSK；分析与仿真。

MODULATION AND DEMODULATION MATLABIMPLEMENTATIONAbstract:The digital modulation is one important aspect of the communication system, the improvement of digital modulation techniques for improved performance of the communication system has an important role. The quality of modern communication systems require transmission distance communication, communication capacity modulation technique is one of the key technologies, people are efforts modulation and demodulation techniques, better modulation and demodulation techniques in modern communication systems. This paper analyzes several digital demodulation system several basic modulation and demodulation method, and then use the basic functions of modulation and demodulation MATLAB simulation verification.By 2ASK, 2FSK 2PSK the basic principles and modem implementation, analyze it, and then design use Simulink simulation software binary modulation and demodulation system model construction, system design, simulation, presentation, resultsthe display, error analysis and performance analysis, this paper focuses on 2ASK 2FSK, 2PSK performance comparison and error analysis. Analysis in the practical application, according to the situation and choose the best modulation.In this paper, MATLAB software platform, to take full advantage of its communications toolbox and signal processing toolbox module, digital modulation and demodulation system design and simulation, and error analysis.Key words:MATLAB; Modulation and demodulation;ASK;FSK;PSK; Analysis and Simulation.目录1 前言 (1)1.1课题研究的背景 (1)1.2MATLAB/SIMULINK简介 (1)1.3通信系统的组成 (2)1.4调制研究的目的和意义 (4)2 2ASK、2FSK、2PSK、2QSK的基本原理和实现 (6)2.12ASK的基本原理和调制解调实现 (6)2.22FSK的基本原理和调制解调实现 (8)2.32PSK的基本原理和调制解调实现 (10)3 SIMULINK的模型建立与仿真 (13)3.1启动SIMULINK (13)3.22ASK的模型建立与仿真 (14)3.32FSK的调制与解调仿真 (20)3.42PSK的调制与解调仿真 (27)4 2ASK,2FSK,2PSK调制解调的M语言实现 (31)4.12ASK调制与解调的M语言实现 (31)4.22FSK调制与解调的M语言实现 (31)4.32PSK调制与解调的M语言实现 (32)结束语 (34)参考文献 (35)附录 (36)致谢 (44)1 前言1.1课题研究的背景伴随着进入20世纪以来，晶体管、集成电路的出现和普及、无线通信的迅速发展。

ASK,FSK,PSK调制

#include<stdio.h>#include<graphics.h>#include<math.h>#include<conio.h>#define N 63#define MAX 1024#define fs 8000#define PI 3.1415926#define L 640#define RAND_MAX 32768#define fc 1000void DFT_FFT(float x[],int xl) ;void Convolution( float x[], float y[], int xl, int yl );int p, a[4];int m,n;float H[N],R[MAX],e[MAX],u[MAX],s[MAX],x[MAX], y[MAX],UU[640];main(){ float U[640];int i;void student_number(),LPF(),GRAPH(),BPF(),modulate(),whitenoise(), panjue(); printf("input your number:");scanf( "%d",&p );student_number();DFT_FFT(u,L);GRAPH( u, 25, UU, 5 );LPF();DFT_FFT(H, L);GRAPH(H,1000, UU ,200);for(i=0;i<640;i++) x=u;for(i=0;i<63;i++) y=H;Convolution( x, y, L, N );DFT_FFT(R, L);GRAPH(R, 80, UU, 2 );modulate( R,L);DFT_FFT(s, L );GRAPH( s,30 ,UU, 3);whitenoise( s);DFT_FFT(s, L);GRAPH(s,25, UU, 3 );BPF() ;DFT_FFT( H, L );GRAPH( H, 150, UU, 20 );for(i=0;i<640;i++) x=u;for(i=0;i<63;i++) y=H;Convolution(x,y,L,N);DFT_FFT(R,L);GRAPH( R, 80, UU, 8 );modulate(R , L );DFT_FFT( s, L);GRAPH( s,80, UU, 8 );LPF();DFT_FFT( H, L);GRAPH( H, 500, UU, 50 );for(i=0;i<640;i++) x=u;for(i=0;i<63;i++) y=H;Convolution(x, y, L, N );DFT_FFT( R,L);GRAPH( R, 100, UU, 2 );panjue(R);DFT_FFT(R,L);GRAPH( R, 25, UU, 5 );}/******************************************基带信号.**********************/void student_number(){int i,j,A[16];a[0]=p/1000;a[1]=p%1000/100;a[2]=p%100/10;a[3]=p%10;for(i=0;i<4;i++){A[4*i+3]=a%2;A[4*i+2]=(a-A[4*i+3])/2;A[4*i+2]%=2;A[4*i+1]=(a-A[4*i+3]-A[4*i+2]*2)/4;A[4*i+1]%=2;A[4*i+0]=(a-A[4*i+3]-A[4*i+2]*2-A[4*i+3]*4)/8;A[4*i+0]%=2;}for(i=0;i<16;i++)for(j=0;j<40;j++){if(A==1) u[40*i+j]=1;else u[40*i+j]=0;}}/************************************低通***********************************/void LPF(){int i;float a,wn[N],hd[N];a=(N-1)/2;for(i=0;i<N;i++){if(i==a) hd=0.05;else hd=sin((PI/20)*(i-a))/(float)(PI*(i-a));}for(i=0;i<N;i++){wn=0.54-0.46*cos(2.0*PI*i/(N-1));H=wn*hd;}}/***************************卷积**********************************/ void Convolution( float x[], float y[], int xl, int yl ){int m,n; float sum;for(n=0;n<(xl+yl-1);n++){sum=0.0;for(m=0;m<=n;m++){if(m>=xl) x[m]=0.0;if((n-m)>=yl) y[n-m]=0.0;sum+=x[m]*y[n-m];}if(n>=(yl-1)/2&&n<(xl+(yl-1)/2))R[n-(yl-1)/2]=sum;}}/**************************带通**********************************/ void BPF(){int i;float a,wn[N]={0.0},hd[N]={0.0};a=(N-1)/2;for(i=0;i<N;i++){if(i==a) hd=0.1;else hd=sin((3*PI/10)*(i-a))/(float)(PI*(i-a))-sin((PI/5)*(i-a))/(float)(PI*(i-a)); }for(i=0;i<N;i++){wn=0.54-0.46*cos(2.0*PI*i/(N-1));H=wn*hd;}}/***********************画图*********************************/ void GRAPH(float x[],int AM,float y[],int PM){int gdriver,mode,i;gdriver=DETECT;initgraph(&gdriver,&mode," ");setbkcolor(0);setcolor(30);line(0,150,640,150);outtextxy(240,70,"------Time------");for(i=0;i<L;i++)line(i,150,i,150-x*AM);line(0,400,640,400);outtextxy(240,350,"------Frequency------");for(i=0;i<L;i++)line(i,400,i,400-y*PM);getch();closegraph();}/**********************调制***************************/ void modulate(float R[] ,int F){int i;for(i=0;i<F;i++){ s=R*cos(2*PI*fc*i/fs); }}/*********************噪声********************************/ void whitenoise( float s[]){int i, j;float r, ri, m[ 640 ],po=0.1;for ( j = 0;j < L;j++ ){m[ j ] = 0.0;for ( i = 0;i < 12;i++ ){r=rand();ri=po/2*(r-RAND_MAX/2)/(RAND_MAX/2);m[ j ] += ri;}s[ j ] = s[ j ] + m[ j ];}}/*********************DFT_FFT**************************/ void DFT_FFT(float x[],int xl){int i,j;float xr[MAX],xi[MAX];for(j=0;j<xl;j++){xr[j]=0.0;xi[j]=0.0;for(i=0;i<xl;i++){xr[j]+=x*cos(2*PI*i*j/xl);xi[j]+=(-1)*x*sin(2*PI*i*j/xl);}UU[j]=sqrt(pow(xr[j],2)+pow(xi[j],2));}}/******************判决*************************/void panjue(float R[]){ int i;for(i=0;i<L;i++){if(R>=0.5) R=1;else R=0.0;}}clear all%二进制随机序列x=[0 1 1 0 0 1 0 1 0 1];%定义一个二进制10元素数组，作为FSK信号输入数据。

二进制数字调制的MATLAB仿真

一、实验目的：1.了解二进制数字调制的工作原理；2.掌握ASK,FSK,及PSK 的波形图。

二、实验原理：对于大多数的数字传输系统来说，由于数字基带信号往往具有丰富的低频成分，而实际的通信信道又具有带通特性，很多信道都不能直接传送基带信号，而必须用基带信号来控制高频载波的某些参量，这种把系带数字信号变换为频带数字信号的过程称为数字解调。

1.二进制振幅键控信号（1）数学表示设信息源发出的是有二进制符号0、1组成的序列，且假设0符号出现的概率为P,1符号出现的概率为1-P,它们彼此独立，则2ASK 信号可表示为：t t s t nT t g a t e c c ns n ωωcos )(cos )]([)(0=-=∑其中，g(t)是持续时间为s T 的矩形脉冲，且 ⎩⎨⎧=P-11P 0概率为概率为n a（2）频谱与带宽设s(t)是单极性随机矩阵脉冲序列，亲切0、1出现是等概的，则2ASK 信号的功率谱密度为)]()([161)()(sin )()(sin 16)(P 22cc sc sc sc sc s e f f f f T f f T f f T f f T f f T f -+++⎪⎪⎭⎫⎝⎛--+++=δδππππ2ASK 信号的带宽是基带脉冲波形带宽的两倍，即s f 2B ASK 2=2．二进制移频键控信号（1）数学表示设信息源发出的是有二进制符号0、1组成的序列，且假定0符号对应于载频w1,1符号对应于载频w2,则2FSK 信号可表示为：)cos()]()cos()]()(210n ns n n ns n t nT t g a t nT t g a t e ϕωϕω+-++-=∑∑其中，g(t)是单个矩形脉冲，脉宽为s T 且⎩⎨⎧=P -11P概率为概率为n a ⎩⎨⎧-=P1P 10概率为概率为n a（2）频谱与带宽])()()()([161])()(sin )()(sin )()(sin )()(sin [16)(P 2211222222211211E f f f f f f f f T f f T f f T f f T f f T f f T f f T f f T f f T f sssssssss -+++-+++--++++--+++=δδδδππππππππ传输2FSK 信号所需频带约为s f f f 2B 12FSK2+-=3．二进制相移键控（1）数学表示设信息源发出的是有二进制符号0、1组成的序列，其信号一般形式可表示为：t nT t g a t e c ns n ωcos )]([)(0∑-=这里，g(t)是单个矩形脉冲，脉宽为s T 且⎩⎨⎧-+=P-11P 1概率为概率为n a（2）频谱与带宽设s(t)是双极性矩形基带信号，且0、1等概出现，则2PSK 信号的功率谱密度为⎪⎪⎭⎫ ⎝⎛--+++=22)()(sin )()(sin 4)(P sc sc sc sc s e T f f T f f T f f T f f T f ππππ 2PSK 信号的带宽为s f 2B PSK 2=三、实验程序： A=1; fc=2; N_sample=20; N=500; Ts=1;dt=Ts/fc/N_sample; t=0:dt:N*Ts-dt; Lt=length(t); d=sign(randn(1,N));dd=sigexpand((d+1)/2,fc*N_sample); gt=ones(1,fc*N_sample); figure(1) subplot(2,2,1); d_NRZ=conv(dd,gt);plot(t,d_NRZ(1:length(t))); axis([0,10,0,1.2]);xlabel('(a)输入信号');subplot(2,2,2);[f,d_NRZf]=T2F(t,d_NRZ(1:length(t))); plot(f,10*log10(abs(d_NRZf).^2/Ts)); axis([-2,2,-50,10]);xlabel('(b)输入信号功率谱密度(dB/HZ)'); ht=A*cos(2*pi*fc*t);s_2ask=d_NRZ(1:Lt).*ht;subplot(2,2,3);plot(t,s_2ask);axis([0,10,-1.2,1.2]);xlabel('(c)2ask');[f,s_2askf]=T2F(t,s_2ask);subplot(2,2,4);plot(f,10*log10(abs(s_2askf).^2/Ts)); xlabel('(d)2ask功率谱密度(dB/HZ)'); figure(2)d_2psk=2*d_NRZ-1;s_2psk=d_2psk(1:Lt).*ht;subplot(2,2,1);plot(t,s_2psk);axis([0,10,-1.2,1.2]);xlabel('(e)2psk');subplot(2,2,2);[f,s_2psk]=T2F(t,s_2psk);plot(f,10*log10(abs(s_2psk).^2/Ts));axis([-fc-4,fc+4,-50,10]);xlabel('(f)2psk功率谱密度(dB/HZ)');sd_2fsk=2*d_NRZ-1;s_2fsk=A*cos(2*pi*fc*t+2*pi*sd_2fsk(1:length(t)).*t); subplot(2,2,3);plot(t,s_2fsk);axis([0,10,-1.2,1.2]);xlabel('(g)2fsk');subplot(2,2,4);[f,s_2fskf]=T2F(t,s_2fsk);plot(f,10*log10(abs(s_2fskf).^2/Ts));axis([-fc-4,fc+4,-50,10]);xlabel('(h)2fsk功率谱密度(dB/HZ)');子函数：①F2T.mfunction [t,st]=F2T(f,sf)%反傅立叶变换df=f(2)-f(1);Fmx=(f(end)-f(1)+df);df=1/Fmx;N=length(sf);T=dt*N;t=0:dt:T-dt;sff=fftshift(sf);st=Fmx*ifft(sff)②T2F.mfunction[f,sf]=T2F(t,st)dt=t(2)-t(1);T=t(end);df=1/T;N=length(st);f=-N/2*df:df:N/2*df-df;sf=fft(st);sf=T/N*fftshift(sf);③ sigexpand.mfunction[out]=sigexpand(d,M)%将输入的序列扩展成间隔N—1个0 N=length(d);out=zeros(M,N);out(1,:)=d;out=reshape(out,1,M*N);四、实验结果及分析：。

基于MATLAB的2ASK和2FSK调制仿真

基于MATLAB的2ASK和2FSK调制仿真2ASK调制仿真一、实验设计1.实验目的通过MATLAB仿真实现2ASK调制过程，了解2ASK调制的原理和过程。

2.实验原理2ASK调制是一种基于振幅调制（AM）的数字调制方式。

将数字信号根据其幅值变化对载波进行调制，从而实现数字信号的传输。

2ASK调制的过程可以分为三个步骤:（1）将数字信号变为模拟信号；（2）将模拟信号进行波形调制；（3）生成2ASK调制信号。

3.实验步骤（1）生成符号序列；（2）将符号序列转为数字信号；（3）将数字信号调制成模拟信号；（4）将模拟信号进行波形调制；（5）生成2ASK调制信号。

4.实验结果（1）生成符号序列：符号序列的生成可以通过MATLAB的randi函数来实现。

代码如下：symbolSequence = randi([0, 1], 1, N);（2）将符号序列转为数字信号：由于二进制数字信号只包含两个数字（0和1），我们可以通过将符号序列中的0用低电平来表示，将1用高电平来表示。

代码如下：digitalSignal = 2 * symbolSequence - 1;（3）将数字信号调制成模拟信号：数字信号调制成模拟信号需要先进行差分编码，然后通过插值法将数字信号转为模拟信号。

代码如下：diffCode = diff(digitalSignal);modulatedSignal = interp1([0:length(diffCode)-1], diffCode, linspace(0, length(diffCode)-1, Fs/Fsymbol));（4）将模拟信号进行波形调制：将模拟信号进行波形调制需要通过乘以载波信号来实现。

代码如下：carrierSignal = cos(2 * pi * Fc * t);modulatedSignal = carrierSignal .* modulatedSignal;（5）生成2ASK调制信号：代码如下：ASKSignal = (modulatedSignal + 1) / 2;二、实验结果通过以上实验步骤，我们可以得到2ASK调制信号。

Matlab的ASK-FSK--PSK程序仿真

1.实验与要求1.1实验任务1.根据题目，查阅有关资料，掌握数字带通调制技术以及扩频通信原理。

2.学习MATLAB软件，掌握MATLAB各种函数的使用。

3.根据数字带通调制原理，运用MATLAB进行编程，仿真调制过程，记录并分析仿真结果。

4.形成设计报告。

1.2设计要求课程设计需要运用MATLAB编程实现2ASK,2FSK,2PSK，2DPSK,FM,AM,PM调制解调过程，并且输出其调制后的波形，画出频谱、功率谱密度图，并比较各种调制的误码率情况，讨论其调制效果。

2．设计原理2.1 二进制数字调制技术原理数字信号的传输方式分为基带传输和带通传输，在实际应用中，大多数信道具有带通特性而不能直接传输基带信号。

为了使数字信号在带通信道中传输，必须使用数字基带信号对载波进行调制，以使信号与信道的特性相匹配。

这种用数字基带信号控制载波，把数字基带信号变换为数字带通信号的过程称为数字调制。

通常使用键控法来实现数字调制，比如对载波的振幅、频率和相位进行键控。

2.1.1、ASK2ASK信号的产生方法通常有两种：模拟调制和键控法。

解调有相干解调和非相干解调。

P=1时f(t)=Acoswt;p=0时f(t)=0;其功率谱密度是基带信号功率谱的线性搬移2.1.2、FSK一个ＦＳＫ信号可以看成是两个不同载波的2ASK信号的叠加。

其解调和解调方法和ASK 差不多。

2FSK信号的频谱可以看成是f1和f2的两个2ASK频谱的组合。

12.1.3、2PSK2PSK以载波的相位变化作为参考基准的，当基带信号为0时相位相对于初始相位为0，当基带信号为1时相对于初始相位为180°。

2.1.4、AM幅度调制是用调制信号去控制高频正弦载波的幅度，使其按调制信号的规律变化的过程。

幅度调制器的一般模型如图2.1.1所示。

2.1.5、FM2.1.6、PM在模拟调制中，一个连续波有三个参数可以用来携带信息而构成已调信号。

当幅度和频率保持不变时，改变载波的相位使之随未调信号的大小而改变，这就是调相的概念。