最优化运输问题
货运运力调度的优化方法与技巧

05
04
调度执行
根据运力规划和路线规划结果,执行 货物运输任务。
优化方法的重要性
01
02
03
04
提高运输效率
优化方法可以帮助合理安排运 输工具和人力,减少运输时间
和成本,提高运输效率。
降低成本
通过优化方法,可以降低运输 过程中的能源消耗和人力成本 ,从而降低整体运输成本。
提高服务质量
优化方法可以确保货物按时、 安全、高效地送达目的地,提 高客户满意度和服务质量。
,确保了运输安全和稳定。
某港口货运运力调度优化案例
要点一
总结词
要点二
详细描述
通过引入先进的港口管理系统,优化了港口货运运力调度 ,提高了港口吞吐量和作业效率。
该港口引入了一套先进的港口管理系统,该系统集成了货 物管理、船舶调度、岸桥管理等多个功能模块。通过该系 统的应用,港口实现了对货物流转和船舶调度的全面优化 ,提高了港口吞吐量和作业效率。同时,该系统还加强了 对港口安全和环保的管理和控制,确保了港口运营的可持 续性。
配载优化
02
根据货物特性、车辆承载能力和路线规划,进行合理的配载优
化,提高运输效率。
车辆维护与保养
03
确保车辆处于良好工作状态,定期进行维护和保养,提高车辆
使用寿命和安全性。
实时监控与调整
实时监控运输状态
通过GPS、北斗等定位系统实时监控车辆位置、速度 、货物状态等信息。
调整运输计划
根据实时监控情况,及时调整运输计划,避免延误和 不必要的损失。
应对突发情况
对于突发情况如交通事故、天气变化等,及时采取应 对措施,确保运输安全和效率。
04
案例分析
奥数讲义_3._最优化问题

最优化问题[知识要点]结合实际,联系生活。
通过列举、计算、对比等手段,选择最佳方法。
有些问题,从部分思考,再全面解决问题,得到最佳对策。
[例题解析]例1 甲地有59吨货物要运到乙地。
大货车的载重量是7吨,小货车的载重量是4吨,大货车运一次耗油14升,小货车运一次耗油9升。
运完这批货物至少耗油多少升?解:14÷7=2(升/吨) 9÷4=2.25(升/吨)2<2.25 尽可能用大货车。
59÷7=8(辆)……3(吨)选8辆大货车和一辆小货车。
14×8+9=121(升)答:运完这批货物至少耗油121升. 。
例2 街道旁有ABCDE 五栋居民楼(见下图B 点为中点),现在要建立一个邮筒,为使五栋楼的居民到邮筒的距离之和最短,邮筒应建立在何处?解:(原则是少向多靠、两边向中间靠。
)所以可参考BC 两点。
B 点:AB +BC +(BC +CD)+(BC +CD +DE)C 点:(AB +BC)+BC +CD +(CD +DE)B 点-C 点=BC答:选C 点。
例3 服装厂的工人每天可以生产4件上衣或7条裤子。
一件上衣和一条裤子为一套。
现有66名工人生产,每天最多能生产多少套服装?66÷(1+74)=42(人) 4×42=168(套) 答:每天最多能生产168套服装.例4 桌子放了60根火柴,甲乙二人轮流取。
每人每次取1—3根,取到最后一根者获胜。
甲有必胜的策略吗?解:60÷(1+3)=15让乙先取。
乙取1个,甲取3个;乙取2个,甲取2两个;乙取3个,甲取1个。
这样可以确保甲胜。
例5在黑板上写下数2、3、4……2010,甲先擦去其中一个数,如此轮流下去,若最后剩下两个数互质时,甲胜;若剩下两个数不互质,乙胜;那么甲有必胜的策略吗?解:把相邻两数分成一组,如:2,(3、4),(5、6),(7、8),(9、10)……2008),(2009、2010)甲先取走2,以后和乙拿同一括号的数即可确保胜利。
突发公共事件下应急物流中的优化运输问题的研究

突发公共事件下应急物流中的优化运输问题的研究一、本文概述随着社会的快速发展和全球化的深入推进,突发公共事件,如自然灾害、疫情爆发、事故灾难等,对人类社会的影响日益显著。
这些事件往往导致物资短缺、交通受阻、信息传递不畅等问题,对应急物流系统提出了巨大的挑战。
因此,如何在突发公共事件下优化运输问题,提高应急物流的效率,成为了当前研究的热点和难点。
本文旨在探讨突发公共事件下应急物流中的优化运输问题。
我们将对突发公共事件和应急物流的概念进行界定,明确研究范围和对象。
我们将分析突发公共事件对运输系统的影响,包括物资需求的变化、运输网络的破坏、运输能力的下降等。
在此基础上,我们将探讨应急物流中优化运输问题的关键要素,如运输路径的选择、运输资源的调配、运输成本的控制等。
接下来,我们将通过文献综述和案例分析的方法,深入探究突发公共事件下应急物流优化运输问题的研究现状和发展趋势。
我们将总结前人的研究成果和经验教训,分析现有研究的不足和局限性,为后续的研究提供借鉴和参考。
我们将提出一种基于多目标优化的应急物流运输模型,并通过仿真实验验证其有效性和可行性。
该模型将综合考虑运输时间、运输成本、运输风险等多个因素,以实现应急物流运输的最优化。
我们期望通过本研究,能够为突发公共事件下的应急物流运输问题提供新的解决思路和方法,为未来的应急物流管理和实践提供有益的参考和指导。
二、文献综述在应对突发公共事件的过程中,应急物流的优化运输问题一直备受关注。
众多学者针对这一领域进行了深入的研究和探讨。
本节将对前人的研究成果进行系统的文献综述,旨在明确研究现状、挖掘研究不足,为本研究的深入展开提供理论基础和研究方向。
在应急物流的研究方面,学者们主要关注了应急物流体系的构建、应急预案的制定与实施、应急资源的调度与分配等方面。
其中,优化运输问题是应急物流研究中的核心内容之一。
运输路径的选择、运输资源的调配、运输过程的优化等问题都受到了广泛关注。
货物配送的最优化设计的数学模型

货物配送的最优化设计的数学模型一、问题的提出。
一公司有二厂,分处a,b两市,另外还有4间具有存贮机构的库房,分别在p,q,r 和s市,公司出售产品给6家客户c1,c2,c3,…,c6,由各库房或直接由工厂向客户供货,配送货物的费用由公司负担单价见下表:受货者供货者a市厂b市厂p库房q r sp库房0.5-q库房0.50.3r库房1.00.5s库房0.20.2客户c11.02.0-1.0--c2--1.50.51.5-c31.5-0.50.52.00.2c42.0-1.51.0-1.5c5---0.50.50.5c61.0-1.0-1.51.5注单位:元/吨:划“-”表示无供货关系.某些客户表示喜欢由某厂或某库房供货,计有:c1—a市厂c2—p库房c5—q库房c6—r库房或s库房a市厂月供货量不能超过150千吨,b市厂月供货量不能超过200千吨.各库房的月最大流通量千吨数为:库房p q r s流通量705010040各客户每月所必须满足的供货量为(单位:千吨)客户c1c2c3c4c5c6要求货量501040356020公司希望确定以下事项:1)如何配货,总费用最低?2)增加工厂和库房的生产能力对配送费用的影响是什么?3)费用单价,工厂和库房生产能力以及客户对供货量的最低要求等,各微小变化对配货方案的影响是什么?4)能不能满足各客户对供货者的喜好选择?如果满足,会引起配送费用提高多少?二、摘要。
在公司给客户配送货物的过程中,有两种情况,一种是由工厂直接向客户提供货物,另一种是由库房向客户提供货物,再结合运输的费用问题我们建立了这个货物配送的最优化设计的数学模型.在这个模型中,我们考虑到了以下几点:1.为了保证模型的一般性,我们不考虑不能配送的问题,对所有可能的运输都设了未知量来建立模型,然后根据模型的条件在处理单价时将不可能运货路线的运输价格设为”无穷大”,在实际处理中给予比一般数据高数量级的数据来进行运算.2.我们将模型中的对象分为三层,第一层为供货者,第三层为受货者,第二层既可以为供货者也可以为受货者,为了使模型更直观,我们在第二层里引入a,b两个工厂加入库房的行列,然后将a,b向a,b运货设为不可能运货路线.3.在模型解答中,因为计算量庞大,为了节约时间,我们调用了matlab里的最优化方法的函数来进行运算.4.另外,在模型的解答过程中,由于运输的单价的相同,我们还发现在满足配送费用最低的情况下配送方案并不唯一,其主要不确定因素我们在模型中给予了讨论。
物流运筹学第4章 运输最优化-精选文档

min
2
0 13 11 6 0 10 4 0 5 7 9 7 0 1 4 4
0 13 6 0 0 5 0 1 7 6 3 0
2 11 4 2 2 min
0 9 (bij ) 2 0
第一步,画出该问题的供销平衡表和单位运价表
超市 仓库 A1 A2 A3
B1
B2
B3
B4
3 1 7
11 9 4
3 2 10
10 8 5
第二步,求初始解
1、最小元素法 超市仓库 A1 A2 A3 销量 3 6 5 6 3 B1 B2 B3 B4 储量 7 4 9
计算过程表 超
市 仓库
A1 A2
X 0
用矩阵描述时为
max z CX
AX b X 0 a 11 a 12 a 1 n A (p ,p , ,p ) 1 2 n a a a 1 m 2 mn m
b为资源向量; c为价值向量; x为决策变量的向量
单纯形法简介
问题要求极小化时数学模型是
Min z c x ij ij
i j
x 1 ,j 1 , 2 n
ij i
ቤተ መጻሕፍቲ ባይዱ
x 1 ,i 1 , 2 n
ij j
xij 1 或 0
例题:某物流公司现有四项运输任务A、B、C、D, 现有甲、乙、丙、丁四辆车,他们完成任务所需时 间如表所示。问应指派何人去完成何工作,使所需 总时间最少?
min z cij xij
i 1 j 1
m
n
x b, j 1 ,2 , ,n
i 1 ij j
最优化理论——运输问题的案例
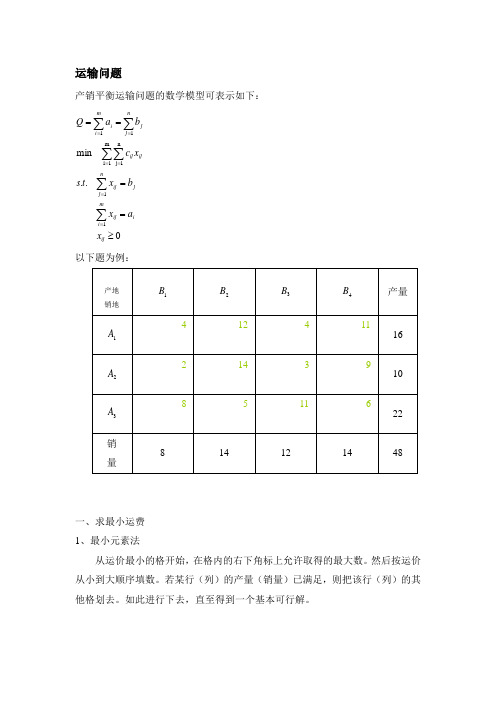
运输问题产销平衡运输问题的数学模型可表示如下:.. min 11m 1i n1j 11≥====∑∑∑∑∑∑======ij i mi ij j nj ij ijij nj jm i i x a x b x t s x c b a Q以下题为例:产地 销地1B 2B 3B 4B产量1A4124 11162A21439103A 8511 622销 量814121448一、求最小运费 1、最小元素法从运价最小的格开始,在格内的右下角标上允许取得的最大数。
然后按运价从小到大顺序填数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
产地 销地1B 2B 3B 4B产量1A4 124 10 116162A2 8143 29103A 85 1411 6822销 量814121448最小运费为:246116685144102382=⨯+⨯+⨯+⨯+⨯+⨯ 2、西北角法从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数。
然后按行(列)标下一格的数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
产地 销地1B 2B 3B 4B 产量1A4 8 12 84 11162A214 6 3 49103A 8511 861122 销814121448量最小运费为:372=6×14+11×8+3×4+10×6+12×8+4×8 3、V ogel (沃格尔)法① 计算出各行各列中最小元素和次小元素差额(罚数),并标出。
② 在罚数最大的行和列中填上尽可能大的数(若有两个罚数最大,则选择最大罚数所在行或所在列运费最小的)。
若有行或列饱和,划去。
③ 重复以上步骤。
产地 销地1B2B3B 4B产量行罚数1 2 3 41A412412 11416 0 0 0 72A28143910 1 1 1 63A 8514116822 1 2销 量 8 14 12 14 48列 罚 数 1 2 5 1 3 2 2 1 3 3 2 1 2 412二、检验是否是最优解 1、闭回路法闭回路:从空格出发,遇到数字格可以旋转90度,最后回到空格所构成的回路;原理:利用检验数的经济含义;检验数:非基变量增加一个单位引起的成本变化量。
数学建模的船队运输最优化问题
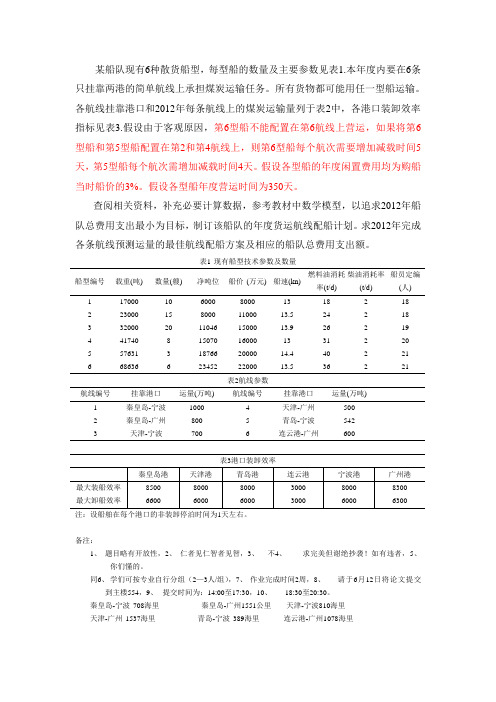
天,第5型船每个航次需增加减载时间4天。假设各型船的年度闲置费用均为购船
当时船价的3%。假设各型船年度营运时间为350天。
查阅相关资料,补充必要计算数据,参考教材中数学模型,以追求2012年船
队总费用支出最小为目标,制订该船队的年度货运航线配船计划。求2012年完成
各条航线预测运量的最佳航线配船方案及相应的船队总费用支出额。
现有船型技术参数及数量船型编号载重吨数量艘净吨位万元船速kn燃料油消耗170001060008000131823000158000110001352432000201104615000139261507016000133118766200001444023452220001353621表2航线参数航线编号挂靠港口运量万吨航线编号挂靠港口运量万吨秦皇岛宁波1000天津广州500秦皇岛广州800青岛宁波542天津宁波700连云港广州600表3港口装卸效率秦皇岛港天津港青岛港连云港宁波港广州港最大装船效率850080008000300080008300最大卸船效率660060006000300060006300注
a62 A62 a63 A63 a64 A64
a65 A65
a66 A66
小写字母代表船数 大写代表船次
各种船往返一次所用的时间
D=2+M/p+M/q+2S/V/24 M:载重量 p:装货率 q:卸货率
S:航线长度 V:船速 2:港口为停靠时间 24:一天 24 小时
1
2
3
4
5
6
秦皇岛-宁 波
11.372
船型编号 载重(吨) 数量(艘)
表1 现有船型技术参数及数量
燃料油消耗 柴油消耗率 船员定编
净吨位 船价 (万元) 船速(kn)
运用线性规划对运输问题进行研究运输问题在企业管理方面的应用

运用线性规划对运输问题进行研究运输问题在企业管理方面的应用一、本文概述随着全球化的推进和市场竞争的日益激烈,运输问题在企业管理中扮演着越来越重要的角色。
如何有效地进行物资运输、降低成本、提高效率,成为了企业运营中必须面对和解决的问题。
线性规划作为一种数学优化技术,为运输问题的研究和解决提供了有力的工具。
本文旨在探讨线性规划在运输问题中的应用,以及它在企业管理中的实际作用。
本文将首先介绍线性规划的基本概念、原理及其在运输问题中的应用原理。
接着,通过具体案例,分析线性规划在运输问题中的实际应用,包括如何建立运输问题的数学模型、如何运用线性规划求解最优运输方案等。
本文还将探讨线性规划在企业管理中的其他应用,如资源分配、生产计划等。
本文将总结线性规划在运输问题和企业管理中的应用效果,并展望未来的发展趋势。
通过本文的研究,我们期望能够帮助企业更好地理解和应用线性规划,优化运输方案,提高运营效率,从而在激烈的市场竞争中获得优势。
也希望本文能为相关领域的研究人员提供参考,推动线性规划在运输问题和企业管理领域的研究和发展。
二、线性规划理论基础线性规划是一种数学方法,用于解决具有线性约束和线性目标函数的优化问题。
它广泛应用于各种领域,包括运输问题。
在企业管理中,线性规划尤其适用于资源分配、生产调度和物流优化等问题。
线性规划问题的基本形式可以描述为:在给定的线性约束条件下,最大化或最小化一个线性目标函数。
这些约束条件和目标函数都是由决策变量的线性组合构成的。
决策变量是在问题中需要优化的变量,例如运输量、生产量等。
在运输问题中,线性规划可以用于优化运输成本、运输时间和运输路线等。
例如,假设一个企业需要将其产品从多个工厂运输到多个销售点,每个工厂和销售点之间的运输成本可能不同。
通过线性规划,企业可以找出一种运输方案,使得总运输成本最低,同时满足各种约束条件,如每个工厂的生产能力、每个销售点的需求量等。
线性规划的理论基础包括线性代数、凸分析和优化理论等。
垃圾运输问题路线最优

垃圾运输问题路线最优城市垃圾收运是由产生垃圾的源头运送至处理处置场的全过程操作,包括3 个阶段:①收集———垃圾从产生源到公共贮存容器的过程;②清运———指清运车沿一定路线清除贮存容器内垃圾并将其转运到垃圾转运站的过程(在一定情况下,清运车可直接将垃圾运送至处理处置场);③中转———指在转运站将垃圾装载至大容量转运车,远途运输至处理处置场。
前1 个阶段需要对垃圾产生源分布情况、垃圾产生量及成分等进行调查和预测;后2 个阶段需要运用最优化技术对清运线路和转运站垃圾分配运输进行优化。
1 城市生活垃圾产生量预测方法城市生活垃圾收运模式的设计是在对生活垃圾产生量作正确预测的条件下进行的,因为设计的收运模式,不仅应满足当前垃圾产生量的需求,而且应该能够应对未来几年的变化。
目前,国内外较为普遍使用的数理统计方法为单指数平滑法、线性回归分析法、灰色系统模型分析法。
1. 1 单指数平滑法Yt+1=aXt+(1-a)Yt。
(1)式中:t 为时间;a 为指数平滑系数,介于0~1;Xt 为t 时垃圾产生量的实际观测值;Yt 为t 时垃圾产生量的预测值;Yt+1 为t+1 时垃圾产生量的预测值。
1. 2 线形回归分析法Y=a0+a1x1+a2x2+…+amxm。
(2)式中:Y 为垃圾预测产生量;xi 为影响垃圾产生的多个因素(i=1,2,…,m);ai 为回归系数(i=1,2,…,m)。
影响垃圾产生的因素有很多,如人口数量、工资收入、消费水平、生活习惯、燃料结构等。
对于众多因素,可以采用变量聚类法,对数据进行预处理。
据介绍,经过数据处理后多元回归分析法中很多变量都属“同解”,经过变量与处理后,实际运算时,相当于一元回归的“人口模式”预测法〔1〕。
1. 3 灰色系统模型分析法灰色系统模型(GM)包含模型的变量维数m和阶数n,记作GM (n,m)。
在生活垃圾产生量预测中普遍使用GM(1,1)模型。
通过对原始的时间序列数据进行累加处理后,数据便会出现明显的指数规律,通过进一步分析,可以进行垃圾产生量预测。
货物配送中的路线规划和优化

货物配送中的路线规划和优化时间就像一把无形的雕刻刀,在任何时刻都在雕刻着人们的生命。
而今天,我们所处的这个时代无疑是一个高速发展的时代,信息技术正在深刻地改变着企业的经营模式。
特别是在电子商务和物流领域,信息技术的应用带来了质的飞跃,使货物配送的效率和成本得到了极大地优化。
本文将探讨货物配送中的路线规划和优化的相关问题。
一、货物配送中路线规划的重要性货物配送中的路线规划和优化是现代物流管理的重要组成部分。
在日常的配送工作中,我们往往要面对复杂的地理环境和各种交通状况,如巨大的交通流量、道路状况的不同、峰值期的拥堵等等,这使得货物配送的路线规划变得复杂而困难。
然而,货物配送中的路线规划和优化对于提高配送效率是极为重要的。
首先,科学的路线规划可以缩短配送路径,从而减少运输时间和物流成本,提高运输速度和货物的安全性。
同时,路线规划也可以避免配送误差,提升配送服务质量,提高客户满意度。
因此说,货物配送中的路线规划是极其重要的。
二、货物配送中路线规划的方法货物配送中路线规划的方法主要有两种:手工规划和智能规划。
手工规划是传统的规划方法,在手工规划中,配送员会根据业务量和经验,结合己有的配送能力进行路线规划。
虽然这种方法较为简单,但需要配送员花费大量的时间和精力去制定每个细节,难以完全控制配送风险,并且难以满足高效、快捷升级的配送需求。
智能规划是一种新型的路线规划方法,其核心是将计算机技术和物流业务相结合,围绕客户需求设置参数,并依据客户的特殊配送要求进行计算。
该方法不依赖对配送员的影响,不受路线障碍和路口严重影响,而是通过智能算法实现自动规划和调度,提升货物配送的速度和准确度。
三、货物配送中路线优化的方法货物配送中路线规划完成后,如何进行路线优化呢?这就要提出路线优化的方法。
路线优化是指在货物配送中对路线进行最优化调整,以达到最低配送成本、最快速配送、最大的交通效益和最大的物流效益。
常见的路线优化方法包括:1.动态路线规划。
运输问题的表上作业法的一个解释

运输问题的表上作业法的一个解释
运输问题的表上作业法,也称作基于选表法或表上方法,是一种分配类型的技术,它是用来求解类似运输问题的一种技术。
这类问题是在现实生活和技术领域中经常被遇到的,它要求将一定数量的物品从某一个地方运输到另一个地方,或者将某种资源从一个地方运输到另一个地方,再或者将某种物品从一个地方运输到多个地方,例如从苹果在北京的仓库运输到上海的几家超市。
与其他分配类型的技术相比,运输问题的表上作业法的优势在于,它可以给出最优的解决方案,而且这种解决方案可以在较短的时间内获得。
它的基本思路是,首先将数据输入到一个表格,如仓库和超市之间的距离或运输成本,然后用一个“对换”算法对表格进行优化,不断“对换”表格中直接相连的数值,使得解决方案到达最优状态,达到最优化。
首先,将运输问题用表格表示,表格中每一行表示从某一出发地到一定目的地的运输距离或运输费用,每一列表示从一定出发地到某一目的地的运输距离或运输费用。
然后,用“费用减少法”对表格进行优化,不断比较当前状态下两点之间的运输成本,如果当前状态下两点之间的运输成本比较大,则以更小的运输成本替换,从而达到最优解。
经过一定的步骤,即可得到运输问题的最优解,计算完成后可得出最小的运输成本,而且可以把最小的运输成本显示出来,使用户能
够清楚明白。
此外,表上作业法在实际应用中还有其他优势,它比较容易实现,只要将数据输入到表格中,即可完成优化,而且计算时间较短。
有时候,表上作业法也可以用来解决更复杂的问题,如经营决策问题、联盟问题和设备调度问题。
总之,运输问题的表上作业法是一种有效的配类型的技术,它可以帮助人们在短时间内得到最优解,最小化运输成本,应用范围也比较广泛,非常适合求解类似运输问题的技术。
运筹学运输问题的方法

运筹学运输问题的方法
运筹学中的运输问题可以通过以下方法进行解决:
1. 确定初始方案:最小元素法、付格尔法和西北角法等,其中最小元素法是先找出运费最小的,然后优先满足。
付格尔法是算出行差额和列差额,依次对差额最大的行或列中运费较小的先分配。
西北角法也是一种求初始可行解的方法。
2. 判定最优解:可以采用闭回路法或者位势法求检验数。
闭回路法是对所选回路上进行“奇+偶-”的操作,而位势法则是直接用公式:检验数=cij-ui-vj。
3. 调整优化解:以检验数<0且最小的数开始入基,对偶数点选择最小的xij出基。
接着为满足表格平衡,使奇数点加上xij,偶数点减xij,记住出基的点为空格点了,这样才能保证有数点一直是m+n-1个。
对于产销不平衡的问题,则考虑增设一个仓库存放多出来的部分,或者增设一个产地弥补不足的部分,这些运费均为0,后做法同上。
4. 重复上述步骤:如果还未得到最优解,则重复步骤2和3,直到求得最优解。
总的来说,运筹学的运输问题需要综合运用多种方法进行求解,通过不断调整和优化解,最终得到最优解。
综合性问题探究---- 运输问题的悖论

运输问题的悖论01 悖论简介02 产生条件03 实际意义01 运输问题的悖论先看一个例子最有运输计划表如下:B1B2B3A1 1 2 3 × 2 35A2 1 × 1 4 4 6 10249最优值为∑∑CijXij=36现将产地A1的产量增加2个单位,销地B2的销量增加2个单位,则最优运输计划表为:B1B2B3A1 1 2 3 × 2 57A2 1 × 1 6 4 6 10269最优值为∑∑CijXij=34从上面的例子可以看到:在产地、销地、单位运价均相同的情况下,运输总量增加了2个单位,但总运价却减少了2个单位,这种奇特的现象称为运输问题悖论。
02 产生条件非退化运输问题悖论出现的条件One在最优运输方案中找到一个非基变量x i0,j0,那么一定可以找到若干个基变量构成唯一一个闭回路。
输入标题Second以非基变量x i0,j0作为第一个顶点出发,将闭回路中的第1,3,5…奇数顶点对应的运价c ij 值取正,第2,4,6…偶数顶点对应的c ij 取值取负,求他们的代数和即为非基变量x i0,j0的检验数λi0,j0定理回顾非退化运输问题悖论出现的条件当我们用表上作业法进行迭代时用到的调整量是闭回路偶顶点上的x i,j 最小值。
0102040506对于非退化问题而言,x i,j的值必然大于0。
在最优运输方案中找到一个非基变量x i0,j0,如果该非基变量的检验数λi0,j0大于该非基变量的运价c i0,j0,当第i0个产地增加产量Y,第j0个销地增加销量Y ,且Y 满足0≤Y ≤min{x i,j |x i,j ≠x i0,j0}时,x i,j 是由x i0,j0出发构成的闭回路上的奇顶点,就会出现总运价下降的情况。
注意非退化运输问题悖论出现的条件第i0个产地增加产量Y,第j个销地增加销量Y后,约束条件变化为:原有最优解无法使新的约束条件继续成立,需要继续迭代。
运筹学最优化原理的例子

运筹学最优化原理的例子
运筹学中的最优化原理有很多应用,以下是其中一些例子:
1. 背包问题:这是一个经典的连续最优化问题。
给定一组物品,每个物品都有自己的重量和价值,目标是选择一些物品放入背包中,使得背包内物品的总价值最大,同时不超过背包的重量限制。
2. 生产计划问题:在生产计划中,需要确定生产哪些产品、生产多少以及如何分配资源。
最优化原理可以用来制定最优的生产计划,使得某种目标函数(如总利润)达到最大或最小。
3. 路径规划问题:在物流和交通运输领域,最优化原理可以用来找到最优的路径规划方案,例如在给定一系列节点和边的情况下,找到一条从起点到终点的最短路径或最低成本路径。
4. 投资组合优化问题:在金融领域,投资者需要决定如何分配他们的资金以最大化收益或最小化风险。
最优化原理可以用来确定最优的投资组合,即在一组可能的投资组合中选择一个最优的组合,使得某个目标函数(如预期收益或风险)达到最优。
5. 调度问题:在生产或服务行业中,需要确定任务的顺序和时间安排以最小化成本或最大化效率。
最优化原理可以用来找到最优的调度方案,使得某个目标函数(如总完成时间或总成本)达到最小或最大。
以上例子只是运筹学中最优化原理的一些应用,实际上还有很多其他的应用领域,如医疗、农业、能源等。
数学建模货运列车编组运输问题

数学建模货运列车编组运输问题数学建模是一门将实际问题抽象化并运用数学方法解决的学科。
货运列车编组运输问题是在实际生产与运输中常遇到的一个问题,即如何合理编组货运列车,以达到效率最大化、成本最小化的目标。
本文将针对这个问题进行深入探讨,并给出一种解决方案。
首先,我们来分析货运列车编组运输问题的背景和影响因素。
货运列车作为运输货物的一种重要方式,具有运载量大、运输成本低的优势。
然而,由于货物种类和数量的不同,以及货物间的相互关系,如何合理编组列车、安排运输路线,成为一个关键问题。
合理的编组方案可以提高运输效率,减少运输成本,提高生产力。
其次,我们来了解一下数学建模在解决货运列车编组运输问题中的应用。
数学建模是通过建立合理的数学模型,运用数学方法来解决实际问题的过程。
在货运列车编组运输问题中,数学建模可以帮助我们确定合适的编组方案。
具体来说,我们可以将问题抽象为一个数学模型,考虑列车的运载限制、货物的属性、运输距离、运输成本等因素,并通过数学方法求解最优解。
接下来,我们来介绍一种常用的数学建模方法——线性规划。
线性规划是一种数学优化方法,用于求解一类特殊的最优化问题。
在货运列车编组运输问题中,我们可以将其建模为一个线性规划问题。
具体来说,我们可以定义目标函数和约束条件,通过线性规划求解器求解最优解。
目标函数可以是最小化运输成本或最大化运输效率,约束条件包括列车的运载限制、货物的属性等。
通过求解线性规划问题,我们可以得到一个最优的编组方案。
除了线性规划,还有其他一些数学建模方法可以用于解决货运列车编组运输问题,如整数规划、动态规划、遗传算法等。
这些方法各有特点,可以根据具体问题的性质选择适合的方法。
然后,我们来讨论一些与货运列车编组运输问题相关的实际案例。
以某货运公司为例,他们需要编组一列货运列车,按照一定的编组规则将货物装载到不同的车厢中,以便快速、高效地运输货物。
该公司采用了数学建模的方法,通过线性规划求解器得到了一个最优的编组方案。
物流管理中的运输优化问题研究

物流管理中的运输优化问题研究随着全球化和信息技术的快速发展,物流管理在我们的日常生活中扮演着越来越重要的角色。
在一个高度竞争的商业环境中,物流成本和效率成为企业获得竞争优势的关键因素之一。
运输作为物流的核心环节,对于物流管理的优化起着至关重要的作用。
1. 运输成本的控制在物流管理中,运输成本是企业最关注的方面之一。
运输成本包括燃料费、人工费、车辆维护费等多个方面。
如何降低这些成本是一个不容忽视的问题。
运输优化可以通过合理的路径规划、装载率优化和运输网络设计来实现。
合理的路径规划能够减少运输距离和时间,降低燃料费用;装载率优化能够最大程度地利用运输工具的容量,减少运输次数和人工费用;运输网络设计能够构建高效的运输网络,提高运输效率。
通过综合考虑这些因素,企业可以实现运输成本的最优化。
2. 运输效率的提升除了成本控制外,物流管理还关注运输效率的提升。
运输效率不仅仅是速度的问题,还包括送达准时性、货物损失率等方面。
运输优化可以通过合理的运输计划和有效的信息流通来实现。
合理的运输计划能够避免不必要的等待时间和中转,提高运输效率;信息流通能够实现货物跟踪和信息共享,减少错误和沟通成本。
提升运输效率既可以提高企业的服务质量,又可以降低运输成本,是物流管理中的重要环节。
3. 物流网络的优化物流网络的优化也是物流管理中的一个重要问题。
物流网络的优化涉及到运输路线的选择、仓储点的布局等方面。
合理的运输路线选择能够减少运输距离和时间,提高运输效率;仓储点的合理布局能够降低中转成本和货物损失率。
物流网络的优化不仅能够降低企业的物流成本,还能够提高物流服务的质量和可靠性。
4. 新技术的应用随着信息技术的快速发展,新技术的应用对物流管理的优化起着越来越重要的作用。
自动化设备、无人机、人工智能等技术的引入能够提高运输效率和准确性。
自动化设备可以实现货物的快速装卸和运输,减少人工操作的错误;无人机可以实现远程快速配送,提高运输效率;人工智能可以进行数据分析和决策支持,提供运输优化的方案。
【精品】运输问题优化模型

运输问题优化模型运输方案问题的优化模型摘要:本文研究运输最优化问题。
运输问题(Transportation Problem)是一个典型的线性规划问题。
一般的运输问题就是要解决把某种产品从若干个产地调运到若干个销地,在每个产地的供应量与每个销地的需求量已知,并知道各地之间的运输单价的前提下,如何确定一个使得总的运输费用最小的方案的问题。
本论文运用线性规划的数学模型来解决此运输问题中总费用最小的问题。
引入x变量作为决策变量,建立目标函数,列出约束条件,借助LINGO软件进行模型求解运算,得出其中的最优解,使得把某种产品从2个产地调运到3个客户的总费用最小。
关键词:LINGO软件运输模型最优化线性规划1问题重述与问题分析1、1 问题重述要把一种产品从产地运到客户处,发量、收量及产地到客户的运输费单价如表1所示。
表1 运输费用表客户1 客户2 客户3 发量产地1 10 4 12 3000 产地2 8 10 3 4000 需求量2000 1500 5000这是一个供求不平衡问题,产品缺少1500个单位,因此决定运输方案应按下列目标满足要求:第一目标,客户1为重要部门,需求量必须全部满足;第二目标,满足其他两个客户至少75%的需要量;第三目标,使运费尽量少;第四目标,从产地2到客户1的运量至少有1000个单位。
1、2 问题分析运输方案就是安排从两个产地向三个客户运送产品的最佳方案,目标是使运费最少。
而从题目来看产品的总量只有7000个单位,客户的需求量却有8500个单位,产品明显的缺了1500各单位,所以至少要按以下要求分配运输,首先客户1为重要部门,需求量必须全部满足,从产地2到客户1的运量至少有1000个单位,即至少向客户1发2000个单位,且从产地2向客户1发的要大于等于1000个单位;其次满足其他两个客户至少75%的需要量,即至少得向客户2发1125个单位,至少向客户3发3750个单位。
最佳的运输方案就是满足了要求中的发量,而让运输费用最少的方案。
最优化理论运输问题

ai
n
bj
(4.2)
i 1
j 1
m
n
如果 ai bj ,就称此运输
mn
Min Z
cij X ij
问题为i非1 平衡j1运输问题,包含
i1 j1
产大于销和销大于产两种情况,
这我们将在第3节介绍。 下面我们只考虑产销平衡
s.t
n
X ij ai
中,目标函数要求运输总费用最小;前m个约束条件的意义
是:由某一产地运往各个销地的物资数量之和等于该产地的
产量;中间n个约束条件的意义是:由各产地运往某一销地
的物资数量之和等于该销地的销量;后mn个约束条件是变量
的非负条件.
11
4.1.2 运输问题数学模型的特点
对于产销平衡运输问题(4.3),将其约束条件加以整理,
= 50 = 70 = 20 = 50 = 60 = 30
上述模型显然是线性规划模型,我们可以使用线性规划的
单纯形法对它进行求解. 但是,当用单纯形法求解运输问题
时,先得给每个约束条件中引入一个人工变量,这样模型
的变量个数就会达到15个,求解是比较繁琐的,因而有必 要寻求更简便的解法.
8
为了说明适于求解运输问题的更好的解法,先看一下运输问 题的一般描述及模型的一般形式. 运输问题的一般形式为:
对工厂1必须有 对工厂2必须有 对工厂3必须有
X11+X12+X13 X21+X22+X23 X31+X32+X33
= 50 = 70 = 20
对商店1必须有 对商店2必须有 对商店3必须有
X11+X21+X31 X12+X22+X32 X13+X23+X33
运输问题的数学模型

运输问题的数学模型
运输问题是指将一定数量的物资从一个地点运输到另一个地点,
在实现最优运输方案的过程中,可能途径多个中间节点。
由于数据可
能很庞大,特别是考虑到影响运输成本的一系列不确定因素,因此,
将运输问题的解决变成一个数学优化模型就显得尤为重要。
数学优化模型是一种描述和尝试求解优化问题的表达型语言,其
中包括一系列变量、目标函数和约束。
根据优化原理,通常优化模型
可以定义为如下公式:
min/max f(x)
s.t. g(x,y) = 0
h(x,y) ≥ 0
其中,f(x)是目标函数,用来描述给定的优化问题的目标;g(x,y) = 0和h(x,y) ≥ 0分别是约束函数,用来限制优化变量的取值,以达到问题的最优解。
运输问题的数学模型包括以下三个部分:
首先,定义运输问题的优化变量。
一般来说,优化变量包括运输量、源点到各中间节点的运输量以及中间节点到收货站的运输量。
其次,描述给定优化变量的目标函数,也就是运输成本最低的最
优化目标,也称为最低成本目标函数:
Minimize Sum[i=1->n] (c(i,j)xij)
其中,c(i,j)是从源点i到收货点j的运输单价,xij是从源点i
到收货点j的运输量。
最后,定义运输问题的限制条件,比如发货量不能大于源点库存;收货量不能大于收货点需求;各中间节点运输出量不能大于运输入量,即xij-xji≥0。
由以上确定的运输问题数学模型,就可以通过解析或者随机算法
等方法进行优化,以获得最优运输解决方案,尽可能地降低运输成本。
货物运输方案

货物运输方案在现代经济中,货物运输是不可或缺的环节。
面对越来越复杂的运输市场,企业如何寻找最优化的货物运输方案是一个必须要考虑的问题。
首先,需要根据货物属性、成本、时效、安全性等要素,综合考虑选择何种运输方式。
目前,常用的运输方式有三种:公路运输、铁路运输和水路运输。
公路运输适用于短途、量少、时效紧的货物运输,而铁路运输适用于远距离、货物重量大的运输;水路运输适用于长距离、大运量、成本低的运输,但时效相对较差。
对于一些特殊的货物,如易爆、易腐、易变形等,需要选择专门的运输方式,如航空运输、低温运输、挂车运输等。
其次,需要根据物流仓储的情况,选择最优的配送方式。
在运输方案中,配送方式也是一个重要考虑因素。
根据物流仓储的情况,有直送、配送、集货等多种选择。
直送适用于货物需要迅速到达目的地时,配送适用于货量较大但发货间隔时间较长的情况,而集货则适用于货量大、发货间隔时间较短的情况。
除此之外,配送时间的选择也是需要注意的因素。
在考虑时效的情况下,经济快递等配送公司可以提供24小时、次日达等服务,更为高效。
最后,需要从运输设备、装卸要素、安全风险等多方面综合考虑,确定货物装载、卸载和安全措施。
货物装卸是一个需要注意的环节,这不仅考验了运输公司的专业水平,也影响了货物运输的成本和安全。
需要考虑合适的装卸设备、作业人员的素质、环境安全等多个因素。
在考虑安全方面,需要考虑货物运输过程中可能出现的安全风险,并采取相应的措施。
例如,对于易爆品货物,需要保证车辆符合相关标准、采取特殊运输措施等,以确保安全。
总之,货物运输方案的优化需要考虑多种因素,从货物属性、成本、时效、安全性等多个方面进行综合评估。
通过合理的选择运输方式、配送方式和安全措施,可以更好地提高运输效率和货物安全保障。
在经济运营中,货物运输方案的制定是企业取得成功的一个重要环节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要:根据运输问题的基本特征,运用最优化的线性规划解决问题,通过实例对运输问题进行优化分析,建立运输问题的线性规划数学模型。
将模型应用于一些特殊的运输问题,从而得到最优化的方案,提高实际运输工作中的经济效益。
关键词:最优化;运输问题;线性规划
1 运输问题的特征
运输问题关心的是以最低的总配送成本把供应中心的任何产品运送到每一个接收中心。
每一个出发地都有一定供应量配送到目的地,每一个目的地都需要一定的需求量。
需求假设:从任何一个出发地到任何一个目的地的货物配送成本和所配送的数量成线性比例关系。
运输问题所需要的数据仅仅是供应量、需求量和单位成本。
这些就是模型参数。
如果一个问题可以完全描述成表1所示的参数表形式,并且符合需求假设和成本假设,那么这个问题(不管其中是否涉及到运输)都适用于运输问题模型,最终目的都是要使配送的总成本最小。
这个模型的参数都包含在参数表中。
下面就通过例题来说明。
A公司是一家汽车生产商,A1、A2是它的工厂,生产的轿车用卡车把它们运送到三个分销仓库:A3、A4、A5。
在下表中列有下列数据:每辆轿车从每个工厂到每个分销仓库所需的运输成本(C ij),每个工厂的供应量,以及每个经销商对轿车的需求量。
求能使运输成本最低的从每个工厂到每个分销仓库运输轿车的数量以及最低的运输成本。
表 1 A公司的运输数据表
解:设X ij(i=1,2;j=1,2,3);为从每个工厂到每个经销商运输轿车的数量,目
标是为了找出能使总运输成本最低的从每个工厂到每个经销商运输轿车的数量。
所以,
目标函数为C=200X11+100X12+300X13+400X21+300X22+200X23
约束条件是:
X11+X12+X13=3000
X21+X22+X23=5000
X11+X21=3000
X12+X22=4000
X31+X32=1000
X ij(i=1,2,j=1,2,3)≥0
用微机很快就可以得出决策变量的下列最优值以及最低的运输成本200万元。
表2 A公司决策变量的最优值表
由上面的例题可以看出,对于一般的运输问题,首先是建立线性规划的模型,模型中包含的内容主要是目标函数和约束条件;然后再应用微机求解。
2 选址
许多公司的管理人员都面临着一个非常重要的决策:在什么地方设置一个新的重要设施。
设施有可能是一个新的工厂、一个新的配送中心、一个新的管理中心或者其他的建筑物。
一般来说,一个建筑物都有几个可供选择的地点。
而且,在经济全球化的今天,这些可供选择的潜在地点很有可能已经超越了国界而在另一个国家中。
在形成决策的过程之中包含了许多很重要的因素,其中一个就是运输成本。
A公司是一家大型石油公司。
公司拥有大型配送网络。
把石油运送到公司的
炼油厂,然后再把石油产品从炼油厂运送到公司的配送中心。
A公司正在持续增加其几种主要产品的市场占有率,因此管理层决定建立一个新的炼油厂来增加公司的产量,接下来要作的决策就是确定在什么地方建设新的炼油厂。
他们确定了三个非常有潜力和吸引力的备选地点。
表中是A公司的一些相关数据,其中A1、A2是已有的炼油厂,B1、B2、B3是被选地点,C1、C2、C3是油田,D1、D2、D3、D4是配送中心。
表3 A公司的相关数据
表4 原油和石油制品的运输成本数据
现在要确定的是每一个新炼油厂建造地点选择带来的总原油运输成本以及每一个新炼油厂建造地点选择带来的总石油制品运输成本。
对于这两种成本来说,一旦确立了建造地点,最优的运输计划也就确定了。
因此,为了找出潜在选择地点的每一种成本,有必要为每一种情况都作出一个最优运输计划,然后再计算出相
应的成本。
以选择在B1建造新的炼油厂为例。
(1)确定最低的总原油运输成本。
设X ij(i=1,2,3, j=1,2,3)为从油田向炼油厂运输原油的数量。
目标函数为:
C1=2X11+4X12+3X13+4X21+5X22+1X23+5X31+7X32+4X33
约束条件:
X11+X12+X13=80
X21+X22+X23=60
X31+X32+X33=100
X11+X21+X31=90
X12+X22+X32=70
X13+X23+X33=80
X ij(i=1,2, j=1,2,3) ≥0
通过微机可以得出决策变量的最优值为:
X11=10 X12=70 X13=0 X21=0 X22=0 X23=60 X31=80 X32=0 X33=20
最低的总原油运输成本为840万元。
(2)确定最低的总石油制品运输成本
设Y ij(i=1,2,3, j=1,2,3,4) 为从炼油厂运输到配送中心的石油制品数量。
目标函数为:
C=5Y11+2Y12+6Y13+8Y14+6Y21+4Y22+3Y23+5Y24+8Y31+6Y32+3Y33+2Y34
Y11+Y12+Y13+Y14=90
Y21+Y22+Y23+Y24=70
Y31+Y32+Y33+Y34=80
Y11+Y21+Y31=60
Y12+Y22+Y32=50
Y13+Y23+Y33=70
Y14+Y24+Y34=6
X ij(i=1,2, j=1,2,3)≥0
通过微机可以得出决策变量的最优值为:
Y11=40 Y12=50 Y13=0 Y14=0 Y21=20 Y22=0 Y23=50 Y24=0 Y31=0 Y32=0 Y33=20 Y34=60
最低的总石油制品的运输成本为750万元。
同理如果选择在B2建造新的炼油厂可以得出最低的总原油运输成本为900万元,最低的总石油运输成本为910万元,如果选择在B3建造新的炼油厂可以得出最低的总原油运输成本为1060万元,最低的总石油运输成本为770万元。
表5 A公司每一个被选厂址所带来的年变动成本
单位:百万
元
经过比较总变动成本,最终可以选择在B1建造新的炼油厂。
3 结束语
所有经理都会遇到有约束条件下的最优化问题,因此线性规划在许多管理问题中都能应用,只要是对生产、制造、投资、财务、工程等求最大利润、最小成本等问题,就基本上可以用线性规划来求解。
作为一个管理人员,应当能够把面临的问题描述为一个线性规划问题并进行分析。
【参考文献】
[1] 胡运权,郭耀煌运筹学教程[M].北京;清华大学出版社,1998
[2] H?克雷格?彼得森,W?克里斯?刘易斯,管理经济学[M].北京;中国人民大学
出版社,2005
[3] 张建中,许绍吉.线性规划[M].北京:科学技术出版社,1997。
