SolidWorks 蜗杆参数方程式驱动建模
solid works参数方程

solid works参数方程
在SolidWorks中,参数方程是一种控制零件或装配体尺寸的方法。
通过定义参数,可以控制模型的尺寸和形状。
具体操作步骤如下:
1. 打开SolidWorks软件,打开需要创建参数方程的模型。
2. 在模型树中选择需要创建参数的尺寸,右击选择“参数”。
3. 在弹出的参数属性对话框中,输入参数名称和参数值,并选择参数类型。
4. 点击“确定”按钮,完成参数的创建。
5. 在设计树中展开“方程式”文件夹,右击空白位置选择“新建方程式”。
6. 在弹出的方程式编辑器中,输入参数方程,例如“D1=D2*0.5”,其中D1和D2为两个需要关联的尺寸。
7. 点击“确定”按钮,完成方程式的创建。
8. 保存并关闭SolidWorks软件,重新打开模型时,即可看到参数方程已经生效。
需要注意的是,参数方程的创建需要一定的SolidWorks使用经验,以及对模型结构和设计要求的了解。
在创建参数方程时,需要仔细考虑参数的命名和参数方程的逻辑关系,以确保模型的可维护性和准确性。
solidworks曲线方程式驱动详解

SolidWorks中的曲线方程式驱动是一种功能,它允许您使用数学方程来定义曲线形状。
通过输入适当的方程式,可以创建各种复杂的曲线和曲面。
以下是使用SolidWorks中曲线方程式驱动的详细步骤:1. 打开SolidWorks软件并创建一个新的零件文件。
2. 在"特征"工具栏中选择"曲线"下的"方程式驱动曲线"选项。
3. 在弹出窗口中,您可以开始定义曲线方程。
在这里,您可以使用数学函数、变量和操作符来构建方程。
4. 您可以在方程框中输入单个方程,也可以使用多个方程来定义复杂的曲线形状。
您可以使用"+"、"-"、"*"和"/"等基本算术操作符,以及sin、cos、tan等常见数学函数。
5. 在输入方程之前,请确保先定义变量。
您可以通过在方程框中输入类似于"X = 2"或"Y = 3"的方程来定义变量。
定义变量后,您可以在其他方程中引用这些变量。
6. 您还可以使用条件语句和循环语句来创建更复杂的曲线形状。
例如,您可以使用if语句根据不同的条件设置曲线的不同部分。
7. 在定义完方程后,单击"应用"或"确定"按钮生成曲线。
SolidWorks将根据您的方程计算曲线的点坐标,并在绘图区域显示出来。
8. 您可以进一步编辑和调整曲线的参数,以满足您的需求。
您可以修改方程中的变量值,添加更多方程或删除不需要的方程。
使用SolidWorks的曲线方程式驱动功能,您可以创建各种复杂的曲线形状,如螺旋线、花瓣形状、椭圆等。
这种方法可以提供更大的灵活性和精确度,使您能够通过数学方式精确控制曲线的形状和特征。
1。
Solidworks2010双头蜗杆的建模
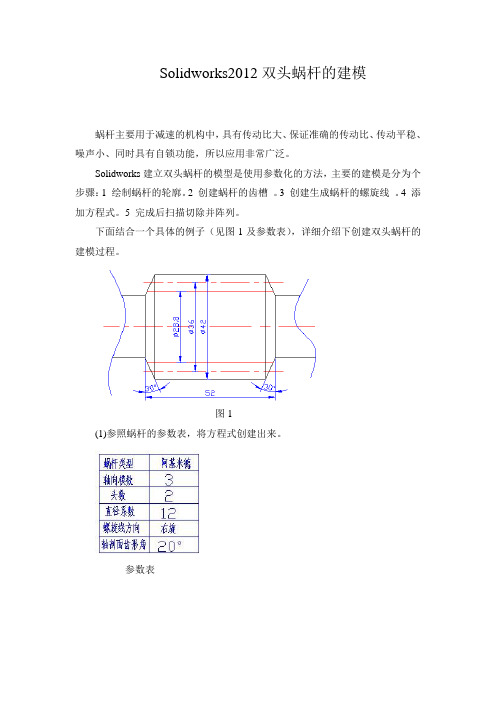
Solidworks2012双头蜗杆的建模蜗杆主要用于减速的机构中,具有传动比大、保证准确的传动比、传动平稳、噪声小、同时具有自锁功能,所以应用非常广泛。
Solidworks建立双头蜗杆的模型是使用参数化的方法,主要的建模是分为个步骤:1 绘制蜗杆的轮廓。
2 创建蜗杆的齿槽。
3 创建生成蜗杆的螺旋线。
4 添加方程式。
5 完成后扫描切除并阵列。
下面结合一个具体的例子(见图1及参数表),详细介绍下创建双头蜗杆的建模过程。
图1(1)参照蜗杆的参数表,将方程式创建出来。
参数表点击图标,进入Solidworks2012的界面。
单击“工具”-“方程式”按钮,并添加方程式(见图2)图2方程式添加完成后,将实行具体的建模过程。
(2)绘制轮廓图形,将轮廓创建出来(见图3),轮廓的二维图(见图1)。
图3(3)创建蜗杆齿槽螺旋线,在右视基准面右边60mm处创建一个辅助的平面,再辅助的平面上以分度圆直径36为基准,画一条螺旋线,将螺旋线的螺距设为“18.85mm”,圈数为“3”,起始的角度设为90,单击“确定”按钮。
在创建导程时,有显示红色的方程式的字母,首先我们添加尺寸,双击尺寸数字下的尺寸线,系统会弹出“修改”的对话框,然后在数字栏中输入=“z1”*“px”即可。
(见图4)图4(4)绘制蜗杆齿槽轮廓,通过螺旋线的起点建立平面,并绘制齿廓。
齿廓的平面草图在创建时也是需要修改尺寸的数值,用如上创建导程的方法创建。
(见图5)图5(5)通过扫描切除的命令将创建出一个齿槽,选择设计树中刚创建的草图和轮廓,单击特征工具栏中的“扫描切除”按钮,然后弹出“扫描切除”属性管理器进行设置。
(见图6)图6(6)完成一条齿槽之后,利用圆周阵列创建出另外的一条齿槽,单击特征工具栏中的“圆周阵列”按钮,选择“视图”——“临时轴”的命令,将显示临时需要的阵列轴,设置轴线为“360度”,实例数为“2”。
(见图7)图7总结,从此例中可以看出,Solidworks2012在蜗杆的设计方面还是比较有强大的功能的,本例我们是利用方程式的驱动来创建蜗杆,但也可以利用方程式来创建蜗轮,齿轮一类的零件,比较容易实现这一类标准且有规则的产品。
Solidworks2010双头蜗杆的建模

Solidworks2012双头蜗杆的建模蜗杆主要用于减速的机构中,具有传动比大、保证准确的传动比、传动平稳、噪声小、同时具有自锁功能,所以应用非常广泛。
Solidworks建立双头蜗杆的模型是使用参数化的方法,主要的建模是分为个步骤:1 绘制蜗杆的轮廓。
2 创建蜗杆的齿槽。
3 创建生成蜗杆的螺旋线。
4 添加方程式。
5 完成后扫描切除并阵列。
下面结合一个具体的例子(见图1及参数表),详细介绍下创建双头蜗杆的建模过程。
图1(1)参照蜗杆的参数表,将方程式创建出来。
参数表点击图标,进入Solidworks2012的界面。
单击“工具”-“方程式”按钮,并添加方程式(见图2)图2方程式添加完成后,将实行具体的建模过程。
(2)绘制轮廓图形,将轮廓创建出来(见图3),轮廓的二维图(见图1)。
图3(3)创建蜗杆齿槽螺旋线,在右视基准面右边60mm处创建一个辅助的平面,再辅助的平面上以分度圆直径36为基准,画一条螺旋线,将螺旋线的螺距设为“18.85mm”,圈数为“3”,起始的角度设为90,单击“确定”按钮。
在创建导程时,有显示红色的方程式的字母,首先我们添加尺寸,双击尺寸数字下的尺寸线,系统会弹出“修改”的对话框,然后在数字栏中输入=“z1”*“px”即可。
(见图4)图4(4)绘制蜗杆齿槽轮廓,通过螺旋线的起点建立平面,并绘制齿廓。
齿廓的平面草图在创建时也是需要修改尺寸的数值,用如上创建导程的方法创建。
(见图5)图5(5)通过扫描切除的命令将创建出一个齿槽,选择设计树中刚创建的草图和轮廓,单击特征工具栏中的“扫描切除”按钮,然后弹出“扫描切除”属性管理器进行设置。
(见图6)图6(6)完成一条齿槽之后,利用圆周阵列创建出另外的一条齿槽,单击特征工具栏中的“圆周阵列”按钮,选择“视图”——“临时轴”的命令,将显示临时需要的阵列轴,设置轴线为“360度”,实例数为“2”。
(见图7)图7总结,从此例中可以看出,Solidworks2012在蜗杆的设计方面还是比较有强大的功能的,本例我们是利用方程式的驱动来创建蜗杆,但也可以利用方程式来创建蜗轮,齿轮一类的零件,比较容易实现这一类标准且有规则的产品。
用SolidWorks精确建立锥面包络蜗杆的三维实体

式中: - !— — —用盘状刀具加工蜗杆时, 蜗杆作螺旋 运动的转角; - - - "! — — —刀具轴与蜗杆轴的夹角; - $ — — —蜗杆的螺旋运动参数。 为了从坐标系 %( 变换到坐标系 % % , 需使用矩阵等式 & % ’ ( %! & ! , 式中: - "! — — —刀具圆锥面 (图 .) 的矢量; - ! %!— — —空间坐标变换矩阵。 其方程式分别为 - & ! ’ ))’*#( $*! + *+($,! )+ ()*+(#! " #) -! , ( /) ! )’* 式中: - )— — —圆锥面上的点距锥顶的距离; — —刀具绕回转轴转动的角度。 $— )’* ! !% ! & !%’ !’ ( & " *+(! # # 触线由如下方程确定 &! ’ &( ), , #! $ ! & % ! $ ! & # , $) ! 式中: - #! — — —刀具圆锥面的法线矢量; %! — — —刀具圆锥面的法线单位矢量; $! — — —刀具圆锥面与蜗杆接触处的相对运 动速度矢量。
(M& 贵州大学 机械工程及自动化学院, 贵州 贵阳’ PP)))N ; !& 华北水利水电学院 机械学院, 河南 郑州’ OP)))) ; N& 广东工贸职业技术学院, 广东 广州’ PM)))); O& 浙江师范大学 交通学院, 浙江 金华’ N!M))) )
摘’ 要: 以 2$%<=+$>?@ 为平台, 应用微分几何, 依据 啮合原理, 使用 #Q *&) 编程, 精确 建立锥面包 络蜗杆的三 维实体。建立了锥 面包络蜗杆的三维实体可用于有限元分析和蜗轮蜗杆副传动的动力学分析。 关键词 : 锥面包络蜗杆; 2$%<=+$>?@ 软件; 扫描 中图分类 号: -7NMM& M : -9MN!& OO’ ’ ’ 文献标识码: Q’ ’ ’ 文章编号: M))* R *OO* ( !))* ) )" R ))!S R )N
SOLIDWORKS工业机器人数字化建模教程 项目五 底盘旋转蜗杆的数字化设计

任务三 创建螺旋线
项目要求
项目实施
绘制螺旋线
现场经验
图5-8【螺旋线/涡状线】属性管理器
图5-9 绘制完成螺旋线
任务三 创建螺旋线
项目要求
项目实施
现场经验
任务四 扫描切除生成螺纹
一、绘制截面草图
图5-10 绘制截面草图中心线
图5-11 绘制截面轮廓线
图5-12 截面尺寸标注
图5-13 完全定义的截面草图
项目要求
项目实施
三、扫描切除 扫描切除的方法如下:
现场经验
方法一
菜单【插入】→【切除】→【扫描】。
方法二
单击【特征】选项卡的【扫描切除】按钮
方法三 单击【特征】工具栏的【扫描切除】按钮
任务四 扫描切除生成螺纹
项目要求
项目实施
现场经验
图5-14【切除-扫描】属性管理器设置和效果预览
图5-15扫描切除生成螺 纹
项目要求
项目实施
现场经验
二、绘制螺旋线,绘制螺旋线的方法如下:
方法一
菜单【插入】→【曲线】→【螺旋线/涡状线】。
方法二
单击【特征】选项卡的【曲线】按钮右侧下三角按钮,
在弹出的下拉列表中选择【螺旋线/涡状线】按钮
方法三
单击【特征】工具栏的【曲线】按钮右侧下三角按钮, 在弹出的下拉列表中选择【螺旋线/涡状线】按钮
SOLIDWORKS工业机器人数字化建模教程
项目五 底盘旋转蜗杆的数字化设计
学习目标
了解用特征进行建模的构思和结构分析。 熟悉3D螺旋线/涡状线、扫描切除特征。 掌握特征扫描、基准轴的使用。
项目要求
项目实施
现场经验
项目引入:本项目要求完成该零件的三维数字化设计。底盘旋转蜗杆是机 械臂中非常重要的传动零件。如图5-1所示。
SolidWorks驱动方程曲线简单教程

SolidWorks中“方程式驱动的曲线”工具的应用自从SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的 X 值以后,Y 值会随着 X 值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X 值表达式中含有变量 T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程类型:正弦函数函数解析式:1正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)2A——振幅、(ωx+φ)——相位、φ——初相3k——偏距、反应图像沿Y轴整体的偏移量4ω目标:模拟交流电的瞬时电压值得正玄曲线图像,周期,φ=,A=2操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
方程式:X1=- ,X2=函数图像:如图 1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式:Yx=1一次函数是一条直线 , y值与对应x值成正比例变化,比值为k 2k、b是常数,x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图 1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式:Yx=1平面内,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
SolidWorks蜗轮蜗杆建模方法

SolidWorks蜗轮蜗杆建模方法一、蜗杆传动概述蜗杆传动由蜗杆和蜗轮组成,按蜗杆形状可分为圆柱蜗杆(图1左图)和环面蜗杆(图1右图)两种类型。
图1 蜗杆传动类型圆柱蜗杆按其螺旋面的形成方式分为阿基米德蜗杆(即普通蜗杆,标记为ZA 蜗杆)与渐开线蜗杆(ZI蜗杆)。
ZA蜗杆便于加工,应用较普遍。
其齿面为螺旋面,其轴向截面齿廓为直线,两相邻齿廓线的夹角2α= 40°。
图2 ZA蜗杆传动蜗杆传动的几何尺寸计算公式如下表1所示。
表1 ZA蜗杆传动几何尺寸计算公式(参看图2)蜗轮咽喉母圆半径:r g2 = a – d a2/2 (公式1)其中,与蜗杆齿形建模有关的分度圆直径、齿顶圆直径、齿根圆直径、蜗杆轴向齿距,蜗杆分度圆柱上的螺旋导程角γ(也称为螺旋升角)等5个参数。
如图3所示为蜗杆分度圆柱面上的螺旋线展开图,图中γ为分度圆上螺旋线的导程角(即升角),p x1为蜗杆轴向齿距,d1为蜗杆分度圆直径,s为蜗杆螺旋线的导程,z1为蜗杆螺旋线的线数。
图3 蜗杆导程角由图3可知,tanγ= s/πd1=z1 p x1/πd1s = πd1·tanγ= z1 p x1 = z1πm (公式2)二、蜗杆、蜗轮零件图如图4、图5所示为蜗杆传动互相啮合的蜗杆和蜗轮的零件图(注:图中所注蜗杆螺旋升角γ有误,应为5°42′38″)。
图4 蜗杆零件图图5 蜗轮零件图零件建模时,先按零件图创建各个特征,其中轮齿部分按齿顶圆尺寸创建齿胚,然后再切出齿形。
三、蜗杆建模1. 按蜗杆零件图(图4)创建齿胚特征,如图6所示。
图6 蜗杆齿胚2. 创建蜗杆齿形齿形由齿形截面沿螺旋线扫描切除形成,因此:1)第一步先创建螺旋线:由于采用扫描切除,所以螺旋线的圈数可以多一些,要超过蜗杆齿形部分的全长(184),故选直径Φ55圆柱的右端面画螺旋线的定义圆,直径为蜗杆的分度圆直径Φ80,如图7所示。
图7 螺旋线定义圆使用此草图创建螺旋线,根据公式2,计算得到螺旋线的螺距为25.12,其余参数见图8所示。
如何用SolidWorks实现蜗轮蜗杆的运动仿真

方法/步骤
1、已经装配好的一对啮合的蜗轮蜗 杆,新建运动算例,并选择动画,如 下图所示:
方法/步骤
2、添加一个旋转马达,并设置好相 关参数。SolidWorks马达是动力的源 泉,能量的源头,它包括旋转马容,以图片内 容为准。
方法/步骤
如何用SolidWorks实现蜗轮 蜗杆的运动仿真?
参考资料:机械设计基础课程设计——基于SolidWorks的实现
《机械设计基础课程设计——基于SolidWorks的实现》是2019年6月清华大学出版社出版的图书, 作者是林秀君、林怡青、谢宋良、吕文阁、成思源。
内容介绍
在实际工作中,我们都会用SolidWorks进行动画制作,可能会不太清楚如何添加一个旋转马达, 来实现零件之间旋转运动的传递,下面我就来做一下蜗轮蜗杆的运动仿真。
3、设置完成后,动画提示条自动添 加模拟动作的时间。当然,你也可以 自己来确定模拟运动的时间,如下图 所示:
方法/步骤
4、点击运算,查看仿真,也可以保 存动画,如下图所示:
方法/步骤
左图表示了本步骤的内容,以图片内 容为准。
感谢观看
基于SolidWorks的蜗轮蜗杆三维参数化

2012届本科毕业论文(设计)论文题目:基于SolidWorks的蜗轮蜗杆三维参数化设计学生姓名:所在院系:所学专业:导师姓名:完成时间:基于SolidWorks的蜗轮蜗杆三维参数化设计摘要本设计以蜗轮蜗杆为研究对象,建立其数学模型,使用Visual Basic语言对SolidWorks2011进行二次开发。
通过录制宏、编辑宏的方法,获得参数化设计的源程序,在Visual Basic 6.0编辑器中对其进行相应的代码替换和修改,最后制作成简单的程序,并添加控件和窗体来实现蜗轮蜗杆的三维参数化实体设计建模。
通过对蜗轮蜗杆的参数化设计,详细说明了基于Visual Basic语言进行的SolidWorks二次开发方法,为初学者提供一个便利的参考,提高了编程效率,可以避免走一些不必要的弯路,也对类似的复杂曲面形状的零部件三维参数化设计提供了借鉴。
蜗轮蜗杆参数化设计与SolidWorks造型软件的开发,不仅实现了蜗轮蜗杆的参数化设计与三维实体造型的结合,缩短了产品设计时间,有利于提高产品开发的效率和质量,同时所完成的三维实体零件模型为后续的进一步研究工作提供了必要的条件。
关键词:蜗轮蜗杆,Visual Basic,SolidWorks 2011,参数化Parametric 3D-Design for Worm and Worm Gear Based onSolidWorksAbstractThis design takes the worm and worm gear as an object,establishes its mathematical model,introduces the theory and method of the Redevelopment approach or SolidWorks2011 with Visual Basic. Modifing and replacing the source program obtained by recording and editing macro in Visual Basic 6.0, finally makes into a simple program. And it helps us to achieve the worm and worm gear three-dimensional parametric solid model by adding the controls and forms.By the Parametric 3D-Design for worm and worm Gear , it makes us understand the secondary development of SolidWorks and Provides a favorable reference for beginners to improve their programming efficiency and avoid detours. It also provides a reference for three-dimensional design of similar parts with complex surface shape . The development of worm and worm gear parametrical design and modeling software brings about the join of gear parametrical design and three- dimensional substance modeling ,shortens the time of design produce ,and benefits the improvement of produce quality and efficiency..It has realized the wormAnd worm gear three-dimensional parametric model, which has provided the essentional condition for the following further research work.Keywords:worm and worm gear , Visual Basic, SolidWorks 2011, parametric目录第一章绪论 (1)1.1蜗轮蜗杆传动特点 (1)1.2SolidWorks二次开发的研究背景和意义 (1)第二章SolidWorks软件的简介 (1)2.1SolidWorks软件的特点 (1)2.2SolidWorks的二次开发功能 (2)2.3 Visual Basic对SolidWorks的简单开发过程 (2)2.3.1宏工具条 (2)2.3.2宏录制及其源代码的简单调试 (3)第三章蜗轮蜗杆的参数化描述 (5)3.1蜗轮蜗杆传动的主要参数及选择 (5)3.2蜗轮蜗杆的参数化计算 (7)第四章蜗轮蜗杆参数化建模的实现 (7)4.1参数化建模中约束参数的提取 (8)4.2数学模型 (8)4.2.1蜗杆的数学模型 (8)4.2.2蜗轮的数学模型 (9)4.3蜗轮蜗杆参数化建模的基本步骤 (10)4.3.1蜗杆的建模步骤 (11)4.3.2运用程序创建蜗杆实体 (11)4.3.3蜗轮的建模步骤 (17)4.3.4运用程序创建蜗轮实体 (18)第五章结论 (24)参考文献 (25)致谢 (26)附录1蜗杆程序 (27)附录2蜗轮程序 (33)第一章绪论1.1蜗轮蜗杆传动特点蜗轮蜗杆传动主要是在空间交错的两轴间传递运动和力的一种传动机构,常见的有圆柱蜗杆传动、环面蜗杆传动、和锥蜗杆传动。
SOLIDWORKS装配体中使用方程式进行参数化设计

SW里的装配体中使用方程式进行参数化设计1、在单个零件里使用方程式的方法:例如如下的一个长方体。
在零件树的注解右击鼠标。
勾选显示特征尺寸。
用…(AJ显示庄解曲.示杼iiL弓寸J旦=示DimXpE注醒田簸然中晒㈤~ 目弼ED到i主解通理旧)蜀朝翩咽显示状志.:H|弟,川析m取目mI五/套洞面目…阳】在隐藏/显示项目中,钩选查看尺寸名称项。
iimulation查看尺寸名部控割尺寸■名称的壶示状态。
也可以在视图菜单中选择显示尺寸名称。
这样只要我们点中零件。
零件就会显示出尺寸及其名称了。
添加方程式。
菜单下拉“工具”二》“方程式”,打开方程式对话框。
法路点[町 分型草图⑸ 3 口阜图闾 网格⑸ 所肓注黑(AJ尺寸5称 捶人田工具 E Simulation ToolboK PhotoView 360 营口炉」帮 E显示⑼修改(MJ 光源与相机© G -—iff 量耿阳 荧群捕获(NJ "廿•国Ctrl+R-। ----------------------除藏所有类型m 基准面阴 活动剖切面(U 基准轴内 临时轴凶 原点(D曲展⑻喝并45阚ku 胱4宣示状态1=! .i 星击史记录 「切,旃11. A 注龌 1••在 Q235:••侬的亚基螭 i5上祝基宫回 !专司Q4SL J 原广在方程式对话框中。
点击“按序排列视图”然后在对应的列里,点选零件显示的尺寸名称即可。
二S E5iirulEtion ri] olb sx 身 口闺甯用(M : = I'l豆庭安田廖拈[心SEZ = mm 醵a£J 块土扫关工具山 标注尺寸t£l 口呵工 S®5(Q)-,枷 芭反/惨友DtsiQn Checke-野正毓i 叫虬 度m 三性MI . 哈营⑹ 几何启折“. 与证免LiFl,“ DimXpert爸冲矶,;玲。
苓I 4我人等新(G 】一 滨三分析必… 厚度!2诲,喔a,.方程式、整钵变量、及尺寸■D2遍草=P1喜草图『二 ,口1侬曰合一疝"/= □2®草图丁名舜数面方程式 冒过海斤有栏区无论是草图尺寸还是特征。
SolidWorks驱动方程曲线简单教程

SolidWorks中“方程式驱动的曲线”工具的应用自从SolidWords自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系) 下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确的数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的 X 值以后,Y 值会随着 X 值的围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值围,X值表达式中含有变量 T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T 的定义域围求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线的关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转化到笛卡尔坐标系以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWords帮助文件详细了解使用方法。
(一)显式方程类型:正弦函数函数解析式:1正弦曲线是一条波浪线,k、ω和φ是常数(k、ω、φ∈R,ω≠0)2A——振幅、(ωx+φ)——相位、φ——初相3k——偏距、反应图像沿Y轴整体的偏移量4ω目标:模拟交流电的瞬时电压值得正玄曲线图像,周期,φ=,A=2操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
方程式:X1=- ,X2=函数图像:如图 1-1 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-1类型:一次函数函数解析式:Yx=1一次函数是一条直线 , y值与对应x值成正比例变化,比值为k 2k、b是常数,x∈R目标:模拟速度—位置曲线,k=4,b=0操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程方程式: Yx=4*x+0函数图像:如图 1-2 所示,使用尺寸标注工具得出图像关键点对应的数值图 1-2类型:二次函数函数解析式:Yx=1平面,到一个定点F和不过F的一条定直线L距离相等的点的轨迹(或集合)称之为抛物线。
solidworks用方程式驱动曲线

solidworks用方程式驱动曲线SolidWorks自从2007版开始,草图绘制工具中添加了“方程式驱动的曲线”工具,用户可通过定义”笛卡尔坐标系”(暂时还不支持其他坐标系)下的方程式来生成你所需要的连续曲线。
这种方法可以帮助用户设计生成所需要的精确数学曲线图形,目前可以定义“显式的”和“参数的”两种方程式。
本文将分别依次介绍这两种方程式的定义方法,以及绘制一些特殊曲线时的注意事项。
“显式方程”在定义了起点和终点处的X 值以后,Y值会随着X值的范围而自动得出;而“参数方程”则需要定义曲线起点和终点处对应的参数(T)值范围,X值表达式中含有变量T,同时为Y值定义另一个含有T值的表达式,这两个方程式都会在T的定义域范围内求解,从而生成需要的曲线。
下面介绍一下笛卡尔坐标系下常用的一些曲线的定义方法,通过图片可以看出所绘制曲线关键位置的数值。
对于有些在其他坐标系下定义的曲线方程,例如极坐标系方程,大家可以使用基本的数学方法先将该坐标系下的曲线方程转换到笛卡尔坐标系,以后就可以重新定义该曲线了。
关于“方程式曲线”对话框其他的选项功能大家可以参照SolidWorks 帮助文件详细了解使用方法。
一、显式方程1.类型:正弦函数(1)函数解析式:。
其中,正弦曲线是一条波浪线,是常数(k 、ω、φ∈R,ω≠0);A是振幅、(ωx+φ)是相位、φ是初相;k是偏距,是反应图像沿Y轴整体的偏移量;且(2)目标:模拟交流电的瞬时电压值得到正弦曲线图像,周期(3)操作:新建零件文件→工具→选择绘图基准面→方程式驱动的曲线,键入如下方程。
(4)方程式:(5)函数图像:如图1所示,使用尺寸标注工具得出图像关键点对应的数值。
2.类型:一次函数(1)函数解析式:。
其中一次函数是一条直线,y值与对应x值成正比例变化,比值为k ;k 、b 是常数,x∈R。
(2)目标:模拟速度—位置曲线,其中k=4,b=0。
(3)操作:新建零件文件→选择基准面→驱动的曲线,键入如下方程。
SolidWorks 蜗杆参数方程式驱动建模
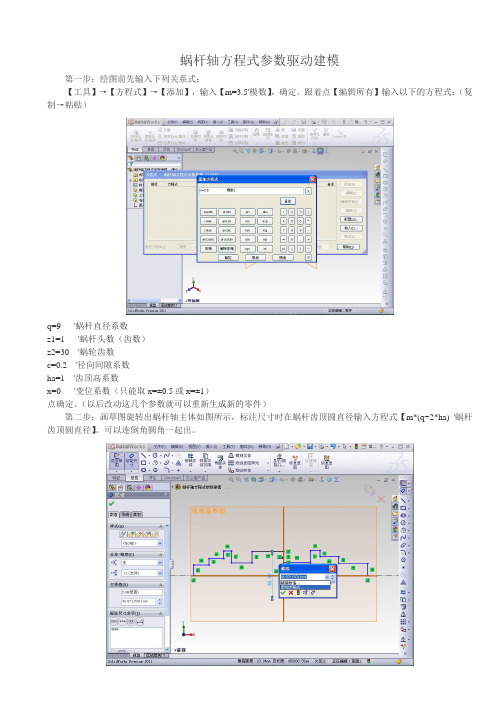
蜗杆轴方程式参数驱动建模第一步:绘图前先输入下列关系式:【工具】→【方程式】→【添加】,输入【m=3.5'模数】,确定。
跟着点【编辑所有】输入以下的方程式:(复制→粘贴)q=9 '蜗杆直径系数z1=1 '蜗杆头数(齿数)z2=30 '蜗轮齿数c=0.2 '径向间隙系数ha=1 '齿顶高系数x=0 '变位系数(只能取x=±0.5或x=±1)点确定。
(以后改动这几个参数就可以重新生成新的零件)第二步:画草图旋转出蜗杆轴主体如图所示,标注尺寸时在蜗杆齿顶圆直径输入方程式【m*(q+2*ha) '蜗杆齿顶圆直径】。
可以连倒角圆角一起出。
【插入】→【曲线】→【螺旋线】双击螺旋线,双击螺距20,添加方程式【PI*m'螺距(即蜗杆轴节(蜗轮周节))】第四步:以螺旋线起头画出蜗杆齿形截面图:中心线离原点高度为蜗杆分度圆半径,方程式为【m*q /2'分度圆半径】,分别标注添加方程式【ha*m'蜗杆齿顶高】、【(ha+c)*m'蜗杆齿根高】、分度圆齿厚【PI*m/2'分度圆齿厚螺距/2】(要先画出两个点来标注)。
以这草图和螺旋线扫描切除出齿形。
然后再完成键槽、加工中心孔、材料等等。
最后的结果:本模型所用的方程式:('这个符号是用来加备注的,跟方程式一起输入方便知道是什么)"m"=3.5 '模数"q"=9 '蜗杆直径系数"z1"=1 '蜗杆头数(齿数)"z2"=30 '蜗轮齿数"c"=0.2 '径向间隙系数"ha"=1 '齿顶高系数"x"=0 '变位系数(只能取x=±0.5或x=±1)"D1@草图1" ="m"*("q"+2*"ha") '蜗杆齿顶圆直径"D1@基准面1" = PI*"m"'螺距"D4@螺旋线/涡状线1" =PI*"m" '螺距(即蜗杆轴节(蜗轮周节))"D3@螺旋线/涡状线1" ="D10@草图1"+2*PI*"m" ' 螺旋长度"D1@草图3" = "m"*"q"/2 '蜗杆分度圆半径"D3@草图3" = "ha"*"m" '蜗杆齿顶高"D4@草图3" = ("ha"+"c")*"m"'蜗杆齿根高"D5@草图3" = PI*"m"/2'分度圆齿厚"D1@基准面2" = "D5@草图1"/2。
蜗杆的三维参数化建模

蜗杆的三维参数化建模下面通过创建具体实例来说明利用Pro/E软件设计阿基米德蜗杆类零件的方法与一般过程。
1.新建文件(1)执行[新建]菜单命令,打开[新建]对话框。
在[名称]文本框输入文件名“wogan”,单击取消[使用缺省模板]复选框的缺省选中状态,保持该对话框中其他缺省设置不变,单击[确定]按钮。
(2)在打开的[新文件选项]对话框中单击选取“mmns-part-solid”选项,单击[确定]按钮,进入零件环境。
2.创建参数(1)打开[参数]对话框。
单击[参数]对话框中的[添加新参数]按钮,输入蜗杆的模数,参数名称取为“M”,保持缺省的“实数”类型不变,将“值”数值为“4”。
输入蜗杆头数“Z”,将“值”数值为“1”。
输入齿形角“ALPHA”,将“值”数值为“20”。
输入蜗杆直径系数“Q”,将“值”数值为“10”。
输入顶隙“C*”,将“值”数值为“0.25”。
输入齿顶高“HA*”,将“值”数值为“1”。
输入基圆导程角“ ”,将“值”数值为“11.309”。
如图2-1图2-1(2)单击[参数]对话框中的[确定]按钮,关闭[参数]对话框。
3.创建关系式(1)依次执行[工具]| [关系]菜单命令,打开[关系]对话框,在[关系]文本框做输入下面的关系式,按“Enter"键换行。
蜗杆分度圆直径:d=m*q=4*10=40mm蜗杆齿顶圆直径:da=d+2*ha=40+2*m=48mm蜗杆齿根圆直径:df=d1-2*hf=40-2*1.2*m=30.4mm蜗杆齿顶高系数:ha*=m蜗杆齿根高系数:hf*=1.2m蜗杆齿高:h=1/2*(da-df)蜗杆齿宽:b=0.75*da蜗杆轴向齿距:pa=m*π=3.14*4=12.566mm螺距:s=d1*π*tg(11.309)=25.132mm(2)输入完成后,单击[关系]对话框中的[确定]按钮,完成关系式的创建。
4.创建圆柱蜗杆坯料(1)单击按钮,激活操控板。
蜗轮参数方程式驱动建模

蜗轮方程式参数驱动建模第一步:绘图前先输入下列关系式:【工具】→【方程式】→【添加】,输入【m=3.5'模数】,确定。
跟着点【编辑所有】输入以下的方程式:(复制→粘贴)q=9 '蜗杆直径系数z1=1 '蜗杆头数(齿数)z2=30 '蜗轮齿数c=0.2 '径向间隙系数ha=1 '齿顶高系数x=0 '变位系数(只能取x=±0.5或x=±1)点确定。
(以后改动这几个参数就可以重新生成新的零件)第二步:画出蜗杆分度圆草图(标注尺寸时添加各方程式【m*q'蜗杆分度圆直径】),其中心离原点为中心距(添加方程式【(q+z2+2*x) *m/2'中心距】)。
再用同个基准面画出蜗轮旋转主体截面图如图所示,标注尺寸时添加各方程式:【m*(z2+2*(ha+x)+2) '蜗轮外圆直径】、【m*q/2-m'蜗轮喉面半径(齿顶圆弧半径)】(同蜗杆分度圆同心)、【arcsin(蜗轮宽度(这个自己输入)/(m*(q+2*ha-0.5)) '蜗轮齿冠(外圆)包角)。
旋转出蜗轮圈如图第三步:用蜗杆分度圆直径作螺旋线基准圆。
【插入】→【曲线】→【螺旋线】。
双击螺旋线,双击螺距20,添加方程式【PI*m'螺距(即蜗杆轴节(蜗轮周节))】第四步:以螺旋线起头为中心画出蜗杆齿形截面图(要倒过来):分别标注添加方程式分度圆齿厚【PI*m/2'分度圆齿厚螺距/2】(要先画出两个点来标注)、【(ha+x)*m'蜗轮齿顶高】、【(ha+c-x)*m'蜗轮齿根高】。
以这草图和螺旋线扫描切除出齿形。
再圆形阵列Z2个齿。
最后蜗轮圈如下:本模型所用的方程式:(’这个符号是用来加备注的,跟方程式一起输入方便知道是什么)"m"=3.5'模数"q"=9 '蜗杆直径系数"z1"=1 '蜗杆头数(齿数)"z2"=30 '蜗轮齿数"c"=0.2 '径向间隙系数"ha"=1 '齿顶高系数"x"=0 '变位系数(只能取x=±0.5或x=±1)"D1@草图1" = ("q"+"z2"+2*"x") *"m"/2'中心距"D2@草图1" = "m"*"q"'蜗杆分度圆直径"D1@草图2" = "m"*("z2"+2*("ha"+"x")+2) '蜗轮外圆直径"D2@草图2" = "m"*"q"/2-"m"'蜗轮喉面半径(齿顶圆弧半径)"D4@草图2" = "D3@草图2"/3"D5@草图2" = "m"*("z2"-4*("ha"+"c"-"x")) '蜗轮齿根圆直径-2*蜗轮齿根高"D6@草图2" = "m"*("z2"-6*("ha"+"c"-"x")) '蜗轮齿根圆直径-4*蜗杆齿根高"D10@草图2" = arcsin(("D3@草图2")/("m"*("q"+2*"ha"-0.5))) '蜗轮齿冠(外圆)包角"D4@螺旋线/涡状线1" = PI*"m"'螺距(即蜗杆轴节(蜗轮周节))"D2@草图3" = PI*"m"/2'分度圆齿厚螺距/2"D3@草图3" = ("ha"+"x")*"m"'蜗轮齿顶高"D4@草图3" = ("ha"+"c"-"x")*"m"'蜗轮齿根高"D1@阵列(圆周)1" = "z2" '蜗轮齿数。
SolidWorks蜗轮参数方程式驱动建模

SolidWorks蜗轮参数方程式驱动建模SolidWorks蜗轮参数方程式驱动建模是一种使用SolidWorks软件来建立蜗轮的三维模型的方法。
蜗轮是一种传动装置,由蜗杆和蜗轮两部分组成,通过蜗杆的旋转来传递动力。
在建模过程中,我们可以使用参数方程式将蜗轮的尺寸和几何特征与其他零件相连接,实现自动调整和驱动。
在SolidWorks软件中,我们可以先创建蜗轮的基本几何形状,然后使用参数方程式来调整其尺寸和位置。
参数方程式允许我们输入一组数学表达式来定义物体的尺寸和位置,而不是手动输入具体的数值。
通过调整这些参数的数值,我们可以自动调整蜗轮的形状和尺寸,使其符合实际需求。
使用参数方程式驱动建模可以极大地简化建模过程。
当我们需要修改蜗轮的尺寸时,只需改变参数方程式中的数值,而不需要手动修改每个零件的尺寸。
这样不仅提高了工作效率,还减少了错误的发生。
在SolidWorks中,我们可以使用几何条件和关联关系来定义蜗轮的参数方程式。
例如,我们可以通过限制蜗杆的螺旋角度和圆心距离来定义蜗轮的齿数和模数。
通过设置这些几何条件和关联关系,我们可以确保蜗轮的尺寸和几何特征与其他零件相连。
除了使用参数方程式来驱动蜗轮的建模,SolidWorks还提供了许多其他功能来优化蜗轮的设计。
例如,我们可以使用运动仿真来模拟蜗轮的运动,并检查其在不同条件下的性能。
还可以使用流体力学分析来评估蜗轮在高速运动时的涡流损失和效率。
总之,SolidWorks蜗轮参数方程式驱动建模是一种高效、准确和灵活的建模方法,可以帮助我们快速创建符合实际需求的蜗轮模型。
通过使用参数方程式来驱动蜗轮的尺寸和几何特征,我们可以自动调整和驱动模型,节省时间和精力,并提高建模效果。
solidworks的方程式驱动的曲线中参数

SolidWorks的方程式驱动的曲线中参数1.引言在S ol id Wo rk s中,方程式驱动的曲线是一种非常强大的工具,它允许我们使用数学方程来控制曲线的形状。
本文将重点介绍S oli d Wo rk s中方程式驱动的曲线中的参数。
2.方程式驱动的曲线简介方程式驱动的曲线是通过输入数学方程来生成曲线的一种方法。
在S o li dW or ks中,我们可以使用多种类型的方程来定义曲线,如线性方程、二次方程、三角函数等。
3. So lidWork s中的参数在使用方程式驱动的曲线时,我们可以定义参数来控制曲线的形状。
参数可以是任何数值,如长度、角度、比例等。
通过修改参数的数值,我们可以实时地改变曲线的形状和特征。
4.方程式驱动的曲线中的参数应用4.1.长度参数在S ol id Wo rk s中,我们可以使用长度参数来控制曲线的长度。
通过改变长度参数的值,我们可以拉伸或收缩曲线,从而改变曲线的形状。
4.2.角度参数除了长度参数,我们还可以使用角度参数来控制曲线的方向和角度。
通过改变角度参数的数值,我们可以旋转或翻转曲线,使其适应不同的设计需求。
4.3.比例参数在方程式驱动的曲线中,比例参数非常常见。
通过改变比例参数的数值,我们可以调整曲线的比例,实现曲线的缩放或拉伸效果。
5.实例演示为了更好地理解方程式驱动的曲线中的参数应用,我们将以一个具体的示例进行演示。
5.1.示例目标我们的目标是创建一个以椭圆为基础的曲线,通过调整参数,实现曲线的旋转和缩放效果。
5.2.操作步骤1.在S ol id Wo rk s中创建一个草图。
2.使用椭圆工具画出一个椭圆。
3.在椭圆的参数框中,定义两个参数:*长度参数*和*角度参数*。
4.通过改变长度参数的值,拉伸或收缩椭圆,观察曲线的形状变化。
5.通过改变角度参数的值,旋转或翻转椭圆,观察曲线的方向和角度变化。
通过以上步骤,我们可以实时地控制曲线的形状,实现所需的设计效果。
蜗轮蜗杆传动SolidWorks参数化建模_米广杰

[1]邓泽民,陈庆合. 职业教育课程设计[M]. 北京: 中国铁道出版社,
序的编写,知道数据库应该如何管理,这样有利于开发学生的思维,锻炼学
2006. 146 - 169.
生分析和解决问 题 的能力,提升学生 的 学 习 兴 趣,实 现 职 业 能 力 培 养 的
[2]肖衍,龙娟.“计算机网络”课程研究性学习的改革与实践[J]. 职
2007. 67 - 94.
( 上接第 129 页) 软件的二次开发,这些 OLE 对象涵盖了全部的 SolidWorks
4 结论
的 OLE 对象属性的设置和对 OLE 对象方法的调用,就可以在用户自己开
为了检验蜗杆蜗轮的三 维 建 模 是 否 正 确,应 将 其 进 行 装 配,并 进 行 干
发的系统中 实 现与 SolidWorks 相同的功能。SolidWorks 中的常 用 对 象 有 涉检验。对于装配好的蜗轮蜗杆,既可以在 SolidWorks 中直接进行分析,也
蜗轮齿数 z2 、蜗杆头数 z1 、模数 m、蜗杆直径系数 q、蜗轮变位系数 x2 、
供了必要的条件。
中心距 a,这些是绘制蜗轮蜗杆时的常用参数,约束了这些变量,蜗杆蜗轮
2 参数化建模的总体思路
就确定好了且是唯一的。
参数化设计是指参数化的尺寸不需用确定的数值表示,改变一个参数
3. 2 蜗杆传动参数化建模的关键算法分析
绘制蜗轮渐开线齿形草 图: 齿 廓 的 生 成 主 要 有 两 种 方 法,一 种 是 用 直
线 段 逼 近 的 方 法,另 一 种 是 先 确 定 齿 廓 上 的 部 分 点,用 曲 线 拟 合 的 方 法。
直线段逼近法计算量比较大,曲线拟合算法简单同时在精度上也不比直线
实例告诉你solidworks方程式如何使用

实例告诉你solidworks方程式如何使用
跟溪风学SolidWorks的头条粉,在SOLIDWORKS中,方程式的使用必不可少,因为很多时候我们的模型可能是根据其他模型变过来的或者和其他模型存在某种关系,这个时候方程式就派上用场了,那么方程式能做什么呢?方程式其实和Excel基本类似,下面我们就看一下吧。
1、打开SOLIDWORKS绘制出相关产品模型,完善产品基本数据。
1.2. 在设计树内找到方程式点击右键进入管理方程式或者工具—【∑方程式】
1.3. 在方程式内找到需要使用条件的尺寸
1.4. 键入你需要的条件,例:如果草图1的尺寸小于65,那么螺栓长度为100,否则为120(D1@凸台-拉伸=IIF(”D1@草图1”<>
1.5. 如果D1@草图1=60,相对应的螺栓长度就应该为100
上述是if语句,其实在SOLIDWORKS 方程式里面还能进行方程式讲特征压缩:
SOLIDWORKS不仅支持条件语句还提供更多的选择,如三角函数等,大家都可以根据自己的需要来选择,能让设计者能更方便和快捷的来设计。
以上就是SolidWorks方程式的应用实例,大家可以再使用的过程中发现更多的技巧,应用到我们的设计当中去。
十天学会SolidWorks视频教程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蜗杆轴方程式参数驱动建模
第一步:绘图前先输入下列关系式:
【工具】→【方程式】→【添加】,输入【m=3.5'模数】,确定。
跟着点【编辑所有】输入以下的方程式:(复制→粘贴)
q=9 '蜗杆直径系数
z1=1 '蜗杆头数(齿数)
z2=30 '蜗轮齿数
c=0.2 '径向间隙系数
ha=1 '齿顶高系数
x=0 '变位系数(只能取x=±0.5或x=±1)
点确定。
(以后改动这几个参数就可以重新生成新的零件)
第二步:画草图旋转出蜗杆轴主体如图所示,标注尺寸时在蜗杆齿顶圆直径输入方程式【m*(q+2*ha) '蜗杆齿顶圆直径】。
可以连倒角圆角一起出。
【插入】→【曲线】→【螺旋线】
双击螺旋线,双击螺距20,添加方程式【PI*m'螺距(即蜗杆轴节(蜗轮周节))】
第四步:以螺旋线起头画出蜗杆齿形截面图:中心线离原点高度为蜗杆分度圆半径,方程式为【m*q /2'分度圆半径】,分别标注添加方程式【ha*m'蜗杆齿顶高】、【(ha+c)*m'蜗杆齿根高】、分度圆齿厚【PI*m/2'分度圆齿厚螺距/2】(要先画出两个点来标注)。
以这草图和螺旋线扫描切除出齿形。
然后再完成键槽、加工中心孔、材料等等。
最后的结果:
本模型所用的方程式:('这个符号是用来加备注的,跟方程式一起输入方便知道是什么)"m"=3.5 '模数
"q"=9 '蜗杆直径系数
"z1"=1 '蜗杆头数(齿数)
"z2"=30 '蜗轮齿数
"c"=0.2 '径向间隙系数
"ha"=1 '齿顶高系数
"x"=0 '变位系数(只能取x=±0.5或x=±1)
"D1@草图1" ="m"*("q"+2*"ha") '蜗杆齿顶圆直径
"D1@基准面1" = PI*"m"'螺距
"D4@螺旋线/涡状线1" =PI*"m" '螺距(即蜗杆轴节(蜗轮周节))"D3@螺旋线/涡状线1" ="D10@草图1"+2*PI*"m" ' 螺旋长度
"D1@草图3" = "m"*"q"/2 '蜗杆分度圆半径
"D3@草图3" = "ha"*"m" '蜗杆齿顶高
"D4@草图3" = ("ha"+"c")*"m"'蜗杆齿根高
"D5@草图3" = PI*"m"/2'分度圆齿厚
"D1@基准面2" = "D5@草图1"/2。
