平抛运动实验(经典题型)

合集下载

(完整版)平抛运动实验专项训练题

甲v 。

乙平抛运动专项训练一.不定项选择题1.平抛物体的运动规律可以概括为两点：①水平方向做匀速运动；②竖直方向做自由落体运动.为了研究平抛物体的运动，可做下面的实验，如图所示，用小锤打击弹性金属片，A 球就水平飞出，同时B 球被松开，做自由落体运动，两球同时落到地面.这个实验（） A.只能说明上述规律中的第①条 B.只能说明上述规律中的第②条 C.不能说明上述规律中的任何一条 D.能同时说明上述两条规律2.平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动，在同一坐标系中作出两分运动的v-t 图线，如图所示.则以下说法正确的是（） A.图线1表示水平分运动的v-t 图线 B.图线2表示竖直分运动的v-t 图线C.t 1时刻物体的速度方向与初速度方向夹角为45°D.若图线2倾角为θ,当地重力加速度为g ，则一定有tan θ=g3.在研究平抛物体的运动的实验中，为了求平抛物体的初速度，需直接测的数据有（） A.小球开始滚下的高度 B.小球在空中飞行的时间C.运动轨迹上某点P 的水平坐标D.运动轨迹上某点P 的竖直坐标4.如图所示，在研究平抛运动时，小球A 沿轨道滑下，离开轨道末端（末端水平）时撞开轻质接触式开关S ，被电磁铁吸住的小球B 同时自由下落.改变整个装置的高度H 做同样的实验，发现位于同一高度的A 、B 两球总是同时落地.该实验现象说明了A 球在离开轨道后（）A.水平方向的分运动是匀速直线运动B.水平方向的分运动是匀加速直线运动C.竖直方向的分运动是自由落体运动D.竖直方向的分运动是匀速直线运动 5.下列哪些因素会使“研究物体平抛运动”实验的误差增大（） A.小球与斜槽之间有摩擦 B.安装斜槽时其末端不水平C.建立坐标系时，以斜槽末端端口位置为坐标原点D.根据曲线计算平抛运动的初速度时，在曲线上取作计算的点离点O 较远 6.如右图所示是物体做平抛运动的x-y 图象,物体从O 点抛出，A 、B 、C 分别为其轨迹上的三点，A 、B 、C 三点的水平距离相等，则A 、B 、C 三点的竖直距离之比为（）A ．1：1：1B ．1：3：5C ．1：4：9D ．不能确定7.一同学做“研究平抛物体的运动”的实验，只在纸上记下重锤线y 方向，忘记在纸上记下斜槽末端位置，并只在坐标纸上描出如图所示曲线。

平抛运动研究典型例题精析

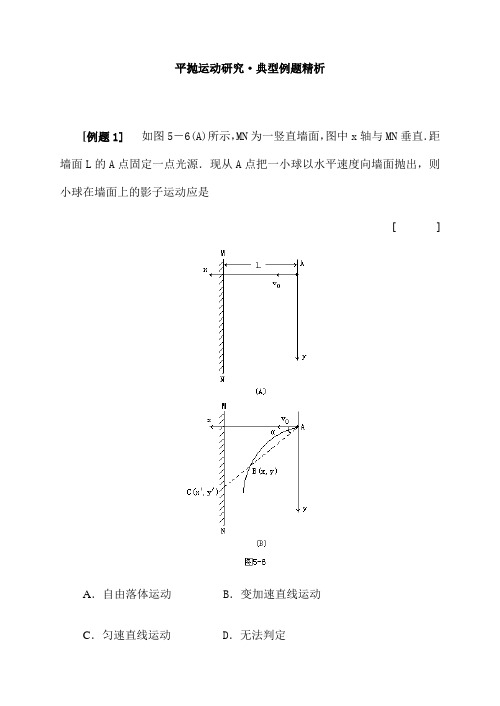
平抛运动研究·典型例题精析[例题1] 如图5－6(A)所示，MN为一竖直墙面，图中x轴与MN垂直．距墙面L的A点固定一点光源．现从A点把一小球以水平速度向墙面抛出，则小球在墙面上的影子运动应是[]A．自由落体运动 B．变加速直线运动C．匀速直线运动 D．无法判定[思路点拨] 小球抛出后为平抛运动，在图中x方向上为匀速直线运动，在y方向上为自由落体运动．故不少同学选择(A)项，而实际上该答案是错误的．问题在于我们研究的并不是小球在竖直方向上的运动，而是在点光源照射下小球在墙上影子的运动．[解题过程] 设小球从A点抛出后经过时间t，其位置B坐标为(x，y)，连接AB并延长交墙面于C(x′，y′)．显然C点就是此时刻小球影子的位置(如图5－6(B)所示)．令AB与x轴夹角为α，则依几何关系，影子位置y′＝L·tanα．故令 gL/2v0＝k，则y′＝k·t．即影子纵坐标y′与时间t是正比例关系，所以该运动为匀速直线运动，应选(C)项．[小结] (1)要认真审清题意：本题所研究的是“点光源照射下小球影子的运动”，否则会差之毫厘，谬之千里．(2)对选择题的分析判断，切莫主观猜测，要做到弃之有理，选之有据．对于需做出定量研究的问题，最好的方法就是将物理图景利用数学语言表达出来，例如在本题中就是写出位移随时间的函数关系．[例题2] 如图5－7所示，M和N是两块相互平行的光滑竖直弹性板．两板之间的距离为L，高度为H．现从M板的顶端O以垂直板面的水平速度v0抛出一个小球．小球在飞行中与M板和N板，分别在A点和B点相碰，并最终在两板间的中点C处落地．求：(1)小球抛出的速度v0与L和H之间满足的关系；(2)OA、AB、BC在竖直方向上距离之比．[思路点拨] 根据平抛运动规律，建立小球在MN之间的运动图景是本题关键之一．小球被水平抛出后，如果没有板面N的作用，其运动轨迹应如图5－8中虚线所示．由于板面光滑弹性良好，故在A点与N板碰后，应满足反射定律，反弹后运动轨迹与虚线，满足以N板为轴的左右对称．第二次在B点与M板相碰情况亦然．本题的另一难点是问题竖直方向运动为自由落体，所以不少同学会认为这三段在竖直方向上距离之比应为：1∶3∶2.5．你是否也有同样的结果呢？[解题过程] (1)分析可知运动的全过程中，小球始终保持其水平速度大小v0不变．设运动全过程飞行时间为t，水平全程长度为S，则又 S＝2.5L，(2)取小球由B到C为一个时间间隔Δt．小球从O抛出到C点落地共经过5个Δt．在此5个Δt中下落高度之比为：1∶3∶5∶7∶9．由于t OA包括第1个Δt和第2个Δt；t AB包括第3个Δt和第4个Δt，故三段竖直距离之比为h OA∶h AB∶h BC＝(1＋3)∶(5＋7)∶9＝4∶12∶9．[小结] (1)注意将平抛运动的一般规律与题目中特定物理条件相结合，才能正确描述题目的物理图景。

平抛运动特经典题型组合

一选择题。

1．做平抛运动的物体，在连续相等的时间间隔内速度增量总是()A．大小相等，方向相同B．大小不等，方向不同C．大小相等，方向不同D．大小不等，方向相同2、为了探究影响平抛运动水平射程的因素，某同学通过改变抛出点的高度及初速度的方法做了6AB．若探究水平射程与高度的关系，可用表中序号为1、3、5的实验数据C．若探究水平射程与高度的关系，可用表中序号为2、4、6的实验数据D．若探究水平射程与初速度的关系，可用表中序号为2、4、6的实验数据3、在冬奥会自由式滑雪比赛中，运动员在较高的雪坡上滑到某一弧形部位处，沿水平方向飞离斜坡，在空中划过一段抛物线后，再落到雪坡上，如图3所示，若雪坡的倾角为θ，飞出时的速度大小为v0则( )A．运动员落回雪坡时的速度大小是B．运动员在空中经历的时间是C．运动员的落点与起飞点的距离是D．运动员的落点与起飞点间竖直高度是4、如图所示，有一带电粒子贴A板沿水平方向射入匀强电场，当偏转电压为U1时，带电粒子沿轨迹①从两板正中间飞出；当偏转电压为U2时，带电粒子沿轨迹②落到B板中间；设两次射入电场的水平速度相同，不计粒子的重力，则电压U1、U2之比为（）A．1:8 B．1:4C．1:2 D．1:15．如右图所示，一小球以v 0＝10 m/s 的速度水平抛出，在落地之前经过空中A 、B 两点．在A 点小球速度方向与水平方向的夹角为45°，在B 点小球速度方向与水平方向的夹角为60°(空气阻力忽略不计，g 取10 m/s 2)，以下判断中正确的是( )A ．小球经过A 、B 两点间的时间t ＝1 s B ．小球经过A 、B 两点间的时间t ＝ sC ．A 、B 两点间的高度差h ＝10 mD ．A 、B 两点间的高度差h ＝15 m6．如图所示，三个小球在离地面不同高度处，同时以相同的速度向左水平抛出，小球A 落到D 点，DE ＝EF ＝FG ，不计空气阻力，每隔相等的时间间隔小球依次碰到地面．则关于三小球( )A ．B 、C 两球也落在D 点 B ．B 球落在E 点，C 球落在F 点C ．三小球离地面的高度AE ∶BF ∶CG ＝1∶3∶5D ．三小球离地面的高度AE ∶BF ∶CG ＝1∶4∶97．如图所示，将一物体从倾角为θ的固定斜面顶端以初速度v 0沿水平方向抛出，物体与斜面接触时速度与斜面之间的夹角为α1.若只将物体抛出的初速度变成21v 0，其他条件不变，物体与斜面接触时速度与斜面之间的夹角为α2，则下列关于α2与α1的关系正确的是( )A ．α2＝21α1 B ．α2＝α1 C ．tan α2＝21tan α1D ．tan α2＝2tan α18.如图所示,小朋友在玩一种运动中投掷的游戏,目的是在运动中将手中的球投进离地面高3 m 的吊环,他在车上和车一起以2m/s 的速度向吊环运动,小朋友抛球时手离地面1.2 m,当他在离吊环的水平距离为2 m 时将球相对于自己竖直上抛,球刚好进入吊环,他将球竖直向上抛出的速度是(g 取)…（）A. 1.8 m/sB. 3.2 m/sC. 6.8 m/sD. 3.6 m/s二、计算题9、遥控赛车比赛中有一个规定项目：飞越“壕沟”。

高考物理平抛运动经典题型汇总与解析

平抛运动专题练习1.（单选）图中给出某一通关游戏的示意图，安装在轨道AB上可上下移动的弹射器，能水平射出速度大小可调节的弹丸，弹丸射出口在B点的正上方，竖直面内的半圆弧BCD的半径为R=2.0m，直径BD水平且与轨道AB处在同一竖直平面内，小孔P和圆心O连线与水平方向夹角为37º，游戏要求弹丸垂直于P点圆弧切线方向射入小孔P就能进入下一关.为了能通关，弹射器离B点的高度和弹丸射出的初速度分别是(不计空气阻力) （）A. B.C. D.2.（多选）如图所示，在高处有小球，速度水平抛出，与此同时，地面上有个小球以速度竖直上抛，两球在空中相遇，则（）A. 从它们抛出到相遇所需的时间是B. 从它们抛出到相遇所需的时间是C. 两球抛出时的水平距离为D. 两球抛出时的水平距离为3.（单选）如图所示，小球甲从A点水平抛出的同时小球乙从B点自由释放，两小球先后经过C点时速度大小相等，方向间夹角为θ=45°，已知BC高h，不计空气的阻力。

由以上条件可知（）A. 甲小球做平抛运动的初速度大小为B. 甲、乙两小球到达C点所用时间之比为1:2C. A、B两点的高度差为D. A、B两点的水平距离为4.（多选）横截面为直角三角形的两个相同斜面如图紧靠在一起，固定在水平面上，它们的竖直边长都是底边长的一半．小球从左边斜面的顶点以不同的初速度向右平抛，最后落在斜面上．其中三个小球的落点分别是a、b、c．图中三小球比较，下列判断正确的是（）A．落在c点的小球飞行时间最长B．落在a点的小球飞行时间最长C．落在c点的小球飞行过程速度变化最快D．落在c点的小球飞行过程速度变化最小5.（单选）如图所示，球网高出桌面H ，网到桌边的距离为L ．某人在乒乓球训练中，从左侧2L处，将球沿垂直于网的方向水平击出，球恰好通过网的上沿落到右侧桌边缘．设乒乓球运动为平抛运动．则（） A ．击球点的高度与网高度之比为2：1 B ．乒乓球在网左右两侧运动时间之比为2：1 C ．乒乓球过网时与落到桌边缘时速率之比为1：2 D ．乒乓球在左、右两侧运动速度变化量之比为1：26.（多选）如图所示，一网球运动员将球在边界处正上方正对球网水平向前击出，球刚好过网落在图中位置（不计空气阻力），相关数据如图，下列说法中正确的是（） A ．击球点高度h 1与球网高度h 2之间的关系为h 1=1.8h 2 B ．若保持击球高度不变，球的初速度满足21gh hs ＜v 0＜112gh h s ，一定落在对方界内 C ．任意降低击球高度（仍大于h 2），只要击球初速度合适，球一定能落在对方界内 D ．任意增加击球高度，只要击球初速度合适，球一定能落在对方界内7.（多选）如图，在同一竖直面内，小球a 、b 从高度不同的两点，分别以初速度v a 和v b 沿水平方向抛出，经过时间t a 和t b 后落到与两抛出点水平距离相等的P 点．若不计空气阻力，下列关系式正确的是（） A ．t a ＞t b B ．t a ＜t b C ．v a ＜v bD ．v a ＞v b8.（多选）如图所示，在水平路面上一运动员驾驶摩擦车跨越壕沟，壕沟两侧的高度差为 0.8m ，水平距离为8m ，则（取 g=10m/s 2）（） A ．运动员跨过壕沟的时间约为 0.4s B ．运动员跨过壕沟的时间约为 0.3s C ．运动员跨过壕沟的初速度至少为 10m/s D ．运动员跨过壕沟的初速度至少为 20m/s9.（单选）如图所示，在光滑的水平面上有小球 A 以初速度 v 0 向左运动，同时刻一个小孩在 A 球正上方以 v 0 的速度将 B 球平抛出去，最后落于 C 点，则（） A ．小球 A 先到达 C 点B ．小球 B 先到达C 点 C ．两球同时到达 C 点D ．不能确定10.（单选）如图所示，从同一条竖直线上两个不同点 P 、Q 分别向右平抛两个小球，平抛的初速度分别为 v 1、v 2，结果它们同时落到水平面上的 M 点处（不考虑空气阻力）．下列说法中正确的是（） A ．一定是 P 先抛出的，并且 v 1=v 2 B ．一定是 P 先抛出的，并且 v 1＜v 2 C ．一定是 Q 先抛出的，并且 v 1=v 2 D ．一定是 Q 先抛出的，并且 v 1＞v 211.（单选）如图，竖直平面内有一段圆弧MN ，小球从圆心O 处水平抛出，若初速度为v a ，将落在圆弧上的a 点，若初速度为v b ，将落在圆弧上的b 点，已知Oa 、Ob 与竖直方向的夹角分别为α、β，不计空气阻力，则初速度大小之比为（） A ．βαsin sin B ．αβcos cos C ．βααβsin sin cos cos D ．αββαcos cos sin sin 12.（多选）如图所示，在某次自由式滑雪比赛中，一运动员从弧形雪坡上沿水平方向飞出后，又落回到斜面雪坡上，若斜面雪坡的倾角为θ，运动员飞出时的速度大小为v 0，不计空气阻力，运动员飞出后在空中的姿势保持不变，重力加速度为g ，则（） A ．运动员落到雪坡时的速度大小为θcos 0v B ．运动员在空中飞行的时间是gv θtan 20 C ．如果v 0大小不同，则运动员落到雪坡时的速度于斜面的夹角也就不同 D ．不论v 0多大，该运动员落到雪坡上时的速度与斜面的夹角都是相同的13.（单选）2007年10月13日，日本、美国、法国、英国、澳大利亚和新西兰在日本东京伊豆大岛海域举行联合海上军事演习，如图所示，若在演习中，离地H 高处的飞机以水平速度v 1发射一颗导弹欲轰炸地面目标P ，反应灵敏的地面拦截系统同时以速度v 2竖直向上发射导弹拦截．设拦截系统与飞机的水平距离为x ，若拦截成功，不计空气阻力，则v 1、v 2的关系应满足（）A ．v 1=v 2B ．v 1=2v x HC ．v 1=v 2 xHD ．v 1=2v H x14.如图所示，射击枪水平放置，射击枪与目标靶中心位于离地面足够高的同一水平线上，枪口与目标靶之间的距离s=36m，子弹射出的水平速度v0=40m/s，子弹从枪口射出的瞬间目标靶由静止开始释放，不计空气阻力，取重力加速度g为10m/s2，求：（1）从子弹由枪口射出开始计时，经多长时间子弹击中目标靶？（2）目标靶由静止开始释放到被子弹击中，下落的距离h为多少？（3）子弹击中目标靶时的速度的大小？15.如图所示，一小球从平台上抛出，恰好落在临近平台的一倾角为α=53°的光滑斜面顶端并沿斜面下滑，已知斜面顶端与平台的高度差h=0.8m，重力加速度g=10m/s2，（sin53°=0.8，cos53°=0.6）求：（1）小球水平抛出的初速度v0是多少；（2）若斜面顶端高H=20.8m，则小球离开平台后经多长时间到达斜面底端．16.如图所示，参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后，落在水平传送带上．已知平台与传送带的高度差H=1.8m，水池宽度s0=1.2m，传送带AB间的距离L0=9.6m．由于传送带足够粗糙，假设选手落到传送带上后瞬间相对传送带静止，经过△t=1.0s反应时间后，立刻以a=2m/s2恒定向右的加速度跑至传送带最右端。

平抛运动测试题及答案范本

平抛运动测试题及答案范本测试题：题目一：假设一颗子弹以80 m/s的初速度从平地的一点射出，求其水平运动的时间。

题目二：一名游泳运动员在比赛中进行平抛运动，投掷角度为45°，求其竖直方向上的运动时间。

题目三：一个小球以12 m/s的速度向上抛出，求其最大高度。

答案范本：题目一答案：假设子弹水平运动时间为t秒，则可以利用水平运动速度的定义 v = S / t，其中 v 为水平初速度，S为水平距离。

根据题目中给出的信息 v = 80 m/s，S = 0（因为水平运动，不受竖直方向上的重力作用，所以水平位移为0）。

代入公式可以得到 t = S / v = 0 / 80 = 0秒。

因此，子弹的水平运动时间为0秒。

题目二答案：由题目给出的投掷角度为45°，可以将水平方向和竖直方向的运动分开计算。

对于水平方向的运动，由于没有水平的外力作用，所以水平速度始终保持不变，即 vt = 0，其中 v为水平速度，t为水平运动时间。

而对于竖直方向的运动，运用自由落体运动的规律，可以得到运动时间 t' = 2 * (v / g)，其中 v为竖直初速度，g为重力加速度。

根据题目中给出的投掷角度，可以得到v = v0 * sinθ，其中 v0为初速度，θ为投掷角度。

代入公式可得t' = 2 * (v0 * sinθ / g)。

由于题目中没有给出具体数值，所以无法计算出游泳运动员在竖直方向上的运动时间的具体数值。

题目三答案：小球的最大高度即为其竖直方向上运动时间的一半所对应的高度。

根据自由落体运动的规律，小球的竖直运动方程可以表示为 h = v0 * t - (1/2) * g * t^2，其中 h为高度，v0为初速度，t为时间，g为重力加速度。

最大高度对应的时间为小球的总运动时间的一半，因此 t' = t / 2。

代入公式可得 h = v0 * t' - (1/2) * g * (t')^2。

平抛运动典型例题(含答案)

[例1] 在倾角为的斜面上的P点, 以水平速度向斜面下方抛出一个物体, 落在斜面上的Q 点, 证明落在Q点物体速度。

解析：设物体由抛出点P运动到斜面上的Q点的位移是, 所用时间为, 则由“分解位移法”可得, 竖直方向上的位移为；水平方向上的位移为。

又根据运动学的规律可得竖直方向上,水平方向上,所以Q点的速度[例2] 如图3所示, 在坡度一定的斜面顶点以大小相同的速度同时水平向左与水平向右抛出两个小球A和B, 两侧斜坡的倾角分别为和, 小球均落在坡面上, 若不计空气阻力, 则A和B两小球的运动时间之比为多少？图3解析: 和都是物体落在斜面上后, 位移与水平方向的夹角, 则运用分解位移的方法可以得到所以有同理则[例3] 如图6所示, 在倾角为的斜面上以速度水平抛出一小球, 该斜面足够长, 则从抛出开始计时, 经过多长时间小球离开斜面的距离的达到最大, 最大距离为多少？图6解析: 将平抛运动分解为沿斜面向下和垂直斜面向上的分运动, 虽然分运动比较复杂一些, 但易将物体离斜面距离达到最大的物理本质凸显出来。

取沿斜面向下为轴的正方向, 垂直斜面向上为轴的正方向, 如图6所示, 在轴上, 小球做初速度为、加速度为的匀变速直线运动, 所以有①②当时, 小球在轴上运动到最高点, 即小球离开斜面的距离达到最大。

由①式可得小球离开斜面的最大距离当时, 小球在轴上运动到最高点, 它所用的时间就是小球从抛出运动到离开斜面最大距离的时间。

由②式可得小球运动的时间为例4: 在平直轨道上以的加速度匀加速行驶的火车上, 相继下落两个物体下落的高度都是2.45m. 间隔时间为1s. 两物体落地点的间隔是2.6m, 则当第一个物体下落时火车的速度是多大？（g 取）分析: 如图所示. 第一个物体下落以的速度作平抛运动, 水平位移 , 火车加速到下落第二个物体时, 已行驶距离 . 第二个物体以的速度作平抛运动水平位移 . 两物体落地点的间隔是2.6m.解: 由位置关系得物体平抛运动的时间 20.7ht s g'=00021002000.710.252()(0.5)0.7s v t v s v t at v s v at t v '===+=+'=+⋅=+⨯由以上三式可得201sin 22sin 2/L gt L t gv m sαα===例5: 光滑斜面倾角为 , 长为L, 上端一小球沿斜面水平方向以速度抛出（如图所示）, 小球滑到底端时, 水平方向位移多大？解：小球运动是合运动, 小球在水平方向作匀速直线运动, 有0s v t = ①沿斜面向下是做初速度为零的匀加速直线运动, 有212L at =② 根据牛顿第二定律列方程sin mg ma θ= ③由①, ②, ③式解得例6: 某一物体以一定的初速度水平抛出, 在某内其速度方向与水平方向成变成 , 则此物体初速度大小是________ , 此物体在内下落的高度是________ （取）选题目的: 考查平抛物体的运动知识的灵活运用.解析：作出速度矢量图如图所示, 其中．分别是及时刻的瞬时速度．在这两个时刻, 物体在竖直方向的速度大小分别为及 , 由矢量图可知：037gt v tg =︒ 0(1)53g t v tg +=︒由以上两式解得017.1/v m s = 97t s =物体在这1s 内下落的高度2211(1)22y g t gt ∆=+- 221919(1)()2727g g =+-17.9m =（1）例7如图, 跳台滑雪运动员经过一段加速滑行后从O 点水平飞出, 经过3.0s 落到斜坡上的A 点. 已知O 点是斜坡的起点, 斜坡与水平面的夹角θ=37°, 运动员的质量m=50kg. 不计空气阻力. （取sin37°=0.60, cos37°=0.80；g 取10m/s2）求: （1）A 点与O 点的距离L ；（2）运动员离开O 点时的速度大小；从O 点水平飞出后, 人做平抛运动, 根据水平方向上的匀速直线运动, 竖直方向上的自由落体运动可以求得A 点与O 点的距离L ；（2）运动员离开O 点时的速度就是平抛初速度的大小, 根据水平方向上匀速直线运动可以求得；设A 点与O 点的距离为L, 运动员在竖直方向做自由落体运动, 则有： Lsin37°=0.5gt2L=gt22sin37°=75m（2）设运动员离开O点的速度为v0, 运动员在水平方向做匀速直线运动,即: Lcos37°=v0t解得: v0=20m/s答: （1）A点与O点的距离是75m；（2）运动员离开O点时的速度大小是20m/s.1: 在倾角为的斜面上的P点, 以水平速度向斜面下方抛出一个物体, 落在斜面上的Q点, 证明落在Q点物体速度。

平抛运动经典题目

平抛运动经典题目1．a 、b 、c 为平抛物体运动轨迹上的三个点，若取a点为坐标系原点，b 、c 坐标如图所示，则小球平抛初速度的大小为 m/s.2．如图所示，在“研究平抛物体运动”的实验中，用一张印有小方格的纸记录轨迹，小方格的边长L=1.25cm 。

若小球在平抛运动途中的几个位置如图中的a 、b 、c 、d 所示，则小球平抛的初速度的计算式为v o = （用L 、g 表示），其值是（取g=9.8m/s 2），小球在b 点的速率是。

3．滑雪运动员以20m ／s 的速度从一平台水平飞出，落地点与飞出点的高度差3．2m 。

不计空气阻力，g 取10m ／s 2。

运动员飞过的水平距离为s ，所用时间为t ，则下列结果正确的是A ．s=16m ，t=0．50sB ．s=16m ，t=0．80sC ．s=20m ，t=0．50sD ．s=20m ，t=0．80s4．船在400米宽的河中横渡，河水流速是2m/s ，船在静水中的航速是4m/s ，试求：（1）要使船到达对岸的时间最短，船头应指向何处？最短时间是多少？航程是多少？（2）要使船航程最短，船头应指向何处？最短航程为多少？渡河时间又是多少？5．以2m/s 的速度水平抛出的物体，在飞行中垂直地撞击在倾角为30º的斜面上A 点，则抛出点O 与A 点的高度差为 m6．如图所示，一光滑的半径为R 的半圆形轨道放在水平面上，一个质量为m 的小球以某一速度冲上轨道，当小球将要从轨道口飞出时，轨道的压力恰好为零，则小球落地点C 距A 处多远?7．如图12所示，一个人用一根长1m ，只能承受74N 拉力的绳子，拴着一个质量为1㎏的小球，在竖直平面内作圆周运动，已知圆心O 离地面h =6m 。

转动中小球在最底点时绳子断了，（1）绳子断时小球运动的线速度多大？（2）绳断后，小球落地点与抛出点间的水平距离。

图12。

平抛运动典型例题

平抛运动典型例题
1.从某高处以6m/s的初速度、30°抛射角斜向上方抛出一石子，落地时石子的速度方向和水平线的夹角为60°，求石子在空中运动的时间和抛出点离地面的高度。

（取g=10m/s2）
2.如图,可视为质点的小球,位于半径为半圆柱体左端点A的正上方某处,以一定的初速度水平抛出小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为,则初速度为:(不计空气阻力,重力加速度为多少。

3.如图所示，在倾角为45O 的斜面底端正上方高H=6.4m 处，将一小球以不同初速度水平抛出，若小球到达斜面时位移最小，重力加速度g=10m/s 2，求：
（1）小球平抛的初速度；
（2）小球落到斜面时的速度。

4如图所示，装甲车在水平地面上以速度s m v /200=沿直线前进，车上机枪的枪管水平，距地面高为h=1.8m 。

在车正前方竖直立一块高为两米的长方形靶，其底边与地面接触。

枪口与靶距离为时，机枪手正对靶射出第一发子弹，子弹相对于枪口的初速度为s m v /800=。

在子弹射出的同时，装甲车开始匀减速运动，行进s=90m 后停下。

装甲车停下后，机枪手以相同方式射出第二发子弹。

（不计空气阻力，子弹看成质点，重力加速度
）
（1）求装甲车匀减速运动时的加速度大小；
（2）当410m 时，求第一发子弹的弹孔离地的高度，并计算靶上两个弹孔之间的距离；
（3）若靶上只有一个弹孔，求L 的范围。

平抛运动实验(经典题型).

平抛运动实验（全面）1．实验目的（1）用实验方法描出平抛物体的运动轨迹（2）从实验轨迹求平抛物体的初速度2．实验原理平抛物体的运动可以看作是水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。

使小球做平抛运动，利用描迹法描出小球运动轨迹，建立坐标系，测出轨迹曲线上某一点的坐标x 和y ，根据公式0x v t =和212y at =，就可求得：02g v x y =，即为做平抛运动的初速度。

3．参考案例（1）案例一：利用平抛运动实验器（如同4-7-1所示）。

A 、斜槽末端切线必须水平B 、每次从同一位置无初速释放小球，以使小球每一次抛出后轨迹相同，每次描出的点在同一轨迹上C 、安装实验装置时，要注意使轨道末端与图板相靠近，并保持它们的相对位置不变D 、要用重垂线把图板校准到竖直方向，使小球运动靠近图板，又不接触图板E 、坐标原点不是槽口末端点，应是球在槽口时，球心在图板上的水平投影点OF 、球的释放高度要适当，使其轨迹不至于太平也不至于太竖直，以减小测量误差G 、计算初速度时，应选离O 点远些的点（2）案例二：利用水平喷出的细水柱显示平抛运动的轨迹。

水从喷嘴中射出，在空中形成弯曲的细水柱，它显示了平抛运动的轨迹。

（3）案例三：利用数码照相机或数码摄像机更精细地探究平抛运动。

(如图4-7-2)图图4、重点难点例析【考点一】平抛运动的实验步骤及注意事项【例1】在“探究平抛运动的运动规律”的实验中，可以描绘出小球平抛运动的轨迹，实验简要步骤如下：A．让小球多次从位置上滚下，记下小球碰到铅笔笔尖的一系列位置。

B．按图安装好器材，注意，记下平抛初位置O点和过O点的竖直线。

C．取下白纸，以O为原点，以竖直线为y轴建立坐标系，用平滑曲线画平抛运动物体的轨迹。

⑴完成上述步骤，将正确的答案填在横线上。

⑵上述实验步骤的合理顺序是。

O xy图4-7-4图4-7-3【变式训练】如图4-7-3所示是研究平抛运动的实验装置简图，图4-7-4是实验后白纸上的轨迹图。

研究平抛运动实验（共6篇）

研究平抛运动实验（共6篇）以下是网友分享的关于研究平抛运动实验的资料6篇，希望对您有所帮助，就爱阅读感谢您的支持。

《实验：研究平抛运动》教案篇1实验：研究平抛运动描绘平抛运动的轨迹【方案一】平抛运动演示仪一、实验目的1．用实验方法描出平抛物体的运动轨迹。

2．从实验轨迹求平抛物体的初速度。

二、实验器材斜槽，铁架台，木板，白纸，小球，图钉，铅笔，有孔的卡片，刻度尺，重锤线。

三、实验原理平抛运动可以看作是水平方向的匀速直线运动和竖直方向的自由落体运动。

让小球做平抛运动，利用描迹法描出小球的运动轨迹，建立坐标系。

测出曲线上的某一点的坐标x和y，根据重力加速度g的数值、利用公式y=gt2/2 求出小球飞行时间t，再利用公式x=vt ，求出小球做平抛运动的初速度。

四、实验步骤1、安装调整斜槽：用图钉把白纸钉在竖直板上，在木板的左上角固定斜槽，可用平衡法调整斜槽，即将小球轻放在斜槽平直部分，能使小球在平直轨道上的任意位置静止，就表明水平已调好。

2、调整木板：用悬挂在槽口的重垂线把木板调整到竖直方向、并使木板平面与小球下落的竖直面平行。

然后把重垂线方向记录到钉在木板的白纸上，固定木板，使在重复实验的过程中，木板与斜槽的相对位置保持不变。

3、确定坐标原点O：把小球放在槽口处，用铅笔记下球在槽口时球心在白纸上的水平投影点O，O即为坐标原点。

4．描绘运动轨迹：使小球每次从斜槽上的同一位置由静止开始滑下，可记录小球平抛轨迹上的一系列位置。

5、计算初速度：取下白纸，以O点为原点画出竖直向下的y轴和水平向右的x轴，用平滑的曲线把这些位置连接起来即得小球做平抛运动的轨迹。

在曲线上选取A、B、C、D、E、F六个不同的点，用刻度尺和三角板测出它们的坐标x和y。

用公式x＝v0t和y＝gt2/2计算出小球的初速度v0，最后计算出v0的平均值，并将有关数据记入表格内。

五、注意事项1、保证斜槽末端的切线水平。

2、方木板必须处在竖直面内且与小球运动轨迹所在的竖直平面平行，并使小球的运动靠近图板但不接触。

(完整版)平抛运动测试题及答案

平抛运动试题一、选择题：1.如图1所示,在光滑的水平面上有一小球ａ以初速度ｖ0运动,同时刻在它的正上方有小球ｂ也以ｖ0初速度水平抛出,并落于ｃ点,则（）A ．小球ａ先到达ｃ点B ．小球ｂ先到达ｃ点C ．两球同时到达ｃ点D ．不能确定2.一个物体从某一确定的高度以ｖ0的初速度水平抛出,已知它落地时的速度为ｖｔ, 那么它的运动时间是（）A ．g v v t 0-B ．g v v t 20-C ．gv v t 222- D ．g v v t 202-3.如图2所示，为物体做平抛运动的ｘ－ｙ图象.此曲线上任意一点P (x ,y )的速度方向的反向延长线交于x 轴上的A 点，则A 点的横坐标为( ) A.0.6xB.0.5xC.0.3xD.无法确定4.下列关于平抛运动的说法正确的是( )A. 平抛运动是非匀变速运动B. 平抛运动是匀速运动图2C. 平抛运动是匀变速曲线运动D. 平抛运动的物体落地时的速度一定是竖直向下的5.将甲、乙、丙三个小球同时水平抛出后落在同一水平面上，已知甲和乙抛射点的高度相同，乙和丙抛射速度相同。

下列判断中正确的是( )A. 甲和乙一定同时落地B. 乙和丙一定同时落地C. 甲和乙水平射程一定相同D. 乙和丙水平射程一定相同6．对平抛运动的物体，若g 已知，再给出下列哪组条件，可确定其初速度大小( ) A ．水平位移 B ．下落高度C ．落地时速度大小和方向D ．落地位移大小和方向7. 关于物体的平抛运动,下列说法正确的是( )A. 由于物体受力的大小和方向不变, 因此平抛运动是匀变速运动;B. 由于物体速度的方向不断变化, 因此平抛运动不是匀变速运动;C. 物体的运动时间只由抛出时的初速度决定,与高度无关;D.平抛运动的水平距离由抛出点的高度和初速度共同决定.8. 把甲物体从2h 高处以速度V 水平抛出,落地点的水平距离为L,把乙物体从h 高处以速度2V 水平抛出,落地点的水平距离为S,比较L 与S,可知( )A.L=S/2 ;B. L=2S;C.L S =12; D.L S =2 . 9．以速度v 0水平抛出一小球，如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等，以下判断正确的是（）A ．此时小球的竖直分速度大小等于水平分速度大小B ．此时小球的速度大小为2 v 0C ．小球运动的时间为2 v 0/gD ．此时小球速度的方向与位移的方向相同10．物体在平抛运动过程中，在相等的时间内，下列哪个量是相等的（） A.位移 B.加速度C.平均速度D.速度的增量图1二、填空题：11．如图3所示的演示实验中，A 、B 两球同时落地，说明。

平抛运动典型分类例题.docx

1．定义水平抛出的物体只在重力作用下的运动．2．特征加速度为重力加速度g 的匀变速曲线运动，轨迹是抛物线．平抛运动的速率随时间变化不是均匀的，但速度随时间的变化是均匀的，要注意区分．4．规律（1）平抛运动如图所示；（2）其合运动及在水平方向上、竖直方向上的运动如下表所示：①从抛出点开始，任意时刻速度偏向角的正切值等于位移偏向角正切值的两倍．②抛物线上某点的速度反向延长线与初速度延长线的交点到抛点的距离等于该段平抛水平位移的一半．③在任意两个相等的t ∆内，速度矢量的变化量v ∆是相等的，即v ∆的大小与t ∆成正比，方向竖直向下．④平抛运动的时间为t =，取决于下落的高度，而与初速度大小无关．水平位移0x v t v == 4．求解方法（1）常规方法：将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动，利用运动的合成及分解来做．（2）特殊方法：巧取参考系来求解，例如：选取具有相同初速度的水平匀速直线运动物体为参考系，平抛物体做自由落体运动；选取自由落体运动的物体为参考系，平抛物体做匀速直线运动．题型一：对平抛性质的理解【例1】关于平抛运动，下列说法正确的是( )A ．是匀变速运动B ．是变加速运动C ．任意两段时间内速度变化量的方向相同D ．任意相等时间内的速度变化量相等【例2】物体在平抛运动过程中，在相等的时间内，下列哪些量是相等的（）A ．速度的增量B ．加速度C ．位移D ．平均速率题型二：对平抛基本公式、规律运用【例3】以速度0v 水平抛出一个小球，如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等，以下判断正确的是( )A ．此时小球的竖直分速度大小等于水平分速度大小B 0C ．小球运动的时间为2v gD ．此时小球的速度方向与位移方向相同【例4】一架飞机水平匀速飞行．从飞机上海隔l s 释放一个铁球，先后释放4个，若不计空气阻力，从地面上观察4个小球( )A ．在空中任何时刻总是捧成抛物线，它们的落地点是等间距的B ．在空中任何时刻总是排成抛物线，它们的落地点是不等间距的C ．在空中任何时刻总在飞机正下方，排成竖直的直线，它们的落地点是等间距的D ．在空中任何时刻总在飞机的正下方，捧成竖直的直线，它们的落地点是不等间距的【例5】在光滑的水平面上有一个小球a 以初速度0v 向右运动，以此同时，在它的正上方有一个小球b 也以0v 的初速度水平向右抛出（如右上图），并落于水平面的c 点，则( ) A ．小球a 先到达c 点B ．小球b 先到达c 点C ．两球同时到达c 点D ．不能确定【例6】甲、乙两球位于同一竖直直线上的不同位置，甲比乙高h ，如图所示，将甲、乙两球分别以1v 、2v 的速度沿同一水平方向抛出，不计空气阻力，下列条件中有可能使乙球击中甲球的是( )A ．同时抛出，且1v <2vB ．甲迟抛出，且1v >2vC ．甲早抛出，且1v >2vD ．甲早抛出，且1v <2v【例7】滑雪运动员以20/m s 的速度从一平台水平飞出，落地点与飞出点的高度差3．2m ．不计空气阻力，取210/g m s =．运动员飞过的水平距离为s ，所用时间为t ,则下列结果正确的是( ) A ．16m, =0.50s s t = B ． 16m, =0.80s s t = C ．20m, =0.50s s t = D ． 20m, =0.80s s t =【例8】一物体从某高度以初速度0v 水平抛出，落地时速度大小为t v ，则它运动时间为（）A ．0t v v g -B ．02t v v g -C ．222t v v g - D题型三：与斜面组合类【例9】如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上．物体与斜面接触时速度与水平方向的夹角φ满足( )A ．tan sin φθ=B ．tan cos φθ=C ． tan tan φθ=D ．tan 2tan φθ=【例10】如图所示，以9.8m/s 的水平初速度v 0抛出的物体，飞行一段时间后，垂直地撞在倾角θ为30° 的斜面上，可知物体完成这段飞行的时间是（）A 、sB 、sC 、s D 、2s【例11】如图所示，相对的两个斜面，倾角分别为37。

平抛运动实验题

10 道平抛运动实验题题目一：在平抛运动实验中，小球从斜槽上滚下，在空中做平抛运动，若小球每次从斜槽上滚下的初始位置不同，下列说法正确的是（）A. 小球平抛的初速度不同B. 小球平抛的运动轨迹不同C. 小球在空中运动的时间不同D. 小球在空中运动的水平位移不同解析：小球每次从斜槽上滚下的初始位置不同，会导致平抛的初速度不同。

因为平抛运动的水平方向是匀速直线运动，初速度不同则水平位移不同；而平抛运动的时间只由下落高度决定，初始位置不同不影响下落高度，所以时间不变。

运动轨迹也会因初速度不同而不同。

答案为ABD。

题目二：平抛运动实验中，下列哪些操作会增大实验误差（）A. 安装斜槽时，其末端不水平B. 确定小球抛出点时，有较大偏差C. 小球每次从斜槽上相同位置由静止释放D. 建立坐标系时，以斜槽末端端口位置为坐标原点解析：安装斜槽时末端不水平，小球做的不是平抛运动，会增大误差；确定小球抛出点有较大偏差，影响数据准确性，增大误差；小球每次从斜槽上相同位置由静止释放是正确操作，不会增大误差；以斜槽末端端口位置为坐标原点可能导致测量误差增大，应该以小球在末端球心位置为坐标原点。

答案为ABD。

题目三：在平抛运动实验中，测得小球平抛的初速度为v₀，当地重力加速度为g，小球下落高度为h，求小球水平位移x。

解析：根据平抛运动规律，竖直方向h = 1/2gt²，可求出运动时间t = √(2h/g)；水平方向做匀速直线运动，水平位移x = v₀t = v₀√(2h/g)。

题目四：平抛运动实验中，若已知小球平抛的水平位移为x，下落高度为h，求小球平抛的初速度v₀。

解析：由h = 1/2gt²可得运动时间t = √(2h/g)；又因为水平位移x = v₀t，所以v₀ = x/t = x/√(2h/g)。

题目五：在平抛运动实验中，实验时忘记记录小球抛出点的位置，只记录了几个点的坐标，已知其中一点坐标为(x₀,y₀)，水平间距为Δx，竖直间距为Δy，求小球平抛的初速度v₀。

平抛运动的经典例题

平抛运动的经典例题
1.一个小球以10m/s的初速度从距离地面15m高的地方平抛，求小球在水平方向上的运动时间和落点的高度。

解：小球在水平方向上做匀速直线运动，其速度vx=10m/s，方向水平向右。

小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

由平抛运动的解析公式可知，水平位移
x=vx*t=10m/s×4s=40m，垂直位移
y=1/2gt^2=1/2×20m/s×4s=80m。

落点高度h=y-x=80m-40m=40m。

2.一个小球以10m/s的初速度从距离地面15m高的地方平抛，求小球到达地面时，竖直方向上的速度大小和方向。

解：小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

小球到达地面时，速度为0，因此竖直方向上的速度大小为
20m/s，方向竖直向下。

3.一个小球以10m/s的初速度从距离地面20m高的地方平抛，求小球到达地面时，竖直方向上的速度大小和方向。

解：小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

小球到达地面时，速度为0，因此竖直方向上的速度大小为
20m/s，方向竖直向下。

(完整版)平抛习题(含答案)

平抛运动1．在平坦的垒球运动场上，击球手挥动球棒将垒球水平击出，垒球飞行一段时间后落地．若不计空气阻力，则()A．垒球落地时瞬间速度的大小仅由初速度决定B．垒球落地时瞬间速度的方向仅由击球点离地面的高度决定C．垒球在空中运动的水平位移仅由初速度决定D．垒球在空中运动的时间仅由击球点离地面的高度决定2．若以抛出点为起点，取初速度方向为水平位移的正方向，在下列各图中，能正确描述做平抛运动的物体的水平位移x的图象的是()3．水平匀速飞行的飞机每隔1 s投下一颗炸弹，共投下5颗，若空气阻力及风的影响不计，则在炸弹落地前()A．这5颗炸弹在空中排列成抛物线B．这5颗炸弹及飞机在空中排列成一条竖直线C．这5颗炸弹在空中各自运动的轨迹均是抛物线D．这5颗炸弹在空中均做直线运动4．如图2所示，在光滑的水平面上有小球A以初速度v0匀速直线运动，同时在它正上方有小球B以v0为初速度水平抛出并落于C点，则()图2A．小球A先到达C点B．小球B先到达C点C．两球同时到达C点D．不能确定5．从水平匀速飞行的直升机上向外自由释放一个物体，不计空气阻力，在物体下落过程中，下列说法正确的是()A．从飞机上看，物体静止B．从飞机上看，物体始终在飞机的后方C．从地面上看，物体做平抛运动D．从地面上看，物体做自由落体运动6.在同一平台上的O点抛出的3个物体，做平抛运动的轨迹如图3所示，则3个物体做平抛运动的初速度v A、v B、v C的关系和3个物体运动的时间t A、t B、t C的关系分别是()图3A．v A>v B>v C，t A>t B>t CB．v A＝v B＝v C，t A＝t B＝t CC．v A<v B<v C，t A>t B>t CD．v A>v B>v C，t A<t B<t C7.图4一水平抛出的小球落到一倾角为θ的斜面上时，其速度方向与斜面垂直，运动轨迹如图4中虚线所示．小球在竖直方向下落的距离与在水平方向通过的距离之比为() A．tan θB．2tan θC. D.8．如图5所示，在同一竖直面内，小球a、b从高度不同的两点，分别以初速度v a和v b 沿水平方向抛出，经过时间t a和t b后落到与两抛出点水平距离相等的P点．若不计空气阻力，下列关系式正确的是()图5A．t a>t b，v a<v b B．t a>t b，v a>v b题号12345678答案斜面长为L，那么抛球的水平初速度v0是________．图610．平抛一物体，当抛出1 s后，它的速度与水平方向成45°角，落地时速度方向与水平方向成60°角，g取10 m/s2.求：(1)物体的初速度大小；(2)物体落地时的速度大小；(3)开始抛出时物体距地面的高度；(4)物体的水平射程．11.将一个物体以10 m/s的初速度从10 m高处水平抛出，不计空气阻力，它落地时的速度大小和方向怎样？所用的时间为多少？(g取10 m/s2)12．在亚西湾某次护航任务中，为了驱赶索马里海盗，我护航官兵从空中直升机上向海盗船水平发射了一颗警告弹，6 s后官兵看到警告弹在海盗船附近爆炸，若爆炸时警告弹的运动方向与水平方向的夹角为30°，空气阻力不计，g＝10 m/s2，求：(1)直升机发射警告弹时的高度；(2)警告弹的初速度；(3)发射警告弹时直升机到海盗船的距离．、课后巩固练1．D 2.C3．BC[炸弹投出后，具有与飞机相同的水平速度，故所有炸弹抛出后均做平抛运动，轨迹是抛物线；炸弹抛出后在竖直方向上自由下落，在水平方向与飞机一样做匀速运动，所以炸弹落地前总在飞机的正下方，落地前炸弹和飞机总排列成一条竖直线．] 4．C[小球B以初速度v0水平抛出并落于C点，其水平方向做匀速直线运动，而在光滑的水平面上有小球A以初速度v0匀速直线运动，所以两球同时到达C点．]5．C[由于飞机在水平方向做匀速运动，当物体自由释放的瞬间，物体具有与飞机相同的水平初速度，则从飞机上看，物体始终处于飞机的正下方，选项B错；物体在重力的作用下在竖直方向做自由落体运动，所以选项A错误；在地面上看，由于物体具有水平方向的速度且只受重力的作用，因此物体做平抛运动，则C对，D错．]6．C[平抛运动的时间只与下落的高度有关，由t＝得t A>t B>t C，由题图可知，在下落高度相同时，水平射程s A<s B<s C，所以v A<v B<v C，故C正确．]7．D[如图所示，设小球抛出时的初速度为v0，则v x＝v0 ①v y＝v0cotθ②v y＝gt ③x＝v0t ④y＝⑤解①②③④⑤得：＝，D正确．]8．A[根据平抛运动的规律可知，小球在空中运动的时间由抛出点到落地点的竖直高度决定，因h a>h b，所以t a>t b；水平位移由初始速度和小球在空中运动的时间决定，因x a ＝x b，所以v a<v b，故A正确．]9．cos θ解析根据题中条件，小球做平抛运动的水平方向的位移x＝L cos θ，竖直方向的位移y ＝L sin θ，则x＝v0t，y＝gt2，故v0＝，将上述条件代入得：v0＝，整理得：v0＝cos θ.点评将平抛运动的规律与斜面的几何关系相结合，是分析此类问题的技巧．10．(1)10 m/s (2)20 m/s(3)15 m(4)10 m解析(1)物体抛出t1＝1 s时，由速度方向可得tan 45°＝，得v0＝10 m/s.(2)物体落地时，由速度方向可得cos 60°＝，得v＝20 m/s.(3)因v y＝v·sin 60°＝gt2，得t2＝s，故h＝gt＝15 m.(4)物体的水平射程x＝v0t2＝10 m.11．17.3 m/s与水平地面的夹角约为54.7° 1.41 s解析设物体从抛出到落地所用时间为t，根据平抛运动的性质可知v x＝v0，v y＝gt，y ＝.所用时间t＝＝s≈1.41 s.落地时的速度大小v＝＝m/s≈17.3 m/s.速度方向与水平地面的夹角为θ，则θ＝arctan ＝arctan ≈54.7°.落地时的速度大小为17.3 m/s，方向与水平地面的夹角约为54.7°，所用时间为1.41 s.12．(1)180 m(2)104 m/s(3)649 m解析(1)直升机的高度h＝gt2＝×10×62 m＝180 m.(2)警告弹爆炸前瞬间在竖直方向上的速度v y＝g·t＝10×6 m/s＝60 m/s所以v0＝＝m/s＝60 m/s≈104 m/s.(3)直升机到海盗船的距离s＝＝m≈649 m.。

物理平抛运动实验题型及解析

物理平抛运动实验题型及解析
在物理中，平抛运动实验是一个重要的实验，它主要考察学生对平抛运动的理解以及实验设计和操作能力。

以下是一些常见的平抛运动实验题型及解析：
1. 基本概念题：
题型：什么是平抛运动？请描述其运动特点。

解析：平抛运动是指一个物体以一定的初速度水平抛出，在重力的作用下，沿曲线轨迹运动。

其运动特点是初速度恒定，仅受重力影响，轨迹为抛物线。

2. 实验设计题：
题型：请设计一个实验来研究平抛运动的轨迹。

解析：可以使用频闪仪或高速摄像机来捕捉平抛运动的轨迹。

通过调整频闪仪或高速摄像机的参数，可以观察和记录物体在不同时刻的位置，从而描绘出其运动轨迹。

3. 数据分析题：
题型：给定一组平抛运动的实验数据，如何计算初速度和落地时间？
解析：通过分析物体的水平位移和竖直位移，结合时间间隔，可以计算出物体的初速度和落地时间。

使用公式$x = v_{0}t$和$y =
\frac{1}{2}gt^{2}$进行计算。

4. 误差分析题：
题型：在平抛运动的实验中，如何减小测量误差？
解析：可以采用多种方法减小误差，例如使用更精确的测量工具、多次测量求平均值、优化实验设计和操作等。

此外，还要注意消除系统误差和随机误差的影响。

5. 综合应用题：
题型：请解释在平抛运动的实验中，为何需要选择合适的实验参数？
解析：选择合适的实验参数是确保实验准确性和可靠性的关键。

例如，选择合适的初速度可以确保平抛运动的轨迹足够长，方便观察和测量；选择合适的时间间隔可以确保能够捕捉到物体在不同时刻的运动状态。

高中物理必修二平抛运动专题训练(经典必练题型)

高中物理必修二平抛运动专题训练（经典必练题型）一、单选题1.以30m/s的水平初速度v0抛出的物体，飞行一段时间后，打在倾角θ为30°的斜面上，此时速度方向与斜面夹角α为60°，（如图所示），则物体在空中飞行的时间为（不计空气阻力，g取10m/s2）（）A. 1.5sB. √3sC. 1.5√3sD. 3√3s2.如图所示，两个挨得很近的小球，从斜面上的同一位置O以不同的初速度v A、v B做平抛运动，斜面足够长，在斜面上的落点分别为A、B，空中运动的时间分别为t A、t B，碰撞斜面前瞬间的速度与斜面的夹角分别为α、β，已知OB=2OA．则有（）A. t A：t B=1：2B. v A：v B=1：2C. α=βD. α>β3.如图所示，滑板运动员以速度v0从距离地面高度为h的平台末端水平飞出，落在水平地面上。

运动员和滑板均可视为质点，忽略空气阻力的影响。

下列说法中正确的是（）A. h一定时，v0越大，运动员在空中运动时间越长B. h一定时，v0越大，运动员落地瞬间速度越大C. 运动员落地瞬间速度与高度h无关D. 运动员落地位置与v0大小无关4.如图所示，以19.6m/s的水平初速v0抛出的物体，飞行一段时间后，垂直地撞在倾角θ为45°的斜面上，可知物体完成这段飞行的时间是（）A. 1sB. 2sC. √3sD. 3s5.如图，可视为质点的小球，位于半径为√3m半圆柱体左端点A的正上方某处，以一定的初速度水平抛出小球，其运动轨迹恰好能与半圆柱体相切于B点．过B点的半圆柱体半径与水平方向的夹角为60°，则初速度为：（不计空气阻力，重力加速度为g=10m/s2）（）A. 5√53m/s B. 4√3m/s C. 3√5m/s D. √152m/s6.如图所示，小球以v0正对倾角为θ的斜面水平抛出，若小球到达斜面的位移最小，则以下说法正确的是（重力加速度为g）（）A. 小球空中运动时间为v0cotθgB. 小球的水平位移大小为2v02cotθgC. 由于不知道抛出点位置，位移大小无法求解D. 小球的竖直位移大小为v04cotθg7.如图所示的光滑斜面长为l，宽为b，倾角为θ，一物块（可看成质点）沿斜面左上方顶点P以初速度v0水平射入，恰好从底端Q点离开斜面，则（）A. 物块由P点运动到Q点所用的时间t=2√2lgsinθB. 物块由P点运动到Q点所用的时间t=2√2lgC. 初速度v0=b√g2lD. 初速度v0=b√gsinθ2l二、计算题（本大题共5小题，共50.0分）8.如图所示，质量为m=0.2kg的小球从平台上水平抛出后，落在一倾角θ=53°的光滑斜面顶端，并恰好无碰撞的沿光滑斜面滑下，顶端与平台的高度差h=0.8m，斜面的高度H=7.2m。