振动与波复习题及答案上课讲义
《大学物理》期末考试复习题(振动与波)

)
(A) 2 ;
答案:(D)
(B)
m1 m2
2
;
(C)
m2 m1
2
;
(D) 2
m2 . m1
一物体作简谐振动,振动方程为
x
A cos(t
1 4
) 。在
t = T/4(T
为周期)时刻,物体的
加速度为 ( )
(A)
2 2
A 2
;
(B)
2 2
A 2 ;
(C)
3 2
A 2
;
(D)
3 2
A 2
。
一弹簧振子,当把它水平放置时,它作简谐振动。若把它竖直放置或放在光滑斜面上,试判
一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的 1/4 时,其动能为振 动总能量的
(A) 7/16 ; (B) 9/16 ; (C) 11/16 ; (D) 15/16 。 []
答案:(D)
第十章 波动
10-1 机械波的几个概念
10-2 平面简谐波的波函数
如图所示,有一平面简谐波沿 x 轴负方向传播,
断下列情况正确的是
(A)竖直放置作简谐振动,在光滑斜面上不作简谐振动;
(B)竖直放置不作简谐振动,在光滑斜面上作简谐振动;
(C)两种情况都作简谐振动;
(D)两种情况都不作简谐振动。
[]
竖直放置 放在光滑斜面上
答案:(C)
同一弹簧振子悬挂相同的质量,分别按如图(a)、(b)、(c)所示的三种方式放置,摩擦力都
(A) 曲线 3,1,2 分别表示 x,v,a 曲线; (B) 曲线 2,1,3 分别表示 x,v,a 曲线; (C) 曲线 1,2,3 分别表示 x,v,a 曲线; (D) 曲线 2,3,1 分别表示 x,v,a 曲线.
振动与波复习题 答案

1.一轻弹簧在60 N 的拉力下伸长30 cm .现把质量为4 kg 的物体悬挂在该弹簧的下端并使之静止 ,再把物体向下拉10 cm ,然 后由静止释放并开始计时.求(1) 物体的振动方程;(2) 物体在平衡位置上方5 cm 时弹簧对物体的拉力;(3) 物体从第一次越过平衡位置时刻起到它运动到上方5 cm 处所需要的最短时间.解: k = f/x =200 N/m ,07.7/≈=m k ω rad/s 2分(1) 选平衡位置为原点,x 轴指向下方(如图所示), t = 0时, x 0 = 10A cos φ ,v 0 = 0 = -A ωsin φ. 解以上二式得 A = 10 cm ,φ = 0. 2分∴ 振动方程x = 0.1 cos(7.07t ) (SI) 1分 (2) 物体在平衡位置上方5 cm 时,弹簧对物体的拉力f = m (g -a ),而a = -ω2x = 2.5 m/s 2∴ f =4 (9.8-2.5) N= 29.2 N 3分(3) 设t 1时刻物体在平衡位置,此时x = 0,即0 = A cos ω t 1或cos ω t 1 = 0.∵ 此时物体向上运动, v < 0∴ ω t 1 = π/2, t 1= π/2ω = 0.222 s 1分再设t 2时物体在平衡位置上方5 cm 处,此时x = -5,即-5 = A cos ω t 1,cos ω t 1 =-1/2∵ v < 0, ω t 2 = 2π/3,t 2=2 π/3ω =0.296 s 2分∆t = t 1-t 2 = (0.296-0.222) s =0.074 s 1分2.一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B 点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm 求: (1) 质点的振动方程; (2) 质点在A 点处的速率.解:由旋转矢量图和 |v A | = |v B | 可知 T /2 = 4秒, ∴ T = 8 s , ν = (1/8) s -1,ω = 2πν = (π /4) s -1 3分 (1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A = t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图) 2分25cos /==φx A cm 1分∴ 振动方程 )434cos(10252π-π⨯=-t x (SI) 1分 (2) 速率 )434sin(41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时,质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==t x v m/s 1分 x 5 cm O v B x A B O t = 0t = 2 st = 4 s φωv A v BA B vx3.质量m = 10 g 的小球与轻弹簧组成的振动系统,按)318cos(5.0π+π=t x 的规律作自由振动,式中t 以秒作单位,x 以厘米为单位,求(1) 振动的角频率、周期、振幅和初相;(2) 振动的速度、加速度的数值表达式;(3) 振动的能量E ;(4) 平均动能和平均势能.解:(1) A = 0.5 cm ;ω = 8π s -1;T = 2π/ω = (1/4) s ;φ = π/3 2分(2) )318sin(1042π+π⨯π-==-t xv (SI) )318cos(103222π+π⨯π-==-t x a (SI) 2分 (3) 2222121A m kA E E E P K ω==+==7.90×10-5 J 3分 (4) 平均动能 ⎰=T K t m T E 02d 21)/1(v ⎰π+π⨯π-=-Tt t m T 0222d )318(sin )104(21)/1( = 3.95×10-5 J = E 21 同理 E E P 21== 3.95×10-5 J 3分4.一质量m = 0.25 kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1.(1) 求振动的周期T 和角频率ω.(2) 如果振幅A =15 cm ,t = 0时物体位于x = 7.5 cm 处,且物体沿x 轴反向运动,求初速v 0及初相φ.(3) 写出振动的数值表达式.解:(1) 1s 10/-==m k ω 1分63.0/2=π=ωT s 1分(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v 0 < 0 由 2020)/(ωv +=x A 得 3.12020-=--=x A ωv m/s 2分π=-=-31)/(tg 001x ωφv 或 4π/3 2分 ∵ x 0 > 0 ,∴ π=31φ (3) )3110cos(10152π+⨯=-t x (SI) 2分 5.一物体作简谐振动,其速度最大值v m = 3×10-2 m/s ,其振幅A = 2×10-2 m .若t = 0时,物体位于平衡位置且向x 轴的负方向运动. 求:(1) 振动周期T ;(2) 加速度的最大值a m ;(3) 振动方程的数值式.解: (1) v m = ωA ∴ω = v m / A =1.5 s -1∴ T = 2π/ω = 4.19 s 3分(2) a m = ω2A = v m ω = 4.5×10-2 m/s 2 2分 (3) π=21φ x = 0.02)215.1cos(π+t (SI) 3分6.一振幅为 10 cm ,波长为200 cm 的一维余弦波.沿x 轴正向传播,波速为 100 cm/s ,在t = 0时原点处质点在平衡位置向正位移方向运动.求(1) 原点处质点的振动方程.(2) 在x = 150 cm 处质点的振动方程.解:(1) 振动方程: )cos(0φω+=t A y A = 10 cm ,ω = 2πν = π s -1,ν = u / λ = 0.5 Hz初始条件: y (0, 0) = 0 0)0,0(>y得 π-=210φ 故得原点振动方程: )21cos(10.0π-π=t y (SI) 2分 (2) x = 150 cm 处相位比原点落后π23, 所以 )2321cos(10.0π-π-π=t y )2cos(10.0π-π=t (SI) 3分 也可写成 t y π=cos 10.0 (SI)7.一平面简谐波沿x 轴正向传播,其振幅为A ,频率为ν ,波速为u .设t = t '时刻的波形曲线如图所示.求(1) x = 0处质点振动方程;(2) 该波的表达式.解:(1) 设x = 0 处质点的振动方程为 )2cos(φν+π=t A y 由图可知,t = t '时 0)2cos(=+'π=φνt A y1分 0)2sin(2d /d <+'ππ-=φννt A t y 1分 所以 2/2π=+'πφνt , t 'π-π=νφ2212分x = 0处的振动方程为 ]21)(2cos[π+'-π=t t A y ν 1分(2) 该波的表达式为 ]21)/(2cos[π+-'-π=u x t t A y ν 3分8.某质点作简谐振动,周期为2 s ,振幅为0.06 m ,t = 0 时刻,质点恰好处在负向最大位移处,求12. x u O t =t ′y(1) 该质点的振动方程;(2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时,形成的一维简谐波的波动表达式,(以该质点的平衡位置为坐标原点);(3) 该波的波长.解:(1) 振动方程 )22cos(06.00π+π=t y )cos(06.0π+π=t (SI) 3分 (2) 波动表达式 ])/(cos[06.0π+-π=u x t y 3分])21(cos[06.0π+-π=x t (SI) (3) 波长 4==uT λ m 2分9.如图所示为一平面简谐波在t = 0 时刻的波形图,设此简谐波的频率为250 Hz ,且此时质点P 的运动方向向下,求(1) 该波的表达式;(2) 在距原点O 为100 m 处质点的振动方程与振动速度表达式.解:(1) 振动方程 )22cos(06.00π+π=t y )cos(06.0π+π=t (SI) 3分(2) 波动表达式 ])/(cos[06.0π+-π=u x t y 3分])21(cos[06.0π+-π=x t (SI) (3) 波长 4==uT λ m 2分10.一平面简谐波沿Ox 轴的负方向传播,波长为λ ,P 处质点的振动规律如图所示.(1) 求P 处质点的振动方程;(2) 求此波的波动表达式;(3) 若图中 λ21=d ,求坐标原点O 处质点的振动方程. 解:(1) 由振动曲线可知,P 处质点振动方程为 ])4/2cos[(π+π=t A y P )21cos(π+π=t A (SI) 3分 (2) 波动表达式为 ])4(2cos[π+-+π=λd x tA y (SI) 3分(3) O 处质点的振动方程 )21cos(0t A y π= 2分.16.。
大学物理振动与波练习题与答案

第二章 振动与波习题答案12、一放置在水平桌面上的弹簧振子,振幅2100.2-⨯=A 米,周期50.0=T 秒,当0=t 时 (1) 物体在正方向的端点;(2) 物体在负方向的端点;(3) 物体在平衡位置,向负方向运动; (4) 物体在平衡位置,向正方向运动。
求以上各种情况的谐振动方程。
【解】:π=π=ω45.02 )m ()t 4cos(02.0x ϕ+π=, )s /m ()2t 4cos(08.0v π+ϕ+ππ=(1) 01)cos(=ϕ=ϕ,, )m ()t 4cos(02.0x π=(2) π=ϕ-=ϕ,1)cos(, )m ()t 4cos(02.0x π+π=(3) 21)2cos(π=ϕ-=π+ϕ, , )m ()2t 4cos(02.0x π+π= (4) 21)2cos(π-=ϕ=π+ϕ, , )m ()2t 4cos(02.0x π-π=13、已知一个谐振动的振幅02.0=A 米,园频率πω4=弧度/秒,初相2/π=ϕ。
(1) 写出谐振动方程;(2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】:)m ()2t 4cos(02.0x π+π= , )(212T 秒=ωπ=15、图中两条曲线表示两个谐振动(1) 它们哪些物理量相同,哪些物理量不同 (2) 写出它们的振动方程。
【解】:振幅相同,频率和初相不同。
虚线: )2t 21cos(03.0x 1π-π= 米实线: t cos 03.0x 2π= 米16、一个质点同时参与两个同方向、同频率的谐振动,它们的振动方程为t 3cos 4x 1= 厘米)32t 3cos(2x 2π+= 厘米试用旋转矢量法求出合振动方程。
【解】:)cm ()6t 3cos(32x π+=17、设某一时刻的横波波形曲线如图所示,波动以1米/秒的速度沿水平箭头方向传播。
(1) 试分别用箭头表明图中A 、B 、C 、D 、E 、F 、H 各质点在该时刻的运动方向;(2) 画出经过1秒后的波形曲线。
大学物理复习题答案(振动与波动)

大学物理1复习题答案一、单选题(在本题的每一小题备选答案中,只有一个答案是正确的,请把你认为正确答案的题号,填入题干的括号内)1.一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。
将它们拿到月球上去,相应的周期分别为'T 1和'T 2。
则有 ( B )A .'T T >11且 'T T >22B .'T T =11且 'T T >22C .'T T <11且 'T T <22D .'T T =11且 'T T =222.一物体作简谐振动,振动方程为cos 4x A t ⎛⎫=+⎪⎝⎭πω,在4Tt =(T 为周期)时刻,物体的加速度为 ( B )A. 2ω B 。
2ω C 。
2ω D2ω3.一质点作简谐振动,振幅为A ,在起始时刻质点的位移为/2A -,且向x 轴的正方向 运动,代表此简谐振动的旋转矢量图为 ( D )AAAAAAC)AxxAAxA B C D4。
两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为)cos(1αω+=t A x .当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为 ( B )A. )π21cos(2++=αωt A x B. )π21cos(2-+=αωt A x . C 。
)π23cos(2-+=αωt A x D. )cos(2π++=αωt A x . 5.波源作简谐运动,其运动方程为t y π240cos 100.43-⨯=,式中y 的单位为m ,t 的单位为s ,它所形成的波形以s m /30的速度沿一直线传播,则该波的波长为 ( A )A .m 25.0B .m 60.0C .m 50.0D .m 32.06.已知某简谐振动的振动曲线如图所示,位移的单位为厘米,时间单位为秒.则此简谐振动的振动方程为: ( B )A .cos x t ππ⎛⎫=+ ⎪⎝⎭22233B .cos x t ππ⎛⎫=+ ⎪⎝⎭42233C .cos x t ππ⎛⎫=- ⎪⎝⎭22233D .cos x t ππ⎛⎫=- ⎪⎝⎭42233二. 填空题(每空2分)1. 简谐运动方程为)420cos(1.0ππ+=t y (t 以s 计,y 以m 计),则其振幅为 0.1 m ,周期为 0。
2.振动和波考试重点和习题答案

第八章 振动和波下面重点要考试内容:1.掌握简谐振动的基本概念、简谐振动的余弦表达式2.掌握旋转矢量表示法、振幅、相位概念、掌握振动能量的公式3.掌握同方向同频率谐振动的合成4.掌握平面简谐波的表达式及其意义、掌握波的能流密度和波的干涉5.理解机械波的产生和传播、惠更斯原理、波的衰减;;理解拍、相互垂直谐振动的合成8-1 试解释下列名词:简谐振动、振幅、频谱分析、基频、频谱图、波动、横波、纵波、波阵面、波的强度。
答: ①简谐振动:质点在弹性力(或准弹性力)作用下所作的振动叫简谐振动,其加速度与离开平衡位置的位移成正比,且方向相反。
②振幅:振动物体离开平衡位置的最大距离称为振幅。
③频谱分析:将任一周期性振动分解为多个简谐振动之和的过程,称为频谱分析。
④基频:一个复杂的振动可以分解为若干个频率不同的简谐振动之和,这些分振动频率中最低的频率称为基频,它与原振动的频率相同。
⑤频谱图:将组成一个复杂振动的各分振动的频率和振幅找出来,按振幅与频率关系列出谱线,这种图称为频谱图。
⑥波动:振动在介质中的传播现象叫波动,它也是一种重要的能量传播过程。
其中简谐振动在介质中传播所形成的波叫简谐波。
⑦横波:波在介质中传播时,如果介质中各质点振动的方向与波的传播方向垂直,则该波叫做横波。
⑧纵波:如果介质中各质点振动的方向与波的传播方向相互平行,则这种波称为纵波。
⑨波阵面:在波传播的介质中,质点振动相位相同的各点连成的面称为波阵面。
⑩波的强度:单位时间内通过垂直于波的传播方向单位面积上的平均能量,称为波的强度。
8-2 有一质点作简谐振动,试分析它在下列位置时的位移、速度、加速度的大小和方向:①平衡位置,向正方向运动;②平衡位置,向负方向运动;③正方向的端点;④负方向的端点。
解: 设该质点的振动方程为:)cos(ϕω+=t A x将它对时间t 分别求一阶导数、二阶导数,可得到速度v 和加速度a 的表达式:)2cos()sin(πϕωωϕωω++=+-==t A t A dt dx v)cos()cos(2222πϕωωϕωω++=+-==t A t A dtxd a 由此可以看出,速度的相位超前位移2π,加速度与位移的相位相反。
振动与波练习(题目与解答)
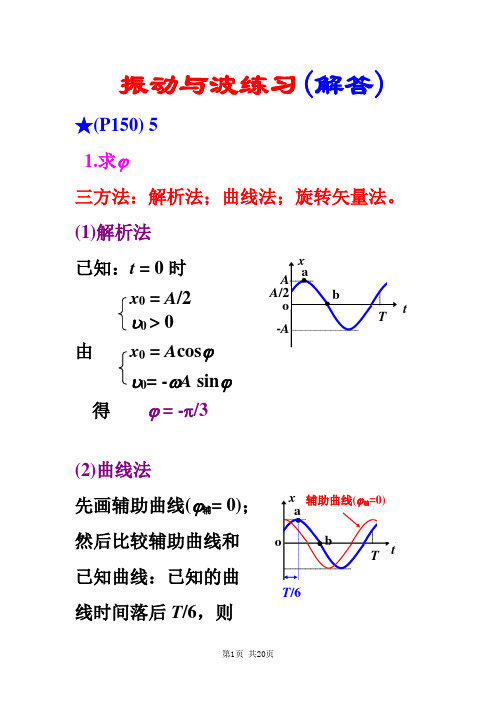
振动与波练习(解答) ★(P150) 51.求ϕ三方法:解析法;曲线法;旋转矢量法。
(1)解析法已知:t = 0时x0 = A/2υ0 > 0由x0 = A cosϕυ= -ωA sinϕ得ϕ = -π/3(2)曲线法先画辅助曲线(ϕ辅= 0)然后比较辅助曲线和已知曲线:已知的曲线时间落后T/6,则位相落后π/3,故已知振动的初相ϕ = -π/3(3)旋转矢量法由图ϕ = -π/3。
2.求a、b点的位相·a点:ξa = A;υa = 0,可得位相= 0。
·b点:ξb = 0;υb = -ωA,可得位相= π/2。
由解析法亦可。
3.求从t = 0到a、b两态的时间由旋转矢量图知,·从t = 0到a态,矢量转过π/3,故∆t a = T/6·从t = 0到b态,矢量转过π/3 + π/2,故 ∆t b = 5T /12 ★ (动力学解题两方法:受力法;能量法。
1.受力法:分析物体在任一位置时受力对m对轮 TR - fR = J β (2) 另 f = k ( y 0 + y ) f 0 = k y 0 = mg a = β Rd 2y d t 2 mg - T = m (1)可得说明振动是SHM ,其角频率为2.能量法:分析物体在任一位置时系统的能量。
·势能零点:平衡位置。
· 两边求导,并用 k y 0 = mg ;υ = ω角R , 可得d t 2 + ( ) y = 0 d 2ykR 2J + mR 2kR 2J + mR 2 ω = √m ( )2 + J ω角2 - m gy+ k (y 0+ y )2 = const.d y d t1 2 1 2 12d t 2 + ( ) y = 0 d 2y kR 2J + mR 2★(P151) 7 用能量法· 势能零点:平衡位置。
· 势能:(ρSy )gy · 系统能量:·两边求导,得 ·角频率为L 为液体总长度,m = ρSLyd y d tm ( )2+ ρS gy 2 = const. 1 2 d t 2 + ( ) y = 0d 2y 2ρSgm 2ρSg m ω = √ 2gL=√★(P160) 2已知x = 0处质元(波源)的振动曲线t(s)此曲线初相= ?1.画x = 25m处质元的振动曲线·由图T = 4 s ;知λ = uT = 20m·x = 0处质元的初相ϕo = - π/2·x = 25m处质元的初相x = 25m处质元的位相比x = 0处质元的落后多少?∆ϕ = k⋅25 = 2.5π,(波数k = 2π/λ = π/10) x = 25m处质元的初相ϕ 25 = - 3π = - π·x = 25m处质元也可先列出振动表达式再画振动曲线:·x = 0处质元(波源)的振动表达式ξ(0, t) = 2 cos(ωt - π/2) cm·x = 25m处质元的振动表达式ξ(25, t) = 2 cos(ωt - π/2- k⋅25) cm= 2 cos(ωt - 3π) cm= 2 cos(ωt - π) cm由此也可画x = 25m处质元的振动曲线。
振动和波综合标准答案

振动和波综合标准答案一、单选题:本大题共6小题,第1小题为3分;从第2小题到第6小题每题4分小计20分;共计23分。
1、◆标准答案:A★ 试题提示:再经T/2时,A.b的运动情况应与原来的运动情况相反,即a点振动到x轴下方的最低点,b恰好通过平衡位置向下运动,并以此画出A.b 间的波形.2、◆标准答案:C3、◆标准答案:D4、◆标准答案:C★ 试题详解:如图A错.周期T满足:0.15s=T,T=0.1s.0.25s相当于周期.故2m处质点此时y轴位移为0,B错.0.1s后,波到达10m处,故C对.10m处质点第一次到达y轴最大位移,用时.波源质点只通过了0.5m路程,D错.5、◆标准答案:D6、◆标准答案:B二、填空题:本大题共11小题,从第7小题到第12小题每题4分小计24分;第13小题为5分;从第14小题到第17小题每题6分小计24分;共计53分。
7、◆标准答案:各个时刻,各个质点★ 试题详解:各个时刻,各个质点8、◆标准答案:29、★ 试题详解: 0,向下10、◆标准答案:2.5,011、★ 试题详解: 16cm,+2cm12、◆标准答案:[3,2],613、◆标准答案:0.2414、★ 试题详解: 16cm/s,如下图所示15、◆标准答案:1000/316、◆标准答案:-4,0.117、◆标准答案:[0,1]、[3,4]三、多选题:本大题共10小题,第18小题为3分;从第19小题到第27小题每题4分小计36分;共计39分。
18、◆标准答案:BD★ 试题提示:波长有三种可能,如图所示,可以看出这三种可能的波长是λ1=2x0,λ2= x0,λ3=2x0/3.经过时间t,a点从平衡位置第一次到达正的最大位移处,说明它的振动周期有两种可能,分别是 T1=4t,T2=4t/3.根据公式v=λ/T,似乎有6种可能的速率,但经过计算,只有5种可能的数值,具体计算过程同学们可以自己去完成.如果经过时间t,b点也到达正的最大位移处,说明只能是中间图所示的情况,即波长λ2=x0,这列波的波速只可能是x0/4t或3x0/4t,选项A不对而选项B正确.如果经过时间t,b点到达负的最大位移处,则可能是两侧图所示的情况,即波长值有两种可能,即λ1=2x0或λ3=2x0/3.这列波的波速可能是x0/2t、3x0/2t、x0/6t三种情况,选项C不对.如果这列波的波速是x0/6t,经过时间t,b点一定到达负的最大位移处,选项D 正确.本题特别强度了波动过程中的两个周期性,计算结果不是唯一的,必须根据题目的具体条件去认真分析.)19、◆标准答案:BD20、◆标准答案:BD21、◆标准答案:ABC★ 试题详解:由题图中看出质点振动的周期T=0.5s,故波的频率f==2Hz,A对.由于P、Q两质点振动反向,故它们之间的距离为,由于波长大于它们之间距离,即n只能取0,即=2m,故=4m,B正确,由v=f知v=4×2=8(m/s),C对.无法确定波的传播方向,D错.22、◆标准答案:AB★ 试题详解:解题过程:从振动图象中知,周期T=4s,又知在t =0时刻,a质点在波谷,b质点在平衡位置且向y轴正方向运动,根据波由a 传向b,可知ab间距离x与波长的关系为即得波长λ的通式波速v=,则波速的通式为案为A、B.思路点拨:从题设条件和图形中,知周期T和波传播方向,确定此波属于单向传播问题.又知道在t=0时刻,a在波谷,b在平衡位置向y轴正方向运动.可是ab间距离x与波长λ关系不明确,波长λ是多值问题,周期T一定,波速也是多值问题,分别列出波长和波速的通式,再分析讨论便可得本题结果.小结:本题属于周期T确定,两点间距离与波长关系不明确,引起波长和波速的多值问题.若本题又未明确波沿直线ab向右传播,还需讨论波向左传播的情况,使题目变成双向多解问题.23、◆标准答案:BD24、◆标准答案:ABD25、◆标准答案:BD26、◆标准答案:ACD27、◆标准答案:ABC★ 试题提示:虽然波速v=λ/T,但不是“最大波速=最大波长/最大周期”.四、作图题:本大题共3小题,第28小题为5分;第29小题为6分;第30小题为8分;共计19分。
C1(振动与波答案)
C1
解: 动 力 学 表 征 式 : F kx
运 动 学 表 征 式 : y A c os[ ( t
x
x
)]
u :波沿传播方向传播距离落后的时间 u
x
u
:波沿传播方向传播距离落后的相位。
振动波动练习题(二) 三、1
大 学 物 理 练 习 册 振 动 波 动
如图所示,以P点在平衡位置向正方向运动作为计时零 点,已知圆频率为ω,振幅为A,简谐波以速度u向轴 的正方向传播,试求:(1)P点的振动方程。(2) 波动方程 u P · 解: t 0, x p 0, v p 0 p O
5 x B 5 m , B 点 的 振 动 方 程 : y B 5 c os t 20 x B 为 原 点 的 波 动 方 程 : y A 5 c os t 20 4 5
10m O A (a) 5m B -5 (b) O 0.5 1.5 t/s
2 3
C1
B
Ek 1 2
3 8
C
2
8 27
D
E k1
27 32
解:
kA
1 2
kx
2
4 9
kA
2
Ek2
3 8
kA
2
E k 2 / E k 1 27 : 32
答案:D
振动波动练习题(一) 二、1
大 学 物 理 练 习 册 振 动 波 动
如图所示,有一条简谐振动曲线,请写出: 振幅A = _____cm,周期T=_____s,圆频率ω=______,初 相位φo=______,振动表达式x =_______cm,振动 速度表达式υ=_______ cm/s,振动加速度表达式a =___________cm/s2,t =3s的相位______。
高考物理力学知识点之机械振动与机械波知识点总复习含答案(1)

高考物理力学知识点之机械振动与机械波知识点总复习含答案(1)一、选择题1.一列横波某时刻的波形图如图甲所示,图乙表示介质中某质点此后一段时间内的振动图象.下列说法正确的是()A.若波沿x轴正方向传播,则图乙表示的是质点N的振动图象B.若波沿x轴负方向传播,则图乙表示的是质点K的振动图象C.若图乙表示的是质点L的振动图象,则波沿x轴正方向传播D.若图乙表示的是质点M的振动图象,则波沿x轴负方向传播2.如图所示,A、B两物体组成弹簧振子,在振动过程中,A、B始终保持相对静止,下列给定的四幅图中能正确反映振动过程中物体A所受摩擦力F f与振子对平衡位置位移x关系的图线为A.B.C.D.3.如图所示,弹簧振子以O点为平衡位置,在M、N两点之间做简谐运动.下列判断正确的是()A.振子从O向N运动的过程中位移不断减小B.振子从O向N运动的过程中回复力不断减小C.振子经过O时动能最大D.振子经过O时加速度最大4.一洗衣机在正常工作时非常平稳,当切断电源后,发现洗衣机先是振动越来越剧烈,然后振动再逐渐减弱,对这一现象,下列说法正确的是()①正常工作时,洗衣机波轮的运转频率比洗衣机的固有频率大;②正常工作时,洗衣机波轮的运转频率比洗衣机的固有频率小;③正常工作时,洗衣机波轮的运转频率等于洗衣机的固有频率;④当洗衣机振动最剧烈时,波轮的运转频率恰好等于洗衣机的固有频率.A.①B.③C.①④D.②④5.如图所示,一列简谐横波向右传播,P、Q两质点平衡位置相距0.15 m。
当P运动到上方最大位移处时,Q刚好运动到下方最大位移处,则这列波的波长可能是()A.0.60 mB.0.20 mC.0.15 mD.0.10 m6.一列简谐横波沿x轴传播,某时刻的波形如图所示,质点a、b均处于平衡位置,质点a正向上运动.则下列说法正确的是A.波沿x 轴负方向传播B.该时刻质点b正向上运动C.该时刻质点a、b的速度相同D.质点a、b的振动周期相同7.下图表示一简谐横波波源的振动图象.根据图象可确定该波的()A.波长,波速B.周期,振幅C.波长,振幅D.周期,波速8.一列简谐横波在某时刻的波形图如图所示,已知图中的质点b比质点a晚0. 5s起振,质点b和质点c平衡位置之间的距离为5m,则该波的波速为A.1m/s B.3m/s C.5m/s D.8m/s9.如图所示为一列沿x轴负方向传播的简谐横波在t1=0时的波形图。
大学物理学振动与波动习题答案

大学物理学(上)第四,第五章习题答案第4章振动P174.4.1 一物体沿x轴做简谐振动,振幅A = 0.12m,周期T = 2s.当t = 0时,物体的位移x = 0.06m,且向x轴正向运动.求:(1)此简谐振动的表达式;(2)t = T/4时物体的位置、速度和加速度;(3)物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m,角频率ω = 2π/T= π.当t = 0时,x = 0.06m,所以cosφ = 0.5,因此φ= ±π/3.物体的速度为v = d x/d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sinφ,由于v > 0,所以sinφ < 0,因此φ = -π/3.简谐振动的表达式为x= 0.12cos(πt –π/3).(2)当t = T/4时物体的位置为x= 0.12cos(π/2–π/3)= 0.12cosπ/6 = 0.104(m).速度为v = -πA sin(π/2–π/3)= -0.12πsinπ/6 = -0.188(m·s-1).加速度为a = d v/d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s-2).(3)方法一:求时间差.当x = -0.06m 时,可得cos(πt1 - π/3) = -0.5,因此πt1 - π/3 = ±2π/3.由于物体向x轴负方向运动,即v< 0,所以sin(πt1 - π/3) > 0,因此πt1 - π/3 = 2π/3,得t1 = 1s.当物体从x= -0.06m处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt2 - π/3) = 0,可得πt2 - π/3 = -π/2或3π/2等.由于t2 > 0,所以πt2 - π/3 = 3π/2,可得t2 = 11/6 = 1.83(s).所需要的时间为Δt = t2 - t1 = 0.83(s).方法二:反向运动.物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间就是它从x= 0.06m,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x0/A),(-π < φ≦π),初位相的取值由速度决定.由于v = d x/d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sinφ,当v > 0时,sinφ < 0,因此φ = -arccos(x0/A);当v < 0时,sinφ > 0,因此φ = arccos(x0/A).可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x0 = A时,φ = 0;当初位置x0 = -A时,φ= π.4.2 已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及到达这些状态的时刻t各是多少?已知周期为T;(2)振动表达式;(3)画出旋转矢量图.[解答]方法一:由位相求时间.(1)设曲线方程为x = A cosΦ,其中A表示振幅,Φ = ωt + φ表示相位.由于x a = A,所以cosΦa = 1,因此Φa = 0.由于x b = A/2,所以cosΦb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t增加,b点位相就应该大于a点的位相,因此Φb = π/3.由于x c = 0,所以cosΦc = 0,又由于c点位相大于b位相,因此Φc = π/2.同理可得其他两点位相为Φd = 2π/3,Φe = π.c点和a点的相位之差为π/2,时间之差为T/4,而b点和a点的相位之差为π/3,时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同,所以到达a点的时刻为t a = T/6.到达b点的时刻为t b = 2t a = T/3.到达c点的时刻为t c = t a + T/4 = 5T/12.到达d点的时刻为t d = t c + T/12 = T/2.到达e点的时刻为t e = t a + T/2 = 2T/3.(2)设振动表达式为x = A cos(ωt + φ),当t = 0时,x = A/2时,所以cosφ = 0.5,因此φ =±π/3;由于零时刻的位相小于a点的位相,所以φ = -π/3,因此振动表达式为cos(2)3tx ATπ=π-.另外,在O时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t轴相交于f点,由于x f= 0,根据运动方程,可得cos(2)03tTππ-=图6.2所以232f t Tπππ-=±. 显然f 点的速度大于零,所以取负值,解得 t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为t a = T /4 + t f = T /6,其位相为203a a t T Φπ=π-=. 由图可以确定其他点的时刻,同理可得各点的位相.4.3如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k= 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅; (2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即mv = (m + M )v 0.解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m + M ) v 02/2 = kA 2/2,所以振幅为A v =-2(m). (2)振动的圆频率为ω=s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为x = A cos(ωt + φ).当t = 0时,x = 0,可得φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为x = 5×10-2cos(40t - π/2)(m).4.4 如图所示,在倔强系数为k的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为0m v v m M ==+这也是它们振动的初速度. 设振动方程为x = A cos(ωt + φ),其中圆频率为ω=物体没有落下之前,托盘平衡时弹簧伸长为x 1,则x 1 = Mg/k .物体与托盘碰撞之后,在新的平衡位置,弹簧伸长为x 2,则x 2 = (M + m )g/k .取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k . 因此振幅为图4.3图4.4A===初位相为arctanvxϕω-==4.5重量为P的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)可以证明:当两根弹簧串联时,总倔强系数为k=k1k2/(k1+ k2),因此固有频率为2πων===.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为2πων===4.6 一匀质细圆环质量为m,半径为R,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]方法一:用转动定理.通过质心垂直环面有一个轴,环绕此轴的转动惯量为I c = mR2.根据平行轴定理,环绕过O点的平行轴的转动惯量为I = I c + mR2 = 2mR2.当环偏离平衡位置时,重力的力矩为M = -mgR sinθ,方向与角度θ增加的方向相反.根据转动定理得Iβ = M,即22dsin0dI mgRtθθ+=,由于环做小幅度摆动,所以sinθ≈θ,可得微分方程22ddmgRt Iθθ+=.摆动的圆频率为ω=周期为2πTω=22==方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为E p = mg(R - R cosθ),绕O点的转动动能为212kE I=ω,总机械能为21(cos)2E I mg R R=+-ωθ.环在转动时机械能守恒,即E为常量,将上式对时间求导,利用ω= dθ/d t,β=dω/d t,得0 = Iωβ + mgR(sinθ)ω,由于ω ≠ 0,当θ很小有sinθ≈θ,可得振动的微分方程22ddmgRt Iθθ+=,从而可求角频率和周期.[注意]角速度和圆频率使用同一字母(b)图4.5ω,不要将两者混淆.4.7 横截面均匀的光滑的U 型管中有适量液体如图所示,液体的总长度为L ,求液面上下微小起伏的自由振动的频率。
振动和波复习题2及答案

振动和波复习题51解:(1) 1s 10/-==m k ω 63.0/2=π=ωT s(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v 0 < 0 由 2020)/(ωv +=x A 得3.12020-=--=x A ωv m/sπ=-=-31)/(tg 001x ωφv 或 4π/3∵ x 0 > 0 ,∴ π=31φ (3) )3110cos(10152π+⨯=-t x (SI) 52、3824解:设弹簧的原长为l ,悬挂m 1后伸长∆l ,则 k ∆l = m 1g , k = m 1g/ ∆l = 2 N/m 取下m 1挂上m 2后, 2.11/2==m k ω rad/s,ω/2π=T =0.56 st = 0时,φcos m 10220A x =⨯-=-,φωsin m/s 10520A -=⨯=-v解得 220201005.2m )/(-⨯=+=ωv x A m=-=-)/(tg 001x ωφv 180°+12.6°=3.36 rad也可取 φ = -2.92 rad振动表达式为 x = 2.05×10-2cos(11.2t -2.92) (SI)或 x = 2.05×10-2cos(11.2t +3.36) (SI)53、3555解:周期 25.0/2=π=ωT s ,振幅 A = 0.1 m,初相 φ = 2π/3,v max = ω A = 0.8π m/s ( = 2.5 m/s ), a max = ω 2A = 6.4π2 m/s 2 ( =63 m/s 2 ).54、5191解: (1) v m = ωA ∴ω = v m / A =1.5 s -1 ∴ T = 2π/ω = 4.19 s(2) a m = ω2A = v m ω = 4.5×10-2 m/s 2(3) π=21φ,x = 0.02)215.1cos(π+t (SI) 55、3558解:(1) )25sin(0.3d d π--==t t x v (SI) t 0 = 0 , v 0 = 3.0 m/s . (2) x m ma F 2ω-== ,A x 21= 时, F = -1.5 N . 56、3410解: (1)已知波的表达式为)2100cos(05.0x t y π-π=与标准形式)/22cos(λνx t A y π-π= 比较得A = 0.05 m , ν = 50 Hz , λ = 1.0 m , u = λν = 50 m/s(2) 7.152)/(max max =π=∂∂=A t y νv m /s322max 22max 1093.44)/(⨯=π=∂∂=A t y a ν m/s 2(3) π=-π=∆λφ/)(212x x ,二振动反相57、5206解:由图,λ = 2 m ,又∵u = 0.5 m/s ,∴ ν = 1 /4 Hz ,T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图. 此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动, ∴ π=21φ ∴ - )2121cos(5.0π+π=t y (SI) 58、3084解:(1) 以O 点为坐标原点.由图可知,该点振动初始条件为 0cos 0==φA y , 0sin 0<-=φωA v所以 π=21φ 波的表达式为 ]21)/(cos[π+-=u x t A y ωω (2) 8/λ=x 处振动方程为 ]21)8/2(cos[π+π-=λλωt A y )4/cos(π+=t A ω 8/3λ=x 的振动方程为,]218/32cos[π+-=λλπωt A y )4/cos(π-=t A ω (3) )21/2sin(/d d π+π--=λωωx t A t y , t = 0,8/λ=x 处质点振动速度 ]21)8/2sin[(/d d π+π--=λλωA t y 2/2ωA -=,t = 0,8/3λ=x 处质点振动速度]21)8/32sin[(/d d π+⨯π--=λλωA t y 2/2ωA = 59 解:(1) )3121cos(10220π+π⨯=-t y (SI) (2) ]31)4141(2cos[1022π+-π⨯=-x t y (SI) (3)t = 1 s 时,波形表达式:)6521cos(1022π-π⨯=-x y (SI) 故有如图的曲线. 60、5516解:设x = 0处质点振动的表达式为 )cos(0φω+=t A y ,已知 t = 0 时,y 0 = 0,且 v 0 > 0 ∴π-=21φ ∴ )2cos(0φν+π=t A y )21100cos(1022π-π⨯=-t (SI) 由波的传播概念,可得该平面简谐波的表达式为)/22cos(0u x t A y νφνπ-+π=)2121100cos(1022x t π-π-π⨯=- (SI) x = 4 m 处的质点在t 时刻的位移,)21100cos(1022π-π⨯=-t y (SI) 该质点在t = 2 s 时的振动速度为 )21200sin(1001022π-π⨯⨯-=-πv = 6.28 m/s 61、3476解:(1) x = λ /4处,)212cos(1π-π=t A y ν , )212cos(22π+π=t A y ν ∵ y 1,y 2反相 ∴合振动振幅 A A A A s =-=2 , 且合振动的初相φ 和y 2的初相一样为π21. 合振动方程 )212cos(π+π=t A y ν x (m)y (m)0u 0.512t = 0-1 -2-(2) x = λ /4处质点的速度 )212sin(2/d d π+ππ-== v t A t y νν)2cos(2π+ππ=t A νν 62、3060解:(1) x = 0点 π=210φ;x = 2点 π-=212φ; x =3点 π=3φ; (2) 如图所示.63、0321解:取如图x 坐标,平衡位置为原点O ,向下为正,m 在平衡位置时弹簧已伸长x 0 0kx mg = ①设m 在x 位置,分析受力, 这时弹簧伸长0x x + )(02x x k T += ② 由牛顿第二定律和转动定律列方程:ma T mg =-1 ③ βJ R T R T =-21 ④ βR a = ⑤联立解得 m R J kx a +-=)/(2 由于x 系数为一负常数,故物体做简谐振动,其角频率为222)/(mRJ kR m R J k +=+=ω 64、3428解:(1) ==t W P / 2.70×10-3 J/s (2) ==S P I /9.00×10-2 J /(s ·m 2) (3) u w I ⋅= ==u I w / 2.65×10-4 J/m 365、3436解:在P 最大限度地减弱,即二振动反相.现二波源是反相的相干波源,故要求因传播路径不同而引起的相位差等于 ± 2k π(k = 1,2,…).由图 =AP 50 cm . ∴ 2π (50-40) /λ = 2k π,∴ λ = 10/k cm ,当k = 1时,λmax = 10 cm波动光学复习题51、解:(1) x = 2kD λ / d ,d = 2kD λ /∆x 此处 k =5∴ d =10 D λ / ∆x =0.910 mm(2) 共经过20个条纹间距,即经过的距离l =20 D λ / d =24 mm(3) 不变52、3613解:原来,δ = r 2-r 1= 0覆盖玻璃后δ=( r 2 + n 2d – d )-(r 1 + n 1d -d )=5λ∴ (n 2-n 1)d =5λ ,125n n d -=λ = 8.0×10-6 m 53、3659解:(1) 明环半径()2/12λ⋅-=R k r ,()Rk r 1222-=λ=5×10-5 cm (2) (2k -1)=2 r 2 / (R λ),对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5故在OA 范围内可观察到的明环数目为50个.54、3660解:(1) 棱边处是第一条暗纹中心,在膜厚度为e 2=21λ处是第二条暗纹中心,依此可知第四条暗纹中心处,即A 处膜厚度 e 4=λ23 xy O 1234t =T /4时的波形曲线 21∴ ()l l e 2/3/4λθ===4.8×10-5 rad(2) 由上问可知A 处膜厚为 e 4=3×500 / 2 nm =750 nm对于λ'=600 nm 的光,连同附加光程差,在A 处两反射光的光程差为 λ'+2124e ,它与波长λ'之比为0.321/24=+'λe .所以A 处是明纹。
(完整word版)振动与波复习题及答案

第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a .则下列计算该振子劲度系数的公式中,错误的是:(A) 2max 2max /x m k v =. (B) x mg k /=.(C) 22/4T m k π=. (D) x ma k /=. [ B ] 2. 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为(A) g l π2. (B) gl22π.(C) g l 322π. (D) gl 3π. [ C ] 3. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为(A) π. (B) π/2. (C) 0 . (D) θ. [ C ]4. 两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(ωt + α).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .(C) )π23cos(2-+=αωt A x . (D) )cos(2π++=αωt A x . [ B ][ ]6. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A) π/6. (B) 5π/6. (C) -5π/6. (D) -π/6. (E) -2π/3. [ ]7. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2.将它们拿到月球上去,相应的周期分别为1T '和2T '.则有(A) 11T T >'且22T T >'. (B) 11T T <'且22T T <'.(C) 11T T ='且22T T ='. (D) 11T T ='且22T T >'. [ D ] 8. 一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动.当重物通过平衡位置且向规定的正方向运动时,开始计时.则其振动方程为: (A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x(C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A xv 21(E) t m /k A x cos = [ B ] 9. 一质点在x 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为(A) 1 s . (B) (2/3) s .(C) (4/3) s . (D) 2 s . [ B ]10.一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为(A) 2221ωA -. (B) 2221ωA . (C) 2321ωA -. (D)2321ωA . [ B ] 11. 两个同周期简谐振动曲线如图所示.x 1的相位比x 2的相位(A) 落后π/2. (B) 超前π/2. (C) 落后π . (D) 超前π.[ B ]12. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为[ B ]13. 一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s .(C) 2.20 s .(D) 2.00 s . [ B ]A21-A21-A21 21A21 AA21-A21-2115. 用余弦函数描述一简谐振子的振动.若其速度~时间(v ~t )关系曲线如图所示,则振动的初相位为(A) π/6. (B) π/3.(C) π/2. (D) 2π/3. (E) 5π/6.[ A ]17. 一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为 (A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ D ]18 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A) kA 2. (B)221kA . (C) (1/4)kA 2. (D) 0. [ D ]19. 一物体作简谐振动,振动方程为)21cos(π+=t A x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为:(A) 1:4. (B) 1:2. (C) 1:1.(D) 2:1. (E) 4:1. [ D ]20.动的初相为 (A) π23. (B) π.(C) π21. (D) 0. [ B ] 二. 填空题21. 在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为 (a) ______________________________;(b) ______________________________;(c) ______________________________.23. 在两个相同的弹簧下各悬一物体,两物体的质量比为4∶1,则二者作简谐振 动的周期之比为___2:1___.24. 一质点作简谐振动,速度最大值v m = 5 cm/s ,振幅A = 2 cm .若令速度具有 正最大值的那一时刻为t = 0,则振动表达式为_____50.02cos()22x t π=-___.25. 一物体作余弦振动,振幅为15×10-2m ,角频率为6π s -1,初相为0.5 π,则21--(c)A/ -A 2cos()2x A t T ππ=+2cos()2x A t T ππ=+2cos()x A t T ππ=+振动方程为 __0.15cos(6)2x t ππ=+(SI).27. 一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m ,初速度为0.09 m/s ,则振幅A =____0.05m_________ ,初相φ =____3arcsin 5-____________.30. 已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为_______1:1__________.31.则此简谐振动的三个特征量为A =_____0.1m________;ω =_____/6rad s π_____;φ =_____3π__________. .34. 已知三个简谐振动曲线如图所示,则振动方程分别为:x 1 =10cos t π______________________, x 2 =10cos()2t ππ- _____________________,x 3 =10cos()t ππ+_______________________.37.一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初相为_____4π_______.振动方程为__0.02cos()4x t ππ=+____________.41. 一作简谐振动的振动系统,振子质量为2 kg ,系统振动频率为1000 Hz ,振 幅为0.5 cm ,则其振动能量为______1002πJ________.43. 一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,t x (cm)则弹簧的劲度系数为____200N/m_______,振子的振动频率为_5πHZ________. 44.两个同方向的简谐振动曲线如图所示.合振动的振幅 为______21A A -___________,合振动的振动方程 为_____212()cos()2x A A t T ππ=-+______. 50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为)612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI)则其合成振动的振幅为___0.01m________,初相为____6π_____.第十章波复习题一、选择题1. 在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计). (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计)[ C ]2. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则 (A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ B ] 3.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5s 时刻的波形图是 [ A ]·---4. 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻 [ D ](A) A 点振动速度大于零. (B) B 点静止不动. (C) C 点向下运动. (D) D 点振动速度小于零.5. 把一根十分长的绳子拉成水平,用手握其一端.维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长. (B) 振动频率越低,波长越长.(C) 振动频率越高,波速越大. (D) 振动频率越低,波速越大.[ B ] 6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则O 点的振动初相φ 为: (A) 0. (B)π21(C) π (D)π23(或π-21) [ B ]7. 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为(A) ])/(cos[0φω+-=u x t A y .(B) )]/([cos u x t A y +=ω.(C) })]/([cos{0φω+-=u x t A y . (D)})]/([cos{0φω++=u x t A y . [ C ]8.如图所示为一平面简谐波在t = 0 时刻的波形图,该波的波速u = 200 m/s ,则P 处质点的振动曲线为[ C ]9. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是 [ A ]xy Ouy(m)ωSA ϖO ′ωSA ϖO′ωϖO ′ωSAϖO ′(A)(B)(C)(D)S10. 一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是(A))314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI). (C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI). [ A ]11. 图示一简谐波在t = 0时刻的波形图,波速 u = 200 m/s ,则P 处质点的振动速度表达式为 [ C ](A))2cos(2.0π-ππ-=t v (SI). (B) )cos(2.0π-ππ-=t v (SI). (C) )2/2cos(2.0π-ππ=t v (SI).(D) )2/3cos(2.0π-ππ=t v (SI).12.在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是(A) A 1 / A 2 = 16. (B)A 1 / A 2 = 4.(C) A 1 / A 2 = 2.(D) A 1 / A 2 = 1 /4. [ C ] 13. 一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为最大值的媒质质元的位置是:(A) o ',b ,d ,f . (B) a ,c ,e ,g .(C) o ',d . (D) b ,f . [ B ]14. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [C ] 15. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中(A) 它的势能转换成动能. (B) 它的动能转换成势能. (C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.[ C ] 16. 如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为)212cos(1π+π=t A y ,则S 2的振动方程为(A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y . [ D ]S17. 两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B)π21. (C) π. (D) π23. [ C ] 18. S 1和S 2是波长均为λ 的两个相干波的波源,相距3λ /4,S 1的相位比S 2超前π21.若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,则在S 1、S 2连线上S 1外侧和S 2外侧各点,合成波的强度分别是(A) 4I 0,4I 0. (B) 0,0.(C) 0,4I 0 . (D) 4I 0,0. [ A ] 19 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ] 20 在波长为λ 的驻波中,两个相邻波腹之间的距离为 (A) λ /4. (B) λ /2.(C) 3λ /4. (D) λ . [ B ] 21.沿着相反方向传播的两列相干波,其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=.在叠加后形成的驻波中,各处简谐振动的振幅是 (A) A . (B) 2A .(C))/2cos(2λx A π. (D) |)/2cos(2|λx A π. [ D ]二、填空题22.一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在 该时刻的运动方向.A _____________;B_____________ ;C ______________ . 23. 一平面简谐波的表达式为)37.0125cos(025.0x t y -= (SI),其角频率ω =__________________________,波速u =______________________,波长λ = _________________.24. 频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________.25. 图为t = T / 4 时一平面简谐波的波形曲线,则其波的表达式为 ______________________________________________.26、一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.S 1S 2Pλ/4-xOP 1P 227、一简谐波沿x 轴正方向传播.x 1和x 2两点处的振动曲线分别如图(a)和(b)所示.已知x 2 .> x 1且x 2 - x 1 < λ(λ为波长),则x 2点的相位比x 1点的相位滞后___________________.28、已知某平面简谐波的波源的振动方程为t y π=21sin 06.0(SI),波速为2 m/s .则在波传播前方离波源 5 m 处质点的振动方程为_-______________________.29、(1)一列波长为λ 的平面简谐波沿x 轴正方向传播.已知在λ21=x处振动的方程为y = A cos ω t ,则该平面简谐波的表达式为______________________________________. (2) 如果在上述波的波线上x = L (λ21>L)处放一如图所示的反射面,且假设反射波的振幅为A ',则反射波的表达式为 _______________________________________ (x ≤L ).30、一平面简谐波沿x 轴负方向传播.已知 x = -1 m 处质点的振动方程为)cos(φω+=t A y ,若波速为u ,则此波的表达式为 _________________________________________________________. 31、一个波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2,在两个球面上分别取相等的面积∆S 1和∆S 2,则通过它们的平均能流之比=21P /P ___________________.32、一点波源发出均匀球面波,发射功率为4 W .不计媒质对波的吸收,则距离 波源为2 m 处的强度是__________________.33、如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3λ 和10 λ / 3 ,λ 为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率___________,波源S 1 的相位比S 2 的相位领 先_________________.34、如图所示,S 1和S 2为同相位的两相干波源,相距为L ,P 点距S 1为r ;波源S 1在P 点引起的振动振幅为A 1,波源S 2在P 点引起的振动振幅为A 2,两波波长都是λ ,则P 点振幅A =_________________________________________________________. 35、两相干波源S 1和S 2的振动方程分别是tA y ωcos 1=和)21cos(2π+=t A y ω.S 1距P 点3个波长,S 2距P 点21/4个波长.两波在P 点引起的两个振动的相位差是____________.36、 S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(λ为波长)如图.已知S 1的初相为π21. (1) 若使射线S 2C 上各点由两列波引起的振动均干涉相消,则S 2的初相应为________________________.(2) 若使S 1 S 2连线的中垂线MN 上各点由两列波引起的 振动均干涉相消,则S 2的初位相应为_______________________.(a)(b)PS S1237、 两列波在一根很长的弦线上传播,其表达式为 y 1 = 6.0×10-2cos π(x - 40t ) /2 (SI) y 2 = 6.0×10-2cos π(x + 40t ) /2 (SI)则合成波的表达式为__________________________________________________; 在x = 0至x = 10.0 m 内波节的位置是_____________________________________ __________________________________;波腹的位置是________________________________________________________. 38、设入射波的表达式为)(2cos 1λνxt A y +π=.波在x = 0处发生反射,反射点为固定端,则形成的驻波表达式为____________________________________. 39、 一驻波表达式为t x A y ππ=100cos 2cos .位于x 1 = 3 /8 m 的质元P 1与位于x 2 = 5 /8 m 处的质元P 2的振动相位差为_____________________________. 40、 在弦线上有一驻波,其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________.。
第10章 振动与波动(习题与答案)讲解

第10章 振动与波动一. 基本要求1. 掌握简谐振动的基本特征,能建立弹簧振子、单摆作谐振动的微分方程。
2. 掌握振幅、周期、频率、相位等概念的物理意义。
3. 能根据初始条件写出一维谐振动的运动学方程,并能理解其物理意义。
4. 掌握描述谐振动的旋转矢量法,并用以分析和讨论有关的问题。
5. 理解同方向、同频率谐振动的合成规律以及合振幅最大和最小的条件。
6. 理解机械波产生的条件。
7. 掌握描述简谐波的各物理量的物理意义及其相互关系。
8. 了解波的能量传播特征及能流、能流密度等概念。
9. 理解惠更斯原理和波的叠加原理。
掌握波的相干条件。
能用相位差或波程差概念来分析和确定相干波叠加后振幅加强或减弱的条件。
10. 理解驻波形成的条件,了解驻波和行波的区别,了解半波损失。
二. 内容提要1. 简谐振动的动力学特征 作谐振动的物体所受到的力为线性回复力,即kx F -= 取系统的平衡位置为坐标原点,则简谐振动的动力学方程(即微分方程)为x tx 222d d ω-= 2. 简谐振动的运动学特征 作谐振动的物体的位置坐标x 与时间t 成余弦(或正弦)函数关系,即)cos(ϕ+ω=t A x由它可导出物体的振动速度 )sin(ϕ+ωω-=t A v 物体的振动加速度 )cos(ϕ+ωω-=t A a 23. 振幅A 作谐振动的物体的最大位置坐标的绝对值,振幅的大小由初始条件确定,即2v ω+=2020x A 4. 周期与频率 作谐振动的物体完成一次全振动所需的时间T 称为周期,单位时间内完成的振动次数γ称为频率。
周期与频率互为倒数,即ν=1T 或 T1=ν 5. 角频率(也称圆频率)ω 作谐振动的物体在2π秒内完成振动的次数,它与周期、频率的关系为 ωπ=2T 或 πν=ω26. 相位和初相 谐振动方程中(ϕ+ωt )项称为相位,它决定着作谐振动的物体的状态。
t=0时的相位称为初相,它由谐振动的初始条件决定,即0x v ω-=ϕtan应该注意,由此式算得的ϕ在0~2π范围内有两个可能取值,须根据t=0时刻的速度方向进行合理取舍。
II2_振动和波+详细解答

振动1. 一倔强系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为1T ,若将此弹簧截去一半的长度,下端挂一质量为12m 的物体,则系统振动周期2T 等于 (A )21T (B )1T (C )1T /2 (D )1T /2 (E )1T /4(C )弹簧的弹性系数问题:一根弹簧,弹性系数为k ,把它截短以后,k 不是减小了,而是增大了。
为什么?因为我们知道胡克定律为:f kx =(力的大小),即 f k x=。
下面两根弹簧,本来材料、长度、弹性系数都是完全一样的,但是把其中的一根截短,加上相等的拉力f ,截短以后的弹簧伸长量要小于原来长度的弹簧的伸长量,弹性系数k 增大了。
f12T = 22k k =,下端挂一质量为12m的物体,则系统振动周期2T 为:2T 1112222T π⎛=== ⎝2. 图(下左)中三条曲线分别表示简谐振动中的位移x ,速度v 和加速度a ,下列说法中那一个是正确的?(A )曲线3、1、2分别表示x 、v 、a 曲线。
(B )曲线2、1、3分别表示x 、v 、a 曲线。
(C )曲线1、3、2分别表示x 、v 、a 曲线。
(D )曲线2、3、1分别表示x 、v 、a 曲线。
(E )曲线1、2、3分别表示x 、v 、a 曲线。
(E )位移x 与加速度a 的曲线时刻都是反相的,从图上看曲线1、3反相,曲线2是速度v 曲线;另外,速度比位移的位相超前2π,加速度比速度的位相超前2π,从图上看曲线3比2超前了2π,3是加速度曲线; 曲线2比1超前了2π,1是位移曲线。
3. 在t =0时,周期为T 、振幅为A 的单摆分别处于图(上右)(a)、(b)、(c)三种状态,若选单摆的平衡位置为x 轴的原点,x 轴正向指向右方,则单摆作小角度摆动的振动表达式分别为(1) ; (2) ; (3) 。
关键是写出初位相,用旋转矢量法最方便:0v (a)(b)t(a )φ= -π/2(b )φ= π/2(c )φ= π所以: (1)Y=Acos (t T π2-2π) (2)Y=Acos (t T π2+2π) (3)Y=Acos (t Tπ2+π)4.一系统作谐振动,周期为T ,以余弦函数表达振动时,初位相为零,在0≤t ≤T /2范围内,系统在t = 、 时刻动能和势能相等。
振动和波复习题1及答案

振动和波复习题一、选择题 1、3002两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(ωt + α).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .(C) )π23cos(2-+=αωt A x . (D) )cos(2π++=αωt A x . [ ]2、3003轻弹簧上端固定,下系一质量为m 1的物体,稳定后在m 1下边又系一质量为m 2的物体,于是弹簧又伸长了∆x .若将m 2移去,并令其振动,则振动周期为(A) g m x m T 122∆π= . (B) gm xm T 212∆π=. (C) g m xm T 2121∆π=. (D) gm m x m T )(2212+π=∆. [ ]3、3396一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6. (B) 5π/6. (C) -5π/6.(D) -π/6. (E) -2π/3. [ ] 4、5501一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为(A) 2221ωA -. (B) 2221ωA . (C) 2321ωA -. (D)2321ωA . [ ] 5、3254一质点作简谐振动,周期为T .质点由平衡位置向x 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为(A) T /4. (B) T /6(C) T /8 (D) T /12 [ ] 6、3031已知一质点沿y轴作简谐振动.其振动方程为)4/3cos(π+=t A y ω.与之对应的振动曲线是 [ ]y当质点以频率ν 作简谐振动时,它的动能的变化频率为 (A) 4 ν. (B) 2 ν . (C) ν. (D)ν21. [ ] 8、3560弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为 (A) kA 2. (B)221kA . (C) (1/4)kA 2. (D) 0. [ ] 9、5182一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的 (A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E)2/3. [ ]10、3562图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为(A) π23. (B) π.(C) π21. (D) 0. [ ]11、3147一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是 [ ]12、3058在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计). (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计) [ ] 13、3066机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则(A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ ]-A/ -A在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反. (B) 大小和方向均相同. (C) 大小不同,方向相同. (D) 大小不同,而方向相反.[ ] 15、5513频率为 100 Hz ,传播速度为300 m/s 的平面简谐波,波线上距离小于波长的两点振动的相位差为π31,则此两点相距(A) 2.86 m . (B) 2.19 m . (C) 0.5 m . (D) 0.25 m . [ ] 16、3407横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻(A) A 点振动速度大于零. (B) B 点静止不动.(C) C 点向下运动. (D) D 点振动速度小于零.[]17、3603一平面简谐波的表达式为 )/(2cos λνx t A y -π=.在t = 1 /ν 时刻,x 1 = 3λ /4与x 2 = λ /4二点处质元速度之比是(A) -1. (B)31. (C) 1. (D) 3 [ ] 18、3149一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是 [ ]19、3069一沿x 轴负方向传播的平面简谐波在t= 2 s 时的波形曲线如图所示,则原点O 的振动方程为 (A) )21(cos 50.0ππ+=t y , (SI).(B) )2121(cos 50.0ππ-=t y , (SI).(C) )2121(cos 50.0ππ+=t y , (SI). (D) )2141(cos 50.0ππ+=t y , (SI). [ ] 20、3087一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是ωSAO ′ωSA ωωSAO ′(A)(B)(C)(D)S(A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [ ] 21、3090一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成势能. (B) 它的势能转换成动能. (C) 它从相邻的一段质元获得能量其能量逐渐增大.(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小. [ ]22、3289图示一平面简谐机械波在t 时刻的波形曲线.若此时A 点处媒质质元的振动动能在增大,则(A) A 点处质元的弹性势能在减小.(B) 波沿x 轴负方向传播.(C) B 点处质元的振动动能在减小.(D) 各点的波的能量密度都不随时间变化. [ ] 23、3308在波长为λ 的驻波中,两个相邻波腹之间的距离为 (A) λ /4. (B) λ /2.(C) 3λ /4. (D) λ . [ ] 24、3598电磁波在自由空间传播时,电场强度E 和磁场强度H(A) 在垂直于传播方向的同一条直线上. (B) 朝互相垂直的两个方向传播. (C) 互相垂直,且都垂直于传播方向. (D) 有相位差π21. [ ] 25、3458在真空中沿着x 轴正方向传播的平面电磁波,其电场强度波的表达式是 )/(2cos 0λνx t E E z -π=,则磁场强度波的表达式是: (A) )/(2cos /000λνμεx t E H y -π=. (B) )/(2cos /000λνμεx t E H z -π=.(C) )/(2cos /000λνμεx t E H y -π-=.(D) )/(2cos /000λνμεx t E H y +π-=. [ ]二、填空题 26、3820将质量为 0.2 kg 的物体,系于劲度系数k = 19 N/m 的竖直悬挂的弹簧的下端.假定在弹簧不变形的位置将物体由静止释放,然后物体作简谐振动,则振动频率为__________,振幅为____________. 27、5187一竖直悬挂的弹簧振子,自然平衡时弹簧的伸长量为x 0,此振子自由振动的周期T =____________________________. 28、3038一水平弹簧简谐振子的振动曲线如图所示.当振子处在位移为零、速度为-ωA 、加速度为零和弹性力为零的状态时,应对应于曲线上的________点.当振子处在位移的绝对值为A 、速度为零、加速度为-ω2A 和弹性力为-kA 的状态时,应对应于曲线上的____________点.29、3567图中用旋转矢量法表示了一个简谐振动.旋转矢量的长度为0.04 m ,旋转角速度ω = 4π rad/s .此简谐振动以余弦函数表示的振动方程为x=__________________________(SI).30、3033一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为 A =_____________;ω =________________; φ =_______________.31、3046一简谐振动的旋转矢量图如图所示,振幅矢量长2 cm ,则该简谐振动的初相为____________.振动方程为_____________.32、3268一系统作简谐振动, 周期为T ,以余弦函数表达振动时,初相为零.在0≤t ≤T 21范围内,系统在t =________________时刻动能和势能相等. 33、3821一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为___________,振子的振动频率为_________. 34、3269一作简谐振动的振动系统,振子质量为2 kg ,系统振动频率为1000 Hz ,振幅为0.5 cm ,则其振动能量为______________. 35、3839两个同方向的简谐振动,周期相同,振幅分别为A 1 = 0.05 m 和A 2 = 0.07 m ,它们合成为一个振幅为A = 0.09 m 的简谐振动.则这两个分振动的相位差为___________rad . 36、5314一质点同时参与了两个同方向的简谐振动,它们的振动方程分别为)41cos(05.01π+=t x ω (SI), )129cos(05.02π+=t x ω (SI),其合成运动的运动方程为x = __________________________.37、5515A ,B 是简谐波波线上的两点.已知,B 点振动的相位比A 点落后π31,A 、B 两点相距0.5 m ,波的频率为 100 Hz ,则该波的波长 λ = ________m ,波速 u = ______m/s .-t一平面简谐波沿x 轴正方向传播,波速u = 100 m/s ,t = 0时刻的波形曲线如图所示.可知波长λ = ____________; 振幅A = __________;频率ν = ____________.40、3342一平面简谐波(机械波)沿x 轴正方向传播,波动表达式为)21cos(2.0x t y π-π= (SI),则x = -3 m 处媒质质点的振动加速度a 的表达式为__________________. 41、3418频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________. 42、3133一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.43、3132一平面简谐波沿Ox 轴正向传播,波动表达式为 ]4/)/(cos[π+-=u x t A y ω,则x 1 = L 1处质点的振动方程是__________________________________;x 2 = -L 2处质点的振动和x 1 = L 1处质点的振动的相位差为φ2 - φ1 =__________________. 44、3135 如图所示为一平面简谐波在t = 2 s 时刻的波形图,该简谐波的表达式是____________________________________________;P 处质点的振动方程是____________________________. (该波的振幅A 、波速u 与波长λ 为已知量)45、3856已知某平面简谐波的波源的振动方程为t y π=21sin06.0 (SI),波速为2 m/s .则在波传播前方离波源5 m 处质点的振动方程为____________________ 46、3343图示一简谐波在t = 0时刻与t = T /4时刻(T 为周期)的波形图,则x 1处质点的振动方程为____________.47、3610一简谐波沿x 轴正方向传播,x 1与x 2两点处的振动曲线分别如图(a)和(b)所示,已知x 2 > x 1且x 2 - x 1 < λ(λ为波长),则这两点的距离为__________________(用波长λ表示).xO P 1P 2L 1L 2/4(a)(b)两相干波源S 1和S 2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y .S 1距P 点3个波长,S 2距P 点 4.5个波长.设波传播过程中振幅不变,则两波同时传到P 点时的合振幅是________________. 49、3126在真空中沿着z 轴的正方向传播的平面电磁波,O 点处电场强度为)6/2cos(900π+π=t E x ν,则O 点处磁场强度为___________________________. (真空介电常量 ε 0 = 8.85×10-12 F/m ,真空磁导率 μ 0 =4π×10-7 H/m ) 50、3460广播电台的发射频率为ν = 640 kHz .已知电磁波在真空中传播的速率为c = 3×108 m/s ,则这种电磁波的波长为___________________.三计算题 51、3828一质量m = 0.25 kg 的物体,在弹簧的力作用下沿x 轴运动,平衡位置在原点. 弹簧的劲度系数k = 25 N ·m -1. (1) 求振动的周期T 和角频率ω.(2) 如果振幅A =15 cm ,t = 0时物体位于x = 7.5 cm 处,且物体沿x 轴反向运动,求初速v 0及初相φ. (3) 写出振动的数值表达式. 52、3824有一轻弹簧,当下端挂一个质量m 1 = 10 g 的物体而平衡时,伸长量为 4.9 cm .用这个弹簧和质量m 2 = 16 g 的物体组成一弹簧振子.取平衡位置为原点,向上为x 轴的正方向.将m 2从平衡位置向下拉 2 cm 后,给予向上的初速度v 0 = 5 cm/s 并开始计时,试求m 2的振动周期和振动的数值表达式. 53、3555一质点按如下规律沿x 轴作简谐振动:)328cos(1.0π+π=t x (SI).求此振动的周期、振幅、初相、速度最大值和加速度最大值. 54、5191一物体作简谐振动,其速度最大值v m = 3×10-2 m/s ,其振幅A = 2×10-2 m .若t = 0时,物体位于平衡位置且向x 轴的负方向运动. 求:(1) 振动周期T ; (2) 加速度的最大值a m ; (3) 振动方程的数值式. 55、3558一质量为0.20 kg 的质点作简谐振动,其振动方程为 )215cos(6.0π-=t x (SI).求:(1) 质点的初速度; (2) 质点在正向最大位移一半处所受的力. 56、3410一横波沿绳子传播,其波的表达式为 )2100cos(05.0x t y π-π= (SI) (1) 求此波的振幅、波速、频率和波长. (2) 求绳子上各质点的最大振动速度和最大振动加速度.(3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差. 57、3864一简谐波沿x 轴负方向传播,波速为1 m/s ,在x 轴上某质点的振动频率为1 Hz 、振幅为0.01 m .t = 0时该质点恰好在正向最大位移处.若以该质点的平衡位置为x 轴的原点.求此一维简谐波的表达式.58、3141 图示一平面简谐波在t = 0 时刻的波形图,求(1) 该波的波动表达式;(2) P 处质点的振动方程.57、5206 沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示,设波速u = 0.5 m/s . 求:原点O 的振动方程.58、3084一平面简谐波沿x 轴正向传播,其振幅和角频率分别为A 和ω ,波速为u ,设t = 0时的波形曲线如图所示.(1) 写出此波的表达式. (2) 求距O 点分别为λ / 8和3λ / 8 两处质点的振动方程.(3) 求距O 点分别为λ / 8和3λ / 8 两处质点在t = 0时的振动速度. 59、3333一简谐波沿Ox 轴正方向传播,波长λ = 4 m , 周期T= 4 s ,已知x = 0处质点的振动曲线如图所示.(1) 写出x = 0处质点的振动方程; (2) 写出波的表达式; (3) 画出t = 1 s 时刻的波形曲线.60、5516平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s .在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动,求x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度. 61、3476平面简谐波沿Ox 轴正方向传播,波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播,波的表达式为 )/(2cos 2λνx t A y +π= 求:(1) x = λ /4 处介质质点的合振动方程;(2) x = λ /4 处介质质点的速度表达式. 62、3060 一个沿x 轴正向传播的平面简谐波(用余弦函数表示)在t = 0时的波形曲线如图所示.(1) 在 x = 0,和x = 2,x = 3各点的振动初相各是多少? (2) 画出t = T / 4时的波形曲线.(m)-(s)-263、0321一定滑轮的半径为R ,转动惯量为J ,其上挂一轻绳,绳的一端系一质量为m 的物体,另一端与一固定的轻弹簧相连,如图所示.设弹簧的劲度系数为k ,绳与滑轮间无滑动,且忽略轴的摩擦力及空气阻力.现将物体m 从平衡位置拉下一微小距离后放手,证明物体作简谐振动,并求出其角频率.64、3428一平面简谐波,频率为300 Hz ,波速为340 m/s ,在截面面积为3.00×10-2 m 2的管内空气中传播,若在10 s 内通过截面的能量为2.70×10-2 J ,求(1) 通过截面的平均能流; (2) 波的平均能流密度; (3) 波的平均能量密度. 65、3436 图中A 、B 是两个相干的点波源,它们的振动相位差为π(反相).A 、B 相距 30 cm ,观察点P 和B 点相距 40 cm ,且AB PB ⊥.若发自A 、B 的两波在P 点处最大限度地互相削弱,求波长最长能是多少.答案一、选择题1、 B2、B3、C4、B5、D6、B7、B8、D9、D 10、B 11、B 12、C 13、B 14、A 15、C 16、D 17、A 18、A 19、C 20、C 21、D 22、B 23、B 24、C 25、C 二、填空题 26、38201.55 Hz ; 0.103 m 27、5187gx /20π28、3038b ,f ; a ,b 29、3567)214cos(04.0π-πt30、303310 cm ; (π/6) rad/s ; π/3 31、3046π/4 ; )4/cos(1022π+π⨯=-t x (SI)32、3268T /8,3T /8 33、3821m BP30 cm40 cm2×102 N/m ; 1.6 Hz 34、32699.90×102 J 35、38391.47 36、5314)1223cos(05.0π+t ω (SI) [ 或)121cos(05.0π-t ω (SI) ] 37、55153 ; 300 38、30630.8 m ; 0.2 m ; 125 Hz 39、3059向下 ; 向上 ; 向上 40、3342)23cos(2.02x t a π+ππ-= (SI)41、3418 2π /5 42、3133])(2cos[212φλν++-π=L L t A y λk L x +-=1 ( k = ± 1,± 2,…)43、3132]4/)/(cos[11π+-=u L t A y ω; ;uL L )(21+ω44、3135]2)2(2cos[π-+-π=u x t u A y λ ; ]2)2(2cos[π+-π=t u A y P λ45、3856)4521sin(06.0π-π=t y46、3343)22cos(1π-π=t T A y x 或写成 )/2sin(1T t A y x π=47、3610 3λ/ 448、35880 49、3126)6/2cos(39.2π+π=t H y ν A/m50、34604.69×102 m 三、计算题51、3828解:(1) 1s 10/-==m k ω 63.0/2=π=ωT s(2) A = 15 cm ,在 t = 0时,x 0 = 7.5 cm ,v 0 < 0由 2020)/(ωv +=x A得 3.12020-=--=x A ωv m/sπ=-=-31)/(tg 001x ωφv 或 4π/3∵ x 0 > 0 ,∴ π=31φ (3) )3110cos(10152π+⨯=-t x (SI)52、3824解:设弹簧的原长为l ,悬挂m 1后伸长∆l ,则 k ∆l = m 1g ,k = m 1g/ ∆l = 2 N/m取下m 1挂上m 2后, 2.11/2==m k ω rad/sω/2π=T =0.56 st = 0时, φcos m 10220A x =⨯-=-φωsin m/s 10520A -=⨯=-v解得 220201005.2m )/(-⨯=+=ωv x A m=-=-)/(tg 001x ωφv 180°+12.6°=3.36 rad也可取 φ = -2.92 rad振动表达式为 x = 2.05×10-2cos(11.2t -2.92) (SI)或 x = 2.05×10-2cos(11.2t +3.36) (SI) 53、3555解:周期 25.0/2=π=ωT s , 振幅 A = 0.1 m , 初相 φ = 2π/3, v max = ω A = 0.8π m/s ( = 2.5 m/s ), a max = ω 2A = 6.4π2 m/s 2 ( =63 m/s 2 ). 54、5191解: (1) v m = ωA ∴ω = v m / A =1.5 s -1∴ T = 2π/ω = 4.19 s(2) a m = ω2A = v m ω = 4.5×10-2m/s 2(3) π=21φ x = 0.02)215.1cos(π+t (SI) 55、3558解:(1) )25sin(0.3d d π--==t t x v (SI) t 0 = 0 , v 0 = 3.0 m/s .(2) x m ma F 2ω-==A x 21=时, F = -1.5 N . 56、3410解: (1)已知波的表达式为)2100cos(05.0x t y π-π= 与标准形式)/22cos(λνx t A y π-π=比较得A = 0.05 m , ν = 50 Hz , λ = 1.0 mu = λν = 50 m/s(2) 7.152)/(max max =π=∂∂=A t y νv m /s322max 22max 1093.44)/(⨯=π=∂∂=A t y a ν m/s 2(3) π=-π=∆λφ/)(212x x ,二振动反相57、5206解:由图,λ = 2 m ,又∵u = 0.5 m/s ,∴ ν = 1 /4 Hz ,T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图.此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ∴ )2121cos(5.0π+π=t y (SI)58、3084解:(1) 以O 点为坐标原点.由图可知,该点振动初始条件为0cos 0==φA y , 0sin 0<-=φωA v所以 π=21φ 波的表达式为 ]21)/(cos[π+-=u x t A y ωω(2) 8/λ=x 处振动方程为]21)8/2(cos[π+π-=λλωt A y )4/cos(π+=t A ω8/3λ=x 的振动方程为]218/32cos[π+-=λλπωt A y )4/cos(π-=t A ω(3) )21/2sin(/d d π+π--=λωωx t A t yt = 0,8/λ=x 处质点振动速度]21)8/2sin[(/d d π+π--=λλωA t y 2/2ωA -=t = 0,8/3λ=x 处质点振动速度]21)8/32sin[(/d d π+⨯π--=λλωA t y 2/2ωA =59、3333x (m)y (m)0u0.512t = 0-1解:(1) )3121cos(10220π+π⨯=-t y (SI) (2)]31)4141(2cos[1022π+-π⨯=-x t y (SI)(3) t = 1 s 时,波形表达式: )6521cos(1022π-π⨯=-x y (SI)故有如图的曲线.60、5516解:设x = 0处质点振动的表达式为 )cos(0φω+=t A y ,已知 t = 0 时,y 0 = 0,且 v 0 > 0 ∴π-=21φ ∴ )2cos(0φν+π=t A y )21100cos(1022π-π⨯=-t (SI)由波的传播概念,可得该平面简谐波的表达式为)/22cos(0u x t A y νφνπ-+π=)2121100cos(1022x t π-π-π⨯=- (SI) x = 4 m 处的质点在t 时刻的位移 )21100cos(1022π-π⨯=-t y (SI)该质点在t = 2 s 时的振动速度为 )21200sin(1001022π-π⨯⨯-=-πv= 6.28 m/s-2-。
大学物理知识总结习题答案(第八章)振动与波动

第八章 振动与波动本章提要1. 简谐振动· 物体在一定位置附近所作的周期性往复运动称为机械振动。
· 简谐振动运动方程()cos x A t ωϕ=+其中A 为振幅,??为角频率,(?t+?)称为谐振动的相位,t =0时的相位??称为初相位。
· 简谐振动速度方程d ()d sin xv A t tωωϕ==-+ · 简谐振动加速度方程222d ()d cos xa A t tωωϕ==-+· 简谐振动可用旋转矢量法表示。
2. 简谐振动的能量· 若弹簧振子劲度系数为k ,振动物体质量为m ,在某一时刻m 的位移为x ,振动速度为v ,则振动物体m 动能为212k E mv =· 弹簧的势能为212p E kx =· 振子总能量为P22222211()+()221=2sin cos k E E E m A t kA t kA ωωϕωϕ=+=++3. 阻尼振动· 如果一个振动质点,除了受弹性力之外,还受到一个与速度成正比的阻尼作用,那么它将作振幅逐渐衰减的振动,也就是阻尼振动。
· 阻尼振动的动力学方程为222d d 20d d x xx t tβω++= 其中,γ是阻尼系数,2mγβ=。
(1) 当22ωβ>时,振子的运动一个振幅随时间衰减的振动,称阻尼振动。
(2) 当22ωβ=时,不再出现振荡,称临界阻尼。
(3) 当22ωβ<时,不出现振荡,称过阻尼。
4. 受迫振动· 振子在周期性外力作用下发生的振动叫受迫振动,周期性外力称驱动力 · 受迫振动的运动方程为22P 2d d 2d d cos x x F x t t t mβωω++= 其中,2k m ω=,为振动系统的固有频率;2C m β=;F 为驱动力振幅。
· 当驱动力振动的频率p ω等于ω时,振幅出现最大值,称为共振。
大学物理D-06振动和波-参考答案

B 2 ;波的周期为 B C lC ;此质元的初相位为
;波长为
2 C
;离波源距离为 l
lC 。
6.1.5 一平面简谐波沿 ox 轴正向传播,波动方程为 y A cos[ (t 振动方程为 为 2 1 二、选择题
x ) ] ,则 x L1 处质点的 u 4
y A cos[ (t
由 t=0 和 t=0.25 时的波形图,得
O
t
x
2 x x 2 10 (t ) ] 0.2 cos[2t x ] (2)波动表式为 y A cos[ ( t ) 0 ] 0.2 cos[ 1 0.6 2 3 2 u
O 点的振动表式为
y 0 | t 0 A cos 0 0 , v 0 | t 0 A sin 0 0 , 0
3 , 4
x1 x3振幅最大 。
2
0 20 , 0 20
5 3 (或 )时, x2 x3振幅最小 4 4
0 , 0 20 84 o 48时, x1 x 2 x3振幅最大 0 0
6.4.2
2
o
4
2
3
4
2
6.2.6 两相干平面简谐波沿不同方向传播,如图所示,波速均为 u 0.40m / s ,其中一列波在 A 点 引 起 的 振 动 方 程 为 y 1 A1 cos( 2 t
2
) ,另一列波在 B 点引起的振动方程为
y 2 A2 cos( 2 t
[ A ] (A)0; (B) /2; (C) ; (D)3 /2。 三、简答题
振动和波题目及答案

1一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为(A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ ] D 2一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为(A)π/6. (B) 5π/6. (C) -5π/6. (D) -π/6. (E) -2π/3. [ ]C 3在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计).(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计)[ ]C4一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的(A) 7/16. (B) 9/16.(C) 11/16. (D) 15/16 [ ]D5一劲度系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为T 1.若将此弹簧截去一半的长度,下端挂一质量为m 21的物体,则系统振动周期T 2等于 (A) 2 T 1 (B) T 1 (C) T 12/(D) T 1 /2 (E) T 1 /4 [ ] D 6已知某简谐振动的振动曲线如图所示,位移的单位为厘米,时间单位为秒.则此简谐振动的振动方程为:(A))3232cos(2π+π=t x .(B) )3232cos(2π-π=t x .(C) )3234cos(2π+π=t x .v 21(D) )3234cos(2π-π=t x .(E) )4134cos(2π-π=t x . [ ]C 7如图所示,质量为m 的物体由劲度系数为k 1和k 2的两个轻弹簧连接,在水平光滑导轨上作微小振动,则系统的振动频率为(A)m k k 212+π=ν . (B) mk k 2121+π=ν . (C) 212121k mk k k +π=ν . (D) )(212121k k m k k +π=ν . [ ]B8如图所示,两列波长为λ 的相干波在P 点相遇.波在S 1点振动的初相是φ 1,S 1到P 点的距离是r 1;波在S 2点的初相是φ 2,S 2到P 点的距离是r 2,以k 代表零或正、负整数,则P 点是干涉极大的条件为:(A) λk r r =-12.(B) π=-k 212φφ.(C)π=-π+-k r r 2/)(21212λφφ.(D) π=-π+-k r r 2/)(22112λφφ.[ ]D 9两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B)π21. (C) π. (D) π23. [ ] C10机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则(A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ ] B11如图所示,一平面简谐波沿x 轴正向传播,已知P 点的振动方程为)cos(0φω+=t A y ,则波的表达式为(A) }]/)([cos{0φω+--=u l x t A y . (B) })]/([cos{0φω+-=u x t A y . (C) )/(cos u x t A y -=ω.(D) }]/)([cos{0φω+-+=u l x t A y . [ ]A12一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是(A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. [ ] C 1在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为(a) ______________________________;(b) ______________________________;(c) ______________________________. )212cos(π-=T t A x π 2分 )212cos(π+=T t A x π 2分)2cos(π+=TtA x π 1分2一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________;与P 1点处质点振动状态相同的那些点的位置是___________________________.])(2cos[212φλν++-π=L L t A y 3分λk L x +-=1 ( k = ± 1,± 2,…) 2分3(c)O P 1P 2两个相干点波源S 1和S 2,它们的振动方程分别是 )21cos(1π+=t A y ω和 )21cos(2π-=t A y ω.波从S 1传到P 点经过的路程等于2个波长,波从S 2传到P 点的路程等于7 / 2个波长.设两波波速相同,在传播过程中振幅不衰减,则两波传到P 点的振动的合振幅为__________________________.2A 3分4图中所示为两个简谐振动的振动曲线.若以余弦函数表示这两个振动的合成结果,则合振动的方程为 =+=21x x x ________________(SI) )21cos(04.0π-πt (其中振幅1分,角频率1分,初相1分) 3分5有两相同的弹簧,其劲度系数均为k .(1)把它们串联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为___________________;(2)把它们并联起来,下面挂一个质量为m 的重物,此系统作简谐振动的周期为___________________________________.k m /22π 2分k m 2/2π 2分 6一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为A =_____________;ω =________________;φ =_______________. 10 cm 1分(π/6) rad/s 1分 π/3 1分 7两个简谐振动曲线如图所示,则两个简谐振动-的频率之比ν1∶ν2=__________________,加速度最大值之比a 1m ∶a 2m =__________________________,初始速率之比v 10∶v 20=____________________.2∶1 1分 4∶1 1分 2∶1 1分 8一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在该时刻的运动方向.A _____________;B _____________ ;C ______________ . 向下 ; 向上 ;向上9两个弹簧振子的周期都是0.4 s , 设开始时第一个振子从平衡位置向负方向运动,经过0.5 s 后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为____________.π3分 10一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为)612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI)则其合成振动的振幅为___________,初相为_______________.1×10-2 m 2分 π/6 2分一如图,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m ,重物的质量m = 6 kg ,重物静止在平衡位置上.设以一水平恒力F = 10 N 向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05 m 时撤去力F .当重物运动到左方最远位置时开始计时,求物体的运动方程.解:设物体的运动方程为 )cos(φω+=t A x .恒外力所做的功即为弹簧振子的能量: F ×0.05 = 0.5 J .2分当物体运动到左方最远位置时,弹簧的最大弹性势能为0.5 J ,即:5.0212=kA J , ∴ A = 0.204 m . 2分 A 即振幅. 4/2==m k ω (rad/s)2ω = 2 rad/s . 2分 按题目所述时刻计时,初相为φ = π.∴ 物体运动方程为 2分)2cos(204.0π+=t x (SI). 2分二如图,一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播,已知A 点的振动方程为t y π⨯=-4cos 1032 (SI).(1) 以A 点为坐标原点写出波的表达式;(2) 以距A 点5 m 处的B 点为坐标原点,写出波的表达式. 解:(1) 坐标为x 点的振动相位为)]/([4u x t t +π=+φω)]/([4u x t +π=)]20/([4x t +π= 2分波的表达式为 )]20/([4cos 1032x t y +π⨯=- (SI) 2分 (2) 以B 点为坐标原点,则坐标为x 点的振动相位为]205[4-+π='+x t t φω (SI) 2分 波的表达式为 ])20(4cos[1032π-+π⨯=-xt y (SI) 2分三如图所示,两相干波源在x 轴上的位置为S 1和S 2,其间距离为d = 30 m ,S 1位于坐标原点O .设波只沿x 轴正负方向传播,单独传播时强度保持不变.x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点.求两波的波长和两波源间最小相位差.解:设S 1和S 2的振动相位分别为φ 1和φ 2.在x 1点两波引起的振动相位差 ]2[]2[1112λφλφx x d π---π-π+=)12(K即 π+=-π--)12(22)(112K x d λφφ ① 2分在x 2点两波引起的振动相位差 ]2[]2[2122λφλφx x d π---π-π+=)32(K 即 π+=-π--)32(22)(212K x d λφφ ② 3分②-①得 π=-π2/)(412λx x6)(212=-=x x λ m 2分由①π+=-π+π+=-)52(22)12(112K x d K λφφ 2分当K = -2、-3时相位差最小π±=-12φφ 1分四ABxu沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示,设波速u = 0.5 m/s . 求:原点O 的振动方程.解:由图,λ = 2 m , 又 ∵u = 0.5 m/s ,∴ ν = 1 /4 Hz , 3分T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图. 2分此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ 2分 ∴ )2121cos(5.0π+π=t y (SI) 3分x (m)y (m)0u 0.512t = 0-1。
第七章 振动和波 题库含答案-大学复习资料

第七章 振动和波 题库及答案一、单选题1、作简谐振动的物体运动至平衡位置向正方向运动时,其位移x 、速度υ、加速度a 为 [设振动方程为x =A cos(ωt+φ)] ()。
A) x =0, υ=0, a =0 B) x =0, υ=ωA , a =0 C) x =A , υ=ωA , a =ω2A D) x = –A , υ= –ωA , a =0 答案: B知识点: 7.1、简谐振动、简谐振动方程 难度: 1 提示:无题解:作简谐振动的物体运动至平衡位置时,其位移x =0、向正方向运动的速度υ=ωA 、加速度a =0,所以B 答案是正确的。
2、一质点作简谐振动,振动方程为x =A cos(ωt +ϕ),当时间t =T / 2(T 为周期)时,质点的速度为 ()。
A) -A ωcos ϕ B) -A ωsin ϕ C) A ωcos ϕ D) A ωsin ϕ 答案: D知识点:7.1、简谐振动、简谐振动方程 难度: 2 提示:无题解:质点作简谐振动的速度方程为)sin(ϕωω+=t A -υ,将t =T / 2代入得ϕωϕωϕωωsin )πsin()2sin(A A -TA -υ=+=+=所以D 答案是正确的。
3、一质点作水平方向的简谐振动,设其向右运动为正方向。
当质点在平衡位置开始向右运动,则初位相为()。
A) 0 B) 2πC) 2π-D) 3π答案: C知识点: 7.1、描述简谐振动的物理量 难度: 2 提示:无题解:设简谐动方程为)cos(ϕω+=t A x , t =0时ϕcos 0A = 0cos =ϕ 2π±=ϕ因为 0sin 0sin 0<>-=ϕϕωA υ 所以 2π-=ϕ 所以C 答案是正确的。
4、一质量为m 的物体,以速度υ(t ) = υ0sin ωt 的规律振动,则振动系统的总机械能为()。
A)221ωm B) ω 20m υ C)2021m υ D)t m υω sin 21220 答案: C知识点: 7.1、简谐振动的能量 难度: 2提示:因物体的速度按υ(t ) = υ0sin ωt 的规律振动,所以物体的振动为简谐振动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
振动与波复习题及答案第九章振动复习题1. 一轻弹簧,上端固定,下端挂有质量为m 的重物,其自由振动的周期为T .今已知振子离开平衡位置为x 时,其振动速度为v ,加速度为a .则下列计算该振子劲度系数的公式中,错误的是:(A) 2max 2max /x m k v =. (B) x mg k /=.(C) 22/4T m k π=. (D) x ma k /=. [ B ] 2. 一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上,(如图所示),作成一复摆.已知细棒绕通过其一端的轴的转动惯量231ml J =,此摆作微小振动的周期为(A) g l π2. (B) g l22π.(C) g l 322π. (D) gl3π. [ C ] 3. 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时.若用余弦函数表示其运动方程,则该单摆振动的初相为 (A) π. (B) π/2. (C) 0 . (D) θ. [ C ]4. 两个质点各自作简谐振动,它们的振幅相同、周期相同.第一个质点的振动方程为x 1 = A cos(ωt + α).当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点正在最大正位移处.则第二个质点的振动方程为(A) )π21cos(2++=αωt A x . (B) )π21cos(2-+=αωt A x .(C) )π23cos(2-+=αωt A x . (D) )cos(2π++=αωt A x . [ B ][ ]6. 一质点作简谐振动.其运动速度与时间的曲线如图所示.若质点的振动规律用余弦函数描述,则其初相应为 (A) π/6. (B) 5π/6. (C) -5π/6.(D) -π/6. (E) -2π/3. [ ]v 217. 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2.将它们拿到月球上去,相应的周期分别为1T '和2T '.则有 (A) 11T T >'且22T T >'. (B) 11T T <'且22T T <'. (C) 11T T ='且22T T ='. (D) 11T T ='且22T T >'. [ D ]8. 一弹簧振子,重物的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动.当重物通过平衡位置且向规定的正方向运动时,开始计时.则其振动方程为:(A) )21/(cos π+=t m k A x (B) )21/cos(π-=t m k A x(C) )π21/(cos +=t k m A x (D) )21/cos(π-=t k m A x(E) t m /k A x cos = [ B ]9. 一质点在x 轴上作简谐振动,振辐A = 4 cm ,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则质点第二次通过x = -2 cm 处的时刻为 (A) 1 s . (B) (2/3) s .(C) (4/3) s . (D) 2 s . [ B ] 10.一物体作简谐振动,振动方程为)41cos(π+=t A x ω.在 t = T /4(T 为周期)时刻,物体的加速度为(A) 2221ωA -. (B) 2221ωA .(C) 2321ωA -. (D) 2321ωA . [ B ]11. 两个同周期简谐振动曲线如图所示.x 1的相位比x 2的相位 (A) 落后π/2. (B) 超前π/2. (C) 落后π . (D) 超前π. [ B ]12. 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为 [ B ]x13. 一简谐振动曲线如图所示.则振动周期是(A) 2.62 s . (B) 2.40 s .(C) 2.20 s . (D) 2.00 s .[ B ]15. 用余弦函数描述一简谐振子的振动.若其速度~时间(v ~t )关系曲线如图所示,则振动的初相位为 (A) π/6. (B) π/3.(C) π/2. (D) 2π/3. (E) 5π/6.[ A ]17. 一弹簧振子作简谐振动,总能量为E 1,如果简谐振动振幅增加为原来的两倍,重物的质量增为原来的四倍,则它的总能量E 2变为 (A) E 1/4. (B) E 1/2.(C) 2E 1. (D) 4 E 1 . [ D ]18 弹簧振子在光滑水平面上作简谐振动时,弹性力在半个周期内所作的功为(A) kA 2. (B) 221kA .(C) (1/4)kA 2. (D) 0. [ D ]19. 一物体作简谐振动,振动方程为)21cos(π+=tA x ω.则该物体在t = 0时刻的动能与t = T /8(T 为振动周期)时刻的动能之比为: (A) 1:4. (B) 1:2. (C) 1:1.(D) 2:1. (E) 4:1. [ D]A21-A21-A21 21A21 AA21-A21-2121--20. 图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为(A) π23. (B) π.(C) π21. (D) 0. [ B ]二. 填空题21. 在t = 0时,周期为T 、振幅为A 的单摆分别处于图(a)、(b)、(c)三种状态.若选单摆的平衡位置为坐标的原点,坐标指向正右方,则单摆作小角度摆动的振动表达式(用余弦函数表示)分别为(a) ______________________________; (b) ______________________________; (c) ______________________________.23. 在两个相同的弹簧下各悬一物体,两物体的质量比为4∶1,则二者作简谐振动的周期之比为___2:1___.24. 一质点作简谐振动,速度最大值v m = 5 cm/s ,振幅A = 2 cm .若令速度具有正最大值的那一时刻为t = 0,则振动表达式为_____50.02cos()22x t π=-___.25. 一物体作余弦振动,振幅为15×10-2 m ,角频率为6π s -1,初相为0.5 π,则 振动方程为 __0.15cos(6)2x t ππ=+(SI).(c)2cos()2x A t T ππ=+2cos()2x A t T ππ=+2cos()x A t T ππ=+27. 一简谐振动的表达式为)3cos(φ+=t A x ,已知 t = 0时的初位移为0.04 m ,初速度为0.09 m/s ,则振幅A =____0.05m_________ ,初相φ=____3arcsin 5-____________.30. 已知两个简谐振动的振动曲线如图所示.两简谐振动的最大速率之比为_______1:1__________31. 一简谐振动用余弦函数表示,其振动曲线如图所示,则此简谐振动的三个特征量为A =_____0.1m________;ω =_____/6rad s π_____;φ =_____3π__________. .34. 已知三个简谐振动曲线如图所示,则振动方程分别为:x 1 =10cos t π______________________,x 2 =10cos()2t ππ- _____________________,x 3 =10cos()t ππ+_______________________.x (cm)37.一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初相为_____4π_______.振动方程为__0.02cos()4x t ππ=+____________.41. 一作简谐振动的振动系统,振子质量为2 kg ,系统振动频率为1000 Hz ,振 幅为0.5 cm ,则其振动能量为______1002πJ________.43. 一弹簧振子系统具有1.0 J 的振动能量,0.10 m 的振幅和1.0 m/s 的最大速率,则弹簧的劲度系数为____200N/m_______,振子的振动频率为_5πHZ________. 44.两个同方向的简谐振动曲线如图所示.合振动的振幅 为______21A A -___________,合振动的振动方程为_____212()cos()2x A A t T ππ=-+______.50. 一个质点同时参与两个在同一直线上的简谐振动,其表达式分别为 )612cos(10421π+⨯=-t x , )652cos(10322π-⨯=-t x (SI) 则其合成振动的振幅为___0.01m________,初相为____6π_____.第十章波复习题t ·--一、选择题1. 在下面几种说法中,正确的说法是:(A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的. (B) 波源振动的速度与波速相同.(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于π计).(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前.(按差值不大于π计) [ C ]2. 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ,则 (A) 其振幅为3 m . (B) 其周期为s 31. (C) 其波速为10 m/s . (D) 波沿x 轴正向传播. [ B ] 3.一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t =0.5 s 时刻的波形图是 [ A ]4. 横波以波速u 沿x 轴负方向传播.t 时刻波形曲线如图.则该时刻 [ D ](A) A 点振动速度大于零. (B) B 点静止不动. (C) C 点向下运动. (D) D 点振动速度小于零.5. 把一根十分长的绳子拉成水平,用手握其一端.维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长. (B) 振动频率越低,波长越长.(C) 振动频率越高,波速越大. (D) 振动频率越低,波速越大.[ B ] 6. 一平面余弦波在t = 0时刻的波形曲线如图所示,则O 点的振动初相φ 为:(A) 0. (B)π21 (C) π (D) π23(或π-21) [ B ] 7. 如图所示,有一平面简谐波沿x 轴负方向传播,坐标原点O 的振动规律为)cos(0φω+=t A y ),则B 点的振动方程为(A)])/(cos[0φω+-=u x t A y .(B) )]/([cos u x t A y +=ω.-xy Ou(C) })]/([cos{0φω+-=u x t A y .(D)})]/([cos{0φω++=u x t A y . [ C ]8.如图所示为一平面简谐波在t = 0 时刻的波形图,该波的波速u = 200 m/s ,则P 处质点的振动曲线为[ C ]9. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是 [ A ]10. 一平面简谐波沿Ox 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处介质质点的振动方程是(A) )314cos(10.0π+π=t y P (SI).(B) )314cos(10.0π-π=t y P (SI). (C) )312cos(10.0π+π=t y P (SI).(D) )612cos(10.0π+π=t y P (SI). [ A ]11. 图示一简谐波在t = 0时刻的波形图,波速 u = 200 m/s ,则P 处质点的振动速度表达式为 [ C ](A) )2cos(2.0π-ππ-=t v(SI).(B) )cos(2.0π-ππ-=t v (SI). (C) )2/2cos(2.0π-ππ=t v (SI).(D) )2/3cos(2.0π-ππ=t v (SI).12.在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是 (A) A 1 / A 2 = 16. (B) A 1 / A 2 = 4.(C) A 1 / A 2 = 2. (D) A 1 / A 2 = 1 /4. [ C ]y(m)ωS A O ′ωSA O′ωAO ′ωSAO ′(A)(B)(C)(D)S13. 一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为最大值的媒质质元的位置是:(A) o ',b ,d ,f . (B) a ,c ,e ,g .(C) o ',d . (D) b ,f . [ B ]14. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零. (C) 动能最大,势能最大. (D) 动能最大,势能为零. [C ]15. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中 (A) 它的势能转换成动能. (B) 它的动能转换成势能.(C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.[ C ] 16. 如图所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=PS ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为)212cos(1π+π=t A y ,则S 2的振动方程为 (A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y .(C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y . [ D ]17. 两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是: (A) 0. (B)π21. (C) π. (D) π23. [ C ] 18. S 1和S 2是波长均为λ 的两个相干波的波源,相距3λ /4,S 1的相位比S 2超前π21.若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,则在S 1、S 2连线上S 1外侧和S 2外侧各点,合成波的强度分别是 (A) 4I 0,4I 0. (B) 0,0.(C) 0,4I 0 . (D) 4I 0,0. [ A ] 19 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同. (C) 振幅相同,相位不同. (D) 振幅不同,相位不同. [ B ] 20 在波长为λ 的驻波中,两个相邻波腹之间的距离为 (A) λ /4. (B) λ /2.(C) 3λ /4. (D) λ . [ B ] 21.沿着相反方向传播的两列相干波,其表达式为)/(2cos 1λνx t A y -π= 和 )/(2cos 2λνx t A y +π=.在叠加后形成的驻波中,各处简谐振动的振幅是 (A) A . (B) 2A .(C) )/2cos(2λx A π. (D) |)/2cos(2|λx A π. [ D ] 二、填空题SS 1S 2Pλ/422.一个余弦横波以速度u 沿x 轴正向传播,t 时刻波形曲线如图所示.试分别指出图中A ,B ,C 各质点在 该时刻的运动方向.A _____________;B_____________ ;C ______________ . 23. 一平面简谐波的表达式为)37.0125cos(025.0x t y -= (SI),其角频率ω =__________________________,波速u =______________________,波长λ = _________________.24. 频率为100 Hz 的波,其波速为250 m/s .在同一条波线上,相距为0.5 m 的两点的相位差为________________.25. 图为t = T / 4 时一平面简谐波的波形曲线,则其波的表达式为 ______________________________________________.26、一平面简谐波沿Ox 轴正方向传播,波长为λ.若如图P 1点处质点的振动方程为)2cos(1φν+π=t A y ,则P 2点处质点的振动方程为_________________________________; 与P 1点处质点振动状态相同的那些点的位置是___________________________.27、一简谐波沿x 轴正方向传播.x 1和x 2两点处的振动曲线分别如图(a)和(b)所示.已知x 2 .> x 1且x 2 - x 1 < λ(λ为波长),则x 2点的相位比x 1点的相位滞后 ___________________.28、已知某平面简谐波的波源的振动方程为t y π=21sin 06.0(SI),波速为2 m/s .则在波传播前方离波源5 m 处质点的振动方程为_-______________________.29、(1)一列波长为λ 的平面简谐波沿x 轴正方向传播.已知在λ21=x 处振动的方程为y = A cos ω t ,则该平面简谐波的表达式为______________________________________.(2) 如果在上述波的波线上x = L (λ21>L )处放一如图所示的反射面,且假设反射波的振幅为A ',则反射波的表达式为 _______________________________________ (x ≤L ).30、一平面简谐波沿x 轴负方向传播.已知 x = -1 m 处质点的振动方程为)cos(φω+=t A y ,若波速为u ,则此波的表达式为 _________________________________________________________.31、一个波源位于O 点,以O 为圆心作两个同心球面,它们的半径分别为R 1和R 2,在两个球面上分别取相等的面积∆S 1和∆S 2,则通过它们的平均能流之比=21P /P ___________________.32、一点波源发出均匀球面波,发射功率为4 W .不计媒质对波的吸收,则距离 波源为2 m 处的强度是__________________.-xOP 1P 2(a)(b)33、如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3λ 和10 λ / 3 ,λ 为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率___________,波源S 1 的相位比S 2 的相位领 先_________________.34、如图所示,S 1和S 2为同相位的两相干波源,相距为L ,P 点距S 1为r ;波源S 1在P 点引起的振动振幅为A 1,波源S 2在P 点引起的振动振幅为A 2,两波波长都是λ ,则P 点振幅A =_________________________________________________________. 35、两相干波源S 1和S 2的振动方程分别是t A y ωcos 1=和)21cos(2π+=t A y ω.S 1距P 点3个波长,S 2距P 点21/4个波长.两波在P 点引起的两个振动的相位差是____________.36、 S 1,S 2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者相距λ23(λ为波长)如图.已知S 1的初相为π21. (1) 若使射线S 2C 上各点由两列波引起的振动均干涉相 消,则S 2的初相应为________________________.(2) 若使S 1 S 2连线的中垂线MN 上各点由两列波引起的 振动均干涉相消,则S 2的初位相应为_______________________. 37、 两列波在一根很长的弦线上传播,其表达式为 y 1 = 6.0×10-2cos π(x - 40t ) /2 (SI) y 2 = 6.0×10-2cos π(x + 40t ) /2 (SI)则合成波的表达式为__________________________________________________; 在x = 0至x = 10.0 m 内波节的位置是_____________________________________ __________________________________;波腹的位置是________________________________________________________. 38、设入射波的表达式为)(2cos 1λνxt A y +π=.波在x = 0处发生反射,反射点为固定端,则形成的驻波表达式为____________________________________. 39、 一驻波表达式为t x A y ππ=100cos 2cos .位于x 1 = 3 /8 m 的质元P 1与位于x 2 = 5 /8 m 处的质元P 2的振动相位差为_____________________________. 40、 在弦线上有一驻波,其表达式为 )2cos()/2cos(2t x A y νλππ=, 两个相邻波节之间的距离是_______________.PS S12。
