-初中数学竞赛常用公式[1].doc-2013

合集下载

初中数学竞赛重要定理公式(代数篇)

初中数学竞赛重要定理、公式及结论代数篇【乘法公式】完全平方公式：(a±b)2=a2±2ab+b2，平方差公式：（a+b）(a-b)=a2-b2，立方和（差）公式：(a±b)(a2 ∓ab+b2)=a3±b3多项式平方公式：(a+b+c+d)2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd二项式定理：(a±b)3=a3±3a2b+3ab2±b3(a±b)4=a4±4a3b+6a2b2±4ab3+b4）(a±b)5=a5±5a4b+10a3b2±10a2b3＋5ab4±b5）…………在正整数指数的条件下，可归纳如下：设n为正整数(a+b)(a2n-1- a2n-2b+a2n-3b2- …＋ab2n-2- b2n-1)=a2n-b2n(a+b)(a2n-a2n-1b+a2n-2b2n-…-ab2n-1+b2n)=a2n+1+b2n+1类似地：（a-b）(a n-1+a n-2b+a n-3b2+…＋ab n-2+b n-1)=a n-b n公式的变形及其逆运算由(a+b)2=a2+2ab+b2得a2+b2=(a+b)2-2ab由(a+b)3=a3+3a2b+3ab2+b3=a3+b3+3ab(a+b)得a3+b3=(a+b)3-3ab(a+b)由公式的推广③可知：当n为正整数时a n-b n能被a-b 整除，a2n+1+b2n+1能被a+b整除，a2n-b2n能被a+b 及a-b整除。

重要公式（欧拉公式）(a+b+c)(a2+b2+c2+ab+ac+bc)=a3+b3+c3-3abc【综合除法】一个一元多项式除以另一个一元多项式，并不是总能整除。

当被除式f(x)除以除式g(x)，(g(x)≠0) 得商式q(x)及余式r(x)时，就有下列等式：f(x)=g(x)q(x)-r(x)其中r(x)的次数小于g(x)的次数，或者r(x)=0。

初中数学竞赛常用公式总结

初中数学竞赛常用公式总结数学竞赛是考验学生逻辑思维、推理能力和数学知识应用的重要考试。

在竞赛中，掌握一些常用的数学公式是非常关键的。

下面将总结初中数学竞赛中常用的公式，帮助竞赛学习者更好地备战。

1. 代数公式（1）二次方程的解：对于一元二次方程ax^2 + bx + c = 0，有以下公式：\[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \]其中，Δ = b^2 - 4ac，称为判别式。

（2）平方差公式：对于任意实数a和b，有以下公式：\[ (a+b)(a-b)=a^2-b^2 \]（3）两点间距离公式：对于平面上任意两点A(x1, y1)和B(x2, y2)，它们之间的距离d可以用以下公式表示：\[ d=\sqrt{(x2-x1)^2+(y2-y1)^2} \]2. 几何公式（1）周长和面积公式：- 矩形的周长C和面积S分别为：C = 2(l + w)，S = lw，其中l和w分别表示矩形的长度和宽度。

- 正方形的周长C和面积S分别为：C = 4s，S = s^2，其中s表示正方形的边长。

- 圆的周长C和面积S分别为：C = 2πr，S = πr^2，其中r表示圆的半径。

- 三角形的周长C和面积S可以根据不同类型的三角形使用不同公式计算（如直角三角形的勾股定理）。

（2）三角函数公式：- 正弦定理：在任意三角形ABC中，有以下公式：\[ \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)} \]其中，a、b、c分别为三角形BC、AC和AB的边长，A、B、C分别为三角形对应的角度。

- 余弦定理：在任意三角形ABC中，有以下公式：\[ c^2 = a^2 + b^2 - 2ab\cos(C) \]- 正弦、余弦和正切的关系：对于任意角θ，有以下公式：\[ \sin(\theta) = \frac{opposite}{hypotenuse}，\cos(\theta) =\frac{adjacent}{hypotenuse}，\tan(\theta) = \frac{opposite}{adjacent} \]其中，opposite表示对边的长度，adjacent表示邻边的长度，hypotenuse表示斜边的长度。

初中数学竞赛中常用重要定理

初中数学竞赛中常用重要定理1、梅涅劳斯定理：假如在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、 E 、F 且D 、E 、F 三点共线，则FB AF EA CE DC BD ••=12、梅涅劳斯定理的逆定理：假如在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ，且满足FB AF EA CE DC BD ••=1，则D 、E 、F 三点共线。

3、塞瓦定理：设O 是△ABC 内任意一点，AO 、BO 、CO 分别交对边于N 、P 、 M ，则1=••PACP NC BN MB AM4、塞瓦定理的逆定理：设M 、N 、P 分别在△ABC 的边AB 、BC 、CA 上，且满足1=••PA CP NC BN MB AM ，则AN 、BP 、CM 相交于一点。

5、广勾股定理的两个推论：推论1：平行四边形对角线的平方和等于四边平方和。

推论2：设△ABC 三边长分别为a 、b 、c ，对应边上中线长分别为m a 、m b 、m c则：m a =2222221a c b -+；m b =2222221b c a -+；m c =2222221c b a -+ 6、三角形内、外角平分线定理：内角平分线定理：如图：假如∠1=∠2，则有AC AB DC BD =外角平分线定理：如图，AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ，则有ACAB DC BD =7、托勒密定理：四边形ABCD 是圆内接四边形，则有AB ·CD+AD ·BC=AC ·BD8、三角形位似心定理：如图，若△ABC 与△DEF 位似，则通过对应点的三直线AD 、BE 、CF 共点于P9、正弦定理、在△ABC 中有R C c B b A a 2sin sin sin ===（R 为△ABC 外接圆半径）余弦定理：a 、b 、c 为△ABC 的边，则有：a 2=b 2+c 2-2bc ·cosA; b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;10、西姆松定理：点P 是△ABC 外接圆周上任意一点，PD ⊥BC ，PE ⊥AC ， PF ⊥AB ，D 、E 、F 为垂足，则D 、E 、F 三点共线，此直线称为西姆松线。

初中数学竞赛重要定理公式(统计篇)

初中数学竞赛重要定理公式（统计篇）
1. 事件概率
- 定义：对某一事件发生的可能性大小的描述。

- 公式：$P(A)=\dfrac{m}{n}$，其中 $A$ 为事件，$m$ 为
$A$ 发生的可能性数，$n$ 为随机试验的总次数。

2. 条件概率
- 定义：事件 $B$ 在已知事件 $A$ 发生的条件下发生的可能性。

- 公式：$P(B|A)=\dfrac{P(A \cap B)}{P(A)}$，其中 $A \cap
B$ 表示事件 $A$ 和事件 $B$ 同时发生的概率。

3. 全概率公式
- 定义：若 $B_1,B_2,...,B_n$ 互不相容，且 $B_1 \cup B_2
\cup ... \cup B_n$ 为必然事件，$A$ 为任意一事件，则有：
$P(A)=\sum_{i=1}^nP(B_i) \cdot P(A|B_i)$
4. 贝叶斯公式
- 定义：反向求解条件概率的公式。

- 公式：$P(B_i|A)=\dfrac{P(B_i) \cdot
P(A|B_i)}{\sum_{j=1}^nP(B_j) \cdot P(A|B_j)}$
5. 排列组合
- 排列：从 $n$ 个不同的元素中，取出 $m$ 个元素，按一定顺序进行排列的个数。

公式：$A_n^m=n \cdot (n-1) \cdot ... \cdot (n-m+1)$
- 组合：从 $n$ 个不同的元素中，取出 $m$ 个元素，不考虑顺序的组合数。

公式：$C_n^m=\dfrac{A_n^m}{m!}=\dfrac{n!}{m!(n-m)!}$。

初中数学竞赛25个定理

初中数学竞赛25个定理
初中数学竞赛25个定理1. 勾股定理：直角三角形斜边的平方等于两腰的平方和。

2. 余弦定理：在任意三角形ABC中，有c²=a²+b²-2abcosC。

3. 正弦定理：在任意三角形ABC中，有a/sinA=b/sinB=c/sinC。

4. 相似三角形的性质：对应角相等，对应边成比例。

5. 平行四边形法则：平行四边形两对邻边互相平分、互为反向共线向量。

6. 向量加减法则：向量之间可以进行加减运算，并且满足交换律、结合律和分配律。

7. 向量数量积公式：设向量a=(x₁,y₁,z₁)和b=(x₂,y₂,z₂)，则
a·b=x₁x₂+y₁y₂+z₁z₂。

8. 圆周率π的计算方法及其性质
9. 等差数列通项公式an=a1+(n-1)d
10. 等比数列通项公式an=a1*q^(n-1)
11. 数列求和公式Sn=n(a1+an)/2
12. 柿子（二次根号不含整系数）判别法
13 .一元二次方程求解公式 x=(-b±√(b^2-4ac))/2a
14 .勾股数存在条件与构造方法
15 .正多面体表面积与体积计算公式
16 .圆锥侧面积与体积计算公式
17 .球表面积与体积计算公式
18 .立体图像展开后各部位长度关系推导方法
19 .概率基本定义及常见问题解决思路
20 .排列组合基础知识点总结
21 .函数定义域、值域以及单调性研究方法
22 .极坐标下曲线参数化表示方式
23 ．复杂图案拼接技巧总结
24 ．代数恒等变换规律总结
25 ．空间几何证明题目思考策略。

初三数学竞赛常用公式

初中数学引申常用公式1.如果在一个顶点周围有k个正n边形的角，由于这些角的和应为，因此k×(n-2)180°／n=360°化为（n-2）(k-2)=4 2 弧长计算公式：L=n兀R／1803. 扇形面积公式：S扇形=n兀R^2／360=LR／24.内公切线长= d-(R-r) 外公切线长= d-(R+r)某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3一些平面几何的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

6、三角形各边的垂直一平分线交于一点。

7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O，垂心为H，从O向BC边引垂线，设垂足不L，则AH=2OL9、三角形的外心，垂心，重心在同一条直线上。

10、（九点圆或欧拉圆或费尔巴赫圆）三角形中，三边中心、从各顶点向其对边所引垂线的垂足，以及垂心与各顶点连线的中点，这九个点在同一个圆上，11、欧拉定理：三角形的外心、重心、九点圆圆心、垂心依次位于同一直线（欧拉线）上12、库立奇大上定理：（圆内接四边形的九点圆）圆周上有四点，过其中任三点作三角形，这四个三角形的九点圆圆心都在同一圆周上，我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。

初中数学竞赛公式及定理精简版

一般定理与公式1、多边形内角和定理n边形的内角的和等于（n-2）×180°2、推论任意多边的外角和等于360°3、等腰梯形性质定理等腰梯形在同一底上的两个角相等4、等腰梯形的两条对角线相等5、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形6、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半L=（a+b）÷2 S=L×h7、比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d8、合比性质如果a／b=c／d,那么(a±b)／b=(c±d)／d9、等比性质如果a／b=c／d=…=m／n(b+d+…+n≠0),那么(a+c+…+m)／(b+d+…+n)=a10、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值11、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值12、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等13、如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项14、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项15、从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等16、如果两个圆相切，那么切点一定在连心线上17、①两圆外离d＞R+r ②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)18、相交两圆的连心线垂直平分两圆的公共弦19、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形20、正三角形面积√3a／4 ，a表示边长21、弧长计算公式：L=nπR／18022、扇形面积公式：S扇形=nπR2／360=LR／223、内公切线长= d-(R-r) 外公切线长= d-(R+r)三角函数定理与公式两角和公式sin(A+B)=sin A·cos B+cos A·sin Bsin(A-B)=sin A·cos B-sin B·cos Acos(A+B)=cos A·cos B-sin A·sin Bcos(A-B)=cos A·cos B+sin A·sin Btan(A+B)=(tan A+tanB)/(1-tanAtanB) tan(A-B)=(tan A-tan B)/(1+tan A·tan B) cot(A+B)=(cotA·cotB-1)/(cot B+cot A) cot(A-B)=(cot A·cot B+1)/(cot B-cot A)倍角公式tan2A=2·tanA/(1-tan2A)cot 2A=(cot 2A-1)/2·cotAcos2a=cos2a-sin2a=2·cos2a-1=1-2·sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cos A)/2) cos(A/2)=-√((1+cos A)/2)tan(A/2)=√(((1-cosA)/(1+cos A)) tan(A/2)=-√((1-cosA)/(1+cosA))cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinA·cosB=sin(A+B)+sin(A-B) 2cosA·sinB=sin(A+B)-sin(A-B)2cosA·cosB=cos(A+B)-sin(A-B) -2sinA·sinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)·sin((A-B)/2) tanA+tanB=sin(A+B)/cosA·cosB tanA-tanB=sin(A-B)/cosA·cosBcot A+cot B·sin(A+B)/sinA·sinB -cot A+cot B·sin(A+B)/sinA·sinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3一些平面几何的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

初中竞赛数学公式定理

初中竞赛数学公式定理好嘞，以下是为您生成的文章：在咱们初中的竞赛数学世界里呀，那公式定理就像是一把把神奇的钥匙，能帮咱们打开一道道难题的大门。

先来说说勾股定理吧。

这可是个超级经典的定理！直角三角形两直角边的平方和等于斜边的平方。

记得有一次，我在课堂上给学生们讲这个定理，有个调皮的小家伙居然说：“老师，这勾股定理不就是告诉咱们直角三角形的三条边在玩‘比大小’的游戏嘛！”大家哄堂大笑，不过这倒也让大家一下就记住了勾股定理的本质。

还有完全平方公式，(a+b)² = a² + 2ab + b²，(a - b)² = a² - 2ab + b²。

这俩公式在解题的时候可太有用啦！有一回，一道竞赛题要求计算一个复杂式子的值，好多同学都抓耳挠腮的。

我就提醒他们：“你们想想完全平方公式呀！”结果呢，有个聪明的同学马上反应过来，巧妙地变形，一下子就把答案给算出来了，那叫一个得意！再说说韦达定理。

在一元二次方程 ax² + bx + c = 0 中，两根 x₁，x₂有 x₁ + x₂ = -b/a ，x₁x₂ = c/a 。

我曾经遇到过一个学生，他总是记不住韦达定理。

我就给他举了个例子，说假如你有两个口袋，一个口袋里有 x₁个糖果，另一个口袋里有 x₂个糖果，那么把两个口袋里的糖果加起来就相当于 -b/a ，两个口袋里糖果相乘就相当于 c/a 。

嘿，这招还真管用，他后来再也没忘过。

还有三角函数的那些定理，像正弦定理、余弦定理。

正弦定理a/sinA = b/sinB = c/sinC ，余弦定理 a² = b² + c² - 2bc cosA 。

有一次在做一道几何题的时候，怎么都找不到解题的突破口，后来我灵机一动，想到了余弦定理，一下子就把角度和边长的关系给搞清楚了，那感觉就像是在黑暗中突然找到了明灯。

平方差公式 (a + b)(a - b) = a² - b²，也是个不能忽视的好宝贝。

初中竞赛重要数学公式归纳总结

初中竞赛重要数学公式归纳总结初中数学竞赛中常用的一些重要公式主要包括代数、几何和概率三个方面。

下面将对这些公式进行归纳总结。

一、代数公式：1.两数和、差与积的关系：(a+b)^2 = a^2 + 2ab + b^2(a-b)^2 = a^2 - 2ab + b^2(a+b)(a-b)=a^2-b^22.平方差：a^2-b^2=(a+b)(a-b)3.二次方程求根公式：对于ax^2 + bx + c = 0，其解为：x = (-b ± √(b^2 - 4ac)) / 2a4.四则运算：a^m*a^n=a^(m+n)a^m/a^n=a^(m-n)(a^m)^n=a^(m*n)(ab)^n = a^n * b^n(a/b)^n=a^n/b^n5.无理数:√a * √b = √(ab)√a/√b=√(a/b)√a+√b≠√(a+b)6.配方法：(a+b)^2 = a^2 + 2ab + b^2(a-b)^2 = a^2 - 2ab + b^27.因式分解：a^2-b^2=(a+b)(a-b)a^3 + b^3 = (a+b)(a^2 - ab + b^2)a^3 - b^3 = (a-b)(a^2 + ab + b^2)a^2 + 2ab + b^2 = (a+b)^2a^2 - 2ab + b^2 = (a-b)^28.绝对值：a*b，=，a，*二、几何公式：1.面积公式：矩形的面积：S=长×宽三角形的面积：S=(底边×高)/2圆的面积：S=πr^22.周长公式：矩形的周长：P=2(长+宽)圆的周长：P=2πr3.直角三角形勾股定理：对于直角三角形ABC，设边长分别为a、b、c，则有：a^2+b^2=c^24.圆内切四边形面积公式：设四边形的边长分别为a、b、c、d，其半周长为s，则其面积S可以用公式表示为：S=√((s-a)(s-b)(s-c)(s-d))5.圆内接四边形面积公式：设四边形的边长分别为a、b、c、d，其半周长为s，则其面积S可以用公式表示为：S = √((s-a)(s-b)(s-c)(s-d) - abcd cos^2((A+C)/2))6.等腰三角形的高公式：设等腰三角形的底边为a，高为h，则其面积S可以用公示表示为：S = (1/2)ah7.同位角与同旁内角对应关系：同位角相等，同旁内角和为180°三、概率公式：1.事件的概率：事件A发生的概率P(A)=A的可能性数/总的可能性数2.互斥事件概率：两个互斥事件A、B均发生的概率P(A∩B)=03.独立事件概率：两个独立事件A、B发生的概率P(A∩B)=P(A)*P(B)4.包含关系的事件概率：一个事件A包含另一个事件B的概率P(B)=P(A∩B)/P(A)以上就是初中数学竞赛常用的一些重要公式的归纳总结。

初中数学竞赛公式及定理精简版

初中数学竞赛公式及定理精简版一般定理及公式1、多边形内角和定理 n边形的内角的和等于（n-2）×180°2、推论任意多边的外角和等于360°3、等腰梯形性质定理等腰梯形在同一底上的两个角相等4、等腰梯形的两条对角线相等5、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形6、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半 L=（a+b）÷2 S=L×h7、比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d8、合比性质如果a／b=c／d,那么(a±b)／b=(c±d)／d9、等比性质如果a／b=c／d=…=m／n(b+d+…+n≠0),那么(a+c+…+m)／(b+d+…+n)=a10、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值11、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值12、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等13、如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项14、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项15、从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等16、如果两个圆相切，那么切点一定在连心线上17、①两圆外离d＞R+r ②两圆外切d=R+r ③两圆相交 R-r＜d＜R+r(R＞r)④两圆内切 d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)18、相交两圆的连心线垂直平分两圆的公共弦19、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形20、正三角形面积√3a／4 ，a表示边长21、弧长计算公式：L=nπR／18022、扇形面积公式：S扇形=nπR2／360=LR／223、内公切线长= d-(R-r) 外公切线长= d-(R+r)三角函数定理及公式两角和公式sin(A+B)=sin A·cos B+cos A·sin B sin(A-B)=sin A·cos B-sin B·cos Acos(A+B)=cos A·cos B-sin A·sin B cos(A-B)=cos A·cos B+sin A·sin Btan(A+B)=(tan A+tan B)/(1-tanAtanB)tan(A-B)=(tan A-tan B)/(1+tan A·tan B)cot(A+B)=(cot A·cotB-1)/(cot B+cot A)cot(A-B)=(cot A·cot B+1)/(cot B-cot A)倍角公式tan 2A=2·tan A/(1-tan 2A) cot 2A=(cot2A-1)/2·cotAcos 2a=cos 2a-sin 2a=2·cos 2a-1=1-2·sin 2a半角公式sin(A/2)=√((1-cos A)/2)sin(A/2)=-√((1-cos A)/2)cos(A/2)=√((1+cos A)/2)cos(A/2)=-√((1+cos A)/2)tan(A/2)=√(((1-cos A)/(1+cos A))tan(A/2)=-√((1-cos A)/(1+cos A)) cot(A/2)=√((1+cos A)/((1-cos A)) cot(A/2)=-√((1+cos A)/((1-cos A))和差化积2sin A·cos B=sin(A+B)+sin(A-B) 2cos A·sin B=sin(A+B)-sin(A-B)2cos A·cos B=cos(A+B)-sin(A-B) -2sin A·sinB=cos(A+B)-cos(A-B)sin A+sin B=2sin((A+B)/2)cos((A-B)/2 cos A+cos B=2cos((A+B)/2)·sin((A-B)/2)tan A+tan B=sin(A+B)/cos A·cos B tan A-tan B=sin(A-B)/cos A·cos Bcot A+cot B·sin(A+B)/sin A·sin B -cot A+cot B·sin(A+B)/sin A·sin B某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3一些平面几何的著名定理1、勾股定理（毕达哥拉斯定理）2、射影定理（欧几里得定理）3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

数学竞赛所有公式

数学竞赛所有公式以下是一份数学竞赛中常用的公式汇总：1. 代数- 二次方程求根公式：对于二次方程 ax^2 + bx + c = 0，其根的公式为 x = (-b ± √(b^2 - 4ac)) / (2a)。

- 因式分解公式：对于一个多项式，可以因式分解为两个乘积，如 a^2 - b^2 = (a + b)(a - b)。

- 奇偶性判定公式：如果一个多项式中所有的指数项系数同奇同偶，则该多项式为偶函数；否则，为奇函数。

2. 几何- 皮亚诺定理（勾股定理）：直角三角形斜边的平方等于两直角边平方和，即 c^2 = a^2 + b^2。

- 正弦定理：在一个三角形中，三条边的比值与对应的正弦值成比例，即 a/sinA = b/sinB = c/sinC。

- 余弦定理：在一个三角形中，两条边和夹角的余弦值成正比，即 a^2 = b^2 + c^2 - 2bc cosA。

3. 概率与统计- 排列组合公式：排列的总数为 n! / (n-k)!，组合的总数为 n! / (k!(n-k)!)。

- 期望值公式：对于离散型随机变量 X，其期望值 E(X) =Σ(xP(x))，其中 x 为随机变量的取值，P(x)为该取值的概率。

- 标准差公式：对于一组数据，其标准差为σ = sqrt(Σ((x-μ)^2 / n))，其中 x 为每个数据点，n为总数据个数，μ为数据的平均值。

4. 微积分- 导数的四则运算：对于函数 f(x) 和 g(x)，其和、差、积、商的导数分别为 (f+g)' = f' + g'，(f-g)' = f' - g'，(f*g)' = f'g + fg'，(f/g)' = (f'g - fg') / g^2。

- 不定积分法则：对于函数 f(x) 和 g(x)，其和、差、积、商的不定积分分别为∫(f+g)dx = ∫fdx + ∫gdx，∫(f-g)dx = ∫fdx - ∫gdx，∫(f*g)dx = ∫fdx * ∫gdx，∫(f/g)dx = ∫(f*dx) / g。

(完整版)初中数学公式大全(整理打印版)

初中数学公式大全初中数学定理、公式汇编一、数与代数1．数与式（1）实数实数的性质：①实数a 的相反数是—a ，实数a 的倒数是a1（a ≠0）； ②实数a 的绝对值： ⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a③正数大于0，负数小于0，两个负实数，绝对值大的反而小。

二次根式：①积与商的方根的运算性质：b a ab ⋅=（a ≥0，b ≥0）；b a b a =（a ≥0，b ＞0）；②二次根式的性质：⎩⎨⎧<-≥==)0()0(2a a a a a a （2）整式与分式①同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，即n m n m a a a +=⋅（m 、n 为正整数）；②同底数幂的除法法则：同底数幂相除，底数不变，指数相减，即nm n m a a a -=÷（a ≠0，m 、n 为正整数，m>n ）；③幂的乘方法则：幂的乘方，底数不变，指数相乘，即n n n b a ab =)(（n 为正整数）；④零指数：10=a （a ≠0）；⑤负整数指数：n n aa 1=-（a ≠0，n 为正整数）； ⑥平方差公式：两个数的和与这两个数的差的积等于这两个数的平方，即22))((b a b a b a -=-+；⑦完全平方公式：两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即2222)(b ab a b a +±=±；分式①分式的基本性质：分式的分子和分母都乘以（或除以）同一个不等于零的整式，分式的值不变，即m b m a b a ⨯⨯=；mb m a b a ÷÷=，其中m 是不等于零的代数式； ②分式的乘法法则：bdac d c b a =⋅； ③分式的除法法则：)0(≠=⋅=÷c bcad c d b a d c b a ； ④分式的乘方法则：n nn ba b a =)(（n 为正整数）； ⑤同分母分式加减法则：cb ac b c a ±=±； ⑥异分母分式加减法则：bccd ab b d c a ±=±； 2．方程与不等式 ①一元二次方程02=++c bx ax (a ≠0）的求根公式：)04(2422≥--+-=ac b aac b b x ②一元二次方程根的判别式：ac b 42-=∆叫做一元二次方程02=++c bx ax （a ≠0）的根的判别式：⇔>∆0方程有两个不相等的实数根；⇔=∆0方程有两个相等的实数根；⇔<∆0方程没有实数根；③一元二次方程根与系数的关系：设1x 、2x 是方程02=++c bx ax （a ≠0）的两个根，那么1x +2x =a b -，1x 2x =ac ；不等式的基本性质：①不等式两边都加上（或减去）同一个数或同一个整式，不等号的方向不变； ②不等式两边都乘以（或除以）同一个正数，不等号的方向不变；③不等式两边都乘以（或除以）同一个负数，不等号的方向改变；3．函数一次函数的图象：函数y=kx+b(k 、b 是常数，k ≠0)的图象是过点（0，b ）且与直线y=kx 平行的一条直线；一次函数的性质：设y=kx+b （k ≠0），则当k>0时，y 随x 的增大而增大；当k<0， y 随x 的增大而减小；正比例函数的图象：函数kx y =的图象是过原点及点（1，k ）的一条直线。

初中竞赛重要数学公式归纳总结

初中竞赛重要数学公式归纳总结数学公式在解决问题、推导证明以及解释数学概念等过程中起着重要的作用。

对于初中生而言，在竞赛中掌握一些重要的数学公式将能极大地提升他们解题的效率和准确性。

本文将就初中竞赛中常见的数学公式进行归纳总结，以便同学们在备战竞赛时能够更好地应用。

1. 代数公式1.1 一次方程：ax + b = 0根据一次方程的一般形式可以得出：x = -b/a1.2 二次方程：ax^2 + bx + c = 0根据二次方程的求解公式可以得出：x = (-b ± √(b^2 - 4ac))/(2a)1.3 等差数列通项公式：an = a1 + (n - 1)d其中，an表示第n项，a1表示首项，d表示公差。

1.4 等比数列通项公式：an = a1 * r^(n - 1)其中，an表示第n项，a1表示首项，r表示公比。

2. 几何公式2.1 长方形面积公式：S = 长 ×宽2.2 正方形面积公式：S = 边长 ×边长2.3 圆的面积公式：S = πr^2其中，S表示面积，r表示半径，π取近似值3.14。

2.4 三角形面积公式：S = 1/2 ×底边长 ×高其中，S表示三角形面积，底边长和高为已知条件。

3. 概率公式3.1 事件A发生的概率：P(A) = 事件A发生的次数 / 总的可能性次数3.2 互斥事件A、B的概率：P(A或B) = P(A) + P(B)其中，P(A或B)表示事件A或事件B发生的概率，P(A)和P(B)分别表示事件A和事件B发生的概率。

3.3 独立事件A、B同时发生的概率：P(A且B) = P(A) × P(B)其中，P(A且B)表示事件A和事件B同时发生的概率，P(A)和P(B)分别表示事件A和事件B发生的概率。

4. 统计学公式4.1 平均数的计算公式：平均数 = 总和 / 数据个数4.2 中位数的计算公式：将数据按照大小排列，若数据个数为奇数，则中位数为中间的那个数；若数据个数为偶数，则中位数为中间两个数的平均数。

初中竞赛重要数学公式归纳总结

初中竞赛重要数学公式归纳总结初中数学竞赛圆的方程公式1、圆的标准方程：在平面直角坐标系中，以点O(a，b)为圆心，以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2。

2、圆的一般方程：方程x^2+y^2+Dx+Ey+F=0可变形为(x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4.故有：(1)、当D^2+E^2-4F 0时，方程表示以(-D/2,-E/2)为圆心，以(√D^2+E^2-4F)/2为半径的圆;(2)、当D^2+E^2-4F=0时，方程表示一个点(-D/2，-E/2);(3)、当D^2+E^2-4F 0时，方程不表示任何图形。

3、圆的参数方程：以点O(a，b)为圆心，以r为半径的圆的参数方程是x=a+r_cosθ, y=b+r_sinθ, (其中θ为参数)圆的端点式：若已知两点A(a1,b1),B(a2,b2)，则以线段AB为直径的圆的方程为 (x-a1)(x-a2)+(y-b1)(y-b2)=0圆的离心率e=0，在圆上任意一点的曲率半径都是r。

经过圆 x^2+y^2=r^2上一点M(a0，b0)的切线方程为 a0_x+b0_y=r^2在圆(x^2+y^2=r^2)外一点M(a0，b0)引该圆的两条切线，且两切点为A,B，则A,B两点所在直线的方程也为 a0_x+b0_y=r^2初中数学竞赛重要定理公式代数篇【乘法公式】完全平方公式：(a±b)2=a2±2ab+b2，平方差公式：(a+b)(a-b)=a2-b2，立方和(差)公式：(a±b)(a2 ab+b2)=a3±b3多项式平方公式：(a+b+c+d)2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd二项式定理：(a±b)3=a3±3a2b+3ab2±b3(a±b)4=a4±4a3b+6a2b2±4ab3+b4)(a±b)5=a5±5a4b+10a3b2±10a2b3+5ab4±b5)…………在正整数指数的条件下，可归纳如下：设n为正整数(a+b)(a2n-1- a2n-2b+a2n-3b2- …+ab2n-2- b2n-1)=a2n-b2n(a+b)(a2n-a2n-1b+a2n-2b2n-…-ab2n-1+b2n)=a2n+1+b2n+1类似地：(a-b)(a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)=a n-b n公式的变形及其逆运算由(a+b)2=a2+2ab+b2得a2+b2=(a+b)2-2ab由(a+b)3=a3+3a2b+3ab2+b3=a3+b3+3ab(a+b) 得a3+b3=(a+b)3-3ab(a+b) 由公式的推广③可知：当n为正整数时a n-b n能被a-b 整除，a2n+1+b2n+1能被a+b整除，a2n-b2n能被a+b 及a-b 整除。

(完整版)初中数学竞赛定理大全

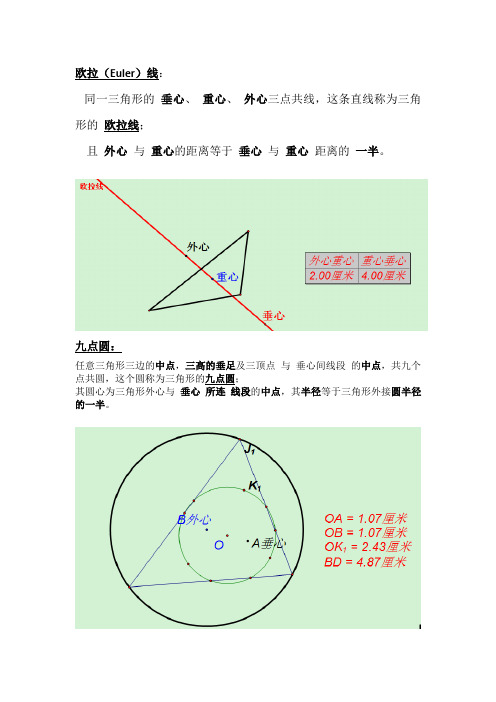
欧拉（Euler）线：同一三角形的垂心、重心、外心三点共线，这条直线称为三角形的欧拉线；且外心与重心的距离等于垂心与重心距离的一半。

九点圆：任意三角形三边的中点，三高的垂足及三顶点与垂心间线段的中点，共九个点共圆，这个圆称为三角形的九点圆；其圆心为三角形外心与垂心所连线段的中点，其半径等于三角形外接圆半径的一半。

费尔马点：已知P为锐角△ABC内一点，当∠APB＝∠BPC＝∠CPA＝120°时，PA＋PB＋PC的值最小，这个点P称为△ABC的费尔马点。

海伦（Heron）公式：塞瓦（Ceva）定理：在△ABC中，过△ABC的顶点作相交于一点P的直线，分别交边BC、CA、AB与点D、E、F，则(BD/DC)·(CE/EA)·(AF/FB)＝1；其逆亦真。

密格尔（Miquel）点：若AE、AF、ED、FB四条直线相交于A、B、C、D、E、F六点，构成四个三角形，它们是△ABF、△AED、△BCE、△DCF，则这四个三角形的外接圆共点，这个点称为密格尔点。

葛尔刚（Gergonne）点:△ABC的内切圆分别切边AB、BC、CA于点D、E、F，则AE、BF、CD三线共点，这个点称为葛尔刚点。

西摩松（Simson）线：已知P为△ABC外接圆周上任意一点，PD⊥BC，PE⊥ACPF⊥AB，D、E、F为垂足，则D、E、F三点共线，这条直线叫做西摩松线。

黄金分割：把一条线段(AB)分成两条线段，使其中较大的线段(AC)是原线段(AB) 与较小线段(BC)的比例中项，这样的分割称为黄金分割。

帕普斯（Pappus）定理：已知点A1、A2、A3在直线l1上，已知点B1、B2、B3在直线l2上，且A1 B2与A2 B1交于点X，A1B3与A3 B1交于点Y，A2B3于A3 B2交于点Z，则X、Y、Z三点共线。

笛沙格（Desargues）定理：已知在△ABC与△A'B'C'中，AA'、BB'、CC'三线相交于点O，BC与B'C'、CA与C'A'、AB与A'B'分别相交于点X、Y、Z，则X、Y、Z三点共线；其逆亦真摩莱（Morley）三角形：在已知△ABC三内角的三等分线中，分别与BC、CA、AB相邻的每两线相交于点D、E、F，则△DEF是正三角形，这个正三角形称为摩莱三角形。

初中数学竞赛公式及定理精简版

一般定理与公式1、多边形角和定理 n边形的角的和等于〔n-2〕×180°2、推论任意多边的外角和等于360°3、等腰梯形性质定理等腰梯形在同一底上的两个角相等4、等腰梯形的两条对角线相等5、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形6、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半 L=〔a+b〕÷2 S=L×h7、比例的根本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d8、合比性质如果a／b=c／d,那么(a±b)／b=(c±d)／d9、等比性质如果a／b=c／d=…=m／n(b+d+…+n≠0),那么(a+c+…+m)／(b+d+…+n)=a10、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值11、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值12、相交弦定理圆的两条相交弦，被交点分成的两条线段长的积相等13、如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项14、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项15、从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等16、如果两个圆相切，那么切点一定在连心线上17、①两圆外离 d＞R+r ②两圆外切d=R+r③两圆相交 R-r＜d＜R+r(R＞r)④两圆切 d=R-r(R＞r) ⑤两圆含d＜R-r(R＞r)18、相交两圆的连心线垂直平分两圆的公共弦19、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形20、正三角形面积√3a／4 ，a表示边长21、弧长计算公式：L=nπR／18022、扇形面积公式：S扇形=nπR2／360=LR／223、公切线长= d-(R-r) 外公切线长= d-(R+r)三角函数定理与公式两角和公式sin(A+B)=sin A·cos B+cos A·sin Bsin(A-B)=sin A·cos B-sin B·cos Acos(A+B)=cos A·cos B-sin A·sin Bcos(A-B)=cos A·cos B+sin A·sin Btan(A+B)=(tan A+tanB)/(1-tanAtanB) tan(A-B)=(tan A-tan B)/(1+tan A·tan B) cot(A+B)=(cotA·cotB-1)/(cot B+cot A) cot(A-B)=(cot A·cot B+1)/(cot B-cot A)倍角公式tan2A=2·tanA/(1-tan2A)cot 2A=(cot 2A-1)/2·cotAcos2a=cos2a-sin2a=2·cos2a-1=1-2·sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cos A)/2) cos(A/2)=-√((1+cos A)/2)tan(A/2)=√(((1-cosA)/(1+cos A)) tan(A/2)=-√((1-cosA)/(1+cosA)) cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA)) 和差化积 2sinA·cosB=sin(A+B)+sin(A-B) 2cosA·sinB=sin(A+B)-sin(A-B) 2cosA·cosB=cos(A+B)-sin(A-B) -2sinA·sinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)·sin((A-B)/2) tanA+tanB=sin(A+B)/cosA·cosB tanA-tanB=sin(A-B)/cosA·cosB cot A+cot B·sin(A+B)/sinA·sinB -cot A+cot B·sin(A+B)/sinA·sinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3一些平面几何的著名定理1、勾股定理〔毕达哥拉斯定理〕2、射影定理〔欧几里得定理〕3、三角形的三条中线交于一点，并且，各中线被这个点分成2：1的两局部4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。

初中数学竞赛常用公式(总6页)

初中数学竞赛常用公式-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除初中数学常用公式1 过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中，垂线段最短7 平行公理经过直线外一点，有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行，这两条直线也互相平行9 同位角相等，两直线平行 10 内错角相等，两直线平行 11 同旁内角互补，两直线平行 12两直线平行，同位角相等 13 两直线平行，内错角相等 14 两直线平行，同旁内角互补 15 定理：三角形两边的和大于第三边 16 推论：三角形两边的差小于第三边17 三角形内角和定理：三角形三个内角的和等于180° 18 推论1：直角三角形的两个锐角互余19 推论2：三角形的一个外角等于和它不相邻的两个内角的和20 推论3：三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理(SAS)：有两边和它们的夹角对应相等的两个三角形全等23 角边角公理( ASA)：有两角和它们的夹边对应相等的两个三角形全等24 推论(AAS)：有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理(SSS)：有三边对应相等的两个三角形全等26 斜边、直角边公理(HL)：有斜边和一条直角边对应相等的两个直角三角形全等27 定理1：在角的平分线上的点到这个角的两边的距离相等28 定理2：到一个角的两边的距离相同的点，在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理：等腰三角形的两个底角相等 (即等边对等角）31 推论1：等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合33 推论3：等边三角形的各角都相等，并且每一个角都等于60°34 等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）35 推论1：三个角都相等的三角形是等边三角形36 推论 2：有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理：线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1：关于某条直线对称的两个图形是全等形43 定理 2：如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线44定理3：两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上45逆定理：如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称46勾股定理：直角三角形两直角边a、b的平方和、等于斜边c的平方，即a2+b2=c247勾股定理的逆定理：如果三角形的三边长a、b、c有关系a2+b2=c2，那么这个三角形是直角三角形48定理：四边形的内角和等于360° 49四边形的外角和等于360°50多边形内角和定理：n边形的内角的和等于（n-2）×180° 51推论：任意多边的外角和等于360°52平行四边形性质定理1：平行四边形的对角相等53平行四边形性质定理2：平行四边形的对边相等54推论：夹在两条平行线间的平行线段相等55平行四边形性质定理3：平行四边形的对角线互相平分56平行四边形判定定理1：两组对角分别相等的四边形是平行四边形57平行四边形判定定理2：两组对边分别相等的四边形是平行四边形58平行四边形判定定理3：对角线互相平分的四边形是平行四边形59平行四边形判定定理4：一组对边平行相等的四边形是平行四边形60矩形性质定理1：矩形的四个角都是直角 61矩形性质定理2：矩形的对角线相等62矩形判定定理1：有三个角是直角的四边形是矩形63矩形判定定理2：对角线相等的平行四边形是矩形64菱形性质定理1：菱形的四条边都相等65菱形性质定理2：菱形的对角线互相垂直，并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半，即S=（a×b）÷267菱形判定定理1：四边都相等的四边形是菱形68菱形判定定理2：对角线互相垂直的平行四边形是菱形69正方形性质定理1：正方形的四个角都是直角，四条边都相等70正方形性质定理：正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角71定理1：关于中心对称的两个图形是全等的72定理2：关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分73逆定理：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称74等腰梯形性质定理：等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理：在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等79 推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰80 推论2：经过三角形一边的中点与另一边平行的直线，必平分第三边81 三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半82 梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半 L=（a+b）÷2 S=L×h83 比例的基本性质：如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d84 平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例85 推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例88 定理如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边86 平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例87 定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似88 相似三角形判定定理1：两角对应相等，两三角形相似（ASA）89 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似90 判定定理2：两边对应成比例且夹角相等，两三角形相似（SAS）91 判定定理3：三边对应成比例，两三角形相似（SSS）92 定理：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似93 性质定理1：相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比94 性质定理2：相似三角形周长的比等于相似比95 性质定理3：相似三角形面积的比等于相似比的平方96 任意锐角的正弦值等于它的余角的余弦值，sinA=cos(90-A)任意锐角的余弦值等于它的余角的正弦值，cosA=sin(90-A)97任意锐角的正切值等于它的余角的余切值，tanA=cot(90-A)任意锐角的余切值等于它的余角的正切值 cotA=tan(90-A)98圆是定点的距离等于定长的点的集合99圆的内部可以看作是圆心的距离小于半径的点的集合100圆的外部可以看作是圆心的距离大于半径的点的集合101同圆或等圆的半径相等102到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆103和已知线段两个端点的距离相等的点的轨迹，是这条线段的垂直平分线104到已知角的两边距离相等的点的轨迹，是这个角的平分线105到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线106定理：不在同一直线上的三点确定一个圆。

-初中数学竞赛常用公式[1].doc-2013

初中数学竞赛重要定理公式(代数篇)

初中数学竞赛常用公式总结

初中数学竞赛中常用重要定理

初中数学竞赛重要定理公式(统计篇)

初中数学竞赛25个定理

初三数学竞赛常用公式

初中数学竞赛公式及定理精简版

初中竞赛数学公式定理

初中竞赛重要数学公式归纳总结

初中数学竞赛公式及定理精简版

数学竞赛所有公式

(完整版)初中数学公式大全(整理打印版)

最新的初中数学竞赛常用公式[].doc

初中竞赛重要数学公式归纳总结

初中竞赛重要数学公式归纳总结

(完整版)初中数学竞赛定理大全

初中数学竞赛公式及定理精简版

初中数学竞赛常用公式(总6页)