初中数学竞赛平面几何常用公式及例题讲解
初中数学竞赛平面几何讲座---巧添辅助-- 妙解竞赛题

初中数学巧添辅助-- 妙解竞赛题在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路.1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化.1.1 作出三角形的外接圆例1如图1,在△ABC中,AB=AC,D是底边BC上一点,E是线段AD上一点且∠BED=2∠CED=∠A.求证:BD=2CD.ABGC DFE 图1例 2 凸四边形ABCD 中,∠ABC =60°,∠BAD =∠BCD =90°, AB =2,CD =1,对角线AC 、BD 交于点O ,如图2.则sin ∠AOB =____.例3 已知:如图3,AB =BC =CA =AD ,AH ⊥CD 于H ,CP ⊥BC ,CP 交AH 于P . 求证:△ABC 的面积S =43AP ·BD .A图3BP QD HC ABCDPO图22 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决. 2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长.2.2 联想直径的性质构造辅助圆例5 已知抛物线y =-x 2+2x +8与x 轴交于B 、C 两点,点D 平分BC .若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____.A EDCB图4图5例6 AD 是Rt △ABC 斜边BC 上的高,∠B 的平行线交AD 于M ,交AC 于N . 求证:AB 2-AN 2=BM ·BN .例7 如图7,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证:EP 2+FQ 2=EF 2.EANCD B FM 12345图6例8 如图8,△ABC 与△A 'B 'C '的三边分别为a 、b 、c 与a '、b '、c ',且∠B =∠B ',∠A +∠A '=180°.试证:aa '=bb '+cc '.同步练习题1. 作一个辅助圆证明:△ABC 中,若AD 平分∠A ,则AC AB =DCBD.2. 已知凸五边形ABCDE 中,∠BAE =3a ,BC =CD =DE ,∠BCD =∠CDE =180°-2a . 求证:∠BAC =∠CAD =∠DAE .3. 在△ABC 中AB =BC ,∠ABC =20°,在AB 边上取一点M ,使BM =AC .求∠AMC 的度数.(1)(2)图8ABCA'B'C'cb a'c'b'3. 如图10,AC 是ABCD 较长的对角线,过C 作CF ⊥AF ,CE ⊥AE .求证:AB ·AE +AD ·AF =AC 2.4. 如图11.已知⊙O 1和⊙O 2相交于A 、B ,直线CD 过A 交⊙O 1和⊙O 2于C 、D ,且AC =AD ,EC 、ED 分别切两圆于C 、D . 求证:AC 2=AB ·AE .6.已知E 是△ABC 的外接圆之劣弧BC 的中点. 求证:AB ·AC =AE 2-BE 2.7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba=1.F DAB EC图10C图11初中数学巧添辅助-- 妙解竞赛题答案在某些数学竞赛问题中,巧妙添置辅助圆常可以沟通直线形和圆的内在联系,通过圆的有关性质找到解题途径.下面举例说明添置辅助圆解初中数学竞赛题的若干思路.1 挖掘隐含的辅助圆解题有些问题的题设或图形本身隐含着“点共圆”,此时若能把握问题提供的信息,恰当补出辅助圆,并合理挖掘图形隐含的性质,就会使题设和结论的逻辑关系明朗化. 1.1 作出三角形的外接圆例1 如图1,在△ABC 中,AB =AC ,D 是底边BC 上一点,E 是线段AD 上一点且∠BED =2∠CED = ∠A .求证:BD =2CD .分析:关键是寻求∠BED =2∠CED 与结论的联系. 容易想到作∠BED 的平分线,但因BE ≠ED ,故不能 直接证出BD =2CD .若延长AD 交△ABC 的外接圆 于F ,则可得EB =EF ,从而获取.证明:如图1,延长AD 与△ABC 的外接圆相交于点F ,连结CF 与BF ,则∠BFA =∠BCA =∠ABC =∠AFC ,即∠BFD =∠CFD .故BF :CF =BD :DC .又∠BEF =∠BAC ,∠BFE =∠BCA ,从而∠FBE =∠ABC =∠ACB =∠BFE . 故EB =EF .作∠BEF 的平分线交BF 于G ,则BG =GF . 因∠GEF =21∠BEF =∠CEF ,∠GFE =∠CFE ,故△FEG ≌△FEC .从而GF =FC . 于是,BF =2CF .故BD =2CD . 1.2 利用四点共圆例2 凸四边形ABCD 中,∠ABC =60°,∠BAD = ∠BCD =90°,AB =2,CD =1,对角线AC 、BD 交于点O ,如图2. 则sin ∠AOB =____.ABGCD FE图1ABCDPO 图2分析:由∠BAD =∠BCD =90°可知A 、B 、C 、D四点共圆,欲求sin ∠AOB ,联想到托勒密定理,只须求出BC 、AD 即可.解:因∠BAD =∠BCD =90°,故A 、B 、C 、D 四点共圆.延长BA 、CD 交于P ,则∠ADP =∠ABC =60°.设AD =x ,有AP =3x ,DP =2x .由割线定理得(2+3x )3x =2x (1+2x ).解得AD =x =23-2,BC =21BP =4-3. 由托勒密定理有BD ·CA =(4-3)(23-2)+2×1=103-12.又S ABCD =S △ABD +S △BCD =233. 故sin ∠AOB =263615 . 例3 已知:如图3,AB =BC =CA =AD ,AH ⊥CD 于H ,CP ⊥BC ,CP 交AH 于P .求证: △ABC 的面积S =43AP ·BD . 分析:因S △ABC =43BC 2=43AC ·BC ,只 须证AC ·BC =AP ·BD ,转化为证△APC ∽△BCD .这由A 、B 、C 、Q 四点共圆易证(Q 为BD 与AH 交点).证明:记BD 与AH 交于点Q ,则由AC =AD ,AH ⊥CD 得∠ACQ =∠ADQ . 又AB =AD ,故∠ADQ =∠ABQ .从而,∠ABQ =∠ACQ .可知A 、B 、C 、Q 四点共圆. ∵∠APC =90°+∠PCH =∠BCD ,∠CBQ =∠CAQ , ∴△APC ∽△BCD . ∴AC ·BC =AP ·BD . 于是,S =43AC ·BC =43AP ·BD . A图3BPQDHC2 构造相关的辅助圆解题有些问题貌似与圆无关,但问题的题设或结论或图形提供了某些与圆的性质相似的信息,此时可大胆联想构造出与题目相关的辅助圆,将原问题转化为与圆有关的问题加以解决. 2.1 联想圆的定义构造辅助圆例4 如图4,四边形ABCD 中,AB ∥CD ,AD =DC =DB =p ,BC =q .求对角线AC 的长.分析:由“AD =DC =DB =p ”可知A 、B 、C 在 半径为p 的⊙D 上.利用圆的性质即可找到AC 与 p 、q 的关系.解:延长CD 交半径为p 的⊙D 于E 点,连结AE . 显然A 、B 、C 在⊙D 上. ∵AB ∥CD ,∴BC =AE . 从而,BC =AE =q .在△ACE 中,∠CAE =90°,CE =2p ,AE =q ,故 AC =22AE CE -=224q p -. 2.2 联想直径的性质构造辅助圆例5 已知抛物线y =-x 2+2x +8与x 轴交于B 、C 两点,点D 平分BC .若在x 轴上侧的A 点为抛物线上的动点,且∠BAC 为锐角,则AD 的取值范围是____.分析:由“∠BAC 为锐角”可知点A 在以定线段BC 为直径的圆外,又点A 在x 轴上侧,从而可确定动点A 的范围,进而确定AD 的取值范围. 解:如图5,所给抛物线的顶点为A 0(1,9), 对称轴为x =1,与x 轴交于两点B (-2,0)、 C (4,0).分别以BC 、DA 为直径作⊙D 、⊙E ,则两圆与抛物线均交于两点P (1-22,1)、A EDCB图4图5Q (1+22,1).可知,点A 在不含端点的抛物线PA 0Q 内时,∠BAC <90°.且有3=DP =DQ <AD ≤DA 0=9,即AD 的取值范围是3<AD ≤9. 2.3 联想圆幂定理构造辅助圆例6 AD 是Rt △ABC 斜边BC 上的高,∠B 的平行线交AD 于M ,交AC 于N .求证:AB 2-AN 2=BM ·BN .分析:因AB 2-AN 2=(AB +AN )(AB -AN )=BM ·BN ,而由题设易知AM =AN ,联想割线定理,构造辅助圆即可证得结论. 证明:如图6,∵∠2+∠3=∠4+∠5=90°, 又∠3=∠4,∠1=∠5, ∴∠1=∠2.从而,AM =AN . 以AM 长为半径作⊙A ,交AB 于F ,交 BA 的延长线于E .则AE =AF =AN . 由割线定理有 BM ·BN =BF ·BE =(AB +AE )(AB -AF ) =(AB +AN )(AB -AN ) =AB 2-AN 2, 即 AB 2-AN 2=BM ·BN .例7 如图7,ABCD 是⊙O 的内接四边形,延长AB 和DC 相交于E ,延长AB 和DC 相交于E ,延长AD 和BC 相交于F ,EP 和FQ 分别切⊙O 于P 、Q .求证:EP 2+FQ 2=EF 2. 分析:因EP 和FQ 是⊙O 的切线,由结论联想到切割线定理,构造辅助圆使EP 、FQ 向EF 转化.证明:如图7,作△BCE 的外接圆交EF 于G ,连 结CG .因∠FDC =∠ABC =∠CGE ,故F 、D 、C 、G 四点共圆.EA N D BFM 12345图6由切割线定理,有 EF 2=(EG +GF )·EF =EG ·EF +GF ·EF =EC ·ED +FC ·FB=EC ·ED +FC ·FB =EP 2+FQ 2,即 EP 2+FQ 2=EF 2.2.4 联想托勒密定理构造辅助圆 例8 如图8,△ABC 与△A 'B ' C '的三边分别为a 、b 、c 与a '、 b '、c ',且∠B =∠B ',∠A +∠A '=180°.试证:aa '=bb '+cc '. 分析:因∠B =∠B ',∠A +∠A '=180°,由结论联想到托勒密定理,构造圆内接四边形加以证明.证明:作△ABC 的外接圆,过C 作CD ∥AB 交圆于D ,连结AD 和BD ,如图9所示. ∵∠A +∠A '=180°=∠A +∠D , ∠BCD =∠B =∠B ',∴∠A '=∠D ,∠B '=∠BCD .∴△A 'B 'C '∽△DCB .有DC B A ''=CB C B ''=DBC A '',即 DC c '=a a '=DB b '.故DC =''a ac ,DB =''a ab .又AB ∥DC ,可知BD =AC =b ,BC =AD =a . 从而,由托勒密定理,得 AD ·BC =AB ·DC +AC ·BD , 即 a 2=c ·''a ac +b ·''a ab . 故aa '=bb '+cc '.练习题(1)(2)图8ABCA'B'C'ca b a'c'b'A BCDa b b c图91. 作一个辅助圆证明:△ABC 中,若AD 平分∠A ,则AC AB =DCBD. (提示:不妨设AB ≥AC ,作△ADC 的外接圆交AB 于E ,证△ABC ∽△DBE ,从而AC AB =DEBD=DCBD.) 2. 已知凸五边形ABCDE 中,∠BAE =3a ,BC =CD =DE ,∠BCD =∠CDE =180°-2a .求证:∠BAC =∠CAD =∠DAE .(提示:由已知证明∠BCE =∠BDE =180°-3a ,从而A 、B 、C 、D 、E 共圆,得∠BAC =∠CAD =∠DAE .)3. 在△ABC 中AB =BC ,∠ABC =20°,在AB 边上取一点M ,使BM =AC .求∠AMC 的度数. (提示:以BC 为边在△ABC 外作正△KBC ,连结KM ,证B 、M 、C 共圆,从而∠BCM =21∠BKM =10°,得∠AMC =30°.) 4.如图10,AC 是ABCD 较长的对角线,过C 作CF ⊥AF ,CE ⊥AE .求证:AB ·AE +AD ·AF =AC 2. (提示:分别以BC 和CD 为直径作圆交AC 于点 G 、H .则CG =AH ,由割线定理可证得结论.) 5. 如图11.已知⊙O 1和⊙O 2相交于A 、B ,直线CD 过A 交⊙O 1和⊙O 2于C 、D ,且AC =AD ,EC 、ED 分别切两圆于C 、D .求证:AC 2=AB ·AE . (提示:作△BCD 的外接圆⊙O 3,延长BA 交⊙O 3 于F ,证E 在⊙O 3上,得△ACE ≌△ADF ,从而AE =AF ,由相交弦定理即得结论.)6.已知E 是△ABC 的外接圆之劣弧BC 的中点. 求证:AB ·AC =AE 2-BE 2.(提示:以BE 为半径作辅助圆⊙E ,交AE 及其延长线于N 、M ,由△ANC ∽△ABM 证AB ·AC =AN ·AM .)7. 若正五边形ABCDE 的边长为a ,对角线长为b ,试证:a b -ba=1. (提示:证b 2=a 2+ab ,联想托勒密定理作出五边形的外接圆即可证得.)FDAEC图10图11。
初中数学竞赛重要定理公式(平面几何篇)

初中数学竞赛重要定理公式(平面几何篇)初中数学竞赛中,平面几何是一个重要的考点。
以下是一些重要的定理、公式和结论。
三角形面积公式(包括海伦公式):三角形的面积S可以用以下公式计算:$S=\sqrt{p(p-a)(p-b)(p-c)}$,其中$p=\frac{1}{2}(a+b+c)$,$a$,$b$,$c$分别为三角形的三条边长。
另外,三角形的面积也可以用以下公式计算:$S=\frac{1}{2}ab\sin C$,其中$a$,$b$为两边,$C$为两边之间的夹角。
还有一个海伦公式:$S=\frac{1}{2}ah_a$,其中$h_a$为三角形顶点$A$到边$BC$的垂线长度,$a$为边$BC$的长度。
XXX定理:对于三角形$\triangle ABC$及其底边上的一点$D$,有$AB^2\cdot DC+AC^2\cdot BD-AD^2\cdotBC=BC\cdot DC\cdot BD$。
XXX定理:对于一个内接四边形,其对角线之积等于两组对边乘积之和,即$AC\cdot BD=AB\cdot CD+AD\cdot BC$。
逆命题也成立。
同时还有广义托勒密定理:$AB\cdotCD+AD\cdot BC\geq AC\cdot BD$。
蝴蝶定理:如果$AB$是圆$O$的弦,$M$是$AB$的中点,弦$CD$,$EF$经过点$M$,$CF$,$DE$交$AB$于$P$,$Q$,则$MP=QM$。
勾股定理(毕达哥拉斯定理):对于一个直角三角形,锐角对边的平方等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍;钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍。
同时还有广义勾股定理。
中线定理(巴布斯定理):对于一个三角形$\triangleABC$,如果$BC$的中点为$P$,则有$AB^2+AC^2=2(AP^2+BP^2)$。
同时,中线的长度可以用以下公式计算:$m_a=\frac{1}{2}\sqrt{2b^2+2c^2-a^2}$。
数学奥赛平面几何

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理:1、梅涅劳斯定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
2、塞瓦定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
3、托勒密定理:四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理:设P 是ABC ∆外接圆上任一点,过P 向ABC ∆的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
5、斯德瓦特定理:设P 是ABC ∆的边BC 边上的任一点,则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理:设ABC ∆和C B A '''∆中有一个角相等或互补(不妨设A=A ')则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理:设ABC ∆和C B A '''∆中有一个边相等,则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明:1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点,且AM:AC=CN:CE=k,如果BMN 三点共线,试求k 。
(IMO23,1982)2、在四边形ABCD 中,ABD ∆、BCD ∆、ABC ∆的面积之比为3:4:1,点M 、N 分别 是AC 、CD 上的点,且AM:AC=CN:CD, 并且BMN 三点共线,求证:M 、N 分别是AC 、 CD 的中点。
平面解析几何的基本公式

平面解析几何的基本公式平面解析几何是数学中的一个重要分支,它研究平面上点、线、圆等几何图形的性质和关系。
在平面解析几何中,有一些基本公式被广泛应用于求解几何问题。
本文将介绍平面解析几何的基本公式,并给出相应的示例和应用。
1. 点到直线的距离公式平面解析几何中,求点到直线的距离是一个常见的问题。
设直线的方程为Ax + By + C = 0,点的坐标为(x0, y0),则点到直线的距离公式如下:d = |Ax0 + By0 + C| / √(A^2 + B^2)示例:求点P(1, 2)到直线2x + 3y - 6 = 0的距离。
解:代入公式,得到d = |2*1 + 3*2 - 6| / √(2^2 + 3^2) = |7| / √13 ≈ 7 / 3.61 ≈ 1.942. 直线的斜率公式及两直线的夹角公式直线的斜率描述了它的方向性质,在平面解析几何中,直线的斜率可以表示为k = tanθ,其中θ为直线与x轴的夹角。
直线斜率和两直线夹角的公式如下:k = (y2 - y1) / (x2 - x1)θ = arctan(k)示例:已知两点A(1, 2)和B(3, 4),求直线AB的斜率和与x轴的夹角。
解:代入公式,得到k = (4 - 2) / (3 - 1) = 2 / 2 = 1,θ = arctan(1) ≈ 45°3. 两直线的垂直和平行判定公式在平面解析几何中,判断两条直线是否垂直可以通过斜率来判断。
若两直线斜率分别为k1和k2,则它们垂直的条件是k1 * k2 = -1。
判断两条直线是否平行可以通过比较斜率来判断。
若两直线斜率分别为k1和k2,则它们平行的条件是k1 = k2。
示例:已知直线L1过点A(1, 2)且斜率为2,直线L2垂直于L1,求直线L2的方程。
解:由L1斜率为2,得到L2斜率为-1/2。
过点A(1, 2)且斜率为-1/2的直线方程为y - 2 = (-1/2)(x - 1),整理得到直线L2的方程为2x + y - 4 = 0。
初中数学66个常考几何模型50个应用题答题公式(二)

初中数学66个常考几何模型50个应用题答题公式(二)初中数学66个常考几何模型50个应用题答题公式1. 模型一:直角三角形•直角三角形的斜边长度 = 根号下(直角边1的长度的平方 + 直角边2的长度的平方)–例题:已知直角三角形的直角边1的长度为3,直角边2的长度为4,求斜边的长度。
•解答:斜边长度 = 根号下(3^2 + 4^2)= 52. 模型二:等边三角形•等边三角形的边长 = 边长–例题:已知等边三角形的边长为6,求周长和面积。
•解答:周长 = 6 + 6 + 6 = 18,面积 = (6 × 6× √3)/ 4 = 9√33. 模型三:等腰三角形•等腰三角形的底边长度 = (底角对边长度× 2)/ sin(顶角的一半)–例题:已知等腰三角形的顶角为60°,底边对应的底角对边长度为5,求底边的长度。
•解答:底边长度 = (5 × 2)/ sin(60°的一半)= 10/ sin(30°) = 10/ = 204. 模型四:等腰梯形•等腰梯形的面积 = (上底 + 下底)× 高 / 2–例题:已知等腰梯形的上底为6,下底为10,高为8,求面积。
•解答:面积 = (6 + 10)× 8 / 2 = 805. 模型五:矩形•矩形的周长 = (长 + 宽)× 2•矩形的面积 = 长× 宽•矩形的对角线长度 = 根号下(长的平方 + 宽的平方)–例题:已知矩形的长为5,宽为3,求周长、面积和对角线的长度。
•解答:周长 = (5 + 3)× 2 = 16,面积= 5 × 3 = 15,对角线长度 = 根号下(5^2 + 3^2)= √34 6. 模型六:菱形•菱形的周长 = 边长× 4•菱形的面积 = 对角线长度1 × 对角线长度2 / 2–例题:已知菱形的边长为6,对角线长度1为8,求周长和面积。
初中数学奥林匹克几何问题梅涅劳斯定理及应用

初中数学奥林匹克几何问题-梅涅劳斯定理及应用第一章涅劳斯定理及应用【基础知识】梅涅劳斯定理设,,分别是的三边,,或其延长线上的点,若,,三点共线,则.①证明如图,过作直线交的延长线于,则,,故.注此定理的证明还有如下正弦定理证法及面积证法.正弦定理证法设,,,在中,有,同理,,,此三式相乘即证.面积证法由,,,此三式相乘即证.梅涅劳斯定理的逆定理设,,分别是的三边,,或其延长线上的点,若,②则,,三点共线.证明设直线交于,则由梅涅劳斯定理,得到.由题设,有,即有.又由合比定理,知,故有,从而与重合,即,,三点共线.有时,也把上述两个定理合写为:设,,分别是的三边,,所在直线(包括三边的延长线)上的点,则,,三点共线的充要条件是.上述①与②式是针对而言的,如图(整个图中有4个三角形),对于、、也有下述形式的充要条件:;;.③第一角元形式的梅涅劳斯定理设,,分别是的三边,,所在直线(包括三边的延长线)上的点,则,,共线的充分必要条件是.④证明如图,可得.同理,,.以上三式相乘,运用梅涅劳斯定理及其逆定理,知结论成立.第二角元形式的梅涅劳斯定理设,,分别是的三边,,所在直线上的点,点不在三边所在直线上,则,,三点共线的充要条件是.⑤证明如图,由,有.同理,,.于是.故由梅涅劳斯定理知,,共线.从而定理获证.注(1)对于④、⑤式也有类似③式(整个图中有4个三角形)的结论.(2)于在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式中的右端均为,③、④、⑤式中的角也可以按①或②式中的对应线段记忆.特别要注意的是三边所在直线上的点为一点或者三点在边的延长线上.【典型例题与基本方法】1.恰当地选择三角形及其截线(或作出截线),是应用梅涅劳斯定理的关键例1如图,在四边形中,,,的面积比是3∶4∶1,点,分别在,上,满足∶∶,并且,,共线.求证:与分别是和的中点.(1983年全国高中联赛题)证明设(),交于.,,..又因,,三点共线,可视为的截线,故由梅涅劳斯定理,得,即.化简整理,得,解得,(舍去).故与分别是和的中点.例2如图1-5,在四边形中,对角线平分,在上取一点,与相交于,延长交于.求证:.(1999年全国高中联赛题)证明记,,,直线与相截,由梅涅劳斯定理,有.故.即,亦即,且只可能为0,故.例3设、分别为四边形的边、上的点,与交于点.若,则.证明如图1-6,只需证得当关于的等角线交于时,、、共线即可.事实上,、、分别为三边所在直线上的三点,且不在其三边所在直线上.又,,,由第二角元形式的梅涅劳斯定理,有.故、、三点共线.注当平分时,即为1999年全国高中联赛题.2.梅涅劳斯定理的逆用(逆定理的应用)与迭用,是灵活应用梅氏定理的一种方法例2另证如图1-5,设,关于的对称点分别为,,易知,,三点共线,连,,只须证明,,三点共线.设,,,则.对,应用梅涅劳斯定理的逆定理,知,,三点共线.故.注在图1-5中,*式也可为,若在的延长上,则*式为.例4如图1-7,与和的三边所在的3条直线都相切,,,,为切点,直线与交于点.求证:.(1996年全国高中联赛题)证法1过作于,延长交直线于点.对及截线应用梅涅劳斯定理,有.由,有.显然,,三点共线,连,,,,则由,有,从而,即.又,则.对,应用梅涅劳斯定理的逆定理,知,,三点共线,即为直线与的交点.故点与点重合,从而.证法2延长交于,直线与的三边延长线都相交,直线与的三边延长线都相交,分别应用(迭用)梅涅劳斯定理,有,.上述两式相除,则有.而,,于是,即.连,,,,,,而,,共线,则,,且,从而,于是.故,即.【解题思维策略分析】梅涅劳斯定理是三角形几何学中的一颗明珠,它蕴含着深刻的数学美,因而它在求解某些平面几何问题,特别是某些平面几何竞赛题中有着重要的应用.1.寻求线段倍分的一座桥梁例5已知的重心为,是边的中点,过作边的平行线交边于,交边于,且与交于点,与交于点.证明:.(1991年第3届亚太地区竞赛题)证明如图1-8,延长交于,则为的中点.由,知,而.对及截线,应用梅涅劳斯定理,有,故.从而,且.同理,,且.由此可知,与的两边分别平行且方向相反,从而,且,故.例6是一个等腰三角形,,是的中点;是的延长线上的一点,使得;是线段上不同于和的任意一点,在直线上,在直线上,使得,,是不同的和共线的,求证:(Ⅰ)若,则;(Ⅱ)若,则.(1994年第35届试题)证明(1)如图1-9,连,,.由,易证,,,四点共圆,,,,四点共圆.则,因此.故.(Ⅱ)由,,对及截线运用梅涅劳斯定理,有,即.于是可证,得,故.例7在凸四边形的边和上取点和,使线段和把对角线三等分,已知,求证:是平行四边形.(1990年第16届全俄竞赛题)证明如图1-10,设,分别交于,,两对角线交于.要证是平行四边形,若证得(或),且即可.由,(等底等高),知,而,故有,从而有.对及截线,及截线,分别应用梅涅劳斯定理,有,①.②由①,②两式相除得.而,故,即有.此时,又有.又由,知,于是①式可写为,即有,亦即.故为平行四边形.2.导出线段比例式的重要途径例8在中,为边上的中线,为的平分线,且交于,为上的点,使.证明.(1997年第58届莫斯科竞赛题)证明如图1-11,延长交于,只须证.由平分,有.①由,有.注意到,对及截线运用梅涅劳斯定理,得.故,由合比定理,有,即为.②由①,②式有,故.例9给定锐角,在边上取点,(位于与之间),在边上取点,(位于与之间),在边上取点,(位于与之间),使得,直线,与可构成一个三角形,直线,与可构成另一个三角形.证明:(1995年第36届1mo预选题)这两个三角形的六个顶点共圆.证明如图1-12,设题中所述两个三角形分别为与.由已知条件,有,,,得,,,此三式相乘得.①对及截线,及截线,分别应用梅涅劳斯定理,得,②,③①,②,③三式相乘化简,得.故.同理,.故.从而点在的外接圆上.同理,可证得,也在的外接圆上.证毕.例10如图1-13,以的底边为直径作半圆,分别与边,交于点和,分别过点,作的垂线,垂足依次为,,线段和交于点.求证:.(-37中国国家队选拔赛题)证法1设直线与交于,连,,则知,直线与相截,直线与相截,迭用梅涅劳斯定理,有,.两式相除,得.在与中,有,,即.将其代入①式,得.又由,有.将其代入②式,得,从而,.而,则,故.证法2作高,连,,则,于是,,..又,,,即,故.对应用梅涅劳斯定理的逆定理,知,,三点共线.由,知.例11如图1-14,设点,分别为锐角的内心和垂心,点,分别为边,的中点.已知射线交边于点(),射线交的延长线于点,与相交于,为的外心.试证:,,三点共线的充分必要条件是和的面积相等.(-2003试题)分析首先证,,三点共线.设为的外心,连,,则.又,因此,,,,四点共圆在的外接圆上与重合,,三点共线.其次,再证.并在三角函数式中,用、、分别表示三内角.证法1设的外接圆半径为,的延长线交于,对及截线,应用梅涅劳斯定理,有.①注意到,则.而,由①式,有.从而.②又对及截线,应用梅涅劳斯定理,有.注意到,有,,即.从而.③由,注意②,③,且为锐角.证法2如图1-14,设直线交于,直线交的延长线于.对及截线,应用梅涅劳斯定理,有.④又由及角平分线性质,即有.令,,,则.由④式,有,即.而,则.又,(由题设知).从而.对及截线,应用梅涅劳斯定理,有.将⑤式代入上式,得,.⑥同理.由,注意⑥,⑦.注例11还有其他证法,可参见笔者另文《关于20XX年中国数学奥林匹克第一题》(《中等数学》20XX年第6期).例12如图1-15,凸四边形的一组对边与的延长线交于,且,过作截线交另一组对边所在直线于,,交对角线所在直线于,.求工业化:.证法1如图1-15,对及直线由梅涅劳斯定理得.对及直线由梅涅劳斯定理得.对及直线由梅涅劳斯定理得.由①②③得,所以,所以,故.证法2设与的延长线相交于.和均被直线所截,迭用梅涅劳斯定理,有,①,②由①②,得.③注意到(直线上的托勒密定理),则③式变为.④又由截和截,迭用梅涅劳斯定理,有,.将此结果代入④式整理,即得欲证结论.注当,④式显然成立,故仍有结论成立.此题是二次曲线蝴蝶定理的推论.3.论证点共直线的重要方法例13如图1-16,的内切圆分别切三边,,于点,,,点是的一个内点,的内切圆也在点处与边相切,并与,分别相切于点,.证明:是圆内接四边形.(1995年第36届预选题)证明由切线长定理,知,,,.设的延长线与的延长线交于,对及截线,应用梅涅劳斯定理,有.对应用梅涅劳斯定理的逆定理,知,,三点共线,故由切割线定理有,.以而,即是圆内接四边形.例14如图1-17,中,内的旁切圆切的两边于和,直线与交于;类似地定义,,和,,.求证:,,三点共线.证明由切线长定理,知,,.对与直线,,分别应用梅涅劳斯定理,有,,.上述三式相乘,有.设切于,切于,则由,可得.同理.又由两内公切线长相等,即,故.同理,,.从而,故对用梅涅劳斯的逆定理,知,,三点共直线.例15如图1-18,设的三边,,所在的直线上的点,,共线,并且直线,,关于,,平分线的对称直线,,分别与,,所在直线交于,,,则,,也共线.证明对及截线应用第一角元形式的梅涅劳斯定理,有.由题设知,,,,,,,从而有,即.故由第一角元形式的梅涅劳斯定理,知,,共线.例16在筝形中,,.过上的一点作一条直线分别交、于、,再过点作一条直线分别交、于、.设与分别与交于、,求证:.证明如图1-19,过作的平行线交直线于,再过作的平行线交直线于,则,.进而.所以.又、、分别为三边所在直线上的点,且点不在三边所在的直线上.由第二角元形式的梅涅劳斯定理的逆定理知、、共线.于是,由,.有.因此,.故.注当,为中点时,即为1989年12月冬令营选拔赛试题.例17如图1-20,四边形内接于圆,其边,的延长线交于点,和的延长线交于点,过作该圆的两条切线,切点分别为,.求证:,,三点共线.(1997年试题)证明设圆心为,连交于,连,,,,则由切割线定理和射影定理,有,从而,,,四点共圆,即有,亦即为的内角的外角平分线.又,则平分.设分别交,于,,于是.同理,.于是,,,所以,,.直线与的三边延长线相交,由梅涅劳斯定理,有.对应用梅涅劳斯定理的逆定理,知,,三点共线.所以,,三点共线.注此例的其他证法,可参见第二章例9,第九章例15等.例18已知的内切圆分别切、、于点、、,线段、分别与该内切圆交于点、,若直线与交于圆外一点.证明、、三点共线.(20XX年香港奥林匹克题)证明如图1-21,由切线长定理有.对及截线应用梅涅劳斯定理,有,即有.设与交于点,由,,,有,,.又对及所在边上的点、、,有.于是,由梅涅劳斯定理的逆定理,知、、三点共线.4.注意与其他著名定理配合运用例19在中,已知,,是处接圆的圆心,直线、分别切于点、,与直线、与直线分别交于点、,与交于点,与直线交于点,又设是直线上的点,且使得,(不同于点)是与的交点,是与的交点,令与直线交于点.证明:.(20XX年韩国奥林匹克题)证明如图1-22,设的延长线与(过点)的切线交于点.由帕斯卡定理知、、三点共线,从而点与重合.由切割线窄弹知,.所以,.①设与交于点,对及截线,截线分别应用梅涅劳斯定理,有,.②注意相交弦定理,有.③由①、②、③,得.例20在梯形中,已知、分别为上、下底,为腰上一点,与交于点,为边上一点,满足,与交于点,与交于点.证明:、、三线共点.(20XX年乌克兰奥林匹克题)证明如图1-23,设直线与、与分别交于点、.先证、、三点共线.由,知,,.有.上述三式相乘,有.对应用梅涅劳斯定理的逆定理,知、、三点共线.考虑和,注意到直线与,与、与分别交于点、、,于是由戴沙格定理,知、、三线共点.【模拟实战】习题A1.在中,点在上,,,分别在,上,,,交于点,求.2.在中,,分别是,的中点,与相交于,与相交于,求∶∶.3.是内一点,引线段,和,使在上,在上,在上.已知,,,,,求的面积.(第7届题)4.设凸四边形的对角线和交于点,过作的平行线分别交,于点,,交的延长线于点,是以为圆心,以为半径的圆上一点,求证:.(1996年全国初中联赛题)5.已知,分别是的边,上的点,且,连交边的延长线于点,求.6.设为等腰()的直角边的中点,在上,且,求证:.7.在中,点和顺次三等分,点和顺次三等分,与,分别交于点,,求四边形与的面积之比.8.,,,分别为四边形的四条边,,,上的点,若,,三直线共点,则,,三直线共点或平行.9.设,,分别是的边,和延长线上的点,又,和分别是外接圆的切线.证明:,,三点共线.(1989年新加坡竞赛题)10.求证:三角形两角的平分线与第三角的外角平分线各与对边所在直线的交点共线.11.已知直径为的圆和圆上一点,设,和分别是这个圆在,,处的切线.设是直线与的交点,是直线与的交点,证明:,,三直线共点.(第6届加拿大竞赛题)12.是中任一点,过作的平行线分别交,于,,又过作的平行线,分别交,于,.求证:,,三线共点.13.在中,为中线,为角平分线,为上的点,使.证明:.(第58届莫斯科奥林匹克题)14.直线交直线,分别于,,点与是线段两侧的直线上两点,且.过的直线交于,交于;过的直线交于,交于.连结和,交直线分别于,.求证:.15.设四边形外切于一圆,,,,分别是,,,边上的切点,若直线与相交于点,则,,三点共线.16.设为的内点,过点的直线,,分别垂直于,,,若交于,交于,交于,证明:,,共线.(-28预选题)17.已知的与它的内切圆相切于点.证明:该圆的圆心在与的两个中点,的连线上.18.已知凸四边形内接于,对角线,相交于点,过分别作直线,,,的垂线,垂足分别是,,,.求证:,,三直线共点或互相平行.19.设为圆外切四边形,又,,,与该圆的切点为,,,.求证:,,,共点.习题B1.是内一点,,分别过,且分别与,交于点,,且分别与,交于点,.求证:,,三线共点.2.在中,为锐角,从上任一点作于,于,点是的垂心,求当点在线段上移动时,点的轨迹.(-7试题)3.在正的边,,上有内分点,,将边分成3∶,线段,,相交所成的(交于,交于)是的面积的时,求的值.(1992年日本奥林匹克预选题)4.在中,,点在上,点在上,的延长线交于.若∶∶,则.5.已知点,,在()的边上,,交于,又与的延长线交于,交于,又与的延长线交于.求证:.(《数学通报》问题1353题)6.圆外切四边形中,,,,边上的切点分别为,,,.与的延长线交于点,与延长线相交于点.求证:(Ⅰ),,,四线共点;(Ⅱ),,,四线共点;(Ⅲ),,,四线共点(假定).7.若凸四边形的对角线与互相垂直,且相交于,过点分别作边,,,的垂线,垂足依次为,,,,并分别交,,,边于,,,,再顺次连接,.,,则;.(-22试题的推广)8.面积为1的的边,上分别有点,,线段,相交于点.点,分别在,上移动,但满足四边形的面枳是面积的两倍这一条件,求面积的最大值.(1992年日本奥林匹克题)9.是边长为2的正方形,为的中点,是的中点,和相交于,和相交于.求四边形的面积.10.是凸四边形所在平面上一点,,,,的平分线分别交,,,于点,,,.(Ⅰ)寻找一点,使是平行四边形;(Ⅱ)求所有这样的点的轨迹.(1995年世界城市际联赛题)11.中,,为内角平分线,点在的内部,且,,求证:射线平分边.(《数学教学》问题536题)12.设为非等腰三角形,内心为,(,2,3)为过与和相切的小圆(增加的下标作模3同余),(,2,3)为圆和的另一交点,证明:,,的外心共线.(-38预选题)。
初中数学竞赛重要定理公式(平面几何篇)

初中数学竞赛重要定理、公式及结论平面几何篇【三角形面积公式(包括海伦公式)】)(为内切圆半径,为外接圆半径,边上的高,表示,其中c b a p R BC h c p b p a p p pr C B A c b a C B A R R abc C ab ah S a a ++=---==++++=====21r ))()(()cot cot (cot 4sin sin sin 24sin 21212222ABC Δ【斯特瓦尔特定理】设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2·DC+AC 2·BD -AD 2·BC =BC·DC·BD .【托勒密定理】圆内接四边形对角线之积等于两组对边乘积之和,即AC·BD=AB·CD+AD·BC ,(逆命题成立).(广义托勒密定理)AB·CD+AD·BC ≥AC·BD .【蝴蝶定理】AB 是△O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,则MP=QM .【勾股定理(毕达哥拉斯定理)(广义勾股定理)】(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍.(2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍.【中线定理(巴布斯定理)】设△ABC 的边BC 的中点为P ,则有)BP 2(AP AC AB 2222+=+中线长:【垂线定理】AB ⊥CD ⇔AC 2-AD 2=BC 2-BD 2 高线长: 【角平分线定理】三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例如△ABC 中,AD 平分△BAC ,则 (外角平分线定理) 角平分线长:【正弦定理】 222222a c b m a -+=bSinC cSinB SinA a bc c p b p a p p a h a ===---=))()((2ACAB DC BD =为周长一半)其中p A c b bc a p bcp c b t a (2cos 2)(2+=-+=为三角形外接圆半径)其中,R R C c B b A a (2sin sin sin ===【余弦定理】 【张角定理】【圆周角定理】同弧所对的圆周角相等,等于圆心角的一半.【弦切角定理】弦切角等于夹弧所对的圆周角.【圆幂定理】(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:)【射影定理(欧几里得定理)】直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
初中平面几何竞赛题

初中平面几何竞赛题题目一:已知在△ABC 中,AB = AC,D 是BC 中点,E 是AD 上一点,求证:BE = CE。
解析:因为AB = AC,D 是BC 中点,根据等腰三角形三线合一性质,AD 垂直平分BC。
所以BE = CE(垂直平分线上的点到线段两端距离相等)。
题目二:在矩形ABCD 中,E、F 分别是AB、CD 上的点,且AE = CF,求证:四边形AECF 是平行四边形。
解析:因为四边形ABCD 是矩形,所以AB△CD,AB = CD。
又因为AE = CF,所以BE = DF。
且BE△DF,所以四边形BEDF 是平行四边形,所以BF△DE。
又因为AB△CD,AE = CF,所以四边形AECF 是平行四边形。
题目三:已知在圆O 中,弦AB 与弦CD 相交于点E,且△AEC = 45°,AE = 3,CE = 5,求圆O 的半径。
解析:连接OA、OC,过O 作OF△AB 于F,OG△CD 于G。
则AF = FB,CG = GD。
因为△AEC = 45°,所以△FEG = 45°,则OF = OG。
设圆O 的半径为r,在Rt△AOF 和Rt△COG 中,根据勾股定理可得:AF² + OF² = r²,CG² + OG² = r²。
又因为AF = (AE + EF)/2,CG = (CE - EG)/2,且EF = EG = OF = OG。
设OF = OG = x,则可得方程组:[(3 + x)/2]² + x² = r²,[(5 - x)/2]² + x² = r²。
解方程组可得r 的值。
题目四:在△ABC 中,△BAC = 90°,AD 是BC 边上的高,E 是BC 中点,求证:AE² = DE² + BD²。
初中几何竞赛试题及答案

初中几何竞赛试题及答案1. 已知一个等腰三角形的顶角为120°,求底角的度数。
答案:等腰三角形的底角相等,设底角为x°,则顶角为120°。
根据三角形内角和为180°,有x + x + 120 = 180,解得x = 30°。
所以底角的度数为30°。
2. 一个圆的半径为5cm,求其周长。
答案:圆的周长公式为C = 2πr,其中r为半径。
将半径r = 5cm代入公式,得 C = 2 × 3.14 × 5 = 31.4cm。
所以圆的周长为31.4cm。
3. 一个矩形的长是宽的两倍,若宽为4cm,求矩形的面积。
答案:设矩形的宽为4cm,则长为2 × 4 = 8cm。
矩形的面积公式为A = 长× 宽,代入数值得A = 8 × 4 = 32cm²。
所以矩形的面积为32cm²。
4. 已知一个直角三角形的两条直角边长分别为3cm和4cm,求斜边的长度。
答案:根据勾股定理,直角三角形的斜边长度c满足c² = a² + b²,其中a和b分别为两条直角边的长度。
将a = 3cm和b = 4cm代入公式,得c² = 3² + 4² = 9 + 16 = 25,所以c = √25 = 5cm。
因此,斜边的长度为5cm。
5. 一个正五边形的内角和是多少度?答案:正五边形有5个内角,每个内角的度数可以通过公式(5-2) × 180° ÷ 5计算得出。
代入数值得(5-2) × 180° ÷ 5 = 3 × 180° ÷ 5 = 540° ÷ 5 = 108°。
所以每个内角的度数为108°,正五边形的内角和为5 × 108° = 540°。
全国初中数学竞赛辅导(初3)第17讲平面几何中的定值问题(20200619101924)

第十七讲平面几何中的定值问题定值问题的证明或计算,一般是通过图形的定量,如线段和定角来讨论的.如果问题中已明确给出定值,那么一般通过线段和角的和、差、倍、分的推导或计算来解决;如果问题中未给出定值,可以利用特殊的方法推测出定值,然后再加以一般化的证明.下面举几个例题,说明上述思考方法.例1 如图3-80.已知△ABC中,AB=AC,P是其底边BC上任一点,设AP交△ABC的外接圆于Q点,求证:AP·AQ为定值.分析欲证AP·AQ为定值,我们先用特殊化方法找出这个定值是什么,然后再给以一般化的证明.为此,我们取P与B(或C)重合,则Q点也必与B(或C)重合,则AP·AQ应等于AB2(定值),以下证明这个推测.证连结BQ.因为AB=AC,所以∠ABC=∠ACB.又因为∠ACB=∠AQB,所以∠ABC=∠AQB.又因为∠BAQ=∠PAB,所以所以 AP·AQ=AB2(定值).注意如果连结QC,将怎样证明?请读者思考.例2 如图3-81.已知△ABC中,AB=AC,如果直线EF,MN都垂直于BC,试证明:不论MN,EF怎样平行移动,只要MN,EF之间的距离不变,五边形AMNFE的周长是一个定值.分析从图3-81中可以发现,如果引AD⊥BC于D,由已知条件可知AB(或AC),AD,NF,BD(或CD)都为定值,因此,若五边形AMNFE的周长转化为以上各线段的表达式,则可判定其为定值.证作AD⊥BC于D,则所以所以又因为所以所以所以由于△ABC为确定的等腰(AB=AC)三角形,所以AD,BD,CD,AB为定值,又因为EF,MN之间距离为定长,所以NF为定值.所以五边形AMNFE的周长为定值.例3 设OA,OB是已知圆O的任意两条半径,过B引BE⊥OA于E,过E作EP⊥AB于P.求证:OP2+EP2为定值(图3-82).分析由已知A,B为⊙O上任意两点,如果固定A,让B在圆上移动,当B点移动到半圆中点时,BE变成了半径r,E与O重合,证延长OP交⊙O于C,D(图3-82).因为在直角三角形AEB中,∠AEB=90°,EP⊥AB于P,所以EP2=AP·PB=CP·PD=(OC-OP)·(OD+OP)=r2-OP2,例4 若P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R(如图3-84),分析根据已知,AC为过圆O内定点P的任意一弦,为了找定值,使AC特殊化,令AC为直径,则P是直径AC上的一个定点,这时由于PC,PQ同时垂直于切线,所以Q,C两点重合.同理A,R也重合(图3-85).于是,下面证明这个推测结论.证在图3-84中,作直径AB,连BC,并过OP作直径EF.由于∠ACB=90°,于是△ABC∽△APR.例4 若P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R(如图3-84),分析根据已知,AC为过圆O内定点P的任意一弦,为了找定值,使AC特殊化,令AC为直径,则P是直径AC上的一个定点,这时由于PC,PQ同时垂直于切线,所以Q,C两点重合.同理A,R也重合(图3-85).于是,下面证明这个推测结论.证在图3-84中,作直径AB,连BC,并过OP作直径EF.由于∠ACB=90°,于是△ABC∽△APR.例4 若P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R(如图3-84),分析根据已知,AC为过圆O内定点P的任意一弦,为了找定值,使AC特殊化,令AC为直径,则P是直径AC上的一个定点,这时由于PC,PQ同时垂直于切线,所以Q,C两点重合.同理A,R也重合(图3-85).于是,下面证明这个推测结论.证在图3-84中,作直径AB,连BC,并过OP作直径EF.由于∠ACB=90°,于是△ABC∽△APR.例4 若P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R(如图3-84),分析根据已知,AC为过圆O内定点P的任意一弦,为了找定值,使AC特殊化,令AC为直径,则P是直径AC上的一个定点,这时由于PC,PQ同时垂直于切线,所以Q,C两点重合.同理A,R也重合(图3-85).于是,下面证明这个推测结论.证在图3-84中,作直径AB,连BC,并过OP作直径EF.由于∠ACB=90°,于是△ABC∽△APR.。
平面几何(竞赛题定理)

1 平面几何的定理模型1:【内心与外接圆】【内心与外接圆】设设I 为△ABC 的内心,射线AI 交△ABC 外接圆于A ′,则有A ′I =A ′B =A ′C .换言之,点A ′必是△IBC 之外心(内心的等量关系之逆也成立). 模型2【内切圆与旁切圆】三角形的一条内角平分线与另两个内角的外角平分线相交于一点,是旁切圆的圆心,称为旁心.旁心常常与内心联系在一起,旁心还与三角形的半周长关系密切. 性质:(1)设AI A 的连线交△ABC 的外接圆于D ,则DI A =DI =DB =DC ;(2)△ABC 的∠A 的内角平分线交外接圆于点D ,以点D 为圆心,DC 为半径作圆,与直线AD 相交于两点I 和I A ,则这两点I 和I A 恰好是△ABC 的内心和旁心。
模型3【垂心性质】△ABC 垂心H 关于三边的对称点在△ABC 的外接圆上,关于三边中点的对称点在△ABC 的外接圆上;三角形任一顶点到垂心的距离等于外心到对边的距离的2倍(AH =|2RcosA |)。
A'IAB CI ADIA BCH'MB'F E D H OCA B模型4【圆幂定理】【圆幂定理】从一定点P 引直线与定圆O 交于两点A 、B ,(A 、B 可能重合为一个点),(记OP =d ), 则P A ·PB 等于点P 对于⊙O 的幂:d 2-r 2所以上面的几个定理(相交弦定理、切割线定理、割线定理及切线长定理)也统称圆幂定理.也统称圆幂定理.ïîïíì<=>=在圆内,在圆上,在圆外,的幂P P P P 000模型5【多圆问题】【多圆问题】 相交两圆的性质相交两圆的性质 性质1:相交两圆的连心线垂直平分公共弦。
:相交两圆的连心线垂直平分公共弦。
性质2:相交两圆的公共弦所在直线平分外公切线线段。
:相交两圆的公共弦所在直线平分外公切线线段。
初中数学竞赛:几何的定值与最值(附练习题及答案)

初中数学竞赛:几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明. 几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法;2.几何定理(公理)法;3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、 逻辑推理与合情想象相结合等思想方法.【例题就解】【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 .思路点拨 如图,作CC ′⊥AB 于C ,DD ′⊥AB 于D ′,DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=21AB 一常数,当CQ 越小,CD 越小,本例也可设AP=x ,则PB=x 10,从代数角度探求CD 的最小值.注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指:(1)中点处、垂直位置关系等;(2)端点处、临界位置等.【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T ,圆交AC 、BC 于M 、N ,则对于所有可能的圆的位置而言, MTN 为的度数( )A .从30°到60°变动B .从60°到90°变动C .保持30°不变D .保持60°不变⌒思路点拨 先考虑当圆心在正三角形的顶点C 时,其弧的度数,再证明一般情形,从而作出判断.注:几何定值与最值问题,一般都是置于动态背景下,动与静是相对的,我们可以研究问题中的变量,考虑当变化的元素运动到特定的位置,使图形变化为特殊图形时,研究的量取得定值与最值.【例3】 如图,已知平行四边形ABCD ,AB=a ,BC=b (a >b ),P 为AB 边上的一动点, 直线DP 交CB 的延长线于Q ,求AP+BQ 的最小值.思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+ (当且仅当b a =时取等号)来求最小值.【例4】 如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A 、B 的点M ,设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N ,证明:线段AK 和BN 的乘积与M 点的选择无关. 思路点拨 即要证AK ·BN 是一个定值,在图形中△ABC 的边长是一个定值,说明AK ·BN 与AB 有关,从图知AB 为△ABM 与△ANB 的公共边,作一个大胆的猜想,AK ·BN=AB 2,从而我们的证明目标更加明确.⌒注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.【例5】已知△XYZ是直角边长为1的等腰直角三角形(∠Z=90°),它的三个顶点分别在等腰Rt△ABC(∠C=90°)的三边上,求△ABC直角边长的最大可能值.思路点拨顶点Z在斜边上或直角边CA(或CB)上,当顶点Z在斜边AB上时,取xy的中点,通过几何不等关系求出直角边的最大值,当顶点Z在(AC或CB)上时,设CX=x,CZ=y,建立x,y的关系式,运用代数的方法求直角边的最大值.注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值;(2)构造二次函数求几何最值.专题训练1.如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为,最小值为.2.如图,∠AOB=45°,角内有一点P,PO=10,在角的两边上有两点Q,R(均不同于点O),则△PQR的周长的最小值为.3.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=5,CD=4,P 在直线MN 上运动,则PB PA -的最大值等于 . 4.如图,A 点是半圆上一个三等分点,B 点是弧AN 的中点,P 点是直径MN 上一动点,⊙O 的半径为1,则AP+BP 的最小值为( )A .1B .22 C .2 D .13-5.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( )A .212π+B .2412π+C .214π+D .242π+6.如图、已知矩形ABCD ,R ,P 户分别是DC 、BC 上的点,E ,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A .线段EF 的长逐渐增大B .线段EF 的长逐渐减小C .线段EF 的长不改变D .线段EF 的长不能确定7.如图,点C 是线段AB 上的任意一点(C 点不与A 、B 点重合),分别以AC 、BC 为边在直线AB 的同侧作等边三角形ACD 和等边三角形BCE ,AE 与CD 相交于点M ,BD 与CE 相交于点N .(1)求证:MN ∥AB ;(2)若AB 的长为l0cm ,当点C 在线段AB 上移动时,是否存在这样的一点C ,使线段MN 的长度最长?若存在,请确定C 点的位置并求出MN 的长;若不存在,请说明理由.(2002年云南省中考题)8.如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足,求证:不管ST 滑到什么位置,∠SPM 是一定角.9.已知△ABC 是⊙O 的内接三角形,BT 为⊙O 的切线,B 为切点,P 为直线AB 上一点,过点P 作BC 的平行线交直线BT 于点E ,交直线AC 于点F .(1)当点P 在线段AB 上时(如图),求证:PA ·PB=PE ·PF ;(2)当点P 为线段BA 延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果不成立,请说明理由.10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE ,其中AF=2,BF=l ,在AB 上的一点P ,使矩形PNDM 有最大面积,则矩形PNDM 的面积最大值是( )A .8B .12C .225D .1411.如图,AB 是半圆的直径,线段CA 上AB 于点A ,线段DB 上AB 于点B ,AB=2;AC=1,BD=3,P 是半圆上的一个动点,则封闭图形ACPDB 的最大面积是( )A .22+B .21+C .23+D .23+12.如图,在△ABC 中,BC=5,AC=12,AB=13,在边AB 、AC 上分别取点D 、E ,使线段DE 将△ABC 分成面积相等的两部分,试求这样线段的最小长度.13.如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.(1)设矩形的边AB=x(米),AM=y(米),用含x的代数式表示y为.(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.①设该工程的总造价为S(元),求S关于工的函数关系式.②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?若能,请列出所有可能的设计方案;若不能,请说明理由.16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).参考答案。
初中竞赛平面几何数学竞赛题目
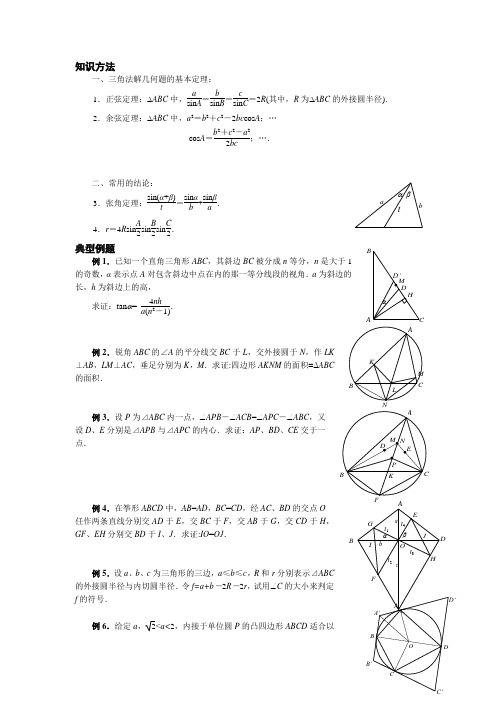
一、三角法解几何题的基本定理:1.正弦定理:∆ABC中,asin A=bsin B=csin C=2R(其中,R为∆ABC的外接圆半径).2.余弦定理:∆ABC中,a2=b2+c2-2bc cos A;…cos A=b2+c2-a22bc;….二、常用的结论:3.张角定理:sin(α+β)t=sinαb+sinβa.4.r=4R sin A2sinB2sinC2.典型例题例1.已知一个直角三角形ABC,其斜边BC被分成n等分,n是大于1的奇数,α表示点A对包含斜边中点在内的那一等分线段的视角.a为斜边的长,h为斜边上的高,求证:tanα=4nha(n2-1).例2.锐角ABC的∠A的平分线交BC于L,交外接圆于N,作LK ⊥AB,LM⊥AC,垂足分别为K,M.求证:四边形AKNM的面积=ΔABC 的面积.例3.设P为⊿ABC内一点,∠APB-∠ACB=∠APC-∠ABC,又设D、E分别是⊿APB与⊿APC的内心.求证:AP、BD、CE交于一点.例4.在筝形ABCD中,AB=AD,BC=CD,经AC、BD的交点O 任作两条直线分别交AD于E,交BC于F,交AB于G,交CD于H,GF、EH分别交BD于I、J.求证:IO=OJ.例5.设a、b、c为三角形的三边,a≤b≤c,R和r分别表示⊿ABC 的外接圆半径与内切圆半径.令f=a+b-2R-2r,试用∠C的大小来判定f的符号.例6.给定a,2<a<2,内接于单位圆P的凸四边形ABCD适合以tαβabAB CAKLMNt3t2t4t1JHEFGBCDAOαβabcIC‘B‘BCDAOA‘⑴ 圆心在这凸四边形内部;⑵ 最大边长为a ,最小边长为4-a 2 ,过点A 、B 、C 、D 依次作圆P 的四条切线l A 、l B 、l C 、l D ,已知l A 与l B ,l B 与l C ,l C 与l D ,l D 与l A 分别交于点A',B',C',D'.求面积之比S 四边形A 'B 'C 'D 'S 四边形ABCD的最大值与最小值.例7.一条直线l 与具有圆心O 的圆ω不相交,E 是l 上的点,OE ⊥l ,M 是l 上不同于E 的点,从M 作w 的两条切线切ω于点A 和B ,C 是MA 的点,使得EC 垂直于MA ,D 是MB 上的点,使得ED 垂直于MB ,直线CD 交OE 于F .求证点F的位置不依赖于点M 的位置.例8.凸四边形的四个角分别为 2α, 2β, 2γ, 2δ,四条边分别为l , m , n , k .求证它的面积 S = (l + m + n + k ) 24(cot α + cot β + cot γ + cot δ) -(l + n -m -k ) 24(tan α + tan β + tan γ + tan δ).例9.在△ABC 的三边中点D 、E 、F 向内切圆引切线,设所引的切线分别与EF 、FD 、DE 交于I 、L 、M .求证:I 、L 、M 三点共线.例10.已知平面上一个半径为R 的定圆⊙O ,A 、B 是⊙O 上两个定点,且A 、B 、O 不共线,C 为异于A 、B 的点,过点A 作⊙O 1与直线BC 切于点C ,过点B 作⊙O 2与直线AC 切于点C ,⊙O 1与⊙O 2相交于DC (异于C 点).求证:(1) CD ≤ R ;(2) 当点C 在⊙O 上移动时,且与A 、B 不重合时,直线CD 过一定点.例11.已知P 是△ABC 内一点,过P 作BC 、CA 、AB 的垂线,其垂足分别为D 、E 、F ,又Q 是△ABC 内的一点,且使得∠ACP = ∠BCQ , ∠BAQ = ∠CAP .证明∠DEF = 90︒的充要条件是Q 为△BDF 的垂心.例12.设点D 、E 、F 分别是△ABC 的边BC 、CA 、AB 上的点,并且△AEF 、△BFD 、△CDE 的内切圆都与△DEF 的内切圆外切.求证AD 、BE 、CF 三线共点.12AB CDE MF OPP lDL MNBαKβA δγrrr r ●●●●BDI E F●●●OACBDEF AC P QXYO 1●3●2M●●O O O ●●I HA J A21MBCO POO ●1.设M 是⊿ABC 的AB 边上的任一点,r 1、r 2、r 分别是ΔAMC 、ΔBMC 、ΔABC 的内切圆半径,ρ1、ρ2、ρ分别是这些三角形在∠ACB 内部的旁切圆半径.求证:r 1ρ1·r 2ρ2=rρ.2.设正方形ABCD 边长为1,试求其内接正三角形面积的最大值与最小值.3.在∠A 内有一定点P ,过点P 作直线交角的两边于B 、C ,问何时PB ·PC 取最小值. 4.在平面上有一个定点P ,考虑所有可能的正三角形ABC ,其中AP =3,BP =2,求CP 长度的最大值.5.设⊿ABC 的三个内角A 、B 、C 分别为α、β、γ,求证:在AB 上有一点D ,使CD 为AD 与BD 的几何中项的充要条件为sin αsin β≤sin 2γ2.6.在梯形ABCD 中(AB ∥CD ),两腰AD 、BC 上分别有点P 、Q 满足∠APB =∠CPD ,∠AQB =∠CQD .求证:点P 与Q 到梯形对角线的交点O 的距离相等.7.在一个非钝角⊿ABC 中,AB >AC ,∠B =45︒,O 与I 分别是⊿ABC 的外心与内心,且2 OI =AB -AC ,求sin A .8.ABCD 内接于圆,AB ∩CD = E ,AD ∩BC = F ,M 、N 为AC 、BD 中点,已知AC = a , BD = b ,求MNEF. 9.△ABC 内心为I ,A 对应的旁心为I a ,II a 分别交BC 、⊙ABC 于A '、M ,N 为 ⌒ABM 的中点,NI 、NI a 分别交⊙ABC 于S 、T .求证S 、A '、T 三点共线.10.设△ABC 内切圆与BC 、CA 、AB 相切于D 、E 、F ,一圆与△ABC 内切圆切于D ,并与△ABC 外接圆切于K ,点M 、N 类似定义.求证DK 、EM 、FN 相交于△DEF 的欧拉线上.γ2γ1βαBCAD。
初中数学竞赛经典几何定理

AB2 = BD2 + AD2
= BD2 +( AC - CD)2
= BD2 + AC2 + CD2 - 2 AC ⋅ CD
= BC2 + AC2 - 2AC ⋅ CD
= a2 + b2 - 2ab ⋅ cosC
即
c2 = a2 + b2 - 2ab ⋅ cosC
那么(*)式得证,则同理其余两式亦得证.
OP2
=
ìïïïïïíïïïïïîRRR222
- PA⋅ PB ( 当P在圆内) ( 当P在圆上) + PA⋅ PB ( 当P在圆外)
证明
作 OK ^ AB 于 K,连 OB,则由垂径定理知 BK = AK ,当 P 在圆内时,
R2 - OP2 = BO2 - OP2 = BK 2 - PK 2
= (BK - PK )( AK + PK )
BD ⋅ AE ⋅ CF =1 AD CE BF
时,可延长 DE 交 BC 的延长线于 F’,那么由 Menelaus
定理
BD AD
⋅
AE CE
⋅
CF BF
' '
=
1
可知
CF = CF ' BF BF '
CF CF '
=
BF BF '
CF CF '
=
BF BF '
=
BF - CF BF '- CF
(中线长公式) (角平分线长公式)
(圆幂定理)
7. 共边比例定理 如图1,△XAB 和△YAB 具有公共边 AB,△XYA 和△XYB 具有公共边 XY,XY 交 AB 于
初中竞赛重要数学公式归纳总结

初中竞赛重要数学公式归纳总结初中数学竞赛圆的方程公式1、圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2。
2、圆的一般方程:方程x^2+y^2+Dx+Ey+F=0可变形为(x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4.故有:(1)、当D^2+E^2-4F 0时,方程表示以(-D/2,-E/2)为圆心,以(√D^2+E^2-4F)/2为半径的圆;(2)、当D^2+E^2-4F=0时,方程表示一个点(-D/2,-E/2);(3)、当D^2+E^2-4F 0时,方程不表示任何图形。
3、圆的参数方程:以点O(a,b)为圆心,以r为半径的圆的参数方程是x=a+r_cosθ, y=b+r_sinθ, (其中θ为参数)圆的端点式:若已知两点A(a1,b1),B(a2,b2),则以线段AB为直径的圆的方程为 (x-a1)(x-a2)+(y-b1)(y-b2)=0圆的离心率e=0,在圆上任意一点的曲率半径都是r。
经过圆 x^2+y^2=r^2上一点M(a0,b0)的切线方程为 a0_x+b0_y=r^2在圆(x^2+y^2=r^2)外一点M(a0,b0)引该圆的两条切线,且两切点为A,B,则A,B两点所在直线的方程也为 a0_x+b0_y=r^2初中数学竞赛重要定理公式代数篇【乘法公式】完全平方公式:(a±b)2=a2±2ab+b2,平方差公式:(a+b)(a-b)=a2-b2,立方和(差)公式:(a±b)(a2 ab+b2)=a3±b3多项式平方公式:(a+b+c+d)2=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd二项式定理:(a±b)3=a3±3a2b+3ab2±b3(a±b)4=a4±4a3b+6a2b2±4ab3+b4)(a±b)5=a5±5a4b+10a3b2±10a2b3+5ab4±b5)…………在正整数指数的条件下,可归纳如下:设n为正整数(a+b)(a2n-1- a2n-2b+a2n-3b2- …+ab2n-2- b2n-1)=a2n-b2n(a+b)(a2n-a2n-1b+a2n-2b2n-…-ab2n-1+b2n)=a2n+1+b2n+1类似地:(a-b)(a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)=a n-b n公式的变形及其逆运算由(a+b)2=a2+2ab+b2得a2+b2=(a+b)2-2ab由(a+b)3=a3+3a2b+3ab2+b3=a3+b3+3ab(a+b) 得a3+b3=(a+b)3-3ab(a+b) 由公式的推广③可知:当n为正整数时a n-b n能被a-b 整除,a2n+1+b2n+1能被a+b整除,a2n-b2n能被a+b 及a-b 整除。
人教版 初三数学竞赛专题:平面几何的定值问题(包含答案)
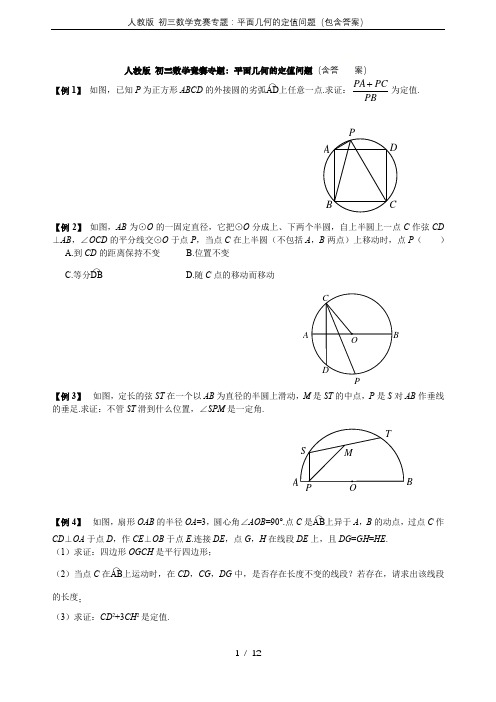
人教版 初三数学竞赛专题:平面几何的定值问题(含答案)【例1】 如图,已知P 为正方形ABCD 的外接圆的劣弧AD⌒上任意一点.求证:PA PC PB为定值.【例2】 如图,AB 为⊙O 的一固定直径,它把⊙O 分成上、下两个半圆,自上半圆上一点C 作弦CD ⊥AB ,∠OCD 的平分线交⊙O 于点P ,当点C 在上半圆(不包括A ,B 两点)上移动时,点P ( ) A.到CD 的距离保持不变 B.位置不变C.等分DB⌒ D.随C 点的移动而移动【例3】 如图,定长的弦ST 在一个以AB 为直径的半圆上滑动,M 是ST 的中点,P 是S 对AB 作垂线的垂足.求证:不管ST 滑到什么位置,∠SPM 是一定角.【例4】 如图,扇形OAB 的半径OA =3,圆心角∠AOB =90°.点C 是AB⌒上异于A ,B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E .连接DE ,点G ,H 在线段DE 上,且DG =GH =HE .(1)求证:四边形OGCH 是平行四边形;(2)当点C 在AB ⌒上运动时,在CD ,CG ,DG 中,是否存在长度不变的线段?若存在,请求出该线段的长度;(3)求证:CD 2+3CH 2是定值.P AB CDAPB【例5】 如图1,在平面直角坐标系xOy 中,点M 在x 轴的正半轴上,⊙M 交x 轴于A ,B 两点,交y 轴于C ,D 两点,且C 为弧AE 的中点,AE 交y 轴于G 点.若点A 的坐标为(-2,0),AE =8. (1)求点C 的坐标;(2)连接MG ,BC ,求证:MG ∥BC ;(3)如图2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.(图1)(图2)【例6】 如图,已知等边△ABC 内接于半径为1的圆O ,P 是⊙O 上的任意一点.求证:P A 2+PB 2+PC 2为定值.【能力训练】1.如图,点A ,B 是双曲线xy 3上的两点,分别经过A ,B 两点向x 轴,y 轴作垂线段.若S 阴影=1,则BOACE HG D A=+21S S _______.(第1题图) (第3题图) (第4题图)2.从等边三角形内一点向三边作垂线段,已知这三条垂线段的长分别为1,3,5,则这个等边三角形的面积是__________.3.如图,OA ,OB 是⊙O 任意两条半径,过B 作BE ⊥OA 于E ,又作OP ⊥AB 于P ,则定值OP 2+EP 2为_________.4.如图,在菱形ABCD 中,∠ABC =120°,F 是DC 的中点,AF 的延长线交BC 的延长线于点E ,则直线BF 与直线DE 所夹的锐角的度数为( )A.30°B.40°C.50°D.60°5.如图,在⊙O 中,P 是直径AB 上一动点,在AB 同侧作A A '⊥AB ,AB B B ⊥',且A A '=AP ,B B '=BP .连接B A '',当点P 从点A 移动到点B 时,B A ''的中点的位置( ) A .在平分AB 的某直线上移动 B.在垂直AB 的某直线上移动 C.在弧AMB 上移动 D.保持固定不移动(第5题图) (第6题图) 6.如图,A ,B 是函数xky =图象上的两点,点C ,D ,E ,F 分别在坐标轴上,且分别与点A ,B ,O 构成正方形和长方形.若正方形OCAD 的面积为6,则长方形OEBF 的面积是( ) A.3 B.6 C.9 D.127.(1)经过⊙O 内或⊙O 外一点P 作两条直线交⊙O 于A ,B 和C ,D 四点,得到如图①~⑥所表示的六种不同情况.在六种不同情况下,P A ,PB ,PC ,PD 四条线段之间在数量上满足的关系式可以用同一个式子表示出来.请你首先写出这个式子,然后只就如图②所示的圆内两条弦相交的一般情况给出它的证明.A ABCDEFAB'(2)已知⊙O 的半径为一定值r ,若点P 是不在⊙O 上的一个定点,请你过点P 任作一直线交⊙O 于不重合的两点E ,F . PE ·PF 的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.8.在平面直角坐标系中,边长为2的正方形OABC 的两顶点A ,C 分别在y 轴,x 轴的正半轴上,点O 在原点,现将正方形OABC 绕O 点顺时针旋转,当A 点第一次落在直线x y =上时停止旋转.旋转过程中,AB 边交直线x y =于点M ,BC 边交x 轴于点N .(1)求OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 与AC 平行时,求正方形OABC 旋转度数;(3)设△MBN 的周长为P ,在正方形OABC 旋转的过程中,P 值是否有变化?请证明你的结论.⑥⑤④③②①P(B )A PB9.如图,AB 是半圆的直径,AC ⊥AB ,AC =AB .在半圆上任取一点D ,作DE ⊥CD ,交直线AB 于点E ,BF ⊥AB ,交线段AD 的延长线于点F .(1)设弧AD 是x °的弧,若要点E 在线段BA 的延长线上,则x 的取值范围是_______.(2)不论点D 取在半圆的什么位置,图中除AB =AC 外,还有两条线段一定相等.指出这两条相等的线段,并予证明.(第9题图) (第10题图)(第11题图)10.如图,内接于⊙O 的四边形ABCD 的对角线AC 与BD 垂直相交于点K ,设⊙O 的半径为R .求证: (1)2222DK CK BK AK +++是定值; (2)2222DA CD BC AB +++是定值.11.如图,设P 是正方形ABCD 外接圆劣弧弧AB 上的一点,求证:DPCP BPAP ++的值为定值.1.等腰△ABC 的底边BC 为定长2,H 为△ABC 的垂心.当顶点A 在保持△ABC 为等腰三角形的情况下 改变位置时,面积S △ABC ·S △HBC 的值保持不变,则S △ABC ·S △HBC =________.2.已知A ,B ,C ,D ,E 是反比例函数xy 16=(x >0)图象上五个整数点(横、纵坐标均为整数),分别过这些点向横轴或纵轴作垂线段,以垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是__________(用含π的代数式表示).P D CB A A折叠,使点A ,B 落在六边形ABCDEF 的内部,记∠C +∠D + )A. ∠1+∠2=900°-2α B. ∠1+∠2=1080°-2α C. ∠1+∠2=720°-α D. ∠1+∠2=360°-21α(第3题图) (第4题图)4.如图,正△ABO 的高等于⊙O 的半径,⊙O 在AB 上滚动,切点为T ,⊙O 交AO ,BO 于M ,N ,则弧MTN ( )A.在0°到30°变化B.在30°到60°变化C.保持30°不变D.保持60°不变5.如图,AB 是⊙O 的直径,且AB =10,弦MN 的长为8.若MN 的两端在圆上滑动时,始终与AB 相交,记点A ,B 到MN 的距离分别为h 1,h 2,则∣h 1-h 2∣等于( )A.5B.6C.7D.8(第5题图) 12GF EDCHBAB6.如图,已知△ABC 为直角三角形,∠ACB =90°,AC =BC ,点A ,C 在x 轴上,点B 坐标为(3,m )(m >0),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B ,D . (1)求点A 的坐标(用m 表示) (2)求抛物线的解析式;(3)设点Q 为抛物线上点P 至点B 之间的一动点,连接PQ 并延长交BC 于点E ,连接BQ 并延长交AC 于点F .试证明:FC (AC +EC )为定值.7.如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A ,B 的点M .设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N .证明线段AK 和BN 的乘积与M 点的选择无关.(第7题图) (第8题图)8.如图,设H 是等腰三角形ABC 两条高的交点,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积S △ABC ·S △HBC 的值变小、变大,还是不变?证明你的结论.9.如图,在平面直角坐标系xOy 中,抛物线10941812--=x x y 与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线BC ,交抛物线于点C ,连接AC .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动.点P 停止运动时,点Q 也同时停止运动.线段OC ,PQ 相交于点D ,过点D 作DE ∥OA ,交CA 于E ,射线QE 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒). (1)求A ,B ,C 三点的坐标和抛物线的顶点坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程; (3)当290<<t 时,△PQF 的面积是否总是定值?若是,求出此值;若不是,请说明理由; (4)当t 为何值时,△PQF 为等腰三角形,请写出解答过程.NKMB AC HCBA(第9题图) (第10题图) 10.已知抛物线C 1:12121+-=x x y ,点F (1,1). (1)求抛物线C 1的顶点坐标;(2)若抛物线C 1与y 轴的交点为A ,连接AF ,并延长交抛物线C 1于点B ,求证:211=+BFAF . (3)抛物线C 1上任意一点P (x P ,y P )(0<x P <1),连接PF ,并延长交抛物线C 1于点 Q (x Q ,y Q ),试判断211=+QFPF 是否成立?请说明理由.11.已知A ,B 是平面上的两个顶点,C 是位于AB 一侧的一个动点,分别以AC ,BC 为边在△ABC 外作正方形ACDE 和正方形BCFG .求证:不论C 在直线AB 同一侧的任何位置,EG 的中点P 的位置不变. 参考答案例 1 延长PC 至E ,使CE =AP ,连结BE ,则△BCE ≌△BAP ,及△PBE 为等腰直角三角形,故PA PC CE PC PEPB PB PB++=== 例2 B 提示:连结AC ,BC ,可以证明P 为APB 的中点. 例3 ∵SP ⊥OP ,OM ⊥ST ,∴S ,M ,O ,P 四点共圆,于是∠SPM =∠SOM =12∠SOT 为定角. 例4 (1)连结OC 交DE 于M ,则OM =CM , EM =DM ,而DG = HE ,则HM =GM 故四边形OGCH 是平行四边形. (2)DG 不变.DE =OC =OA =3 .DG =13DE =13×3=1. (3)设CD =x ,延长OG 交CD 于N ,则CN =DN =12 x ,229CE x =- , 2214DN x = .∴22394ON x =-,而ON =32CH ,∴22143CH x =-.故CD 2+3CH 2=x 2+3(4-13x 2)=x 2+12-x 2为定值. 例5 ⑴C (0,4) ⑵先求得AM =CM =5,连接MC 交AE 于N ,由△AO G ∽△ANM ,得OG AO MN AN =,O G =32,38OG OM OC OB ==,又∠BOC =∠G OM ,∴△G OM ∽△COB ,∠G MO =∠CBO ,得M G ∥BC .⑶连结DM ,则DM ⊥PD ,DO ⊥PM ,DO 2=OM •OP ,OP =163.动点F 在⊙M 的圆周上运动时,从特殊位置探求OFPF的值.当F 与点A 重合时,2316523OF AO PF AP ===-;当点F 与点B 重合时,8316583OF OB PF PB ===+;当点F 不与点A ,B 重合时,连接OF 、PF 、MF ,∴DM 2=MO •MP ,∴FM 2=MO •MP ,即FM MPOM FM=,又∠OMP =∠FMP ,∴△MFO ∽△MPF ,35OF MO PF MF ==,故OF PF 的比值不变,比值为35. 例6 ∠BPC =120°,在△BPC 中,由余弦定理得BC 2=PB 2+PC 2-2PB •PC =BC 2,又由上托勒密定理得BC •P A +PC •AB ,而AB =BC =AC ,∴P A =PB +PC ,从而P A 2+ PB 2+ PC 2= (PB +PC )2+ PB 2+ PC 2=2 (PB 2+PC 2+PB •PC )=2BC 2=2×()23=6.故P A 2+PB 2+PC 2为定值.A 级 1.4提示:∵S 1+S 阴= S 2+S 阴=xy =3,∴S 1+S 2=2xy -2S 阴=6-2=4.2.273 提示:1+3+5=9是等边三角形的高. 3.r 2提示:先考查OB 与OA 垂直的情形.4.D 提示:延长BF 交DE 于点M ,连接BD ,则△BCD 为等边三角形,BF 平分∠CBD .∵F 为CD 中点,且AD ∥CE ,∴△ADF 与△ECF 关于点F 中心对称.∴CE =AD =CD ,∴∠CEM=30°,∠DMF=60°,5.D 提示:A′B′的中点均在⊙O 的上半圆的中点处. 6.B 提示:S 正方形OCAD =OD •OC =A A x y k ==6,∴S OEBF =OE •OF =x B •y B k ==6. 7.⑴略⑵当点P在⊙O 内时,过P 作直径CD ,则PE •PF =PD •PC =r 2-OP 2为定值;当点P 在⊙O 外时,PE •PF 为定值22OP r -.结论:过不在圆上的一个定点任作一条直线与圆相交,则这点到直线与圆相交点的两条线段长的积为定值. 8.⑴2π⑵22.5° ⑶P 值无变化.理由如下:如图,延长BA 交y 轴于E 点,可证明△OAE ≌△OCN ,得OE =ON ,AE =CN ,又∠MOE =∠MON =45°,OM =ON ,∴△OME ≌△OMN ,得MN =ME =AM +AE =AM +CN .∴P =MN +BN +BM =AM +CM +CN +BN +BM =AB +AC =4.9.⑴0<x <90 ⑵BE =BF 提示:连接BD ,可证明△BDF ∽△ADB ,△BDE ∽△ADC . 10.⑴作OP ⊥BD 于P ,OQ ⊥AC 于Q ,连接AO ,则AO 2=()()221122BK DK CK AK ⎡⎤⎡⎤-++⎢⎥⎢⎥⎣⎦⎣⎦,又AK •CK =BK •DK ,得AK 2+BK 2+CK 2+DK 2=4R 2为定值. ⑵作直径DE ,连接AE ,BE ,CE ,AB 2+CD 2=4R 2,AD 2+BC 2=4R 2,故AB 2+BC 2+CD 2+DA 2=8K 2为定值. 11.设正方形的边长为a ,根据托勒密定理,对于四边形APBC 和四边形APBD ,有CP •a =AP •a +BP •2a ,DP •a =BP •a +AP •2a ,两式相加并整理得(CP +DP )a =(AP +BP )(a +2a ),从而21AP BPCP DP+=-+为定值.B 级1.1 提示:不妨设∠A 为锐角,AD ,BE ,CF 为△ABC 的三条高,H 为垂心,由AB =AC 知∠HBD =∠HCD =∠HAE ,∠HDC =∠CDA =90°,故R t △CHD ∽R t △ACD .∴AD DC DC HD =,即AD •HD =DC 2=14BC 2=1.∴S △ABC •S △HBC =2111224BC AD BC HD BC ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭=1.当∠A ≥90°时,结论成立.2.13π-26 提示:∵A ,B ,C ,DE 是反比例函数y =16x(x >0)图象上五个整数点,由图象可知,这些点的横坐标分别为1,2,4,8,16.∴五个正方形的边长分别为1,3,4,2,1.∴这五人橄榄形的面积总和是2221111112211122222444424242πππ⎡⎤⎛⎫⎛⎫⎛⎫⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=5π-10+8π-16=13π-26. 3.B 提示:如图,设F A 的延长线与CB 的延长线交于点P ,G A ′的延长线与HB ′的延长线交于点P ′.由对称性可知∠1=2∠APP ′,∠2=2∠BPP ′.∴∠1+∠2=2∠APB .∵∠APB =540°-α,∴∠1+∠2=1080°-2α. 4.D 5.B 提示:如图,设AB 与MN 交于点C ,过点O 作OD ⊥MN 于D ,连接FO 并延长交EB 于G .由垂径定理,得OD =2254-=3.由△AFO ≌△B G O ,得AF =B G ,即h 1=B G .由AF ⊥MN ,BE ⊥MN ,得△FOD ∽△F G E .∴12OD FO GE FG ==.∴E G =2OD =6,∴12h h AF BE -=-=E G =6. 6.⑴A (3-m ,0) ⑵y =x 2-2x +1 ⑶过点Q 作QM ⊥AC 于M ,过点Q 作QN ⊥BC 于N ,设Q 点的坐标为(x ,x 2-2x +1),则QM =CN =(x -1)2,MC =QN=3-x .∵QM ∥CE ,∴PQM ∽△PEC .∴QM PMEC PC=,即()2112x x EC--=,得EC =2(x -1).∵QN ∥CF ,∴△BQN ∽△BFC .∴QN BN FC BC =,即()24134x x FC ---=,得FC =41x +.又AC =4,∴FC (AC +EC )=()44211x x +-⎡⎤⎣⎦+=8为定值. 7.提示:易证△ABK ∽△BNA ,故AK •BN =AB 2为定值,即AK 与BN 的乘积与M 点的选择无关. 8.提示:S △ABC •S △HBC =116BC 4,由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积S △ABC •S △HBC 保持不变. 9.⑴A (18,0),B (0,-10),顶点坐标为(4,-989)⑵若四边形PQCA 为平行四边形,由于QC ∥P A ,故只要QC =P A 185. ⑶即可,而P A =18-4t ,CQ =t ,故18-4t =t ,得t =设点P 运动t s ,则OP =4t ,CQ =t ,0<t <4.5.说明P在线段OA 上,且不与点O ,A 重合.由于QC ∥OP 知△QDC ∽△PDO ,故144QD QC t DP OP t ===.同理QC ∥AF ,故14QC CE AF EA ==,即14t AF =,∴AF =4t =OP .∴PF =P A +AF =P A +OP =18.又点Q 到直线PF 的距离d =10,∴S △PQF =12•PF •d =12×18×10=90.于是S △PQF 的面积总为定值90. ⑷由前面知道,P (4t ,0),F (18+4t ,0),Q (8-t ,-10),0≤t ≤4.5.构造直角三角形后易得PQ 2=(4t -8+t )2+102=,FQ 2=(18+4t -8+t )2+102=(5t +10)2+100.①若FP =FQ ,即182=(5t +10)2+100,故25(t +2)2=224,(t +2)2=24425.∵2≤t +2≤6.5,∴t +2=244414255=.∴t = 4145-2. ②若QP =QF ,即(5t -8)2+100=(5t +10)2+100,即(5t -8)2=(5t +10)2,无0≤t ≤4.5的t 满足. ③若PQ =PF ,即(5t -8)2+100=182,∴(5t -8)2=224.由于224≈15,又0≤5t ≤22.5,∴-8≤5t -8≤14.5,14.52=22984124⎛⎫= ⎪⎝⎭<224.故没有t (0≤t ≤4.5)满足此方程.综上所述,当t =4145-2时,△PQ R 为等腰三角形. 10.⑴C 1的顶点坐标为(1,12). ⑵略 ⑶作PM ⊥AB 于M ,作QN ⊥AB 交AB 延长线于N ,∴PM =1-y P ,FM =1-x P .在R t △PMF 中,PF 2=(1-y P )2+(1-x P )2=1-2y P +y P 2+1-2x P +x P 2,又∵点P 在抛物线上,∴y P =12x P 2-x P +1,∴PF 2=1-x P 2+2x P -2+y P 2+1-2x P +x P 2=y P 2,∴PF =y P ,同理,QF =y Q ,易证△PMF ∽△QNF ,则PM QN PF QF =,∴11Q P y y PF QF --=,即11PF QF PF QF --=,∴11PF QF+=2. 11.先从特殊情况出发.当△ABC 是等腰直角三角形时,点P 与点C 重合,此时点P 的位置在AB 的中垂线上,且到AB的距离为12AB ,如图①所示.下面就一般情况来证明上面的结论(结论②所示).过C ,E ,G 分别作直线AB 的垂线CH ,EM ,G N ,垂足分别是H ,M ,N .容易证明△AEM ≌△ACH ,△B G N ≌△BCH .从而有AM =CH =BN ,EM =AH ,G N =BH .这样,线段AB 的中点O 也是线段MN 的中点,连接OP ,则OP 是梯形EMN G 的中位线,从而OP ⊥AB ,OP =12(EM +G N )= 12(AH +BH )=12AB .∴无论点C 在AB 同一侧的位置如何,E G 中点P 的位置不变.。
初中数学66个常考几何模型50个应用题答题公式(一)

初中数学66个常考几何模型50个应用题答题公式(一)初中数学66个常考几何模型及50个应用题解答公式一、直线和角1. 直线的斜率公式斜率公式用于计算直线的斜率,即直线上两点的纵坐标之差与横坐标之差的比值。
斜率公式为:k = (y2 - y1) / (x2 - x1)例如,已知两点A(2, 4)和B(5, 9),则直线AB的斜率为:k = (9 - 4) / (5 - 2) = 5 / 32. 同位角公式同位角公式用于计算同位角的性质。
当两条直线被一条截线相交时,同位角相等。
例如,直线l1和直线l2被直线l相交,角1和角2为同位角,则有:角1 = 角23. 对顶角公式对顶角公式用于计算对顶角的性质。
当两条直线被一条截线相交时,对顶角互为补角。
例如,直线l1和直线l2被直线l相交,角1和角2为对顶角,则有:角1 + 角2 = 180°二、平行线和三角形1. 平行线的性质公式平行线的性质公式包括平行线定理和平行线的判定定理。
平行线定理表示若两条直线与一直线交叉,使得同位角或内错角互为补角,则这两条直线平行。
平行线的判定定理表示若两条直线的斜率相等且至少有一对对应角相等,则这两条直线平行。
2. 三角形的内角和公式三角形的内角和公式表示三角形三个内角的和等于180°。
例如,对于任意三角形ABC,其内角A、B和C满足:角A + 角B + 角C = 180°三、相似三角形和勾股定理1. 相似三角形的性质公式相似三角形的性质公式包括AAA相似定理、AA相似定理和SAS相似定理。
AAA相似定理表示若两个三角形的对应角相等,则这两个三角形相似。
AA相似定理表示若两个三角形的两个对应角相等,则这两个三角形相似。
SAS相似定理表示若两个三角形的一个角相等,两个对边比值相等,则这两个三角形相似。
2. 勾股定理勾股定理用于计算直角三角形的边长关系。
设直角三角形的两条直角边长度分别为a和b,斜边长度为c,则有:c^2 = a^2 + b^2例如,已知直角三角形的一条直角边长度为3,另一条直角边长度为4,则斜边的长度为:c = sqrt(3^2 + 4^2) = 5以上是初中数学66个常考几何模型和50个应用题的一些解答公式的列举和说明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面积公式A bc B ac C ab S ABC sin 2
1sin 21sin 21===∆
))()((c p b p a p p S ABC ---=∆ 2/)(c b a p ++=
和角公式
A B B A B A cos sin cos sin )sin(+=+ A B B A B A sin sin cos cos )cos(-=+
B A B A B A tan tan 1tan tan )tan(-+=+ 差角公式
A B B A B A cos sin cos sin )sin(-=- A B B A B A sin sin cos cos )cos(+=- B
A B A B A tan tan 1tan tan )tan(+-=-
常用角度的三角比
相关练习题:
1.已知ABC ∆中,,75 =∠B ,60 =∠C ,10=BC 求AB 与AC 的长及三角形的面积
2.求证面积公式A bc B ac C ab S ABC sin 2
1sin 21sin 21===∆
3.求证海伦公式 ))()((c p b p a p p S ABC ---=∆ 2/)(c b a p ++=
4. 已知ABC ∆中,,7=AB ,8=BC ,9=AC 求sinA , sinB , sinC
5.在等腰三角形ABC 中,AB=1,∠A=900,点E 为腰AC 中点,点F 在底边BC 上,且FE ⊥BE ,求△CEF 的面积。
6.已知四边形ABCD 内接于直径为3的圆O ,对角线AC 是直径,对角线AC 和BD 的交点是P ,AB=BD ,且PC=0.6,求四边形ABCD 的周长.
7.在△ABC 中,∠ABC =600,点P 是△ABC 内的一点,使得∠APB =∠BPC =∠CPA ,且PA =8,PC =6,则PB = 。
A B C E F A
B C
P
8. 在△ABC 中,∠ACB =90°.
(1)当点D 在斜边AB 内部时,求证:AB
BD AD BC BD CD -=-222. (2)当点D 与点A 重合时,第(1)小题中的等式是否存在?请说明理由.
(3)当点D 在BA 的延长线上时,第(1)小题中的等式是否存在?请说明理由.
9. ABC ∆中,3=AB ,4=AC ,5=BC ,D 是BC 上一点,若ABD ∆、ACD ∆的内心连线与AD 垂直,则AD =______。
B
10. D 是边长为1的正三角形ABC 的边BC 上一点,CD BD <,AD 的中垂线EF 分别交AB 、AC 于E 、F ,点G 在BE 上,且CG ∥FE 。
求证:(1)BD GE =;(2)若
GDB BED ∠=∠,求BD 。
C B
B A C
D。
