悬臂梁受力计算表格
悬臂梁 计算公式

悬臂梁计算公式悬臂梁计算公式。
悬臂梁是一种常见的结构形式,广泛应用于工程建筑中。
它的设计和计算是工程设计中的重要内容,对于确保结构的安全性和稳定性至关重要。
在本文中,我们将介绍悬臂梁的计算公式及其应用。
悬臂梁的计算公式主要包括静力学原理和材料力学原理。
静力学原理是指根据平衡条件和力的平衡条件来计算悬臂梁的受力情况,而材料力学原理则是指根据材料的力学性质来计算悬臂梁的受力情况。
下面我们将分别介绍这两方面的计算公式。
首先是静力学原理。
根据力的平衡条件,悬臂梁在受力时会受到弯矩和剪力的作用。
弯矩和剪力是悬臂梁受力的两个基本参数,它们的计算公式如下:1. 弯矩的计算公式。
悬臂梁的弯矩可以根据悬臂梁的受力情况和外力情况来计算。
一般情况下,悬臂梁的弯矩可以使用以下公式来计算:M = F L。
其中,M表示弯矩,F表示作用在悬臂梁上的外力,L表示悬臂梁的长度。
2. 剪力的计算公式。
悬臂梁的剪力也可以根据悬臂梁的受力情况和外力情况来计算。
一般情况下,悬臂梁的剪力可以使用以下公式来计算:V = F。
其中,V表示剪力,F表示作用在悬臂梁上的外力。
以上是悬臂梁在静力学原理下的计算公式。
接下来我们将介绍悬臂梁在材料力学原理下的计算公式。
材料力学原理是指根据材料的力学性质来计算悬臂梁的受力情况。
材料力学原理下的计算公式主要包括应力和应变的计算公式。
1. 应力的计算公式。
悬臂梁在受力时会产生应力,应力的计算公式如下:σ = M y / I。
其中,σ表示应力,M表示弯矩,y表示悬臂梁截面上某点到受力轴线的距离,I表示悬臂梁的惯性矩。
2. 应变的计算公式。
悬臂梁在受力时会产生应变,应变的计算公式如下:ε = σ / E。
其中,ε表示应变,σ表示应力,E表示悬臂梁的弹性模量。
以上是悬臂梁在材料力学原理下的计算公式。
这些计算公式可以帮助工程师和设计师在设计悬臂梁时准确计算悬臂梁的受力情况,确保悬臂梁的结构安全和稳定。
除了上述的计算公式,还需要考虑悬臂梁的边界条件和约束条件,以及材料的强度和稳定性等因素。
各种梁的弯矩剪力计算(大全)表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
悬臂梁受集中载荷的应力变形计算

悬臂梁受集中载荷的应力变形计算悬臂梁是一种常见的结构,在工程中应用广泛。
在设计和分析悬臂梁时,经常需要计算受集中载荷作用下的应力和变形。
本文将对悬臂梁受集中载荷的应力和变形计算进行详细阐述。
一、悬臂梁受集中载荷的应力计算1.弯曲应力计算当悬臂梁受到集中荷载作用时,会产生弯曲应力。
弯曲应力是由于载荷作用引起梁的弯曲变形而产生的。
计算弯曲应力可使用弯曲应力公式:σ=(M*y)/I其中,σ为弯曲应力,M为弯矩,y为弦纤维上离中轴线的距离,I 为截面转动惯量。
在悬臂梁上的集中荷载作用下,弯矩可通过以下公式计算:M=F*L其中,M为弯矩,F为集中荷载,L为悬臂梁的长度。
对于矩形截面的悬臂梁,截面转动惯量I可通过以下公式计算:I=(b*h^3)/12其中,I为截面转动惯量,b为矩形截面的宽度,h为矩形截面的高度。
2.剪切应力计算除了弯曲应力外,悬臂梁还会受到剪切应力的作用。
剪切应力是指梁截面内部不同层次之间的相对滑动所产生的应力。
计算剪切应力可使用剪切应力公式:τ=(V*Q)/(b*I)其中,τ为剪切应力,V为剪力,Q为梁截面的截面模量,b为截面的宽度,I为截面转动惯量。
悬臂梁上的剪力可通过以下公式计算:V=F其中,V为剪力,F为集中荷载。
悬臂梁的截面模量Q可通过以下公式计算:Q=(b*h^2)/6其中,Q为截面模量,b为截面的宽度,h为截面的高度。
二、悬臂梁受集中载荷的变形计算1.弯曲变形计算悬臂梁受到集中载荷作用时,会产生弯曲变形。
弯曲变形是指悬臂梁由于受到集中载荷作用发生的弯曲现象。
计算弯曲变形可使用弯曲变形公式:δ=(M*L^2)/(2*E*I)其中,δ为弯曲变形,M为弯矩,L为悬臂梁的长度,E为弹性模量,I为截面转动惯量。
2.剪切变形计算悬臂梁除了弯曲变形外,还会受到剪切变形的作用。
剪切变形是指梁截面内部不同层次之间的相对滑动所产生的变形。
计算剪切变形可使用剪切变形公式:θ=(V*L)/(G*Q)其中,θ为剪切变形,V为剪力,L为悬臂梁的长度,G为剪切模量,Q为截面模量。
悬臂梁计算公式一览表

悬臂梁计算公式一览表悬臂梁是一种常见的工程结构,常用于吊车起重、桥梁和建筑物中。
在设计和分析悬臂梁时,我们需要使用一系列的计算公式来确定其受力和变形情况。
下面是悬臂梁计算中常用的公式一览表:1. 弯矩公式(弯矩与力的关系)弯矩是悬臂梁受到外力作用产生的抗弯形变的指示。
对于集中力的悬臂梁,弯矩公式为:M = F * L其中,M为弯矩,F为作用在悬臂梁上的力,L为悬臂梁的长度。
2. 最大弯矩公式在悬臂梁上不同位置的弯矩大小不同。
最大弯矩是指悬臂梁上弯矩大小最大的位置。
对于集中力的悬臂梁,最大弯矩公式为:M_max = F * L其中,M_max为最大弯矩,F为作用在悬臂梁上的力,L为悬臂梁的长度。
3. 剪力公式(剪力与力的关系)剪力是指作用在悬臂梁上截面两侧的力的大小。
对于集中力的悬臂梁,剪力公式为:V = F其中,V为剪力,F为作用在悬臂梁上的力。
4. 获取剪力和弯矩图的公式剪力和弯矩图是对悬臂梁受力情况的图形表示。
对于集中力的悬臂梁,剪力和弯矩图的公式为:V = V0 - FM = M0 - F * x其中,V为截面处的剪力大小,M为截面处的弯矩大小,V0和M0为截面处离开力作用点时的剪力和弯矩大小,F为作用在悬臂梁上的力,x为距离力作用点的距离。
5. 变形公式(变形与力的关系)变形是悬臂梁在受力作用下产生的长度、角度或形状的改变。
对于悬臂梁的弹性变形,变形公式为:δ = (F * L^3) / (3 * E * I)其中,δ为悬臂梁在力作用下的弹性变形,F为作用在悬臂梁上的力,L为悬臂梁的长度,E为材料的弹性模量,I为悬臂梁的截面惯性矩。
这些公式是悬臂梁设计和分析中的基本工具。
通过使用这些公式,工程师可以计算悬臂梁的弯矩、剪力、变形等参数,以确保悬臂梁在使用中安全可靠。
同时,这些公式也可以帮助工程师优化设计,减少材料使用量,提高工程效率。
需要注意的是,上述公式适用于一些简化情况下的悬臂梁设计和分析。
(完整版)梁的内力计算

(2) 荷载简化一一将荷载简化为集中力、线分布力或力偶等;
(3) 支座简化——主要简化为以下三种典型支座:
(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4—3(a)所示。这
种支座只限制梁在沿垂直于支承平面方向的位移, 其支座反力过铰心且垂直于支
(1)求支座反力
正,如图4-7(c)o
由
Y0
Q2
qa
0
得
Q2qa
由
M20
m2
a小
qa 0
2
得
m2
2
qa
2
(4)求3-3截面(D截面左侧边一点)内力
取右端为脱离体,3-3截面无限靠近D点,线分布力q的分布长度趋于0,则3-3
截面上Q=0,M=0o
2.2截面法直接由外力求截面内力的法则
上例说明了运用截面法求任一截面内力的方法。因脱离体的平衡条件丫0的 含义为:脱离体上所有外力和内力在丫轴方向投影的代数和为零。其中只有剪力Q为未知量,移到方程式右边即得直接由外力求任一截面剪力的法则:
对称平面内,称为弯矩
则得
由Mc0,有YaxM0
则得MYaX
注意此处是对截面形心C取矩,因剪力Q通过截面形心C点,故在力矩方程中为 零。同样可取右脱离体,由平衡方程求出梁截面m-n上的内力Q和M,其结果与 左脱离体求得的Q M大小相等,方向(或转向)相反,互为作用力与反作用力 关系。
为使梁同一截面内力符号一致,必须联系到变形状态规定它们的正负号。 若从梁m-n处取一微段梁dx,由于剪力Q作用会使微段发生下错动的剪切变形。 我们规 定:使微段梁发生左端向上而右端向下相对错动的剪力Q为正(如图4—6(a)),反之为负(如图4—6(b));使微段梁弯曲为向下凸时的弯矩M为正,反之为负
简支梁和悬臂梁的弯矩挠度计算

0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
0
0
0
#DIV/0!
悬臂梁计算书.rtf

悬臂梁计算书项目名称_____________ 日期_____________设计者_____________ 校对者_____________2、材性:Q345弹性模量 E = 206000 MPa剪变模量 G = 79000 MPa质量密度ρ = 7850 kg/m3线膨胀系数α = 12x10-6 / °c泊松比ν = 0.30屈服强度 f y = 345 MPa抗拉、压、弯强度设计值 f = 310 MPa抗剪强度设计值 f v = 180 MPa截面面积 A = 3804 mm2自重 W = 0.293 kN/m面积矩 S = 186267 mm3抗弯模量 I = 41558000 mm4抗弯刚度 W = 332464 mm3塑性发展系数γ = 1.05二、荷载信息1、恒荷载2、活荷载(1)、均布荷载,35.00kN/m,荷载分布:满布三、组合信息1、内力组合、工况(1)、恒载工况(2)、活载工况(3)、1.20恒+1.40活(4)、1.35恒+1.4x0.7活2、挠度组合、工况(1)、恒载工况(2)、活载工况(3)、1.0恒+1.0活四、内力、挠度计算1、弯矩图(kN.m)(1)、恒载工况最大正应力与设计强度比值最大稳定应力与设计比值若有局稳字样,表示局部稳定不满足(1)、内力范围、最大挠度(a)、内力范围:弯矩设计值 0.00~78.78 kN.m剪力设计值 -0.00~131.31 kN(b)、最大挠度:最大挠度2.58mm,最大挠跨比1/928(挠度允许值见《钢结构设计规范》(GB 50017-2003)附录A.1)(2)、强度应力最大剪应力τ = V max * S / I / t w= 131.31 * 186267 / 41558000 / 6.0 * 1000= 98.1 MPa ≤ f v = 180 MPa 满足!最大正应力σ = M max / γ / W= 78.78 / 1.05 / 332464 * 1e6= 225.7 MPa ≤ f = 310 MPa 满足!(3)、稳定应力受压翼缘自由长度 l1 = 1200 mm面外回转半径 i = 34.4 mm面外长细比λ = 1200 / 34.4 = 34.9按 GB 50017--2003 第127页公式(B.5-1) 计算:整体稳定系数φb = 1.07 - λ2/44000 * 235/fy= 1.07 - 34.92 /44000 * 235 / 345= 1.03 > 1.0 取 1.0最大压应力σ = M max / φb / W= 78.78 / 1.00 / 332464 * 1e6= 237.0 MPa ≤ f = 310 MPa 满足!(4)、局部稳定腹板稳定验算:腹板高 h w = 234 mm,腹板厚 t w = 6.0 mm腹板高厚比为 234 / 6.0 = 39.0 ≤ 80√(235/fy)无局部压应力时可不配置加劲肋!(GB50017--2003 第26页 4.3.2)翼缘稳定验算:受压下翼缘外伸宽度 b = 72.0 mm,翼缘厚 t = 8.0 mm受压下翼缘外伸宽度与厚度之比为 72.0 / 8.0 = 9.0 ≤ 13√(235/fy)满足!(GB50017--2003 第32页 4.3.8)(5)、验算结论:满足!。
各类梁的弯矩力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lqasF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
悬臂梁配筋计算案例

悬臂梁配筋计算案例一、案例基本情况。
假设我们有一个悬臂梁,就像一个从墙上伸出去的手臂一样,这梁的长度呢,咱就设定为3米。
这梁上面承受着均布荷载,啥叫均布荷载呢?就好比你在这悬臂梁上均匀地铺满了小砖头,每个地方受力都差不多。
这个均布荷载的大小是每米20千牛(kN/m),这就像是每个小砖头对梁产生的压力啦。
二、计算步骤。
1. 弯矩计算。
对于悬臂梁,弯矩的计算公式是M=(1)/(2)ql^2,这里的q就是均布荷载,l 是梁的长度。
把数值带进去哈,q = 20kN/m,l = 3m,那么弯矩M=(1)/(2)×20×3^2=90kN·m。
这个弯矩呢,就像是一个扭转的力量,要让梁弯起来,咱得根据这个力量来配钢筋,让钢筋来抵抗这个弯矩。
2. 确定混凝土和钢筋的强度等级。
咱就假设混凝土用的是C30的,它的抗压强度设计值f_c=14.3N/mm^2。
钢筋呢,就用HRB400的,它的抗拉强度设计值f_y=360N/mm^2。
这就好比是我们找了一群强壮的“士兵”(钢筋),让它们在混凝土这个“阵地”里抵抗外力。
3. 计算梁的截面尺寸。
咱先假设梁的截面是矩形的,宽度 b = 300mm,高度h = 500mm。
这个尺寸就像梁的身材一样,不同的身材对抵抗弯矩的能力是有影响的哦。
4. 配筋计算。
根据弯矩平衡公式M≤slantα_1f_cbx(h_0-(x)/(2)),这里的α_1对于C30混凝土取1.0,h_0=h a_s,假设钢筋的保护层厚度a_s=40mm,那么h_0=500 40 =460mm。
首先我们要找到受压区高度x,把已知的值都带进去这个弯矩平衡公式里,经过一番计算(这个计算有点像解谜题呢),可以得到x的值。
然后根据公式A_s=(M)/(f_y)(h_{0-(x)/(2))}来计算受拉钢筋的面积A_s。
算出来A_s之后,我们就可以根据钢筋的面积去选择合适的钢筋根数和直径啦。
比如说,如果算出来A_s=1000mm^2,我们可能会选择3根直径20mm的HRB400钢筋,因为一根直径20mm的HRB400钢筋的面积大概是314.2mm²,3根就差不多能满足要求啦。
悬臂梁挠度计算公式

悬臂梁挠度计算公式
根据应变-位移公式,我们可以得到悬臂梁在受力下的挠度计算公式。
公式为:
δ=(P*L^3)/(3*E*I)
其中,δ代表悬臂梁的挠度,P代表悬臂梁上的受力,L代表悬臂梁
的长度,E代表悬臂梁的弹性模量,I代表悬臂梁的截面转动惯量。
这个公式是基于悬臂梁的假设条件以及材料的线性弹性特性。
假设悬
臂梁所受的力是集中作用于梁的一端,且力的作用方向与梁的轴线一致。
此外,该公式还假设悬臂梁的材料是线性弹性材料,即满足胡克定律。
在工程实际中,悬臂梁的材料通常是钢、混凝土、木材等,这些材料
的弹性模量和截面转动惯量可以通过实验或材料手册得到。
根据这些参数,可以进行悬臂梁挠度的计算。
需要注意的是,悬臂梁的挠度公式是在假设条件下得出的近似解,并
且只适用于线性弹性材料、小挠度和小变形的情况。
对于非线性弹性材料、大变形或大挠度的情况,需要采用更加复杂的方法来进行挠度的计算。
总之,悬臂梁的挠度计算公式是用来计算悬臂梁在受力作用下的挠度
的公式。
该公式是基于应变-位移公式和力学平衡条件推导得到的,适用
于线性弹性材料、小挠度和小变形的情况。
在实际工程中,需要根据具体
的材料参数和假设条件来进行准确的挠度计算。
悬臂梁的挠度计算公式

悬臂梁的挠度计算公式悬臂梁的挠度计算公式均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 8pl^3/(384EI)=1pl^3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 6.81pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式: Ymax = 6.33pl^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).挠度计算公式:Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q 作用下,EI是梁的弯曲刚度)挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。
各类梁的弯矩剪力计算汇总表
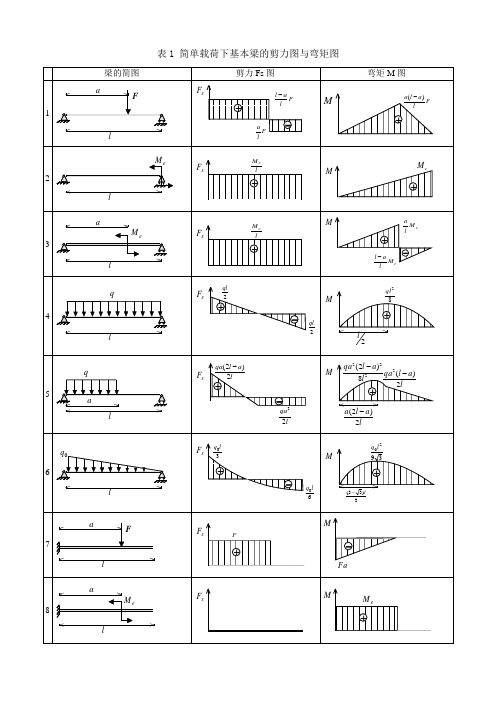
表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
悬臂梁形变计算公式

悬臂梁的形变计算公式可以通过梁的弯曲理论得到。
下面列举了常见的悬臂梁形变计算公式:
1. 梁的弯曲形变(El):
El = (W * L^3) / (3 * E * I)
其中,El为梁的弯曲形变,W为悬臂梁上作用的外力,L为悬臂梁的长度,E为悬臂梁的弹性模量,I为悬臂梁的截面惯性矩。
2. 梁的挠度(δ):
δ= (W * L^3) / (3 * E * I)
其中,δ为梁的挠度。
3. 梁的剪切形变(γ):
γ= (V * L) / (G * A)
其中,γ为梁的剪切形变,V为悬臂梁上作用的切力,G为悬臂梁的剪切模量,A为悬臂梁的截面面积。
需要注意的是,上述公式只适用于简单的悬臂梁,并假设梁的截面是均匀的。
对于复杂的悬臂梁形变计算,可能需要考虑材料非均匀性、梁的扭转、悬臂梁形状、剪切变形等因素,并采用更为复杂的理论和计算方法。
