初三数学超难训练题(附答案)
初三超难数学试卷上册答案

---初三上册数学试卷(虚构)一、选择题(每题5分,共50分)1. 已知函数f(x) = 2x + 1,则f(-3)的值为:A. -5B. -7C. -9D. -11答案:A解题过程:将x = -3代入函数f(x) = 2x + 1,得到f(-3) = 2(-3) + 1 = -6 + 1 = -5。
2. 下列各组数中,存在勾股数的是:A. (3, 4, 5)B. (5, 12, 13)C. (6, 8, 10)D. (7, 9, 12)答案:B解题过程:勾股数满足a² + b² = c²。
计算选项B中的数,5² + 12² = 25 + 144 = 169 = 13²,因此(5, 12, 13)是勾股数。
3. 已知等腰三角形ABC中,AB = AC,AD是高,则∠BAC的度数为:A. 30°B. 45°C. 60°D. 90°答案:C解题过程:在等腰三角形中,底角相等,且底边上的高也是底边的中线。
因此,∠BAC = ∠BAD + ∠CAD =90°/2 + 90°/2 = 60°。
4. 下列哪个图形是轴对称图形:A. 等边三角形B. 长方形C. 梯形D. 正方形答案:D解题过程:正方形是轴对称图形,因为它有两条对称轴,分别是两条对角线。
5. 若一元二次方程x² - 4x + 3 = 0的两根分别为a和b,则a + b的值为:A. 2B. 3C. 4D. 5答案:C解题过程:根据韦达定理,一元二次方程ax² + bx + c = 0的两根之和等于-b/a。
因此,a + b = -(-4)/1 = 4。
二、填空题(每题5分,共50分)6. 已知sinα = 1/2,且α在第二象限,则cosα的值为______。
答案:-√3/2解题过程:在第二象限,sinα > 0,cosα < 0。
初三数学超难试题及答案

初三数学超难试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数y=ax^2+bx+c(a≠0)的对称轴?A. x=-b/2aB. x=b/2aC. x=a/2bD. x=b/2c答案:A2. 已知等腰三角形的两边长分别为3和6,那么这个三角形的周长是多少?A. 12B. 15C. 18D. 21答案:B3. 在一次函数y=kx+b中,若k>0且b<0,则该函数的图像不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:C4. 一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B5. 计算下列二次根式中,哪个是同类二次根式?A. √2和√8B. √3和√12C. √5和√20D. √6和√24答案:C6. 一个数的立方等于8,那么这个数是多少?A. 2B. -2C. 2和-2D. 以上都不对答案:C7. 一个长方体的长、宽、高分别为2cm、3cm、4cm,那么这个长方体的体积是多少?A. 24cm³B. 36cm³C. 48cm³D. 52cm³答案:A8. 已知一个角的余角是30°,那么这个角的度数是多少?A. 60°B. 90°C. 120°D. 150°答案:A9. 一个数的相反数是-5,那么这个数是多少?A. 5B. -5C. 0D. 10答案:A10. 计算:(1/2)^-1的值是多少?A. 2B. -2C. 1/2D. -1/2答案:A二、填空题(每题4分,共20分)1. 一个数的绝对值是5,那么这个数可以是______。
答案:±52. 一个角的补角是120°,那么这个角的度数是______。
答案:60°3. 一个正数的倒数是1/4,那么这个数是______。
答案:44. 一个三角形的内角和是______。
(完整版)初中数学几何题(超难)及答案分析

(完整版)初中数学⼏何题(超难)及答案分析⼏何经典难题1、已知:如图,O 是半圆的圆⼼,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初三)2、已知:如图,P 是正⽅形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三⾓形.(初⼆)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正⽅形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正⽅形.(初⼆)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .5、已知:△ABC 中,H 为垂⼼(各边⾼线的交点)(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初三)A P C D BA FG CE B O D D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 BF6、设MN 是圆O 外⼀直线,过O 作OA ⊥MN 于A ,⾃A,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初三)7、如果上题把直线MN 由圆外平移⾄圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初三)8、如图,分别以△ABC 的AC 和BC 为⼀边,在△ABC 的外侧作正⽅形ACDE 和正⽅形CBFG ,点P是EF 的中点.求证:点P 到边AB 的距离等于AB 的⼀半.N9、如图,四边形ABCD 为正⽅形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初⼆)10、如图,四边形ABCD 为正⽅形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .11、设P 是正⽅形ABCD ⼀边BC求证:PA =PF .(初⼆)12、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E E P13、已知:△ABC 是正三⾓形,P 是三⾓形内⼀点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初⼆)14、设P 是平⾏四边形ABCD 内部的⼀点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初⼆)15、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)16、平⾏四边形ABCD 中,设E 、F 分别是BC 、AB 上的⼀点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .17、设P 是边长为1的正△ABC 内任⼀点,L =PA +PB +PC ,求证:≤L <2.AP C B PA D CB CB D AFPDECBA18、已知:P 是边长为1的正⽅形ABCD 内的⼀点,求PA +PB +PC 的最⼩值.19、P 为正⽅形ABCD 内的⼀点,并且PA =a ,PB =2a ,PC =3a ,求正⽅形的边长.20、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.CCD解答1.如下图做GH ⊥AB,连接EO 。
较难的初三试卷数学及答案

一、选择题(每题5分,共50分)1. 若 \(a > 0\),\(b < 0\),则以下不等式中正确的是:A. \(a + b > 0\)B. \(a - b < 0\)C. \(ab > 0\)D. \(a \div b > 0\)2. 函数 \(y = 2x - 1\) 的图像是一条:A. 斜率为正的直线B. 斜率为负的直线C. 水平直线D. 垂直直线3. 在等腰三角形ABC中,底边BC=8cm,腰AB=AC=10cm,那么顶角A的度数是:A. 30°B. 45°C. 60°D. 75°4. 若 \(x^2 - 5x + 6 = 0\),则 \(x^2 + 5x + 6 =\)?A. 0B. 1C. 2D. 35. 在平面直角坐标系中,点A(2, 3),点B(-3, -4),那么线段AB的中点坐标是:A. (-1, -1)B. (-1, 1)C. (1, -1)D. (1, 1)6. 若 \(a, b, c\) 是等差数列的前三项,且 \(a + b + c = 12\),\(abc = 27\),则该数列的公差是:A. 1B. 2C. 3D. 47. 在直角坐标系中,点P(1, 2)关于原点对称的点是:A. (1, -2)B. (-1, 2)C. (-1, -2)D. (1, 2)8. 若 \(x^2 + y^2 = 25\),\(x + y = 5\),则 \(x - y\) 的值为:A. 3B. 4C. 5D. 69. 在△ABC中,∠A = 30°,∠B = 45°,则∠C的度数是:A. 75°B. 105°C. 135°D. 165°10. 若 \(a, b, c\) 是等比数列的前三项,且 \(a + b + c = 27\),\(abc = 27\),则该数列的公比是:A. 1B. 3C. 9D. 27二、填空题(每题5分,共50分)11. 若 \(x^2 - 4x + 3 = 0\),则 \(x^2 + 4x + 3 =\)________。
九年级数学选择题(难)100道附解析

41.如图,已知点A1,A2,…,A2011在函数 位于第二象限的图象上,点B1,B2,…,B2011在函数 位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形 、 ,…, 都是正方形,则正方形 的边长为
A. 2010B. 2011 C. 2010 D. 2011
A.2 B.4 C.8 D.16
33.如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1单位长度分别沿B-A-D-C和B-C-D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平房单位),S与t的函数图象如图2所示,则下列结论错误的是()
A.当t=4秒时,S=4
24.如图,反比例函数 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为()
A.1 B.2 C.3 D.4
25.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP= ,AE= ,则能反映 与 之间函数关系的大致图象是()
A. B. C. D.
15.如图,已知菱形ABCD的边长为2㎝, ,点M从点A出发,以1㎝/s的速度向点B运动,点N从点A同时出发,以2㎝/s的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动.则△AMN的面积 (㎝2)与点M运动的时间 (s)的函数的图像大致是()
16.已知反比例函数的图象过点M(-1,2),则此反比例函数的表达式为
A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S2
23.已知在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
较难的初三试卷数学答案

一、选择题(每题5分,共25分)1. 已知函数f(x) = 2x - 3,若f(x) > 0,则x的取值范围是()A. x > 1.5B. x < 1.5C. x > 3D. x < 3答案:A2. 在△ABC中,∠A = 45°,∠B = 60°,则∠C的度数是()A. 75°B. 90°C. 105°D. 120°答案:C3. 已知等差数列{an}中,a1 = 3,公差d = 2,则第10项an =()A. 19B. 21C. 23D. 25答案:C4. 若等比数列{bn}中,b1 = 2,公比q = 3,则第n项bn =()A. 2 × 3^(n-1)B. 2 × 3^nC. 6 × 3^(n-1)D. 6 × 3^n答案:A5. 下列函数中,在其定义域内单调递减的是()A. y = x^2B. y = 2x - 1C. y = log2xD. y = √x答案:B二、填空题(每题5分,共25分)6. 已知函数f(x) = x^2 - 4x + 3,若f(x) = 0,则x的值为______。
答案:1或37. 在△ABC中,若AB = 5,AC = 6,BC = 7,则△ABC的面积是______。
答案:158. 等差数列{an}中,a1 = 1,公差d = 3,则第10项an =______。
答案:289. 等比数列{bn}中,b1 = 4,公比q = 1/2,则第n项bn =______。
答案:4 × (1/2)^(n-1)10. 函数y = 2x + 3的图像上,一点P(x, y)到y轴的距离是______。
答案:|x|三、解答题(共50分)11. (15分)已知函数f(x) = x^2 - 2ax + a^2,若f(x) ≥ 0恒成立,求实数a的取值范围。
中考最难数学试题及答案

中考最难数学试题及答案一、选择题(每题3分,共15分)1. 下列哪个数是无理数?A. √2B. 0.33333(无限循环)C. πD. 1/3答案:A、C2. 已知方程x^2 + 4x + 4 = 0,求x的值。
A. -2B. -1C. 2D. 4答案:A3. 如果一个角的正弦值是1/2,那么这个角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C4. 一个长方体的长、宽、高分别是a、b、c,其体积是?A. abcB. a + b + cC. a/b + b/c + c/aD. (a + b + c)/3答案:A5. 下列哪个表达式等于0?A. (x - 1)(x + 1)B. (x - 1)(x - 1)C. (x - 1)^2D. x^2 - 1答案:A二、填空题(每题3分,共15分)6. 一个圆的半径是5,那么它的面积是________。
答案:25π7. 如果一个数的立方根等于它本身,那么这个数可以是________、________或________。
答案:1,-1,08. 一个直角三角形的两条直角边分别是3和4,斜边的长度是________。
答案:59. 一个数的相反数是-5,那么这个数是________。
答案:510. 一个数的绝对值是它本身,那么这个数是________或________。
答案:非负数,非正数三、解答题(共70分)11. 解不等式:3x - 5 < 2x + 8。
答案:首先将不等式中的项进行移项,得到3x - 2x < 8 + 5,简化后得到x < 13。
12. 已知一个二次函数的顶点是(1, -4),并且它的对称轴是直线x = 1,求这个二次函数的解析式。
答案:设二次函数的解析式为y = a(x - 1)^2 - 4,由于对称轴是x = 1,所以顶点的x坐标为1,不需要进一步求解a的值,函数的解析式已经确定。
初三数学 二次函数较高难度综合题(含详细答案)

绝密★启用前2015-2016学年度二次函数学校:___________姓名:___________班级:___________考号:___________一、选择题1.二次函数c bx ax y ++=2(a ≠0)的图像如图所示,其对称轴为x =1,有如下结论:① c <1 ②2a +b =0 ③2b <4a c ④若方程02=++c bx ax 的两个根为1x ,2x ,则1x +2x =2.则结论正确的是【 】A. ①②B. ①③C. ②④D. ③④2.如图是二次函数2y=ax +bx+c 的部分图象,由图象可知不等式2ax +bx+c<0的解集是【 】A .1<x<5-B .x>5C .x<1-且x>5D .x <-1或x >53.二次函数2y ax bx c =++的图象如图所示,则反比例函数a y x=与一次函数y bx c =+在同一坐标系中的大致图象是( ).4.在同一平面直角坐标系内,一次函数y =ax +b 与二次函数y =ax 2+8x +b 的图象可能是( )5.如图是二次函数y=ax 2+bx+c 图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc <0;②2a ﹣b=0;③4a+2b+c <0;④若(﹣5,y 1),(0,y 2)是抛物线上两点,则y 1<y 2,其中说法正确的是( )A .①②B .②③C .①②④D .②③④6.若函数y=mx ²+(m+2)12m+1的图象与x 轴只有一个交点,那么m 的值为( )A .0B .0或2C .2或-2D .0,2或-27.已知二次函数y=ax 2+bx +c (a ≠0)的图像如图,有下列5个结论:①abc >0;②b<a +c ;③4a +2b +c >0;④2c <3b ;⑤a +b >m (am +b )(m ≠1的实数)其中正确的结论个数有( )-1O x =1y xA 、2个B 、3个C 、4个D 、5个8.已知抛物线2(41)21y x m x m =-++-与x 轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y 轴的交点在点(0,12-)的下方,那么m 的取值范围是( )A .1164m << B .16m < C .14m > D .全体实数9.在同一坐标系中,函数2y ax b =+与2y bx ax =+的图象,只可能是下图中的( )A .B .C .D .10.在同一平面直角坐标系中,函数y=kx+k 和函数y=﹣kx 2+4x+4(k 是常数,且k ≠0)的图象可能是( )A .B .C .D .11.若二次函数222y ax bx a =++-(a b ,为常数)的图象如下,则a 的值为( )A .1 D 12.抛物线222y x x =-+-经过平移得到2y x =-,平移方法是( )A .向右平移1个单位,再向下平移1个单位B .向右平移1个单位,再向上平移1个单位C .向左平移1个单位,再向下平移1个单位D .向左平移1个单位,再向上平移1个单位13.已知二次函数y =ax 2+bx +c 的图象如图所示,其对称轴为直线x =−1,给出下列结果:(1)b 2>4ac ;(2)abc >0;(3)2a +b =0;(4)a +b +c >0;(5)a −b +c <0.则正确的结论是( )A .(1)(2)(3)(4)B .(2)(4)(5)C .(2)(3)(4)D .(1)(4)(5)二、填空题(题型注释)14.如图,抛物线2y ax bx c =++(0a >)的对称轴是过点(1,0)且平行于 y 轴的直线,若点P (4,0)在该抛物线上,则4a ﹣2b+c 的值为 .15.已知二次函数2y ax bx c =++的图象与x 轴交于点(-2,0),(x 1,0)且1<x 1<2,与y 轴正半轴的交点在点(0,2)的下方,下列结论:①a <b <0;②248b ac a ->-;③4a+c <0;④2a -b+l ﹤0.其中正确的结论是(填写序号) .16.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,给出以下结论:①a+b+c <0;②a-b+c <0;③b+2a <0;④abc >0.其中所有正确结论的序号是______.A .②③B .①②C .③④D .①④17. 抛物线a bx ax y 32-+=经过A (1-,0)、C (0,3-)两点,与x 轴交于另一点B 。
初三数学重点难点几何题及答案
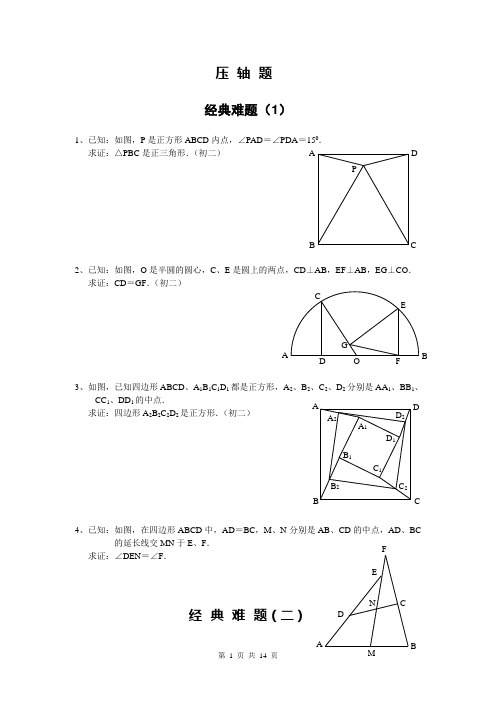
压轴题 经典难题(1)1、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)2、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CD BA FG CEBO D A P C D BPCG FB QA DE 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)· A D H EM C B O · GAO D B EC Q P NM · O Q PB DE C N M · A AFD ECB2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)D E DA CB F F EP C B A O D BFAECP AP C B P A D CB C B DA4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初三数学难题精选答案及讲解

1、如果将点P 绕定点M 旋转180°后与点Q 重合,那么称点P 与点Q 关于点M 对称,定点M 叫做对称中心。
此时,M 是线段PQ 的中点。
如图,在平面直角坐标系中,△ABO 的顶点A ,B ,O 的坐标分别为(1,0),(0,1),(0,0)。
点列P 1,P 2,P 3,…中的相邻两点都关于△ABO 的一个顶点对称:点P 1与点P 2关于点A 对称,点P 2与点P 3关于点B 对称,点P 3与点P 4关于点O 对称,点P 4与点P 5关于点A 对称,点P 5与点P 6关于点B 对称,点P 6与点P 7关于点O 对称…对称中心分别是A ,B ,O ,A ,B ,O ,…,且这些对称中心依次循环。
已知点P 1的坐标是(1,1),则点P 2017的坐标为 。
解:P 2的坐标是(1,-1),P 2017的坐标是(1,-1)。
理由:作P 1关于A 点的对称点,即可得到P 2(1,-1),P 3(-1,3),P 4(1,-3),P 5(1,3),P 6(-1,-1),又回到原来P 1的坐标,P 7(-1,-1);由此可知,每6个点为一个周期,作一次循环,2017÷6=336…1,循环了336次后又回到了原来P 1的坐标,故P 2017的坐标与P 1的坐标一样为(1,1)。
点评:此题主要考查了平面直角坐标系中中心对称的性质,以及找规律问题,根据已知得出点P 的坐标每6个一循环是解题关键.2、如图①,已知△ABC 是等边三角形,点E 在线段AB 上,点D 在直线BC 上,且DE=EC ,将△BCE 绕点C 顺时针旋转60°至△ACF ,连接EF 。
试证明:AB=DB+AF 。
【类比探究】(1)如图②,如果点E 在线段AB 的延长线上,其它条件不变,线段AB 、DB 、AF 之间又有怎样的数量关系?请说明理由。
(2)如果点E 在线段BA 的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB ,DB ,AF 之间数量关系,不必说明理由。
初三数学超难试卷及答案

一、选择题(每题5分,共50分)1. 已知函数f(x) = x^3 - 3x,若f(x)在x=1处取得极值,则该极值是()。
A. 0B. -2C. 2D. 4答案:A解析:f'(x) = 3x^2 - 3,令f'(x) = 0,得x = ±1。
当x < -1时,f'(x) > 0;当-1 < x < 1时,f'(x) < 0;当x > 1时,f'(x) > 0。
因此,f(x)在x=1处取得极大值0。
2. 在△ABC中,AB=AC=5,BC=6,点D在BC上,且BD=DC=2,若点E在AC上,且AE=3,则△ADE的面积是()。
A. 6B. 8C. 9D. 12答案:B解析:由题意知,△ABC为等腰三角形,所以∠ABC=∠ACB。
由BD=DC,得∠BDC=∠BDC。
因此,△BDC与△BDA相似。
由相似三角形的性质,得AD/AB =BD/BC,即AD/5 = 2/6,解得AD=5/3。
由勾股定理,得DE=√(AD^2 - AE^2) =√((5/3)^2 - 3^2) = √(25/9 - 9) = √(-56/9)。
由于面积不能为负,所以此题无解。
3. 已知数列{an}的通项公式为an = n^2 - 2n + 1,则数列的前10项和S10等于()。
A. 55B. 110C. 165D. 220答案:C解析:数列的前10项分别为1, 0, 1, 4, 9, 16, 25, 36, 49, 64。
因此,S10 = 1 + 0 + 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 = 220。
4. 已知函数g(x) = ax^2 + bx + c在x=1处取得极值,且g(0) = 3,g(2) = 5,则a、b、c的值分别为()。
A. 1, -2, 3B. -1, 2, 3C. 1, 2, 3D. -1, -2, 3答案:A解析:由g(0) = 3,得c = 3。
初三数学超难试题及答案

初三数学超难试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次函数的一般形式?A. y = ax^2 + bx + cB. y = ax^3 + bx^2 + cx + dC. y = ax^2 + bx + c + dD. y = ax^2 + bx + c - d答案:A2. 如果一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 75πD. 100π答案:B3. 一个等腰三角形的两边长分别为6和8,那么它的周长是多少?A. 20B. 22C. 24D. 26答案:C4. 以下哪个选项是不等式x > 2的解?A. x = 1B. x = 2C. x = 3D. x = 0答案:C5. 一个数的平方根是它本身的数是?A. 0B. 1C. -1D. 以上都是答案:D6. 一个三角形的内角和是多少度?A. 90°B. 180°C. 270°D. 360°答案:B7. 以下哪个选项是方程2x - 3 = 7的解?A. x = 5B. x = 3C. x = 2D. x = 4答案:A8. 一个正数的倒数是?A. 比它小的数B. 比它大的数C. 0D. 1除以这个数答案:D9. 以下哪个选项是方程x^2 - 5x + 6 = 0的解?A. x = 2B. x = 3C. x = 6D. x = 9答案:A10. 一个数的立方根是它本身的数是?A. 0B. 1C. -1D. 以上都是答案:D二、填空题(每题4分,共20分)11. 一个数的绝对值是它本身,那么这个数是______。
答案:非负数12. 如果一个角的补角是120°,那么这个角是______。
答案:60°13. 一个数的相反数是-5,那么这个数是______。
答案:514. 一个直角三角形的两直角边长分别为3和4,那么它的斜边长是______。
答案:515. 如果一个数的平方是25,那么这个数是______。
中考巨难数学试卷及答案

一、选择题(每题5分,共50分)1. 已知函数f(x) = 2x^3 - 3x^2 + 4x + 1,若f(x)在x=1处的切线斜率为k,则k的值为:A. 1B. 2C. 3D. 4答案:B解析:由导数的定义,f'(x) = 6x^2 - 6x + 4,代入x=1得f'(1) = 6 - 6 + 4= 4,所以切线斜率k=4。
2. 在等差数列{an}中,a1=1,公差d=2,则第10项an的值为:A. 19B. 20C. 21D. 22答案:A解析:由等差数列的通项公式an = a1 + (n-1)d,代入a1=1,d=2,n=10,得an= 1 + (10-1)×2 = 1 + 18 = 19。
3. 已知三角形ABC中,AB=AC,BC=4,则角A的正弦值为:A. 1/2B. √2/2C. √3/2D. 1答案:C解析:由勾股定理,AB=AC=√(BC^2/4) = √(4^2/4) = √4 = 2。
在直角三角形ABC中,sinA = 对边/斜边 = BC/AB = 4/2 = 2。
4. 若复数z满足|z-1|+|z+1|=4,则复数z对应的点在复平面上的轨迹是:A. 矩形B. 等腰梯形C. 矩形D. 等腰梯形答案:B解析:由复数的几何意义,|z-1|表示点z到点(1,0)的距离,|z+1|表示点z到点(-1,0)的距离。
因为|z-1|+|z+1|=4,所以点z到这两个点的距离之和为4,对应的轨迹是一个等腰梯形。
5. 已知函数f(x) = ax^2 + bx + c,若f(1) = 2,f'(2) = 6,则a+b+c的值为:A. 2B. 3C. 4D. 5答案:B解析:由导数的定义,f'(x) = 2ax + b,代入x=2得f'(2) = 4a + b = 6。
又因为f(1) = a + b + c = 2,解得a+b+c=3。
二、填空题(每题5分,共25分)6. 已知函数f(x) = x^2 - 4x + 3,则f(x)的图像与x轴的交点坐标为______。
初三超难数学试卷及答案

一、选择题(每题5分,共50分)1. 已知等差数列{an}中,a1=3,公差d=2,则第10项a10等于:A. 15B. 17C. 19D. 212. 下列函数中,定义域为实数集R的是:A. y = √(x^2 - 4)B. y = 1/xC. y = |x|D. y = √(-x)3. 在直角坐标系中,点A(1, 2),点B(-3, 4),点C(m, n)在直线y = kx + b上,且ABC是等腰直角三角形,则m和n的值分别为:A. m=1,n=2B. m=-1,n=2C. m=1,n=-2D. m=-1,n=-24. 若等比数列{an}中,a1=2,公比q=√2,则数列的前n项和S_n等于:A. 2^nB. 2^n - 1C. 2^(n+1) - 2D. 2^(n+1) - 15. 已知函数f(x) = ax^2 + bx + c,若f(-1) = 0,f(1) = 0,且f(0) = 3,则a、b、c的值分别为:A. a=1,b=0,c=3B. a=1,b=0,c=-3C. a=-1,b=0,c=3D. a=-1,b=0,c=-36. 在等边三角形ABC中,点D在边BC上,且BD = DC,若∠BDC = 60°,则∠ADC等于:A. 30°B. 60°C. 90°D. 120°7. 若方程x^2 - 4x + 3 = 0的两个根分别为α和β,则(α+β)^2的值为:A. 16B. 14C. 12D. 108. 在平面直角坐标系中,点P(a, b)到原点O的距离为√(a^2 + b^2),若点P在直线y = x上,则a和b的值分别为:A. a=1,b=1B. a=1,b=-1C. a=-1,b=1D. a=-1,b=-19. 若函数y = log_2(x+1)的图像关于直线y = x对称,则该函数的定义域为:A. (-1, +∞)B. [0, +∞)C. (0, +∞)D. (-∞, -1)10. 在平面直角坐标系中,点A(2, 3),点B(-3, 4),若直线AB的斜率为k,则k 的值为:A. -1/5B. 1/5C. 5D. -5二、填空题(每题5分,共25分)11. 若等差数列{an}中,a1=1,公差d=2,则第n项an的表达式为______。
初三数学重点难点几何题及答案
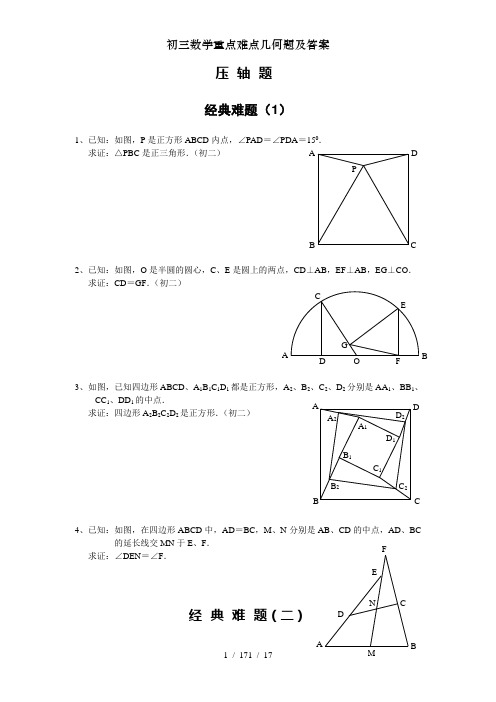
压轴题 经典难题(1)1、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)2、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A FG CEBO D A P C D BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初三数学难考试卷及答案

1. 下列各数中,属于有理数的是()A. √3B. πC. 2/3D. √-1答案:C2. 下列各式中,正确的是()A. 2^3 = 2^2 × 2B. (a+b)^2 = a^2 + b^2C. (a-b)^2 = a^2 - b^2D. (a+b)(a-b) = a^2 - b^2答案:D3. 已知函数f(x) = 2x - 1,若f(x) > 0,则x的取值范围是()A. x > 1/2B. x < 1/2C. x > 1D. x < 1答案:A4. 下列各式中,与x^2 - 4x + 4 = 0同解的是()A. x^2 + 4x + 4 = 0B. x^2 - 4x - 4 = 0C. x^2 + 4x - 4 = 0D. x^2 - 4x + 5 = 0答案:B5. 已知一次函数y = kx + b(k≠0),若k > 0,b < 0,则函数图象在()A. 第一、三象限B. 第一、二象限C. 第一、四象限D. 第二、四象限答案:C二、填空题(每题5分,共20分)6. 已知二次函数y = ax^2 + bx + c(a≠0),若a > 0,b < 0,则函数图象开口向上,顶点坐标为()。
答案:(-b/2a,c - b^2/4a)7. 若两个数x和y满足x^2 + y^2 = 1,则x + y的取值范围是()。
答案:(-√2,√2)8. 已知一次函数y = kx + b(k≠0),若k < 0,b > 0,则函数图象在()。
答案:第二、四象限9. 若二次函数y = ax^2 + bx + c(a≠0)的顶点坐标为(h,k),则函数图象的对称轴方程是()。
答案:x = h10. 若一次函数y = kx + b(k≠0)的图象经过点(2,3),则k和b的值分别是()。
答案:k = 1/2,b = 5/2三、解答题(每题10分,共20分)11. 已知二次函数y = -x^2 + 2x + 1,求该函数的顶点坐标和开口方向。
超难的初三数学试卷及答案

1. 若实数a、b满足a + b = 5,ab = 6,则a² + b²的值为:A. 29B. 25C. 21D. 112. 在直角坐标系中,点A(2,3)关于直线y = x的对称点为:A.(3,2)B.(-3,-2)C.(-2,3)D.(2,-3)3. 已知函数f(x) = 2x + 1,若f(x)的值域为[3,7],则x的取值范围为:A. [1,3]B. [1,2]C. [2,3]D. [1,4]4. 在等腰三角形ABC中,AB = AC,AD是底边BC上的高,且AD = 6,AB = 8,则BC的长度为:A. 10B. 12C. 14D. 165. 若等差数列{an}的前n项和为Sn,且S5 = 15,S10 = 50,则公差d为:A. 1B. 2C. 3D. 46. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数为:A. 75°B. 105°C. 120°D. 135°7. 已知函数f(x) = x² - 4x + 3,若f(x)在区间[1,3]上的最大值为2,则x的值为:A. 1B. 2C. 3D. 48. 在平面直角坐标系中,点P的坐标为(-2,3),点Q在直线y = -x上,且PQ = 5,则点Q的坐标为:A.(3,-2)B.(-3,2)C.(2,-3)D.(-2,3)9. 若x,y是方程x² - 4x + 4 = 0的两个实数根,则x + y的值为:A. 2B. 4C. 6D. 810. 在△ABC中,若AB = AC,且∠B = 30°,则∠A的度数为:A. 60°B. 90°C. 120°D. 150°11. 若等差数列{an}的首项为2,公差为3,则第10项an的值为______。
12. 在直角坐标系中,点A(1,2)关于原点的对称点为______。
初三的高难度数学试卷答案

1. 已知等差数列{an}中,a1=2,d=3,则a10的值为()A. 29B. 32C. 35D. 38答案:C解析:由等差数列的通项公式an=a1+(n-1)d,代入a1=2,d=3,n=10,得a10=2+(10-1)×3=35。
2. 若x2+2x-3=0,则x+1的值为()A. 1B. -2C. 3D. -1答案:A解析:将x+1代入原方程,得(x+1)2+2(x+1)-3=0,即x2+4x=0,解得x=0或x=-4,因此x+1=1或-3,选A。
3. 已知正方形的对角线长为10,则该正方形的面积为()A. 50B. 100C. 200D. 500答案:B解析:设正方形的边长为a,则a2+(a/√2)2=10,解得a=5√2,所以正方形的面积为a2=50。
4. 若函数f(x)=x2-2x+1在区间[1,2]上的最大值为4,则函数g(x)=2x2-4x+1在区间[1,2]上的最大值为()A. 3B. 4C. 5D. 6答案:C解析:由f(x)=x2-2x+1在区间[1,2]上的最大值为4,可知f(x)在区间[1,2]上的最大值点为x=2,所以g(x)在区间[1,2]上的最大值点为x=2,代入g(x)得g(2)=2×22-4×2+1=5。
5. 已知等比数列{an}中,a1=1,q=2,则a6的值为()A. 64B. 32C. 16D. 8答案:A解析:由等比数列的通项公式an=a1×q^(n-1),代入a1=1,q=2,n=6,得a6=1×2^(6-1)=64。
二、填空题(每题5分,共25分)1. 若函数f(x)=ax2+bx+c在区间[1,2]上的最大值为3,则a+b+c=()答案:5解析:由题意可知,函数f(x)在区间[1,2]上的最大值点为x=2,代入f(x)得f(2)=4a+2b+c=3,所以a+b+c=5。
2. 若函数g(x)=2x+1在区间[-1,1]上的最小值为-1,则g(x)在区间[-2,2]上的最大值为()答案:5解析:由题意可知,函数g(x)在区间[-1,1]上的最小值点为x=-1,代入g(x)得g(-1)=-1,所以g(x)在区间[-2,2]上的最大值点为x=2,代入g(x)得g(2)=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习一1.已知BC 是半径为2cm 的圆内的一条弦,点A 为圆上除点B C ,外任意一点,若BC =,则BAC ∠的度数为 .2.若a b ,均为整数,当1x =时,代数式2x ax b ++的值为0,则b a 的算术平方根为 . 3.如图(1),在等腰三角形ACB 中,5AC BC ==,8AB =,D 为底边AB 上一动点(不与点A B ,重合),DE AC ⊥,DF BC ⊥,垂足分别为E F ,,则DE DF +44条,从位置A 出右行进,两步向上行进,如果用用数字“1”表示向右行进,数字“2”表示向上行进,那么“11221”与“11212”就表示两种符合要求的不同走法,请你思考后回答:符合要求的不同走法共有 种. 5.(1)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果n a (n 为正整数)表示这个数列的第n 项,那么18a = ,n a = ; (2)如果欲求232013333+++++的值,可令232013333S =+++++……………………………………………………① 将①式两边同乘以3,得………………………………………………………② 由②减去①式,得S = .(3)用由特殊到一般的方法知:若数列123n a a a a ,,,,,从第二项开始每一项与前一项之比的常数为q ,则n a = (用含1a q n ,,的代数式表示),如果这个常数1q ≠,那么123n a a a a ++++= (用有含1a q n ,,的代数式表示).练习二1.如图(4),在ABC △中,5AB =,3BC =,4AC =,动点E (与点A C ,不重合)在AC 边上,EF AB ∥交BC 于F 点.(1)当ECF △的面积与四边形EABF 的面积相等时,求CE 的长; (2)当ECF △的周长与四边形EABF 的周长相等时,求CE 的长;(3)试问在AB 上是否存在点P ,使得EFP △为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF 的长.图(2) 图(1)2.如图(5),已知平行四边形ABCD 的顶点A 的坐标是(016),,AB 平行于x 轴,B C D ,,三点在抛物线2425y x =上,DC 交y 轴于N 点,一条直线OE 与AB 交于E 点,与DC 交于F 点,如果E 点的横坐标为a ,四边形ADFE 的面积为1352.(1)求出B D ,两点的坐标; (2)求a 的值;(3)作ADN △的内切圆P ,切点分别为M K H ,,,求tan PFM ∠的值.练习三1.有甲、乙、丙三种商品,如果购甲3件、乙2件,丙1件共需315元钱,购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需 元钱.2.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面3.如图,在34⨯的矩形方格图中,不包含阴影部分的矩形个数是 个. 4.如图,当四边形PABN 的周长最小时,a =.5.如图,ABC △内接于O ,60BAC ∠=,点D 是BC 的中点.BC AB ,边上的高AE CF ,相交于点H .图(4)图(5)(2题1(3题图)x(4题图)试证明:(1)FAH CAO ∠=∠;(2)四边形AHDO 是菱形.练习四5.阅读下列内容后,解答下列各题:几个不等于0的数相乘,积的符号由负因数的个数决定. 例如:考查代数式(1)(2)x x --的值与0的大小 当1x <时,10x -<,20x -<,(1)(2)0x x ∴--> 当12x <<时,10x ->,20x -<,(1)(2)0x x ∴--< 当2x >时,10x ->,20x ->,(1)(2)0x x ∴--> 综上:当12x <<时,(1)(2)0x x --< 当1x <或2x >时,(1)(2)0x x --> (1+(2x 满足 时,(2)(1)(3)(4)0x x x x ++--<(3)运用你发现的规律,直接写出当x 满足 时,(7)(8)(9)0x x x -+-<. 6.“512”汶川大地震后,某药业生产厂家为支援灾区人民,准备捐赠320箱某种急需药品,该厂家备有多辆甲、乙两种型号的货车,如果单独用甲型号车若干辆,则装满每车后还余20箱未装;如果单独用同样辆数的乙型号车装,则装完后还可以再装30箱,已知装满时,每辆甲型号车比乙型号车少装10箱. (1)求甲、乙两型号车每辆车装满时,各能装多少箱药品?(2)已知将这批药品从厂家运到灾区,甲、乙两型号车的运输成本分别为320元/辆和350元/辆.设派出甲型号车u 辆,乙型号车v 辆时,运输的总成本为z 元,请你提出一个派车方案,保证320箱药品装完,且运输总成本z 最低,并求出这个最低运输成本为多少元?练习五1.已知25350x x --=,则22152525x x x x --=-- . 2.把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止.那么2007,2008,2009,2010这四个数中 可能是剪出的纸片数. 3.阅读材料: 如图,ABC △中,AB AC =,P 为底边BC 上任意一点,点P 到两腰的距离分别为12r r ,,腰上的高为h ,连接AP ,则ABP ACP ABC S S S +=△△△. 即:12111222AB r AC r AB h +=12r r h ∴+=(定值).(1)理解与应用如图,在边长为3的正方形ABCD 中,点E 为对角线BD 上的一点,且BE BC =,F 为CE 上一点,FM BC ⊥于M ,FN BD ⊥于N ,试利用上述结论求出FM FN +的长.(2)类比与推理如果把“等腰三角形”改成“等边三角形”,那么P 的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边ABC △内任意一点P 到各边的距离分别为123r r r ,,,等边ABC △的高为h ,试证明123r r r h ++=(定值).(3)拓展与延伸若正n 边形12n A A A 内部任意一点P 到各边的距离为12n r r r ,请问是12n r r r +++是否为定值,如果是,请合理猜测出这个定值.练习六1.如图所示,将ABC △沿着DE 翻折,若1280∠+∠=°,则B ∠=.2.已知Rt ABC △的周长是4+2,则ABC S =△ . 3.我市部分地区近年出现持续干旱现象,为确保生产生活用水,某村决定由村里提供一点,村民捐一点的办法筹集资金维护和新建一批储水池.该村共有243户村民,准备维护和新建的储水池共有20个,费用和可供使用的户数及用地情况如x y 万元.(1)求y 与x 之间的函数关系; (2)满足要求的方案各有几种;(3)若平均每户捐2000元时,村里出资最多和最少分别是多少? 4.如图所示,已知点(10)A -,,(30)B ,,(0)C t ,,且0t >,tan 3BAC ∠=,抛物线经ACPr 1r 2 h DCB A ENF M C A B P r 1r 3 r 2h过A 、B 、C 三点,点(2)P m ,是抛物线与直线:(1)l y k x =+的一个交点. (1)求抛物线的解析式;(2)对于动点(1)Q n ,,求PQ QB +的最小值; (3)若动点M 在直线l 上方的抛物线上运动,求AMP △的边AP 上的高h 的最大值.练习七1.已知2510m m --=,则22125m m m-+=___________. 2.下面的方格图案中的正方形顶点叫做格点,图1中以格点为顶点的等腰直角三角形共有4个,图2中以格点为顶点的等腰直角三角形共有___________个,图3中以格点为顶点的等腰直角三角形共有___________个,图4中以格点为顶点的等腰直角三角形共有___________个.3.已知非负数a b c ,,满足条件75a b c a +=-=,,设S a b c =++的最大值为m ,最小值为n ,则m n -的值为___________.4.如图,在ABC △中,AB AC =,点E F 、分别在AB 和AC 上,CE 与BF 相交于点D ,若AE CF D =,为BF 的中点,AE AF :的值为___________.5.如图,抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点,与y 轴交于C 点. (1)请求出抛物线顶点M 的坐标(用含m 的代数式表示),A B 、两点的坐标; (2)经探究可知,BCM △与ABC △的面积比不变,试求出这个比值;(3)是否存在使BCM △为直角三角形的抛物线?若存在,请求出;如果不存在,请说明 理由.练习八1.阅读理解:我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点()()1122P x y Q x y ,、,的对称中心的坐标为1212.22x x y y ++⎛⎫⎪⎝⎭, 观察应用:(1)如图,在平面直角坐标系中,若点()()120123P P -、,的对称中心是点A ,则点A 的坐标为_________; (2)另取两点()()1.62.110.B C --,、,有一电子青蛙从点1P 处开始依次关于点A B C 、、作循环对称跳动,即第一次跳到点1P 关于点A 的对称点2P 处,接着跳到点2P 关于点B 的对称点3P 处,第三次再跳到点3P 关于点C 的对称点4P 处,第四次再跳到点4P 关于点A 的对称点5P 处,…则点38P P 、的坐标分别为_________、_________. 拓展延伸:(3)求出点2012P 的坐标,并直接写出在x 轴上与点O A CB x y2012P 、点C 构成等腰三角形的点的坐标.2.如图,在Rt ABC △中,90C ∠=°,点E 在斜边AB 上,以AE 为直径的O ⊙与BC 相切于 点.D(1)求证:AD 平分.BAC ∠ (2)若3 4.AC AE ==,①求AD 的值;②求图中阴影部分的面积.练习九1.若201120121m =-,则54322011m m m --的值是_________2.如图,在△ABC 中,点D 、E 分别是边AB 、AC 的中点,DF 过EC 的中点G 并与BC 的延长线交于点F ,BE 与DE 交于点O .若△ADE 的面积为S ,则四边形B0GC 的面积= _________3.已知263(5)36(3)m n m m n -+----,则m n -=4.在直角坐标系中,正方形1111A B C O 、2221A B C C 、…、n n n n-1A B C C 按如图所示的方式放置,其中点123A A A 、、、…、n A 均在一次函数y kx b =+的图象上,点123C 、C 、C 、…、n C 均在x 轴上.若点1B 的坐标为(1,1),点2B 的坐标为(3,2),则点n A 的坐标为_________5.小英和小明姐弟二人准备一起去观看端午节龙舟赛.但因家中临时有事,必须留下一人在家,于是姐弟二人采用游戏的方式来确定谁去看龙舟赛.游戏规则是:在不透明的口袋中分别放入2个白色和1个黄色的乒乓球,它们除颜色外其余都相同.游戏时先由小英从口袋中任意摸出1个乒乓球记下颜色后放回并摇匀,再由小明从口袋中摸出1个乒乓球,记下颜色.如果姐弟二人摸到的乒乓球颜色相同.则小英赢,否则小明赢.(1)请用树状图或列表的方法表示游戏中所有可能出现的结果. (2)这个游戏对游戏双方公平吗?请说明理由.练习十1.同学们,我们曾经研究过n ×n 的正方形网格,得到了网格中正方形的总数的表达式为2222123...n ++++.但n 为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道1011223...(1)(1)(1)3n n n n n ⨯+⨯+⨯++-⨯=+-时,我们可以这样做:(1)观察并猜想:2212+=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2) 222123++=(1+0)×1+(1+1)×2+(l+2)×3 =1+0×1+2+1×2+3+2×3=(1+2+3)+(0×1+1×2+2×3)22221234+++=(1+0)×1+(1+1)×2+(l+2)×3+ ___________ =1+0×1+2+1×2+3+2×3+ ___________ =(1+2+3+4)+(___________) …(2)归纳结论:2222123...n ++++=(1+0)×1+(1+1)×2+(1+2)×3+…[1+(n-l )]n =1+0×1+2+1×2+3+2×3+…+n+(n-1)×n =(___________)+[ ___________] = ___________+ ___________ =16×___________(3 )实践应用:通过以上探究过程,我们就可以算出当n 为100时,正方形网格中正方形的总个数是_________。
