离散数学及应用课后习题答案
离散数学及其应用集合论部分课后习题答案

34、设A,B为集合,证明:如果 ,则 。
证明:(反证法)
设 ,则 ,
所以 ;
所以
但是 。
与 矛盾。
37、设A,B,C为任意集合,证明: 。
证明:
对任意 ,由于 ,所以 且 所以
因此, 。
P121:习题七
5、设A,B为任意集合,证明
若 ,则 。
证明:
所以有
9、设 ,列出下列关系R
(2)
(3)
解答:
(2)不是,由于 集合较小,
①自反性:
②对称性,
但是传递性不满足, ,但是 。
(3)不是,满足对称性、传递性,但是不满足自反性
取 ,但是 不为奇数,所以 。
(5)满足
①自反性:
②对称性:
③传递性:
下面证明
若 ,则 ,所以
若 ,则 ,所以
所以 ,同理可证,
所以
所以 。因此满足传递性。
27、设 A上的等价关系
(2)不存在反函数,因为不是双射函数;
(3)
22、对于以下集合A和B,构造从A到B的双射函数。
(1)
(2)
(3)
(4)
解答:
(1)
(2)
(3)
(4)
作业答案:集合论部分
P90:习题六
5、确定下列命题是否为真。
(2)
(4)
(6)
解答:(2)假(4)真(6)真
8、求下列集合的幂集。
(5)
(6)
解答:
(5)集合的元素彼此互不相同,所以 ,所以该题的结论应该为
(6)
9、设 , , , ,求下列集合。
(1)
(2)
解答:
(1)
离散数学课后习题答案(最新)

习题参考解答习题1.11、(3)P:银行利率降低Q:股价没有上升P∧Q(5)P:他今天乘火车去了北京Q:他随旅行团去了九寨沟PQ(7)P:不识庐山真面目Q:身在此山中Q→P,或~P→~Q(9)P:一个整数能被6整除Q:一个整数能被3整除R:一个整数能被2整除T:一个整数的各位数字之和能被3整除P→Q∧R ,Q→T2、(1)T (2)F (3)F (4)T (5)F(6)T (7)F (8)悖论习题 1.31(3))()()()()()(R P Q P R P Q P R Q P R Q P →∨→⇔∨⌝∨∨⌝⇔∨∨⌝⇔∨→(4)()()()(())()(()())(())()()()()P Q Q R R P P R Q R P P R R P Q R P P R P R Q R Q P ∧∨∧∨∧=∨∧∨∧=∨∨∧∧∨∧=∨∧∨∧∨∧∨=右2、不, 不, 能习题 1.41(3) (())~((~))(~)()~(~(~))(~~)(~)P R Q P P R Q P P R T P R P R Q Q P R Q P R Q →∧→=∨∧∨=∨∧=∨=∨∨∧=∨∨∧∨∨、主合取范式)()()()()()()()()()()()()()())(())(()()(())()())(()((Q P R P Q R P Q R R Q P R Q P R Q P Q P R Q P R P Q R P Q R R Q P R Q P R Q P R Q P Q Q P R P P Q R R R Q Q P P R Q R P P Q R P P Q R P ∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∧∧∨⌝∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∨⌝∧∧∨∨⌝∧⌝∧∨∨⌝∧∨⌝∧⌝=∧∨⌝∧∨⌝=∨⌝∧∨⌝=→∧→ ————主析取范式(2) ()()(~)(~)(~(~))(~(~))(~~)(~)(~~)P Q P R P Q P R P Q R R P R Q Q P Q R P Q R P R Q →∧→=∨∧∨=∨∨∧∧∨∨∧=∨∨∧∨∨∧∨∨ 2、()~()(~)(~)(~~)(~)(~~)P Q R P Q R P Q P R P Q R P Q R P R Q →∧=∨∧=∨∧∧=∨∨∧∨∨∧∨∨∴等价3、解:根据给定的条件有下述命题公式:(A →(C ∇D ))∧~(B ∧C )∧~(C ∧D )⇔(~A ∨(C ∧~D )∨(~C ∧D ))∧(~B ∨~C )∧(~C ∨~D )⇔((~A ∧~B )∨(C ∧~D ∧~B )∨(~C ∧D ∧~B )∨(~A ∧~C )∨(C ∧~D ∧~C )∨(~C ∧D ∧~C ))∧(~C ∨~D )⇔((~A ∧~B )∨(C ∧~D ∧~B )∨(~C ∧D ∧~B )∨(~A ∧~C )∨(~C ∧D ∧~C )) ∧(~C ∨~D )⇔(~A ∧~B ∧~C )∨(C ∧~D ∧~B ∧~C )∨(~C ∧D ∧~B ∧~C )∨ (~A ∧~C ∧~C )∨(~C ∧D ∧~C ∧~C )∨(~A ∧~B ∧~D )∨(C ∧~D ∧~B ∧~D )∨(~C ∧D ∧~B ∧~D )∨(~A ∧~C ∧~D )∨ (~C ∧D ∧~C ∧~D )(由题意和矛盾律)⇔(~C ∧D ∧~B )∨(~A ∧~C )∨(~C ∧D )∨(C ∧~D ∧~B )⇔(~C ∧D ∧~B ∧A )∨ (~C ∧D ∧~B ∧~A )∨ (~A ∧~C ∧B )∨ (~A ∧~C ∧~B )∨ (~C ∧D ∧A )∨ (~C ∧D ∧~A )∨(C ∧~D ∧~B ∧A )∨(C ∧~D ∧~B ∧~A )⇔(~C ∧D ∧~B ∧A )∨ (~A ∧~C ∧B ∧D )∨ (~A ∧~C ∧B ∧~D )∨(~A ∧~C ∧~B ∧D )∨ (~A ∧~C ∧~B ∧~D )∨(~C ∧D ∧A ∧B )∨ (~C ∧D ∧A ∧~B )∨ (~C ∧D ∧~A ∧B )∨ (~C ∧D ∧~A ∧~B )∨(C ∧~D ∧~B ∧A )∨(C ∧~D ∧~B ∧~A ) ⇔(~C ∧D ∧~B ∧A )∨ (~A ∧~C ∧B ∧D )∨ (~C ∧D ∧A ∧~B )∨ (~C ∧D ∧~A ∧B ) ∨(C ∧~D ∧~B ∧A )⇔(~C ∧D ∧~B ∧A )∨ (~A ∧~C ∧B ∧D )∨(C ∧~D ∧~B ∧A ) 三种方案:A 和D 、 B 和D 、 A 和C习题 1.51、 (1)需证()(())P Q P P Q →→→∧为永真式()(())~(~)(~())~~(~)(()(~))~(~)(~)()P Q P P Q P Q P P Q P P P Q P Q TP Q P Q T P Q P P Q →→→∧=∨∨∨∧∨=∨∨∧∨=∨∨∨=∴→⇒→∧(3)需证S R P P →∧⌝∧为永真式SR P P T S F S R F S R P P ⇒∧⌝∧∴⇔→⇔→∧⇔→∧⌝∧3A B A B ⇒∴→ 、为永真式。
离散数学习题答案解析

离散数学习题答案解析(总16页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p:李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语∧解:设p:王强学过法语;q:刘威学过法语;则命题符号化的结果是p q(9)只有天下大雨,他才乘班车上班→解:设p:天下大雨;q:他乘班车上班;则命题符号化的结果是q p (11)下雪路滑,他迟到了解:设p:下雪;q:路滑;r:他迟到了;则命题符号化的结果是()∧→p q r 15、设p:2+3=5.q:大熊猫产在中国.r:太阳从西方升起.求下列复合命题的真值:(4)()(())∧∧⌝↔⌝∨⌝→p q r p q r解:p=1,q=1,r=0,∧∧⌝⇔∧∧⌝⇔,p q r()(110)1p q r⌝∨⌝→⇔⌝∨⌝→⇔→⇔(())((11)0)(00)1∴∧∧⌝↔⌝∨⌝→⇔↔⇔()(())111p q r p q r19、用真值表判断下列公式的类型:(2)()→⌝→⌝p p q解:列出公式的真值表,如下所示:由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值: (4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值: (2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式, 所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式, 所以成假赋值为100。
离散数学及其应用张剑妹课后答案

离散数学及其应用张剑妹课后答案1、14.在防治新型冠状病毒的例行体温检查中,检查人员将高出37℃的部分记作正数,将低于37℃的部分记作负数,体温正好是37℃时记作“0”。
记录一被测人员在一周内的体温测量结果分别为+1,-3,-5,+1,-6,+2,-4,那么,该被测者这一周中测量体温的平均值是(??)[单选题] *A.1℃B.31℃C.8℃(正确答案)D.69℃2、37、已知A(3,﹣2),B(1,0),把线段AB平移至线段CD,其中点A、B分别对应点C、D,若C(5,x),D(y,0),则x+y的值是()[单选题] *A.﹣1B.0C.1(正确答案)D.23、下列计算正确的是()[单选题] *A. a2+a2=2a?B. 4x﹣9x+6x=1C. (﹣2x2y)3=﹣8x?y3(正确答案)D. a6÷a3=a24、如果四条不共点的直线两两相交,那么这四条直线()[单选题] *A、必定在同一平面内B、必定在同一平面内C可能在同一平面内,也可能不在同一平面内(正确答案)D、无法判断5、-330°是第()象限角?[单选题] *第一象限(正确答案)第二象限第三象限第四象限6、6.若x是- 3的相反数,|y| = 5,则x + y的值为()[单选题] *A.2B.8C. - 8或2D.8或- 2(正确答案)7、18.下列说法正确的是()[单选题] *A.“向东10米”与“向西10米”不是相反意义的量B.如果气球上升25米记作+25米,那么-15米的意义就是下降-15米C.如果气温下降6℃,记为-6℃,那么+8℃的意义就是下降8℃D.若将高1米设为标准0,高20米记作+20米,那么-05米所表示的高是95米(正确答案)8、下列计算正确的是( ) [单选题] *A. 9a3·2a2=18a?(正确答案)B. 2x?·3x?=5x?C. 3 x3·4x3=12x3D. 3y3·5y3=15y?9、计算的结果是( ) [单选题] *A. -p2?(正确答案)B. p2?C. -p1?D. p1?10、已知二次函数f(x)=2x2-x+2,那么f(0)的值为()。
离散数学及其应用第2版课后练习题含答案

离散数学及其应用第2版课后练习题含答案1. 引言《离散数学及其应用》是一本经典的离散数学教材,是计算机科学和数学专业的必修课程。
本文将为读者提供《离散数学及其应用》第2版课后练习题的答案,并希望能够帮助读者加深对离散数学的理解。
2. 答案解析第一章习题 1.11.给定一组七个数字 {1, 3, 3, 4, 6, 9, 12},请给出这组数字的中位数。
答案:中位数为 4。
2.给出两个整数 a 和 b 的三进制表示: a = 111011,b = 101101。
求 a + b。
答案:a + b = 1011000。
3.证明奇奇数的积为奇数。
答案:令两个奇数分别为 2n + 1 和 2m +1,则有:(2n + 1) × (2m + 1) = 4nm + 2n + 2m + 1 = 2(2nm + n + m) + 1,即奇奇数的积还是一个奇数。
习题 1.21.证明:如果一个整数 n 能同时被 2 和 3 整除,则它也能被 6 整除。
答案:首先,n 能同时被 2 和 3 整除,则分别有 n = 2k 和 n = 3m。
联立方程组 2k = 3m,得 k = (3/2)m。
因此,n = 2k = (3m/2) × 2 = 3m× (2/2) = 6m,可以被 6 整除。
2.求 10010 的八进制表示。
答案:将 10010 转换为四位一组的二进制数,得 0010 0100。
将 0010 和 0100 分别转换为八进制数,得 2 和 4。
因此,10010 的八进制表示为 24。
3.已知 547a5 是 11 的倍数,求 a 的值。
答案:根据 11 的倍数的规律,将 547a5 中的奇数位数字相加,再将偶数位数字相加,然后将两个和的差求出来: (5 + 7 + a) - (4 + 5) = 13 + a - 9 = a + 4。
因为547a5 是 11 的倍数,所以 a + 4 也必须是 11 的倍数。
(完整版)离散数学及其应用(课后习题)

习题1.12. 指出下列命题是原子命题还是复合命题。
(3)大雁北回,春天来了。
(4)不是东风压倒西风,就是西风压倒东风。
(5)张三和李四在吵架。
解:(3)和(4)是复合命题,(5)是原子命题。
习题1.21. 指出下列命题的真值:(1)若224+>,则太阳从西方升起。
解:该命题真值为T (因为命题的前件为假)。
(3)胎生动物当且仅当是哺乳动物。
解:该命题真值为F (如鸭嘴兽虽是哺乳动物,但不是胎生动物)。
2. 令P :天气好。
Q :我去公园。
请将下列命题符号化。
(2)只要天气好,我就去公园。
(3)只有天气好,我才去公园。
(6)天气好,我去公园。
解:(2)P Q →。
(3)Q P →。
(6)P Q ↔。
习题1.32. 将下列命题符号化(句中括号内提示的是相应的原子命题的符号表示): (1)我去新华书店(P ),仅当我有时间(Q )。
(3)只要努力学习(P ),成绩就会好的(Q )。
(6)我今天进城(P ),除非下雨(Q )。
(10)人不犯我(P ),我不犯人(Q );人若犯我,我必犯人。
解:(1)P Q →。
(3)P Q →。
(6)Q P ⌝→。
(10)()()P Q P Q ⌝→⌝∧→。
习题1.41. 写出下列公式的真值表: (2)()P Q R ∨→。
解:该公式的真值表如下表:2. 证明下列等价公式:(2)()()()P Q P Q P Q ∨∧⌝∧⇔⌝↔。
证明:()(()()) ()()) ()() ()()P Q P Q P Q P Q P Q P Q P Q P Q P Q ⌝↔⇔⌝∧∨⌝∧⌝⇔⌝∧∧⌝⌝∧⌝⇔⌝∧∧∨⇔∨∧⌝∧(4)()()()P Q P R P Q R →∧→⇔→∧。
证明:()()()() () ()P Q P R P Q P R P Q R P Q R →∧→⇔⌝∨∧⌝∨⇔⌝∨∧⇔→∧3. 甲、乙、丙、丁4人参加考试后,有人问他们谁的成绩最好,甲说,不是我。
离散数学及其应用数理逻辑部分课后习题答案

作业答案:数理逻辑部分P14:习题一1、下列句子中,哪些是命题?在是命题的句子中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道?(3 答:简单命题,真命题。
(9)吸烟请到吸烟室去! 答:不是命题。
(12)8是偶数的充分必要条件是8能被3整除。
答:复合命题,假命题。
14、讲下列命题符号化。
(6)王强与刘威都学过法语。
答::p 王强学过法语;:q 刘威学过法语。
符号化为:p q ∧(10)除非天下大雨,他就乘班车上班。
答::p 天下大雨;:q 他乘班车上班。
符号化为:p q →(13)“2或4是素数,这是不对的”是不对的。
答::p 2是素数;:q 4是素数。
符号化为:(())p q ⌝⌝∨15、设:p 2+3=5. :q 大熊猫产在中国。
:r 太阳从西方升起。
求下列复合命题的真值。
(2)(())r p q p →∧↔⌝(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→ 解答: p 真值为1;q 真值为1;r 真值为0.(2)p q ∧真值为1;()r p q →∧真值为1;p ⌝真值为0;所以(())r p q p →∧↔⌝真值为0.(4)p q r ∧∧⌝真值为1,p q ⌝∨⌝真值为0,()p q r ⌝∨⌝→真值为1;所以()(())p q r p q r ∧∧⌝↔⌝∨⌝→真值为1.19、用真值表判断下列公式的类型。
(4)()()p q q p →→⌝→⌝所以为重言式。
(7)所以为可满足式。
P36:习题二3、用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出其成真赋值。
(1)()p q q ⌝∧→ 解答:()(())(())()10p q q p q q p q q p q q ⌝∧→⇔⌝⌝∧∨⇔⌝⌝∨⌝∨⇔⌝⌝∨⌝∨⇔⌝⇔所以为永假式。
(2)(())()p p q p r →∨∨→ 解答:(())()(())()()()1()1p p q p r p p q p r p p q p r p r →∨∨→⇔⌝∨∨∨⌝∨⇔⌝∨∨∨⌝∨⇔∨⌝∨⇔ 所以因为永真式。
离散数学及其应用第三版第二章计数问题课后答案

离散数学及其应用第三版第二章计数问题课后答案1、从3点到6点,分针旋转了多少度?[单选题] *90°960°-1080°(正确答案)-90°2、由数字1、2、3、4、5可以组成多少个不允许有重复数字的三位数?()[单选题]*A、125B、126C、60(正确答案)D、1203、已知5m-2n-3=0,则2??÷22?的值为( ) [单选题] *A. 2B. 0C. 4D. 8(正确答案)4、7.已知点A(-2,y1),B(3,y2)在一次函数y=-x+b的图象上,则( ) [单选题]* A.y1 > y2(正确答案)B.y1 < y2C.y1 ≤y2D.y1 ≥y25、若3x+4y-5=0,则8?·16?的值是( ) [单选题] *A. 64B. 8C. 16D. 32(正确答案)6、16.若过多边形的每一个顶点只有6条对角线,则这个多边形是()[单选题] * A.六边形B.八边形C.九边形(正确答案)D.十边形7、计算-(a-b)3(b-a)2的结果为( ) [单选题] *A. -(b-a)?B. -(b+a)?C. (a-b)?D. (b-a)?(正确答案)8、函数式?的化简结果是()[单选题] *A.sinα-cosαB.±(sinα-cosα)(正确答案)C.sinα·cosαD.cosα-sinα9、8.一个面积为120的矩形苗圃,它的长比宽多2米,苗圃长是()[单选题] *A 10B 12(正确答案)C 13D 1410、函数y=kx(k是不为0的常数)是()。
[单选题] *正比例函数(正确答案)一次函数反比例函数二次函数函数11、4、已知直角三角形的直角边边长分别是方程x2-14x+48=0的两个根,则此三角形的第三边是()[单选题] *A、6B、10(正确答案)C、8D、212、4.已知第二象限的点P(-4,1),那么点P到x轴的距离为( ) [单选题] *A.1(正确答案)B.4C.-3D.313、27.下列各函数中,奇函数的是()[单选题] *A. y=x^(-4)B. y=x^(-3)(正确答案)C .y=x^4D. y=x^(2/3)14、-120°用弧度制表示为()[单选题] *-2π/3(正确答案)2π/3-π/3-2π/515、函数y= 的最小正周期是()[单选题] *A、B、(正确答案)C、2D、416、下列说法中,正确的是()[单选题] *A、第一象限角是锐角B、第一象限角是锐角(正确答案)C、小于90°的角是锐角D、第一象限的角不可能是钝角17、1.(必修1P5B1改编)若集合P={x∈N|x≤2 022},a=45,则( ) [单选题] * A.a∈PB.{a}∈PC.{a}?PD.a?P(正确答案)18、9.已知关于x,y的二元一次方程组的解满足x+y=8,则k的值为( ) [单选题] * A.4B.5C.-6D.-8(正确答案)19、8.如果直角三角形的三条边为2,4,a,那么a的取值可以有()[单选题] *A. 0个B. 1个C. 2个D. 3个(正确答案)20、7.把点平移到点,平移方式正确的为()[单选题] *A.先向左平移3个单位长度,再向下平移2个单位长度B.先向左平移3个单位长度,再向上平移2个单位长度C.先向右平移3个单位长度,再向下平移2个单位长度D.先向右平移3个单位长度,再向上平移2个单位长度(正确答案)21、35、下列判断错误的是()[单选题] *A在第三象限,那么点A关于原点O对称的点在第一象限.B在第二象限,那么它关于直线y=0对称的点在第一象限.(正确答案)C在第四象限,那么它关于x轴对称的点在第一象限.D在第一象限,那么它关于直线x=0的对称点在第二象限.22、22、在平面直角坐标系中,已知点P,在轴上有点Q,它到点P的距离等于3,那么点Q的坐标是()[单选题] *(0,3)(0,5)(0,-1)(0,5)或(0,-1) (正确答案)23、5.下列说法中正确的是()[单选题] *A.没有最大的正数,但有最大的负数B.没有最小的负数,但有最小的正数C.没有最小的有理数,也没有最大的有理数(正确答案)D.有最小的自然数,也有最小的整数24、4.小亮用天平称得牛奶和玻璃杯的总质量为0.3546㎏,用四舍五入法将0.3546精确到0.01的近似值为()[单选题] *A.0.35(正确答案)B.0.36C.0.354D.0.35525、下列表示正确的是()[单选题] *A、0={0}B、0={1}C、{x|x2 =1}={1,-1}(正确答案)D、0∈φ26、22.如图棋盘上有黑、白两色棋子若干,找出所有使三颗颜色相同的棋在同一直线上的直线,满足这种条件的直线共有()[单选题] *A.5条(正确答案)B.4条C.3条D.2条27、已知2x=8,2y=4,则2x+y=()[单选题] *A 、32(正确答案)B 、33C、16D、428、28.已知点A(2,3)、B(1,5),直线AB的斜率是()[单选题] *A.2B.-2C.1/2D.-1/2(正确答案)29、x3??(m为正整数)可写成( ) [单选题] *A. x3+x?B. x3-x?C. x3·x?(正确答案)D. x3?30、已知x-y=3,x2-y2=12,那么x+y的值是( ??) [单选题] *A. 3B. 4(正确答案)C. 6D. 12。
离散数学及其应用(原书第8版本科教学版)肯尼思奇数题答案

离散数学及其应用(原书第8版本科教学版)肯尼思奇数题答案1. 引言离散数学是数学的一个重要分支,研究的对象是离散的数学结构,包括集合、逻辑、代数、图论等。
离散数学在计算机科学、信息技术、密码学等领域有着广泛的应用。
本文主要介绍《离散数学及其应用(原书第8版本科教学版)》一书中的肯尼思奇数题答案。
2. 肯尼思奇数题肯尼思奇数题是《离散数学及其应用》一书中的习题(Chapter 8, Exercise 52)。
题目如下:肯尼思有一袋子里装有若干只标有0或1的球。
每次他从袋子里取出一只球,查看其上的数字,并且将其放回袋子内。
他这样做999次。
最后,他从袋子里取出一个球独立地、查看其上的数字,并根据这个数字决定选课还是买彩票。
假设他在这999次中取出的数字的比例非常接近他最后一次取出的数字的比例:- 如果比例大于等于0.5,则他选择选课;- 如果比例小于0.5,则他选择买彩票。
试问肯尼思选择选课的概率是多少?3. 解答为了解决这个问题,我们可以应用一个离散数学中的概率理论的知识:大数定律(The Law of Large Numbers)。
大数定律指出,对于一个随机试验,若试验次数足够多,那么实验结果呈现的相对频率就接近于该事件的概率。
首先,我们定义一些符号: - N:在肯尼思进行999次试验后,比例大于等于0.5的次数。
- n:在肯尼思进行999次试验后,总共取出的球的数量。
- p:从袋子中取出一只球之后,它上面标有1的概率。
我们的目标是求解肯尼思选择选课的概率。
根据大数定律,我们可以得出以下等式:lim(N/n) = p这里,lim表示随着试验次数趋近无穷大,我们求得的相对频率趋近于概率。
根据题目信息,我们已经知道最后一次取出的球的数字将成为肯尼思决定选课还是买彩票的依据。
因此,我们可以得出以下等式:lim(N/n) = lim(N/(n+1)) = p注意,这个等式的右边是固定的,我们希望求解的是左边的lim(N/n)。
离散数学习题的答案解析

离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p :李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语解:设p :王强学过法语;q :刘威学过法语;则命题符号化的结果是p q ∧(9)只有天下大雨,他才乘班车上班解:设p :天下大雨;q :他乘班车上班;则命题符号化的结果是q p →(11)下雪路滑,他迟到了解:设p :下雪;q :路滑;r :他迟到了;则命题符号化的结果是()p q r ∧→15、设p :2+3=5.q :大熊猫产在中国.r :太阳从西方升起.求下列复合命题的真值:(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→解:p=1,q=1,r=0, ()(110)1p q r ∧∧⌝⇔∧∧⌝⇔,(())((11)0)(00)1p q r ⌝∨⌝→⇔⌝∨⌝→⇔→⇔()(())111p q r p q r ∴∧∧⌝↔⌝∨⌝→⇔↔⇔19、用真值表判断下列公式的类型:(2)()p p q →⌝→⌝解:列出公式的真值表,如下所示:20、求下列公式的成真赋值:(4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒00p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值:(2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式,所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值:(2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式,所以成假赋值为100。
离散数学课后习题答案 (2)

离散数学课后习题答案1. 第一章习题答案1.1 习题一答案1.1.1 习题一.1 答案根据题意,设集合A和B如下:Set A and BSet A and B在此情况下,我们可以得出以下结论:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }。
因此,习题一.1的答案为:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b,2), (b, 3) }。
1.1.2 习题一.2 答案根据题意,集合A和B如下所示:Set A and BSet A and B根据集合的定义,习题一.2要求我们判断以下命题的真假性:a)$A \\cap B = \\{ 2, 3 \\}$b)$\\emptyset \\in B$c)$A \\times B = \\{ (a, 2), (b, 1), (b, 3) \\}$d)$B \\subseteq A$接下来,我们来逐个判断这些命题的真假性。
a)首先计算集合A和B的交集:$A \\cap B = \\{ x\\,|\\, x \\in A \\, \\text{且} \\, x \\in B \\} = \\{ 2, 3 \\}$。
因此,命题a)为真。
b)大家都知道,空集合是任意集合的子集,因此空集合一定属于任意集合的幂集。
根据题意,$\\emptyset \\in B$,因此命题b)为真。
c)计算集合A和B的笛卡尔积:$A \\times B = \\{ (x, y) \\,|\\, x \\in A \\, \\text{且} \\, y \\in B \\} = \\{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \\}$。
应用离散数学(方景龙)课后答案

令原子命题 p :若下雪超过 20 公分,学校就停课, q :若温度低于 −10°C ,学校就 停课,则同或和异或分别符号化为: p ∨ q 和 ( p ∧ ¬q) ∨ (¬p ∧ q) 。
我认为该语句想表示的是“同或”。
6. 给出下列各蕴涵形式命题的逆命题、否命题和逆否命题。 (1)如果今天下雪,我明天就去滑雪。 (2)只要有测验,我就来上课。 (3)只有当正整数没有 1 和它自己以外的因数时,它才是质数。 解 (1)逆命题:如果我明天去滑雪,就今天会下雪;否命题:如果今天不下雪,我 明天就不去滑雪;逆否命题:如果我明天没去滑雪,今天就没下雪。 (2)逆命题:我来上课,就有测验;否命题:只要没有测验,我就不来上课;逆否命 题:我不来上课,就没有测验。 (3)逆命题:正整数是质数,则它没有 1 和它自己以外的因数;否命题:只有当正整 数有 1 和它自己以外的因数时,它才不是质数;逆否命题:正整数不是质数,则它有 1 和它 自己以外的因数。
§1.1 命题和逻辑连接词
习题 1.1
1. 下列哪些语句是命题,在是命题的语句中,哪些是真命题,哪些是假命题,哪些命题
的真值现在还不知道?
(1)中国有四大发明。
(2)你喜欢计算机吗?
(3)地球上海洋的面积比陆地的面积大。
(5) 2 + 3 = 6 。
(4)请回答这个问题!
(6) x + 7 < 10 。
(1)你的车速没有超过每小时 120 公里。 (2)你的车速超过了每小时 120 公里,但没接到超速罚款单。 (3)你的车速若超过了每小时 120 公里,将接到一张超速罚款单。 (4)你的车速不超过每小时 120 公里,就不会接到超速罚款单。 (5)你接到一张超速罚款单,但你的车速没超过每小时 120 公里。 (6)只要你接到一张超速罚款单,你的车速就肯定超过了每小时 120 公里。
3离散数学及其应用 英文版 第6版 课后答案(美 Kennenth H.Rosen 著) 机械工业出版社

P.161.14.f) If I did not buy a lottery ticket this week, then I did not win the million dollar jackpot on Friday.g) I did not buy a lottery ticket this week, and I did not win the million dollar jackpot on Friday.h ) Either I did not buy a lottery ticket this week, or else I did buy one and won the million dollar jackpot on Friday.10.a) r ∧┐q b) p ∧ q∧ r c)r → pd) p ∧┐q ∧ r e) (p ∧q) → r f) r↔ ( q ∨ p)20.a) If I am to remember to send you the address, then you will have to send me ane-mail message.(This has been slightly reworded so that the tenses make more sense.)b) If you were born in the United States, then you are a citizen of this country.c) If you keep your textbook, then it will be a useful reference in your future courses.(The word "then" is understood in English, even if omitted.)d) If their goaltender plays well, then the Red Wings will win the Stanley Cup.e) If you get the job, then you had the best credentials.f) If there is a storm, then the beach erodes.g) If you log on to the server, then you have a valid password.h) If you don’t begin your climb too late, then you will reach the summit.33.c)P.261.28.a) Kwame will not take a job in industry and he will not go to graduate school.b) Yoshiko doesn’t know Java or she doesn’t know calculus.c) James is not young or he is not strong.d) Rita will not move to Oregon and she will not move to Washington.10.a)c)12.a) Assume the hypothesis is true. Then p is false. Since p∨q is true, we conclude that q must be true.Here is a more "algebraic" solution:[┐p∧(p ∨q)]→q <=> ┐[┐p∧(p ∨q)]∨q <=> ┐┐p∨┐(p∨q)∨q <=> p∨┐(p∨q)∨q <=> (p ∨q)∨┐(p∨q) <=> Tc) Assume the hypothesis is true. Then p is true, and since the second part of the hypothesis is ture, we conclude that q is also true, as desired.51.((p ↓ p) ↓ q )↓((p ↓ p) ↓ q )7.The graph is planar.20.The graph is not homeomorphic to K3,3, since by rerouting the edge between a and h we seethat it is planar.22.Replace each vertex of degree two and its incident edges by a single edge. Then the result isK3,3 : the parts are {a,e,i} and {c,g,k}. Therefore this graph is homeomorphic to K3,3.23.The graph is planar.25. The graph is not planar.9.83. 3F E8. 310.417. time slot 1: Math 115, Math 185; time slot 2: Math 116, CS 473;time slot 3: Math 195, CS 101; time slot 4: CS 102time slot 5: CS 273P.461.33. a) true b) false c) false d) false5. a) There is a student who spends more than 5 hours every weekday in class.b) Every student spends more than 5 hours every weekday in class.c) There is a student who does not spend more than 5 hours every weekday in class.d) No student spends more than 5 hours every weekday in class.9. a) x(P(x)∧Q(x)) b) x(P(x)∧﹁Q(x))c) x(P(x)∨Q(x)) d) x﹁(P(x)∨Q(x))16. a) true b) false c) true d) false24. Let C(x) be the propositional function “x is in your class.”a)x P(x) and x(C(x)→P(x)), where P(x) is “x has a cellular phone.”b) x F(x) and x(C(x)∧F(x)), where F(x) is “x has seen a foreign movie.”c)x﹁S(x) and x(C(x)∧﹁S(x)), where S(x) is “x can swim.”d)x E(x) and x(C(x)→E(x)), where E(x) is “x can solve quadratic equations.”e)x﹁R(x) and x(C(x)∧﹁R(x)), where R(x) is “x wants to be rich.”62.a) x (P(x)→﹁S(x)) b)x(R(x)→S(x))c) x (Q(x)→P(x))d)x(Q(x)→﹁R(x))e) Yes. If x is one of my poultry, then he is a duck (by part(c)), hence not willing to waltz (part (a)). Since officers are always willing to waltz (part (b)), x is not an officer.1.412.d)x┐C(x, Bob)h)x y (I(x) ∧((x≠y) →┐ I(y)))k)x y( I(x) ∧┐C(x, y))n)x y z ((x≠y) ∧┐ (C(x, z) ∧ C(y, z)))14.a) x H(x), where H(x) is “x can speak Hindi”and the universe of the discourse consists of all students in this class.b) x y P(x, y), where P(x, y) is “x plays y.” and the universe of the discourse for xconsists of all students in this class, and the universe of the discourse for y consists of all sports.c) x A(x) ∧┐H(x) , where A(x) is “x has visited Alaska.” , H(x) is “x has visited Hawaii” and the universe of the discourse for x consists of all students in this class.d) x y L(x, y), where L(x, y) is “x has learned programming language y” and theuniverse of the discourse for x consists of all students in this class, and the universe of the discourse for y consists of all programming languages.e) x z y (Q(y,z) →P(x, y)), where P(x, y) is“x has taken course y.”, Q(y, z) is“course y is offered by department z.”, and the universe of the discourse for x consists of all students in this class, the universe of the discourse for y consists of all courses in this school, and the universe of the discourse for z consists of all departments in this school.f)x y z ( (x≠y) ∧P(x, y)∧ ((x≠y≠z) →┐P(x, z))), where P(x, y) is “x andy grew up in the same town.” and the universe of the discourse for x, y, z consists of all students in this class.g) x y z C(x, y) ∧G(y, z), where C(x, y) is “x has chatted with y”, G(y, z) is “yis in chat group z”, the universe of the discourse for x, y consists of all students in this class, and the universe of the discourse for z consists of all chat group in this class.a) There is an additive identity for the real numbers.d) The product of two nonzero numbers is nonzero for the real numbers.38.b) There are no students in this class who have never seen a computer.d) There are no students in this class who have taken been in at least one room of every building on campus.1.5(1)(┐r∧(q→p))→(p→(q∨r)) <=> ┐(┐r∧(┐q∨p))∨(┐p∨(q∨r)) <=>(q∧┐p)∨(┐p∨q∨r)<=> (┐p∨q∨r∨q)∧(┐p∨q∨r∨┐p) <=> (┐p∨q∨r) <=> ∏3 <=> ∑0,1,2,4,5,6,7 (2) P.726. Let r be the proposition "It rains", let f be the proposition "It is foggy", let s be the proposition "The sailing race will be held", let l be the proposition "The lifesaving demonstration will go on", and let t be the proposition "The trophy will be awarded". We are given premises (┐r∨┐f)→(s∧l), s→t, and ┐t. We want to conclude r. We set up the proof in two columns, with reasons. Note that it is valid to replace subexpressions by other expressions logically equivalent to them.Step Reason1. ┐t Hypothesis2. s→t Hypothesis3. ┐s Modus tollens using Steps 1 and 24. (┐r∨┐f)→(s∧l) Hypothesis5. (┐(s∧l))→┐(┐r∨┐f) Contrapositive of step 46. (┐s∨┐l)→(r∧f) De Morgan's law and double negative7. ┐s∨┐l Addition, using Step 38. r∧f Modus ponens using Step 6 and 79. r Simplification using Step 8First, using the conclusion of Exercise 11, we should show that the argument form with premises (p ∧t) → (r ∨s), q→ (u ∧t), u→p, ┐s, q, and conclusion r is valid. Then, we use rules of inference from Table 1.Step Reason1. q Premise2. q→ (u ∧t)P remise3. u ∧t Modus ponens using Steps 1 and 24. u Simplification using Step 35. u→p Premise6. p Modus ponens using Steps 3 and 47. t Simplification using Step 38. p ∧t Conjunction using Steps 6 and 79. (p ∧t) → (r ∨s) Premise10. r ∨s Modus ponens using Steps 8 and 911. ┐s Premise12. r Disjunctive syllogism using Steps 10 and 11 14.b)Let R(x) be “x is one of the five roommates,” D(x) be “x has taken a course in discrete mathematics,” and A(x) be “x can take a course in algorithms.” The premises are x (R(x) → D(x)), x (D(x) → A(x)) and R(Melissa). Using the first premise andUniversal Instantiation, R(Melissa) → D(Melissa) follows. Using the third premise and Modus Ponens, D(Melissa) follows. Using the second premise and Universal Instantiation, A(Melissa) follows. So do the other roommates.d) Let C(x) be “x is in the class,”F(x) be “x has been to France,” and L(x) be “x hasvisited Louvre.” The premises are x(C(x) ∧F(x)) and x (F(x) → L(x)). From thefirst premise and Existential Instantiation imply that C(y) ∧F(y) for a particularperson y. Using Simplification, F(y) follows. Using the second premise and Universal Instantiation F(y) → L(y) follows. Using Modus Ponens, L(y) follows. UsingExistential Generalization, x(C(x) ∧L(x)) follows.24. The errors occur in steps (3), (5) and (7).For steps (3) and (5), we cannot assume, as is being done here, that the c that makes P(x) true is the same as the c that makes Q(x) true at the same time. For step (7), it is not a conjunction and there is no such disjunction rule.29.Step Reason1. x ┐P(x) Premise2. ┐P(c) Existential instantiation from (1)3. x (P(x) ∨Q(x)) Premise4. P(c) ∨Q(c) Universal instantiation from (3)5. Q(c) Disjunctive syllogism from (2) and (4)6. x (┐Q(x) ∨S(x)) Premise7. ┐Q (c) ∨S(c) Universal instantiation from (6)8. S(c) Disjunctive syllogism from (5) and (7)9. x (R(x) →┐S(x)) Premise10. R(c) →┐S(c) Universal instantiation from (9)11. ┐R(c) Modus tollens from (8) and (10)12. x ┐R(x) Existential generalization from (11)P.861.637.Suppose that P1→P4→P2→P5→P3→P1. To prove that one of these propositions implies any of the others, just use hypothetical syllogism repeatedly.P.1031.713.a) This statement asserts the existence of x with a certain property. If we let y=x, then we see that P(x) is true. If y is anything other than x, then P(x) is not true. Thus, x is the unique element that makes P true.b) The first clause here says that there is an element that makes P true. The second clause says that whenever two elements both make P true, they are in fact the same element. Together these say that P is satisfied by exactly one element.c) This statement asserts the existence of an x that makes P true and has the further property that whenever we find an element that makes P true, that element is x. In other words, x is the unique element that makes P true.P.1202.19.T T F T T F16. Since the empty set is a subset of every set, we just need to take a set B that contains Φ as an element. Thus we can let A = Φ and B = {Φ} as the simplest example.20 .The union of the sets in the power set of a set X must be exactly X. In other words, we can recover X from its power set, uniquely. Therefore the answer is yes.22.a) The power set of every set includes at least the empty set, so the power set cannot be empty. Thus Φ is not the power set of any set.b) This is the power set of {a}c) This set has three elements. Since 3 is not a power of 2, this set cannot be the power set of any set.d) This is the power set of {a,b}.28.a) {(a,x,0), (a,x,1), (a,y,0), (a,y,1), (b,x,0), (b,x,1), (b,y,0), (b,y,1), (c,x,0), (c,x,1), (c,y,0), (c,y,1)}c) {(0,a,x), (0,a,y), (0,b,x), (0,b,y), (0,c,x), (0,c,y), (1,a,x), (1,a,y), (1,b,x), (1,b,y), (1,c,x), (1,c,y)}P.1302.214. Since A = (A - B)∪(A∩B), we conclude that A = {1,5,7,8}∪{3,6,9} ={1,3,5,6,7,8,9}. Similarly B = (B - A)∪(A ∩ B) = {2,10}∪{3,6,9} = {2,3,6,9,10}. 24. First suppose x is in the left-hand side. Then x must be in A but in neither B nor C. Thus x∈A - C, but x B - C, so x is in the right-hand side. Next suppose that x is in the right-hand side. Thus x must be in A - C and not in B - C. The first of theseimplies that x∈A and x C. But now it must also be the case that x B, since otherwise we would have x∈B - C. Thus we have shown that x is in A but in neitherB nor C, which implies that x is in the left-hand side.40. This is an identity; each side consists of those things that are in an odd number of the sets A,B,and C.P147.2.335a) This really has two parts. First suppose that b is in f(S∪T). Thus b=f(a) for somea∈S∪T. Either a ∈S, in which case b∈f(S), or a∈T, in which case b∈f(T). Thus in either case b∈ f(S) ∪f(T). This shows that f(S∪T) ⊆f(S) ∪f(T), Conversely, suppose b∈f(S) ∪f(T). Then either b∈f(S) or b∈f(T). This means either that b=f(a) for some a∈S or that b=f(a) for some a ∈T. In either case, b=f(a) for some a∈S∪T, so b∈f(S∪T). This shows that f(S) ∪f(T) ⊆f(S∪T), and our proof is complete. b)Suppose b∈f(S∩T). Then b=f(a) for some a∈S∩T. This implies that a∈S anda∈T , so we have b∈f(S) and b∈f(T). Therefore b∈f(S)∩f(T), as desired.52In some sense this question is its own answer—the number of integers between a and b, inclusive, is the number of integers between a and b, inclusive. Presumably we seek an express involving a, b, and the floor and/or ceiling function to answer this question. If we round a up and round b down to integers, then we will be looking at the smallest and largest integers just inside the range of the integers we want to count, respectively. These values are of course ⎡⎤a and ⎣⎦b, respectively. Then the answer isb-+1 (just think of counting all the integers between these two values, ⎣⎦⎡⎤aincluding both ends—if a row of fenceposts one foot apart extends for k feet, then there are k +1 fenceposts). Note that this even works when, for example, a=0.3 and b=0.7 .P1622.434.a) This is countable. The integers in the set are ±1,±2,±4,±5,±7,andso on. We can listthese numbers in the order 1, -1 , 2, -2, 4, -4,…, thereby establishing the desired correspondence. In other words, the correspondence is given by 1↔1,2↔-1,3↔2,4↔-2,5↔4,and so on.b) This is similar to part(a);we can simply list the elements of the set in order ofincreasing absolute value, listing each positive term before its correspondingnegative:5,-5,10,-10,15,-15,20,-20,30,-30,40,-40,45,-45,50,-50,……c) This is countable but a little tricky. We can arrange the numbers in a 2-dimensionaltable as follows:1..1 0.11 0.111 0.1111 0.11111 ……1.1 1 1.1 1.11 1.111 1.1111 ……1.1111 11.1 11.11 11.111 11.1111 ……1111.111 111.1 111.11 111.111 111.1111 ……………………………………d) This set is not countable. We can prove it by the same diagonalization argument aswas used to prove that the set of all reals is uncountable in Example 21.All we need to do is choose d i=1 when d ii=9 and choose d i=9 when d ii=1 or d ii is blank(if the decimal expansion is finite)46.We know from Example 21 that the set of real numbers between 0 and 1 is uncountable. Let us associate to each real number in this range(including 0 but excluding 1) a function from the set of positive integers to the set {0,1,2,3,4,5,6,7,8,9} as follows: If x is a real number whose decimal representation is 0.d1d2d3…(with ambiguity resolved by forbidding the decimal to end with an infinite string of9's),then we associate to x the function whose rule is given by f(n)=d n. clearly this is a one-to-one function from the set of real numbers between 0 and 1 and a subset of the set of all functions from the set of positive integers the set {0,1,2,3,4,5,6,7,8,9}.Two different real numbers must have different decimal representations, so the corresponding functions are different.(A few functions are left out, because of forbidding representations such as 0.239999…)Since the set of real numbers between 0 and 1 is uncountable, the subset of functions we have associated with them must be uncountable. But the set of all such functions has at least this cardinality, so it, too, must be uncountable.P1913.21. The choices of C and k are not unique.a) Yes C = 1, k = 10 b) Yes C = 4, k = 7 c) Nod) Yes C = 5, k = 1 e) Yes C = 1, k = 0 f) Yes C = 1, k = 29. x2+4x+17 ≤ 3x3 for all x>17, so x2+4x+17 is O(x3), with witnesses C = 3, k=17. However, if x3 were O(x2+4x+17), then x3≤C(x2+4x+17) ≤ 3Cx2for some C, for all sufficiently large x, which implies that x≤ 3C, for all sufficiently large x, which is impossible.P2093.419.a) no b) no c) yes d) no31.a) GR QRW SDVV JRb) QB ABG CNFF TBc) QX UXM AHJJ ZXP2183.513.a) Yes b) No c) Yes d) Yes17a) 2 b) 4 c) 12P2804.122.A little computation convinces us that the answer is that n2 ≤ n! for n= 0, 1, and all n≥ 4. (clearly the inequality doesn’t hold for n=2 or n=3) We will prove by mathematical induction that the inequality holds for all n≥ 4. The base case is clear, since 16 ≤ 24. Now suppose that n2 ≤ n! for a given n≥ 4. We m ust show that (n+1)2≤ (n+1)!. Expanding the left-hand side, applying the inductive hypothesis, and then invoking some valid bounds shows this:n2 + 2n+ 1 ≤ n! + 2n + 1≤ n! + 2n + 1 = n! + 3n≤ n! + n·n≤ n! + n·n!≤ (n+1)n! = (n+1)!P2934.231.Assume that the well-ordering property holds. Suppose that P(1) is true and that the conditional statement [P(1)∧P(2) ∧···∧P(n)] →P(n+1) is true for every positive integer n. Let S be the set of positive integers n for which P(n) is false. We will show S=Ø. Assume that S≠Ø, then by the well-ordering property there is a least integer m in S. We know that m cannot be 1 because P(1) is true. Because n=m is the least integer such that P(n) is false, P(1), P(2),…,P(m-1) are true, and m-1 ≥1. Because [P(1)∧P(2) ∧···∧P(m-1)] →P(m) is true, it follows that P(m) must also be true, which is a contradiction. Hence, S= Ø.P3084.310.The base case is that S m(0)=m. The recursive part is that S m(n+1) is the successor of S m(n)(i.e., S m(n)+1)12.The base case n=1 is clear, since f12=f1f2=1. Assume the inductive hypothesis. Thenf12+f22+…+f n2+f n+12 = f n+12+f n f n+1= f n+1(f n+1+f n)= f n+1f n+2, as desired.31.If x is a set or variable representing set, then x is well-formed formula. if x and y are all well-formed formulas, then x, (x∪y), (x∩y) and (x-y) are all well-formed formulas.50.Let P(n) be “A(1, n) = 2n .”BASIC STEP: P(1) is true, because P(1) = A(1, 1) = 2 = 21.INDCUTIVE STEP: Assume that P(m) is true, that is A(1, m) = 2m and m≥1. Then P(m+1) = A(1, m+1) = A(0, A(1, m))= A(0, 2m)=2·2m=2m+1.So A(1, n) = 2n whenever n≥159.b) Not well defined. F(2) is not defined since F(0) isn’t.Also, F(2) is ambiguous.d) Not well defined. The definition is ambiguous about n=1.P3445.13.a) 104b) 10512.We use the sum rule, adding the number of bit strings of each length up to 6. If we include the empty string, then we get 20 + 21 + 22 + 23 + 24 + 25 + 26= 27–1=12720.a) Every seventh number is divisible by 7. Therefore there are 999 / 7=142such numbers. Note that we use the floor function, because the k th multiple of 7 does not occur until the number 7k has been reached.b) For solving this part and the next four parts, we need to use the principle of inclusion-exclusion. Just as in part(a), there are 999/11=90 numbers in our range divisible by 11, and there are 999/77=12 numbers in our range divisible by both 7 and 11 (the multiples of 77 are the numbers we seek). If we take these 12 numbers are away from the 142 numbers divisible by 7, we see that there are 130 numbers in our range divisible by 7 but not by 11.c) as explained in part(b), the answer is 12.d) By the principle of inclusion-exclusion, the answer, using the data from part (b), is 142+90-12=220.e) If we subtract from the answer to part(d) the number of numbers divisible by neither of them; so the answer is 220-12=208.f) If we subtract the answer to part(d) from the total number of positive integers less than 1000, we will have the number of numbers divisible by exactly one of them; so the answer is 999-220=779.g) If we assume that numbers are written without leading 0s, then we should break the problem down into three cases-one-digit numbers, two-digit numbers. Clearly there are 9 one-digit numbers, and each of them has distinct digits. There are 90 two-digit numbers (10 through 99), and all but 9 of them have distinct digits. An alternativeway to compute this is to note that the first digit must be 1 through 9 (9 choices) and the second digit must be something different from the first digit (9 choices out of the 10 possible digits), so by the product rule, we get 9*9=81 choices in all. This approach also tells us that there are 9*9*8=648 three-digit numbers with distinct digits (again, work from left to right-in the ones place, one 8 digits are left to choose from). 80 the final answer is 9+81+648=738.h) It turns out to be easier to count the odd numbers with distinct digits and subtract from our answer to part(g), so let us proceed that way. There are 5 odd one-digit numbers. For two-digit numbers, first choose the one digit (5 choices), then choose the tens digits (8 choices), since neither the ones digit value not 0 is available); therefore there are 40 such two-digit numbers. (Note that this is not exactly half of 81.) For the three-digit numbers, first choose the ones digit (5 choices), then the hundreds digit (8 choices), then the tens digit (8 choices), giving us 320 in all. So there are 5+40+320=365 odd numbers with distinct digits. Thus the final answer is 738-365=373.35.a) 若n=1, 为2;若n=2, 为2; 若n>=3, 为0b) 对于n>1, 为22 n;若n=1, 为1;c) 2(n-1) (注:n可映射到0,1两种可能)44.First we count the number of bit strings of length 10 that contain five consecutive 0’s. We will base the count on where the string of five or more consecutive 0’s starts. If it starts in the first bit, then the first five bits are all 0’s, but there is free choice for the last five bits; therefore there are 25 = 32 such strings. If it starts in the second bit, then the first bit must be a 1, the next five bits are all 0’s, but there is free choice for the last four bits; therefore there are 24 = 16 such strings. If it starts in the third bit, then the second bit must be a 1 but the first bit and the last three bits are arbitrary; therefore there are 24= 16 such strings. Similarly, there are 16 such strings that have the consecutive 0’s starting in each of positions four, five ,and six. This gives us a total of 32+5×16=112 strings that contain five consecutive 0’s. Symmetrically, there are 112 strings that contain five consecutive 1’s. Clearly there are exactly two strings that contain both (0000011111,1111100000). Therefore by the inclusion-exclusion principle, the answer is 2*(112)-2=222.52.We draw the tree, with its root at the top. We show a branch for each of the possibilities 0 and 1, for each bit in order, except that we do not allow three consecutive 0’s. Since there are 13 leaves, the answer is 13.second bitthird bitfourth bitP3535.26.There are only d possible remainders when an integer is divided by d, namely 0, 1, …, d-1. By the pigeonhole principle, if we have d+1 remainders, then at least two must be the same.10.The midpoint of the segment whose endpoints are (a,b) and (c,d) is ( ( a + c ) / 2, ( b + d ) / 2). We are concerned only with integer values of the original coordinates. Clearly the coordinates of these fractions will be integers as well if and only if a and c have the same parity (both odd or both even) and b and d have the same parity. Thus what matters in this problem is the parities of coordinates. There are four possible pairs of parities: (odd,odd), (odd, even), (even, even) and (even,odd). Since we are given five points, the pigeonhole principle guarantees that at least two of them will have the same pair of parties. The midpoint of the segment joining these two points will therefore have integer coordinates.38.a) T b) Tc) T1 ≤a1< a2 < …< a75≤ 125 , and 26 ≤a1 + 25 < a2 + 25 < …< a75 + 25 ≤ 150.Now either of these 150 numbers are precisely all the number from 1 to 150, or else by the pigeonhole principle we get, as in Exercise 37, a i = a j + 25 for some i and j and we are done. In the former case, however, since each of the number a i + 25 is greater than or equal to 26, the numbers 1, 2, … , 25 must all appear among the a i’s. But since the a i’s are increasing, the only way this can happen is if a1=1, a2 =2 , …, a25=25. Thus there were exactly 25 matches in the first25 hours.d) TWe need a different approach for this part, an approach, incidentally, that works for many numbers besides 30 in this setting. Let a1, a2 , …a75 be as before, and note that 1 ≤a1< a2 < …< a75≤ 125. By the pigeonhole principle two of the numbers among a1, a2 , …a 31 are congruent modulo 30. If they differ by 30, then we have our solution. Otherwise they differ by 60 or more, so a 31 ≥ 61. Similarly, among a 31through a 61 ,either we find a solution, or two numbers must differ by 60 or more; therefore we assume that a 61 ≥ 121. But this means that a 66 ≥ 126, a contradiction.注:38题d 因为30大于25,不能用解决a,b,c的方法解决,所以适用一种新的方法(这种方法对前面3问同样适用的)。
离散数学及其应用图论部分课后习题答案
(2)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(3)构成了初级通路,因为点不重复;
(4)不构成通路,因为边 不存在;
(5)构成通路,但是不为简单通路和初级通路,因为有重复的边
(6)构成了回路,但是不为简单回路和初级回路,因为有重复的边
(7)构成了初级通路;
(8)简单通路,但是不为初级通路,有重复边。
23、用Dijkstra标号法求图9.22中各图从顶点 到其余各点的最短路径和距离。
解答
步骤
1
2
3
4
5
6
7பைடு நூலகம்
到 最短路为 ,路长为6;
到 最短路为 ,路长为3;
到 最短路为 ,路长为5;
到 最短路为 ,路长为6;
到 最短路为 ,路长为12;
到 最短路为 ,路长为7;
那么对于n阶m条边的无向图G是 棵树组成的森林,在任意两棵树中分别找一点进行连一条边,那么得到的图则为n阶m+1条边的无向图G是 棵树组成的森林,
那么 ,所以 。
方法二:设 棵树中,分别有 个顶点和 条边, ,则有
, , ,即可得证。
19、求图10.17中两个带权图的最小生成树。
解答:
P204:习题十一
16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
解答:
(1)三条边一共提供6度;所以点度序列可能是
①3,3,0,0,0,0;②3,2,1,0,0,0;③3,1,1,1,0,0;④2,2,2,0,0,0;⑤2,2,1,1,0,0;⑥2,1,1,1,1,0;⑦1,1,1,1,1,1;
由于是简单图,①②两种情形不可能
离散数学习题的答案解析

离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p :李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语解:设p :王强学过法语;q :刘威学过法语;则命题符号化的结果是p q ∧(9)只有天下大雨,他才乘班车上班解:设p :天下大雨;q :他乘班车上班;则命题符号化的结果是q p →(11)下雪路滑,他迟到了解:设p :下雪;q :路滑;r :他迟到了;则命题符号化的结果是()p q r ∧→15、设p :2+3=5.q :大熊猫产在中国.r :太阳从西方升起.求下列复合命题的真值:(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→解:p=1,q=1,r=0, ()(110)1p q r ∧∧⌝⇔∧∧⌝⇔,(())((11)0)(00)1p q r ⌝∨⌝→⇔⌝∨⌝→⇔→⇔()(())111p q r p q r ∴∧∧⌝↔⌝∨⌝→⇔↔⇔19、用真值表判断下列公式的类型:(2)()p p q →⌝→⌝解:列出公式的真值表,如下所示:20、求下列公式的成真赋值:(4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒00p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值:(2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式,所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值:(2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式,所以成假赋值为100。
离散数学习题答案解析

离散数学习题答案习题一及答案:(P14-15) 14、将下列命题符号化:(5)李辛与李末是兄弟解:设p :李辛与李末是兄弟,则命题符号化的结果是p (6)王强与刘威都学过法语解:设p :王强学过法语;q :刘威学过法语;则命题符号化的结果是p q ∧(9)只有天下大雨,他才乘班车上班解:设p :天下大雨;q :他乘班车上班;则命题符号化的结果是q p → (11)下雪路滑,他迟到了解:设p :下雪;q :路滑;r :他迟到了;则命题符号化的结果是()p q r ∧→15、设p :2+3=5.q :大熊猫产在中国. r :太阳从西方升起. 求下列复合命题的真值:(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→ 解:p=1,q=1,r=0,()(110)1p q r ∧∧⌝⇔∧∧⌝⇔,(())((11)0)(00)1p q r ⌝∨⌝→⇔⌝∨⌝→⇔→⇔ ()(())111p q r p q r ∴∧∧⌝↔⌝∨⌝→⇔↔⇔19、用真值表判断下列公式的类型: (2)()p p q →⌝→⌝解:列出公式的真值表,如下所示:由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值: (4)()p q q ⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩ 所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值: (2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨,此即公式的主析取范式, 所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值: (2)()()p q p r ∧∨⌝∨解:原式()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔,此即公式的主合取范式,所以成假赋值为100。
离散数学及其应用课后习题答案

离散数学及其应用课后习题答案【篇一:离散数学及其应用(课后习题)】出下列命题是原子命题还是复合命题。
(3)大雁北回,春天来了。
(4)不是东风压倒西风,就是西风压倒东风。
(5)张三和李四在吵架。
解:(3)和(4)是复合命题,(5)是原子命题。
习题1.21. 指出下列命题的真值:(1)若2?2?4,则太阳从西方升起。
解:该命题真值为t(因为命题的前件为假)。
(3)胎生动物当且仅当是哺乳动物。
解:该命题真值为f(如鸭嘴兽虽是哺乳动物,但不是胎生动物)。
2. 令p:天气好。
q:我去公园。
请将下列命题符号化。
(2)只要天气好,我就去公园。
(3)只有天气好,我才去公园。
(6)天气好,我去公园。
解:(2)p?q。
(3)q?p。
(6)p?q。
习题1.32. 将下列命题符号化(句中括号内提示的是相应的原子命题的符号表示):(1)我去新华书店(p),仅当我有时间(q)。
(3)只要努力学习(p),成绩就会好的(q)。
(6)我今天进城(p),除非下雨(q)。
(10)人不犯我(p),我不犯人(q);人若犯我,我必犯人。
解:(1)p?q。
(3)p?q。
(6)?q?p。
(10)(?p??q)?(p?q)。
习题1.41. 写出下列公式的真值表:(2)p?(q?r)。
解:该公式的真值表如下表:2. 证明下列等价公式:(2)(p?q)??(p?q)??(p?q)。
证明:?(p?q)??((p?q)?(?p??q))??(p?q)??(?p??q))??(p?q)?(p?q) ?(p ?q)??(p?q)(4)(p?q)?(p?r)?p?(q?r)。
证明:(p?q)?(p?r)?(?p?q)?(?p?r)??p?(q?r)?p?(q?r)3. 甲、乙、丙、丁4人参加考试后,有人问他们谁的成绩最好,甲说,不是我。
乙说:是丁。
丙说:是乙。
丁说:不是我。
已知4个人的回答只有一个人符合实际,问成绩最好的是谁?解:设a:甲成绩最好。
b:乙成绩最好。
离散数学及其应用习题答案

离散数学及其应用习题答案离散数学是一门研究离散结构的数学学科,它在计算机科学、信息科学、电子工程等领域中有着广泛的应用。
通过学习离散数学,我们可以培养出逻辑思维、抽象思维和解决问题的能力。
在学习离散数学的过程中,习题是不可或缺的一部分。
本文将回答一些离散数学中的常见习题,帮助读者更好地理解和应用离散数学的知识。
1. 集合论习题1.1 求解集合的交、并、差运算对于给定的集合A={1,2,3,4}和B={3,4,5,6},求解A∩B、A∪B和A-B。
解答:A∩B={3,4},A∪B={1,2,3,4,5,6},A-B={1,2}。
1.2 判断集合关系对于给定的集合A={1,2,3,4}和B={3,4,5,6},判断A是否是B的子集。
解答:A不是B的子集,因为A中的元素2不属于B。
2. 图论习题2.1 判断图的连通性给定一个无向图G,其顶点集合为V={1,2,3,4},边集合为E={(1,2),(2,3),(3,4)},判断图G是否连通。
解答:图G是连通的,因为任意两个顶点之间都存在一条路径。
2.2 求解最短路径给定一个有向图G,其顶点集合为V={A,B,C,D},边集合为E={(A,B,2),(A,C,3),(B,D,4),(C,D,1)},求解从顶点A到顶点D的最短路径。
解答:最短路径为A-C-D,路径长度为4。
3. 命题逻辑习题3.1 判断命题的真假给定命题P: "如果今天下雨,那么我就带伞",命题Q: "我带了伞",判断P→Q 的真假。
解答:由于P和Q都是真命题,且"真命题→真命题"为真命题,所以P→Q为真命题。
3.2 求解命题的合取范式给定命题P: "如果今天下雨,那么我就带伞",命题Q: "我没有带伞",将P∧Q 转化为合取范式。
解答:P∧Q的合取范式为"(¬P∨¬Q)"。
离散数学及其应用答案徐凤生

习题1.判断下列语句是否是命题,为什么?若是命题,判断是简单命题还是复合命题?(1)离散数学是计算机专业的一门必修课。
(2)李梅能歌善舞。
(3)这朵花真美丽!(4)3+2>6。
(5)只要我有时间,我就来看你。
(6)x=5。
(7)尽管他有病,但他仍坚持工作。
(8)太阳系外有宇宙人。
(9)小王和小张是同桌。
(10)不存在最大的素数。
解在上述10个句子中,(3)是感叹句,因此它不是命题。
(6)虽然是陈述句,但它没有确定的值,因此它也不是命题。
其余语句都是可判断真假的陈述句,所以都是命题。
其中:(1)、(4)、(8)、(9)、是简单命题,、(2)、(5)、(7)、(10)是复合命题。
2.判断下列各式是否是命题公式,为什么?(1)(P→(P∨Q))。
(2)(⌝P→Q)→(Q→P)))。
(3)((⌝P→Q)→(Q→P))。
(4)(Q→R∧S)。
(5)(P∨QR)→S。
(6)((R→(Q→R)→(P→Q))。
解(1)是命题公式。
(2)不是命题公式,因为括号不配对。
(3)是命题公式。
(4)是命题公式。
(5)不是命题公式,因为QR没有意义。
(6)不是命题公式,因为R→(Q→R)→(P→Q)没有意义。
3.将下列命题符号化:(1)我们不能既划船又跑步。
(2)我去新华书店,仅当我有时间。
(3)如果天下雨,我就不去新华书店。
(4)除非天不下雨,我将去新华书店。
(5)张明或王平都可以做这件事。
(6)“2或4是素数,这是不对的”是不对的。
(7)只有休息好,才能工作好。
(8)只要努力学习,成绩就会好的。
(9)大雁北回,春天来了。
(10)小张是山东人或河北人。
解(1)符号化为⌝(P∧Q),其中,P:我们划船,Q:我们跑步。
(2)符号化为Q→R,其中,R:我有时间,Q:我去新华书店。
(3)符号化为P→⌝Q,其中,P:天下雨,Q:我去新华书店。
(4)符号化为⌝P→Q,其中,P:天下雨,Q:我去新华书店。
(5)符号化为P∧Q,其中,P:张明可以做这件事,Q:王平可以做这件事。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
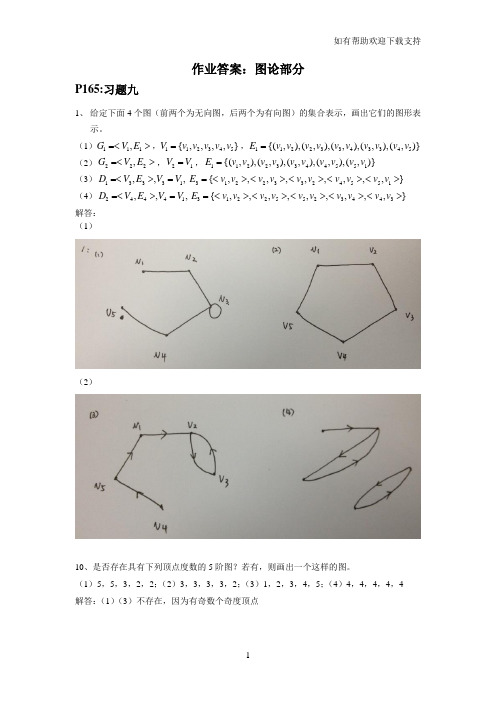
离散数学及应用课后习题答案【篇一:离散数学及其应用图论部分课后习题答案】p165:习题九1、给定下面4个图(前两个为无向图,后两个为有向图)的集合表示,画出它们的图形表示。
(1)g1??v1,e1?,v1?{v1,v2,v3,v4,v5},e1?{(v1,v2),(v2,v3),(v3,v4),(v3,v3),(v4,v5)} (2)g2??v2,e2?,v2?v1,e1?{(v1,v2),(v2,v3),(v3,v4),(v4,v5),(v5,v1)} (3)d1??v3,e3?,v3?v1,e3?{?v1,v2?,?v2,v3?,?v3,v2?,?v4,v5?,?v5,v 1?} (4)d2??v4,e4?,v4?v1,e3?{?v1,v2?,?v2,v5?,?v5,v2?,?v3,v4?,?v4,v 3?} 解答:(1)(2)10、是否存在具有下列顶点度数的5阶图?若有,则画出一个这样的图。
(1)5,5,3,2,2;(2)3,3,3,3,2;(3)1,2,3,4,5;(4)4,4,4,4,4 解答:(1)(3)不存在,因为有奇数个奇度顶点。
14、设g是n(n?2)阶无向简单图,g是它的补图,已知?(g)?k1,?(g)?k2,求?(g),(g)。
解答:?(g)?n?1?k2;?(g)?n?1?k1。
15、图9.19中各对图是否同构?若同构,则给出它们顶点之间的双射函数。
解答:(c)不是同构,从点度既可以看出,一个点度序列为4,3,3,3,3而另外一个为4,4,3,3,1(d)同构,同构函数为12f(x)345解答:(1)三条边一共提供6度;所以点度序列可能是x?ax?bx?c x?dx?e16、画出所有3条边的5阶简单无向图和3条边的3阶简单无向图。
①3,3,0,0,0,0;②3,2,1,0,0,0;③3,1,1,1,0,0;④2,2,2,0,0,0;⑤2,2,1,1,0,0;⑥2,1,1,1,1,0;⑦1,1,1,1,1,1;由于是简单图,①②两种情形不可能图形如下:(2)三条边一共提供6度,所以点度序列可能为①3,3,0;②3,2,1;③2,2,2 由于是简单图,①②两种情形不可能21、在图9.20中,下述顶点序列是否构成通路?哪些是简单通路?哪些是初级通路?哪些是回路?哪些是简单回路?哪些是初级回路?(1)a,b,c,d,b,e;(2)a,b,e,d,b,a;(3)a,d,c,e,b;(4)d,b,a,c,e;(5)a,b,c,d,e,b,d,c;(6)a,d,b,e,c,b,d;(7)c,d,a,b,c;(8)a,b,c,e,b 解答:(1)构成通路,且为初级通路,因为点不重复(2)构成了回路,但是不为简单回路和初级回路,因为有重复的边(a,b) (3)构成了初级通路,因为点不重复;(4)不构成通路,因为边(a,c)不存在;(5)构成通路,但是不为简单通路和初级通路,因为有重复的边(d,c) (6)构成了回路,但是不为简单回路和初级回路,因为有重复的边(d,b) (7)构成了初级通路;(8)简单通路,但是不为初级通路,有重复边。
23、用dijkstra标号法求图9.22中各图从顶点v1到其余各点的最短路径和距离。
v1到v2最短路为v1?v2,路长为6; v1到v3最短路为v1?v3,路长为3; v1到v4最短路为v1?v3?v4,路长为5;v1到v5最短路为v1?v3?v4?v5,路长为6; v1到v6最短路为v1?v2?v6,路长为12;v1到v7最短路为v1?v3?v4?v5?v7,路长为7; v1到v8最短路为v1?v3?v4?v5?v7?v8,路长为10;(2)略。
25、图9.23中各图有几个连通分支?给出它们所有的连通分支。
解答:(a)有两个连通分支:aec和bdf;(b)有三个连通分支:abd、c和ef;(c)连通图,只有一个连通分支;(d)两个连通分支:afbgd和ech。
38、写出图9.27的关联矩阵。
1100000010?111000?00?1000?1? 解答:?0??0000?11?110?1100?110??【篇二:离散数学及其应用(课后习题)】出下列命题是原子命题还是复合命题。
(3)大雁北回,春天来了。
(4)不是东风压倒西风,就是西风压倒东风。
(5)张三和李四在吵架。
解:(3)和(4)是复合命题,(5)是原子命题。
习题1.21. 指出下列命题的真值:(1)若2?2?4,则太阳从西方升起。
解:该命题真值为t(因为命题的前件为假)。
(3)胎生动物当且仅当是哺乳动物。
解:该命题真值为f(如鸭嘴兽虽是哺乳动物,但不是胎生动物)。
2. 令p:天气好。
q:我去公园。
请将下列命题符号化。
(2)只要天气好,我就去公园。
(3)只有天气好,我才去公园。
(6)天气好,我去公园。
解:(2)p?q。
(3)q?p。
(6)p?q。
习题1.32. 将下列命题符号化(句中括号内提示的是相应的原子命题的符号表示):(1)我去新华书店(p),仅当我有时间(q)。
(3)只要努力学习(p),成绩就会好的(q)。
(6)我今天进城(p),除非下雨(q)。
(10)人不犯我(p),我不犯人(q);人若犯我,我必犯人。
解:(1)p?q。
(3)p?q。
(6)?q?p。
(10)(?p??q)?(p?q)。
习题1.41. 写出下列公式的真值表:(2)p?(q?r)。
解:该公式的真值表如下表:2. 证明下列等价公式:(2)(p?q)??(p?q)??(p?q)。
证明:(pq)((pq)(pq))(pq)(pq))(pq)(pq) (p q)(pq)(4)(p?q)?(p?r)?p?(q?r)。
证明:(p?q)?(p?r)?(?p?q)?(?p?r)??p?(q?r)?p?(q?r)3. 甲、乙、丙、丁4人参加考试后,有人问他们谁的成绩最好,甲说,不是我。
乙说:是丁。
丙说:是乙。
丁说:不是我。
已知4个人的回答只有一个人符合实际,问成绩最好的是谁?解:设a:甲成绩最好。
b:乙成绩最好。
c:丙成绩最好。
d:丁成绩最好。
四个人所说的命题分别用p、q、r、s表示,则p??a;q??a??b??c?d;r??a?b??c??d;s??d。
则只有一人符合实际的命题k符号化为k?(p??q??r??s)?(?p?q??r??s)?(?p??q?r??s)?(?p??q??r?s) p??q??r??s??a??(?a??b??c?d)??(?a?b??c??d)?d ??a?(a?b cd)(abcd)d (ad)(abcd)(abcd)(abcd)(abd)(abcd)(acd)0;同理,pqrsaabcd(abcd)d0; pqr s?a??(?a??b??c?d)??a?b??c??d?d?0; ?p??q??r?s?a??(?a? bcd)(abcd)d a(abcd)(abcd)d ad.所以,当k为真时,a??d为真,即甲的成绩最好。
习题1.52. 证明下列各蕴含式:(3)p?(q?r)?(p?q)?(p?r)。
证明:方法一:真值表法(列出命题公式(p?(q?r))?((p?q)?(p?r))的真值表)。
方法二:等值演算法(p?(q?r))?((p?q)?(p?r))??(p?(q?r))?((p?q)?(p?r))??(?p?(?q?r)) (?p?q)?(?p?r)?(p?qr)?(pq)?(?p?r)(pqr)((ppr)(qpr))(pqr)(qpr)(pqpr)(qqpr)(rqpr)1.方法三:分析法(1)直接分析法:若前件p?(q?r)为真,分两种情况:(i)p为假,则p?q为真,p?r为真,(p?q)?(p?r)为真。
(ii)p为真,则q?r为真,此时若q为真,则r为真,则p?q为真,p?r为真,(p?q)?(p?r)为真;若q为假,则p?r为假,(p?q)?(p?r)为真。
综上,若前件为真,后件必为真,故该蕴含式成立。
(2)间接分析法:若后件(p?q)?(p?r)为假,则p?q为真,p?r为假。
由p?r为假可知,p为真,r为假。
再由p?q可知,q为真。
此时q?r 为假,p?(q?r)为假,即前件为假。
故蕴含式成立。
5. 叙述下列各个命题的逆换式和逆反式,并以符号写出。
(1)如果下雨,我不去。
解:设p:天下雨。
q:我去。
逆换式:如果我不去,天就下雨。
符号表示为?q?p。
逆反式:如果我去,天就不下雨。
符号表示为q??p。
(2)仅当你走我将留下。
解:设p:我留下。
q:你走。
逆换式:如果你走,我就留下。
符号表示为:q?p。
逆反式:如果你不走,我就不留下。
符号表示为:?q??p。
习题1.62. 将下列命题公式用只含?和?的等价式表达,并要求尽可能简单。
(1)(p?q)??p.解: (p?q)??p?(p?? p)?q?0?q?0.(2)(p?(q??r))??p?q.解: (p?(q??r))??p?q?(?p?(q??r))?(?p?q??r)p qpqp?q(?pqp)q(pq)q(r)(pq)r(pq)(pq)(p(pq)(pqr)(pq).(3)?p??q?(?r?p).(?p?q? ?r?p q解:?p??q?(?r?p)??p??q?(r?p)(pqr)(pqp)(pqr)0 pqr(pqr).习题1.76.求下列命题公式的主析取范式和主合取范式:(1)((p?q)?r)?p.解:((p?q)?r)?p??(?(p?q)?r) ?p?((p?q)??r)?p?(p?q?p)?(p??r)?(p? q?(r??r))?(p?(q??q)? ?r?(p?q?r)?(p?q??r)?(p?q?r)?(p?q??r)?m0?m1?m3(主合取范式)m2m4m5m6m7.(主析取范式)(pq)(p r(pqr)(pq r(pq r)【篇三:《离散数学》试题及答案】合a,b,其中a={1,2,3}, b= {1,2}, 则a - b=____________________;__________________________ .3. 设集合a = {a, b}, b = {1, 2}, 则从a到b的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式g=?(p?q)∧r,则g的主析取范式是_____________________________________________________________________________________ ____.5.设g是完全二叉树,g有7个点,其中4个叶点,则g的总度数为__________,分枝点数为________________.___________________;a-b= _____________________ .7. 设r是集合a上的等价关系,则r所具有的关系的三个特性是______________________, ________________________,_______________________________.8. 设命题公式g=?(p?(q?r)),则使公式g为真的解释有__________________________,_____________________________,__________________________.9. 设集合a={1,2,3,4}, a上的关系r1 = {(1,4),(2,3),(3,2)}, r1 = {(2,1),(3,2),(4,3)}, 则 r1?r2 = ________________________,r2?r1 =____________________________,=________________________.10. 设有限集a, b,|a| = m, |b| = n, 则| |?(a?b)| =_____________________________.11 设a,b,r是三个集合,其中r是实数集,a = {x | -1≤x≤1, x?r}, b = {x | 0≤x 2, x?r},则a-b = __________________________ , b-a = __________________________ , a∩b =__________________________ , .13. 设集合a={2, 3, 4, 5, 6},r是a上的整除,则r以集合形式(列举法)记为_________________________________________________________________ _.14. 设一阶逻辑公式g = ?xp(x)??xq(x),则g的前束范式是__________________________ _____. 15.设g是具有8个顶点的树,则g中增加_________条边才能把g变成完全图。
