2020新高考试卷内容分析(浙江卷)

合集下载

2020年1月高考英语浙江卷真题解析(1)

2020年1月高考英语浙江卷真题解析第一节（共10小题；每小题2.5分，满分25分）阅读下列短文，从每题所给的A 、B 、C 和D 四个选项中，选出最佳选项，并在答题纸上将该项涂黑。

AI never knew anyone who’d grown up in Jackson without being afraid of Mrs. Calloway , our librarian. She ran Jackson’s Carnegie Library absolutely by herself. SILENCE in big black letters was on signs hung everywhere. If she thought you were dressed improperly,she sent you straight back home to change your clothes. I was willing; I would do anything to read.My mother was not afraid of Mrs. Calloway. She wished me to have my own library card to check out books for myself. She took me in to introduce m e. “Eudora is nine y ears old and has my permission to read any book she wants from the shelves, children or adults,” Mother said.Mrs. Calloway made her own rules about books. You could not take back a book to the library on the same day you’d taken it out; it made no difference to her that you’d read every word in it and needed another to start. You could take out two books at a time and two only. So two by two, I read library books as fast as I could go, rushing them home in the basket of my bicycle. From the minute I reached our house, I started to read. I knew this was extreme happiness, knew it at the time.My mother shared this feeling of mine. Now, I think of her as reading so much of the time while doing something else. I remember her reading a magazine while taking the part of the Wolf in a game of “Little Red Riding H ood” with my brother’s two daughters. She’d just look up at the right time, long enough to answer — in character — “The better to eat you with, my dear,” and go back to her place in the magazine article.21. Which of the following best describes Mrs. Calloway?A. Quiet.B. Strict.C. Humorous.D. Considerate.22. What do the underlined words “this feeling” refer to in the last paragraph?A. Desire to read.B. Love for Mrs. Calloway.C. Interest in games.D. Fear of the library rules.23. Where is the text probably from?A. A guidebook.B. An autobiography.答案与解析21. B 推理判断题根据第一段中的If she thought you were dressed improperly, she sent you straight back hometo change your clothes.可知Mrs. Calloway对衣着严格要求以及第三段中她对图书借阅严格规定可知，Mrs.Calloway是一位严格的图书管理员。

2020年浙江省高考生物试卷(7月)(含详细解析)

8．高等动物胚胎干细胞分裂过程中，发生在同一时期的是（）
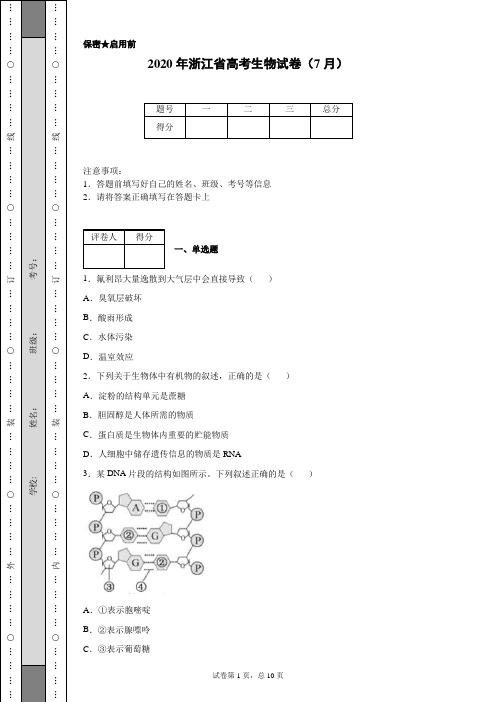
A．核糖体的增生和环沟的形成
B．染色体的出现和纺锤体的出现
C．染色单体的形成和着丝粒的分裂
D．中心体的复制和染色体组数的加倍
9．人体甲状腺分泌和调节示意图如下，其中TRH表示促甲状腺激素释放激素，TSH表示促甲状腺激素，“+”表示促进作用，“-”表示抑制作用。据图分析，下列叙述正确的是（）
B．中性粒细胞吞入的细菌可被溶酶体中的多种酶降解
C．溶酶体是由脂双层构成的内、外两层膜包被的小泡
D．大量碱性物质进入溶酶体可使溶酶体中酶的活性发生改变
5．对人群免疫接种是预防传染性疾病的重要措施。下列叙述错误的是（）
A．注射某种流感疫苗后不会感染各种流感病毒
B．接种脊髓灰质炎疫苗可产生针对脊髓灰质炎病毒的抗体
保密★启用前
2020年浙江省高考生物试卷（7月）
题号
一
二
三
总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
评卷人
得分
一、单选题
1．氟利昂大量逸散到大气层中会直接导致（）
A．臭氧层破坏
B．酸雨形成
C．水体污染
D．温室效应
2．下列关于生物体中有机物的叙述，正确的是（）
C．营养级是指处于食物链同一环节上同种生物的总和
D．食物链中的各营养级之间能量传递效率是相同的
12．下列关于“肺炎双球菌转化实验”的叙述，正确的是（）
A．活体转化实验中，R型菌转化成的S型菌不能稳定遗传
B．活体转化实验中，S型菌的荚膜物质使R型菌转化成有荚膜的S型菌
C．离体转化实验中，蛋白质也能使部分R型菌转化成S型菌且可实现稳定遗传

2020年高考化学浙江卷(1月选考)附答案解析版

化学试卷第1页（共12页）化学试卷第2页（共12页）绝密★启用前浙江省2020年1月普通高校招生选考科目考试化学可能用到的相对原子质量：H 1 Li 7 C12 N14 O16 Na 23 Mg 24Al 27 Si 28 S 32 Cl 35.5 K 39 Ca 40 Mn 55 Fe 56 Cu 64 I127 Ba 137一、选择题（本大题共25小题，每小题2分，共50分。

每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1.有共价键的离子化合物是（）A .22Na OB .24H SOC .22CH ClD .SiC 2.萃取碘水中的碘并分液，需要用到的仪器是（）ABC D3.下列属于有机物，又是电解质的是（）A .己烷B .乙酸C .葡萄糖D .纯碱4.反应()2222MnO 4HCl MnCl Cl 2H O ++↑+△浓中，氧化产物是（） A .2MnOB .HClC .2MnClD .2Cl 5.下列物质的名称不正确．．．的是（）A .NaOH ：烧碱B .4FeSO ：绿矾C .：甘油D .：3−甲基己烷6.下列表示不正确．．．的是（）A .羟基的电子式：B .乙烯的结构简式：22CH CHC .氯原子的结构示意图：D .3NH 分子的球棍模型：7.下列说法不正确．．．的是（）A .168O 和188O 互为同位素B .金刚石和石墨互为同素异形体C .和互为同系物D .323CH COOCH CH 和322CH CH CH COOH 互为同分异构体 8.下列说法不正确．．．的是（）A .二氧化硅导电能力强，可用于制造光导纤维B .石灰石在高温下可用于消除燃煤烟气中的2SOC .钠着火不能用泡沫灭火器灭火D .利用催化剂可减少汽车尾气中有害气体的排放 9.下列说法不正确．．．的是（）A .()344Cu NH SO ⎡⎤⎣⎦可通过4CuSO 溶液与过量氨水作用得到B .铁锈的主要成分可表示为232Fe O H O nC .钙单质可以从4TiCl 中置换出TiD .可用2H 还原MgO 制备单质Mg 10.下列说法不正确．．．的是（）A .天然气的主要成分甲烷是高效，较洁净的燃料B .石油的分馏、煤的气化和液化都是物理变化C .石油的裂化主要是为了得到更多的轻质油D .厨余垃圾中蕴藏着丰富的生物质能 11.下列有关实验说法，不正确．．．的是（）A .碱液不慎溅到手上，先用大量水冲洗，再用饱和硼酸溶液洗，最后用水冲洗B .KCl 和2MnO 的混合物经溶解、过滤，洗涤、干燥，可分离出2MnOC .用容量瓶配制溶液，定容时若加水超过刻度线，立即用滴管吸出多余液体D .火柴头的浸泡液中滴加3AgNO 溶液，稀3HNO 和2NaNO 溶液，可检验火柴头是否-------------在------------------此------------------卷------------------上-------------------答-------------------题-------------------无--------------------效---------------- 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________化学试卷第3页（共12页）化学试卷第4页（共12页）含有氯元素12.下列关于铝及其化合物说法，不正确．．．的是（）A .明矾可用作净水剂和消毒剂B .利用铝热反应可冶炼高熔点金属C .铝可用作包装材料和建筑材料D .氢氧化铝可用作治疗胃酸过多的药物 13.不能．．正确表示下列变化的离子方程式是（）A .3BaCO 溶于盐酸：2322BaCO 2H Ba CO H O ++++↑+B .3FeCl 溶液腐蚀铜板：3222Fe Cu2Fe Cu +++++C .苯酚钠溶液中通入少量2CO ：D .醋酸钠水解：323CH COO H O CH COOH OH--++14.下列说法不正确．．．的是（）A .强酸、强碱、重金属盐等可使蛋白质变性B .用新制氢氧化铜悬浊液（必要时可加热）能鉴别甲酸、乙醇、乙醛C .乙酸乙酯中混有的乙酸，可加入足量的饱和23Na CO 溶液，经分液除去D .向苯和苯酚的混合液中加入浓溴水，充分反应后过滤，可除去苯中少量的苯酚15.下列关于的说法，正确的是（）A .该物质可由n 个单体分子通过缩聚反应生成B .0.1mol 该物质完全燃烧，生成33.6L （标准状况）的2COC .该物质在酸性条件下水解产物之一可作汽车发动机的抗冻剂D .1mol 该物质与足量NaOH 溶液反应，最多可消耗3mol n NaOH 16.下列说法正确的是（）A .同一原子中，在离核较远的区域运动的电子能量较高B .原子核外电子排布，先排满K 层再排L 层，先排满M 层再排N 层C .同一周期中，随着核电荷数的增加，元素的原子半径逐渐增大D .同一周期中，ⅡA 与ⅢA 族元素原子的核电荷数都相差1 17.下列说法不正确．．．的是（）A .pH 7＞的溶液不一定呈碱性B .中和pH 和体积均相等的氨水、NaOH 溶液，所需HCl 的物质的量相同C .相同温度下，pH 相等的盐酸、3CH COOH 溶液中，()OH c -相等 D .氨水和盐酸反应后的溶液，若溶液呈中性，则()()4ClNH c c -+=18.在氯碱工业中，离子交换膜法电解饱和食盐水示意图如下，下列说法不正确．．．的是（）离子交换膜A .电极A 为阳极，发生氧化反应生成氯气B .离子交换膜为阳离子交换膜C .饱和NaCl 溶液从a 处进，NaOH 溶液从d 处出D .OH -迁移的数量等于导线上通过电子的数量19.在干燥的HCl 气流中加热22MgCl 6H O ，能得到无水2MgCl 。

2020年浙江省高考数学试卷(解析版)

ii解析分析i作dhac交ac于h连接bh由题意可知dh平面abc即有dhbcbcbhefbc可得dhefbhef平面bhd即证得efdbdfch所以df与平面dbc所成角即为ch与平面dbc所成角作hgbd接cg即可知hcg即为所求角再解三角形即可求出df与平面dbc详解作dhac交ac于h连接bh平面adfc平面abc而平面adfc平面abcacdh平面adfcdh平面abc而bc平面abc即有dhbc45acbacdcdchbcchbccos45bhchbcchbcbcbhbcchbhbcefbc所以dhefbhef而bhdh平面bhdefdbdfch所以df与平面dbc所成角即为与ch平面dbc作hgbd连接cg由1可知bc平面bhd因为所以平面bcd平面bhd而平面bcd平面bhdbdhg平面bhdhg平面bcd
1 3
1 2
2
1
1
1 2
2
1
2
1 3
2
7 3
.
故选：A
【点睛】本小题主要考查根据三视图计算几何体的体积，属于基础题.
6. 已知空间中不过同一点的三条直线 m，n，l，则“m，n，l 在同一平面”是“m，n，l 两两相交”的（）
A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件
台体的体积公式V
1 3 (S1
S1S2 S2 )h
其中 S1, S2 分别表示台体的上、下底面积， h 表示台体的高
柱体的体积公式V Sh 其中 S 表示柱体的底面积， h 表示柱体的高锥体的体积公式V 1 Sh
3 其中 S 表示锥体的底面积， h 表示锥体的高球的表面积公式
S 4 R2
【合等差数列的性质即可判断各等式是否成立．【详解】对于 A，因为数列 an 为等差数列，所以根据等差数列的下标和性质，由 4 4 2 6 可得， 2a4 a2 a6 ，A 正确；对于 B，由题意可知， bn1 S2n2 S2n a2n1 a2n2 ， b1 S2 a1 a2 ， ∴ b2 a3 a4 ， b4 a7 a8 ， b6 a11 a12 ， b8 a15 a16 ． ∴ 2b4 2 a7 a8 ， b2 b6 a3 a4 a11 a12 ．根据等差数列的下标和性质，由 3 11 7 7, 4 12 8 8 可得 b2 b6 a3 a4 a11 a12 =2a7 a8 =2b4 ，B 正确；对于 C， a42 a2a8 a1 3d 2 a1 d a1 7d 2d 2 2a1d 2d d a1 ，

浙江高考语文试卷考点分析(含答案)

浙江高考语文试卷考点分析（含答案）下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!专业课原理概述部分一、选择题1. 下列哪个选项是浙江高考语文试卷的基本组成部分？A. 诗歌鉴赏B. 数学应用C. 历史分析D. 物理实验2. 浙江高考语文试卷中，文言文阅读主要考察的是哪方面的能力？A. 现代文学B. 古代文化C. 科学推理D. 美术鉴赏3. 在浙江高考语文试卷中，论述类文本阅读主要考查的是哪种类型的文本？A. 小说B. 论文C. 诗歌D. 戏剧4. 下列哪一项不是浙江高考语文试卷中的写作部分？A. 作文B. 小作文C. 应用文D. 翻译5. 浙江高考语文试卷的阅读理解部分主要考查的是哪种能力？A. 数据分析B. 文学欣赏C. 历史理解D. 物理实验二、判断题1. 浙江高考语文试卷的考试时间为3小时。

2020年浙江省高考数学试卷-解析版

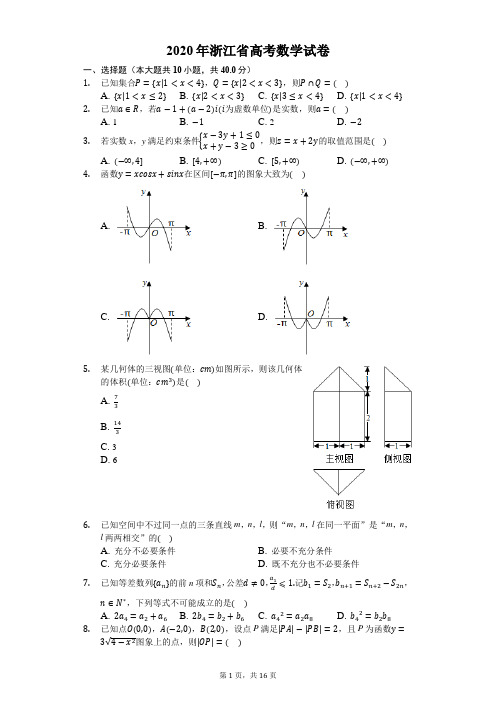
2020年浙江省高考数学试卷一、选择题（本大题共10小题，共40.0分）1. 已知集合P ={x|1<x <4}，Q ={x|2<x <3}，则P ∩Q =( )A. {x|1<x ≤2}B. {x|2<x <3}C. {x|3≤x <4}D. {x|1<x <4}2. 已知a ∈R ，若a −1+(a −2)i(i 为虚数单位)是实数，则a =( )A. 1B. −1C. 2D. −2 3. 若实数x ，y 满足约束条件{x −3y +1≤0x +y −3≥0，则z =x +2y 的取值范围是( )A. (−∞,4]B. [4,+∞)C. [5,+∞)D. (−∞,+∞)4. 函数y =xcosx +sinx 在区间[−π,π]的图象大致为( )A.B.C.D.5. 某几何体的三视图(单位：cm)如图所示，则该几何体的体积(单位：cm 3)是( )A. 73 B. 143 C. 3 D. 66. 已知空间中不过同一点的三条直线m ，n ，l ，则“m ，n ，l 在同一平面”是“m ，n ，l 两两相交”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 已知等差数列{a n }的前n 项和S n ，公差d ≠0，a1d⩽1.记b 1=S 2，b n+1=S n+2−S 2n ，n ∈N ∗，下列等式不可能成立的是( )A. 2a 4=a 2+a 6B. 2b 4=b 2+b 6C. a 42=a 2a 8D. b 42=b 2b 8 8. 已知点O(0,0)，A(−2,0)，B(2,0)，设点P 满足|PA|−|PB|=2，且P 为函数y =3√4−x 2图象上的点，则|OP|=( )A. √222B. 4√105C. √7D. √109.已知a，b∈R且a，b≠0，若(x−a)(x−b)(x−2a−b)≥0在x≥0上恒成立，则()A. a<0B. a>0C. b<0D. b>010.设集合S，T，S⊆N∗，T⊆N∗，S，T中至少有两个元素，且S，T满足：①对于任意x，y∈S，若x≠y，都有xy∈T；②对于任意x，y∈T，若x<y，则yx∈S；下列命题正确的是()A. 若S有4个元素，则S∪T有7个元素B. 若S有4个元素，则S∪T有6个元素C. 若S有3个元素，则S∪T有5个元素D. 若S有3个元素，则S∪T有4个元素二、填空题（本大题共7小题，共36.0分）11.我国古代数学家杨辉、宋世杰等研究过高阶等差数列求和问题，如数列{n(n+1)2}就是二阶等差数列，数列{n(n+1)2}，(n∈N∗)的前3项和______．12.二项展开式(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a4=______；a1+a2+a3=______．13.已知tanθ=2，则cos2θ=______；tan(θ−π4)=______．14.已知圆锥的侧面积(单位：cm2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是______．15.已知直线y=kx+b(k>0)与圆x2+y2=1和圆(x−4)2+y2=1均相切，则k=______，b=______．16.盒中有4个球，其中1个红球，1个绿球，2个黄球，从盒中随机取球，每次取1个不放回，直到取出红球为止，设此过程中取到黄球的个数为ξ，则P(ξ=0)=______，E(ξ)=______．17.已知平面向量e1⃗⃗⃗ ，e2⃗⃗⃗ 满足|2e1⃗⃗⃗ −e2⃗⃗⃗ |≤√2，设a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ，b⃗ =3e1⃗⃗⃗ +e2⃗⃗⃗ ，向量a⃗，b⃗ 的夹角为θ，则cos2θ的最小值为______．三、解答题（本大题共5小题，共74.0分）18.在锐角△ABC中，角A,B,C的对边分别为a,b,c.已知2bsinA−√3a=0．(1)求角B；(2)求cosA+cosB+cosC的取值范围．19.如图，三棱台ABC−DEF中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC=2BC．(1)证明：EF⊥DB；(2)求DF与面DBC所成角的正弦值．⋅20.已知数列{a n}，{b n}，{c n}满足a1=b1=c1=1，c n+1=a n+1−a n，c n+1=b nb n+2c n(n∈N∗)．(1)若{b n}为等比数列，公比q>0，且b1+b2=6b3，求q的值及数列{a n}的通项公式；(2)若{b n}为等差数列，公差d>0，证明：c1+c2+c3+⋯+c n<1+1，n∈N∗．d21.如图，已知椭圆C1：x2+y2=1，抛物线C2：y2=2px(p>0)，点A是椭圆C1与2抛物线C2的交点．过点A的直线l交椭圆C1于点B，交抛物线C2于点M(B,M不同于A)．(1)若p=1，求抛物线C2的焦点坐标；16(2)若存在不过原点的直线l使M为线段AB的中点，求p的最大值．22.已知1<a≤2，函数f(x)=e x−x−a.其中e=2.718281828459…为自然对数的底数．(1)证明：函数y=f(x)在(0,+∞)上有唯一零点；(2)记x0为函数y=f(x)在(0,+∞)上的零点，证明：(ⅰ)√a−1≤x0≤√2(a−1)；(ⅰ)x0f(e x0)≥(e−1)(a−1)a．答案和解析1.【答案】B【解析】解：集合P ={x|1<x <4}，Q ={x|2<x <3}，则P ∩Q ={x|2<x <3}．故选：B ．直接利用交集的运算法则求解即可．此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2.【答案】C【解析】【分析】本题考查复数的基本概念，是基础题．利用复数的虚部为0，求解即可．【解答】解：a ∈R ，若a −1+(a −2)i(i 为虚数单位)是实数，可得a −2=0，解得a =2．故选：C ．3.【答案】B【解析】解：画出实数x ，y 满足约束条件{x −3y +1≤0x +y −3≥0所示的平面区域，如图：将目标函数变形为−12x +z2=y ，则z 表示直线在y 轴上截距，截距越大，z 越大，当目标函数过点A(2,1)时，截距最小为z =2+2=4，随着目标函数向上移动截距越来越大，故目标函数z =2x +y 的取值范围是[4,+∞)．故选：B ．作出不等式组表示的平面区域；作出目标函数对应的直线；结合图象判断目标函数z =x +2y 的取值范围．本题考查画不等式组表示的平面区域、考查数形结合求函数的最值．4.【答案】A【解析】解：y =f(x)=xcosx +sinx ，则f(−x)=−xcosx −sinx =−f(x)，∴f(x)为奇函数，函数图象关于原点对称，故排除B ，D ，当x =π时，y =f(π)=πcosπ+sinπ=−π<0，故排除B ，故选：A ．先判断函数的奇偶性，再判断函数值的特点．本题考查了函数图象的识别，掌握函数的奇偶性额函数值得特点是关键，属于基础题．5.【答案】A【解析】解：由题意可知几何体的直观图如图，下部是直三棱柱，底面是斜边长为2的等腰直角三角形，棱锥的高为2，上部是一个三棱锥，一个侧面与底面等腰直角三角形垂直，棱锥的高为1，所以几何体的体积为：12×2×1×2+13×12×2×1×1=73．故选：A．画出几何体的直观图，利用三视图的数据求解几何体的体积即可．本题考查三视图求解几何体的体积，判断几何体的形状是解题的关键．6.【答案】B【解析】【分析】本题借助空间的位置关系，考查了充分条件和必要条件，属于基础题．由m，n，l在同一平面，则m，n，l相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行，根据充分条件，必要条件的定义即可判断．【解答】解：空间中不过同一点的三条直线m，n，l，若m，n，l在同一平面，则m，n，l相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行．故m，n，l在同一平面”是“m，n，l两两相交”的必要不充分条件，故选：B．7.【答案】B【解析】解：在等差数列{a n}中，a n=a1+(n−1)d，S n+2=(n+2)a1+(n+2)(n+1)2d，S2n=2na1+2n(2n−1)2d，b1=S2=2a1+d，b n+1=S n+2−S2n=(2−n)a1−3n2−5n−22d．∴b2=a1+2d，b4=−a1−5d，b6=−3a1−24d，b8=−5a1−55d．A.2a4=2(a1+3d)=2a1+6d，a2+a6=a1+d+a1+5d=2a1+6d，故A正确；B.2b4=−2a1−10d，b2+b6=a1+2d−3a1−24d=−2a1−22d，若2b4=b2+b6，则−2a1−10d=−2a1−22d，即d=0不合题意，故B错误；C.若a42=a2a8，则(a1+3d)2=(a1+d)(a1+7d)，即a12+6a1d+9d2=a12+8a1d+7d2，得a1d=d2，∵d≠0，∴a1=d，符合a1d⩽1，故C正确；D.若b42=b2b8，则(−a1−5d)2=(a1+2d)(−5a1−55d)，即2(a1d )2+25a1d+45=0，则a1d有两不等负根，满足a1d⩽1，故D正确．∴等式不可能成立的是B．故选：B．由已知利用等差数列的通项公式判断A与C；由数列递推式分别求得b2,b4,b6,b8，分析B，D成立时是否满足公差d≠0，a1d⩽1判断B与D．本题考查数列递推式，等差数列的通项公式与前n项和，考查转化思想和计算能力，是中档题．8.【答案】D【解析】解：点O(0,0)，A(−2,0)，B(2,0).设点P满足|PA|−|PB|=2，可知P的轨迹是双曲线x21−y23=1的右支上的点，P为函数y=3√4−x2图象上的点，即y236+x24=1在第一象限的点，联立两个方程，解得P(√132,3√32)，所以|OP|=√134+274=√10．故选：D．求出P满足的轨迹方程，求出P的坐标，即可求解|OP|．本题考查圆锥曲线的综合应用，曲线的交点坐标以及距离公式的应用，是中档题．9.【答案】C【解析】【分析】本题考查不等式恒成立问题，注意三次函数的图象，考查分类讨论思想和转化思想，属于中档题．先由x=0时，不等式ab(−2a−b)⩾0恒成立，可得1a +2b⩽0，则a,b至少有一个是小于0的，再按a<0,b<0，a<0,b>0，a>0,b<0，讨论可得结论．【解答】解：由题意知，x=0时，不等式ab(−2a−b)⩾0恒成立，即ab(2a+b)⩽0，∵ab≠0，∴可得1a +2b⩽0，则a,b至少有一个是小于0的，(1)若a<0,b<0，由图象知，(x−a)(x−b)(x−2a−b)⩾0在x⩾0时恒成立，符合题意；(2)若a<0,b>0，2a+b>0，(x−a)(x−b)(x−2a−b)⩽0在x≥0上恒成立，则b=2a+b，得a=0，矛盾，不符合题意．(3)若a>0,b<0，(x−a)(x−b)(x−2a−b)⩾0在x⩾0时恒成立，则a=2a+b，则a+b=0，符合题意．综合，b<0成立．故选：C．10.【答案】A【解析】【分析】本题考查命题的真假的判断与应用，集合的基本运算，利用特殊集合排除选项是选择题常用方法，属于较难题．利用特殊集合排除选项，推出结果即可．【解答】解：取：S ={1,2，4}，则T ={2,4，8}，S ∪T ={1,2，4，8}，4个元素，排除C ． S ={2,4，8}，则T ={8,16，32}，S ∪T ={2,4，8，16，32}，5个元素，排除D ； S ={2,4，8，16}则T ={8,16，32，64，128}，S ∪T ={2,4，8，16，32，64，128}，7个元素，排除B ；故选：A ．11.【答案】10【解析】【分析】本题考查数列求和，数列通项公式的应用，是基本知识的考查．求出数列的前3项，然后求解即可．【解答】解：数列{a n }满足a n =n(n+1)2，可得a 1=1，a 2=3，a 3=6，所以S 3=1+3+6=10．故答案为：10．12.【答案】80；130【解析】【分析】本题考查二项式定理的应用，只有二项式定理系数以及项的系数的区别，属于基础题．直接利用二项式定理的通项公式，求解即可．【解答】解：∵(1+2x)5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5，则a 4=C 54⋅24=80．a 1+a 2+a 3=C 51⋅2+C 52⋅4+C 53⋅8=130．故答案为：80；130．13.【答案】−35， 13【解析】解：tanθ=2，则cos2θ=cos 2θ−sin 2θcos 2θ+sin 2θ=1−tan 2θ1+tan 2θ=1−41+4=−35． tan(θ−π4)=tanθ−tanπ41+tanθtanπ4=2−11+2×1=13．故答案为：−35；13．利用二倍角公式以及同角三角函数基本关系式求解第一问，利用两角和与差的三角函数转化求解第二问．本题考查二倍角公式的应用，两角和与差的三角函数以及同角三角函数基本关系式的应用，是基本知识的考查．14.【答案】1【解析】解：∵圆锥侧面展开图是半圆，面积为2π，设圆锥的母线长为a ，则12×a 2π=2π，∴a =2，∴侧面展开扇形的弧长为2π，设圆锥的底面半径OC =r ，则2πr =2π，解得r =1．故答案为：1．利用圆锥的侧面积，求出母线长，求解底面圆的周长，然后求解底面半径．本题考查圆锥的母线长的求法，注意利用圆锥的弧长等于底面周长这个知识点．15.【答案】√33 ；−2√33【解析】解：由条件得C 1(0,0)，r 1=1，C 2(4,0)，r 2=1，因为直线l 与C 1，C 2都相切，故有d 1=√1+k 2=1，d 2=√1+k 2=1，则有√1+k 2=√1+k 2，故可得b 2=(4k +b)2，整理得k(2k +b)=0，因为k >0，所以2k +b =0，即b =−2k ，代入d 1=√1+k 2=1，解得k =√33，则b =−2√33，故答案为：√33；−2√33．根据直线l 与两圆都相切，分别列出方程d 1=√1+k2=1，d 2=√1+k 2=1，解得即可．本题考查直线与圆相切的性质，考查方程思想，属于中档题．16.【答案】13 ；1【解析】解：由题意知，随机变量ξ的可能取值为0，1，2；计算P(ξ=0)=14+14×13=13；P(ξ=1)=1 2×13 +14×23×12+24×13×12=13；P(ξ=2)=1−13−13=13；所以E(ξ)=0×13+1×13+2×13=1．故答案为：13，1．由题意知随机变量ξ的可能取值为0，1，2；分别计算P(ξ=0)、P(ξ=1)和P(ξ=2)，再求E(ξ)的值．本题考查了离散型随机变量的分布列与数学期望的计算问题，是中档题．17.【答案】2829【解析】【分析】本题考查了平面向量的数量积与夹角的运算问题，是中档题．设e1⃗⃗⃗ 、e2⃗⃗⃗ 的夹角为α，由题意求出cosα≥34；再求a⃗，b⃗ 的夹角θ的余弦值cos2θ的最小值即可．【解答】解：设e1⃗⃗⃗ 、e2⃗⃗⃗ 的夹角为α，由e1⃗⃗⃗ ，e2⃗⃗⃗ 为单位向量，满足|2e1⃗⃗⃗ −e2⃗⃗⃗ |≤√2，所以4e1⃗⃗⃗ 2−4e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=4−4cosα+1≤2，解得cosα≥34；又a⃗=e1⃗⃗⃗ +e2⃗⃗⃗ ，b⃗ =3e1⃗⃗⃗ +e2⃗⃗⃗ ，且a⃗，b⃗ 的夹角为θ，所以a⃗⋅b⃗ =3e1⃗⃗⃗ 2+4e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=4+4cosα，a⃗2=e1⃗⃗⃗ 2+2e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=2+2cosα，b⃗ 2=9e1⃗⃗⃗ 2+6e1⃗⃗⃗ ⋅e2⃗⃗⃗ +e2⃗⃗⃗ 2=10+6cosα；则cos2θ=(a⃗ ⋅b⃗)2a⃗2×b⃗2=(4+4cosα)2(2+2cosα)(10+6cosα)=4+4cosα5+3cosα=43−835+3cosα，所以cosα=34时，cos2θ取得最小值为43−835+3×34=2829．故答案为2829．18.【答案】解：(1)∵2bsinA=√3a，∴2sinBsinA=√3sinA，∵sinA≠0，∴sinB=√32，，∴B=π3，(2)∵△ABC为锐角三角形，B=π3，∴C=2π3−A，，△ABC为锐角三角形，，，解得，，，，∴cosA+cosB+cosC的取值范围为(√3+12,32 ]．【解析】本题考查了正弦定理，三角函数的化简，三角函数的性质，考查了运算求解能力和转化与化归能力，属于中档题．(1)根据正弦定理可得sinB=√32，结合角的范围，即可求出，(2)根据两角和差的余弦公式，以及利用正弦函数的性质即可求出．19.【答案】解：(1)证明：作DH⊥AC，且交AC于点H，∵面ADFC⊥面ABC，面ADFC∩面ABC=AC，DH⊂面ADFC，∴DH⊥面ABC，BC⊂面ABC，∴DH⊥BC，∴在Rt△DHC中，CH=CD⋅cos45°=√22CD，∵DC=2BC，∴CH=√22CD=√22⋅2BC=√2⋅BC，∴BCCH =√22，又∠ACB=45°，∴△BHC是直角三角形，且∠HBC=90°，∴HB⊥BC，又∵DH⊂面DHB，HB⊂面DHB，DH∩HB=H，∴BC⊥面DHB，∵DB⊂面DHB，∴BC⊥DB，∵在三棱台DEF−ABC中，EF//BC，∴EF⊥DB．(2)设BC=1，则BH=1，HC=√2，在Rt△DHC中，DH=√2，DC=2，在Rt△DHB中，DB=√DH2+HB2=√2+1=√3，作HG⊥BD于G，∵BC⊥面DHB，HG⊂面DHB，∴BC⊥HG，而BC⊂面BCD，BD⊂面BCD，BC∩BD=B，∴HG⊥面BCD，∵GC⊂面BCD，∴HG⊥GC，∴△HGC是直角三角形，且∠HGC=90°，设DF与面DBC所成角为θ，则θ即为CH与面DBC的夹角，且sinθ=sin∠HCG=HGHC =√2，∵在Rt△DHB中，DH⋅HB=BD⋅HG，∴HG=DH⋅HBBD =√2⋅13=√63，∴sinθ=√2=√63√2=√33．【解析】本题主要考查空间直线互相垂直的判定和性质，以及直线与平面所成角的几何计算问题，考查了空间想象能力和思维能力，平面与空间互相转化是能力，几何计算能力，以及逻辑推理能力，本题属综合性较强的中档题．(1)题根据已知条件，作DH⊥AC，根据面面垂直，可得DH⊥BC，进一步根据直角三角形的知识可判断出△BHC是直角三角形，且∠HBC=90°，则HB⊥BC，从而可证出BC⊥面DHB，最后根据棱台的定义有EF//BC，根据平行线的性质可得EF⊥DB；(2)题先可设BC=1，根据解直角三角形可得BH=1，HC=√2，DH=√2，DC=2，DB=√3，然后找到CH与面DBC的夹角即为∠HCG，根据棱台的特点可知DF与面DBC 所成角与CH与面DBC的夹角相等，通过计算∠HCG的正弦值，即可得到DF与面DBC 所成角的正弦值．20.【答案】(1)解：由题意，b2=q，b3=q2，∵b1+b2=6b3，∴1+q=6q2，整理，得6q2−q−1=0，解得q=−13(舍去)，或q=12，∴c n+1=b nb n+2⋅c n=1b n+2b n⋅c n=1q2⋅c n=1(12)2⋅c n=4⋅c n，∴数列{c n}是以1为首项，4为公比的等比数列，∴c n=1⋅4n−1=4n−1，n∈N∗．∴a n+1−a n=c n+1=4n，则a1=1，a2−a1=41，a3−a2=42，……a n−a n−1=4n−1，各项相加，可得a n=1+41+42+⋯+4n−1=1−4n1−4=4n−13．(2)证明：依题意，由c n+1=b nb n+2⋅c n(n∈N∗)，可得b n+2⋅c n+1=b n⋅c n，两边同时乘以b n+1，可得b n+1b n+2c n+1=b n b n+1c n，∵b1b2c1=b2=1+d，∴数列{b n b n+1c n}是一个常数列，且此常数为1+d，b n b n+1c n=1+d，∴c n=1+db n b n+1=1+dd⋅db n b n+1=(1+1d)⋅b n+1−b nb n b n+1=(1+1d)(1b n−1b n+1)，∴c1+c2+⋯+c n=(1+1d)(1b1−1b2)+(1+1d)(1b2−1b3)+⋯+(1+1d)(1b n−1b n+1)=(1+1d)(1b1−1b2+1b2−1b3+⋯+1b n−1b n+1)=(1+1d)(1b1−1b n+1)=(1+1d)(1−1b n+1)<1+1d，∴c1+c2+⋯+c n<1+1d，故得证．【解析】本题主要考查数列求通项公式，等差数列和等比数列的基本量的运算，以及和式不等式的证明问题．考查了转化与化归思想，整体思想，方程思想，累加法求通项公式，裂项相消法求和，放缩法证明不等式，以及逻辑推理能力和数学运算能力，属于综合题．(1)先根据等比数列的通项公式将b2=q，b3=q2代入b1+b2=6b3，计算出公比q的值，然后根据等比数列的定义化简c n+1=b nb n+2⋅c n可得c n+1=4c n，则可发现数列{c n}是以1为首项，4为公比的等比数列，从而可得数列{c n}的通项公式，然后将通项公式代入c n+1=a n+1−a n，可得a n+1−a n=c n+1=4n，再根据此递推公式的特点运用累加法可计算出数列{a n}的通项公式；(2)通过将已知关系式c n+1=b nb n+2⋅c n不断进行转化可构造出数列{b n b n+1c n}，且可得到数列{b n b n+1c n}是一个常数列，且此常数为1+d，从而可得b n b n+1c n=1+d，再计算得到c n=1+db n b n+1，根据等差数列的特点进行转化进行裂项，在求和时相消，最后运用放缩法即可证明不等式成立．21.【答案】解：(1)p =116，则 p 2=132，则抛物线C 2的焦点坐标(132,0)，(2)由题意可设直线l ：x =my +t (m ≠0,t ≠0)，点A (x 0,y 0)，将直线l 的方程代入椭圆C 1：x 22+y 2=1得(m 2+2)y 2+2mty +t 2−2=0∴点M 的纵坐标y M =−mtm 2+2。

2020年浙江省名校联盟新高考创新物理试卷(一)(含答案解析)

2020年浙江省名校联盟新高考创新物理试卷（一）一、单选题（本大题共13小题，共39.0分）1.下列说法正确的是()A. 米、牛顿、秒是国际单位制中的基本单位B. 力、速度、路程均为矢量C. 只有细小的物体才可看成质点D. 静止的物体也有惯性2.如图所示，一个质量为M的人站在台秤上，用跨过定滑轮的绳子将质量为m的物体自高处放下，不考虑滑轮与绳子间的摩擦，当物体以加速度a加速下降(a<g)时，台秤的读数为()A. (M−m)g+maB. (M+m)g−maC. (M−m)gD. (M−m)g−ma3.某弹簧的劲度系数k=5×103N/m，在弹性限度内，当它伸长2.5cm时，产生的弹力是()A. 125NB. 50NC. 5ND. 12.5N4.如图为一个简易的冲击式水轮机模型，水流自水平的水管流出，水流轨迹与下边放置的轮子边缘相切，水冲击轮子边缘上安装的挡水板，可使轮子连续转动。

当该装置工作稳定时，可近似认为水到达轮子边缘时的速度与轮子边缘的线速度相同。

调整轮轴O的位置，使水流与轮边缘切点对应的半径与水平方向成θ=37°角。

测得水从管口流出速度v0=3m/s，轮子半径R=0.1m。

不计挡水板的大小，不计空气阻力。

取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8。

则可知()A. 水管出水口距轮轴O的水平距离x=1.2mB. 水管出水口距轮轴O的竖直距离ℎ=0.86mC. 该装置工作稳定时，轮子的转动角速度ω=30rad/sD. 该装置工作稳定时，轮子的转动周期T大于0.2s5.关于历史上对于物体受力和运动的研究，下列说法正确的是()A. 亚里士多德首先提出，轻重物体下落一样快B. 伽利略认为物体的运动需要力来维持C. 牛顿最早将逻辑推理(和数学推演)与实验相结合，开创了近代自然科学研究的方法D. 伽利略在研究自由落体运动时，巧妙利用斜面“冲淡”重力，证明了自由落体运匀变速直线运动6.机场的安检门可以利用涡流探测人身上携带的金属物品，安检门中接有线圈，线圈中通以交变电流关于其工作原理，以下说法正确的是()A. 人身上携带的金属物品会被地磁场磁化，在线圈中产生感应电流B. 人体在线圈交变电流产生的磁场中运动，产生感应电动势并在金属物品中产生感应电流C. 线圈产生的交变磁场不会在金属物品中产生交变的感应电流D. 金属物品中感应电流产生的交变磁场会在线圈中产生感应电流7.某区域电场线如图所示，左右对称分布，A、B为区域上两点。

浙江新高考研究卷创新卷技术(4)

A．1 或 2
B．2 或 3
C．3 或 4
D．4 或 5
《浙江省新高考创新卷》技术（四）第 3 页共 16 页
二、非选择题（本大题共 4 小题，其中第 13 小题 4 分，第 14 小题 8 分，第 15 小题 7 分，第 16 小题 7 分，共 26 分）
13．杭州市某区 2020 年面向社会招聘教师入围人员名单，并用 Excel 软件进行数据处理，如图所示。
致数据丢失 5．使用 GoldWave 软件编辑某音频文件，部分界面如下
图所示：
《浙江省新高考创新卷》技术（四）第 1 页共 16 页
下列说法正确的是
A．执行“静音”操作，左声道最后 5 秒钟是静音
B．执行“删除”操作并按原参数保存，音频文件存储容量变小
C．将“保存选定部分为”操作，参数默认，则音频文件大小约为 430KB
A．int(Rnd*90+10)
B．int(Rnd*13)*7+14
C．int(Rnd*84)+14
D．int(Rnd*86)+14
8．某算法的部分流程图如右图所示，执行该
流程图后，s 的值为
A．27
B．63
C．48
D．36
9．“A”的 ASCII 码值为 65，有如下 VB 程序段：
s1=text1．text
（1）总成绩是将“笔试成绩”与“面试成绩”分别乘以对应的权重后相加所得。通过 F3 单元格中的公式，对 F4:F8 进行自动填充，F4 单元格中显示结果是 ▲ （单选，填字母:A．＃ VALUE！/B．85.00/C．0.00 /D．＃DIV/0！）。
（2）若要正确计算“总成绩”列的数据，可对 F3 单元格中的公式进行修改，并对 F4:F44 进行自动填充，则 F3 单元格中的公式是 ▲ 。

2020年浙江省高考语文试题(解析版)

2020年普通高等学校招生全国统一考试（浙江卷）语文试题一、语言文字运用（共20分）1.下列各句中，没有错别字且加点字的注音全都正确的一项是（）。

A. 浙江诗路文化带以诗词文化为主线，结合水系古道，将各地旖．（yǐ）旎风光串联成富有诗情画意的山水旅游线路，让游客徜．（táng）徉在江南美景中。

B. 历经千年沧桑，觥．（gōng）筹交错的场面早已湮．（yān）没于历史深处，但留存至今的一件件青铜器足以让人们浮想联篇，去回味那个钟鸣鼎食的时代。

C. 生态文学应更多创作体现绿色发展理念讴．（ōu）歌美好生活的作品，致力于鞭挞．（dá）滥杀野生动物、肆意破坏环境的恶劣行为，提高全社会的生态文明素养。

D. 北方的季节泾．（jīng）渭分明，春季的风一寸寸吹向大地，为山川褪去寒衣，一点点着．（zhuó）上春色，东风过处，整个原野为之一振，草木葳蕤，生机勃勃。

【答案】D【1题详解】A项，“徜（táng）徉”读音错，应为“cháng”。

徜徉，1.犹徘徊，盘旋往返。

2.犹彷徨，心神不宁貌。

3.安闲自得貌。

B项，“浮想联篇”字形错，应为“浮想联翩”。

浮想联翩，联翩：鸟飞的样子，比喻连续不断。

指许许多多的想象不断涌现出来。

C项，“鞭挞（dá）”读音错，应为“tà”。

鞭挞，原指鞭打，现多形容无情地指责披露。

故选D。

阅读下面的文字，完成各题。

屏幕中的剧情风生水起．．．．，扣人心弦。

屏幕上方一行又一行的字符络绎不绝，争先恐后。

某些字符甚至悬浮于屏幕中央，仿佛不忍退场。

【甲】“弹幕”是这些字符获得的形象称谓——那些字符如同密集射击的炮弹在夜空展开了眼花缭乱的一幕。

弹幕通常是对屏幕中剧情的即时评论，短小精悍．．．．。

【乙】评论内容五花八门，崇拜、感叹、剧透、调侃、吐槽，也包含了“前方高能反应”“美爆了”“劝你善良”……等弹幕文化的常用语。

【丙】弹幕文化显示出既丰富又单调的双重特征：一方面群情踊跃，图文并茂；另一方面彼此重复，似曾相识。

2024年高考生物真题完全解读(1月浙江卷)

【详解】A、试管动物的培育属于胚胎工程，没有禁止，A正确；
B、我过目前不反对转基因的食品的生产，B正确；
C、中国政府禁止生殖性克隆，支持治疗性克隆，C正确；
D、生物武器致病能力强、攻击范围广，世界范围内应全面禁止生物武器，D错误。
故选D。
2.下列不属于水在植物生命活动中作用的是（）
A.物质运输的良好介质B.保持植物枝叶挺立
如第1题的生物技术与安全伦理、第5题生物多样性的保护、第7题快递小哥勇救落水者弘扬社会主义核心价值观、第15题通过生物防治减少环境污染、第22和23题应用生物技术研究植物生理及遗传学问题、第24题应用生物学原理服务生产生活实践，理解生物科学技术的进步及其对社会发展和个人生活的影响，引导学生敬畏生命，落实保护环境等社会责任，彰显生物学试题的育人价值。
一、稳中有变，体现创新性
试题命制延续往次选考卷风格，试卷题型结构、命题立意、考点分布、能力要求等基本稳定，同时适当调整和创新。选择题由原20题40分调整为19题38分。试题呈现略有调整。
如第20题结合光合作用实验测得数据，通过相关性分析，得出结论；第23题运用DNA琼脂糖凝胶电泳等分子生物学手段分析遗传现象；第24题在生态学研究过程中考查实验设计并完善实验思路等。
2、精练反思，提升解题能力
学生在首考前已经做了不少的习题，但是部分学生认为做题越多，见识越广，考试分数就会越高，因此只顾埋头刷题，很少抬头思考,没有认真分析、总结、归纳，分析解决问题的关键能力缺乏。也没有好好利用自己的错题资源，分析出错的原因，面对新试题情境时，往往会答不到点上或者答不全。二轮选考复习需要精选题目，首选历年高考真题，其次是各个地市模拟试题。反复研究题干信息，结合上下文，体会得出答案的逻辑思维过程,不断修正自己的偏差，提升解题能力。要跳出“想当然”，基于事实和证据有理有据地分析推理，不断总结和形成自身的规范解题思路，比如人体血浆pH为7.35~7.4，血细胞在体外培养时，也应该模拟体内环境，培养T细胞时，培养基的pH应该维持在中性偏碱。很多学生受到CO2培养箱的影响，认为CO2溶于水是酸性的，所以培养基应该是酸性的，忽略了CO2培养箱的作用是“调节”pH的相对稳定。

2020年浙江省高考数学试卷-含详细解析

2020年浙江省⾼考数学试卷-含详细解析2020年浙江省⾼考数学试卷副标题题号⼀⼆三总分得分⼀、选择题（本⼤题共10⼩题，共40.0分）1. 已知集合P ={x|1A. {x|1B. {x|2C. {x|3≤x <4}D. {x|12. 已知a ∈R ，若a ?1+(a ?2)i(i 为虚数单位)是实数，则a =( )A. 1B. ?1C. 2D. ?2 3. 若实数x ，y 满⾜约束条件{x ?3y +1≤0x +y ?3≥0，则z =x +2y 的取值范围是( )A. (?∞,4]B. [4,+∞)C. [5,+∞)D. (?∞,+∞)4. 函数y =xcosx +sinx 在区间[?π,π]的图象⼤致为( )A.B.C.D.5. 某⼏何体的三视图(单位：cm)如图所⽰，则该⼏何体的体积(单位：cm 3)是( )A. 73 B. 143 C. 3 D. 66. 已知空间中不过同⼀点的三条直线m ，n ，l ，则“m ，n ，l 在同⼀平⾯”是“m ，n ，l 两两相交”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.已知等差数列{a n}的前n项和S n，公差d≠0，a1d1.记b1=S2，b n+1=S n+2?S2n，n∈N?，下列等式不可能成⽴的是()A. 2a4=a2+a6B. 2b4=b2+b6C. a42=a2a8D. b42=b2b88.已知点O(0,0)，A(?2,0)，B(2,0)，设点P满⾜|PA|?|PB|=2，且P为函数y=3√4?x2图象上的点，则|OP|=()A. √222B. 4√105C. √7D. √109.已知a，b∈R且a，b≠0，若(x?a)(x?b)(x?2a?b)≥0在x≥0上恒成⽴，则()A. a<0B. a>0C. b<0D. b>010.设集合S，T，S?N?，T?N?，S，T中⾄少有两个元素，且S，T满⾜：①对于任意x，y∈S，若x≠y，都有xy∈T；②对于任意x，y∈T，若xx∈S；下列命题正确的是()A. 若S有4个元素，则S∪T有7个元素B. 若S有4个元素，则S∪T有6个元素C. 若S有3个元素，则S∪T有5个元素D. 若S有3个元素，则S∪T有4个元素⼆、填空题（本⼤题共7⼩题，共36.0分）11.我国古代数学家杨辉、宋世杰等研究过⾼阶等差数列求和问题，如数列{n(n+1) 2}就是⼆阶等差数列，数列{n(n+1)}，(n∈N?)的前3项和______．12.⼆项展开式(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a4=______；a1+a2+a3=______．13.已知tanθ=2，则cos2θ=______；tan(θ?π4)=______．14.已知圆锥的侧⾯积(单位：cm2)为2π，且它的侧⾯展开图是⼀个半圆，则这个圆锥的底⾯半径(单位：cm)是______．15.已知直线y=kx+b(k>0)与圆x2+y2=1和圆(x?4)2+y2=1均相切，则k=______，b=______．16.盒中有4个球，其中1个红球，1个绿球，2个黄球，从盒中随机取球，每次取1个不放回，直到取出红球为⽌，设此过程中取到黄球的个数为ξ，则P(ξ=0)=______，E(ξ)=______．17.已知平⾯向量e1 ，e2 满⾜|2e1??? ?e2??? |≤√2，设a?=e1 +e2 ，b? =3e1 +e2 ，向量a?，b? 的夹⾓为θ，则cos2θ的最⼩值为______．三、解答题（本⼤题共5⼩题，共74.0分）18.在锐⾓△ABC中，⾓A,B,C的对边分别为a,b,c.已知2bsinA?√3a=0．(1)求⾓B；(2)求cosA+cosB+cosC的取值范围．19.如图，三棱台ABC?DEF中，⾯ADFC⊥⾯ABC，∠ACB=∠ACD=45°，DC=2BC．(1)证明：EF⊥DB；(2)求DF与⾯DBC所成⾓的正弦值．20.已知数列{a n}，{b n}，{c n}满⾜a1=b1=c1=1，c n+1=a n+1?a n，c n+1=b nb n+2c n(n∈N?)．(1)若{b n}为等⽐数列，公⽐q>0，且b1+b2=6b3，求q的值及数列{a n}的通项公式；(2)若{b n}为等差数列，公差d>0，证明：c1+c2+c3+?+c n<1+1，n∈N?．d21.如图，已知椭圆C1：x2+y2=1，抛物线C2：y2=2px(p>0)，点A是椭圆C1与抛物线C2的交点．过点A的直线l交椭圆C1于点B，交抛物线C2于点M(B,M不同于A)．(1)若p=1，求抛物线C2的焦点坐标；16(2)若存在不过原点的直线l使M为线段AB的中点，求p的最⼤值．22.已知1底数．(1)证明：函数y=f(x)在(0,+∞)上有唯⼀零点；(2)记x0为函数y=f(x)在(0,+∞)上的零点，证明：(ⅰ)√a?1≤x0≤√2(a?1)；(ⅰ)x0f(e x0)≥(e?1)(a?1)a．答案和解析1.【答案】B【解析】解：集合P ={x|1直接利⽤交集的运算法则求解即可．此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键． 2.【答案】C【解析】解：a ∈R ，若a ?1+(a ?2)i(i 为虚数单位)是实数，可得a ?2=0，解得a =2．故选：C ．利⽤复数的虚部为0，求解即可．本题考查复数的基本概念，是基础题． 3.【答案】B【解析】解：画出实数x ，y 满⾜约束条件{x ?3y +1≤0x +y ?3≥0所⽰的平⾯区域，如图：将⽬标函数变形为?12x +z2=y ，则z 表⽰直线在y 轴上截距，截距越⼤，z 越⼤，当⽬标函数过点A(2,1)时，截距最⼩为z =2+2=4，随着⽬标函数向上移动截距越来越⼤，故⽬标函数z =2x +y 的取值范围是[4,+∞)．故选：B ．作出不等式组表⽰的平⾯区域；作出⽬标函数对应的直线；结合图象判断⽬标函数z =x +2y 的取值范围．本题考查画不等式组表⽰的平⾯区域、考查数形结合求函数的最值． 4.【答案】A【解析】解：y =f(x)=xcosx +sinx ，则f(?x)=?xcosx ?sinx =?f(x)，∴f(x)为奇函数，函数图象关于原点对称，故排除B ，D ，当x =π时，y =f(π)=πcosπ+sinπ=?π<0，故排除B ，故选：A ．先判断函数的奇偶性，再判断函数值的特点．本题考查了函数图象的识别，掌握函数的奇偶性额函数值得特点是关键，属于基础题． 5.【答案】A【解析】解：由题意可知⼏何体的直观图如图，下部是直三棱柱，底⾯是斜边长为2的等腰直⾓三⾓形，棱锥的⾼为2，上部是⼀个三棱锥，⼀个侧⾯与底⾯等腰直⾓三⾓形垂直，棱锥的⾼为1，所以⼏何体的体积为：12×2×1×2+13×12×2×1×1=73．故选：A．画出⼏何体的直观图，利⽤三视图的数据求解⼏何体的体积即可．本题考查三视图求解⼏何体的体积，判断⼏何体的形状是解题的关键．6.【答案】B【解析】【分析】本题借助空间的位置关系，考查了充分条件和必要条件，属于基础题．由m，n，l在同⼀平⾯，则m，n，l相交或m，n，l有两个平⾏，另⼀直线与之相交，或三条直线两两平⾏，根据充分条件，必要条件的定义即可判断．【解答】解：空间中不过同⼀点的三条直线m，n，l，若m，n，l在同⼀平⾯，则m，n，l相交或m，n，l有两个平⾏，另⼀直线与之相交，或三条直线两两平⾏．故m，n，l在同⼀平⾯”是“m，n，l两两相交”的必要不充分条件，故选：B．7.【答案】B【解析】解：在等差数列{a n}中，a n=a1+(n?1)d，S n+2=(n+2)a1+(n+2)(n+1)2d，S2n=2na1+2n(2n?1)2d，b1=S2=2a1+d，b n+1=S n+2?S2n=(2?n)a1?3n2?5n?22d．∴b2=a1+2d，b4=?a1?5d，b6=?3a1?24d，b8=?5a1?55d．A.2a4=2(a1+3d)=2a1+6d，a2+a6=a1+d+a1+5d=2a1+6d，故A正确；B.2b4=?2a1?10d，b2+b6=a1+2d?3a1?24d=?2a1?22d，若2b4=b2+b6，则?2a1?10d=?2a1?22d，即d=0不合题意，故B错误；C.若a42=a2a8，则(a1+3d)2=(a1+d)(a1+7d)，即a12+6a1d+9d2=a12+8a1d+7d2，得a1d=d2，∵d≠0，∴a1=d，符合a1d1，故C正确；D.若b42=b2b8，则(?a1?5d)2=(a1+2d)(?5a1?55d)，即2(a1d )2+25a1d+45=0，则a1d有两不等负根，满⾜a1d1，故D正确．∴等式不可能成⽴的是B．故选：B．由已知利⽤等差数列的通项公式判断A与C；由数列递推式分别求得b2,b4,b6,b8，分析B，D成⽴时是否满⾜公差d≠0，a1 d1判断B与D．本题考查数列递推式，等差数列的通项公式与前n项和，考查转化思想和计算能⼒，是中档题．8.【答案】D【解析】解：点O(0,0)，A(?2,0)，B(2,0).设点P满⾜|PA|?|PB|=2，可知P的轨迹是双曲线x21?y23=1的右⽀上的点，P为函数y=3√4?x2图象上的点，即y236+x24=1在第⼀象限的点，联⽴两个⽅程，解得P(√132,3√32)，所以|OP|=√134+274=√10．故选：D．求出P满⾜的轨迹⽅程，求出P的坐标，即可求解|OP|．本题考查圆锥曲线的综合应⽤，曲线的交点坐标以及距离公式的应⽤，是中档题．9.【答案】C【解析】解：由题意知，x=0时，不等式ab(?2a?b)?0恒成⽴，即ab(2a+b)?0，∵ab≠0，∴可得1a +2b0，则a,b⾄少有⼀个是⼩于0的，(1)若a<0,b<0，(x?a)(x?b)(x?2a?b)?0在x?0时恒成⽴，符合题意；(2)若a<0,b>0，则2a+b(3)若a>0,b<0，则2a+b>b，当2a+b=a时，(x?a)(x?b)(x?2a?b)?0在x?0时恒成⽴，符合题意．综合，b<0成⽴．故选：C．本题考查不等式恒成⽴问题，注意三次函数的图象，考查分类讨论思想和转化思想，属于中档题．10.【答案】A【解析】解：取：S={1,2，4}，则T={2,4，8}，S∪T={1,2，4，8}，4个元素，排除C．S={2,4，8}，则T={8,16，32}，S∪T={2,4，8，16，32}，5个元素，排除D；S={2,4，8，16}则T={8,16，32，64，128}，S∪T={2,4，8，16，32，64，128}，7个元素，排除B；故选：A．利⽤特殊集合排除选项，推出结果即可．本题考查命题的真假的判断与应⽤，集合的基本运算，利⽤特殊集合排除选项是选择题常⽤⽅法，难度⽐较⼤．11.【答案】10【解析】【分析】本题考查数列求和，数列通项公式的应⽤，是基本知识的考查．求出数列的前3项，然后求解即可．【解答】解：数列{a n}满⾜a n=n(n+1)2，可得a1=1，a2=3，a3=6，所以S3=1+3+6=10．故答案为：10．12.【答案】80 130【解析】解：∵(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a4=C54?24=80．a1+a2+a3=C51?2+C52?4+C53?8=130．故答案为：80；130．直接利⽤⼆项式定理的通项公式，求解即可．本题考查⼆项式定理的应⽤，只有⼆项式定理系数以及项的系数的区别，是基本知识的考查．13.【答案】?351 3【解析】解：tanθ=2，则cos2θ=cos2θ?sin2θcos2θ+sin2θ=1?tan2θ1+tan2θ=1?41+4=?35．tan(θ?π4)=tanθ?tanπ41+tanθtanπ4=2?11+2×1=13．故答案为：?35；13．利⽤⼆倍⾓公式以及同⾓三⾓函数基本关系式求解第⼀问，利⽤两⾓和与差的三⾓函数转化求解第⼆问．本题考查⼆倍⾓公式的应⽤，两⾓和与差的三⾓函数以及同⾓三⾓函数基本关系式的应⽤，是基本知识的考查．14.【答案】1【解析】解：∵圆锥侧⾯展开图是半圆，⾯积为2π，设圆锥的母线长为a，则12×a2π=2π，∴a=2，∴侧⾯展开扇形的弧长为2π，设圆锥的底⾯半径OC=r，则2πr=2π，解得r=1．故答案为：1．利⽤圆锥的侧⾯积，求出母线长，求解底⾯圆的周长，然后求解底⾯半径．本题考查圆锥的母线长的求法，注意利⽤圆锥的弧长等于底⾯周长这个知识点．15.【答案】√33?2√33【解析】解：由条件得C1(0,0)，r1=1，C2(4,0)，r2=1，因为直线l与C1，C2都相切，故有d 1=√1+k 2=1，d 2=√1+k 2=1，则有√1+k 2=√1+k 2，故可得b 2=(4k +b)2，整理得k(2k +b)=0，因为k >0，所以2k +b =0，即b =?2k ，代⼊d 1=√1+k 2=1，解得k =√33，则b =?2√33，故答案为：√33；?2√33．根据直线l 与两圆都相切，分别列出⽅程d 1=√1+k 2=1，d 2=√1+k 2=1，解得即可．本题考查直线与圆相切的性质，考查⽅程思想，属于中档题．16.【答案】13 1【解析】解：由题意知，随机变量ξ的可能取值为0，1，2；计算P(ξ=0)=C 11C 41+C 11?C 11C 41?C 31=13；P(ξ=1)=C 21?C 11A 42+C 21C 11A 22C 11A 43=13； P(ξ=2)=A 22?C 11A 43+C 22C 11A 33A 22C 11A 44=13；所以E(ξ)=0×13+1×13+2×13=1．故答案为：13，1．由题意知随机变量ξ的可能取值为0，1，2；分别计算P(ξ=0)、P(ξ=1)和P(ξ=2)，再求E(ξ)的值．本题考查了离散型随机变量的分布列与数学期望的计算问题，是中档题．17.【答案】2829【解析】解：设e 1 、e 2 的夹⾓为α，由e 1 ，e 2 为单位向量，满⾜|2e 1??? ?e 2??? |≤√2，所以4e 1 2?4e 1 ?e 2 +e 2 2=4?4cosα+1≤2，解得cosα≥34；⼜a ? =e 1 +e 2 ，b ? =3e 1 +e 2 ，且a，b ? 的夹⾓为θ，所以a ? ?b ? =3e 1 2+4e 1 ?e 2 +e 2 2=4+4cosα， a ? 2=e 1 2+2e 1 ?e 2 +e 2 2=2+2cosα，b ? 2=9e 1 2+6e 1 ?e 2 +e 2 2=10+6cosα；则cos 2θ=(a ? ?b)2a2×b2=(4+4cosα)2(2+2cosα)(10+6cosα)=4+4cosα5+3cosα=43?835+3cosα，所以cosα=34时，cos 2θ取得最⼩值为43?835+3×34=2829．故答案为：2829．设e1 、e2 的夹⾓为α，由题意求出cosα≥34；再求a?，b? 的夹⾓θ的余弦值cos2θ的最⼩值即可．本题考查了平⾯向量的数量积与夹⾓的运算问题，是中档题．18.【答案】解：(1)∵2bsinA=√3a，∴2sinBsinA=√3sinA，∵sinA≠0，∴sinB=√32，，∴B=π3，(2)∵△ABC为锐⾓三⾓形，B=π∴C=2π3A，，△ABC为锐⾓三⾓形，，，解得，，，，∴cosA+cosB+cosC的取值范围为(√3+12,32 ]．【解析】本题考查了正弦定理，三⾓函数的化简，三⾓函数的性质，考查了运算求解能⼒和转化与化归能⼒，属于中档题．(1)根据正弦定理可得sinB=√32，结合⾓的范围，即可求出，(2)根据两⾓和差的余弦公式，以及利⽤正弦函数的性质即可求出．19.【答案】解：(1)证明：作DH⊥AC，且交AC于点H，∵⾯ADFC⊥⾯ABC，⾯ADFC∩⾯ABC=AC，DH?⾯ADFC，∴DH⊥⾯ABC，BC?⾯ABC，∴DH⊥BC，∴在Rt△DHC中，CH=CD?cos45°=√22CD，∵DC=2BC，∴CH=√22CD=√222BC=√2BC，∴BCCH =√22，⼜∠ACB=45°，∴△BHC是直⾓三⾓形，且∠HBC=90°，∴BC⊥⾯DHB，∵DB?⾯DHB，∴BC⊥DB，∵在三棱台DEF?ABC中，EF//BC，∴EF⊥DB．(2)设BC=1，则BH=1，HC=√2，在Rt△DHC中，DH=√2，DC=2，在Rt△DHB中，DB=√DH2+HB2=√2+1=√3，作HG⊥BD于G，∵BC⊥⾯DHB，HG?⾯DHB，∴BC⊥HG，⽽BC?⾯BCD，BD?⾯BCD，BC∩BD=B，∴HG⊥⾯BCD，∵GC?⾯BCD，∴HG⊥GC，∴△HGC是直⾓三⾓形，且∠HGC=90°，设DF与⾯DBC所成⾓为θ，则θ即为CH与⾯DBC的夹⾓，且sinθ=sin∠HCG=HGHC =√2，∵在Rt△DHB中，DH?HB=BD?HG，∴HG=DH?HBBD =√2?1√3=√63，∴sinθ=√2=√63√2=√33．【解析】本题主要考查空间直线互相垂直的判定和性质，以及直线与平⾯所成⾓的⼏何计算问题，考查了空间想象能⼒和思维能⼒，平⾯与空间互相转化是能⼒，⼏何计算能⼒，以及逻辑推理能⼒，本题属综合性较强的中档题．(1)题根据已知条件，作DH⊥AC，根据⾯⾯垂直，可得DH⊥BC，进⼀步根据直⾓三⾓形的知识可判断出△BHC是直⾓三⾓DF与⾯DBC 所成⾓的正弦值．20.【答案】(1)解：由题意，b2=q，b3=q2，∵b1+b2=6b3，∴1+q=6q2，整理，得6q2?q?1=0，解得q=?13(舍去)，或q=12，∴c n+1=b nb n+2?c n=1b n+2b nc n=1q2c n=1(12)2c n=4c n，∴数列{c n}是以1为⾸项，4为公⽐的等⽐数列，∴c n=1?4n?1=4n?1，n∈N?．∴a n+1?a n=c n+1=4n，则a1=1，a2?a1=41，a3?a2=42，a na n1=4n1，各项相加，可得a n=1+41+42+?+4n?1=1?4n1?4=4n?13b n+2c n(n∈N?)，可得b n+2?c n+1=b n?c n，两边同时乘以b n+1，可得b n+1b n+2c n+1=b n b n+1c n，∵b1b2c1=b2=1+d，∴数列{b n b n+1c n}是⼀个常数列，且此常数为1+d，b n b n+1c n=1+d，∴c n=1+db n b n+1=1+dddb n b n+1=(1+1d)?b n+1?b nb n b n+1=(1+1d)(1b n1b n+1)，∴c1+c2+?+c n=(1+1d)(1b11b2)+(1+)(1b21b3)+?+(1+ 1d)(1b n1b n+1 )=(1+1 d)(1b11b2+1b21b3 +?+1b nb n+1)=(1+1d)(1b11b n+1)=(1+1d)(1?1b n+1)<1+1d，∴c1+c2+?+c n<1+1d，故得证．【解析】本题主要考查数列求通项公式，等差数列和等⽐数列的基本量的运算，以及和式不等式的证明问题．考查了转化与化归思想，整体思想，⽅程思想，累加法求通项公式，裂项相消法求和，放缩法证明不等式，以及逻辑推理能⼒和数学运算能⼒．本题属综合性较强的偏难题．(1)先根据等⽐数列的通项公式将b2=q，b3=q2代⼊b1+b2=6b3，计算出公⽐q的值，然后根据等⽐数列的定义化简c n+1=b nb n+2c n可得c n+1=4c n，则可发现数列{c n}是以1为⾸项，4为公⽐的等⽐数列，从⽽可得数列{c n}的通项公式，然后将通项公式代⼊c n+1=a n+1?a n，可得a n+1?a n=c n+1=4n，再根据此递推公式的特点运⽤累加法可计算出数列{a n}的通项公式；(2)通过将已知关系式c n+1=b nb n+2c n不断进⾏转化可构造出数列{b n b n+1c n}，且可得到数列{b n b n+1c n }是⼀个常数列，且此常数为1+d ，从⽽可得b n b n+1c n =1+d ，再计算得到c n =1+d，根据等差数列的特点进⾏转化进⾏裂项，在求和时相消，最后运⽤放缩法即可证明不等式成⽴．21.【答案】解：(1)p =116，则?p 2=132，则抛物线C 2的焦点坐标(132,0)，(2)由题意可设直线l ：x =my +t (m ≠0,t ≠0)，点A (x 0,y 0)，将直线l 的⽅程代⼊椭圆C 1：x 22+y 2=1得(m 2+2)y 2+2mty +t 2?2=0∴点M 的纵坐标y M =?mtm 2+2。

2020年高考地理浙江卷(1月选考)及答案

海等南方沿海省市，形成了“北菜南运”格局。完成 5、6 题。
5.“北菜南运”的主要原因是
（）
A.南方市场需求大
B.北方耕地面积增大
C.北方蔬菜品种多
D.南方蔬菜种植减少
6.“北菜南运”有利于北方地区农业
（）
①粗放经营 ②规模化经营 ③集约化生产 ④“小而全”生产
A.①②
B.②③
C.③④
D.①④
下图为我国两大资源跨区域调配工程的局部示意图。完成 7、8 题。
下图分别为1沿经向分布折线图图中t为t1与t2251月亚欧大陆45n以北t较大的主要原因是亚洲低压与大洋副热带高压形成热力差异北大西洋暖流增加西部海岸温度大陆中部高原的存在缩小了东西沿岸温差季风影响了东部陆地与海洋间温差三非选择题本大题共4小题共45长江与鄱阳湖之间存在径流相互补给的季节变化
毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________
④季风影响了东部陆地与海洋间温差
A.①②
B.①③
C.②④
D.③④
（）（）
三、非选择题（本大题共 4 小题，共 45 分）
26.阅读材料，完成下列问题。（10 分）长江与鄱阳湖之间存在径流相互补给的季节变化。下图 1 为西太平洋副热带高压脊
季节变化示意图，图 2 为长江与鄱阳湖相互补给频率的年内分布图（频率越高一般表示径流量补给越大）。
27.阅读材料，完成下列问题。（10 分）材料一下图为中亚地区略图。
材料二乙地为所在国棉花主产区，棉花播种面积约占该地种植总面积的 40%，所产棉花大部分出口到俄罗斯、中国，已发展成为重要棉花输出基地。（1）指出甲地径流的主要补给类型，分析城镇沿甲河分布的原因。（6 分）（2）说明乙地是重要棉花输出基地的主要原因。（4 分） 28.阅读材料，完成下列问题。（12 分）材料一皖江城市带在长江经济带位置示意图。

2020年高考物理浙江卷(1月选考)附答案解析版

聚变前要先使原有的原子结构破坏发生类似裂变然后重新组合成新的原子发生聚变有质量亏损会对外再次释放能量因此核聚变中平均每个核子放出的能量比裂变中平均每个核子的大故c错误
毕业学校
姓名
考生号
绝密★启用前
在
浙江省 2020 年 1 月普通高校招生选考科目考试
物理
一、选择题Ⅰ（本题共 13 小题，每小题 3 分，共 39 分。每小题列出的四个
效物理试卷第 5 页（共 8 页）
18.（1）小明同学用多用电表测量一未知电阻器的阻值。经过规范操作后，所选欧姆挡
倍率及指针位置分别如图甲、乙所示，则此电阻器的阻值为
。
（2）在“测绘小灯泡的伏安特性曲线”实验中：
①如图丙所示，已经连接了一部分电路，请在答题纸上对应位置将电路连接完整。 ②合上开关后，测出 9 组 I、U 值，在 I U 坐标系中描出各对应点，如图丁所示。请在
D. 大量氢原子从n 4 能级向低能级跃迁时可辐射出 2 种频率的可见光
15.如图所示，波长为a 和 b 的两种单色光射入三棱镜，经折射后射出两束单色光 a和
b ，则这两束光
（）
A. 照射同一种金属均有光电子逸出，光电子最大初动能 EKa EKb B. 射向同一双缝干涉装置，其干涉条纹间距xa xb
（）
5.如图所示，钢球从斜槽轨道末端以v0 的水平速度飞出，经过时间 t 落在斜靠的挡板 AB
中点。若钢球以2v0 的速度水平飞出，则
（）
A. 下落时间仍为t
B. 下落时间为2t
C.下落时间为 2t
D. 落在挡板底端 B 点 6.小明在一根细橡胶管中灌满食盐水，两端用粗铜丝塞住管口，形成一段封闭的盐水柱。
（填“甲”或“乙”）所

2020年高考数学浙江卷附答案解析版

故选：D. 【考点】等差数列的性质应用 8.【答案】D 【解析】因为| PA | | PB | 2＜4 ，所以点 P 在以 A, B 为焦点，实轴长为2 ，焦距为4 的双曲线的右支上，由
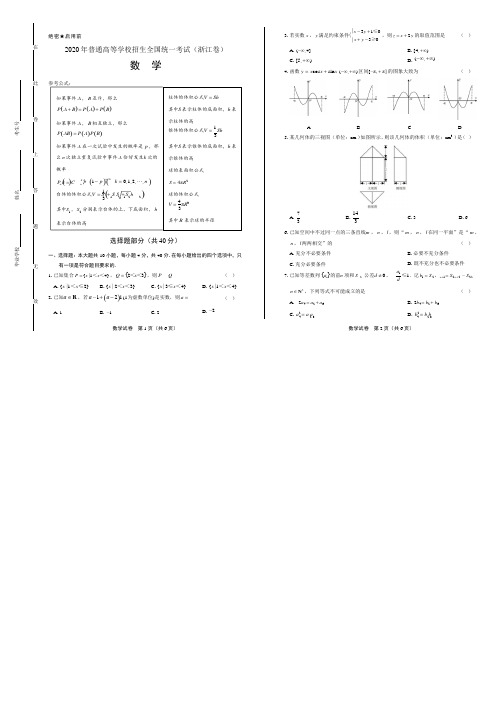
c 2 ， a 1 可得， b2 c2 a2 4 1 3 ，即双曲线的右支方程为 x 2 y2 1x＞0 ，而点 P 还在函数
（Ⅱ）若数列 bn为等差数列，且公差d＞0 ，证明：c 1c 2
c ＜n1
1 (n N
d
) ．*
此
卷
21.如图，已知椭圆C1:
x2 y 2
12，抛物线C
:y
2 2 p2x p
＞0 ，点 A 是椭圆C 1与抛物线
C2 的交点，过点 A 的直线l 交椭圆C1 于点 B ，交抛物线C2 于 M（ B ，M 不同于 A ）．
故选：B 【考点】交集概念【考查能力】基本分析求解 2. 【答案】C
【解析】因为a 1 a 2i 为实数，所以a 2 0 ，∴a 2
故选：C 【考点】复数概念【考查能力】基本分析求解 3. 【答案】B 【解析】绘制不等式组表示的平面区域如图所示，
目标函数即： y 1 x 1 z ， 22
，则
z
x
2
y
的取值范围是
A. (,4] C.[5, )
B.[4, ) D. (, )
4.函数 y xcosx sinx (,) 区间[–π, π] 的图象大致为
（）（）
A
B
C
D
5.某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm3 ）是（）
A. 7
B. 14
3
3
C.3
毕业学校
姓名
考生号

浙江省2020年7月新高考信息技术和通用技术命题思路与试题评析

技术（信息技术）信息技术学科组本次试卷根据高校人才选拔要求和国家课程标准，坚持科学、准确、公平和规范的原则，立足本学科基础知识、基本技能以及核心素养，突出考查学生分析和解决问题的能力。

试卷沿承往年的考试试题形式，保持难度、区分度等方面稳定，与此同时，考虑题目的综合性、灵活性和创新性，使本次试卷平实而不失品味，大气而不失精致，全面考查学生的学科能力和素养。

一、紧扣教材，立足基本概念和原理本次命题突出考查学科的基本概念和原理，紧扣教材，贴近教学。

第1题从信息技术工具、应用等角度综合考查信息技术的基本概念，引导学生关注信息技术的应用及发展趋势。

第2题从网页基本概念、网络信息的检索和应用等角度考查网络基础知识。

第3题从信息管理角度分析数据表设计的合理性，考查数据库基础知识。

第4、7、8题分别考查进制转换、逻辑表达式、流程图等基础知识。

第11、12题立足考查对分查找和冒泡排序算法的基本思想，具有一定的灵活性，旨在引导教学关注基本算法原理，避免对代码的机械记忆。

二、结合应用，落实学科方法和能力考查本次命题以信息技术应用为背景，创设了贴近生活的问题情境，突出考查学生运用学科思想和方法，分析、解决问题的能力。

第13题综合考查运用公式、图表、筛选、排序等方法分析、处理数据的能力。

采用开放性操作序列的多项选择形式，突出数据分析能力，弱化操作步骤的机械记忆。

第14题以多媒体作品设计、制作过程为线索，综合考查作品设计的方法，矢量图、元件与实例、关键帧等知识的应用，问题设计弱化操作性记忆，突出对概念和方法的理解。

第15、16题分别以考场分配、温度数据分析为背景，考查算法理解和程序设计能力。

三、关注素养，多角度考查计算思维算法与程序设计模块的试题命制，多角度考查计算思维。

第10题要求学生通过逻辑推理，理解所给的最值求解算法，从一组形式相同的语句中选择、补全程序，考查学生的逻辑思维和算法思维能力。

第11题采用标记数组探究对分算法查找过程，从微观考查学生算法思维。

2020年浙江省高考语文试卷(有详细解析)

2020年浙江省高考语文试卷班级：___________姓名：___________得分：___________一、单选题（本大题共2小题，共6.0分）1.下列各句中，没有错别字且加点字的注音全都正确的一项是（）A. 浙江诗路文化带以诗词文化为主线，结合水系、古道，将各地旖．（yǐ）旎风光串联成富有诗情画意的山水旅游线路，让游客徜．（táng）徉在江南美景中。

C. 生态文学应更多创作体现绿色发展理念、讴．（ōu）歌美好生活的作品，致力于鞭挞．（dá）滥杀野生动物、肆意破坏环境的恶劣行为，提高全社会的生态文明素养。

2.下列各句中，没有语病的一项是（）A. 新冠肺炎疫情来势汹汹，严重威胁全人类的健康与福祉，也暴露了全球公共卫生治理上的短板，推进全球公共卫生治理体系改革的必要性。

B. 长征五号B运载火箭自从首次飞行任务展开以来，各参研参试单位和全体同志团结拼搏，经历严峻考验，克服重重困难，获得了最后的胜利。

C. 互联网的快速发展为打贏脱贫攻坚战提供了新思路，各地广泛开展的网络扶贫活动，让扶贫工作受益范围更广，使更多的群众有了存在感。

D. 汽车影院以停车空间为电影放映场地，通常设置超大银幕，观众坐在私家车内就可以看到大银幕上清晰稳定的图象和车内收音机上接收的电影原声。

二、现代文阅读（本大题共2小题，共30.0分）3.阅读下面的文字，完成各题。

材料一：一般来说，阅读是和文字相关联的。

当然，人们有时也会把欣赏一幅好画说成“读画”。

用在这里的“读”，强调的是欣赏的深度了，就此也微妙地点出了看画与读画间的差异。

2024年高考生物真题完全解读(6月浙江卷)

2024年1月的生物试题题型与2023年6月的的题型大体一致，小范围调整，选择题由19题重新恢复至20题共40分，非选择题为5题由62分恢复至60分，文字量由6410缩减至6143，一定程度上降低了考生的阅读量，整体降低了试卷难度。与2023年的试题相比，2024年的选择题增加了对图表信息的考查，由1张表3幅图增加至1张表7幅图，依然侧重真实情景的考查以及对题干信息的解读能力；2024年的非选择题更加注重实验技能的培养，5道大题均涉及到了实验分析能力、实验设计能力以及具体应用能力；同时减少了对于课本基础知识的填空考查，更多的需要学生结合题目进行分析，整体来说，增加了试卷难度；试题中的情景多样化，通过情景的推进和转变逐步考查学生的各方面能力，情景之间前后联系，逐渐加深考查难度。试题题意简练，难度适宜，承续了近几年浙江高考生物试题命制风格，情境丰富，创新设问方式，引导考生减少死记硬背和机械刷题。
酒精发酵和醋酸发酵
14
微生物培养
19
PCR
20
电泳
23
植物组织培养；次生代谢产物；基因工程；测序；实验设计与探究
1、回归教材，落实学科基础
教材是《课程标准》具化和细化后的资源，是获取生物学学科知识、落实生物学核心素养的关键性载体和主要的学习资源。高考试题虽然都是依照《课程标准》命制，但是很多知识的落脚点还是在教材上。生物选考中结合教材内容的考查非常多，比如第2题的染色体结构变异，第3题进化的证据，第5题的群落演替，第9题的DNA分子结构。在复习过程中切忌抛弃教材，而过分依赖教辅用书和机械刷题，教材要切实成为学习和复习的最重要资源。第一轮复习的时候要结合《课程标准》，熟读教材，关注教材的角角落落，踏踏实实梳理和理解生物学基本概念，厘清知识点之间的内在逻辑，优化知识结构。第二轮复习要立足教材去做题，对于做错的题目要去教材上寻找答题的依据，收集错题，做好笔记，以免重蹈覆辙。从考试题目回归教材，双向互动，夯实学科基础。

2020年浙江省高考生物试题及解析(浙江卷)

2020年普通高等学校招生全国统一考试（浙江卷）生物试题一、选择题1.下列疾病中不属于遗传病的是( )A. 流感B.唇裂C. 白化病D.21-三体综合征【答案】A【分析】遗传病是指由于生殖细胞或受精卵里的遗传物质发生改变，从而使发育成的个体所患的疾病，包括单基因遗传病、多基因遗传病和染色体异常遗传病。

【详解】A、流感是由于流感病毒入侵人体而引起的，人体遗传物质没有发生改变，不属于遗传病，A正确；B、唇裂属于多基因遗传病，B错误；C、白化病是由常染色体上的隐性致病基因控制的疾病，属于单基因遗传病，C错误D、21-三体综合征是由于体细胞中21号染色体多一条引起的，属于染色体异常遗传病，D错误。

2.下列关于人类与环境的叙述，错误的是( )A. 酸雨会破坏水体生态平衡B. 人口在地球上可以不断地增长C. 生物圈是地球上最大的生态系统D. 人类活动会影响臭氧层的稳定【答案】B【分析】生物圈是指地球上全部生物及其生存的环境。

人类、生物和环境共处于生物圈中。

人类正面临三大全球生态问题：人口、环境和资源。

悉心维护地球的生态环境已经成为人类生存和持续发展的必要条件。

【详解】A、酸雨能杀死水生生物、破坏水体生态平衡，A正确；B、地球的资源是有限的，食物的生产也是有限的，人类生存的唯一出路就是设法降低出生率，做到自我控制，最终使全球人口保持在一个稳定的水平上，B错误；C、生物圈是指地球上全部生物及其生存的环境，是地球上最大的生态系统，C正确；D、最近30多年的研究表明，人类活动正在干扰和破坏着大气圈上臭氧层的自然平衡，D正确。

3.下列关于艾滋病和HIV的叙述，正确的是( )A. 艾滋病属于先天性免疫缺乏病B. HIV由蛋白质和DNA组成C. 艾滋病患者免疫功能严重衰退D. HIV通过性接触和握手等途径传播【答案】C【分析】艾滋病是英文AIDS的译名。

AIDS是获得性免疫缺陷综合征一词的英文缩写。

这是一种新发现的通过体液传播的疾病。

专题07+2020年7月浙江卷(遇熊脱险)-近年新高考英语真题读后续写解析+讲评课件

Tdhoneeb. Tighidsawyascaonmeeofathloasset.timThese. alarm rang at 6 a.m. The pair went down the stairs quietly to the kitchen. They decided to boil the
As Elli and I cooked dinner, a young male polar bear who was playing in a nearby lake sniffed, and smelled our spaghetti and garlic bread. The hungry bear followed his nose to our camp, which was surrounded by a high, wire fence. He clawed, bit, and shoved the wire mesh. He stood on his hind legs and pushed at the wooden fence posts.Terrified, Elli and I tried all the bear defense actions we knew. We yelled at the bear, banged pots, and fired blank shotgun shells into the air. Sometimes loud noises like these will scare bears off. Not this polar bear-he just growled and went back to trying to tear down the fence with his massive paws.