七年级数学下册.平移练习题新人教版

合集下载

(新人教版)数学七年级下册：5.4《平移》教案和习题(含答案)

《平移》教案一、教学目标1.经历观察、分析、操作、欣赏以及抽象、归纳等过程，以及与他人合作交流探索的过程，进一步发展空间观念，增强审美意识，学会用运动的观点分析问题.2.通过实例，认识图形平移，了解平移的特征，理解平移的含义，会进行点的平移.3.理解平移前后两个图形对应点连线平行且相等的性质，能解决简单的平移问题.二、教学重点与难点重点：图形平移的特征和作平移图形.难点：平移的性质探索和理解.三、教学过程（一）创设情境，引入新课1.感受平移，体验新知你坐过公车和搭过电梯吗？它是一种什么样的运动？这样的运动在生活中还有哪些现象？（活动1：学生讨论）2.观察图形，形成印象生活中有许多美丽的图案，他们都有着共同的特点，请同学们欣赏下面图案.观察上面图形，我们发现他们都有一个局部和其他部分重复，如果给你一个局部，你能复制他们吗？学生思考讨论，并回答问题.(1)它们有什么共同的特点？(2)能否根据其中的一部分绘制出整个图案？（活动2：师生交流.）这些美丽的图案是由若干个相同的图案组合而成的，每个图形都有“基本图形”，而“基本图形”是什么？如第一个图形是中间一个正方形，上、下有正立与倒立的正三角形，下排的左图中的“基本图形”是鸽子与橄榄枝；下排右图中的“基本图形”是上、下一对面朝右与面朝左的人头像组成的图案.3.实践探索，得出新知探究：设计一个简单的图案，利用一张半透明的纸附在上面，绘制一排形状，大小完全一样的图案如：引导学生找规律，发现平移特征，回答下面问题：1、图形经过平移后，_______图形的位置，________图形的形状，________图形的大小.(填“改变”或“不改变”)2、经过平移，每一组对应点所连成的线段________.归纳 (活动3：分组讨论)平移：(1)把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同. (2)新图形中的每一点，都是由原图形中的某一个点移动后得到的，这两个点是对应点. (3)连接各组对应的线段平行且相等.图形的这种变换，叫做平移变换，简称平移简单归纳为两点：1.平移的方向. 2.平移的距离四、典例剖析，深化巩固1. 把鱼往左平移8cm.(假设每小格是1cm2)五、小结(学生回答)：这节课你学了什么？知道了什么？学会了什么？六、课后作业必做题：教科书习题：3.6题《平移》习题1、决定平移的基本要素是＿＿＿＿和＿＿＿＿。

(新人教版)七年级下册数学：5.4《平移》练习题及答案

平移练习题◆回顾归纳1．平移的要素：（1）平移的_________；（2）平移的_________．2．（1）平移：将一个图形沿某个方向_________叫平移．（2）平移的性质：对应点的连结线段_________且_________．3．平移作图方法：（1）找出已知图形上的关键点；（2）过这些点沿指定_______平移，使平移_______等于已知距离；（3）依次作出各个_______点，连结所平移后的点得平移图形．◆课堂测控知识点平移（1）将线段AB•向北偏东方向平移5cm，•则点A•平移方向_______，•平移距离为______．（2）1．经过平移后的图形与______形状和大小都不改变．2．下列物体运动中平移的是_________（填序号）．（1）打乒乓球的运动；（2）手表上指针的运动；（3）汽车在笔直公路上运动；（4）车轮的滚动．3．如图1所示的“田”字格可以看成由________平移得到的．图1 图2 图34．如图2所示，线段b向右平移3格，再向上平移______格，能与线段______重合．5．如图3所示，三角形ABC向下（右）平移_______格，再向右（下）平移_____得到三角形A′B′C′，图形的面积相等，形状不变．6．下列各组图形可以通过平移得到另一个图形的是（）A B C D7．（经典题）如图4所示，长方形ABCD中，对角线AC，BD交于点O．DE∥AC，CE ∥BC．那么三角形EDC可以看成什么三角形平移得到的，指出平移方向，并求出平移距离？图4◆课后测控1．将正方形ABCD向北偏东30°方向平移4cm，•则对角线交点O•向________•平移______cm．2．如图5所示，BC垂直于水平面，高5.196m，现要建造阶梯，•每级台阶不超过20cm，则至少要建_______级台阶（不足20cm，按一级台阶计算）图5 图6 图73．在5×5方格纸中将图6（1）中的图形N平移后的位置如图6（2）中所示，那么正确的平移方法是（）A．先向下移动1格，再向左移动1格B．先向下移动1格，再向左移动2格C．先向下移动2格，再向左移动1格D．先向下移动2格，再向左移动2格4．（互动探究题）如图7所示，在网格中，有三角形ABC，将A点平移到P点，画出三角形ABC平移后的图形．[解答]（1）将A点向_______（或向______）平移______格（或_____格）．（2）再向_____（或向_____）平移______格（或_______格），得点P．（3）同理B，C与A点平移次数方向距离一样，易得B′，C′．（4）连结PB′，PC′，B′C′得到三角形ABC平移后的三角形PB′C′．5．（经典题）如图所示，一块边长为8米的正方形土地，上面修了横竖各两条道路，宽都是1米，空白的部分种上各种花草，请利用平移的知识求出种花草的面积？◆拓展创新6．如图所示，在长方形ABCD中，AB=10cm，BC=6cm，试问将长方形ABCD•沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2？答案:回顾归纳1．（1）方向（2）距离2．（1）移动（2）平行或在同一条直线上，相等3．（2）方向；距离（3）对应课堂测控1．（1）北偏东；5cm （2）原图形 2．（3）3．小正方形包括中间四个小圆圈为基本图形4．2，c 5．3（或2），2（或3）6．C（点拨：A，B，D都不能通过平移得到）7．由三角形AOB，向右平移，平移距离为AD长．解题技巧：由平移图形的特征：大小，形状不变，猜想是△AOB．课后测控1．北偏东30°；4 2．26（点拨：519.620=26）3．C（点拨：或向左平移1格，再向下平移2格）4．（1）右；（下）；4；（5）（2）下；（右）；5；（4）（3），（4）图略5．将两条道路平移得到如图所示，则空白面积为（8-2）（8-2）=36（m2）思路点拨：运用平移思想方法是求这类面积问题最佳途径．6．设平行线段AE=x，A到E，E到F，则BE=AB-AE=10-x，因为BC=6，所以6（10-x）=24，•解得x=6，向右平移6cm．解题规律：扣住HEBC面积为24cm2，运用方程思想求解．。

人教版七年级下册数学平移课时练习题(含答案)

人教版七年级下册数学5.4平移课时练习题（含答案）一、单选题1．“水是生命之源，滋润着世间万物”国家节水标志由水滴，手掌和地球变形而成．寓意：像对待掌上明珠一样，珍惜每一滴水!以下通过平移节水标志得到的图形是（）A．B．C．D．2．在下列现象中，属于平移的是（）A．月亮绕地球运动B．翻开书中的每一页纸张C．教室可移动黑板的左右移动D．投掷出去的铅球3．下列几种运动中属于平移的有（）①水平运输带上砖的运动；②笔直的铁路上行驶的动车（忽略车轮的转动）；③升降机上下做机械运动；④足球场上足球的运动．A．4种B．3种C．2种D．1种4．如图，在平面直角坐标系中，已知点A(2，1)，B(3，－1)，平移线段AB，使点B落在点B1（－1，－2）处，则点A的对应点A1的坐标为（）A．(0，－2)B．（－2，0）C．（0，－4）D．（－4，0）5．佳佳将坐标系中一图案横向拉长2倍，又向右平移2个单位长度，若想变回原来的图案，需要变化后的图案上各点坐标（）A．纵坐标不变，横坐标减2 B．纵坐标不变，横坐标先除以2，再均减2C．纵坐标不变，横坐标除以2 D．纵坐标不变，横坐标先减2，再均除以26．如图，ΔABC是直角三角形，它的直角边AB=6，BC=8，将ΔABC沿边BC的方向平移到ΔDEF 的位置，DE交AC于点G，BE=2，ΔCEG的面积为13.5，下列结论：①ΔABC平移的距离是4：②DG=1.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是（）A．①②B．②③C．③④D．②④7．如图所示，将三角形ABC平移得到三角形EFG，则图中共有平行线(含虚线)()A．3对B．4对C．5对D．6对8．如图，△ABC沿直线BC向右平移得到△DEF，已知EC=2，BF=8，则CF的长为（）A．3B．4C．5D．69．如图，将△ABC向右平移8个单位长度得到△DEF，且点B，E，C，F在同一条直线上，若EC＝4，则BC的长度是（）A．11B．12C．13D．1410．如图，在平面直角坐标系xOy中，将四边形ABCD先向上平移，再向左平移得到四边形A1B1C1D1，已知A1(−3,5),B1(−4,3),A(3,3)，则点B坐标为（）A．(1,2)B．(2,1)C．(1,4)D．(4,1)11．如图，在平面直角坐标系中，▱AOBC的顶点O与原点重合，顶点B在x轴正半轴上，顶点A 的坐标为(−1，2)．按以下步骤作图：先以点O为圆心，适当长为半径作弧，分别交边OA，OB于点D，E；再分别以点D，E为圆心，大于12DE的长为半径作弧，两弧在∠AOB内交于点F，作射线OF交AC边于点G．则点G的坐标为（）A．(3−√5，2)B．(√5，2)C．(√5−2，2)D．(√5−1，2) 12．如图，在数轴上，点A表示1，现将点A沿数轴做如下移动；第一次将点A向左移动3个单位长度到达点A1，第二次将点A向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种移动规律移动下去，第n次移动到点A n，如果点A n与原点的距离不小于17，那么n的最小值是（）A．9B．10C．11D．12二、填空题13．如图，将△ABC沿直线BC方向平移3个单位得到△DEF，若BC=5，则BF=．14．如图，将△ABC沿BC方向平移至△DEF处.若EC＝2BE＝2，则CF的长为.15．在平面直角坐标系中，将点A(9，-7)向左平移2个单位长度，则平移后对应的点A‘的坐标是。

人教版七年级下册数学第5章5.4平移习题课件1

三角形DEF. (1)图中有哪些相等的线段，有哪些平行的线段？
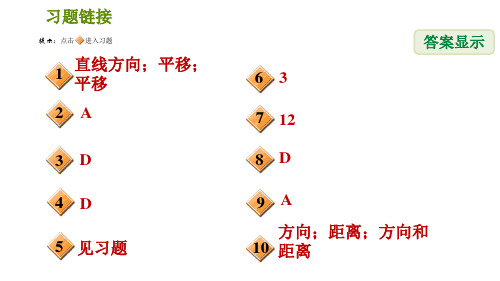
解：相等的线段有：AB＝DE，BC＝ EF，AC＝DF，AD＝BE＝CF；平行的线段有：AB∥DE，BC∥EF， AC∥DF，AD∥BE∥CF.
素质一练通 (2)若∠ABC＝60°，∠ACB＝70°，直接写出∠DEF和
∠DFE的度数．
素质一练通 (2)求证AB⊥E′D′.
证明：由平移的性质知CE∥C′E′，∠CED＝ ∠C′E′D′＝60°， ∴∠BE′C′＝∠A＝30°.∴∠BE′D′＝90°. ∴AB⊥E′D′.
精彩一题 17．【教材P31习题T6变式】如图，图形的操作过程(本题4个
图形中的长方形均相同，长为a，宽为b)：在图①中，将
新知基本功
10．平移是由平移的_方__向____和__距___离__决定的，所以在平移作图时，要先明确图形原来的位置及平移的 _方__向__和__距___离______，再画图．
新知基本功 11．下列平移作图错·误·的是( C )
新知基本功 12．如图，在10×6的网格中，每个小正方形的边长都是1
素质一练通 15．如图，将直角三角形ABC沿AB方向平移得到直角三角形
DEF.已知BE＝5，EF＝8，CG＝3，求图中阴影部分的面积．解：∵直角三角形ABC沿AB方向平移得到直角三角形DEF， ∴三角形ABC的面积与三角形DEF的面积相等， BC＝EF，BC∥BF.
素质一练通
∴三角形ABC的面积－三角形DBG的面积＝三角形DEF的面积－三角形DBG的面积，四边形GBEF为梯形． ∴阴影部分的面积与梯形GBEF的面积相等． ∵EF＝8，CG＝3， ∴BG＝BC－CG＝EF－CG＝5. 又∵BE＝5，∴阴影部分的面积＝(5＋8)×5× 12＝32.5.

人教版七年级数学下册第七章第二节用坐标表示平移习题(含答案) (31)

人教版七年级数学下册第七章第二节用坐标表示平移习题（含答案)一、单选题1．将点(-3，4)向右平移3个单位、向下平移2个单位后的坐标为( ) A．(-6，0) B．(6，0) C．(0，-2) D．(0，2)【答案】D【解析】【分析】根据平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，即可求解．【详解】解：横坐标右移加，左移减；纵坐标上移加，下移减，将点A（-3，4）向右平移3个单位，再向下平移2个单位，得到的点A′的坐标是（0，2）．故选：D．【点睛】本题主要考查了在平面直角坐标系中，图形的平移与图形上某点的平移相同，难度适中．2．在平面直角坐标系中，点M（﹣1，3），先向右平移2个单位，再向下平移4个单位，得到的点的坐标为（）A．（﹣3，﹣1）B．（﹣3，7）C．（1，﹣1）D．（1，7）【答案】C【解析】【分析】直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．【详解】解：点M（﹣1，3），先向右平移2个单位，再向下平移4个单位，得到的点的坐标为（﹣1+2，3﹣4），即（1，﹣1），故选：C．【点睛】本题主要考查了坐标与图形变化−平移，平移中点的变化规律：左右移动改变点的横坐标，左减，右加；上下移动改变点的纵坐标，下减，上加．3．已知点A的坐标为(1，3)，点B的坐标为(3，1)，将线段AB沿某一方向平移后，点A的对应点的坐标为(﹣2，1)，则点B的对应点的坐标为( ) A．(6，3) B．(0，3) C．(6，﹣1) D．(0，﹣1)【答案】D【解析】【分析】根据点A、点A的对应点的坐标确定出平移规律，然后根据规律求解点B 的对应点的坐标即可．【详解】解：由题意A （1，3）的对应点的坐标为（-2，1），∴平移规律为横坐标减3，纵坐标减2，∴点B （3，1）的对应点的坐标为（0，-1）．故选：D ．【点睛】本题考查了坐标与图形变化-平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，本题根据对应点的坐标确定出平移规律是解题的关键．4．抛物线23y x =先向下平移1个单位，再向左平移2个单位，所得的抛物线是（）A ．23(2)1y x =+-.B ．23(2)1y x =-+C ．2(2)1y x =--D ．23(2)1y x =++ 【答案】A【解析】【分析】根据函数图象平移的法则“左加右减，上加下减”的原则进行解答即可．【详解】由“上加下减”的原则可知，将抛物线y=3x 2先向向下平移1个单位可得到抛物线y=3x 2-1；由“左加右减”的原则可知，将抛物线y=3x 2-1先向左平移2个单位可得到抛物线23(2)1y x =+-.故选A.本题考查二次函数图象与几何变换，解题的关键是掌握函数图象平移的法则“左加右减，上加下减”的原则.5．将点A(3, 1)向上平移2个单位得到点B , 点B 的坐标是( )A ．(5,3)B ．(1, 3)C ．(3, 3)D ．(5, 1)【答案】C【解析】【分析】根据点的平移规律，向上平移2个单位，将纵坐标加2即可.【详解】点A(3, 1)向上平移2个单位，纵坐标加2得(3, 3)，故B 的坐标是(3, 3)，选C.【点睛】本题考查点的平移，熟练掌握上下平移是改变纵坐标，左右平移改变横坐标是关键，与函数图像平移的“左加右减”要进行区分. 6．点()34--，先向上平移5个单位，再向右平移4个单位后的坐标为（）A ．()20，B ．()71-，C ．()19-，D ．()11，【答案】D【解析】【分析】根据坐标系中点的平移规律，上下平移改变纵坐标，左右平移改变横坐标，即可解答.向上平移5个单位，纵坐标为-4+5=1，向右平移4个单位，横坐标为-3+4=1，所以平移后的坐标为()11，，故选D.【点睛】本题考查坐标系中点的平移，熟记平移规律是解题的关键.7．将△ABC向左平移2个单位长度后得到△A'B'C'．若点A的坐标是（－3，7），则点A'的坐标是( )A．(－5，5) B．(－1，9) C．(－5，7) D．(－1，7)【答案】C【解析】【分析】根据平移点的变化规律（横坐标右移加，左移减；纵坐标上移加，下移减）求解．【详解】解：∵△ABC向左平移2个单位长度后得到△A′B′C′，∴点A（-3，7）向左平移2个单位长度后得到的点A′的坐标为（-5，7）．故选：C．【点睛】本题考查了坐标与图形变化——平移：在平面直角坐标系内，把一个图形各个点的横坐标都加上（或减去）一个整数a，相应的新图形就是把原图形向右（或向左）平移a个单位长度；如果把它各个点的纵坐标都加（或减去）一个整数a，相应的新图形就是把原图形向上（或向下）平移a个单位长度．8．在平面直角坐标系中，将点（2，3）向右平移2个单位，所得到的点的坐标是（）A．（2，5 ）B．（4，3 ）C．（0，3 ）D．（2，1 ）【答案】B【解析】【分析】把点（2，3）的横坐标加2，纵坐标不变得到（4，3），就是平移后的对应点的坐标．【详解】点（2，3）向右平移2个单位长度后得到的点的坐标为（4，3）．故选B．【点睛】本题考查了坐标与图形变化﹣平移．掌握平移的规律是解答本题的关键．9．在如图所示的网格中，有两个完全相同的直角三角形纸片，如果把其中一个三角形纸片先横向平移m格，再纵向平移n格，就能使它的一条边与另一个三角形纸片的一条边重合，拼接成一个四边形，那么m n 的结果（）A．只有一个确定的值B．有两个不同的值C．有三个不同的值D．有三个以上不同的值【答案】B【解析】【分析】根据使一个三角形的一条边与另一个三角形的一条边重合，分情况讨论平移方式，然后分别求出m+n即可.【详解】解：①上边的三角形向右平移两个单位，向下平移三个单位，此时m+n=5；②上边的三角形向右平移两个单位，向下平移五个单位，此时m+n=7；③上边的三角形向左平移两个单位，向下平移三个单位，此时m+n=5；所以m n+的结果有两个不同的值，故选B.【点睛】本题考查图形的平移，根据题目要求判断出平移方式是解题关键.A B，其中点A，B的对应点分别10．如图，线段AB经过平移得到线段''A B 为点'A，'B，这四个点都在格点上．若线段AB上有一个点(),P a b，则点P在''上的对应点P'的坐标为（）A ．()2,3a b -+B ．()2,3a b --C ．()2,3a b ++D ．()2,3a b ++ 【答案】A【解析】【分析】先根据点A 到它的对应点'A 的平移规律即可得到线段AB 到线段''A B 的平移规律，从而得到点P 到对应点P' 的平移规律，即可得到P'的坐标【详解】解：∵点A （1，﹣1）到它的对应点'A （﹣1，2）的平移规律是：先向左平移2个单位，再向上平移3个单位，∴AB 到线段''A B 的平移规律是：先向左平移2个单位，再向上平移3个单位，∴点(),P a b 平移后对应点P'的坐标为：()2,3a b -+故选A.【点睛】此题考查的是坐标与图形的变化——平移：横坐标为左减右加，纵坐标为上加下减，掌握点的平移规律是解决此题的关键.。

七年级数学下册第五章相交线与平行线5.4平移习题含解析新版新人教版

5.4平移一．选择题（共12小题）1．如图,若△DEF是由△ABC经过平移后得到,已知A,D之间的距离为1,CE＝2,则EF是（）A．1 B．2 C．3 D．42．如图图形中,把△ABC平移后能得到△DEF的是（）A．B．C．D．3．下列图形中,可以由其中一个图形通过平移得到的是（）A．B．C．D．4．同桌读了：“子非鱼焉知鱼之乐乎？”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问：由图中所示的图案通过平移后得到的图案是（）A．B．C．D．5．通过平移,可将如图中的福娃“欢欢”移动到图（）A．B．C．D．6．下列图形中,哪个可以通过如图平移得到（）A．B．C．D．7．如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若△ABC的面积为20cm2,则四边形A1DCC1的面积为（）A．10cm2B．12cm2C．15cm2D．17cm28．下列运动属于平移的是（）A．荡秋千B．地球绕着太阳转C．风筝在空中随风飘动D．急刹车时,汽车在地面上的滑动9．下列现象属于平移的是（）①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走．A．③B．②③C．①②④D．①②⑤10．下列运动属于平移的是（）A．电风扇扇叶的转动B．石头从山顶滚到山脚的运动C．缆车沿索道从山顶运动到山脚D．足球被踢飞后的运动11．如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块（）A．向右平移1格,向下3格B．向右平移1格,向下4格C．向右平移2格,向下4格D．向右平移2格,向下3格12．如图所示,将图中阴影三角形由甲处平移至乙处,下面平移方法中正确的是（）A．先向上移动1格,再向右移动1格B．先向上移动3格,再向右移动1格C．先向上移动1格,再向右移动3格D．先向上移动3格,再向右移动3格二．填空题（共8小题）13．如图,∠1＝70°,直线a平移后得到直线b,则∠2﹣∠3＝°．14．如图,将边长为3个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD 的周长为．15．如图,将△ABC沿射线AC平移得到△DEF,若AF＝17,DC＝7,则AD＝．16．小明把自己的左手手印和右手手印按在同一张白纸上,左手手印（填“能”或“不能”）通过平移与右手手印完全重合．17．如图,四边形ABCD平移到四边形A′B′C′D′的位置,这时可把四边形A′B′C′D′看作先将四边形ABCD向右平移格,再向下平移2格．18．下面生活中的物体的运动情况可以看成平移的是．（1）摆动的钟摆；（2）在笔直的公路上行驶的汽车；（3）随风摆动的旗帜；（4）摇动的大绳；（5）汽车玻璃上雨刷的运动；（6）从楼顶自由落下的球（球不旋转）．19．将线段AB平移1cm,得到线段A′B′,则点A到点A′的距离是cm．20．如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC＝3cm,则A′C＝cm．5.4平移同步基础习题解析卷一．选择题（共12小题）1．如图,若△DEF是由△ABC经过平移后得到,已知A,D之间的距离为1,CE＝2,则EF是（）A．1 B．2 C．3 D．4【分析】根据平移的性质,结合图形可直接求解．【解答】解：观察图形可知：△DEF是由△ABC沿BC向右移动BE的长度后得到的,根据对应点所连的线段平行且相等,得BE＝AD＝1．∴EF＝BC＝BE+EC＝1+2＝3,故选：C．2．如图图形中,把△ABC平移后能得到△DEF的是（）A．B．C．D．【分析】根据图形平移的性质对各选项进行逐一分析即可．【解答】解：A、△DEF由△ABC平移而成,故本选项正确；B、△DEF由△ABC对称而成,故本选项错误；C、△DEF由△ABC旋转而成,故本选项错误；D、△DEF由△ABC对称而成,故本选项错误．故选：A．3．下列图形中,可以由其中一个图形通过平移得到的是（）A．B．C．D．【分析】根据平移的性质,结合图形对小题进行一一分析,选出正确答案．【解答】解：∵只有B的图形的形状和大小没有变化,符合平移的性质,属于平移得到；故选：B．4．同桌读了：“子非鱼焉知鱼之乐乎？”后,兴高采烈地利用电脑画出了几幅鱼的图案,请问：由图中所示的图案通过平移后得到的图案是（）A．B．C．D．【分析】根据图形平移的性质对各选项进行逐一分析即可．【解答】解：A、由图中所示的图案通过旋转而成,故本选项错误；B、由图中所示的图案通过翻折而成,故本选项错误C、由图中所示的图案通过旋转而成,故本选项错误；D、由图中所示的图案通过平移而成,故本选项正确．故选：D．5．通过平移,可将如图中的福娃“欢欢”移动到图（）A．B．C．D．【分析】根据平移的性质,结合图形,对选项进行一一分析,排除错误答案．【解答】解：A、属于图形旋转所得到,故错误；B、属于图形旋转所得到,故错误；C、图形形状大小没有改变,符合平移性质,故正确；D、属于图形旋转所得到,故错误．故选：C．6．下列图形中,哪个可以通过如图平移得到（）A．B．C．D．【分析】看哪个图形相对于所给图形的形状与大小没有改变,并且对应线段平行且相等即可．【解答】解：A、没有改变图形的形状,对应线段平行且相等,符合题意,故此选项正确；B、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误；C、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误；D、对应线段不平行,不符合平移的定义,不符合题意,故此选项错误．故选：A．7．如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若△ABC的面积为20cm2,则四边形A1DCC1的面积为（）A．10cm2B．12cm2C．15cm2D．17cm2【分析】根据平移的性质可得△A1B1C1的面积等于△ABC的面积,再根据平移的性质求出B1C＝BC,CD＝AC,然后利用相似三角形的性质解决问题即可．【解答】解：∵△ABC沿BC方向平移得到△A1B1C1,∴△A1B1C1的面积＝20cm2,B1C＝BC,CD＝AC,∵CD∥A1C1,∴△B1CD∽△B1C1A1,∴：＝1：4,∴＝×20＝5,∴四边形A1DCC1的面积＝20﹣5＝15cm2．故选：C．8．下列运动属于平移的是（）A．荡秋千B．地球绕着太阳转C．风筝在空中随风飘动D．急刹车时,汽车在地面上的滑动【分析】判断是否是平移现象,要根据平移的性质进行,即图形平移前后的形状和大小没有变化,只是位置发生变化．【解答】解：A、荡秋千不符合平移的性质,不属于平移,故本选项错误；B、地球绕着太阳转不符合平移的性质,不属于平移,故本选项错误；C、风筝在空中随风飘动,不符合平移的性质,故本选项错误；D、急刹车时,汽车在地面上的滑动,符合平移的性质,故本选项正确．故选：D．9．下列现象属于平移的是（）①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走．A．③B．②③C．①②④D．①②⑤【分析】根据平移的定义即可作出判断．【解答】解：①②⑤都是平移现象；③④是旋转．故选：D．10．下列运动属于平移的是（）A．电风扇扇叶的转动B．石头从山顶滚到山脚的运动C．缆车沿索道从山顶运动到山脚D．足球被踢飞后的运动【分析】判断是否是平移现象,要根据平移的性质进行,即图形平移前后的形状和大小没有变化,只是位置发生变化．【解答】解：A、B、D中,物体在运动的过程中,不断的旋转,不是平移；C、缆车沿索道从山顶运动到山脚符合平移的性质,是平移．故选：C．11．如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块（）A．向右平移1格,向下3格B．向右平移1格,向下4格C．向右平移2格,向下4格D．向右平移2格,向下3格【分析】找到两个图案的最右边移动到一条直线,最下边移动到一条直线上的距离即可．【解答】解：上面的图案的最右边需向右平移2格才能与下面图案的最右边在一条直线上,最下边需向下平移4格才能与下面图案的最下面重合,故选C．12．如图所示,将图中阴影三角形由甲处平移至乙处,下面平移方法中正确的是（）A．先向上移动1格,再向右移动1格B．先向上移动3格,再向右移动1格C．先向上移动1格,再向右移动3格D．先向上移动3格,再向右移动3格【分析】根据图形,对比图甲与图乙中位置关系,进行分析即可．【解答】解：要将图中阴影三角形由甲处平移至乙处,可选用先向上移动3格,再向右移动1格或先向右移动1格,再向上移动3格,故选：B．二．填空题（共8小题）13．如图,∠1＝70°,直线a平移后得到直线b,则∠2﹣∠3＝110 °．【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可．【解答】解：延长直线,如图：,∵直线a平移后得到直线b,∴a∥b,∴∠5＝180°﹣∠1＝180°﹣70°＝110°,∵∠2＝∠4+∠5,∵∠3＝∠4,∴∠2﹣∠3＝∠5＝110°,故答案为：110．14．如图,将边长为3个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD 的周长为13 ．【分析】根据平移的性质易得AD＝BE＝2,那么四边形ABFD的周长即可求得．【解答】解：∵将边长为3个单位的等边△ABC沿边BC向右平移2个单位得到△DEF, ∴AD＝BE＝2,各等边三角形的边长均为3．∴四边形ABFD的周长＝AD+AB+BE+FE+DF＝13．15．如图,将△ABC沿射线AC平移得到△DEF,若AF＝17,DC＝7,则AD＝ 5 ．【分析】根据平移的性质得出AD＝CF,再利用AF＝17,DC＝7,即可求出AD的长．【解答】解：∵将△ABC沿射线AC平移得到△DEF,AF＝17,DC＝7,∴AD＝CF,∴AF﹣CD＝AD+CF,∴17﹣7＝2AD,∴AD＝5,故答案为：5．16．小明把自己的左手手印和右手手印按在同一张白纸上,左手手印不能（填“能”或“不能”）通过平移与右手手印完全重合．【分析】左手手印与右手手印是左右对称的图形,故不能通过平移使之完全重合．【解答】解：由于左手手印和右手手印是轴对称图形,故左手手印不能通过平移与右手手印完全重合．故本题答案为：不能．17．如图,四边形ABCD平移到四边形A′B′C′D′的位置,这时可把四边形A′B′C′D′看作先将四边形ABCD向右平移 5 格,再向下平移2格．【分析】找到一对对应点,例如D与D′,观察图形,根据平移的性质,即可求出答案．【解答】解：四边形ABCD平移到四边形A′B′C′D′的位置,这时可把四边形A′B′C′D′看作先将四边形ABCD向右平移5格,再向下平移2格．故答案为5．18．下面生活中的物体的运动情况可以看成平移的是（2 ）（6）．（1）摆动的钟摆；（2）在笔直的公路上行驶的汽车；（3）随风摆动的旗帜；（4）摇动的大绳；（5）汽车玻璃上雨刷的运动；（6）从楼顶自由落下的球（球不旋转）．【分析】根据平移的性质,对题材中的条件进行一一分析,选出正确答案．【解答】解：（1）摆动的钟摆,方向发生改变,不属于平移；（2）在笔直的公路上行驶的汽车沿直线运动,属于平移；（3）随风摆动的旗帜,形状发生改变,不属于平移；（4）摇动的大绳,方向发生改变,不属于平移；（5）汽车玻璃上雨刷的运动,方向发生改变,不属于平移；（6）从楼顶自由落下的球沿直线运动,属于平移．∴可以看成平移的是（2）（6）．19．将线段AB平移1cm,得到线段A′B′,则点A到点A′的距离是 1 cm．【分析】根据题意,画出图形,由平移的性质直接求得结果．【解答】解：在平移的过程中各点的运动状态是一样的,现在将线段平移1cm,则每一点都平移1cm,即AA′＝1cm,∴点A到点A′的距离是1cm．20．如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC＝3cm,则A′C＝ 1 cm．【分析】先根据平移的性质得出AA′＝2cm,再利用AC＝3cm,即可求出A′C的长．【解答】解：∵将△ABC沿射线AC方向平移2cm得到△A′B′C′,∴AA′＝2cm,又∵AC＝3cm,∴A′C＝AC﹣AA′＝1cm．故答案为：1．。

人教版七年级数学下册 7-2-2用坐标表示平移(同步练习)

第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移班级：姓名：知识点1用坐标表示点的平移1.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A.(0,1)B.(2,-1)C.(4,1)D.(2,3)2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,点B的坐标是()A.(-5,3)B.(1,3)C.(1,-3)D.(-5,-1)3.点P(2,-3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P'的坐标是.4.将点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',则点A'的坐标是.5.将点A(1,-3)向右平移2个单位长度,再向下平移2个单位长度后得到点B(a,b),则ab=.6.(1)如图,将点A向右平移几个单位长度可得到点B()A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度(2)将点A向下平移5个单位长度后,将重合于图中的()A.点CB.点FC.点DD.点E(3)将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A',将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B',则A'与B'相距()A.4个单位长度B.5个单位长度C.6个单位长度D.7个单位长度(4)点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G',则G'的坐标为()A.(6,5)B.(4,5)C.(6,3)D.(4,3)7.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是()A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)知识点2用坐标表示图形的平移8.将一个三角形的三个顶点的坐标分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是()A.(6,0),(3,2),(8,-6)B.(-1,-5),(2,-7),(3,-1)C.(1,5),(2,-7),(-3,1)D.(-1,5),(2,-7),(-3,1)9.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则点P平移后的坐标是()A.(-2,-4)B.(-2,4)C.(2,-3)D.(-1,-3)10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2),(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.11.如图,三角形OAB 的顶点B 的坐标为(4,0),把三角形OAB 沿x 轴向右平移得到三角形CDE.如果CB=1,那么OE 的长为.12.如图,A,B 的坐标分别为(1,0),(0,2),若将线段AB 平移至A 1B 1,A 1,B 1的坐标分别为(2,a),(b,3),则a+b=.13.如图,梯形A'B'C'D'可以由梯形ABCD 经过怎样的平移得到?对应点的坐标有什么变化?综合点学科内综合14.如图,点A,B 的坐标分别为(1,2),(4,0),将三角形AOB 沿x 轴向右平移,得到三角形CDE,已知DB=1,则点C 的坐标为.15.如图,三角形A'B'C'是由三角形ABC 平移后得到的,已知三角形ABC 中一点P(x 0,y 0)经平移后对应点为P'(x 0+5,y 0-2).(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A',B',C'的坐标;(2)试说明三角形A'B'C'是如何由三角形ABC平移得到的;(3)请直接写出三角形A'B'C'的面积为_____.拓展训练拓展点坐标中的规律探究16.如图,三角形DEF 是三角形ABC 经过某种变换后得到的图形,分别写出点A 与点D,点B 与点E,点C 与点F 的坐标,并观察它们的关系,如果三角形ABC 中任一点M 的坐标(x,y),那么它的对应点N的坐标是什么?第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移答案与点拨1.A(点拨:点A'的横坐标为2-2=0,纵坐标为1,∴A'的坐标为(0,1).故选A.)2.B(点拨:∵A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,∴1+2=3,-2+3=1;点B的坐标是(1,3).故选B.)3.(-2,-2)(点拨:点(2,-3)向左平移4个单位长度,横坐标为:2-4=-2,向上平移1个单位长度,纵坐标为:-3+1=-2,∴点P'(-2,-2).)4.(-7,3)(点拨:点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',∴A'的坐标是(-3-4,-2+5),即(-7,3).)5.-15(点拨:将点A向右平移2个单位长度,纵坐标不变,横坐标增加2,此时点的坐标为(3,-3),再向下平移2个单位长度,横坐标不变,纵坐标减2,此时的坐标为(3,-5),即点B坐标为(3,-5),∴a=3,b=-5,∴ab=3×(-5)=-15.)6.(1)B(2)D(3)A(点拨:先分别找到A',B'的位置,再观察它们之间的距离.)(4)D7.D(点拨:逆向思考,把点(-3,2)先向右平移5个单位长度,再向下平移3个单位长度可得到A点坐标.)8.A(点拨:将平移后各点横坐标加4,纵坐标减1,可得到平移前的点的坐标分别是:(2+4,1-1),(-1+4,3-1),(4+4,-5-1),即(6,0),(3,2),(8,-6).)9.A(点拨:由图形知点P的坐标为P(-4,-1),由平移规律得平移后P点的坐标是(-4+2,-1-3)即(-2,-4).故选A.)10.(5,4)(点拨:左眼坐标由(-4,2)到(3,4)是向右平移7个单位长度,又向上平移2个单位长度,右眼由(-2,2)作同样的平移得坐标为(5,4).)11.7(点拨:因为三角形OAB的顶点B的坐标为(4,0),所以OB=4,所以OC=OB-CB=4-1=3,因此平移的距离为3.因为把三角形OAB沿x轴向右平移得到三角形CDE,所以CE=OB=4,所以OE=OC+CE=3+4=7.)12.2(点拨:∵A,B的坐标分别为(1,0),(0,2),若将线段AB平移至A1B1,A1,B1的坐标分别为(2,a),(b,3),可知线段AB向右平移了1个单位长度,向上平移了1个单位长度,则a=0+1=1,b=0+1=1,则a+b=1+1=2.)13.可由ABCD向左平移7个单位长度,向上平移7个单位长度得到.各对应点的坐标横坐标减7,纵坐标加7.14.(4,2)(点拨:O与D是一对对应点,因此平移距离为OD=OB-DB=4-1=3,因此平行规律为向右平移3个单位长度,所以A(1,2)的对应点C的坐标为(4,2).)15.(1)A'(4,0),B'(1,3),C'(2,-2)(2)三角形ABC向右平移5个单位长度,再向下平移2个单位长度(或先下平移2个单位长度,再向右平移5个单位长度)即可得到三角形A'B'C'.(3)616.A(4,3),D(-4,-3),B(3,1),E(-3,-1),C(1,2),F(-1,-2);N(-x,-y)。

【★】人教版七年级下册数学课时练《5-4 平移》(含答案)

《5.4 平移》课时练1．下面生活中的物体的运动情况可以看成平移的是（）A．摆动的钟摆B．在笔直的公路上行驶的汽车C．随风摆动的旗帜D．汽车玻璃上雨刷的运动2．如图，在一块长方形草地上原有一条等宽的笔直小路，现在要把这条小路改为同样宽度的等宽弯曲小路，则下列结论正确的有（）A．改造后小路的长度不变B．改造后小路的长度变小C．改造后草地部分的面积变小D．改造后草地部分的面积不变3．如图为一只小兔，将图进行平移，得到的图形可能是下列选项中的（）A．B．C．D．4．如图，将直线CD向上平移到AB的位置，若∠1＝130°，则D的度数为（）A．130°B．50°C．45°D．35°5．如图，将△ABC向右平移acm（a＞0）得到△DEF，连接AD，若△ABC的周长是36cm，则四边形ABFD的周长是（）A．（36+a）cm B．（72+a）cm C．（36+2a）cm D．（72+2a）cm 6．如图，用平移三角尺的方法可以检验出图中平行线共有（）A．3对B．4对C．5对D．6对7．下列图形中，不能通过其中一个四边形平移得到的是（）A．B．C．D．8．将周长为8的△ABC沿BC方向右移2个单位长度得到△DEF，则四边形ABFD的周长为（）A．12 B．14 C．10 D．169．如图，一块形状为长方形ABCD的场地，长AB＝98米，宽AD＝46米，A、B两处入口E小路宽都为1米，两小路汇合处路口宽2米，其余部分种植草坪，那么草坪的面积为（）A．4320平方米B．4410平方米C．4416平方米D．4508平方米10．下面的每组图形中，左面的图形平移后可以得到右面图形的是（）A．B．C．D．11．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则平移的距离为（）A．3 B．4 C．5 D．612．如图，将△ABC沿BC方向平移得到△DEF，使点B的对应点E恰好落在边BC的中点上，点C的对应点F在BC的延长线上，连接AD．下列结论一定正确的是（）A．∠B＝∠F B．AC⊥DE C．BC＝DF D．AC平分DE 13．如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD 的周长是（）A．16 cm B．18 cm C．20 cm D．21 cm14．如图图形中，把△ABC平移后能得到△DEF的是（）A．B．C．D．15．如图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（）A．100米B．99米C．98米D．74米16．一个长方形花园，长为a，宽为b，中间有两条互相垂直的宽为c的路，则可种花的面积为．17．如图，将Rt△ABC沿BC方向平移得到Rt△DEF，如果AB＝12cm，BE＝5cm，DH＝4cm，则图中阴影部分面积为cm2．18．白云宾馆在装修时，准备在主楼梯上铺上红地毯．已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图所示，则购买这种地毯至少需要元．19．如图，一块长方形草地，长为20米，宽为10米，草地上有一条弯曲的小路（小路任何地方的宽度都是2米），请你写出小路部分所占的面积是米2．20．如图，边长为8cm的正方形ABCD先向上平移4cm，再向右平移2cm，得到正方形A′B′C′D′，此时阴影部分的面积为．21．如图，将三角形ABC水平向右平移得到三角形DEF，A，D两点的距离为1，CE＝2，∠A＝72°，则：（1）AC和DF的关系式为，．（2）∠1＝（度）；（3）BF＝．22．作图：△DEF是△ABC平移后的图形，F是C的对应点，画出△ABC．（保留画图痕迹）23．如图1，直线CB∥OA，∠A＝∠B＝120°，E，F在BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF．（1）求∠AOB及∠EOC的度数；（2）如图2，若平行移动AC，那么∠OCB：∠OFB的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；参考答案1．B 2．D 3．C 4．B 5．C 6．D 7．D 8．A 9．A 10．D 11．A 12．D 13．C 14．A 15．C16．ab﹣ac﹣bc+c2．17．50．18．504．19．20．20．24cm2．21．AC＝DF，AC∥DF；108°；4．22．解：如图所示：△ABC即为所求．23．解：（1）∵CB∥OA∴∠BOA+∠B＝180°，∴∠BOA＝180°﹣120°＝60°，∵∠FOC＝∠AOC，OE平分∠BOF∴∠EOC＝∠EOF+∠FOC＝∠BOF+∠FOA＝（∠BOF+∠FOA）＝×60°＝30°；（2）不变．∵CB∥OA∴∠OCB＝∠COA，∠OFB＝∠FOA，∵∠FOC＝∠AOC∴∠COA＝∠FOA，即∠OCB：∠OFB＝1：2．。

新人教版七年级数学下册同步练习5.4平移(练习卷+解析版)

21．（10 分）如图所示，张三打算在院落种上蔬菜．已知院落为东西长为 32 米，南北宽为 20 米的长方形，为了行走方便，要修筑同样宽度的三条小路，东西两条，南北一条，余下的部分种上各类蔬菜．若每条小路的宽均为 1 米．（1）求蔬菜的种植面积；（2）若每平方米的每季蔬菜的值为 3 元，成本为 1 元，这个院落每季的产值是多少？
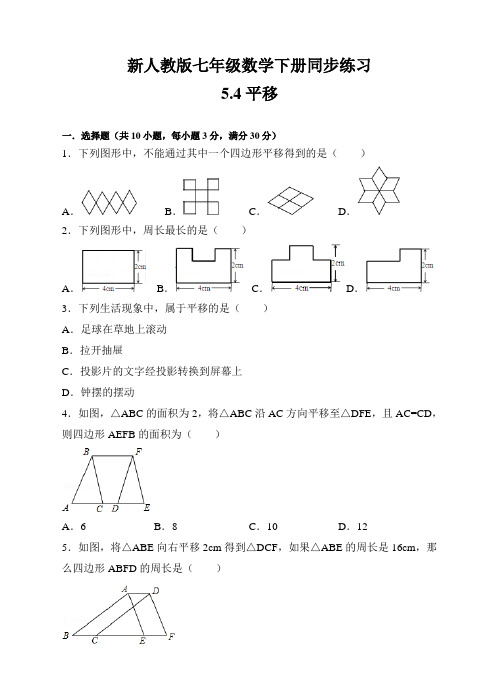
18．（8 分）如图，在方格纸中，每个小正方形的边长均为 1 个单位长度有一个 △ABC，它的三个顶点均与小正方形的顶点重合．（1）将△ABC 向右平移 3 个单位长度，得到△DEF（A 与 D、B 与 E、C 与 F 对应），请在方格纸中画出△DEF；（2）在（1）的条件下，连接 AE 和 CE，请直接写出△ACE 的面积 S，并判断 B 是否在边 AE 上．
C、由图形可得其周长为：12cm，
D、由图形可得其周长为：12cm，
故最长的是 B．
故选：B．
3．下列生活现象中，属于平移的是（）
A．足球在草地上滚动
B．拉开抽屉
C．投影片的文字经投影转换到屏幕上
D．钟摆的摆动
解：A．足球在草地上滚动方向变化，不符合平移的定义，不属于平移
B．拉开抽屉符合平移的定义，属于平移；
解：∵将线段 DC 沿着 CB 的方向平移 7cm 得到线段 EF，
∴EF=DC=4cm，FC=7cm， ∵AB=AC，BC=12cm， ∴∠B=∠C，BF=5cm， ∴∠B=∠BFE， ∴BE=EF=4cm， ∴△EBF 的周长为：4+4+5=13（cm）．故答案为：13． 14．如图，∠1=70°，直线 a 平移后得到直线 b，则∠2﹣∠3= 110 °．
A．12
B．24
C．21

人教版七年级下册数学 5

人教版七年级下册数学5.4平移专题练习一.单选题（共 10 小题）1、如图，△ABC 中，∠ABC=90°沿BC 所在的直线向右平移得到△DEF ，下列结论中不一定成立的是（）A ．EC=CFB ．∠DEF=90°C ．AC ＝DFD ．AC ∥DF2、如图是一个基本图形，将其平移四次，把得到的新图形结合起来，能得到的图案是（）A ．B ．C ．D ．3、如图，在三角形ABC 中，90,3cm,4cm BAC AB AC ∠=︒==，把三角形ABC 沿着直线BC 向右平移2.5cm 后得到三角形DEF ，连接,AE AD ，有以下结论：①AC DF ∥；②AD CF ∥；③ 2.5cm CF =；④DE AC ⊥．其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个4、如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是( )A ．平行四边形B ．等腰梯形C ．正六边形D ．圆5、如图，将边长为5cm 的等边三角形ABC 沿边BC 向右平移3cm ，得到△DEF ，则四边形ADFB 的周长为（）cm ．A ．20B ．21C ．22D ．23 6、如图，面积为12cm 2的△ABC 沿BC 方向平移到△DEF 的位置，平移的距离是边BC 长的2倍，则图中四边形ACED 的面积为（）A ．24cm 2B ．36cm 2C ．48cm 2D ．无法确定7、如图，面积为2cm 2的△ABC ，沿BC 方向平移至△DEF 的位置，平移的距离是边BC 长的2倍，则图中的四边形ACED 的面积为（）A ．4cm 2B ．6cm 2C ．8cm 2D ．10cm 28、如图所示，三张正方形纸片①，②，③分别放置于长()a b +，宽()a c +的长方形中，正方形①，②，③的边长分别为a ，b ，c ，且a b c >>，则阴影部分周长为（）A ．42a c +B ．42a b +C ．4aD ．422a b c ++9、经过平移，ABC ∆移到DEF ∆的位置，如图，下列结论：①AD BE CF ==，且////AD BE CF ；②//AB DE ，//BC EF ，BC EF =；③AB DE =，BC EF =，AC DF =．正确的有( )A ．0个B ．1个C ．2个D ．3个10、如图，将△ABC 沿直线AB 向右平移后到达△BDE 的位置，连接CD 、CE ，若△ACD 的面积为6，则△BCE 的面积为（）A ．5B ．6C ．10D ．3二.填空题（共 8 小题）1、在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是_____．2、如图，△ABC 的面积为10，BC ＝4，现将△ABC 沿着射线BC 平移a 个单位（a ＞0），得到新的△A'B'C'，则△ABC 所扫过的面积为_____．3、如图，将直角△ABC 沿斜边AC 的方向平移到△DEF 的位置，DE 交BC 于点G ，BG=4，EF=10，则线段GC 的长 ______________．4、如图，若DEF ∆是由ABC ∆平移后得到的，已知点A 、D 之间的距离为1，2CE =，则BC =_______．5、如图，O 是正六边形ABCDEF 的中心，下列图形：△OCD ，△ODE ，△OEF ，△OAF ，△OAB ，其中可由△OBC 平移得到的有_________个．6、如图所示是一座楼房的楼梯，高1 m ，水平距离是2.8 m ．如果要在台阶上铺一种地毯，那么至少要买这种地毯________7、如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路，宽均为1米，其它部分均种植花草．则种植花草的面积______．8、如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到△DEF的位置，AB ＝10，DO ＝4，平移距离为6，则阴影部分面积为__三.解答题（共 6 小题）1、如图，平面内点A ，B 沿同一方向，平移相同距离分别得到点C ，D ，连接AB ，BC ，延长AC 到点E ，连接BE ，DE ，BC 恰好平分∠ABE ．(1)若∠ACB ＝100°，∠CBE ＝40°，求∠EBD 的度数；(2)若∠AED ＝∠ABC+∠EBD ，求证：BC//DE ．2、（1）动手操作如图1，在55⨯的网格中，将线段AB 向右平移，得到线段A B ''，连接AA '，BB '． ①线段AB 平移的距离是_________；②四边形ABB A ''的面积_________；（2）如图2，在55⨯的网格中，将折线ACB 向右平移3个单位长度，得到折线AC B '''．①画出平移后的折线AC B '''；②连接AA '，BB '，多边形ACBB C A '''的面积_________；（3）拓展延伸如图3，在一块长为a 米，宽为b 米的长方形草坪上，修建一条宽为m 米的小路（小路宽度处处相同），直接写出剩下的草坪面积_________．3、如图，在方格纸内将三角形ABC 经过平移后得到三角形111A B C ，图中标出了点A 的对应点1A ，解答下列问题．(1)在网格中画出三角形.111A B C .；(2)连接，1AA ，1BB ，则所得正方形.11AA B B .的面积是______，它的边长AB 是______．4、如图，在66⨯的正方形网格中，每个小正方形的边长为1，点A ，B ，C ，D ，E ，F ，P 均为格点（格点是指每个小正方形的顶点），请完成下列问题：(1)利用直尺画图：在图1中，过P 点画直线AB 的平行线和垂线；(2)平移图2中的三条线段AB 、CD 、EF 中的两条，使平移后三条线段首尾顺次相接组成一个三角形；（只画出一个三角形即可）(3)图2中所组成的三角形的面积为______．5、画图并填空：如图，在12⨯8 的方格纸中，每个小正方形的边长都为1 ，△ABC 的顶点都在方格纸的格点上，将△ABC 按照某方向经过一次平移后得到△A' B'C ' ，图中标出了点C 的对应点C ' ．（1）请画出△A' B'C ' ；（2）利用方格纸，在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ；（3）点F 为方格纸上的格点（异于点B ），若S ∆ACB = S ∆ACF ，则图中格点F 共有个．（请在方格纸中标出点F ）6、平移和轴对称是数学中两种重要的图形运动．(1)平移①把笔尖放在数轴的原点处，先向负方向移动5个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？用算式表示以上过程及结果是（）．A ．(5)(2)7+++=+B ．(5)(2)3++-=+C ．(5)(2)3-++=-D ．(5)(2)7-+-=-②一机器人从原点O 开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳，当它跳2022次时，落在数轴上的点表示的数是________．(2)轴对称若对折纸条，表示-1的点与表示3的点重合，则表示2022的点与表示________的点重合．(3)若数轴上M ，N 两点对应的数分别表示为m ，n ，将点M 向正方向平移5个单位得到1M ，将点N 向负方向平移3个单位长度得到1N ，且1M ，1N 两点经对折后重合，对折的中间点表示的数为多少？（用含有m ，n 的式子表示）。

人教版初中七年级下册数学《平移》检测练习题

七年级下5.4《平移》检测题一、选择题1、在以下现象中：①温度计中液面上升或下降，②用打气筒打气时活塞的移动，③钟摆的摆动，④传送带带着瓶装饮料的移动。

其中平移的有（）A 、①②④B 、①③C 、②③D 、②④ 2、如图所示ABC ∆平移到C B A '''∆，则图中平行相等的线段有_____对（） A 、3对 B 、4对 C 、5对 D 、6对3、在平移过程中，对应线段（）A 、互相平行且相等B 、互相垂直且相等C 、互相平行（或在同一条直线上）且相等D 、相交且相等 4、如图，ABC ∆平移后得到FDE ∆，则和BD 对应的线段是（） A 、DC B 、DE C 、CE D 、以上都不对(4题图) (5题图)5、DEF ∆经过平移后得到ABC ∆，则C ∠的对应角和ED 的对应边分别是（） A 、F ∠、AC B 、BOD ∠、BA C 、F ∠、BA D 、BOD ∠、AC 二、填空题1、平移后，对应线段________________________________，对应角__________2、如图DEF ∆，ABC ∆是沿BC 方向平移后的图形，试判断FCGD 四边形S 与GAB S E 四边形的面积关系是______________BAC C 'B 'A 'BECAFDAB EC FD OABG ECF D(2题图) (3题图)3、如图，直角ABO ∆的周长为100，在其内部有4个小直角三角形，则这4个小直角三角形周长之和为（）A 、90B 、100C 、110D 、1204、在长为a m ，宽为b m 的一块草坪上修了一条1m 宽的笔直小路，则余下草坪的面积可表示为__________m 2，现为增加美感，把这条小路改为竖直方向的宽恒为1m 的弯曲小路，则此时余下草坪的面积为__________ m 25、如图，平移ABC ∆可得到DEF ∆，若A ∠=50°，C ∠=60°，则E ∠=__________，EDF ∠=__________，F ∠=__________，DOB ∠=__________(4题图) (5题图) (6题图)6、如图，是一块钜形ABCD 的场地，长AB =101米，宽AD =52米，从A 、B 两处入口的中路宽都为1米，两小路汇合处路口宽为2米，其余部分种植草坪面积为__________米2 三、解答题1、如图，将Rt ABC ∆沿AB 方向平移AD 距离得到Rt DEF ∆，已知BE =5，EF =8，CG =3，求ADBEFC O图中阴影部分面积。

2022-2023学年人教版七年级数学下册《5-4平移》同步达标测试题(附答案)

2022-2023学年人教版七年级数学下册《5.4平移》同步达标测试题（附答案）一．选择题（共8小题，满分32分）1．下列现象中是平移的是（）A．翻开书中的每一页纸张B．飞碟的快速转动C．将一张纸沿它的中线折叠D．电梯的上下移动2．汉字“王、人、木、水、口、立”中能通过单独平移组成一个新的汉字的有（）A．1个B．2个C．3个D．4个3．要用一根铁丝弯成如图所示的铁框，则这根铁丝至少长（）米？A．2.5m B．5m C．4m D．无法确定4．如图，直线AB∥CD，EG平分∠AEF，EH⊥EG，且平移EH恰好到GF，则下列结论：①EH平分∠BEF；②EG＝HF；③FH平分∠EFD；④∠GFH＝90°．其中正确的结论个数是（）A．1个B．2个C．3个D．4个5．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则平移的距离为（）A．3B．4C．5D．66．如图，将直角△ABC沿斜边AC的方向平移到△DEF的位置，DE交BC于点G，BG＝4，EF＝10，△BEG的面积为4，下列结论：①∠A＝∠BED；②△ABC平移的距离是4；③BE＝CF；④四边形GCFE的面积为16，正确的有（）A．②③B．①②③C．①③④D．①②③④7．如图，△ABC中，∠ABC＝90°，沿BC所在的直线向右平移得到△DEF，下列结论中不一定成立的是（）A．EC＝CF B．∠DEF＝90°C．AC＝DF D．AC∥DF8．如图，∠C＝90°，将直角三角形ABC沿着射线BC方向平移5cm，得三角形A'B'C'，已知BC＝3cm，AC＝4cm，则阴影部分的周长为（）A．16cm B．18cm C．20cm D．22cm二．填空题（共6小题，满分24分）9．如图，直线m与∠AOB的一边射线OB相交，∠3＝120°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2﹣∠1＝．10．如图，△ABC中，AB＝AC，BC＝12cm，点D在AC上，DC＝4cm，将线段DC沿CB 方向平移7cm得到线段EF，点E、F分别落在边AB、BC上，则△EBF的周长是cm．11．如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条”之”字路，余下部分绿化，道路的宽为2米，则绿化的面积为m2．12．如图，直角三角形DEF是直角三角形ABC沿BC平移得到的，如果AB＝8，BE＝3，DH＝2，则图中阴影部分的面积是．13．如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm2．14．如图，在三角形ABC中，∠C＝90°，AC+BC＝17，AB＝13，则内部五个小直角三角形周长的和为．三．解答题（共8小题，满分64分）15．某酒店在重新装修后，准备在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平方米的售价为40元，主楼梯道宽为3米，其侧面如图所示；铺设梯子的红地毯至少需要多长？花费至少多少元？16．（1）图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形．（2）若长方形长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积．（3）如图④，在宽为10m，长为40m的长方形菜地上有一条弯曲的小路，小路宽为1m，求这块菜地的面积．17．如图，粗线A→C→B和细线A→D→E→F→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线．①比较两条线路的长短（简要在下图上画出比较的痕迹）；②小丽坐出租车由体育馆B到少年宫A，假设出租车的收费标准为：起步价为7元，3千米以后每千米1.8元，用代数式表示出租车的收费m元与行驶路程s（s＞3）千米之间的关系；③如果这段路程长4.5千米，小丽身上有10元钱，够不够小丽坐出租车由体育馆到少年宫呢？说明理由．18．如图，已知直线AB∥CD，∠A＝∠C＝100°，E，F在CD上，且满足∠DBF＝∠ABD，BE平分∠CBF．（1）直线AD与BC有何位置关系？请说明理由；（2）求∠DBE的度数；（3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC＝∠ADB？若存在，求出∠ADB；若不存在，请说明理由．19．如图，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG＝24cm，WG＝8cm，CW ＝6cm，求阴影部分面积．20．如图，在边长为1的正方形网格中，平移△ABC，使点A平移到点D．（1）画出平移后的△DEF；（2）求△ABC的面积．21．在一次数学课上，张老师让同学们独立完成课本第23页7．选择题（2）如图1，如果AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝A.180°B.270°C.360°D.540°（1）请你也完成这道题；（2）在同学们都正确解答这道题后，张老师对这道题进行了变式：在（1）中AB∥EF不变，将点C移动到点C1位置（如图2所示），写出∠BAC1，∠AC1E，∠C1EF之间的数量关系，并证明．请你和这个班的同学一起解答这道题吧；（3）善于思考的小明想：将图1平移至与图2重合（如图3所示），当AC1，EC1分别平分∠BAC，∠CEF时，那么∠ACE与∠AC1E之间有怎样的数量关系？请你直接写出结果，不需要证明．22．将下列方格纸中的△ABC向右平移8格，再向上平移2格，得到△A1B1C1．（1）画出平移后的三角形；（2）若BC＝3，AC＝4，则A1C1＝；（3）连接AA1，BB1，则线段AA1与BB1的关系是．参考答案一．选择题（共8小题，满分32分）1．解：A不是沿某一直线方向移动，不属于平移．B不是沿某一直线方向移动，不属于平移．C新图形与原图形的形状和大小不同，不属于平移．因此C错误．故选：D．2．解：“人”平移得到“从”，“木”平移得到“林”，“水”平移得到“淼”，“口”平移得到“品”，所以通过平移组成一个新的汉字的有4个．故选：D．3．解：这根铁丝至少长：（1.5+1）×2＝5m，故选：B．4．解：∵EG平分∠AEF，∴∠AEG＝∠GEF＝∠AEF，∵HE⊥GE于E，∴∠GEH＝90°，∴∠GEF+∠HEF＝90°，∴∠AEG+∠BEH＝90°，∴∠BEH＝∠FEH，∴EH平分∠BEF；故①正确，∵平移EH恰好到GF，∴四边形EGFH是平行四边形，∴EG∥FH，EG＝HF；故②正确；∴∠GEF＝∠EFH，∵AB∥CD，∴∠AEF＝∠DFE，∵∠GEF＝∠AEF，∴∠EFH＝∠EFD，∴FH平分∠EFD；故③正确；∵四边形EGFH是平行四边形，∠GEH＝90°，∴四边形EGFH是矩形，∴∠GFH＝90°，故④正确，∴正确的结论有4个，故选：D．5．解：由平移的性质可知，BE＝CF，∵BF＝8，EC＝2，∴BE+CF＝8﹣2＝6，∴BE＝CF＝3，∴平移的距离为3，故选：A．6．解：∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的，且A、D、C、F 四点在同一条直线上，∴BE∥AC，AB∥DE，BC＝EF，BE＝CF，故③正确；由图形的平移知，ED∥AB，AC∥BE，∴∠EDC＝∠A，∠EDC＝∠BED，∴∠A＝∠BED，故①正确；∵BG＝4，∴AD＝BE＞BG，∴△ABC平移的距离＞4，故②错误；∵EF＝10，∴CG＝BC﹣BG＝EF﹣BG＝10﹣4＝6，∵△BEG的面积等于4，∴BG•GE＝4，∴GE＝2，∴四边形GCFE的面积＝（6+10）×2＝16，故④正确；故选：C．7．解：∵Rt△ABC沿直角边BC所在的直线向右平移得到△DEF，∴AC∥DF，△ABC≌△DEF，∴∠ACB＝∠DFE，∠DEF＝∠ABC＝90°，AC＝DF，BC＝EF，∴BC﹣CE＝EF﹣CE，即BE＝CF，∴选项B、C、D正确，不符合题意，选项A错误，符合题意；故选：A．8．解：在Rt△ACB中，AB＝＝＝5（cm），∵AA′＝BB′＝5cm，∴CB′＝BB′﹣BC＝5﹣3＝2（cm），∴阴影部分的周长＝AC+CB′+A′B′+AA′＝4+2+5+5＝16（cm）．故选：A．二．填空题（共6小题，满分24分）9．解：作OC∥m，如图，∵直线m向上平移直线m得到直线n，∴m∥n，∴OC∥n，∴∠1＝∠BOC，∠2+∠AOC＝180°，∠AOC＝∠3﹣∠1，∴∠2+∠3﹣∠1＝180°，∴∠2﹣∠1＝180°﹣120°＝60°，故答案为：60°．10．解：∵将线段DC沿着CB的方向平移7cm得到线段EF，∴EF＝DC＝4cm，FC＝7cm，CD∥EF，∴∠C＝∠EFB，∵AB＝AC，BC＝12cm，∴∠B＝∠C，BF＝12﹣7＝5cm，∴∠B＝∠EFB，∴BE＝EF＝4cm，∴△EBF的周长为：4+4+5＝13（cm）．故答案为：13．11．解：如图，把两条”之”字路平移到长方形地块ABCD的最上边和最左边，则余下部分EFGH是矩形．∵CF＝32﹣2＝30（米），CG＝20﹣2＝18（米），∴矩形EFCG的面积＝30×18＝540（平方米）．答：绿化的面积为540m2．故答案为：540．12．解：∵Rt△ABC沿BC方向平移得到Rt△DEF，∴AB＝DE＝8，S△ABC＝S△DEF，∴阴影部分面积＝梯形ABEH的面积，∵DH＝2，∴EH＝8﹣2＝6，∴阴影部分面积＝×（6+8）×3＝21．故答案为21．13．解：由题意，阴影部分是矩形，长为5﹣2＝3（cm），宽为3﹣1＝2（cm），∴阴影部分的面积＝2×3＝6（cm2），故答案为6．14．解：由平移的性质可知内部五个小直角三角形的直角边的和等于AC+BC＝17，斜边的和等于13，∴内部五个小直角三角形周长的和＝17+13＝30，故答案为30．三．解答题（共8小题，满分64分）15．解：地毯的长度至少为：2.6+5.8＝8.4米；8.4×3×40＝1008（元）．答：铺设梯子的红地毯至少需要8.4米，花费至少1008元．16．解：（1）如图：；（2）三个图形中除去阴影部分后剩余部分的面积：①ab﹣b；②ab﹣b；③ab﹣b；（3）40×10﹣10×1＝390（m2）．答：这块菜地的面积是390m2．17．解：①如图所示：两条线路的长相等；②由题意可得：m＝7+1.8（s﹣3）＝1.8s+1.6；③小丽坐出租车由体育馆到少年宫，钱够，理由：由②得：m＝7+1.8×1.5＝9.7（元）．小丽坐出租车由体育馆到少年宫10元够．18．解：（1）直线AD与BC互相平行，理由：∵AB∥CD，∴∠A+∠ADC＝180°，又∵∠A＝∠C∴∠ADC+∠C＝180°，∴AD∥BC；（2）∵AB∥CD，∴∠ABC＝180°﹣∠C＝80°，∵∠DBF＝∠ABD，BE平分∠CBF，∴∠DBE＝∠ABF+∠CBF＝∠ABC＝40°；（3）存在．设∠ABD＝∠DBF＝∠BDC＝x°．∵AB∥CD，∴∠BEC＝∠ABE＝x°+40°；∵AB∥CD，∴∠ADC＝180°﹣∠A＝80°，∴∠ADB＝80°﹣x°．若∠BEC＝∠ADB，则x°+40°＝80°﹣x°，得x°＝20°．∴存在∠BEC＝∠ADB＝60°．19．解：由平移的性质，梯形ABCD的面积＝梯形EFGH的面积，CD＝HG＝24cm，∴阴影部分的面积＝梯形DWGH的面积，∵CW＝6cm，∴DW＝CD﹣CW＝24﹣6＝18cm，∴阴影部分的面积＝（DW+HG）•WG＝（18+24）×8＝168cm2．答：阴影部分面积是168cm2．20．解：（1）所作图形如图所示：；（2）S△ABC＝4×4﹣×1×4﹣×2×3﹣×2×4＝7．21．解：（1）∵AB∥CD∥EF，∴∠A+∠ACD＝180°，∠E+∠ECD＝180°，∴∠A+∠ACD+∠E+∠ECD＝360°，即∠BAC+∠ACE+∠CEF＝360°，故选：C．（2）∠BAC1+∠C1EF＝∠AC1E，如图，过C1作C1G∥AB，∵AB∥EF，∴C1G∥AB∥EF，∴∠A＝∠AC1G，∠E＝∠EC1G，∴∠A+∠E＝∠AC1G+∠EC1G＝∠AC1E；（3）∠C+2∠AC1E＝360°，理由：由（1）可得，∠BAC+∠C+∠CEF＝360°，由（2）可得，∠C1＝∠BAC1+∠C1EF，又∵AC1，EC1分别平分∠BAC，∠CEF，∴∠BAC＝2∠BAC1，∠CEF＝2∠C1EF，∴2∠BAC1+∠C+2∠C1EF＝360°，即2（∠BAC1+∠C1EF）+∠C＝360°，∴∠C+2∠AC1E＝360°．22．解：（1）△A1B1C1如图所示；（2）A1C1＝AC＝4；（3）AA1∥BB1且AA1＝BB1．。

人教版七年级数学下册 5.4 平移同步练习试题含答案

5.4 平移一．选择题（共8小题）1．下列现象中是平移的是（）A．将一张纸沿它的中线折叠B．电梯的上下移动C．飞碟的快速转动D．翻开书中的每一页纸张2．在下图所示的四个三角形中，能由△ABC经过平移得到的是（）A．B．C．D．3．下列现象属于平移的是（）①打气筒活塞的轮复运动，②电梯的上下运动，③钟摆的摆动，④转动的门，⑤汽车在一条笔直的马路上行走．A．③B．②③C．①②④D．①②⑤4．如图所示，共有3个方格块，现在要把上面的方格块与下面的两个方格块合成一个长方形的整体，则应将上面的方格块（）A．向右平移1格，向下3格B．向右平移1格，向下4格C．向右平移2格，向下4格D．向右平移2格，向下3格5．下列图形中，不能通过其中一个四边形平移得到的是（）A．B．C．D．6．下列四组图形中，平移其中一个三角形可以得到另一个三角形的一组图形是（）A．B．C．D．7．下列平移作图错误的是（）A．B．C．D．8．下列平移作图不正确的是（）A．B．C．D．二．填空题（共6小题）9．如图，将△ABC沿BC方向平移到△DEF，若A、D间的距离为1，CE＝2，则BF＝．10．如图，将周长为8的△ABC沿BC方向向右平移1.5个单位得到△DEF，则四边形ABFD的周长为．11．如图，△ABC平移后的图形是△A′B′C′，其中C与C′是对应点，请画出平移后的三角形△A′B′C′．（作图题）12．如图，在一块长为20m，为10m的长方形草地上，修建两条宽为2m的长方形小路，则这块草地的绿地面积（图中空白部分）为m213．如图，在△ABC中，∠B＝90°，BC＝5cm，AB＝12cm，则图中4个小直角三角形周长的和为．14．如图是一块长方形ABCD的场地，长AB＝a米，宽AD＝b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为米2．三．解答题（共6小题）15．如图，将三角形ABC水平向右平移得到三角形DEF，A，D两点的距离为1，CE＝2，∠A＝70°．根据题意完成下列各题：（1）AC和DF的数量关系为；AC和DF的位置关系为；（2）∠1＝度（3）BF＝．16．如图，已知直线AB∥CD，∠A＝∠C＝100°，E，F在CD上，且满足∠DBF＝∠ABD，BE平分∠CBF．（1）直线AD与BC有何位置关系？请说明理由；（2）求∠DBE的度数；（3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC＝∠ADB？若存在，求出∠ADB；若不存在，请说明理由．17．如图，将△ABC沿直线AB向右平移后到达△BDE的位置．（1）若AC＝6cm，则BE＝cm；（2）若∠CAB＝50°，∠BDE＝100°，求∠CBE的度数．18．如图，平面直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为（3，2）．（1）填空：点A的坐标是，点B的坐标是；（2）将△ABC先向左平移3个单位长度，再向上平移1个单位长度，画出平移后的△A1B1C1；（3）求△ABC的面积．19．如图，在正方形网格中有一个△ABC，按要求进行下列作图（只借助网格，需要写出结论）．（1）过点B画出AC的平行线；（2）画出三角形ABC向右平移5格，在向上平移2格后的△DEF；（3）若每一个网格的单位长度为a，求三角形ABC的面积．20．如图，凯瑞酒店准备进行装修，把楼梯铺上地毯．已知楼梯的宽度是2米，楼梯的总长度为8米，总高度为6米，已知这种地毯每平方米的售价是60元．请你帮老板算下，购买地毯多少钱？参考答案一．选择题（共8小题）1．B．2．C．3．D．4．C．5．D．6．A．7．C．8．C．二．填空题（共6小题）9．BF＝BE+EC+CF＝4．10．11．11．作法：（1）连接CC′，过点C作A′C′∥AC，且相等，再过点A′，作A′B′∥AB且相等，连接A′、B′、C′，△A′B′C′就是所画的三角形．12．144．13．3014．（ab﹣a﹣2b+2）．三．解答题（共6小题）15．解：（1）AC和DF的关系式为AC＝DF，AC∥DF．（2）∵三角形ABC水平向右平移得到三角形DEF，∴AB∥DE，∵∠A＝70°，∴∠1＝110（度）；（3）BF＝BE+CE+CF＝2+1+1＝4．故答案为：AC＝DF，AC∥DF；110；4；16．解：（1）直线AD与BC互相平行，理由：∵AB∥CD，∴∠A+∠ADC＝180°，又∵∠A＝∠C∴∠ADC+∠C＝180°，∴AD∥BC；（2）∵AB∥CD，∴∠ABC＝180°﹣∠C＝80°，∵∠DBF＝∠ABD，BE平分∠CBF，∴∠DBE＝∠ABF+∠CBF＝∠ABC＝40°；（3）存在．设∠ABD＝∠DBF＝∠BDC＝x°．∵AB∥CD，∴∠BEC＝∠ABE＝x°+40°；∵AB∥CD，∴∠ADC＝180°﹣∠A＝80°，∴∠ADB＝80°﹣x°．若∠BEC＝∠ADB，则x°+40°＝80°﹣x°，得x°＝20°．∴存在∠BEC＝∠ADB＝60°．17．解：（1）∵将△ABC沿直线AB向右平移得到△BDE，∴△ABC≌△BDE，∴BE＝AC＝6cm，故答案为：6；（2）由（1）知△ABC≌△BDE，∴∠DBE＝∠CAB＝50°、∠BDE＝∠ABC＝100°，∴∠CBE＝180°﹣∠ABC﹣∠DBE＝30°．18．解：（1）点A的坐标是：（4，﹣1），点B的坐标是：（5，3）；故答案为：（4，﹣1），（5，3）；（2）如图所示：△A1B1C1，即为所求；（3）．19．解：（1）如图，直线BP为所作．（2）如图，△DEF为所作；（3）三角形ABC的面积＝×3a×2a＝3a2．20．解：如图，利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为8米，6米，即可得地毯的长度为6+8＝14（米），地毯的面积为14×2＝28（平方米），故买地毯至少需要28×60＝1680（元）．购买地毯需要1680元．。

人教版数学七年级下册第五章《平移》小测与答案

人教版数学七年级下册第五章《平移》小测测试时间:15分钟一、选择题1.下列现象中是平移的是( )A.将一张纸沿它的中线折叠B.飞碟的快速转动C.电梯的上下移动D.翻开书中的每一页纸张2.甲骨文是我国古代的一种文字,是汉字的早期形式,下列甲骨文中,能用平移来分析其形成过程的是( )3.如图,长方形ABCD的对角线AC=5,AB=3,BC=4,则图中五个小长方形的周长之和为( )A.7B.9C.14D.184.如图是两个有重叠的直角三角形,可以看作是将直角三角形ABC沿着BC方向平移5个单位长度得到了直角三角形DEF,其中AB=8,BE=5,DH=3,则下列结论正确的有( )①AC∥DF;②HE=5;③CF=5;④四边形DHCF的面积为32.5.A.1个B.2个C.3个D.4个二、填空题5.如图所示,在正方形网格中,为了把三角形ABC平移到三角形A'B'C',可以先将三角形ABC 向右平移格,再向上平移格.6.如图,将三角形ABO沿着射线AD的方向平移10 cm得到三角形DCE,连接OE,则OE= cm.7.如图,在一块长为a米、宽为b米的长方形地上,有一条弯曲的柏油马路,马路的任何地方的水平宽度都是2米,其他部分都是草地,则草地的面积为平方米.8.如图所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的路(阴影部分),余下部分绿化,小路的宽为2 m,则绿化的面积为m2.三、解答题9.某宾馆重新装修后,准备在大厅的楼梯上铺设一种红地毯,已知这种地毯每平方米售价为50元,楼梯宽2 m,楼梯侧面及相关数据如图所示,求买地毯需要多少元.10.如图,在直角三角形ABC中,∠ACB=90°,BC=3 cm,AC=4 cm,将三角形ABC沿BC方向平移1 cm得到三角形A'B'C'.求四边形ABC'A'的面积.11.如图,方格纸中每个小正方形的边长都是1,三角形ABC是格点三角形(三个顶点都在格点上).三角形ABC经过平移后得到三角形A'B'C',点B恰好落在点B'处,(1)请画出平移后得到的三角形A'B'C';(2)三角形A'B'C'的面积等于;(3)在线段PQ上是否存在格点M,使得△MA'C'的面积是△MA'B'面积的2倍?若存在,请画出所有这样的格点M1,M2,…,若不存在,请说明理由.人教版数学七年级下册第五章《平移》小测答案一、选择题1.答案 C A.将一张纸沿它的中线折叠,不是沿某一直线方向移动,不属于平移,不符合题意;B.飞碟的快速转动,不是沿某一直线方向移动,不属于平移,不符合题意;C.电梯的上下移动是平移,符合题意;D.翻开书中的每一页纸张,不是沿某一直线方向移动,不属于平移,不符合题意.故选C.2.答案 D 由图可知,D 可利用图形的平移得到.故选D.3.答案 C 图中五个小长方形的周长之和=AB+BC+CD+AD=3+4+3+4=14.故选C.4.答案 D 由平移的性质可得AC∥DF,AB=DE=8,CF=BE=5,S 三角形ABC =S 三角形DEF ,∵DH=3,∴HE=DE-DH=8-3=5,∴S 四边形DHCF =S 梯形ABEH =12(EH+AB)·BE=12×(5+8)×5=652=32.5, 故①②③④都正确,故选D.二、填空题5.答案 5;3解析由题图可知,先将三角形ABC 向右平移5格,再向上平移3格,可以得到三角形A'B'C', 故答案为5;3.6.答案 10解析 ∵三角形ABO 沿着射线AD 的方向平移10 cm 得到三角形DCE,∴AD=OE=10 cm.故答案为10.7.答案 (ab-2b)解析由题可得,平移之后如图:则草地的面积是(ab-2b)平方米.故答案为(ab-2b).8.答案 560解析利用平移可得,绿化的面积为(30-2)×(22-2)=560(m 2).故答案为560.三、解答题9.解析如图,利用平移线段,把楼梯的横、竖分别向上、向左平移,构成一个矩形,则该矩形的长,宽分别为6米,4米,∴地毯的长度为6+4=10(米),地毯的面积为10×2=20(平方米), ∴买地毯需要20×50=1 000(元).10.解析 ∵三角形ABC 沿BC 方向平移1 cm,得到三角形A'B'C',∴AA'=CC'=1 cm,AA'∥BC',∴BC'=BC+CC'=3+1=4 cm,∵∠ACB=90°,∴四边形ABC'A'是梯形且AC 是梯形的高,∴四边形ABC'A'的面积=12×(1+4)×4=10 cm 2. 11.解析 (1)画出平移后得到的三角形A'B'C'如图所示.(2)三角形A'B'C'的面积等于3×6-12×3×3-12×2×3-12×1×6=152,故答案为152. (3)如图所示,点M 1、M 2即为所求.。

人教版数学七年级下册《5.4平移》基础训练（含答案）

人教版数学七年级下册5.4平移基础训练一、选择题1.下列运动属于平移的是( D )A.荡秋千B.地球绕着太阳转C.风筝在空中随风飘动D.急刹车时，汽车在地面上的滑动2. 下列各网格中的图形是用其图形中的一部分平移得到的是( C )A. B. C. D.3.如图，两个直角三角形重叠在一起，将其中一个三角形沿着BC边平移到△DEF 的位置，∠B=90°，AB=10，DH=2，平移距离为3，则阴影部分的面积为（ C ）A. 20B. 24C. 27D. 364.如图，三角形ADE是由三角形DBF沿BD所在直线平移得到的，AE，BF的延长线交于点C,若∠BFD=45°,则∠C的度数是( C )A.43°B.44°C.45°D.46°5. 两个三角形是通过平移得到的,下列说法错误的是( D )A. 平移过程中,两三角形周长不变B. 平移过程中,两三角形面积不变C. 平移过程中,两三角形的对应线段一定相等D. 平移过程中,两三角形的对应边必平行6.甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，能用其中一部分平移得到的是（ D ）A. B. C. D.7.如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线( D )A.a户最长B.6户最长C.c户最长D.一样长8. 如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A'的坐标是( B )A. (6,1)B. (0,1)C. (0,-3)D. (6,-3)9.如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（ A ）A. 2B. 3C. 23D. 3210.如图，将三角形ABC沿BC方向平移得到三角形DEF,若BC=4，EC=1，则平移的距离为( D )A.7B.6C.4D.3二、填空题11.如图，在四边形ABCD中，AD∥BC,若∠B与∠C互余，将AB，DC分别平移到EF和EG的位置，则∠FEG的度数为 .【答案】90°12.如图，平移△ABC可得到△DEF，如果∠C=60°，AE=7cm，AB=4cm，那么∠F= ______ 度，DB= ______ cm．【答案】60；113.如图是“俄罗斯方块”游戏的一个画面，若使左上角的图形经平移插入到下面空白的A处，应先向平移格，再向平移格.【答案】右 1 下 314.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是cm2.【答案】16815.如图，矩形ABCD中，AB=5,BC=8，则矩形内部五个小矩形的周长之和为_________.【答案】26三、解答题''';16.(1)如图，平移三角形ABC，使点A平移到点A'，画出平移后的三角形A B C (2)在(1)的条件下，指出点A,B,C 的对应点，并指出AB,BC,AC的对应线段和∠A，∠B, ∠C的对应角.【答案】(1)如图所示.(2)点A ，B ，C 的对应点分别是点A B C '''，，,线段AB,BC ，AC 的对应线段分别是A B B C A C ''''''，，，∠A,∠B ，∠ACB 的对应角分别A A B C A C B '''''''∠∠∠，，. 17. 如图所示,已知在△ABC 中,BC =4 cm,把△ABC 沿BC 方向平移2 cm 得到△DEF.问:(1)图中与∠A 相等的角有多少个?(2)图中的平行线共有多少对?请分别写出来. (3)BE ∶BC ∶BF 的值是多少?(1) 【答案】共有3个,分别是∠D ,∠EMC ,∠AMD. (2) 【答案】两对,AB ∥DE ,AC ∥DF.(3) 【答案】∵△ABC 沿BC 方向平移2 cm, ∴BE =CF =2 cm . 又∵BC =4 cm, ∴BF =6 cm .∴BE ∶BC ∶BF =1∶2∶3.18.关注生活数学：某宾馆重新装修后考虑在大厅内的主楼梯上铺设地毯，已知主楼梯宽3m ，其剖面图如图所示，请计算铺此楼梯，需要购买地毯多少平方米？解析：由平移的性质，可知地毯的长为AB +BC = 1.2 +2.4= 3.6(m) ,3.6×3=10.8(m2).故需要购买地毯10.8平方米.19. 如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路,余下部分绿化,小路的宽为2 m,则绿化的面积为多少?【答案】如图所示,把两条小路平移到长方形地块ABCD的最上边和最左边,则余下部分EFCG是长方形.∵CF=32-2=30(m),CG=20-2=18(m),∴长方形EFCG的面积=30×18=540(m2). 答:绿化的面积为540m2.20.已知：如图，△ABC的面积为84，BC=21，现将△ABC沿直线BC向右平移a （0＜a＜21）个单位到△DEF的位置．（1）求BC边上的高；（2）若AB=10，①求线段DF的长；②连结AE，当△ABE时等腰三角形时，求a的值．【答案】解：（1）作AM⊥BC于M，∵△ABC的面积为84，×BC×AM=84，∴12解得，AM=8，即BC边上的高为8；（2）①在Rt△ABM中，BM=√AB2−AM2=6，∴CM=BC-BM=15，在Rt△ACM中，AC=√AM2+CM2=17，由平移的性质可知，DF=AC=17；②当AB=BE=10时，a=BE=10；当AB=AE=10时，BE=2BM=12，则a=BE=12；当EA=EB=a时，ME=a-6，在Rt△AME中，AM2+ME2=AE2，即82+（a-6）2=a2，，解得，a=253．则当△ABE时等腰三角形时，a的值为10或12或253。

2022-2023学年人教版七年级数学下册《5-4平移》同步练习题(附答案)

2022-2023学年人教版七年级数学下册《5.4平移》同步练习题（附答案）一．选择题1．如图是第七届世界军人运动会的吉祥物“兵兵”，将图中的“兵兵”通过平移可得到下列选项中的（）A．B．C．D．2．如图所示：某公园里有一处长方形风景欣赏区ABCD，AB长50米，BC宽25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小明同学在假期沿着小路的中间行走（图中虚线），则：小明同学所走的路径长约为（）米．（小路的宽度忽略不计）A．150米B．125米C．100米D．75米3．下列运动属于平移的是（）A．荡秋千B．地球绕着太阳转C．风车的转动D．急刹车时，汽车在地面上的滑动4．如图，将△ABC沿着某一方向平移一定的距离得到△DEF，则下列结论：①AD＝CF；②AC∥DF；③∠ABC＝∠DFE；④∠DAE＝∠AEB．其中正确的是（）A．仅①②B．仅①②④C．仅①②③D．①②③④5．如图，将直线CD向上平移到AB的位置，若∠1＝130°，则D的度数为（）A．130°B．50°C．45°D．35°6．如图，将△ABC向右平移acm（a＞0）得到△DEF，连接AD，若△ABC的周长是36cm，则四边形ABFD的周长是（）A．（36+a）cm B．（72+a）cm C．（36+2a）cm D．（72+2a）cm 7．如图，△ABC沿BC方向平移到△DEF的位置，若BE＝2cm，则平移的距离为（）A．1B．2C．3D．48．如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知BE＝4，EF＝8，CG＝3，则图中阴影部分的面积为（）A．16B．20C．26D．129．下列说法正确的个数是（）①同位角相等；②同旁内角互补，两直线平行；③若a∥b，b∥c，则a∥c；④直线外一点到这条直线的距离是指这一点到这条直线的垂线段；⑤在连接直线外一点与直线上各点的线段中，垂线段最短；⑥平移既改变图形的位置，也改变图形的形状与大小．A．2个B．3个C．4个D．5个10．如图，表示直线a平移得到直线b的两种画法，下列关于三角板平移的方向和移动的距离说法正确的是（）A．方向相同，距离相同B．方向不同，距离不同C．方向相同，距离不同D．方向不同，距离相同11．如图，直线m与∠AOB的一边射线OB相交，∠3＝120°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2﹣∠1＝．12．如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm2．13．在长为a（m），宽为b（m）一块长方形的草坪上修了一条宽2（m）的笔直小路，则余下草坪的面积可表示为m2；先为了增加美感，把这条小路改为宽恒为2（m）的弯曲小路（如图），则此时余下草坪的面积为m2．14．如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则道路的面积为．15．如图是一个会场的台阶的截面图，要在上面铺上地毯，则所需地毯的长度是．16．如图的网格纸中，每个小方格都是边长为1个单位的正方形，三角形ABC的三个顶点都在格点上．（每个小方格的顶点叫格点）（1）画出三角形ABC向上平移4个单位后的三角形A1B1C1；（2）画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2；（3）经过（1）次平移线段AC划过的面积是．17．已知AB＝13，CD＝8，M和N分别为线段AB，CD的中点．（1）若BC重合，D在线段AB上，如图1，求MN的长度．（2）①如果将图1的线段CD沿着AB向右平移n个单位，求MN的长度与n的数量关系．②当n为多少的时，MN的长度为9．（3）如果AB保持长度和位置不变，点D保持图1的位置不变，改变DC的长度，将点C沿着直线AB向右移动m个单位，其余条件不变，①BN+BC；②MN﹣BC，请问以上两个式子哪一个式子的值是定值，定值是多少？18．在直角三角形ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，△ABC沿AB方向平移至△DEF，若AE＝8cm，DB＝2cm．（1）AC和DF的关系为．（2）∠BGF＝°．（3）求△ABC沿AB方向平移的距离．19．如图，AN∥DM，点B在AN上（点B与点A不重合），点C在DM上（点C与点D 不重合），∠DAB＝∠BCD．（1）那么AD∥BC吗？试说明理由；（2）若平行移动BC，保持∠ABC＝100°；点E、F在DC上，且满足∠F AC＝∠BAC，AE平分∠DAF．①小红发现可求出∠EAC的度数，请你帮助小红写出求∠EAC的度数的过程；②在平行移动BC的过程中，是否存在某种情况，使∠BCA＝∠DEA？若存在，请直接写出∠BCA的度数；若不存在，请说明理由．20．已知点C在射线OA上．（1）如图①，CD∥OE，若∠AOB＝90°，∠OCD＝120°，求∠BOE的度数；（2）在①中，将射线OE沿射线OB平移得O′E'（如图②），若∠AOB＝α，探究∠OCD 与∠BO′E′的关系（用含α的代数式表示）；（3）在②中，过点O′作OB的垂线，与∠OCD的平分线交于点P（如图③），若∠CPO′＝90°，探究∠AOB与∠BO′E′的关系．参考答案一．选择题1．解：将图中的“兵兵”通过平移可得到图为：故选：C．2．解：由平移的性质可知，由于小路的宽度忽略不计，因此说行走的路程为AD+AB+BC＝25+50+25＝100（米），故选：C．3．解：A、荡秋千，不符合题意；B、地球绕着太阳转，不符合题意；C、风车的转动，不符合题意；D、急刹车时，汽车在地面上的滑动，属于平移变换，符合题意；故选：D．4．解：∵△ABC沿着某一方向平移一定的距离得到△DEF，∴①AD∥CF，正确；②AC＝DF，正确；③∠ABC＝∠DEF，故原命题错误；④∠DAE＝∠AEB，正确．所以，正确的有①②④．故选：B．5．解：∵∠1和∠2是邻补角，∴∠1+∠2＝180°，∵∠1＝130°，∴∠2＝180°﹣∠1＝50°，∵AB∥CD，∴∠D＝∠2＝50°，故选：B．6．解：∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF，∴AD＝a，BF＝BC+CF＝BC+a，DF＝AC，又∵AB+BC+AC＝36cm，∴四边形ABFD的周长＝AD+AB+BF+DF＝a+AB+BC+a+AC＝（36+2a）（cm）．故选：C．7．解：△ABC沿BC方向平移到△DEF的位置，若BE＝2cm，则平移的距离为2cm，故选：B．8．解：由平移的性质可知，S△ABC＝S△DEF，EF＝BC＝8，∵CG＝3，∴BG＝BC﹣CG＝5，∴S阴＝S梯形EFGB＝（5+8）×4＝26，故选：C．9．解：①同位角相等，错误，只有两直线平行，才有同位角相等；②同旁内角互补，两直线平行，正确；③若a∥b，b∥c，则a∥c，正确；④直线外一点到这条直线的距离是指这一点到这条直线的垂线段的长度，故本小题错误；⑤在连接直线外一点与直线上各点的线段中，垂线段最短，正确；⑥平移只改变图形的位置，不改变图形的形状与大小，故本小题错误；综上所述，正确的有②③⑤共3个．故选：B．10．解：由图和平移可得：三角板平移的方向不同，距离不同，故选：B．二．填空题11．解：作OC∥m，如图，∵直线m向上平移直线m得到直线n，∴m∥n，∴OC∥n，∴∠1＝∠BOC，∠2+∠AOC＝180°，∠AOC＝∠3﹣∠1，∴∠2+∠3﹣∠1＝180°，∴∠2﹣∠1＝180°﹣120°＝60°，故答案为：60°．12．解：由题意，阴影部分是矩形，长为5﹣2＝3（cm），宽为3﹣1＝2（cm），∴阴影部分的面积＝2×3＝6（cm2），故答案为6．13．解：余下草坪的长方形长仍为a，宽为（b﹣2），则面积为a（b﹣2）＝ab﹣2a；长方形的长为a，宽为b﹣2．余下草坪的面积为：a（b﹣2）＝ab﹣2a，故答案为：（ab﹣2a），（ab﹣2a）．14．解：将道路分别向左、向上平移，得到草地为一个长方形，长方形的长为20﹣2＝18（米），宽为10﹣2＝8（米），则草地面积为18×8＝144米2．∴道路的面积为20×10﹣144＝56米2故答案为：56米2．15．解：楼梯的长为5m，高为2.5m，则所需地毯的长度是5+2.5＝7.5（m）．故答案为：7.5m．三．解答题16．解：（1）如图，A1B1C1即为所求；（2）如图，△A2B2C2即为所求；（3）经过（1）次平移线段AC划过的面积＝4×4＝16．故答案为：16．17．解：（1）∵M和N分别为线段AB，CD的中点，∴AM＝BM＝AB，CN＝DN＝CD，∵MN＝BM﹣CN＝AB﹣CD，∵AB＝13，CD＝8，∴MN＝﹣＝；（2）①∵线段CD沿着AB向右平移n个单位，∴BC＝n，∵MN＝BM﹣BN＝AB﹣（CN﹣BC）＝AB﹣CD+BC，∵AB＝13，CD＝8，∴MN＝+n；②∵MN＝9，∴+n＝9，∴n＝；（3）∵点C沿着直线AB向右移动m个单位，∴BC＝m，∵点D保持位置不变，∴CD＝8+m，∵N是CD的中点，∴CN＝DN＝CD＝（8+m）＝4+m，∴BN＝CN﹣BC＝4+m﹣m＝4﹣m，当0＜m≤8时，∴BN+BC＝4﹣m+m＝4，MN﹣BC＝（BM﹣BN）﹣BC＝AB﹣BN﹣BC＝﹣（4﹣m）﹣m＝；∴BN+BC是定值4，MN﹣BC是定值；当m＞8时，N点在B点右侧，∵BN＝BC﹣CN＝m﹣4﹣m＝m﹣4，MN＝BM+BN＝+m﹣4＝m+，∴BN+BC＝m﹣4+m＝m﹣4，MN﹣BC＝m+﹣m＝，∴BN+BC不是定值，MN﹣BC是定值；综上所述：无论m取何值，MN﹣BC的值都是定值．18．解：（1）∵△ABC沿AB方向平移至△DEF，∴AC＝DF，AC∥DF，故答案为：AC＝DF，AC∥DF；（2）由平移的性质得出AC∥DF，∴∠ACB＝∠DGB＝90°，∴∠BGF＝180°﹣90°＝90°，故答案为：90；（3）由平移得AD＝BE，AE＝8cm，DB＝2cm，∴AD＝BE＝＝3（cm），∴平移的距离为3cm；19．（1）解：结论：AD∥BC．理由：∵AB∥CD，∴∠D+∠DAB＝180°，∵∠DAB＝∠BCD，∴∠D+∠BCD＝180°，∴AD∥BC．（2）①∵AD∥BC，∴∠DAB+∠ABC＝180°，∵∠ABC＝100°，∴∠DAB＝80°，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠EAC＝∠DAF+∠F AB＝（∠DAF+∠F AB）＝40°．②存在．理由：∵AD∥BC，∴∠DAC＝∠ACB，∵CD∥AB，∴∠DEA＝∠EAB，∵∠ACB＝∠DEA，∴∠DAC＝∠EAB，∴∠DAE＝∠CAB，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠DAE＝∠EAF＝∠F AC＝∠CAB＝20°，∴∠ACB＝∠DAC＝60°．20．解：（1）∵CD∥OE，∴∠AOE＝∠OCD＝120°，∴∠BOE＝360°﹣∠AOE﹣∠AOB＝360°﹣90°﹣120°＝150°；（2）∠OCD+∠BO′E′＝360°﹣α．证明：如图②，过O点作OF∥CD，∵CD∥O′E′，∴OF∥O′E′，∴∠AOF＝180°﹣∠OCD，∠BOF＝∠E′O′O＝180°﹣∠BO′E′，∴∠AOB＝∠AOF+∠BOF＝180°﹣∠OCD+180°﹣∠BO′E′＝360°﹣（∠OCD+∠BO′E′）＝α，∴∠OCD+∠BO′E′＝360°﹣α；（3）∠AOB＝∠BO′E′．证明：∵∠CPO′＝90°，∴PO′⊥CP，∵PO′⊥OB，∴CP∥OB，∴∠PCO+∠AOB＝180°，∴2∠PCO＝360°﹣2∠AOB，∵CP是∠OCD的平分线，∴∠OCD＝2∠PCO＝360°﹣2∠AOB，∵由（2）知，∠OCD+∠BO′E′＝360°﹣α＝360°﹣∠AOB，∴360°﹣2∠AOB+∠BO′E′＝360°﹣∠AOB，∴∠AOB＝∠BO′E′．。

人教版数学七年级下册7 2 2 用坐标表示平移同步练习(含解析)

第七章平面直角坐标系7.2坐标方法的简单应用7.2.2用坐标表示平移基础过关全练知识点1坐标系中点的平移1.(2022广东中考)在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( )A.(3,1)B.(-1,1)C.(1,3)D.(1,-1)2.在平面直角坐标系中,将点P(-3,4)平移至原点,则平移方式可以是( )A.先向左平移3个单位,再向上平移4个单位B.先向右平移4个单位,再向上平移3个单位C.先向左平移3个单位,再向下平移4个单位D.先向右平移3个单位,再向下平移4个单位3.如图,在平面直角坐标系xO1y中,点A的坐标为(2,2).如果将x轴向上平移6个单位长度,将y轴向左平移4个单位长度,交于点O2,点A 的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )A.(-6,4)B.(6,-4)C.(-4,-6)D.(6,8)知识点2坐标系中图形的平移4.如图,点A,B的坐标分别为(-3,1),(-1,-2),若将线段AB平移至A1B1的位置,点A1,B1的坐标分别为(a,4),(3,b),则a+b的值为( )A.2B.3C.4D.55.如图,△ABC经过一定的平移得到△A'B'C',如果△ABC上的点P的坐标为(a,b),那么这个点在△A'B'C'上的对应点P'的坐标为( )A.(a-2,b-3)B.(a-3,b-2)C.(a+3,b+2)D.(a+2,b+3)6.三角形ABC中一点P(x,y)经过平移后对应点为P1(x+4,y-2),将三角形ABC进行同样的平移得到三角形A1B1C1,若点A的坐标为(-4,5),则点A1的坐标为.7.【教材变式·P86T9变式】如图所示,四边形ABCO中,AB∥OC,BC ∥AO,A、C两点的坐标分别为(-√3,√5)、(-2√3,0),A、B两点间的距离等于O、C两点间的距离.(1)点B的坐标为;(2)将这个四边形向下平移2√5个单位长度后得到四边形A'B'C'O',请你写出平移后四边形四个顶点的坐标.8.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(1,0),B(4,0),C(3,3),D(1,4).(1)描出A、B、C、D四点的位置,并顺次连接A、B、C、D各点,组成一个封闭图形;(2)四边形ABCD的面积是;(3)四边形ABCD向左平移5个单位长度,再向上平移1个单位长度得到四边形A'B'C'D',在图中画出四边形A'B'C'D',并写出A'、B'、C'、D'的坐标.能力提升全练9.(2021重庆丰都期末,10,★★☆)将点P(m+2,2-m)向右平移2个单位长度得到点Q,且Q在y轴上,那么点P的坐标为( )A.(6,-2)B.(-2,6)C.(2,2)D.(0,4)10.【新素材·密码确定】(2022山东济宁兖州期末,5,★★☆)一组密码的一部分如图,为了保密,不同的情况下可以采用不同的密码.若输入数字密码(7,7),(8,5),对应的中转口令是“数学”,最后输出的口令为“文化”,按此方法,若输入数字密码(2,7),(3,4),则最后输出的口令为( )A.垂直B.平行C.素养D.相交11.【代数推理】(2022福建厦门思明湖滨中学期末,9,★★☆)在平面直角坐标系中,将A(n2,1)沿着x轴的正方向平移3+n2个单位后得到B点.有四个点M(-2n2,1)、N(3n2,1)、P(n2,n2+4)、Q(n2+1,1),一定在线段AB上的是( )A.点MB.点QC.点PD.点N12.【易错题】(2021湖北武汉江岸期末,14,★★☆)如图,第一象限内有两点P(m-4,n),Q(m,n-3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是.素养探究全练13.【抽象能力】如图,已知点A1(1,1),点A1向上平移1个单位,再向右平移2个单位,得到点A2;点A2向上平移2个单位,再向右平移4个单位,得到点A3;点A3向上平移4个单位,再向右平移8个单位,得到点A4,……,按这个规律平移得到点A n,则点A n的横坐标为.14.【抽象能力】(2022北京师大附中期末)对于平面直角坐标系xOy 中的图形G和图形G上的任意点P(x,y),给出如下定义:将点P(x,y)平移到P'(x+t,y-t)称为将点P进行“t型平移”,点P'称为将点P进行“t型平移”的对应点;将图形G上的所有点进行“t型平移”称为将图形G进行“t型平移”.例如:将点P(x,y)平移到P'(x+1,y-1)称为将点P进行“1型平移”,将点P(x,y)平移到P'(x-1,y+1)称为将点P进行“-1型平移”.已知点A(1,1)和点B(3,1).(1)将点A(1,1)进行“1型平移”后的对应点A'的坐标为;(2)①将线段AB进行“-1型平移”后得到线段A'B',点P1(2,3),P2(1.5,2),P3(3,0)中,在线段A'B'上的点是;②若线段AB进行“t型平移”后与坐标轴有公共点,则t的取值范围是.答案全解全析基础过关全练1.A将点(1,1)向右平移2个单位后,横坐标加2,所以平移后点的坐标为(3,1),故选A.2.D将点P(-3,4)的横坐标加3,纵坐标减4即可得原点的坐标(0,0),故可以先向右平移3个单位,再向下平移4个单位.3.B新坐标系如图所示,点A在新坐标系中的坐标为(6,-4),故选B.4.A∵点A,B的坐标分别是为(-3,1),(-1,-2),线段AB平移至A1B1的位置后,A1(a,4),B1(3,b),∴线段AB向右平移了4个单位,向上平移了3个单位,∴a=1,b=1,∴a+b=2,故选A.5.C点B的坐标为(-2,0),点B'的坐标为(1,2),横坐标增加了1-(-2)=3,纵坐标增加了2-0=2,∵△ABC上点P的坐标为(a,b),∴点P'的横坐标为a+3,纵坐标为b+2,∴点P'的坐标为(a+3,b+2),故选C.6.答案(0,3)解析∵三角形ABC中任意一点P(x,y)经过平移后对应点为P1(x+4,y-2),∴该点先向右平移了4个单位长度,又向下平移了2个单位长度,又-4+4=0,5-2=3,∴点A的对应点A1的坐标为(0,3).7.解析(1)∵C点的坐标为(-2√3,0),∴OC=2√3.∵AB∥OC,AB=OC,∴将A点向左平移2√3个单位长度得到B点,又∵A点的坐标为(-√3,√5),∴B点的坐标为(-√3−2√3,√5),即(-3√3,√5).(2)∵将四边形ABCO向下平移2√5个单位长度后得到四边形A'B'C'O',∴A'点的坐标为(-√3,-√5),B'点的坐标为(-3√3,-√5),C'点的坐标为(-2√3,-2√5),O'点的坐标为(0,-2√5).8.解析(1)如图..(2)四边形ABCD的面积是172(3)四边形A'B'C'D'如图.其中A'(-4,1)、B'(-1,1)、C'(-2,4)、D'(-4,5).能力提升全练9.B将点P(m+2,2-m)向右平移2个单位长度后得到的点Q的坐标为(m+4,2-m),∵点Q(m+4,2-m)在y轴上,∴m+4=0,即m=-4,则点P 的坐标为(-2,6),故选B.10.D输入数字密码(7,7),(8,5),对应的中转口令是“数学”,最后输出的口令为“文化”,可得平移规律为向左平移1格,向下平移2格,所以输入数字密码(2,7),(3,4),得最后输出的口令为“相交”,故选D.11.B∵将A(n2,1)沿着x轴的正方向平移3+n2个单位后得到B点,∴B(2n2+3,1),∴点B在点A右侧,且AB与x轴平行,AB上的点都距离x轴1个单位,因为点M(-2n2,1)距离x轴1个单位,当n≠0时,M 点在点A左侧,当n=0时,M点跟A点重合,所以点M不一定在线段AB上.点N(3n2,1)距离x轴1个单位,可看作将点A沿着x轴的正方向平移2n2个单位后得到的,不一定在线段AB上.点P(n2,n2+4)在点A 右侧,且距离x轴n2+4个单位,不在线段AB上.点Q(n2+1,1)距离x 轴1个单位,可看作将A(n2,1)沿着x轴的正方向平移1个单位后得到的,一定在线段AB上.所以一定在线段AB上的是点Q.故选B.12.答案(0,3)或(-4,0)解析设平移后点P、Q的对应点分别是P'、Q'.分两种情况:①P'在y轴上,Q'在x轴上,则P'的横坐标为0,Q'的纵坐标为0,∴点P'的纵坐标为n+0-(n-3)=3,∴点P平移后的对应点的坐标是(0,3);②P'在x轴上,Q'在y轴上,则P'的纵坐标为0,Q'的横坐标为0,∴点P'的横坐标为m-4+0-m=-4,∴点P平移后的对应点的坐标是(-4,0).综上可知,点P平移后的对应点的坐标是(0,3)或(-4,0).素养探究全练13.答案2n-1解析由题意知,点A1的横坐标为1=21-1,点A2的横坐标为3=22-1,点A3的横坐标为7=23-1,点A4的横坐标为15=24-1,……,则点A n的横坐标为2n-1.14.解析(1)将点A(1,1)进行“1型平移”后的对应点A'的坐标为(2,0),故答案为(2,0).(2)①如图,将线段AB进行“-1型平移”后得到线段A'B',点P1(2,3),P2(1.5,2),P3(3,0)中,线段A'B'上的点是P2.②若线段AB进行“t型平移”后与坐标轴有公共点,则t的取值范围是-3≤t≤-1或t=1.。

(人教版数学)初中7年级下册-同步练习-7.2.2 用坐标表示平移-七年级数学人教版(下册)(解析版

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．
1．如图所示，将点A向右平移几个单位长度可得到点B
A．3个单位长度B．4个单位长度
C．5个单位长度D．6个单位长度
【答案】B
长度，故选B．
2．如图所示，将点A向下平移5个单位长度后，将重合于图中的
A．点CB．点F
C．点DD．点E
【答案】D
16．三角形ABC沿x轴正方向平移2个单位长度，再沿y轴负方向平移1个单位长度得到三角形EFG．
（1）写出三角形EFG的三个顶点坐标；
（2）求三角形EFG的面积．
（1）如图所示：
点E（4，1），点F（0，–2），点G（5，–3）；
（2）S三角形EFG=4×5– ×4×3– ×1×5– ×1×4= ．
9．已知三角形ABC，A(–3，2)， B(1，1)，C(–1，–2)，现将三角形ABC平移，使点A到点(1，–2)的位置上，则点B，C的坐标分别为______，________.
【答案】(5，–3)；(3，–6)
点C横坐标为：–1+4=3；纵坐标为：–2+（–4）=–6；
∴ B点的坐标为（5，–3），C点的坐标为（3，–6）．
（2）分别过A、C两点作x轴的平行线，过B、D两点作y轴的平行线，围成矩形，利用“割补法”求四边形ABCD的面积．如图，用矩形EFGH围住四边形ABCD，则
S四边形ABCD=S矩形EFGH–S三角形ABE–S三角形 BCF–S三角形CDG–S三角形ADH
=3×4– ×1×2– ×1×2– ×2×2– ×1×3=6.5．
6．三角形ABC三个顶点的坐标分别是A（2，1），B（1，3），C（3，0），将三角形ABC向左平移3个单位长度，再向下平移1个单位长度，则平移后三个顶点的坐标为

平移(专项练习)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题5.18 平移（专项练习）一、单选题1．下列现象中，属于平移现象的是（）A ．方向盘的转动B ．行驶的自行车的车轮的运动C ．电梯的升降D ．钟摆的运动2．在下列汽车标志的图案中，能用图形的平移来分析其形成过程的是（）A ．B ．C ．D ．3．如图，ABC 沿直线m 向右平移2cm ，得到DEF ，下列说法错误的是（）A ．//AC DFB ．AB DE =C ．2cm CF =D ．2cm DE = 4．如图，ABC 沿射线BC 方向平移到DEF （点E 在线段BC 上），如果8cm BC =，5cm EC =，那么平移距离为（）A ．3cmB ．5cmC ．8cmD ．13cm5．有以下说法：①①ABC 在平移的过程中，对应线段一定相等；①①ABC 在平移过程中，对应线段一定平行；①①ABC 在平移过程中，周长保持不变；①①ABC 在平移过程中，对应角分别相等. 正确的是（）A．①①①①B．①①①C．①①①D．①①①6．如图，在一块长方形草地上原有一条等宽的笔直小路，现在要把这条小路改为同样宽度的弯曲小路，则改造后草地部分的面积（）A．变大B．不变C．变小D．无法确定7．下列平移作图不正确的是（）A．B．C．D．8．定义：将一个图形L沿某个方向平移一段距离后，该图形在平面上留下的痕迹称之为图形L在该方向的拖影．如图，四边形ABB′A′是线段AB水平向右平移得到的拖影．则将下面四个图形水平向右平移适当距离，其拖影是五边形的是()A．B．C．D．9．如图所示，将边长为8cm的正方形ABCD先向上平移4cm，再向右平移2cm，得到正方''''，此时阴影部分的面积为（）形A B C DA ．224cmB ．226cmC ．218cmD ．220cm10．小红同学在某数学兴趣小组活动期间，用铁丝设计并制作了如图所示的三种不同的图形，请您观察甲、乙、丙三个图形，判断制作它们所用铁丝的长度关系是（）A ．制作甲种图形所用铁丝最长B ．制作乙种图形所用铁丝最长C ．制作丙种图形所用铁丝最长D ．三种图形的制作所用铁丝一样长二、填空题11．下列生活中的物体的运动情况可以看成平移的是____．（1）摆动的钟摆；（2）在笔直的公路上行驶的汽车；（3）随风摆动的旗帜；（4）汽车玻璃上雨刷的运动；（5）从楼顶自由落下的球（球不旋转）．12．如图所示是一座楼房的楼梯，高1 m ，水平距离是2.8 m ．如果要在台阶上铺一种地毯，那么至少要买这种地毯________13．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到①DEF 的位置，AB ＝10，DO ＝4，平移距离为6，则阴影部分面积为__14．如图，将ABC ∆沿着射线BC 的方向平移，得到DEF ∆，若13EF =，7EC =，则平移的距离为__．15．如图，将△ABC平移到△A’B’C’的位置（点B’在AC边上），若△B=55°，△C=100°，则△AB’A’的度数为_____°．16．如图，在长方形ABCD中，线段AC，BD相交于O，DE//AC，CE//BD，BC=2cm，那么三角形EDC可以看作由____平移得到的，连接OE，则OE=____cm．17．如图，在长为9m，宽为7m的矩形场地上修建两条宽度都为1m且互相垂直的道路，剩余部分进行绿化，则绿化面积共有______2m．18．如图，公园里长为20米宽为10米的长方形草地内修建了宽为1米的道路，则草地面积是________平方米．三、解答题19．如图示，每个小方格的边长为1，把三角形ABC 先向右平移5个格再向下平移2个格得到三角形DNF ．(1) 在方格中画出平移后的三角形DNF ．(2) 计算平移后三角形DNF 的面积．20．如图所示的正方形网格中，每个小正方形的边长都为1个单位长度，三角形ABC 的顶点都在正方形网格的格点上，将三角形ABC 向上平移m 个单位，再向右平移n 个单位，平移后得到三角形A B C '''，其中图中直线l 上的点A '是点A 的对应点。