第十四章 生存分析
生存分析

19.2.1 寿命表法(life table method)
例21-1 收集374名某恶性肿瘤患者的随访资料,取时间区 间均为1年,整理结果见下午表,试估计各年生存率。
解析:
该生存资料为大样本,生存时间粗略且含有删失数据。
方法原理:
寿命表法
1. 计算期初有效例数,注意删失数据
期初有效例数=期初病例数-期内删失数/2
表19-2 30例膀胱肿瘤患者生存资料的原始记录表
编 号
1 2 3
年龄 肿瘤 肿瘤大 是否 (岁) 分级 小/cm 复发
62 64 52 I I II ≤3.0 ≤3.0 ≤3.0 0 0 1
手术日期
02/10/1996 03/05/1996 04/09/1996
终止观 察日期
12/30/2000 12/03/1999
期间死亡人数:k 初人口数:n 末人口数:n-k
⑴ 死亡概率(probability of death):表示某单位时
段开始存活的个体,在该时段内死亡的可能性;
如年死亡概率。
某年内死亡人数 死亡概率(q) 某年年初人口数
注意:如果年内有删失,则分母用校正人口数: 校正人口数 = 年初人口数—删失例数/2
19 生存分析
常用的回归分析:
回归分析
1个因变量Y Y是数值 变量
两个因变量 (结局分类变量+时间)
④
生存分析
Cox回归
Y是分类 型变量
① 一元回归
1个自变量X
② 多重回归
2个以上自变量X
③ Logistic 回归
Logistic regression
Simple regression
Multiple regression
《卫生统计学》课后思考题答案

《卫生统计学》课后思考题答案第一章绪论答:某人打靶100次,中靶次数少于等于5,那么该人一次打中靶的概率≤0.05,即可称该人一次打中靶的事件为小概率事件,可以视为很可能不发生。
第二章调查研究设计1、调查研究有何特点?答:(1)不能人为施加干预措施(2)不能随机分组(3)很难控制干扰因素(4)一般不能下因果结论2、四种常用的抽样方法各有什么特点?(2)系统抽样:优点是易于理解、操作简便,被抽到的观察单位在总体中分布均匀,抽样误差较单纯随机抽样小;缺点是在某些情况下会出现偏性或周期性变化。
(3)分层抽样:优点是抽样误差小,各层可以独立进行统计分析,适合大规模统计;缺点是事先要进行分层,操作麻烦。
(4)整群抽样:优点是易于组织和操作大规模抽样调查;缺点是抽样误差大。
3、调查设计包括那些基本内容?答:(1)明确调查目的和指标(2)确定调查对象和观察单位(3)选择调查方法和技术(4)估计样本大小(5)编制调查表答:(1)分析项目直接整理计算的必须的内容;(2)备查项目保证分析项目填写得完整和准确的内容;(3)其他项目大型调查表的前言和表底附注。
第三章实验设计1、简述实验设计的特点。
答:(1)研究者能人为设置处理因素(2)受试对象可以接受何种处理因素或水平是由随机分配而定的。
2、简述一般选择受试对象的原则。
答:(1)受试对象能从临床试验中受益(2)受试对象具有代表性(3)受试对象具有依从性(4)受试对象可以是志愿者。
3、什么是混杂因素?设计时怎样控制混杂因素?答:混杂因素是指影响实验效应并与处理因素同时存在的非处理因素。
可以通过采取排除、平衡、或标准化的办法来控制混杂因素的影响。
4、什么是随机化?怎样实现随机抽样和随机分组?答:随机化就是使样本具有较好的代表性,使各组受试对象在重要的非处理因素方面具有较好的均衡性,提高实验结果的可比性。
一般用随机数字表、随机排列表或统计软件包来实现随机抽样和随机分组。
答:(1)有算术均数、几何均数和中位数、众数、调和数等。
生存分析的基本方法

生存分析的基本方法生存分析是一种用于研究生命过程中事件发生率的统计方法。
它可以应用于医学、流行病学、社会科学等领域,用于分析和预测个体的生存时间或事件发生的概率。
本文将介绍生存分析的基本方法,包括生存函数、风险比、半生存时间、生存曲线和生存率表等。
生存分析的基本思想是通过比较观察时间和事件发生时间来估计生存率或者事件发生率。
观察时间是指个体从开始被观察到事件发生之间的时间段,也称为生存时间。
事件发生时间是指个体从开始被观察到事件发生的时间点。
生存函数是生存分析的核心概念之一。
生存函数描述的是个体在给定时间内存活下来的概率。
生存函数通常用S(t)表示,其中t是给定的时间点。
生存函数是一个在[0,1]区间上的递减函数,表示从0时刻到t时刻存活下来的概率。
风险比是生存分析的另一个重要概念。
风险比表示在一个时间段内,某个因素对事件发生率的影响。
风险比通常用hazard表示,是一个在[0,∞)区间上的非负数。
风险比越大,表示事件发生的风险越高。
半生存时间是指个体在给定的时间段内生存下来的时间的中位数。
它是生存数据的一个重要指标,可以用来描述生存数据的分布情况。
半生存时间越长,表示生存能力越强。
生存曲线是用来描述不同时间段个体存活下来的比例。
生存曲线通常是一个递减的曲线,随着时间的推移,曲线的斜率越来越陡峭,表示个体存活的概率逐渐减小。
生存率表是一种用表格形式表示的生存数据汇总。
生存率表通常包括时间段、观察个体数、事件发生个体数、累积观察个体数、累积事件发生个体数和生存函数等内容。
生存率表可以帮助研究人员更直观地了解生存数据的分布情况。
生存分析的方法还包括生存回归分析、生存树分析、生存指标筛选等。
生存回归分析是一种用于分析多个因素对生存数据的影响的方法,可以用来确定生存数据中重要的预测因素。
生存树分析是一种用于构建生存数据分类模型的方法,可以用于预测个体的存活概率。
生存指标筛选是一种用于选择生存数据中重要的预测指标的方法,可以帮助研究人员更准确地预测个体的生存时间。
生存分析(survivalanalysis)

⽣存分析(survivalanalysis)⼀、⽣存分析(survival analysis)的定义 ⽣存分析:对⼀个或多个⾮负随机变量进⾏统计推断,研究⽣存现象和响应时间数据及其统计规律的⼀门学科。
⽣存分析:既考虑结果⼜考虑⽣存时间的⼀种统计⽅法,并可充分利⽤截尾数据所提供的不完全信息,对⽣存时间的分布特征进⾏描述,对影响⽣存时间的主要因素进⾏分析。
⽣存分析不同于其它多因素分析的主要区别点:⽣存分析考虑了每个观测出现某⼀结局的时间长短。
应⽤场景 什么是⽣存?⽣存的意义很⼴泛,它可以指⼈或动物的存活(相对于死亡),可以是患者的病情正处于缓解状态(相对于再次复发或恶化),还可以是某个系统或产品正常⼯作(相对于失效或故障),甚⾄可是是客户的流失与否等。
在⽣存分析中,研究的主要对象是寿命超过某⼀时间的概率。
还可以描述其他⼀些事情发⽣的概率,例如产品的失效、出狱犯⼈第⼀次犯罪、失业⼈员第⼀次找到⼯作等等。
在某些领域的分析中,常常⽤追踪的⽅式来研究事物的发展规律,⽐如研究某种药物的疗效,⼿术后的存活时间,某件机器的使⽤寿命等。
在医学研究中,常常⽤追踪的⽅式来研究事物发展的规律。
如,了解某药物的疗效,了解⼿术的存活时间,了解某医疗仪器设备使⽤寿命等等。
对⽣存资料的分析称为⽣存分析。
所谓⽣存资料就是描述寿命或者⼀个发⽣时间的数据。
更详细的说⼀个⼈的⽣存时间的长短与许多因素有联系的,研究因素与⽣存时间的联系有⽆及程度⼤⼩,称为⽣存分析。
例如研究病⼈感染了病毒后,多长时间会死亡;⼯作的机器多长时间会发⽣崩溃等。
这⾥“个体的存活”可以推⼴抽象成某些关注的事件。
所以SA就成了研究某⼀事件与它的发⽣时间的联系的⽅法。
这个⽅法⼴泛的⽤在医学、⽣物学等学科上,近年来也越来越多⼈⽤在互联⽹数据挖掘中,例如⽤survival analysis去预测信息在社交⽹络的传播程度,或者去预测⽤户流失的概率。
⽣存分析研究的内容 1.描述⽣存过程 研究⽣存时间的分布特点,估计⽣存率及平均存活时间,绘制⽣存曲线等,根据⽣存时间的长短,可以估算出各个时点的⽣存率,并根据⽣存率来估计中位⽣存时间,也可以根据⽣存曲线分析其⽣存特点,⼀般使⽤Kaplan-Meier法和寿命表法。
生存分析(2012年)推荐课件

合格的 研究对象
试验组 对照组
出现结果 尚未出现结果 失访、脱落
伴随因素 干扰因素
随访研究(follow-up study)示意图
【例题】
某医院泌尿外科医师选择1996-2000年间经手术 治疗的膀胱肿瘤患者,对可能影响膀胱肿瘤术后 生存的因素进行了调查,随访截止日期为2000年 12月30日。
➢ 1 有2个效应变量:(1)生存时间(天数),(2) 结局(死亡与否、是否阳性等)
➢ 2 截尾数据:如表21-1中的1号、 3号和4号病人 未观察到底,不知他们究竟能活多长时间。 处理截尾数据时两种错误的做法:
✓ 错误1:丢弃截尾数据,只考虑确切数据。(损失 了信息)
✓ 错误2:将截尾数据当作确切数据处理。(低估了 生存时间的平均水平)。
生存时间资料的特点
➢ 3. 分布类型复杂:生存时间常呈正偏态分布。 在处理正偏态分布数据时两种错误的做法: 错误1:采用平均生存时间而不是采用中位生存时
间来表示生存时间的平均水平。
错误2:采用常规t检验或方差分析进行组间比较。
(应采用log-rank检验比较几组生存时间 )
二、生存分析的统计描述指标
h(t)h0(t)exp(1x1 ...pxp)
h0(t)为t时刻的风险函数。
Cox回归模型的模型假定:任两个个体风险之比不 随时间的变化而变化。
Assumption of proportional hazard( PH假定)
R Rh h0 0tte ex x 1 p 1 p X Xji1 1 2 2X Xij2 2 ............
生存分析 Survival Analysis
生存分析基础知识

生存分析基础知识生存分析是一种统计方法,用于研究个体在特定时间段内生存的概率和生存时间的分布。
它广泛应用于医学、生物学、社会科学等领域,帮助研究人员了解个体的生存状况和预测生存时间。
本文将介绍生存分析的基础知识,包括生存函数、生存率、危险比和生存曲线等概念。
一、生存函数和生存率生存函数是描述个体在特定时间点存活的概率。
通常用S(t)表示,其中t为时间点。
生存函数的定义为:S(t) = P(T > t)其中T表示个体的生存时间,P(T > t)表示个体的生存时间大于t的概率。
生存函数的取值范围为0到1,随着时间的增加,生存函数逐渐减小。
生存率是描述个体在特定时间段内存活的概率。
通常用s(t)表示,其中t为时间段的起始点。
生存率的定义为:s(t) = P(t ≤ T < t + Δt)其中Δt表示时间段的长度。
生存率可以通过生存函数计算得到:s(t) = S(t) - S(t + Δt)生存率的取值范围也是0到1,随着时间的增加,生存率逐渐减小。
二、危险比危险比是用来比较两组个体生存状况的指标。
通常用hazard ratio (HR)表示,表示一组个体相对于另一组个体的生存风险。
危险比的定义为:HR = h1(t) / h2(t)其中h1(t)和h2(t)分别表示两组个体在时间点t的危险函数。
危险函数描述了在给定时间点个体发生事件(如死亡)的概率。
如果HR大于1,表示第一组个体的生存风险高于第二组个体;如果HR小于1,表示第一组个体的生存风险低于第二组个体。
三、生存曲线生存曲线是描述个体在不同时间点的生存概率的曲线。
通常用Kaplan-Meier曲线表示,该曲线基于生存函数估计得到。
生存曲线可以帮助研究人员观察个体的生存状况和预测生存时间。
在生存曲线上,横轴表示时间,纵轴表示生存概率。
生存曲线可以根据不同的因素进行分组比较,以了解不同因素对生存的影响。
四、生存分析方法生存分析有多种方法,常用的包括Kaplan-Meier方法和Cox比例风险模型。
生存分析知识总结

生存分析知识总结一、生存分析的基本概念生存分析是将事件的结果和出现此结果所经历的时间结合起来分析的统计分析方法。
研究生存现象和响应时间数据及其统计规律的一门学科。
对一个或多个非负随机变量(生存时间)进行统计分析研究。
对生存时间进行分析和推断,研究生存时间和结局与众多影响因素间关系及其程度的统计分析方法。
在综合考虑相关因素(内因和外因)的基础上,对涉及生物学、医学(临床、流行病)、工程(可靠性)、保险精算学、公共卫生学、社会学和人口学(老龄问题、犯罪、婚姻)、经济学(市场学)等领域中,与事件(死亡,疾病发生、发展和缓解,失效,状态持续)发生的时间(也叫寿命、存活时间或失效时间,统称生存时间)有关的问题提供相关的统计规律的分析与推断方法的学科。
生存时间也叫寿命、存活时间、失效时间等等。
比如:医学上包括疾病发生时间、治疗后疾病复发时间;可靠性工程系为元件或系统失效时间;犯罪学方面是重罪犯人的假释时间;社会学上指首次婚姻持续时间;人口学上包括母乳喂养新生儿断奶时间;经济学包括经济危机爆发时间、发行债券的违约时间;保险精算学包括保险人的索赔时间、保险公司某一索赔中所付保费;汽车工业包括汽车车轮转数;市场学中有报纸和杂志的篇幅和订阅费。
这些也可以说明,生存时间可以不是具体的时间。
二、生存分析的历史生存分析方法最早可上溯至十九世纪的死亡寿命表。
现代的生存分析则开始于二十世纪三十年代工业科学中的相关应用。
二次世界大战时期,武器装备的可靠性研究,这一研究兴趣延续到战后。
此时生存分析都集中在参数模型。
二十世纪六七十年代,医学研究中大量临床试验的出现,要求方法学有新的突破,导致了生存分析的研究开始转向非参数方法。
D.R. Cox在72年提出的比例风险模型为此做出了划时代的贡献。
现在,生存分析方法的在医学领域得到了广泛的应用,而通过医学研究要求的不断提高,这一方法也得到了飞速的发展。
三、生存分析的研究目的,内容和具体方法(一)研究目的主要由以下五个方面1.描述生存过程:估计不同时间的总体生存率,计算中位生存期,绘制生存函数曲线。
Removed_生存分析知识总结14

生存分析知识总结一、生存分析的基本概念生存分析是将事件的结果和出现此结果所经历的时间结合起来分析的统计分析方法。
研究生存现象和响应时间数据及其统计规律的一门学科。
对一个或多个非负随机变量(生存时间)进行统计分析研究。
对生存时间进行分析和推断,研究生存时间和结局与众多影响因素间关系及其程度的统计分析方法。
在综合考虑相关因素(内因和外因)的基础上,对涉及生物学、医学(临床、流行病)、工程(可靠性)、保险精算学、公共卫生学、社会学和人口学(老龄问题、犯罪、婚姻)、经济学(市场学)等领域中,与事件(死亡,疾病发生、发展和缓解,失效,状态持续)发生的时间(也叫寿命、存活时间或失效时间,统称生存时间)有关的问题提供相关的统计规律的分析与推断方法的学科。
生存时间也叫寿命、存活时间、失效时间等等。
比如:医学上包括疾病发生时间、治疗后疾病复发时间;可靠性工程系为元件或系统失效时间;犯罪学方面是重罪犯人的假释时间;社会学上指首次婚姻持续时间;人口学上包括母乳喂养新生儿断奶时间;经济学包括经济危机爆发时间、发行债券的违约时间;保险精算学包括保险人的索赔时间、保险公司某一索赔中所付保费;汽车工业包括汽车车轮转数;市场学中有报纸和杂志的篇幅和订阅费。
这些也可以说明,生存时间可以不是具体的时间。
二、生存分析的历史生存分析方法最早可上溯至十九世纪的死亡寿命表。
现代的生存分析则开始于二十世纪三十年代工业科学中的相关应用。
二次世界大战时期,武器装备的可靠性研究,这一研究兴趣延续到战后。
此时生存分析都集中在参数模型。
二十世纪六七十年代,医学研究中大量临床试验的出现,要求方法学有新的突破,导致了生存分析的研究开始转向非参数方法。
D.R. Cox在72年提出的比例风险模型为此做出了划时代的贡献。
现在,生存分析方法的在医学领域得到了广泛的应用,而通过医学研究要求的不断提高,这一方法也得到了飞速的发展。
三、生存分析的研究目的,内容和具体方法(一)研究目的主要由以下五个方面1.描述生存过程:估计不同时间的总体生存率,计算中位生存期,绘制生存函数曲线。
生存分析

0 indicates loss to follow-up
X
o
O
X X X
1994
1995
1996 年份
1997
1998
1999
生存时间图示
X
X indicates event
0 indicates loss to follow-up
X X o X X 0 12 24 36 48 生存时间(月) 60 72
生存分析
Survival Analysis
吴静 公共卫生学院流行病与卫生统计学系
前
言
生存分析(survival analysis)是将事件的 结果和出现这一结果所经历的时间结合起来 分析的一类统计分析方法 生存分析是队列研究和临床试验的重要分析 方法之一 生存分析不同于其它多因素分析的主要区别 点就是生存分析考虑了每个观测出现某一结 局的时间长短
1995.06.04 死亡 1998.08.25 死亡 1994.03.18 失访 2000.12.30 存活 1995.03.17 死亡 1996.08.16 死于其它
1476 2417 876+ 2250+ 265 985+
生存时间的类型
完全数据(complete data) 是指从观察的起 始事件一直达到观察的终点事件,即观察对象 完整的生存时间,是生存分析最重要的资料。 不完全数据(incomplete data)在随访研究中, 由于某种原因未能观察到随访对象发生事先定 义的终点事件(为其他终点事件或生存结局), 无法得知随访对象的确切生存时间,这种现象 称为删失(censoring),也称截尾或终检。包 含删失的数据即为不完全数据,它所提供关于 生存时间的信息是不完全的。
《生存分析》PPT幻灯片PPT

截尾数据
截尾数据(censored data)在随访工作中,由于某种原 因未能观察到病人的明确结局(即终止事件),所以 不知道该病人的确切生存时间,它所提供关于生存时 间的信息是不完全的。
产生截尾现象的原因: ①病人失访 ②病人的生存期超过了研究的终止期
③在动物实验中,达到了事先规定的终止事件
生存时间资料的特点
生存时间资料常因失访等原因造成观察不完全,因而在资料搜集、统计 分析和质量控制等方面均有其显著的特点。
生存时间资料有如下显著特点: (1)效应变量有2个 一是生存时间(天数),二是结局(死亡与否、是否阳性 等)。 (2)存在截尾数据 如有些病人未观察到底,不知他们究竟能活多长时间。 (3)分布类型复杂 生存时间资料常通过随访获得,因观察时间长且难以控 制混杂因素,故其分布常呈偏态,影响因素较多,规律难以估测。
各种生存数据的表示
×
X
×
X
o
O
1994
1995
×
X
1996
1997
年份
1998 1999
各种生存数据的表示
×
X × X ×
X
o
X 1994 1995 1996 1997 1998 1999 2000
死亡概率
死亡概率(mortality probability)记为q, 是指死于某时段内的可能性的大小。
因此,生存时间资料不宜简单地计算死亡率,也不能简单地计算生存时 间的平均数,必须将两者结合起来分析才能准确地反映疗效和预后的好 坏程度,即必须用生存分析方法作统计分析。
病例随访资料分析
• 基本概念 • 小样本未分组资料分析 • 大样本分组资料分析
基本概念
• 生存时间 • 完全数据 • 截尾数据 • 死亡概率 • 生存概率 • 生存率
卫生统计学第十四章生存分析

做对人数:0
所占比例: 0%
题号: 9 本题分数: 4.2
以死亡为终止事件的随访资料分析中,应选用的指标是
A. 发病率
B. 患病率
C. 出生率
D. 生存率
E. 死亡率
正确答案: D
答案解析:以死亡为终止事件的随访资料分析中,应选用的指标是生存率。
一、题型:A1
题号: 1 本题分数: 4.2
无截尾数据时,直接法计算5年生存率公式中的分母是
A. 所有观察对象数
B. 所有活满5年的对象数
C. 所有5年内死亡的对象数
D. 5年内死于本病的对象数
E. 5年内死于本病及活满5年的对象数
正确答案: A
A B C D E
正确答案: B
答案解析:生存时间按在研究期内是否观察到终点事件将资料分为完全数据和截尾数据。完全数据是观察到终点事件出现,而截尾数据则没有观察到终点事件。研究开始时间是1995年1月,终点事件是观察对象发现胃癌,时间单位是月,研究终止时间是2000年1月。1题设观察对象在研究时间内观察到终点事件,它是完全数据。2题设观察对象在研究时间内并未观察到终点事件,它是截尾数据。3题设观察对象对象终止观察时并未观察到终点事件,它是截尾数据。4题设观察对象在研究时间内观察到终点事件,它是完全数据。
答案:
答案解析:直接法计算6年生存率公式的分母是观察满6年的人数,包括6年内死于本病及活满6年的观察对象数。
做答人数:2
做对人数:0
所占比例: 0%
题号: 6 本题分数: 4.2
生存率的标准误
A. 是反映平均水平的指标
B. 可用生存率曲线来比较
第十四章 生存分析的Stata实现
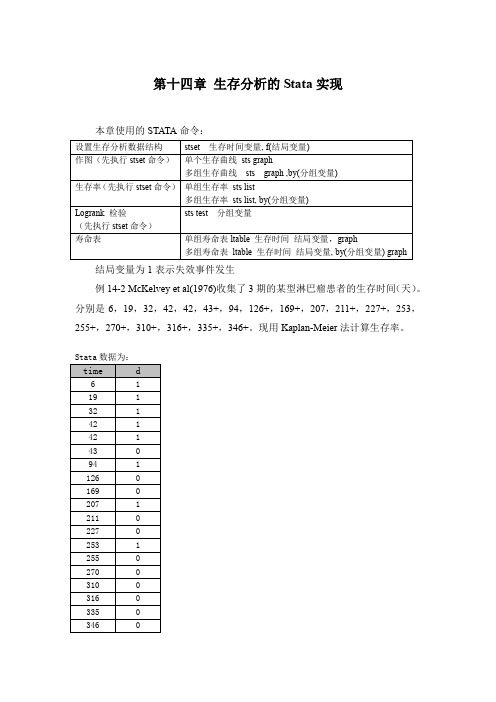
第十四章生存分析的Stata实现本章使用的STATA命令:结局变量为1表示失效事件发生例14-2 McKelvey et al(1976)收集了3期的某型淋巴瘤患者的生存时间(天)。
分别是6,19,32,42,42,43+,94,126+,169+,207,211+,227+,253,255+,270+,310+,316+,335+,346+。
现用Kaplan-Meier法计算生存率。
Stata命令为:stset time,failure(d) sts liststs graph结果为:例14-3 下面是来自于Berkson & Gage(1950)的一个研究队列。
为了叙述方便,把原来的出院后的生存时间改称为某恶性肿瘤术后生存时间。
共有374名患者进入研究队列。
表14-3 寿命表法计算生存率的计算用表(1) (2) (3) (4) (5) (6) (7) (8) (9)序号术后生存年数期初观察例数期内死亡期内截尾人数校正期初人数死亡概率生存概率生存率t n d c n c=n-c/2 q=d/n c p=1-q S(t)1 0~374 90 0 374 0.2406 0.7594 0.75942 1~284 76 0 284 0.2676 0.7324 0.55613 2~208 51 0 208 0.2452 0.7548 0.41984 3~157 25 12 151 0.1656 0.8344 0.35035 4~120 20 5 117.5 0.1702 0.8298 0.29076 5~957 9 90.5 0.0773 0.9227 0.26827 6~79 4 9 74.5 0.0537 0.9463 0.25388 7~66 1 3 64.5 0.0155 0.9845 0.24989 8~62 3 5 59.5 0.0504 0.9496 0.237210 9~54 2 5 51.5 0.0388 0.9612 0.228011 10+47 21 26 34 0.6176 0.3824 0.0872 Stata数据格式为:Stata命令为:stset time [weight=w],failure(d=1) ltable time d [weight=w],graph结果为:例14-4 在例14-3中介绍了McKelvey et al收集了19名3期淋巴瘤病人的生存资料,该研究者还同时收集了4期淋巴瘤病人的生存数据共61例:4,6,10,11,11,11,13,17,20,20,21,22,24,24,29,30,30,31,33,34,35,39,40,41+,43+,45,46,50,56,61+,61+,63,68,82,85,88,89,90,93,104,110,134,137,160+,169,171,173,175,184,201,222,235+,247+,260+,284+,290+,291+,302+,304+,341+,345+。
生存分析入门及其应用领域

生存分析入门及其应用领域生存分析是统计学中一种重要的分析方法,主要用于研究个体在特定时间内生存的概率和影响因素。
生存分析可以帮助我们了解不同因素对生存时间的影响程度,预测个体的生存概率,评估治疗效果等。
本文将介绍生存分析的基本概念、常用方法以及在医学、生物学、社会科学等领域的应用。
一、生存分析基本概念生存分析是一种统计方法,用于研究个体在特定时间内生存的概率和影响因素。
在生存分析中,我们通常关注以下几个重要概念:1. 生存时间(Survival Time):生存时间是指个体从特定起始时间到达某一事件(比如死亡、疾病复发等)发生时的时间间隔。
生存时间可以是连续的,也可以是离散的。
2. 存活函数(Survival Function):存活函数是描述个体在给定时间内存活下来的概率。
通常用S(t)表示,其中t为时间点。
存活函数的值范围在0到1之间,随着时间的增加逐渐减小。
3. 风险函数(Hazard Function):风险函数是描述在给定时间点个体发生事件的概率。
通常用h(t)表示,表示在t时刻发生事件的概率密度。
风险函数的倒数称为生存时间的概率密度函数。
4. 生存曲线(Survival Curve):生存曲线是描述个体在不同时间点的存活概率的曲线图。
生存曲线可以帮助我们直观地了解个体的生存情况。
二、生存分析常用方法生存分析有多种方法,常用的包括Kaplan-Meier方法、Cox比例风险模型等。
下面将介绍其中两种常用方法:1. Kaplan-Meier方法:Kaplan-Meier方法是用于估计存活函数的一种非参数方法。
该方法考虑了在不同时间点发生事件的个体数和存活个体数的比例,通过累积乘积法计算存活函数的估计值。
Kaplan-Meier方法适用于右偏分布的生存数据,常用于临床试验和生存分析中。
2. Cox比例风险模型:Cox比例风险模型是一种用于分析生存数据的半参数方法。
该模型可以同时考虑多个影响因素对生存时间的影响程度,通过估计风险比(Hazard Ratio)来评估不同因素的影响。
生存分析概述及实例分析

实例演示:选择一个具体的实例如癌症患者的 生存分析演示整个操作流程和结果分析
软件使用技巧和注意事项
选择合适的软件:根据数据特点和 需求选择合适的生存分析软件如 SPSS、R、SS等。
数据预处理:确保数据质量进行数 据清洗、缺失值处理等。
模型选择:根据研究目的和数据 特点选择合适的生存分析模型如 Kpln-Meier法、Cox比例风险模 型等。
实例选择:选择具有代表性的实例 进行分析如癌症患者生存率分析、 心脏病患者生存率分析等
数据类型:包括患者的年龄、性别、 疾病类型、治疗方式、生存时间等
添加标题
添加标题
添加标题
添加标题
数据来源:数据来源包括医院、科 研机构、政府机构等确保数据的准 确性和可靠性
数据处理:对数据进行清洗、整理、 转换等操作确保数据的可用性和可 分析性
生存函数的估计方法
非参数法:Kpln-Meier法、 Nelson-len法等
半参数法:Cox-Snell法、lenJohnsen法等
添加标题
添加标题
参数法:Cox比例风险模型、 Fine-Gry模型等
添加标题
添加标题
贝叶斯方法:Byesin生存分析、 Byesin网络模型等
生存函数的比较方法
非参数法:Kpln-Meier法、Nelson-len 法等
生存函数的概念
添加 标题
生存函数:描述个体生存概率随时间变化的 函数
添加 标题
生存函数形式:S(t) = P(T>t)其中S(t)表示 生存函数P(T>t)表示在t时刻仍然存活的概率
添加 标题
生存函数的特点:非负、单调不减、在t=0 时等于1
添加 标题
生存函数的应用:用于估计个体的生存概率分 析影响生存时间的因素预测个体的生存时间等
14生存分析

◦ 计算恰在每一时q刻i ti 之前的p生i 存人数
◦ 计算复发概率Sˆ (ti ) 和生存概率 ◦ 计算生存率
Kaplan-Meier methods
第三节 多变量Cox回归分析
生存分析的多变量分析方法特点:
1. Logistic回归不能同时处理结局变量和生存时间。 2.生存时间分布类型的复杂性不满足多元线性回
归条件的要求。 3.多元线性回归与Logistic回归均不能利用不完
全数据提供的信息。
一、Cox回归模型
1.模型的基本形式
h(t , X ) h0(t)exp(1 X1 2 X 2 m X m )
h0 (t )exp(1 X1 2 X 2
h0(t )exp(1 X
* 1
2X
* 2
mXm)
m
X
* m
)
exp[ 1 (
X1
X
* 1
)
2
(
X
2
X
* 2
)
m(Xm
X
* m
)]
比例风险假定,PH假定比值HR与h0(t)无关,即在时 间t上为常数。
(1)到研究结束时结局仍未发生
(2)失访
(3)结局起因于其他原因
生存数据的特点 ◦同时考虑生存结局和生存时间 ◦生存时间可能含有删失数据 ◦生存时间的分布很复杂,通常不服从正态分布
图14-1 生存时间原始记录示意图
十四、生存分析

124,143,12+,159+,190+,196+,197+,205+,219+
浙江大学医学院流行病与卫生统计学教研室
沈毅
Kaplan-meier过程
浙江大学医学院流行病与卫生统计学教研室
沈毅
Kaplan-meier过程
时间变量 结局变量
分组变量
浙江大学医学院流行病与卫生统计学教研室
沈毅
Kaplan-meier过程
当变量为二分类变量时,一般以死亡、复发、恶化等为 终结事件,如本例就是以恶化为终结事件,标记值为1,所 以在Single value框中输入1;如果生存状态变量取值为连续 变量时,则在Range of values 框分别输入下限值和上限值。 浙江大学医学院流行病与卫生统计学教研室 沈毅
浙江大学医学院流行病与卫生统计学教研室
做出的生存曲线不同
统计学检验方法不同:Life Tables过程采用Wilcoxon法 ,Kaplan-Meier过程 用Log rank 法、Breslow法、Tarone-are法
浙江大学医学院流行病与卫生统计学教研室
沈毅
Cox回归模型 上面介绍的两种生存分析方法只能研究一至两 个因素对生存时间的影响,当生存时间的影响因 素有多个时,它们就无能为力了,下面介绍Cox Regression过程,这是一种专门用于生存时间多 变量分析的统计方法。
Cox回归模型
例3 数据pancer.sav是关于胰脏癌术中接受放疗会否延长病人生存时间
的研究。该研究的终点为死亡,接受手术被定义为计算生存时间的起点。 由于该研究是一项未经随机化的观察研究,要正确估计术中接受放疗提 高患者生存时间的效果,还需考虑对其他因子的效果进行调整。
生存分析(卫管2011).ppt

• 寿命表法 (life-table method )
适用于大样本的分组生存时间资料 –比较生存过程:对数秩检验(log-rank test) –生存时间的影响因素分析:Cox 回归分析 –生存率的预测: Cox 回归模型
21.03.2019 31
六、未分组资料的生存分析
0 . 5 0 5 0 , 0 . 9 9 5 0
21.03.2019
ˆ ˆ S ( t ) 1 . 9 6 S E S ( t ) 0 . 7 5 0 01 . 9 60 . 1 2 5 0 3 3
据表示患者至少活了多少个月)。
化疗组:1,2,3,5,6,9+,11, 13,16,26,37+
放化疗联合组:10,11+,14,18, 22, 22,26 ,32,38,
40+,42+ 欲比较两种治疗措施的疗效应采用何种统计分析方法?
21.03.2019 3
+ • 化疗组:1,2,3,5,6,9 ,11, 13,16, + 26,37 (月) + • 放化疗联合组:10,11 ,14,18, 22, 22, + + 26 ,32,38,40 ,42 (月) 卡方检验: 存活 死亡 化疗组 2 9 联合组 3 8
正偏态(positive skewness)数据 • 两种错误的做法: • 错误1:采用平均生存时间而不是采用中位 生存时间来表示生存时间的平均水平。 • 错误2:采用常规 t 检验或方差分析进行组 间比较。(应采用log-rank检验比较几组 生存时间 )
21.03.2019 17
生存分析的统计描述指标
1、死亡概率、生存概率 2、生存率及其标准误 3、生存曲线 4、半数生存期(中位数) 及四分位
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章生存分析的Stata实现
本章使用的STATA命令:
结局变量为1表示失效事件发生
例14-2 McKelvey et al(1976)收集了3期的某型淋巴瘤患者的生存时间(天)。
分别是6,19,32,42,42,43+,94,126+,169+,207,211+,227+,253,255+,270+,310+,316+,335+,346+。
现用Kaplan-Meier法计算生存率。
Stata命令为:
stset time,failure(d) sts list
sts graph
结果为:
例14-3 下面是来自于Berkson & Gage(1950)的一个研究队列。
为了叙述方便,把原来的出院后的生存时间改称为某恶性肿瘤术后生存时间。
共有374名患者进入研究队列。
表14-3 寿命表法计算生存率的计算用表
(1) (2) (3) (4) (5) (6) (7) (8) (9)
序号术后生存
年数
期初观察
例数
期内
死亡
期内截尾
人数
校正期初
人数
死亡
概率
生存
概率
生存率t n d c n c=n-c/2 q=d/n c p=1-q S(t)
1 0~374 90 0 374 0.2406 0.7594 0.7594
2 1~284 76 0 284 0.2676 0.7324 0.5561
3 2~208 51 0 208 0.2452 0.7548 0.4198
4 3~157 2
5 12 151 0.165
6 0.8344 0.3503
5 4~120 20 5 117.5 0.1702 0.8298 0.2907
6 5~95
7 9 90.5 0.0773 0.9227 0.2682
7 6~79 4 9 74.5 0.0537 0.9463 0.2538
8 7~66 1 3 64.5 0.0155 0.9845 0.2498
9 8~62 3 5 59.5 0.0504 0.9496 0.2372
10 9~54 2 5 51.5 0.0388 0.9612 0.2280
11 10+47 21 26 34 0.6176 0.3824 0.0872 Stata数据格式为:
Stata命令为:
stset time [weight=w],failure(d=1) ltable time d [weight=w],graph
结果为:
例14-4 在例14-3中介绍了McKelvey et al收集了19名3期淋巴瘤病人的生存资料,该研究者还同时收集了4期淋巴瘤病人的生存数据共61例:4,6,10,11,11,11,13,17,20,20,21,22,24,24,29,30,30,31,33,34,35,39,40,41+,43+,45,46,50,56,61+,61+,63,68,82,85,88,89,90,93,104,110,134,137,160+,169,171,173,175,184,201,222,235+,247+,260+,284+,290+,291+,302+,304+,341+,345+。
要比较3期淋巴瘤患者和4期淋巴瘤患者的生存率是否有差异。
Stata命令为:
stset time,failure(d=1) sts test group
sts graph,by(group) 结果:
P=0.0096,3期淋巴瘤患者和4期淋巴瘤患者的生存率有差别。
