1万以内素数表
魅力无穷的梅森素数

魅力无穷的梅森素数——香港科技大学方程2004年5月15日,美国国家海洋和大气局顾问、数学爱好者乔希·芬德利(Josh Findley)用一台装有2.4GH奔腾处理器的个人计算机,找到了目前世界上已知最大Z的梅森素数。
该素数为2的24036583次方减1(即224036583-1),它有7235733位数,如果用普通字号将这个数字连续写下来,它的长度可达3万米!它是2000多年来人类发现的第41个梅森素数,也是目前已知的最大素数。
世界上许多著名的新闻媒体和科学刊物都对这一消息进行了报道和评介,认为这是数学研究和计算技术中最重要的突破之一。
也许会有人感到奇怪:素数不就是在大于1的整数中只能被1和其自身整除的数吗?在数学和计算机科学高度发达的今天,为什么发现一个已知的最大素数竟如此困难?找到一个已知的最大梅森素数竟成了科学上的大事?是的,魅力无穷的梅森素数具有许多特异的性质和现象,千百年来一直吸引着众多的数学家和数学爱好者对它进行研究;虽然已经揭示了一些规律,但围绕着它仍然有许多未解之谜,等待着人们去探索。
梅森素数的由来马林·梅森(Marin Mersenne,1588–1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物。
他与大科学家伽利略、笛卡尔、费马、帕斯卡、罗伯瓦、迈多治等是密友。
虽然梅森致力于宗教,但他却是科学的热心拥护者,在教会中为了保卫科学事业做了很多工作。
他捍卫笛卡儿的哲学思想,反对来自教会的批评;也翻译过伽里略的一些著作,并捍卫了他的理论;他曾建议用单摆来作为时计以测量物体沿斜面滚下所需时间,从而使惠更斯发明了钟摆式时钟。
梅森对科学所作的主要贡献是他起了一个极不平常的思想通道作用。
17世纪时,科学刊物和国际会议等还远远没有出现,甚至连科学研究机构都没有创立,交往广泛、热情诚挚和德高望众的梅森就成了欧洲科学家之间的联系的桥梁。
许多科学家都乐于将成果寄给他,然后再由他转告给更多的人。
总复习因数倍数质数合数

)。
10、9个连续偶数的和是90,这9个连续偶数分别是(
)。
11、7个连续自然数的和为35,这7个自然数分别是(
)。
2021/1/4
27
• 一个房间长40分米,宽32分米要在地面铺上边长最大的正方形瓷砖,共需要多少块这样的瓷砖?
2021/1/4
28
• 一块瓷砖长12厘米,宽10厘米,要铺成一个正方形地面,这个正方形地面的边长至少是多少 厘米?面积是多少?要多少块这样的瓷砖?
2021/1/4
3
因数和倍数
如果整数a能被整数b整除(b≠0)就叫做b的 倍数就叫做a的因数。
因数
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数 是它本身。
因数和倍数是相 互依存的
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有
倍
最大的倍数。
数
2021/1/4
4
能被2、3、5整除的数的特征 能被2整除的数的特征: 能被5整除的数的特征: 能被3整除的数的特征:
4
)三,最小的合数是( 2
),最小的奇数是
1
0
2021/1/4
10
分解质因数 每一个合数都可以写成几个质数相乘的形式,这几个质数叫做这个合数的质因数。
把一个合数用几个质因数相乘的形式表示出来,叫做分解质因数。
分解质因数的方法:短除法
把30分解质因数
2 30 3 15 5
把30分解质因数正确的做法是( )
80
17 10
17×10=170(个)
答:一共可裁出170。
2021/1/4
20
一堆糖果,如果平均分给4个小朋友,还剩3块;如果平均分给5个小朋友,还缺1块;如果平 均分给6个小朋友,还缺1块。这堆糖果最少有多少块?
小升初专题复习1:数的认识-中

(进入美妙的世界啦~) 还记得以前所学过所有的数吗?分别有哪些? 知识 典例(注意咯,下面可是黄金部分!)知识点一、数的分类及其概念整数的含义:像…-3,-1,0,1,2,3,…这样的数统称整数。
正数和负数的含义:像1,+5,6,…这样的数叫做正数;像-3,-2,-9,…这样的数叫做负数。
占位0是最小的自然数,0是偶数,0的作用 表示起点表示界线自然数 1是最小的一位数,是自然数的基本单位;1既不是质数,也不是合数。
数的意义: 是整数的一部分,可表示基数也可以表示序数意义:把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数。
表示其中一份的数就是分数单位分数 真分数——分子比分母小(小于1)分类: 假分数——分子大于或等于分母(大于或等于1)带分数——分子比分母大(大于1)意义:把整体“1平均”分成10份、100份、1000份……这样的一份或几份是十分之几,百分之几,千分之几……可以用小数表示 有限小数按小数部分分小数 无限小数 纯循环小数分类 纯小数 循环小数按整数部分分 混循环小数带小数例1、请你把这些数填入相应的圈里。
36、-9 、0.7、+20.4、-56 、100、-13、-261、+4.8、109、π、3.010101、1.333…… 正数: 负数:自然数: 整数:小数: 分数:导入数的认识变式练习:1、π,3.14,3.1415,3.104四个数按从大到小排列应该是(),其中π是()小数。
2、16÷11的商用循环小数的简写法表示是(),它是()循环小数。
3、三个连续自然数中,第二个数是第一个数的2倍,第三个数是第一个数的3倍,这三个自然数之和为()。
知识点二、数的读写和改写数的读写:1、整数的读法:从高位到低位,一级一级地读,每级末尾的0都不读,其他数位连续有几个0都只读一个0。
2、整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
自然数是否为素数的两个判定方法

设 6n 一1
(6 1一 1) (6j + l ) , 则 61 !j + i一j
设 n 一6 k + ; (可 以有 多种 写 法 ) , 则 6 i
一j 二6k 十r .
!j + i
, {i j 一k , _ ∀ 二 #. _ _ _ _ , __~ , ., _ 令 } * 泣 ,一 ; .则 , ∃+ 万 一 ∀ 一 O,方 程 有 整 数 解
综 上所 述 :二 (3 00) = 2 + 32 + 28 = 62.
n+ i
,
或 6n + 1 = (61 + l ) (6j + 1 ) ∗ , 变 形 得 j
n + 7
上面解题过程是求 武x ) 的一种方法 , 然而对
于一个 比较 大 的数 , 是 否 有简单 实用 (最好 能形 成
6 1+ 1 ∀
注 意到 1 , 8 = 6 , l , 1 ; 9 一2 , 4 . 所 以 , 6n 一 1 型 合 数 的个 数
+ 2 + 1 + (1 一 1)+ l = 18.
,一 昌 是 正 整 数 .
合 数 的充 分性 显 然 成 立. 由此 我 得 到 以下 重 要结论 . 定 理 3 (l )
~ ~ 一~ ~
一 6 1一
1 关1 = 8 , 1 关2 = 1 5 , 1 关3 = 2 2 , 1 补4 = 2 9 , 1 关 5 = 3 6 , 1 关6 = 4 3 ;2 关2 = 2 8 , 2 关3 = 4 1 .
充 分 性 显 然 成 立 . 以下 我 们 证 明 必
【新版】北师大版小学数学1-6年级总复习知识点汇总

2017年北师大版小学1-6年级总复习知识点第一部分:数与代数一、数的认识1、整数2、小数、分数、百分数二、数的运算1、数的意义2、计算与应用3、估算4、运算律三、式与方程四、正、反比例五、常见的量六、探索规律第二部分:图形与几何一、图形的认识二、图形与测量三、图形的运动四、图形与位置第三部分:统计与概率一、统计二、可能性第四部分:解决问题的策略第一部分:数与代数(教材第63 ~88页)一、数的认识(一)整数(教材第63~67页)知识点1:整数1.整数的定义:像-3,-2,-1,0,1,2,3,…这样的数称为整数。
整数的个数是无限的。
在整数中,大于零的数称为正整数,小于零的数称为负整数。
正整数、零与负整数统称为整数。
0既不是正整数,也不是负整数。
2.整数的计数单位和数位。
(1)整数数位顺序表。
(2)数的分级:按照我国的计数习惯,整数从个位起,每四个数位是一级。
个位、十位、百位、千位是个级,表示多少个一;万位、十万位、百万位、千万位是万级,表示多少个万;亿位、十亿位、百亿位、千亿位是亿级,表示多少个亿……(3)计数单位:一(个)、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿……都是整数的计数单位。
(4)数位:在计数时,计数单位按照一定的顺序排列起来,它们所占的位置叫数位。
3.整数的读法:先分级,再读数,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其他数位连续有几个0都只读一个零。
4.整数的写法:从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在哪一个数位上写0。
知识点2:自然数1.自然数的定义:我们在数物体的时候,用来表示物体个数的0,1,2,3,4,5,……叫作自然数。
“0”是最小的自然数,自然数的个数是无限的,没有最大的自然数。
2.自然数的基本单位:任何非“0”的自然数都是由若干个“1”组成的,因此“1”是自然数的基本单位。
3.“0"的含义:一个物体也没有,用“0"表示,但并不是说“0”只表示没有物体,它还有多方面的含义。
《数的认识》总复习精品 课件

•
三、从晨昏到日暮,从清贫到富足,从 少年到 老迈, 从相遇 到余生 ,只想 和你十 指相扣 ,从此 再不分 开。
•
四、你的名字,是我读过最短的情诗。 我很喜 欢你, 像春去 秋来, 海棠花 开。
•
五、秒回的人应该很温柔吧,因为一直 在等喜 欢的人 ,也舍 不得让 喜欢的 人等。
•
六、多想和你有一个长久的未来,陪你 走完这 一生。 让所有 人祝福 我们, 彼此温 暖,互 不辜负 。
•
十二、世上最好的缘,便是有个聊得来 的伴, 永远不 嫌你的 话多, 不厌其 烦且久 处不厌 ,永远 会陪在 身边, 念你冷 暖,且 懂你悲 欢。
•
十三、你相信吗,未来要和你共度一生 的那个 人,其 实在与 你相同 的时间 里,也 忍受着 同样的 独。那 个人一 定也怀 着满心 的期待 ,拥着 一腔孤 勇,穿 过茫茫 人海, 也要来 与你相 见。
•
八、总要允许有人错过你,才能赶上最 好的相 遇。总 有人真 诚地爱 着你, 相爱, 从来都 不是一 个人的 事,先 经营好 自己, 最好的 爱情是 你刚好 成熟我 刚好温 柔。
九、没有人不想和你同坐一辆豪华轿车 ,但你 需要的 ,却是 轿车坏 了还会 和你一 起搭巴 士的人 。环境 影响下 ,公司 面临改 革,需 要裁员 ,高学 历出身 的她赫 然在列 。
• 完成《精讲精练》第8页的6、7、8、9、10、 11
用
四张数字卡片,能摆出多少个不同
的两位数?先摆一摆,再写出来。
什么是偶数? 能被2整除的数叫做偶数
什么是奇数? 不能被2整除的数叫做奇数
什么是素数? 50以内的素数:
只有1 和本身两个因数的数, 最小的素数是2
2、3、5、7、11、13、17、19、23、 29、31、37、41、43、47
1.3.1像素

数码相机性能像素虽然数码相机已经逐渐成为摄影爱好者的首选,但其得到如此迅猛的发展也不过几年的时间,在数码相机刚刚诞生之初,像素对不少人来说都是一个全新的事物。
即使是现在也有不少入门者对此不甚理解。
为了帮助那些刚刚涉足数码摄影领域的新手更好的了解数码相机和掌握数码摄影,这里就来说说数码相机的像素。
像素,译自英文Pixel,图像元素(Picture element)的简称,是单位面积中构成图像的点的个数。
每个像素都有不同的颜色值。
单位面积内的像素越多,分辨率越高,图像的效果就越好。
像素有时被简称为pel (picture element的缩写)。
数码相机的像素分为最大像素数和有效像素数。
最大像素:英文名称为Maximum Pixels,所谓的最大像素是经过插值运算后获得的。
插值运算通过设在数码相机内部的DSP芯片,在需要放大图像时用最临近法插值、线性插值等运算方法,在图像内添加图像放大后所需要增加的像素。
插值运算后获得的图像质量不能够与真正感光成像的图像相比。
在市面上,有一些商家会标明“经硬件插值可达XXX像素”,这也是相同的原理,只不过在图像的质量和感光度上,以最大像素拍摄的图片清晰度比不上以有效像素拍摄的。
最大像素,也直接指CCD/CMOS感光器件的像素,一些商家为了增大销售额,只标榜数码相机的最大像素,在数码相机设置图片分辨率的时候,的确也有拍摄最高像素的分辨率图片,但是,用户要清楚,这是通过数码相机内部运算而得出的值,再打印图片的时候,其画质的减损会十分明显。
有效像素:有效像素数英文名称为Effective Pixels。
与最大像素不同,有效像素数是指真正参与感光成像的像素值。
最高像素的数值是感光器件的真实像素,这个数据通常包含了感光器件的非成像部分,而有效像素是在镜头变焦倍率下所换算出来的值。
以美能达的DiMAGE7为例,其CCD像素为524万(5.24Megapixel),因为CCD有一部分并不参与成像,有效像素只为490万。
数学珍宝梅森素数:迄今人类仅发现47个

数学瑰宝梅森素数:迄今人类仅发现 47个10月13日信息,尽人皆知,素数也叫质数,是只好被和自己整除的数,如2、3、5、7、11等等。
2300年前,古希腊数学家欧几里得就已证明素数有无量多个,并提出一些素数可写成“2p-1”的形式,这里的指数p也是一个素数。
这类特别形式的素数拥有独到的性质和无量的魅力,千百年来向来吸引着众多的数学家(包含数学大师费马、笛卡尔、哥德巴赫、欧拉、高斯、哈代等)和无数的业余数学喜好者对它进行研究。
而17世纪法国数学家、法兰西科学院奠定人马林·梅森是此中成就较为卓著的一位,因今后代将“2p-1”型的素数称为“梅森素数”。
迄今为止,人类仅发现47个梅森素数。
因为这类素数珍异而迷人,它被人们称为“数学瑰宝”。
梅森素数向来是数论研究的一项重要内容,也是此刻科学研究的热门和难点之一。
貌似简单研究极难梅森素数貌似简单,但研究难度却极大。
它不单需要高妙的理论和熟练的技巧,并且还需要进行艰巨的计算。
1772年,有“数学英豪”美誉的瑞士数学大师欧拉在双目失明的状况下,靠默算证了然231-1(即2147483647)是第8个梅森素数。
这个拥有10位的素数,可谓当时世界上已知的第1 页最大素数。
欧拉的坚强毅力与解题技巧令人赞美不已;法国大数学家拉普拉斯说的话,或许能够代表我们的心声:“读读欧拉,他是我们每个人的老师。
”在“手算笔录”的年月,人们千辛万苦,仅找到12个梅森素数。
而计算机的产生加快了梅森素数研究进度。
1952年,美国数学家拉婓尔·鲁滨逊等人使用SWAC型计算机在短短的几个月内,就找到了5个梅森素数:2521-1、2607-1、21279-1、22203-1和22281-1。
研究梅森素数不单极富挑战性,并且对研究者来说有一种巨大的骄傲感。
1963年6月2日夜晚8点,当第23个梅森素数211213-1经过大型计算机被找到时,美国广播企业(ABC)中止了正常的节目播放,在第一时间公布了这一重要信息。
小学数学知识点总结大全(非常全面)

小学数学知识点大全第一章数和数的运算一、概念(一)整数1、整数的意义自然数和 0 都是整数。
2、自然数我们在数物体的时候,用来表示物体个数的1, 2, 3⋯⋯叫做自然数。
一个物体也没有,用0 表示。
0 也是自然数。
3、计数单位一(个)、十、百、千、万、十万、百万、千万、亿⋯⋯都是计数单位。
其中“一”是计数的基本单位。
10 个 1 是 10,10 个 10 是 100⋯⋯每相邻两个计数单位之间的进率都是 10。
这样的计数法叫做十进制计数法。
4、数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5、整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。
每一级末尾的 0 都不读出来,其它数位连续有几个 0 都只读一个零。
6、整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
7、一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
⑴准确数:在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
例如把 1254300000 改写成以万做单位的数是 125430 万;改写成以亿做单位的数 12.543 亿。
⑵ 近似数:根据实际需要,我们还可以把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。
例如: 1302490015 省略亿后面的尾数是 13 亿。
⑶四舍五入法:求近似数,看尾数最高位上的数是几,比 5 小就舍去,是 5 或大于 5 舍去尾数向前一位进 1。
这种求近似数的方法就叫做四舍五入法。
8、整数大小的比较:位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
以此类推。
(二)小数1、小数的意义把整数 1 平均分成 10 份、 100 份、 1000 份⋯⋯得到的十分之几、百分之几、千分之几⋯⋯可以用小数表示。
北师大版六年级数学下册《数与代数》第40-67页[2]-2
![北师大版六年级数学下册《数与代数》第40-67页[2]-2](https://img.taocdn.com/s3/m/de19f36e3b3567ec102d8a80.png)
晴
今天是2007年2月29日,早上从睡梦 中醒来已经七点钟了,我立刻从床上爬起 来,马上穿衣、洗脸、刷牙,不知不觉中 已 经 过 了 2 0 小 时 。 该 吃 饭 了 , 我 端 起 一 杯牛奶一饮而尽,又吃了200千克面包, 一个煎鸡蛋。吃过早餐,我从抽屉里拿了 9 角 钱 冲 出 了 家 门 , 因 为 今 天 是 爸 爸 生 日,要买生日礼物呢!
或≈21(亿)(五入)
北师大版
六年级
数学下册
第45-47页
的内容
北流市新圩中心小学
1、剪一张长方形纸条,以它的长度为单位测量周围物体的长度。
可以用小数或分数表示
1、分数、小数的产生。
用一个单位的长度进行度量时,出现 量不尽的情形,这样可以将1个单位再平均 分成几份,由此产生了分数。如果平均分 成10份,就产生了小数。
从上面的资料中你了解 到什么?你能解释一下这些 数据的具体意义吗?你有哪 些体会和感想?
大家谈
北师大版六年级数学下册
知识梳理——货币、时间、质量单位及换算
货币单位:1元=10角 1角=10分 质量单位:1吨=1000千克 1千克=1000克 时间单位:1小时=60分=3600秒 1分=60秒
1年=12个月 1日=24时
自然数
数
负整数
分数(小数) (百分数)(比)
1.整数包括(正整数)、( 负整数)、和( 零 )
2.自然数的个数是无限的,没有最大的自然数。 最小的自然数是( 1 )
(2).我们可以用下图中的点表示所学的数。
-1 21
3 13 3
4
5
(2 ) 5
4.5
-2 -1
六年级下册数学素材 整数的认识知识点总结 苏教版
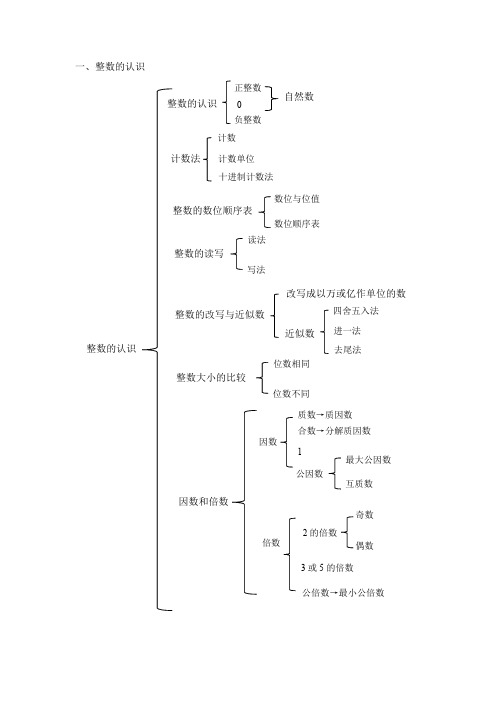
一、整数的认识整数的认识整数的认识正整数计数法自然数整数的数位顺序表整数的读写改写成以万或亿作单位的数整数的改写与近似数近似数负整数计数计数单位十进制计数法数位与位值数位顺序表读法写法四舍五入法进一法去尾法整数大小的比较位数相同位数不同因数和倍数因数质数→质因数合数→分解质因数1公因数最大公因数互质数倍数2的倍数奇数偶数3或5的倍数公倍数→最小公倍数一、自然数(非负整数)1.自然数的定义自然数是表示物体的个数,0、1、2、3、4,…都是自然数。
2.自然数“0”的含义0表示一个物体也没有,是最小的自然数,没有最大的自然数,所以自然数的个数是无限的。
0是除它本身之外任意自然数的倍数,即0能被除它本身之外的任何一个自然数整除。
“0”不仅可以表示没有,还可以表示特定的数值。
如:今天的温度是0摄氏度,不能说今天没有温度。
在引入负数的概念后,0还是正数与负数的分界线。
正数都比0大,负数都比0小。
3.自然数“1”的含义自然数的基本单位是“1”,任何非0的自然数都可以看成是由若干个“1”组成的,如0加上一个单位就是1,1加上一个单位就是2,再加上一个单位就是3等。
二、整数1.整数的定义正整数、零、负整数统称为整数。
2.正整数:正整数是除0以外的自然数。
如:1,5,6,12,95,154,9555,…都是正整数。
3.负整数:负整数就是在除0以外的自然数的前面加上负号所得到的数。
如:-15,-45,-100,-9555,-165156…都是负整数。
三、计数法1.计数:计数就是数数。
如:桌子上有一些糖果,一个一个地数,两个两个地数,十个十个地数都是计数。
2.计数单位:个、十、百、千、万、十万、百万、…都是计数单位。
3.十进制:每相邻两个计数单位之间的进率是10,是目前应用较多的一种记数方法。
十进制遵循“满十进一”的原则,如10个一等于1个十,10个十等于1个百,10个百等于1个千等。
除了十进制以外,其他的还有二进制(逢二进一),十六进制(逢十六进一)等。
小学数学顺口溜

一、年月日一三五七八十腊(12月),三十一天永不差;四六九冬(11月)三十日;平年二月二十八,闰年二月把一加。
二、100以内的质数口诀2、3、5、7和11,13后面是17,19、23、29,(十九、二三、二十九)31、37、41,(三一、三七、四十一) 43、47、53,(四三、四七、五十三)59、61、67,(五九、六一、六十七) 71、73、79,(七一、七三、七十九)83、89、97。
(八三、八九、九十七)三、多位数读法歌读数要从高位起,哪位是几就读几,每级末尾若有零,不必读出记心里,其他数位连续零,只读一个就可以,万级末尾加读万,亿级末尾加读亿。
四、多位数写法歌写数要从高位起,哪位是几就写几,哪一位上没单位,用0占位要牢记。
五、多位数大小比较歌位数不同比大小,位数多的大,位数少的小,位数相同比在小,高位比起就知道.六、运算顺序歌打竹板,响连天,各位同学听我言,今天不把别的表,单把四则运算聊一聊,混合试题要计算,明确顺序是关键。
同级运算最好办,从左到右依次算,两级运算都出现,先算乘除后加减。
遇到括号怎么办,小括号里算在先,中括号里后边算,次序千万不能乱,每算一步都检查,又对又快喜心间七、“除”的意义看到“除”,圈一圈,“除”字前面是除数,“除”字后面被除数,位置交换别忘了八、商中间或末尾有0的除法我是0,本事大,除法运算显神通。
不够商1我来补,有了空位我就坐。
别人要想把我除,常胜将军总是我.九、认识钟表跑的最快是秒针,个儿高高,身材好;跑的最慢是时针,个儿短短,身材胖.不高不矮是分针,匀速跑步作用大十、量角中心对顶点0线对一边,一边读刻度内外要分辨十一、计量单位间的换算大化小,用乘好。
小化大,除不差.十二、大月、小月的记忆:七前单月大,八后双月大.十三、我是1厘米1厘米,很淘气,仔细找,才见你。
指甲盖1厘米,伸出手指比一比。
长短和我差不多,大约就是一厘米. 100个我是1米,我是米的小兄弟, 物体长了别用我,要不一定累死你.十四、大于号、小于号的用法大于号、小于号。
数与数的运算

数和数的运算一、概念(一)整数1.整数的意义自然数和0都是整数。
2.自然数我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3.计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4.数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5.数的整除整数a除以整数b(b≠0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b 能整除a。
如果数a能被数b(b≠0)整除,a就叫做b的倍数,b就叫做a的因数(或a的因数)。
倍数和因数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的因数。
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
例如:10的因数有1、2、5、10,其中最小的因数是1,最大的因数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12……其中最小的倍数是3,没有最大的倍数。
个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
能被2整除的数叫做偶数。
不能被2整除的数叫做奇数。
0也是偶数。
自然数按能否被2整除的特征可分为奇数和偶数。
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数),100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数,例如4、6、8、9、12都是合数。
1不是质数也不是合数,自然数除了1外,不是质数就是合数。
素数

素数素数就是质数。
它除了能表示为它自己和1的乘积以外,不能表示为任何其它两个整数的乘积。
例如,15=3*5,所以15不是素数;又如,12=6*2=4*3,所以12也不是素数。
另一方面,13除了等于13*1以外,不能表示为其它任何两个整数的乘积,所以13是一个素数。
有的数,如果单凭印象去捉摸,是无法确定它到底是不是素数的。
有些数则可以马上说出它不是素数。
一个数,不管它有多大,只要它的个位数是2、4、5、6、8或0,就不可能是素数。
此外,一个数的各位数字之和要是可以被3整除的话,它也不可能是素数。
但如果它的个位数是1、3、7或9,而且它的各位数字之和不能被3整除,那么,它就可能是素数(但也可能不是素数)。
没有任何现成的公式可以告诉你一个数到底是不是素数。
你只能试试看能不能将这个数表示为两个比它小的数的乘积。
找素数的一种方法是从2开始用“是则留下,不是则去掉”的方法把所有的数列出来(一直列到你不想再往下列为止,比方说,一直列到10,000)。
第一个数是2,它是一个素数,所以应当把它留下来,然后继续往下数,每隔一个数删去一个数,这样就能把所有能被2整除、因而不是素数的数都去掉。
在留下的最小的数当中,排在2后面的是3,这是第二个素数,因此应该把它留下,然后从它开始往后数,每隔两个数删去一个,这样就能把所有能被3整除的数全都去掉。
下一个未去掉的数是5,然后往后每隔4个数删去一个,以除去所有能被5整除的数。
再下一个数是7,往后每隔6个数删去一个;再下一个数是11,往后每隔10个数删一个;再下一个是13,往后每隔12个数删一个。
……就这样依法做下去。
你也许会认为,照这样删下去,随着删去的数越来越多,最后将会出现这样的情况;某一个数后面的数会统统被删去崮此在某一个最大的素数后面,再也不会有素数了。
但是实际上,这样的情况是不会出现的。
不管你取的数是多大,百万也好,万万也好,总还会有没有被删去的、比它大的素数。
事实上,早在公元前300年,希腊数学家欧几里得就已证明过,不论你取的数是多大,肯定还会有比它大的素数,假设你取出前6个素数,并把它们乘在一起:2*3*5*7*11*13=30030,然后再加上1,得30031。
小学数学知识点及易错题型总结

小学数学重点模块知识点汇总整数1、自然数:正整数和0。
最小的自然数是0,没最大自然数。
自然数和0都是整数。
2、计数单位:个、十、百、千、万、十万、百万、千万、亿等等。
3、每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4、数位:计数单位按照一定的顺序排列起来,它们所占的位置。
5、整除:整数a除以整数b(b≠0) , 商是整数而没余数,就说a能被b整除,或者说b 能整除a。
a就做b的倍数, b就做a的约数(或a的因数)。
倍数和约数是相互依存的。
(1)个位上是0、2、4、6、8的数,都能被2整除;个位上是0或5的数,都能被5整除;一个数的各位上的数的和能被3整除,都能被3整除;一个数的末两位数能被4 (或25)整除,这个数就能被4 (或25)整除;一个数的末三位数能被8 (或125)整除,这个数就能被8 (或125)整除。
(2)能被2整除的数叫做偶数。
不能被2整除的数叫做奇数。
0也是偶数。
6、约数倍数:一个数的倍数的个数是无限的,其中最小的倍数是它本身。
一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
7、质数合数:(1)一个数如果只有1和它本身两个约数,这样的数叫做质数(或素数),最小的质数时2,100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
(2)一个数如果除了1和它本身还有别的约数,这样的数叫做合数。
最小的合数4.(3)1不是质数也不是合数,自然数除了1外,不是质数就是合数。
如果把自然数按其约数的个数的不同分类,可分为质数、合数和1。
8、质因数:每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数,例如15=3×5, 3和5叫做15的质因数。
(1)把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
自然数学之素数公式

自然数学之素数公式一.素数的判别:素数也称为质数,它是只能被1和自身整除的自然数。
所以人们在判断一个数是不是素数素数就需要将这个数逐一除以这个数开平方内的所有素数。
即我们常用的筛法。
但这方法有一缺点,需要相当多的素数储备。
当一个数相当大,我们储备的素数不够多时,我们就无法判别。
那么有没有其他方法能判别和获得素数呢?有!就是要在此发表的素数公式。
这个公式不是凭空想象出来的,是根据自然数学的基础理论和定律获得。
二.自然数学的简单介绍:物体,时间,数量是自然数学的三个要素。
它们的的定义是:1,物体:具有质量为物,占有空间为体,统称为物体。
2,时间:物体的变化过程为时间。
3,数量:在物体不变的情况下,对指定范围内的同一概念物体的计量。
这样自然数学和应用数学的数字在数轴的表现方式就会产生了明显的不同。
现在的应用数学的数值在数轴的表现方式是这样的:每个数都是数轴上的一个点。
自然数学的数值在数轴的表现方式这样的:每个数都是数轴上的一个线段。
从上可以看到0和负数在自然数学中都是自然数。
为什么将0和负数归入自然数和自然数的基础理论等以后有机会再作详细介绍。
三,素数公式:这个公式非常简单,如果用自然数学表达,可能会让人产生误会。
用应用数学有两个表达方式。
它们的计算方法是一样的。
同余式:函数式:获得素数公式的原理和定律等讲解自然数学基础理论时再公布。
四:为什么命名为素数公式:将以上公式作为组合公式:把2,3,4,……n/2分别代人a,如果公式全部成立,那么n必定是素数。
否则必定是合数。
将以上公式单独应用:1:a为2,3,4,……n/2中的任意一个数,n代人素数等式必然成立。
2:等式不成立,代人n的数必定不是素数。
3:有极少量的合数也能使得公式成立,但比例很小。
且当数字越大,能使公式成立的合数越少,准确率越高。
五:公式的计算和与筛法的对照:我们知道a的n次方是一个相当大的数,但公式的余数必定小于n。
我们可以用因式分解方法解决。
梅森素数

梅森数(Mersenne number)是指形如2^p-1的正整数,其中指数p是素数,常记为Mp 。
若Mp是素数,则称为梅森素数(Mersenne prime)。
p=2,3,5,7时,Mp都是素数,但M11=2047=23×89不是素数。
已发现的最大梅森素数是p=43,112,609的情形,此时 Mp 是一个12,978,189位数。
如果用普通字号将这个巨数连续写下来,其长度可超过50公里!是否有无穷多个梅森素数是数论中未解决的难题之一。
概念也许会有人感到奇怪:素数不就是在大于1的整数中只能被1和其自身整除的数吗?古希腊数学大师欧几里得早就证明了素数有无穷多个,既然有无穷个,那么就应该有一个素数数列的公式,为了寻找这个公式,人们耗尽了巨大的心血(参见百度百科“素数分布”)。
在数学和计算机科学高度发达的今天,为什么发现一个已知的最大素数竟如此困难?找到一个已知的最大梅森素数竟成了科学上的大事?是的,魅力无穷的梅森素数具有许多特异的性质和现象,千百年来一直吸引着众多的数学家和数学爱好者对它进行研究;虽然已经揭示了一些规律,但围绕着它仍然有许多未解之谜,等待着人们去探索。
由来马林·梅森(Marin Mersenne,1588–1648)是17世纪法国著名的数学家和修道士,也是当时欧洲科学界一位独特的中心人物。
他与大科学家伽利略、笛卡尔、费马、帕斯卡、罗伯瓦、迈多治等是密友。
虽然梅森致力于宗教,但他却是科学的热心拥护者,在教会中为了保卫科学事业做了很多工作。
他捍卫笛卡儿的哲学思想,反对来自教会的批评;也翻译过伽里略的一些著作,并捍卫了他的理论;他曾建议用单摆来作为时计以测量物体沿斜面滚下所需时间,从而使惠更斯发明了钟摆式时钟。
梅森对科学所作的主要贡献是他起了一个极不平常的思想通道作用。
17世纪时,科学刊物和国际会议等还远远没有出现,甚至连科学研究机构都没有创立,交往广泛、热情诚挚和德高望众的梅森就成了欧洲科学家之间的联系的桥梁。
自然数学之素数公式

自然数学之素数公式一.素数的判别:素数也称为质数,它是只能被1和自身整除的自然数。
所以人们在判断一个数是不是素数素数就需要将这个数逐一除以这个数开平方内的所有素数。
即我们常用的筛法。
但这方法有一缺点,需要相当多的素数储备。
当一个数相当大,我们储备的素数不够多时,我们就无法判别。
那么有没有其他方法能判别和获得素数呢?有!就是要在此发表的素数公式。
这个公式不是凭空想象出来的,是根据自然数学的基础理论和定律获得。
二.自然数学的简单介绍:物体,时间,数量是自然数学的三个要素。
它们的的定义是:1,物体:具有质量为物,占有空间为体,统称为物体。
2,时间:物体的变化过程为时间。
3,数量:在物体不变的情况下,对指定范围内的同一概念物体的计量。
这样自然数学和应用数学的数字在数轴的表现方式就会产生了明显的不同。
现在的应用数学的数值在数轴的表现方式是这样的:每个数都是数轴上的一个点。
自然数学的数值在数轴的表现方式这样的:每个数都是数轴上的一个线段。
从上可以看到0和负数在自然数学中都是自然数。
为什么将0和负数归入自然数和自然数的基础理论等以后有机会再作详细介绍。
三,素数公式:这个公式非常简单,如果用自然数学表达,可能会让人产生误会。
用应用数学有两个表达方式。
它们的计算方法是一样的。
同余式:函数式:获得素数公式的原理和定律等讲解自然数学基础理论时再公布。
四:为什么命名为素数公式:将以上公式作为组合公式:把2,3,4,……n/2分别代人a,如果公式全部成立,那么n必定是素数。
否则必定是合数。
将以上公式单独应用:1:a为2,3,4,……n/2中的任意一个数,n代人素数等式必然成立。
2:等式不成立,代人n的数必定不是素数。
3:有极少量的合数也能使得公式成立,但比例很小。
且当数字越大,能使公式成立的合数越少,准确率越高。
五:公式的计算和与筛法的对照:我们知道a的n次方是一个相当大的数,但公式的余数必定小于n。
我们可以用因式分解方法解决。
