东华大学信号与系统作业答案
信号与系统习题部分参考答案

信号与系统第三章习题部分参考答案3-2 已知连续时间周期信号()⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=35sin 432cos 2t t t f ππ。
将其表示成复指数傅立叶级数形式,求n F ,并画出双边幅度谱和相位谱。
解:由于()t f 为连续的时间周期信号。
由于题易知T=61ω=3π又()⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=35sin 432cos 2t t t f ππ即有2=a 12=a 45=b 200==a F ()2121222=−=jb a F ()221555j jb a F −=−=431F F F ==故()53322212t j tj jee tf ππ−+=又nn F F −=其双边幅度谱如图 3-2-1所示易知43210ϕϕϕϕϕ====25πϕ−=25πϕ=−其相位谱如图 3-2-2所示15w −12w −012w 15w wnF 0F 2 15−F 2−F 2F 5F 图 3-2-115w −015w wnϕ2π2π−图3-2-2 相位谱3-4 如题图3-4所示信号,求指数形式和三角形式的傅里叶级数。
所示信号,求指数形式和三角形式的傅里叶级数。
()t f 1EE −T2/T 题图3-4t()t f 21T t()t f 31TT−00T−T 24T 4T −t()t f 61TT−04T 4T −2T 2T −()t f 5()t f 4A TT2T−A TT−4T 4T−00()a ()b ()c()d()e ()f ttt解:(a ) 由于)(1t f 为奇函数故有为奇函数故有 00=a })sin()sin([2202∫∫+=−TT n dt nwt dt nwt T E b=]1)[cos(2−ππn n E0 n=2k N k ∈πn E4− n=2k+1 N k ∈∴ ]))12sin((121)5sin(51)3sin(31)[sin(4)(1⋅⋅⋅++++⋅⋅⋅⋅+++−=wt k k wt wt wt E t f π=)sin(]1)[cos(121nwt n nEn −−∑∞=ππ]1)[cos()(21−−=−=ππn n E j jb a F n n njnwt jnwt n e n n E j e F t f }1)[cos(1)(1−−==∑∑+∞∞−+∞∞−ππ3-8:设()()ωF t f ↔,试用()ωF 表示下列各信号的频谱。
信号与系统练习及答案

信号与系统练习及答案一、单项选择题1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( ) A .tu(t) B .(t-1)u(t-1) C .tu(t-1) D .2(t-1)u(t-1) 2.积分式⎰-δ+δ++4422)]dt-(t 2(t))[23(t t的积分结果是( )A .14B .24C .26D .283.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )4.周期矩形脉冲的谱线间隔与( ) A .脉冲幅度有关 B .脉冲宽度有关 C .脉冲周期有关D .周期和脉冲宽度有关5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( )A .不变B .变窄C .变宽D .与脉冲宽度无关6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号()A .一定相同B .一定不同C .只能为零D .可以不同7.f(t)=)(t u e t的拉氏变换为F (s )=11-s ,且收敛域为( )A .Re[s]>0B .Re[s]<0C .Re[s]>1D .Re[s]<18.函数⎰-∞-δ=2t dx)x ()t (f 的单边拉氏变换F (s )等于( )A .1B .s1 C .e -2sD .s1e -2s9.单边拉氏变换F (s )=22++-s e)s (的原函数f(t)等于( )A .e -2t u(t-1)B .e -2(t-1)u(t-1)C .e -2t u(t-2)D .e -2(t-2)u(t-2)答案: BCCCBDCDA二.填空题1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
3.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示,试作出信号x(t)的波形图,并加以标注。
题图1-51- 6 试画出下列信号的波形图:1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图:⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角,并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下,试写出各自系统的输入输出方程。
(完整版)信号与系统练习及答案

信号与系统练习及答案一、单项选择题1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( )A .tu(t)B .(t-1)u(t-1)C .tu(t-1)D .2(t-1)u(t-1)2.积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是( ) A .14 B .24 C .26 D .283.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )4.周期矩形脉冲的谱线间隔与( )A .脉冲幅度有关B .脉冲宽度有关C .脉冲周期有关D .周期和脉冲宽度有关 5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( ) A .不变 B .变窄 C .变宽D .与脉冲宽度无关 6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号()A .一定相同 B .一定不同 C .只能为零 D .可以不同7.f(t)=)(t u e t 的拉氏变换为F (s )=11-s ,且收敛域为( ) A .Re[s]>0B .Re[s]<0C .Re[s]>1D .Re[s]<1 8.函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F (s )等于( ) A .1 B .s 1 C .e -2s D .s1e -2s 9.单边拉氏变换F (s )=22++-s e )s (的原函数f(t)等于( ) A .e -2t u(t-1) B .e -2(t-1)u(t-1) C .e -2t u(t-2)D .e -2(t-2)u(t-2)答案: BCCCBDCDA二.填空题1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
3.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。
信号与系统课后习题与解答第三章
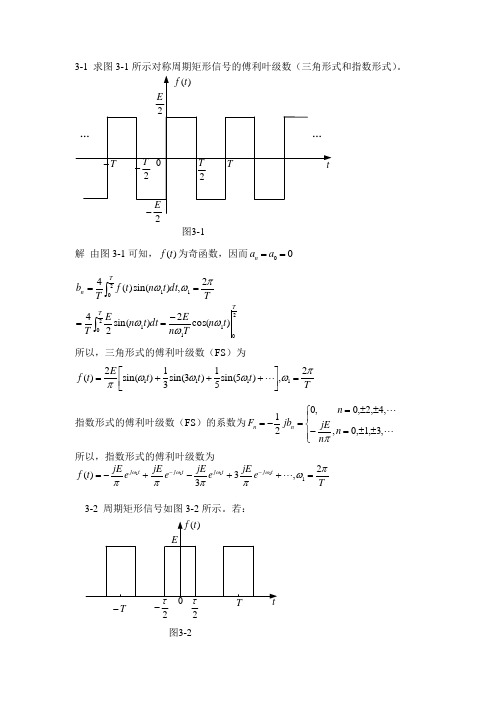
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统课后答案(全)
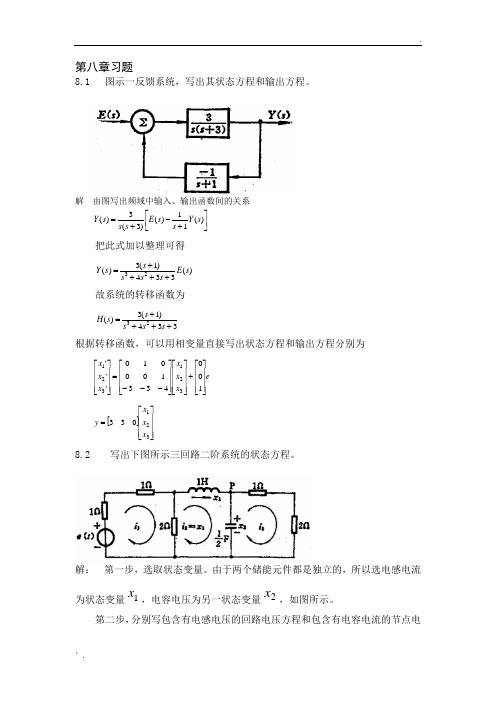
第八章习题8.1 图示一反馈系统,写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数,可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解:第一步,选取状态变量。
由于两个储能元件都是独立的,所以选电感电流为状态变量1x,电容电压为另一状态变量2x,如图所示。
第二步,分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程,并代入元件参数,则有112122'ixxx+--=312'21ixx-=第三步,上两式中1i和3i不是状态变量,要把它们表为状态变量。
由第一个回路有1124xie-=,即112141xei+=由第三个回路有323ix=,即2331xi=把1i和3i分别代入第二步中两式,并经整理,最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路,这里的激励函数)(t e是一压控电流源,输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解:第一步,选状态变量。
因为电感电流和电容电压等三个变量都是独立的,所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步,分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步,消去非状态变量。
信号与系统课后答案第八章作业答案后半部分

频率响应为
H
(e jΩ
)
=
H
(z)
|z = e jΩ
=
4 ⎡⎣ejΩ −1⎤⎦
3
⎡⎢⎣e
jΩ
−
1 3
⎤ ⎥⎦
经计算得极点为 p = 1 ,零点为 z = 1。 3
H(e jΩ)
(Ω)
幅频响应图(横坐标进行了归一化处理)
(c)Yx (z) =
y(−1) + 2 y(−2) + 2 y(−1)z−1 1− z−1 − 2z−2
=
8⋅ z +1⋅ 3 z−2 3
z, z +1
z
>2
其逆
z
变换即零输入响应为
yx
(n)
=
8 3
⋅
2n
u(n)
+
1 3
⋅
(−1)n
u(n)
(d)根据上面计算的零输入和零状态响应可知系统的完全响应为
f (n) = (−1)n u(n) , y(−1) = 0 , y(−2) = 1;
解:(1)将原式两边取单边 Z 变换得,
Y (z) −[z−1Y (z) + y(−1)] − 2[z−2Y (z) + y(−2) + y(−1)z−1] = F (z) + z−1F (z)
整理得:
Y (z)
=
题图 8-23
根据系统框图可得 h(n) = h1(n) ∗[h2 (n) + h3 (n)] ,故 h(n) = δ (n) ∗[h2 (n) + h3(n)] = u(n) + u(n − 2)
东华大学信号与线性系统课程设计答案

东华⼤学信号与线性系统课程设计答案答案东华⼤学信号与线性系统课程设计班级:学号:姓名:东华⼤学信息学院⽬录实验⼀连续信号的时域分析 (3)实验⼆连续时间系统的时域分析 (8)实验三连续信号的频域分析 (14)实验四连续系统的频域分析 (22)实验五信号采样与重建 (33)实验六离散时间信号和系统分析 (39)实验总结 (46)实验⼀连续信号的时域分析⼀、实验⽬的1、熟悉MATLAB 软件。
2、掌握常⽤连续信号与离散信号的MATLAB 表⽰⽅法。
⼆、实验设备安装有matlab6.5 以上版本的PC 机⼀台。
三、实验原理四、实验内容1、⽤MATLAB表⽰连续信号:tAe ,Acos(ω0 t +?),Asin(ω0 t +?)。
源程序:clcclearclosesyms t;f1=2*exp(t);f2=2*cos(3*t+4);f3=2*sin(3*t+4);subplot(2,2,1);ezplot(f1,[-10,2]);title('f(t)=2e^t');grid on;subplot(2,2,2);ezplot(f2,[-5,5]);xlabel('t');title('f(t)=2cos(3t+4)');grid on;subplot(2,2,3);ezplot(f3,[-5,5]);xlabel('t');title('f(t)=2sin(3t+4)');grid on2、⽤MATLAB表⽰抽样信号(sinc(t))、矩形脉冲信号(rectpuls(t, width)) 及三⾓脉冲信号(tripuls(t, width, skew))。
源程序:clcclearcloset=-5:0.01:5;f1=sinc(t);f2=3*rectpuls(t,4);f3=3*tripuls(t,4,0);subplot(2,2,1);plot(t,f1);xlabel('t');title('f(t)=sinc(t)');grid on;subplot(2,2,2)plot(t,f2);xlabel('t');title('f(t)=3rectpuls(t,4)');grid on;axis([-5,5,-1,4]);subplot(2,2,3);xlabel('t');title('f(t)=3rectpuls(t,4,0)');grid on;axis([-5,5,-1,4]);3、编写如图3 的函数并⽤MATLAB 绘出满⾜下⾯要求的图形。
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集? 解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
信号与系统第5章习题答案

第5章连续时间信号的抽样与量化5.1试证明时域抽样定理。
证明:设抽样脉冲序列是一个周期性冲激序列,它可以表示为T(t)(tnT)sn由频域卷积定理得到抽样信号的频谱为:1F s ()F()T 2()1 T snFns式中F()为原信号f(t)的频谱,T ()为单位冲激序列T (t)的频谱。
可知抽样后信 号的频谱()F 由F()以s 为周期进行周期延拓后再与1T s 相乘而得到,这意味着如果 s s2,抽样后的信号f s (t)就包含了信号f(t)的全部信息。
如果s2m ,即抽样m 间隔 1 Tsf2m,则抽样后信号的频谱在相邻的周期内发生混叠,此时不可能无失真地重建 原信号。
因此必须要求满足1 Tsf2 m,f(t)才能由f s (t)完全恢复,这就证明了抽样定理。
5.2确定下列信号的最低抽样频率和奈奎斯特间隔:2t (1)Sa(50t)(2)Sa(100)2t (3)Sa(50t)Sa(100t)(4)(100)(60)SatSa解:抽样的最大间隔 T s 12f 称为奈奎斯特间隔,最低抽样速率f s 2f m 称为奈奎m斯特速率,最低采样频率s 2称为奈奎斯特频率。
m(1)Sa(t[u(50)u(50)],由此知m50rad/s ,则50)5025 f , m由抽样定理得:最低抽样频率50 f s 2f m ,奈奎斯特间隔1 T 。
sf50s2t(2))Sa(100)(1100200脉宽为400,由此可得radsm200/,则100f,由抽样定理得最低抽样频率m200f s2f m,奈奎斯特间隔1T。
sf200s(3)Sa[(50)(50)],该信号频谱的m50rad/s(50t)uu50Sa(100t)[u(100)u(100)],该信号频谱的m100rad/s10050Sa(50t)Sa(100t)信号频谱的m100rad/s,则f,由抽样定理得最低m抽样频率100f s2f m,奈奎斯特间隔1T。
大学信号与系统习题答案

⼤学信号与系统习题答案§ 1.1 信号与系统信号(signal)消息(Message):在通信系统中,⼀般将语⾔、⽂字、图像或数据统称为消息。
信号(Signal):指消息的表现形式与传送载体。
信息(Information):⼀般指消息中赋予⼈们的新知识、新概念,定义⽅法复杂,将在后续课程中研究。
信号是消息的表现形式与传送载体,消息是信号的传送内容。
如电信号传送声⾳、图像、⽂字等。
电信号是应⽤最⼴泛的物理量,如电压、电流、电荷、磁通等。
系统(system)系统(system):由若⼲相互作⽤和相互依赖的事物组合⽽成的,具有稳定功能的整体。
如太阳系、通信系统【-----为传送消息⽽装设的全套技术设备(包括传输信道),其⽅框如下图所⽰:消息信号】、控制系统、经济系统、⽣态系统等。
系统可以看作是变换器、处理器。
电系统具有特殊的重要地位,某个电路的输⼊、输出是完成某种功能,如微分、积分、放⼤,也可以称系统。
在电⼦技术领域中,“系统”、“电路”、“⽹络”三个名词在⼀般情况下可以通⽤。
信号理论与系统理论信号理论信号分析:研究信号的基本性能,如信号的描述、性质等。
信号传输:通信的⽬的是为了实现消息的传输。
原始的光通信系统——古代利⽤烽⽕传送边疆警报;声⾳信号的传输——击⿎鸣⾦。
利⽤电信号传送消息。
1837年,莫尔斯(F.B.Morse)发明电报;1876年,贝尔(A.G.Bell)发明电话利⽤电磁波传送⽆线电信号。
1901年,马可尼(G.Marconi)成功地实现了横渡⼤西洋的⽆线电通信;全球定位系统GPS(Global Positioning System);个⼈通信具有美好的发展前景光纤通信带来了更加宽⼴的带宽。
信号的传输离不开信号的交换。
信号处理:对信号进⾏某种加⼯或变换。
其⽬的是:消除信号中的多余内容;滤除混杂的噪声和⼲扰;将信号变换成容易分析与识别的形式,便于估计和选择它的特征参量。
信号处理的应⽤已遍及许多科学技术领域。
(完整版)信号与系统专题练习题及答案

(完整版)信号与系统专题练习题及答案信号与系统专题练习题一、选择题1.设当t<3时,x(t)=0,则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1B t=1和t=2C t>-1D t>-22.设当t<3时,x(t)=0,则使)2()1(t x t x -?-=0的t 值为 D 。
A t>2或t>-1B t=1和t=2C t>-1D t>-23.设当t<3时,x(t)=0,则使x(t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34.信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/25.下列各表达式中正确的是B A. )()2(t t δδ= B.)(21)2(t t δδ= C. )(2)2(t t δδ= D. )2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B 。
A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统7. 已知系统的激励e(t)与响应r(t)的关系为:)()(2t e t r = 则该系统为 C 。
A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统 8. ?∞-=td ττττδ2sin )( A 。
A 2u(t) B )(4t δ C 4 D 4u(t)10.dt t t )2(2cos 33+??-δπ等于 B 。
A 0 B -1 C 2 D -211.线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置;B 激励信号的形式;C 系统起始状态;D 以上均不对。
12.若系统的起始状态为0,在x (t)的激励下,所得的响应为 D 。
A 强迫响应;B 稳态响应;C 暂态响应;D 零状态响应。
《信号与系统》第一二章自测题及参考答案

第一、二章自测题1、判断题(1)若x (t )是一连续时间周期信号,则y (t )=x (2t )也是周期信号。
(2)两个周期信号之和一定是周期信号。
(3)所有非周期信号都是能量信号。
(4)两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
(5)若)()()(t h t x t y *=,则)1()2()1(+*-=-t h t x t y 。
(6)一个系统的自由响应就等于它的零输入响应。
(7)一个系统的零状态响应就等于它的自由响应。
(8)零状态响应是指系统没有激励时的响应。
(9)系统的单位冲激响应是指系统在冲激信号作用下的全响应。
(10)两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号? (1)3cos(15)0()0t t f t t π≥⎧=⎨<⎩ (2)50()0te tf t t -⎧≥=⎨<⎩ (3)()6sin23cos3f t t t =+(4)|2|()20sin2t f t e t -=3、填空题 (1)已知)()4()(2t t t f ε+=,则)(''t f =__________________。
(2)=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
(3)=-⎰∞∞-dt t )(92δ_________________________ 。
(4)=-⎰∞∞-dt t t e t j )(0δω_________________________ 。
(5)信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 (1)100()(), 0f t u t t t =-> (2)2()cos3[()(4)]f t t u t u t π=--(3)3()[sin ]f t u t π=5、已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形图。
信号与系统考试题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
大学考试试卷《信号与系统》及参考答案

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。
《信号与系统》课程习题与解答
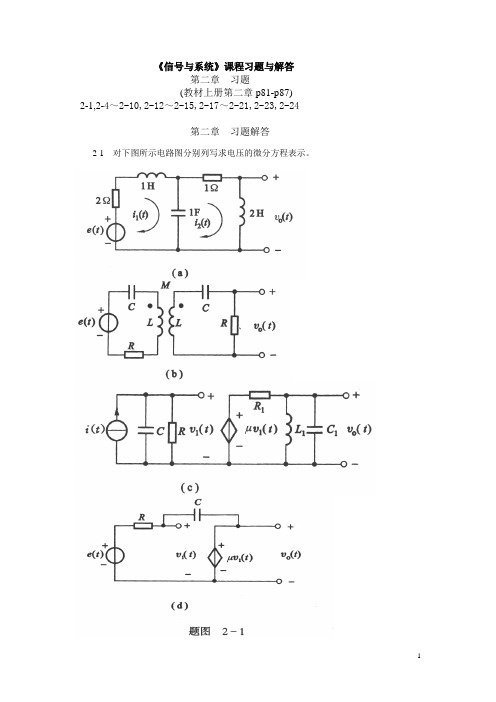
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统作业答案

信号与系统作业答案一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确3.冲击信号的拉氏变换结果是一个常数。
正确4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 。
全通系统2.单位冲击信号的拉氏变换结果是 。
( 1 )3.单位阶跃信号的拉氏变换结果是 。
(1 / s)4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用ωj 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 。
广义傅立叶变换6、单边拉普拉斯变换(LT)的定义式是:⎰∞-=0)()(dt e t f s F st . 7、双边拉普拉斯变换(LT)的定义式是:⎰∞∞--=dt e t f s F st )()(.三、计算题1. 求出以下传递函数的原函数1)F (s )=1/s解:)()(t u t f =2)F(s)=11+s 解:f (t)=)(t u et - 3)F(s)= )1(12-s s 解:F(s)= )1(12-s s =)1)(1(1+-s s s =15.0-+s 15.0++s -s 1 f (t)= +-)(5.0t u e t -)(5.0t u e t )(t u2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
L [)](t δ=⎰+∞∞--dt e t st )(δ=1L [u (t)]= ⎰+∞∞--dt e t u st )(=⎰+∞-0dt e st =s 1 3、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s ,试求)0(f =? 答案:0lim )(lim )(lim )0(20==⋅==∞→∞→→s s s F s t f f s s t 5、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 答案:由终值定理 02.0)100010()10)(2(lim )(lim )(200=++++==∞→→s s s s s s s sF f s s5、求)()(3t u t t f =的拉氏变换 答案:46)]([s t f L =(Re(s) > 0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
(完整版)信号与系统练习及答案

信号与系统练习及答案一、单项选择题1.已知信号f (t )的波形如题1图所示,则f (t )的表达式为( )A .tu(t)B .(t-1)u(t-1)C .tu(t-1)D .2(t-1)u(t-1)2.积分式⎰-δ+δ++4422)]dt -(t 2(t))[23(t t 的积分结果是( ) A .14 B .24 C .26 D .283.已知f(t)的波形如题3(a )图所示,则f (5-2t)的波形为( )4.周期矩形脉冲的谱线间隔与( )A .脉冲幅度有关B .脉冲宽度有关C .脉冲周期有关D .周期和脉冲宽度有关 5.若矩形脉冲信号的宽度加宽,则它的频谱带宽( ) A .不变 B .变窄 C .变宽D .与脉冲宽度无关 6.如果两个信号分别通过系统函数为H (j ω)的系统后,得到相同的响应,那么这两个信号()A .一定相同 B .一定不同 C .只能为零 D .可以不同7.f(t)=)(t u e t 的拉氏变换为F (s )=11-s ,且收敛域为( ) A .Re[s]>0B .Re[s]<0C .Re[s]>1D .Re[s]<1 8.函数⎰-∞-δ=2t dx )x ()t (f 的单边拉氏变换F (s )等于( ) A .1 B .s 1 C .e -2s D .s1e -2s 9.单边拉氏变换F (s )=22++-s e )s (的原函数f(t)等于( ) A .e -2t u(t-1) B .e -2(t-1)u(t-1) C .e -2t u(t-2)D .e -2(t-2)u(t-2)答案: BCCCBDCDA二.填空题1.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
2.已知x(t)的傅里叶变换为X (j ω),那么x (t-t 0)的傅里叶变换为_________________。
3.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为_________________。
