徐亚宁 信号与系统全部作业的参考答案汇编
精品文档-信号与系统分析(徐亚宁)-第4章

F2= s/(s^2+w0^2)
第4章 连续时间信号与系统的复频域分析
【例4-10】用MATLAB求解【例4-3】, 设τ=1 解 求解的代码如下: %program ch4-10 R=0.02; t=-2:R:2; f=stepfun(t, 0)-stepfun(t, 1); S1=2*pi*5; N=500; k=0:N; S=k*S1/N; L=f*exp(t′*s)*R; L=real(L);
本例中
和
的ROC均为
Re[s]>0,
极点均在s=0处。但
有一个s=0的零点,
抵消了该处的极点,相应地ROC扩大为整个s平面。
第4章 连续时间信号与系统的复频域分析 4.2.3 复频移(s域平移)特性
【例4-4】
, s0为任意常数 (4-12)
求e-atcosω0tU(t)及e-atsinω0tU(t)的象函数。
第4章 连续时间信号与系统的复频域分析
1. s 借助复平面(又称为s平面)可以方便地从图形上表示 复频率s。如图4-1所示,水平轴代表s Re[s]或σ, 垂直轴代表s的虚部,记为Im[s]或jω, 水平 轴与垂直轴通常分别称为σ轴与jω轴。如果信号f(t)绝 对可积,则可从拉氏变换中得到傅里叶变换:
f= exp(-t)+2*t*exp(-2*t)-exp(-2*t)
第4章 连续时间信号与系统的复频域分析
【例4-9】 用MATLAB求解【例4-2】 解 求解的代码如下:
%program ch4-9 syms w0t; F1=laplace(sin(w0*t)) F2=laplace(cos(w0*t))
(4-2)
信号与系统考题参考解答(完整版)

《信号与系统》作业参考解答第一章(P16-17)1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。
证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 (m ,n 为正整数) 解:由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == (m ,n 为正整数) 1-5 试判断下列信号是否是周期信号。
若是,确定其周期。
(1)t t t f πsin 62sin 3)(+= (2)2)sin ()(t a t f =(8)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解:(1)因为t 2sin 的周期为π,而t πsin 的周期为2。
显然,使方程n m 2=π (m ,n 为正整数)成立的正整数m ,n 是不存在的,所以信号t t t f πsin 62sin 3)(+=是非周期信号。
(2)因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。
(8)由于)4/cos(k π的周期为8)4//(21==ππN ,)8/sin(k π的周期为16)8//(22==ππN ,)2/cos(k π的周期为4)2//(23==ππN ,且有16412321=⨯=⨯=⨯N N N所以,该信号是周期16=N 的周期信号。
1-10 判断下列系统是否为线性时不变系统,为什么?其中)(t f 、][k f 为输入信号,)(t y 、][k y 为零状态响应。
(1))()()(t f t g t y = (2))()()(2t f t Kf t y += 解:(1)显然,该系统为线性系统。
信号与系统课后习题参考答案

信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号?题图1-11-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。
题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。
⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。
1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。
题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。
试做出当输⼊为时,响应得波形图。
题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。
题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。
⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。
第⼆章习题2-1试计算下列各对信号得卷积积分:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。
已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。
2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。
信号与系统分析徐亚宁第1章

第1章 绪论
例如,当飞机驾驶员和空运交通管制台通信时,通 信会受到驾驶舱的背景噪声影响而使通信系统恶化,在 这种情况下,需要设计一个系统,使通信信号经过该系 统的处理后,保留需要的信号(此处指驾驶员的声音)而排 除不需要的信号(驾驶舱的背景噪声);再比如,在接收来 自卫星探测的太空图像时,一般由于成像设备的缺陷和 大气影响,收到的图像可能非常不清晰,需要设计一个 图像处理系统来补偿图像的某些恶化,或者根据应用要 求增强图像的某些特征,如突出图像上的某些线条等。
第1章 绪论 用时间函数来表示信号,我们可以根据信号在对应 时间函数取值的连续性与离散性,将信号划分为连续时 间信号与离散时间信号(简称连续信号与离散信号)。
第1章 绪论
如果在所考虑的时间区间内,除有限个间断点外, 对于任意时间值都有确定的函数值与之对应,这样的 信号称为连续信号(例如前面提到的放大器中的电压信号), 通常用f(t)表示,例如
f1(t)=10 cos?t
f2 (t)=???01,,
t>0 t<0
或者可用波形表示离散信号f1(n)和f2(n),如图1-3所示。
第1章 绪论 图1-2 连续时间信号
第1章 绪论
实际上,连续信号就是函数的定义域是连续的。至 于值域,可以是连续的,也可以不连续。 如果函数的定 义域和值域都是连续的,则称该信号为模拟信号。但在 实际应用中,模拟信号和连续信号两词往往不予区分。
第1章 绪论 综上所述,信号可以定义为带有信息的随时间变化 的物理量。信号有电信号和非电信号,本课程着重研究 电信号的分析、处理和传输。
第1章 绪论
系统和信号是密不可分的,系统对输入的特定信号 (输入信号)响应,然后产生另外一些信号(输出信号)。我 们将系统定义为具有特定功能的整体,由若干相互作用 和相互依赖的事物组合而成。系统的概念不仅适用于自 然科学领域,还适用于社会科学领域,例如企业会根据 产品的产量、货存与销售速率等信息建立一个经验系统, 用来研究如何根据市场销售状况调节生产速度,使产品 既不脱销也不积压,以节省资金提高收益。本书主要讨 论处理电信号的系统,一般是具有某些特定功能的电路, 因此,在本书中,电路与系统二者通用。图1-1就是一个 典型的通信系统示意图。
信号与系统课后习题答案汇总

第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--=(9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列,周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sin π的功率为1/2,因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sinn n επ在),0(∞区间上的功率,其功率为1/2。
2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t), 0 , f(0 )且 4 ;已知 f(t)f(2t) 的波形如图所示,试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立,
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
(a)y(t) dx(t) dt
时不变、线性、因果、 稳定
( b) y(t)co3t)sx((t) 时变、线性、因果、稳 定
(c)y(t) 2t x()d
(d)y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
(3)4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
( 4)(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
(5)t (t2)(t2)dt4t (t2)d t4u(t2)
《信号与系统(第2版》【附录+习题答案】

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统课后习题答案汇总

可编辑第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t e t x -= (2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2cos )]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=t d t x ττδ)1()((14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t e t x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin )(π=解 功率有限信号。
n 4sinπ是周期序列,周期为8。
(5) )(2sin )(t t t x επ= 解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin )(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sinπ的功率为1/2,因此)(4sin n n επ在),(∞-∞区间上的功率为1/4。
(完整版)信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统课后答案(PDF)
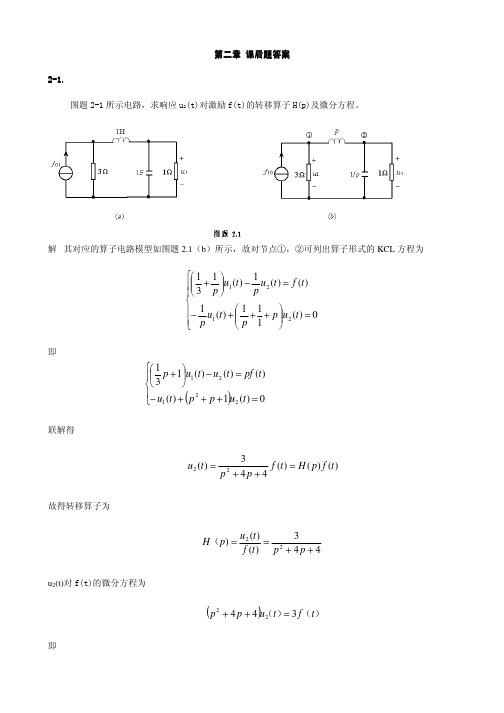
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
信号与系统课后习题答案汇总

第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n (3) )(2sin )(t t tx επ= (5) )]4()([4cos )(--=-t t t et x tεεπ(7) t t t t x 2cos)]2()([)(πδδ--= (9) )2()1(2)()(-+--=t t t t x εεε)5- (11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε (13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:(3) t t x π2sin )(=解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
(4) n n x 4sin)(π=解 功率有限信号。
n 4sin π是周期序列,周期为8。
(5) )(2sin )(t t t x επ=解 功率有限信号。
由题(3)知,在),(∞-∞区间上t π2sin 的功率为1/2,因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。
如果考察)(2sin t t επ在),0(∞区间上的功率,其功率为1/2。
(6) )(4sin)(n n n x επ=解 功率有限信号。
由题(4)知,在),(∞-∞区间上n 4sin π的功率为1/2,因此)(4sinn n επ在),(∞-∞区间上的功率为1/4。
如果考察)(4sin n n επ在),0(∞区间上的功率,其功率为1/2。
精品文档-信号与系统分析(徐亚宁)-第3章

第3章 连续时间信号与系统的频域分析 (3-5)
其中 (3-6)
第3章 连续时间信号与系统的频域分析
这里,若将周期信号分解为式(3-5)的傅里叶级数,则
y=quad(FUN, A, B) 其中FUN是被积函数,是字符串或函数句柄; A,B分 别是积分下限和上限。利用该函数、 傅里叶级数的系数可 由下式求出
Fn=quad(FUN, -T/2, T/2)/T 其中T是信号的周期。
第3章 连续时间信号与系统的频域分析
【例3-6】 利用MATLAB求图3-9所示周期方波的傅里叶函数, 给出幅度谱和相位谱; 然后将求得的系数代入公式
从式(3-3)和式(3-4)可知,an与bn都是nω0的函数,所 以An和φn也都nω0的函数。若n取负值,可知an和An是n的偶 函数,bn与φn是n的奇函数。如果将An对nω0的关系 绘成图形,nω0用ω表示,即ω=nω0,n=0, 1, 2,…,以 ω为横轴,所对应的An为纵轴,就可以画成一种线图, 直观地表明信号f(t)的各频率分量的振幅。
(3-10)
(3-11)
第3章 连续时间信号与系统的频域分析
可见,Fn也应该是nω0的函数,且|Fn|为n的偶函数,φn 为n的奇函数。将nω0用ω代替,也可以得到|Fn|~ω的关系 和φn~ω的关系,以ω为横轴,|Fn|与φn为纵横,画出 |Fn|~ω的谱线,称为(复数)幅度谱。画出φn~ω的谱线,称 为(复数)相位谱。二者共同组成信号的复数频谱(复频谱)。 值得注意的是,Fn中的n可取负整数,故ω有正有负,即复频 谱中不仅包括正频率项,而且含有负频率项,所以经常称复 频谱为双边谱,如图3-4所示; 而称图3-1所示的频谱为单边 谱。
信号与系统课后习题参考答案

题图2-10
2-11已知系统得微分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-12已知系统得差分方程与起始条件,试求系统得零输入响应。
⑴
⑵
⑶
2-13已知系统得微分方程,试求系统得单位冲激响应。
⑴
⑵
⑶
2-14已知系统得差分方程,试求系统得单位样值响应。
1-1试分别指出以下波形就是属于哪种信号?
题图1-1
1-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所示,试作出下列各信号得波形图,并加以标注。
题图1-3
⑴⑵⑶
⑷⑸⑹
⑺⑻⑼
1-4已知信号与波形如题图1-4中所示,试作出下列各信号得波形图,并加以标注。
题图1-4
⑴⑵⑶
⑷⑸⑹
⑵
⑶
⑷
⑸
⑹
2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)
⑵
⑶
⑷
⑸
⑹
2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-3
2-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-4
2-5已知,试求:
⑴⑵⑶
并作出她们得图形。
2-6系统如题图2-6所示,试求系统得单位冲激响应。已知其中各子系统得单位冲激响应分别为:
3-5设有一周期信号x(t),其复振幅为:
⑴x(t)就是实函数吗?⑵x(t)就是偶函数吗?⑶就是偶函数吗?
3-6设x(t)就是一基波频率为Ω得周期信号,其复振幅为,试用表示以下周期信号得复振幅。
⑴⑵
精品文档-信号与系统分析(徐亚宁)-第5章

第5章 离散信号与系统的时域分析 以上三种序列之间有如下关系:
(5-7) (5-8) (5-9)
第5章 离散信号与系统的时域分析
4. 单边指数序列anU(n)
f(n)=anU(n)
(5-10)
anU(n)的波形如图5-5所示。
此外,还有因果斜升序列nU(n), 正弦(余弦)序列
sinω0n或cosω0h等。
5.1.2 1. 单位样值(Unit Sample)信号δ(n)
δ(n)的波形如图5-2(a)所示。
(5-1)
第5章 离散信号与系统的时域分析 图 5-2 δ(n)、δ(n-m)和δ(n+m)的波形
第5章 离散信号与系统的时域分析
此序列只在n=0处取单位值1, 其余样点上都为零。 δ(n)也称为“单位取样”、“单位函数”、“单位脉冲” 或“单位冲激”。δ(n)对于离散系统分析的重要性,类 似于δ(t)对于连续系统分析的重要性,但δ(t)是一种 广义函数,可理解为在t=0处脉宽趋于零,幅度为无限大 的信号;而δ(n)则在n=0处具有确定值,其值等于1
第5章 离散信号与系统的时域分析
【例5-1】 绘制单位阶跃序列U(n) 解 MATLAB
%program ch5-1 n=[-2:10]; un=[zeros(1, 2)ones(1, 11)]; stem(n, un); xlabel(′n′); ylabel(′u(n)′); grid on; axis([-2 10 -0.2 1.2]) 运行结果如图5-6所示。
第5章 离散信号与系统的时域分析 图 5-9 斜变序列
第5章 离散信号与系统的时域分析
5.2 离散信号的基本运算及MATLAB实现
像连续信号一样,离散信号也可以进行相应的变换和运算, 这里只介绍利用
信号与系统,徐亚宁

j
1 2
f t e
j t
dt
f t
F
j t j e d
10
典型非周期信号的傅里叶变换
g t Sa 2
e
at
U t
1 a j
d t 1
U (t ) d 1 j
第2章 连续时间信号与系统的时域分析
• 一、常用信号及其基本运算 • 二、阶跃信号与冲激信号
1. 单位阶跃
定义: U(t) =
U (t)
0
1
t <0 t >0
1 0
t
2. 单位冲激
定义: δ(t) = 0 ∞ t≠0 t=0 且 d t dt
d (t)
1
(1) 0
5
t
3. 冲激信号的性质
s at e U t U t 1 1 sa
(3) 单位冲激: d t
1
15
二、单边拉普拉斯变换的性质
1. 线性特性 a1 f1 t a2 f 2 t a1 F1 s a2 F2 s 2. 时移特性
f t t 0 U t t 0 F s e f t e
f
n
t
s F s
n
n 1
s
n 1 m
f
m
0
16
m 0
(2) 复频域微分 t f t
dF s ds
,
t
n
f t
d F (s) ds
n
n
7. 积分定理
(1) 时域积分 若下限为 0 , 则: 下限为-∞, 则:
徐亚宁 信号与系统全部作业的参考答案

2 f1 t t0
y1 t t0 ,所以是时不变的。
2 f t1
,即输出由当前时刻的输入决定,所以系统是
f 2 t y2 t ,则 y1 t f1 t cos 2t ,
y2 t f 2 t cos 2t
a1 f1 t a2 f 2 t y t a1 f1 t a2 f 2 t cos 2t a1 f1 t cos 2t a2 f 2 t cos 2t ,
波形见(b)
1 (c) f1 t * f 2 t f1 t * f 2 1 t 2 t 1 2 t 1 * f 2 t
t0 0 t 1 t 1
2 f 2
1
t 1 2 f21 t 1 ,而
e t t dt
t
(14) f t e
1 2 3 2
t
n
t n dt
解:(2) f t
d 0 e t t dt
(8)因为 1 t t 1 , 所以 f t 2 t 3 4 1 t dt 2 t 3 4 t 1 dt 2 t 3 4
y t a1 y1 t a2 y2 t ,所以是非线性的。
② 时不变性
2f t 设 f1 t y1 t , 则 y1 t e 1 ,
y1 t t0 e
2 f1 t t0
设 f1 t t0 y2 t , 则 y2 t e ③ 因果性 因为对任意时刻 t1, y t1 e 因果的。 (5) y t f t cos 2t ① 线性: 设 f1 t y1 t , 那么
徐亚宁 信号与系统全部作业的参考答案汇编

-1
01
t
-1
7
f1(t)
1
sint[U(t)-U(tπ)
0
1t
(e)
f2(t) 2 1
0
t
解:(a) f1 t * f2 t f1 t * t 1 t 1 f1 t 1 f1 t 1 ,故波形如
下:
f(t) 1
f(t) 2(1-e-1)
-3
-1
01
3t
(a)
0
t
(b)
(b) f1 t* f2 t
第一章
1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。其中 X(0-)为 系统的初始状态。
(2) y t e2 f t
(5) y t f t cos 2t
(8) y t f 2t
解:(2) y t e2 f t
① 线性:
设 f1 t y1 t , f2 t y2 t ,则 y1 t e2 f1t,
2.52 求下列系统的零输入响应,零状态响应和全响应。
(1) yt 3yt 2y t f t , f t 2etU t , y 0 1, y0 2
解:特征方程为: 2 3 2 0 ,特征根为: 1 1, 2 2 , (1)求零输入响应
由特征根得 yx t 为: yx t C1et C2e2t t 0 ;代入初始条件并求解,有:
CC21
2 ,所以 1
yx
t
2et
e2t
t0
2.26 系统框图如图 2-58 所示,试列出系统的微分方程,求单位冲激响应。
yt
f (t)
-1
y (t)
解:(1)如图,加法器的输出方程为:
yt f t yt ,整理后即得系统的微分方程为: yt yt f t
精品文档-信号与系统分析(徐亚宁)-第6章

第6章 离散信号与系统的z域分析
6.2.4 若
,则
(6-18)
第6章 离散信号与系统的z域分析
6.2.5 z域微分(时域线性加权)
若
,R1<|z|<R2, 则
(6-19)
第6章 离散信号与系统的z域分析
【例6-7】 求uU(n)的z 解 因为
由z域微分性质,可得
(6-20)
第6章 离散信号与系统的z域分析 6.2.6 卷积定理
f(n)=2U(n)-(0.5)nU(n)=[2-(0.5)n]U(n)
第6章 离散信号与系统的z域分析
【例6-10】 已知
,|z|>1 , 求
f(n)。
解 因为
由式(6-25)和式(6-26)可得展开式
所以
因为|z|>1, 所以 f(n)=6δ(n)+2δ(n-1)+8U(n)-13(0.5)nU(n)
域及相应的序列f(n)。
解 F(z)的两个极点是z1=1和z2=0.5, 故其可能的收敛域为 |z|<0.5, 0.5<|z|<1或|z|>1。先将F(z)展开为
第6章 离散信号与系统的z域分析 其中
所以
第6章 离散信号与系统的z域分析
(1) 若收敛域为|z|<0.5, 则两个极点均在收敛域的外 侧,因此这两项的逆变换是反因果序列,由式(6-27)得
则
(6-22)
式中, C是F1(λ)与
收敛域公共部分内逆时
针方向的围线。这里对收敛域及积分围线的选取限制较严,从
而限制了它的应用,不再赘述。
第6章 离散信号与系统的z域分析 6.3 逆z变换
与拉氏变换类似,用z变换分析离散系统时,往往需要从 变换函数F(z)确定对应的时间序列,即求F(z)的逆z变换。 求逆z变换的方法有留数法、幂级数展开法(长除法)和部分分 式展开法。下面我们只讨论用部分分式展开法求有理函数的逆 变换。
信号与系统第三版徐亚宁第三章

第三章3.12 求下列信号的傅里叶变换(2)()/21U t - (4) ()2jt e t δ-- (6)()()211t e t δ--- (8)()()1U t U t --解:(2)因为 ()()/212U t U t -=-,所以 ()()21/21j U t e j ωπδωω-⎡⎤-↔+⎢⎥⎣⎦ (4)因为 ()()222jt j e t e t δδ---=-,所以,()()212j jt e t e ωδ-+--=↔ (6)因为 ()()()2111t e t t δδ---=-,所以,()()211t j e t e ωδ----↔(8)因为 ()()()33 1.5U t U t g t --=-,所以()() 1.53332j U t U t Sa eωω-⎛⎫--↔ ⎪⎝⎭3.14 已知信号()1f t 和()2f t 的带宽分别为1ω和2ω,并且12ωω>,求下列信号的带宽。
(1)()()12f t f t(2)()()12f t f t * (3)()()122f t f t +(4)()()212*f t f t(5)()()1221f t f t -(1)()()()()()12121*2f t f t F j F j F j ωωωπ↔=,根据卷积的性质可知()F j ω 带宽为12ωω+;(2)因为()()()()()1212f t f t F j F j F j ωωω*↔=,所以()F j ω的带宽为2ω; (3)因为()()()()()121222f t f t F j F j F j ωωω=↔=+,所以()F j ω的带宽为1ω;(4)因为()()()()()()1221121*2f t f t F j F j F j F j ωωωωπ⎡⎤*↔=⎢⎥⎣⎦,所以()F j ω的带宽为2ω;(5)因为 ()()()()12121121*222j f t f t F j F j F j e ωωωωπ-⎡⎤⎛⎫⎡⎤-↔=⎪⎢⎥⎣⎦⎝⎭⎣⎦ ,所以()F j ω的带宽为122ωω+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 f1 t t0 y2 t , 则 y2 t e2 f1tt0 y1 t t0 ,所以是时不变的。
③ 因果性
因为对任意时刻 t1, y t1 e2 f t1 ,即输出由当前时刻的输入决定,所以系统是
因果的。
(5) y t f t cos 2t
① 线性:
设 f1 t y1 t , f2 t y2 t ,则 y1 t f1 t cos 2t, y2 t f2 t cos 2t
③ 因果性
因为对任意时刻 t1, y t1 f 2t1 ,当 t1 0 时, t1 2t1 ,即输出由未来时刻
的输入决定,所以系统是非因果的。
2
第二章
2.12 (a)已知信号 f(t)如图所示,试分别画出下列信号的波形。
(1)f(1-t)
(2)f(2t+2)
(3)f(2-t/3) (4)[f(t)+f(2-t)]U(1-t)
f(t) 2 1
-1
1
-1
23t
解:(1)先将 f(t)向左移 1 得 f(t+1)(见图(a)):
f(t+1) 2 1
-2
12t
-1
f(1-t) 2 1
-2
12
t
-1
图(a)
图(b)
然后反折即得 f(1-t)(见图(b))。 (2)首先 f(t)向左移 2 得 f(t+2)(见图 a):
f(t+2) 2 1
t 1
(10) f t
et
t
t
dt
et
t 0
et
2
t0
(14)冲激串 t n 中只有 两个:δ(t)和δ(t+1)落在积分区间 n
[-3/2 1/ t
e 2 t
3 2
n
t n dt
e 2 t
3
t
1
t dt
e1
1
2
2.25 已知激励为零时刻加入,求下列系统的零输入响应。
f(2t+2) 2 1
-3
01t
-3/2
0 1/2 t
-1
-1
图(a)
图(b)
然后将 f(t+2)的波形压缩为 1/2 即得 f(2t+2)的波形(见图 b)。
3
(3) 首先 f(t)向左移 2 得 f(t+2)(见图 a):
f(t+2) 2 1
f(t/3+2) 2 1
-3
01t
-9
03 t
-1
-1
图(a)
图(b)
然后将 f(t+2)的波形扩展 3 倍即得 f(2+t/3)的波形(见图 b)。 最后将 f(2+t/3)进行反折即得 f(2-t/3)的波形(见图 c):
f(2-t/3)
2 1
-3
36 9
t
图(c) )
(4) 先作出 f(2-t)的波形 和 U(1-t)的波形(见图 a 和图 b):
(1) yt y t f t , y 0 2, y0 0
(3) yt 3yt 2y t f t , y 0 1, y0 0
解:(1)特征方程为: 2 1 0 ,特征根为 1 i, 2 i ,因此,yx(t) 为:
yx t C1eit C2eit t 0 ,代入初始条件并求解,有:
d dt
e3t
t
(8)
f
t
2
t3 4
1 t dt
(10)
f
t
et
t t
dt
1
(14) f t
e 2 t
3 2
n
t n dt
解:(2)
f
t
d dt
e0
t
t
(8)因为 1 t t 1 ,
所以 f t 2 t3 4 1 t dt 2 t3 4 t 1dt 2 t3 4 10
第一章
1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。其中 X(0-)为 系统的初始状态。
(2) y t e2 f t
(5) y t f t cos 2t
(8) y t f 2t
解:(2) y t e2 f t
① 线性:
设 f1 t y1 t , f2 t y2 t ,则 y1 t e2 f1t,
y2 t e2 f2t
那么
a1 f1
t
a2 f2
t
y t
e e e ,显然, 2a1 f1ta2 f2t
2a1 f1t 2a2 f2 t
y t a1y1 t a2 y2 t ,所以是非线性的。
② 时不变性
设 f1 t y1 t , 则 y1 t e2 f1t , y1 t t0 e2 f1tt0
那么
a1 f1 t a2 f2 t y t a1 f1 2t a2 f2 2t a1 f1 2t a2 f2 2t , 显然 y t a1y1 t a2 y2 t ,所以系统是线性的。
② 时不变性
设 f1 t y1 t , 则 y1 t f1 2t , y1 t t0 f1 2t t0 设 f1 t t0 y2 t , 则 y2 t f1 2t t0 y1 t t0 ,所以系统是时变的。
设 f1 t t0 y2 t , 则 y2 t f1 t t0 cos 2t y1 t t0 ,所以是时变的。
③ 因果性
因为对任意时刻 t1, y t1 f t1 cos 2t1 ,即输出由当前时刻的输入决定,所以
系统是因果的。
1
(8) y t f 2t
① 线性:
设 f1 t y1 t , f2 t y2 t ,则 y1 t f1 2t , y2 t f2 2t
5
iCC11
C2 2 iC2 0
C1
f(2-t) 2 1
U(1-t) 1
-1
12 3
t
1
t
图(a) )
图(b) )
然后作出 f(t)+f(2-t)的波形(见图 c): 最后乘以 U(1-t)后的波形如图 d。
4
f(2-t)+f(t)
3
3
2t
1
t
图(c) )
图(d) )
2.16 利用冲激信号及其各阶导数的性质,计算下列各式:
(2)
f
t
那么
a1 f1 t a2 f2 t y t a1 f1 t a2 f2 t cos 2t a1 f1 t cos 2t a2 f2 t cos 2t ,
显然 y t a1y1 t a2 y2 t ,所以系统是线性的。
② 时不变性
设 f1 t y1 t , 则 y1 t f1 t cos 2t, y1 t t0 f1 t t0 cos 2t t0
