abaqus 回弹
abaqus 中回弹问题总结

我建议你参考A B A Q U S E x a m p l e p r o b l e m s m a n u a l 1.3.7A x i s y m m e t r i c f o r m i n g o f a c i r c u l a r c u p1.5.1 Springback of two-dimensional draw bending1.5.2 Deep drawing of a square box回弹中注意把系统改成双精度,否则有些问题是算不了的,或者显示有问题。
隐式计算回弹中的设置参考maunal中的13.5.5 Springback analysis in ABAQUS/Standard谈谈我的体会,或许对你有点帮助。
使用动力显示算法模拟成形过程,静力隐式算法分析回弹的回弹预测方法,在静力隐式求解时由于接触条件的变化,计算复杂零件的回弹收敛很困难。
为使计算收敛,大概可以从以下几个方面进行调整:1. 减小计算的步长? ?这种方法对简单形状的零件比较有效,对复杂零件来说基本上没有用。
2. 调整固定点? ?我在附图中的回弹分析中,尝试了A点固定,B点固定,C点固定三种方式。
对A,B两点固定的计算中,无论计算步长多小,都不收敛。
而在C点固定时,很快求出了结果。
所以,我觉得把固定点选在零件几何中心或回弹量对称的点上可能效果比较好。
当然,如过约束点是已经给定的可以结合第3种方法尝试。
3. 逐步去掉约束? ?把约束条件不要一次去掉,可以分几个分析步取消,也会增加收敛概率。
可能还有其它办法,这只是我做回弹分析的一点体会,希望对你有用。
我也是用了一些时间才计算出来的,重要的是多思考,多尝试。
ABAQUS常见问题汇总- 2.0版回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
abaqus 弯曲回弹冲压成形模拟分析设置注意事项

ABAQUS弯曲回弹分析详细操作及其注意事项abaqus 冲压成形模拟分析设置注意事项1.做回弹分析时,回弹模型一定和调用的.odb文件在同一个文件夹。
用file-set workdirectory设置工作文件夹。
2.做回弹分析时,一定要赋予回弹零件材料特性。
并且要对零件进行不在同一直线上的三点约束。
回弹分析步骤:1.在成形模块下,右键creat model,展开新建的model- parts右键-import-.odb(同一文件夹),选BLANK-1,改名字BLANK.设置如下。
2.赋BLANK零件和成形时一样的材料属性。
建立截面,赋截面的步骤和成形相同。
3.assembly:把BLANK零件进行装配。
4.step:选“静态”。
output-restart-intervals(1);5.load:BC 三点锁定predefined field-creat6.JOB模块,和成形操作相同。
选BLANK零件-出现“edit predefined field”对话框,设置如下,其中JOB NAME中的名字一定和成形的odb的名字一致。
updata选项要选中。
abaqus后处理的数据提取:(1)节点或单元的显示在modul为mesh,part为BLANK的情况下,菜单view—part display options—mesh —选show node labels 或show element labels以显示节点号或单元号;(2)建立路径在modul 为visualization时,菜单tool-path-creat建立路径;(3)建立XY曲线菜单tool—XY data-create XY data—选path-在XY data from path中设置显示的纵坐标和横坐标的内容。
角度的测量:在零件状态下,菜单tool—datum—两点建轴,query测量角度即可。
abaqus回弹分析实例:在分析步之间传递数据

Abaqus Example Problems Guide1.5.1 Springback of two-dimensional draw bendingProducts: Abaqus/Standard Abaqus/Explicit是用explicit进行成形,然后使用standard分析回弹Problem description这个例子描述了在93年成形模拟数值会议中报道的基准测试。
这个基准包括使用三种材料描述六种问题以及两种不同的夹持力。
六个问题中的一个描述如下。
原文见Taylor等人在93年的论文。
坯料初始尺寸350*35,厚度0.78.问题本质上是个平面应变问题(垂直于模型平面的尺寸是35mm)。
夹持力是2.45kN,夹具的质量是5kg。
摩擦系数0.144坯料为低碳钢,材料为弹塑性材料,弹性为各向同性,对于塑性使用Hill 异性屈服准则。
材料的性质如下:Young's modulus = 206.0 GPaPoisson's ratio = 0.3Density = 7800.Yield stress = 167.0 MPaAnisotropic yield criterion: =1.0, =1.0402, =1.24897, =1.07895, =1.0, =1.0此例是对称问题,只取一半建模。
坯料使用一行175个一阶壳单元建模。
对称的边界条件施加到对称面上。
边界条件施加到了坯料所有的节点上以模拟平面应变的条面;建模平面外的尺寸是5mm;因此,坯料的加持力经过了粗略缩放。
成形的过程由explicit中的两个分析步完成。
坯料的加持力在第一个分析步施加。
加载使用平滑分析步,以将惯性效应最小化。
第二个分析步,通过设定冲头刚体参考点的速度冲头下行70mm。
速度使用triangular smooth step amplitude 功能施加,初始速度和最终速度都是0,峰值速度在这个过程之间。
abaqus计算回弹的方法

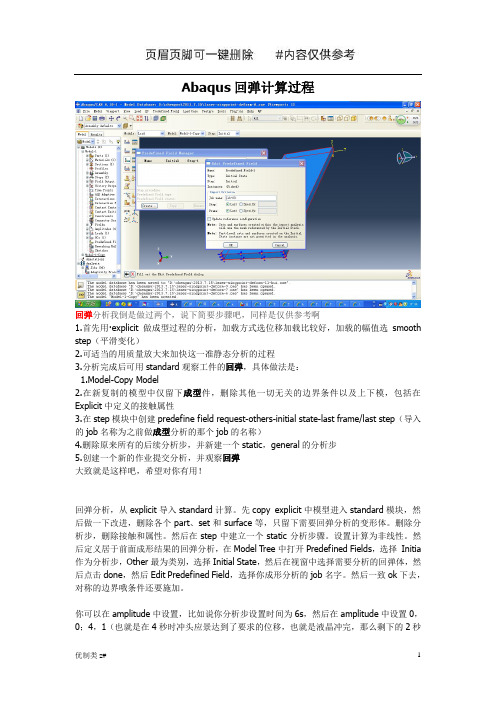
Abaqus回弹计算过程回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊1.首先用·explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹,具体做法是:1.Model-Copy Model2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)4.删除原来所有的后续分析步,并新建一个static,general的分析步5.创建一个新的作业提交分析,并观察回弹大致就是这样吧,希望对你有用!回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择Initia 作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
Abaqus中显示动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
Abaqus 中显示动力学分析步骤【精选文档】

准静态分析—-ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响.ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用.当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易.此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟.但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
(完整版)Abaqus中显示动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
Abaqus中显示动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
abaqus计算回弹的方法(实用荟萃)
Abaqus回弹计算过程回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊1.首先用·explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹,具体做法是:1.Model-Copy Model2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)4.删除原来所有的后续分析步,并新建一个static,general的分析步5.创建一个新的作业提交分析,并观察回弹大致就是这样吧,希望对你有用!回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择Initia 作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
abaqus单元形状 -回复

abaqus单元形状-回复Abaqus 单元形状Abaqus 是一个用于有限元分析的强大软件工具,广泛应用于工程领域。
在进行有限元分析时,选择合适的单元形状是至关重要的。
Abaqus 提供了各种各样的单元形状,以满足不同分析问题的需求。
本文将一步一步地回答关于Abaqus 单元形状的问题,并讨论它们的适用性和特点。
1. 什么是Abaqus 单元形状?Abaqus 单元形状是指在有限元分析中使用的几何形状。
单元形状可以是简单的几何形状,如线段、三角形和矩形,也可以是复杂的几何形状,如曲线、曲面和体积。
每个Abaqus 单元形状都涉及到不同的数学算法和方程,以模拟材料和结构在不同条件下的力学行为。
2. Abaqus 中有哪些常见的单元形状?Abaqus 中有许多常见的单元形状,下面是其中一些常见的单元形状:- 线单元(1D 单元):线单元是用来模拟沿一维方向传输力和位移的结构的。
常见的线单元有两个节点的二节点线单元和三个节点的三节点线单元。
- 二维单元(2D 单元):二维单元是用来模拟平面内的结构问题的。
常见的二维单元有三个节点的三角形单元和四个节点的矩形单元。
- 三维单元(3D 单元):三维单元是用来模拟立体结构问题的。
常见的三维单元有四个节点的四面体单元和八个节点的立方体单元。
除了上述常见的单元形状,Abaqus 还提供了许多其他类型的单元形状,如壳单元、梁单元、悬臂梁单元等。
可以根据具体的分析需求选择适当的单元形状。
3. 如何选择适当的Abaqus 单元形状?选择适当的Abaqus 单元形状是根据分析需求和所模拟的问题而定的。
以下是选择适当单元形状的一些建议:- 如果模拟的结构是一维结构,比如悬臂梁,那么选择线单元是最合适的选择。
- 如果模拟的结构是二维结构,如平面板或薄壳结构,那么选择二维单元是最合适的选择。
对于具有曲率的结构,需要选择更高阶的二维单元,如六节点三角形单元。
- 如果模拟的结构是三维结构,如实体结构体,那么选择三维单元是最合适的选择。
基于Abaqus数值模拟厚板冲压件回弹影响因素研究

由塑性原理可知,板材越厚成形件弯曲时变形抗力
越大,且弯曲时体现出来的塑性、应力分布、应变状况、
材料流动状况等也会发生较大的变化,进而体现出与薄
板不一样的回弹特性[2]。基于此,本文拟采用 Abaqus 有
限元软件对 V 形厚板冲压件的回弹过程进行数值模拟,
《模具制造》2024 年第 3 期
1.058 减小到 0.963,降低了 8.9%。
1.06
1.04
1.02
1.00
0.98
0.96
1.0
70
表面会与凹模圆角产生摩擦,增大板材外表面受到的拉
回弹量/mm
2.0
50
60
W 数值/mm
对于 V 形件而言,成形时板材流入凹模时,板材外
大,回弹数值增加的幅度明显增加。
2.5
40
(3)摩擦系数对回弹的影响。
增大到 R15mm,回弹数值达到了 2.617mm,且随着 R 角增
3.0
30
图7
从成形件变形过程及塑性成形原理分析可知,V 形
参数对成形件回弹数值会产生影响,因此,开展了各因
0.5
0.0
影响回弹的因素分析
件 R 角、凹模开口宽度、凸模成形速度、接触摩擦系数等
1.0
0.10
0.12
0.14 0.16
Z 3 个方向的旋转自由度均设置为 0,X 和 Y 方向平动自
由度也设置为 0,Z 方向运动不做约束。凸模施加位移载
(b)
图4
V 形件数值模拟结果
a——成形件应力分布云图
b——成形件应变分布云图
提取了成形件料厚分布云图,如图 5 所示。从图 5
荷,运行时间为 0.1s。网格采用四边形网格,凸模和凹模
Abaqus中显示动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
abaqus方盒拉深的有限元分析CAE

¾ Shape: Shell ¾ Type: Planar ¾ Approximate size: 0.5
点击对话框中下方的
1.1 板坯建模
3. 进入参数化建模的sketch界面,进行几何建模 点击 建立矩形边界组成的面 根据绘图窗口下方的提示输入角点坐标 回车 回车
7.1 定义板坯边界条件
只显示板坯,隐藏其他物体
双击目录树中的Loads
选择 Create Boundary Conditions Mechanical Symmetry….
Continue
选择板坯X=0的那条边
在弹出的对话框中选择 XSYMM
用相同的方法定义Y=0的那条边为YSYMM
7.2 定义凸模边界条件
本例的主要目的就是展示在Abaqus中如何应用 Explitcit 和 Implicit 来分析成形及回弹问题。
简介
几何信息(mm) : 200×200 × 0.82 的板料,凹模口尺寸为102.5 × 102.5, 四角导圆半径为
10, 凸模截面尺寸100 × 100 ,各棱边导圆半径为10.
6.1 划分板坯的网格
首先双击目录树的Parts,然后选择Blank,这时屏幕上只显示板坯。
在第一个按钮组中选择Seed Edge: By Number,定义边界上
的节点数量
选择板坯的左边和下边,点击中键确认
输入20 , 选择Done 确认 本例中单元类型采用默认的S4R单元
选择按钮Mesh Part
只显示凸模,隐藏其他物体
双击目录树中的Loads
ABAQUS使用解答(整理)

ABAQUS使用解答(整理)Abaqus 使用问答Q:abaqus的图形如何copy?A:file>print>file格式为png,可以用Acdsee打开。
Q:用Abaqus能否计算[Dep]不对称的问题?A:可以,并且在step里面的edit step对话框other里面的matrix solver有个选项。
Q: 弹塑性矩阵【D】与ddsdde有何联系?A: stress=D*stran;d(stress)=ddsdde*d(stran)。
Q:在abaqus中,如果采用umat,利用自己的本构,如何让abaqus明白这种材料的弹塑性应变,也就是说,如何让程序返回弹性应变与塑性应变,好在output中输出,我曾想用最笨地方法,在uvarm中定义输出,利用getvrm获取材料点的值,但无法获取增量应力,材料常数等,研究了帮助中的例子,umatmst3.inp,umatmst3.for,他采用mises J2 流动理论,我在output history 显示他已进入塑性状态,但他的PE仍然为0!!?A: 用uvar( )勉强成功。
Q: 本人在用umat作本构模型时,*static,1,500,0.000001,0.1 此时要求的增量步很多,即每次增量要很小,*static1,500 时,在弹性向塑性过度时,出现错误,增量过大,出现尖点.?A: YOU CAN TRY AS FOLLOWS:*STEP,EXTRAPOLATION=NO,INC=2000000*STATIC0.001,500.0,0.00001,0.1。
Q: 模型中存在两个物体的接触,计算过程中报错,怎么回事?A: 接触问题不收敛有两个方面不妨试试:一、在*CONTACT PAIR 里调试ADJUST参数;二、调一些模型参数,比如FRICTION等。
Q: 在边界条件和加载时,总是有initial这个步,然后是我们自己定义的加载步,请问这个initial步,主要作用是什么?能不能去掉?A: 不能去掉,所有的分析都有,是默认的步。
abaqus 谐响应实现方式 -回复

abaqus 谐响应实现方式-回复Abaqus软件是一种用于有限元分析的强大工具,广泛应用于工程领域。
谐响应是其中一种常见的分析方式,用于评估结构在周期性负载下的稳定性和疲劳寿命。
本文将一步一步地介绍如何在Abaqus中实现谐响应分析。
第一步:建立几何模型在进行谐响应分析之前,我们需要先建立一个几何模型以描述要分析的结构。
可以使用Abaqus提供的几何建模工具创建模型,也可以导入其他CAD软件生成的几何数据。
确保几何模型准确地反映了结构的形状和尺寸。
第二步:定义材料特性和截面属性在Abaqus中,我们需要为结构定义材料特性和截面属性。
材料特性包括材料的弹性模量、泊松比、密度等等。
截面属性是指结构的截面形状和尺寸,例如梁的截面高度和宽度。
这些参数对于分析结构的谐响应特性至关重要。
第三步:应用谐响应荷载在Abaqus中,可以通过定义周期性荷载来模拟谐响应。
可以根据具体分析需要选择不同类型的谐响应荷载模型,例如简谐荷载、随机振动荷载等。
对于简谐荷载,我们需要指定振荡的频率和幅值。
可以通过在谐响应分析步骤中添加荷载来应用谐响应荷载。
第四步:设置边界条件在Abaqus中,需要定义适当的边界条件来约束结构的自由度。
这些边界条件包括固定支座、自由度的约束或加载。
确保边界条件能够合理地模拟实际结构的约束情况。
第五步:设置分析步骤和参数在进行谐响应分析之前,需要设置分析步骤和参数。
可以选择隐式或显式求解器,根据具体分析需求设置步长和收敛准则等参数。
合理设置这些参数可以提高计算效率和准确性。
第六步:执行谐响应分析一切准备就绪后,可以执行谐响应分析。
Abaqus将根据定义的几何模型、材料特性、荷载和边界条件,进行求解并得到谐响应结果。
这些结果包括结构的振动频率、模态形态和应力响应等。
第七步:分析结果和后处理在完成谐响应分析后,我们可以对分析结果进行后处理。
Abaqus提供了丰富的后处理工具,可以用来可视化结果、绘制模态振型、计算结构的疲劳寿命等。
abaqus计算回弹的方法

回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊1.首先用·explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹,具体做法是:Model2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)4.删除原来所有的后续分析步,并新建一个static,general的分析步5.创建一个新的作业提交分析,并观察回弹大致就是这样吧,希望对你有用!回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择Initia作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
系列教程13ABAQUSExplicit准静态分析

13 ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit 在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型成为很大时,显式过程比隐式过程需要较少的系统资源。
关于隐式与显式过程的详细比较请参见第2.4节“隐式和显式过程的比较”。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
目标是在保持惯性力的影响不显著的前提下用最短的时间进行模拟。
准静态(Quasi-static)分析也可以在ABAQUS/Standard中进行。
当惯性力可以忽略时,在ABAQUS/Standard中的准静态应力分析用来模拟含时间相关材料响应(蠕变、膨胀、粘弹性和双层粘塑性)的线性或非线性问题。
关于在ABAQUS/Standard中准静态分析的更多信息,请参阅ABAQUS分析用户手册(ABAQUS Analysis User’s Manual)的第6.2.5节“Quasi-static analysis”。
13.1 显式动态问题类比为了使你能够更直观地理解在缓慢、准静态加载情况和快速加载情况之间的区别,我们应用图13-1来类比说明。
