初中三年级数学下册切线长定理习题课件北师大版
北师大版初三数学下册《3.7切线长定理》习题课件(附答案)

(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
(1)证明:如图,连接OC. ∵BD是⊙O的切线, ∴∠ABD=90°.
∵AB是⊙O的直径,∴∠ACB=90°.
∴∠ACO+∠BCO=90°,∠BCD=90°. ∵点E是BD的中点, 1 ∴CE= BD=BE. 2 ∴∠BCE=∠CBE. ∵∠CBE+∠ABC=90°,
∵DF是⊙O的切线,
∴OD⊥DF. ∴∠EDF=90°-60°=30°. ∴∠DFE=90°. ∴DF⊥CE.
∴CF=EF.
(2)解: 相等.理由如下:
当点E运动至与点B重合时,BC是⊙O的切线, ∵⊙O的切线DF交BC于点F,
∴BF=DF.
∴∠BDF=∠DBF. ∵AB是直径, ∴∠ADB=∠BDC=90°. ∴∠FDC=∠C. ∴DF=CF. ∴BF=CF.
DH=BC+AD,
即AB+CD=BC+AD. (2)过点B作⊙O的切线,交AD于点M. 由(1)可知BM+CD=BC+MD. ∵AB<AM+BM,
∴AB+BM+CD<AM+BM+BC+MD,
即AB+CD<BC+AD.
∵AB=2,∴OE=DE.
∴△ODE是等边三角形. ∴∠ODE=∠OED=60°. ∵DE∥AB, ∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°.
∴△AOD和△BOE是等边三角形.
∴∠OAD=∠OBE=60°.
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°. ∴△CDE是等边三角形.
BD BC 2 1 , ∵tan A= AB AC 4 2 1 1 5 . ∴BD= AB 5. CE BD 2 2 2
12.【中考•泸州】如图,⊙O与Rt△ABC的直角边AC和斜 边AB分别相切于点C,D,与边BC相交于点F,OA与 CD相交于点E,连接FE并延长交AC边于点G. (1)求证:DF∥AO;
3.7 切线长定理,北师大版,最新版
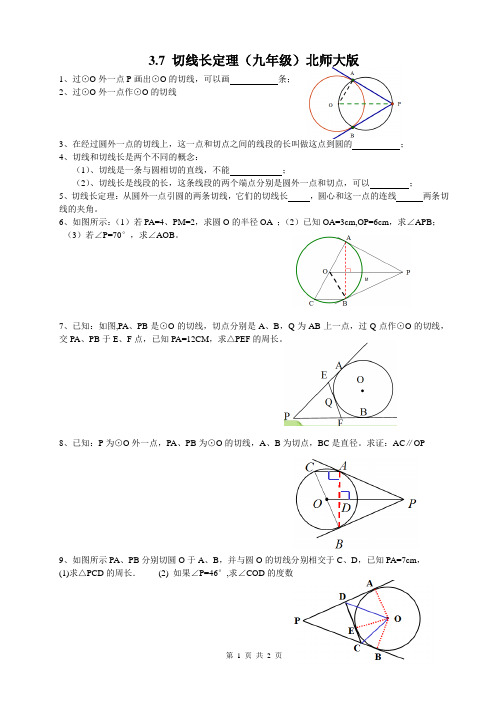
3.7 切线长定理(九年级)北师大版1、过⊙O外一点P画出⊙O的切线,可以画条;2、过⊙O外一点作⊙O的切线3、在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的;4、切线和切线长是两个不同的概念:(1)、切线是一条与圆相切的直线,不能;(2)、切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以;5、切线长定理:从圆外一点引圆的两条切线,它们的切线长,圆心和这一点的连线两条切线的夹角。
6、如图所示:(1)若PA=4、PM=2,求圆O的半径OA ;(2)已知OA=3cm,OP=6cm,求∠APB;(3)若∠P=70°,求∠AOB。
7、已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。
8、已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,BC是直径。
求证:AC∥OP9、如图所示PA、PB分别切圆O于A、B,并与圆O的切线分别相交于C、D,已知PA=7cm,(1)求△PCD的周长.(2) 如果∠P=46°,求∠COD的度数DL M N A B C O P10、如图,四边形ABCD 的边AB 、BC 、CD 、DA 和圆⊙O 分别相切于点L 、M 、N 、P ,求证: AD+BC=AB+CD11、如图,△ABC 中,∠C =90º ,它的内切圆O 分别与边AB 、BC 、CA 相切于点D 、E 、F ,且BD=12,AD=8,求⊙O 的半径r.12、如图,AB 是⊙O 的直径,AD 、DC 、BC 是切线,点A 、E 、B 为切点,(1)求证:OD ⊥ OC(2)若BC=9,AD=4,求OB 的长.13、如图,AB 是⊙O 的直径,AD 、DC 、BC 是切线,点A 、E 、B 为切点,若BC=9,AD=4,求OE 的长.。
3.7 切线长定理课件(共19张PPT) 北师大版九年级下册数学

点,可以度量.
预习导学
3.过圆外一点画圆的两条切线,它们的切线长 相等 .
·导学建议·
在引入时,教师可找实物悠悠球,拆开球,出示球的剖面,
球的整体和中心轴可分别抽象成圆形,被拉直的线绳可抽象成
线段.
预习导学
1.如图,PA、PB是☉O的切线,切点分别是A、B,若PB=5
A.32°
B.48°
C.60°
D.66°
(1)写出此图中相等的线段.
(2)请你设计一种可以通过计算求出直径
的测量方法.(写出主要解题过程)
合作探究
解:(1)根据切线长定理,知AB=AC.
(2)如图,连接OB、OA.
根据切线长定理,得∠OAB=60°.
在直角三角形AOB中,OB= AB,
则只需测得AB的长,即可求得圆的直径.
合作探究
如图,P为☉O外一点,PA、PB为☉O的切线,A和B是切
学习.
预习导学
根据条件画出图形:已知☉O外一点P,过点P作☉O的切线,
可以画几条?
你有几种方法?
预习导学
切线长的概念
阅读教材本课时相关内容,并回答下列问题.
1.过圆外一点作圆的切线,这点和 切点 之间的 线段
叫做这点到圆的切线长.
预习导学
2.切线和切线长有何区别?
切线和切线长是两个不同的概念,切线是直线,不能度量;
合作探究
(2)∵CD是☉O的切线,∴CA=CE,DB=DE,
∴AC+BD=CD,
△PCD的周长=PC+PD+CD=PC+PD+AC+BD=PA+
PB=20.
合作探究
如图,AB是☉O的直径,点C为☉O外一点,CA、CD
北师版数学下册3.7切线长定理(练习题课件)

解:直线 CD 与⊙O 相切.理由如下: 连接 OC. ∵CB=CD,CO=CO,OB=OD, ∴△OCB≌△OCD(SSS). ∴∠ODC=∠OBC=90°. ∴OD⊥CD.∴直线 CD 与⊙O 相切.
(2)若 BE=2,DE=4,求⊙O 的半径及 AC 的长. 解:设⊙O 的半径为 r.∴OE=4-r. 在 Rt△ OBE 中,∵OE2=OB2+EB2,∴(4-r)2=r2+22. 解得 r=1.5,即⊙O 的半径为 1.5.∵tan E=OBEB=CDDE, ∴12.5=C4D.∴CD=BC=3. 在 Rt△ ABC 中,AC= AB2+BC2= 32+32=3 2.
11.【2019·资阳】如图,AC 是⊙O 的直径,PA 切⊙O 于点 A, PB 切⊙O 于点 B,且∠APB=60°. (1)求∠BAC 的度数;
解:∵PA 切⊙O 于点 A,PB 切⊙O 于点 B, ∴PA=PB,∠PAC=90°. ∵∠APB=60°,∴△APB 是等边三角形,∴∠BAP=60°, ∴∠BAC=∠PAC-∠BAP=30°.
4.将一把直尺,含 60°角的直角三角尺和光盘如图摆放,AB=3, 则光盘的直径是( ) A.3 B.3 3 C.6 D.6 3
【点拨】如图,设三角尺与光盘的切点为 C,光盘所在圆的圆心 为 O,连接 OA,OB,则∠BAC=120°. 易知 AO 平分∠BAC,∴∠OAB=60°,∴∠AOB=30°, ∴在 Rt△ ABO 中,OA=2AB=6, ∴OB= OA2-AB2=3 3.∴光盘的直径为 6 3,故选 D. 【答案】D
证明:如图,连接OD,OE.∵AB=2, ∴OA=OD=OE=OB=1. ∵DE=1,∴OD=OE=DE.∴△ODE是等边三角形. ∴∠ODE=∠OED=60°.∵DE∥AB,∴∠AOD=∠ODE=60°, ∠ EOB = ∠ OED = 60°. ∴ △ AOD 和 △BOE 都 是 等 边 三 角 形.∴∠OAD=∠OBE=60°.∵DE∥AB,∴∠CDE=∠OAD= 60° , ∠ CED = ∠ OBE = 60°. ∴ △ CDE 是 等 边 三 角 形 . ∵ DF 是 ⊙O的切线,∴OD⊥DF.∴∠EDF=90°-60°=30°.∴∠DFE= 90°.∴DF⊥CE.∴CF=EF.
北师大版九年级下册数学3.7【教学课件】《切线长定理》 (共22张PPT)

O
P
B 图2
北京师范大学出版社 九年级 | 下册
1、如图, PA和PB分别与⊙O相切于点A、B ,点P到⊙O的切线长可以用哪一 条线段的长来表示?
A
2、思考:点P到⊙O的切线有几条?
O P
B 图2
北京师范大学出版社 九年级 | 下册
3、既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条 线段之间一定存在着某种关系,你能发现是什么关系呢?
A
D
C P
O
B
E
北京师范大学出版社 九年级 | 下册
中考 试题
1、如图,过⊙O外一点作⊙O的切线PA、PB,A、B为切点,C为弧AB
1 上一点,设∠APB= 求证:∠ACB= 90 2
A
.
O
C
P
B
北京师范大学出版社 九年级 | 下册
中考 试题
2.如图,PA、PB 切⊙O于A、B,PO 交AB 于E,下列等式
E
北京师范大学出版社 九年级 | 下册
问题3:如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三 角形的内切圆,图8中存在切线长定理吗?
O 图8
O
O
问题4:如果有一张三角形的铁皮,如何在它的上面截下一块圆形的用料 ,并且使圆的面积尽可能最大?
北京师范大学出版社 九年级 | 下册
问题5:请同学们先在课堂练习本上作出有关已知⊙O的四条切线,如图9, 再互相交流与讨论四条切线围成的四边形(即圆的外切四边形)有什么性质, 发现结论并加以证明。 结论:圆的外切四边形的两组对边的和相等.
A
O
P
B 图2
北京师范大学出版社 九年级 | 下册
九年级数学北师大版下册课件:第三章 3.7 切线长定理(共26张PPT)

∵∠CBA=70°,∴∠ADC=110°,∠ODC=60
°.又∵OP⊥CD,∴∠OQD=90°. ∴OQ=OD·sin60°=2× 23= 3. ∴DQ=OD·cos60°=1. ∵PD 是切线,∴∠PDO=90°.∴∠PDC=30°. ∴PQ=DQ·tan30°=1× 33= 33. ∴OP=PQ+QO=4 3 3.
探究二:如图,△ABC 的内切圆⊙O 与 BC,CA,
AB 分别相切于点 D,F,E,且 AB=9 cm,BC=14 cm, CA=13 cm,求 AE,BD,CF 的长.
解:设 AE=x,BD=y,CF=z,
由切线长定理列方程组xy+ +yz= =91, 4,得xy= =45, , x+z=13, z=9.
∴OD=CD=4-x,∵∠A=∠A,∠ADO=∠ACB,∴
△ADO∽△ACB,∴AADC=BODC,即x4=4-6 x,∴x=1.6.
7. (2018·绵阳)如图,AB 是⊙O 的直径,点 D 在 ⊙O 上(点 D 不与 A,B 重合),直线 AD 交过点 B 的切
线于点 C,过点 D 作⊙O 的切线 DE 交 BC 于点 E. (1)求证:BE=CE; (2)若 DE∥AB,求 sin∠ACO 的值.
∴BC=2r,AC=2 2r, 在 Rt△COB 中,∴OC= 5r,
又∵S△ACO=21·AO·BC=21·AC·OH,
∴r×2r=2 2r×OH,∴OH= 22r,
在
Rt△COH
OH 中,∴sin∠ACO=OC=
225rr=
1100.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10
初三下数学课件(北师大)-切线长定理
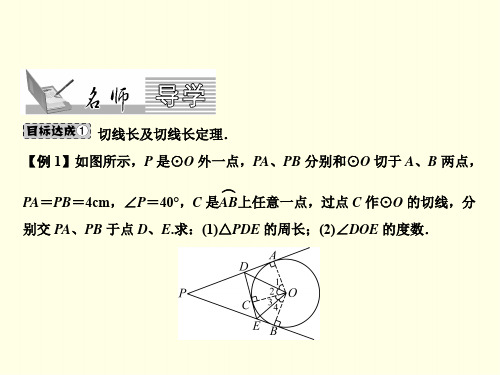
12.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,
A、B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD、BE 于点 M、 3
解:(1)△ABC 为等腰三角形,∵△ABC 的内切圆⊙O 与 AB、BC、AC 分 别相切于点 D、E、F,∴∠CFO=∠CEO=∠BDO=∠BEO=90°,∵四边
︵︵ 形内角和为 360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵EF=DE, ∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC 为等腰三角形;
切线长定理的综合运用. 【例 2】如图所示,在△ABC 中,∠C=90°,AC=8,AB=10,点 P 在 AC 上,AP=2,若⊙O 的圆心在线段 BP 上,且⊙O 与 AB、AC 都相切,则⊙ O 的半径是( A )
A.1 C.172
B.45 D.94
【思路分析】如图所示,过点 O 作 OD⊥AC,OE⊥AB,OF⊥BC,垂足分 别为 D、E、F,CP=AC-AP=8-2=6,BC= AB2-AC2= 102-82=6. ∴CP=CB,∴∠CPB=∠CBP=45°,设⊙O 的半径为 r,则 OD=OE=DP =r,BF=OF=6-r,AD=AE=r+2,BE=8-r,在 Rt△BOE 中,由勾 股定理,得 BE2+OE2=BO2,而 BO2=BF2+OF2,即(8-r)2+r2=2(6-r)2, ∴r=1.
⊙O 的切线条数为( C )
A.0 条
B.1 条
C.2 条
D.无数条
下册 切线长定理-秋九年级北师大版数学全一册作业课件PPT

15、愚痴的人,一直想要别人了解他。有智慧的人,却努力的了解自己。 8、不是某人使我烦恼,而是我拿某人的言行来烦恼自己。 7 、思忆常会在夜静灯昏时翻开甜酸苦辣也成了一道最凄美的风景线,陈旧的美无法在代谢中泯灭。 20 、机会靠自己争取,命运需自己把握,生活是自己的五线谱,威慑呢们不亲自演奏好它? 让内心强大的句子
11、成长是一件很漫长的事。从你呱呱落地开始到你最终闭上眼睛那一刻为止,你无时无刻不在成长。成长不只是有身体的不断变化,还有 你知识的不断增加、感情的不断丰富和智慧的不断提高
5、不要为没有达到目标而沮丧,因为你在出发前就已经明白了挫折的意义。这成长的烦恼,也正是我成长快乐,我应该从容地面对它。唯 有挫折,才能让我进步,让我迈向成功的方向,为我修建成功的道路。
17、我觉得长大仿佛就在一念之间。落雨了,会自然而然的带一把伞,独自一人撑一把伞,漫步在迷蒙的细雨中,用心去感受着独特的浪漫
与温馨,而不会再像小时候一样一头扎进雨帘中嬉闹,满不在乎自己被浇成一支落汤鸡。当听到别人夸奖自己时脸上会突然飘来几朵红云,而 不像小时候一样只会歪着脑袋傻笑……哦!长大的感觉是什么?长大的感觉是雨后萌芽的翠绿的嫩芽,花瓣上滚动的羞涩的露珠儿。 13 、如果青春是醺人欲醉的海风,那么自信就是这和风前行的路标;如果青春是巍峨入云的高耸,那么拼搏就是这山脉层层拔高的动力;如果青 春是高歌奋进的谱曲,那么坚强就是这旋律奏响的最强音! 16 、在被动地生与死之间,种种美好的的愿望,让我们主动地去满足自己种种莫明其妙的反感,让我们去争取。总有一天,我们老了,面朝 大海,看千帆竞发,百舸争流,匆匆的来,也匆匆地去,我们不会伤感,也不应伤感。
北师大版九年级数学下册第三章《 3-7 切线长定理》优课件(共20张PPT)

如图:用两根带有刻度的木条做一个夹角为60°的 工具尺,你能用它量出一个圆的半径吗?
若量出角的顶点到切点的距离为10cm,试求这个圆 半径的近似值。
三角形的外接圆: 三角形的内切圆:
学科网
A
A
O
B
C
B
I C
D
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月4日星期一2022/4/42022/4/42022/4/4 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/42022/4/42022/4/44/4/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/42022/4/4April 4, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
谢谢观赏
You made my day!
我们,还在路上……
学科网
A
O
·
P
B
① PA=PB
连结OA、OB、
② PO平分∠APB ∵PA、PB与⊙O相切,点
A、B是切点
∴OA⊥AP,OB⊥BP
A O
·
∴∠OAP=∠OBP=90°
∵OA=OB,OP=OP
1 ∴Rt△AOP≌Rt△BOP 2 P ∴PA=PB
∠1 =∠2
B
切线长定理
从圆外一点可以引圆的两条切 线,
B
┐ E
C
【例题】
【例1】△ABC的内切圆⊙O与BC,CA,AB分别相切于
点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,
初中数学《切线长定理》公开课ppt北师大版1

•
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
•
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
证明∵:PA、DC为⊙O的切线
∴DA=DE (切线长定理)
同理可证 CE=CB,PA=PB D
又∵C△PCD=PD+PC+CD
=PD+PC+DE+CE P
E
A ·O
=PA+PB =7+7
C B
=14 cm
练 一练 探究∠BOC与∠A有何数量关系?
4、如图,△ABC中,∠ ABC∠=A6=04°0°,∠ACB=80 °,点O
2、如果作辅助线把OP连接起
O
P
来,∠APO和∠ BPO又有何关系?
B
∠APO=∠ BPO
你能证明你的猜想吗?
推理论证
已知:从⊙O外的一点P引两条切线PA, PB,切点分别是A、B. 求证: AP=BP, ∠OPA=∠OPB
证明:连接OA,OB
A
∵PA,PB与⊙O相切,
点A,B是切点。
∴OA⊥PA,OB⊥PB
CE=9 cm
C
课堂小结
1、切线长概念 经过圆外一点作圆的切线,这点和切点之间的 线段的长,叫做这点到圆的切线长。
2、切线长定理 从圆外一点可以引圆的两条切线,它们的切线长相 等,这一点和圆心的连线平分两条切线的夹角。
3、与三角形各边 都相切的圆 ,叫做三角形 的 内切圆.
