广州中考数学压轴题汇总
广州各区数学中考一模压轴题汇总

一、选择填空2、如图6,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=5.下列结论:①△APD≌△AEB;②点B到直线AE的距离为2;③EB⊥ED;④S△APD+S△APB=1+6;⑤S正方形ABCD=4+6.其中正确结论的序号是* .(二)黄浦区图6(三)铁一中学1、定义[]c b a ,,为函数c bx ax y ++=2的特征函数,下面给出特征数为[]m m m 2-11,,+-的函数的一些结论:①当3=m 时,函数图像的顶点坐标是()8-1-,;②当1>m 时,函数图像截x 轴所得的线段长度定点。
其中正确的结论有( ) A .1个 B .2个C .3个D . 4个2、如图,在平面直角坐标系中,矩形OABC的顶点CA、分别在x轴的负半轴、y轴的正半轴上,点B(四)白云区第16题图(六) 番禺区1、抛物线92-=x y 与x 轴交于A 、B 两点,点P 在函数xy 3=的图像上,若△PAB 为直角三角形,则满足条件的点P 的个数为( )【A 】2个; 【B 】3个; 【C 】4个; 【D 】6个.2、直线y=x-2与x 轴、y 轴分别交于点B 、C ,与反比例函数xk y =(k>0)的图象在第一象限交于点A ,连接OA ,若S △AOB :S △BOC=1:2,则k 的值为( )(七)海珠区10、正方形ABCD 中,对角线AC 、BD 相交于点O ,DE 平分∠ADO 交AC 于点E ,把△ADE 沿AD 翻折,得到△ADE ’。
点F 是DE 的中点,连接AF 、BF 、E ’F ’。
若AE=2.下列结论:①AD垂直平分EE ’;②tan ∠ADE=12-;③122-=-∆∆ODE ADE C C ;④223'+=AEFE S 四边形。
其中结论正确的是( )第16题图16、设关于x 的方程04)4(2=--+k x k x 有两个不相等的实数根21,x x ,且2120x x <<<,那么k 的取值范围是(八)花都区10. 如图,在矩形ABCD 中,点F 在AD 上,点E 在BC 上,把这个矩形沿EF 折叠后,使点D 恰好落在BC 边上的G 点处,若矩形面积为60AFG ∠=︒,2GE BG =,则折痕EF 的长为( D ) A .4 B. C .2 D.16.如图,30MON ∠=︒,点1B 在边OM上,1OB =过点1B 作11A B OM ⊥交ON 于点1A ,以11A B 为边在11B OA ∆外侧作等边三角形111C B A ∆,再过点1C 作22A B OM ⊥,分别交OM ,ON 于点2B 、2A ,再以22A B 为边在22B OA ∆的外侧作等边三角形222C B A ∆……按此规律进行下去,则第3个等边三角形333C B A ∆的周长为 ,第n 个等边三角形n n n C B A ∆的周长为 .(用含n 的代数式表示)272 136()2n -(九)华工附中10.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,并且关于x 的一元二次方程20ax bx c m ++-=有两个不相等的实数根,下列结论:①240b ac -<;②0abc >;③0a b c -+<;④2m >-.其中,正确的个数有( ). A .1 B .2C .3D .416.已知二次函数222y x mx =++,当2x >时,y 的值随x 值的增大而增大,则实数m 的取值范围是__________.(十)广雅10.如图,在平面直角坐标系中,正三角形OAB 的顶点B 的坐标为(2,0),点A 在第一象限内,将△OAB 沿直线OA 的方向平移至'''B A O △的位置,此时点'A 的横坐标为3,则点'B 的坐标为( )A.(4,32)B.(3,33)C.(4,33)D.(3,32)16.如图,在矩形ABCD 中,E 是AD 边的中点,BE ⊥AC,垂足为点F ,连接DF.分析下列四个结 论:①△AEP ∽△CAB ;②CF=2AF ;③DF=DC ;④43tan =∠CAD .其中正确的结论是_____.(十一)四中10.如图,PA 、PB 切○O 于A 、B 两点,CD 切○O 于点E 交PA ,PB 于C ,D. 若○O 的半径为r ,△PCD 的周长等于3r ,则tan ∠APB 的值是( ) A. B.C.D.16.如图,已知:点A是双曲线在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限,随着点A的运动,点C得位置也不断变化,但点C始终在双曲线>上运动,则k的值是。
10-14年广州中考数学压轴题及答案详解

24. (2014?广州)(本小题满分14分)已知平面直角坐标系中两定点A( -1, 0), B( 4, 0),抛物线「过点A B,顶点为C.点P( m n)( n<0)为抛物线上一点.(1) 求抛物线的解析式与顶点C的坐标.(2) 当/ APB为钝角时,求m的取值范围.(3) 若」,当/ APE为直角时,将该抛物线向左或向右平移t ( • I )个单位,点P、2 2C移动后对应的点分别记为「-、」,是否存在t ,使得首尾依次连接A E」所构成的多边形的周长最短?若存在,求t值并说明抛物线平移的方向;若不存在,请说明理由.【考点】动点问题.(1)二次函数待定系数法;(2) 存在性问题,相似三角形;(3) 最终问题,轴对称,两点之间线段最短a-b-2^0解得:;16滋+ 4占-4 = 01 , 3抛物线解析式为;' ■::2 2一b 3 3 1 .顶点横坐标,将:- 代入抛物线得r -2a2 2 2] 3⑵如图,当二七三—时,设' ,1 2 3沪一沪一2过-作直线' | 轴,.;匸匚亠;一MED-出FD.AE_DF_1 a~-2b = -2【答案】(1)解:依题意把.丨「的坐标代入得:_x,-_x n~ 22 2 4-心.. ------------------------ =------------------ ------ (注意用整体代入法)知+1 2 3严-尹2解得—丄工.:——二当「在止丄N之间时,―二—.丁「或二:•〔:: 一时,_■_■ 11 为钝角.(3)依题意m>3,且山哥二吋■■刊3厂2)设丨'移动- :厂向右,-,向左)玖3+盒*(和厂字)2 8连接又匚「’」的长度不变.四边形周长最小,只需最小即可将一"一]沿T轴向右平移5各单位到处13三“「上一最小,且最小为,此时「「--2医讣+—兰2 8[(3^t)k+b = 2"直+2 28 即^ "'I.:28 28二宀厶:」,解得:28 281541;沿.T轴对称为厂•••当且仅当、B、r三点共线时, 二■:.J., 设过的直线为-二,代入如图7,梯形O中,土」二,八E J厂-,丄’:,芒;—四,二:|,点二为线段CD上一动点(不与点C重合),ABCS 关于BE的轴对称图形为丄三,连接一丁,设二,..,_匸「的面积为的面积为:.(1)当点「落在梯形ABCD的中位线上时,求.丁的值;、、一爲…卄(2)试用」.表示,,并与出」.的取值氾围;S.(3)当的外接圆与,丄相切时,求,的值.【答案】解:(1)如图1,£:为梯形丄二「二的中位线,则CH 二HB=2,过点匸作>:丄上二于点丄,则有:厂厂一、一;.工一’厂一■.在―二中,有.在二_ a 中,■■一 d 口厂卩工丁又m ::.<-■-- ■丿厂-+解得:(2)如图2,二:交」「于点「,厂r二「了与吭上关于,亏对称, 则有:—二,又-亠」二:伽-出CJ 护黑€又川二上与二—关于丄丄对称,-工;「二•'江岚,-,「门二";|-- 二邑二涯二隆二工(0“金)■ 5 汕16(3)如图3,当m;文的外接圆与,匕,相切时,则匚「为切点• 的圆心落在丄丄的中点,设为二则有.口」”过点[作,「丄y丄汇.mT 连接—「得恥=耐?,则陀=『罔占韦i又匸亠二一―亠..色辿」x2石丄耐+竺+《丄+竺2 2 2 2 2 2 2 解得:.〔—「*•[ :...-二丄匚(舍去).笙匕(J2+20舛川9-8常右16 16① ② ③24. (2013?广州)(本小题满分14分)已知AB是O O的直径,AB=4,点C在线段AB的延长线上运动,点D在O O上运动(不与点B重合),连接CD,且CD=OA.(1) 当OC= 2 .2时(如图12),求证:CD是O O的切线;(2) 当OC> 2.2时,CD所在直线于O O相交,设另一交点为E,连接AE.①当D为CE中点时,求△ ACE的周长;②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE-ED的值;若不存在,请说明理由。
2024广东中考数学压轴题

2024广东中考数学压轴题一、在直角坐标系中,抛物线y = ax2 + bx + c与x轴交于点A(-3,0)和B(1,0),且与y 轴交于点C(0,3)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 抛物线的对称轴是直线x = -1(答案:D)二、已知三角形ABC的三边长为a,b,c,且满足a2 + b2 + c2 = 10a + 6b + 8c - 50。
则下列判断三角形ABC的形状中,正确的是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形(答案:D)三、函数y = (x - 1)/(x + 2)中,当x的值增大时,y的值会:A. 一直增大B. 一直减小C. 在某个区间内增大,在另一个区间内减小D. 保持不变(答案:C)四、已知四边形ABCD是平行四边形,且AB = 6,BC = 8,对角线AC与BD相交于点O,则下列关于O点到AB和BC的距离d1和d2的说法正确的是:A. d1 + d2 = 14B. d1 × d2 = 24C. d1/d2 = AB/BCD. d12 + d22 = AB2 + BC2(答案:B)五、圆O的半径为5,点P在圆O外,且OP = 8。
过点P作圆O的两条切线,分别与圆O 相切于点A和B。
则弦AB的长度为:A. 6B. 4√3C. 5√2D. 2√15(答案:A)六、在数轴上,点A表示的数为-2,点B表示的数为3。
若点C表示的数为x,且满足AC + BC = 8,则x的值为:A. -3或4B. -4或3C. -3或-1D. 2或-5(答案:B)七、已知二次函数y = ax2 + bx + c的图像经过点(1,0),(2,0)和(3,4)。
下列说法正确的是:A. a > 0B. b < 0C. c = 0D. 函数的顶点在x轴上(答案:A)八、正方形ABCD的边长为4,点E在边AB上,且AE = 1。
广州中考数学压轴题(学生版)

1.如图,以O 为原点的直角坐标系中,A 点的坐标为(0,1),直线1交x 轴于点B 。
P 为线段上一动点,作直线⊥,交直线1于点C 。
过P 点作直线平行于x 轴,交y 轴于点M ,交直线1于点N 。
(1)当点C 在第一象限时,求证:△≌△;(2)当点C 在第一象限时,设长为m ,四边形的面积为S ,请求出S 与m 间的函数关系式,并写出自变量m 的取值范围;(3)当点P 在线段上移动时,点C 也随之在直线1上移动,△是否可能成为等腰三角形?如果可能,求出所有能使△成为等腰三角形的点P 的坐标;如果不可能,请说明理由。
说明:●考查字母运算能力 ● 分类讨论思想,取值范围内解的有效性 ●2.关于x 的二次函数y =2+(k 2-4)x +22以y 轴为对称轴,且与y 轴的交点在x 轴上方.(1)求此抛物线的解析式(2)设A 是y 轴右侧抛物线上的一个动点,过点A 作垂直x 轴于点B,再过点A 作x 轴的平行线交抛物线于点D ,过D 点作垂直x 轴于点C, 得到矩形.设矩形的周长为C ,点A 的横坐标为x ,试求C 关于x 的函数关系式;(3)当点A 在y 轴右侧的抛物线上运动时,矩形能否成为正方形.若能,请求出此时正方形的周长;若不能,请说明理由.x 第1题图 第2题图说明:●考查字母运算能力●分类讨论思想,取值范围内解的有效性●方法多样化,易错点为用字母表示边长时,注意边长的非负性3.如图所示, 在平面直角坐标系中, 矩形的边长、分别为12、6, 点A、C 分别在y轴的负半轴和x轴的正半轴上, 抛物线2经过点A、B, 且18a + c = 0.(1)求抛物线的解析式.(2)如果点P由点A开始沿边以1的速度向终点B移动, 同时点Q由点B开始沿边以2的速度向终点C移动.①移动开始后第t秒时, 设△的面积为S, 试写出S与t之间的函数关系式, 并写出t的取值范围.②当S取得最大值时, 在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形如第3题图果存在, 求出R点的坐标, 如果不存在, 请说明理由.说明:●图形必须准确,存在性问题如果不会做,可通过画图判断(答存在得分的机会大得多)4.已知二次函数2++c与x轴交于A(-1,0)、B(1,0)两点.(1)求这个二次函数的关系式;(2)若有一半径为r 的⊙P ,且圆心P 在抛物线上运动,当⊙P 与两坐标轴都相切时,求半径r 的值.(3)半径为1的⊙P 在抛物线上,当点P 的纵坐标在什么范围内取值时,⊙P 与y 轴相离、相交?说明:●考查画图能力和字母运算能力 ●分类讨论思想,取值范围内解的有效性 ● 方法多样化,易错点为用字母表示边长时,注意边长的非负性5.如图示已知点M 的坐标为(4,0),以M 为圆心,以2为半径的圆交x 轴于A 、B ,抛物线c bx x y ++=261过A 、B 两点且与y 轴交于点C .(1)求点C 的坐标并画出抛物线的大致图象(2)过C 点作⊙M 的切线,求直线的解析式.说明:●图形必须准确,画切线后巧妙解法是利用两直线平行,K 相等 ●易错点为漏解(过圆外一点作圆的切线有两条) ● 两直线垂直,K 互为负倒数可以使用6.如图,在ABC ∆中,∠A 90=°,10=BC , ABC ∆的面积为25,点D 为AB 边上的任意一点(D 不与A 、B 重合),过点D 作DE ∥BC ,交AC 于点E .设x DE =以DE 为折线将△ADE 翻折,所得的DE A '∆与梯形DBCE 重叠部分的面积记为y.(1).用x 表示∆的面积;第5题图(2).求出0﹤x≤5时y与x的函数关系式;(3).求出5﹤x﹤10时y与x的函数关系式;(4).当x取何值时,y的值最大?最大值是多少?说明:●考查画图能力和字母运算能力●分类讨论思想,取值范围内解的有效性●方法多样化,在设未知数或用字母表示未知量时,要充分发挥“勾股、相似、锐角三角函数”的作用,挖掘题目中的特殊角(特殊比值)来巧妙运算7.在△中,∠A=90°,=4,3,M是上的动点(不与A、B重合),过点M作∥交于点N. 以为直径作⊙O,并在⊙O内作内接矩形,令. 当x为何值时,⊙O与直线相切?8.如图,直线334y x=+和x轴y轴分别交与点B、A,点C是的中点,过点C向左方作射线⊥y轴,点D是线段上一动点,不和B重合,⊥于点P,⊥于点E,连接。
2024中考备考重难点07中考数学选填压轴题练习(21大题型)(原卷版)

重难点07 中考数学选填压轴题练习一.根的判别式(共1小题)1.(2023•广州)已知关于x的方程x2﹣(2k﹣2)x+k2﹣1=0有两个实数根,则的化简结果是()A.﹣1B.1C.﹣1﹣2k D.2k﹣3二.函数的图象(共1小题)2.(2023•温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.【问题】路线①③⑥⑦⑧各路段路程之和为()A.4200米B.4800米C.5200米D.5400米三.动点问题的函数图象(共1小题)3.(2023•河南)如图1,点P从等边三角形ABC的顶点A出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点B.设点P运动的路程为,图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.D.四.反比例函数系数k的几何意义(共1小题)4.(2023•宁波)如图,点A,B分别在函数y=(a>0)图象的两支上(A在第一象限),连结AB交x 轴于点C.点D,E在函数y=(b<0,x<0)图象上,AE∥x轴,BD∥y轴,连结DE,BE.若AC =2BC,△ABE的面积为9,四边形ABDE的面积为14,则a﹣b的值为,a的值为.五.反比例函数图象上点的坐标特征(共2小题)5.(2023•德州)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(6,3),D是OA的中点,AC,BD交于点E,函数的图象过点B.E.且经过平移后可得到一个反比例函数的图象,则该反比例函数的解析式()A.y=﹣B.C.D.6.如图,O是坐标原点,Rt△OAB的直角顶点A在x轴的正半轴上,AB=2,∠AOB=30°,反比例函数y=(k>0)的图象经过斜边OB的中点C.(1)k=;(2)D为该反比例函数图象上的一点,若DB∥AC,则OB2﹣BD2的值为.六.反比例函数与一次函数的交点问题(共1小题)7.(2023•湖州)已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t,p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠﹣2),点C(t,m)和点D(t+2,n)在函数的图象上.当p﹣m与q﹣n的积为负数时,t的取值范围是()A.或B.或C.﹣3<t<﹣2或﹣1<t<0D.﹣3<t<﹣2或0<t<1七.二次函数图象与系数的关系(共3小题)8.(2023•乐至县)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,且过点(1,0).现有以下结论:①abc<0;②5a+c=0;③对于任意实数m,都有2b+bm≤4a﹣am2;④若点A(x1,y1)、B(x2,y2)是图象上任意两点,且|x1+2|<|x2+2|,则y1<y2,其中正确的结论是()A.①②B.②③④C.①②④D.①②③④9.(2023•丹东)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点为A(﹣3,0),与y轴交于点C,点D是抛物线的顶点,对称轴为直线x=﹣1,其部分图象如图所示,则以下4个结论:①abc>0;②E(x1,y1),F(x2,y2)是抛物线y=ax2+bx(a≠0)上的两个点,若x1<x2,且x1+x2<﹣2,则y1<y2;③在x轴上有一动点P,当PC+PD的值最小时,则点P的坐标为;④若关于x的方程ax2+b(x﹣2)+c =﹣4(a≠0)无实数根,则b的取值范围是b<1.其中正确的结论有()A.1个B.2个C.3个D.4个10.(2023•河北)已知二次函数y=﹣x2+m2x和y=x2﹣m2(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为()A.2B.m2C.4D.2m2八.二次函数图象上点的坐标特征(共1小题)11.(2023•广东)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac 的值为()A.﹣1B.﹣2C.﹣3D.﹣4九.二次函数与不等式(组)(共1小题)12.(2023•西宁)直线y1=ax+b和抛物线(a,b是常数,且a≠0)在同一平面直角坐标系中,直线y1=ax+b经过点(﹣4,0).下列结论:①抛物线的对称轴是直线x=﹣2;②抛物线与x轴一定有两个交点;③关于x的方程ax2+bx=ax+b有两个根x1=﹣4,x2=1;④若a >0,当x<﹣4或x>1时,y1>y2.其中正确的结论是()A.①②③④B.①②③C.②③D.①④一十.三角形中位线定理(共1小题)13.(2023•广州)如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点M是边AC上一动点,点D,E分别是AB,MB的中点,当AM=2.4时,DE的长是.若点N在边BC上,且CN=AM,点F,G分别是MN,AN的中点,当AM>2.4时,四边形DEFG面积S的取值范围是.一十一.矩形的性质(共2小题)14.(2023•宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连结AE,AD,设△AED,△ABE,△ACD的面积分别为S,S1,S2,若要求出S﹣S1﹣S2的值,只需知道()A.△ABE的面积B.△ACD的面积C.△ABC的面积D.矩形BCDE的面积15.(2023•河南)矩形ABCD中,M为对角线BD的中点,点N在边AD上,且AN=AB=1.当以点D,M,N为顶点的三角形是直角三角形时,AD的长为.一十二.正方形的性质(共2小题)16.如图,在边长为4的正方形ABCD中,点G是BC上的一点,且BG=3GC,DE⊥AG于点E,BF∥DE,且交AG于点F,则tan∠EDF的值为()A.B.C.D.17.(2023•湖州)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形ABCD,相邻图形之间互不重叠也无缝隙,①和②分别是等腰Rt△ABE和等腰Rt△BCF,③和④分别是Rt△CDG和Rt△DAH,⑤是正方形EFGH,直角顶点E,F,G,H分别在边BF,CG,DH,AE上.(1)若EF=3cm,AE+FC=11cm,则BE的长是cm.(2)若,则tan∠DAH的值是.一十三.正多边形和圆(共1小题)18.(2023•河北)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.则图2中:(1)∠α=度;(2)中间正六边形的中心到直线l的距离为(结果保留根号).一十四.扇形面积的计算(共1小题)19.(2023•温州)图1是4×4方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图2),过左侧的三个端点作圆,并在圆内右侧部分留出矩形CDEF作为题字区域(点A,E,D,B在圆上,点C,F在AB上),形成一幅装饰画,则圆的半径为5.若点A,N,M在同一直线上,AB∥PN,DE=EF,则题字区域的面积为.一十五.轴对称-最短路线问题(共1小题)20.(2023•安徽)如图,E是线段AB上一点,△ADE和△BCE是位于直线AB同侧的两个等边三角形,点P,F分别是CD,AB的中点.若AB=4,则下列结论错误的是()A.P A+PB的最小值为3B.PE+PF的最小值为2C.△CDE周长的最小值为6D.四边形ABCD面积的最小值为3一十六.翻折变换(折叠问题)(共2小题)21.(2023•乐至县)如图,在平面直角坐标系xOy中,边长为2的等边△ABC的顶点A、B分别在x轴、y 轴的正半轴上移动,将△ABC沿BC所在直线翻折得到△DBC,则OD的最大值为.22.(2023•南京)如图,在菱形纸片ABCD中,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB′⊥AD,垂足为F.若CF=4cm,FB′=1cm,则BE=cm.一十七.旋转的性质(共1小题)23.(2023•西宁)如图,在矩形ABCD中,点P在BC边上,连接P A,将P A绕点P顺时针旋转90°得到P A′,连接CA′,若AD=9,AB=5,CA′=2,则BP=.一十八.相似三角形的判定与性质(共2小题)24.(2023•杭州)如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.设=k,若AD=DF,则=(结果用含k的代数式表示).25.(2023•广东)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为.一十九.相似三角形的应用(共1小题)26.(2023•南京)如图,不等臂跷跷板AB的一端A碰到地面时,另一端B到地面的高度为60cm;当AB 的一端B碰到地面时,另一端A到地面的高度为90cm,则跷跷板AB的支撑点O到地面的高度OH是()A.36cm B.40cm C.42cm D.45cm二十.解直角三角形(共1小题)27.(2023•丹东)如图,在平面直角坐标系中,点O是坐标原点,已知点A(3,0),B(0,4),点C在x 轴负半轴上,连接AB,BC,若tan∠ABC=2,以BC为边作等边三角形BCD,则点C的坐标为;点D的坐标为.二十一.解直角三角形的应用(共1小题)28.(2023•杭州)第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD中,∠ABF>∠BAF,连接BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1:n,tanα=tan2β,则n=()A.5B.4C.3D.2。
广州中考数学压轴题汇总

广州中考压轴题汇总选择题(2014·广州)如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③=;④(a﹣b)2?S△EFO=b2?S△DGO.其中结论正确的个数是()A.4个B.3个C.2个D.1个(2015·广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为()A.10 B.14 C.10或14 D.8或10(2016·广州)定义运算:a?b=a(1﹣b).若a,b是方程x2﹣x+m=0(m<0)的两根,则b?b﹣a?a的值为()A.0 B.1 C.2 D.与m有关(2017·广州)a≠0,函数y=与y=﹣ax2+a在同一直角坐标系中的大致图象可能是()A.B.C.D.(2017·广州)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到A n.则△OA2A2018的面积是()A.504m2B.m2 C.m2 D.1009m2填空题(2014·广州)若关于x的方程x2+2mx+m2+3m﹣2=0有两个实数根x1、x2,则x1(x2+x1)+x22的最小值为.(2015·广州)如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.(2016·广州)如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB 绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是.(2017·广州)如图,平面直角坐标系中O是原点,?OABC的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是;④OD=其中正确的结论是(填写所有正确结论的序号).(2018·广州)如图,CE是?ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE :S△COD=2:3.其中正确的结论有.(填写所有正确结论的序号)解答题(2014·广州24)已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时,求m的取值范围;(3)若m>,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.(2014·广州25)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,连接CF.设CE=x,△BCF的面积为S1,△CEF的面积为S2.(1)当点F落在梯形ABCD的中位线上时,求x的值;(2)试用x表示,并写出x的取值范围;(3)当△BFE的外接圆与AD相切时,求的值.(2015·广州24)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.(1)试探究筝形对角线之间的位置关系,并证明你的结论;(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.(2015·广州25)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1?x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.(1)求点C的坐标;(2)当y1随着x的增大而增大时,求自变量x的取值范围;(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.(2016·广州24)已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B(1)求m的取值范围;(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.(2016·广州25)如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°(1)求证:BD是该外接圆的直径;(2)连结CD,求证:AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.(2017·广州24)如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.(1)求证:四边形OCED是菱形;(2)连接AE,若AB=6cm,BC=cm.①求sin∠EAD的值;②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.(2017·广州)如图,AB是⊙O的直径,=,AB=2,连接AC.(1)求证:∠CAB=45°;(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD.①试探究AE与AD之间的数量关系,并证明你的结论;②是否为定值?若是,请求出这个定值;若不是,请说明理由.(2018·广州24)已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=﹣的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求的值.(2018·广州25)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.。
挑战压轴题解答题(真题汇编压轴特训)-2024年中考数学冲刺 挑战压轴题专题汇编(广州卷)(原卷版)

03挑战压轴题(解答题一)(1)尺规作图:将法);(2)在(1)所作的图中,连接V①求证:ABD②若tan BAC∠2.(2022·广东广州·统考中考真题)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆的AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD = 1.6m,BC =5CD.(1)求BC的长;(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.条件①:CE = 1.0m;条件②:从D处看旗杆顶部A的仰角α为54.46°.注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin54.46°≈0.81,cos54.46°≈0.58,tan54.46°≈1.40.(1)求A 、B 两点的坐标;(2)设PAO V 的面积为S ,求S 关于x 的函数解析式:并写出x 的取值范围;(3)作PAO V 的外接圆C e ,延长PC 交C e 于点Q ,当POQ △的面积最小时,求C e 的半径.(1)沿AC BC 、剪下ABC V ,则ABC V 是_______三角形(填“锐角______.(2)分别取半圆弧上的点E 、F 和直径AB 上的点G 、H .已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm 的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);2.(2022上·陕西西安·九年级校考期中)如图,在等边ABC V 中,点D 是AB 边上的一个动点(不与点A ,B 重合),以CD 为边作等边EDC △,AC 与DE 交于点F ,连接AE .(1)求证:ADF BCD △∽△;(2)若:5:2AB BD =,且20AB =,求ADF △的面积.3.(2022·安徽合肥·统考一模)如图,在正方形ABCD 中,9AB =,E 为AC 上一点,以AE 为直角边构造等腰直角AEF △(点F 在AB 左侧),分别延长FB ,DE 交于点H ,DH 交线段BC 于点M ,AB 与EF 交于点G ,连结BE .(1)求证:AFB AED≅V V (2)当62AE =时,求sin MBH ∠的值.(3)若BEH △与DEC V 的面积相等,记△(1)当点D 与圆心O 重合时,如图2所示,求DE 的长.(2)当CEF △与ABC V 相似时,求cos BDE ∠的值.6.(2023下·安徽蚌埠·九年级校考开学考试)如图,矩形ABCD 中,8AB =厘米,12BC =厘米,P 、Q 分别是AB 、BC 上运动的两点,若点P 从点A 出发,以1厘米/秒的速度沿AB 方向运动,同时,点Q 从点B 出发以2厘米/秒的速度沿BC 方向运动,设点P ,Q 运动的时间为x 秒.(1)设PBQ V 的面积为y ,求y 与x 之间的函数关系式及自变量x 的取值范围;(2)当x 为何值时,以P ,B ,Q 为顶点的三角形与BDC V 相似?7.(2021下·湖北随州·七年级统考期末)阅读材料:在平面直角坐标系中,二元一次方程0x y -=的一个解11x y =⎧⎨=⎩可以用一个点(1,1)表示,二元一次方程有无数个解,以方程0x y -=的解为坐标的点的全体叫作方程0x y -=的图象.一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程0x y -=的图象称为直线0x y -=.直线x -y =0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M (x 0,y 0)的坐标满足不等式x -y ≤0,那么点M (x 0,y 0)就在直线x -y =0的上方区域内。
2023广州中考数学压轴题

中考数学试卷一、单项选择题(共12分)1.如图,在三角形ABC中D,E分别是AB和AC上的点,且DE平行BC,AE 比EC=5/2,D E=10,则BC的长为()。
A.16B.14C.12D.112.一元二次方程x2﹣3x=0的根是()A.x=3 B.x1=0,x2=﹣3C.x1=0,x2=√3 D.x1=0,x2=33.如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()A.4对 B.3对C.2对D.1对4.如图,一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了()A.4圈B.3圈C.5圈D.3.5圈5.一个由相同正方体堆积而成的几何体如图所示,从正面看,这个几何体的形状是()。
A.B.C.D.二、填空题(共24分)6.小明和小红在阳光下行走,小明身高1.75米,他的影长2.0米,小红比小明矮7厘米,此刻小红的影长是()米。
7.将抛物线y=﹣x2向右平移一个单位,所得函数解析式为。
(x<0)图象上的点,过点A8.如图,在平面直角坐标系中,点A是函数y=kx作y轴的垂线交y轴于点B,点C在x轴上,若△ABC的面积为1,则k的值为()。
9.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y 轴上的某一点为位似中心,作位似图形ABCD,且点B、F的坐标分别为(-4,4)、(2,1)则位似中心的坐标为()。
10.两圆的半径分别为3和5,当这两圆相交时,圆心距d的取值范围是。
三、解答题(共20分)11.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD =21,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动(到A点不停),动点Q从点C出发,在线段CB上以每秒一个单位长的速度向点B 运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒)。
广东中考数学压轴题
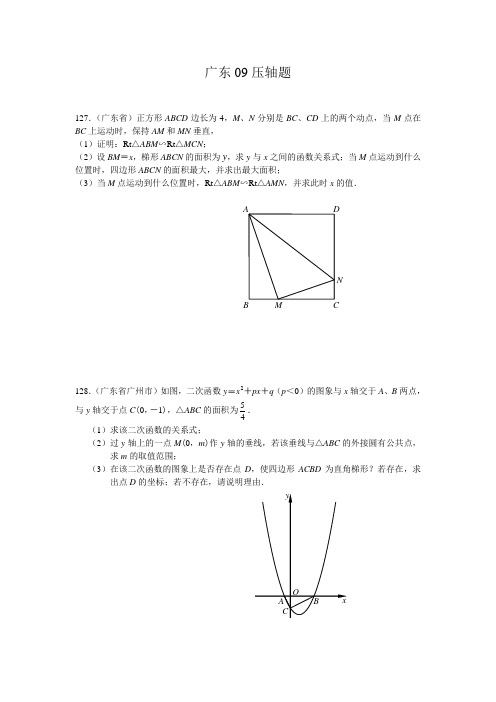
广东09压轴题127.(广东省)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt △ABM ∽Rt △MCN ;(2)设BM =x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 的面积最大,并求出最大面积;(3)当M 点运动到什么位置时,Rt △ABM ∽Rt △AMN ,并求此时x 的值.128.(广东省广州市)如图,二次函数y =x2+px +q (p <0)的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45. (1)求该二次函数的关系式;(2)过y 轴上的一点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有公共点,求m 的取值范围;(3)在该二次函数的图象上是否存在点D ,使四边形ACBD 为直角梯形?若存在,求出点D 的坐标;若不存在,请说明理由.M B CND A129.(广东省深圳市)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△P AB是否有最大面积?若有,求出此时P点的坐标及△P AB的最大面积;若没有,请说明理由.130.(广东省深圳市)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结P A,若P A=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?备用图131.(广东省深圳市)已知:Rt △ABC 的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB 与x 轴重合(其中OA <OB ),直角顶点C 落在y 轴正半轴上(如图1).(1)求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式. (2)如图2,点D 的坐标为(2,0),点P (m ,n )是该抛物线上的一个动点(其中m >0,n >0),连接DP 交BC 于点E .①当△BDE 是等腰三角形时,直接写出....此时点E 的坐标. ②又连接CD 、CP (如图3),△CDP 是否有最大面积?若有,求出△CDP 的最大面积和此时点P 的坐标;若没有,请说明理由.132.(广东省珠海市)已知抛物线y =x2-32mx 与x 轴相交于点A 、B ,抛物线的顶点为C .(1)试用含m 的代数式表示AB 的长度; (2)当△ABC 为等边三角形时,求点C 的坐标; (3)在(2)的条件下,如何平移抛物线,使AC =213AB ?133.(广东省佛山市)如图1,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A 处沿着木柜表面爬到柜角C 1处. (1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB =4,BC =4,CC 1=5时,求蚂蚁爬过的最短路径的长; (3)求点B 1到最短路径的距离. A Bxy O 图1C A B x y O PD E图2 C A BPxy O D E 图3 C 备用图 图1134.(广东省茂名市)已知:如图,直线l :y =31x +b ,经过点M (0,41),一组抛物线的顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3),…,B n (n ,y n )(n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:A 1(x 1,0),A 2(x 2,0),A 3(x 3,0),…,A n +1(x n +1,0)(n 为正整数),设x 1=d (0<d <1). (1)求b 的值;(2)求经过点A 1、B 1、A 2的抛物线的解析式(用含d 的代数式表示)(3)定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”.探究:当d (0<d <1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的d 的值.135.(广东省湛江市)已知矩形纸片OABC 的长为4,宽为3,以长OA 所在的直线为x 轴,O 为坐标原点建立平面直角坐标系;点P 是OA 边上的动点(与点OA 不重合),现将△POC 沿PC 翻折得到△PEC ,再在AB 边上选取适当的点D ,将△P AD 沿PD 翻折,得到△PFD ,使得直线PE 、PF 重合.(1)若点E 落在BC 边上,如图①,求点P 、C 、D 的坐标,并求过此三点的抛物线的函数关系式;(2)若点E 落在矩形纸片OABC 的内部,如图②,设OP =x ,AD =y ,当x 为何值时,y 取得最大值?(3)在(1)的情况下,过点P 、C 、D 三点的抛物线上是否存在点Q ,使△PDQ 是以PD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q 的坐标.136.(广东省肇庆市)如图,⊙O 的直径AB =2,AM 和BN 是它的两条切线,DE 切⊙O 于E ,交AM 于D ,交BN 于C .设AD =x ,BC =y . (1)求证:AM ∥BN ;(2)求y 关于x 的关系式;(3)求四边形ABCD 的面积S ,并证明:S≥2.137.(广东省清远市)如图,已知一个三角形纸片ABC ,BC 边的长为8,BC 边上的高为6,∠B 和∠C 都为锐角,M 为AB 上一动点(点M 与点A 、B 不重合),过点M 作MN ∥BC ,交AC 于点N ,在△AMN 中,设MN 的长为x ,MN 上的高为h . (1)请你用含x 的代数式表示h .(2)将△AMN 沿MN 折叠,使△AMN 落在四边形BCNM 所在平面,设点A 落在平面的点为A 1,△A 1MN 与四边形BCNM 重叠部分的面积为y ,当x 为何值时,y 最大,最大值为多少?138.(广东省梅州市)如图,矩形ABCD 中,AB =5,AD =3.点E 是CD 上的动点,以AE 为直径的⊙O 与AB 交于点F ,过点F 作FG ⊥BE 于点G . (1)当E 是CD 的中点时:①tan ∠EAB 的值为______________; ②证明:FG 是⊙O 的切线;(2)试探究:BE 能否与⊙O 相切?若能,求出此时DE 的长; 若不能,请说明理由.NB C N M A139.(广东省梅州市)如图,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.(1)直接写出直线L的解析式;(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.1。
(完整版)广东中考数学省卷压轴题汇总
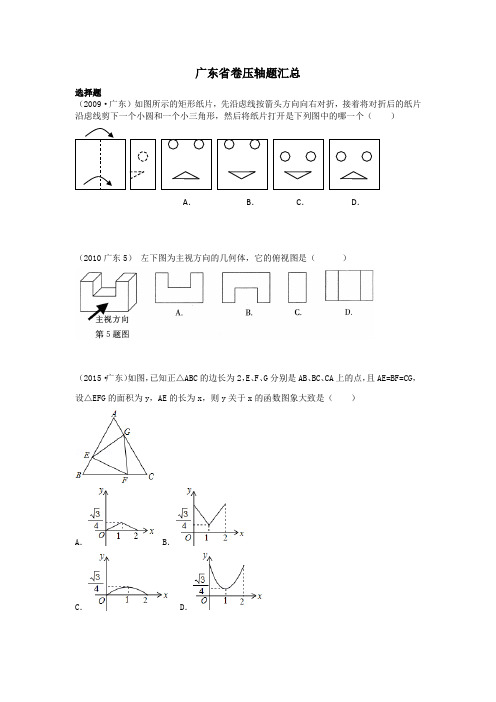
广东省卷压轴题汇总选择题(2009·广东)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( )(2010广东5) 左下图为主视方向的几何体,它的俯视图是( )(2015·广东)如图,已知正△ABC 的边长为2,E 、F 、G 分别是AB 、BC 、CA 上的点,且AE=BF=CG ,设△EFG 的面积为y ,AE 的长为x ,则y 关于x 的函数图象大致是( )A .B .C .D .C .D . A . B .(2016·广东)如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则△APC的面积y与点P运动的路程x之间形成的函数关系图象大致是()A.B.C.D.(2017·广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③ B.②③ C.①④ D.②④(2018·广东)如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为()A.B.C.D.填空题(2009)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖 __________块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表示).……(1)(2)(3)第10题图(2010广东10)如图(1),已知小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形A 1B 1C 1D 1;把正方形A 1B 1C 1D 1边长按原法延长一倍得到新正方形A 2B 2C 2D 2(如图(2));以此下去…, 则正方形A 4B 4C 4D 4的面积为 .(2011广东10)如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1和△D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…,则正六角星形A 4F 4B 4D 4C 4E 4的面积为_________________.(2012•广东)如图,在▱ABCD 中,AD=2,AB=4,∠A=30°,以点A 为圆心,AD 的长为半径画弧交AB 于点E ,连接CE ,则阴影部分的面积是 _________ (结果保留π).题10图(1)A 1BCD AFEBCD A FEB CD A FEB 1C 1F 1 D 1 E 1 A 1B 1C 1F 1 D 1 E 1 A 2B 2C 2F 2 D 2E 2 题10图(2)题10图(3)(2013•广东)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是_________ (结果保留π).(2014•广东)如图,ABC∠=︒,∆绕点A顺时针旋转45︒得到△AB C'',若90BAC==,则图中阴影部分的面积等于.AB AC(2015.广东)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是.(2016·广东)如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA、PB、PC,若PA=a,则点A到PB和PC的距离之和AE+AF= .(2017·广东)如图,矩形纸片ABCD中,AB=5,BC=3,先按图(2)操作:将矩形纸片ABCD 沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按图(3)操作,沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为.(2018·广东)如图,已知等边△OA1B1,顶点A1在双曲线y=(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为.解答题(2009.广东)正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点, 当M 点在BC 上运动时,保持AM 和MN 垂直, (1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积;(3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求此时x 的值.DM AB C第22题图N(2010广东20)已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.∆是等腰三角形;(1)求证:EGB∆绕点F逆时针旋转最小____度时,四边形ACDE成为以(2)若纸片DEF不动,问ABCED为底的梯形(如图(2)).求此梯形的高.(2011广东22)如图,抛物线1417452++-=x x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0).(1)求直线AB 的函数关系式;(2)动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N . 设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;(3)设在(2)的条件下(不考虑点P 与点O ,点C 重合的情况),连接C M ,BN ,当t 为何值时,四边形BCMN 为平行四边形?问对于所求的t 值,平行四边形BCMN 是否菱形?请说明理由.(2012•广东21)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求tan∠ABG的值;(3)求EF的长.(2012•广东22)如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).(2013•广东24)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;(3)求证:BE是⊙O的切线.(2013•广东25)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA 方向平行移动,当点F运动到点A时停止运动.(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC= _________ 度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.(2014•广东24)如图,O是ABC⊥于点D,∆的外接圆,AC是直径,过点O作OD AB延长DO交O于点P,过点P作PE AC⊥于点E,作射线DE交BC的延长线于F点,连接PF.π(1)若60AC=,求劣弧PC的长;(结果保留)POC∠=︒,12(2)求证:OD OE=;(3)求证:PF是O的切线.(2014•广东25)如图,在ABC=,8=.点AD cmBC cm⊥于点D,10∆中,AB AC=,AD BCP从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(0)t>.(1)当2t=时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的PEF∆的面积最大时,求∆的面积存在最大值,当PEF 线段BP的长;(3)是否存在某一时刻t,使PEF∆为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.(2015•广东24)⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.(2015•广东25)如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm(1)填空:AD= (cm),DC= (cm)(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A →D,C→B方向运动,当N点运动到B点时,M、N两点同时停止运动,连接MN,求当M、N 点运动了x秒时,点N到AD的距离(用含x的式子表示)(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.(参考数据sin75°=,sin15°=)(2016·广东24)如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.(1)求证:△ACF∽△DAE;(2)若S△AOC=,求DE的长;(3)连接EF,求证:EF是⊙O的切线.(2016·广东25)如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.(2017·广东24)如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当=时,求劣弧的长度(结果保留π)(2017·广东25)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C 的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为;(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)①求证:=;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y 的最小值.(2018·广东24)如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.(1)证明:OD∥BC;(2)若tan∠ABC=2,证明:DA与⊙O相切;(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.(2018·广东24)已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC= °;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N 沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y 取得最大值?最大值为多少?。
2024年中考数学压轴题型(广东专用)专题04特殊平行四边形中全等相似与最值问题(学生版)

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B (1)将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型(三点共线)• B(2)费马点模型:将边以A 为顶点逆时针旋转60。
,得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. (2023-r 东深圳•中考真题)(1)如图,在矩形ABCD 中,E 为AD 边上一点,连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证:AABE^AFCB ;②若S 矩形倔8 = 2。
时,则BECF=(2)如图,在菱形ABCD 中,cosA = |,过。
作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时,求EF BC 的值.(3)如图,在平行四边形ABCD 中,匕4 = 60。
,AB = 6, AD=5,点E 在CD 上,且CE = 2,点F 为BC 上一点,连接时,过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时,请直接写出AG 的长.D,E E a C C A B AB备用图2.(2022广东广州•中考真题)如图,在菱形ABCQ中,0BAD=120°,AB=6,连接8Q.⑴求BQ的长;⑵点E为线段BQ上一动点(不与点B,。
重合),点E在边AQ上,且BE二也DF,①当CE±AB时,求四边形的面积;②当四边形的面积取得最小值时,CE+右CT的值是否也最小?如果是,求CE+也CF的最小值;如果不是,请说明理由.题型一特殊平行四边形中全等相似计算1.(2024-P东汕头•一模)(1)如图1,在矩形ABCD中,E为AD边上一点,连接8E,①若BE=BC,过。
2023年广州中考数学压轴题回忆版

2023年广州中考数学压轴题回忆版一、题目回忆1. 下列各组数据中,哪一组数据的方差最大?A. 1,2,3,4,5B. 6,7,9,10,11C. 21,23,25,27,29D. 33,35,37,39,412. 已知直角三角形ABC中,∠B=90°,AB=3,BC=4,则AC=?A. 5B. 6C. 7D. 83. 一张半径为5cm的圆被一块长为12cm、宽为16cm的矩形纸片的一个长边所切割,则切割后圆的面积为多少?A. 10πB. 12πC. 15πD. 16π4. 已知集合A={3,4,5,6},集合B={4,5,6,7},则A∩B=?A. {4,5,6}B. {4,5,6,7}C. {3,4,5,6,7}D. 空集5. 下列函数中,哪一个是奇函数?A. y=x^3+2x^2B. y=3x^2+4xC. y=x^4+x^2D. y=3x^3+5x二、解题思路1. 题目一是考察对方差计算的理解和运用。
方差是指一组数据与其平均数之差的平方和的平均数,用于衡量数据的分散程度。
在选择答案时,需要计算每组数据的方差并做对比,选择分散程度最大的一组。
2. 题目二是利用勾股定理求解直角三角形的边长。
根据勾股定理,直角三角形的两个直角边的平方和等于斜边的平方。
结合AB和BC的已知条件,可以求得AC的长度。
3. 题目三是利用几何图形的面积计算。
首先确定圆的面积,然后根据题目所给的矩形纸片的长度和宽度,计算出被矩形纸片遮盖的圆形面积,最后利用减法得出切割后的圆的面积。
4. 题目四是利用集合的交集概念进行计算。
需要将两个集合进行交集运算,得到同时属于A和B的元素的集合。
5. 题目五是判断函数的奇偶性。
奇函数是指当自变量x变为-x时,函数值与原来的函数值互为相反数的函数。
需要对每个函数进行奇函数的特性判断,得出最终答案。
三、解题方法1. 方差的计算方法是先求出一组数据的平均数,然后将每个数据与平均数的差的平方相加,再求平均数,即可得到方差。
广东数学中考压轴题汇编

16. 如图,Rt △ABC 的直角边BC 在x 轴上,直线3232-=x y 经 过直角顶点B ,且平分△ABC 的面积,BC=3,点A 在反比例 函数xky =图像上,则k = . 23.如图,在平面直角坐标系中,直线2+=x y 与坐标轴交于A 、B 两点,点A 在x 轴上, 点B 在y 轴上,C 点的坐标为(1,0),抛物线c bx ax y ++=2经过点A 、B 、C . (1)求该抛物线的解析式;(2)根据图像直接写出不等式2)1(2>+-+c x b ax 的解集;(3)点P 是抛物线上一动点,且在直线AB 上方,过点P 作AB 的 垂线段,垂足为Q 点.当PQ=22时,求P 点坐标.24.如图,四边形ABCD 的顶点在⊙O 上,BD 是⊙O 的直径,延长CD 、BA 交于点E ,连接AC 、BD 交于点F ,作AH ⊥CE ,垂足为点H ,已知∠ADE=∠ACB .(1)求证:AH 是⊙O 的切线;(2)若OB=4,AC=6,求sin ∠ACB 的值; (3)若32=FO DF ,求证:CD=DH .25. 如图,在平面直角坐标系中,矩形OABC 的顶点B 坐标为(4,6),点P 为线段OA 上一动点(与点O 、A 不重合),连接CP ,过点P 作PE ⊥CP 交AB 于点D ,且PE=PC ,过点P 作 PF ⊥OP 且PF=PO (点F 在第一象限),连结FD 、BE 、BF ,设OP=t . (1)直接写出点E 的坐标(用含t 的代数式表示): ; (2)四边形BFDE 的面积记为S ,当t 为何值时,S 有最小值,并求出最小值; (3)△BDF 能否是等腰直角三角形,若能,求出t ;若不能,说明理由.10.如图,△ABC 中,∠ACB=90°,∠A=30°,AB=16.点P 是斜边AB 上一点.过点P 作PQ ⊥AB ,垂足为P ,交边AC (或边CB )于点Q ,设AP=x ,△APQ 的面积为y ,则y 与x 之间的函数图象大致为( )23. 如图所示,将矩形ABCD 沿AF 折叠,使点D 落在BC 边的点E 处,过点E 作EG∥CD 交AF 于点G ,连接DG . (1)求证:四边形EFDG 是菱形; (2)求证:EG 2=GF×AF;,则矩形ABCD 的 (第23题图)24. 如图所示,△OAB 中,OA=OB=10,∠AOB=80°,以点O 为圆心,6为半径的优弧MN ⌒分别交OA 、OB 于点M 、N. (1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′. 求证:AP = BP ′; (2)点T 在左半弧上,若AT 与弧MN ⌒相切于点T ,求点T 到OA 的距离; (3)设点Q 在优弧MN ⌒上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.25. 如图所示,已知抛物线y =x 2+bx +c 与x 轴交于A 、B 两点 (点A 在点B 左侧),与y 轴交于点C(0,-3),对称轴是直线x =1, 直线BC 与抛物线的对称轴交于点D . (1)求抛物线的函数表达式;(2)求直线BC 的函数表达式; (3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P在第三象限.①当线段PQ 34AB =时,求tan∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标.24.如图,正方形ABCD 的边长为2,点M 是BC 的中点,P 是线段MC 上的一个动点(不与M ,C 重合),以AB 为直径作⊙O ,过点P 作⊙O 的切线,交AD 于点F ,切点为E . (1)求证:OF ∥BE ;(2)设BP =x ,AF =y ,求y 关于x 的函数解析式,并写出自变量x 的取值范围;(3)延长DC ,FP 交于点G ,连接OE 并延长交直线DC 于H ,问是否存在点P ,使△EFO ∽△EHG (E ,F ,O 分别与E ,H ,G 为对应点),如果存在,试求(2)中x 和y 的值,如果不存在,请说明理由.25.如图,已知抛物线经过原点O ,顶点为A (1,1),且与直线y=x ﹣2交于B ,C 两点. (1)求抛物线的解析式及点C 的坐标;(2)求证:△ABC 是直角三角形;(3)若点N 为x 轴上的一个动点,过点N 作MN⊥x 轴与抛物线交于点M ,则是否存在以O ,M ,N 为顶点的三角形与△ABC 相似?若存在,请求出点N 的坐标;若不存在,请说明理由.23.如图,已知一次函数y=23x ﹣3与反比例函数xky =的图象相交于点A (4,n ),与x 轴相交于点B .(1) 填空:n 的值为 ,k 的值为 ; (2) 以AB 为边作菱形ABCD ,使点C 在x 轴正半轴上,点D 在第一象限,求点D 的坐标; (3) 考察反比函数xky =的图象,当2y ≥-时,请直接写出自变量x 的取值范围.24.如图,△ABC 的边AB 为⊙O 的直径,BC 与圆交于点D ,D 为BC 的中点,过D 作DE⊥AC 于E . (1)求证:AB=AC ;(2)求证:DE 为⊙O 的切线; (3)若AB=13,sinB=,求CE 的长.25.如图,抛物线y=ax 2+bx+c 与x 轴交于点A 和点B (1,0),与y 轴交于点C (0,3),其对称轴l 为x=﹣1.(1)求抛物线的解析式并写出其顶点坐标;(2)若动点P 在第二象限内的抛物线上,动点N 在对称轴l 上. ①当PA⊥NA,且PA=NA 时,求此时点P 的坐标;②当四边形PABC 的面积最大时,求四边形PABC 面积的最大值及此时点P 的坐标.24. 如图,⊙O 是四边形ABCD 的外接圆,AC 是直径,分别延长AB 、CD 相交于点E ,AC=AE ,过点D 作DF∥BC 于点F. (1)求证:DF 是⊙O 的切线; (2)求证:AC·DF = AD·DE;(3)若M 是弧AB 的中点,连接MD 交弦AB 于点H , 若AB :AF=3:5,证明:AH = AF.25. 已知,把Rt △ABC 和Rt △DEF 按图1摆放(点C 与E 重合),点B ,C ,E ,F 始终在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8,BC=6,EF=10.如图2,△DEF 从图1位置出发,以每秒1个单位的速度沿CB 向△ABC 匀速运动,同时,点P 从点A 出发,沿AB 以每秒1个单位的速度向点B 匀速运动,AC 与△DEF 的直角边相交于点Q ,当E 到达终点B 时,△DEF 与点P 同时停止运动,连接PQ ,设移动的时间为t (s ).解答下列问题: (1)当D 在AC 上时,求t 的值;(2)连接PE ,设四边形APEQ 的面积为y (cm 2),求y 与t 之间的函数关系式;(3)在P 点运动过程中,是否存在点P ,使△APQ 为等腰三角形?若存在,求出t 的值;若不存在,说明理由.22、正方形ABCD 边长为4,M,N 分别是BC ,CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直。
挑战压轴题填空题(真题汇编压轴特训)-2024年中考数学冲刺 挑战压轴题专题汇编(广州卷)(解析版)

02挑战压轴题(填空题)<≤【答案】 1.23S【分析】根据三角形中位线定理可得形DEFG是平行四边形,结合【详解】解:∵点D,E分别是由题意得,DE AM ∥,且DE ∴1122DE AM x ==,又F 、G 分别是MN AN 、的中点,∴FG AM ∥,12FG AM =,【答案】120°/120度75°/75度【分析】如图,以AB为边向右作等边△ABE,连接EP′.利用全等三角形的性质证明∠BEP′=90°,推出点P′在射线EP′上运动,如图1中,设EP′交BC于点O,再证明△BEO是等腰直角三角形,可得结论.【详解】解:如图,以AB为边向右作等边△ABE,连接EP′.∵△BPP′是等边三角形,∴∠ABE=∠PBP′=60°,BP=BP′,BA=BE,∴∠ABP=∠EBP′,在△ABP和△EBP′中BA BEABP EBPBP BP'=⎧⎪∠=∠⎨='⎪⎩,∴△ABP≌△EBP′(SAS),∴∠BAP=∠BEP′=90°,∴点P′在射线EP′上运动,如图1中,设EP′交BC于点O,当点P′落在BC上时,点P′与O重合,此时∠PP′C=180°-60°=120°,当CP′⊥EP′时,CP′的长最小,此时∠EBO=∠OCP′=30°,51【点睛】本题考查了正方形的综合问题,掌握特殊四边形、相似三角形的判定与性质及等腰三角形的性质是解题的关键.【答案】15 4【分析】如图,连接PC交AB于直角三角形求出AC,PA,利用相似三角形的性质求出题.【详解】解:如图,连接PC交AB∵AC⊥BC,∴∠ACB=90°,∵BC=23,∠BAC=30°,∴AB=2BC=43,AC=3BC=6,∵∠EPB=∠EBP=60°,(1)∠AEB 的度数为 (2)若15EBA ∠=︒,【答案】 135° 【分析】(1)如图,连接∵E 是△ADC 的内心,∠∴∠ACE =12∠ACD ,∠EAC ∴∠AEC =180°−12(∠ACD 在△AEC 和△AEB 中,【详解】【答案】171++/117【分析】连接CE,AE',可证AE'=的圆,当E F'经过圆心半径为1【详解】解:如图,连接CE四边形ABCD是正方形,=∴∠=︒,AD CDADC90ADE CDE∴∠+∠=︒,90将DE绕D顺时针旋转∠=DE DE'∴=,EDE'∴22AF AD DF =+224117=+=,FE AF AE ''∴=+171=+;【答案】17【分析】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,由V V,可得BE≅BDE BDF=,由勾股定理可求解.AE CF∠=BD DE,BDE2==∴∠=∠=︒,90BDE BDF()SAS∴≅V V,BDE BDF∠=∠BE BF∴=,BEA BFA【答案】8【分析】本题考查动点最值问题法求线段长等知识,在Rt PBE△中,求出在等腰ABCV中,∴在Rt△ABD中,ABsinAD ABDAB∴∠==在Rt PBE△中,sin313【答案】5【分析】本题考查了正方形的综合题,关键是借助相似三角形对应边成比例解决问题.先画出点E 运动的路线EE ',过E 作EF AQ ⊥,交AQ 于点F ,根据EAF CAB △∽△,可得EF AF =,设cm EF x =,则()3cm BF x =-,()4.5cm QF x =-,再根据EQF DQA V V ∽,可求得EF E F '、,利用勾股定理可得EE '.【详解】解:当点P 在点A 处时,如图,,23cm BP BQ BP == ,,15cm BQ .∴=,当点P 运动到点B 时,如图,,所以点E 运动的路线EE ',如图,,过E 作EF AQ ⊥,交AQ 于点F ,即90AFE EFQ ∠=∠=︒,∵四边形ABCD 为正方形,【答案】32【分析】本题考查了垂线段最短,等边三角形的性质,全等三角形的判定和性质等知识,取连接DK ,EK ,由V AE 绕点A 顺时针旋转∵ABC V 是等边三角形,∴60BAC ∠=︒,3AD =∵线段AE 绕点A 顺时针旋转∴60PAE ∠=︒,AE =∴60PAE BAC ∠=∠=︒【答案】23【分析】本题考查三角形的重心,涉及相似三角形的判定与性质,于G ,延长CG 交AB 于点F ,证明V 据3AC =,得21CD AD ==,,进而根据勾股定理求出【详解】解:过G 作GD AC ⊥于G ,延长∵ 90GD AC BAC ⊥∠=︒,,∴ DE AB ∥,90CDG CAF ==∠∠又∵ DCG ACF ∠=∠,∴ DCG ACF V V ∽,∴ CD DG CG ==,【答案】26【分析】连接,,OA AC OC ,OF CF ,先求出AD =后利用勾股定理求出OE 则52OA OC OF ===,12AOD AOC ∴∠=∠,弦CD AB ⊥于点E ,CD ∴142CE CD ==,∴2225BC CE BE =+=设OC x =,则2=-OE x ,2C BAD ∠=∠ ,设BAD ∠=α,则2C α∠=,90ABD ∠=︒ ,90ADB ADE α∠=︒-=∠ ,180EDC ADB ADE ∴∠=︒-∠-∠=ED EC ∴=,【答案】AP的长为25或2或10【分析】分三种情况:PA'平行于行于x轴时,过点C作CN PA⊥于的坐标,从而求得CM AM,,再由折叠性质得PA '平行于x 轴时,如图,过点设AP a =,点5512P m m ⎛⎫+ ⎪⎝⎭,,则则5512A m a m ⎛⎫++ ⎪⎝'⎭,,50,12M ⎛ ⎝当P 靠近A 且PA '平行于x 轴时,延长设AP a =,点5512P m m ⎛⎫+ ⎪⎝⎭,,则0m <,则5512A m a m ⎛⎫-+ ⎪⎝'⎭,,50,512M m ⎛⎫+ ⎪⎝⎭,∴555321212CM m m ⎛⎫=+-=+ ⎪⎝⎭,PM =综上,AP 的长为25或2或10.【点睛】本题考查了一次函数图象上点的坐标特征,平行线的性质,等腰三角形的性质角平分线的性质,勾股定理,等积法,利用等积法是解题的关键与难点.17.(2024上·山东济南·八年级统考期末)平面直角坐标系中,点123B B B ⋯,,,在x 轴上,11122233OA B B A B B A B ⋯V V V ,,是等腰直角三角形.【答案】94,设22A C m =,33A C n =,点()111A ,,1111OC A C ∴==,【答案】8【分析】如图,记AB BC 、1122DP BC AB DQ ===,证明()SAS FDQ EDC V V ≌1124BM PM BP AB ===又∵D 是AC 的中点,∴DP DQ 、是ABC V 的中位线,∴1122DP BC AB DQ ===∴四边形BPDQ 是菱形,∴1122DP BQ BC AB ===∵等边DFE △,【答案】3212+2【分析】(1)连结AB,取AB的中点D,连结CD 以定点D为圆心,1为半径的圆上运动,所以当点即得OC的最小值;(2)连结AB,取AB的中点D,连结DM,ODC为AP的中点,M 为AC 的中点,1122DM BC ∴==,所以点M 在以定点D 为圆心,90AOB ∠=︒Q ,2OA =,OB 2222AB OA OB ∴=+=,1。
广州中考数学压轴题汇总
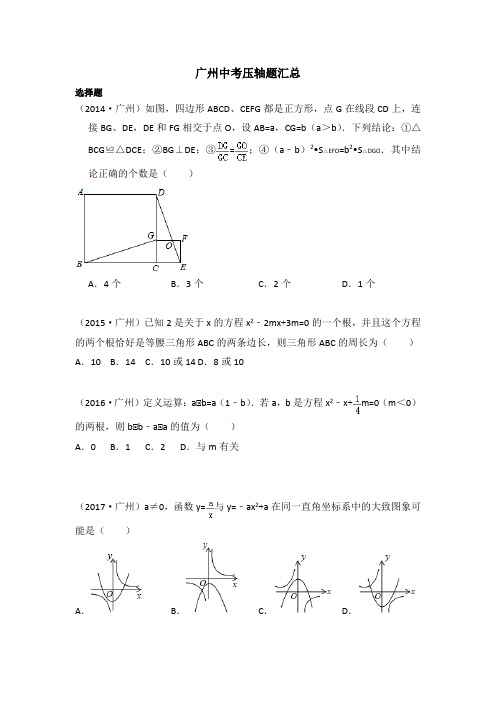
广州中考压轴题汇总选择题(2014·广州)如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③=;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是()A.4个B.3个C.2个D.1个(2015·广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为()A.10 B.14 C.10或14 D.8或10(2016·广州)定义运算:a⋆b=a(1﹣b).若a,b是方程x2﹣x+m=0(m<0)的两根,则b⋆b﹣a⋆a的值为()A.0 B.1 C.2 D.与m有关(2017·广州)a≠0,函数y=与y=﹣ax2+a在同一直角坐标系中的大致图象可能是()A.B.C.D.(2017·广州)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到A n.则△OA2A2018的面积是()A.504m2B.m2 C.m2 D.1009m2填空题(2014·广州)若关于x的方程x2+2mx+m2+3m﹣2=0有两个实数根x1、x2,则x1(x2+x1)+x22的最小值为.(2015·广州)如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.(2016·广州)如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB 绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是.(2017·广州)如图,平面直角坐标系中O是原点,▱OABC的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是;④OD=其中正确的结论是(填写所有正确结论的序号).(2018·广州)如图,CE是▱ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE :S△COD=2:3.其中正确的结论有.(填写所有正确结论的序号)解答题(2014·广州24)已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.(1)求抛物线的解析式和顶点C的坐标;(2)当∠APB为钝角时,求m的取值范围;(3)若m>,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.(2014·广州25)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,连接CF.设CE=x,△BCF的面积为S1,△CEF的面积为S2.(1)当点F落在梯形ABCD的中位线上时,求x的值;(2)试用x表示,并写出x的取值范围;(3)当△BFE的外接圆与AD相切时,求的值.(2015·广州24)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.(1)试探究筝形对角线之间的位置关系,并证明你的结论;(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.(2015·广州25)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.(1)求点C的坐标;(2)当y1随着x的增大而增大时,求自变量x的取值范围;(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.(2016·广州24)已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B(1)求m的取值范围;(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.(2016·广州25)如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°(1)求证:BD是该外接圆的直径;(2)连结CD,求证:AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.(2017·广州24)如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD的对称图形为△CED.(1)求证:四边形OCED是菱形;(2)连接AE,若AB=6cm,BC=cm.①求sin∠EAD的值;②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.(2017·广州)如图,AB是⊙O的直径,=,AB=2,连接AC.(1)求证:∠CAB=45°;(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD.①试探究AE与AD之间的数量关系,并证明你的结论;②是否为定值?若是,请求出这个定值;若不是,请说明理由.(2018·广州24)已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=﹣的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求的值.(2018·广州25)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.。
初中数学中考压轴题及答案详解(广东篇)

专题训练122. 如图,抛物线923212--=x x y 与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC 、AC 。
(1)求AB 和OC 的长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合)。
过点E 作直线l 平行BC ,交AC 于点D 。
设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围; (3)在(2)的条件下,连接CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π)。
参考答案: 解:(1)令y=0,即0923212=--x x , 整理得 01832=--x x , 解得:31-=x ,62=x , ∴ A (—3,0),B (6,0) 令x = 0,得y = —9, ∴ 点C (0,—9)∴ 9)3(6=--=AB ,99=-=OC , (2)281992121=⨯⨯=⋅=∆OC AB S ABC, ∵ l ∥BC ,∴ △ADE ∽△ACB , ∴22ABAE S S ABC=∆,即229281m S = ∴ 221m S =,其中90<<m 。
(3)88129212192122+⎪⎭⎫ ⎝⎛--=-⨯⨯=-=∆∆∆m m m S S S ADEACE CDE , ∵ 021<-∴ 当29=m 时,S △CDE 取得最大值,且最大值是881。
这时点E (23,0),yA OB xElCD题22图∴29236=-=-=OE OB BE ,133962222=+=+=OC OB BC , 作EF ⊥BC ,垂足为F ,∵∠EBF=∠CBO ,∠EFB=∠COB , ∴△EFB ∽△COB ,∴CB BEOC EF =,即133299=EF ∴132627=EF , ∴ ⊙E 的面积为:πππ5272913262722=⎪⎭⎫⎝⎛⨯=⋅=EF S 。
押广东省卷第11-15题(因式分解、二次根式的运算、一元二次方程、不等式的应用、图形面积)(解析版)

押广东省卷第11-15题押题方向一:因式分解3年广州省卷真题考点命题趋势2023年广州省卷第11题因式分解从近年广州省卷中考来看,因式分解是近几年广州深圳的常考题,考查比较简单;预计2024年广州省卷还将继续重视因式分解的考查。
1.(2023·广东·中考真题)因式分解:2.9x -=.【答案】()()33x x -+【分析】本题考查了因式分解,根据算术平方根因式分解,即可求解.【详解】解:29x -=()()33x x -+,故答案为:()()33x x -+.因式分解是核心考点,常在填空题中出现。
多项式的因式分解,先提取公因式,再利用平方差、完全平方公式分解即可.1.因式分解:22024-=x x .【答案】()2024-x x 【分析】本题考查了分解因式.根据式子的特点将公因数提取出来即可.【详解】解:22024x x -式子中含有公因数x ,∴()220242024x x x x -=-,故答案为:()2024-x x .2.分解因式2363a a -+的结果是.【答案】()231a -/()231a -+【分析】本题考查了综合提取公因式法和公式法因式分解,解题的关键是正确找出公因式,熟练掌握完全平方公式()2222a b a ab b +=++.先提取公因式3,再利用完全平方公式进行因式分解即可.【详解】解:2363a a -+()2321a a =-+()231a =-,故答案为:()231a -.3.因式分解:()()224ax y b y x -+-=.【答案】()()()22x y a b a b -+-【分析】本题考查了因式分解的应用,熟练掌握因式分解的方法是解答本题的关键.因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.先提取公因式,再用平方差公式分解.【详解】解:()()224ax y b y x -+-()()224a x y b x y =---()()224x y a b =--()()()22x y a b a b =-+-.故答案为:()()()22x y a b a b -+-.6,7x y x y +=-=,则22.【答案】42【分析】本题考查因式分解,代数式求值,利用平方差公式法进行因式分解后,代值计算即可,掌握平方差公式法因式分解,是解题的关键.【详解】解:∵6,7x y x y +=-=,∴()()226742x y x y x y -=+-=⨯=;故答案为:42.5.若5x y -=,6xy =则22x y xy -=,2222x y +=.【答案】3074【分析】第一个空先利用提公因式法因式分解,再代入计算即可;第二个空利用完全平方公式变形后,代入计算即可.【详解】解:22()6530x y xy xy x y -=-=⨯=;()222222()22251274x y x y xy ⎡⎤+=-+=⨯+=⎣⎦.故答案为:30,74.【点睛】本题考查代数式求值,掌握因式分解法和熟练利用完全平方公式是解题关键.押题方向二:二次根式的运算3年广东省真题考点命题趋势2023年广东省卷第12题二次根式的运算从近年广东省中考来看,二次根式的运算是常考题型,难度简单;预计2024年广东省卷还将继续重视对二次根式的运算的考查。
广州等七地数学中考压轴题解析汇编

3
PH 3
∴∠ P=30° ∵∠ P+∠ PDH=9°0 ,∠ PDH+ ∠ BDE=90°
∴∠ BDE=30° ∵DE 是⊙O 的直径 ∴∠ DBE=90° ∵ DE=2 r=50
∴ BD=DE ·cos∠BDE=50 ×
3 =25 3
2
( 3)过点 O 作 OF⊥ AC 于 F,作 OG⊥ AB 于 G,则四边形 OFHG 是矩形
∴∠ PDE=90°,即 PD⊥ DE
∴ PD 与⊙ O 相切
( 2)连接 BE 。
∵ AC ⊥ BD
∴∠ AHD=9°0
∴ tan∠ ADB=
AH
3
=
DH 4
∴ DH= 4 AH 3
∵ PA= 4 3 3 AH 3
学习好资料
欢迎下载
∴ PH=PA+AH= 4 3 AH 3
∵在 Rt△PHD 中, tan∠ P= DH
m m2
解得 m= 5 1 或 5 1(舍去 )
∴ AE= 5 1
∵∠ DOC= ∠EAO= ∠ OCD ∴ CE=AE
∴ ED=CE - CD=AE - CD= 5 1 - 2= 5 1
∴ AE · ED=( 5 1 )( 5 1 )=4
E D
D
A
O
C
B
A
O
FB C
【 2013·广州· 25 题 】已知抛物线 y1= ax2 bx c(a 0, a c) 过点 A(1,0) ,顶点为 B,且
∴CD2 =4
∵ OC= 2 2 ∴ OC2=8
∵ OC2=OD 2+CD 2
∴△ ODC 是直角三角形,且∠ ODC=9°0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州中考压轴题汇总
选择题
(2014·广州)如图,四边形ABCD 、CEFG 都是正方形,点G 在线段CD 上,连接
BG 、DE ,DE 和FG 相交于点O ,设AB=a ,CG=b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③
=;④(a ﹣b )2•S △EFO =b 2•S △DGO .其中结论正确的
个数是( )
A .4个
B .3个
C .2个
D .1个
(2015·广州)已知2是关于x 的方程x 2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC 的两条边长,则三角形ABC 的周长为( )
A .10
B .14
C .10或14
D .8或10
(2016·广州)定义运算:a ⋆b=a (1﹣b ).若a ,b 是方程x 2﹣x+m=0(m <0)的两根,则b ⋆b ﹣a ⋆a 的值为( )
A .0
B .1
C .2
D .与m 有关
(2017·广州)a ≠0,函数y=与y=﹣ax 2+a 在同一直角坐标系中的大致图象可
能是()
A.B.C.D.
(2017·广州)在平面直角坐标系中,一个智能机器人接到如下指令:从原点O 出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走
路线如图所示,第1次移动到A
1,第2次移动到A
2
,…,第n次移动到A
n
.则△
OA
2A
2018
的面积是()
A.504m2B.m2C.m2D.1009m2填空题
(2014·广州)若关于x的方程x2+2mx+m2+3m﹣2=0有两个实数根x
1、x
2
,
则x
1(x
2
+x
1
)+x
2
2的最小值为.
(2015·广州)如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.
(2016·广州)如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是.
(2017·广州)如图,平面直角坐标系中O是原点,▱OABC的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是;④OD=
其中正确的结论是(填写所有正确结论的序号).
(2018·广州)如图,CE是▱ABCD的边AB的垂直平分线,垂足为点O,CE与DA 的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S
四边形AFOE :S
△COD
=2:3.
其中正确的结论有.(填写所有正确结论的序号)
解答题
(2014·广州24)已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
(2014·广州25)如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=3,BC=4,CD=5.点E为线段CD上一动点(不与点C重合),△BCE关于BE的轴对称图形为△BFE,
连接CF.设CE=x,△BCF的面积为S
1,△CEF的面积为S
2
.
(1)当点F落在梯形ABCD的中位线上时,求x的值;(2)试用x表示,并写出x的取值范围;
(3)当△BFE的外接圆与AD相切时,求的值.
(2015·广州24)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.
(2015·广州25)已知O为坐标原点,抛物线y
1
=ax2+bx+c(a≠0)与x轴相交
于点A(x
1,0),B(x
2
,0),与y轴交于点C,且O,C两点间的距离为3,x
1
•x
2
<0,|x
1|+|x
2
|=4,点A,C在直线y
2
=﹣3x+t上.
(1)求点C的坐标;
(2)当y
1
随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y
1
向左平移n(n>0)个单位,记平移后y随着x的增大而增大
的部分为P,直线y
2
向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.
(2016·广州24)已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B
(1)求m的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;
(3)当<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.
(2016·广州25)如图,点C为△ABD的外接圆上的一动点(点C不在上,且不与点B,D重合),∠ACB=∠ABD=45°
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.
(2017·广州24)如图,矩形ABCD的对角线AC,BD相交于点O,△COD关于CD 的对称图形为△CED.
(1)求证:四边形OCED是菱形;
(2)连接AE,若AB=6cm,BC=cm.
①求sin∠EAD的值;
②若点P为线段AE上一动点(不与点A重合),连接OP,一动点Q从点O出发,以1cm/s的速度沿线段OP匀速运动到点P,再以1.5cm/s的速度沿线段PA匀速运动到点A,到达点A后停止运动,当点Q沿上述路线运动到点A所需要的时间最短时,求AP的长和点Q走完全程所需的时间.
(2017·广州)如图,AB是⊙O的直径,=,AB=2,连接AC.
(1)求证:∠CAB=45°;
(2)若直线l为⊙O的切线,C是切点,在直线l上取一点D,使BD=AB,BD所在的直线与AC所在的直线相交于点E,连接AD.
①试探究AE与AD之间的数量关系,并证明你的结论;
②是否为定值?若是,请求出这个定值;若不是,请说明理由.
(2018·广州24)已知抛物线y=x2+mx﹣2m﹣4(m>0).
(1)证明:该抛物线与x轴总有两个不同的交点;
(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.
①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;
②若点C关于直线x=﹣的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求的值.
(2018·广州25)如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
