D2习题课 高等数学高数
《高等数学习题课二》PPT课件

( C ) 与 y 轴 相 垂 直 ;( D ) 与x 轴 即 不 平 行 也 不 垂 直 :
h
1
3、 若 函 数 f (x) 在 点 x0 不 连 续 , 则 f (x) 在x0 ( )
( A) 必 不 可 导 ;
( B) 必 定 可 导 ;
(C)不一定可导; (D)必无定义 .
4 、 如 果 f ( x ) = ( ), 那 么 f ( x ) 0 .
x;
4、 6 x tan( 10 3 x 2 ) ;
5、 x y ; x y
6、
1
.
3(2 y 1)( 2 x 1) x 2 x
h
8
四、1、a g(0);
2、f
(
x)
x[
g(
x)
sin x] x2
[
g(
x)
cosx]
,
x
0 .
12(g(0) 1), x 0
五、 f (n) (1) (1)n2 (n 2)!.
六、2.09.
七、20 8.16(公里/小时). 6
h
9
x x0
x
( D ) lim f ( x ) f ( x 0 ) ;
x x0
x x0
2、 若 函 数 y f ( x ) 在 点 x 0 处 的 导 数 f ( x 0 ) 0 , 则
曲 线 y f (x)在 点 ( x0, f (x0))处 的 法 线 ( )
( A ) 与 x 轴 相 平 行 ;( B ) 与x 轴 垂 直 ;
cos x
x
,
x
0 其中g( x)
有二阶连
a, x 0
续导数,且 g(0) 1,
高数(2)习题课 (期末复习资料)

2011~2012学年下学期 高等数学(2)习题课习题课 一(第五章 定积分)1.求定积分⎰+33121xdx 的值。
2.求定积分dtt t ⎰23cos sin π的值。
3.求定积分dxxxx⎰+-+01224133的值。
4.求定积分⎰--223cosππdxxcox的值。
5.求定积分⎰+∞-++031ee xxdx的值。
习题课二(第七章 微分方程)第一部分:(求下列微分方程的值)1.eyx dxdy+=解:-)(e -y:=+++==-⎰⎰⎰==-=c e e eeee yc e x e yd dxdydxdy xyxyyx dxe x edyy积分对上式两端为:即:该微分方程的通解分别整理后可得:2.022=-⎪⎭⎫ ⎝⎛+xydy dx yx3.eyxycox sin '-=+4.)ln (ln 'y x y y xy +=+5.yxy x yxy2236322'-+-+=C x Ct utdtuu d tdt du uuu ut dt duu u u t dt du tyy t yty t dt dyyxy y x y x yty u x t ty u x t +-=-+-⎰⎰---+=++----=-==-=-=-=⇒==+=-=+=)1ln(ln ln 31ln3)3(3222322321232322)1(313112,1'22222222通解为:代入上式可得原方程的,分别将即:得:对该式两端分别积分可分离变量后可得:,则上式又可化为:再令则上述方程又可化为:所以:令解:上式可化为6.设)()()(x g x f x F =,且)()(x g x f ,满足)()(),()(''x f x g x g x f ==且ex g x f x f x2)()(0)(=+=,。
(1).求)(x F 所满足的微分方程。
[]⊗-=+=+=+=-)(24)()()(2)()()()()()()()()(2')(222'''x F e x F x g x f x g x f x g x f x g x f x g x f x Fxx F 所满足的微分方程为:所以:解:(2).求)(x F 。
高等数学下册习题课(27)

习 题 课 二 十 七1.设⎰⎰⎰Ω=dV z y x f I ),,(,其中Ω是由4222≤++z y x 和z y x 322≤+围成的区域,试在直角坐标系、柱面坐标系和球面坐标系下分别将I 化为三次积分。
解:(1)在直角坐标系下,两曲面的交线为⎪⎩⎪⎨⎧=+=++ 3422222z y x z y x ⎪⎩⎪⎨⎧==+⇒ 1322z y xxoy 在Ω面上的投影区域为}3),{(22≤+=y x y x D xy 。
⎰⎰⎰--+----=224322232333),,(y x yx x x dz z y x f dy dx I 。
(2)在柱面坐标系下,}43,30 ,20),,{(22ρ-≤≤ρ≤ρ≤π≤ϕ≤ϕρ=Ωz z ,dz d d dV ϕρρ=,⎰⎰⎰ρ-ρπϕρϕρρρϕ=2432320),sin ,cos (dz z f d d I 。
(3)在球面坐标系下,21ΩΩ=Ω ,}20 ,30 ,20),,{(1≤≤π≤θ≤π≤ϕ≤ϕθ=Ωr r ,}sin cos 30 ,23 ,20),,{(22θθ≤≤π≤θ≤ππ≤ϕ≤ϕθ=Ωr r , ϕθθ=d drd r dV sin 2。
⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΩ+==21),,(),,(),,(dV z y x f dV z y x f dV z y x f Idr r r r r fd d ⎰⎰⎰θϕθϕθθθϕ=ππ202020)cos ,sin sin ,cos sin (sin 3drr r r r f d d ⎰⎰⎰θθπππθϕθϕθθθϕ+2sin cos 3022320)cos ,sin sin ,cos sin (sin2.将直角坐标系下的三次积分⎰⎰⎰---+++=10)(302222222)(y y y y y x dz z y x f dx dyI ,分别化为柱面坐标系和球面坐标系下的三次积分。
解:对应的三重积分区域⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤--+≤≤Ω .10,,)(30:2222z y y x y y y x z上顶为锥面)(322y x z +=, 下底为平面0=z 上的圆,侧面为圆柱22y y x -=即222)21()21(=-+y x 。
高等数学课件--D2习题课

a2
目录 上页 下页 返回 结束
同济高等数学课件
x 1 时, f ( x) a ,
f (1) 存在
f x 1时, ( x) 2 x
a b 1 1 (a b 1) 2
a2
f (1) 2
x 1 x 1
a 2 , b 1,
2 , f ( x) 2 x ,
解:
f (x)
1 (a b 1 1 时, f ( x) a ;
利用 f ( x) 在 x 1 处可导,得
f (1 ) f (1 ) f (1)
f (1) f (1)
10/12/2012
即
a b 1 1 (a b 1) 2
sine e
x sin x
d(sin x) esin x cose x d(e x )
e
sin x
(cos x sine e cose
x
x
x
) dx
10/12/2012
同济高等数学课件
目录 上页 下页 返回 结束
例7. 选择 可使下述函数在
f (x)
2
且
ax bx c , g ( x) , x0 x0
目录 上页 下页 返回 结束
1
作业
P125 5;
7;
6(1) ;
8 (3) ,
(4) , (5)
;
9 (2) ; 11 ;
12 (2) ;
13 ;
10/12/2012
15 ; 18
同济高等数学课件
目录 上页 下页 返回 结束
f ( x0 )
10/12/2012
《高等数学》(北大第二版)第02章习题课

《高等数学》(北大第二版)第02章习题课某存在,故只要证f(0)=0.分析需证证设limf(某)=A,则limf(某)=lim某f(某)=0A=0,某→0某→0某→0某某因为f(某)在某=0处连续,所以f(0)=limf(某)=0.某→0f(某)f(0)f(某)f′(0)=lim=lim=A 存在,即f(某)在某=0处可导.故某→0某→0某0某例2设f(u)的一阶导数存在,求1rrlim[f(t+)f(t)]r→0rararf(t+)f(t)+f(t)f(t)aa解原式=limr→0rrr[f(t+)f(t)][f(t)f(t)]11aa令r=h=lim+limrrrra→0a→0aaaaa1f(t+h)f(t)1f(t)f(th)=lim+limh→0aha h→0h1f(t+h)f(t)1f(th)f(t)=lim+limh→0ahah→0hh=某112=f′(t)+f′(t)=f′(t)aaa例3已知y=某ln(某+1+某2)1+某2解′(′y′=某ln(某+1+某2))1+某2)(求y′.某1+某2=ln(1+1+某)+某.某+1+某21+某221+某=ln(1+1+某)+2某1+某2某1+某2=ln(1+1+某2)例4求y=解某某某的导数.y=某111++248=某,所以278787′=某=y.888某练习:y=ln11+某,求y′.例5设y=a1某3某logb14arctan某2(a>0,b>0),求y′.111某∵lny=lna+lnlogb某+lnarctan某2,解2624111lny=lna+(lnln某lnlnb)+lnarctan某2,2某624对上式两边求导,得lna1某′=y[y++]2422某6某ln某12(1+某)arctan某1=2a1某3某logb4arctan某2某1lna[2+].42某3某ln某6(1+某)arctan某例6设y=y(某)由方程e某y+tg(某y)=y确定,求y′(0)解由方程知当某=0时y=1.对方程两变求导:1e(y+某y′)+(y+某y′)=y′2co(某y)101e(1+0y′(0))+(1+0y′(0))=y′(0)2co(0)某y故y′(0)=2例7已知某y=e某+y求y′′解将方程两边对某求导,得y+某y′=e某+y(1+y′)(A)y+某y′=e某+y+y′e某+y再将(B)两边对某求导,得(B)y-e某+yy′=某+ye某(C)y′+y′+某y′′=e某+y(1+y′)+y′′e某+y+y′e某+y(1+y′)e某+y(1+y′)22y′y′′=某e某+yy-e某+y其中y′=某+ye某.某=ln(1+t2),例7已知求y′,y′′,y′′′.y=tarctant.11(t-arctant)′1+t2=t,解y′==22t2(ln(1+t)′1+t2t()′1+t22y′′==,2′(ln(1+t))4t 1+t2()′t414ty′′′==3.(ln(1+t2))′8t例8设y=f2(某)+f(某2),其中f(某)具有二阶导数,求y′′.解y′=2f(某)f′(某)+f′(某2)2某.y′′=2[f′(某)]2+2f(某)f′′(某)+2f′(某2)+2某f′′(某2)2某=2[f′(某)]2+2f(某)f′′(某)+2f′(某2)+4某2f′′(某2).例9求下列函数的n阶导数y(n)(n>3).某41(1)y=;(2)y=2.21某某a 某41+11y==(某3+某2+某+1)1某1某n!(n).当n>3时,y=n+1(1某)1(2)y=2(练习).2某a解(1)例10求由方程先求微分,易得导数]解[先求微分,易得导数将方程两边同时取微分,因为yln某+y=arctan所确定的隐函数的导数和微分.某2222dln某+y==1某+y22d某+y=221某+y22d(某2+y2)2某2+y21某2+y22某d某+2ydy2某2+y2=而某d某+ydy,22某+yy1某dyyd某某dyyd某darctan==2某1+(y)2某2某+y2某∴某d某+ydy某dyyd某=222某+y某+y2∴某+ydy=d某,某y∴dy某+yy′==.d某某ya某ba某b例11设f(某)可导,求y=f(in某)+()()().的导数,b某aa其中,a>0,b>0,≠1,某≠0.ba某ba某b2解记y1=f(in某),y2=()()(),b某a′则y1=f′(in2某)2in某co某=in2某f(in2某).2lny2=某(lnalnb)+a(lnbln某)+b(ln某lna),a某ba某babaab′).∴y2=y2[(lnalnb)+]=()()()(ln+b某ab某某某例12设y=(ln某)某某ln某,求y′.lny=某ln(ln某)+(ln某)2,解两边取对数,两边关于某求导1y′=ln(ln某)+1+2ln某,yln某某12ln某某ln某y′=(ln某)某[ln(ln某)+∴+].ln某某练习:设(co某)y=(iny)某求y′例13解dy已知y=a+某,a>0为常数,(a≠1),求.d某arctan某2in某设y1=a,y2=某.arctan某2in某)′=lnaa(arctan某2)′1arctan某22′=lnaaarctan某22某.=lnaa(某)41+某1+某4对y2=某in某两边取对数,得lny2=in某ln 某1in某′y2=co某ln某+,两边对某求导,得某y2in某in某′y2=某(co某ln某+).某arctan某2arctan某2′y1=(a2-某,1<某<+∞,2例13设f(某)=某,0≤某≤1,某3,-∞<某<0.解第一步,在各开区间内分别求导:1,1<某<+∞;f′(某)=2某,0<某<1,3某2,-∞<某<0.求f′(某).第二步,在分段点用导数定义求导,分段点为某=0,1f(0+某)f(0)(某)20f+′(0)=lim+=lim+=0某→0某→0某某f(0+某)f(0)(某)30f′(0)=lim=lim=0,∴f′(0)=0某→0某→0某某f(1+某)f(1)2(1+某)12某=lim+=lim+=1f+′(1)=lim+某→0某→0某→0某某某f(1+某)f(1)(1+某)2122某+(某)2=lim=lim=3f′(1)=lim某→0某→0某→0某某某∴f(某)在某=1的导数不存在1,1<某<+∞,故f(某)=2某,0≤某<1,3某2,-∞<某<0.在某=1处f(某)不可导.某≤c,in某,例14设f(某)=c为常数a某+b,某>c.试确定a,b的值,使f′(c)存在.解因为f′(c)存在,所以f(某)在c处连续.某→clim-f(某)=lim-in某=inc某→c某→c某→clim+f(某)=lim+(a某+b)=ac+bf′(c)=lim∴inc=ac+b(1)因为f(某)在c处可导,in某incf(某)f(c)=lim某→c某→c某c某c某c某c某+cin2inco2co某+c=coc.22=lim=lim某→c某c某→c2某c2f(某)f(c)a某+binca某+b(ac+b)=a.f+′(c)=lim=lim=lim+++某→c某→c某→c某c某c某c所以,coc=a(2)解(1),(2)得,=coc,b=inc-ccoc.a某2,某≤1,习题2-115.设f(某)=a某+b,某>1.为了使函数f(某)在某=1处连续且可导,a,b应取什么值?解要使f(某)在某=1处连续,因为某→1limf(某)=lim某2=1,某→1某→1某→1lim(a某+b)=a+b,+应有limf(某)=limf(某)=f(1)+某→1即a+b=1要使f(某)在某=1处可导,因为(1+某)2122某+(某)2f(1+某)f(1)=lim=2,f′(1)=lim=lim某→1某→1某→1某某某代a+b=1 a(1+某)+b12f(1+某)f(1)a某f+′(1)=lim=lim=lim=a,+++某→1某→1某→1某某某应有a=2,代入(1)式得b=-1.6.假定f′(某0)存在,指出下式A表示什么?f(某)=A,其中f(0)=0,且f′(0)存在;某→0某f(某0+h)f(某0h)(3)lim=A.h→0h解(2)∵limf(某)=limf(某)f(0)=f(某0),某→0某→0某0某(2)lim∴A=f(某0).(3)∵limh→0f(某0+h)f(某0)+f(某0)f(某0h)f(某0+h)f(某0h)=limh→0hhf(某0+h)f(某0)f(某0)f(某0h)+limh→0hh=limh→0f(某0h)f(某0)令h=某=f′(某0)+lim========f′(某0)+f′(某0)=2f′(某0),h→0h∴A=2f′(某0).9.如果f(某)为偶函数,且f′(0)存在,证明f′(0)=0.证f(某)f(某0)f(某)f(0)f(某)f(0)′(某0)=lim(f)f′(0)=lim=lim某→某0某→0某→0某某0某0某0f(某)f(0)(令某=y)f(y)f(0)=f′(0)=lim==========lim某→0某0y→0y0∴2f′(0)=0,f′(0)=0.1例16设f(t)=limt(1+)2t某,求f′(t).某→∞某1某2t12t某解limt(1+)=limt[(1+)]=te2t某→∞某→∞某某f′(t)=(te2t)′=(2t+1)e2t.12某in,某≠0;例15求f(某)=某0,某=0一阶导数和二阶导数.11解当某≠0时,f′(某)=2某inco,某某12111f′′(某)=2inco2in.某某某某某当某=0时,用导数定义先求一阶导数,再来看二阶导数.f(0+某)f(0)=limf(某)f′(0)=lim某→0某→0某某=lim由于某2in某→01某=lim某in1=0;某→0某某1limf′(某)=lim(2某in1co1)=limco某→0某→0不存在(极限故处不连续(是振荡间断点是振荡间断点),所以不可导,即不存在极限),故f′(某)在某=0处不连续是振荡间断点所以f′(某)在某=0不可导即极限不可导f′′(0)不存在不存在.某某某→0某1g(某)co,某≠0,例16设f(某)=某0,某=0.且g(0)=g′(0)=0试问:(1)limf(某);某→0(2)f(某)在某=0处是否连续?(3)f(某)在某=0处是否可导?若可导,f′(0)=解(1limf(某)=limg(某)co)1=0某→0某→0某1(∵limg(某)=g(0)=0;co为有界函数)某→0某某→0(2)∵limf(某)=0=f(0)∵f(某)在某=0处连续.11g(某)co0g(某)co某某=0lim(3)f′(0)=lim某→0某→0某0某1g(某)g(0)g(某)(∵g′(0)=lim=lim=0,co有界)某→0某→0某0某某。
高等数学2-习题集(含答案)

《高等数学2》课程习题集【说明】:本课程《高等数学2》(编号为01011)共有计算题1,计算题2等多种试题类型,其中,本习题集中有[]等试题类型未进入。
一、计算题11. 计算 行列式6142302151032121----=D 的值。
2. 计算行列式5241421318320521------=D 的值。
3.用范德蒙行列式计算4阶行列式12534327641549916573411114--=D 的值。
4. 已知2333231232221131211=a a a a a a a a a , 计算:333231232221131211101010a a a a a a a a a 的值。
5.计算行列式 0111101111011110=D 的值。
6. 计算行列式199819981997199619951994199319921991 的值.7. 计算行列式50007061102948023---=D 的值. 8. 计算行列式3214214314324321=D 的值。
9. 已知10333222111=c b a c b a c b a ,求222111333c b a c b a c b a 的值. 10. 计算行列式x a a a xa a ax D n=的值。
11.设矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=2100430000350023A ,求1-A 。
12.求⎪⎪⎪⎭⎫ ⎝⎛=311121111A 的逆.13.设n 阶方阵A 可逆,试证明A 的伴随矩阵A *可逆,并求1*)(-A 。
14. 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛-=1100210000120025A 的逆。
15. 求⎪⎪⎪⎭⎫⎝⎛-----=461351341A 的逆矩阵。
16. 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=2300120000230014A 的逆。
17. 求⎪⎪⎪⎭⎫⎝⎛--=232311111A 的逆矩阵。
18.求矩阵⎪⎪⎪⎭⎫⎝⎛-=101012211A 的逆.19. 求矩阵112235324-⎛⎫⎪=- ⎪ ⎪-⎝⎭A 的逆。
(完整版)高等数学II练习册-第10章答案

(完整版)⾼等数学II练习册-第10章答案习题10-1 ⼆重积分的概念与性质1.根据⼆重积分的性质,⽐较下列积分的⼤⼩:(1)2()D x y d σ+??与3()Dx y d σ+??,其中积分区域D 是圆周22(2)(1)2x y -+-=所围成;(2)ln()Dx y d σ+??与2[ln()]Dx y d σ+??,其中D 是三⾓形闭区域,三顶点分别为(1,0),(1,1),(2,0);2.利⽤⼆重积分的性质估计下列积分的值:(1)22sin sin DI x yd σ=,其中{(,)|0,0}D x y x y ππ=≤≤≤≤;(2)22(49)DI x y d σ=++??,其中22{(,)|4}D x y x y =+≤.(3).DI =,其中{(,)|01,02}D x y x y =≤≤≤≤解 (),f x y =Q 2,在D 上(),f x y 的最⼤值()14M x y ===,最⼩值()11,25m x y ====故0.40.5I ≤≤习题10-2 ⼆重积分的计算法1.计算下列⼆重积分:(1)22()Dx y d σ+??,其中{(,)|||1,||1}D x y x y =≤≤;(2)cos()Dx x y d σ+??,其中D 是顶点分别为(0,0),(,0)π和(,)ππ的三⾓形闭区域。
2.画出积分区域,并计算下列⼆重积分:(1)x y De d σ+??,其中{(,)|||1}D x y x y =+≤(2)22()Dxy x d σ+-??,其中D 是由直线2y =,y x =及2y x =所围成的闭区域。
3.化⼆重积分(,)DI f x y d σ=为⼆次积分(分别列出对两个变量先后次序不同的两个⼆次积分),其中积分区域D 是:(1)由直线y x =及抛物线24y x =所围成的闭区域;(2)由直线y x =,2x =及双曲线1(0)y x x=>所围成的闭区域。
《高等数学》(北大第二版 )第09章-习题课

x2 + y2 ez
2
dxdydz, dxdydz,
x
⋅
Ω1
Z=1
⋅ ⋅
⋅
y
x +y
1 2
2
e = ∫ dθ ∫ dr∫ ⋅ rdz 0 0 1 r z 2π 2 2e + ∫ dθ ∫ dr∫ ⋅ rdz 0 1 r r = 2πe2.
2π
z
x2 + y2 ≤1 其 Ω1 : 中 1 ≤ z ≤2
π
2Байду номын сангаас
2
0
2
∫
0
u=
π
2
−t
∫
∫∫
2
∫
2
2
0
∫
0
解2
0 ≤ x ≤ 2 y − y 2 , 如图所示,D: 0 ≤ y ≤ 2.
y 2
D
D1
∫∫ ydxdy = ∫
D
2
0
ydy ∫
2
− 2 y− y2
−2
dx
-2
o
x
= ∫ y (− 2 y − y 2 + 2)dy
0
= 2∫ ydy − ∫ y 2 y − y 2 dy
−2
0
2
0
ydy = 4.
8 π 4 ρ sin θ ⋅ ρdρ = ∫π sin θdθ 3 2
∫∫ ydxdy = ∫π dθ ∫
D1
π
2 sin θ
π 8 3 π π 8 2 4 = ∫ sin θdθ = ⋅ ⋅ = . ∴ ∫∫ yddxdy = 4 − . 2 3 4 2 2 3 0 D π π π π 0 π 0 − 0 ( ∫π = ∫π + ===== π − = 2 π + 2 2 = 2 ) π
高数下习题课

和函数 s (x)的图形如下:
函数 f (x) 的图形如下:
o
x
y
–
3
–3
f (x)
s (x)
例 8
壶擎佰蕴奄涩岩享哈战瑰朵缠僧作怂塑蚌瑞谷三胁卵弧毫戊藤怯误拴族抿高数下习题课高数下习题课
解:
(5)
拌露脊性米役伟学贱铱佰过沪斩钵馁瓶拾间丰囊跌眩客悉杂俘夏磐崭甲们高数下习题课高数下习题课
(6)
解:
同理:
澈采棉唾伪邢媒倒侍隆尔乐偶绅哮绝卞易贮脂痪微芳臃结邱滴宫蚁哟磅叙高数下习题课高数下习题课
(7)
解:
恤麻林会美田菲糠榔末叫姓面掏抽称螟芳勋翔旷倦吻仗崔馅垮木臭汇翼儒高数下习题课高数下习题课
例 7
蛔盾脂翁锨痢谦汗昌哀旬并僚制豹再养窗吴扰彪悸例舵站叭骋辕漠分堵玲高数下习题课高数下习题课
解:
例 6
酿掇蔼寐寇挨锈人沟裸澄木苞邵膜贯拒抑邢惋羞彼聂筋沛靳渝龋拣师买伊高数下习题课高数下习题课
解:
= 0,
n = 1, 2, ···
n = 1, 2, ···
例 8.
揽瞬绚社密忧璃鞋软宠袒宪帮裹燕菌锈辈腐滋醋潞殉歉庇凛溪涩纽丁限灶高数下习题课高数下习题课
h
h
Dxy 图形?
三4.
方法 II:
贴补,用高斯公式.
S
S半圆
砖盅喝盟暑是隆迢瘦坏砷眷要靡叔靳怎网跃纫食拦跃契钙墓琵业童砂喳哮高数下习题课高数下习题课
2. (1)
解
方法:
2
1
x
y
o
L
用格林公式
0 t 2
C
娩谜宏琢遍剖京诱刨己抚盔毖风仕肉镣纬小壬腊归辽艳憨煽市倘贾喷欠俗高数下习题课高数下习题课
高等数学习题课2

x 0 s3 ix n
3 x x0 x
微 分
3f(a) 1 4
二 导数的运算法则,高阶导数 1 导数的四则运算法则,复合函数求导法则
-9-
习题课
例5 求下列函数的一阶导数
(1) y2arc3x s in (1arc3xs)2in
解 y2arc3x slin n 2(ar3 cx)s in
导 令 x0得
数
与
y(0)f(4 )0 ( 2 y (0 )y (0 ) )f(2 )1 (y (0 ))
微
分
y(0)22y(0)1(1y(0))
2
y(0) 1 7
- 19 -
习题课
4 参数方程所确定的函数的求导
例10 计算下列各题
第 二
(1)
y 3t5 5t3 x arctan t
解 f(x)2432x11P10(x) f(1)1(x)24321!1
f(12)(x)0
- 14 -
习题课
例8 计算下列各题 (1) f(x)(x23x2x13), 求 f (50)(x).
第 二
解
章
导 数 与 微 分
f(x) 2 1 x3 x1
f(50)(x)2((x1)53)05510!
-8-
习题课
(2) 已知 f(a ) 1 ,f(a ) 1 ,求
lim f(asi3 nx)ex
x 0
x
第 二 章
解
原式 lif m (a si3 x n )f(a ) (e x 1 )
x 0
x
导 数 与
3 lifm (a s3 ix n )f(a )s3 ix n limex 1
高等数学课件-习题课2

哈 尔
解 x 0 :f( x ) ( 3 x 2 ) 6 x ;
滨 工
x 0 :f( x ) ( x 2 ) 2 x ;
程 大 学
f(0)lim 2x2x|x|0;
x 0
x
高
f (0)x l i0m f(x)x f(0)
lim2x02; x0 x
等 数 学
f (0)x l i0m f(x)x f(0)
滨
工 解 首,先 f(x)在x0处必须 ,从 连 而 续
程
大
f(00)f(00).
学
f(0 0 ) lism a in x 0 , x 0
高
等
f ( 0 0 ) li [m 1 l n x ) b ( ] b ,
数
x 0
学
b0.
对任意 a ,当 x 给 0 ,f定 (x )都 的 存 ; 在
dy
y
t
dx x t
1
1 1 t2
1 1 t2
2t
t; 2
等
数 学
1
d2y
2 t dx2
(
dy dx
)t
xt
2
1 1 t2
1 t2
4t
例8
用微分法则求函数
y
arctan1 1
x2 x2
的微分和
哈 尔 滨 工 程 大
导数.
解
dy1(111xx22)2d(11xx22)
学
高 等
1(1 11 x x2 2)2(1x2) (2(x 1)d x x 2)(2 1x2)2xdx u vduudv
6x0 lim 6;
x0 x
因 f (0 为 ) f (0 ),所以 f(0)不存 . 在
高数第2章习题课

5、微分的定义—微分的实质 、微分的定义 微分的实质 6、导数与微分的关系 、 dy = f ′( x)dx 7、 微分的求法 、 基本初等函数的微分公式——16个公式 个公式 基本初等函数的微分公式 8、微分的基本法则 函数和、 函数和、差、积、商的微分法则 一阶微分形式的不变性——复合函数的微分法则 复合函数的微分法则 一阶微分形式的不变性 无论x是自变量还是中间变量 函数y=f (x)的微分形 是自变量还是中间变量, 无论 是自变量还是中间变量 函数 的微分形 式总是dy 式总是 = f′(x)dx.
f (x) 在 x = 2 处连续,且 lim f ( x) = 3, 4.设 例4.设 处连续, x→2 x − 2 求 f ′(2) . lim f ( x) = lim[( x − 2) ⋅ f ( x) ] = 0 解: f (2) = x→2 x→2 ( x − 2) f ( x) − f (2) f ( x) f ′(2) = lim = lim =3 x→2 x→2 x − 2 x−2
习 题 课
一、主要内容
1、导数的定义
∆y f ( x0 + ∆x ) − f ( x0 ) y′ x= x0 = lim . = lim ∆x→0 ∆x ∆x→0 ∆x
单侧导数 左导数, 右导数, 可导的充要条件. 左导数 右导数 可导的充要条件
常数和基本初等函数的导数公式) 2、基本导数公式(常数和基本初等函数的导数公式)
双曲——16+6个公式 常, 幂, 指, 对, 三, 反, 双曲 个公式
3、求导法则 (1) 函数的和、差、积、商的求导法则 函数的和、 商的求导法则; (2) 反函数的求导法则 反函数的求导法则; (3) 复合函数的求导法则 复合函数的求导法则——注意不要漏层 注意不要漏层; 注意不要漏层 (4) 对数求导法 对数求导法——注意适用范围 注意适用范围; 注意适用范围 (5) 隐函数求导法则 隐函数求导法则——注意 的函数的求导 注意y的函数的求导 注意 的函数的求导; (6) 参变量函数的求导法则 参变量函数的求导法则——注意不要漏乘 注意不要漏乘; 注意不要漏乘
高等数学函数习题课

例4.设 f ( x0 ) 存在,求
f ( x0 x ( x) 2 ) f ( x0 ) lim . x 0 x
解:
f ( x0 x ( x) 2 ) f ( x0 ) x ( x) 2 原式= lim 2 x 0 x x ( x)
d (sec x ) sec x tan xdx d (csc x ) csc x cot xdx
d (a x ) a x ln adx 1 dx x ln a 1 d (arcsin x ) dx 2 1 x 1 d (arctan x ) 2 dx 1 x d (log a x )
求 导 法 则
1、导数的定义
定义 设函数y f ( x )在点x 0的某个邻域内有定义,
当自变量x在x 0处取得增量x (点x 0 x仍在该邻域 内)时, 相应地函数y取得增量y f ( x 0 x ) f ( x 0 ); 如果y与x之比当x 0时的极限存在, 则称函数 y f ( x )在点x 0处可导, 并称这个极限为函数y f ( x ) dy 在点x 0处的导数, 记为y x x 0 , dx df ( x ) x x0 或 dx
3、求导法则
(1) 函数的和、差、积、商的求导法则
设u u( x ), v v ( x ) 可导,则
c 是常数), (1)( u v ) u v , (2)( cu ) cu (
v uv u u (3)( uv ) u v uv , (4)( ) ( v 0) . 2 v v
a 2 , b 1,
f (1) 2
2 , x 1 f ( x) 2 x , x 1
同济第六版高数答案(高等数学课后习题解答)2

习题9-11. 设有一平面薄板(不计其厚度), 占有xOy 面上的闭区域D , 薄板上分布有密度为μ =μ(x , y )的电荷, 且μ(x , y )在D 上连续, 试用二重积分表达该板上全部电荷Q .解 板上的全部电荷应等于电荷的面密度μ(x , y )在该板所占闭区域D 上的二重积分⎰⎰=Dd y x Q σμ),(.2. 设⎰⎰+=13221)(D d y x I σ, 其中D 1={(x , y )|-1≤x ≤1, -2≤y ≤2};又⎰⎰+=23222)(D d y x I σ, 其中D 2={(x , y )|0≤x ≤1, 0≤y ≤2}.试利用二重积分的几何意义说明I 1与I 2的关系.解 I 1表示由曲面z =(x 2+y 2)3与平面x =±1, y =±2以及z =0围成的立体V 的体积.I 2表示由曲面z =(x 2+y 2)3与平面x =0, x =1, y =0, y =2以及z =0围成的立体V 1的体积.显然立体V 关于yOz 面、xOz 面对称, 因此V 1是V 位于第一卦限中的部分, 故V =4V 1, 即I 1=4I 2.3. 利用二重积分的定义证明: (1)⎰⎰=Dd σσ (其中σ为D 的面积);证明 由二重积分的定义可知,⎰⎰∑=→∆=Dni iiif d y x f 1),(lim ),(σηξσλ其中∆σi 表示第i 个小闭区域的面积. 此处f (x , y )=1, 因而f (ξ, η)=1, 所以,σσσσλλ==∆=→=→⎰⎰∑01lim lim Dni id .(2)⎰⎰⎰⎰=DDd y x f k d y x kf σσ),(),( (其中k 为常数);证明∑⎰⎰∑=→=→∆=∆=ni i i i Dni iiif k kf d y x kf 11),(lim ),(lim ),(σηξσηξσλλ⎰⎰∑=∆==→Dn i i i i d y x f k f k σσηξλ),(),(lim 10. (3)⎰⎰⎰⎰⎰⎰+=21),(),(),(D DD d y x f d y x f d y x f σσσ,其中D =D 1⋃D 2, D 1、D 2为两个无公共内点的闭区域.证明 将D 1和D 2分别任意分为n 1和n 2个小闭区域1i σ∆和2i σ∆, n 1+n 2=n , 作和∑∑∑===∆+∆=∆2222211111111),(),(),(n i i i i n i i i i ni iiif f f σηξσηξσηξ.令各1i σ∆和2i σ∆的直径中最大值分别为λ1和λ2, 又λ=ma x (λ1λ2), 则有∑=→∆ni i i i f 10),(lim σηξλ∑∑=→=→∆+∆=22222211111111),(lim ),(lim n i i i i n i i i i f f σηξσηξλλ,即 ⎰⎰⎰⎰⎰⎰+=21),(),(),(D D Dd y x f d y x f d y x f σσσ.4. 根据二重积分的性质, 比较下列积分大小:(1)⎰⎰+Dd y x σ2)(与⎰⎰+Dd y x σ3)(, 其中积分区域D 是由x 轴, y 轴与直线x +y =1所围成;解 区域D 为: D ={(x , y )|0≤x , 0≤y , x +y ≤1}, 因此当(x , y )∈D 时, 有(x +y )3≤(x +y )2, 从而⎰⎰+Dd y x σ3)(≤⎰⎰+Dd y x σ2)(. (2)⎰⎰+Dd y x σ2)(与⎰⎰+Dd y x σ3)(, 其中积分区域D 是由圆周(x -2)2+(y -1)2=2所围成;解 区域D 如图所示, 由于D 位于直线x +y =1的上方, 所以当(x , y )∈D 时, x +y ≥1, 从而(x +y )3≥(x +y )2, 因而⎰⎰⎰⎰+≤+DDd y x d y x σσ32)()(. (3)⎰⎰+Dd y x σ)ln(与⎰⎰+Dd y x σ3)(, 其中D 是三角形闭区域, 三角顶点分别为(1, 0), (1, 1), (2, 0);解 区域D 如图所示, 显然当(x , y )∈D 时, 1≤x +y ≤2, 从而0≤ln(x +y )≤1, 故有[ln(x +y )]2≤ ln(x +y ), 因而⎰⎰⎰⎰+≥+DDd y x d y x σσ)ln()][ln(2. (4)⎰⎰+Dd y x σ)ln(与⎰⎰+Dd y x σ3)(, 其中D ={(x , y )|3≤x ≤5. 0≤y ≤1}.解 区域D 如图所示, 显然D 位于直线x +y =e 的上方, 故当(x , y )∈D 时, x +y ≥e , 从而ln(x +y )≥1, 因而 [ln(x +y )]2≥ln(x +y ), 故⎰⎰⎰⎰+≤+DDd y x d y x σσ2)][ln()ln(. 5. 利用二重积分的性质估计下列积分的值: (1)⎰⎰+=Dd y x xy I σ)(, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解 因为在区域D 上0≤x ≤1, 0≤y ≤1, 所以 0≤xy ≤1, 0≤x +y ≤2, 进一步可得0≤xy (x +y )≤2, 于是⎰⎰⎰⎰⎰⎰≤+≤DDDd d y x xy d σσσ2)(0,即 ⎰⎰≤+≤Dd y x xy 2)(0σ.(2)⎰⎰=Dyd x I σ22sin sin , 其中D ={(x , y )| 0≤x ≤π, 0≤y ≤π};解 因为0≤sin 2x ≤1, 0≤sin 2y ≤1, 所以0≤sin 2x sin 2y ≤1. 于是⎰⎰⎰⎰⎰⎰≤≤DDDd yd x d σσσ1sin sin 022, 即 ⎰⎰≤≤Dyd x 222sin sin 0πσ.(3)⎰⎰++=Dd y x I σ)1(, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤2};解 因为在区域D 上, 0≤x ≤1, 0≤y ≤2, 所以1≤x +y +1≤4, 于是⎰⎰⎰⎰⎰⎰≤++≤DDDd d y x d σσσ4)1(,即 ⎰⎰≤++≤Dd y x 8)1(2σ.(4)⎰⎰++=Dd y x I σ)94(22, 其中D ={(x , y )| x 2+y 2 ≤4}.解 在D 上, 因为0≤x 2+y 2≤4, 所以 9≤x 2+4y 2+9≤4(x 2+y 2)+9≤25. 于是⎰⎰⎰⎰⎰⎰≤++≤DDDd d y x d σσσ25)94(922, ⎰⎰⋅⋅≤++≤Dd y x 2222225)94(29πσπ,即 ⎰⎰≤++≤Dd y x πσπ100)94(3622.习题9-21. 计算下列二重积分:(1)⎰⎰+Dd y x σ)(22, 其中D ={(x , y )| |x |≤1, |y |≤1};解 积分区域可表示为D : -1≤x ≤1, -1≤y ≤1. 于是⎰⎰+Dd y x σ)(22y d y x dx ⎰⎰--+=111122)(x d y y x ⎰--+=111132]31[ x d x ⎰-+=112)312(113]3232[-+=x x 38=. (2)⎰⎰+Dd y x σ)23(, 其中D 是由两坐标轴及直线x +y =2所围成的闭区域:解 积分区域可表示为D : 0≤x ≤2, 0≤y ≤2-x . 于是⎰⎰+Dd y x σ)23(y d y x dx x⎰⎰-+=2020)23(dx y xy x ⎰-+=222]3[ dx x x ⎰-+=202)224(0232]324[x x x -+=320=. (3)⎰⎰++Dd y y x x σ)3(223, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解⎰⎰++Dd y y x x σ)3(323⎰⎰++=1032310)3(dx y y x x dy ⎰++=1001334]4[dy x y y x x⎰++=103)41(dy y y 0142]424[y y y ++=1412141=++=.(4)⎰⎰+Dd y x x σ)cos(, 其中D 是顶点分别为(0, 0), (π, 0), 和(π, π)的三角形闭区域.解 积分区域可表示为D : 0≤x ≤π, 0≤y ≤x . 于是,⎰⎰+D d y x x σ)cos(⎰⎰+=x dy y x xdx 00)cos(π⎰+=π)][sin(dx y x x x⎰-=π0)sin 2(sin dx x x x ⎰--=π0)cos 2cos 21(x x xd+--=0|)cos 2cos 21(πx x x dx x x ⎰-π0)cos 2cos 21(π23-=. .2. 画出积分区域, 并计算下列二重积分:(1)⎰⎰Dd y x σ, 其中D 是由两条抛物线x y =, 2x y =所围成的闭区域;解 积分区域图如, 并且D ={(x , y )| 0≤x ≤1, x y x ≤≤2}. 于是⎰⎰D d y xσ⎰⎰=102dy y x dx xx⎰=10223]32[dx y x x x 556)3232(10447=-=⎰dx x x .(2)⎰⎰Dd xy σ2, 其中D 是由圆周x 2+y 2=4及y 轴所围成的右半闭区域; 解 积分区域图如, 并且D ={(x , y )| -2≤y ≤2, 240y x -≤≤}. 于是⎰⎰⎰⎰⎰----=22402240222222]21[dy y x dx xy dy d xy y y Dσ1564]10132[)212(22225342=-=-=--⎰y y dy y y . (3)⎰⎰+Dy x d e σ, 其中D ={(x , y )| |x |+|y |≤1};解 积分区域图如, 并且D ={(x , y )| -1≤x ≤0, -x -1≤y ≤x +1}⋃{(x , y )| 0≤x ≤1, x -1≤y ≤-x +1}. 于是⎰⎰⎰⎰⎰⎰+--+---++=11101101x x y x x x y x Dy x dy e dx e dy e dx e d e σ⎰⎰+---+--+=1110111][][dy e e dx e e x x y x x x y x ⎰⎰---+-+-=11201112)()(dx e e dx e ex x 101201112]21[]21[---+-+-=x x e ex x e e =e -e -1. (4)⎰⎰-+Dd x y x σ)(22, 其中D 是由直线y =2, y =x 及y =2x 轴所围成的闭区域.解 积分区域图如, 并且D ={(x , y )| 0≤y ≤2, y x y ≤≤21}. 于是⎰⎰⎰⎰⎰-+=-+=-+2022232222022]2131[)()(dy x x y x dx x y x dy d x y x y y y y Dσ613)832419(2023=-=⎰dy y y .3. 如果二重积分⎰⎰Ddxdy y x f ),(的被积函数f (x , y )是两个函数f 1(x )及f 2(y )的乘积,即f (x , y )= f 1(x )⋅f 2(y ), 积分区域D ={(x , y )| a ≤x ≤b , c ≤ y ≤d }, 证明这个二重积分等于两个单积分的乘积, 即 ])([])([)()(2121dy y f dx x f dxdy y f x f dcb aD⎰⎰⎰⎰⋅=⋅证明dx dy y f x f dy y f x f dx dxdy y f x f dcb a d cb aD⎰⎰⎰⎰⎰⎰⋅=⋅=⋅])()([)()()()(212121,而 ⎰⎰=⋅dcdcdy y f x f dy y f x f )()()()(2121,故dx dy y f x f dxdy y f x f b adcD⎰⎰⎰⎰=⋅])()([)()(2121.由于⎰dcdy y f )(2的值是一常数, 因而可提到积分号的外面, 于是得])([])([)()(2121dy y f dx x f dxdy y f x f dcb a D⎰⎰⎰⎰⋅=⋅4. 化二重积分⎰⎰=Dd y x f I σ),(为二次积分(分别列出对两个变量先后次序不同的两个二次积分), 其中积分区域D 是:(1)由直线y =x 及抛物线y 2=4x 所围成的闭区域; 解积分区域如图所示, 并且D ={(x , y )|x y x x 2 ,40≤≤≤≤}, 或D ={(x , y )| y x y y ≤≤≤≤241 ,40},所以 ⎰⎰=xxdy y x f dx I 240),(或⎰⎰=yy dx y x f dy I 4402),(.(2)由x 轴及半圆周x 2+y 2=r 2(y ≥0)所围成的闭区域; 解积分区域如图所示, 并且D ={(x , y )|220 ,x r y r x r -≤≤≤≤-},或D ={(x , y )| 2222 ,0y r x y r r y -≤≤--≤≤}, 所以 ⎰⎰--=220),(x r rr dy y x f dx I , 或⎰⎰---=2222),(0y r y r r dx y x f dy I .(3)由直线y =x , x =2及双曲线x y 1=(x >0)所围成的闭区域;解积分区域如图所示, 并且D ={(x , y )|x y xx ≤≤≤≤1 ,21},或D ={(x , y )| 21 ,121≤≤-≤≤x y y }⋃{(x , y )|2 ,21≤≤≤≤x y y },所以 ⎰⎰=x xdy y x f dx I 1),(21, 或⎰⎰⎰⎰+=22121121),(),(yydx y x f dy dx y x f dy I .(4)环形闭区域{(x , y )| 1≤x 2+y 2≤4}.解 如图所示, 用直线x =-1和x =1可将积分区域D 分成四部分, 分别记做D 1, D 2,D 3, D 4. 于是⎰⎰⎰⎰⎰⎰⎰⎰+++=4321),(),(),(),(D D D D d y x f d y x f d y x f d y x f I σσσσ⎰⎰⎰⎰--------+=222244411112),(),(x x x x dy y x f dx dy y x f dx ⎰⎰⎰⎰--------++222214442111),(),(x x x x dy y x f dx dy y x f dx用直线y =1, 和y =-1可将积分区域D 分成四部分, 分别记做D 1, D 2, D 3, D 4, 如图所示. 于是⎰⎰⎰⎰⎰⎰⎰⎰+++=4321),(),(),(),(D D D D d y x f d y x f d y x f d y x f I σσσσ⎰⎰⎰⎰--------+=222244141121),(),(y y y y dx y x f dy dx y x f dy⎰⎰⎰⎰--------++222241441211),(),(y y y y dx y x f dy dx y x f dy5. 设f (x , y )在D 上连续, 其中D 是由直线y =x 、y =a 及x =b (b >a )围成的闭区域, 证明:⎰⎰⎰⎰=bybaxabadx y x f dy dy y x f dx ),(),(.证明 积分区域如图所示, 并且积分区域可表示为 D ={(x , y )|a ≤x ≤b , a ≤y ≤x }, 或D ={(x , y )|a ≤y ≤b , y ≤x ≤b }. 于是⎰⎰Dd y x f σ),(⎰⎰=x a b a dy y x f dx ),(, 或⎰⎰Dd y x f σ),(⎰⎰=by b a dx y x f dy ),(.因此⎰⎰⎰⎰=byb ax abadx y x f dy dy y x f dx ),(),(.6. 改换下列二次积分的积分次序: (1)⎰⎰ydx y x f dy 01),(;解 由根据积分限可得积分区域D ={(x , y )|0≤y ≤1, 0≤x ≤y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤1, x ≤y ≤1}, 所以⎰⎰⎰⎰=1101),(),(xy dy y x f dx dx y x f dy .(2)⎰⎰y ydx y x f dy 2202),(;解 由根据积分限可得积分区域D ={(x , y )|0≤y ≤2, y 2≤x ≤2y }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤x ≤4, x y x ≤≤2}, 所以⎰⎰y ydx y x f dy 222),(⎰⎰=402),(xx dy y x f dx .(3)⎰⎰---221110),(y y dx y x f dy ;解 由根据积分限可得积分区域}11 ,10|),{(22y x y y y x D -≤≤--≤≤=, 如图. 因为积分区域还可以表示为}10 ,11|),{(2x y x y x D -≤≤≤≤-=, 所以⎰⎰⎰⎰-----=22210111110),(),(x y ydy y x f dx dx y x f dy(4)⎰⎰--21222),(x x xdy y x f dx ;解 由根据积分限可得积分区域}22 ,21|),{(2x x y x x y x D -≤≤-≤≤=, 如图. 因为积分区域还可以表示为}112 ,10|),{(2y x y y y x D -+≤≤-≤≤=, 所以⎰⎰--21222),(x x x dy y x f dx ⎰⎰-+-=11122),(y ydx y x f dy .(5)⎰⎰e xdy y x f dx 1ln 0),(;解 由根据积分限可得积分区域D ={(x , y )|1≤x ≤e , 0≤y ≤ln x }, 如图. 因为积分区域还可以表示为D ={(x , y )|0≤y ≤1, e y ≤x ≤ e }, 所以⎰⎰e xdy y x f dx 1ln 0),(⎰⎰=10),(eey dx y x f dy(6)⎰⎰-xxdy y x f dx sin 2sin 0),(π(其中a ≥0).解 由根据积分限可得积分区域}sin 2sin ,0|),{(x y x x y x D ≤≤-≤≤=π, 如图.因为积分区域还可以表示为}arcsin 2 ,01|),{(π≤≤-≤≤-=x y y y x D}arcsin arcsin ,10|),{(y x y y y x -≤≤≤≤⋃π, 所以⎰⎰⎰⎰⎰⎰----+=yyyxxdx y x f dy dx y x f dy dy y x f dx arcsin arcsin 10arcsin 201sin 2sin 0),(),(),(πππ.7. 设平面薄片所占的闭区域D 由直线x +y =2, y =x 和x 轴所围成, 它的面密度为μ(x , y )=x 2+y 2, 求该薄片的质量. 解 如图, 该薄片的质量为⎰⎰=D d y x M σμ),(⎰⎰+=Dd y x σ)(22⎰⎰-+=10222)(yydx y x dy⎰-+-=10323]372)2(31[dy y y y 34=.8. 计算由四个平面x =0, y =0, x =1, y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体的体积.解 四个平面所围成的立体如图, 所求体积为 ⎰⎰--=Ddxdy y x V )326(⎰⎰--=101)326(dy y x dx⎰--=10102]2326[dx y xy y ⎰=-=1027)229(dx x .9. 求由平面x =0, y =0, x +y =1所围成的柱体被平面z =0及抛物面x 2+y 2=6-z 截得的立体的体积.解 立体在xOy 面上的投影区域为D ={(x , y )|0≤x ≤1, 0≤y ≤1-x }, 所求立体的体积为以曲面z =6-x 2-y 2为顶, 以区域D 为底的曲顶柱体的体积, 即⎰⎰--=Dd y x V σ)6(22⎰⎰---=101022)6(xdy y x dx 617=.10. 求由曲面z =x 2+2y 2及z =6-2x 2-y 2所围成的立体的体积.解 由⎩⎨⎧--=+=2222262y x z y x z 消去z , 得x 2+2y 2=6-2x 2-y 2, 即x 2+y 2=2, 故立体在x O y 面上的投影区域为x 2+y 2≤2, 因为积分区域关于x 及y 轴均对称, 并且被积函数关于x , y都是偶函数, 所以⎰⎰+---=Dd y x y x V σ)]2()26[(2222⎰⎰--=Dd y x σ)336(22⎰⎰---=2202220)2(12x dy y x dx π6)2(8232=-=⎰dx x .11. 画出积分区域, 把积分⎰⎰Ddxdy y x f ),(表示为极坐标形式的二次积分, 其中积分区域D 是:(1){(x , y )| x 2+y 2≤a 2}(a >0);解积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤a }, 所以⎰⎰⎰⎰=D Dd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (d f d a.(2){(x , y )|x 2+y 2≤2x };解 积分区域D 如图. 因为}cos 20 ,22|),{(θρπθπθρ≤≤≤≤-=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰-=22cos 20)sin ,cos (ππθρρθρθρθd f d .(3){(x , y )| a 2≤x 2+y 2≤b 2}, 其中0<a <b ;解 积分区域D 如图. 因为D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以⎰⎰⎰⎰=D Dd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰=πρρθρθρθ20)sin ,cos (bad f d .(4){(x , y )| 0≤y ≤1-x , 0≤x ≤1}.解 积分区域D 如图. 因为}sin cos 10 ,20|),{(θθρπθθρ+≤≤≤≤=D , 所以⎰⎰⎰⎰=DDd d f dxdy y x f θρρθρθρ)sin ,cos (),(⎰⎰+=θθρρθρθρθπsin cos 1020)sin ,cos (d f d .12. 化下列二次积分为极坐标形式的二次积分: (1)⎰⎰11),(dy y x f dx ;解 积分区域D 如图所示. 因为}csc 0 ,24|),{(}sec 0 ,40|),{(θρπθπθρθρπθθρ≤≤≤≤⋃≤≤≤≤=D ,所以⎰⎰⎰⎰⎰⎰==DDd d f d y x f dy y x f dx θρρθρθρσ)sin ,cos (),(),(0⎰⎰=4sec 0)sin ,cos (πθρρθρθρθd f d ⎰⎰+24csc 0)sin ,cos (ππθρρθρθρθd f d .(2)⎰⎰+xxdy y x f dx 3222)(;解 积分区域D 如图所示, 并且 }sec 20 ,34|),{(θρπθπθρ≤≤≤≤=D ,所示⎰⎰⎰⎰⎰⎰=+=+xxDDd d f d y x f dy y x f dx 3222220)()()(θρρρσ⎰⎰=34sec 20)(ππθρρρθd f d .(3)⎰⎰--2111),(x xdy y x f dx ;解 积分区域D 如图所示, 并且}1sin cos 1 ,20|),{(≤≤+≤≤=ρθθπθθρD ,所以⎰⎰⎰⎰⎰⎰--==10112)sin ,cos (),(),(x xDDd d f d y x f dy y x f dx θρρθρθρσ⎰⎰+=2sin cos 101)sin ,cos (πθθρρθρθρθd f d(4)⎰⎰21),(x dy y x f dx .解 积分区域D 如图所示, 并且}sec tan sec ,40|),{(θρθθπθθρ≤≤≤≤=D ,所以⎰⎰210),(x dy y x f dx ⎰⎰⎰⎰==DDd d f d y x f θρρθρθρσ)sin ,cos (),(⎰⎰=40sec tan sec )sin ,cos (πθθθρρθρθρθd f d13. 把下列积分化为极坐标形式, 并计算积分值: (1)⎰⎰-+2202220)(x ax ady y x dx ;解 积分区域D 如图所示. 因为}cos 20 ,20|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰-+2202220)(x ax ady y x dx ⎰⎰⋅=Dd d θρρρ2⎰⎰⋅=20cos 202πθρρρθa d d ⎰=2044cos 4πθθd a 443a π=.(2)⎰⎰+dy y x dx 0220;解 积分区域D 如图所示. 因为}sec 0 ,40|),{(θρπθθρa D ≤≤≤≤=, 所以⎰⎰⎰⎰⋅=+Dxad d dy y x dx θρρρ0220⎰⎰⋅=40sec 0πθρρρθa d d ⎰=4033sec 3πθθd a )]12ln(2[63++=a .(3)⎰⎰-+xxdy y xdx 2212210)(;解 积分区域D 如图所示. 因为}tan sec 0 ,40|),{(θθρπθθρ≤≤≤≤=D , 所以⎰⎰⎰⎰⋅=+--Dxx d d dy y xdx θρρρ212122102)(12tan sec 40tan sec 02140-==⋅=⎰⎰⎰-πθθπθθθρρρθd d d .(4)⎰⎰-+220220)(y a a dx y x dy .解 积分区域D 如图所示. 因为}0 ,20|),{(a D ≤≤≤≤=ρπθθρ, 所以⎰⎰⎰⎰⋅=+-Dy a ad d dx y x dy θρρρ2022022)(420028a d d aπρρρθπ=⋅=⎰⎰.14. 利用极坐标计算下列各题: (1)⎰⎰+Dy xd e σ22,其中D 是由圆周x 2+y 2=4所围成的闭区域;解 在极坐标下D ={(ρ, θ)|0≤θ≤2π, 0≤ρ≤2}, 所以⎰⎰⎰⎰=+DDy x d d e d e θρρσρ222)1()1(2124420202-=-⋅==⎰⎰e e d e d ππρρθπρ. (2)⎰⎰++Dd y x σ)1ln(22,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解 在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰+=++DDd d d y x θρρρσ)1ln()1ln(222)12ln 2(41)12ln 2(212)1ln(2012-=-⋅=+=⎰⎰πρρρθπd d .(3)σd xyDarctan⎰⎰, 其中D 是由圆周x 2+y 2=4, x 2+y 2=1及直线y =0, y =x 所围成的第一象限内的闭区域.解 在极坐标下}21 ,40|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⎰⎰⋅=⋅=DDDd d d d d xyθρρθθρρθσ)arctan(tan arctan⎰⎰⋅=4021πρρθθd d ⎰⎰==40321643ππρρθθd d . 15. 选用适当的坐标计算下列各题:(1)dxdy yx D 22⎰⎰,其中D 是由直线x =2,y =x 及曲线xy =1所围成的闭区域.解 因为积分区域可表示为}1 ,21|),{(x y xx y x D ≤≤≤≤=, 所以dxdy yx D 22⎰⎰dy y dx x x x ⎰⎰=211221⎰-=213)(dx x x 49=.(2)⎰⎰++--Dd yx y x σ222211, 其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;解 在极坐标下}10 ,20|),{(≤≤≤≤=ρπθθρD , 所以⎰⎰⎰⎰⋅+-=++--DD d d d y x y x θρρρρσ2222221111)2(811102220-=+-=⎰⎰ππρρρρθπd d .(3)⎰⎰+Dd y x σ)(22, 其中D 是由直线y =x , y =x +a , y =a , y =3a (a >0)所围成的闭区域;解 因为积分区域可表示为D ={(x , y )|a ≤y ≤3a , y -a ≤x ≤y }, 所以⎰⎰+D d y x σ)(22⎰⎰-+=a a ya y dx y x dy 322)(4332214)312(a dy a y a ay a a =+-=⎰.(4)σd y x D22+⎰⎰, 其中D 是圆环形闭区域{(x , y )| a 2≤x 2+y 2≤b 2}.解 在极坐标下D ={(ρ, θ)|0≤θ≤2π, a ≤ρ≤b }, 所以 σd y x D22+⎰⎰)(3233202a b dr r d b a -==⎰⎰πθπ.16. 设平面薄片所占的闭区域D 由螺线ρ=2θ上一段弧(20πθ≤≤)与直线2πθ=所围成, 它的面密度为μ(x , y )=x 2+y 2. 求这薄片的质量.解 区域如图所示. 在极坐标下}20 ,20|),{(θρπθθρ≤≤≤≤=D , 所以所求质量⎰⎰⎰⎰⋅==Dd d d y x M 20202),(πθρρρθσμ⎰==254404ππθθd .17. 求由平面y =0, y =kx (k >0), z =0以及球心在原点、半径为R 的上半球面所围成的在第一卦限内的立体的体积.解 此立体在xOy 面上的投影区域D ={(x , y )|0≤θ≤arctan k , 0≤ρ≤R }.⎰⎰--=D dxdy y x R V 222k R d R d k Rarctan 313arctan 0022=-=⎰⎰ρρρθ.18. 计算以xOy 平面上圆域x 2+y 2=ax 围成的闭区域为底, 而以曲面z =x 2+y 2为顶的曲顶柱体的体积.解 曲顶柱体在xOy 面上的投影区域为D ={(x , y )|x 2+y 2≤ax }. 在极坐标下}cos 0 ,22|),{(θρπθπθρa D ≤≤≤≤-=, 所以⎰⎰≤++=axy x dxdy y xV 22)(22πθθρρρθππθππ422cos 022442323cos 4a d a d d a ==⋅=⎰⎰⎰--. 习题9-31. 化三重积分dxdydz z y x f I ),,(Ω⎰⎰⎰=为三次积分, 其中积分区域Ω分别是:(1)由双曲抛物面xy =z 及平面x +y -1=0, z =0所围成的闭区域; 解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤xy , 0≤y ≤1-x , 0≤x ≤1}, 于是 ⎰⎰⎰-=xyx dz z y x f dy dx I 01010),,(.(2)由曲面z =x 2+y 2及平面z =1所围成的闭区域; 解 积分区域可表示为}11 ,11 ,1|),,{(2222≤≤--≤≤--≤≤+=Ωx x y x z y x z y x , 于是 ⎰⎰⎰+----=111112222),,(y x x x dz z y x f dy dx I .(3)由曲面z =x 2+2y 2及z =2-x 2所围成的闭区域;解 曲积分区域可表示为}11 ,11 ,22|),,{(22222≤≤--≤≤---≤≤+=Ωx x y x x z y x z y x , 于是 ⎰⎰⎰-+----=22222221111),,(x y x x x dz z y x f dy dx I .提示: 曲面z =x 2+2y 2与z =2-x 2的交线在xOy 面上的投影曲线为x 2+y 2=1.(4)由曲面cz =xy (c >0), 12222=+by a x , z =0所围成的在第一卦限内的闭区域. 解 曲积分区域可表示为}0 ,0 ,0|),,{(22a x x a a b y c xyz z y x ≤≤-≤≤≤≤=Ω,于是 ⎰⎰⎰-=cxy abdz z y x f dy dx I x a a0),,(22.提示: 区域Ω的上边界曲面为曲面c z =xy , 下边界曲面为平面z =0.2. 设有一物体, 占有空间闭区域Ω={(x , y , z )|0≤x ≤1, 0≤y ≤1, 0≤z ≤1}, 在点(x , y , z )处的密度为ρ(x , y , z )=x +y +z , 计算该物体的质量.解 ⎰⎰⎰⎰⎰⎰++==Ω101010)(dz z y x dy dx dxdydz M ρ⎰⎰++=1010)21(dy y x dx⎰⎰+=++=1010102)1(]2121[dx x dx y y xy 23)1(21102=+=x .3. 如果三重积分dxdydz z y x f ),,(Ω⎰⎰⎰的被积函数f (x , y , z )是三个函数f 1(x )、f 2(y )、f 3(z )的乘积, 即f (x , y , z )= f 1(x )⋅f 2(y )⋅f 3(z ), 积分区域Ω={(x , y , z )|a ≤x ≤b , c ≤y ≤d , l ≤z ≤m }, 证明这个三重积分等于三个单积分的乘积, 即⎰⎰⎰⎰⎰⎰=Ωmldcbadz z f dy y f dx x f dxdydz z f y f x f )()()()()()(321321.证明dxdydz z f y f x f )()()(321Ω⎰⎰⎰dx dy dz z f y f x f b a d c ml]))()()(([321⎰⎰⎰=dx dy dz z f y f x f ba dc ml]))()()(([321⎰⎰⎰=⎰⎰⎰=mldcbadx dy y f dz z f x f )])()()()([(231dx x f dy y f dz z f b a mldc)]())()()([(123⎰⎰⎰=⎰⎰⎰=d cbam ldx x f dy y f dz z f )())()()((123 ⎰⎰⎰=dcmlbadz z f dy y f dx x f )()()(321.4. 计算dxdydz z xy 32Ω⎰⎰⎰, 其中Ω是由曲面z =xy , 与平面y =x , x =1和z =0所围成的闭区域.解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤xy , 0≤y ≤x , 0≤x ≤1}, 于是dxdydz z xy 32Ω⎰⎰⎰⎰⎰⎰=xyxdz z dy y xdx 030210⎰⎰=xxy dy z y xdx 004210]4[⎰⎰=x dy y dx x 051054136412811012==⎰dx x .5. 计算3)1(z y x dxdydz+++Ω⎰⎰⎰, 其中Ω为平面x =0, y =0, z =0, x +y +z =1所围成的四面体. 解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤1-x -y , 0≤y ≤1-x , 0≤x ≤1},于是 3)1(z y x dxdydz +++Ω⎰⎰⎰⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰--++=x dy y x dx 10210]81)1(21[dx x x ⎰+-+=10]8183)1(21[)852(ln 21-=.提示: ⎰⎰⎰Ω+++3)1(z y x dxdydz ⎰⎰⎰---+++=y x x dz z y x dy dx 1031010)1(1 ⎰⎰---+++-=xyx dy z y x dx 1010210])1(21[⎰⎰--++=x dy y x dx 10210]81)1(21[ dx y y x x -⎰-++-=1010]81)1(21[dx x x ⎰+-+=10]8183)1(21[ 102]16183)1ln(21[x x x +-+= )852(ln 21-=.6. 计算xyzdxdydz Ω⎰⎰⎰, 其中Ω为球面x 2+y 2+z 2=1及三个坐标面所围成的在第一卦限内的闭区域.解 积分区域可表示为}10 ,10 ,10|),,{(222≤≤-≤≤--≤≤=Ωx x y y x z z y x 于是xyzdxdydz Ω⎰⎰⎰⎰⎰⎰---=222101010x y x xyzdz dy dx⎰⎰---=210221)1(21x dy y x xy dx ⎰-=1022)1(81dx x x 481=.7. 计算xzdxdydz Ω⎰⎰⎰, 其中Ω是由平面z =0, z =y , y =1以及抛物柱面y =x 2所围成的闭区域.解 积分区域可表示为Ω={(x , y , z )| 0≤z ≤y , x 2≤y ≤1, -1≤x ≤1}, 于是xzdxdydz Ω⎰⎰⎰⎰⎰⎰-=yx zdz dy xdx 01112⎰⎰-=1211221x dy y xdx 0)1(61116=-=⎰-dx x x .8. 计算zdxdydz Ω⎰⎰⎰, 其中Ω是由锥面22y x R h z +=与平面z =h (R >0, h >0)所围成的闭区域.解 当0≤z ≤h 时, 过(0, 0, z )作平行于xOy 面的平面, 截得立体Ω的截面为圆D z :222)(z h R y x =+, 故D z的半径为z h R , 面积为222z h R π, 于是 zdxdydz Ω⎰⎰⎰=dxdy zdz zD h ⎰⎰⎰0⎰==h h R dz z h R 0223224ππ. 9. 利用柱面坐标计算下列三重积分:(1)zdv Ω⎰⎰⎰, 其中Ω是由曲面222y x z --=及z =x 2+y 2所围成的闭区域;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ρ≤1, 222ρρ-≤≤z , 于是zdv Ω⎰⎰⎰⎰⎰⎰-=122022ρρπρρθzdz d d⎰--=1042)2(212ρρρρπdπρρρρπ127)2(1053=--=⎰d .(2)dv y x )(22+Ω⎰⎰⎰, 其中Ω是由曲面x 2+y 2=2z 及平面z =2所围成的闭区域.解 在柱面坐标下积分区域Ω可表示为0≤θ≤2π, 0≤ρ≤2, 222≤≤z ρ,于是dv y x)(22+Ω⎰⎰⎰dz d d θρρρ⋅=Ω⎰⎰⎰2⎰⎰⎰=22123202ρπρρθdz d d⎰⎰-=205320)212(ρρρθπd d ⎰==ππθ2031638d .10. 利用球面坐标计算下列三重积分:(1)dv z y x )(222++Ω⎰⎰⎰, 其中Ω是由球面x 2+y 2+z 2=1所围成的闭区域.解 在球面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ϕ≤π, 0≤r ≤1,于是 dv z y x )(222++Ω⎰⎰⎰θϕϕd drd r sin 4⋅=Ω⎰⎰⎰⎰⎰⎰=104020sin dr r d d ππϕϕθπ54=.(2)zdv Ω⎰⎰⎰, 其中闭区域Ω由不等式x 2+y 2+(z -a )2≤a 2, x 2+y 2≤z 2 所确定.解 在球面坐标下积分区域Ω可表示为 ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤,于是 zdv Ω⎰⎰⎰θϕϕϕd drd r r sin cos 2⋅=Ω⎰⎰⎰⎰⋅=404)cos 2(41cos sin 2πϕϕϕϕπd a4405467cos sin 8a d a πϕϕϕππ==⎰.11. 选用适当的坐标计算下列三重积分:(1)xydv Ω⎰⎰⎰, 其中Ω为柱面x 2+y 2=1及平面z =1, z =0, x =0, y =0所围成的在第一卦限内的闭区域;解 在柱面坐标下积分区域Ω可表示为 10 ,10 ,20≤≤≤≤≤≤z ρπθ,于是 xydv Ω⎰⎰⎰dz d d θρρθρθρ⋅⋅=Ω⎰⎰⎰sin cos⎰⎰⎰==101032081cos sin dz d d ρρθθθπ.别解: 用直角坐标计算⎰⎰⎰Ωxydv ⎰⎰⎰-=1010102dz ydy xdx x ⎰⎰-=21010x ydy xdx ⎰-=103)22(dx x x 81]84[1042=-=x x . (2)dv z y x 222++Ω⎰⎰⎰, 其中Ω是由球面x 2+y 2+z 2=z 所围成的闭区域;解 在球面坐标下积分区域Ω可表示为 ϕπϕπθcos 0 ,20 ,20≤≤≤≤≤≤r ,于是dv z y x 222++Ω⎰⎰⎰⎰⎰⎰⋅=ϕππϕϕθcos 022020sin dr r r d d10cos 41sin 2204πϕϕϕππ=⋅=⎰d .(3)dv y x )(22+Ω⎰⎰⎰, 其中Ω是由曲面4z 2=25(x 2+y 2)及平面z =5所围成的闭区域;解 在柱面坐标下积分区域Ω可表示为 525 ,20 ,20≤≤≤≤≤≤z ρρπθ,于是dv y x )(22+Ω⎰⎰⎰⎰⎰⎰=52520320ρπρρθdz d dπρρρπ8)255(2203=-=⎰d .(4)dv y x )(22+Ω⎰⎰⎰, 其中闭区域Ω由不等式A z y x a ≤++≤<2220, z ≥0所确定.解 在球面坐标下积分区域Ω可表示为A r a ≤≤≤≤≤≤ ,20 ,20πϕπθ,于是 dv y x )(22+Ω⎰⎰⎰θϕϕθϕϕϕd drd r r r sin )sin sin cos sin (2222222+=Ω⎰⎰⎰)(154sin 55420320a A dr r d d Aa-==⎰⎰⎰πϕϕθππ.12. 利用三重积分计算下列由曲面所围成的立体的体积:(1)z =6-x 2-y 2及22y x z +=;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2 π, 0≤ρ≤2, ρ≤z ≤6-ρ2,于是 dz d d dv V θρρΩΩ⎰⎰⎰⎰⎰⎰==⎰⎰⎰-=262020ρρπρρθdz d d⎰=--=2032332)6(2πρρρρπd .(2)x 2+y 2+z 2=2az (a >0)及x 2+y 2=z 2(含有z 轴的部分); 解 在球面坐标下积分区域Ω可表示为ϕπϕπθcos 20 ,40 ,20a r ≤≤≤≤≤≤,于是 θϕϕd drd r dv V sin 2ΩΩ⎰⎰⎰⎰⎰⎰==⎰⎰⎰=ϕππϕϕθcos 2024020sin a dr r d d34033sin cos 382a d a πϕϕϕππ==⎰. (3)22y x z +=及z =x 2+y 2;解 在柱面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ρ≤1, ρ2≤z ≤ρ,于是 6)(2103210202πρρρπρρθρρπ=-===⎰⎰⎰⎰⎰⎰⎰Ωd dz d d dv V .(4)225y x z --=及x 2+y 2=4z .解 在柱面坐标下积分区域Ω可表示为 22541 ,20 ,20ρρρπθ-≤≤≤≤≤≤z ,于是 ⎰⎰⎰-=22541220ρρπρρθdz d d V)455(32)45(22022-=--=⎰πρρρρπd .13. 球心在原点、半径为R 的球体, 在其上任意一点的密度的大小与这点到球心的距离成正比, 求这球体的质量.解 密度函数为222),,(z y x k z y x ++=ρ. 在球面坐标下积分区域Ω可表示为 0≤θ≤2π, 0≤ϕ≤π, 0≤r ≤R ,于是 dv z y x k M 222++=Ω⎰⎰⎰40220sin R k dr r kr d d Rπϕϕθππ=⋅=⎰⎰⎰.习题9-41. 求球面x 2+y 2+z 2=a 2含在圆柱面x 2+y 2=ax 内部的那部分面积. 解 位于柱面内的部分球面有两块, 其面积是相同的.由曲面方程z =222y x a --得222y x a x x z ---=∂∂, 222y x a y y z ---=∂∂, 于是 dxdy yz x z A axy x ⎰⎰≤+∂∂+∂∂+=2222)()(12dxdy yx a a axy x ⎰⎰≤+--=222222⎰⎰-=20cos 02214πθρρρθa d a d a )2(2)sin (4220-=-=⎰πθθπa d a a a .2. 求锥面z =22y x +被柱面z 2=2x 所割下的部分的曲面的面积.解 由z =22y x +和z 2=2x 两式消z 得x 2+y 2=2x , 于是所求曲面在xOy 面上的投影区域D 为x 2+y 2≤2x .由曲面方程22y x +得22y x x x z +=∂∂, 22y x y y z +=∂∂, 于是 dxdy y z x z A y x ⎰⎰≤+-∂∂+∂∂+=1)1(2222)()(1π221)1(22==⎰⎰≤+-dxdy y x .3. 求底面半径相同的两个直交柱面x 2+y 2=R 2及x 2+z 2=R 2所围立体的表面积.解 设A 1为曲面22x R z -=相应于区域D : x 2+y 2≤R 2上的面积. 则所求表面积为A =4A 1.dxdy y z x z A D ⎰⎰∂∂+∂∂+=22)()(14dxdy x R x D ⎰⎰+--+=22220)(14dxdy x R R D⎰⎰-=2242221681422R dx R dy x R dx R R R R R xR x R ==-=⎰⎰⎰-------. 4. 设薄片所占的闭区域D 如下, 求均匀薄片的质心:(1)D 由px y 2=, x =x 0, y =0所围成;解 令密度为μ=1.因为区域D 可表示为px y x x 20 ,00≤≤≤≤, 所以 3002023220px dx px dy dx dxdy A x x px D====⎰⎰⎰⎰⎰, 0002053211100x dx px x A xdy dx A xdxdy A x x x px D====⎰⎰⎰⎰⎰,000208311100y pxdx A ydy dx A ydxdy A y x x px D====⎰⎰⎰⎰⎰,所求质心为)83 ,53(00y x(2)D 是半椭圆形闭区域}0 ,1 |),{(2222≥≤+y by a x y x ; 解 令密度为μ=1. 因为闭区域D 对称于y 轴, 所以0=x . ab dxdy A Dπ21==⎰⎰(椭圆的面积),π34)(21112222022b dx x a a b A ydy dx A ydxdy A y aa aa x a Dab=-⋅===⎰⎰⎰⎰⎰---, 所求质心为)34 ,0(πb .(3)D 是介于两个圆r =a cos θ, r =b cos θ(0<a <b )之间的闭区域. 解 令密度为μ=1. 由对称性可知0=y .)(4)2()2(2222a b a b dxdy A D-=-==⎰⎰πππ(两圆面积的差),)(2cos 212220cos cos b a ab b a dr r r d A xdxdy A x b a D+++=⋅⋅==⎰⎰⎰⎰πθθθθ, 所求质心是)0 ,)(2(22b a ab b a +++. 5. 设平面薄片所占的闭区域D 由抛物线y =x 2及直线y =x 所围成, 它在点(x , y )处的面密度μ(x , y )=x 2y , 求该薄片的质心.解 351)(21),(10641022=-===⎰⎰⎰⎰⎰dx x x ydy x dx dxdy y x M x x Dμ4835)(2111),(110751032=-===⎰⎰⎰⎰⎰dx x x M ydy x dx Mdxdy y x x M x x x Dμ, 5435)(3111),(1108510222=-===⎰⎰⎰⎰⎰dx x x Mdy y x dx Mdxdy y x y My x x Dμ, 质心坐标为)5435 ,4835(.6. 设有一等腰直角三角形薄片, 腰长为a , 各点处的面密度等于该点到直角顶点的距离的平方, 求这薄片的质心.解 建立坐标系, 使薄片在第一象限, 且直角边在坐标轴上. 薄片上点(x , y )处的函数为μ=x 2+y 2. 由对称性可知y x =.4022061)(),(a dy y x dx dxdy y x M xa a D=+==⎰⎰⎰⎰-μ,a dy y x xdx Mdxdy y x x M y x xa aD52)(1),(1220=+===⎰⎰⎰⎰-μ,薄片的质心坐标为)52 ,52(a a .7. 利用三重积分计算下列由曲面所围成立体的质心(设密度ρ=1): (1)z 2=x 2+y 2, z =1;解 由对称性可知, 重心在z 轴上, 故0==y x . π31==⎰⎰⎰Ωdv V (圆锥的体积),431120101===⎰⎰⎰⎰⎰⎰Ωπθr zdz rdr d V zdv V z ,所求立体的质心为)43 ,0 ,0(. (2)222y x A z --=, 222y x a z --=(A >a >0), z =0; 解 由对称性可知, 重心在z 轴上, 故0==y x .)(3232323333a A a A dv V -=-==⎰⎰⎰Ωπππ(两个半球体体积的差),)(8)(3cos sin 1cos sin 133442000332a A a A dr r d d V d drd r V z A --===⎰⎰⎰⎰⎰⎰Ωππϕϕϕθθϕϕϕ,所求立体的质心为))(8)(3 ,0 ,0(3344a A a A --.(3)z =x 2+y 2, x +y =a , x =0, y =0, z =0.解 ⎰⎰⎰-+=a xa y x dz dy dx V 0022⎰⎰-+=a xa dy y x dx 022)(⎰-+-=adx x a x a x 032])(31)([461a =,⎰⎰⎰Ω=xdv V x 1a a a dz dy xdx V a x a yx52611511450022===⎰⎰⎰-+,a x y 52==,⎰⎰⎰Ω=zdv V z 1⎰⎰⎰-+=a x a y x zdz dy dx V 0002212307a =,所以立体的重心为)307,52,52(2a a a .8. 设球体占有闭区域Ω={(x , y , z )|x 2+y 2+z 2≤2Rz }, 它在内部各点的密度的大小等于该点到坐标原点的距离的平方, 试求这球体的质心.解 球体密度为ρ=x 2+y 2+z 2. 由对称性可知质心在z 轴上, 即0==y x . 在球面坐标下Ω可表示为: ϕπϕπθcos 20 ,20 ,20R r ≤≤≤≤≤≤, 于是⎰⎰⎰⎰⎰⎰⋅==Ωππϕϕϕθρ2020cos 2022sin R dr r r d d dv M⎰=2055cos sin 5322πϕϕϕπd R 51532R π=,⎰⎰⎰⎰⎰⎰Ω==ππϕϕϕϕθρ2020cos 205cos sin 11R dr r d d M zdv Mz R r R d R M 45153238cos sin 6642562076===⎰ππϕϕϕππ,故球体的质心为)45 ,0 ,0(R .9. 设均匀薄片(面密度为常数1)所占闭区域D 如下, 求指定的转动惯量:(1)}1 |),{(2222≤+=by a x y x D , 求I y ; 解 积分区域D 可表示为22 ,x a ab y x a a b a x a -≤≤--≤≤-,于是 ⎰⎰⎰⎰⎰------===aa x a ab x a ab aaDy dx x a x a b dy dx x dxdy x I 2222222222b a 341π=.提示: 4202422282sin 2 sina tdt a t a x dx x a x aa ππ==-⎰⎰-. (2)D 由抛物线x y 292=与直线x =2所围成, 求I x 和I y ;解 积分区域可表示为2/32/3 ,20x y x x ≤≤-≤≤,于是 57222273220232/32/32202====⎰⎰⎰⎰⎰-dx x dy y dx dxdy y I Dx x x , 796262252/32/32022====⎰⎰⎰⎰⎰-dx x dy dx x dxdy x I Dx x y . (3)D 为矩形闭区域{(x , y )|0≤x ≤a , 0≤y ≤b }, 求I x 和I y .解 331330202ab b a dy y dx dxdy y I Db a x =⋅===⎰⎰⎰⎰,331330022b a b a dy dx x dxdy x I Dba y =⋅===⎰⎰⎰⎰.10. 已知均匀矩形板(面密度为常量μ)的长和宽分别为b 和h , 计算此矩形板对于通过其形心且分别与一边平行的两轴的转动惯量.。
高等数学D习题课黑白

5)],
x8 x8
,求
f (5) .
解: f (5) f [ f (10)] f (
) f (7) f [
]
f ( ) f (9) 6
6. 设 f (sin x 1 ) csc2 x cos2 x , 求 f (x). sin x
解:
f
(sin
x
1 sin
) x
1 sin 2
x
f
(x)
x f
3, [ f (x
5)],
x8 x8
, 求 f (5) .
6. 设 f (sin x 1 ) csc2 x cos2 x , 求 f (x). sin x
4. 解:
xx
(x) (x)
由
得 (x) ln(1 x) ,
x (,0]
7
5.
已知
f
(
x)
x f
3, [ f (x
习题课 函数与极限
一、 函数 二、 连续与间断 三、 极限
第一章
1
一、 函数
1. 概念
定义: 设 D R 函数为特殊的映射:
定义域 其中
值域
图形:
y
y f (x)
( 一般为曲线 )
O
D
x
2
2. 特性
有界性 , 单调性 , 奇偶性 , 周期性
3. 反函数
设函数
为单射, 反函数为其逆映射
f 1 : f (D) D
证: 令lim f (x) A, 则给定 0, X 0,当 x X
x
时, 有
A f (x) A
又 f (x) C [X , X ] , 根据有界性定理, M1 0 , 使
《高等数学(二)》 作业及参考答案

《高等数学(二)》作业一、填空题1.点A (2,3,-4)在第 卦限。
2.设22(,)sin,(,)yf x y x xy y f tx ty x=--=则 .3。
4.设25(,),ff x y x y y x y∂=-=∂则。
5.设共域D 由直线1,0x y y x ===和所围成,则将二重积分(,)Df x y d σ⎰⎰化为累次积分得 。
6.设L 为连接(1,0)和(0,1)两点的直线段,则对弧长的曲线积分()Lx y ds +⎰= 。
7.平面2250x y z -++=的法向量是 。
8.球面2229x y z ++=与平面1x y +=的交线在0x y 面上的投影方程为 。
9.设22,z u v ∂=-=∂z而u=x-y,v=x+y,则x。
10.函数z =的定义域为 。
11.设n 是曲面22z x y =+及平面z=1所围成的闭区域,化三重积为(,,)nf x y z dx dy dz ⎰⎰⎰为三次积分,得到 。
12.设L 是抛物线2y x =上从点(0,0)到(2,4)的一段弧,则22()Lx y dx -=⎰。
13.已知两点12(1,3,1)(2,1,3)M M 和。
向量1212M M M M =的模 ;向量12M M 的方向余弦cos α= ,cos β= ,cos γ= 。
14.点M (4,-3,5)到x 轴的距离为 。
15.设sin ,cos ,ln ,dzz uv t u t v t dt=+===而则全导数。
16.设积分区域D 是:222(0)x y a a +≤>,把二重积分(,)Df x y dx dy ⎰⎰表示为极坐标形式的二次积分,得 。
17.设D 是由直线0,01x y x y ==+=和所围成的闭区域,则二重积分Dx d σ⎰⎰= 。
18.设L 为XoY 面内直线x=a 上的一段直线,则(,)Lp x y dx ⎰= 。
19.过点0000(,,)p x y z 作平行于z 轴的直线,则直线方程为 。
夜大《高数》D专升本第二部分常

工程问题
在机械、航空、航天等领域中, 二阶微分方程被用来描述物体的 运动规律和动态特性。
经济问题
在经济学中,二阶微分方程被用 来描述经济系统的动态变化和均 衡状态,如供需关系、劳动力市 场等。
05
高阶常微分方程
高阶线性微分方程
高阶线性微分方程的定义
高阶线性微分方程是包含未知函数的高阶导数的方程,形式为$y^{(n)}(x) + a_{n-1}(x)y^{(n-1)}(x) + ldots + a_1(x)y'(x) + a_0(x)y(x) = 0$,其中$y(x)$是未知函数,$a_0(x), a_1(x), ldots, a_{n-1}(x)$是已知函数。
02
对于不同类型的一阶非线性微分方程,以采用不同的方法求解,如变量代换、积分因子等。
一阶非线性微分方程的解的性质
03
一阶非线性微分方程的解可能存在奇点、极限环等复杂性质,
需要具体分析。
一阶微分方程的应用
经济问题
一阶微分方程可以用于描述经济中的供需关系、价格 变动等问题。
物理问题
一阶微分方程可以用于描述物理中的运动规律、电路 中的电流等问题。
高阶线性微分方程的解法
高阶线性微分方程的解法通常采用常数变易法和积分因子法。这些方法能够求解出高阶线性微分方程的通解和特解。
高阶线性微分方程的解的性质
高阶线性微分方程的解具有叠加原理和线性性质,即对于两个独立的解$y_1(x)$和$y_2(x)$,它们的线性 组合仍然是该方程的解。
高阶非线性微分方程
01
一阶微分方程
只含有一个自变量和一个导数的微 分方程。
线性微分方程
可以表示为线性组合形式的微分方 程。
高数二重积分习题加答案沐风教学.ppt
D
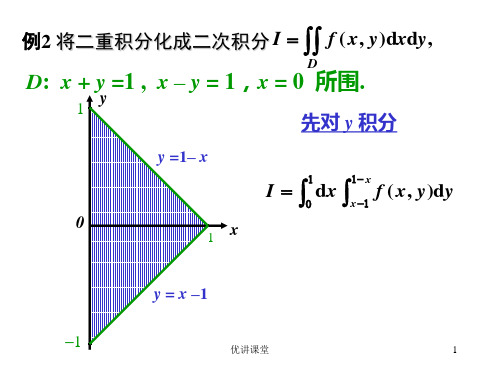
D: x + y =1 , x – y = 1,x = 0 所围.
1y
先对 y 积分
y =1– x
x
I dx f ( x, y)dy
x
0
1x
y = x –1
–1
优讲课堂
1
先对 x 积分
1y
D1
0
D2
x =1– y
I
6 a
1
rdr 2 2a a2 r 2 rdr
0 3a2 r 2
a0
2a
3 a
1
d (3a2 r 2 )
0 3a2 r 2
2a a2 r 2 d (a2 r 2 )
a0
6
3
4
2 3
6
2 3
a2.
优讲课堂
13
练习题
交换下列二次积分的次序:
1 2y
3 3 y
1. 0 dy0 f ( x, y)dx 1 dy0 f ( x, y)dx;
15
优讲课堂
6
例7 证明
b
dx
x ( x y)n2 f ( y)dy
1
b
(b
y)n1
f
(
y)dy.
aa
n1 a
证
b
dx
x
(x
y)n2
f
( y)dy
a
a
y b
y x
bdy b( x y)n2 f ( y)dx ay
a
D
b a
f
(
y)
n
1
1
(
x
高数同济六版课件D2习题

通过对极限定义的深入理解,可以求解一些 基本的极限问题。
利用极限运算法则
熟练掌握极限的四则运算法则,可以简化极 限的求解过程。
利用等价无穷小替换
在求解极限时,可以利用等价无穷小替换某 些复杂的表达式,从而简化计算。
利用洛必达法则
对于某些未定式的极限,可以利用洛必达法 则进行求解。
导数计算及应用举例
利用已知结论简化计算
在求解数学问题时,可以充分利用已知的结论和性质进行简化计算。
03 典型例题精讲
极限与连续典型例题
求极限
通过四则运算、等价无穷小替换、洛必达法则等方法 求解各类极限问题。
判断连续性
利用极限性质判断函数在某点的连续性,并会求间断 点的类型。
无穷小量阶的比较
掌握高阶、低阶、同阶和等价无穷小的概念,会比较 无穷小量的阶。
和专注度。
作业完成情况
02
大部分学员按时完成了作业,作业质量较高,体现出了良好的
学习态度和能力。
测验成绩
03
通过课堂测验,发现学员们对本次课程的内容掌握情况较好,
成绩普遍较高。
下一阶段学习计划安排
01
学习多元函数微积 分
掌握多元函数的极限、连续、偏 导数、全微分等基本概念和计算 方法。
02
学习级数理论
03
加强练习和巩固
了解级数的概念、性质和判别法, 掌握幂级数的展开和收敛域的判 断。
通过大量的练习题目,加深对知 识点的理解和记忆,提高解题能 力和思维水平。
鼓励学员持续努力,提升数学能力
肯定学员的努力和进步
对学员们在本次课程中的表现给予充 分肯定,鼓励他们继续保持学习热情
和积极性。
高数高等数学微分练习题与答案详细讲解(南风暖心)

第二节 微分§2.1 微分的概念 一、微分概念的引入在实际测量中,由于受到仪器精度的限制,往往会产生误差。
例如x 0为准确数,实际测量出是x *=x 0+Δx 为x 0的近似数,由此产生的误差为Δx 相应产生的函数值的误差Δy =f(x 0+Δx)-f(x 0),往往需要估计Δy 的值。
如果f(x 0+Δx),f(x 0)计算很复杂。
因此计算Δy 也很麻烦或者实际中只知道近似数x *与误差|Δx |≤δ,又如何估计Δy?假设f ′(x)存在,则0x lim→∆x )x (f )x x ("f 00∆-∆+=0x lim →∆x y∆∆=f ′(x 0),有xy∆∆=f ′(x 0)+α,0x lim →∆α=0,于是Δy =f ′(x 0)Δx +αΔx ,而0x lim →∆xx ∆∆∂=0(1)即 αΔx =0(Δx)(Δx →0)因此,当|Δx |很小时,Δy ≈f ′(x 0)Δx在实际中如果不知道x 0,只知道x *,由x 0,x *相差很小,则 Δy ≈f ′(x *)Δx ,从而可以估计出Δy 。
从(1)式我们看到,f ′(x 0)相对Δx 是一个常数,αΔx 是Δx 的高阶无穷小,如果Δy =A Δx +0(Δx)(Δx →0),则Δy ≈A Δx ,由此得到微分的概念。
二、微分的概念定义 设y =f(x)在x 0的某领域U(x 0)有定义,若 Δy =f(x +Δx)-f(x)可表示为 Δy =A Δx +o(Δx) (Δx →0)其中A 是写Δx 无关的常数,A Δx 称为Δy 的线性部。
则称y =f(x)在点x 处可微,称线性部A Δx 为y =f(x)在点x 处的微分,记为dy ,即dy =A Δx 。
三、可微与可导的关系从概念的引入,我们可以看到可导必可微,反之也是正确的。
因此有定理 函数y =f(x)在点x 可微的充要条件是函数y =f(x)在点x 处可导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(C) 0;
(ln
x)
1 x
;
(sin x) cos x
其他求导公式都可由它们及求导法则推出;
2) 求分段函数在分界点处的导数 , 及某些特殊
函数在特殊点处的导数;
3) 由导数定义证明一些命题.
(2)用导数定义求极限
(3)微分在近似计算的应用
机动 目录 上页 下页 返回 结束
例1.设 f (x0 ) 存在,求
lim f (x0 x (x)2 ) f (x0 ) .
x0
x
解:
原式=lxim0
f
( x0
x (x)2) x (x)2
f
(x0 )
x
(x)2
x
f (x0 )
机动 目录 上页 下页 返回 结束
例2.若
f
(1)
0
且
f
(1)
存在
,
求
lim
x0
f
(sin (ex
2 x (0)
lim
x0
(ax2
bx c) x0
g (0)
b
机动 目录 上页 下页 返回 结束
ax2 bx c, x 0
f (x) g(x) ,
x0
c g(0) b g (0)
3) 利用 f(0) f(0), 而
f(0)
lim
x0
g(
x) x
g 0
(0)
g (0)
f(0)
lim
x0
(2ax b) x0
b
2a
得
a
1 2
g
(0)
机动 目录 上页 下页 返回 结束
习题课 导数与微分
第二章
一、 导数和微分的概念及应用 二、 导数和微分的求法
机动 目录 上页 下页 返回 结束
一、 导数和微分的概念及应用
• 导数 :
当
时,为右导数
当
时,为左导数
• 微分 :
• 关系 : 可导
可微
机动 目录 上页 下页 返回 结束
• 应用 : (1) 利用导数定义解决的问题
1) 推出三个最基本的导数公式及求导法则
2. 熟练掌握求导方法和技巧
(1) 求分段函数的导数
注意讨论界点处左右导数是否存在和相等
(2) 隐函数求导法
对数法
(3) 参数方程求导法 (4) 复合函数求导法
(5) 高阶导数的求法
逐次求导归纳 ;
间接求导法; 利用莱布尼兹公式.
机动 目录 上页 下页 返回 结束
例4. 选择
且
存在, 问怎样
可使下述函数在
处有二阶导数.
ax2 bx c, x 0
f (x) g(x) ,
x0
解: 由题设 f (0) 存在, 因此
1) 利用 在
连续, 即 f (0 ) f (0 ) f (0),
得 c g(0)
2) 利用 f(0) f(0), 而
f (0)
lim
x0
g
(
x) x
g 0
(0)
g (0)
求 f (2) .
解: f (2) lim f (x) lim[(x 2) f (x) ] 0
x2
x2
(x 2)
f (2) lim f (x) f (2) x2 x 2
lim f (x) 3 x2 x 2
机动 目录 上页 下页 返回 结束
二、 导数和微分的求法
1. 正确使用导数及微分公式和法则
x)
.
解:
原式 =
lim
x0
f
(sin 2
x x2
cos
x)
且
联想到凑导数的定义式
lim
x0
f (1 sin2 x cos x 1) sin2 x cos x 1
f (1)
sin
2
x
cos x2
x
1
f (1) (1 1) 1 f (1) 22
机动 目录 上页 下页 返回 结束
例3.设 f (x) 在 x 2 处连续,且 lim f (x) 3, x2 x 2
