现代计量经济学模型体系解析
(财务知识)建立计量经济学模型的步骤和要点最全版

(财务知识)建立计量经济学模型的步骤和要点建立计量经济学模型的步骤和要点壹、理论模型的设计对所要研究的经济现象进行深入的分析,根据研究的目的,选择模型中将包含的因素,根据数据的可得性选择适当的变量来表征这些因素,且根据经济行为理论和样本数据显示出的变量间的关系,设定描述这些变量之间关系的数学表达式,即理论模型。
生产函数就是壹个理论模型。
理论模型的设计主要包含三部分工作,即选择变量、确定变量之间的数学关系、拟定模型中待估计参数的数值范围。
1、确定模型所包含的变量在单方程模型中,变量分为俩类。
作为研究对象的变量,也就是因果关系中的“果”,例如生产函数中的产出量,是模型中的被解释变量;而作为“原因”的变量,例如生产函数中的资本、劳动、技术,是模型中的解释变量。
确定模型所包含的变量,主要是指确定解释变量。
能够作为解释变量的有下列几类变量:外生经济变量、外生条件变量、外生政策变量和滞后被解释变量。
其中有些变量,如政策变量、条件变量经常以虚变量的形式出现。
严格他说,上述生产函数中的产出量、资本、劳动、技术等,只能称为“因素”,这些因素间存在着因果关系。
为了建立起计量经济学模型,必须选择适当的变量来表征这些因素,这些变量必须具有数据可得性。
于是,我们能够用总产值来表征产出量,用固走资产原值来表征资本,用职工人数来表征劳动,用时间作为壹个变量来表征技术。
这样,最后建立的模型是关于总产值、固定资产原值、职工人数和时间变量之间关系的数学表达式。
下面,为了叙述方便,我们将“因素”和“变量”间的区别暂时略去,都以“变量”来表示。
关键在于,在确定了被解释变量之后,怎样才能正确地选择解释变量。
首先,需要正确理解和把握所研究的经济现象中暗含的经济学理论和经济行为规律。
这是正确选择解释变量的基础。
例如,在上述生产问题中,已经明确指出属于供给不足的情况,那么,影响产出量的因素就应该在投入要素方面,而在当前,壹般的投入要素主要是技术、资本和劳动。
计量经济学模型的核心内容

计量经济学模型的核心内容计量经济学是经济学的一个重要分支,旨在通过建立经济学模型来解释和预测经济现象。
计量经济学模型是计量经济学研究的核心内容,它能够帮助研究者对经济现象进行量化分析和预测。
下面将介绍计量经济学模型的核心内容。
一、模型的假设计量经济学模型建立在一系列假设的基础上,这些假设是为了简化和抽象经济现象,使得模型能够更好地描述实际情况。
常见的假设包括理性行为假设、市场均衡假设、完全竞争假设等。
这些假设为模型提供了基本的框架,使得研究者能够对经济问题进行具体的分析和预测。
二、模型的变量计量经济学模型中包含多个变量,这些变量代表了经济现象中的各个要素。
常见的变量包括经济产出、价格、就业率、利率等。
通过对这些变量的测量和分析,可以揭示它们之间的关系和相互影响,进而理解和解释经济现象的发生和演变。
三、模型的结构计量经济学模型的结构是指模型中各个变量之间的关系和相互作用方式。
常见的模型结构包括线性模型、非线性模型、动态模型等。
线性模型假设模型中的变量之间存在线性关系,非线性模型则允许变量之间存在非线性关系。
动态模型则考虑了时间的因素,使得模型能够更好地反映经济现象的变化和演化。
四、模型的估计计量经济学模型的估计是指通过实证分析来确定模型中的参数值。
估计模型参数的方法有很多种,常见的方法包括最小二乘法、极大似然法、广义矩估计法等。
通过对模型参数的估计,可以得到模型对经济现象的解释和预测结果。
五、模型的检验计量经济学模型的检验是指通过统计方法对模型的有效性和适用性进行检验。
常见的检验方法包括假设检验、拟合优度检验、残差分析等。
通过对模型的检验,可以评估模型在描述和预测经济现象方面的准确性和可靠性。
六、模型的应用计量经济学模型的应用范围广泛,可以用于解释和预测各种经济现象。
例如,可以利用计量经济学模型来研究货币政策对经济增长的影响,分析贸易政策对国际贸易的影响,预测股票市场的走势等。
通过应用计量经济学模型,可以更好地理解和解释经济现象,并为政策制定提供科学依据。
计量经济学分析模型

计量经济学分析模型摘要改革开放以来,我国经济呈迅速而稳定的增长趋势,由于分配机制和收入水平的变化,城镇居民生活水平在达到稳定小康之后,消费结构和消费水平都出现了一些新的特点。
本文旨在对近几年,我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。
首先,我们综合了几种关于收入和消费的主要理论观点;本文根据相关的数据统计数据,运用一定的计量经济学的研究方法,进而我们建立了理论模型。
然后,收集了相关的数据,利用EVIEWS软件对计量模型进行了参数估计和检验,并加以修正。
最后,我们对所得的分析结果和影响消费的一些因素作了经济意义的分析,并相应提出一些政策建议。
并找到影响居民消费的主要因素。
关键词:居民消费;城镇居民;回归;Eviews目录摘要 (II)前言 (1)1 问题的提出 (2)2 经济理论陈述 (3)2.1西方经济学中有关理论假说 (3)2.2有关消费结构对居民消费影响的理论 (4)3 相关数据收集 (6)4 计量经济模型的建立 (9)5 模型的求解和检验 (10)5.1计量经济的检验 (10)5.1.1模型的回归分析 (10)5.1.2拟合优度检验: (11)5.1.3 F检验 (11)5.1.4 T检验 (12)5.2 计量修正模型检验: (12)5.2.1 Y与的一元回归 (13)5.2.2拟合优度的检验 (13)5.2.3 F检验 (14)5.2.4 T检验: (15)5.3经济意义的分析: (15)6 政策建议 (16)结论 (17)参考文献 (19)城镇居民消费模型分析前言近年来,改革开放的影响不断加大,人民的物质文化生活水平日益提高,消费水平和消费结构都有了一定的调整,随着城镇化程度的提高,城镇居民消费在整个国民经济中的地位日益重要,因此,对其进行计量经济分析的十分有必要的。
本文旨在对近15年我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。
人均收入和消费支出的有关数据进行了计量经济的检验,通过两者之间的动态关系研究发现,居民人均收入与消费支出有长期的均衡关系,据此建立了居民人均收入和消费支出之间的长期均衡模型。
计量经济学的体系框架

计量经济学的体系框架一、引言计量经济学是经济学的一个重要分支,通过运用统计学和数学的方法来研究经济现象。
它旨在通过建立经济模型、收集和分析数据,来验证经济理论以及对经济政策的评估和预测。
本文将介绍计量经济学的体系框架,包括经济模型的构建、数据的收集和处理、估计和推断、以及结果的解释和政策分析。
二、经济模型的构建经济模型是计量经济学分析的基础,它是对经济现象或经济行为的简化描述。
构建经济模型需要明确的理论基础,并根据研究问题选择适当的变量和关系形式。
模型的构建可以通过宏观经济模型、微观经济模型和计量经济模型等方法进行。
三、数据的收集和处理数据的收集是计量经济学的重要一环。
研究者需要根据研究问题明确需要收集哪些数据,并选择适当的数据来源和采样方法。
同时,数据的处理也是不可忽视的环节。
研究者需要对数据进行清洗、转换和整理,以保证数据的质量和可用性。
四、估计和推断估计和推断是计量经济学的核心任务。
研究者通过建立经济模型和利用收集到的数据,运用统计学的方法对模型的参数进行估计,并进行推断。
常用的估计方法包括最小二乘法、极大似然估计和仪器变量法等。
推断则通过假设检验和置信区间等方法对参数进行分析和解释。
五、结果的解释和政策分析结果的解释是计量经济学研究的重要一步。
研究者需要对估计结果进行解读和分析,以及对模型的合理性进行评估。
同时,研究者还需要将研究结果与经济理论相结合,进行经济政策的分析和评估。
通过研究结果的解释和政策分析,可以为决策者提供科学的建议和参考。
六、结论计量经济学的体系框架包括经济模型的构建、数据的收集和处理、估计和推断,以及结果的解释和政策分析等步骤。
它通过运用统计学和数学的方法来研究经济现象,并提供科学的经济政策建议。
在实际应用中,研究者需要结合具体问题和研究目标来选择适当的方法和模型,并进行合理的数据收集和处理,以获得可靠的研究结果。
计量经济学的发展为我们深入理解经济现象和解决实际问题提供了有力的工具和方法。
计量经济学模型-经济管理学院

第二节 建立计量经济学模型的步骤 和要点
理论计量经济学的研究程序 一旦某种估计方法被提出,有 关的理论探讨就须遵循图1-2所示的 逻辑化程序。
估计方法
不可靠
可靠 估计方法的统计可靠性
拒绝该理论
估计方法适用的假定条件 若假定条件被满足 如何判定假定条件是否获得满足 若假定条件不能被满足
接受该理论
后果
• 经济计量模型由系统或方程组成,方程由 变量和系数组成。其中,系统也是由方程 组成。
怎样看待计量经济模型?
• 广义地说,一切包括经济、数学、统计三 者的模型;
• 狭义地说,仅只用参数估计和假设检验的 数理统计方法研究经验数据的模型。
• 事实上,理论研究需要经验数据的检验, 而经验研究也需要理论分析的指导,我们 不能只搞没有计量的理论,更不能搞“没 有理论的计量”—统计“炼金术”
经济计量模型的一般形式
n
Y b0 bi xi i 1
Y :被解释变量
xi:解释变量 b0,bi:参数
:服从正态分布的随机变量 正是由于的随机性导致Y的随机性。 服从正态分布,Y也服从正态分布。
三、计量经济学的内容体系
⒈ 广义计量经济学和狭义计量经济学 广义计量经济学是利用经济理论、数学以及统计学定量研究
关系: 外生变量数值的变化能够影响内生变量的变化 内生变量却不能反过来影响外生变量
3.按经济活动形态分:流量、存量;
被解释变量与解释变量
在单方程模型中,变量分为两类:被解释变量与解释变量
• 作为研究对象的变量,也就是因果关系中的“果”,例如 生产函数中的产出量,是模型中的被解释变量,在单一方 程模型中,处于左端
内生变量与外生变量
内生变量 • 是所研究的经济系统的模型本身确定的 • 是该模型求解的结果 • 属于应变量
计量经济学模型应用分析

计量经济学模型应用分析计量经济学是一门以数据为基础,运用数学、统计学和经济学等相关学科分析和解释经济现象的学科。
在实践中,计量经济学主要通过建立各种经济模型来分析和预测现实经济问题。
在本文中,我们将探讨计量经济学模型的应用分析。
一、单因素模型单因素模型是一种简单的计量经济学模型,其特点是只考虑一个因素对经济变量的影响。
例如,研究公路通行费对公路使用量的影响,或者研究利率对消费者支出的影响。
在这种模型中,经济变量(因变量)被解释为一个单独的影响因素(自变量)的函数。
通常,单因素模型采用线性回归来描述变量之间的关系。
回归模型的基本形式为:Y= a + bX + ε其中,Y是因变量(例如,需求或价格),X是自变量(例如,收入或成本),a和b是常数,ε是误差项(通常性质是随机的)。
a反映了Y在X=0时的值,b反映了Y随X的变化。
单因素模型在经济学实践中应用广泛。
例如,研究收入水平对消费支出的影响,研究通货膨胀率对股票价格的影响,以及研究贸易政策对贸易流量的影响。
单因素模型提供了一个可靠的方法来评估影响因素对因变量的影响程度。
二、多重线性回归模型多重线性回归模型是一种计量经济学模型,它允许解释因变量在多个自变量(或因素)下的变化。
该模型的形式为:Y= a + b1X1 + b2X2 +......+ bnXn + ε在此模型中,Y是因变量,X1、X2、...、Xn是自变量(或因素),a、b1、b2等是回归系数,ε是观测误差。
回归系数反映了因变量与自变量之间的关系。
具体而言,回归系数越大,自变量对因变量的影响越大。
多重线性回归模型具有广泛的应用范围。
例如,它可以用于研究成本对价格的影响,对劳动力市场的影响以及对经济增长的影响。
此外,多重线性回归模型还可以用于评估因素之间的相互作用,这是单因素模型无法实现的。
三、时间序列模型时间序列模型是一种专门用于描述和预测时间序列数据的计量经济学模型。
时间序列数据是指按时间顺序收集的数据。
计量经济学回归分析模型

计量经济学回归分析模型计量经济学是经济学中的一个分支,通过运用数理统计和经济理论的工具,研究经济现象。
其中回归分析模型是计量经济学中最为常见的分析方法之一、回归分析模型主要用于确定自变量与因变量之间的关系,并通过统计推断来解释这种关系。
回归分析模型中的关系可以是线性的,也可以是非线性的。
线性回归模型是回归分析中最为常见和基础的模型。
它可以表示为:Y=β0+β1X1+β2X2+...+βkXk+ε其中,Y代表因变量,X1,X2,...,Xk代表自变量,β0,β1,β2,...,βk代表回归系数,ε代表随机误差项。
回归模型的核心是确定回归系数。
通过最小二乘法估计回归系数,使得预测值与实际观测值之间的差异最小化。
最小二乘法通过使得误差的平方和最小化来估计回归系数。
通过对数据进行拟合,我们可以得到回归系数的估计值。
回归分析模型的应用范围非常广泛。
它可以用于解释和预测经济现象,比如价格与需求的关系、生产力与劳动力的关系等。
此外,回归分析模型还可以用于政策评估和决策制定。
通过分析回归系数的显著性,可以判断自变量对因变量的影响程度,并进行政策建议和决策制定。
在实施回归分析模型时,有几个重要的假设需要满足。
首先,线性回归模型要求因变量和自变量之间存在线性关系。
其次,回归模型要求自变量之间不存在多重共线性,即自变量之间没有高度相关性。
此外,回归模型要求误差项具有同方差性和独立性。
在解释回归分析模型的结果时,可以通过回归系数的显著性来判断自变量对因变量的影响程度。
显著性水平一般为0.05或0.01,如果回归系数的p值小于显著性水平,则说明该自变量对因变量具有显著影响。
此外,还可以通过确定系数R^2来评估模型的拟合程度。
R^2可以解释因变量变异的百分比,值越接近1,说明模型的拟合程度越好。
总之,回归分析模型是计量经济学中非常重要的工具之一、它通过分析自变量和因变量之间的关系,能够解释经济现象和预测未来走势。
在应用回归分析模型时,需要满足一定的假设条件,并通过回归系数和拟合优度来解释结果。
计量经济学模型分析方法
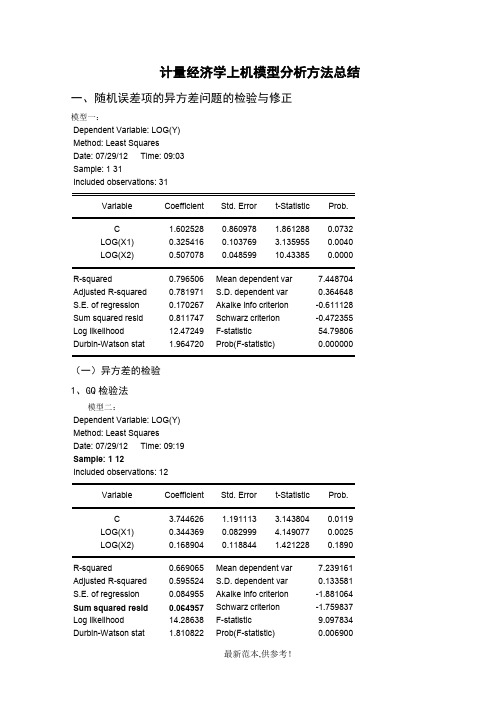
计量经济学上机模型分析方法总结一、随机误差项的异方差问题的检验与修正模型一:Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:03Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C 1.602528 0.860978 1.861288 0.0732LOG(X1) 0.325416 0.103769 3.135955 0.0040LOG(X2) 0.507078 0.048599 10.43385 0.0000R-squared 0.796506 Mean dependent var 7.448704 Adjusted R-squared 0.781971 S.D. dependent var 0.364648 S.E. of regression 0.170267 Akaike info criterion -0.611128 Sum squared resid 0.811747 Schwarz criterion -0.472355 Log likelihood 12.47249 F-statistic 54.79806 Durbin-Watson stat 1.964720 Prob(F-statistic) 0.000000(一)异方差的检验1、GQ检验法模型二:Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:19Sample: 1 12Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.C 3.744626 1.191113 3.143804 0.0119LOG(X1) 0.344369 0.082999 4.149077 0.0025LOG(X2) 0.168904 0.118844 1.421228 0.1890R-squared 0.669065 Mean dependent var 7.239161 Adjusted R-squared 0.595524 S.D. dependent var 0.133581 S.E. of regression 0.084955 Akaike info criterion -1.881064 Sum squared resid 0.064957 Schwarz criterion -1.759837 Log likelihood 14.28638 F-statistic 9.097834 Durbin-Watson stat 1.810822 Prob(F-statistic) 0.006900模型三:Dependent Variable: LOG(Y)Method: Least SquaresDate: 07/29/12 Time: 09:20Sample: 20 31Included observations: 12Variable Coefficient Std. Error t-Statistic Prob.C -0.353381 1.607461 -0.219838 0.8309LOG(X1) 0.210898 0.158220 1.332942 0.2153LOG(X2) 0.856522 0.108601 7.886856 0.0000R-squared 0.878402 Mean dependent var 7.769851Adjusted R-squared 0.851381 S.D. dependent var 0.390363S.E. of regression 0.150490 Akaike info criterion -0.737527Sum squared resid 0.203824 Schwarz criterion -0.616301Log likelihood 7.425163 F-statistic 32.50732Durbin-Watson stat 2.123203 Prob(F-statistic) 0.000076进行模型二和模型三两次回归,目的仅是得到出去中间7个样本点以后前后各12个样本点的残差平方和RSS1和RSS2,然后用较大的RSS除以较小的RSS即可求出F统计量值进行显著性检验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#学术探讨#现代计量经济学模型体系解析*李子奈刘亚清内容提要:本文对现代计量经济学模型体系进行了系统的解析,指出了现代计量经济学的各个分支是以问题为导向,在经典计量经济学模型理论的基础上,发展成为相对独立的模型理论体系,包括基于研究对象和数据特征而发展的微观计量经济学、基于充分利用数据信息而发展的面板数据计量经济学、基于计量经济学模型的数学基础而发展的现代时间序列计量经济学、基于非设定的模型结构而发展的非参数计量经济学,并对每个分支进行了扼要的描述。
最后在/交叉与综合0的方向上提出了现代计量经济学模型理论的研究前沿领域。
关键词:经典计量经济学时间序列计量经济学微观计量经济学一、引言计量经济学自20世纪20年代末30年代初诞生以来,已经形成了十分丰富的内容体系。
一般认为,可以以20世纪70年代为界将计量经济学分为经典计量经济学(Classical Econometrics)和现代计量经济学(Mo dern Eco no metr ics),而现代计量经济学又可以分为四个分支:时间序列计量经济学(Tim e Ser ies Econo metrics)、微观计量经济学(M-i cro-econometrics)、非参数计量经济学(Nonpara-m etric Econometrics)以及面板数据计量经济学(Panel Data Eco nom etrics)。
这些分支作为独立的课程已经被列入经济学研究生的课程表,独立的教科书也已陆续出版,应用研究已十分广泛,标志着它们作为计量经济学的分支学科已经成熟。
据此提出三个问题:一是经典计量经济学的地位问题。
既然现代计量经济学模型体系已经成熟,而且它们都是在经典模型理论的基础上发展的,那么经典模型还有应用价值吗?是不是凡是采用经典模型的研究都是低水平和落后的?二是现代计量经济学的各个分支的发展导向问题。
即它们是如何发展起来的?三是现代计量经济学进一步创新和发展的基点在哪里?回答这些问题,对于正确理解计量经济学的学科体系,对于计量经济学的课程设计和教学内容安排,对于正确评价计量经济学理论和应用研究的水平,对于进一步推动中国的计量经济学理论研究,都是十分有益的。
现代计量经济学的各个分支是以问题为导向,以经典计量经济学模型理论为基础而发展起来的。
所谓/问题0,包括研究对象和表征研究对象状态和变化的数据。
研究对象不同,表征研究对象状态和变化的数据具有不同的特征,用以进行经验实证研究的计量经济学模型既然不同,已有的模型理论方法不适用了,就需要发展新的模型理论方法。
按照这个思路,就可以用图1简单地描述经典计量经济学模型与现代计量经济学模型各个分支之间的关系。
本文试图从方法论的角度对现代计量经济学模型的发展,特别是现代计量经济学模型与经典计量经济学模型之间的关系进行较为系统的讨论,以期对未来我国计量经济学的发展研究提供借鉴和启示。
本文的内容安排如下:首先分析经典计量经济学模型的基础地位,明确它在现代的应用价值,同时对发生于20世纪70年代的/卢卡斯批判0的实质进行讨论;然后依次讨论时间序列计量经济学、微观计量经济学、非参数计量经济学以及面板数据计量经济学的发展,回答它们是以什么问题为导向,以什么为目的而发展的;最后以/现代计量经济学模型体系的分解与综合0为题,讨论现代计量经济学的前沿研究领域以及从对我国计量经济学理论的创新和发展)22)*本文受国家社会科学基金重点项目(08AJY001,计量经济学模型方法论基础研究)的资助。
提出建议。
图1 经典计量经济学与现代计量经济学二、经典计量经济学模型的基础地位11经典计量经济学模型的特征。
如果将20世纪70年代以前发展并广泛应用的计量经济学称为/经典0的,它们具有显著的共同特征,李子奈(2002)对此作出如下概括。
在理论方法方面的特征可以简要概括为:(1)模型类型)))参数模型、随机模型;(2)模型导向)))理论导向;(3)模型结构)))线性模型、因果分析模型;(4)数据类型)))截面数据、时间序列数据、被解释变量具有服从正态分布的连续观测值;(5)估计方法)))仅利用样本信息、最小二乘方法、最大似然方法。
在应用方面的特征可以简要概括为:(1)应用模型方法论基础)))实证分析、经验分析;(2)应用模型的功能)))结构分析、政策评价、经济预测、理论检验与发展;(3)应用模型的领域)))传统的应用领域,例如生产、需求、消费、投资、货币需求、就业、福利以及宏观经济等。
21经典计量经济学的发展。
有4位经济学家因为在经典计量经济学领域作出重要贡献而获得诺贝尔经济学奖,他们是弗里希(R.Frisch)、丁伯根(J.Tinberg en)、哈维尔莫(Tr ygv e H aav elm o )和克莱因(R.Klein)。
关于他们的贡献的描述,实际上就是关于经典计量经济学发展的描述。
经典计量经济学领域最早获得诺贝尔奖的是1969年第一届的获得者弗里希和丁伯根。
弗里希在1933年首先提出了计量经济学的定义,并第一个运用计量经济学的方法分析资本主义的经济波动,首创描述资本主义经济周期的数学模型,最早把导致经济波动的因素区分为扩散作用和冲击作用两大类,将两者结合起来解释资本主义经济周期,为当代经济周期理论奠定了重要基础。
弗里希提出了周期动态模型,其模型有三个关键要素:有关资本起动消费增长的加速机效应;资本起动与资本完成之间的酝酿期;消费与库存现金之间的关系。
这三个要素是弗里希能够建立起经济周期的动态模型的基础。
对存在持续性周期的解释方面,弗里希强调经济关系中随机干扰的重要性。
弗里希把经济计量方法应用到经济分析中,他试图把经济、数学和统计分析结合在一起阐明经济问题,这对后面经典计量经济学模型的发展奠定了基础。
丁伯根被称为计量经济学模型发展之父,他主要发展了动态计量经济模型来分析经济问题。
丁伯根(1969)指出,计量经济模型应该是:/(1)编一个要考虑的变量目录;(2)编一份变量必须服从的方程或关系的清单;(3)检验方程是否能成立,包括如果有的话,估计它们的系数。
由于特别是(3)的结果,我们可能必须修改(1)和(2),使模型体现的理论达到满意的真实程度。
然后,模型可以用于各种目的,即,解决各种问题。
0这对于经典计量经济学模型的发展具有重要的指导意义。
丁伯根在数量经济学理论上有三个贡献:一是提出了现代动态经济分析和/蛛网理论0;二是根据历史统计资料,利用数学和数理统计方法,对各种商业循环理论进行统计检验;三是首次用48个方程式为美国建立了完整的宏观经济计量模型,设法定量地明确各个因素的重要性,以便检验现有许多商业循环学说的解释价值,在模型中并且借助统计分析测定反应系数和/前导及滞后0。
他把通行的统计方法用于宏观经济问题的研究,从而开创了一个全新的经济学分支,即经验宏观经济学。
同时他在现代经济政策理论上的新贡献,就是把他在荷兰中央计划局的经验和在经济政策的广阔领域内参加讨论的结果,提高为系统的经济政策理论,成为规划短期经济政策的基础。
丁伯根在计量经济学方面的先驱著作对以后方法论的发展有很大的作用。
哈维尔莫于1943年发表于/Econometrica 0的论文/联立方程系统的统计学内涵0和于1944年完成的博士论文/计量经济学中的概率论方法0,奠定了计量经济学的概率论基础,提出了联立方程计量经济学模型系统的识别和估计理论,并因此获得1989年诺贝尔经济学奖。
20世纪30年代,经济理论的经验检验受到重视,两个与经济理论检验的可能性相联系的基本问题备受关注。
一是经济关系经常蕴含于大量的个体或企业的行为之中,而反映经济关系的经济理论不可能与所有个体或企业的数据完全吻合,那么什么是好的或者比较好的?二是经济学家不可能进行类似于自然科学中的可控实验,)23)5经济学动态62010年第5期而从市场中得到的观察是不同条件下同时发生的不同的行为互相作用的结果,利用这些观察去识别、估计、检验经济理论,如何才能反映其中的相互影响?哈维尔莫的研究表明,如果用随机方程的形式表达经济理论,上述第一个问题可以得到解决,数理统计方法能够从经验观察的随机样本中得到关于经济关系的严格的结论。
为了解决上述第二个问题,哈维尔莫发展了联立方程模型的分析框架,完善了识别和估计理论。
克莱因通过他的研究以及对各国研究团体的指导,促进了有关计量经济模型的研究和使用这些模型对经济政策的实际效果进行分析的可行性的研究。
由于克莱因的大力推动,计量经济模型获得了广泛地应用,克莱因也因此获得1980年诺贝尔经济学奖。
克莱因的主要理论贡献是:以公认的经济学说为基础,根据对现实经济中实际数据所作的经验性估算,建立经济体制的数学模型,并用以分析经济波动和经济政策,预测经济趋势。
在包括周期研究、随机波动、动态乘数反应、方案分析以及预报等理论性经济分析和公共政策的问题上,运用各种模型系统。
所研究的模型包括发展中经济、中央计划经济和工业化市场经济以及这些经济的国际贸易和金融关系。
主要有/克莱因)戈德伯格模型0、/布鲁金斯模型0、/沃顿模型0和/世界连接模型0。
克莱因的学术成就是将计量经济学方法和凯恩斯主义宏观经济学分析结合起来,创立了宏观计量经济学。
他第一次完整地把凯恩斯的经济理论表述为数学形式,不仅在结构、规模和先进的估算方法论方面是现代宏观模型的鼻祖,而且也是正式地用于经济波动预测的第一个计量经济模型,对后来美国和其他国家建立的宏观计量经济模型有深远而普遍的影响。
31/卢卡斯批判0的背景与实质。
所谓/卢卡斯批判0,即发生于20世纪70年代,以卢卡斯(E.Lu-cas)、萨金特(J.Sarg ent)、西姆斯(A.Sims)等为代表的对经典计量经济学的批判。
第二次世界大战以后,凯恩斯主义盛行,西方发达资本主义国家经济经历了一段稳步增长的黄金时期,科技进步促进了生产力的极大发展,国家干预政策使经济中的一些矛盾得以化解。
但进入20世纪70年代,主要资本主义国家经济开始陷入/滞胀0局面。
经济停滞和通货膨胀并存的现实使凯恩斯主义在理论上无法自圆其说,在实践中无能为力,以凯恩斯主义为理论导向的经典计量经济学模型同时也受到了质疑。
卢卡斯将理性预期加入经济周期理论,提出了公众是有理性的,他们能够对政府的经济政策和其他经济信息作出合理的反应并相应地调整他们的经济行为。
作为政府制定经济政策依据的凯恩斯经济学,没有考虑到公众的理性预期,因而制定的经济政策难以取得理想的效果。
同时他指出这些模型中预先设定好的描述经济稳定的参数不是不变的,因为人们的理性预期而经常更改他们的行为模式,在现实经济中这些参数是广泛变动的,使得这些经济计量模型的结果和预期是无效的。
卢卡斯(1976)提出,理性预期使得经济主体改变行为模式,应该从计量经济学模型的原始设定开始重新对模型进行设定,而且常参数模型不再适用。
