方差分析两两比较
方差分析和协方差分析的比较研究

方差分析和协方差分析的比较研究一、引言方差分析和协方差分析是统计分析中常用的两种方法,但它们在应用前需要进行一定的选择和比较,以便得出更为准确的结果。
本文旨在比较方差分析和协方差分析的特点和用途,并探究它们之间的异同,为合理应用提供指导。
二、方差分析方差分析是一种多元统计方法,通常用于检验两个或两个以上总体均值是否相等,应用范围很广,包括医学、工业、农业等多个领域。
方差分析的主要目的是比较各总体的平均数是否相等。
例如,研究一批根据不同方法制备的药品的药效,可采用方差分析来检验各总体的平均数是否相等。
(一)方差分析的优点1. 方差分析适用于多种不同方法和不同总体的比较。
2. 方差分析可以检验多个总体的均值是否存在显著的差异。
3. 方差分析可以分析多种影响因素对种群的影响。
(二)方差分析的缺点1. 方差分析对数据的正态性和方差齐性要求比较高。
2. 方差分析需要样本数量足够大才能具有较高的准确度。
3. 方差分析对数据的标准差值较为敏感,不适用于某些非正态分布的数据。
三、协方差分析协方差分析是一种多元统计方法,通常用于探究一个或多个自变量与因变量之间的关系。
协方差分析适合于多个决策变量之间相互影响,以及影响因素存在交互作用的情况。
(一)协方差分析的优点1. 协方差分析能够查明决策变量之间的相互作用关系。
2. 协方差分析能够比较这些变量之间的各种组合。
3. 协方差分析能够有效减少决策变量之间的复杂性。
(二)协方差分析的缺点1. 协方差分析对数据的要求比较高,需要具有一定的正态分布性和方差齐性。
2. 协方差分析需要较多的样本数,才能保证分析结果的准确性。
3. 协方差分析结果对自变量选取的灵敏度很高,需要仔细选择自变量。
四、方差分析和协方差分析的不同之处1. 方差分析的主要目的是检验不同总体均值是否相等,而协方差分析则是比较各种影响因素的影响大小。
2. 方差分析只能比较一个因素的影响,而协方差分析可以比较多个因素的影响。
方差分析中的两两比较

一、均数间的多沉比较(Multipie Comparison)要领的采用:之阳早格格创做1、如二个均数的比较是独力的,大概者虽有多个样本的均数,但是预先已计划佳要搞某几对付均数的比较,则没有管圆好分解的截止怎么样,均应举止比较,普遍采与LSD法大概Bonferroni法;2、如果预先已计划举止多沉比较,正在圆好分解得到有统计意思的F考验值后,不妨利用多沉比较举止探干脆分解,此时比较要领的采用要根据钻研手段战样本的本量.比圆,需要举止多个真验组战一个对付照组比较时,可采与Dunnett法;如需要举止任性二组之间的比较而各组样本的容量又相共时,可采与Tukey法;若各组样本的容量没有相共时,可采与Scheffe法;若预先已计划举止多沉比较,且圆好分解截止已有隐著没有共,则没有该举止多沉比较;3、偶尔间钻研者预先有对付特定几组均值比较的思量,那时不妨没有必Post hoc举止险些所有均值拉拢的二二比较,而是通过Contrasts中相映的树坐去真止;4、末尾需要注意的是,如果组数较少,如3组、4组,百般比较要领得到的截止没有共没有会很大;如果比较的组数很多,则要慎沉采用二二均值比较的要领.5、LSD法:即最小隐著好法;是最简朴的比较要领之一,它本去不过t考验的一种简朴变形,已对付考验程度搞所有矫正,不过正在尺度误估计上充分利用了样本疑息.它普遍用于计划佳的多沉比较;6、Sidak法:它是正在LSD法上加进了Sidak矫正,通过矫正落矮屡屡二二比较的一类过失率,达到所有比较最后甲类过失率为α的手段;7、Bonferroni法:它是Bonferroni矫正正在LSD法上的应用.8、Scheffe法:它真量上是对付多组均数间的线性拉拢是可为0搞假设考验(即所谓的Contrasts),多用于各组样本容量没有等时的比较;9、Dunnett法:时常使用于多个真验组与一个对付照组间的比较,果此使用此法时,应当指定对付照组;10、S-N-K法:它是根据预先造定的规则将各组均数分为多身材集,而后利用Studentized Range分散举止假设考验,并根据均数的个数安排总的犯一类过失的概率没有超出α;11、Tukey法:那种要领央供各组样本容量相共,它也是利用Studentized Range分散举止各组均数间的比较,与S-N-K法分歧,它是统造所有比较中最大的一类过失(即甲类过失)的概率没有超出α;12、Duncan法:思路与S-N-K法相似,只没有过考验统计量遵循的是Duncan′s Multiple Range分散;13、还需注意的是,SPSS共时给出了圆好没有齐性时的4种考验要领,但是从担当程度战宁静性瞅,圆好没有齐性时尽管没有搞多沉比较.二、各组均数的粗细比较(Contrast)对付于具备4组均值的比较,正在Coefficient如果依次输进数字3,-1,-1,-1,则表示要考验本假设Ho:μ1=(μ2+μ3+μ4)/3;三、一元单果素圆好分解1、一元单果素圆好分解包罗二种数教模型:(1)独力模型;(2)接互模型;设二果素为A战B,则有(1)独力模型:应变量Y的变更=A果素效率+B果素效率+随机效率(2)接互模型:Y的变更=A的效率+B的效率+AB接互效率+随机效率2、正在接互模型中,每个格子内起码要有二个样本个案,那样才搞把接互效率分散出去.3、对付于考验而止,最先经常考验接互效率的效率是可隐著;如果没有隐著,则将接互效率并进随机效率,而后按独力模型考验;4、如果接互效率隐著,进一步的考验则要根据变量A战B的属性有所变更:分为牢固模型、随机模型战混同模型.详睹卢淑华课本的相闭真量.。
r语言 三组间两两比较方法

在R语言中,有多种方法可以进行三组间的两两比较。
以下是一些常见的方法:1. t检验(pairwise.t.test):当数据满足正态性和方差齐性假设时,可以使用t检验来进行两两比较。
该函数会对每对组进行t检验,计算出每对之间的差异显著性水平和置信区间。
```Rpairwise.t.test(data$group, data$value, p.adjust.method = "bonferroni")```2. 方差分析(ANOVA):如果数据不满足t检验的假设条件,可以使用方差分析来进行两两比较。
可以使用ANOVA函数进行方差分析,然后使用posthoc函数进行多重比较。
```Rmodel <- aov(value ~ group, data = data)posthoc <- TukeyHSD(model)```3. 非参数检验(Kruskal-Wallis检验):当数据不满足正态性和方差齐性假设时,可以使用非参数方法进行两两比较,如Kruskal-Wallis检验。
可以使用kruskal.test函数进行Kruskal-Wallis检验,然后使用pairwise.wilcox.test函数进行多重比较。
```Rkruskal.test(value ~ group, data = data)pairwise.wilcox.test(data$value, data$group, p.adjust.method = "bonferroni")```这些方法都可以用于进行三组间的两两比较,具体应该根据数据的性质和实验设计来选择合适的方法。
在进行多重比较时,通常需要考虑到多重比较校正以控制错误率。
常见的多重比较校正方法包括Bonferroni校正、Holm校正等。
方差分析后的两两比较方法选择,真的无迹可寻吗?

⽅差分析后的两两⽐较⽅法选择,真的⽆迹可寻吗?两两⽐较⽅法的选择,⼤概是统计学界争议最多的⼀个话题了,直⾄今天,也没有⼀个完全统⼀的说法。
所以,本⽂虽然说是两两⽐较⽅法的选择,但更多的是在基于以往⽂献的基础上,再结合作者本⼈的经验和理解,给读者⼀些提⽰。
两两⽐较的⽅法太多了,正因为太多了,所以往往⼤家都不知道给怎么选择。
⽐如SAS提供了12种两两⽐较⽅法让⼈选择,SPSS更是毫不吝啬地给出了18种⽅法让你选择。
我想任何⼀个⾮统计专业的⼈都有同⼀个感觉:你在耍我们吗?毫⽆提⽰地给出10多种⽅法,让我⼀个毫⽆统计背景的⼈⾃⼰选择。
就像是医⽣给你10多种药,⼀脸怜悯地对你说:回家⾃⼰看着吃啊,你觉得哪个好就吃哪个。
关键是,明知道我们没有这个判别⼒,为什么要给我们这么多的两两⽐较⽅法,还得让我们⾃⼰选择?正是统计学家太多了,每个⼈都能根据⾃⼰的理念提出⼀种⽅法,⽽这些⽅法看起来似乎都没错,那怎么办?只好都放在软件中,你⾃⼰跟着感觉⾛吧。
下⾯就来说⼏种⽐较常见的两两⽐较⽅法的选择,希望给⼤家稍微理清⼀点思路。
先声明⼀下,以下结论是参考了不少国外课本和⽂献,加上⾃⼰的⼀点经验,⽽且只给出结论性的内容,不给出公式和证明,喜欢追根究底的朋友可以⾃⼰看专业书籍。
为什么要⽤两两⽐较⽅法呢?⼤多数两两⽐较⽅法的⽬的都是为了控制假阳性,因为两两⽐较次数多了,容易产⽣假阳性的结果。
⾸先说医学统计课本中最喜欢介绍的3种⽅法:LSD、SNK和Bonferroni法。
我⼤概翻了⼀下国内的医学统计学教程,⼏乎都是这3种⽅法,但似乎都没有说什么情况下⽤。
LSD法其实就相当于t检验,只不过它需要在⽅差分析⼀定要有统计学差异的情况下才⽤。
所以LSD法并没有控制假阳性错误。
⼀般情况下,如果你在设计初期就有很明确的⽬的,可以考虑这种⽅法,因为每⼀对⽐较都是有特定意义的,不⽤⾮得控制假阳性错误。
SNK法是先按多组均值⼤⼩排序,然后按⼀个有点类似于t检验的公式分别⽐较(不过误差计算不同)。
多组间两两比较的方法

多组间两两比较的方法一种多组间两两比较的方法就是采用一种叫做“多元方差分析(multivariate analysis of variance,MANOVA)”的统计方法。
虽然这项分析看上去很复杂,但它的核心思想其实很简单。
MANOVA的假设是不同组之间的平均值有显著差异。
为了证明这一假定,将所有变量以向量形式表示出来,然后用F-检验或ADONIS检验来测试其相似性。
如果P值小于0.05,说明这些变量之间存在显著差异。
然后,再使用T检验或Tukey-Kramer HSD检验来测试不同组之间的差异性。
如果P值也小于0.05,则表明不同组之间存在显著差异。
此外,也可以使用ANOVA或Kruskal-Wallis H检验来对多组进行两两比较。
ANOVA是一种广泛使用的多元分析方法,它通过F-test来测试变量之间的差异性。
而Kruskal-Wallis H检验是一种非参数方法(nonparametric method ),它用H-test来测试不同样本中数字大小的差异性。
如果P值小于0.05,则表明不同样本之间存在显著差异。
此外,也可以使用Wilcoxon rank sum test or Wilcoxon signed rank test 来对两个独立样本进行两两比较, 这是一种常用的非参数方法, 首先将样本中所有数字从小到大依序重新加上正序号(rank),然后再将正序号相加, 如果rank sum 差别大, 则表明样本中数字大小有显著差别, P值小于0.05时即表明样本中数字大小有显著性差别. Wilcoxon signed rank test 测试的是相对数字大小而不是相对数字大小, 其测试命题是: 给定样本A, B, 样本A中x > y的概率是否要大于样本B中x > y的概率.最后, 还可以使用G-test或Fisher’s exact test来对两个独立样本进行两两比较。
G-test是一种基于卡方分布的统计方法,它用来测试相关性,如果P值小于0.05,则表明不同样本之间存在显著差异。
方差分析【范本模板】

1. 三组样本均数的比较,先进行单因素方差分析,P<0.05。
再进行两两比较,发现第一组与第二组差别无统计学意义,第二组与第三组差别也无统计学意义,但第一组与第三组之间差别有统计学意义,于是(10.0分)A。
三组样本来自于同一总体B.第一组和第三组来自于两个不同的总体,但尚无法判断第二组究竟来自于哪个总体C.第二组来自的总体位于第一组和第三组所来自的总体之间D.该两两比较为模糊结论,说明计算中发生了错误2。
成组设计方差分析中,若处理因素无作用,理论上应有________(10.0分)A.F=0B。
F=1C.F<1D。
F〈1。
963。
单因素方差分析中,组间变异主要反映的是(10。
0分)A。
处理因素的作用B。
抽样误差C。
测量误差D.随机误差,包括个体差异和测量误差4。
为研究溶液温度对液体植物的影响,将水温控制在三个水平上,则称这种方差分析是(10。
0分)A.单因素三水平方差分析B.三因素方差分析C。
双因素三水平方差分析D。
双因素方差分析5. 单因素方差分析中,n代表总的样本含量,r代表组数,并计算F统计量,其分子与分母的自由度各为(10。
0分)A。
r, nB.r—n, n—rC。
r-1,n—rD。
n-r,r—16。
对三个组进行多个样本的方差齐性检验(Bartlett法),得到P<0。
05,按alpha=0。
05的水准,可认为(10。
0分)A.三组样本方差不全相等B。
三组样本均数不全相等C.三组总体方差不全相等D.三组总体均数不全相等7. 当组数等于2时,对于同一资料,方差分析结果与t检验结果(10.0分)A.方差分析更准确B.完全等价且F=√tC。
t检验更准确D.完全等价且t=√F8. 配对设计资料,若满足正态性和方差齐性。
要对两样本均数的差别做比较,可选择(10.0分)A.秩和检验B.成组t检验C。
随机区组设计的方差分析D.卡方检验9. 完全随机设计资料,若满足正态性和方差齐性。
方差分析两两比较

方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有:Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant dif ference t test) 。
这两种方法不管方差分析的结果如何——即便对于P稍大于检验水平α进行所关心组别间的比较。
LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
方差分析中均值比较的方法

方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有: Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant dif ference t test) 。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
方差分析两两比较

方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有:Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant dif ference t test) 。
这两种方法不管方差分析的结果如何——即便对于P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
方差分析两两比较知识分享

方差分析两两比较方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有: Dunnett-t 检验、LSD-t 检验(Fisher ’s least s ignificant difference ttest) 。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
一年多点区域试验数据的方差分析(spss)
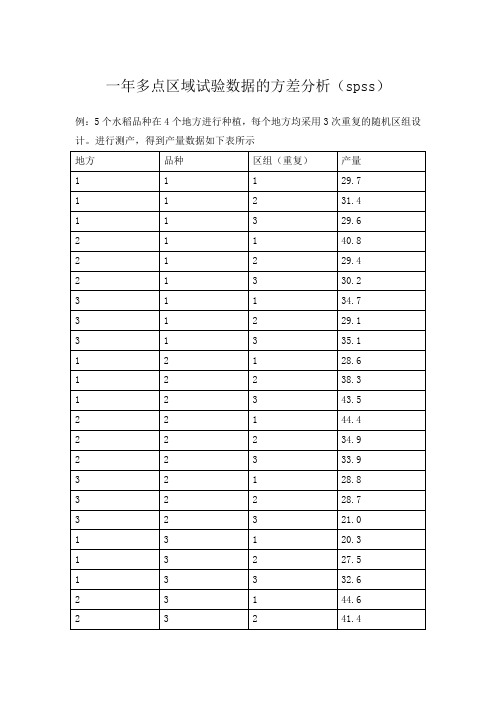
一年多点区域试验数据的方差分析(spss)例:5个水稻品种在4个地方进行种植,每个地方均采用3次重复的随机区组设计。
进行测产,得到产量数据如下表所示1、按照上表格式在excel中整理好数据2、将数据导入或复制粘贴至spss的“数据”窗口,并在视图窗口进行命名。
如图所示3、点击【分析】,然后选择【一般线性模型】,【单变量】。
4、打开【单变量】对话框,将产量选入因变量,其余分组变量选入固定因子5、打开【模型】,选择【设定】,然后设定地方、品种、区组的主效应,设定品种与地方的交互作用。
设定完成后点击继续6、打开两两比较或事后比较(26版以上spss)对话框,选择ducan法或LSD 法,并将地方和品种选入右边对话框进行两两比较。
点击继续。
7、回到【单变量】对话框。
点击确定,输出最后结果主体间效应的检验因变量: 产量df 均方 F Sig.源III 型平方和校正模型771.621a13 59.355 1.455 .212截距38592.602 1 38592.602 946.185 .000地方299.060 2 149.530 3.666 .042品种13.474 3 4.491 .110 .953区组40.207 2 20.103 .493 .617地方 * 品种418.880 6 69.813 1.712 .165误差897.327 22 40.788总计40261.550 36校正的总计1668.947 35a. R 方 = .462(调整 R 方 = .145)从上面可以看出试验点差异显著。
地方*品种差异不显著说明,品种在不同实验点的结果比较一致。
地方的两两比较结果如下。
产量Duncan地方N 子集1 23.00 12 29.10831.00 12 32.9583 32.95832.00 12 36.1583Sig. .154 .233已显示同类子集中的组均值。
基于观测到的均值。
误差项为均值方 (错误) = 40.788。
方差分析中的两两比较

一、均数间的多重比较(Multipie Comparison)方法的选择:1、如两个均数的比较是独立的,或者虽有多个样本的均数,但事先已计划好要做某几对均数的比较,则不管方差分析的结果如何,均应进行比较,一般采用LSD法或Bonferroni 法;2、如果事先未计划进行多重比较,在方差分析得到有统计意义的F检验值后,可以利用多重比较进行探索性分析,此时比较方法的选择要根据研究目的和样本的性质。
比如,需要进行多个实验组和一个对照组比较时,可采用Dunnett法;如需要进行任意两组之间的比较而各组样本的容量又相同时,可采用Tukey法;若各组样本的容量不相同时,可采用Scheffe法;若事先未计划进行多重比较,且方差分析结果未有显著差别,则不应进行多重比较;3、有时候研究者事先有对特定几组均值比较的考虑,这时可以不用Post hoc进行几乎所有均值组合的两两比较,而是通过Contrasts中相应的设置来实现;4、最后需要注意的是,如果组数较少,如3组、4组,各种比较方法得到的结果差别不会很大;如果比较的组数很多,则要慎重选择两两均值比较的方法。
5、LSD法:即最小显著差法;是最简单的比较方法之一,它其实只是t检验的一种简单变形,未对检验水准做任何校正,只是在标准误计算上充分利用了样本信息。
它一般用于计划好的多重比较;6、Sidak法:它是在LSD法上加入了Sidak校正,通过校正降低每次两两比较的一类错误率,达到整个比较最终甲类错误率为α的目的;7、Bonferroni法:它是Bonferroni校正在LSD法上的应用。
8、Scheffe法:它实质上是对多组均数间的线性组合是否为0做假设检验(即所谓的Contrasts),多用于各组样本容量不等时的比较;9、Dunnett法:常用于多个实验组与一个对照组间的比较,因此使用此法时,应当指定对照组;10、S-N-K法:它是根据预先制定的准则将各组均数分为多个子集,然后利用Studentized Range分布进行假设检验,并根据均数的个数调整总的犯一类错误的概率不超过α;11、Tukey法:这种方法要求各组样本容量相同,它也是利用Studentized Range分布进行各组均数间的比较,与S-N-K法不同,它是控制所有比较中最大的一类错误(即甲类错误)的概率不超过α;12、Duncan法:思路与S-N-K法相似,只不过检验统计量服从的是Duncan′s MultipleRange分布;13、还需注意的是,SPSS同时给出了方差不齐性时的4种检验方法,但从接受程度和稳定性看,方差不齐性时尽量不做多重比较。
方差分析下两两对比如何进行芬香邀请码X1K36A(spssau文章)

方差分析下两两对比如何进行?(SPSSAU文章)展开全文当我们想研究不同组别下,多组数据的差异性时,通常会选择方差分析。
但是方差分析只能得到一个显著性的结果,具体是那些组别有显著差异,我们无法得知。
因而还需要对两两组别进行对比。
事后检验正是基于方差分析基础上进行,对比两两组别的差异。
方差分析事后比较事后检验的方法有多种,但功能均一致,只是在个别点或使用场景上有小区别。
SPSSAU目前共提供LSD,Scheffe,Tukey,Bonferroni校正,Tamhane T2常见的五种方法,其中LSD方法最常使用。
分析时,首先判断方差分析的p值是否呈现出显著性,如果呈现出显著性,则说明不同组别数据具有显著性差异,差异可通过平均值进行对比;然后可通过事后检验判断具体两两组别之间的差异情况。
如果说X仅两组,则不需要进行事后检验;如果方差分析显示P值大于0.05即说明各个组别之间没有差异性,此时也不需要进行事后检验。
非参数的事后多重比较当数据呈现严重的偏态或方差不齐,可考虑使用非参数分析,同样可以进行两两对比。
如果进行非参数检验Kruskal-Wallis时发现呈现出显著性,可以继续深入研究,对比两两组别之间的差异性,选中“Nemenyi两两比较”即可输出结果。
如果Kruskal-Wallis检验显示没有差异性,则不需要进行两两比较。
案例分析1、背景研究人员希望了解游客对于某旅游地不同方面满意度(交通满意度、住宿满意度、服务满意度、景区满意度)是否存在不同的态度差异。
满意度均由五级量表题统计得出。
2、操作(1)首先检验数据正态性、方差齐性,以选择适合的分析方法。
SPSSAU-正态图可以看到数据基本呈现钟型分布,由于现实研究中收集的样本量较少,很难得到完全符合正态分布的数据,因而只要数据分布基本上可以用一个钟形的正态曲线描绘,即可说明数据基本满足正态分布性。
然后进行方差齐性检验,如果方差齐则使用方差分析,如果方差不齐则使用非参数检验。
三组间两两比较统计方法

三组间两两比较统计方法
三组间两两比较统计方法,这可真是个有趣的话题啊!想象一下,就好像是在一场激烈的比赛中,要找出每两组之间的差异和特点。
方差分析,这可是个厉害的家伙呢!它就像是一个超级侦探,能敏锐地察觉到三组数据之间的不同。
通过它,我们可以清楚地看到每组数据的独特之处,这难道不神奇吗?
还有 t 检验,哇哦,它也毫不逊色呀!它就像是一把精准的尺子,能精确地衡量出两组之间的细微差别。
有时候,那些微小的差异就像是隐藏在数据海洋中的珍珠,而 t 检验就能把它们找出来,这是多么了不起啊!
两两比较的时候,不就像是在一个大舞台上,每组都在展示自己的风采,而我们就是那个评判者,要公正地给它们打分。
这不就和选美比赛有点像嘛,要从众多佳丽中选出最出众的那一个。
在这个过程中,我们需要仔细观察,认真分析,不能有一丝马虎。
这可不是闹着玩的,这关系到我们能否得出正确的结论。
要是不小心弄错了,那可就糟糕啦!
难道不是吗?我们对待统计方法就得像对待珍贵的宝物一样,小心翼翼地呵护,仔仔细细地研究。
每一个步骤都要严谨,每一个数据都要准确。
只有这样,我们才能在三组间两两比较中找到真正有价值的信息。
我们不能随随便便就下结论,要像侦探破案一样,不放过任何一个蛛丝马迹。
有时候,一个小小的细节就能改变整个结果呢!这可不是开玩笑的呀!
总之,三组间两两比较统计方法是一个充满挑战和乐趣的领域。
我们要用心去探索,用智慧去发现,这样才能在这个数据的世界里游刃有余。
让我们一起加油吧,去挖掘那些隐藏在数据背后的秘密!。
讲个明白:为什么方差分析后两两比较不能直接用t检验?

讲个明白:为什么方差分析后两两比较不能直接用t检验?为什么两两比较不能用t检验在医学研究中,方差分析,卡方检验,秩和检验等方法都会碰到多组数据的比较,多组均数、多组率、多组中位数的比较。
多组数据比较紧跟着的是两两比较。
很多人对为什么两两比较不能直接用t检验、直接用两样本率的卡方检验,直接用两样本秩和检验表示困惑。
现在我以方差分析后的两两比较为例,做一些通俗易懂的介绍。
但凡学过《医学统计学》的朋友,可能都了解一些,多组均数往往采用方差分析,而方差检验只能说明多组之间总体均数不全相同,不能说明任何两组之间存在着统计学差异。
可在此基础上开展多重比较的方法(俗称两两比较),以探索两组两组之间有没有统计学差异。
怎么比较?两组均数比较,我们之前讲过用t检验,这里多次两两比较可以直接用t检验吗?不能!多组数据两两比较用t检验会增加一类错误α,也就是假阳性错误。
这意味着本来你的研究应该是阴性结果,但如果两两比较用t 检验,您的结果可能就是阳性。
一般情况下,我们一项研究的一类错误α值设定为0.05,因此,我们才有P<0.05,有统计学意义的结论。
但是这个结论存在一定的风险,或者说,我们的结论可能5%的可能性是错误的,是假的阳性结论。
5%的假阳性是公认的可以被接受的,但是如果一个项目多次两两比较,假阳性的概率可不是5%的概率了。
原理如下:当有k个均数需作两两比较时,同时比较的次数共有c= k(k-1)/2。
设每次检验所用Ⅰ类错误的概率水准为α,累积Ⅰ类错误的概率为α’,则在对同一实验资料进行c次t检验时,在样本彼此独立的条件下,根据概率乘法原理,其累积Ⅰ类错误概率α’与c有下列关系:α’=1-(1-α)c例如,设α=0.05,c=3(即k=3),其累积Ⅰ类错误的概率为α’=1-(1-0.05)3=1-(0.95)3 = 0.143 本来假设检验假阳性错误是5%,现在有14.3%,太多了。
容易把阴性结果说成阳性!虽然,可能发表文章是很有利的,但是这是不合适的。
单因素方差分析

单因素方差分析(ANOVA):两两比较检验Post-Hoc选项详解添加时间:2014-5-5分享到:0One-Way ANOVA:两两比较检验后,务必进行Post Hoc检验,也称事后分析,或称为两两比较分析。
但具体算法有很多种,各自有哪些差别呢?一旦确定均值间存在差值,两两范围检验和成对多重比较就可以确定哪些均值存在差值了。
范围检验识别彼此间没有差值的同类均值子集。
成对多重比较检验每一对均值之间的差分,并得出一个矩阵,其中星号指示在 0.05 的 alpha 水平上的组均值明显不同。
一、假定方差齐性Tukey's 真实显著性差异检验、Hochberg’s GT2、Gabriel 和Scheffé 是多重比较检验和范围检验。
其他可用的范围检验为 Tukey 的 b、S-N-K (Student-Newman-Keuls)、Duncan、R-E-G-W F(Ryan-Einot-Gabriel-Welsch F 检验)、R-E-G-W Q(Ryan-Einot-Gabriel-Welsch 范围检验)和 Waller-Duncan。
可用的多重比较检验为 Bonferroni、Tukey's 真实显著性差异检验、Sidak、Gabriel、Hochberg、Dunnett、Scheffé 和 LSD(最小显著性差异)。
详细剖析• 最小显著差法(LSD). 使用 t 检验执行组均值之间的所有成对比较。
对多个比较的误差率不做调整。
LSD法侧重于减少第二类错误,此法精度较差,易把不该判断为显著的差异错判为显著,敏感度最高。
LSD法的使用:在进行试验设计时就确定各处理只是固定的两个两个相比,每个处理平均数在比较中只比较一次。
例如,在一个试验中共有4个处理,设计时已确定只是处理1与处理2、处理3与处理4(或1与3、2与4;或1与4、2与3)比较,而其它的处理间不进行比较。
因为这种比较形式实际上不涉及多个均数的极差问题,所以不会增大犯I型错误的概率。
8.2单因素方差分析及两两比较

人文与管理学院方差分析单因素方差分析及两两比较处理因素施加于实验对象的措施或方法,或者实验对象本身所具有的某种属性或特征。
处理因素的不同状态。
水平完全随机设计是按随机化的原则将实验对象随机分配到处理因素的不同水平组(处理组),各组分别接受不同的处理,通过比较各组间均数差异有无统计学意义来分析处理因素的效应。
这种设计仅设计一个处理因素,但该因素可以有多个水平,因此又称为单因素方差分析(One-way ANOVA)。
各组例数可以相等也可以不等,相等时各组均衡可比性较好。
F统计量服从基于正态分布理论的F分布,因此单因素方差分析由如下应用条件:1)各样本是相互独立的随机样本2)各样本来自正态分布总体3)各总体方差相等,即方差齐需要说明的是,实际操作过程中,对于方差齐性的要求并不是非常严格,不符合方差齐性的数据也可以做方差分析。
各样本的总体是否服从正态分布,通过正态性检验来判断。
方差是否相等则通过方差齐性检验判断,常用Levene检验。
Levene检验不依赖于总体分布形式,适合于任意分布资料,能够对两组或多组样本进行方差齐性检验。
若资料不满足上述条件,可进行数据转换,对转换后的数据进行正态性和方差齐性检验,满足条件后,进行方差分析,或直接采用非参数检验方法进行分析。
例8-1观察参苓降脂片对高脂血症模型大鼠甘油三酯(TG)的影响,将高脂血症大鼠随机分为4组,每组9只,对照组不给予任何处理,低剂量组、中剂量组和高剂量组分别灌服参苓降脂片0.41g/kg体重、0.82g/kg体重、1.23g/kg体重,连续给药20天后,测定各组大鼠TG水平。
例8-1结果如表8-1所示。
试分析不同剂量的参苓降脂片降脂效果是否相同。
例8-1首先判断单因素方差分析应用条件是否满足:1、根据研究设计和实验观察可知,本资料满足独立性和随机性。
例8-12、由于各组样本含量均不大于50,所以采用Shapiro-Wilk统计量进行正态性检验。
方差分析与多重比较

方差分析与多重比较方差分析是一种统计分析方法,用于比较多个个体、组或处理之间的平均数差异。
它的主要目的是确定因素对于所观察到的变量是否具有显著影响。
在进行方差分析之后,如果发现了显著差异,那么就需要进行多重比较来确定哪些组或处理之间存在着实质性的差异。
1. 方差分析方差分析可以分为单因素和多因素方差分析。
单因素方差分析用于比较一个因素对于变量的影响,而多因素方差分析则考虑了多个因素的影响。
方差分析的原假设是各组或处理的均值相等,备择假设是各组或处理的均值不相等。
方差分析模型的基本假设是各组或处理的观测值是来自于正态分布总体。
在进行方差分析之前,需要检验各组或处理的观测值是否满足方差齐性的假设。
如果方差齐性假设成立,则可以使用方差分析方法进行推断;如果方差齐性假设不成立,则需要采取相应的修正方法,如Welch方法。
方差分析的结果通常以F统计量的形式呈现,根据F统计量的显著性水平,可以判断各组或处理之间是否存在显著差异。
2. 多重比较在进行方差分析后,如果发现了显著差异,则需要进行多重比较来确定具体是哪些组或处理之间存在着实质性的差异。
多重比较可以采用多种方法,常用的方法包括两两比较法、多重t 检验法和Tukey HSD法等。
在进行多重比较时,需要对比较结果进行适当的校正,以控制错误发现率。
两两比较法是最直观的方法,它通过对所有可能的组合进行t检验或其他适当的检验来确定差异的组合。
然而,当组数较多时,两两比较会导致多个假设检验,从而增加了错误发现的可能性。
多重t检验法是通过对多个均值进行比较来确定差异的组合。
不同于两两比较,多重t检验可以同时比较多个组之间的差异,从而减少错误发现的机会。
然而,多重t检验法需要进行适当的校正,以控制错误发现率。
Tukey HSD(Honestly Significant Difference)法是一种经典的多重比较方法,它通过估计多个均值之间的差异来确定差异的组合。
Tukey HSD法可以提供一个整体的比较结果,并以置信区间的形式表示差异的大小。
方差分析两两比较.pptx

3.1 Bonferroni t 检验
基本思想是:如果三个样本均数经 ANOVA 检验差异有统计学意义(α=0.05), 需对每两个均数进行比较,共需比较的次数为 3 次,由于每进行一次比较犯I 类 错误的概率是α=0.05,那么比较 3 次至少有一次犯I 类错误的概率就是: α’=1-0.953≈0.1426>0.05。因此,要使多次比较犯 I 类错误的概率不大于原 检验水准α,现有的检验水准应该进行调整,用 α’=α/m 作为检验水准的调 整值,两两比较得出的 P 值与其进行比较。该方法的思想适用于所有的两两比较, 并且该方法的适用范围很广,不仅仅限于方差分析,例如相关系数的检验和卡方 检验也适用。Bonferroni t 检验的方法和思想容易理解,操作简便,但是严格 地控制了I 类错误的同时增大了Ⅱ类错误的发生概率,在结论的给出方面是一种 比较保守的方法。
学海无涯
Dunnett’s 是一种基于学生化极差的适用于方差不齐情况时两两比较的方 法。
实验组和对照组的样本均数和样本含量。需特别指出的是 Dunnett—t 检验 有专门的界值表,不同于t 检验的界值表 。
一般认为,比较组数k≥3 时,任何两个样本的平均数比较会牵连到其它平 均数的对比关系,而使比较数再也不是两个相互独立的样本均数的比较.这是 LSD-t 无法克服的缺点。Dunnett—t 针对这一问题提出.在同一显著水平上两个
1. LSD-t 检验即最小显著法,是 Fisher 于 1935 年提出的, 多用于检验某 一 对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的 方 差分析没有推翻无效假设 H0 时也可以应用。该方法实质上就是 t 检验,检验 水 准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均 数 统一估计出一个更为稳健的标准误, 因此它一般用于事先就已经明确所要实 施 对比的具体组别的多重比较。由于该方法本质思想与 t 检验相同, 所以只适 用 于两个相互独立的样本均数的比较。LSD 法单次比较的检验水准仍为α , 因 此可以认为该方法是最为灵敏的两两比较方法.另一 方面,由于 LSD 法侧重于 减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I 类错误的倾向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析中均值比较的方法
最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具
体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1.事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有: Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant difference t test) 。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验
某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
1.2 Dunnett-t(新复极差法)检验,Duncan 1955年在Newman及Keuls的复极差法(muhiple range method)基础上提出,该方法与Tukey法相类似。
适用于n-1个试验组与一个对照组均数差别的多重比较,多用于证实性研究。
Dunnett-t统计量的计算公式与LSD-t检验完全相同。
实验组和对照组的样本均数和样本含量。
需特别指出的是Dunnett—t检验有专门的界值表,不同于t检验的界值表。
一般认为,比较组数k≥3时,任何两个样本的平均数比较会牵连到其它平均数的对比关系,而使比较数再也不是两个相互独立的样本均数的比较.这是LSD-t无法克服的缺点。
Dunnett—t针对这一问题提出.在同一显著水平上两个
均数的最小显著差数随着这二个平均数在多个平均数中所占的极差大小而不同,根据不同平均数间的对比关系来调整相应的显著差别(critical range)的大小。
2.多个均数的两两事后比较:适用于探索性研究,即各处理组两两问的对比关系都要回答,一般要将各组均数进行两两组合,分进行检验。
常用的方法有:SNK-q(Student-Newman-Keuls q)法、Duncan法、Tukey法和Scheffe法。
值得注意的是,这几种方法对数据有具体的要求和限制。
而文献中我最常见的是Tukey法与SNK-q法,。
2.1 SNK-q检验
对于SNK-q检验,检验的统计量是q,所以又称为q检验。
SNK-q检验的原理是根据所包含不同数目的平均数的极差调整各自的显著性水准,限制了实验的误差.保证在做所有比较时,不易犯第1类错误。
2.2 Tukey法
Tukey法(Tukey’S Honestly Significant DiferenceTukey’s HSD)的原理与SNK-q检验基本相同,但是,该方法要求各比较组样本含量相同,它将所有对比组中I类错误最大者控制在α之内。
研究显示:这种方法有较高的检验效能(与LSD法比较),具有很好的稳定性,适用于大多数场合下的两两比较,计算简便。
但是,Tukey法是基于比较组全部参与比较这一假设下进行的,因此在只比较指定的某几组总体均数时并不适用,建议选择Dunnett法或者是Bonferroni方法,因为这两种方法会给出较高效能的检验结果。
2.3 Scheffe法
与一般的多重比较不同,Scheffe法的实质是对多组均数间的线性组合是否为0进行假设检验,多用于对比组样本含量不等的资料。
在单因素的多重比较问题中,除了要逐对比较因素水平的平均效应之外,有时还有可能要比较因素水平平均效应的线性组合。
例如将有基本相同的因素水平平均效应的几个组,构成一个综合组。
因此可能检验这样的假设:
显然,前面讨论的参数的两两比较属于一类特殊的对比。
Scheffe法可以同时检验所有可能的对比,即同时检验任何一组对比。
Scheffe法的优点是可以检验任意的线性对比。
在这方面,Tukey法不如Scheffe法。
但是在单纯作逐对因素效应均值的比较时,Schefe法的效率不如Tukey法高。
也就是说,Schefe法更易于将显著的差异判定为不显著(Tukey法认为)。
在实际场合,当单纯作逐对均值
比较时,建议用Tukey法;而当要做多个一般的线性对比检验时。
就要用Scheffe法。
Scheffe法检验实质上对F值进行了简单的校正,将比较的组数纳入考虑的范畴,该方法的检验统计量代表了最大可能的累积I类错误的概率。
遗憾的是,由于控制I类错误时的“矫枉过正”.会最终导致较大的Ⅱ类错误的概率。
3.探索性研究和证实性研究均适用的检验方法:
3.1 Bonferroni t检验
基本思想是:如果三个样本均数经ANOVA检验差异有统计学意义(α=0.05),需对每两个均数进行比较,共需比较的次数为3次,由于每进行一次比较犯I类错误的概率是α=0.05,那么比较3次至少有一次犯I类错误的概率就是:α’=1-0.953≈0.1426>0.05。
因此,要使多次比较犯I类错误的概率不大于原检验水准α,现有的检验水准应该进行调整,用α’=α/m作为检验水准的调整值,两两比较得出的P值与其进行比较。
该方法的思想适用于所有的两两比较,并且该方法的适用范围很广,不仅仅限于方差分析,例如相关系数的检验和卡方检验也适用。
Bonferroni t检验的方法和思想容易理解,操作简便,但是严格地控制了I类错误的同时增大了Ⅱ类错误的发生概率,在结论的给出方面是一种比较保守的方法。
3.2 Sidak检验
该方法通过Sidak校正降低每次两两比较的I类错误概率,以达到最终整个比较的I类错误发生率不超过α的目的。
Bonferroni t检验与Sidak检验相似,Bon.ferroni t检验是检验的近似计算,但是由于Bonferroni t检验在计算上容易实现,所以应用较广。
相比较而言,Bonferroni t检验在给出推断结论时更为审慎。
不容易得到拒绝零假设的结果。
两种检验在对比组数增加、比较组不独立时,推断结论更趋保守。
以上方法都必须在满足方差齐性的前提条件时才可以应用,另外还有一些方法是在不满足方差齐性时多重比较的方法:Tamhane’s T2,Dunnetts’s T3, Games-Howell, Games-Howell。
Tamhane’s T2是一种基于t检验原理的两两比较方法。
该方法比较保守。
Dunnetts’s T3则是以最大的t值(studentized maximum modulus)为基础的。
Games-Howell检验方法是比较宽大的一种两两比较方法。
Games-Howell 方法将方差不齐的组数作为一个影响因素纳入考虑范畴。
严重的方差不齐和样本含量过小都会使I类错误的概率增加。
Games-Howell检验基于Welch’s对t检验的自由度进行校正,并使用了学生化极差作为统计量。
该检验适用于样本含量小且方差不齐(轻度方差不齐例外)时的情况。
该方法是方差不齐时的一种较好的方法。
Dunnett’s是一种基于学生化极差的适用于方差不齐情况时两两比较的方法。
