正弦和余弦函数的图像及性质..
合集下载
正弦、余弦、正切函数图象及其性质
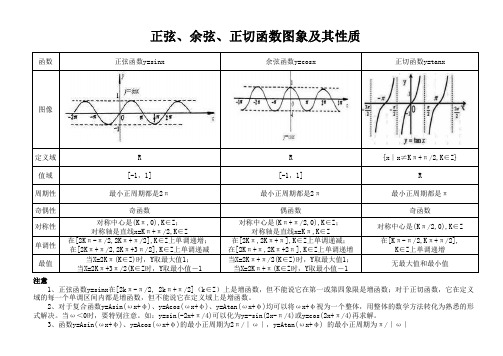
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1，1][-1，1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z；对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z；对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增；在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减；在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时，Y取最大值1；当X=2Kπ+3π/2(K∈Z时，Y取最小值－1当X=2Kπ+π/2(K∈Z)时，Y取最大值1；当X=2Kπ+π(K∈Z时，Y取最小值－1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2]（k∈Z）上是增函数，但不能说它在第一或第四象限是增函数；对于正切函数，它在定义域的每一个单调区间内都是增函数，但不能说它在定义域上是增函数。
2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体，用整体的数学方法转化为熟悉的形式解决。
当ω＜0时，要特别注意。
如：y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。
3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣，y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。
正弦函数和余弦函数的图像与性质
x 10, 3 2 , 0, 2 , 3
3. 求最小正周期： (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1]，最大值是 1，最小值是 1.
当 cos x 1时，x 2k (k Z). 当 cos x 1 时，x (2k 1) (k Z).
（2）周期性
一般地，对于函数 f ( x)，如果存在一个常数 T (T 0)， 使得当 x 取定义域 D 内的任意值时，都有 f ( x T ) f ( x) 成立，那么函数 f ( x) 叫做周期函数，常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说，如果在所有的周期中 存在一个最小正数，那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解： 偶函数； (1)
(2) f ( x) cos 2 x，偶函数；
2 (k Z)
(3)sin x 1 x 2k
x
，但 x 可以取 ，即 f ( x)的定义域不关于原点对称， 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增：k , k (k Z)， 减：k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解： x cos x 2 k , 2 k 2 6 6
3. 求最小正周期： (1) f ( x) 3sin x 4cos x (2) f ( x) sin 2 x (3) f ( x) sin 2 x cos 2 x
y cos x , x R 的值域是 [1,1]，最大值是 1，最小值是 1.
当 cos x 1时，x 2k (k Z). 当 cos x 1 时，x (2k 1) (k Z).
（2）周期性
一般地，对于函数 f ( x)，如果存在一个常数 T (T 0)， 使得当 x 取定义域 D 内的任意值时，都有 f ( x T ) f ( x) 成立，那么函数 f ( x) 叫做周期函数，常数 T 叫做函数 f ( x) 的周期。对于一个周期函数 f ( x) 来说，如果在所有的周期中 存在一个最小正数，那么这个最小正数叫做函数 f ( x) 的 最小正周期。
解： 偶函数； (1)
(2) f ( x) cos 2 x，偶函数；
2 (k Z)
(3)sin x 1 x 2k
x
，但 x 可以取 ，即 f ( x)的定义域不关于原点对称， 2 2
f ( x) 是非奇非偶函数。
(4) f ( x)
1 sin 2 x sin x 1 1 sin 2 x sin x 1
5 3 增：k , k (k Z)， 减：k , k (k Z) 8 8 8 8
(4) y log 1 2cos x 3
2
3 解： x cos x 2 k , 2 k 2 6 6
正弦余弦函数的图像性质(周期、对称、奇偶)
4π
6π
正弦函数y=sinx的图 象
-
-
-
x
-
每隔2π ，图象重复出现
− 6π − 4π
-
y
即对任意x，y = sin x + 2π） sin x （ =
1-1-
− 2π
-
o
2π
4π
6π
如果令f（x）＝ 如果令 （ ）＝sinx，则 f（x＋2π）＝ （x) ， （ ＋ ）＝f（ ）＝ ）＝ 抽象 f (x +T) = f(x)
y
2
+ kπ，k ∈ Z
（kπ，0）,k∈Z ， ） ∈
余 弦函 数 y=cosx的 图象 的
1-
− 4π
-
− 2π
-
o
- 1心： 无数个 对称中心：
-
-
x
0 k （ + kπ， ）（ ∈ z） 2
π
巩固运用
例4、判断下列函数的奇偶 性 5 （1） f（ x） 2sin （2x＋ π）； = 2
-
-
-
-
x
-
正弦余弦函数对称性
正弦函数.余弦函数的图象和性质 正弦函数 余弦函数的图象和性质
y
正弦 函数 y=sinx的 图象 的
1-
− 6π
对称轴： 无数条 对称轴：
x=
− 6π
-
对称轴： 无数条 对称轴： x=kπ， x=kπ，k∈Z
-
− 4π
-
− 2π
-
o
-1 -
2π
4π
6π
x
π
对称中心： 无数个 对称中心：
答： T =
2π
正弦、余弦函数的图像和性质PPT优质课件
作三角函数图象
描几点何法法:作查图三的角关函键数是表如得何三利角用函单数位值圆,描中点角(xx的,s正in弦x),线连，线巧. 妙地
如移:动x 到 直3 角查坐表标y系内s，i从n3而确0.8定对6应6的0点 (x,sinx).
y
描点 (3 ,0.866)0
1-
y
P
-Hale Waihona Puke 023 2
2
x
1 -
3
O M 1x
2020/12/10
9
练习：（1）作函数 y=1+3cosx，x∈[0,2π]的简图 (２)作函数 y=2sinx-1，x∈[0,2π]的简图
（1） y
x
2020/12/10
10
四川省天全中学数学组
2005.03
2020/12/10
11
余弦曲线
-
-
y-
1
-
6
4
2
o
-1
2
4
6
由于 ycox scosx)(sin [(x) ]sin x()
几何法：作三角函数线得三角函数值，描点(x,sinx),连线
如: x
3
作
3
的正弦线 MP ,
平移定点 (x, MP)
2020/12/10
5
函数 y six ,n x 0 ,2图象的几何作法
y
作法: (1) 等分
(2) 作正弦线
1-
P1
p
/ 1
(3) 平移 (4) 连线
6
o1
M -11A
o 6
3
正 弦 函 数、余 弦 函数的图象和性质
2020/12/10
1
正弦函数和余弦函数的图像与性质
10
18
(2) 因为
π ＜ 2 π ＜ 3 π ＜π ，
23
4
且
y ＝sin x
在[ π ，π] 上是减函数，
2
所以 sin 2 π ＞ sin 3 π ．
3
4
例8.判断f(x)=xsin(+x)奇偶性
解 函数的定义域R关于原点对称 f (x) xsin( x) xsin x
f (x) (x)sin(x) f (x) f (x) f (x)
y
1
-2 - o 2 3
-1
4 x
定义域
R
值域
[1,1]
x 2k (k Z ) 时
2
最
值
ymax=1 x 2k (k Z ) 时
2
ymin= 1
y= 0 x k (k Z)
R [1,1]
x 2k (k Z) 时 ymax=1 x 2k (k Z ) 时 ymin= 1
是减函数。
② 函数y=cos(x+/2),xR ( A )
A 是奇函数； B 是偶函数； C 既不是奇函数也不是偶函数； D 有无奇偶性不能确定。
2 不通过求值，比较下列各组中两个三角函数值的大小：
sin 250 >_ sin 260
cos15 / 8>_ cos14 / 9
cos515 >_ cos530
y
1-
-
o
π 6
π 3
π 2
2π 3
5π 6
π
7 6
4π 3
3π 2
5π 3
11π 6
2π
x
-1 -
图象的最高点: ( π ，1)； 2
正弦函数和余弦函数的图像与性质.ppt
, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式：cos x sin x, x [ , ]
-2
五个关键点：(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时， -6
余弦函数取得最大值1；-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时，
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值，及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦函数、余弦函数的图象_优质课件
3) y 3sin(1 x ), x R 一般
35
结论：
函数y Asin(x )及y Acos(x ), x R
( A,,为常数, A 0, 0)的周期T 2
新课讲解. 正弦函数、余弦函数的性质 (三)关于奇偶性（复习）
一般地, •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= f( x )，那么就说f( x )是偶函数 •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= -f( x )，那么就说f( x )是奇函数
小结回顾
正切函数的基本性质
4 5
应用提升
练习1：试着画出y | tan x | 和y tan | x |
并讨论它们的单调性，周期性和奇偶性.
练习2.如果、
(
,
)且
tan
cot
,
2
那么必有（ ）
A.
B.
C. 3 D. 3
2
2
应用提升
例3.求函数y tan x 1 的定义域 3 tan x
例4.试讨论函数y loga tan x的单调性
2
2
y=cosx
y cos x : 定义域为R，值域[1,1]
1
最-6大 值1,此-5时 x
2-k4; 最小值-3-1,
此时x
-2
2k
-;
-1
2 3 2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
(2) y sin x, y cosx与y Asin(x ), y Acos(x )间的换元思想
正弦函数余弦函数的图像与性质
三角函数在物理学中的应用
振动与波动
正弦和余弦函数是描述简谐振动和波动的基本函 数，广泛应用于声学、光学等领域。
交流电
交流电的电压和电流是时间的正弦或余弦函数， 用于驱动各种电器设备。
磁场与电场
在电磁学中，正弦和余弦函数用于描述磁场和电 场的分布和变工程中的许多振动问题都可以用 正弦和余弦函数来描述，如桥梁 振动、车辆振动等。
周期性
正弦函数具有周期性， 其周期为2π。
奇偶性
正弦函数是奇函数，满 足sin(-x) = -sin(x)。
余弦函数的定义
定义
余弦函数是三角函数的另一种形式，定义为直角三角形中锐角的邻边与斜边的比值，记作 cos(x)。
周期性
余弦函数也具有周期性，其周期为2π。
奇偶性
余弦函数是偶函数，满足cos(-x) = cos(x)。
奇偶性
总结词
正弦函数是奇函数，而余弦函数是偶 函数。
详细描述
奇函数满足$f(-x) = -f(x)$，偶函数满 足$f(-x) = f(x)$。对于正弦函数， $sin(-x) = -sin(x)$；对于余弦函数， $cos(-x) = cos(x)$。
最值与振幅
总结词
正弦函数和余弦函数都具有最大值和最小值，这取决于它们的振幅。
正弦函数余弦函数的图像与性质
目录
• 正弦函数与余弦函数的定义 • 正弦函数与余弦函数的图像 • 正弦函数与余弦函数的性质 • 正弦函数与余弦函数的应用 • 正弦函数与余弦函数的扩展知识
01 正弦函数与余弦函数的定 义
正弦函数的定义
定义
正弦函数是三角函数的 一种，定义为直角三角 形中锐角的对边与斜边 的比值，记作sin(x)。
正弦函数、余弦函数的图像和性质
-
图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法，求下列不等式的解集：
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数： 3 （ ）y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法，求下列不等式的解集：
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数： 3 （ ）y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
正弦函数 余弦函数的图像和性质ppt
1
1
0 0
0
y
2 1 -
1
0
1
1 -
o
2
3 2
2
x
作函数 y= sinx + 小值
y= sinx+
1 2
1 2
3 2
cosx草图，求y的最大值和最
解：用辅角公式化简函数
3 cosx 2
= sinxcos 3 + cosxsin 3 = sin(x+ 3 )
X+ 3
0 －
3
o
1-
x
6
-
4
-
2
2
-1 -
4
6
-
因为终边相同的角的三角函数值相同，所以y=sinx的图象在……， 4 ,2 , 2 , 0 , 0 , 2 , 2 , 4 , y ……与y=sinx,x∈[0,2π ]的图象相同
2
1 2
1
1
1
0
0 1
1 -
o
2
3 2
2
x
练习 : 作函数 y=－cosx，x∈[0,2π]的草图
作函数 y= sinx + 小值
1 2
3 2
cosx草图，求y的最大值和最
练习：作函数y= －cosx,x∈[0,2π]的草图 解: 列表
X
0
2
1
3 2
2
1
cosx -cosx
描点法: 查三角函数表得三角函数值,描点 ( x, sin x),连线.
如: x 查表 y sin 3 0.8660 3 ) 描点 ( ,0.8660 3
6.1 正弦函数和与弦函数的图像与性质docx
6.1 正弦函数和余弦函数的图像与性质
1.定义
型如sin (x R)y x =∈的函数叫做正弦函数.
型如cos (x R)y x =∈的函数叫做余弦函数.
2.图像
sin (x R)y x =∈
cos (x R)y x =∈
3.周期性
一般地，对于函数f(x)，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有f(x ＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T 叫做这个函数的周期. 对于一个周期函数f(x)，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.
正弦函数、余弦函数都是周期函数，2k π(k ∈Z 且k ≠0)都是它的周期，最小正周期是2π.
例1 作出下列函数的大致图像
（1）[]1cos ,0,2y x x π=+∈ （2）[]y sinx,0,2x π=-∈
（3）[]sin ,0,2y x x π=∈ （4）[]y sin 2,0,2x x π=∈
例2.求下列函数的定义域与值域
（1）1sin 22y x =
（2）y
例3.求函数2sin 33y x π⎛
⎫=-+ ⎪⎝⎭
的最大值与最小值，并求使其取得最大值、最小值的x 的集合
例4.矩形ABCD 的四个顶点分别在矩形A ’B ’C ’D ’的四条边上，AB=a ，BC=b ，如果AB 与A ’B ’的夹角为α，那么当α为和值时，矩形A ’B ’C ’D ’的周长最大？。
《正余弦函数图像》课件
余弦函数基本概念介绍
定义与特点
余弦函数是周期性变化的函数，描述了单位圆上一个点的横坐标随角度变化而变化的规律。
公式
余弦函数公式为y = A * cos(B * (x - C)) + D，其中A、B、C、D分别影响振幅、周期、相位 和纵坐标偏移。
图像特征
余弦函数图像呈现周期性的波浪曲线，对称于x轴和y轴，振幅与A值相关。
《正余弦函数图像》PPT 课件
本课程将介绍正弦函数和余弦函数的基本概念，探索它们的图像及性质，比 较分析两者的图像，并以小测验来巩固所学知识。最后给出结论和参考资料。
正弦函数基本概念介绍
1 定义与特点
正弦函数是周期性变化的函数，描述了单位圆上一个点的纵坐标随角度变化而变化的规 律。
2 公式
正弦函数公式为y = A * sin(B * (x - C)) + D，其中A、B、C、D分别影响振幅、周期、相 位和纵坐标偏移。
相似性
正弦函数和余弦函数都是周 期性的函数，呈现波动或波 浪形状的图像。
差异性
相位差：正弦函数和余弦函 数的图像相位差90度。
振幅：正弦函数图像纵向的 上下震动幅度，而余弦函数 图像横向的左右震动幅度。
应用
正弦函数常用于描述周期性 变化的现象，如音波、电流 等；余弦函数通常用于描述 旋转变化的现象，如天体运 动等。
余弦函数图像及性质
1
调节振幅
2
余弦函数图像的振幅可以通过改变A
的值来调节，振幅表示纵向的上下震
动幅度。
3
波动与震动
余弦函数图像呈现连续的波动曲线， 每个周期具有相同的形状，与正弦函 数的图像相位差90度。
平移与初始位置
改变C的值可以使整个图像左右平移， 影响图像的起始位置。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
-
-
-
-
-
－1
用诱导公式来作余弦函数y=cosx,x∈R的的图像 y= cosx = cos(-x) = sin[
y
2
-(-x)] = sin(x+ 2 )
从图像中我们看到cosx由sinx 向左平移 2 个单位后得到
1
-
4
2
o
-ቤተ መጻሕፍቲ ባይዱ
2
4
x
-
-
因为终边相同的角的三角函数值相同，所以y=cosx的图象在……， 4 ,2 , 2 ,0, 0,2 , 2 ,4 , ……与y=cosx,x∈[0,2π]的图象 形状相同
0 －
3
x y
2 6
2 3
3 2
7 6
2
5 3
0
1
0
－1
0
y=sin(x+ 3 )图像如下所示
y
最大值为 1，最小值为－1
2
-
1
-
3
2 3
2
x
-
-
-
-
o
-
1
2
想一想?
正弦曲线、余弦曲线，它们图象有何特征？
y
正弦函数 y sin x , x R
的图象
1
3 2
2
1
0 0
0
y
2 1 -
1
0
1
1 -
o
2
3 2
2
x
作函数 y= sinx + 小值
y= sinx+
1 2
1 2
3 2
cosx草图，求y的最大值和最
解：用辅角公式化简函数
3 cosx 2
= sinxcos 3 + cosxsin 3 = sin(x+ 3 )
换元法
X+ 3
6
4
2
o
1-
2
4
6
x
-
6
余弦函数
-
正弦、余弦函数y=sinx,y=cosx的图象
y
o x
4
y co s x , x R
的图象
2
-
-1-
-
-
2
1-
4
余弦函数 y
cos x , x R 的图象
-
0
-
-
-
-
,2
, 2
, 4 ,
y 正弦函数 .余弦函数的图象和性质
1-
图象的最高点
2
( 1) 2 ,
o
－1
-
3 2
2
x
与x轴的交点
(0,0) ( ,0) (2 ,0)
( 32, 1)
图象的最低点
简图作法 (五点作图法) (1) 列表(列出对图象形状起关键作用的五点坐标) (2) 描点(定出五个关键点) (3) 连线(用光滑的曲线顺次连结五个点)
....
描点法: 查三角函数表得三角函数值,描点 ( x, sin x),连线.
y sin 如: x 3 0.8660 3 查表 ) 描点 ( 3 ,0.8660
y
P
3
y 1 1
O
M
x 0
2
的从 点而 确 定 对 应
1
- 3 2
2
-
x
1 -
坐巧 标妙 系地 内移 ，动 到 直 角
2 1 -
2
1 2
1
1
1
0
0 1
1 -
o
2
3 2
2
x
练习 : 作函数 y=－cosx，x∈[0,2π]的草图
作函数 y= sinx + 小值
1 2
3 2
cosx草图，求y的最大值和最
练习：作函数y= －cosx,x∈[0,2π]的草图 解: 列表 cosx -cosx
X
0
1
1
2
1 2
x
y
0
6
3
2
2 3
3 2
5 6
1 2
0
7 6
4 3
3 2
5 3
11 6
2
0
3 2
1
1 2
3 2
1
23
1 2
0
(2).描点
y 1 0
2
- 3 2
2
-
x
(3).连线
1 -
y
正弦曲线
1
-
4
2
o
-
2
4
-
因为终边相同的角的三角函数值相同，所以y=sinx的图象在……， 4 ,2 , 2 ,0, 0,2 , 2 ,4 ,……与y=sinx,x∈[0,2π]的图象 形状相同
o
x
6
-
4
2
2
-1 -
4
6
-
因为终边相同的角的三角函数值相同，所以 y=sinx的图象在……， 4 ,2 , 2 , 0 , 0 , 2 , 2 , 4 , y ……与y=sinx,x∈[0,2π ]的图象相同
-
-
-
-
-
－1
想一想
请观察正弦曲线、余弦曲线的形状 和位置,说出它们的异同点.
y 正弦函数.余弦函数的图象和性质 正弦函数 y sin x , x R 的图象
1-
它们的形状相 同，且都夹在 两条平行直线 y=1与y=－1 之间。但它们 的位置不同， 正弦曲线交y 轴于原点，余 弦曲线交y轴 于点（0，1）.
几何法： 作三角函数线得三角函数值,描点 ( x, sin x) ,连线
如: x 作 3 的正弦线 MP, 3 平移定点 ( x, MP)
用几 单何 位法 圆作 中图 角的 的关 正键 弦是 线如 ，何 利
(x,sinx).
x
正弦函数.余弦函数的图象和性质 函数
y sin x, x 0,2 图象的几何作法
授课教师：谷元芳
正弦函数.余弦函数的图象和性质
想一想?
1. sinα、cosα、tanα的几何意义.
y
T 1 P
正弦线MP
余弦线OM
o
M
A 1
x
正切线AT
三角问题
几何问题
正弦函数.余弦函数的图象和性质
新课:
1.函数 y sin x, x 0,2 图象的几何作法
利用三角函数线 作三角函数图象
1
图象的最高点
(0,1) (2 ,1)
o
－1
2
3 2
2
3 2 ,0) ( 2 ,0) 与x轴的交点(
图象的最低点 ( ,1)
正弦函数.余弦函数的图象和性质
例题
作函数y=sinx+1,x∈[0,2π]的简图 解: 列表
x
sin x sin x 1
0
0
2
描点作图
0
3 2
y
正弦、余弦函数y=sinx,y=cosx的图象
o x
1-
-
-
-
-
-
6
-
4
2
2
-1 -
4
6
-
4 , 2 因为终边相同的角的三角函数值相同，所以 y=cosx的图象在……， , 2 , 0 , ……与y=cosx,x∈[0,2π ]的图象相同
作法: (1) 等分 (2) 作正弦线 (3) 平移 (4) 连线
y
1
/ p1
-
o-1
6
-A
o
－1
6
3
-
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2
x
正弦函数.余弦函数的图象和性质
2.用描点法作出函数图象的主要步骤是怎样的？
(1).列表
y sin x, x 0,2