华理大学物理第6章习题课
大学物理第6章习题参考答案

第六章习题解答6-1 解:首先写出S 点的振动方程 若选向上为正方向,则有:0c o s02.001.0ϕ=- 21cos 0-=ϕ,0s i n 00>-=ϕωυA 0sin 0<ϕ 即 πϕ320-=或π34 初始相位 πϕ320-=则 m t y s )32cos(02.0πω-=再建立如图题6-1(a)所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为: ux t =∆则该波的波动方程为:m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0若坐标原点不选在S 点,如习题6-1图(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为: uL x t -=∆则该波的波方程为:m uL x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0若P 点选在S 点左侧,P 点比S 点超前时间为ux L -,如习题6-1图(c)所示,则⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0u x L t y⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t∴不管P 点在S 点左边还是右边,波动方程为: ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t y6-2 解(1)由习题6-2图可知, 波长 m 8.0=λ 振幅A=0.5m习题6-1图习题6-1图频率 Hz 125Hz 8.0100===λuv周期 s 10813-⨯==vT ππυω2502==(2)平面简谐波标准波动方程为: ⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u xt A y 由图可知,当t=0,x=0时,y=A=0.5m ,故0=ϕ。
将ϕπωω、、、u v A )2(=代入波动方程,得:m )100(250cos 5.0⎥⎦⎤⎢⎣⎡-=x t y π(3) x =0.4m 处质点振动方程.⎥⎦⎤⎢⎣⎡-=)1004.0(250cos 5.0t y π m )250cos(5.0ππ-=t6-3 解(1)由习题6-3图可知,对于O 点,t=0时,y=0,故2πϕ±=再由该列波的传播方向可知,00<υ取 2πϕ=由习题6-3图可知,,40.0m OP ==λ且u=0.08m/s ,则ππλππω52rad/s 40.008.0222====u v rad/s可得O 点振动表达式为:m t y )252cos(04.00ππ+=(2) 已知该波沿x 轴正方向传播,u=0.08m/s,以及O 点振动表达式,波动方程为:m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ(3) 将40.0==λx 代入上式,即为P 点振动方程:m t y y p ⎥⎦⎤⎢⎣⎡+==ππ2152cos 04.00 (4)习题6-3图中虚线为下一时刻波形,由图可知,a 点向下运动,b 点向上运动。
大学物理第06章习题分析与解答.doc

6-1某一热力学系统经历一个过程后,吸收了400J的热量,并对环境做功300J,则系统的内能()o(A)减少了100J (B)增加了100J (C)减少了700J (D)增加了700J解:由热力学第一定律2 = AE + W可得AE = 2 - VV = 400 - 300=100J 故选B6-2对于理想气体系统来说,在下列过程中,哪个过程中系统所吸收的热量、内能的增量和对外做功三者均为负值( )?(A) 等容降压过程(B)等温膨胀过程(C)绝热膨胀过程(D)等压压缩过程解:等容过程不做功,故A不正确;等温过程内能不变,故B不正确;绝热过程与外界不交换热量,故C不正确;对于等压压缩过程:体积减小,系统对外界做负功,表现为外界对系统做功;易知压缩过程温度降低,则内能减少;等压过程e p = vC^T ,温度降低,则必放热。
故选D6-3系统分别经过等压过程和等体过程,如果两过程中的温度增加值相等,那么()o(A)等压过程吸收的热量小于等体过程吸收的热量(B)等压过程吸收的热量等于等体过程吸收的热量(C)等压过程吸收的热量大于等体过程吸收的热量(D)无法确定解:等压过程吸收的热量Q p = vC^T ;等容过程吸收的热量e v=^c v Ar,由于C p > C v ,故选 C6-4 一台工作于温度分别为327°C和27°C的高温热源与低温热源之间的卡诺热机,每经历一次循环吸热2000J ,则对外界做功( )o(A) 2000J ( B ) 1000J ( C ) 4000J ( D ) 500J解:卡诺热机循环效率?/= —=1-^=1- —则W = 1000J,故选BQ吸心600 26・5系统从外界获得的能量,一部分用来_______ ,另一部分用来对外界做功。
解:详见热力学第一定律6-6空气压缩机在一次压缩过程中,活塞对气缸内的气体做功为2xlO4J,同时气体的内能增加了1.5X104J O试问:此压缩过程中,气体_______________ (填“吸收”或“放出”)的热量等于 ___________ J。
大学物理A第六章习题选解,DOC

第六章真空中的静电场习题选解6-1三个电量为q -的点电荷各放在边长为r 的等边三角形的三个顶点上,电(的中(2)粒子的质量为: 由牛顿第二定律得:6-3如图所示,有四个电量均为C q 610-=的点电荷,分别放置在如图所示的1,2,3,4点上,点1与点4距离等于点1与点2的距离,长m 1,第3个电荷位于2、4两电荷连线中点。
求作用在第3个点电荷上的力。
解:由图可知,第3个电荷与其它各电荷等距,均为2r =。
各电荷之间均为斥力,且第2、4两电荷对第三电荷的作用力大小相等,方向相反,两力平衡。
由库仑定律,作用于电荷3的力为题6-3图 题6-3图力的方向沿第1电荷指向第3电荷,与x 轴成45角。
6-4在直角三角形ABC 的A 点放置点电荷C q 91108.1-⨯=,B 点放置点电荷C q 92108.4-⨯-=,已知0.04,0.03BC m AC m ==,试求直角顶点C 处的场强E 。
E 题6-5图6-6如图所示,一根很长的绝缘棒,均匀 带电,单位长度上的电荷量为λ,试求距棒的一端垂直距离为d 的P 点处的电场强度。
解:建立如图所示坐标,在棒上任取一线 元dx 在P 点产生的场强为dE 题6-6图场强dE 可分解成沿x 轴、y 轴的分量 题6-6图P 点场强dE E E y x02242πελ=+= 方向与Y 轴夹角为ϕarctan45xyE E ϕ== 6-7一根带电细棒长为l 2,沿x 轴放置,其一端在原点,电荷线密度Ax =λ(A 为正的常数)。
求x 轴上,l b x 2+=处的电场强度。
解:在坐标为x 处取线元dx ,带电量为Axdx dq =,该线元在P 点的场强为dE ,,在方求在这个圆洞轴线上距洞心r 处一点P 的场强。
解:开了一个圆洞的无限大均匀带电 平面,相当于一个无限大均匀带电平面又 加了一块带异号电荷,面密度σ相同的圆 盘。
距洞心r 处P 点的场强式中+E 为无限大均匀带电平面在P 点产生的场强题6-9图方向垂直于平面向外-E 为半径为R 的均匀带负电圆盘在其轴线上距中心为r 处的P 产生的场强。
大学物理课后答案——第六章 管靖主编

第六章 习题6.1 三个相同的点电荷放置在等边三角形的三个顶点上,在此三角形的中心应放置怎样的电荷,才能使作用在每一点电荷上的合力为零?解 设等边三角形的边长为a,则由顶点到中心的距离为;顶点处电荷为q ,中心处电荷为Q ,Q 与q 反号.考虑到等边三角形的对称性,可知Q 受其它三个电荷的合力为零,与Q 的大小无关;顶点处三个电荷q 所受合力的大小相同.上方顶点处电荷q受其它三个电荷的作用力如题解图 6.1所示,合力为零要求题解图6.102cos30F F =即22024q aπε⨯=可求出3Q q =.6.2 半径为R 的半圆形带电曲线,如题图 6.2所示,线上单位长度带有电荷η,求圆心O 点的场强. 题图6.2解 在带电曲线上取一个长度为d l 的电荷元,其电量d d q l η=.电荷元在O 点的场强为d E,如题解图 6.2.由于电荷分布对Ox 轴对称,所以全部电荷在O 点产生的总场强沿y 方向的分量之和为零,O 点的总场强E 沿Ox 方向,(d )x E E i =⎰.由于d =d lR θ,所以200d cos cos d cos d d 44x l E E R Rηθηθθθπεπε⋅=== 于是222200cos (d )(sin )44E i |i R R ππππηθηθθπεπε--==⎰02i Rηπε= 6.3 电量均为9410C -⨯的四个点电荷置于正方形的四个顶点,各顶点距正方形中心O点5cm .试求:(1)O 点的场强和电势;(2)将点电荷90110C q -=⨯从无穷远处移到O 点,电场力作功多少?电势能的改变为多少?解 (1)根据场强迭加原理,O 点的场强12340E E E E E =+++=根据电势迭加原理,O 点的电势12340144qrϕϕϕϕϕπε=+++=⨯99291040104510.--⨯⨯⨯=⨯⨯328810().V =⨯ (2)电场力作功0(0)A q ϕ=--93101028810..-=-⨯⨯⨯628810(J).-=-⨯电势能的改变为6p 28810(J)E A .-∆=-=⨯6.4 半径为R 的半圆形带电曲线,如题图 6.2所示,线上单位长度带有电荷η,求圆心O 点的电势.解 在带电曲线上取一个长度为d l 的电荷元,其电量d d ql η=.参见题解图6.2,d =d l R θ.则O 点的电势为001d 1d 44q l r R ηϕπεπε==⎰⎰20001d 444ππηπηηθπεπεε-===⎰6.5 已知空气的击穿场强为6310V m ⨯,测得某次闪电的火花长100m .(1)求这次发生的闪电两端的电势差;(2)设闪电时通过的电量为30C ,问这次闪电消耗多大能量?解 (1)闪电两端的电势差68310100310(V)U Ed ϕ=∆==⨯⨯=⨯(2)次闪电消耗多大能量8931030910(J)E qU ==⨯⨯=⨯6.6 如题图6.6所示,匀强电场E 与半径为R 的半球面1S 的轴线平行,试计算通过此半球面的E通量.若以半球面的边线为边,另取一个任意形状的曲面2S ,问2S 的电通量多大?请说明理由. 题图6.6解 以半球面1S 的边缘为边界作一个平面0S ,此平面为一个圆,面积为2R π.由于E与0S面垂直,所以通过0S 面的E通量2R E Φπ=.因为通过1S 面和2S 面的E 通量与通过0S 面的E 通量相等,故通过1S 面和2S 面的E通量均为2R E Φπ=.6.7 设地球表面附近的场强约为200Vm ,方向指向地心,试求地球所带总电量.解 在地球表面外、沿地球表面作一个球面,以此球面为高斯面,设地球所带总电量为Q ,地球半径66.410m R =⨯,由高斯定理20d 4SQ E S E R πε⋅=-⨯=⎰⎰所以地球所带总电量204Q E R επ=-⨯⨯1262885102004314(6410)...-=-⨯⨯⨯⨯⨯⨯59110(C).=-⨯6.8 一块厚度为d 的无限大平板均匀带电,电荷密度为ρ,求板内外电场E的分布.解 垂直于平板表面作横截面,如题解图 6.8;图中虚线为与表面平行、距离两表面等距离(均为2d )的平面AB .由于带电平板无限大,电荷分布对平面AB 对称,可知电场强度E与平板表面垂直,在距离平面AB 距离相等处电场强度的大小E 相同.作对平面AB 对称的闭合高斯面S ,高斯面S 由与平面AB 平行的两个底面1S 和2S 和与平面AB正交的柱面3S 组成,两个底面1S 和2S 到平面AB 的距离均为l .因1S 和2S 的E 通量相等,12ES ES =;3S 的E 通量为零;当2dl ≤时,根据高斯定理1110122E S lS ρε=即可求出10l E ρε=;当2d l >时,根据高斯定理 211012E S S d ρε=可求出22dE ρε=.平板带正电,E 垂直表面向外,平板带负电,E垂直表面向内.6.9 如题图6.9所示, 在半径分别为1R 、2R 的两个同心薄球面上均匀分布着电荷1Q 和2Q .(1)求I 、II 、III区场强E的分布;(2)求I 、II 、III 区的电势分布. 题图6.9解 由于电荷分布对球心O 具有球对称性,故电场分布也对球心O 具有球对称性,可知电场线为过O 点的放射状半直线,场强E沿半径方向,在到O 点的距离r 相同处,场强大小E 相等.(1)设研究的场点到O 点的距离为r ,以O 为圆心、r 为半径的球面为高斯面,E与高斯面正交.根据高斯定理,在I 区,1rR <,有211d 40E S E r π⋅=⋅=⎰⎰所以10E =.在II 区,12R r R <<,则由21204Q E r πε⋅=可求出12204Q E rπε=.在III 区,2rR >,则由212304Q Q E r πε+⋅=可求出123204Q Q E r πε+=.(2)取参考点在无穷远,积分路径沿半径方向,沿电场线积分. 在III 区,2rR >,121233200()d d 44rr Q Q Q Q r E l r r r ϕπεπε∞∞++=⋅==⎰⎰ 在II 区,12R r R <<,22212233220()d d d ()4R R rR rQ r E l E l r R r ϕϕπε∞=⋅+⋅=+⎰⎰⎰21122002d 44R rQ Q Q r rR πεπε+=+⎰12021()4Q Q r R πε=+在I 区,1rR <,12121123()d d d R R rR R r E l E l E l ϕ∞=⋅+⋅+⋅⎰⎰⎰122101210()()4Q Q R R R ϕπε=+=+6.10 半径为R 的无限长圆柱体均匀带电,电荷密度为ρ,求场强和电势的分布(参考点选在该圆柱面上).解 由于均匀带电圆柱体无限长,电荷分布对圆柱轴线轴对称;所以电场线在垂直于圆柱轴线的平面内,为过圆柱轴线的放射状半直线.用以圆柱轴线为轴,两底面与圆柱轴线垂直的闭合圆柱面为高斯面,如题解图 6.10.高斯面的两底面半径为r ,与E 平行,E 通量为零;圆柱侧面长度为l ,与E 正交,E通量2rlE ϕπ=.在带电圆柱体内部,rR <,由高斯定理可得2110d 2r l E S rlE πρπε⋅==⎰⎰所以102rE ρε=.在带电圆柱体外部,r R >,由高斯定理可得 题解图6.102220d 2R lE S rlE πρπε⋅==⎰⎰因此2202R E rρε=.圆柱带正电时,E 沿半径方向向外;圆柱带负电时,E沿半径方向指向轴线.参考点选在带电圆柱的圆柱面上,积分路径沿半径方向,沿电场线积分.在带电圆柱体内部,r R <,电势为22100d d ()24RR rr r E l r R r ρρϕεε=⋅==-⎰⎰在带电圆柱体内部,rR >,电势为22200d d ln 22RR rr R R RE l r r r ρρϕεε=⋅==⎰⎰6.11 如题图 6.11所示,三块平行放置的金属板A 、B 、C ,面积均为S .B 、C 板接地,A 板带电量Q ,其厚度可忽略不计.设A 、B 板间距为l ,B 、C 板间距为d .因d 很小,各金属板可视为无穷大平面.试求:(1)B 、C 板上的感应电荷;(2)空间的场强及电势分布. 题图6.11解 因d 很小,各金属板可视为无穷大平面,所以除边缘部分外,可认为E沿Oz 方向,z 相同处E 的大小相同,即()z E E z k =.(1)设B 、C 表面的面电荷密度为1σ、2σ、3σ、4σ如题解图6.11所示.由于B 、C 板接地,故B 、C 板电势与无穷远相同,电势均为零.若B 、C 板外表面带有电荷,必有电场线连接板外表面与无穷远,则B 、C 板电势与无穷远不同,因此可知B 、C 板外表面不带电荷,即140σσ==.作高斯面为闭合圆柱面如题解图 6.11,两底面在B 、C 板内部、与Oz 垂直,侧面与Oz 平行,由高斯定理2301d 0()Q E S Sσσε⋅==++⎰⎰ 即23QSσσ+=-(1) 根据叠加原理,Ⅰ区E为五个无穷大带电平面产生的场强的叠加,即 题解图6.1133221000000000022222222z Q S Q S E σσσσεεεεεεεε=+---=--同理,Ⅱ区电场强度322000222z Q S E σσεεε=+-因为A 、B 间的电压AB U 与A 、C 板的电压AC U 相等,12()z z E l E d l -=-3322000000()()()222222Q S Q S l d l σσσσεεεεεε---=+-- 即232Q d lS dσσ--=-(2)联立求解(1)(2)式得:2d l Q d S σ-=-,3l Qd Sσ=-.所以B 、C 板内表面分别带电22d l Q S Q d σ-=⋅=-,33lQ S Q dσ=⋅=- (2) 321000222z Q S E σσεεε=--0001()222d l l Q d d S εεε-=--+0()d l QdSε-=-111d d zzE l E l ϕ=⋅=-⋅⎰⎰0()d l Qz dSε-=322000222z Q S E σσεεε=+-0001()222d l l Q d d S εεε-=-++0lQdSε=211d d dd zz E l E l ϕ=⋅=⋅⎰⎰ 0()lQ d z dSε=-6.12 点电荷q 放在电中性导体球壳的中心,壳的内外半径分别为1R 和2R ,如题图6.12所示.求场强和电势的分布.解 由于电荷q 位于球心O ,导体球壳对球心O 具有球对称性,故感应电荷和电场的分布也对球心O 具有球对称性;可知感应电荷均匀分布在导体球壳的内外表面上;电场线为过O 点的放射状半直线,场强E沿半径方向,在到O 点的距离r 相同处,场强大小E 相等.设球壳内表面带电1Q ,外表面带电2Q .用以O 点为球心,12R r R <<为半径的球面为高斯面,根据高斯定理101d 0()E S q Q ε⋅==+⎰⎰可知1Q q =-;由于导体球壳电中性,由120Q Q +=,所以2Q q =.根据叠加原理,场强和电势分别为点电荷q 、均匀带电1Q 和2Q 的球面的场强和电势的叠加.考虑到在电荷球对称分布情况下,在电荷分布区以外的场强和电势与总电量集中在球心的点电荷的场强和电势的表达式相同.取参考点在无穷远;2rR >时,121220044q Q Q q E r r πεπε++==,1210044q Q Q qr rϕπεπε++==21R r R ≥≥时,112004q Q E r πε+== ,12100202444q Q Q qr R R ϕπεπεπε+=+=1r R <时,1204q E rπε=12100102012111()4444Q Q q qrR R r R R ϕπεπεπεπε=++=-+ 6.13 一半径为A R 的金属球A 外罩有一个同心金属球壳B ,球壳很薄,内外半径均可看成B R ,如题图 6.13所示.已知A 带电量为A Q ,B 带电量为B Q .试求:(1)A 的表面1S ,B 的内外表面2S 、3S 上的电量;(2)A 、B 球的电势(设无穷远电势为零). 题图6.13解 由于金属球A 和同心金属球壳B 对球心O 具有球对称性,故电荷和电场的分布也对球心O 具有球对称性;可知电荷均匀分布在导体球壳的内外表面上;电场线为过O 点的放射状半直线,场强E沿半径方向,在到O 点的距离r 相同处,场强大小E 相等.(1)金属球A 带电A Q 分布于A 的外表面1S ;设金属球壳B 内表面带电2Q ,外表面带电3Q ,23B Q Q Q +=.用以O 点为球心、B rR =为半径、位于球壳B 金属内部的球面为高斯面,根据高斯定理A 201d 0()E S Q Q ε⋅==+⎰⎰可知2A Q Q =-;由于23B Q Q Q +=,所以3A B Q Q Q =+.(2)根据叠加原理,电势为三个均匀带电球面产生电势的叠加,即B r R ≥区域,A 23A B10044Q Q Q Q Q r rϕπεπε+++==B r R =即为B 球的电势A BB 0B4Q Q R ϕπε+=.B A R r R >≥区域,3A 2A B200B 0B 0B1()4444Q Q Q Q Q r R R r R ϕπεπεπεπε=++=+A r R =即为A 球的电势A BA 0A B1()4Q Q R R ϕπε=+. 6.14同轴传输线是由两个很长且彼此绝缘的同轴金属直圆柱构成,如题图6.14所示.设内圆柱体的半径为1R ,外圆柱体的内半径为2R .使内圆柱带电,单位长度上的电量为η,试求内外圆柱间的电势差. 题图6.14解 由于两个同轴金属直圆柱可视为无限长、对圆柱轴线O 轴对称;所以电荷和电场的分布也对圆柱轴线O 轴对称;电场线在垂直于圆柱轴线的平面内,为过圆柱轴线的放射状半直线;场强E沿半径方向,在到轴线O 的距离r 相同处,场强大小E 相等.用以圆柱轴线为轴,两底面与圆柱轴线垂直的闭合圆柱面为高斯面.高斯面的两底面与圆柱轴线O 垂直,半径为r ,21R r R >>;两底面与E 平行,E 通量为零;圆柱侧面长度为l ,与E 正交,E通量2rlE ϕπ=.由高斯定理10d 2l E S rlE ηπε⋅==⎰⎰可得02Erηπε=.沿电场线积分,由1R 沿半径到2R ,内外圆柱间的电势差2221112001d d d ln 22R R R R R R R U E l E r r r R ηηπεπε=⋅===⎰⎰⎰。
华东理工大学《大学物理》第六章 气体动理论习题及答案

ΔT = 2ΔE m Ri M
= 2 ×1012 ×1.6 ×10 −19 0.1× 8.31× 3
= 1.28×10 −7 K
6、质量为 50.0g、温度为 180c的氮气装在容积为 10.0 升的密闭绝热容器内,容器以 v=200m/s的速率作匀速直线运动,若容器突然停止运动,其定向运动的动能全部转化为 分子热运动的动能,那么,平衡后氮气的温度和压强将各增大多少?
解:(1)Q v = ∴z =
8RT
P = nkT
πM
2πd 2 vn = 4d 2 N 0 P 3πm
M
E
E = m 6 RT M2
(2) v p =
2RT = M
2E 3m
(3) εk
=
3 2
kT
=
ME 2N A m
(其中NA为阿伏伽德罗常数)
12、一真空管的真空度为 1.33×10-3Pa,试求在 270C时单位体积的分子数及分子平均自 由程。设分子的有效直径d=3.0×10-10m。 解: n = P = 1.33 × 10 −3 = 3.22 × 1017 个 m 3
× 300
= 1.00 ×10 −8 J
3) εk转总 = NkT = 1.61×1012 ×1.38×10−23 × 300 = 6.67 ×10−9 J
4) εk总 = εk平总 + εk转总 = 1.67 ×10−8 J
39
大学物理习题册题解
5、一能量为 1012eV的宇宙射线粒子,射入一氖管中,氖管中含有氖气 0.1mol。如果宇 宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气温度升高多少度? 解:等容吸热 ΔE = m i RΔT
华理大学物理习题册六答案

即
2 x (2k 1) 200 2
x 50 (2k 1)cm
k 0,1,2
(3)振幅最大: cos 即
2 x k 200
2 x 1
x 100 k
46
(k 0,1,2 )
大学物理上习题册参考解答
y 11、 一列波长为λ 的平面简谐波沿 x 轴的正方向传播, 已 知 x=λ /2 处质点的振动方程为 y =Acosω t。 (1)求该平面简谐波的方程; (2)若在 x=3λ /4 的 P 点处放一如图所示的反射面,求
A 0.20 (m)
u 2.5m / s
x )] 2.5 2.5 2
2.5 1.25 1 s 2
u 2 .5 2 (m) 1.25
(2) y 0.20 cos(2.5t L) L 根据旋转矢量图可知,只有反相的各点才能速度相等而方向相反
x 25 m 处的振动方程
v y 2 10 2 sin[ t ] 2 2 a y t 1 2 10 2 ( ) 2 cos[ t ] 0 2 2
v(1) 102 m s
(2)根据波动方程
x y 2 10 2 cos[ (3 ) ] 2 10 2 cos[ x ] 2 5 2 10 y0 x (2k 1) 10 2 3 x 10 (k ) k 0,1,2 2
A 0. 2 2 x cos t 比较可得 T
u
47 m / s T
(2)相邻节点间距离 (3) v
0. 2 ( m ) 2 16
dy 15 cos 16 x sin 750 t dt
华理大物答案

第六章 气体动理论1. 水银气压计中混进了一个气泡,因此它的读数比实际气体小些,当精确的气压计的水银柱为0.768m 时,它的水银柱只有0.748m 高,此时管中水银面到管顶距离为0.08m ,试问此气压计的水银柱为0.734m 高时,实际的气压是多少?(把空气当作理想气体,并设温度不变)。
解:设第一次测得的空气泡的压强和体积汞汞汞(d 02.0d )748.0768.0hd P 1=-=∆= s 08.0V 1=(s 为截面积)第二次测得空气泡的压强和体积s 094.0s )08.0734.0748.0(V 2=+-=汞汞d 017.0s 094.0s 08.0d 02.0V V P P 2112=⨯== 实际压强 )Pa (10999.01033.1751.0d 017.0d 734.0'P 552⨯=⨯⨯=+=汞汞2、可用下面方法测定气体的摩尔质量。
先在容积为V 的容器内装入被测量的气体,测出其压强为P 1,温度为T ,并称出容器连同气体的质量为m 1。
然后放掉一部分气体,这时压强降到P 2,再称出容器连同气体的质量为m 2,假定温度保持不变,试求该气体的摩尔质量。
解:设容器的质量为m开始时)1(T V P R M m m 11=- 放气后 )2(TV P R M m m 22=- 解得 2121P P m m V RT M --⋅=3、某容器内分子数密度为1026m -3,每个分子的质量为3×10-27kg ,设其中1/6分子数以速率v=200ms -1垂直地向容器的一壁运动,而其余5/6分子或者离开此壁,或者平行此壁方向运动,且分子与容器壁的碰撞为完全弹性。
问:(1)每个分子作用于器壁 的冲量为多少?(2)每秒碰在器壁单位面积上的分子数n 0为多少?(3)作用在器壁上的压强为多少?解:(1) 2427102.12001032v 2P I --⨯=⨯⨯⨯=μ=∆=(kg m/s )(2) s m 10316110200vn 61n 228260⋅⨯=⨯⨯==个 (3) Pa 104102.11031P n P 324280⨯=⨯⨯⨯=∆⋅=-4、有一容积为10cm 3的电子管,当温度为300k 的时候,用真空泵把管内空气抽成压强为5×10-6mmHg 的高真空,问此时管内有多少个空气分子?此空气分子的平均平动动能的总和是多少?平均转动动能的总和是多少?平动动能的总和是多少?(1mmHg=133.3Pa 空气分子可认为是刚性双原子分子)解:由理想气体状态方程RT PV ν=知空气的摩尔数RTPV =ν 1)个122366A A 1061.13001038.1101032.133105kT PV N RT PV N N ⨯=⨯⨯⨯⨯⨯⨯===ν=--- 2)J 1000.13001038.1231061.1kT 23N 82312k --⨯=⨯⨯⨯⨯⨯==ε平总 3)J 1067.63001038.11061.1NkT 92312k --⨯=⨯⨯⨯⨯==ε转总4)J 1067.18k k k -⨯=ε+ε=ε转总平总总5、一能量为1012eV 的宇宙射线粒子,射入一氖管中,氖管中含有氖气0.1mol 。
大学物理第六章静电场习题答案

大学物理第六章静电场习题答案(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第六章静电场习题6-1 电量都是q的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)(2)这种平衡与三角形的边长有无关系?解:(1)如图任选一点电荷为研究对象,分析其受力有1230F F F F=++=合y轴方向有()()21322232cos242433304q qQF F Fa aqq Qaθπεπεπε=+=+=+=合得33Q q=-(2)这种平衡与三角形的边长无关。
6-2 两小球的质量都是m,都用长为l的细绳挂在同一点,它们带有相同电量,静止时两线夹角为2θ,如图所示。
设小球的半径和线的质量都可以忽略不计,求每个小球所带的电量。
解:对其中任一小球受力分析如图所示,有⎪⎩⎪⎨⎧===22)sin2(π41sincosθεθθlqFTmgTe解得θπεθtan4sin2mglq=6-3 在氯化铯晶体中,一价氯离子Cl-与其最邻近的八个一价铯离子Cs+构成如图所示的立方晶格结构。
(1)求氯离子所受的库仑力;(2)假设图中箭头所指处缺少一个铯离子(称作晶格缺陷),求此时氯离子所受的库仑力。
(1)由对称性可知F1= 0(2)2912222001.9210N43q q eFr aπεπε-===⨯方向如图所示6-4 长l= cm的直导线AB上均匀地分布着线密度95.010C mλ-=⨯的正电荷。
试求:(1)在导线的延长线上与导线B端相距15.0cma=处P点的场强;(2)在导线的垂直平分线上与导线中点相距25.0d cm=处Q点的场强。
解:(1)如图所示,在带电直线上取线元x d,其上电量q d在P点产生场强为20)(d π41d x a xE P -=λε2220)(d π4d x a x E E llP P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l -=ελ 用15=l cm ,9100.5-⨯=λ1m C -⋅,5.12=a cm 代入得21074.6⨯=P E 1C N -⋅ 方向水平向右(2)同理 2220d d π41d +=x xE Q λε 方向如图所示由于对称性可知⎰=l Qx E 0d ,即Q E只有y 分量22222220dd d d π41d ++=x x x E Qyλε22π4d d ελ⎰==lQyQy E E ⎰-+2223222)d (d l l x x2220d 4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Q y Q E E 1C N -⋅ 方向沿y 轴正向*6-5 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量。
大学物理第六章课后习题答案

第六章静电场中的导体与电介质6 —1将一个带正电的带电体A从远处移到一个不带电的导体B附近,则导体B的电势将()(A)升高(B)降低(C)不会发生变化(D)无法确定分析与解不带电的导体B相对无穷远处为零电势。
由于带正电的带电体A移到不带电的导体B附近时,在导体B的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A)。
6 —2 将一带负电的物体M靠近一不带电的导体N,在N的左端感应出正电荷,右端感应出负电荷。
若将导体N的左端接地(如图所示),则()(B)N上的正电荷入地(A )N上的负电荷入地(C)N上的所有电荷入地地(D)N上所有的感应电荷入题6-2图分析与解导体N接地表明导体N为零电势,即与无穷远处等电势,这与导体N在哪一端接地无关。
因而正确答案为( A )。
6 —3如图所示将一个电量为q的点电荷放在一个半径为R的不带电的导体球附近,点电荷距导体球球心为d,参见附图。
设无穷远处为零电势,则在导体球球心0点有()(A)E =0,V —4 n^d(B)E J,V L4 n%d 4 n %d (C)E = 0,V = 0题6-3图分析与解 达到静电平衡时导体内处处各点电场强度为零。
点电荷 q 在导 体球表面感应等量异号的感应电荷土 q',导体球表面的感应电荷土 q'在球心 0点激发的电势为零,0点的电势等于点电荷q 在该处激发的电势。
因而正 确答案为(A )。
6 -4根据电介质中的高斯定理,在电介质中电位移矢量沿任意一个闭合 曲面的积分等于这个曲面所包围自由电荷的代数和。
下列推论正确的是()(A )若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内一定没有 自由电荷 (B)若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内电荷的代 数和一定等于零 (C) 若电位移矢量沿任意一个闭合曲面的积分不等于零,曲面内一定有 极化电荷 (D) 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 (E)介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零,表明曲面内自由电荷的代数和等于零; 由于电介质会改变自由电荷的空间分布, 介质 中的电位移矢量与自由电荷与位移电荷的分布有关。
华南理工大学大学物理各章节习题及答案汇编
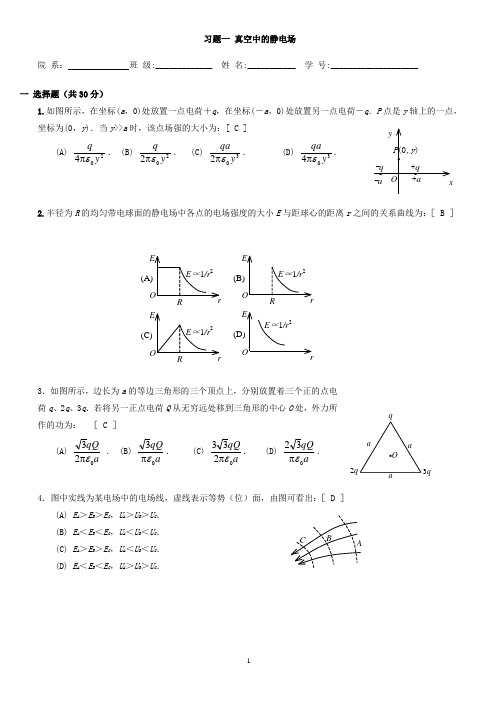
习题一 真空中的静电场院 系: 班 级:_____________ 姓 名:___________ 学 号:____________________一 选择题(共30分)1.如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是y 轴上的一点,坐标为(0,y ).当y >>a 时,该点场强的大小为:[ C ] (A)204y q επ. (B)202y q επ. (C)302y qa επ. (D) 304yqa επ.2.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为:[ B ]3.如图所示,边长为a 的等边三角形的三个顶点上,分别放置着三个正的点电荷q 、2q 、3q .若将另一正点电荷Q 从无穷远处移到三角形的中心O 处,外力所作的功为: [ C ](A) a qQ 023επ . (B) a qQ 03επ. (C) a qQ 0233επ. (D) aqQ 032επ.4.图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:[ D ] (A) E A >E B >E C ,U A >U B >U C . (B) E A <E B <E C ,U A <U B <U C . (C) E A >E B >E C ,U A <U B <U C . (D) E A <E B <E C ,U A >U B >U C .E Or(D) E ∝1/r 23q2q5.半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为: [ B ]6.在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为: (A)2012a Q επ. (B) 206a Q επ. (C) 203a Q επ. (D) 20aQεπ. [C ]7.图示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的. (A) 半径为R 的均匀带电球面. [ B ](B) 半径为R 的均匀带电球体.(C) 半径为R 的、电荷体密度为=A r (A 为常数)的非均匀带电球体. (D) 半径为R 的、电荷体密度为=A/r (A 为常数)的非均匀带电球体.8.选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302r U R . (B) R U 0. (C) 20r RU . (D) r U 0. [ C ]9. 设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负):[C ]10. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的:(A) 2倍. (B) 22倍. (C) 4倍. (D) 42倍. [ B ]E O rE ∝1/rE Or(D) E ∝1/rR E Or(C) E ∝1/rE Or(A) E ∝1/rO R rE E ∝1/r 2OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x11.如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd的电场强度通量等于:(A) 06εq . (B) 012εq . (C) 024εq . (D) 048εq. [ C ]二 填空题1.电荷分别为q 1,q 2,q 3的三个点电荷分别位于同一圆周的三个点上,如图所示.设无穷远处为电势零点,圆半径为R ,则b 点处的电势U =___________ . ()32102281q q q R++πε2.图中所示以O 为心的各圆弧为静电场的等势(位)线图,已知U 1<U 2<U 3,在图上画出a 、b 两点的电场强度的方向,并比较它们的大小.E a = E b (填<、=、>).3.两根相互平行的“无限长”均匀带正电直线1、2,相距为d ,其电荷线密度分别为λ1和λ2如图所示,则场强等于零的点与直线1的距离a 为_____________ .d 211λλλ+4.如图所示,两同心带电球面,内球面半径为r 1=5 cm ,带电荷q 1=3×10-8C ;外球面半径为r 2=20 cm , 带电荷q 2=-6×108C ,设无穷远处电势为零,则空间另一电势为零的球面半径r = __________________.10 cm5.已知某静电场的电势函数U =a ( x 2+ y ),式中a 为一常量,则电场中任意点的电场强度分量E x =-2ax ,E y = -a ,E z = 0.6.如图所示.试验电荷q ,在点电荷+Q 产生的电场中,沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为 0 ;从d 点移到无穷远处的过程中,电场力作功为qQ / (4πε0R ).7.一个带电荷q 、半径为R 的金属球壳,壳内是真空,壳外是介电常量为ε 的无限大各向同性均匀电介质,则此球壳的电势U =________________.Rqεπ48.在点电荷q 的电场中,把一个-1.0×10-9C 的电荷,从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处,克服电场力作功 1.8×10-5 J ,则该点电荷q =-2×10-7库伦.(真空介电常量0=8.85×10-12C 2·N -1·m -2)A b caq2 q 1 q 3OOU 1U 2U 3abλ2a d 12q 1 q 2 r 1r 2+Q R q d∞三 计算题1.厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为σ.试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差.解:选坐标如图.由高斯定理,平板内、外的场强分布为:E = 0 (板内) )2/(0εσ±=x E (板外)1、2两点间电势差⎰=-2121d x E U U x x x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ )(20a b -=εσ 2.一环形薄片由细绳悬吊着,环的外半径为R ,内半径为R /2,并有电荷Q 均匀分布在环面上.细绳长3R ,也有电荷Q 均匀分布在绳上,如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上).解:先计算细绳上的电荷在O 点产生的场强.选细绳顶端作坐标原点O ,x 轴向下为正.在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412RQx R dx R Q E R εεπ=-π=⎰ 圆环上的电荷分布对环心对称,它在环心处的场强E 2=0由此,合场强 i R Qi E E20116επ== 方向竖直向下.3.电荷Q (Q >0)均匀分布在长为L 的细棒上,在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q >0 )的点电荷,求带电细棒对该点电荷的静电力. 解:沿棒方向取坐标Ox ,原点O 在棒中心处.求P 点场强: ()()20204d 4d d x a xx a q E -π=-π=ελε 3分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 4分 方向沿x 轴正向. 点电荷受力:==qE F ()2204πL a qQ-ε 方向沿x 轴正方向. 3分1σda1σd abxOO R 3RR /2E 1xR3R x xOPL+Q OaP O L/2L/2d x d q a。
大学物理6章习题课简
后在两极板间充满某种各向同性、均匀电介质,则电
场强度的大小E、电容C、电压U、电场能量W四个量
各自与充入介质前相比较,增大(↑)或减小(↓)的情形为
(A) E↑,C↑,U↑,W↑.
(B) E↓,C↑,U↓,W↓.
(C) E↓,C↑,U↑,W↓.
(D) E↑,C↓,U↓,W↑.
[ B]
例 一空气电容器充电后切断电源,电容器
例 A、B两个导体球,半径之比为2:1, A球带正电Q,B球不带电. 若使两球接触后 再分离,当两球相距为R时,求两球间的静 电力(设R远大于两球半径).
Q
A
B
解 两球接触后电势相等,电荷重新分配 .
由 VA VB 即 得 qA rA 2
qB rB
qA qB
4π 0rA 4π 0rB 又 qA qB Q
R U r0 E0 ln r0
R U r0 E0 ln r0
dU /d r0 E0 ln(R / r0 ) E0 0
显然有
dБайду номын сангаас U dr2 0
0
r0 R / e
故当 r0 R / e 时电容器可承受最高的电压.
U RE / e 147KV
max
0
O R1 R2
r
解:设导体球带电q,取无穷远处为电势零点,则
导体球电势:
U0
q
4 0r
QQ1 1qQ2
O R1 R2
q
r
内球壳电势:
U1
Q1 q
4 0 R1
Q2
4 0 R2
二者等电势,即 q Q1 q Q2 4 0 r 4 0 R1 4 0 R2
解得
q r(R2Q1 R1Q2 ) R2 (R1 r)
物理化学第六章练习学习习题

第六章化学动力学(三)计算题1.293K时,敌敌畏在酸性介质中水解反响的速率常数为0.01127d-1。
若敌敌畏水解为一级反响,试求其水解反响的半衰期。
解:t1/2=ln2/k=0.6931/0.01127d-1=61.5d2.某人工放射性元素放出a粒子的半衰期为15h。
求该试样分解速率常数和分解 80%所需的时间。
解:放射性元素分解为一级反响,k=ln2/t1/2=0.6931/15h=0.04621h-1t=-ln(1-x)/k=-ln(1-0.8)/0.04621h-1=34.83h二级反响规律某溶液含有NaOH和CH3CO2C2H5,浓度均为0.0100mol·dm-3。
在308.2K时,反响经600s后有55.0% 的分解。
已知该皂化反响为二级反响。
在该温下,计算:反响速率常数?1200s能分解多少?分解50.0%的时间?解:(1)反响为NaOH+CH3CO2C2H5→CH3CO2Na+C2H5 OH该反响为二级且初浓度相同,故有dcA/dt=kcA2,cA=cA0(1-x),积分后得k=(1/t)(1/cA-1/cA0)=x/tcA0(1-x)=0.550/[600s×0.0100mol·dm-3×(1-0.550)]=0.204dm3·mol-1·s-1x=1/(1+1/ktc A0)=1/[1+1/(0.204dm3·mol-1·s-1×1200s×0.0100mol·dm-3)]0.710=71.0%t1/2=1/kc A0=1/(0.204dm3·mol-1·s-1×0.0100mol·dm-3)=490s4.溶液反响A+2B→2C+2D的速率方程为dc B/dt=kc A c B。
20℃下,反响开始时只有两反响物,其初浓度分别为0.01mol·dm-3和0.02mol·dm-3,反响26h后,测定c B=0.01562mol·dm-3,试求k。
大学物理课后习题答案第六章-大学物理第六章

第6章 真空中的静电场 习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷0q 位于点电荷q +的右侧,它受到的合力才可能为0,所以200200)1(π4)1(π42-=+x qq x qq εε故 223+=x2. 电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解:(1) 以A 处点电荷为研究对象,由力平衡知,q '为负电荷,所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。
3. 如图所示,半径为R 、电荷线密度为1λ的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dl dq 1λ=,dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε根据电荷分布的对称性知,0==z y E E23220)(41cos R x xdqdE dE x +==πεθR Oλ1λ2lxy z式中:θ为dq 到场点的连线与x 轴负向的夹角。
⎰+=23220)(4dq R x xE x πε232210)(24R x Rx+⋅=πλπε232201)(2R x xR +=ελ下面求直线段受到的电场力。
在直线段上取dx dq 2λ=,dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ 方向沿x 轴正方向。
大学物理第六章习题解答和分析

6-1频率为Hz 41025.1⨯=ν的平面简谐纵波沿细长的金属棒传播,棒的弹性模量211/1090.1m N E ⨯=,棒的密度33/106.7m Kg ⨯=ρ.求该纵波的波长.分析 纵波在固体中传播,波速由弹性模量与密度决定。
解:波速ρ/E u =,波长νλ/u =0.4m λ==6-2一横波在沿绳子传播时的波方程为:))(5.2cos(04.0SI x t y ππ-= (1)求波的振幅、波速、频率及波长; (2)求绳上的质点振动时的最大速度;(3)分别画出t=1s 和t=2s 的波形,并指出波峰和波谷.画出x=1.0m 处的质点的振动曲线并讨论其与波形图的不同.分析 与标准方程比较即可确定其特征参量。
解:(1)用比较法,由)2cos()5.2cos(04.0x t A x t y λπϕωππ-+=-=得0.04A m = /2 2.5/2 1.25Hz νωπππ=== 2, 2.0m ππλλ== 2.5/u m s λν== (2)0.314/m A m s νω==(3)t=1(s)时波形方程为:)5.2cos(04.01x y ππ-= t=2(s)时波形方程为:)5cos(04.02x y ππ-= x=1(m)处的振动方程为:)5.2cos(04.0ππ-=t y6-3 一简谐波沿x 轴正方向传播,t=T/4时的波形图如题图6-3所示虚线,若各点的振动以余弦函数表示,且各点的振动初相取值区间为(-π,π].求各点的初相.题图6-2分析 由t=T/4时的波形图(图中虚线)和波的传播方向,作出t=0时的波形图。
依旋转矢量法可求t=0时的各点的相位。
解:由t=T/4时的波形图(图中虚线)和波的传播方向,作出 t=0时的波形图(图中实线),依旋转矢量法可知 质点1的初相为π; 质点2的初相为π/2; 质点3的初相为0; 质点4的初相为-π/2.6-4 有一平面谐波在空间传播,如题图6-4所示.已知A 点的振动规律为)t cos(A y ϕ+ω=,就图中给出的四种坐标,分别写出它们波的表达式.并说明这四个表达式中在描写距A 点为b 处的质点的振动规律是否一样?分析 无论何种情况,只需求出任意点x 与已知点的相位差,同时结合相对坐标的传播方向(只考虑相对于坐标方向的正负关系)即可求解波的表达。
华理大学物理第6章习题课

【填空题5】
vp
Nf v dv
vf v dv
v0
f v dv
v0
f v dv
v0
【填空题6】一容器内装有气体,n,T,平衡态下 分子与器壁发生完全弹性碰撞。若碰撞时有20%的 分子被吸收,则此时的压强变为 ?
p nkT =0.8nkT 0.2nkT p nkT =0.8nkT 0.1nkT =0.9nkT
E 4 E0
(4)气体单位体积内的内能变为原来的几倍?
E E0
V 2 V0
【计算题7】N个同种分子,在温度T1(Ⅰ曲线)和T2
(II曲线) (T1>T2)时,麦克斯韦速率分布情况如图
所示。若图中阴影面积为A,则在T1、T2时气体中分子
的运动速率小于V0的分子数之差为多少?对应于曲线Ⅱ f (v) 的最概然速率VP为多少?
第六章 气体动理论
m 理想气体状态 PV RT 方程: M 理想气体的压强
分压定律: P P 1 P 2
统 计 规 律
理想气体的温度:
2 P 3
k
i 能量按自由度均分 kT 多原子分子:i =6 2 原理: i m i 理想气体的内能: E N ( kT ) RT 2 M 2 分子速率分布函数 d N f ( v )dv 3 N v 2 2 f v d v 1 2
v 0 2v
(3)求全部粒子的平均速率
a v v0
v v0 v0 v 2v0 v 2v0
0 a a d v 1 vdv v 2 a v 0 v v0 0 0
1 1 S a2v0 1 a v0 2
华理大学物理第6章气体动理论3

占据势能较低的状态。
平衡态下温度为 T 的气体中,位置在 x~x+dx, y~y+dy, z~z+dz 中, 且速度在 vx ~ vx+dvx , vy ~
vy+dvy ,vz ~ vz+dvz 区间的分子数为 dN (r ,v ) Ce /kT dv x dvydv z dxdydz
式中 =k+p 是分子的总能量, C 是与位置坐标
( p dp)S gSdh pS 0
dp gdh
dp n gdh p dp
平衡态下气体的温度处处 相同,气体的压强为
p nkT dp kTdn
h+dh
dh
h
p (非均匀的稳定分布)
kTdn n gdh
dn g dh
n kT
n
n dn h g dh
n n0 0 kT
T2 T1
gh
n n0e kT
T1
T2
O
h
在重力场中,粒子数密度随高度增大而减小, 越
大,n 减小越迅速;T 越高,n 减小越缓慢。
gh
gh
p nkT n0kTe kT p0e kT (等温气压公式)
式中 p0 是高度为零处的压强。
二、玻耳兹曼分布律
gh
n n0e kT
p gh
快
M
4.分子间平均碰撞次数:z 2nv d 2 5.85 10 9 s 1 乱
(其中:d 3.281010 m)
解:按气体分子算术平均速率公式 算得
v 8RT
M
v
8RT =
M
88.31 273 3.14 2103
m
/
s
华南理工大学大学物理习题答案

上册习题一一、选择题1.C ; 2.D ; 3.B ,B ; 4.D ; 5.D 。
二、填空题1.答案:(1)12a gτ=-;(2)2ρ2.答案:(1)48i j - ;(2)2j - ;(3)224x y =-。
3.答案:(1)20()v bt a n b R τ-=- ;(2)224v s n R Rb ππ∆== 4.答案:01012020cos sin cos sin tg v v tg θθθθθθ+=+5.答案:(1)2230.4m/s n a =;(2)24.8m/s a τ=;(3)2.67rad三、计算题1.答案:(1)2002a v a t t τ=+;(2)2300126a x a t t τ=+ 2.答案:11n -。
3.答案:2203x h a v s =-;0x v v s =-4. 答案:(1)2109m s a -=⋅,与法向成12.4角;(2)m 1722=s 。
5.答案:20v x yud =,即运动轨迹为抛物线。
习题二一、选择题 1.A ; 2.B ; 3.B ; 4.D ,C ; 5.B 。
二、填空题1.答案:64.2310J ⨯。
2.答案:()kt m F dt x d -=1022;⎪⎭⎫ ⎝⎛-+=20021kt t m F v v ;⎪⎭⎫ ⎝⎛-+=3200312kt t m F t v x 。
3.答案:202(2)2()()mM m M v f m M l s +=++;202()Mm E v M m ∆=+。
4.答案:54N s I =⋅;27m/s v =。
5.答案:0.2。
三、计算题1.答案:(1)211 1.96m/s 5a g ==;221 1.96m/s 5a g ==;2335.88m/s 5a g ==。
(2)10.16 1.568N T g ==;20.080.784N T g ==。
2.答案:(1)5.09Km/h ;(2) 1.77Km/h -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N v2 4 e N 2 kT v vp
1 v2p N 4 2 e v N p
32
32
2 kT
v v
2
2kT
v2 p 2 p
, v 0.02v p
0.08
v 0.02v p
e 1.67%
气体的内能是2.45×10 6J,氦分子平均动能是6×1021J,求氢气质量M。(玻耳兹曼常量k=1.38×10-23
J· K-1,摩尔气体常量R=8.31J· mol-1· k-1)
1 3 2 v k T 6 1 0 21 J 2 2
mH 5 m He 3 2 E RT RT 2 . 45 10 6 M He 2 MH 2
o
v1 v2
v
1) 表示在温度为T 的平衡状态下 ,速率在v 附近单位速率区间 的分 子数占总数的百分比 . 2)表示气体分子的速率处于v附 近单位速率区间的概率。
1)速率位于v→v+dv内分子数
dN f (v) N dv
d N N f (v )d v
N
v2 v1
速率位于v1→v2区间的分子数
v 0 2v
(3)求全部粒子的平均速率
a v v0
v v0 v0 v 2v0 v 2v0
0 a a d v 1 vdv v 2 a v 0 v v0 0 0
1 1 S a2v0 1 a v0 2
v0
( 2)
v 0 v0
2 1 2 n v nk 2 3 3 kT 单原子分子:i =3 双原子分子:i =5 2
0
平均碰撞频率 平均自由程
Z 2nd v v z
2
f v 4 e 2 kT
2 kT
v
n n 0e
Ep
kT
f ( v)
物理意义
S
vp
0
1 2 v f v dv 2
(1)速率大于vp的分子数占总分子数的比例 (2)分子的平均平动动能
【填空题2】
p nkT
m NA n M V
n 1 n p nkT 1 nkT 1.92 105 Pa
【填空题3】求气体分子速率与最可然速率之差不 超过1%的分子数占全部分子的百分率为 ?
2
【计算题4】容器内储有质量为m,摩尔质量为M的理想 气体,容器以速度V作定向运动,今使容器突然停止, 问在(1)单原子分子和(2)双原子刚性分子这两种情 况下系统温度的改变和分子速度平方平均值的增量?
MV =T iR
2
1 m i 2 mV E = RT 2 M 2 3 1 2 3 2 v kT k = v kT 2 2
第六章 气体动理论
m 理想气体状态 PV RT 方程: M 理想气体的压强
分压定律: P P 1 P 2
统 计 规 律
理想气体的温度:
2 P 3
k
i 能量按自由度均分 kT 多原子分子:i =6 2 原理: i m i 理想气体的内能: E N ( kT ) RT 2 M 2 分子速率分布函数 d N f ( v )dv 3 N v 2 2 f v d v 1 2
N f ( v )dv
2)速率位于v1→v2区间的分子数占总数的百分比
3)求与速率有关的物理量
N ( v1 v 2 ) v 2 S v f ( v )d v 1 N
1)速率区间0~vp的分子数占总分子数的百分比
N VP dN f (v)dv f (v)dv N N 0
0 0
Nf 2 v d v NA Nf 2 v d v 0 V0 v0
v0
V0
f (v )
N f v dv N A
2 0
Ⅱ
A
N N A N 1 A
T2 v0 T1
Ⅰ
vp
v
T v p2
2)分子的平均速率
d N N f v d v
v d N v N f v d v
v f v dv
0
v
2
v dN v N f v dv
0
N
2
0
N
v
v f v dv
0
【例1】一瓶氦气和一瓶氮气密度相同,分子平均平动
动能相同,而且它们都处于平衡状态。则它们温度相 同?压强相同?分子数密度相同?总分子数相同?
E 4 E0
(4)气体单位体积内的内能变为原来的几倍?
E E0
V 2 V0
【计算题7】N个同种分子,在温度T1(Ⅰ曲线)和T2
(II曲线) (T1>T2)时,麦克斯韦速率分布情况如图
所示。若图中阴影面积为A,则在T1、T2时气体中分子
的运动速率小于V0的分子数之差为多少?对应于曲线Ⅱ f (v) 的最概然速率VP为多少?
【计算题2】P241 6-12 假设有N个电子组成的电子气,
其速率分布函数f(v)与v的关系如图所示。求:(1)a的
大小(用N,v0表示);(2)0—v0间粒子的平均速率;
f ( v) 解:(1) a a f v v 2a v0 v0 v 2v0 0 根据归一化条件:
Ⅱ
A f1 v d v f 2 v d v
0 v0
v0
A
0
V0 0
Ⅰ
v
v0
N 2 N 1 V V0 N f 2 v d v N f1 v d v
0
v0
N 2 N 1 V V N f 2 v d v N f 1 v d v 0
vdN
0 v0 0
v0
v Nf v d v
0 v0 0
dN
2 v0 3 Nf v d v
( 3)
v v f v d v v f ( v ) d v v f v d v v 0
2 v0 v0 0 0 v0
【计算题3】将1kg氦气和Mkg氢气混合,平衡后混合
0
0
vd N vN f v d v
0
vp
4)分子速率大于vp的分子数
N f v d v
【选择题3 】
C
NAfA(v)+NBfB(v) NA+NB
【选择题4 】
b
8RT v M z 2 d nv
2
1 2 d 2 n
【填空题1】
f v dv
0
v0
2 V i 3 2 2 2 3 3k MV 3V kMN A 3V 2 v k T 3 2 iR i RN A i V i5 5
【计算题6】一定质量的某种理想气体,先经过等容过程 使其热力学温度增高为原来的4倍,再经过等温过程使其 体积膨胀为原来的2倍,则经此过程后: (1)分子的平均碰撞的频率变为原来的几倍?
【计算题1】氢分子的质量为3.3×10-24 g,如果每秒有 约1023 个氢分子沿着与容器器壁的法线成45°角的方 向以105 cm/s的速率撞击在2.0cm2 面积上(碰撞是完 全弹性的),则此氢气的压强为多少? 解:一个分子撞击给予器壁的冲量
Ii 2μ v x 2μ v cos 45
每秒钟内分子给予器壁的总冲量
45
I N 2 μ v c o s 4 5 ( F Δ t)
F
3
F N 2 μ v cos 4 5 P S S
2 2 3.3 10 10 10 23 3 2 2.33 10 Pa 4 2.0 10
27
【填空题5】
vp
Nf v dv
vf v dv
v0
f v dv
v0
f v dv
v0
【填空题6】一容器内装有气体,n,T,平衡态下 分子与器壁发生完全弹性碰撞。若碰撞时有20%的 分子被吸收,则此时的压强变为 ?
p nkT =0.8nkT 0.2nkT p nkT =0.8nkT 0.1nkT =0.9nkT
答:(1)T1=T2
( 2) P 1
k
3 kT 2
P2
1
( 3) n
n
2
2 P nk 3 m PM m ( PV RT ) V RT M
(4)不一定相同
P1M
1
P2M
2
m N nV n
【选择题1 】
2H2O 2H2 O2
6 5 E0 2 RT E 3 RT 2 2 15 3 E RT 6 RT RT 2 2 3 RT E 1 2 E0 6 RT 4
【选择题2】已知总分子数N,f(v)为速率分布函数,
则下列表示式是否正确?
N 1)速率在v1—v2之间的分子数 f v dv v1 N
v2
多次观察某一分子,发现其速率处在v1—v2之间的概率
2)最概然速率vp是分子速率的最大值。
3)在整个速率范围内分子速率的总和 v f v d v v
1
【填空题4】一容器内盛有密度为ρ的单原子理想气 体,其压强为p,此气体分子的方均根速率为 单位体积内气体的内能是 ? ?
m RT RT p M V MBiblioteka 3RT 3p v M
