大学概率论习题二详解
概率论与数理统计浙大第四版答案 第二章

概率论与数理统计习题二参考答案1、将一颗骰子抛掷两次,以X 1表示两次所得点数之和,以X 2表示两次得到的点数的最小者,试分别求X 1和X 2的分布律。
解:X 1可取2、3、4、5、6、7、8、9、10、11、123616161)1,1()2(1=×===P X P36261616161)"1,2""2,1(")3(1=×+×=∪==P X P 363616161616161)"1,3""2,2""3,1(")4(1=×+×+×=∪∪==P X P …… 所以X 1的分布律为X 1 2 3 4 5 6 7 8 9 10 11 12 P k 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36 X 2可取的数有1、2、3、4、5、6P (X 2=1)=P ()="1,6""1,5""1,4""1,3""1,2""6,1""5,1""4,1""3,1""2,1""1,1"∪∪∪∪∪∪∪∪∪∪3611所以X 2的分布律为 X 2 1 2 3 4 5 6 P k 11/36 9/36 7/36 5/36 3/36 1/36 2、10只产品中有2只是次品,从中随机地抽取3只,以X 表示取出次品的只数,求X 的分布律。
解:X 可取0、1、2{}310380C C X P ==157={}15713102812===C C C X P {}15123101822===C C C X P3、进行重复独立试验。
概率论第二章习题答案

概率论第二章习题答案习题1:离散型随机变量及其分布律设随机变量X表示掷一枚公正的六面骰子得到的点数。
求X的分布律。
解答:随机变量X的可能取值为1, 2, 3, 4, 5, 6。
由于骰子是公正的,每个面出现的概率都是1/6。
因此,X的分布律为:\[ P(X=k) = \frac{1}{6}, \quad k = 1, 2, 3, 4, 5, 6 \]习题2:连续型随机变量及其概率密度函数设随机变量Y表示从标准正态分布中抽取的数值。
求Y的概率密度函数。
解答:标准正态分布的概率密度函数为高斯函数,其形式为:\[ f(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}, \quad -\infty < y < \infty \]习题3:随机变量的期望值已知随机变量X的分布律为:\[ P(X=k) = p_k, \quad k = 1, 2, ..., n \]求X的期望值E(X)。
解答:随机变量X的期望值定义为:\[ E(X) = \sum_{k=1}^{n} k \cdot p_k \]习题4:随机变量的方差继续使用习题3中的随机变量X,求X的方差Var(X)。
解答:随机变量X的方差定义为期望值的平方与每个值乘以其概率之和的差:\[ Var(X) = E(X^2) - (E(X))^2 \]其中,\( E(X^2) = \sum_{k=1}^{n} k^2 \cdot p_k \)习题5:二项分布设随机变量X表示n次独立伯努利试验中成功的次数,每次试验成功的概率为p。
求X的分布律和期望值。
解答:X服从参数为n和p的二项分布。
其分布律为:\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, ..., n \]X的期望值为:\[ E(X) = np \]结束语:以上是概率论第二章的一些典型习题及其解答。
概率论第二章习题及答案

三、一些常用的离散型随机变量
1) Bernoulli分布 如果随机变量 X 的分布律为
PX 0 1 p q , PX 1 p
或
P{ X k } p q
X P
k 1 k
(k 0 , 1)
1 p
0 1-p
则称随机变量 X 服从参数为 p 的 Bernoulli分布. 记作 X ~ B1 , p . 其中0 p 1 为参数
第二章 随机变量及其分布
一、 随机变量的定义
设E是一个随机试验,S是其样本空间.若对每一个
S , 都有唯一确定的一个实 数X 与之对应 , 则称
X 为一个随机变量.
S
X
R
第二章 习题课
二、离散型随机变量的分布律
设离散型随机变量 X 的所有可能取值为 x1 , x2 , , xk , 并设
如果连续型随机变量X 的密度函数为 (I)
1 2 2 x f x e 2 其中 , 0 为参数, 则称随机变量X 服从参数为 , 2 的
正态分布.记作
f (x)
x 2
X ~ N ,
2
0
第二章 随机变量及其分布
4)几 何 分 布
若随机变量 X 的分布律为
PX k q k 1 p
k 1, 2,
其中 p 0,q 0,p q 1
则称随机变量 X 服从参数为 p的几何分布.
返回主目录
第二章 随机变量及其分布
5)超 几 何 分 布
如果随机变量 X 的分布律为
x
f ( t )dt,
概率论与数理统计(第三版)课后答案习题2

第二章 随机变量2.1 X 2 3 4 5 6 7 8 9 10 11 12 P 1/361/181/121/95/361/65/361/91/121/181/362.2解:根据1)(0==∑∞=k k XP ,得10=∑∞=-k kae,即1111=---eae 。
故 1-=e a2.3解:用X 表示甲在两次投篮中所投中的次数,X~B(2,0.7) 用Y 表示乙在两次投篮中所投中的次数, Y~B(2,0.4) (1) 两人投中的次数相同P{X=Y}= P{X=0,Y=0}+ P{X=1,Y=1} +P{X=2,Y=2}=1122020*********2222220.70.30.40.60.70.30.40.60.70.30.40.60.3124C C C C C C ⨯+⨯+⨯=(2)甲比乙投中的次数多P{X >Y}= P{X=1,Y=0}+ P{X=2,Y=0} +P{X=2,Y=1}=12211102200220112222220.70.30.40.60.70.30.40.60.70.30.40.60.5628C C C C C C ⨯+⨯+⨯=2.4解:(1)P{1≤X ≤3}= P{X=1}+ P{X=2}+ P{X=3}=12321515155++= (2) P {0.5<X<2.5}=P{X=1}+ P{X=2}=12115155+= 2.5解:(1)P{X=2,4,6,…}=246211112222k +++=11[1()]1441314k k lim→∞-=-(2)P{X ≥3}=1―P{X <3}=1―P{X=1}- P{X=2}=1111244--=2.6解:设i A 表示第i 次取出的是次品,X 的所有可能取值为0,1,212341213124123{0}{}()(|)(|)(|)P X P A A A A P A P A A P A A A P A A A A ====18171615122019181719⨯⨯⨯= 1123412342341234{1}{}{}{}{}2181716182171618182161817162322019181720191817201918172019181795P X P A A A A P A A A A P A A A A P A A A A ==+++=⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=12323{2}1{0}{1}1199595P X P X P X ==-=-==--=2.7解:(1)设X 表示4次独立试验中A 发生的次数,则X~B(4,0.4)34314044(3)(3)(4)0.40.60.40.60.1792P X P X P X C C ≥==+==+=(2)设Y 表示5次独立试验中A 发生的次数,则Y~B(5,0.4)345324150555(3)(3)(4)(5)0.40.60.40.60.40.60.31744P X P X P X P X C C C ≥==+=+==++=2.8 (1)X ~P(λ)=P(0.5×3)= P(1.5)0 1.51.5{0}0!P X e -=== 1.5e -(2)X ~P(λ)=P(0.5×4)= P(2)0122222{2}1{0}{1}1130!1!P X P X P X e e e ---≥=-=-==--=-2.9解:设应配备m 名设备维修人员。
天津理工大学概率论与数理统计第二章习题答案详解

第2章一维随机变量 习题2一. 填空题:1.设 离 散 型 随 机 变 量 ξ 的 分 布 函 数 是 (){}x P x F ≤=ξ, 则 用 F (x) 表 示 概 {}0x P =ξ = __________。
解:()()000--x F x F 2.设 随 机 变 量 ξ 的 分 布 函 数 为 ()()+∞<<∞-+=x arctgx x F π121 则 P{ 0<ξ<1} = ____14_____。
解: P{ 0<ξ<1} = =-)0(F )1(F 143.设 ξ 服 从 参 数 为 λ 的 泊 松 分 布 , 且 已 知 P{ ξ = 2 } = P{ ξ = 3 },则 P{ ξ = 3 }= ___2783e - 或 3.375e -3____。
4.设 某 离 散 型 随 机 变 量 ξ 的 分 布 律 是 {}⋅⋅⋅===,2,1,0,!k k C k P Kλξ,常 数 λ>0, 则 C 的 值 应 是 ___ e -λ_____。
解:{}λλλλξ-∞=∞=∞==⇒=⇒=⇒=⇒==∑∑∑e C Ce k C k Ck P KK KK K 11!1!105 设 随 机 变 量 ξ 的 分 布 律 是 {}4,3,2,1,21=⎪⎭⎫⎝⎛==k A k P kξ则 ⎭⎬⎫⎩⎨⎧<<2521ξP = 0.8 。
解:()A A k P k 161516181412141=⎪⎭⎫ ⎝⎛+++==∑=ξ 令15161A = 得 A =1615()()212521=+==⎪⎭⎫ ⎝⎛<<ξξξp p P 8.041211516=⎥⎦⎤⎢⎣⎡+=6.若 定 义 分 布 函 数 (){}x P x F ≤=ξ, 则 函 数 F(x)是 某 一 随 机 变 量 ξ 的 分 布 函 数 的 充 要 条 件 是F ( x ) 单 调 不 减 , 函 数 F (x) 右 连 续 , 且 F (- ∞ ) = 0 , F ( + ∞ ) = 17. 随机变量) ,a (N ~2σξ,记{}σ<-ξ=σa P )(g ,则随着σ的增大,g()σ之值 保 持 不 变 。
概率论第二章习题解答(全)

概率论第二章习题1考虑为期一年的一张保险单,若投保人在投保一年内意外死亡,则公司赔付20万元,若投保人因其它原因死亡,则公司赔付5万元,若投保人在投保期末自下而上,则公司无需传给任何费用。
若投保人在一年内因意外死亡的概率为0.0002,因其它原因死亡的概率为0.0010,求公司赔付金额的分崣上。
解设赔付金额为X ,则X 是一个随机变量,取值为20万,5万,0,其相应的概率为0.0002;0.0010;0.9988,于是得分布律为X20(万)5万0xp 0.00020.00100.99882.(1)一袋中装有5只球,编号为1,2,3,4,5。
在袋中同时取3只,以X 表示取出的3只球中的最大号码,写出随机变量X 的分布律(2)将一颗骰子抛掷两次,以X 表示两次中得到的小的点数,试求X 的分布律。
解(1)在袋中同时取3个球,最大的号码是3,4,5。
每次取3个球,其总取法:35541021C ⋅==⋅,若最大号码是3,则有取法只有取到球的编号为1,2,3这一种取法。
因而其概率为22335511{3}10C P X C C ====若最大号码为4,则号码为有1,2,4;1,3,4;2,3,4共3种取法,其概率为23335533{4}10C P X C C ====若最大号码为5,则1,2,5;1,3,5;1,4,5;2,3,5;2,4,5;3,4,5共6种取法其概率为25335566{5}10C P X C C ====一般地3521)(C C x X p x -==,其中21-x C 为最大号码是x 的取法种类数,则随机变量X 的分布律为X 345xp 101103610(2)将一颗骰子抛掷两次,以X 表示两次中得到的小的点数,则样本点为S ={(1,1),(1,2),(1,3),…,(6,6)},共有36个基本事件,X 的取值为1,2,3,4,5,6,最小点数为1,的共有11种,即(1,1,),(1,2),(2,1)…,(1,6),(6,1),11{1}36P X ==;最小点数为2的共有9种,即(2,2),(2,3),(3,2),…,(3,6),(6,3),9{2}36P X ==;最小点数为3的共有7种,7{3}36P X ==;最小点数为4的共有5种,5{4}36P X ==;最小点数为5的共有3种,3{5}36P X ==;最小点数为6的共有1种,1{6}36P X ==于是其分布律为X 123456kp 11369367365363361363设在15只同类型的产品中有2只次品,在其中取3次,每次任取1只,作不放回抽样,以X 表示取出的次品的次数,(1)求X 的分布律;(2)画出分布律的图形。
概率论与数理统计习题解答 (2)

x<0 0 ≤ x <1 x ≥1
1/ 2
P{ X < 1 / 2} = P{X > 3 / 2} =
−∞ ∞
∫ f ( x)dx = ∫ 2 xdx =1/ 4 或 P{X < 1/ 2} = F (1/ 2) = 1/ 4
0
1/ 2
3/ 2
∫
∞
f ( x)dx =
3/ 2
∫ 0dx = 0
或
P{X > 3 / 2} = 1 − P{X ≤ 3 / 2} = 1 − F (3 / 2) = 1 − 1 = 0
x<0 0 ≤ x <1 x ≥1
求
(1)常数 A
(2)概率密度函数
(3) P{X < 1 / 2} ; P{X > 3 / 2} ;
P{0 ≤ X ≤ 2} 。
解法一:由于连续型随机变量 X 的分布函数是连续的
⎧0 ⎪ ∴ 1 = F( 1 ) = lim F ( x) = lim Ax = A f ( x) = F ' ( X ) = ⎨ 2 x x⎯ ⎯→ 1 x⎯ ⎯→ 1 ⎪0 ⎩
+∞
所以一年中该地区受台风袭击次数为 3~5 的概率为 0.547027 11、有 10 台机床,每台发生故障的概率为 0.08, 而 10 台机床工作独立,每台 故障只需一个维修工人排除。问至少要配备几个维修工人,才能保证有故障而 不能及时排除的概率不大于 5%。 解:随机变量 X 示发生故障的机床的台数则 设配备 n 个维修工人 (0 ≤ n < 10) 则“有故障而不能及时排除”事件为
−1 r k −r (2) P{X = k } = Ckr − , k = r , r + 1,...... 1 p (1 − p )
《概率论与数理统计》第02章习题解答.docx

P{ X = 1} = P[人(瓦U瓦)U孔A ] = 0.8(0.2 + 0.2-0.04) + 0.2 x (0.8)2
= 0.416
P{X=2} =P( £%為)=(0.8)3=0.512
3、据信有20%的美国人没有任何健康保险,现任意抽查12个美国人,以X表示15人无 任何健康保险的人数(设各人是否有健康保险是相互独立的),问X服从什么分布,写出X的分布律,并求下列情况下无任何健康保险的概率
解:(1)P{X>1}=f(x)dx=j"-(4-x2)dr = (-X- — X3)
"9927
(2)―叫刃’叩沟心]刃
22
27
10-R
£二0丄2,…,10
27■■
592
(3)P{y=2}=C^(—)2x(—)8=0.2998
s99s9?
p{r>2}= 1- p{r=0} - p{y=1}= 1-(—)° x(―)10- ^0(—)J(—)9= 0.5778
J;(0.2 + 1.2y)dy
—oo
y v _1
-1 < y < 0
0<y<\
0
0.2y + 0.2
0.6/+0.2j + 0.2
1
y <-1
0<y<l
沖1
P{0<Y<0.5} = F(0.5)-F(0) = 0.2+0.2x0.5 + 0.6x(0.5)2-0.2 = 0.25
P{y > 0.1} = 1-F(0」)=1一0.2-0.2x0」一0.6x0= 0.774
概率论与数理统计习题二及答案

此时, PX
2
62
1 2 2
1 62 2
65 2!
1 6 2
15 64
。
5. 某商店出售某种物品,根据以往的经验,每月销售量 X 服从参数 4 的泊松分布,
问在月初进货时,要进多少才能以 99%的概率充分满足顾客的需要?
解:设至少要进 n 件物品,由题意 n 应满足 PX n 1 0.99, PX n 0.99,
pi
i 1 25
(i 1, 2,3, 4,5) 。
解:要说明题中给出的数列,是否是随机变量的分布律,只要验证 pi 是否满足下列二
个条件:其一条件为 pi 0,i 1,2,,其二条件为 pi 1。
i
依据上面的说明可得(1)中的数列为随机变量的分布律;(2)中的数列不是随机变量
的分布律,因为
PX
10
10
1 5
x
e 5 dx
e2
;
(2)设 Y 表示某顾客五次去银行未等到服务的次数,则 Y 服从 n 5, p e2 的二项
分布,所求概率为
PY 1 PY 0 PY 1
5 0
e
2
0 1 e2
5
5 1
e
2
1 e2
4
1 4e2 1 e2 4
12. 设随机变量 X 服从 N (0,1) ,借助于标准正态分布的分布函数表计算:(1)P(X 2.2) ;
P(0 X 1) ;( 3) X 的 分 布 函 数 。
解 :( 1) 系 数
A必须满足
Ae
x
dx
1, 由 于
e
x
为偶函数,所以
Ae
x
dx
20
概率论第二章习题参考解答

概率论第二章习题参考解答1. 用随机变量来描述掷一枚硬币的试验结果. 写出它的概率函数和分布函数. 解: 假设ξ=1对应于"正面朝上",ξ=0对应于反面朝上. 则 P (ξ=0)=P (ξ=1)=0.5 . 其分布函数为⎪⎩⎪⎨⎧≥<≤<=11105.000)(x x x x F 2. 如果ξ服从0-1分布, 又知ξ取1的概率为它取0的概率的两倍, 写出ξ的分布律和分布函数.解: 根据题意有 P (ξ=1)=2P (ξ=0) (1) 并由概率分布的性质知 P (ξ=0)+P (ξ=1)=1 (2) 将(1)代入(2)得3P (ξ=0)=1, 即P (ξ=0)=1/3 再由(1)式得 P (ξ=1)=2/3因此分布律由下表所示ξ0 1 P 1/32/3而分布函数为⎪⎩⎪⎨⎧>=<≤<=11103/100)(x x x x F 3. 如果ξ的概率函数为P {ξ=a }=1, 则称ξ服从退化分布. 写出它的分布函数F (x ), 画出F (x )的图形. 解: ⎩⎨⎧≥<=ax a x x F 10)(, 它的图形为4. 一批产品分一,二,三级, 其中一级品是二级品的两倍, 三级品是二级品的一半, 从这批产品中随机地抽取一个检验质量, 用随机变量描述检验的可能结果, 写出它的概率函数. 解 设ξ取值1,2,3代表取到的产品为一,二,三级, 则根据题意有 P (ξ=1)=2P (ξ=2) (1)P (ξ=3)=P (ξ=2)/2 (2) 由概率论性质可知P (ξ=1)+P (ξ=2)+P (ξ=3)=1 (3)(1),(2)代入(3)得:2P (ξ=2)+P (ξ=2)+P (ξ=2)/2=1解得P (ξ=2)=2/7, 再代回到(1)和(2)得 P (ξ=1)=4/7, P (ξ=3)=1/7 则概率函数为)3,2,1(271)(3=⨯==-i i P i ξ或列表如下:5. 一批产品20个, 其中有5个次品, 从这批产品中随意抽取4个, 求这4个中的次品数ξ的分布律.解: 基本事件总数为420C n =,有利于事件{ξ=i }(i =0,1,2,3,4)的基本事件数为ii i C C n -=4155, 则001.01731911718192051234)4(031.0171952121545171819201234)3(2167.01718191415231212141545171819201234)2(4696.01718191314151231314155171819201234)1(2817.01719137123412131415171819201234)0(445420115354202152542031515420415=⋅⋅=⋅⋅⋅⋅⋅⋅⋅====⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅===C C P C C C P C C C P C C C P C C P ξξξξξ 6. 一批产品包括10件正品, 3件次品, 有放回地抽取, 每次一件, 直到取得正品为止, 假定每件产品被取到的机会相同, 求抽取次数ξ的概率函数.解: 每次抽到正品的概率相同, 均为p =10/13=0.7692, 则每次抽到次品的概率q =1-p =0.2308则ξ服从相应的几何分布, 即有),3,2,1(1331310)(1=⎪⎭⎫⎝⎛⋅===-i pq i P i i ξ7. 上题中如果每次取出一件产品后, 总以一件正品放回去, 直到取得正品为止, 求抽取次数ξ的分布律.解: 这样抽取次数就是有限的, 因为总共只有3件次品, 即使前面三次都抽到次品,第四次抽时次品已经全部代换为正品, 因此必然抽到正品, 这样ξ的取值为1,2,3,4.不难算出,0027.0131132133)4(0328.01312132133)3(1953.01311133)2(7692.01310)1(=⋅⋅===⋅⋅===⋅=====ξξξξP P P Pξ的分布律如下表所示:8. 自动生产线在调整之后出现废品的概率为p , 当在生产过程中出现废品时立即重新进行调整, 求在两次调整之间生产的合格品数ξ的概率函数.解: 事件ξ=i 说明生产了i 次正品后第i +1次出现废品, 这是i +1个独立事件的交(1次发生i 次不发生, 因此有P (ξ=i )=p (1-p )i , (i =0,1,2,…)9. 已知随机变量ξ只能取-1,0,1,2四个值, 相应概率依次为cc c c 167,85,43,21, 确定常数c 并计算P {ξ<1|ξ≠0}.解: 根据概率函数的性质有1}2{}1{}0{}1{==+=+=+-=ξξξξP P P P即1167854321=+++cc c c 得2.3125163716710128167854321==+++=+++=c 设事件A 为ξ<1, B 为ξ≠0, (注: 如果熟练也可以不这样设)则32.0258167852121}2{}1{}1{}1{)0{}01{)()(}0|1{==++==+=+-=-==≠≠⋂<==≠<ξξξξξξξξξP P P P P P B P AB P P 10. 写出第4题及第9题中各随机变量的分布函数. 解: 第4题:⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=31327/6217/410)(x x x x x F第9题:当x <-1时: F (x )=P (ξ≤x )=0 当-1≤x <0时: F (x )=P (ξ≤x )=P (ξ=-1)=2162.03125.22121=⨯=c 当0≤x <1时: F (x )=P (ξ≤x )=P (ξ=-1)+P (ξ=0)=5405.03125.243214321=⎪⎭⎫ ⎝⎛+=+c c 当1≤x <2时: F (x )=P (ξ≤x )=P (ξ=-1)+P (ξ=0)+P (ξ=1)=8108.03125.2854321854321=⎪⎭⎫ ⎝⎛++=++c c c 当x ≥2时: F (x )=P (ξ≤x )=1 综上所述, 最后得:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤--<=21218108.0105405.0012162.010)(x x x x x x F 11. 已知ξ~⎪⎩⎪⎨⎧<<=其它1021)(x xx ϕ, 求ξ的分布函数F (x ), 画出F (x )的图形.解: 当x <0时: F (x )=0;当0≤x <1时:xx xt x t dt t dt t dt dt t x F xxx=-==+-⋅==+==+--∞-∞-⎰⎰⎰⎰00012112121210)()(12102100ϕ 当x ≥1时: F (x )=1 综上所述, 最后得⎪⎩⎪⎨⎧≥<≤<=111000)(x x xx x F 图形为12. 已知ξ~⎩⎨⎧<<=其它0102)(x x x ϕ, 求P {ξ≤0.5}; P (ξ=0.5);F (x ).解: 25.005.020)(}5.0{225.0025.005,0|=-==+==≤⎰⎰⎰∞-∞-x xdx dx dx x P ϕξ, 因ξ为连续型随机变量, 因此取任何点的概率均为零, 所以P {ξ=0.5}=0,求F (x ): 当x <0时, F (x )=0 当0≤x <1时, 220|20)()(x t tdt dt dt t x F xxx==+==⎰⎰⎰∞-∞-ϕ 当x ≥1时, F (x )=1 综上所述, 最后得:⎪⎩⎪⎨⎧≥<≤<=111000)(2x x x x x F 13. 某型号电子管, 其寿命(以小时计)为一随机变量, 概率密度⎪⎩⎪⎨⎧≥=其它0100100)(2x x x ϕ, 某一个电子设备内配有3个这样的电子管, 求电子管使用150小时都不需要更换的概率.解: 先求一个电子管使用150小时以上的概率P (ξ≥150)为:3215010012100100)()150(|150121502150==+-===≥∞++-+∞+∞⎰⎰x dx xdx x P ϕξ 则3个这样的电子管构成贝努里独立试验概型, 试验三次发生三次的概率为2963.027832)3(33==⎪⎭⎫⎝⎛=p14. 设连续型随机变量ξ的分布函数为:⎪⎩⎪⎨⎧≥<≤<=111000)(2x x Ax x x F 求系数A ; P (0.3<ξ<0.7); 概率密度φ(x ).解: 因ξ是连续型随机变量, 因此F (x )也必是连续曲线, 则其在第二段(0,1)区间的曲线必能和第三段(1,+∞)的曲线接上, 则必有 A ×12=1, 即A =1. 则分布函数为⎪⎩⎪⎨⎧≥<≤<=111000)(2x x x x x F P (0.3<ξ<0.7)=F (0.7)-F (0.3)=0.72-0.32=0.49-0.09=0.4概率密度φ(x )为⎩⎨⎧<≤='=其它0102)()(x x x F x ϕ15. 服从柯西分布的随机变量ξ的分布函数是F (x )=A +B arctg x , 求常数A ,B ;P {|ξ|<1}以及概率密度φ(x ). 解: 由F (-∞)=0, 得A +Barctg (-∞)=02=-πB A(1)再由F (+∞)=1,得12)arctg(=+=+∞+πB A B A(2)综和(1),(2)两式解得π1,21==B A 即x x F arctg 121)(π+=5.0214411111)1()1()11()1|(|==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--==--=--=<<-=<πππππξξarctg arctg F F P P2111)()(x x F x +⋅='=πϕ16. 服从拉普拉斯分布的随机变量ξ的概率密度||)(x Ae x -=ϕ, 求系数A 及分布函数F (x ).解: 这实际上是一个分段函数, φ(x )可重新写为⎩⎨⎧<≥=-0)(x Aex Ae x xxϕ 根据性质1)(=⎰+∞∞-dx x ϕ, 又因φ(x )为偶函数, 因此有1222)(|==-==∞+-+∞-+∞∞-⎰⎰A Aedx Aedx x x xϕ, 则有A =1/2因此⎪⎩⎪⎨⎧<≥==--02102121)(||x e x e ex x x x ϕ.求分布函数F (x ). 当x <0时, 有xxtxt x e e dt e dt t x F 212121)()(====∞-∞-∞-⎰⎰ϕ当x ≥0时, 有x x xtxt t x e e e dt e dt e dt t x F ----∞-∞--=+-=-=+==⎰⎰⎰21121212121212121)()(00ϕ 综上所述, 最后得⎪⎩⎪⎨⎧≥-<=-0211021)(x e x ex F x x17. 已知⎩⎨⎧<<+-=其它01031212)(~2x x x x ϕξ, 计算P {ξ≤0.2|0.1<ξ≤0.5}解: 设事件A ={ξ≤0.2}, B ={0.1<ξ≤0.5}, 则要计算的是条件概率P (A |B ), 而)()()|(B P AB P B A P =, 而事件AB ={ξ≤0.2}∩{0.1<ξ≤0.5}={0.1<ξ≤0.2} 因此有148.03.006.0004.06.024.0032.0)1.0301.06001.04()2.0304.06008.04()364(d )31212()(}2.01.0{)(2.01.0232.01.022.01.0=-+-+-=⨯+⨯-⨯-⨯+⨯-⨯==+-=+-==≤<=⎰⎰x x x xx x dx x P AB P ϕξ256.03.006.0004.05.15.15.0)1.0301.06001.04()5.0325.06125.04()364(d )31212()(}5.01.0{)(5.01.0235.01.025.01.0=-+-+-=⨯+⨯-⨯-⨯+⨯-⨯==+-=+-===≤<=⎰⎰x x x xx x dx x P B P ϕξ最后得5781.0256.0148.0)()()|(}5.01.0|2.0{====≤<≤B P AB P B A P P ξξ18. 已知xxce x +-=2)(~ϕξ, 确定常数c .解: 首先证明普阿松广义积分π=⎰+∞∞--x e xd 2, 因为函数2x e -并不存在原函数, 因此需要一技巧. 令⎰+∞∞--=x eI x d 2, 则⎰⎰⎰+∞∞-+∞∞-+-+∞∞--=⎥⎦⎤⎢⎣⎡=y x e x e I y x x d d d )(22222作极坐标代换, 令θθsin ,cos r y r x ==, 则积分区间为全平面, 即θ从0积到2π, r 从0积到+∞, 且θd d d d r r y x =, 因此有πππθπ====∞+-+∞-+∞-⎰⎰⎰020202222)d(212rr r e r e rdr ed I , 所以I =π.现确定常数c , 由性质1)(=⎰+∞∞-dx x ϕ,1d d 41)21(414141212222====⎰⎰⎰+∞∞---+∞∞-+-⋅⋅+-+∞∞-+-πcedx ecex cex cex x x xx得421πe c =19. 已知⎩⎨⎧>>=-其它)0()(~λλϕξλa x e c x x, 求常数c 及P {a -1<ξ≤a +1}.解: 由性质1)(=⎰+∞∞-dx x ϕ得1d d 0)(|==-=+=-∞+-+∞-∞-+∞∞-⎰⎰⎰aax ax ace ce x e c x dx x λλλλϕ 解得 aec λ=, 因此有⎩⎨⎧>>=--其它)0()()(λλϕλa x e x a x则λλλλλλϕξ---+---+--=-==+==+≤<-⎰⎰⎰⎰e e due x ex x x a a P u u a aa x a a a a 1d d 0d )()11(|111)(111求边缘概率分布, 与是否独立?解: 按下表计算ξ与η的边缘分布:得的边缘分布如下表所示:当i =1及j =0时,因202.026.0}0{}1{0}0,1{)2(0)1(110⨯====≠====ηξηξP P p p P p因此ξ与η相互间不独立.21. 假设电子显示牌上有3个灯泡在第一排, 5个灯泡在第二排. 令ξ,η分别表示在某一规定时间内第一排和第二排烧坏的灯泡数. 若ξ与η的联合分布如下表所示: 试计算在规定时间内下列事件的概率: (1) 第一排烧坏的灯泡数不超过一个; (2) 第一排与第二排烧坏的灯泡数相等;(3) 第一排烧坏的灯泡数不超过第二排烧坏的灯泡数.解: 假设事件A 为第一排烧坏的灯泡数不超过一个, B 为第一排与第二排烧坏的灯泡数相等, C 为第一排烧坏的灯光数不超过第二排烧坏的灯泡数. 则事件A 发生的概率为上表中头两排概率之和52.008.006.005.004.002.001.009.007.005.003.001.001.0)(104=++++++++++++==∑∑==i j ij p A P事件B 发生的概率为上表中从0行0列开始的斜对角线之和14.006.005.002.001.0)(3=+++==∑=i ii p B P事件C 发生的概率为上表中斜对角线上右的各个数相加(包括斜对角线上的数), 但为减少运算量, 也可以考虑其逆事件C 的概率, 然后用1减去它. 而C 的概率为上表中斜对角线的左下角的所有概率之和(不包括斜对角线):89.011.01)04.001.003.001.001.001.0(1)(1)(=-=+++++-=-=C P C P22. 袋中装有标上号码1,2,2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求(ξ,η)的分布律(袋中各球被取机会相同).解: 因为有两个2一个1, 因此第一次取到2号的概率为P (ξ=2)=2/3, 第一次取到1号的概率为P (ξ=1)=1/3. 第一次取到2号后还剩下一个2号一个1号, 则在此条件下第二次取到1号的概率P (η=1|ξ=2)=P (η=2|ξ=2)=1/2. 而第一次取到1号后还剩下两个2号, 因此这时P (η=1|ξ=1)=0, P (η=2|ξ=1)=1. 综上所述并用乘法法则可得312132)2|2()2()2,2(312132)2|1()2()1,2(31131)1|2()1()2,1(0031)1|1()1()1,1(22211211=⨯=========⨯=========⨯=========⨯========ξηξηξξηξηξξηξηξξηξηξP P P p P P P p P P P p P P P p23. (ξ , η)只取下列数组中的值:)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12. 列出(ξ,η)的概率分布表, 写出关于η的边缘分布. 解: 从上面数组可知ξ只取-1,0,2这三个值, 而η只取0,31,1这三个值, 因此总共可构成九个. 概率分布表及η的边缘分布计算如下即η的边缘分布率如下表所示24. 袋中装有标上号码1,2,2,3的4个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求(ξ,η)的分布律(袋中各球被取机会相同).解: 第一次取到号码1,2,3的概率为P{ξ=1}=P(ξ=3)=1/4P{ξ=2}=1/2在第一次取到号码i条件下,第二次取到号码j的概率各为P{η=1|ξ=1}=P{η=3|ξ=3}=0P{η=2|ξ=1}=P{η=2|ξ=3}=2/3P{η=3|ξ=1}=P{η=1|ξ=3}=1/3P{η=1|ξ=2}=P{η=3|ξ=2}=1/3P{η=2|ξ=2}=1/3则p11=P{ξ=1,η=1}=P{ξ=1}P{η=1|ξ=1}=0p12=P{ξ=1,η=2}=P{ξ=1}P{η=2|ξ=1}=1/6p13=P{ξ=1,η=3}=P{ξ=1}P{η=3|ξ=1}=1/12p21=P{ξ=2,η=1}=P{ξ=2}P{η=1|ξ=2}=1/6p22=P{ξ=2,η=2}=P{ξ=2}P{η=2|ξ=2}=1/6p23=P{ξ=2,η=3}=P{ξ=2}P{η=3|ξ=2}=1/6p31=P{ξ=3,η=1}=P{ξ=3}P{η=1|ξ=3}=1/12p32=P{ξ=3,η=2}=P{ξ=3}P{η=2|ξ=3}=1/6p33=P{ξ=3,η=3}=P{ξ=3}P{η=3|ξ=3}=025. 表示随机地在1-4的4个整数中取出的一个整数,η表示在1-ξ中随机地取出的一个整数值,求(ξ,η)的联合概率分布.解: 因ξ取四个数中的任何一个概率相等, 因此有P{ξ=i}=1/4, (i=1,2,3,4)而在ξ=i的条件下, (i=1,2,3,4), η取1到i的概率也相同,为1/i, 即P{η=j|ξ=i}=1/i, (i=1,2,3,4;j=1-i)因此有p ij=P{ξ=i,η=j}=P{ξ=i}P{η=j|ξ=i}=1/(4i), (i=1,2,3,4; j=1-i),联合概率分布如下表所示:26. 已知(ξ,η)~⎪⎩⎪⎨⎧≤≤+=其它04,0)sin(),(πϕy x y x c y x ,试确定常数c 并求η的边缘概率密度.解: 根据性质1),(=⎰⎰+∞∞-+∞∞-dydx y x ϕ, 有1)12(]220122[)]4sin([sin )]4cos([cos )]cos([)sin(40440404040=-=+--=+-=+-=+-=+⎰⎰⎰⎰c c x x c x x dx c y x dx c dydx y x c ππππππππ解得12)12)(12(12121+=+-+=-=c ,因此,⎪⎩⎪⎨⎧≤≤++=其它04,0)sin()12(),(πϕy x y x y x求η的边缘概率密度: 当40π≤≤y 时:)8sin(22)12()]4cos()[cos 12()cos()12()sin()12(),()(4042ππϕϕκπ+-+==+-+==++-=++==⎰⎰∞+∞-y y y y x dx y x dx y x y上式后一等式利用了三角函数公式2sin 2sin2cos cos A B A B B A -+=-, 而计算三角函数8sin π的值, 又是在已知224cos=π的前提下,利用半角公式2cos 12sin θθ-=得222222124cos18sin-=-=-=ππ当y 取区间]4,0[π之外的值时, 0)(1=y ϕ.因此最后得:⎪⎩⎪⎨⎧≤≤+-+=其它040)8sin(22)12()(2ππϕy y y27. 已知ξ服从参数p =0.6的0-1分布, 在ξ=0及ξ=1条件下, 关于η的条件分布分别如下二表所示:求二元随机变量(,)的联合概率分布, 以及在≠1时关于的条件分布. 解: 根据题意已知P {ξ=0}=1-p =1-0.6=0.4, P {ξ=1}=p =0.6 则根据乘法法则有:p 01=P {ξ=0,η=1}=P {ξ=0}P {η=1|ξ=0}=0.4×(1/4)=0.1 p 02=P {ξ=0,η=2}=P {ξ=0}P {η=2|ξ=0}=0.4×(1/2)=0.2 p 03=P {ξ=0,η=3}=P {ξ=0}P {η=3|ξ=0}=0.4×(1/4)=0.1 p 11=P {ξ=1,η=1}=P {ξ=1}P {η=1|ξ=1}=0.6×(1/2)=0.3 p 12=P {ξ=1,η=2}=P {ξ=1}P {η=2|ξ=1}=0.6×(1/6)=0.1 p 13=P {ξ=1,η=3}=P {ξ=1}P {η=3|ξ=1}=0.6×(1/3)=0.2由表中可以算出P {η≠1}=1-P {η=1}=1-(p 01+p 11)=1-0.4=0.6 P {ξ=0,η≠1}=p 02+p 03=0.2+0.1=0.3 P {ξ=1,η≠1}=p 12+p 13=0.1+0.2=0.3 因此有5.06.03.0}1{}1,1{}1|1{5.06.03.0}1{}1,0{}1|0{==≠≠==≠===≠≠==≠=ηηξηξηηξηξP P P P P P则在η≠1时关于ξ的条件分布律如下表所示:28. 第22题中的两个随机变量ξ与η是否独立?当ξ=1时η的条件分布是什么?: , 因为 P {ξ=1}=1/3, P {η=1}=1/3 而P {ξ=1,η=1}=0≠P {ξ=1}P {η=1} 在ξ=1条件下, 因13/13/1}1{}2,1{}1|2{03/10}1{}1,1{}1|1{================ξηξξηξηξξηP P P P P P因此在此条件下η服从单点分布或退化分布, 只取值为2, 取值为2的条件概率为1.=p i (1)p j (2), 算得联合分布律如下表所示 根据此联合分布律可算出43129611211)2/1,2/1()1,1(1)0(1)0(121484481161)1,0()3,2()1(==--==-==-=-=-==+-=≠+==+===+=-===+ηξηξηξηξηξηξηξP P P P P P P30. 测量一矩形土地的长与宽, 测量结果得到如下表所示的分布律(长与宽相互独立), 求周解: 因ζ=2ξ+2η, 可知ζ的取值为96,98,100,102,104, 又因ξ与η独立, 因此有 P {ζ=96}==P {ξ=29}P {η=19}=0.3×0.3=0.09P {ζ=98}=P {ξ=29}P {η=20}+P {ξ=30}P {η=19}=0.3×0.4+0.5×0.3=0.27 P {ζ=100}=P {ξ=29}P {η=21}+P {ξ=30}P {η=20}+P {ξ=31}}P {η=19}==0.3×0.3+0.5×0.4+0.2×0.3=0.35P {ζ=102}=P {ξ=30}P {η=21}+P {ξ=31}P {η=20}=0.3×0.5+0.2×0.4=0.23 P {ζ=104}=P {ξ=31}P {η=21}=0.2×0.3=0.06η的分布.解: 因周长=2πR , 面积=πR , 因此当半径R 取值10,11,12,13时, ξ的取值为62.83, 69.12,32. 一个商店每星期四进货, 以备星期五,六,日3天销售, 根据多周统计, 这3天销售件数 ξ问三天销售总量∑==31i iξη这个随机变量可以取哪些值?如果进货45件, 不够卖的概率是多少? 如果进货40件, 够卖的概率是多少?解: 因η的取值为ξ1,ξ2,ξ3三个随机变量可能取值之和, 因此可能的取值为从10+13+17=40到12+15+19=46之间的每一个整数值, 即40,41,42,43,44,45,46. 因此, 如进货15件, 不够卖的概率在η取值为46时出现, 即 P {η=46}=P {ξ1=12}P {ξ2=15}P {ξ3=19}=0.1×0.1×0.1=0.001 如进货40件, 够卖的概率发生在η取值为40时出现, 即P {η=40}=P {ξ1=10}P {ξ2=13}P {ξ3=17}=0.2×0.3×0.1=0.006 33. 求出第22题中ξ+η的分布律.ξ与η的联合分布律如下表: 则P {+=2}=P {=1,=1}=0P {ξ+η=3}=P {ξ=1,η=2}+P {ξ=2,η=1}=2/3 P {ξ+η=4}=P {ξ=2,η=2}=1/334. 求出第23题中ξ-η的分布律 解: 因(ξ , η)只取下列数组中的值:)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12.因此ξ-η也只取0-0=0, -1-1=-2, -1-1/3=-4/3, 2-0=2这四个值, 相应的概率也还是依次为1/6, 35. 已知P {ξ=k }=a /k , P {η=-k }=b /k (k =1,2,3), ξ与独立, 确定a ,b 的值; 求出(ξ,η)的联合概率分布以及ξ+η的概率分布. 解: 由概率分布的性质有131211}{31=⎪⎭⎫⎝⎛++==∑=a k P k ξ, 解得 5455.0116312111==++=a,191411}{31=⎪⎭⎫⎝⎛++=-=∑=b k P k η 解得 7347.04936914111==++=b 因此有P {ξ=1}=0.5455, P {ξ=2}=0.5455/2=0.2727, P {ξ=3}=0.1818 P {η=-1}=0.7347, P {η=-2}=0.1837, P {η=-3}=0.0816 因ξ与η独立, 则有p 11=P {ξ=1,η=-1}=P {ξ=1}P {η=-1}=0.5455×0.7347=0.4008 p 12=P {ξ=1,η=-2}=P {ξ=1}P {η=-2}=0.5455×0.1837=0.1002 p 13=P {ξ=1,η=-3}=P {ξ=1}P {η=-3}=0.5455×0.0816=0.0445 p 21=P {ξ=2,η=-1}=P {ξ=2}P {η=-1}=0.2727×0.7347=0.2004 p 22=P {ξ=2,η=-2}=P {ξ=2}P {η=-2}=0.2727×0.1837=0.0501 p 23=P {ξ=2,η=-3}=P {ξ=2}P {η=-3}=0.2727×0.0816=0.0223 p 31=P {ξ=3,η=-1}=P {ξ=3}P {η=-1}=0.1818×0.7347=0.1336 p 32=P {ξ=3,η=-2}=P {ξ=3}P {η=-2}=0.1818×0.1837=0.0333 p 33=P {ξ=3,η=-3}=P {ξ=3}P {η=-3}=0.1818×0.0816=0.0148计算+的概率分布: P {ξ+η=-2}=p 13=0.0445P {ξ+η=-1}=p 12+p 23=0.1002+0.0223=0.1225P {ξ+η=0}=p 11+p 22+p 33=0.4008+0.0501+0.0148=0.4657 P {ξ+η=1}=p 21+p 32=0.2004+0.0333=0.2337 P{ξ+η=2}=p 31=0.1336即ξ+η的概率分布率如下表所示36. 已知服从区间[0,1]上的均匀分布, 求的函数=3+1的概率分布. 解: 根据题意知ξ的概率密度φξ(x )为⎩⎨⎧≤≤=其它0101)(x x ξϕ 则η的分布函数为)31(}31{}13{}{)(-=-≤=≤+=≤=x F x P x P x P x F ξηξξη 对其求导得η的概率密度与ξ的概率密度间的关系为⎪⎩⎪⎨⎧≤≤=⎪⎩⎪⎨⎧≤-≤=-=-'='=其它其它041310131031)31(31)31(31)()(x x x x F x F x ϕϕξηη即η服从在区间[1,4]上的均匀分布.37. 已知ξ~⎪⎩⎪⎨⎧>+=其它0)1(2)(2x x x πϕ, ξηln =, 求η的概率密度.解: 求η的分布函数F η(x )为)(}{}{ln }{)(x x e F e P x P x P x F ξηξξη=≤=≤=≤=因e x 总大于0, 而当x 大于0时F ξ(x )为x t t t dt t x F x xxarctg 2arctg 2d )1(2)()(|002πππϕξ==+==⎰⎰∞- 因此有x x e e F x F arctg 2)()(πξη==则η的概率密度为其分布函数的求导:xx ee x F x 212)()(+⋅='=πϕηη。
概率论与数理统计第二章课后习题及参考答案.

概率论与数理统计第二章课后习题及参考答案1.离散型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=≤=.4,1,42,7.0,21,2.0,1,0)()(x x x x x X P x F 求X 的分布律.解:)0()()(000--==x F x F x X P ,∴2.002.0)01()1()1(=-=----=-=F F X P ,5.02.07.0)02()2()2(=-=--==F F X P ,3.07.01)04()4()4(=-=--==F F X P ,∴X 的分布律为2.设k a k X P 32()(==, ,2,1=k ,问a 取何值时才能成为随机变量X 的分布律.解:由规范性,a a a n n k k 2321]32(1[32lim)32(11=--=⋅=+∞→∞+=∑,∴21=a ,此时,k k X P 32(21)(⋅==, ,2,1=k .3.设离散型随机变量X 的分布律为求:(1)X 的分布函数;(2)21(>X P ;(3))31(≤≤-X P .解:(1)1-<x 时,0)()(=≤=x X P x F ,11<≤-x 时,2.0)1()()(=-==≤=X P x X P x F ,21<≤x 时,7.0)1()1()()(==+-==≤=X P X P x X P x F ,2≥x 时,1)2()1()1()()(==+=+-==≤=X P X P X P x X P x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=.2,1,21,7.0,11,2.0,1,0)(x x x x x F .(2)方法1:8.0)2()1()21(==+==>X P X P X P .方法2:8.02.01)21(121(1)21(=-=-=≤-=>F X P X P .(3)方法1:1)2()1()1()31(==+=+-==≤≤-X P X P X P X P .方法2:101)01()3()31(=-=---=≤≤-F F X P .4.一制药厂分别独立地组织两组技术人员试制不同类型的新药.若每组成功的概率都是0.4,而当第一组成功时,每年的销售额可达40000元;当第二组成功时,每年的销售额可达60000元,若失败则分文全无.以X 记这两种新药的年销售额,求X 的分布律.解:设=i A {第i 组取得成功},2,1=i ,由题可知,1A ,2A 相互独立,且4.0)()(21==A P A P .两组技术人员试制不同类型的新药,共有四种可能的情况:21A A ,21A A ,21A A ,21A A ,相对应的X 的值为100000、40000、60000、0,则16.0)()()()100000(2121====A P A P A A P X P ,24.0)()()()40000(2121====A P A P A A P X P ,24.0)()()()60000(2121====A P A P A A P X P ,36.0)()()()0(2121====A P A P A A P X P ,∴X 的分布律为5.对某目标进行独立射击,每次射中的概率为p ,直到射中为止,求:(1)射击次数X 的分布律;(2)脱靶次数Y 的分布律.解:(1)由题设,X 所有可能的取值为1,2,…,k ,…,设=k A {射击时在第k 次命中目标},则k k A A A A k X 121}{-== ,于是1)1()(--==k p p k X P ,所以X 的分布律为1)1()(--==k p p k X P , ,2,1=k .(2)Y 的所有可能取值为0,1,2,…,k ,…,于是Y 的分布律为1)1()(--==k p p k Y P , ,2,1,0=k .6.抛掷一枚不均匀的硬币,正面出现的概率为p ,10<<p ,以X 表示直至两个面都出现时的试验次数,求X 的分布律.解:X 所有可能的取值为2,3,…,设=A {k 次试验中出现1-k 次正面,1次反面},=B {k 次试验中出现1-k 次反面,1次正面},由题知,B A k X ==}{,=AB ∅,则)1()(1p p A P k -=-,p p B P k 1)1()(--=,p p p p B P A P B A P k X P k k 11)1()1()()()()(---+-=+=== ,于是,X 的分布律为p p p p k X P k k 11)1()1()(---+-==, ,3,2=k .7.随机变量X 服从泊松分布,且)2()1(===X P X P ,求)4(=X P 及)1(>X P .X 100000060000400000P0.160.240.240.36解: )2()1(===X P X P ,∴2e e2λλλλ--=,∴2=λ或0=λ(舍去),∴224e 32e !42)4(--===X P .)1()0(1)1(1)1(=-=-=≤-=>X P X P X P X P 222e 31e 2e 1----=--=.8.设随机变量X 的分布函数为⎩⎨⎧<≥+-=-.0,0,0,e )1(1)(x x x x F x 求:(1)X 的概率密度;(2))2(≤X P .解:(1)⎩⎨⎧<≥='=-.0,0,0,e )()(x x x x F x f x ;(2)2e 31)2()2(--==≤F X P .9.设随机变量X 的概率密度为xx Ax f e e )(+=-,求:(1)常数A ;(2))3ln 210(<<X P ;(3)分布函数)(x F .解:(1)⎰⎰+∞∞--+∞∞-+==xAx x f xx d e e d )(1A A x A x x x 2|e arctan d e 21e 2π==+=∞+∞-∞+∞-⎰,∴π2=A .(2)61|e arctan 2d e e 12)3ln 210(3ln 2103ln 210==+=<<⎰-x xx x X P ππ.(3)x xx x xx t t f x F e arctan 2d e e 12d )()(ππ=+==⎰⎰∞--∞-.10.设连续型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<-+-≤=.a x a x a a x B A a x x F ,1,,arctan ,,0)(其中0>a ,试求:(1)常数A ,B ;(2)概率密度)(x f .解:(1) 2arcsin (lim )0()(0)(π⋅-=+=+-=-=+-→B A a x B A a F a F a x ,1)(lim )0()(2==+==⋅++→x F a F a F B A a x π,∴21=A ,π1=B .(2)⎪⎩⎪⎨⎧≥<-='=.a x a x x a x F x f ,0,,1)()(22π.11.设随机变量X 的概率密度曲线如图所示,其中0>a .(1)写出密度函数的表达式,求出h ;(2)求分布函数)(x F ;(3)求)2(a X aP ≤<.解:(1)由题设知⎪⎩⎪⎨⎧≤≤-=其他.,0,0,)(a x x ah h x f 2d )(d )(10ahx x a h h x x f a=-==⎰⎰+∞∞-,∴ah 2=,从而⎪⎩⎪⎨⎧≤≤-=其他.,0,0,22)(2a x x a a x f .y hO a x(2)0<x 时,0d 0d )()(===⎰⎰∞-∞-xxt t t f x F ,a x <≤0时,220202d )22(d 0d )()(a x a x t t a a t t t f x F xx-=-+==⎰⎰⎰∞-∞-,a x ≥时,1)(=x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.a x a x axa x x x F ,1,0,2,0,0)(22.(3)41411(1)2()()2(=--=-=≤<a F a F a X a P .12.设随机变量X 在]6,2[上服从均匀分布,现对X 进行三次独立观察,试求至少有两次观测值大于3的概率.解:由题意知⎪⎩⎪⎨⎧≤≤=其他.,0,62,41)(x x f ,记3}{>=X A ,则43d 41)3()(63==>=⎰x X P A P ,设Y 为对X 进行三次独立观测事件}3{>X 出现的次数,则Y ~43,3(B ,所求概率为)3()2()2(=+==≥Y P Y P Y P )(()(333223A P C A P A P C +=3227)43(41)43(333223=+⋅=C C .13.设随机变量X 的概率密度为⎩⎨⎧<<=其他.,0,10,3)(2x x x f 以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数,求:(1)}21{≤X 至少出现一次的概率;(2)}21{≤X 恰好出现两次的概率.解:由题意知Y ~),3(p B ,其中81d 321(2102==≤=⎰x x X P p ,(1)}21{≤X 至少出现一次的概率为512169)811(1)1(1)0(1)1(33=--=--==-=≥p Y P Y P .(2)}21{≤X 恰好出现两次的概率为51221811(81()1()2(223223=-=-==C p p C Y P .14.在区间],0[a 上任意投掷一个质点,以X 表示这个质点的坐标.设这个质点落在],0[a 中任意小区间内的概率与这个小区间的长度成正比例.试求X 的分布函数.解:0<x 时,事件}{x X ≤表示X 落在区间],0[a 之外,是不可能事件,此时0)()(=≤=x X P x F ;a x ≤≤0时,事件}{x X ≤发生的概率等于X 落在区间],0[x 内的概率,它与],0[x 的长度x 成正比,即x k x X P x F =≤=)()(,a x =时,1)(=≤x X P ,所以a k 1=,则此时axx F =)(;a x ≥时,事件}{x X ≤是必然事件,有1)(=x F ,综上,⎪⎪⎩⎪⎪⎨⎧≥<≤<=,a x a x a x x x F ,1,0,,0,0)(.15.设X ~),2(2σN ,又3.0)42(=<<X P ,求)0(>X P .解:)24222()42(σσσ-<-<-=<<X P X P 3.0)0(2(=Φ-Φ=σ,∴8.03.0)0()2(=+Φ=Φσ,∴8.0)2()2(1)0(1)0(=Φ=-Φ-=≤-=>σσX P X P .16.设X ~)4,10(N ,求a ,使得9.0)10(=<-a X P .解:)10()10(a X a P a X P <-<-=<-)22102(a X a P <-<-=)2()2(a a -Φ-Φ=9.01)2(2=-Φ=a,∴95.0)2(=Φa,查标准正态分布表知645.12=a,∴290.3=a .17.设X ~)9,60(N ,求分点1x ,2x ,使得X 分别落在),(1x -∞,),(21x x ,),(2∞x 的概率之比为3:4:5.解:由题知5:4:3)(:)(:)(2211=><<<x X P x X x P x X P ,又1)()()(2211=>+<<+<x X P x X x P x X P ,∴25.041)(1==<x X P ,33.031)(21==<<x X x P ,125)(2=>x X P ,则5833.0127)(1)(22==>-=≤x X P x X P .25.0)360()360360()(111=-Φ=-<-=<x x X P x X P ,查标准正态分布表知03601<-x ,∴03601>--x ,则75.0)360(1)360(11=-Φ-=--Φx x 查标准正态分布表,有7486.0)67.0(=Φ,7517.0)68.0(=Φ,75.02)68.0()67.0(=Φ+Φ,∴675.0268.067.03601=+=--x ,即975.571=x .5833.0360()360360()(222=-Φ=-≤-=≤x x X P x X P ,查标准正态分布表知5833.0)21.0(=Φ,∴21.03602=-x ,即63.602=x .18.某高校入学考试的数学成绩近似服从正态分布)100,65(N ,如果85分以上为“优秀”,问数学成绩为“优秀”的考生大致占总人数的百分之几?解:设X 为考生的数学成绩,则X ~)100,65(N ,于是)85(1)85(≤-=>X P X P )1065851065(1-≤--=X P 0228.09772.01)2(1=-=Φ-=,即数学成绩为“优秀”的考生大致占总人数的2.28%.19.设随机变量X 的分布律为求2X Y =的分布律.解:Y 所有可能的取值为0,1,4,9,则51)0()0(====X P Y P ,307)1()1()1(==+-===X P X P Y P ,51)2()4(=-===X P Y P ,3011)3()9(====X P Y P ,∴Y 的分布律为20.设随机变量X 在)1,0(上服从均匀分布,求:(1)X Y e =的概率密度;(2)X Y ln 2-=的概率密度.解:由题设可知⎩⎨⎧<<=其他.,0,10,1)(x x f ,(1)当0≤y 时,=≤}{y Y ∅,X 2-1-013P5161511513011X 0149P51307513011∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;e 0<<y 时,)e ()()(y P y Y P y F X Y ≤=≤=)(ln )ln (y F y X P X =≤=,此时,yy f y y y F y F y f X XY X 1)(ln 1)(ln )(ln )()(=='⋅'='=;e ≥y 时,1)()(=≤=y Y P y F Y ,0)(=y f Y ;∴⎪⎩⎪⎨⎧<<=其他.,0,e 0,1)(y y y f Y .(2)当0≤y 时,=≤}{y Y ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;当0>y 时,)e ()ln 2()()(2y Y X P y X P y Y P y F -≥=≤-=≤=)e (1)e (122y X y F X P ---=<-=,此时,222e 21)e ()e ()()(yy y X Y X F y F y f ---='⋅'-='=;∴⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY .21.设X ~)1,0(N ,求:(1)X Y e =的概率密度;(2)122+=X Y 的概率密度;(3)X Y =的概率密度.解:由题知22e 21)(x X xf -=π,+∞<<∞-x ,(1)0≤y 时,=≤=}e {y Y X ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;0>y 时,)(ln )ln ()e ()()(y F y X P y P y Y P y F X X Y =≤=≤=≤=,此时,2)(ln 2e 21)(ln 1)(ln )(ln )()(y X XY X y f yy y F y F y f -=='⋅'='=π;综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2)(ln 2y y y f y Y π.(2)1<y 时,=≤+=}12{2y X Y ∅,∴0)()(=≤=y Y P y F Y ;1≥y 时,21()12()()(22-≤=≤+=≤=y X P y X P y Y P y F Y )2121(-≤≤--=y X y P 当1=y 时,0)(=y F Y ,故1≤y 时,0)(=y F Y ,0)(=y f Y ;当1>y 时⎰⎰------==210221212d e22d e21)(22y x y y x Y x x y F ππ,此时,41e)1(21)()(---='=y Y Y y y F y f π,综上,⎪⎩⎪⎨⎧≤>-=--.1,0,1,e )1(21)(41y y y y f y Y π.(3)0<y 时,=≤=}{y X Y ∅,∴0)()()(=≤=≤=y X P y Y P y F Y ,0≥y 时,)()()()(y X y P y X P y Y P y F Y ≤≤-=≤=≤=)()(y F y F X X --=,0=y 时,0)(=y F Y ,∴0≤y 时,有0)(=y F Y ,0)(=y f Y ;0>y 时,22e 22)()()()()(y X X Y Y Y yf y f y F y F y f -=-+=-'+'=π,综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 22)(22y y y f yY π.22.(1)设随机变量X 的概率密度为)(x f ,+∞<<∞-x ,求3X Y =的概率密度.(2)设随机变量X 的概率密度为⎩⎨⎧>=-其他.,00,e )(x x f x 求2X Y =的概率密度.解:(1)0=y 时,0)()(=≤=y Y P y F Y ,0)(=y f Y ;0≠y 时,)()()()()(333y F y X P y X P y Y P y F X Y =≤=≤=≤=,3233331())(()()(-⋅=''='=y y f y y F y F y f XY Y ;∴⎪⎩⎪⎨⎧=≠=-.0,0,0),(31)(332y y y f y y f Y .(2)由于02≥=X Y ,故当0<y 时,}{y Y ≤是不可能事件,有0)()(=≤=y Y P y F Y ;当0≥y 时,有)()(()()()(2y F y F y X y P y X P y Y P y F X X Y --=≤≤-=≤=≤=;因为当0=y 时,0)0()0()(=--=X X Y F F y F ,所以当0≤y 时,0)(=y F Y .将)(y F Y 关于y 求导数,即得Y 的概率密度为⎪⎩⎪⎨⎧≤>-+=.,;,000)](([21)(y y y f y f y y f X X Y ,⎪⎩⎪⎨⎧≤>+=-.0,0,0),e e (21y y yyy .23.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他.,0,0,2)(2ππx xx f 求X Y sin =的概率密度.解:由于X 在),0(π内取值,所以X Y sin =的可能取值区间为)1,0(,在Y 的可能取值区间之外,0)(=y f Y ;当10<<y 时,使}{y Y ≤的x 取值范围是),arcsin []arcsin ,0(ππy y - ,于是}arcsin {}arcsin 0{}{ππ<≤-≤<=≤X y y X y Y .故)arcsin ()arcsin 0()()(ππ<≤-+≤<=≤=X y P y X P y Y P y F Y ⎰⎰-+=ππyX y X x x f x x f arcsin arcsin 0d )(d )(⎰⎰-+=ππππyy x xx xarcsin 2arcsin 02d 2d 2,上式两边对y 求导,得22222121)arcsin (21arcsin 2)(yyy yyy f Y -=--+-=ππππ;综上,⎪⎩⎪⎨⎧<<-=其他.,0,10,12)(2y y y f Y π.。
河海大学概率论与数理统计2习题二参考答案

概率统计——习题二参考解答2.1 (1)2001500110110090400CC C P =;(2).120015001991100140020015002001100CC C CC P --=2.2 测试5次,即就是从10个晶体管中不放回地抽取5个晶体管,基本事件的总数为510A 。
设事件A 表示“经过5次测试,3个次品都已找到”,这就是说在前4次测试中有2次找到次品,而在第5次测试时找到了最后一个次品,由于3个次品均可以在最后一次被测试到, 所以事件A 所包含的基本事件为!32724A C ,因此,所求概率为201!3)(5102724==AA C A P2.3 设1B ={所取的三个字母中不含a},2B ={所取的三个字母中不含b}。
另见,212121,,B B C B B B B B A =⋃==,从而145)()(383621===CC B B P A P ,2825)()()()()(383638373837212121=-+=-+=⋃=C C C C C C B B P B P B P B B P B P ,5615)()(38261121===CC C B B P C P 。
2.4 (见指南1.11) P =1-P (无成双)=!4/9101112215121)(1441242681241246⋅⋅⋅⋅-=-=-C C C C C=1-16/33=17/33≈0.515.2.5 由于},,,,,,,{ THTT HTHH THH HTT TT HH S =故(1) P =P ({HH ,TT ,HTT ,THH ,HTHH ,THTT ,HTHTT ,THTHH })1615)1248(161)3211618141(2=+++=+++=;(2).324/114/12)41(2)212121(21242=-⋅==++++=∑∞=k k kP2.6 设i A ——第i 人取得红球,则由乘法公式即得 .10,,2,1,101)( ==i A P i2.7 证明:因为)()()()(AB P B P A P B A P -+=⋃,而0)(≥AB P ,所以)()()(B P A P B A P +≤⋃,又B A AB ⋃⊂,故)()(B A P AB P ⋃≤,又由于 1)()()()(1-+=--B P A P B P A P =)())(1()(1)()(AB P B A P AB P B A P AB P ≤⋃--=-⋃+, 从而, 有)()()()()()(1B P A P B A P AB P B P A P +≤⋃≤≤--2.8 (1))()()()()()()()|(B A P B P A P B A P A P B A P BA P B A B P -+-=⋃=⋃/314.0)4.01()3.01(4.0)3.01(=--+---=;(2))()|()()()()()()(AB P B A P AB P A P AB P B P A P B A P -+=-+=⋃.31)31)(41](12/11[41)|()(]1)|(1[)(=-+=-+=A B P A P B A P A P2.9 设A 1、A 2——分别表示取出的零件来自第一、二箱,B 1、B 2——分别表示第 一、二次取出的零件是一等品,则(1)522121)|()()|()()(1301181501102121111=+=+=C C C C A B P A P A B P A P B P ;(2).4856.0294932305/2)//(21)()()|(23021825021012112≈⨯⨯=+==C C C C B P B B P B B P2.10 设i H ——飞机被击中i 次,i =0,1,2,3, B ——飞机被击落,则.)|()()(3∑==i i iH B P HP B P其中 ;1)|(),|(,2.0)|(,0)|(3210===H B P H B P H B P H B P36.0)7.0)(5.01)(4.01()7.01)(5.0)(4.01()7.01)(5.01(4.0)(1=--+--+--=H P , 41.0)7.0)(5.0)(4.01()7.0)(5.01)(4.0()7.01)(5.0(4.0)(2=-+-+-=H P ,14.0)7.0)(5.0(4.0)(3==H P ;故.458.014.0)6.0(41.0)2.0(36.0)|()()(3=++==∑=i i iH B P HP B P2.11 设A 1、A 2、A 3、A 4——分别表示朋友乘火车、轮船、汽车、飞机来,B ——朋友迟到。
概率论第二章课后习题答案

概率论与数理统计第二章习题[])()()()()式,有利用(显然)()(则若))(()()(从而)()()()(的可加性,有:互不相容,因此由概率与而)(则解:AB P A P AB A P B A P A AB AB A P B A P A B B P A P B A P B A P B P B A B P A P B A B C A B A A B -=-=-⊂-=-⊄-=--+=-=--=⊂**.132)(1)()()(1)()()()|()4(2.05.01.0)()()|()3(25.04.01.0|)2(8.0)1(.2=--=--=========-+=B P AB P A P B P B A P B P B A P B A P A P AB P A B P B P AB P B A P AB P B P A P B A P )()()()()()()(解:7.0)(1)|(1)|()4(4.0)(1)|(1)|()3(72.0)()()()()()()()()2(3.0)()()()()()()|(1.3=-=-==-=-==⋅-+=-+===⋅==A PB A P B A P B P A B P A B P B P A P B P A P AB P B P A P B A P B P B P B P A P B P AB P B A P )解:()()()()()(”成立时“或当)()(”成立时“)(当)()()()()()()(解:B P A P B A P A P AB P A AB B A B AB P A P B A A AB P B A P B P A P AB P B P A P B A P +≤≤≤∴⊆=∅==≤∴⊆==≥+∴-+= 0.4)()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()解:(C P B A P C P B A P C P B P A P C B A P C B A P C P AB P C P B P A P ABC P C AB P B A P C P AB P B P A P C P B P A P B P A P C P C P B P A P C P B P C P A P ABC P BC P AC P BC AC P C B A P ⋅-=⋅=⋅⋅==-⋅=⋅⋅===-+=-+=-+=-+==][][3][2][][][1.7832.04.03.06.03.04.03.06.04.06.03.04.06.0)()()()()()()()()(3.04.0200150)(4.06.0150100)(6.020*******.8=⨯⨯+⨯-⨯-⨯-++=+---++===⨯==⨯======ABC P CA P BC P AB P C P B P A P C B A P D P C P B P A P D C B A )(“击中目标”米处射击”“相距米处射击”“相距米处射击”“相距解:设2112632112|31812|6)2(3.0185|8)1(.9222222222222111111111=++++============ )()()()()()()(”“点数和大于“点数和为奇数”)()()()()(”“点数和为“点数和为偶数”解:B P B A P B A P A P B A P A B P B A A P B P A P B A P A B P B A5360160126047514131413141513151413151413151.10=+-=⨯⨯+⨯-⨯-⨯-++=+---++=======)()()()()()()()()(,)(,)(“丙破译密码”“乙破译密码”“甲破译密码”解:ABC P BC P AC P AB P C P B P A P C B A P C P B P A P C B A61|1011|.11110=====)()()()()()(解:B P AB P B A P C A P AB P A B P1025515510530520|12C C C C C A B P A P AB P B A ⋅⋅=⋅===)()()(球各半”“第二次取出的黄、白球”“第一次取出的全是黄。
概率论习题2答案

习题22.1 (2)抛掷一颗匀称质骰子两次, 以X 表示前后两次出现点数之和,求X 的概率分布,并验证其满足(2.2.2)式。
2.1解:样本空间为{})6,6(),....,1,2(),16(),...,2,1(),1,1(=Ω,且每个样本点出现的概率均为361,X 的所有可能的取值为2,3,4,5,6,7,8,9,10,11,12,且有 {}{}{}363)2,2(),1,3(),3,1()4(,362)1,2(),2,1()3(,361)1,1()2(=========P X P P X P P X P类似地,365)6(,364)5(====X P X P ,365)8(,366)7(====X P X P ,363)10(,364)9(====X P X P ,361)12(,362)11(====X P X PX 的概率分布为36118112191365613659112118136112111098765432kp X 满足:1362/652636543212366)(122=⨯⨯+=+++++==∑=k k X P 2.2设离散随机变量X 的概率分布为 {}kP X k ae -==, k=1,2,…,试确定常数.a2.2解:由于11111)(1--∞=-∞=-====∑∑e e a aek X P k kk ,故1111-=-=--e ee a2.3 甲、乙两人投篮,命中率分别为0.7,和0.4,今甲、乙两人各投篮两次,求下列事件的概率:(1)两人投中的次数相同 ; (2)甲比乙投中的次数多。
2.3解:设Y X ,分别为甲、乙投中的次数,则有)4.0,2(~),7.0,2(~B Y B X ,因此有2,1,0,)6.0()4.0()(,)3.0()7.0()(2222=====--k C k Y P C k X P k k kk k k(1) 两人投中次数相同的概率为∑======23142.0)()()(k k Y P k X P Y X P(2) 甲比乙投中次数多的概率为5628.0)]1()0()[2()0()1()()()(2==+==+===<==>∑=Y P Y P X P Y P X P k Y P k X P Y X P k 2.4设离散随机变量X 的概率分布为 {}12kP X k ==, k=1,2,….求 (1){}2,4,6,...P X =; (2){}2.5P X ≥;2.4解:(1){}4.015615321)3()2()1(31==++==+=+==≤≤X P X P X P X P (2){}2.01531521)2()1(5.25.0==+==+==<<X P X P X P2.5设离散随机变量X 的概率分布为 {}15kk X P ==, k=1,2,3,4,5.求(1){}13P X ≤≤; (2){}0.5 2.5P X <<;2.5解:(1){}314/114/14121)2(,...6,4,21121=-======∑∑∑∞=∞=∞=k k k k k k X P X P (2)25.0412/118/121)()3(33==-====≥∑∑∞=∞=k kk k X P X P 2.6 设事件A 在每次试验中发生的概率为0.4,当A 发生3次或3次以上时,指示灯发出信号,求下列事件的概率.(1)进行4次独立试验,指示灯发出信号; (2)进行5次独立试验,指示灯发出信号;2.6解:设X 为4次独立试验时事件A 发生的次数,设Y 为5次独立试验时事件A 发生的次数,则有)4.0,5(~),4.0,4(~B Y B X (1)所求概率为:1792.04.06.04.04)4.01(4.0)4.01(4.0)4()3()3(434444434334=+⨯⨯=-+-==+==≥--C C X P X P X P(2)所求概率为:31744.04.06.04.056.04.010)4.01(4.0)4.01(4.0)4.01(4.0)5()4()3()3(5423555554544535335=+⨯⨯+⨯⨯=-+-+-==+=+==≥---C C C Y P Y P Y P Y P2.7 某城市在长度为t (单位:小时)的时间间隔内发生火灾的次数X 服从参数为0.5t 的泊松分布,且与时间间隔的2无关,求下列事件的概率. (1)某天中午12点到下午15点末发生火灾;(2)某天中午12点到下午16点至小发生两次火灾。
概率论第二版课后习题答案第二章(龙版)
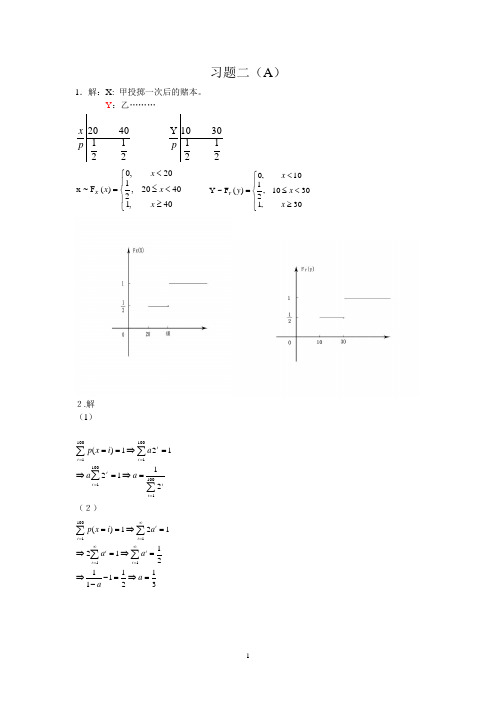
习题二(A )1.解:X: 甲投掷一次后的赌本。
Y :乙……… 21214020p x 21213010Y p ⎪⎩⎪⎨⎧≥<≤<=40,14020,2120,0)(F ~x x x x x X ⎪⎩⎪⎨⎧≥<≤<=30,13010,2110,0)(F ~Y x x x y Y2.解(1)∑∑∑∑=====⇒=⇒=⇒==10011001100110012112121)(i ii i i i ia a a i x p(2)31211112112121)(1110011=⇒=--⇒=⇒=⇒=⇒==∑∑∑∑∞=∞==∞=a a a a ai x p i i i i i i i3.解 21 51 101512 0 25X --p 4.解(1)X:有放回情形下的抽取次数。
P (取到正品)=107C C 11017=P (取到次品)=103 107)103( 107)103( 107 103,107i 3 2 1X 1-i 2 ⋅p(2)Y:无放回情形下。
778192103 87 92103 97 103 1074 3 2 1 Y ⋅⋅⋅⋅⋅⋅p5.解54511)5(1)3(1)3P(=-=-=-=-≤-=->X p X p X 542)P(X 0)P(X )2()33()3X P(==+=+-==<<-=<X p X p 107)5()2()3()1()21P(2)1()21X P(=-=+==-<+>=-<++>+=>+X p X p X p X p X X p6.解(1)根据分布函数的性质11)1()(2lim 1lim 1=⇒=⇒=++→→A Ax F x F x x (2))5.0()8.0()8.05.0(F F X P -=≤<225.08.0-==0.39 7.解:依据分布满足的性质进行判断: (1)+∞<<∞-x单调性:+∞<<<⇒<x x F x F x x 0).()(2121在时不满足。
江西财经大学概率论第二章习题解答

1 2.5 11 0.5 12.50.5
1 0.9938 0.6915 0.6977
4由正态分布密度函数的对称性得k 3
13
2021年6月3日6时26分
第
P44 2.4.4 X ~ N 1600, 2 , X 1600 ~ N 0,1
二 章
习
题
P 1200 X 2000
P
1200 1600
2021年6月3日6时26分
第
P36练习2.2
二 章
习
3 解: X的分布律为
题 解
PX
k
C C k nk M NM CNn
,k
0,1, 2,
, min n, M
答
2021年6月3日6时26分
P36练习2.2
4 解:A=其中含a个白球b个黑球
1
P
A
CaCb C ab
+
2
P
A
CaCb
习 题
解
1 P X 2 1 P X 2 1 P X 0 P X 1 答
1 C80 0.30 0.78 C81 0.31 0.77 0,.7447
2 n 1 p 8 1 0.3 2.7 2
击中2次的概率最大。
P X 2 C820.32 0.76 0.2965
解 答
分布函数为 x在2的左边,取<号, 不左连续
0
1
F
x
1
36
2
36 36
往下累加
x2
规律:小x左闭右开
2 x3
x在2的右边,取 号, 右连续
3 x4
2021年6月3日6时26分
P37 练习2.3 题2
大学概率论——第二章 习题解

P X n 0.00023
查表知: n 15
所以仓库在月初要库存此种商品15件,才能
保证当月不脱销的概率为0.99977。
P81 13、设随机变量X的分布函数为
0 2 F x x 1 x0 0 x 1 x 1
1 P 0.3 X 0.7 , P( X ) 求 1) 2
1 1 1 C C 1 5 2 P X 2 5 2 4 6
1 1 11 C C 1 6 2 P X 2 6 2 36 6
所以X2的分布律为:
X2
P
1
1 36
2 1 12
3
5 36
4 7 36
5 1 4
6 11 36
P80 5、箱子里装有a个白球,b个黑球,从中一次
F A
2
B 1
1 1 x , 3) f x F x 2 2 1 x 1 x
1
P81 15、设随机变量X的概率密度为
0 x 1 x 求:1)X的分布函数; f x 2 x 1 x 2 P X 0.5 , 2 ) 0 其他 P X 1.3 , P 0.2 X 1.2 .
3 1 P X 1 10 2 6 12 1 1 P X 1 12 2 6 36
P X 1 11
2 1 2 6 18
所以X1的分布律为:
X1 2 3 4
P
1 1 1 36 18 12
5 1 9
6 5 36
7 8 1 5 6 36
9 1 9
10
2)X的概率密度。
解: 1) P 0.3 X 0.7 F 0.7 F 0.3
概率论与数理统计习题二答案

概率论与数理统计习题二答案概率论与数理统计习题二答案概率论与数理统计是一门重要的数学学科,广泛应用于各个领域。
习题是学习这门学科的重要方式之一,通过解答习题可以巩固理论知识,提高问题解决能力。
本文将针对概率论与数理统计习题二给出详细的答案解析。
1. 设事件A和事件B为两个相互独立的事件,且P(A) = 0.3,P(B) = 0.4。
求P(A并B)和P(A或B)。
解析:由于事件A和事件B是相互独立的,所以P(A并B) = P(A) * P(B) = 0.3 * 0.4 = 0.12。
而P(A或B) = P(A) + P(B) - P(A并B) = 0.3 + 0.4 - 0.12 = 0.58。
2. 一批产品中有10%的次品,从中随机抽取5个产品进行检验,求恰好有3个次品的概率。
解析:设事件A为恰好有3个次品,事件B为抽取的5个产品中有3个次品。
根据二项分布的概率公式,P(B) = C(5, 3) * (0.1)^3 * (0.9)^2 = 10 * 0.001 * 0.81 = 0.0081。
因此,恰好有3个次品的概率为0.0081。
3. 一批产品的质量服从正态分布,已知平均值为μ,标准差为σ。
从中随机抽取一个样本,样本容量为n。
求样本均值的期望值和方差。
解析:样本均值的期望值为总体均值μ,样本均值的方差为总体方差除以样本容量n。
因此,样本均值的期望值为μ,方差为σ^2/n。
4. 设X和Y是两个随机变量,它们的协方差为Cov(X, Y) = 5,方差分别为Var(X) = 9,Var(Y) = 16。
求随机变量Z = 2X + 3Y的方差。
解析:根据随机变量的性质,Var(Z) = Var(2X + 3Y) = 4Var(X) + 9Var(Y) +12Cov(X, Y) = 4 * 9 + 9 * 16 + 12 * 5 = 36 + 144 + 60 = 240。
5. 设X服从参数为λ的指数分布,即X ~ Exp(λ)。
《概率论与数理统计》习题二答案解析

《概率论与数理统计》习题及答案习题二1•一袋中有5只乒乓球,编号为1 , 2, 3, 4, 5,在其中同时取3只,以X 表示取出的3只 球中的最大号码,写出随机变量 X 的分布律•【解】X =3,4,5 3P(X =4) 3 =0.3 C 5C 2P(X =5)3=0.6C52•设在15只同类型零件中有 2只为次品,在其中取 3次,每次任取1只,作不放回抽样, 以X 表示取出的次品个数,求: (1)X 的分布律; (2)X 的分布函数并作图;(3)1 3 3P{X }, P{1 :: X }, P{1 乞 X }, P{1 :: X :: 2}.2 2 2【解】X =0,1,2. C 13 P(X =2)13C15P(X =3) C ;= 0.1P(X =0) C 13C152235P(X =1)C ;C 23C 512 35丄 3534 34 门 0 2' 2' ' '35 3533 12P(1 _ X ) = P(X =1)P(1 :: X 厂2 2 3534 1P(1 ::: X ::2) = F(2) _ F(1)_ P(X =2) =1 0.35 35 3•射手向目标独立地进行了 3次射击,每次击中率为 0.8,求3次射击中击中目标的次数的 分布律及分布函数,并求 3次射击中至少击中 2次的概率. 【解】设X 表示击中目标的次数.则X=0,1,2,3.P(X = 0) = (0.2)3 = 0.0081 2P(X =1)70.8(0.2) =0.096 P(X 二 2) =C 3(O.8)2O.2 = 0.384P(X =3) =(0.8)3 =0.512故X 的分布律为 X 0 1 2 3 P0.0080.0960.3840.512分布函数” 0,X <00.008, 0 兰 xc1F(X )» 0.104, 1^x<20.488, 2 兰x<31,x^3P(X — 2) = P(X =2) P(X =3^ 0.8964.( 1)设随机变量X 的分布律为P{X=k}= a -,k!其中k=0, 1, 2,…,入〉0为常数,试确定常数 a.(2)设随机变量X 的分布律为P{ X=k}= a/N ,k=1, 2,…,N ,试确定常数a.0,x ::: 0 22 0 _ x :: 13534 1 _x :: 2351, x_2F(x)= (2)当 x<0 时,F (x ) =P (X w x ) =0当 0 w x<1 时, F (x ) 当 1 w x<2 时, F (x ) 22 =P (X w x ) =P(X=0)=- 35 34 =P (X w x ) =P(X=0)+P(X=1)=-35当x >2时,F 故X 的分布函数(x ) =P (X w x ) =1 1 1 22P(X =)★(;) ,2 2 353 3P(1 ::: X ) = F(:)-【解】(1)由分布律的性质知二:• k1 P(X 二k) =a aLe'k z0 k^o k!故 a = e_,(2)由分布律的性质知N Na1 =為P(X =k) akw k a N即 a = 1.5•甲、乙两人投篮,投中的概率分别为0.6,0.7,今各投3次,求:(1)两人投中次数相等的概率;(2)甲比乙投中次数多的概率.【解】分别令X、Y表示甲、乙投中次数,贝U X~b (3, 0.6) Y~b(3,0.7)(1) P(X 二Y)二P(X =0,Y =0) P(X =1,Y =1) P(X =2,Y =2)P(X =3,Y =3)3 3 1 2 1 2-(0.4) (0.3) C30.6(0.4) C30.7(0.3) +2 2 2 23 3C3(0.6) 0.4C3(0.7) 0.3 (0.6) (0.7)=0.32076(2) P(X Y) = P(X =1,Y =0) P(X =2,Y =0) P(X =3,Y =0)P(X =2,Y =1) P(X =3,Y =1) P(X =3,Y =2)1 2 3 2 2 3-C30.6(0.4) (0.3) C3(0.6) 0.4(0.3)3 3 2 2 1 2(0.6) (0.3) C3(0.6) 0.4C30.7(0.3)(0.6)3C;0.7(0.3)2(0.6)3C:(0.7)20.3=0.2436•设某机场每天有 200架飞机在此降落,任一飞机在某一时刻降落的概率设为 0.02,且设各飞机降落是相互独立的•试问该机场需配备多少条跑道,才能保证某一时刻飞机需立即降 落而没有空闲跑道的概率小于0.01(每条跑道只能允许一架飞机降落)?【解】设X 为某一时刻需立即降落的飞机数,则X~b(200,0.02),设机场需配备 N 条跑道,则有P(X ■ N) <0.01200即送 C k 00(O.O2)k (O.98)200上 £0.01k =N 1利用泊松近似-np = 200 0.02 = 4.血 e 44kP(X_N)0.01宀k!查表得N > 9.故机场至少应配备 9条跑道.7. 有一繁忙的汽车站,每天有大量汽车通过,设每辆车在一天的某时段出事故的概率为0.0001,在某天的该时段内有 1000辆汽车通过,问出事故的次数不小于 2的概率是多少(利 用泊松定理)?【解】设X 表示出事故的次数,则 X~b (1000, 0.0001)P(X _2) =1 -P(X =0) -P(X =1)0.1 0.1=1 —e - 0.1 e8.已知在五重贝努里试验中成功的次数 X 满足P{X=1}= P{X=2},求概率P{X=4}.【解】设在每次试验中成功的概率为p ,则14 2 2 3C 5p(1 - p) 9p (1 - p)9.设事件A 在每一次试验中发生的概率为 0.3,当A 发生不少于3次时,指示灯发出信号 (1)进行了 5次独立试验,试求指示灯发出信号的概率;(2)进行了 7次独立试验,试求指示灯发出信号的概率.【解】(1)设X 表示5次独立试验中 A 发生的次数,则 X~6 ( 5, 0.3)5P(X 工3)=送 c 5(0.3)k (0.7)5^ =0.16308k=3⑵ 令Y 表示7次独立试验中 A 发生的次数,则 Y 〜b ( 7,0.3)故 所以P(X =4)=C :(1)4拿10 2437 ■—k k 7 —kP(Y^3)=送C k(0.3)k(0.7)7=0.35293 k=310•某公安局在长度为t 的时间间隔内收到的紧急呼救的次数X 服从参数为(1/2) t 的泊松分63 1 13.进行某种试验,成功的概率为一,失败的概率为一.以X 表示试验首次成功所需试验的次44数,试写出X 的分布律,并计算 X 取偶数的概率. 【解】X =1,2,,k,|||1 k —1 p (x =k )y4P(X =2) P(X =4)P(X =2k)谱64 W …布,而与时间间隔起点无关(时间以小时计)(1) (2) 【解】(1) 求某一天中午12时至下午 求某一天中午12时至下午3P(X =0)3时没收到呼救的概率; 5时至少收到1次呼救的概率.5(2) P(X _1) =1 — P(X =0) =1 -k k2 _k11.设 P{X=k}= C 2P (1 - p) ,k=0,1,2mm4_mP{ Y=m}= C 4 p (1 - p)m=0,1,2,3,45分别为随机变量 X , Y 的概率分布,如果已知 P{X > 1}=,试求P{ Y > 1}.954I 解】因为P(X 牛,故P(X (9)P(X ::: 1) = P(X =0) =(1 - P)2故得24(仆)飞1 「3从而P(Y _1) =1 _P(Y =0) =1_(1_ p)465 0.80247810.001,试求在这 2000册书中 12•某教科书出版了 2000册,因装订等原因造成错误的概率为 恰有5册错误的概率. 【解】令X 为2000册书中错误的册数,则X~b(2000,0.001).利用泊松近似计算,■ - np 二 2000 0.001 二 2P(X =5)「255!-0.001811 514•有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险•在一年中每个人死亡的概率为0.002,每个参加保险的人在 1月1日须交12元保险费,而在死亡时家属可从 保险公司领取2000元赔偿金•求: (1) 保险公司亏本的概率; (2)保险公司获利分别不少于 10000元、20000元的概率.【解】以“年”为单位来考虑.(1) 在1月1日,保险公司总收入为 2500 X 12=30000元. 设1年中死亡人数为 X ,则X~b(2500,0.002),则所求概率为P(2000X • 30000) =P(X 15) P(X <14)由于n 很大,p 很小,入=np=5,故用泊松近似,有:4 e'5kP(X 15) = 10.000069k 竺k !⑵P(保险公司获利不少于 10000)= P(30000 -2000X _ 10000) =P(X < 10)20000) = P(30000 -2000X 一20000) = P(X 乞5)5 _5 k_ e 5 0.615961 k =0 k!即保险公司获利不少于 20000元的概率约为62% 15.已知随机变量 X 的密度函数为f(x)=Ae ,「8 <x<+ ,求:(1) A 值;(2) P{0<X<1}; (3) F(x).【解】(1)由 f (x)dx =1得1=Ae ^dx =2 Ae "dx =2A--:: 01 故 A . 2⑵ p(0 :X ::1)匚 0「dxs (1-e')⑶当x<0时,x1 1F (x )=[石 e x dx 匚 e x10k =0k!0.986305即保险公司获利不少于 10000元的概率在 98%以卜.P (保险公司获利不少于中任意小区间内的概率与这小区间长度成正比例,试求 X 的分布函数 【解】 由题意知X~ U [0,a ],密度函数为故当x<0时F (x ) =0 当 0< x w a 时 F(x)=当 x >0 时,F(x)= f^e X dx + 2 -::22 [-e~dx o 2F(x) =1 x 0 -e , x :::0 1」e 」x_0 2 16•设某种仪器内装有三只同样的电子管,电子管使用寿命 100, X —100,x x ::100. 在开始150小时内没有电子管损坏的概率; 在这段时间内有一只电子管损坏的概率; F ( x ). X 的密度函数为f(x)= 0,求: (1)(2) (3) 【解】 (1) 150 100 1 P(X < 150) r dx . ' )応 x 2 3 3 2 3 8 P 1 <P(X 150)]3 珂2)3 二石 3 2/⑵卩2 二 c ;3(2)2 ⑶当 x<100 时 F (x ) =0 x 当 x > 100 时 F(x) f (t)dtJ JO O 100 x 」(t )d t100f (t )dtx豁1t 2100x i 0,x _100x ::17•在区间]0, a ]上任意投掷一个质点,以 X 表示这质点的坐标,设这质点落在]1f (X )二 a' 0,0乞x 乞a其他xx;f (t )dt 「0x1 xf(眄0了蔦当 x>a 时,F (x ) =1即分布函数x F(x)二l a 1,18.设随机变量X 在[2 , 5]上服从均匀分布•现对 值大于3的概率. 【解】X~U [2,5],即Pf(x) = 3’【0,故所求概率为119•设顾客在某银行的窗口等待服务的时间X(以分钟计)服从指数分布E(-).某顾客在窗口55次,以Y 表示一个月内他未等 P{Y > 1}.> _xf(x)二孑5【0,该顾客未等到服务而离开的概率为Y~b(5,e 冷,即其分布律为P(Y =k) =c 5(e')k (1—e')5=k =0,1,2,3,4,5P(Y 一1)=1 -P(Y = 0) =1 -(1-e‘)5 =0.516720.某人乘汽车去火车站乘火车,有两条路可走.第一条路程较短但交通拥挤,所需时间X 服从N (40, 102);第二条路程较长,但阻塞少,所需时间 X 服从N (50, 42).(1)若动身时离火车开车只有 1小时,问应走哪条路能乘上火车的把握大些?(2) 又若离火车开车时间只有 45分钟,问应走哪条路赶上火车把握大些? 【解】(1)若走第一条路,X~N (40, 102),则「0, x :: 0P(X 3)=Qdx =3 3X 进行三次独立观测,求至少有两次的观测其他p=c 3(2)21 c 3(2)3 3 3 3 20 27等待服务,若超过10分钟他就离开•他一个月要到银行 到服务而离开窗口的次数,试写出 Y 的分布律,并求1【解】依题意知X ~ E(”),即其密度函数为x'5dx = -2ef x —4060—40 )斗 P(X :::60) = P(2) =0.97727V 1010 丿若走第二条路,X~N ( 50, 42),则X 「50 60「50 P(X ::: 60) = P(2.5) = 0.9938++V 441故走第二条路乘上火车的把握大些•(2)若 X~N (40, 102),则P(X :::45)=P X -4° :: 45一4° =::,(0.5)=0.6915I 10 10 丿若 X~N (50 , 42),则:::45 -5° = : :」(_1.25)4=1 -门(1.25) =0.1056故走第一条路乘上火车的把握大些.21•设 X~N (3,22),(1) 求 P{2<X<5}, P{4<X <10} , P{ | X |> 2}, P{X >3}; (2)确定 c 使 P{X > c}= P{X < c}.【解】(1) P(2:::X E5)=P 口」3 空口V 2 2 2 丿()2 () 2= 0.8413 -1 0.6915 =0.5328 P(—4 ::X —10) =P i.X 色一!^3V 222 丿 =O.9996P(| X | 2) = P(X 2) P(X :: -2)f X -3 2_3]丄 f X -3 _2_3; =P --------- > ------ (+P ---------- < ---------I 2 2丿 12 2丿 “—①i —丄①i —5匚①I 丄r —①i-l 2丿I 2丿12丿 12丿-0.6915 1 -0.9938 =0.6977P(X ::45) = P X -50—4X —3 3-3P(X 3) = P() J —::」(0) =0.5⑵c=322. 由某机器生产的螺栓长度(cm ) X~N (10.05,0.062),规定长度在10.05土 0.12内为合格品 求一螺栓为不合格品的概率.=1一门(2)亠处(一2)=2[1-::」(2)]二 0.045623. 一工厂生产的电子管寿命 X (小时)服从正态分布 N (160, (I),若要求P{120 v X < 200 =>0.8,允许i 最大不超过多少?(1) 求常数A , B ;(2) 求 P{X W 2} , P{X > 3}; (3)求分布密度f (x ).匹 F(x)=1 「A = 1【解】(1)由 … 得伽+F (x)巳监F(x)旧一1(2) P(X _2) = F(2) =1 -e ,'P(X 3) =1 _F(3) =1 _(1_eA )25.设随机变量X 的概率密度为・x,f (x )=」2 - x,0,求X 的分布函数F (x ),并画出f (x )及F (x )f (x^ F (x)0,x 一0 x :: 0 【解】P(|X -10.05| 0.12) =PX —10.05 0.060.12>0.06』【解】P(120::"200)=P 1^1坐3 乞叱型 故24.设随机变量X 分布函数为40-31.251.29F (x )A Be*,0,x 一0,x 0.0 空 x :: 1,仁 x :: 2,【解】当x<0时F (x ) =0xtdt当 1W x<2 时 F(x)二 f (t)dt1-0tdt (2-t)dt1 2x22 2 2x2x -1x 当 x >2 时 F (x) f (t)dt = 126•设随机变量X 的密度函数为(1) f(x)=ae_ |x|,入 >0;f(x)二 2c 'X2e当 x W 0 时 F (x) = J 』(x)dx =访e% = 2,当 0W x<1 时 F(x)=xJ (t)仁x.f(t)dtF(x)二x 22x 2x -1,21,x :: 0x _2⑵f(x)= 试确定常数 【解】(1)由bx, 12,x 0,0 ■ x :: 1, 1 < x < 2,其他•a,b ,并求其分布函数 F ( x )."f (x)dx =1知 1J JO O2ax 2 3即密度函数为当 x>0 时 F (x) =(x)dx =J :eMdx 壮专e —x dx故其分布函数x _01 f (x)2, |x 0,当 x < 0 时 F (x ) =0当 0<x<1 时 F(x) f (x)dx f(x)dx 亠 I f (x)dx当 1 w x<2 时 F(x)二 J-f (x)d ^j-Qdx当 x > 2 时 F (x ) =1 故其分布函数为广0, 2xJF(x)二 23_12 x1,27•求标准正态分布的上:-分位点,(1) : =0.01,求 z ; (2) : =0.003,求 z-., z-./2. 【解】(1) P(X Z.H0.01即 :G( z :.)=0.09故z —2.33x=0xdxx 21 八-3 - 2F(x)1丄」 2(2)由 1 = f°°f(x)dx = f1bxdx — dxx得即X 的密度函数为b=1x, 0 : x :: 1其他xdx1严x-0 0 ■ x ■■■ 1 1 < x ::即心(zj =0.012a(2)由 P(X .乙)=0.003得 1 (zj =0.003即 :•:」(乙)=0.997 查表得乙.=2.75由 P(X z ./2) =0.0015 得1-:」(Z-./2)=0.0015即 ■->( Z") =0.9985查表得z :./2 =2.96求Y=X 的分布律.【解】Y 可取的值为0, 1, 4, 9P(Y =0) =P(X =0)」5P(Y =1) = P(X =「1) P(X =1)=1 -~6 15301 p (Y =4) =P(X - -2): 5 11 P(Y =9) = P(X =3)=3029•设 P{X=k}=( 1): k=1,2,…,令Y 「1,当X 取偶数时 1-1,当X 取奇数时.求随机变量X 的函数Y 的分布律.【解】P(Y =1) =P(X =2) P(X =4) "I P(X =2k)川=G )2 G )4 川(1)2k 川2 2 2 1 1 1 =()/(1 厂4 4 3P(Y =—1) = 1 — P(Y =1) = 2 30•设 X~N (0, 1).(1) 求Y=e X 的概率密度; (2) 求Y=2X 2+1的概率密度; (3)求Y= | X |的概率密度•【解】(1)当 y w 0 时,F Y (y)二 P(Y 曲)=0x当 y>0 时,F Y (y) =P(Y 空 y) =P(e < y^P(X < ln y)In y二:i- fX (x)dx(2) P(Y =2X 2 1 _1) = 1当 y w 1 时 F Y (y) =P (丫 乞 y) =02当 y>1 时 F Y (y) =P (丫 乞 y) =P(2X 1 乞 y)(y J)/2「一 R f X (x)dx故 f 丫(y)=f F 丫(y)三民:f x (厅]+f x 「F]]⑶ P(Y-0)=1当 y w 0 时 F Y (y)二 P (Y — y) =0dF y (y)11 1 j n 2y /2 JEW ,y 0= PX 2 哼二P< X <4y 4)/4e , y 1当 y>0 时 F Y (y) = P(| X 国 y)二 P( —y 乞 X 乞 y)y二 y f x (x)dx故 f Y (y):F Y (y )二 f x (y) f x (-y)dy31. 设随机变量X~U (0,1),试求:(1) Y=e x 的分布函数及密度函数; (2)Z= -21 nX 的分布函数及密度函数【解】(1) P(0 ::X :::1) =1故 p( 1 ::: Y 二 e ::: e) 1 当 y _1 时 F Y (y) =P(Y 乞 y) =0当 1<y<e 时 FY (y) =P(e X 乞 y) =P(X On y)In y「0 dx=lnyX当 y 》e 时 F Y (y)二 P(e < y) = 1 即分布函数J, y^e故Y 的密度函数为口 f Y (y)二 y,0,(2) 由 P ( 0<X<1) =1 知P(Z 0) =1当 z w 0 时,F z (z) =P(Z Ez) =0当 z>0 时,F Z (z)二 P(Z 乞 z)二 P(—2ln X ^z)=P(ln X _ -自二 P(X _e 亠2)y 0,F /(y)=七n y,y 乞1 1 ::1 ::y e故Z的密度函数为32. 设随机变量X的密度函数为2xf(x)= n io,0 ::xn其他.试求Y=sinX的密度函数.【解】P(0 Y:::1) =1当y w o 时,F Y(y)二P(Y ^y) =0当0<y<1 时,F Y(y)二P(Y 空y)二P(sin x 乞y)二P(0 :: X M arcsin y) P( n- arcsin y 玄X ::narcsiny 2x n2x2dx 2dx0 n -arcsin y 彳=4( arcsiny)2 1- arcsin®2n n2 .arcs in yn当y》1 时,F Y(y)=1故Y的密度函数为33. 设随机变量X的分布函数如下:z/2即分布函数I z/2 dx = 1 - eu a -----z<0-z/21-ez 0zMX』2,X 』2,18试填上(1),(2),(3)项.F(x) = 1 x‘(2)X-(3) •19【解】由lim F(x) =1知②填1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学概率论习题二详解(A )1、从1,2,3,4四个数码中先后任意取出两个数码(每次取一个,取后不还原),写出下列每个随机变量可能的取值: (1)=X 两个数码的数字和;(2)=Y 第一个数码与第二个数码的数字差; (3)=Z 数码为偶数的个数;(4)=W 数码为1数的个数。
解(1)3,4,5,6,7; (2),,,123---321,,; (3)0,1,2; (4)0,1 2、随机投两颗骰子,以X 表示其点数之和,写出X 可能的取值及其概率,并求)9(>X P .解 X 可能的取值:2,3,…,12;取这些值的概率:12987323613361,,,,,,/)(/)()( ==⎩⎨⎧--==i i i i i X P 18591210===>∑=i i X P X P )()( 3、设随机变量X 的分布列为4,3,2,1,2)(===i Ci X P i求C 的值。
解∑==4112i iC15/16=C4、某人进行射击,每次射击的命中率为0.02,独立射击400次,求至少击中两次的概率。
解 设击中次数为X ,则).,(~020400B X)()()()(101212=-=-=<-=≥X P X P X P X P3994009800204009801.).(.--= 99720.≈5、某厂需要12只集成电路装配仪表,要到外地采购,已知该型号集成电路的不合格品率为0.1,问需要采购几只才能以99%的把握保证其中合格的集成电路不少于12只?解 设采购n 只,不合格品数为X ,显然).,(~10n B X以题意∑-=-=-≤=≥-1290101212n k k n k k nCn X P X n P ..)()(n 取多少呢?取15=n ,94440312.)()(=≤=≥-X P X n P 取16=n ,98300412.)()(=≤=≥-X P X n P 取17=n ,99530512.)()(=≤=≥-X P X n P可见,只需要采购17只就能有99%把握保证其中合格的集成电路不少于12只。
6、在500个人的团队中,求恰有6个人的生日在元旦的概率。
解 每一个人的生日在元旦的概率3651=p ,则该团队中生日在元旦的人数),(~3651500B X 。
依题意要求494665003651136516)()()(-==C X P 由于36991.=np ,采用泊松分布近似≈=)6(X P 0023063699163699166.!.!.≈=--e eλλ7、从某商店过去的销售记录知道:某种商品每月的销售数可以用参数10=λ的泊松分布来描述,为了以%95以上的把握保证不脱销,问商店在月初至少应进多少件?(已知9166.0!1010140≈-=∑e k k k ,9513.0!1010150≈-=∑e k k k )解 令商店该商品的月销售量为X ,设每月进货N 件。
则)(~10P X 。
依题意要求95.0)(≥≤N X P即 95010100.!≥-=∑e k Nk k查泊松分布表得,14=N 和15时,有 950916601010140..!<≈-=∑e k k k ,95095130101015..!>≈-=∑e k k k 于是,为了以%95以上的把握保证不脱销,商店在月底至少应进15件 8、若随机变量X 只取一个值a ,即 1==)(a X P 求X 的分布函数)(x F ,并作出图形。
解 X 的分布函数为:ax ax x F <≥⎩⎨⎧=01)(9、在10台计算机中有2台感染了病毒,现在一台一台地抽样检查,求在发现首台未感染病毒者时已经检查过计算机的台数X 的分布函数.解 先求X 的概率分布.易见,X 有0,1,2等3个可能值,且.;; 451458541}2{45891082}1{54108}0{=--===⨯⨯=====X X X P P P 于是X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=≤=.,;,;,;,2 1 214544 1054 0 0 }{)(x x x x x X x F P10、已知随机变量X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=5 1 524320410 0 )(x x x x x F ,,,, 求随机变量X 的概率分布。
解 易见)(x F 有0,2,5等3个间断点,故随机变量X 有3个可能值.由于{}{}{},,,41431)05()5(5424143)02()2(241)00()0(0=-=--===-=--===--==F F X F F X F F X P P P 可见随机变量X 的概率分布为⎪⎪⎭⎫ ⎝⎛414241520~X . 11、已知连续型随机变量X 的分布函数⎪⎩⎪⎨⎧>≤≤<=1,110,0,0)(2x x Ax x x F求(1)系数A ;(2)X 落入)7.0,3.0(内的概率;(3)X 的密度函数。
解 (1)因为11=+→)(lim x F x ,A F =)(1 又连续型随机变量X 的分布函数)(x F 连续 则1=A(2)X 的分布函数为:⎪⎩⎪⎨⎧>≤≤<=1110002x x x x x F )(故4030703070703022...).().()..(=-=-=<<F F X P(3)X 的密度函数为:⎩⎨⎧≤≤=其它1002x x x p )( 12、已知连续型随机变量X 的分布函数(柯西分布) Barctgx A x F +=)( 求(1)系数A 、B ;(2))1(≤X P ;(3)X 的密度函数。
解 (1)12=+=+∞→πBA x F x )(lim02=-=-∞→πBA x F x )(lim解得 50.=A ,π1=B(2)X 的分布函数为arctgx x F π121+=)( 因此,21111=--=≤)()()(F F X P (3)X 的密度函数为)()(211x x p +=π 13、设随机变量X 的概率密度函数为⎩⎨⎧=,0,)(x x p λ 其他20<<x ,求(1)常数λ;(2))31(<<X P ;(3)X 的分布函数)(x F 。
解 (1)122==⎰λλxdx 2/1=λ(2) )(31<<X P 432121==⎰xdx(3)X 的分布函数2200141)()(2≥<≤<⎪⎩⎪⎨⎧==⎰∞-x x x x dt t x F xφ 14、设随机变量X 的密度函数为+∞<<∞-=-x ce x p x,)(求(1)常数c ;(2))10(<<X P 。
解 (1)1220===⎰⎰+∞-+∞∞--c dx e c dx cex x21/=c(2))(10<<X P )(e dx e x 11212110-==⎰-15、设随机变量X 的密度⎩⎨⎧<<=其他10,0,2)(x x x f 现对X 进行n 次独立重复观测,以n v 表示观测值不大于1.0的次数,求n v 的概率分布。
解 令01.02)1.0(1.00==≤=⎰xdx X P p)01.0,(~n B v n即n k q p qp C k v P kn kkn n ,,1,0,99.0,01.0,)( =====-16、某型号电子管寿命(小时)为一随机变量,密度函数为其它100,0,100)(2≥⎪⎩⎪⎨⎧=x x x p某一电子设备内配有3个这样的电子管,求电子管使用150小时都不需要更换的概率。
解 令=i A “第i 个电子管不需要更换”,X 为电子管的使用寿命=)(321A A A P 331321)]150([)]([)()()(≥==X P A P A P A P A P而321001)150(1)150(1501002=-=<-=≥⎰dx x X P X P 所以278)32()(3321==A A A P或 令=i X “第i 个电子管的使用寿命”,则278)150()150()150(321=≥≥≥X P X P X P 。
17、设随机变量X 和Y 相互独立,且都服从[1,3]上的均匀分布。
记事件}{a X A ≤=,}{a Y B >=,已知97)(=+B A P ,求常数a 。
解 97)211(211)()()()()(=----=-+=+a a B P A P B P A P B A P 解得37,35=a18、设随机变量X 服从参数21=λ的指数分布,计算:(1))3(≥X P ;(2))36(>>X X P 。
解 ⎪⎩⎪⎨⎧≤>-=-01)(21x x ex F x (1)23)3(1)3(-=-=≥e F X P (2) 由指数分布的无记忆性得)36(>>X X P 23)3(-=≥=e X P 19、设随机变量)1,0(~N X ,求:(1))33.202.0(≤≤X P ;(2))2(-<X P ;(3))3(>X P 。
解 (1)482105080099010020332332020...).().()..(=-=Φ-Φ=≤≤X P(2)022809772012122..)()()(=-=Φ-=-Φ=-<X P (3))()()(333>+-<=>X P X P X P)()(313Φ-+-Φ= )(322Φ-=9987022.⨯-= 00260.=20、设随机变量)10,50(~2N X ,(1)求)20(≤X P ;(2)求)70(>X P ;(3)求常数a ,使得90.0)(=<a X P 。
解(1))(20≤X P 00130998701313105020..)()()(=-=Φ-=-Φ=-Φ=(2))()(70170≤-=>X P X P 977201211050701.)()(-=Φ-=-Φ-= 02280.=(3)9001050.)()(=-Φ=<a a X P 查表得2811050.≈-a 862.≈a21、某种电子元件在电源电压不超过200伏,200~240伏,超过240伏三种情况下损坏的概率分别为0.1,0.001及0.2,设电源电压)25,220(~2N X ,求:(1)此种电子元件的损坏率;(2)此种电子元件损坏时,电源电压在200~240伏的概率。
解 令1A =“电压不超过200伏”2A =“电压在200~240伏” 3A =“电压过240伏” =B “电子元件损坏”2119.0)8.0(1)8.025220()200()(1=Φ-=-<-=<=X P X P A P2119.0)8.0(1)8.025220()240()(3=Φ-=>-=>=X P X P A P5762.0)(2=A P(1))()()()()()()(332211A B P A P A B P A P A B P A P B P ++=064.02.02119.0001.05762.01.02119.0=⨯+⨯+⨯=(2)009.0)()()()(222==B P A B P A P B A P22、已知X 的密度函数是)(x p X ,且14-=X Y ,求Y 的密度函数)(x p Y 。
