设计SAR ADC驱动电路,第一部分:ADC工作原理详解
sar adc工作原理

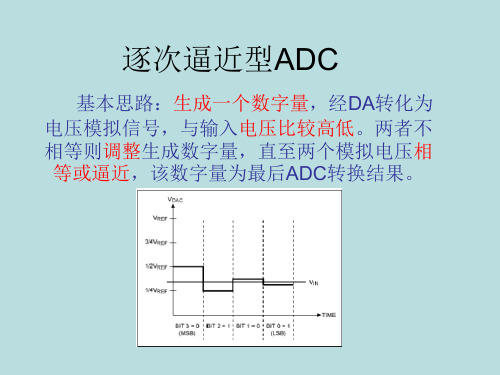
sar adc工作原理SAR ADC,全称为成功逼近寻址(Successive Approximation Register)模数转换器,其工作原理是通过逐位逼近的方式对模拟信号进行数字转换。
该转换器通常由比较器、逼近寄存器和数字/模拟转换器等组成。
首先,从输入端获取模拟信号并经过采样保持器进行采样。
接下来,比较器将采样信号与内部电路中的参考电压进行比较,然后将结果提供给逼近寄存器。
逼近寄存器是该转换器中的关键部分,它通过一个控制电路进行控制,决定每一位数字转换的值。
该寄存器开始比较的第一位是最高位,然后是次高位,以此类推到最低位的比较完成。
当比较器的输出与寄存器的控制电路匹配时,就生成了相应的数字输出。
为了更好地理解SAR ADC的工作原理,下面对其三个主要组成部分进行详细介绍:1. 比较器比较器是SAR ADC中最常见的组成部分之一。
它的作用是将输入信号与参考电压进行比较,并将结果提供给逼近寄存器。
比较器通常由操作放大器(Op-Amp)和其他元件组成。
在比较器中,操作放大器接收到输入信号和参考电压后,将这两个信号进行比较,并输出高或低电平。
这个输出信号表示了输入信号与参考电压之间的关系。
2. 逼近寄存器逼近寄存器是SAR ADC转换器中的另一个关键部分。
它通过内部的控制电路来控制数字转换的过程,在每次比较后将输出保存在逼近寄存器中。
逼近寄存器接收到比较器输出信号后,将这个信号与输入信号进行比较,并将比较结果存储在寄存器中。
然后,逼近寄存器通过逐位逼近的方式,将数字输出精度逐渐提高。
这个过程通过一个非常简单的二进制算法来完成,其时间复杂度为O (n)。
3. 数字/模拟转换器数字/模拟转换器将逼近寄存器中存储的数字转换成模拟信号。
这个过程通常通过一个数字/模拟转换器电路来完成。
根据芯片制造商的不同,这个电路有多种实现方式,例如使用相位选择边缘检测器(Phase-Selecting Edge Detector)或者集成运算放大器等。
sar adc工作原理

sar adc工作原理
Sar ADC是一种基于逐次逼近型原理的模数转换器,用于将模拟信号转换为数字信号。
其工作原理如下:
1. 输入采样:模拟信号经过输入采样电路进入Sar ADC。
采样电路通常包括采样保持电路,用于获取并保持输入信号的电压值。
2. 比较器:Sar ADC中通常含有一个或多个比较器,用于将输入信号与DAC(数字模拟转换器)产生的参考电压进行比较。
比较器输出的结果可以表示输入信号是高于还是低于参考电压。
3. DAC调整:Sar ADC通过DAC调整参考电压的数值。
它通
过逐次逼近的过程将DAC输出的电压调整到与输入信号最接
近的电压值。
4. SAR逼近:在每次逼近中,Sar ADC将DAC输出的电压与
输入信号进行比较。
根据比较结果,SAR逼近逻辑电路会决
定在当前位上是否为1或0。
每次逼近完成后,该位的比较结
果会被保存。
5. 逼近结束:当所有位都完成逼近后,Sar ADC会将逼近结果输出为数字信号。
这些数字信号可以用于数值处理、计算或其他应用。
需要注意的是,Sar ADC的工作速度和分辨率可能会受到多个因素的影响,例如比较器速度、电源噪声、采样保持电路的稳
定性等等。
为了达到较高的性能,Sar ADC经常需要在电路设计和优化过程中进行仔细考虑和调整。
设计SARADC驱动电路第一部分ADC工作原理详解

设计SARADC驱动电路第一部分ADC工作原理详解
SAR ADC(Successive Approximation Register 成功逼近寄存器)是一种常用的数字电路,它可以将模拟信号转换为数字信号。
借助于它,可以实现模拟-数字的转换,并且可以同时采集多个模拟信号。
SAR ADC 会根据以上信号的不同来决定其最终的输出,其最终输出是基于输入模拟信号的比较来决定的。
一个SARADC一般由一个模拟前端,一个成功逼近寄存器和一个比较器构成。
模拟前端的功能是将输入模拟信号转换为一个标准的参考值,例如一个标准的电压参考值。
成功逼近寄存器会将这个标准参考值分解成一系列二进制位,从而估计出输入信号的数字输出。
最后,比较器会将这个数字结果与输入模拟信号进行比较,以确定最终的输出结果。
SARADC具有较高的抗干扰能力,转换精度也比较高,因此它被广泛应用于通信、测量、检测等领域中。
接下来,让我们来具体看一下SARADC的工作原理。
一个SARADC的工作原理如下:
1.首先,输入模拟信号被一个模拟前端转换为一个标准的参考值,例如一个标准的电压参考值。
2.然后,这个参考值被一个成功逼近寄存器分解成一系列二进制位,并估计出输入信号的数字输出。
3.最后,比较器会将这个数字结果与输入模拟信号进行比较,以确定最终的输出结果。
saradc基本结构及其原理_概述及解释说明

saradc基本结构及其原理概述及解释说明1. 引言1.1 概述引言部分将对saradc的基本结构及其原理进行概述和解释说明。
saradc 是一种模拟数字转换器,用于将模拟信号转换为数字信号。
它在电子领域中具有广泛应用,特别是在数据采集和信号处理方面。
了解saradc的基本结构和工作原理对于深入理解其功能和优势至关重要。
1.2 文章结构本文将按照以下结构进行介绍:- 第一部分将介绍saradc的基本结构,包括其组成部分和相互之间的关系。
通过了解saradc的基本结构,读者可以更好地理解它的内部工作原理。
- 第二部分将详细解释saradc的工作原理。
我们将探讨数字化过程、采样频率、量化误差等关键概念,并阐述它们与saradc原理之间的联系。
- 第三部分将以实例应用和案例研究为基础,介绍不同领域中saradc的具体应用情况,并对这些案例进行详细分析。
通过实际案例,读者可以从不同角度深入了解saradc的实际运用和效果。
- 第四部分将探讨saradc的局限性和改进方向。
我们将分析saradc存在的一些局限性,并提出相应的改进建议,以期在实际应用中能够更好地解决问题。
- 最后,我们将对文章进行总结回顾,并对saradc未来发展进行展望。
1.3 目的本文旨在通过介绍saradc的基本结构及其原理,帮助读者了解这一技术在模拟信号转换中的作用和重要性。
同时,通过实例应用和案例研究,让读者深入了解saradc在不同领域中的实际应用情况和效果。
最后,我们将探讨saradc 存在的局限性,并提出改进方向和可能遇到的挑战,并为未来saradc技术发展展示出一条可行的道路。
2. saradc基本结构及其原理:2.1 saradc基本结构:saradc是一种模拟数字转换器,它用于将输入的模拟信号转换为数字信号。
它由多个关键部分组成,包括模拟输入端、采样保持电路、比较器、参考电压、计数器和数字输出端。
2.2 saradc原理解释:saradc的工作原理基于逐次逼近法。
sar adc的控制逻辑电路

sar adc的控制逻辑电路摘要:1.引言2.sar adc 的工作原理3.sar adc 的控制逻辑电路设计4.控制逻辑电路的工作流程5.总结正文:1.引言在当今的数字电子技术中,模数转换器(ADC)是至关重要的组成部分。
其中,串行接口的逐次逼近型(SAR)模数转换器广泛应用于各种领域。
SAR ADC 具有高速、高精度和低功耗等特点,但它的性能在很大程度上取决于控制逻辑电路的设计。
本文将详细介绍SAR ADC 的控制逻辑电路。
2.SAR ADC 的工作原理SAR ADC 的工作原理是通过逐次逼近的方式,将模拟信号转换为数字信号。
在转换过程中,比较器对输入信号与参考电压进行比较,产生阶梯信号。
控制逻辑电路根据阶梯信号,对SAR ADC 的内部状态进行控制,完成模数转换。
3.SAR ADC 的控制逻辑电路设计SAR ADC 的控制逻辑电路主要包括时钟控制、数据锁存、地址选择和驱动等部分。
时钟控制部分负责产生所需的时钟信号,为整个SAR ADC 提供同步;数据锁存部分用于锁存输入信号,保证数据在传输过程中的稳定性;地址选择部分用于选择需要转换的模拟信号通道;驱动部分负责将控制信号传输至SAR ADC 的各个部分,实现对ADC 的控制。
4.控制逻辑电路的工作流程SAR ADC 的控制逻辑电路工作流程如下:(1)初始化:根据输入信号的幅度和分辨率要求,配置SAR ADC 的相关参数,如基准电压、比较器增益等。
(2)时钟控制:产生所需的时钟信号,为SAR ADC 提供同步。
(3)数据锁存:将输入信号锁存,以保证数据在传输过程中的稳定性。
(4)地址选择:根据需要转换的模拟信号通道,选择相应的地址。
(5)驱动:将控制信号传输至SAR ADC 的各个部分,实现对ADC 的控制。
(6)模数转换:在控制逻辑电路的驱动下,SAR ADC 开始进行模数转换,将模拟信号转换为数字信号。
5.总结SAR ADC 的控制逻辑电路是整个模数转换器的关键部分,影响着SAR ADC 的性能。
sar adc原理

sar adc原理
逐次逼近型模数转换器(SAR ADC)是一种常用的模拟到数字转换器(ADC)技术。
它通过将模拟输入信号与逐步逼近的数字比较器进行比较,逐位确定输出的数字编码。
SAR ADC基于一个重要的原理:成功逼近。
它使用一个逐次逼近的过程来近
似输入信号的大小。
具体过程如下:
首先,SAR ADC将输入信号与量化电平(参考电压)进行比较。
通过开始时
的第一个比特位,它可以判断输入信号是大于还是小于参考电平。
如果输入信号小于参考电平,比特位则为0,否则为1。
然后,SAR ADC进入逐步逼近过程。
它将继续将参考电平分成两个部分,并
使用上一比特位的值来确定选择哪个部分。
然后,它将继续将所选的部分再次细分,直到最后一个比特位。
整个逼近过程是迭代的,每一步都通过比较输入信号与逼近的电平来确定下一
步的操作。
最终,SAR ADC通过迭代逼近,得出最接近输入信号的数字编码。
SAR ADC具有许多优点。
首先,它提供了高精度的转换结果。
其次,SAR ADC的转换速度相对较快,适用于高速数据处理和实时应用。
此外,它也具备较
低的功耗和较小的面积需求,适合集成在芯片中。
总结起来,SAR ADC是一种基于逐步逼近的模数转换器,通过迭代比较输入
信号和逼近电平,最终得出准确的数字编码。
它广泛应用于诸如通信系统、传感器接口以及嵌入式系统等领域。
sar adc的控制逻辑电路

sar adc的控制逻辑电路摘要:1.引言2.sar adc 的工作原理3.sar adc 的控制逻辑电路设计4.控制逻辑电路的工作原理5.总结正文:1.引言SAR ADC(逐次逼近型模数转换器)是一种常见的模数转换器,广泛应用于各种电子设备中。
其工作原理是通过逐步逼近输入信号的幅度,将其转换为数字信号。
在SAR ADC 中,控制逻辑电路起着关键作用,负责控制整个转换过程。
2.sar adc 的工作原理SAR ADC 的工作原理是通过比较输入信号与参考电压,逐步逼近输入信号的幅度,将其转换为数字信号。
在转换过程中,需要对输入信号进行采样、量化、编码等操作。
其中,采样阶段需要控制采样时钟的时序,量化阶段需要根据输入信号幅度调整量化级数,编码阶段需要将量化结果转换为数字信号。
3.sar adc 的控制逻辑电路设计SAR ADC 的控制逻辑电路主要包括采样控制电路、量化控制电路和编码控制电路。
采样控制电路负责产生采样时钟,量化控制电路负责调整量化级数,编码控制电路负责将量化结果转换为数字信号。
4.控制逻辑电路的工作原理采样控制电路的工作原理是根据输入信号的幅度,控制采样时钟的时序。
当输入信号的幅度超过设定阈值时,采样控制电路会启动采样过程,使输入信号被采样并转换为数字信号。
量化控制电路的工作原理是根据输入信号的幅度,调整量化级数。
当输入信号的幅度较高时,量化控制电路会增加量化级数,以获得更高的分辨率;当输入信号的幅度较低时,量化控制电路会减少量化级数,以降低功耗和提高转换速度。
编码控制电路的工作原理是将量化结果转换为数字信号。
通过对量化结果进行编码,可以将数字信号表示为二进制数,方便后续处理和传输。
5.总结SAR ADC 的控制逻辑电路在模数转换过程中起着关键作用。
通过对采样、量化和编码等环节的控制,实现对输入信号的有效转换。
全差分sar adc工作原理

全差分sar adc工作原理全差分SAR ADC是一种常见的模数转换器,它在许多应用中被广泛使用。
本文将介绍全差分SAR ADC的工作原理及其应用。
全差分SAR ADC是一种基于逐次逼近法的模数转换器。
它采用了差分输入和输出结构,具有较高的抗干扰能力和较好的线性性能。
在全差分SAR ADC中,输入信号首先经过一个差分放大器,将其转换为差分信号。
差分信号随后进入一个采样保持电路,将其保持在一个固定的电平上。
接下来,差分信号被逐次逼近法进行逐位比较,从而得到模拟输入信号的数字表示。
全差分SAR ADC的核心是逐次逼近法。
逐次逼近法是一种将模拟信号逐位转换为数字信号的方法。
在每一次逼近过程中,ADC会将一个参考电压与输入信号进行比较,以确定输入信号的最高位是0还是1。
然后,ADC会根据比较结果调整参考电压的大小,进而逼近输入信号的下一位。
这个过程将一直进行下去,直到得到输入信号的完整数字表示。
全差分SAR ADC的工作原理可以通过以下步骤来描述:1. 采样保持:输入信号首先被采样保持电路采样并保持在一个固定的电平上。
采样保持电路的作用是将输入信号在逼近过程中保持不变,以确保逼近过程的准确性。
2. 逐次逼近:在每一次逼近过程中,ADC会将一个参考电压与输入信号进行比较。
比较结果将决定输入信号的最高位是0还是1。
根据比较结果,ADC会调整参考电压的大小,以逼近输入信号的下一位。
3. 数字输出:逐次逼近过程将一直进行下去,直到得到输入信号的完整数字表示。
最终的数字输出将作为ADC的输出结果。
全差分SAR ADC具有许多优点。
首先,它采用了差分输入和输出结构,具有较高的抗干扰能力和较好的线性性能。
其次,逐次逼近法具有较高的转换精度和较低的功耗。
此外,全差分SAR ADC还具有较小的面积和较低的成本,适用于集成电路的制造。
全差分SAR ADC在许多应用中得到了广泛的应用。
例如,在通信系统中,全差分SAR ADC可以用于将模拟信号转换为数字信号,以进行数据的传输和处理。
sar adc工作原理

sar adc工作原理
SAR(Successive Approximation Register)ADC是一种广泛应
用于模拟信号转换为数字信号的模数转换器,其工作原理如下:
1. 输入信号采样:首先,SAR ADC会对输入信号进行采样。
采样是指将模拟信号离散化,并将其转换为数字形式。
采样可以通过模拟开关电路来实现,它根据一个时钟信号,将输入信号的电压值存储在一个或多个采样保持电容中。
2. 对比器比较:在采样之后,ADC会使用一个对比器来比较
采样保持电容中的电压值与一个参考电压的大小关系。
对比器会将比较结果转换为数字信号,以确定输入信号的电压是高于还是低于参考电压。
3. DAC输出:接下来,ADC会通过一系列的数字模拟转换器(DAC)来生成一个输出数字信号。
DAC会将对比器输出的
比较结果作为输入,并通过调整DAC的模拟输出电压来逼近
输入信号的实际电压值。
这个过程称为逐次逼近。
4. 精度确认:逐次逼近过程会重复多次,直到得到足够精确的数字输出。
ADC会在每次逼近之后与一个内部的参考值进行
比较,以判断逼近的程度。
一旦逼近足够精确,ADC会停止
逼近过程,并将最终的数字输出传输到外部设备或处理器。
总结来说,SAR ADC的工作原理是通过采样、比较和逼近的
过程,将模拟信号转换为数字信号。
它基于对比器和逐次逼近来测量和逼近输入信号的电压值,最终生成一个数字输出。
噪声整形SAR_ADC设计

噪声整形SAR_ADC设计噪声整形SAR_ADC是一种用于模拟信号数字化转换的关键电路,它在许多应用领域中发挥着重要作用。
本文将介绍噪声整形SAR_ADC的设计原理、工作原理以及其在电子系统中的应用。
噪声是电子系统中不可避免的现象,它来自于各种源头,如电源噪声、电路元件的热噪声以及外部干扰等。
在信号的采集和处理过程中,噪声会对信号的准确性和精度产生不良影响。
因此,噪声整形SAR_ADC的设计就是为了尽可能地降低噪声的干扰,提高信号的采集精度。
噪声整形SAR_ADC的设计原理基于逐次逼近寻找最佳比较电压来实现信号的模拟信号数字化转换。
其工作原理可以简要描述如下:首先,输入的模拟信号经过采样保持电路进行采样,然后由比较器与DAC进行逐次逼近比较,以找到最佳比较电压。
接着,通过数字控制逻辑电路对比较结果进行编码,最终输出数字信号。
在整个转换过程中,噪声整形电路起到了关键作用,它通过滤波、抑制和校准等技术手段来降低噪声的干扰,提高信号的采集质量。
噪声整形SAR_ADC在许多电子系统中都有广泛的应用。
在通信系统中,它被用于信号的调制和解调;在医疗设备中,它用于生物信号的采集和处理;在工业控制系统中,它被用于传感器信号的采集和反馈控制等。
通过合理设计和优化,噪声整形SAR_ADC可以实现高速、高精度和低功耗的特性,适应不同应用场景的需求。
总之,噪声整形SAR_ADC的设计是电子系统中不可或缺的一部分。
它通过降低噪声的干扰,提高信号的采集精度,为信号的后续处理和应用提供了可靠的数据基础。
随着科技的不断进步和应用需求的不断提高,噪声整形SAR_ADC的设计将继续发展和创新,为电子系统的性能提升和功能扩展提供更好的支持。
SarADC原理--ADC从0开始学
VCOMMON < 0 (即VIN > ½ VREF),比较器输出为逻辑 1,MSB电容的自由端保持连接至VREF。 VIN < ½ VREF,比较器输出为逻辑0。MSB电容的自 由端连接至地。 接下来,下一个较小电容的自由端连接至VREF,将 新的VCOMMON电压与地电位进行比较。 继续上述过 程,直至所有位的值均确定下来。 VCOMMON = -VIN + S0×VREF/2 + S2×VREF/4 + S3×VREF/8 + ... + SN× VREF/2N-1 (SN为比较器输出状态(1和0)/ADC输出位)
第二个电容: 1638C=819C+...+4C+2C+C+C=1/2*3276C 3C2=CE Q=CU,U_上升1/4VREF
同理,第N电容改接VREF时同样电荷再 分配,U_上升1/2NVREF
电容切换至地时,则U_下降相同大小的电压
R-2R电阻网络D/A转换电路
u0=-Rf(a1×IR/2 + a2×IR/4 + a3×IR/8 + ... + aN× IR/2N) =-VRRf/R(a1×1/2 + a2×1/4 + a3×1/8 + ... + aN× 1/2N) (aN为输入的二进制数码1或0)
•
•
• 电容式DAC包括一个由N个按照二进制加权 排列的电容和一个“空LSB”电容组成的阵 列。包含采样/保持电路。
采样-保持电路
UC=1,S闭合:u0=ui,输出 跟随输入变化并向电容C充 电。 UC=0,S断开:u0保持断开 瞬间的输入信号
采样
公共端接地,所有自由端接到VIN。UC=VIN(1-e-t/RC). 采样后,公共端与地断开,自由端与VIN断开,电容 阵列获得了与电容成比例的电荷量。Q=CU. 自由端接地,公共端=-VIN。U+比U_高VIN。
sar adc工作原理

sar adc工作原理
SAR ADC(Successive Approximation Register ADC)是一种逐次逼近寄存器ADC,它是一种较为常见的模数转换器(ADC)。
它的工作原理基于比较器和译码器,通过逐次逼近的方法将输入模拟信号转换为数字信号。
下面是SAR ADC的工作原理:
1. 采样与保持:输入的模拟信号首先被采样成一个保持信号,以便后续处理。
采样过程通常由采样电容完成。
2. 参考电压生成:参考电压由一个内部电压源生成,它与输入保持信号的电压范围相同。
3. 比较器:参考电压与保持信号进行比较,比较器输出一个二进制码,表示输入信号的大小是否大于或小于参考电压。
4. 逐次逼近:SAR ADC 中的逐次逼近是指通过多次比较来逐步逼近输入信号的真实值。
在第一次比较后,如果输出二进制码为 1,则表示输入信号大于参考电压,反之则表示输入信号小于参考电压。
在第二次比较时,将根据第一次比较的结果调整参考电压,直到最终得到输入信号的真实值。
这个过程可以使用二进制搜索算法来实现。
5. 数字输出:在逐次逼近过程中,得到的二进制码代表了输入信号的数字输出。
这个数字输出可以被微处理器或其他数字电路所处理。
总的来说,SAR ADC 的工作原理是通过逐次逼近的方法将输入模拟信号转换为数字信号。
它的主要优点是简单、可靠,且价格相对较低,因此在一些需要对模拟信号进行数字化处理的场合得到了广泛应用。
清华大学李福乐老师集成电路设计SARADC

OR: CLt = 2L − k ⋅ Ca
Cu
k Cu
两段结构的线性化设计
相邻跨段bit 的权重满足 2倍关系
Ca = k ⋅ CLt Cu 2L − k Cu
( ) CLt ≥ 2L −1 Cu
Ca ≥ 1 Cu Ca > k Cu
k =1 k >1
从电容匹配角度出发,我们总是希望Ca、Cd、CLt由整数个Cu构成,由此, 我们的一个设计任务是,在M,L,k确定的情况下,确定Ca, Cd, CLt的值, 使得它们满足ADC线性要求,同时为Cu的整数倍:
σ (INLh ) =
整个转换器的INL定义:
[ ] INL
=
max
INL1,
INL2 ,L,
INL 2
N
−1
h σ (Cu )
Cu
zINL只取决于电容面积,而与是否分段、是否采用温度码控制无关; zINL通常是电容面积优化的主要限制因素
INL的分布很复杂,但其满足预定指标的概率一定对应于σ(Cu)/Cu 的值,可以用数值分析的方法求出它们之间的关系,用于实际设计
CIt = 2M kCu
Cd1 = kCu
结论:
1)ADC的增益误差只取决于总采样电容与接到参考的总电容之比, MSB段接地的Cd1或寄生不会改变ADC增益误差; 2)通常在MSB段增加Cd1=kCu,且令Cd1对输入采样,这样可使得 LSB段不参与输入采样,降低ADC输入电容,且不会导致增益误差
寄生电容分析
OR: CLt = 2L − k ⋅ Ca
Cu
k Cu
思路:利用二段设计结论,先分两段设计,再对高位段分两段设计
以一个10bit CDAC为例,采用4‐4‐2分段结构:
sar adc 原理

sar adc 原理一、什么是sar adcsar adc,即逐次逼近式调制转换器(Successive Approximation Register Analog-to-Digital Converter),是一种常用的模数转换器。
它通过逐步逼近的方式将模拟信号转换为数字信号,具有较高的精度和较低的功耗,广泛应用于各种电子设备中。
二、sar adc的工作原理sar adc的核心是一个逐次逼近寄存器(Successive Approximation Register,SAR),它通过将模拟输入信号与一系列参考电压进行比较,逐步逼近输入信号的真实值。
具体来说,sar adc的工作流程如下:1. 初始化:将逐次逼近寄存器的比较器复位,并设置参考电压范围。
2. 开始转换:sar adc接收模拟输入信号,并将其与逐次逼近寄存器中的比较器进行比较。
3. 逐位逼近:sar adc从最高有效位(Most Significant Bit,MSB)开始,将比较结果与当前逼近寄存器的对应位进行比较。
如果输入信号大于逼近值,则该位为1,否则为0。
4. 更新逼近值:根据逐次逼近寄存器的比较结果更新逼近值,然后进行下一位的比较,直到逼近寄存器的最低有效位(Least Significant Bit,LSB)。
5. 转换完成:当逼近寄存器的最低有效位比较完成后,sar adc的转换过程结束,输出数字信号。
sar adc的精度取决于逼近寄存器的位数和参考电压的精度。
通常情况下,逼近寄存器的位数越多,精度越高,但转换速度也会相应降低。
三、sar adc的应用sar adc由于其较高的精度和较低的功耗,被广泛应用于各种电子设备中。
以下是sar adc的一些常见应用场景:1. 通信系统:sar adc可用于无线通信系统中的基带信号处理、调制解调器和射频收发器中的数字前端等。
2. 数字信号处理:sar adc可用于音频、视频和图像处理等领域,将模拟信号转换为数字信号进行处理。
SAR型ADC原理简析

SAR 型ADC 原理简析
逐次逼近寄存器型(SAR)模拟数字转换器(ADC)是采样速率低
于5Msps (每秒百万次采样)的中等至高分辨率应用的常见结构。
SAR ADC 的分辨率一般为8 位至16 位,具有低功耗、小尺寸等特点。
这些特点使该类型ADC 具有很宽的应用范围,例如便携/电池供电仪表、笔输入量化器、工业控制和数据/信号采集等。
顾名思义,SAR ADC 实质上是实现一种二进制搜索算法。
所以,当内部电路运行在数兆赫兹(MHz)时,由于逐次逼近算法的缘故,ADC 采样速率仅是该数值的几分之一。
SAR ADC 的架构
尽管实现SAR ADC 的方式千差万别,但其基本结构非常简单(见图1)。
模拟输入电压(VIN)由采样/保持电路保持。
为实现二进制搜索算法,N 位寄存器首先设置在中间刻度(即:100.。
.00,MSB 设置为1)。
这样,DAC 输出(VDAC)被设为VREF/2,VREF 是提供给ADC 的基准电压。
然
后,比较判断VIN 是小于还是大于VDAC。
如果VIN 大于VDAC,则比较
器输出逻辑高电平或1,N 位寄存器的MSB 保持为1。
相反,如果VIN 小于VDAC,则比较器输出逻辑低电平,N 位寄存器的MSB 清0。
随后,SAR 控。
分段电容sar adc原理

分段电容sar adc原理分段电容SAR ADC原理一、引言分段电容逐次逼近型(Successive Approximation Register, 简称SAR)模数转换器(ADC)是一种常用的高精度ADC转换器。
它通过逐次逼近的方式,将模拟信号转换为数字信号。
本文将详细介绍分段电容SAR ADC的原理和工作流程。
二、分段电容SAR ADC的原理分段电容SAR ADC主要由以下几个部分组成:数字控制逻辑、比较器、DAC(数字模拟转换器)、分段电容阵列和采样保持电路。
1. 数字控制逻辑:数字控制逻辑负责控制ADC的工作流程。
它通过逐次逼近的方式,逐位地对模拟输入信号进行逼近,最终得到数字输出。
2. 比较器:比较器的作用是将DAC输出的模拟电压与输入信号进行比较,输出比较结果。
比较器通常采用高速运算放大器来实现。
3. DAC:DAC将数字控制逻辑输出的二进制码转换为相应的模拟电压输出,用于与输入信号进行比较。
4. 分段电容阵列:分段电容阵列是分段电容SAR ADC的核心组成部分。
它通过将总电容分为多个小电容单元,并通过开关控制,实现对电容的分段调节。
分段电容阵列的每个小电容单元与DAC的输出端相连,通过调节每个小电容单元的电容值,可以得到不同电压的输出。
5. 采样保持电路:采样保持电路用于将输入信号进行采样,并在转换过程中保持其稳定。
采样保持电路通常由开关和电容组成,通过控制开关的状态,将输入信号进行采样并保持在电容上。
三、分段电容SAR ADC的工作流程分段电容SAR ADC的工作流程可以分为以下几个步骤:1. 初始化:首先,数字控制逻辑将比特位数设定为要转换的目标精度,并将比特位数设置为最高有效位(Highest Significant Bit, 简称HSB)。
2. 比较:数字控制逻辑将DAC输出的电压与输入信号进行比较。
如果DAC输出的电压大于输入信号,则将当前比特位设为1,否则设为0。
3. 逼近:根据当前比特位的值,数字控制逻辑调整分段电容阵列的电容值,使得DAC输出的电压逼近输入信号的电压。
SAR ADC 外部驱动电路设计流程

SAR ADC 外部驱动电路设计流程章节一:介绍SAR ADC外部驱动电路SAR ADC(Successive Approximation Register Analog-to-Digital Converter),顾名思义,是一种逐次逼近寄存器型的模拟信号到数字信号转换器。
SAR ADC要求输入信号是单端信号,因此在实际应用中需要添加外部驱动电路,将双端信号转换为单端信号。
本篇文章将详细介绍SAR ADC的外部驱动电路设计流程。
SAR ADC由一系列模拟电路和数字电路组成,其中外部驱动电路是连接模拟电路和输入信号的桥梁,同时承担着滤波、抗干扰等作用。
因此,优秀的SAR ADC外部驱动电路设计具有至关重要的作用。
章节二:SAR ADC外部驱动电路设计细节1.输入信号采集首先需要考虑的是如何采集输入信号。
通常采用差动信号放大器差分输入的方式,将双端信号转换为单端信号,并进行滤波处理。
在实际应用中,差动信号放大器的电源要求较高,一般采用电压稳压器电路来保证供电的稳定性。
2.滤波SAR ADC外部驱动电路的一个重要作用就是滤波,保证输入信号的质量。
常用的滤波电路有低通滤波、带通滤波、高通滤波等。
需要根据不同的应用场景选择合适的滤波电路。
3.抗干扰SAR ADC受到外界干扰时,很容易出现转换误差。
因此,在设计SAR ADC外部驱动电路时,需要考虑如何抗干扰。
常用的抗干扰电路有屏蔽电路、滤波电路、提高信噪比等。
4.缓冲SAR ADC通常具有较低的输入电阻和较高的输入电容。
因此在长距离传输时,需要考虑信号损失的问题。
这时,需要增加缓冲电路,将输入信号放大并保持稳定。
5.时序SAR ADC在转换过程中需要稳定的时序驱动。
外部驱动电路需要根据芯片的时序电气特性,在合适的时间点提供驱动信号。
同时,还需要考虑信号的延迟和同步问题。
章节三:SAR ADC外部驱动电路设计注意事项1.电源噪声SAR ADC的转换精度和稳定性对电源噪声比较敏感。
sar adc 原理

sar adc 原理SAR ADC原理简介SAR ADC(Successive Approximation Register Analog-to-Digital Converter)是一种常用的模数转换器,广泛应用于各种电子设备中。
它的工作原理基于逐次逼近,通过将输入信号与一系列数字比较器进行比较,逐步生成数字输出。
SAR ADC的基本结构包括比较器,逐次逼近寄存器(SAR)和数字电路。
比较器是SAR ADC的核心部件,用于将输入信号与参考电压进行比较。
逐次逼近寄存器(SAR)则是用于逐步逼近生成数字输出的关键部分。
数字电路用于控制SAR ADC的工作流程。
SAR ADC的工作流程如下:1. 首先,将待转换的模拟信号与参考电压进行比较。
比较器将输出一个比较结果,表示输入信号与参考电压的大小关系。
2. 根据比较结果,SAR将根据比较器的输出来更新逐次逼近寄存器(SAR)中的比特位。
逐次逼近寄存器(SAR)是一个n位的二进制寄存器,用于存储逐步逼近过程中的比特位。
3. 在逼近过程中,SAR ADC会根据比较器的输出结果逐步调整逐次逼近寄存器(SAR)中的比特位。
具体来说,它会从最高有效位(MSB)开始,逐个比特地进行逼近,直到逼近到最低有效位(LSB)。
4. 在每次逼近过程中,SAR ADC会将逐次逼近寄存器(SAR)中的比特位与参考电压进行比较,并根据比较结果来调整下一个比特位的值。
这个过程会一直进行,直到逼近到最低有效位(LSB)。
5. 最后,当逼近过程完成后,SAR ADC会将逐次逼近寄存器(SAR)中的比特位的值输出为数字信号。
这个数字信号就是SAR ADC的输出结果。
SAR ADC具有以下几个特点:1. 高精度:由于SAR ADC采用逐次逼近的方式进行转换,可以实现高精度的模拟到数字转换。
逐步逼近的过程可以逐渐减小误差,从而提高转换精度。
2. 快速转换速度:SAR ADC的转换速度比较快,适用于对转换速度要求较高的应用场景。
sar adc的控制逻辑电路

sar adc的控制逻辑电路【最新版】目录1.SAR ADC 简介2.SAR ADC 的控制逻辑电路组成3.SAR ADC 的控制逻辑电路工作原理4.SAR ADC 的控制逻辑电路应用实例5.总结正文一、SAR ADC 简介SAR(Successive Approximation Register)ADC 即连续近似寄存器ADC,是一种串行输出的模数转换器。
它通过连续逼近的方式将模拟信号转换为数字信号,具有较高的转换精度和较低的功耗。
SAR ADC 广泛应用于各类电子设备中,如通信、计算机、仪器仪表等领域。
二、SAR ADC 的控制逻辑电路组成SAR ADC 的控制逻辑电路主要由以下几个部分组成:1.控制器:控制器是 SAR ADC 的核心部分,负责整个转换过程的控制。
它接收启动信号、时钟信号和基准电压,生成控制信号,以控制比较器、译码器和寄存器等模块的工作。
2.比较器:比较器是将模拟信号与基准电压进行比较的模块。
根据比较结果,比较器输出信号控制译码器和寄存器,实现模拟信号的逐步逼近。
3.译码器:译码器是将控制器输出的控制信号转换为具体的控制命令,如选择合适的基准电压、控制寄存器更新等。
4.寄存器:寄存器用于存储转换过程中的中间结果。
在每次转换过程中,寄存器根据译码器的控制信号更新其存储值,以实现模拟信号的逐步逼近。
5.选择器:选择器根据控制器的控制信号选择合适的基准电压,以便与模拟信号进行比较。
三、SAR ADC 的控制逻辑电路工作原理SAR ADC 的控制逻辑电路工作原理如下:1.启动 SAR ADC:接收到启动信号后,控制器开始工作,输出时钟信号控制整个转换过程。
2.选择基准电压:控制器根据需要选择合适的基准电压,以便与模拟信号进行比较。
3.逐步逼近:比较器将模拟信号与基准电压进行比较,根据比较结果输出信号,控制器根据信号控制译码器和寄存器。
译码器根据控制器的信号选择合适的基准电压,并控制寄存器更新其存储值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Designing SAR ADC Drive Circuitryby Rick Downs, Applications Engineering Manager and Miro Oljaca, Systems Engineer Data Acquisition Products, Texas Instruments, IncorporatedPart I: A Detailed Look at SAR ADC OperationDesigning buffer circuitry for driving successive-approximation (SAR) ADCs requires knowledge of the load that the inputs present. Specifications in data sheets may mislead the user into thinking that analog inputs, for example, are static when in fact they are a very dynamic load. This three-part article will look at the architecture of modern SAR ADCs, and examine the conversion process in detail. In this first part the operation of a modern SAR ADC is discussed. A detailed, step-by-step analysis is then given, illustrating the sampling and conversion process. The final part discusses charge distribution during the sampling process. This analysis will give the user of these devicesa better understanding of the inner operations of a charge-redistribution ADC.1. The SAR ADC StructureFig. 1: Representative SAR Input StageFig. 1 shows a representative three bits of a typical SAR ADC (the ADS8361). Looking at this example, we will examine a three-bit conversion sequence. For our analysis, we will assume that the most significant bit (MSB) capacitor has a value of 20 pF. The capacitor nearest to the MSB capacitor will have half its value, or 10 pF and the least significant bit (LSB) capacitor will have one-quarter of the MSB capacitor value, or 5 pF.A termination capacitor has the same value as the LSB capacitor. The effect of this is that the sum of all the capacitors below the MSB capacitor becomes 20 pF, or the same value as the MSB capacitor.The positive analog input, VIN+, is sampled by the MSB capacitor through switch S2 and the capacitive conversion network, composed of three capacitors and two switches (S5 and S6). The negative analog input, VIN-, is sampled by two MSB-valued capacitors in series through switch S1. These two analog inputs, positive and negative, permit this ADC converter to sample differential signals.The reference voltage is applied to the REFIN input, internally buffered and distributed to all switches that are part of the conversion process. Switches S3 and S4 are connected to the buffered Vmid voltage. The value of Vmid is approximately 2.4 V with a 5-V supply; it will vary in direct proportion with the supply voltage. This buffer is important for proper charge distribution during the sampling period.The comparator input signals are connected in parallel to switches S3 and S4. During conversion, the comparator output will be processed by the control logic, which will properly set up switches S2, S5 and S6. (Note that this type of architecture is for the ADS8361 and similar, bipolar input range parts. Other parts may have a similar structure, but are not identical.)2. The Sampling Process in DetailAt the end of the conversion process, the ADS8361 automatically goes into the sampling process. The positions of switches S5 and S6 in the capacitive conversion network are unknown, as well as the position of switch S2. Switch S2 can be closed to either ground or the reference voltage. The status of the switches depends on the results of the previous conversion.Fig. 2: Beginning of the Sampling PeriodWe know that switch S1 is connected to the reference voltage, VREF. The sampling process initiates closing switches S3 and S4. This short-circuits the comparator inputs and connects them to VMID. This initial phase of the sampling cycle is shown in Fig. 2.Because the positions of switches S5 and S6 are unknown, the equivalent capacitance of the network is also unknown. For proper sampling, however, the capacitive conversion network must have an equivalent capacitance that is equal to the MSB capacitor value. To obtain this capacitance, switches S5 and S6 in this step must connect the associated capacitors to the ground terminal. In this way, the positive input, as well as the negative input, of the comparator will be connected over the MSB capacitor equivalent value to ground. This configuration is shown in Fig. 3.Fig. 3: Resetting the Value of the Capacitive Conversion NetworkUp to this point, all changes (such as charge distribution and switch positions) only affect the internal operation. The analog input signals were not affected by these changes. In the next step, input switches S1 and S2 close, and the input signal is sampled on the input MSB capacitors. This period is the most critical period and to have accurate results from the conversion, the input buffer must be capable of charging the sampling MSB capacitors to the proper value. The sampling of the input signal is shown in Fig. 4.Fig. 4: Sampling of the Input SignalAfter charging the sampling capacitor with the input voltage, preparation for the conversion cycle starts with opening switches S3 and S4 when the charge on the sampling capacitors will be frozen. Disconnecting the MSB capacitors from the analog inputs VIN+ and VIN- indicates the end of the sampling period. The next step connects the MSB capacitors with switches S1 and S2 to the reference voltage, VREF. Fig. 5 shows the end of the sampling period and the start of the conversion cycle.Fig. 5: Start of the Conversion Cycle.This representative analysis is for a 3-bit ADC, or a capacitive conversion network that is composed of three capacitors and two switches. This capacitive conversion network can be replaced with the real one (for N-bits SAR ADC) shown in Fig. 6.Fig. 6: Capacitive Conversion Network for N-Bits SAR ADCThe sampling (or MSB) capacitor connected to switch S0 has the standard value, C. The capacitive conversion network, as presented in Fig. 6, has an equivalent capacitive value equal to the value of the MSB capacitor. For the N-Bit SAR ADC, the capacitive conversion network will be composed of N+1 capacitors and N switches.The first capacitor has a value that is one-half of the standard MSB capacitor value, or (0.5*C). The second capacitor has a value that is one-fourth the value of C, the third one has a value that is one-eighth the value of C, and so on. The last two capacitors each have a value that is (1/2N) of the value of C. For a 12-bit SAR ADC, N is 12; for a 14-Bit SAR ADC, N is 14, and so on.The resolution of the SAR ADC is equivalent to the number of switches and capacitors that are in the capacitive conversion network, and their respective values.3. Charge Distribution During the Sampling ProcessTo explain the matter of charge distribution during the sampling and conversion period, Fig. 7 presents a simplified circuit, equivalent to that of Fig. 1.Fig. 7: Simplified SAR ADC CircuitThe sampling or MSB capacitor (CP1), connected to switch S2 and the positive input, has the standard value C. The sampling capacitor (CN1) that is connected to switch S1 and the negative input also has the standard value C. The capacitive conversion network as presented in Fig. 6 has an equivalent capacitive value equal to the value of the MSB capacitor, and is presented as capacitor (CP2) in Fig. 7. The comparator negative input has voltage VCNEG and the positive input VCPOS.The measured signal is connected to the positive input VIN+ and negative input VIN-. As described in section 2, the sampling of the input signal starts by closing switches S3 and S4. In this way, the positive input voltage, VCPOS, to the comparator is equal to the middle voltage, VMID. At the same time, the negative input voltage VCNEG to the comparator is also equal to the middle voltage, VMID. The next step is to close switch S5 to VGND. Switches S1 and S2 remain open. Now the ADC is ready to sample the input signal. The sampling process starts by closing input switches S1 and S2 to the input analog signal.After a transition period of approximately 500 ns (depending on the applied input buffer circuit), the voltages stabilize and the new situation is present. The existing configuration from Fig. 7 demonstrates the positive charge, QPS, that charges capacitors CP1 and CP2. Equation 1 explains this charge distribution sequence.21)()(P GND MID P IN MID PS C V V C V V Q ×−+×−=+Eq. 1Following the same procedure, the negative charge QNS that charges capacitors CN1 and CN2 is described by Equation 2:21)()(N GND MID N IN MID NS C V V C V V Q ×−+×−=−Eq. 2The next step in the sampling process starts when switches S3 and S4 open. In this way, the negative VCNEG and positive VCPOS input voltages into the comparator are not tied together anymore. The charge QPS on the capacitors CP1 and CP2 as well the charge QNS on the capacitors CN1 and CN2 will be frozen. The input switches S1 and S2 open next. To start the comparing or the conversion process, switches S1 and S2 close to the VREF position. Now the charge of the two capacitors CP1 and CP2 is distributed as explained by Equation 3:211)()(P GND CPOS P REF CPOS PC C V V C V V Q ×−+×−=Eq. 3Following the same process, the charge of capacitors CN1 and CN2 is described by Equation (4):211)()(N GND CNEG N REF CNEG NC C V V C V V Q ×−+×−=Eq. 4The charge of capacitors CP1 and CP2 during the sampling and conversion processes is the same. Combining Equation 1 and Equation 3 and substituting the voltage VGND with 0, the result is Equation 5:Eq. 5A similar calculation is applied to the negative side of the input stage. If the charge of capacitors CN1 and CN2 during the sampling and conversion process is the same, combining Equation 2 and Equation 4 and substituting the voltage VGND with 0 produces Equation 6:Eq. 6Equations 5 and 6 present the positive input voltage VCPOS and negative input voltage VCNEG into the comparator as a function of the positive input voltage VIN+ and negative input voltage VIN-. Capacitors CN1 and CN2 are equal and have the same value. The negative input comparator voltage VCNEG (referring to Equation 6) is constant during the entire conversion period, and can be described by Equation 7:Eq. 7The conversion process is accomplished by comparing the dynamic signal VCPOS (described by Equation 5) with a constant voltage VCNEG (described by Equation 7). Fig. 7 shows that capacitor CP2 is an equivalent presentation. During the conversion process, capacitor CP2 will change its value from the maximum value equal to MSB capacitor, CP1, to the lower value so that the difference between voltages VCPOS and VCNEG is minimized.4. ConversionThe sampling of the input signal ends and conversion begins when switches S3 and S4 are opened, capturing the input analog signal. Next, the sample switches S1 and S2 are opened, as explained in Section 3. The descriptions in this section refer to Fig. 7:.The Negative Input SignalFirst, we look at the negative input signal side. The comparator negative input node at S3 is VCNEG. The negative input signal side is set up as an input-signal-voltage-dependent reference for the comparator. Switch S1 switches from VIN- to VREF. The charge stored in the negative input signal side capacitors CN1 and CN2, during conversion QNC1, is equivalent to the charge stored during sampling QNS. The charge sum on capacitors CN1 and CN2 is conserved. Thus, the VCNEG is described by Equation 7 and remains constant during conversion.In the case of single-ended signals, VIN- is connected and equal to VREF, so as a consequence very little charge redistribution occurs on the negative input signal side after sampling. When a differential signal is sampled, the VIN- will differ from VREF; then the charge redistributes, presenting a load on the reference buffer circuit.The Positive Input SignalOn the positive input signal side, the transition from sampling into testing the MSB is similar to the negative input signal side. We will refer to the comparator positive input node at S4 as VPOS. The positive input signal side is set up as a variable input signal voltage for the comparator. The switch S2 switches from VIN+ to VREF and switch S5 remains connected to ground. The charge stored in the positive input signal side capacitors CP1 and CP2, during conversion QPC1, is equivalent to the charge stored during sampling QPS. The charge on the total capacitor array is the same during conversion as during sampling. The charge sum on capacitors CP1 and CP2 is conserved. Thus, the VPOS is described by Equation 5 and is variable during conversion.As in the first instance, switch S2 is connected to VREF, switch S5 to ground, and capacitors CP1 and CP2 have the same value, so Equation 5 can be rewritten as Equation 8:Eq. 8Testing the BitsAt the end of the first clock cycle, voltages VCPOS and VCNEG are compared by the comparator, resolving the value of the MSB to either a 1 or a 0. This value will be latched into the SAR control logic. If the value is 1, the CP1 capacitor remains connected over switch S2 to VREF. If the value is 0, it will be connected over the same switch to ground.To understand the rest of the conversion process, we need to refer to the capacitive conversion network presented in Fig. 6. At the same clock edge, the control logic of the SAR converter shifts to test the next most significant bit, which is referred to as bit 2. Switch S1 from Fig. 6 switches from ground to VREF. The charge on the capacitor array will again be redistributed, placing a load on the reference buffer.The state of the capacitor array is now a function of the decision made during the MSB test. Each bit test that follows will be a function of the preceding bit test. The voltage on VCPOS becomes dependent on which capacitors from the capacitive conversion network are connected to VREF and which are connected to ground. Under these conditions, the positive input voltage to comparator can be described by Equation 9:9Eq. where ∑CREF represents the sum of the capacitors tied to the reference voltage.Now, assume that the first bit tested high. The MSB capacitor is held at the reference voltage, and the second bit is tied to the reference for testing. Referring to Fig. 6 and replacing C with 20 pF, there will now be 30 pF of capacitance tied to the reference voltage. The voltage across this capacitance is given by Equation 10:10Eq.The 30 pF occurs because the MSB sampling capacitor C (with the value of 20 pF) is tied to VREF as a result of the first decision, and the next capacitor connected to switch S1 with the value of (0.5*C), or 10 pF, is also tied to VREF for testing.The End of ConversionThis sequence continues until the final bit is tested. We can assume that at the end of the conversion, the negative input signal into the comparator, VCNEG, is equal to the positive input signal into the comparator, VCPOS. Combining Equation 7 and Equation 9, we can relate VCPOS and VCPOS by Equation 11. The purpose of the conversion is to drive the positive input signal into the comparator VCPOS to an approximately equivalent value of VCNEG:11Eq.It is insightful to note that for any given resolution, with any given input signal, the state of the capacitors at the end of conversion is given by Equation 12, which is obtained by solving Equation 11 for the input signal, or (VIN+ − VIN−):Eq.12 The more positive the value of the input signal (or VIN+ − VIN−), the greater the proportion of capacitors tied to the reference voltage. At positive full-scale, +VREF, all capacitors from the capacitor conversion network will be tied to VREF. Alternately, if VIN+−VIN− is equal to -VREF, then no capacitors are tied to VREF, or all of them are tied to ground.Since the ratio of the sum of the capacitors, or ΣCREF/C, is in the range of 0 to 2, then from Equation 12 we can see that the input analog signal VIN+−VIN− is in the range of –VREF up to +VREF.Note that the ADS8361 complements the most significant bit in the output code. The MSB indicates negative signals with a 1. If the MSB is a 1 internally, indicating the input signal is positive, it will be a 0 in the output code.ConclusionIn this article, a better understanding of the internal operation of a modern SAR ADC is gained by looking at the sampling and conversion process in detail. The load that a SAR ADC presents to its driver circuitry was also examined and design criteria developed in order to optimize solutions for this difficult design problem.About The AuthorsRick Downs is applications engineering manager for Texas Instruments' Data Acquisition Products group in Tucson, AZ. Over the past 20 years, he has held various positions in applications and marketing of analog semiconductors, with focuses on audio, data acquisition, digital temperature sensors and battery management products. Rick holds a bachelor of science in Electrical Engineering from the University of Arizona, and has three patents. He has authored several articles and application notes on analog topics, and prepared and delivered several seminars on data acquisition.Miroslav Oljacac has over 17 years of design and manager experience in the field of motor control and power conversion. His design experience ranges from the several watt to megawatt range. Miroslav currently specify and support products that provides motor control solutions targeted at high precision motor control applications. He earned his BSEE and MSEE degrees in electrical engineering from the Electrotechnical University in Belgrade (Yugoslavia) in 1986 and 1988.Miroslav is a member of the AEI, CNI, IEE and IEEE. He also holds the following titles: Eur Ing, Dott.Ing., MSc and CEng. He can be reached at oljaca_miroslav@。
