立体几何证明题专题(教师版)
专题4:立体几何中垂直关系的证明基础练习题

12.证明见解析
【分析】
在等腰三角形PAB中, 是 的中点,可得 ,利用线面垂直的判定定理可证 平面 ,利用线面垂直的性质定理,即可得证.
【详解】
证明:∵ 是 的中点, ,
∴ ,
∵ 底面 ,
∴ ,
又∵ ,即
∴ 平面 ,
∴ ,
∵ 平面 , 平面 ,
∴ 平面 ,
∵ 平面 ,
∴ .
8.证明见解析
【分析】
由平面 ⊥平面 得到 ⊥平面 ,进一步得到 ⊥ ,再结合直径所对圆周角为直角得到 ⊥ , ⊥平面 ,从而得到证明.
【详解】
由题设知,平面 ⊥平面 ,交线为 .
因为 ⊥ , 平面 ,所以 ⊥平面 ,故 ⊥ .
因为 为 上异于 , 的点,且 为直径,所以 ⊥ .
又 = ,所以 ⊥平面 .
∴点O为三角形ABC的垂心,∴BO⊥AC
又因PO⊥AC,所以AC⊥PBO
故PB⊥AC
考点:证明异面直线垂直.
7.见解析
【分析】
由已知中P为正方形ABCD所在平面外一点,PA⊥面ABCD,结合正方形的几何特征,我们易得到BC⊥平面PAB,由线面垂直的性质得到BC⊥AE,结合已知中AE⊥PB,及线面垂直的判定定理,得到AE⊥平面PBC,最后再由线面垂直的判定定理,即可得到AE⊥PC.
【点睛】
此题考查线面垂直的性质和判定的综合应用,利用线面垂直得线线垂直.
5.证明见解析
【分析】
先证直线 平面 ,再证平面 ⊥平面 .
【详解】
证明:∵ 是圆的直径, 是圆上任一点, , ,
平面 , 平面 ,
,又 ,
平面 ,又 平面 ,
平面 ⊥平面 .
【点睛】
2020年高考数学解答题核心:立体几何综合问题(专项训练)(教师版)

专题08 立体几何综合问题(专项训练)1.如图,菱形ABCD 中,∠ABC =60°,AC 与BD 相交于点O ,AE ⊥平面ABCD ,CF ∥AE ,AB =AE =2. (1)求证:BD ⊥平面ACFE ;(2)当直线FO 与平面BED 所成的角为45°时,求异面直线OF 与BE 所成的角的余弦值大小.【答案】见解析【解析】(1)因为四边形ABCD 是菱形,所以BD ⊥AC .因为AE ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥AE .因为AC ∩AE =A ,所以BD ⊥平面ACFE .(2)以O 为原点,OA →,OB →的方向为x ,y 轴正方向,过O 且平行于CF 的直线为z 轴(向上为正方向),建立空间直角坐标系,则B (0,3,0),D (0,-3,0),E (1,0,2),F (-1,0,a )(a >0),OF →=(-1,0,a ).设平面EBD 的法向量为n =(x ,y ,z ),则有⎩⎪⎨⎪⎧n ·OB →=0,n ·OE →=0,即⎩⎨⎧3y =0,x +2z =0,令z =1,则n =(-2,0,1),由题意得sin 45°=|cos 〈OF →,n 〉|=|OF →·n ||OF →||n |=|2+a |a 2+1·5=22.因为a >0,所以解得a =3.所以OF →=(-1,0,3),BE →=(1,-3,2),所以cos 〈OF →,BE →〉=OF →·BE →|OF →|·|BE →|=-1+610·8=54.故异面直线OF 与BE 所成的角的余弦值为54.2.(2019·河南郑州模拟)如图,在△ABC 中,∠ABC =π4,O 为AB 边上一点,且3OB =3OC =2AB ,已知PO ⊥平面ABC ,2DA =2AO =PO ,且DA ∥PO .(1)求证:平面PBAD ⊥平面COD ;(2)求直线PD 与平面BDC 所成角的正弦值.【答案】见解析【解析】(1)证明:因为OB =OC ,又因为∠ABC =π4,所以∠OCB =π4,所以∠BOC =π2,即CO ⊥AB .又PO ⊥平面ABC ,OC ⊂平面ABC ,所以PO ⊥OC .又因为PO ,AB ⊂平面PAB ,PO ∩AB =O ,所以CO ⊥平面PAB ,即CO ⊥平面PBAD .又CO ⊂平面COD ,所以平面PBAD ⊥平面COD .(2)以OC ,OB ,OP 所在射线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示.设|OA |=1,则|PO |=|OB |=|OC |=2,|DA |=1.则C (2,0,0),B (0,2,0),P (0,0,2),D (0,-1,1),所以PD →=(0,-1,-1),BC →=(2,-2,0),BD →=(0,-3,1).设平面BDC 的法向量为n =(x ,y ,z ),所以⎩⎪⎨⎪⎧n ·BC →=0,n ·BD →=0,所以⎩⎪⎨⎪⎧2x -2y =0,-3y +z =0,令y =1,则x =1,z =3,所以n =(1,1,3).设PD 与平面BDC 所成的角为θ,则sin θ=⎪⎪⎪⎪⎪⎪⎪⎪PD →·n |PD →||n |=⎪⎪⎪⎪⎪⎪1×0+1×(-1)+3×(-1)02+(-1)2+(-1)2×12+12+32=22211.即直线PD 与平面BDC 所成角的正弦值为22211. 3.(2019·湖北武汉调考)如图, 四棱锥S -ABCD 中,AB ∥CD ,BC ⊥CD ,侧面SAB 为等边三角形,AB =BC =2,CD =SD =1.(1)证明:SD ⊥平面SAB ;(2)求AB 与平面SBC 所成角的正弦值.【答案】见解析【解析】方法一 (1)证明:建立如图所示的空间直角坐标系Cxyz ,则D (1,0,0),A (2,2,0),B (0,2,0),设S (x ,y ,z ),则x >0,y >0,z >0,且AS →=(x -2,y -2,z ,),BS →=(x ,y -2,z ).DS→=(x -1,y ,z ).由|AS →|=|BS →|,得(x -2)2+(y -2)2+z 2=x 2+(y -2)2+z 2,得x =1,由|DS →|=1得y 2+z 2=1,①由|BS →|=2得y 2+z 2-4y +1=0,②由①②解得y =12,z =32,所以S ⎝ ⎛⎭⎪⎫1,12,32,AS →=⎝⎛⎭⎪⎫-1,-32,32,BS →=⎝ ⎛⎭⎪⎫1,-32,32,DS →=⎝ ⎛⎭⎪⎫0,12,32,所以DS →·AS →=0,DS →·BS →=0,所以DS ⊥AS ,DS ⊥BS ,又AS ∩DS =S ,所以SD ⊥平面SAB .(2)设平面SBC 的一个法向量为m =(a ,b ,c ),BS →=⎝ ⎛⎭⎪⎫1,-32,32,CB →=(0,2,0),AB →=(-2,0,0),由⎩⎪⎨⎪⎧m ·BS →=0,m ·CB →=0得⎩⎪⎨⎪⎧a -32b +32c =0,2b =0,所以可取m =(-3,0,2),故AB 与平面SBC 所成的角的正弦值为cos 〈m ,AB →〉=m ·AB →|m |·|AB →|=-2×(-3)7×2=217. 方法二 (1)证明:如下图,取AB 的中点E ,连接DE ,SE ,则四边形BCDE 为矩形,所以DE =CB =2,所以AD =DE 2+AE 2= 5.因为侧面SAB 为等边三角形,AB =2,所以SA =SB =AB =2,且SE =3,又SD =1,所以SA 2+SD 2=AD 2,SE 2+SD 2=ED 2,所以SD ⊥SA ,SD ⊥SB ,又AS ∩DS =S ,所以SD ⊥平面SAB .(2)作S 在DE 上的射影G ,因为AB ⊥SE ,AB ⊥DE ,AB ⊥平面SDE ,所以平面SDE ⊥平面ABCD ,两平面的交线为DE ,所以SG ⊥平面ABCD ,在Rt △DSE 中,由SD ·SE =DE ·SG 得1×3=2×SG ,所以SG =32,作A 在平面SBC 上的射影H ,则∠ABH 为AB 与平面SBC 所成的角,因为CD ∥AB ,AB ⊥平面SDE ,所以CD ⊥平面SDE ,所以CD ⊥SD ,在Rt △CDS 中,由CD =SD =1,求得SC = 2.在△SBC 中,SB =BC =1,SC =2,所以S △SBC =12×2×22-12=72,由V A -SBC =V S -ABC 得13·S △SBC ·AH =13·S △ABC ·SG ,即13×72×AH =13×12×2×2×2,得AH =2217,所以sin ∠ABH =AHAB =217,故AB 与平面SBC 所成的角的正弦值为217. 4.(2019·安徽江南名校联考)如图,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,DC =6,AD =8,BC=10,∠PAD =45°,E 为PA 的中点. (1)求证:DE ∥平面BPC ;(2)线段AB 上是否存在一点F ,满足CF ⊥DB ?若存在,试求出二面角F -PC -D 的余弦值;若不存在,请说明理由.【答案】见解析【解析】(1)证明:取PB 的中点M ,连接EM 和CM ,过点C 作CN ⊥AB ,垂足为点N .因为CN ⊥AB ,DA ⊥AB ,所以CN ∥DA ,又AB ∥CD ,所以四边形CDAN 为平行四边形,所以CN =AD =8,DC =AN =6,在Rt △BNC 中,BN =BC 2-CN 2=102-82=6,所以AB =12,而E ,M 分别为PA ,PB 的中点,所以EM ∥AB 且EM =6,又DC ∥AB ,所以EM ∥CD 且EM =CD ,四边形CDEM 为平行四边形,所以DE ∥CM .因为CM ⊂平面PBC ,DE ⊄平面PBC ,所以DE ∥平面BPC .(2)由题意可得DA ,DC ,DP 两两互相垂直,如图,以D 为原点,DA ,DC ,DP 分别为x ,y ,z 轴建立空间直角坐标系Dxyz ,则A (8,0,0),B (8,12,0),C (0,6,0),P (0,0,8).假设AB 上存在一点F 使CF ⊥BD ,设点F 坐标为(8,t,0),则CF →=(8,t -6,0),DB →=(8,12,0),由CF →·DB →=0得t =23.又平面DPC 的法向量为m =(1,0,0),设平面FPC 的法向量为n =(x ,y ,z ).又PC →=(0,6,-8),FC →=⎝ ⎛⎭⎪⎫-8,163,0.由⎩⎪⎨⎪⎧n ·PC →=0,n ·FC →=0得⎩⎪⎨⎪⎧6y -8z =0,-8x +163y =0,即⎩⎪⎨⎪⎧z =34y ,x =23y ,不妨令y =12,有n =(8,12,9).则cos 〈n ,m 〉=n ·m |n ||m |=81×82+122+92=817.又由图可知,该二面角为锐二面角,故二面角F -PC -D 的余弦值为817.5.(2017·山东卷)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是DF的中点.(1)设P是CE上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.【答案】见解析【解析】(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP,又BP⊂平面ABP,所以BE⊥BP,又∠EBC=120°,因此∠CBP=30°.(2)方法一取EC的中点H,连接EH,GH,CH.因为∠EBC=120°,所以四边形BEHC为菱形,所以AE=GE=AC=GC=32+22=13.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM=13-1=2 3.在△BEC中,由于∠EBC=120°,由余弦定理得EC2=22+22-2×2×2×cos120°=12,所以EC=23,因此△EMC为等边三角形,故所求的角为60°.方法二 以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (-1,3,0),故AE →=(2,0,-3),AG →=(1,3,0),CG →=(2,0,3),设m =(x 1,y 1,z 1)是平面AEG 的一个法向量.由⎩⎪⎨⎪⎧m ·AE →=0,m ·AG →=0可得⎩⎨⎧2x 1-3z 1=0,x 1+3y 1=0.取z 1=2,可得平面AEG 的一个法向量m =(3,-3,2). 设n =(x 2,y 2,z 2)是平面ACG 的法向量. 由⎩⎪⎨⎪⎧n ·AG →=0,n ·CG →=0可得⎩⎨⎧x 2+3y 2=0,2x 2+3z 2=0.取z 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2).所以cos 〈m ,n 〉=m ·n |m |·|n |=12.由图可得此二面角为锐二面角,故所求的角为60°.6.(2017·全国卷Ⅲ)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD =∠CBD ,AB =BD . (1)证明:平面ACD ⊥平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D -AE -C 的余弦值.【答案】见解析【解析】(1)证明:由题设可得△ABD ≌△CBD ,从而AD =CD . 又△ACD 是直角三角形,所以∠ADC =90°. 取AC 的中点O ,连接DO ,BO ,则DO ⊥AC ,DO =AO . 又因为△ABC 是正三角形,故BO ⊥AC , 所以∠DOB 为二面角D -AC -B 的平面角. 在Rt △AOB 中,BO 2+AO 2=AB 2,又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2, 故∠BOD =90°.所以平面ACD ⊥平面ABC .(2)由题设及(1)知,OA ,OB ,OD 两两垂直,以O 为坐标原点,OA →的方向为x 轴正方向,|OA →|为单位长度,建立如图所示的空间直角坐标系Oxyz ,则A (1,0,0),B (0,3,0),C (-1,0,0),D (0,0,1).由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得E ⎝ ⎛⎭⎪⎫0,32,12,故AD →=(-1,0,1),AC →=(-2,0,0),AE →=⎝⎛⎭⎪⎫-1,32,12.设n =(x ,y ,z )是平面DAE 的法向量,则⎩⎪⎨⎪⎧ n ·AD →=0,n ·AE →=0,即⎩⎪⎨⎪⎧-x +z =0,-x +32y +12z =0,可取n =⎝ ⎛⎭⎪⎫1,33,1.设m 是平面AEC 的法向量,则⎩⎪⎨⎪⎧m ·AC →=0,m ·AE →=0,同理可取m =(0,-1,3),则cos 〈n ,m 〉=n·m |n||m|=77.所以二面角D -AE -C 的余弦值为77.。
新课标立体几何常考证明题汇总
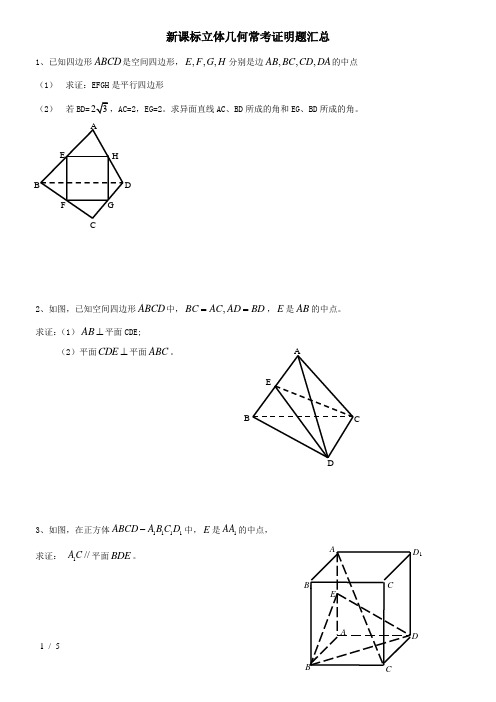
新课标立体几何常考证明题汇总1、已知四边形ABCD 是空间四边形,,,,E F G H 分别是边,,,AB BC CD DA 的中点 (1) 求证:EFGH 是平行四边形(2) 若BD=AC=2,EG=2。
求异面直线AC 、BD 所成的角和EG 、BD 所成的角。
2、如图,已知空间四边形ABCD 中,,BC AC AD BD ==,E 是AB 的中点。
求证:(1)⊥AB 平面CDE;(2)平面CDE ⊥平面ABC 。
3、如图,在正方体1111ABCD A BC D -中,E 是1AA 的中点, 求证: 1//AC 平面BDE 。
AED 1CB 1DAAHGFEDCB AEDBC4、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .5、已知正方体1111ABCD A BC D -,O 是底ABCD 对角线的交点. 求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D .7、正方体ABCD —A 1B 1C 1D 1中.(1)求证:平面A 1BD ∥平面B 1D 1C ; (2)若E 、F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD . 证明:8、四面体ABCD 中,,,AC BD E F =分别为,AD BC 的中点,且22EF AC =, 90BDC ∠=,求证:BD ⊥平面ACDSDCBAD 1ODB AC 1B 1A 1CA1NMPCBA9、如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB =(1)求证:MN AB ⊥;(2)当90APB ∠=,24AB BC ==时,求MN 的长。
10、如图,在正方体1111ABCD A BC D -中,E 、F 、G 分别是AB 、AD 、11C D 的中点.求证:平面1D EF ∥平面BDG .11、如图,在正方体1111ABCD A BC D -中,E 是1AA 的中点. (1)求证:1//AC 平面BDE ; (2)求证:平面1A AC ⊥平面BDE .12、已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角.13、如图,在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 的菱形,侧面PAD 是等边三角形,且平面PAD 垂直于底面ABCD .(1)若G 为AD 的中点,求证:BG ⊥平面PAD ; (2)求证:AD PB ⊥;(3)求二面角A BC P --的大小.14、如图1,在正方体1111ABCD A BC D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1AO ⊥平面MBD .考点:线面垂直的判定,运用勾股定理寻求线线垂直 15、如图2,在三棱锥A-BCD 中,BC =AC ,AD =BD ,作BE ⊥CD ,E为垂足,作AH ⊥BE 于H.求证:AH ⊥平面BCD .16、证明:在正方体ABCD -A 1B 1C 1D 1中,A 1C ⊥平面BC 1D17、如图,过S 引三条长度相等但不共面的线段SA 、SB 、SC ,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC ⊥平面BSC .18.(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC ⊥BC . (1) 求证:平面AB1C1⊥平面AC1;(2) 若AB1⊥A1C ,求线段AC 与AA1长度之比;(3) 若D 是棱CC1的中点,问在棱AB 上是否存在一点E ,使DE ∥平面AB1C1?若存在,试确定点E 的位置;若不存在,请说明理由.AC111。
人教A版必修二立体几何线线垂直证明线面垂直习题
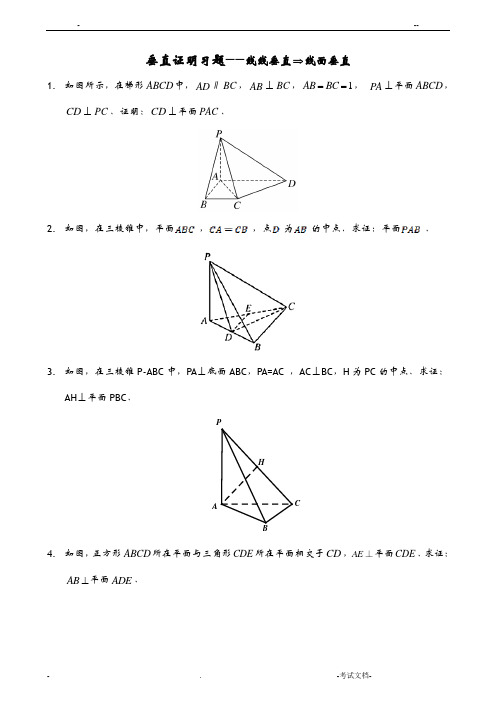
垂直证明习题——线线垂直⇒线面垂直1.如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,1AB BC==,PA⊥平面ABCD,CD⊥PC.证明:CD⊥平面PAC.2.如图,在三棱锥中,平面,,点为的中点.求证:平面.3.如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AC ,AC⊥BC,H为PC的中点.求证:AH⊥平面PBC.HA C4.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.求证:AB⊥平面ADE.5.如图所示,已知P ABC-为正三棱锥,设D为PB的中点,且AD PC⊥.求证:PC⊥平面PAB.6.如图所示,已知四棱锥P ABCD-中,底面ABCD为菱形,PA⊥平面ABCD,60ABC∠=E 是BC的中点.证明:AE⊥平面PAD.B CAD7.如图,四面体P ABC-中,PA⊥平面ABC,1PA AB==,3BC=,2AC=.证明:BC⊥平面PAB.8.如图,四面体ABCD中,O、E分别是BD、BC的中点,2AB AD==2CA CB CD BD====.求证:AO⊥平面BCD.9. 如图,在三棱锥P ABC -中,G 是棱PA 的中点,PC AC ⊥,且2PB AB AC BC ====, 1.PC =求证:直线BG ⊥平面PAC .10. 如图,在三棱锥P ABC -中,PA ⊥面,,2,ABC AC AB PA AD DC AE AB ⊥====,,22,3ABC AC AB PA DC AE AB ⊥====.求证:DE ⊥平面PAE .11. 如图,在三棱锥P ABC -中PA ⊥底面ABC ,D 为BC 上一点,24AC AB ==,7BD CD ==.证明:AD ⊥平面PAB .12. 如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 是矩形,1A D 与1AD 交于点E .证明:AE ⊥平面ECD .13. 己知三棱111,ABC A B C -柱1A 点在底面ABC 上的射影恰为AC 的中点D ,90BCA ︒∠=,2,AC BC ==又知11.BA AC ⊥求证:11AC A BC ⊥平面.14. 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PD ⊥平面ABCD ,E 为棱PB 的中点,2PB =,1PD =,45BPC ∠=︒.证明:PC ⊥平面ADE .15. 如图,已知ABC △是正三角形,EA ,CD 都垂直于平面ABC ,且2EA AB ==,1DC =,F 是BE 的中点,AF ⊥平面EDB .16. 如图,在直三棱柱111ABC A B C -中,AC BC ⊥,22AB =,2BC =,12AA =.证明:1A C ⊥平面11AB C .17. 如图,在五面体ABCDEF 中,四边形CDEF 为矩形,AD CD ⊥.证明: AB ⊥平面ADF .18. 如图,四棱锥S ABCD -中,SD ⊥底面ABCD ,//AB CD ,AD DC ⊥,1AB AD ==,2DC =,2SD =,E 为棱SB 的中点.求证:SC ⊥平面ADE .垂直证明习题——线线垂直⇒线面垂直(教师版)1. 如图所示,在梯形ABCD 中,AD ∥BC ,AB ⊥BC ,1AB BC ==, PA ⊥平面ABCD ,CD ⊥PC .证明:CD ⊥平面PAC .【解析】证明:∵PA ⊥平面ABCD ,CD ⊂平面ABCD , ∴PA ⊥CD .又PC ⊥CD , PA PC P =,PA ⊂平面PAC ,PC ⊂平面PAC ,∴CD ⊥平面PAC . 2. 如图,在三棱锥中,平面,,点为的中点.求证:平面.【解析】因为,点为中点,所以.因为平面,平面,所以.又因为,所以平面.(等腰三角形提供垂直)3.如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AC ,AC⊥BC,H为PC的中点.求证:AH⊥平面PBC.HA C【解析】等腰三角形提供垂直.4.如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE.求证:AB⊥平面ADE.【解析】(正方形提供垂直)5.如图所示,已知P ABC-为正三棱锥,设D为PB的中点,且AD PC⊥.求证:PC⊥平面PAB.【解析】正三棱锥中PC AB⊥.6.如图所示,已知四棱锥P ABCD-中,底面ABCD为菱形,PA⊥平面ABCD,60ABC∠=E是BC的中点.证明:AE⊥平面PAD.EB CADP【解析】有一个角是600的菱形提供垂直.7.如图,四面体P ABC-中,PA⊥平面ABC,1PA AB==,3BC=,2AC=.证明:BC⊥平面PAB.【解析】(勾股定理)8.如图,四面体ABCD中,O、E分别是BD、BC的中点,2AB AD==,2CA CB CD BD====.求证:AO⊥平面BCD.【解析】证明:连接OC,∵BO=DO,AB=AD,∴AO⊥BD,∵BO=DO,BC=CD,∴CO⊥BD.在△AOC中,由题设知13AO CO==,AC=2,∴AO 2+CO 2=AC 2,∴∠AOC =90°,即AO ⊥OC . ∵AO ⊥BD ,BD ∩OC =O , ∴AO ⊥平面BCD .(勾股定理)9. 如图,在三棱锥P ABC -中,G 是棱PA 的中点,PC AC ⊥,且2PB AB AC BC ====,1.PC =求证:直线BG ⊥平面PAC .【解析】连接CG ,因为BP BA =,所以BG PA ⊥. 由已知得1522CG PA ==,112BG =,所以222BG CG BC +=,所以BG CG ⊥, 又PA CG G ⋂=,所以BG ⊥平面.PAC (勾股定理)10. 如图,在三棱锥P ABC -中,PA ⊥面,,2,ABC AC AB PA AD DC AE AB ⊥====,,22,3ABC AC AB DC AE AB ⊥====.求证:DE ⊥平面PAE .【解析】AB AC ⊥,3AB =,3AC AD DC =+=tan 3ACB AB∴==,60B ︒∴=又3AE AB ==,ABE ∴为正三角形,30DAE DAB BAE ︒∴∠=∠-∠=又2AD =,3AE =,由余弦定理可知222?·cos 1DE AD AE AD AE DAE =+-∠=,222AE DE AD ∴+=,根据勾股定理可知AE DE ⊥.又PA ABC 面⊥,PA DE ∴⊥,DE PAE ∴⊥面.(勾股定理)11. 如图,在三棱锥P ABC -中PA ⊥底面ABC ,D 为BC 上一点,24AC AB ==,7BD CD ==.证明:AD ⊥平面PAB .【解析】证明:在ABC ∆中,24AC AB ==,7BD CD ==,2(27)41627cos 2272ABC +-∠==⨯⨯, 所以在ABD ∆中,227472273AD =+-⨯⨯⨯=,故3AD =. 因为222437AB AD BD +=+==,所以AB AD ⊥.(勾股定理)因为PA ⊥底面ABC ,所以PA AD ⊥,又PA AB A =,所以AD ⊥平面PAB .12. 如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 是矩形,1A D 与1AD 交于点E .证明:AE ⊥平面ECD .【解析】证明:因为四棱柱1111ABCD A B C D -是直四棱柱,所以1AA ⊥平面ABCD ,则1AA CD ⊥ . 又CD AD ⊥,1AA AD A =,所以CD ⊥平面11AA D D ,所以CD AE ⊥. 因为1AA AD ⊥,1AA AD =,所以11AA D D 是正方形,所以AE ED ⊥.又CD ED D =,所以AE ⊥平面ECD .(直棱柱提供垂直)13. 己知三棱111,ABC A B C -柱1A 点在底面ABC 上的射影恰为AC 的中点D ,90BCA ︒∠=,2,AC BC ==又知11.BA AC ⊥求证:11AC A BC ⊥平面.【解析】在三棱柱111ABC A B C -中,由BCA 90∠=︒得BC AC ⊥,因为1A D ⊥底ABC ,所以1A D BC ⊥,且1A D AC D ⋂=,所以BC ⊥面1A AC , 又由1AC ⊂平面1A AC ,所以1BC AC ⊥, 因为11BA AC ⊥,1BA BC B ⋂=,由线面垂直的判定定理,可得1AC ⊥平面1A BC .(射影提供垂直)14. 如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PD ⊥平面ABCD ,E 为棱PB 的中点,2PB =,1PD =,45BPC ∠=︒.证明:PC ⊥平面ADE .【解析】取PC 的中点F ,连接EF ,FD ,则EF AD ∥.由题知PD ⊥平面ABCD ,PD ⊂面PDC ,所以面PDC ⊥平面ABCD ,又底面ABCD 为矩形,故AD ⊥平面PDC ,所以AD PC ⊥,在Rt CB P ∆中,2PB =,45BPC ∠=︒,则2CB =.因为1PD =,所以3BD =,1CD =,即△CDP 为等腰三角形,又F 为PC 的中点,所以DF PC ⊥.因为DF AD D ⋂=,所以PC ⊥平面ADF ,即PC ⊥平面ADE .15. 如图,已知ABC △是正三角形,EA ,CD 都垂直于平面ABC ,且2EA AB ==,1DC =,F是BE 的中点,AF ⊥平面EDB .【解析】因M 是AB 的中点,△ABC 是正三角形,所以CM ⊥AB又 EA 垂直于平面ABC ∴CM ⊥AE ,又 AE ∩AB =A ,所以CM ⊥面EAB ,∵AF ⊂面EAB∴CM ⊥AF ,又CM ∥FD ,从而FD ⊥AF ,因F 是BE 的中点,EA =AB ,所以AF ⊥EB .EB ,FD 是平面EDB 两条相交直线,所以AF ⊥平面EDB .16. 如图,在直三棱柱111ABC A B C -中,AC BC ⊥,22AB =,2BC =,12AA =.证明:1A C ⊥平面11AB C .【解析】由题意,三棱柱111ABC A B C -为直三棱柱,所以1CC BC ⊥,又因为AC BC ⊥,1AC CC C =,AC ⊂平面11ACC A ,1CC ⊂平面11ACC A , 所以BC ⊥平面11ACC A ,又因为1AC ⊂平面11ACC A ,所以1BC A C ⊥, 又因为11BC B C ,所以111B C AC ⊥, 在Rt ABC ∆中,22AB =,2BC =,AC BC ⊥,所以2AC =,又因为12AA =,所以四边形11ACC A 为正方形,所以11A C AC ⊥.因为1111B C AC C =,11B C ⊂平面11AB C ,1AC ⊂平面11AB C ,所以1A C ⊥平面11AB C . 17. 如图,在五面体ABCDEF 中,四边形CDEF 为矩形, AD CD ⊥.证明: AB ⊥平面ADF .【解析】证明:因为CD AD ⊥,CD DF ⊥,AD DF D ⋂=, 所以CD ⊥平面ADF , 因为四边形CDFE 为矩形,所以//EF CD .又EF ⊄平面ABCD ,CD ⊂平面ABCD ,所以//EF 平面ABCD .因为//EF 平面ABCD ,EF ⊂平面ABEF ,平面ABEF平面ABCD AB =,所以//EF AB , 又//,EF CD 所以//,CD AB又CD ⊥平面ADF ,所以AB ⊥平面ADF18. 如图,四棱锥S ABCD -中,SD ⊥底面ABCD ,//AB CD ,AD DC ⊥,1AB AD ==,2DC =,2SD =,E 为棱SB 的中点.求证:SC ⊥平面ADE .【解析】取BC 的中点F ,连结EF ,AF .如图:因为SD ⊥底面ABCD 所以SD AD ⊥,又因为AD DC ⊥且SD DC D =,所以AD ⊥平面SDC ,得AD SC ⊥.又因为CD ⊥面ASD 且//AB CD 所以AB ⊥面ASD ,在Rt ∆SAD 中2,1,3SD AD SA ===,在Rt ∆SAB 中1,2AB SB ==,F 为BC 的中点,故112AE SB ==, 在t R SCD ∆中2,2,6SD CD SC ===,所以162EF SC ==, 在ABD ∆中,1,2AB AD BD ===,故45ABD ∠=,在CBD ∆中,2BD BC ==,故90DBC ∠=,在ABF ∆中,21,,1352AB BF ABF ==∠= ,由余弦定理知10AF =, 在AEF ∆中,1AE =,6EF =,10AF =满足勾股定理所以AE EF ⊥,从而AE SC ⊥.所以SC ⊥平面ADE .。
高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点。
1)证明EFGH是平行四边形。
2)已知BD=23,AC=2,EG=2,求异面直线AC、BD所成的角和EG、BD所成的角。
2.如图,已知空间四边形ABCD中,BC=AC,AD=BD,E 是AB的中点。
1)证明AB垂直于平面CDE。
2)证明平面CDE垂直于平面ABC。
3.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
证明A1C平行于平面BDE。
4.已知三角形ABC中∠ACB=90,SA垂直于面ABC,AD垂直于SC。
证明AD垂直于面SBC。
5.已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点。
1)证明C1O平行于面AB1D1.2)证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。
1)证明AC垂直于平面B1D1D。
2)证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。
1)证明平面A1BD平行于平面B1DC。
2)已知E、F分别是AA1、CC1的中点,证明平面EB1D1平行于平面FBD。
8.四面体ABCD中,AC=BD,E、F分别为AD、BC的中点,且EF=AC/2,∠XXX。
证明BD垂直于平面ACD。
9.如图P是△ABC所在平面外一点,PA=PB,CB垂直于平面PAB,M是PC的中点,N是AB上的点,AN=3NB。
1)证明XXX垂直于AB。
2)当∠APB=90,AB=2BC=4时,求MN的长度。
10.如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、AD、C1D1的中点。
证明平面D1EF平行于平面BDG。
11.如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点。
1)证明A1C平行于平面BDE。
2)证明平面A1AC垂直于平面BDE。
12、已知矩形ABCD,PA垂直于平面ABCD,AB=2,PA=AD=4,E为BC的中点。
立体几何证明题精选

立体几何证明题精选1.在多面体中,矩形ABB1A1和ACC1A1,AC垂直于BC。
证明BC垂直于平面ACC1A1,同时在线XXX上存在一点M,使得DE与平面A1MC平行。
2.在三棱锥P-ABC中,D,E,F分别是棱PC,AC,AB 的中点。
已知PA垂直于AC,PA=6,BC=8,DF=5.证明PA 平行于平面DEF,同时平面BDE垂直于平面ABC。
3.在四棱锥P-ABCD中,AP垂直于平面PCD,AD平行于BC,AB和BC分别为线段AD和PC的中点。
证明AP平行于平面BEF,同时BE垂直于平面PAC。
4.在四棱锥P-ABCD中,底面ABCD是平行四边形,BA=BD=BC=1,AD=2,PA=PD=√5,E和F分别是棱AD和PC的中点。
证明EF平行于平面PAB,同时平面PBC垂直于平面ABCD。
5.在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB垂直于BC,AA1=AC=2,BC=1,E和F分别是A1C1和BC的中点。
证明平面ABE垂直于平面B1BCC1,C1F平行于平面ABE,同时求三棱锥E-ABC的体积。
6.在四棱锥P-ABCD中,底面ABCD为矩形,PA垂直于平面ABCD,E为PD的中点。
证明PB平行于平面AEC,同时若AP=1,AD=3,则三棱锥P-ABD的体积为2/3,求A到平面PBC的距离。
7.在四棱锥中,平面ACD和平面ABD的交线为直线L,平面ABC和平面ACD的交线为直线M,平面ABC和平面ABD的交线为直线N,P为直线L上一点,Q为直线M上一点,R为直线N上一点,且PQR平行于平面ABCD,证明PR 平行于直线BD,同时求四面体PQRD的体积。
8.在长方体ABCD-A1B1C1D1中,底面A1B1C1D1为正方形,O为BD的中点,E为棱AA1上任意一点。
证明BD垂直于EC1,同时若AB=2,AE=2,OE垂直于EC1,则AA1的长度为2√2.。
立体几何专题

立体几何专题1. (北京文) (18) (本小题 14 分)如图,在四棱锥 P-ABCD 中,底面 ABCD 为矩形, 平面 PAD⊥平面 ABCD , PA⊥ PD , PA=PD , E , F 分别为 AD , PB 的中点.( Ⅰ ) 求证: PE ⊥BC ; (Ⅱ)求证:平面 PAB ⊥平面 PCD ; (Ⅲ) 求证: EF∥平面 PCD.2. (北京理) (16) (本小题 14 分)如图, 在三棱柱 ABC- A 1B 1C 1 中, CC 1 」平面 ABC , D , E , F , G 分别为 AA 1,AC , A 1C 1,BB 1 的中点, AB=BC= 5, AC= AA 1 =2.( Ⅰ ) 求证: AC⊥平面 BEF ; ( Ⅱ ) 求二面角B-CD-C 1 的余弦值; (Ⅲ) 证明: 直线 FG 与平面 BCD 相交.3. (江苏) (15) (本小题满分 14 分)在平行六面体ABCD 一 A B C D 中,AA = AB, AB 」B C .求证: (1) AB∥平面A B C; (2) 平面ABB A 」平面A BC.4. (浙江) (19) (本题满分 15 分)如图,已知多面体 ABCA1B1C1,A1A, B1B, C1C均垂直于平面 ABC,∠ABC=120°, A1A=4, C1C=1, AB=BC=B1B=2.(Ⅰ)证明:AB1 ⊥平面A1B1C1;(Ⅱ)求直线 AC1 与平面 ABB1 所成的角的正弦值.1 1 1 1 1 1 1 1 1 1 1 1 1第 2 页共 10 页5. (天津文) (17)(本小题满分 13 分)如图,在四面体 ABCD 中,△ABC 是等边三角形,平面 ABC⊥平面 ABD,点 M 为棱AB 的中点, AB=2, AD= 2 3 ,∠BAD=90°.( Ⅰ )求证:AD⊥BC;( Ⅱ ) 求异面直线 BC 与 MD 所成角的余弦值;(Ⅲ)求直线 CD 与平面 ABD 所成角的正弦值.6. (天津理) (17)(本小题满分 13 分)如图,AD∥BC 且 AD=2BC,AD 」CD , EG∥AD且 EG=AD,CD∥FG 且 CD=2FG,DG 」平面ABCD, DA=DC=DG=2.(I)若 M 为 CF 的中点, N 为 EG 的中点,求证:MN∥平面CDE;(II)求二面角E BC F 的正弦值;(III)若点 P 在线段 DG 上,且直线 BP 与平面 ADGE 所成的角为60°,求线段 DP 的长.7. (全国卷一文)(18)(12 分)如图, 在平行四边形 ABCM 中, AB = AC = 3, ∠ACM = 90, 以 AC 为折痕 将△ ACM 折起,使点 M 到达点 D 的位置,且 AB⊥DA. (1)证明:平面 ACD ⊥平面 ABC ;(2) Q 为线段 AD 上一点, P 在线段 BC 上, 且 BP = DQ = DA , 求三棱锥3Q ABP 的体积.8. (全国卷一理)(18)(12 分)如图, 四边形 ABCD 为正方形, E, F 分别为 AD, BC 的中点, 以 DF 为折 痕把 △DFC 折起,使点 C 到达点 P 的位置,且 PF 」BF . (1)证明:平面 PEF 」平面 ABFD ; (2)求 DP 与平面 ABFD 所成角的正弦值 .29. (全国卷二文)( 19) (12 分)如图,在三棱锥P ABC 中,AB = BC = 2 2,PA = PB = PC = AC = 4,O为AC 的中点.(1)证明:PO 」平面ABC;(2)若点M 在棱 BC 上,且MC = 2MB,求点C 到平面POM 的距离.10. (全国卷二理)(20)(12分)如图,在三棱锥P ABC 中,AB = BC = 2 2,PA = PB = PC = AC = 4,O 为AC 的中点.(1)证明:PO 」平面ABC;(2) 若点M 在棱BC 上,且二面角M PA C 为30,求PC 与平面 PAM 所成角的正弦值.POA CMB11. (全国卷三文)(19)(12分)如图,矩形ABCD所在平面与半圆弧 CD 所在平面垂直,M 是CD 上异于C, D 的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM 上是否存在点 P ,使得MC∥平面PBD ?说明理由.12. (全国卷三理)(19)(12分)如图,边长为 2 的正方形ABCD所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C, D 的点.(1)证明:平面 AMD⊥平面BMC;(2) 当三棱锥M ABC 体积最大时,求面 MAB 与面MCD所成二面角的正弦值.13. (12 分)如图,四棱锥 P-ABCD 中,侧面 PAD 为等比三角形且垂直于底面 ABCD,1AB = BC = AD, 三BAD = 三ABC = 90o , E 是 PD 的中点.2(1) 证明:直线CE/ / 平面 PAB(2) 点 M 在棱 PC 上,且直线 BM 与底面 ABCD 所成锐角为45o ,求二面角 M-AB-D 的余弦值14. (12 分)如图,在四棱锥 P-ABCD 中, AB//CD,且三BAP = 三CDP = 90(1)证明:平面 PAB⊥平面PAD;(2)若 PA=PD=AB=DC, 三APD = 90 ,求二面角 A-PB-C 的余弦值.15. (12 分)如图,四面体 ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD= ∠CBD,AB=BD.(1) 证明:平面ACD⊥平面 ABC;(2) 过 AC 的平面交 BD 于点 E,若平面 AEC 把四面体 ABCD 分成体积相等的两部分,求二面角 D –AE –C 的余弦值.16.如图,在四棱锥 P-ABCD 中,底面 ABCD 为正方形,平面PAD⊥平面 ABCD,点 M在线段 PB 上, PD//平面 MAC, PA=PD= 6, AB=4.(I)求证: M 为 PB 的中点;(II)求二面角 B-PD-A 的大小;(III)求直线 MC 与平面 BDP 所成角的正弦值.17.如图,在三棱锥 P-ABC 中,PA⊥底面 ABC,三BAC = 90o .点 D, E, N 分别为棱PA, PC, BC 的中点, M 是线段 AD 的中点, PA=AC=4, AB=2.(Ⅰ)求证: MN∥平面BDE;(Ⅱ)求二面角 C-EM-N 的正弦值;7(Ⅲ) 已知点 H 在棱 PA 上,且直线 NH 与直线 BE 所成角的余弦值为,求线段 AH21的长.18.如图,几何体是圆柱的一部分,它是由矩形为旋转轴旋转得到的,是的中点.(Ⅰ)设是(Ⅱ)当上的一点,且,求的大小;,,求二面角的大小.(及其内部) 以边所在直线19. (本题满分 15 分)如图,已知四棱 P–ABCD,△PAD 是以 AD 为斜边的等腰直角三角形,BC∥AD,D⊥AD, PC=AD=2DC=2CB, E 为 PD 的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE 与平面PBC 所成角的正弦值.。
第一讲-立体几何证明题

ABCDP EF 第一讲:立体几何证明题1、如图,在四棱锥ABCD P -中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD ,1==DC PD ,E 是PC 的中点,作PB EF ⊥交PB 于点F .(I) 证明: PA ∥平面EDB ;(II) 证明:PB ⊥平面EFD ;(III) 求三棱锥DEF P -的体积.2、如图,已知四棱锥P ABCD -的底面为等腰梯形,AB ∥CD ,AC BD ⊥,垂足为H ,PH 是四棱锥的高。
(Ⅰ)证明:平面PAC ⊥ 平面PBD ; (Ⅱ)若6AB =,APB ADB ∠=∠=60°,求四棱锥P ABCD -的体积。
3、如图,矩形A B C D 中,A B E AD 平面⊥,2===BC EB AE ,F 为CE 上的点,且A C EBF 平面⊥. (Ⅰ)求证:BCE AE 平面⊥; (Ⅱ)求证;BFD AE 平面//;(Ⅲ)求三棱锥BGF C -的体积.4、如图,正方形ABCD 和四边形ACEF 所在的平面互相垂直。
EF//AC ,AB=2,CE=EF=1 (Ⅰ)求证:AF//平面BDE ; (Ⅱ)求证:CF ⊥平面BDF;ABCDHPABCDEFABCDEFG5、在如图所示的几何体中,四边形ABCD 是正方形,BCD A MA 平面⊥,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点,且2MA PD A D ==.(Ⅰ) 求证:平面PDC EFG 平面⊥;(Ⅱ)求三棱锥的体积之比与四棱锥ABCD P MAB P --.6、如图所示,矩形ABCD 中,AD ⊥平面ABE ,AE=EB=BC=2,F 为CE 上的点,且BF ⊥平面ACE (1)求证:AE ⊥平面BCE ;(2)求证:AE ∥平面BFD ;(3)求三棱锥C-BGF 的体积。
7、在三棱锥S —ABC 中,∠SAB =∠SAC =∠ACB =90°,且AC =BC =5,SB =55。
高中立体几何证明题

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1},E,F分别是AB,BC的中点,求证:EF∥平面A_{1}C_{1}D。
解析1. 连接AC。
- 在 ABC中,因为E,F分别是AB,BC的中点,所以EF∥ AC。
2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中:- AC∥ A_{1}C_{1}。
- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。
- 又A_{1}C_{1}⊂平面A_{1}C_{1}D,EFnot⊂平面A_{1}C_{1}D。
- 根据线面平行的判定定理,所以EF∥平面A_{1}C_{1}D。
题2在三棱柱ABC - A_{1}B_{1}C_{1}中,D是AB的中点,求证:AC_{1}∥平面CDB_{1}。
解析1. 连接BC_{1},交B_{1}C于点E。
- 在三棱柱ABC - A_{1}B_{1}C_{1}中,E为BC_{1}的中点。
2. 因为D是AB的中点:- 所以在 ABC_{1}中,DE∥ AC_{1}。
- 又DE⊂平面CDB_{1},AC_{1}not⊂平面CDB_{1}。
- 根据线面平行的判定定理,可得AC_{1}∥平面CDB_{1}。
二、线面垂直的证明题3在四棱锥P - ABCD中,底面ABCD是正方形,PA = PB = PC = PD,求证:PA⊥平面ABCD。
解析1. 连接AC,BD交于点O,连接PO。
- 因为底面ABCD是正方形,所以O为AC,BD中点。
- 又PA = PC,PB = PD,根据等腰三角形三线合一的性质:- 可得PO⊥ AC,PO⊥ BD。
- 而AC∩ BD = O,AC⊂平面ABCD,BD⊂平面ABCD。
- 根据直线与平面垂直的判定定理,所以PO⊥平面ABCD。
- 又PA = PB = PC = PD,AO = BO = CO = DO,所以 PAO≅ PBO≅ PCO ≅ PDO。
专题6 立体几何(文科)解答题30题 教师版--高考数学专题训练

专题6立体几何(文科)解答题30题1.(贵州省贵阳市2023届高三上学期8月摸底考试数学(文)试题)如图,在直三棱柱111ABC A B C -中,1CA CB ==,90BCA ∠=︒,12AA =,M ,N 分别是11A B ,1A A 的中点.(1)求证:1BN C M ⊥;(2)求三棱锥1B BCN -的体积.2.(广西普通高中2023届高三摸底考试数学(文)试题)如图,多面体ABCDEF中,∠=︒,FA⊥平面ABCD,//ED FA,且22 ABCD是菱形,60ABC===.AB FA ED(1)求证:平面BDE⊥平面FAC;(2)求多面体ABCDEF的体积.))如图所示,取中点G ,连接3.(江西省五市九校协作体2023届高三第一次联考数学(文)试题)如图多面体ABCDEF 中,四边形ABCD 是菱形,60ABC ∠=︒,EA ⊥平面ABCD ,//EA BF ,22AB AE BF ===.(1)证明:平面EAC ⊥平面EFC ;(2)求点B 到平面CEF 的距离.(2)设B 到平面CEF 的距离为因为EA ⊥平面ABCD ,AC 因为//EA BF ,EA ⊥平面ABCD 且BC ⊂平面ABCD ,所以BF 因为60ABC ∠=︒,2AB =4.(新疆乌鲁木齐地区2023届高三第一次质量监测数学(文)试题)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,AD BC ∥,且2PA AD CD ===,3BC =,E 是PD 的中点,点F 在PC 上,且2PF FC =.(1)证明:DF ∥平面PAB ;(2)求三棱锥P AEF -的体积.(2)作FG PD ⊥交PD 于点G 因为PA ⊥面ABCD ,所以PA 又AD CD ⊥,PA 与AD 交于点所以CD ⊥面PAD ,CD PD ⊥又FG PD ⊥,所以//FG CD ,所以所以PF FG PC CD =,得43FG =,因为E 为PD 中点,所以P AEF D AEF F ADE V V V ---===5.(新疆阿克苏地区柯坪湖州国庆中学2021-2022学年高二上学期期末数学试题)如图所示,已知AB ⊥平面BCD ,M ,N 分别是AC ,AD 的中点,BC CD ⊥.(1)求证://MN 平面BCD ;(2)求证:CD BM ⊥;【答案】(1)证明见解析;(2)证明见解析.【分析】1)根据中位线定理,可得//MN CD ,即可由线面平行的判定定理证明//MN 平面BCD ;(2)由已知推导出AB CD ⊥,再由CD BC ⊥,得CD ⊥平面ABC ,由此能证明CD BM ⊥;【详解】(1)M ,N 分别是AC ,AD 的中点,//MN CD ∴,MN ⊂/ 平面BCD ,且CD ⊂平面BCD ,//MN ∴平面BCD ;(2)AB ⊥Q 平面BCD ,M ,N 分别是AC ,AD 的中点,AB CD ∴⊥,BC CD ⊥ ,,AB BC B AB BC =⊂ ,平面ABC ,CD \^平面ABC ,BM ⊂ 平面ABC ,CD BM ∴⊥.6.(内蒙古乌兰浩特第一中学2022届高三全真模拟文科数学试题)如图在梯形中,//BC AD ,22AB AD BC ===,23ABC π∠=,E 为AD 中点,以BE 为折痕将ABE 折起,使点A 到达点P 的位置,连接,PD PC ,(1)证明:平面PED ⊥平面BCDE ;(2)当2PC =时,求点D 到平面PEB 的距离.因为PE PD =,F 为ED 因为平面PED ⊥平面BCDE 因为21122PF ⎛⎫=-= ⎪⎝⎭设D 到平面PEB 的距离为7.(山西省运城市2022届高三5月考前适应性测试数学(文)试题(A 卷))如图,四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,侧面11ADD A 为矩形,22AB AD ==,160D DB ∠=︒,1BD AA =(1)证明:平面ABCD ⊥平面11BDD B ;(2)求三棱锥11D BCB -的体积.8.(黑龙江省八校2021-2022学年高三上学期期末联合考试数学(文)试题)已知直三棱柱111ABC A B C -中,AC BC =,点D 是AB 的中点.(1)求证:1BC ∥平面1C AD ;(2)若底面ABC 边长为2的正三角形,1BB =11B A DC -的体积.【答案】(1)证明见解析(2)1【分析】(1)连接1AC 交1AC 于点E ,连接DE ,由三角形中位线定理,得1DE BC ∥,进而由线面平行的判定定理即可证得结论;(2)利用等体积转化1111B A DC C A B D V V --=,依题意,高为CD ,再求底面11A B D 的面积,进而求三棱锥的体积.【详解】(1)连接1AC 交1AC 于点E ,连接DE∵四边形11AAC C 是矩形,∴E 为1AC 的中点,又∵D 是AB 的中点,∴1DE BC ∥,又∵DE ⊂平面1C AD ,1BC ⊄平面1C AD ,∴1BC ∥面1C AD .(2)∵AC BC =,D 是AB 的中点,∴AB CD ⊥,9.(青海省西宁市2022届高三二模数学(文)试题)如图,V是圆锥的顶点,O是底面圆心,AB是底面圆的一条直径,且点C是弧AB的中点,点D是AC的中点,2AB=,VA=.2(1)求圆锥的表面积;又D 是AC 的中点,所以OD AC ⊥,又VO OD O ⋂=,VO ⊂平面VOD ,OD ⊂平面VOD所以AC ⊥平面VOD ,又AC ⊂平面VAC ,所以平面VAC ⊥平面VOD .10.(河南省郑州市2023届高三第一次质量预测文科数学试题)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD ⊥AB ,AB DC ,2AD DC AP ===,1AB =,点E 为棱PC 的中点.(1)证明:平面PBC ⊥平面PCD ;(2)求四棱锥E ABCD -的体积;又点E 为棱PC 的中点,BE 由勾股定理得2AC AD =+∵△PAC 为直角三角形,E 111.(江西省部分学校2023届高三上学期1月联考数学(文)试题)如图,在正三棱柱111ABC A B C -中,12AA AB ==,D ,E 分别是棱BC ,1BB 的中点.(1)证明:平面1AC D ⊥平面1ACE .(2)求点1C 到平面1ACE 的距离.(2)连接1EC .因为1AA 由正三棱柱的性质可知因为ABC 是边长为2的等边三角形,所以故三棱锥11A CC E -的体积以15A E CE ==,1A E 则1ACE △的面积212S =12.(广西玉林、贵港、贺州市2023届高三联合调研考试(一模)数学(文)试题)在三棱锥-P ABC 中,底面ABC 是边长为2的等边三角形,点P 在底面ABC 上的射影为棱BC 的中点O ,且PB 与底面ABC 所成角为π3,点M 为线段PO 上一动点.(1)证明:BC AM ⊥;(2)若12PM MO =,求点M 到平面PAB 的距离.AO BC ∴⊥,点P 在底面ABC 上的投影为点PO ∴⊥平面ABC , PO BC ∴⊥,13.(广西南宁市第二中学2023届高三上学期第一次综合质检数学(文)试题)如图,D ,O 是圆柱底面的圆心,ABC 是底面圆的内接正三角形,AE 为圆柱的一条母线,P 为DO 的中点,Q 为AE 的中点,(1)若90APC ∠=︒,证明:DQ ⊥平面PBC ;(2)设2DO =,圆柱的侧面积为8π,求点B 到平面PAC 的距离.∴//,AQ PD AQ PD =,∴四边形AQDP 为平行四边形,∴//DQ PA .又∵P 在DO 上,而OD ∴O 为P 在ABC 内的投影,且ABC 是圆内接正三角形∴三棱锥-P ABC 为正三棱锥∴PAB PAC PBC △≌△≌△∴APB APC BPC ∠=∠=∠即,PA PC PA PB ⊥⊥.∵PC PB P = ,,PB PC14.(江西省吉安市2023届高三上学期1月期末质量检测数学(文)试题)如图,在四棱锥P -ABCD 中,AB CD ,12AD CD BC PA PC AB =====,BC PA ⊥.(1)证明:平面PBC ⊥平面PAC ;(2)若PB =D 到平面PBC 的距离.又BC PA ⊥,PA AC A = 所以BC ⊥平面PAC ,又BC (2)因为BC ⊥平面PAC ,由22PB =,BC PC =,得15.(江西省部分学校2023届高三下学期一轮复习验收考试(2月联考)数学(文)试题)如图,在长方体1111ABCD A B C D -中,1AB AD ==,1AA =E 在棱1DD 上,且1AE A D ⊥.(1)证明:1AE A C ⊥;(2)求三棱锥1E ACD -的体积.【答案】(1)证明见解析;)在平面11ADD A 中,由AE ⊥1AD DE AA AD =,所以12112A DE S DE AD =⋅= 16.(新疆兵团地州学校2023届高三一轮期中调研考试数学(文)试题)如图1,在等腰梯形ABCD 中,M ,N ,F 分别是AD ,AE ,BE 的中点,4AE BE BC CD ====,将ADE V 沿着DE 折起,使得点A 与点P 重合,平面PDE ⊥平面BCDE ,如图2.(1)证明:PC∥平面MNF.(2)求点C到平面MNF的距离.17.(宁夏银川市第一中学2023届高三上学期第四次月考数学(文)试题)如图1,在直角梯形ABCD 中,,90,5,2,3AB DC BAD AB AD DC ∠==== ∥,点E 在CD 上,且2DE =,将ADE V 沿AE 折起,使得平面ADE ⊥平面ABCE (如图2).(1)求点B 到平面ADE 的距离;(2)在线段BD 上是否存在点P ,使得CP 平面ADE ?若存在,求三棱锥-P ABC 的体积;若不存在,请说明理由..18.(陕西省汉中市2023届高三上学期教学质量第一次检测文科数学试题)如图,多面体ABCDEF 中,四边形ABCD 为菱形,60,ABC FA ∠=⊥ 平面,ABCD FA ED ∥,且22AB FA ED ===.(1)求证:BD FC ⊥;(2)求点A 到平面FBD 的距离.19.(内蒙古赤峰市2022届高三下学期5月模拟考试数学(文科)试题)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,60PAB PAD BAD ∠=∠=∠= .(1)证明:BD ⊥平面PAC ;(2)若23AB PA ==,,求四棱锥P ABCD -的体积.解:如图,记AC 与BD 的交点为因为底面ABCD 为菱形,故又60PAB PAD BAD ∠=∠=∠=又PO AC O = ,故BD ⊥平面(2)解:因为2,3,AB PA ==∠20.(内蒙古2023届高三仿真模拟考试文科数学试题)如图,在四棱锥P ABCD -中,四边形ABCD 是直角梯形,AD AB ⊥,//AB CD ,22PB CD AB AD ===,PD =,PC DE ⊥,E 是棱PB 的中点.(1)证明:PD ⊥平面ABCD ;(2)若F 是棱AB 的中点,2AB =,求点C 到平面DEF 的距离.,AB AD=AB AD⊥,2BD∴=为棱PB中点,DE PBE∴⊥,又∴⊥平面PBC,又BC⊂平面DE在直角梯形ABCD中,取CD中点 ,DM AB=2CD AB∴=,又DM ∴四边形ABMD为正方形,BM∴∴===,又BC BM AD AB222BD DE⊂平面PBD ,,=BD DE D21.(山西省晋中市2022届高三下学期5月模拟数学(文)试题)如图,在三棱锥-P ABC中,PAB 为等腰直角三角形,112PA PB AC ===,PC ,平面PAB ⊥平面ABC .(1)求证:PA BC ⊥;(2)求三棱锥-P ABC 的体积.∴OP AB ⊥,22OP =,AB =又∵平面PAB ⊥平面ABC ,平面∴OP ⊥平面ABC .22.(山西省太原市2022届高三下学期三模文科数学试题)已知三角形PAD 是边长为2的正三角形,现将菱形ABCD 沿AD 折叠,所成二面角P AD B --的大小为120°,此时恰有PC AD ⊥.(1)求BD 的长;(2)求三棱锥-P ABC 的体积.∵PAD 是正三角形,∴PM AD ⊥,又∴,PC AD PC PM P⊥=I ∴AD ⊥平面PMC ,∴AD MC ⊥,故ACD 为等腰三角形23.(陕西省联盟学校2023届高三下学期第一次大联考文科数学试题)如图,在四棱锥P ABCD -中,底面ABCD 是长方形,22AD CD PD ===,PA 二面角P AD C--为120︒,点E 为线段PC 的中点,点F 在线段AB 上,且12AF =.(1)平面PCD ⊥平面ABCD ;(2)求棱锥C DEF -的高.824.(陕西省榆林市2023届高三上学期一模文科数学试题)如图,在四棱锥P ABCD -中,平面PAD ⊥底面,,60,ABCD AB CD DAB PA PD ∠=⊥ ∥,且2,22PA PD AB CD ====.(1)证明:AD PB ⊥;(2)求点A 到平面PBC 的距离.(2)因为AB CD ,所以∠2222BC BD CD BD CD =+-⋅由222BD BC CD =+,得BC 25.(陕西省宝鸡教育联盟2022-2023学年高三下学期教学质量检测(五)文科数学试题)如图,在三棱柱111ABC A B C -中,平面11ABB A ⊥平面ABC ,四边形11ABB A 是边长为2的菱形,ABC 为等边三角形,160A AB ∠=︒,E 为BC 的中点,D 为1CC 的中点,P为线段AC上的动点.AB平面PDE,请确定点P在线段AC上的位置;(1)若1//-的体积.(2)若点P为AC的中点,求三棱锥C PDE(2)解:如图,取AB 的中点∵四边形11ABB A 为边长为2∴12A B =,1AA B 为等边三角形,26.(山西省运城市2022届高三上学期期末数学(文)试题)如图,在四棱锥P -ABCD中,底面ABCD 是平行四边形,2APB π∠=,3ABC π∠=,PB =,24PA AD PC ===,点M 是AB 的中点,点N 是线段BC 上的动点.(1)证明:CM⊥平面PAB;(2)若点N到平面PCM BNBC的值.27.(2020届河南省许昌济源平顶山高三第二次质量检测文科数学试题)如图,四棱锥P ABCD -中,//AB CD ,33AB CD ==,2PA PD BC ===,90ABC ∠=︒,且PB PC =.(1)求证:平面PAD ⊥平面ABCD ;(2)求点D 到平面PBC 的距离.因为//AB CD ,33AB CD ==,所以四边形ABCD 为梯形,又M 、E 为AD 、BC 的中点,所以ME 为梯形的中位线,28.(青海省海东市2022-2023学年高三上学期12月第一次模拟数学(文)试题)如图,在直三棱柱111ABC A B C -中,ABC 是等边三角形,14AB AA ==,D 是棱AB 的中点.(1)证明:平面1ACD ⊥平面11ABB A .(2)求点1B 到平面1A CD 的距离.由题意可得11A B D △的面积因为ABC 是边长为4的等边三角形,且29.(河南省十所名校2022-2023学年高三阶段性测试(四)文科数学试题)如图,在四棱锥P —ABCD 中,PC BC ⊥,PA PB =,APC BPC ∠=∠.(1)证明:PC AD ⊥;(2)若AB CD,PD AD ⊥,PC =,且点C 到平面PAB AD 的长.∵PA PB =,APC BPC ∠=∠∴90PCA PCB ∠=∠=︒,即∵PC BC ⊥,AC BC = ∴PC ⊥平面ABCD ,又∵PA PB =,E 为AB 中点∴PE AB ⊥,由(1)知AC BC =,E 为∵PE CE E = ,,PE CE 30.(河南省部分重点中学2022-2023学年高三下学期2月开学联考文科数学试题)如图,在直三棱柱111ABC A B C -中,5AB AC ==,16BB BC ==,D ,E 分别是1AA 和1B C 的中点.(1)求证:平面BED ⊥平面11BCC B ;(2)求三棱锥E BCD -的体积.。
2022学年高三上(编号1-25)立体几何大题汇编(教师版)

,即
令 ,则
面 法向量为
平面 与平面 夹角的余弦值为
,即
, (舍)
4:(2023届广东梅州中学高三上阶段性考试解析第20题)
4:如图,在四棱锥 中,四边形 为直角梯形, , ,平面 平面 , , , .
(1)证明: ;
(2)若四棱锥 的体积为 ,
求平面 与平面 所成的锐二面角的余弦值.
方法提供与解析:(浙江绍兴+谢柏军)
方法提供与解析:(浙江绍兴+谢柏军)
(1)解析: 是正方形
,
直三棱柱
, , 、 面 ,
面
面
面 面
(2)解析: 面
、 分别为 、 中点
以 为原点, 为 轴, 为 轴, 为 轴建立坐标系
, , ,
设面 的法向量为
,即
令 ,则 ,
面
面 的法向量为
平面 与平面 夹角的余弦值为
10:(2023届重庆市巴蜀中学月考卷(一)解析第19题)
方法提供与解析:(衢州张小臣)
解析:(1)证明:取 的中点 ,连接 .
因为 是等边 的中线,所以 .
因为 是棱 的中点, 为 的中点,
所以 ,且 .
因为 ,所以 ,且 ,
所以四边形 是平行四边形,所以 .
因为 , 为 的中点,所以 ,从而 .
高中立体几何证明平行的专题

FGG A B CD ECA BDE F DE B 1A 1C 1CM 立体几何——平行的证明【例1】如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ;分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四边形'【例2】如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1,BC =2,CD =1+3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC 。
(Ⅰ)求证:BC ⊥面CDE ; (Ⅱ)求证:FG ∥面BCD ; &分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形;【例3】已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证:(Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F GM AD CD BD BC AM EFG 求证:E F BACDP (第1题图)AE;PEDCBAAB 1ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC ∠=∠=//=12AD BE //=12AF,G H ,FA FD BCHG ,,,C D F E ) 利用平行四边形的性质【例9】正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心,M 为BB 1的中点, 求证: D 1O21中点为PD E 求证:AE ∥平面PBC ; ~分析:取PC 的中点F ,连EF 则易证ABFE 是平行四边形【例11】在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB=90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF。
立体几何证明题专题(教师版)

立体几何证明题考点1:点线面的位置关系及平面的性质例1.下列命题:①空间不同三点确定一个平面;②有三个公共点的两个平面必重合;③空间两两相交的三条直线确定一个平面;④三角形是平面图形;⑤平行四边形、梯形、四边形都是平面图形;⑥垂直于同一直线的两直线平行;⑦一条直线和两平行线中的一条相交,也必和另一条相交;⑧两组对边相等的四边形是平行四边形.其中正确的命题是________.【解析】由公理3知,不共线的三点才能确定一个平面,所以知命题①错,②中有可能出现两平面只有一条公共线(当这三个公共点共线时),②错.③空间两两相交的三条直线有三个交点或一个交点,若为三个交点,则这三线共面,若只有一个交点,则可能确定一个平面或三个平面.⑤中平行四边形及梯形由公理2可得必为平面图形,而四边形有可能是空间四边形,如图(1)所示.在正方体ABCD—A′B′C′D′中,直线BB′⊥AB,BB′⊥CB,但AB与CB不平行,∴⑥错.AB∥CD,BB′∩AB=B,但BB′与CD不相交,∴⑦错.如图(2)所示,AB=CD,BC=AD,四边形ABCD不是平行四边形,故⑧也错.【答案】④2.若P是两条异面直线l、m外的任意一点,则( )A.过点P有且仅有一条直线与l、m都平行B.过点P有且仅有一条直线与l、m都垂直C.过点P有且仅有一条直线与l、m都相交D.过点P有且仅有一条直线与l、m都异面答案 B解析对于选项A,若过点P有直线n与l,m都平行,则l∥m,这与l,m异面矛盾.对于选项B,过点P与l、m都垂直的直线,即过P且与l、m的公垂线段平行的那一条直线.对于选项C,过点P与l、m都相交的直线有一条或零条.对于选项D,过点P与l、m都异面的直线可能有无数条.3.已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定A.与a,b都相交B.只能与a,b中的一条相交C.至少与a,b中的一条相交D.与a,b都平行答案 C解析若c与a,b都不相交,则c与a,b都平行,根据公理4,则a∥b,与a,b异面矛盾.考点2:共点、共线、共面问题例1.下列各图是正方体和正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的图形是【解析】①在A中易证PS∥QR,∴P、Q、R、S四点共面.②在C中易证PQ∥SR,∴P、Q、R、S四点共面.③在D中,∵QR⊂平面ABC,PS∩面ABC=P且P∉QR,∴直线PS与QR为异面直线.∴P、Q、R、S四点不共面.④在B中P、Q、R、S四点共面,证明如下:取BC中点N,可证PS、NR交于直线B1C1上一点,∴P、N、R、S四点共面,设为α.可证PS∥QN,∴P、Q、N、S四点共面,设为β.∵α、β都经过P、N、S三点,∴α与β重合,∴P、Q、R、S四点共面.【答案】 D2.空间四点中,三点共线是这四点共面的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案 A3.下面三条直线一定共面的是( )A.a、b、c两两平行B.a、b、c两两相交C.a∥b,c与a、b均相交D.a、b、c两两垂直答案 C4.已知三个平面两两相交且有三条交线,试证三条交线互相平行或者相交于一点.【解析】设α∩β=a,β∩γ=b,γ∩α=c,由a⊂β,b⊂β,则a∩b=O,如图(1),或a∥b,如图(2),若a∩b=O,O∈a,a⊂α,则O∈α,O∈b,b⊂γ,则O∈γ,又γ∩α=c,因此O∈c;若a∥b,a⊄γ,b⊂γ,则a∥γ,又a⊂α,α∩γ=c,则a∥c.因此三条交线相交于一点或互相平行.5.如图所示,已知空间四边形ABCD中,E、H分别是边AB,AD的中点,F,G分别是边BC,CD上的点,且CFCB=CGCD=23.(1)求证:三条直线EF,GH,AC交于一点.(2)若在本题中,AEEB=CFFB=2,AHHD=CGGD=3,其他条件不变.求证:EH、FG、BD三线共点.【解析】(1)∵E,H分别是AB,AD的中点,∴由中位线定理可知,EH綊12BD.又∵CFCB=CGCD=23,∴在△CBD中,FG∥BD,且FG=23BD.∴由公理4知,EH∥FG,且EH<FG.∴四边形EFGH是梯形,EH、FG为上、下两底.∴两腰EF、GH所在直线必相交于一点P.∵P∈直线EF,EF⊂平面ABC,∴P∈平面ABC.同理可得P∈平面ADC.∴P在平面ABC和平面ADC的交线上.又∵面ABC∩面ADC=AC,∴P∈直线AC.故EF、GH、AC三直线交于一点.(2)∵AEEB=CFFB=2,∴EF∥AC.又AHHD=CGGD=3,∴HG∥AC,∴EF∥HG,且EF>HG.∴四边形EFGH为梯形.设EH与FG交于点P,则P∈平面ABD,P∈平面BCD.∴P 在两平面的交线BD 上. ∴EH 、FG 、BD 三线共点.考点3:异面直线的夹角1.在正方体ABCD -A 1B 1C 1D 1中,E 为AB 的中点.求BD 1与CE 所成角的余弦值.【解析】 连接AD 1,A 1D 交点为M ,连接ME ,MC ,则∠MEC (或其补角)即为异面直线BD 1与CE 所成的角,设AB =1,CE =52,ME =12BD 1=32,CM 2=CD 2+DM 2=32. 在△MEC 中,cos ∠MEC=CE 2+ME 2-CM 22CE ·ME =1515,因此异面直线BD 1与CE 所成角的余弦值为1515.2.如图,若正四棱柱ABCD -A 1B 1C 1D 1的底面边长为2,高为4,则异面直线BD 1与AD 所成角的正切值是______.答案 53.已知正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB ,E 为AA 1中点,则异面直线BE 与CD 1所成角的余弦值为 A.1010 B.15 C.31010 D.35答案 C解析 连接BA 1,则CD 1∥BA 1,于是∠A 1BE 就是异面直线BE 与CD 1所成的角(或补角),设AB =1,则BE =2,BA 1=5,A 1E =1,在△A 1BE 中,cos ∠A 1BE =5+2-125·2=31010,选C. 4.已知正方体ABCD -A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与BC 所成角的余弦值为________. 【解析】 取A 1B 1的中点F ,连接EF ,FA ,则有EF ∥B 1C 1∥BC ,∠AEF 即是直线AE 与BC 所成的角或其补角.设正方体ABCD —A 1B 1C 1D 1的棱长为2a ,则有EF =2a ,AF =2a2+a 2=5a ,AE =2a2+2a2+a 2=3a .在△AEF 中,cos ∠AEF =AE 2+EF 2-AF 22AE ·EF =9a 2+4a 2-5a 22×3a ×2a =23.因此,异面直线AE 与BC 所成的角的余弦值是23.【答案】2 3考点4:直线与平面平行的判定与性质1.下列命题中正确的是________.①若直线a不在α内,则a∥α;②若直线l上有无数个点不在平面α内,则l∥α;③若直线l与平面α平行,则l与α内的任意一条直线都平行;④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;⑥平行于同一平面的两直线可以相交.答案⑤⑥解析a∩α=A时,a不在α内,∴①错;直线l与α相交时,l上有无数个点不在α内,故②错;l ∥α时,α内的直线与l平行或异面,故③错;a∥b,b∥α时,a∥α或a⊂α,故④错;l∥α,则l与α无公共点,∴l与α内任何一条直线都无公共点,⑤正确;如图,长方体中,A1C1与B1D1都与平面ABCD 平行,∴⑥正确.2.给出下列四个命题:①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行;②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行;③若平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行;④若两条平行直线中的一条与一个平面平行,则另一条也与这个平面平行.其中正确命题的个数是________个.答案 1解析命题①错,需说明这条直线在平面外.命题②错,需说明这条直线在平面外.命题③正确,由线面平行的判定定理可知.命题④错,需说明另一条直线在平面外.3.已知不重合的直线a,b和平面α,①若a∥α,b⊂α,则a∥b;②若a∥α,b∥α,则a∥b;③若a∥b,b⊂α,则a∥α;④若a∥b,a⊂α,则b∥α或b⊂α,上面命题中正确的是________(填序号).答案④解析①若a∥α,b⊂α,则a,b平行或异面;②若a∥α,b∥α,则a,b平行、相交、异面都有可能;③若a ∥b ,b ⊂α,a ∥α或a ⊂α.4.正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP =DQ .求证:PQ ∥平面BCE .【证明】 方法一 如图所示. 作PM ∥AB 交BE 于M , 作QN ∥AB 交BC 于N , 连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD . 又AP =DQ ,∴PE =QB . 又PM ∥AB ∥QN ,∴PM AB =PE AE =QB BD ,QN DC =BQBD.∴PM AB =QN DC. ∴PM 綊QN ,即四边形PMNQ 为平行四边形. ∴PQ ∥MN .又MN ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE .方法二 如图,连接AQ ,并延长交BC 延长线于K ,连接EK . ∵AE =BD ,AP =DQ , ∴PE =BQ ,∴AP PE =DQBQ .又AD ∥BK ,∴DQ BQ =AQ QK,∴AP PE =AQQK,∴PQ ∥EK .又PQ ⊄平面BCE ,EK ⊂平面BCE , ∴PQ ∥平面BCE .方法三 如图,在平面ABEF 内,过点P 作PM ∥BE ,交AB 于点M ,连接QM . ∴PM ∥平面BCE .又∵平面ABEF ∩平面BCE =BE , ∴PM ∥BE ,∴AP PE =AMMB.又AE =BD ,AP =DQ ,∴PE =BQ . ∴AP PE =DQ BQ ,∴AM MB =DQ QB. ∴MQ ∥AD .又AD ∥BC ,∴MQ ∥BC ,∴MQ ∥平面BCE .又PM ∩MQ =M , ∴平面PMQ ∥平面BCE .又PQ ⊂平面PMQ , ∴PQ ∥平面BCE .5.一个多面体的直观图和三视图如图所示(其中M ,N 分别是AF ,BC 中点).<1>求证:MN ∥平面CDEF ; <2>求多面体A —CDEF 的体积.解析 (1)证明 由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB =BC =BF =2,DE =CF =22,∴∠CBF =90°.取BF 中点G ,连接MG ,NG ,由M ,N 分别是AF ,BC 中点,可知:NG ∥CF ,MG ∥EF .又MG ∩NG =G ,CF ∩EF =F ,∴平面MNG ∥平面CDEF ,∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ,由于三棱柱ADE —BCF 为直三棱柱,∴AH ⊥平面CDEF ,且AH = 2. ∴V A -CDEF =13S 四边形CDEF ·AH =13×2×22×2=83.6.若P 为异面直线a ,b 外一点,则过P 且与a ,b 均平行的平面 A .不存在 B .有且只有一个 C .可以有两个 D .有无数多个答案 B7.如图,在正方体ABCD —A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,且CM =DN ,求证:MN ∥平面AA 1B 1B .【证明】 方法一 如右图,作ME ∥BC ,交BB 1于E ;作NF ∥AD ,交AB 于F ,连接EF ,则EF ⊂平面AA 1B 1B .∵BD =B 1C ,DN =CM , ∴B 1M =BN .∵ME BC =B 1M B 1C ,NF AD =BN BD,∴ME BC =BN BD =NFAD,∴ME =NF . 又ME ∥BC ∥AD ∥NF , ∴MEFN 为平行四边形. ∴NM ∥EF .又∵MN ⊄面AA 1B 1B , ∴MN ∥平面AA 1B 1B .方法二 如图,连接CN 并延长交BA 的延长线于点P ,连接B 1P ,则B 1P ⊂平面AA 1B 1B . ∵△NDC ∽△NBP , ∴DN NB =CNNP.又CM =DN , B 1C =BD ,CM MB 1=DN NB =CN NP, ∴MN ∥B 1P .∵B 1P ⊂平面AA 1B 1B , ∴MN ∥平面AA 1B 1B .方法三 如右图,作MP ∥BB 1,交BC 于点P ,连接NP . ∵MP ∥BB 1,∴CM MB 1=CP PB. ∵BD =B 1C ,DN =CM , ∴B 1M =BN .∵CM MB 1=DN NB, ∴CP PB =DNNB,∴NP ∥DC ∥AB . ∴平面MNP ∥平面AA 1B 1B . ∴MN ∥平面AA 1B 1B .8.如图所示,四棱锥P —ABCD 中,底面ABCD 为正方形,PD ⊥平面ABCD ,PD =AB =2,E ,F ,G 分别为PC 、PD 、BC 的中点.(1)求证:PA ∥平面EFG ; (2)求三棱锥P —EFG 的体积.解析 (1)证明 如图,取AD 的中点H ,连接GH ,FH .∵E ,F 分别为PC ,PD 的中点, ∴EF ∥CD .∵G ,H 分别是BC ,AD 的中点, ∴GH ∥CD .∴EF ∥GH ,∴E ,F ,H ,G 四点共面. ∵F ,H 分别为DP ,DA 的中点,∴PA ∥FH . ∵PA ⊄平面EFG ,FH ⊂平面EFG , ∴PA ∥平面EFG .(2)∵PD ⊥平面ABCD ,CG ⊂平面ABCD ,∴PD ⊥CG . 又∵CG ⊥CD ,CD ∩PD =D ,∴GC ⊥平面PCD . ∵PF =12PD =1,EF =12CD =1,∴S △PEF =12EF ·PF =12.又GC =12BC =1,∴V P —EFG =V G —PEF =13×12×1=16.9.如图所示,a ,b 是异面直线,A 、C 与B 、D 分别是a ,b 上的两点,直线a ∥平面α,直线b ∥平面α,AB ∩α=M ,CD ∩α=N ,求证:若AM =BM ,则CN =DN .【证明】 连接AD 交平面α于E 点,并连接ME ,NE . ∵b ∥α,ME ⊂平面ABD ,平面α∩面ABD =ME , ∴ME ∥BD .又在△ABD 中AM =MB , ∴AE =ED .即E 是AD 的中点.又a ∥α,EN ⊂平面ACD ,平面α∩面ADC =EN , ∴EN ∥AC ,而E 是AD 的中点. ∴N 必是CD 的中点,∴CN =DN .10.如图,在三棱柱ABC -A 1B 1C 1中,E 为AC 上一点,若AB 1∥平面C 1EB ,求:AE ∶EC .【解析】 连接B 1C 交BC 1于点F , 则F 为B 1C 中点. ∵AB 1∥平面C 1EB ,AB 1⊂平面AB 1C ,且平面C 1EB ∩平面AB 1C =EF .∴AB1∥EF,∴E为AC中点.∴AE∶EC=1∶1.【答案】1∶1考点5:面面平行的判定及性质1.设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )A.m∥β且l1∥αB.m∥l1且n∥l2 C.m∥β且n∥βD.m∥β且n∥l2答案 B解析因m⊂α,l1⊂β,若α∥β,则有m∥β且l1∥α,故α∥β的一个必要条件是m∥β且l1∥α,排除A.因m,n⊂α,l1,l2⊂β且l1与l2相交,若m∥l1且n∥l2,因l1与l2相交,故m与n也相交,∴α∥β;若α∥β,则直线m与直线l1可能为异面直线,故α∥β的一个充分而不必要条件是m∥l1且n∥l2,应选B.2.棱长为1的正方体ABCD—A1B1C1D1中,点P,Q,R分别是面A1B1C1D1,BCC1B1,ABB1A1的中心,给出下列结论:①PR与BQ是异面直线;②RQ⊥平面BCC1B1;③平面PQR∥平面D1AC;④过P,Q,R的平面截该正方体所得截面是边长为2的等边三角形.以上结论正确的是________.(写出所有正确结论的序号)答案③④解析由于PR是△A1BC1的中位线,所以PR∥BQ,故①不正确;由于RQ∥A1C1,而A1C1不垂直于面BCC1B1,所以②不正确;由于PR∥BC1∥D1A,PQ∥A1B∥D1C,所以③正确;由于△A1BC1是边长为2的正三角形,所以④正确.故填③④.3.已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心.<1>求证:平面G1G2G3∥平面ABC;<2>求S△G1G2G3∶S△ABC.【解析】(1)如图,连接PG1、PG2、PG3并延长分别与边AB、BC、AC交于点D、E、F.连接DE、EF、FD.则有PG1∶PD=2∶3,PG2∶PE=2∶3.∴G1G2∥DE.又G1G2不在平面ABC内,∴G1G2∥平面ABC.同理G2G3∥平面ABC.又因为G1G2∩G2G3=G2,∴平面G1G2G3∥平面ABC.(2)由(1)知PG 1PD =PG 2PE =23,∴G 1G 2=23DE . 又DE =12AC ,∴G 1G 2=13AC . 同理G 2G 3=13AB ,G 1G 3=13BC . ∴△G 1G 2G 3∽△CAB ,其相似比为1∶3.∴S △G 1G 2G 3∶S △ABC =1∶9.4.给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题:①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β;②若α∥β,l ⊂α,m ⊂β,则l ∥m ;③若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n .其中真命题为________.答案 ③解析 ①中当α与β不平行时,也能存在符合题意的l 、m .②中l 与m 也可能异面.③中 ⎭⎪⎬⎪⎫l ∥γl ⊂ββ∩γ=m ⇒l ∥m ,同理l ∥n ,则m ∥n ,正确.5.如图所示,正方体ABCD —A 1B 1C 1D 1中,M 、N 、E 、F 分别是棱A 1B 1,A 1D 1,B 1C 1,C 1D 1的中点.求证:平面AMN ∥平面EFDB .【证明】 连接MF ,∵M 、F 是A 1B 1、C 1D 1的中点,四边形A 1B 1C 1D 1为正方形,∴MF A 1D 1.又A 1D 1 AD ,∴MF AD .∴四边形AMFD 是平行四边形.∴AM ∥DF .∵DF ⊂平面EFDB ,AM ⊄平面EFDB ,∴AM ∥平面EFDB ,同理AN ∥平面EFDB .又AM 、AN ⊂平面ANM ,AM ∩AN =A ,∴平面AMN ∥平面EFDB .6.在正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别是C 1C ,B 1C 1,C 1D 1的中点,求证:平面MNP ∥平面A 1BD . 证明 方法一如图(1)所示,连接B 1D 1.∵P ,N 分别是D 1C 1,B 1C 1的中点,∴PN∥B1D1.又B1D1∥BD,∴PN∥BD.又PN⊄平面A1BD,∴PN∥平面A1BD.同理:MN∥平面A1BD.又PN∩MN=N,∴平面PMN∥平面A1BD.方法二如图(2)所示,连接AC1,AC,∵ABCD-A1B1C1D1为正方体,∴AC⊥BD.又CC1⊥平面ABCD,∴AC为AC1在平面ABCD上的射影,∴AC1⊥BD.同理可证AC1⊥A1B,∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN.∴平面PMN∥平面A1BD.7.如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E、F分别在线段AB,CD上,且AE∶EB=CF∶FD.求证:EF∥β.【证明】①当AB,CD在同一平面内时,由α∥β,α∩平面ABDC=AC,β∩平面ABDC=BD,∴AC∥BD.∵AE∶EB=CF∶FD,∴EF∥BD.又EF⊄β,BD⊂β,∴EF∥β.②当AB与CD异面时,设平面ACD∩β=DH,且DH=AC,∵α∥β,α∩平面ACDH=AC,∴AC∥DH.∴四边形ACDH是平行四边形.在AH上取一点G,使AG∶GH=CF∶FD,又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH.又EG∩GF=G,∴平面EFG∥平面β.∵EF⊂平面EFG,∴EF∥β.综上,EF∥β.8.已知:如图,斜三棱柱ABC—A1B1C1中,点D、D1分别为AC、A1C1上的点.(1)当A 1D 1D 1C 1的值等于何值时,BC 1∥平面AB 1D 1; (2)若平面BC 1D ∥平面AB 1D 1,求ADDC 的值.【解析】 (1)如图,取D 1为线段A 1C 1的中点,此时A 1D 1D 1C 1=1,连接A 1B 交AB 1于点O ,连接OD 1. 由棱柱的性质,知四边形A 1ABB 1为平行四边形,所以点O 为A 1B 的中点.在△A 1BC 1中,点O 、D 1分别为A 1B 、A 1C 1的中点,∴OD 1∥BC 1.又∵OD 1⊂平面AB 1D 1,BC 1⊄平面AB 1D 1,∴BC 1∥平面AB 1D 1.∴A 1D 1D 1C 1=1时,BC 1∥平面AB 1D 1. (2)由已知,平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O ,因此BC 1∥D 1O ,同理AD 1∥DC 1.∴A 1D 1D 1C 1=A 1O OB ,A 1D 1D 1C 1=DC AD. 又∵A 1O OB =1,∴DC AD =1,即AD DC =1. 考点6:线线、线面垂直1.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列四个命题,其中真命题是A .若a ∥α,b ∥α,则a ∥bB .若a ∥α,b ∥β,a ∥b ,则α∥βC .若a ⊥α,b ⊥β,a ⊥b ,则α⊥βD .若a 、b 在平面α内的射影互相垂直,则a ⊥b答案 C解析 与同一平面平行的两条直线不一定平行,所以A 错误;与两条平行直线分别平行的两个平面未必平行,所以B 错误;如图(1),设OA ∥a ,OB ∥b ,直线OA 、OB 确定的平面分别交α、β于AC 、BC ,则OA ⊥AC ,OB ⊥BC ,所以四边形OACB 为矩形,∠ACB 为二面角α-l -β的平面角,所以α⊥β,C 正确;如图(2),直线a 、b 在平面α内的射影分别为m 、n ,显然m ⊥n ,但a 、b 不垂直,所以D 错误,故选C.2.“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件答案 B 3.若m ,n 表示直线,α表示平面,则下列命题中,正确命题的个数为①⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α ② ⎭⎪⎬⎪⎫n ⊥αm ⊥α⇒m ∥n ③ ⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n ④ ⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥αA .1B .2C .3D .4答案 C解析 ①②③正确,④错误.4.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,PA =AB =BC ,E 是PC 的中点.求证:(1)CD ⊥AE ;(2)PD ⊥平面ABE .【证明】 (1)∵PA ⊥底面ABCD ,∴CD ⊥PA .又CD ⊥AC ,PA ∩AC =A ,故CD ⊥平面PAC ,AE ⊂平面PAC .故CD ⊥AE .(2)∵PA =AB =BC ,∠ABC =60°,故PA =AC .∵E 是PC 的中点,故AE ⊥PC .由(1)知CD ⊥AE ,从而AE ⊥平面PCD ,故AE ⊥PD .易知BA ⊥PD ,故PD ⊥平面ABE .5.设l 是直线,α,β是两个不同的平面( )A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若l ⊥α,α⊥β,则l ⊥βD .若α⊥β,l ∥α,则l ⊥β答案 B解析 A 项中由l ∥α,l ∥β不能确定α与β的位置关系,C 项中由α⊥β,l ⊥α可推出l ∥β或l⊂β,D项由α⊥β,l∥α不能确定l与β的位置关系.6.设b,c表示两条直线,α,β表示两个平面,下列命题中真命题是A.若b⊂α,c∥α,则b∥cB.若b⊂α,b∥c,则c∥αC.若c∥α,c⊥β,则α⊥βD.若c∥α,α⊥β,则c⊥β答案 C解析如果一条直线平行于一个平面,它不是与平面内的所有直线平行,只有部分平行,故A错;若一条直线与平面内的直线平行,该直线不一定与该平面平行,该直线可能是该平面内的直线,故B 错;如果一个平面与另一个平面的一条垂线平行,那么这两个平面垂直,这是一个真命题,故C对;对D来讲若c∥α,α⊥β,则c与β的位置关系不定,故选C.7. 在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,∠A1DE =90°,求证:CD⊥平面A1ABB1.证明连接A1E,EC,∵AC=BC=2,∠ACB=90°,∴AB=2 2.设AD=x,则BD=22-x.∴A1D2=4+x2,DE2=1+(22-x)2,A1E2=(22)2+1.∵∠A1DE=90°,∴A1D2+DE2=A1E2.∴x= 2.∴D为AB的中点.∴CD⊥AB.又AA1⊥CD,且AA1∩AB=A,∴CD⊥平面A1ABB1.8.如图,长方体ABCD—A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.<1>证明:BD⊥EC1;<2>如果AB=2,AE=2,OE⊥EC1,求AA1的长.【解析】(1)如图,连接AC,A1C1,AC与BD相交于点O.由底面是正方形知,BD⊥AC.因为AA1⊥平面ABCD,BD⊂平面ABCD,所以AA1⊥BD.又由AA1∩AC=A,所以BD⊥平面AA1C1C.再由EC1⊂平面AA1C1C知,BD⊥EC1.(2)设AA1的长为h,连接OC1.在Rt△OAE中,AE=2,AO=2,故OE2=(2)2+(2)2=4.在Rt△EA1C1中,A1E=h-2,A1C1=2 2.故EC 21=(h -2)2+(22)2. 在Rt △OCC 1中,OC =2,CC 1=h ,OC 21=h 2+(2)2. 因为OE ⊥EC 1,所以OE 2+EC 21=OC 21.即4+(h -2)2+(22)2=h 2+(2)2,解得h =3 2.所以AA 1的长为3 2.考点7:面面垂直1.△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE =CA =2BD ,M 是EA 的中点,求证:①DE =DA ;②平面BDM ⊥平面ECA ;③平面DEA ⊥平面ECA .【证明】 ①取EC 的中点F ,连接DF .∵BD ∥CE ,∴DB ⊥BA .又EC ⊥BC ,在Rt △EFD 和Rt △DBA 中,∵EF =12EC =BD ,FD =BC =AB , ∴Rt △EFD ≌Rt △DBA ,∴DE =DA .②取CA 的中点N ,连接MN 、BN ,则MN 綊12EC . ∴MN ∥BD ,∴N 点在平面BDM 内.∵EC ⊥平面ABC ,∴EC ⊥BN .又CA ⊥BN ,∴BN ⊥平面ECA .∵BN ⊂平面BDM ,∴平面BDM ⊥平面ECA .③∵DM ∥BN ,BN ⊥平面ECA ,∴DM ⊥平面ECA ,又DM ⊂平面DEA ,∴平面DEA ⊥平面ECA .2.已知平面PAB ⊥平面ABC ,平面PAC ⊥平面ABC .AE ⊥平面PBC ,E 为垂足.①求证:PA ⊥平面ABC ;②当E 为△PBC 的垂心时,求证:△ABC 是直角三角形.【证明】 ①在平面ABC 内取一点D ,作DF ⊥AC 于F .平面PAC ⊥平面ABC ,且交线为AC ,∴DF ⊥平面PAC .又PA ⊂平面PAC ,∴DF ⊥PA .作DG ⊥AB 于G ,同理可证:DG ⊥PA . DG 、DF 都在平面ABC 内,∴PA ⊥平面ABC .②连接BE 并延长交PC 于H ,∵E 是△PBC 的垂心,∴PC ⊥BH .又已知AE 是平面PBC 的垂线,PC ⊂平面PBC ,∴PC ⊥AE .又BH ∩AE =E ,∴PC ⊥平面ABE .又AB ⊂平面ABE ,∴PC ⊥AB .∵PA ⊥平面ABC ,∴PA ⊥AB .又PC ∩PA =P ,∴AB ⊥平面PAC .又AC ⊂平面PAC ,∴AB ⊥AC .即△ABC 是直角三角形.3.如图所示,在斜三棱柱A 1B 1C 1-ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC .(1)若D 是BC 的中点,求证:AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1,求证:截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥侧面BB 1C 1C 的充要条件吗?请你叙述判断理由.【证明】 (1)∵AB =AC ,D 是BC 的中点,∴AD ⊥BC .∵底面ABC ⊥侧面BB 1C 1C ,且交线为BC ,∴由面面垂直的性质定理可知AD ⊥侧面BB 1C 1C .又∵CC 1⊂侧面BB 1C 1C ,∴AD ⊥CC 1.(2)方法一 取BC 1的中点E ,连接DE 、ME .在△BCC 1中,D 、E 分别是BC 、BC 1的中点.∴DE 綊12CC 1. 又AA 1綊CC 1,∴DE 綊12AA 1. ∵M 是AA 1的中点(由AM =MA 1知),∴DE 綊AM .∴AMED 是平行四边形,∴AD 綊ME .由(1)知AD ⊥面BB 1C 1C ,∴ME ⊥侧面BB 1C 1C .又∵ME ⊂面BMC 1,∴面BMC 1⊥侧面BB 1C 1C .方法二 延长B 1A 1与BM 交于N (在侧面AA 1B 1B 中),连接C 1N .∵AM =MA 1,∴NA 1=A 1B 1.又∵AB =AC ,由棱柱定义知△ABC ≌△A 1B 1C 1.∴AB =A 1B 1,AC =A 1C 1.∴A 1C 1=A 1N =A 1B 1.在△B 1C 1N 中,由平面几何定理知:∠NC 1B 1=90°,即C 1N ⊥B 1C 1.又∵侧面BB 1C 1C ⊥底面A 1B 1C 1,交线为B 1C 1,∴NC 1⊥侧面BB 1C 1C .又∵NC 1⊂面BNC 1,∴截面C 1NB ⊥侧面BB 1C 1C ,即截面MBC 1⊥侧面BB 1C 1C .(3)结论是肯定的,充分性已由(2)证明.下面仅证明必要性(即由截面BMC 1⊥侧面BB 1C 1C 推出AM =MA 1,实质是证明M 是AA 1的中点), 过M 作ME 1⊥BC 1于E 1.∵截面MBC 1⊥侧面BB 1C 1C ,交线为BC 1.∴ME 1⊥面BB 1C 1C .又由(1)知AD ⊥侧面BB 1C 1C ,∵垂直于同一个平面的两条直线平行,∴AD ∥ME 1,∴M 、E 1、D 、A 四点共面.又∵AM ∥侧面BB 1C 1C ,面AME 1D ∩面BB 1C 1C =DE 1,∴由线面平行的性质定理可知AM ∥DE 1.又AD ∥ME 1,∴四边形AME 1D 是平行四边形.∴AD =ME 1,DE 1綊AM .又∵AM ∥CC 1,∴DE 1∥CC 1.又∵D 是BC 的中点,∴E 1是BC 1的中点.∴DE 1=12CC 1=12AA 1. ∴AM =12AA 1,∴MA =MA 1. ∴AM =MA 1是截面MBC 1⊥侧面BB 1CC 1的充要条件.考点8:平行与垂直的综合问题1.如图所示,在直角梯形ABEF 中,将DCEF 沿CD 折起使∠FDA =60°,得到一个空间几何体.(1)求证:BE ∥平面ADF ;(2)求证:AF ⊥平面ABCD ;(3)求三棱锥E —BCD 的体积.【解析】 (1)由已知条件,可知BC ∥AD ,CE ∥DF ,折叠之后平行关系不变.又因为BC ⊄平面ADF ,AD ⊂平面ADF ,所以BC ∥平面ADF .同理CE ∥平面ADF .又因为BC ∩CE =C ,BC ,CE ⊂平面BCE ,所以平面BCE ∥平面ADF .所以BE ∥平面ADF .(2)由于∠FDA =60°,FD =2,AD =1,所以AF 2=FD 2+AD 2-2×FD ×AD ×cos FDA =4+1-2×2×1×12=3.即AF = 3. 所以AF 2+AD 2=FD 2.所以AF ⊥AD .又因为DC ⊥FD ,DC ⊥AD ,AD ∩FD =D ,所以DC ⊥平面ADF .又因为AF ⊂平面ADF ,所以DC ⊥AF .因为AD ∩DC =D ,AD ,DC ⊂平面ABCD ,所以AF ⊥平面ABCD .(3)因为DC ⊥EC ,DC ⊥BC ,EC ,BC ⊂平面EBC ,EC ∩BC =C ,所以DC ⊥平面EBC .又因为DF ∥EC ,AD ∥BC ,∠FDA =60°,所以∠ECB =60°.又因为EC =1,BC =1,所以S △ECB =12×1×1×32=34. 所以V E -BCD =V D -EBC =13×DC ×S △ECB =13×1×34=312. 2.如图1,在Rt △ABC 中,∠C =90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点.将△ADE 沿DE 折起到△A 1DE 的位置,使A 1F ⊥CD ,如图2.<1>求证:DE ∥平面A 1CB ;<2>求证:A 1F ⊥BE ;<3>线段A 1B 上是否存在点Q ,使A 1C ⊥平面DEQ ?说明理由.【解析】 (1)因为D ,E 分别为AC ,AB 的中点,所以DE ∥BC .又因为DE ⊄平面A 1CB ,所以DE ∥平面A 1CB .(2)由已知得AC ⊥BC 且DE ∥BC ,所以DE ⊥AC .所以DE ⊥A 1D ,DE ⊥CD ,所以DE ⊥平面A 1DC .而A 1F ⊂平面A 1DC ,所以DE ⊥A 1F .又因为A 1F ⊥CD ,所以A 1F ⊥平面BCDE .所以A 1F ⊥BE .(3)线段A 1B 上存在点Q ,使A 1C ⊥平面DEQ .理由如下:如图,分别取A 1C ,A 1B 的中点P ,Q ,连接PQ ,QE ,PD ,则PQ ∥BC .因为DE ∥BC ,所以DE ∥PQ .所以平面DEQ 即为平面DEP .由(2)知,DE ⊥平面A 1DC ,所以DE ⊥A 1C .又因为P 是等腰三角形DA 1C 底边A 1C 的中点,所以A 1C ⊥DP .所以A 1C ⊥平面DEP .从而A 1C ⊥平面DEQ .故线段A 1B 上存在点Q ,使得A 1C ⊥平面DEQ .3.如图,四棱锥P -ABCD 中,四边形ABCD 为矩形,△PAD 为等腰三角形,∠APD =90°,平面PAD ⊥平面ABCD ,且AB =1,AD =2,E 、F 分别为PC 、BD 的中点.<1>证明:EF ∥平面PAD ;<2>证明:平面PDC ⊥平面PAD ;<3>求四棱锥P —ABCD 的体积.解析 (1)证明:如图,连接AC .∵四边形ABCD 为矩形且F 是BD 的中点,∴F 也是AC 的中点.又E 是PC 的中点,EF ∥AP ,∵EF ⊄平面PAD ,PA ⊂平面PAD ,∴EF ∥平面PAD .(2)证明:∵面PAD ⊥平面ABCD ,CD ⊥AD ,平面PAD ∩平面ABCD =AD ,∴CD ⊥平面PAD .∵CD ⊂平面PDC ,∴平面PDC ⊥平面PAD .(3)取AD 的中点为O .连接PO .∵平面PAD ⊥平面ABCD ,△PAD 为等腰直角三角形,∴PO ⊥平面ABCD ,即PO 为四棱锥P —ABCD 的高.∵AD =2,∴PO =1.又AB =1,∴四棱锥P —ABCD 的体积V =13PO ·AB ·AD =23.21。
(完整版)立体几何证明垂直专项含练习题及答案.doc

精品字里行间精品文档立体几何证明 ------ 垂直一. 复习引入1.空间两条直线的位置关系有: _________,_________,_________三种。
2.(公理 4)平行于同一条直线的两条直线互相 _________.3.直线与平面的位置关系有 _____________,_____________,_____________三种。
4.直线与平面平行判定定理 : 如果 _________的一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行5.直线与平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么 _________________________.6.两个平面的位置关系 :_________,_________.7.判定定理 1:如果一个平面内有 _____________直线都平行于另一个平面,那么这两个平面平行 .8.线面垂直性质定理:垂直于同一条直线的两个平面 ________.9.如果两个平行平面同时和第三个平面相交,那么它们的________平行 .10.如果两个平面平行,那么其中一个平面内的所有直线都 _____于另一个平面 . 二.知识点梳理知识点一、直线和平面垂直的定义与判定定义语言描述如果直线l 和平面α内的任意一条直线都垂直,我们就说直线 l 与平面互相垂直,记作 l ⊥α图形判定一条直线与一个平面内的两条相交直线都垂直,则这条直线与该平面垂直 .条件 b 为平面α内的任一直线,而 l 对这l ⊥m, l ⊥n,m∩n=B,m ,一直线总有 l ⊥αn结论l ⊥l ⊥要点诠释:定义中“平面内的任意一条直线”就是指“平面内的所有直线”,这与“无数条直线”不同(线线垂直线面垂直)知识点二、直线和平面垂直的性质性质语言描述一条直线垂直于一个平面,那么这条垂直于同一个平面的两条直线平行.直线垂直于这个平面内的所有直线图形条件结论知识点三、二面角Ⅰ .二面角:从一条直线出发的两个半平面所组成的图形叫二面角(dihedral angle). 这条直线叫做二面角的棱,这两个半平面叫做二面角的面. 记作二面角-AB-. (简记P-AB-Q)二面角的平面角的三个特征:ⅰ.点在棱上ⅱ.线在面内ⅲ .与棱垂直Ⅱ .二面角的平面角:在二面角-l-的棱l上任取一点O,以点O为垂足,在半平面,内分别作垂直于棱 l 的射线 OA 和 OB ,则射线 OA 和 OB 构成的AOB叫做二面角的平面角.作用:衡量二面角的大小;范围:001800.知识点四、平面和平面垂直的定义和判定定义判定文字描述两个平面相交,如果它们所成的二面一个平面过另一个平面的垂线,则这角是直二面角,就说这两个平面垂两个平面垂直直.图形结果α∩β =lα-l-β=90oα⊥β(垂直问题中要注意题目中的文字表述,特别是“任何”“ 随意”“无数”等字眼)三.常用证明垂直的方法立体几何中证明线面垂直或面面垂直都可转化为线线垂直,而证明线线垂直一般有以下的一些方法:( 1)通过“平移”。
人教高中数学必修二1-2章立体几何证明题定理推论汇总

立体几何公理、定理推论汇总一、公理及其推论公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内。
符号语言:,,,A l B l A B l a a a ÎÎÎÎÞÌ作用:作用: ① 用来验证直线在平面内;用来验证直线在平面内;② 用来说明平面是无限延展的。
用来说明平面是无限延展的。
公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
(那么它们有且只有一条通过这个公共点的公共直线)(那么它们有且只有一条通过这个公共点的公共直线)符号语言:P l P l a b a b ÎÞ=Î且作用:①作用:① 用来证明两个平面是相交关系;用来证明两个平面是相交关系;② 用来证明多点共线,多线共点。
用来证明多点共线,多线共点。
公理3 经过不在同一条直线上的三点,有且只有一个平面。
经过不在同一条直线上的三点,有且只有一个平面。
符号语言:,,,,A B C A B C Þ不共线确定一个平面推论1 经过一条直线和这条直线外的一点,有且只有一个平面。
经过一条直线和这条直线外的一点,有且只有一个平面。
符号语言:A a A a a a a ÏÞÎÌ有且只有一个平面,使,推论2 经过两条相交直线,有且只有一个平面。
经过两条相交直线,有且只有一个平面。
符号语言:a b P a b a a a Ç=ÞÌÌ有且只有一个平面,使,推论3 经过两条平行直线,有且只有一个平面。
经过两条平行直线,有且只有一个平面。
符号语言://a b a b a a a ÞÌÌ有且只有一个平面,使,公理3及其推论的作用:用来证明多点共面,多线共面。
及其推论的作用:用来证明多点共面,多线共面。
立体几何证明(教师版)
立体几何证明1.(2021·北京师大附中高一期末)已知四棱锥P ABCD -的底面为直角梯形,//,90,AB DC DAB PA ∠=⊥平面ABCD ,且112PA AD DC AB ====,M 是棱PB 上的动点.(1)求证:平面PAD ⊥平面PCD ;(2)若//PD 平面ACM ,求PM MB的值; (3)当M 是PB 中点时,设平面ADM 与棱PC 交于点N ,求截面ADNM 的面积.2.(2021·北京·人大附中高一期末)如图,已知正方体1111ABCD A B C D -,点E 为棱1CC 的中点.(1)证明:1AC ∥平面BDE .(2)证明1AC BD ⊥.3.(2021·北京·汇文中学高一期末)如图1,已知菱形AECD 的对角线AC ,DE 交于点F ,点E 为AB 的中点.将三角形ADE 沿线段DE 折起到PDE 的位置,如图2所示.(1)求证:DE PC ⊥;(2)试问平面PFC 与平面PBC 所成的二面角是否为90︒,如果是,请证明;如果不是,请说明理由;(3)在线段PD ,BC 上是否分别存在点M ,N ,使得平面//CFM 平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.4.(2021·北京·首都师范大学附属中学高一期末)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,O ,M 分别为BD ,PC 的中点.设平面PAD 与平面PBC 的交线为l .(1)求证://OM 平面PAD ;(2)求证://BC l ;(3)在棱PC 上是否存在点N (异于点C ),使得//BN 平面PAD ?若存在,求出PN PC的值;若不存在,说明理由.5.(2021·北京·101中学高一期末)已知正四棱柱1111ABCD A B C D -中,M 是1DD 的中点.(1)求证:1//BD 平面AMC ;(2)求证:1AC BD ⊥;(3)在线段1BB 上是否存在点P ,当1BP BB λ=时,平面11//A PC 面AMC ?若存在,求出λ的值并证明;若不存在,请说明理由.6.(2021·北京师大附中高一期末)在正方体1111ABCD A B C D -中,E 为1CC 中点.(1)求证:1//BC 平面1AD E ;(2)求证:1A D ⊥平面11ABC D .7.(2021·北京·汇文中学高一期末)如图所示,在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .(1)求证://MN 平面ABD ;(2)若MN CD ⊥,BD CD ⊥,求证:平面CBD ⊥平面ABD .8.(2019·北京师大附中高一期末)如图,在三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=,2AB AC ==,1AA ,M N 分别为1,BC CC 的中点,P 为侧棱1BB 上的动点(Ⅰ)求证:平面APM ⊥平面11BB C C ;(Ⅱ)若P 为线段1BB 的中点,求证:1//A N 平面APM ;(Ⅲ)试判断直线1BC 与平面APM 是否能够垂直.若能垂直,求PB 的值;若不能垂直,请说明理由9.(2019·北京师大附中高一期末)如图,已知四棱锥S ABCD-,底面ABCD是边长为2的菱形,60∠=,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,ABCE为线段AD的中点SD平面MAC;(Ⅰ)求证://⊥;(Ⅱ)求证:SE AC-的体积(Ⅲ)求三棱锥M ABC-中,PA⊥平面ABCD,底10.(2019·北京·101中学高一期末)如图,在四棱锥P ABCD部ABCD为菱形,E为CD的中点.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.11.(2019·北京·中央民族大学附属中学高一期末)在四面体ABCD 中,CB =CD ,AD BD ⊥,且E ,F 分别是AB ,BD 的中点,求证:(I )直线EF ACD 面;(II )EFC BCD ⊥面面.12.(2020·北京师大附中高一期末)如图,四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,E 是PA 的中点.(1)求证://CD 平面PAB ;(2)求证://PC 平面BDE ;(3)证明:BD CE ⊥.13.(2021·北京·人大附中高一期末)如图1,已知△ABD 和△BCD 是两个直角三角形,∠BAD =∠BDC =2π.现将△ABD 沿BD 边折起到1A BD 的位置,如图2所示,使平面1A BD ⊥平面BCD .(1)求证:平面1A BC ⊥平面1A CD ;(2)1A C 与BD 是否有可能垂直,做出判断并写明理由.14.(2020·北京·101中学高一期末)如图1,在△ABC 中,D ,E 分别为AB ,AC 的中点,O 为DE 的中点,AB AC ==4BC =.将△ADE 沿DE 折起到△1A DE 的位置,使得平面1A DE ⊥平面BCED ,F 为1A C 的中点,如图2.(1)求证://EF 平面1A BD ;(2)求证:平面1A OB ⊥平面1A OC ;(3)线段OC 上是否存在点G ,使得OC ⊥平面EFG ?说明理由.15.(2020·北京师大附中高一期末)如图,在多面体ABCDEF 中,底面ABCD 为矩形,侧面ADEF 为梯形,//AF DE ,DE AD ⊥,DC DE =.⊥;(Ⅰ)求证:AD CEBF平面CDE;(Ⅱ)求证://(Ⅲ)判断线段BE上是否存在点Q,使得平面ADQ⊥平面BCE?并说明理由.-中,平面16.(2020·北京·中国人民大学附属中学朝阳学校高一期末)在三棱锥P ABC⊥.设D,E分别为PA,AC中点.PAC⊥平面ABC,PA AC⊥,AB BCDE平面PBC;(Ⅰ)求证://(Ⅱ)求证:BC⊥平面PAB;(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.答案:1.(1)证明见解析;(2)12;【分析】 (1) 要证平面PAD ⊥平面PCD ,只需证明DC ⊥平面PAD ,利用线面垂直的判定可证DC ⊥平面PAD .(2) 根据题意,作出点M ,再利用相似三角形求PM MB的值 (3) 从四点共面角度出发,利用平面向量基本定理确定点N 的位置,再求截面面积.【详解】(1)证明:因为90DAB ∠=,所以AB AD ⊥,又//AB DC ,所以DC AD ⊥.因为PA ⊥平面ABCD ,DC ⊂平面ABCD ,所以PA DC ⊥.又AD ,PA 在平面PAD 内,且相交于点A ,所以DC ⊥平面PAD . 又DC ⊂平面PCD ,所以平面PAD ⊥平面PCD .(2)如图,连接AC ,BD 相交于点E ,过点E 作//EM PD ,交PB 于点M . 因为//EM PD ,PD ⊄平面ACM ,EM ⊂平面ACM ,所以//PD 平面ACM . 故上述所作点M 为使得//PD 平面ACM 的点M .如图在梯形ABCD 中,有//AB DC ,112AD DC AB === 令()22DE DB DA DC DA DC λλλλ==+=+, 因为A ,E ,C 三点共线,所以21λλ+=,13λ=.即13DE DB =,所以23BE DB =,12DE BE =. 因为//EM PD ,所以BME BPD ,12DE P MB BE M ==. (3)设PN PC μ=, 因为,,,A D N M 四点共面,所以存在实数m ,n ,使得AN mAD nAM =+. 因为()12AN AP PN AP PC AD AB AP μμμμ=+=+=++-,22n n mAD nAM mAD AB AP +=++, 又AD ,AB ,AP 为一组基底, 所以,,2212m n n μμμ⎧⎪=⎪⎪=⎨⎪⎪-=⎪⎩解得23m n ==. 所以2233AN AD AM =+.因为PA ⊥平面ABCD ,AD ⊂平面ABCD ,所以PA AD ⊥. 又AD AB ⊥,PA ,AB 在平面PAB 内,且相交于点A , 所以AD ⊥平面PAB ,又AM ⊂平面PAB ,所以AD AM ⊥. 在四边形AMND 中,AD AM ⊥,1AD =,AM = 因为2233AN AD AM =+,点N 到AM 的距离为2233AD =,点N 到AD的距离为23AM . 所以截面ADNM的面积1121223ADN AMNS S S =+=⨯+2.(1)见解析;(2)见解析【详解】试题分析:(1)连结AC 交BD 于F ,连结EF ,通过正方形对角线的性质以及三角形中位线可得112EF AC ,根据线面平行判定定理可得结果;(2)通过证明BD ⊥平面1ACC 可得结论.试题解析:(1)证明:连结AC 交BD 于F ,连结EF ,正方形ABCD 中,AC 与BD 互相平分,∴F 为AC 中点,在1ACC 中,∵E ,F 分别为1CC 与AC 中点,∴112EF AC ,∵EF ⊂平面BDE ,1AC ⊄平面BDE ,∴EF 平面BDE .(2)证明:在正方形ABCD 中,AC BD ⊥,在正方体1111ABCD A B C D -中, 1CC ⊥平面ABCD ,∵BD ⊂平面ABCD ,∴1CC BD ⊥,∵1AC CC C ⋂=,∴BD ⊥平面1ACC ,∵1AC ⊂平面1ACC ,∴1AC BD ⊥.3.(1)证明见解析;(2)平面PFC 与平面PBC 所成的二面角为90︒,证明见解析;(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明见解析. 【分析】(1)根据线面垂直的判定可证得DE ⊥平面PCF ,由线面垂直性质可证得结论; (2)根据平行关系可证得BC ⊥平面PCF ,由面面垂直的判定可证得两平面垂直,由此得到所成角为90︒;(3)利用平行四边形和三角形中位线性质可证得线线平行关系,由此证得线面平行和面面平行,从而确定存在满足条件的,M N . 【详解】(1)四边形AECD 为菱形,AC DE ∴⊥,即DE PF ⊥,DE CF ⊥, 又,PF CF ⊂平面PCF ,PFCF F =,DE ∴⊥平面PCF ,PC ⊂平面PCF ,DE PC ∴⊥.(2)平面PFC 与平面PBC 所成的二面角为90︒,证明如下:E 为AB 中点且四边形AECD 为菱形,//BE CD ∴,∴四边形BCDE 为平行四边形,//BC DE ∴,由(1)知:DE ⊥平面PCF ,BC ∴⊥平面PCF ,又BC ⊂平面PBC ,∴平面PCF ⊥平面PBC ,即平面PFC 与平面PBC 所成的二面角为90︒.(3)存在满足条件的,M N ,,M N 分别为,PD BC 中点,证明如下:由(2)知:四边形BCDE 为平行四边形,又,F N 分别为,DE BC 中点,//EF CN ∴,∴四边形EFCN 为平行四边形,//CF EN ∴,又EN ⊂平面PEN ,CF ⊄平面PEN ,//CF ∴平面PEN ;,M F 分别为,PD DE 中点,MF ∴为PDE △中位线,//MF PE ∴,又PE ⊂平面PEN ,MF ⊄平面PEN ,//MF ∴平面PEN ,又MFCF F =,,MF CF ⊂平面FCM ,∴平面//CFM 平面PEN .【点睛】本题考查立体几何中线线垂直关系、面面垂直与平行关系的证明问题,涉及到线面垂直的判定与性质、面面垂直的判定、线面平行与面面平行的判定等定理的应用,属于常考题型.4.(1)证明见解析;(2)证明见解析;(3)不存在,理由见解析. 【分析】(1)连接AC , 易知O 为AC 的中点,进而得//AP OM ,再结合线面平行的判定定理即可证明;(2)由题知//BC 平面PAD ,进而根据线面平行的性质定理即可证明//BC l ;(3))假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD ,进而在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E ,故平面//BEN 平面PAD ,进而得//BE AD ,另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾,故不存在. 【详解】解:(1)证明:连接AC ,因为底面ABCD 为平行四边形,O 为BD 的中点, 所以O 为AC 的中点,因为M 为PC 的中点, 所以在APC △中,//AP OM ,因为OM ⊄平面PAD ,AP ⊂平面PAD , 所以//OM 平面PAD(2)因为底面ABCD 为平行四边形, 所以//AD BC ,因为AD ⊂平面PAD ,BC ⊄平面PAD , 所以//BC 平面PAD ,因为平面PAD 与平面PBC 的交线为l ,BC ⊂平面PBC , 所以//BC l(3)假设在棱PC 上存在点N (异于点C ),使得//BN 平面PAD , 在平面PDC 中,过点N 作PD 的平行线EN ,交DC 于E , 因为EN ⊄平面PAD ,PD ⊂平面PAD ,所以//EN 平面PAD , 因为EN BN N ⋂=,所以平面//BEN 平面PAD , 因为BE ⊂平面BEN ,所以//BE 平面PAD ,又因为BE ⊂平面ABCD ,平面ABCD 平面PAD AD =,所以//BE AD 另一方面,在平行四边形ABCD 中,BE 与AD 不平行,矛盾, 所以在棱PC 上不存在点N (异于点C ),使得//BN 平面PAD .5.(1)证明见解析;(2) 证明见解析;(3)在线段1BB 上存在点P ,当12λ=时,平面11//A PC 平面AMC . 【分析】(1) 利用线面平行的判定定理证明1//BD 平面AMC ;(2) 利用线面垂直的判定定理证明AC ⊥平面11BB D D ,则有1AC BD ⊥; (3) 先确定λ的值,再根据面面平行的判定定理证明两平面平行. 【详解】因为四棱柱1111ABCD A B C D -是正四棱柱,所以底面ABCD 为正方形,侧棱垂直底面,侧面均为矩形.(1)证明:记AC 和BD 相交于点N ,因为ABCD 为正方形,所以N 为BD 的中点.又M 是1DD 的中点, 所以1//MN BD .又1BD ⊄平面AMC ,MN ⊂平面AMC , 所以1//BD 平面AMC .(2)证明:因为ABCD 为正方形,所以AC BD ⊥.因为1D D ⊥平面ABCD ,AC ⊂平面ABCD ,所以1D D AC ⊥. 又BD ,1D D 在平面11BB D D 内,且相交于点D , 所以AC ⊥平面11BB D D .又1BD ⊂平面11BB D D , 所以1AC BD ⊥.(3) 在线段1BB 上存在点P ,当12λ=,即112BP BB =时,平面11//A PC 面AMC . 理由如下:当112BP BB =时,P 为1BB 的中点. 取1CC 的中点G ,连接1PC ,GB ,则有1//PC GB .连接MG ,因为四边形11CC D D 是矩形,M 是1DD 的中点,G 是1CC 的中点, 所以//MG CD ,MG CD =.在正方形ABCD 中,有,//CD AB ,CD AB =.所以//MG AB ,MG AB =,四边形ABGM 为平行四边形. 有//BG AM ,又1//PC GB ,所以1//PC AM ,又1PC ⊄平面AMC ,AM ⊂平面AMC ,所以1PC //平面AMC . 同理可证:1//PA 平面AMC .又1PC ,1PA 在平面11A PC 内,且相交于点P , 所以平面11//A PC 平面AMC . 6.(1)证明见解析;(2) 证明见解析. 【分析】(1)先证明四边形11ABC D 为平行四边形,得到11//BC AD ,再利用线面平行的判定定理证明1//BC 平面1AD E ;(2)先证明11A D AD ⊥,再由线面垂直的性质得到1AB A D ⊥,最后由线面垂直的判定定理证明1A D ⊥平面11ABC D.(1)证明:在正方体1111ABCD A B C D -中, 有//AB CD ,11//CD C D ,所以11//AB C D .又11AB C D =,所以四边形11ABC D 为平行四边形,有11//BC AD . 又1BC ⊄平面1AD E ,1AD ⊂平面1AD E , 所以1//BC 平面1AD E(2)证明:因为1A D ,1AD 为正方形的对角线,所以11A D AD ⊥. 因为AB ⊥平面11AA D D ,1A D ⊂平面11AA D D ,所以1AB A D ⊥. 又1AD ,AB 在平面11ABC D 内,且相交于点A , 所以1A D ⊥平面11ABC D .7.(1)证明见解析;(2)证明见解析. 【分析】(1)由//MN AB ,利用直线与平面平行的判断定理,证明//MN 平面ABD .(2)推导出BA DC ⊥,DC BD ⊥,从而CD ⊥平面ABD ,由此能证明平面ABD ⊥平面BCD . 【详解】(1)∵在三棱锥A BCD -中,点M 、N 分别在棱BC 、AC 上,且//MN AB .MN ⊄平面ABD ,AB 平面ABD ,∴//MN 平面ABD(2)∵MN CD ⊥,//MN AB ,∴AB CD ⊥, ∵BD CD ⊥,ABBD B =∴CD ⊥平面ABD , ∵CD ⊂平面BCD ∴平面ABD ⊥平面BCD . 【点睛】本题考查的是空间中平行与垂直的证明,较简单.8.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)直线BC 1与平面APM 不能垂直,详见解析 【分析】(Ⅰ)由等腰三角形三线合一得AM BC ⊥;由线面垂直性质可得1AM BB ⊥;根据线面垂直的判定定理知AM ⊥平面11BB C C ;由面面垂直判定定理证得结论;(Ⅱ)取11C B 中点D ,可证得1//A D AM ,//DN MP ;利用线面平行判定定理和面面平行判定定理可证得平面1//A DN 平面APM ;根据面面平行性质可证得结论;(Ⅲ)假设1BC ⊥平面APM ,由线面垂直性质可知1BC PM ⊥,利用相似三角形得到111C B PB MB BB =,从而解得BP 长度,可知满足垂直关系时,P 不在棱1BB 上,则假设错误,可得到结论.(Ⅰ)AB AC =,M 为BC 中点 AM BC ∴⊥1AA ⊥平面ABC ,11//AA BB 1BB ∴⊥平面ABC又AM ⊂平面ABC 1AM BB ∴⊥ 1,BB BC ⊂平面11BB C C ,1BB BC B = AM ∴⊥平面11BB C C又AM ⊂平面APM ∴平面APM ⊥平面11BB C C (Ⅱ)取11C B 中点D ,连接11,,,A D DN DM B C,D M 分别为11,C B CB 的中点 1//DM AA ∴且1DM AA = ∴四边形1A AMD 为平行四边形 1//A D AM ∴又1A D ⊄平面APM ,AM ⊂平面APM 1//A D ∴平面APM,D N 分别为111,C B CC 的中点 1//DN B C ∴又,P M 分别为1,BB CB 的中点 1//MP B C ∴ //DN MP ∴ 又DN ⊄平面APM ,MP ⊂平面APM //DN ∴平面APM 1,A D DN ⊂平面1A DN ,1A DDN D = ∴平面1//A DN 平面APM又1A N ⊂平面1A DN 1//A N ∴平面APM(Ⅲ)假设1BC ⊥平面APM ,由PM ⊂平面APM 得:1BC PM ⊥设PB x =,x ⎡∈⎣当1BC PM ⊥时,11BPM B C B ∠=∠ Rt PBM ∴∆∽11Rt B C B ∆ 111C B PB MB BB =∴由已知得:MB11C B =1BB=,解得:x ⎡=⎣ ∴假设错误 ∴直线1BC 与平面APM 不能垂直【点睛】本题考查立体几何中面面垂直、线面平行关系的证明、存在性问题的求解;涉及到线面垂直的判定与性质、线面平行的判定、面面平行的判定与性质定理的应用;处理存在性问题时,常采用假设法,通过假设成立构造方程,判断是否满足已知要求,从而得到结论. 9.(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)12【分析】(Ⅰ)连接BD ,交AC 于点O ;根据三角形中位线可证得//MO SD ;由线面平行判定定理可证得结论;(Ⅱ)由等腰三角形三线合一可知SE AD ⊥;由面面垂直的性质可知SE ⊥平面ABCD ;根据线面垂直性质可证得结论;(Ⅲ)利用体积桥的方式将所求三棱锥体积转化为14S ABCD V -;根据已知长度和角度关系分别求得四边形面积和高,代入得到结果. 【详解】(Ⅰ)证明:连接BD ,交AC 于点O四边形ABCD 为菱形 O ∴为BD 中点 又M 为SB 中点 //MO SD ∴MO ⊂平面MAC ,SD ⊄平面MAC //SD ∴平面MAC (Ⅱ)SAD ∆为正三角形,E 为AD 中点 SE AD ∴⊥平面SAD ⊥平面ABCD ,平面SAD ⋂平面ABCD AD =,SE ⊂平面SADSE ∴⊥平面ABCD ,又AC ⊂平面ABCD SE AC ∴⊥ (Ⅲ)M 为SB 中点 11112443M ABC M ABCD S ABCD ABCDV V V SSE ---∴===⨯⋅又2AB BC AD CD SA SD ======,60ABC ∠= 2AC ∴=,12222sin 60232ABCDABC SS ∆==⨯⨯⨯=由(Ⅱ)知,SE AD ⊥ SE ∴=11122M ABC V -=⨯∴ 【点睛】本题考查立体几何中线面平行、线线垂直关系的证明、三棱锥体积的求解问题;涉及到线面平行判定定理、面面垂直性质定理和判定定理的应用、体积桥的方式求解三棱锥体积等知识,属于常考题型. 10.(Ⅰ)见解析; (Ⅱ)见解析; (Ⅲ)见解析. 【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论;(Ⅱ)由几何体的空间结构特征首先证得线面垂直,然后利用面面垂直的判断定理可得面面垂直;(Ⅲ)由题意,利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点. 【详解】(Ⅰ)证明:因为PA ⊥平面ABCD ,所以PA BD ⊥; 因为底面ABCD 是菱形,所以AC BD ⊥; 因为PAAC A =,,PA AC ⊂平面PAC ,所以BD ⊥平面PAC .(Ⅱ)证明:因为底面ABCD 是菱形且60ABC ∠=︒,所以ACD ∆为正三角形,所以AE CD ⊥, 因为//AB CD ,所以AE AB ⊥;因为PA ⊥平面ABCD ,AE ⊂平面ABCD , 所以AE PA ⊥; 因为PA AB A = 所以AE ⊥平面PAB ,AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .(Ⅲ)存在点F 为PB 中点时,满足//CF 平面PAE ;理由如下:分别取,PB PA 的中点,F G ,连接,,CF FG EG , 在三角形PAB 中,//FG AB 且12FG AB =;在菱形ABCD 中,E 为CD 中点,所以//CE AB 且12CE AB =,所以//CE FG 且CE FG =,即四边形CEGF 为平行四边形,所以//CF EG ; 又CF⊄平面PAE ,EG ⊂平面PAE ,所以//CF 平面PAE .【点睛】本题主要考查线面垂直的判定定理,面面垂直的判定定理,立体几何中的探索问题等知识,意在考查学生的转化能力和计算求解能力. 11.(I )证明见解析. (II )证明见解析. 【详解】证明:(I )E ,F 分别为AB ,BD 的中点EF AD ⇒}EF ADAD ACD EF ACD EF ACD⇒⊂⇒⊄面面面. (II )}}}EF ADEF BDAD BD CD CB CF BD BD EFCF BD EF CF F⇒⊥⊥=⇒⊥⇒⊥⋂=面为的中点,又BD BCD ⊂面,所以EFC BCD ⊥面面.12.(1)证明见解析;(2)证明见解析;(3)证明见解析. 【分析】(1)根据底面是正方形,得到CDAB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥. 【详解】(1)∵四棱锥P ABCD -的底面是正方形, ∴CDAB ,∵CD CD ⊄平面PAB ,AB 平面PAB ,∴CD ∥平面PAB . (2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.13.(1)证明见解析;(2)1A C 与BD 不可能垂直,证明见解析.【分析】(1)证得1A B ⊥平面1A CD ,结合面面垂直的判定定理即可得出结论;(2)假设1A C 与BD 垂直,然后推出与已知条件11A B A D ⊥矛盾,即可得出1A C 与BD 不可能垂直.【详解】(1)因为平面1A BD ⊥平面BCD ,平面1A BD 平面BCD =BD ,CD ⊂平面BCD ,CD ⊥BD ,所以CD ⊥平面1A BD ,又因为1A B ⊂平面1A BD ,所以CD ⊥1A B ,又因为11A B A D ⊥,1A D CD D =,所以1A B ⊥平面1A CD ,且1A B ⊂平面1A BC ,所以平面1A BC ⊥平面1A CD ;(2)假设1A C 与BD 垂直,又因为CD ⊥BD ,且1AC CD C ⋂=,所以DB ⊥平面1A CD ,又因为1A D ⊂平面1A CD ,所以1DB A D ⊥,这与11A B A D ⊥矛盾,故假设不成立,即1A C 与BD 不可能垂直.23.(1)见解析;(2)见解析;(3)见解析【解析】试题分析:(1)取线段1A B 的中点H ,由三角形中位线性质以及平行四边形性质得四边形DEFH 为平行四边形,即得//EF HD .再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得1A O DE ⊥.再根据面面垂直性质定理得1A O ⊥平面BCED ,即得1CO A O ⊥,根据勾股定理得CO BO ⊥,所以由线面垂直判定定理得 CO ⊥平面1A OB ,最后根据面面垂直判定定理得结论,(3)假设线段OC 上存在点G ,使得OC ⊥平面EFG ,则EO EC =,与条件矛盾.试题解析:解:(1)取线段1A B 的中点H ,连接HD ,HF .因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 //DE BC ,12DE BC =. 因为 H ,F 分别为1A B ,1A C 的中点,所以 //HF BC ,12HF BC =, 所以 //HF DE ,HF DE =,所以 四边形DEFH 为平行四边形,所以 //EF HD . 因为 EF ⊄平面1A BD , HD ⊂平面1A BD ,所以 //EF 平面1A BD .(2)因为在△ABC 中,D ,E 分别为AB ,AC 的中点,所以 AD AE =.所以11A D A E =,又O 为DE 的中点,所以 1A O DE ⊥.因为平面1A DE ⊥平面BCED ,且1AO ⊂平面1A DE , 所以 1A O ⊥平面BCED ,所以 1CO A O ⊥.在△OBC 中,4BC =,易知 OB OC ==所以 CO BO ⊥,所以 CO ⊥平面1A OB ,所以 平面1A OB ⊥平面1A OC .(3)线段OC 上不存在点G ,使得OC ⊥平面EFG .否则,假设线段OC 上存在点G ,使得OC ⊥平面EFG ,连接 GE ,GF ,则必有 OC GF ⊥,且OC GE ⊥.在Rt △1A OC 中,由F 为1A C 的中点,OC GF ⊥,得G 为OC 的中点.在△EOC 中,因为OC GE ⊥,所以EO EC =,这显然与1EO =,EC =所以线段OC 上不存在点G ,使得OC ⊥平面EFG .14.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析【分析】(I )由AD ⊥DE ,AD ⊥CD 可得AD ⊥平面CDE ,故而AD ⊥CE ;(II )证明平面ABF ∥平面CDE ,故而BF ∥平面CDE ;(III )取CE 的中点P ,BE 的中点Q ,证明CE ⊥平面ADPQ 即可得出平面ADQ ⊥平面BCE .【详解】(Ⅰ)由底面ABCD 为矩形,知AD CD ⊥.又因为DE AD ⊥,DE CD D ⋂=,所以AD ⊥平面CDE .又因为CE ⊂平面CDE ,所以AD CE ⊥.(Ⅱ)由底面ABCD 为矩形,知//AB CD ,又因为AB ⊄平面CDE ,CD ⊂平面CDE ,所以//AB 平面CDE .同理//AF 平面CDE ,又因为AB AF A ⋂=,所以平面//ABF 平面CDE .又因为BF ⊂平面ABF ,所以//BF 平面CDE .(Ⅲ)结论:线段BE 上存在点Q (即BE 的中点),使得平面ADQ ⊥平面BCE . 证明如下:取CE 的中点P ,BE 的中点Q ,连接,,AQ DP PQ ,则//PQ BC .由//AD BC ,得//PQ AD .所以,,,A D P Q 四点共面.由(Ⅰ),知AD ⊥平面CDE ,所以AD DP ⊥,故BC DP ⊥.在△CDE 中,由DC DE =,可得DP CE ⊥.又因为BC CE C ⋂=,所以DP ⊥平面BCE .又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE (即平面ADQ ⊥平面BCE ).即线段BE 上存在点Q (即BE 中点),使得平面ADQ ⊥平面BCE【点睛】本题考查了线面垂直、面面垂直的判定与性质定理的应用,线面平行的判定,熟练运用定理是解题的关键,属于中档题.15.(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析.【分析】(Ⅰ)证明以DE ∥平面PBC ,只需证明DE ∥PC ;(Ⅱ)证明BC ⊥平面PAB ,根据线面垂直的判定定理,只需证明PA ⊥BC ,AB ⊥BC ;(Ⅲ)当点F 是线段AB 中点时,证明平面DEF ∥平面PBC ,可得平面DEF 内的任一条直线都与平面PBC 平行.【详解】(Ⅰ)证明:因为点E 是AC 中点,点D 为PA 的中点,所以//DE PC .又因为DE ⊄面PBC ,PC ⊂面PBC ,所以DE ∥平面PBC .(Ⅱ)证明:因为平面PAC ⊥面ABC ,平面PAC ∩平面ABC =AC ,又PA ⊂平面PAC ,PA ⊥AC , 所以PA ⊥面ABC ,因为BC ⊂平面ABC ,所以PA ⊥BC .又因为AB ⊥BC ,且PA ∩AB =A ,所以BC ⊥面PAB .(Ⅲ)当点F 是线段AB 中点时,过点D ,E ,F 的平面内的任一条直线都与平面PBC 平行. 取AB 中点F ,连EF ,连DF .由(Ⅰ)可知DE ∥平面PBC .因为点E 是AC 中点,点F 为AB 的中点,所以EF ∥BC .又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以EF ∥平面PBC .又因为DE ∩EF =E ,所以平面DEF ∥平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.故当点F 是线段AB 中点时,过点D ,E ,F 所在平面内的任一条直线都与平面PBC 平行.【点睛】本题考查线面平行,考查线面垂直,考查面面平行,考查学生分析解决问题的能力,掌握线面平行、线面垂直、面面垂直的判定定理是关键.16.(1)证明见解析;(2)证明见解析;(3)证明见解析.【分析】(1)根据底面是正方形,得到CD AB ,再利用线面平行判定定理证明.(2)连结AC ,BD ,交于点O ,连结OE ,由中位线定理得到OE PC ∥,再利用线面平行判定定理证明.(3)根据底面是正方形,得到BD AC ⊥,由侧棱PA ⊥底面ABCD ,得到BD PA ⊥,从而BD ⊥平面ACE ,由此能证明BD CE ⊥.【详解】(1)∵四棱锥P ABCD -的底面是正方形,∴CD AB ,∵CD ⊄平面PAB ,AB平面PAB , ∴CD ∥平面PAB .(2)如图所示:连结AC ,BD ,交于点O ,连结OE ,∵四棱锥P ABCD -的底面是正方形,∴O 是AC 中点,∵E 是PA 的中点.∴OE PC ∥,∵PC ⊄平面BDE ,OE ⊂平面BDE ,∴PC 平面BDE .(3)∵四棱锥P ABCD -的底面是正方形,侧棱PA ⊥底面ABCD ,∴BD AC ⊥,BD PA ⊥,∵AC PA A ⋂=,∴BD ⊥平面ACE ,∵CE ⊂平面ACE ,∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理,线面垂直的判定定理,还考查了转化化归的思想和逻辑推理的能力,属于中档题.。
专题 立体几何之所成角-(人教A版2019必修第二册) (教师版)

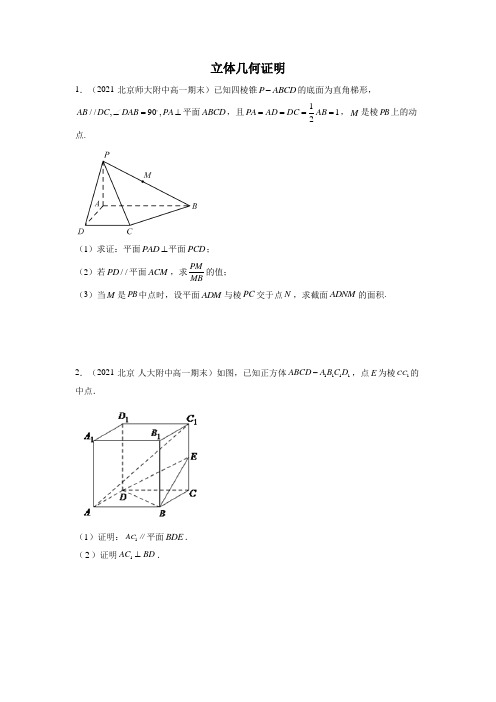
立体几何之所成角1 异面直线所成的角①范围(0∘ ,90∘];②作异面直线所成的角:平移法.如图,在空间任取一点O,过O作a′ // a ,b′ // b,则a′ ,b′所成的θ角为异面直线a ,b所成的角.特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角.2 线面所成的角①定义如下图,平面的一条斜线(直线l)和它在平面上的射影(AO)所成的角,叫做这条直线和这个平面所成的角.一条直线垂直平面,则θ=90°;一条直线和平面平行或在平面内,则θ=0°.②范围[0∘ ,90∘]3 二面角①定义从一条直线出发的两个半平面所组成的图形叫做二面角.在二面角的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则射线OA和OB 构成的∠AOB叫做二面角的平面角.②范围[0° ,180°].【题型一】异面直线所成的角【典题1】如图,正方体ABCD—A1B1C1D1中,点E ,F分别是AA1,AD的中点,则CD1与EF所成角为()A.0°B.45°C.60°D.90°【解析】连结A1D、BD、A1B,∵正方体ABCD—A1B1C1D1中,点E ,F分别是AA1,AD的中点,EF∥A1D,∵A1B∥D1C,∴∠DA1B是CD1与EF所成角,∵A1D=A1B=BD ,∴∠DA1B=60°.∴CD1与EF所成角为60°.故选 C.【点拨】①找异面直线所成的角,主要是把两条异面直线通过平移使得它们共面,可平移一条直线也可以同时平移两条直线;②平移时常利用中位线、平行四边形的性质;【典题2】如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1 ,AD 的中点,那么异面直线OE和FD1所成角的余弦值等于.【解析】取BC的中点G.连接GC1,则GC1∥FD1,再取GC的中点H,连接HE、OH,则∵E是CC1的中点,∴GC1∥EH,∴∠OEH为异面直线所成的角.在△OEH中,OE=√3,HE=√52,OH=√52.由余弦定理,可得cos∠OEH=OE 2+EH2−OH22OE⋅EH=3⋅√2=√155.故答案为√155【点拨】本题利用平移法找到异面直线所成的角(∠OEH)后,确定含有该角的三角形(△OEH),利用解三角形的方法(正弦定理,余弦定理等)把所求角∠OEH最终求出来.【典题3】如图,已知P是平行四边形ABCD所在平面外一点,M,N分别是AB ,PC的中点.(1)求证:MN∥平面PAD;(2)若MN=BC=4 ,PA=4√3,求异面直线PA与MN所成的角的大小.【解析】(1)证明:取PD中点Q,连AQ、QN,则AM∥QN,且AM=QN,∴四边形AMNQ为平行四边形∴MN∥AQ又∵AQ在平面PAD内,MN不在平面PAD内∴MN∥面PAD;(2)解方法一∵MN∥AQ∴∠PAQ即为异面直线PA与MN所成的角∵MN=BC=4 ,PA=4√3,∴AQ=4,设PQ=x,根据余弦定理可知cos∠AQD+cos∠AQP=0即16+x 2−488x +16+x2−168x=0,解得x=4在三角形AQP中,AQ=PQ=4 ,AP=4√3∴cos∠PAQ=2×4×4√3=√32,即∠PAQ=30°∴异面直线PA与MN所成的角的大小为30°方法二过点A作AH⊥PD交PD于H,如图∵MN=BC=4,∴H是QD的中点设HD=x,则QH=x,PQ=2x,在Rt△AQD和Rt△APH利用勾股定理可得AH2=16−x2=48−9x2,解得x=2∴cos∠PAQ=PHAP =4√3=√32,即∠PAQ=30°∴异面直线PA与MN所成的角的大小为30°【点拨】本题中所成角∠PAQ找到后,无法在一个三角形里求出,此时把问题转化为平面几何问题, 再利用解三角形的方法进行求解.【题型二】线面所成的角【典题1】如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB= 2CD=2BC,EA⊥EB.(1)求证:AB⊥DE;(2)求直线EC与平面ABE所成角的正弦值.【解析】(1)证明:取AB中点O,连接EO,DO.∵EB=EA,∴EO⊥AB.∵四边形ABCD为直角梯形,AB=2CD=2BC,AB⊥BC,∴四边形OBCD为正方形,∴AB⊥OD.又∵EO∩OD=O,∴AB⊥平面EOD.∴AB⊥ED.(2)∵平面ABE⊥平面ABCD,且AB⊥BC,∴BC⊥平面ABE.则∠CEB为直线EC与平面ABE所成的角.设BC=a,则AB=2a,BE=√2a,∴CE=√3a,在直角三角形CBE中,sin∠CEB=CBCE =√3=√33.即直线EC与平面ABE所成角的正弦值为√33.【点拨】本题中的“直线EC与平面ABE所成的角”是根据线面角的定义直接在题目原图上找到的,在含所求角∠CEB的直角三角形CBE中求出角度!【典题2】如图,四边形ABCD为正方形,PA⊥平面ABCD,且AB=4,PA=3,点A在PD上的射影为G点,E点在AB边上,平面PEC⊥平面PDC.(1)求证:AG∥平面PEC;(2)求BE的长;(3)求直线AG与平面PCA所成角的余弦值.【解析】(1)证明:∵CD ⊥AD,CD ⊥PA∴CD ⊥平面PAD ∴CD ⊥AG,又PD ⊥AG∴AG ⊥平面PCD作EF ⊥PC 于F,因面PEC ⊥面PCD∴EF ⊥平面PCD∴EF ∥AG,又AG ⊄面PEC,EF ⊂面PEC,∴AG ∥平面PEC(2)由(1)知A 、E 、F 、G 四点共面,又AE ∥CD ∴AE ∥平面PCD∴AE ∥GF ∴四边形AEFG 为平行四边形,∴AE =GF∵PA =3,AD =AB =4 ∴PD =5,AG =125, 在Rt △PAGP 中,PG 2=PA 2−AG 2=8125 ∴PG =95 又GF CD =PG PD∴GF =3625 ∴AE =3625,故BE =6425(3)∵EF ∥AG,所以AG 与平面PAC 所成角等于EF 与平面PAC 所成的角,过E 作EO ⊥AC 于O 点,易知EO ⊥平面PAC,又EF ⊥PC,∴OF 是EF 在平面PAC 内的射影∴∠EFO 即为EF 与平面PAC 所成的角EO =AEsin45°=3625×√22=18√225,又EF =AG =125,∴sin∠EFO=EOEF =18√225×512=3√210故cos∠EFO=√1−sin2∠EFO=√8210所以AG与平面PAC所成角的余弦值等于√8210.【点拨】①若在题目中不能直接找到所求线面角,则可用“作高法”确定所求角,比如下图中,求直线AP与平面α所成的角,具体步骤如下:(1) 如图,过点P作平面α的高PO,垂足为O,则AO是线段AP在平面α上的投影;(2) 找到所求角θ;(3) 求解三角形APO进而求角θ.(此方法关键在于找到垂足O的位置,证明到PO⊥平面α,如本题中EO⊥平面PAC的证明)②本题若直接求“AG与平面PAC所成角”,过点G做高有些难度,则由EF∥AG,能把“AG与平面PAC所成角”转化为“EF与平面PAC所成的角”,这方法称为“间接法”吧.【典题3】如图,正四棱锥S-ABCD中,SA=AB=2,E,F,G分别为BC,SC,CD的中点.设P为线段FG上任意一点.(Ⅰ)求证:EP⊥AC;(Ⅰ)当P为线段FG的中点时,求直线BP与平面EFG所成角的余弦值.【解析】证明:(Ⅰ)连接AC交BD于O,∵S-ABCD是正四棱锥,∴ SO⊥平面ABCD,∴SO⊥AC,又∵AC⊥BD,SO∩BD=O,∴AC⊥平面SBD,∴AC⊥SD,∵F,G分别为SC,CD的中点,∴SD∥FG,∴AC⊥GF,同理AC⊥EF,∴AC⊥平面GEF,又∵PE⊂平面GEF,∴EP⊥AC.(Ⅰ) 方法一过B作BH⊥GE于点H,连接PH,∵BD⊥AC,BD∥GF,∴BH∥AC,由(Ⅰ)知:AC⊥平面GEF,∴BH⊥平面GEF,∴∠BPH就是直线BP与平面EFG所成的角,∵SA=AB=2,∴在Rt△BHP中,解得BH=√22,PH=√132,PB=√152,(易知△BHE是等腰直角三角形,又由斜边BE=1,∴BH=√22;在三角形PGH中,PG=12,GH=3√22,∠PGH=π4,用余弦定理可得PH=√132)则cos∠BPH=PHPB =√19515,故直线BP与平面EFG所成角的余弦值为√19515.方法二设过点B作平面EFG的垂直,垂直为T,则∠BPT就是直线BP与平面EFG所成的角,BT是点B到平面PGE的距离,由已知条件可求GF=EF=1,GE=√2,则∠GFE=90°,∴S△PEG=12S△GFE=12×12=14,由于P、F是中点,易得点P到平面ABCD的距离ℎ1=14SO=√24,而S△GEB=12S△GCB=12×1=12,对于三棱锥P−GEB,由V B−PEG=V P−GEB⇒13×BT×S△PEG=13×ℎ1×S△GEB⇒112BT=√224⇒BT=√22,在正四棱锥S-ABCD中可求PB=√152,(方法较多,提示过点P作平面ABCD的高PI)∴sin∠BPT=BTBP =√3015∴cos∠BPT=√1−sin∠BPT=√19515,故直线BP与平面EFG所成角的余弦值为√19515.【点拨】①本题第二问中方法一就是用“做高法”,计算量有些大;方法二是觉得垂足H的位置难确定,可设点B到平面EFG的投影为T(即垂足),再用“等积法”求高BT,则sin∠BPT=BTBP,可求所求角∠BPT,这种方法称为“等积法”;②思考:上一题试试用“等积法”!【题型三】二面角【典题1】如图,在棱长为a的正方体ABCD-A1B1C1D1中,AC 与BD相交于点O.求二面角 A1-BD-A 的正切值.【解析】在正方体中BD⊥平面A1ACC1,∴AO⊥BD,A1O⊥BD,∴二面角A1-BD-A的平面角为∠A1OA由题中的条件求出:AO=√22a ,AA1=a∴tan∠A1OA=√22a=√2,所以二面角 A1-BD-A 的正切值为√2.【点拨】本题根据二面角的定义找到二面角二面角A1-BD-A的平面角为∠A1OA,再在三角形AOA1内用解三角形的方法求解角∠A1OA.【典题2】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=√6,点E是棱PB的中点.(1)求直线AD与平面PBC的距离;(2)若AD=√3,求二面角A-EC-D的平面角的余弦值.【解析】(1)在矩形ABCD中,AD∥BC,从而AD∥平面PBC,故直线AD与平面PBC的距离为点A到平面PBC的距离,因PA⊥底面ABCD,故PA⊥AB,可得△PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB ∴BC⊥AE,从而AE⊥平面PBC,故AE之长即为直线AD与平面PBC的距离,在Rt△PAB中,PA=AB=√6,所以AE=12PB=12√PA2+AB2=√3(2)过点D作DF⊥CE于F,过点F做FG⊥CE,交AC于G,连接DG,则∠DFG为所求的二面角的平面角.由(1)知BC⊥AE,又AD∥BC,得AD⊥AE,从而DE=√AE2+AD2=√6在Rt△CBE中,CE=√BE2+BC2=√6,由CD=√6,所以△CDE为等边三角形,故F为CE的中点,且DF=CD•sinπ3=3√22因为AE⊥平面PBC,故AE⊥CE,又FG⊥CE,知FG∥AE.∴G点为AC的中点,FG=12AE=√32,则在Rt△ADC中,DG=12√AD2+CD2=32,所以cos∠DFG=DF 2+FG2−DG22DF⋅FG=√63【点拨】若在题目中不能直接得到所求二面角,就需要构造出二面角,比如本题求二面角A-EC-D,解题具体步骤如下(1) 过点D作DF⊥EC,过点F作FG⊥EC交AC于点D,则二面角∠DFG为所求的二面角的平面角;(2) 确定含角∠DFG的三角形DFG,利用解三角形的方法求出角∠DFG,常见的是求出三角形三边再用余弦定理.【典题3】如图,已知三棱锥P-ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点.(1)求证:PC⊥BC.(2)求二面角M-AC-B的大小.【解析】(1)证明:由PA⊥平面ABC,∴PA⊥BC,又因为∠ACB=90°,即BC⊥AC.∴BC⊥面PAC,∴PC⊥BC.(2)取AB中点O,连结MO、过O作HO⊥AC于H,连结MH,∵M是PB的中点,∴MO∥PA,又∵PA⊥面ABC,∴MO⊥面ABC.∴∠MHO为二面角M-AC-B的平面角.设AC=2,则BC=2√3,MO=1,OH=√3,在Rt△MHO中,tan∠MHO=MOHO =√3=√33.二面角M-AC-B的大小为30∘.【点拨】求二面角也可以转化为线面角,比如求二面角D-AB-C,解题思路如下过点D作DE⊥AB,则二面角D-AB-C等于直线ED与平面ABC所成的角或其补角,若过点D作DF⊥平面ABC,则二面角D-AB-C是锐角,等于角∠DEF;二面角D-AB-C是钝角,等于角∠DEF的补角.1(★)在正方体ABCD﹣A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是()A.0 <θ <π2B.0 <θ≤π2C.0≤θ≤π3D.0 <θ≤π3【答案】D【解析】∵A1B∥D1C,∴CP与A1B成角可化为CP与D1C成角.∵△AD1C是正三角形可知当P与A重合时成角为π3,∵P不能与D1重合因为此时D1C与A1B平行而不是异面直线,∴0 <θ≤π3.故选D.2(★★)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.O1,O2,O2′分别为AB ,BC ,DE的中点,F为弧AB的中点,G为弧BC的中点.则异面直线AF与GO2′所成的角的余弦值为.【答案】√1010【解析】如图,连接AF、FB、BG、GC,∵F为半圆弧AFB的中点,G为半圆弧BGC的中点,由圆的性质可知,G、B、F三点共线,且AF=CG,FB=GB,AB=BC,∴△AFB≌△CGB,∴AF∥CG,则∠CGO2′即为所求的角或其补角,又∵半径为1,高为2,且△AFB,△CG B都是等腰Rt△,∴CG=√2,CO2′=GO2′=√1+22=√5,∴在△CGO2′中,cos∠CGO2′=√52√22√522√2⋅√5=√1010,即异面直线AF与GO2′所成的角余弦值√1010.故答案为√1010.3 (★★)如图所示,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点, MN⊥平面A1DC.(1)求证:AD1⊥平面A1DC;(2)求MN与平面ABCD所成的角.【答案】(1) 见解析(2)π4【解析】(1)证明:由ABCD-A1B1C1D1为正方体,得CD⊥平面ADD1A1,AD1⊂平面ADD1A1∴CD⊥AD1,又AD1⊥A1D,且A1D∩CD=D,∴AD1⊥平面A1DC;(2)解:∵MN⊥平面A1DC,又由(1)知AD1⊥平面A1DC,∴MN∥AD1,∴AD1与平面ABCD所成的角,就是MN与平面ABCD所成的角,∵D1D⊥平面ABCD,∴∠D1AD即为AD1与平面ABCD所成的角,,由正方体可知∠D1AD=π4∴MN与平面ABCD所成的角为π.44(★★★) 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P ,Q分别为AE,AB的中点.(1)证明:PQ∥平面ACD;(2)求AD与平面ABE所成角的正弦值.【答案】(1) 见解析(2)√55【解析】(1)证明:因为P,Q分别为AE,AB的中点,所以PQ∥EB.又DC∥EB,因此PQ∥DC,又PQ 平面ACD,从而PQ∥平面ACD.(2)如图,连接CQ,DP,因为Q为AB的中点,且AC=BC,所以CQ⊥AB.因为DC⊥平面ABC,EB∥DC,所以EB⊥平面ABC,因此CQ⊥EB. 故CQ⊥平面ABE.EB=DC,所以四边形CQPD为平行四边形,故DP∥CQ,因此DP⊥平面ABE,由(1)有PQ∥DC,又PQ=12∠DAP为AD和平面ABE所成的角,在Rt△DP A中,AD=√5,DP=1,sin∠DAP=√5,即AD与平面ABE5。
立体几何证明题目

立体几何证明题目一、直线与平面平行的证明题目1:在正方体ABCD - A_1B_1C_1D_1中,E为DD_1的中点,求证:BD_1∥平面AEC。
解析:1. 连接BD交AC于O点。
- 在正方体中,底面ABCD是正方形,根据正方形对角线的性质,对角线互相平分,所以O为BD的中点。
2. 连接OE。
- 因为E为DD_1的中点,在三角形BD_1D中,O是BD中点,E是DD_1中点,根据三角形中位线定理,中位线平行于第三边且等于第三边的一半,所以OE∥ BD_1。
3. 又因为OE⊂平面AEC,BD_1not⊂平面AEC。
- 根据直线与平面平行的判定定理,如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行,所以BD_1∥平面AEC。
二、平面与平面平行的证明题目2:已知四棱锥P - ABCD中,底面ABCD是平行四边形,点M,N分别在PA,BD上,且PM:MA = BN:ND。
求证:平面MNQ∥平面PBC(设AC∩ BD = Q,连接MQ、NQ)。
解析:1. 因为四边形ABCD是平行四边形,AC∩ BD = Q,所以AQ = QC,BQ=QD。
- 由于PM:MA = BN:ND,在三角形PAQ中,(PM)/(MA)=(BN)/(ND),可得MQ∥ PC。
- 理由是:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
2. 在三角形ABD中,(BN)/(ND)=(PM)/(MA),可得NQ∥ AD。
- 又因为底面ABCD是平行四边形,AD∥ BC,所以NQ∥ BC。
3. 因为MQ∥ PC,MQnot⊂平面PBC,PC⊂平面PBC,根据直线与平面平行的判定定理,可得MQ∥平面PBC。
- 同理,NQ∥ BC,NQnot⊂平面PBC,BC⊂平面PBC,可得NQ∥平面PBC。
4. 又因为MQ∩ NQ = Q,MQ⊂平面MNQ,NQ⊂平面MNQ。
- 根据平面与平面平行的判定定理,如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,所以平面MNQ∥平面PBC。
必修二立体几何经典证明题

B 1C BADC 1A 1必修二立体几何经典证明试题1. 如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(I)证明:平面BDC 1⊥平面BDC(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.1. 【解析】(Ⅰ)由题设知BC ⊥1CC ,BC ⊥AC ,1CC AC C ⋂=,∴BC ⊥面11ACC A , 又∵1DC ⊂面11ACC A ,∴1DC BC ⊥,由题设知01145A DC ADC ∠=∠=,∴1CDC ∠=090,即1DC DC ⊥,又∵DC BC C ⋂=, ∴1DC ⊥面BDC , ∵1DC ⊂面1BDC , ∴面BDC ⊥面1BDC ;(Ⅱ)设棱锥1B DACC -的体积为1V ,AC =1,由题意得,1V =1121132+⨯⨯⨯=12,由三棱柱111ABC A B C -的体积V =1,∴11():V V V -=1:1, ∴平面1BDC 分此棱柱为两部分体积之比为1:1.2. 如图5所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//AB CD ,PD AD =,E 是PB 的中点,F 是CD 上的点且12DF AB =,PH 为△PAD 中AD 边上的高. (1)证明:PH ⊥平面ABCD ;(2)若1PH =,2AD =1FC =,求三棱锥E BCF -的体积;(3)证明:EF ⊥平面PAB .【解析】(1)证明:因为AB ⊥平面PAD ,所以PH AB ⊥。
因为PH 为△PAD 中AD 边上的高,所以PH AD ⊥。
因为AB AD A =,所以PH ⊥平面ABCD 。
(2)连结BH ,取BH 中点G ,连结EG 。
因为E 是PB 的中点,所以//EG PH 。
因为PH ⊥平面ABCD 所以EG ⊥平面ABCD 。
则1122EG PH ==, 111332E BCF BCF V S EG FC AD EG -∆=⋅=⋅⋅⋅⋅=2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MB1NB
∴
CPDN
=,∴NP∥DC∥AB.
PBNB
∴平面MNP∥平面AA1B1B.
∴MN∥平面AA1B1B.
7.如图所示,四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别为
PC、PD、BC的中点.
(1)求证:PA∥平面EFG;
(2)求三棱锥P—EFG的体积.
APAM
MB.
=
PE
又AE=BD,AP=DQ,∴PE=BQ.
∴
APDQ
=,∴
PEBQ
AMDQ
QB.
=
MB
∴MQ∥AD.又AD∥BC,
∴MQ∥BC,∴MQ∥平面BCE.又PM∩MQ=M,
∴平面PMQ∥平面BCE.又PQ?平面PMQ,
∴PQ∥平面BCE.
5.一个多面体的直观图和三视图如图所示(其中M,N分别是AF,BC中点).
若a∥b,a?γ,b?γ,则a∥γ,又a?α,α∩γ=c,则a∥c.
因此三条交线相交于一点或互相平行.
4.如图所示,已知空间四边形ABCD中,E、H分别是边AB,AD的中点,F,G分别是边BC,CD上的点,
且
CF
=
CB
CG2
=.
CD3
(1)求证:三条直线EF,GH,AC交于一点.
(2)若在本题中,
AE
命题③正确,由线面平行的判定定理可知.
命题④错,需说明另一条直线在平面外.
3.已知不重合的直线a,b和平面α,
①若a∥α,b?α,则a∥b;
②若a∥α,b∥α,则a∥b;
③若a∥b,b?α,则a∥α;
④若a∥b,a?α,则b∥α或b?α,
上面命题中正确的是________(填序号).
答案④
解析①若a∥α,b?α,则a,b平行或异面;②若a∥α,b∥α,则a,b平行、相交、异面都
【答案】④
2.若P是两条异面直线l、m外的任意一点,则()
A.过点P有且仅有一条直线与l、m都平行
B.过点P有且仅有一条直线与l、m都垂直
C.过点P有且仅有一条直线与l、m都相交
D.过点P有且仅有一条直线与l、m都异面
答案B
解析对于选项A,若过点P有直线n与l,m都平行,则l∥m,这与l,m异面矛盾.
C.至少与a,b中的一条相交
D.与a,b都平行
答案C
解析若c与a,b都不相交,则c与a,b都平行,根据公理4,则a∥b,与a,b异面矛盾.
考点2:共点、共线、共面问题
例1.下列各图是正方体和正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的图形是
【解析】①在A中易证PS∥QR,
∴P、Q、R、S四点共面.
对于选项B,过点P与l、m都垂直的直线,即过P且与l、m的公垂线段平行的那一条直线.
对于选项C,过点P与l、m都相交的直线有一条或零条.
对于选项D,过点P与l、m都异面的直线可能有无数条.
1
3. 已知异面直线a,b分别在平面α,β内,且α∩β=c,那么直线c一定
A.与a,b都相交
B.只能与a,b中的一条相交
______.
答案5
3.已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为AA1中点,则异面直线BE与CD1所成角的余弦值为
A.
10
10
B.
1
5
C.
310
10
D.
3
5
答案C
解析连接BA1,则CD1∥BA1,于是∠A1BE就是异面直线BE与CD1所成的角(或补角),设AB=1,则
BE=2,BA1=5,A1E=1,在△A1BE中,cos∠A1BE=
C.可以有两个D.有无数多个
答案B
6.如图,在正方体ABCD—A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
【证明】方法一如右图,作ME∥BC,交BB1于E;作NF∥AD,交AB于F,连接EF,则EF?平面
AA1B1B.
∵BD=B1C,DN=CM,
∴B1M=BN.
5
有可能;③若a∥b,b?α,a∥α或a?α.
4.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ
∥平面BCE.
【证明】方法一如图所示.
作PM∥AB交BE于M,
作QN∥AB交BC于N,
连接MN.
∵正方形ABCD和正方形ABEF有公共边AB,∴AE=BD.
②在C中易证PQ∥SR,
∴P、Q、R、S四点共面.
③在D中,∵QR?平面ABC,
PS∩面ABC=P且P?QR,
∴直线PS与QR为异面直线.
∴P、Q、R、S四点不共面.
④在B中P、Q、R、S四点共面,证明如下:
取BC中点N,可证PS、NR交于直线B1C1上一点,∴P、N、R、S四点共面,设为α.
可证PS∥QN,∴P、Q、N、S四点共面,设为β.
∴
DNCN
=.又CM=DN,
NBNP
CM
B1C=BD,
=
MB1
DNCN
=,
NBNP
∴MN∥B1P.∵B1P?平面AA1B1B,
∴MN∥平面AA1B1B.
方法三如右图,作MP∥BB1,交BC于点P,连接NP.
∵MP∥BB1,∴
CMCP
=
.
MB1PB
∵BD=B1C,DN=CM,
∴B1M=BN.∵
CMDN
∵α、β都经过P、N、S三点,∴α与β重合,∴P、Q、R、S四点共面.
【答案】D
2.空间四点中,三点共线是这四点共面的()
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
答案A
3.下面三条直线一定共面的是()
A.a、b、c两两平行
B.a、b、c两两相交
C.a∥b,c与a、b均相交
∵
MEB1M
=,
BCB1C
NFBN
=,
ADBD
7
∴
MEBN
==
BCBD
NF
,∴ME=NF.
AD
又ME∥BC∥AD∥NF,
∴MEFN为平行四边形.
∴NM∥EF.又∵MN?面AA1B1B,
∴MN∥平面AA1B1B.
方法二如图,连接CN并延长交BA的延长线于点P,连接B1P,则B1P?平面AA1B1B.
∵△NDC∽△NBP,
①若直线a不在α内,则a∥α;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α平行,则l与α内的任意一条直线都平行;
④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行;
⑤若l与平面α平行,则l与α内任何一条直线都没有公共点;
⑥平行于同一平面的两直线可以相交.
答案⑤⑥
解析a∩α=A时,a不在α内,∴①错;直线l与α相交时,l上有无数个点不在α内,故②错;l
D.a、b、c两两垂直
答案C
4.已知三个平面两两相交且有三条交线,试证三条交线互相平行或者相交于一点.
【解析】设α∩β=a,β∩γ=b,γ∩α=c,
2
由a?β,b?β,则a∩b=O,如图(1),
或a∥b,如图(2),若a∩b=O,
O∈a,a?α,则O∈α,O∈b,b?γ,则O∈γ,
又γ∩α=c,因此O∈c;
6
<1>求证:MN∥平面CDE;F
<2>求多面体A—CDEF的体积.
解析(1)证明由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB=BC=BF=2,
DE=CF=22,∴∠CBF=90°.
取BF中点G,连接MG,NG,由M,N分别是AF,BC中点,可知:NG∥CF,MG∥EF.又MG∩NG=G,CF
有EF=2a,AF=2a
22
+a=5a,AE=2a
2
+2a
22
+a=3a.在△AEF中,cos∠AEF=
222222
AE+EF-AF9a+4a-5a2
==
.因此,异面直线AE与BC所成的角的余弦值是
2AE·EF2×3a×2a3
2
3
.
4
【答案】
2
3
考点4:直线与平面平行的判定与性质
1.下列命题中正确的是________.
角,设AB=1,CE=
5
,ME=
2
1
2
B.
=
22
在△MEC中,cos∠MEC
=
222
CE+ME-CM
=
2CE·ME
15
,因此异面直线BD1与CE所成角的余弦值为
15
15
.
15
2.如图,若正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的正切值是
∩EF=F,
∴平面MNG∥平面CDEF,∴MN∥平面CDEF.
(2)作AH⊥DE于H,由于三棱柱ADE—BCF为直三棱柱,∴AH⊥平面CDE,F且AH=2.
1
∴VAS
-CDEF=
3
18
四边形CDEF·AH=×2×22×2=.
33
5.若P为异面直线a,b外一点,则过P且与a,b均平行的平面
A.不存在B.有且只有一个
又AP=DQ,∴PE=QB.
又PM∥AB∥QN,∴
PMPEQB
==,
ABAEBD
QN
=
DC
BQ
BD.
∴
PMQN
=
.
ABDC
∴PM綊QN,即四边形PMNQ为平行四边形.
∴PQ∥MN.又MN?平面BCE,PQ?平面BCE,
