初三数学猜想与归纳
中考数学风向标 专题一 归纳与猜想

2
1 1 n1 1 1 π 8 =4.第 n 个半圆的面积为 π 2 =π22n-5. 2 2 2 2
答案:4 p22n-5 小结与反思:对于图形找规律的题目,首先应找出哪些部
分发生了变化,再探索变化的部分是按照什么规律变化的.
a), ∴左边=右边,原等式成立. 小结与反思:解这类数字猜想题,最好在草稿纸上按顺序
排好每个数字,然后写多几个,找到规律就可以了.
几何图形中的猜想
例题:(2012 年广东广州)如图 Z1-1,在标有刻度的直线 l 上,从点 A 开始,以 AB=1 为直径画半圆,记为第 1 个半圆; 以 BC=2 为直径画半圆,记为第 2 个半圆;以 CD=4 为直径 画半圆,记为第 3 个半圆;以 DE=8 为直径画半圆,记为第 4
个半圆„„按此规律,继续画半圆,则第 4 个半圆的面积是第
3 个半圆面积的 _____ 倍 , 第 n 个 半 圆 的 面 积 为_______ (结果保留p).
图 Z1-1
解析:根据规律找出每个半圆的半径,第 n 个半圆的直径 为 2n 1.
-
1 1 π 16 : 第 4 个半圆的面积∶第 3 个半圆面积= 2 2
第四部分 中考专题突破
专题一 归纳与猜想
归纳与猜想问题是指给出一定条件(可以是有规律的算式、
图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜
想,得出结论,进而加以验证的数学探索题.
其解题思维过程是:从特殊情况入手→探索发现规律→综
合归纳→猜想得出结论→验证结论,这类问题有利于培养学生
思维的深刻性和创造性.
式为“数字对称等式”. (1)根据上述各式反映的规律填空,使式子成为“数字对称
中考数学思想方法 【猜想归纳】数式规律中的猜想归纳思想(学生版+解析版)

数式规律中的猜想归纳思想知识方法精讲1.规律型:数字的变化类探究题是近几年中考命题的亮点,尤其是与数列有关的命题更是层出不穷,形式多样,它要求在已有知识的基础上去探究,观察思考发现规律.(1)探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法,通常将数字与序号建立数量关系或者与前后数字进行简单运算,从而得出通项公式.(2)利用方程解决问题.当问题中有多个未知数时,可先设出其中一个为x,再利用它们之间的关系,设出其他未知数,然后列方程.2. 猜想归纳思想归纳猜想类问题也是探索规律型问题,这类问题一般给出一组具有某种有规律的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,通过认真观察、分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论。
考查学生的归纳、概括、类比能力。
有利于培养学生思维的深刻性和创造性。
解决归纳猜想类问题的基本思路是“观察→归纳→猜想→证明(验证)”,具体做法:(1)认真观察所给的一组数、式、图等,发现它们之间的关系;(2)根据它们之间的关系分析、概括,归纳它们的共性和蕴含的变化规律,猜想得出一个一般性的结论;(3)结合题目所给的材料情景证明或验证结论的正确性。
归纳猜想类问题可以分成四大类:(1)数式归纳猜想题这类题通常是先给出一组数或式子,通过观察、归纳这组数或式子的共性规律,写出一个一般性的结论。
找出题目中规律,即不变的和变化的,变化的部分与序号的关系是解这类题的关键。
(2)图形归纳猜想题此类题通常给出一组图形的排列(或操作得到一系列的图形)探求图形的变化规律,以图形为载体考查图形所蕴含的数量关系。
其解题关键是找出相邻两个图形之间的位置关系和数量关系。
(3)结论归纳猜想题结论归纳猜想题常考数值结果、数量关系及变化情况。
发现或归纳出周期性或规律性变化,是解题的关键。
(4)类比归纳猜想题类比归纳猜想题通常是指由两类对象的具有某些相同或相似的性质,和其中一类对象的某些已知的性质,推断出另一类对象也具有这些性质的一种题型,有时也指两个对象在研究方法、学习过程上类比,考查类比归纳推理能力。
初中数学九年级中考复习《归纳猜想型问题》专题讲解导学教案

I■••・・•••
—1? — , — ,
1 2223233434
解答下面的问题:
(1) 若n为正整数,请你猜想1—=;
n(n+1)
(2)证明你猜想的结论;
1 1 1 1
(3) 求和:+++…+.
1汉22汉33汉42009汇2010
【分析】(1)根据色的定义规则,可知a23=4,92^—3,85^—6,35^—7.则有
1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答:.(填“能”或“不能”)
(2)设AA=AA=A2Ab=1.
1二=度;
2若记小棒A2n-Байду номын сангаасA2n的长度为Qn(门为正整数,如AA=a1, AA=a2,),求此时&2,的值,并直接
活动二:
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中AA为第1根小棒,且AA= AA.数学思考:
考点二:猜想图形规律
根据一组相关图形的变化规律,从中总结通过图形的变化所反映的规律。其中,以图形为
载体的数字规律最为常见。猜想这种规律,需要把图形中的有关数量关系列式表达出来,再对
所列式进行对照,仿照猜想数式规律的方法得到最终结论。Zzz6ZB2Ltk
例1.(2011重庆)下列图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个
(3)若已经向右摆放了3根小棒,则3=,二2=,3=;(用含二的式子表示)0YujCfmUCw
(4)若只能摆放4根小棒,求二的范围.
图乙
【分析】(1)显而易见,能
(2)①22.5
②方法一:
-AA=AA2=AA=1,AiA_LA2A3,…AiA=f12,AA=1+^/2 .
归纳猜想型问题(含解析)

归纳猜想型问题一、中考专题诠释归纳猜想型问题在中考中越来越被命题者所注重。
这类题要求根据题目中的图形或者数字,分析归纳,直观地发现共同特征,或者发展变化的趋势,据此去预测估计它的规律或者其他相关结论,使带有猜想性质的推断尽可能与现实情况相吻合,必要时可以进行验证或者证明,依此体现出猜想的实际意义。
二、解题策略和解法精讲归纳猜想型问题对考生的观察分析能力要求较高,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的持续热点。
三、中考考点精讲考点一:猜想数式规律通常给定一些数字、代数式、等式或者不等式,然后猜想其中蕴含的规律。
一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式。
例1 (2013•巴中)观察下面的单项式:a,-2a2,4a3,-8a4,…根据你发现的规律,第8个式子是.点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.对应训练1.(2013•株洲)一组数据为:x,-2x2,4x3,-8x4,…观察其规律,推断第n个数据应为.考点二:猜想图形规律根据一组相关图形的变化规律,从中总结通过图形的变化所反映的规律。
其中,以图形为载体的数字规律最为常见。
专题复习 归纳与猜想(含答案)-

①1×12=1-12 ②2×23=2-23 ③3×34=3-34④4×45=4-45 ……专题复习 归纳与猜想归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。
其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图二、基础知识整理猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
★ 范例精讲【归纳与猜想】例1【河北实验区05】观察右面的图形(每个正方形的边长均为1)和相应等式,探究其中的规律:⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:⑵猜想并写出与第n 个图形相对应的等式。
解:⑴5×56=5-56⑵11+-=+⨯n nn n n n 。
例2〖归纳猜想型〗将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一片又按同样的方法剪成四小片,再将其中的一小片正方形纸片剪成四片,⑵如果剪n 次共有A n 个正方形,试用含n 、A n 的等式表示这个规律; ⑶利用上面得到的规律,要剪得22个正方形,共需剪几次? ⑷能否将正方形剪成2004个小正方形?为什么? ⑸若原正方形的边长为1,设a n 表示第n 次所剪的正方形的边长,试用含n 的式子表示a n ;⑹试猜想a 1+a 2+a 3+…+a n 与原正方形边长的关系,并画图示意这种关系.解:⑴100×3+1=301,规律是:本次剪完后得到的小正方形的个数比上次剪完后得到的小正方形的个数多3个;⑵A n =3n +1;⑶若A n =22,则3n +1=22,∴n =7,故需剪7次; ⑷若A n =2004,则3n +1=2004,此方程无自然数解, ∴不能将原正方形剪成2004个小正方形;⑸a n =12n ;⑹a 1=12<1,a 1+a 2=12+14=34<1,a 1+a 2+a 3=12+14+18=78<1,……从而猜想到:a 1+a 2+a 3+…+a n <1.直观的几何意义如图所示。
中考数学复习专题1-归纳猜想型问题

中考数学复习专题一:归纳猜想型问题归纳猜想型问题也是探索规律型问题,其特点是:给出一组具有某种特定关系的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,要求通过观察分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论.考点一:猜想数式规律通常给定一些数字、代数式、等式或者不等式,然后猜想其中蕴含的规律。
一般解法是先写出数式的基本结构,然后通过横比(比较同一等式中不同部分的数量关系)或纵比(比较不同等式间相同位置的数量关系)找出各部分的特征,改写成要求的格式。
例1 (2012•沈阳)有一组多项式:a+b 2,a 2﹣b 4,a 3+b 6,a 4﹣b 8,…,请观察它们的构成规律,用你发现的规律写出第10个多项式为 .例2 (2012•珠海)观察下列等式:以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”. (1)根据上述各式反映的规律填空,使式子称为“数字对称等式”: ①52× = ×25; ② ×396=693× . (2)设这类等式左边两位数的十位数字为a ,个位数字为b ,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a 、b ),并证明. 考点二:猜想图形规律根据一组相关图形的变化规律,从中总结通过图形的变化所反映的规律。
其中,以图形为载体的数字规律最为常见。
猜想这种规律,需要把图形中的有关数量关系列式表达出来,再对所列式进行对照,仿照猜想数式规律的方法得到最终结论。
例3 1.(2012•重庆)下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )A . 50B . 64C .68 D .72 例4 (2012•荆门)已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2012个图形中直角三角形的个数有( )A . 8048个B . 4024个C . 2012个D . 1066个考点三:猜想坐标变化例5(2012•德州)如图,在一单位为1的方格纸上,△A 1A 2A 3,△A 3A 4A 5,△A 5A 6A 7,…,都是斜边在x 轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A 1A 2A 3的顶点坐标分别12×231=132×21, 13×341=143×31, 23×352=253×32, 34×473=374×43, 62×286=682×26, …为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2012的坐标为.例7 (2012•鸡西)如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2012的坐标为.考点四:猜想数量关系数量关系的表现形式多种多样,这些关系不一定就是我们目前所学习的函数关系式。
2024初中数学总复习第二板块热点问题突破专题四归纳与猜想新人教版

专题四归纳与猜想专题提升演练1.视察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,……依据你所发觉的规律,请干脆写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1的值为()A.100B.1 000C.10 000D.100 0002.将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示58的有序数对是()A.(11,3)B.(3,11)C.(11,9)D.(9,11)3.如图,在平面直角坐标系中,有若干个整数点,其依次按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),依据这个规律探究可得,第56个点的坐标为.4.如图所示,将形态、大小完全相同的“”和线段依据肯定规律摆成下列图形,第1幅图形中“”的个数为a1,第2幅图形中“”的个数为a2,第3幅图形中“”的个数为a3,…,以此类推,则1a1+1 a2+1a3+…+1a19= .5.【问题情境】如图①,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)证明:AM=AD+MC.(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延长】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图②,探究展示(1)(2)中的结论是否成立?请分别作出推断.证明:延长AE,BC并交于点N,如图①甲,图①甲∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.∵AE平分∠DAM,∴∠DAE=∠MAE.∴∠ENC=∠MAE.∴MA=MN.在△ADE和△NCE中,{∠aaa=∠aaa,∠aaa=∠aaa, aa=aa,∴△ADE≌△NCE(AAS).∴AD=NC.∴MA=MN=NC+MC=AD+MC.(2)AM=DE+BM成立.图①乙证明:过点A作AF⊥AE,交CB的延长线于点F,如图①乙所示.∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC.∵AF⊥AE,∴∠FAE=90°.∴∠FAB=90°-∠BAE=∠DAE.在△ABF和△ADE中,{∠aaa=∠aaa, aa=aa,∠aaa=∠a=90°,∴△ABF≌△ADE(ASA).∴BF=DE,∠F=∠AED.∵AB∥DC,∴∠AED=∠BAE.∵∠FAB=∠EAD=∠EAM,∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM.∴∠F=∠FAM.∴AM=FM.∴AM=FB+BM=DE+BM.(3)①结论AM=AD+MC仍旧成立.证明:延长AE,BC并交于点P,如图②甲.图②甲∵四边形ABCD是矩形,∴AD∥BC.∴∠DAE=∠EPC.∵AE平分∠DAM,∴∠DAE=∠MAE.∴∠EPC=∠MAE.∴MA=MP.在△ADE和△PCE中,{∠aaa=∠aaa,∠aaa=∠aaa, aa=aa,∴△ADE≌△PCE(AAS).∴AD=PC.∴MA=MP=PC+MC=AD+MC.②结论AM=DE+BM不成立.证明:假设AM=DE+BM成立.过点A作AQ⊥AE,交CB的延长线于点Q,如图②乙所示.图②乙∵四边形ABCD是矩形,∴∠BAD=∠D=∠ABC=90°,AB∥DC.∵AQ⊥AE,∴∠QAE=90°.∴∠QAB=90°-∠BAE=∠DAE.∴∠Q=90°-∠QAB=90°-∠DAE=∠AED.∵AB∥DC,∴∠AED=∠BAE.∵∠QAB=∠DAE=∠EAM,∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠QAB=∠QAM.∴∠Q=∠QAM.∴AM=QM.∴AM=QB+BM.∵AM=DE+BM,∴QB=DE.在△ABQ和△ADE中,{∠aaa=∠aaa,∠aaa=∠a=90°, aa=aa,∴△ABQ≌△ADE(AAS).∴AB=AD.与条件“AB≠AD”冲突,故假设不成立.∴AM=DE+BM不成立.。
专题复习-中考数学归纳与猜想(含答案)-
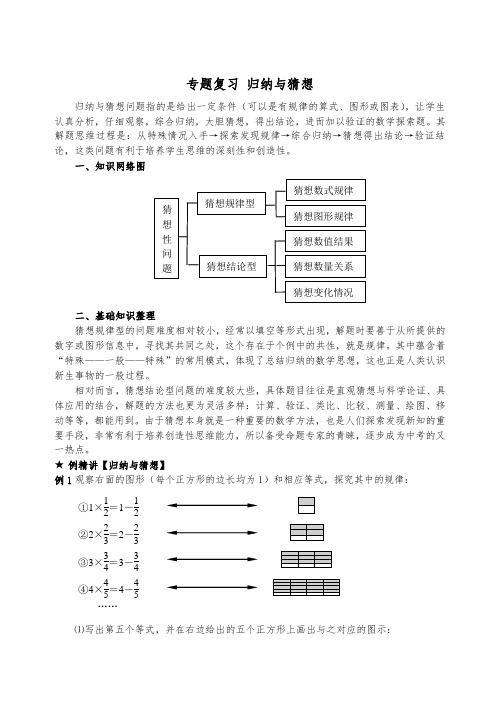
①1×12=1-12 ②2×23=2-23 ③3×34=3-34④4×45=4-45 ……专题复习 归纳与猜想归纳与猜想问题指的是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察,综合归纳,大胆猜想,得出结论,进而加以验证的数学探索题。
其解题思维过程是:从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论,这类问题有利于培养学生思维的深刻性和创造性。
一、知识网络图二、基础知识整理猜想规律型的问题难度相对较小,经常以填空等形式出现,解题时要善于从所提供的数字或图形信息中,寻找其共同之处,这个存在于个例中的共性,就是规律。
其中蕴含着“特殊——一般——特殊”的常用模式,体现了总结归纳的数学思想,这也正是人类认识新生事物的一般过程。
相对而言,猜想结论型问题的难度较大些,具体题目往往是直观猜想与科学论证、具体应用的结合,解题的方法也更为灵活多样:计算、验证、类比、比较、测量、绘图、移动等等,都能用到。
由于猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养创造性思维能力,所以备受命题专家的青睐,逐步成为中考的又一热点。
★ 例精讲【归纳与猜想】例1观察右面的图形(每个正方形的边长均为1)和相应等式,探究其中的规律:⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:⑵猜想并写出与第n 个图形相对应的等式。
解:⑴5×56=5-56⑵11+-=+⨯n nn n n n 。
例2〖归纳猜想型〗将一正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一片又按同样的方法剪成四小片,再将其中的一小片正方形纸片剪成四片,如此循环进行下去,将结果填在下表中,并解答所提出的问题:⑴如果能剪100次,共有多少个正方形?据上表分析,你能发现什么规律? ⑵如果剪n 次共有A n 个正方形,试用含n 、A n 的等式表示这个规律; ⑶利用上面得到的规律,要剪得22个正方形,共需剪几次? ⑷能否将正方形剪成2004个小正方形?为什么?⑸若原正方形的边长为1,设a n 表示第n 次所剪的正方形的边长,试用含n 的式子表示a n ;⑹试猜想a 1+a 2+a 3+…+a n 与原正方形边长的关系,并画图示意这种关系.解:⑴100×3+1=301,规律是:本次剪完后得到的小正方形的个数比上次剪完后得到的小正方形的个数多3个;⑵A n =3n +1;⑶若A n =22,则3n +1=22,∴n =7,故需剪7次; ⑷若A n =2004,则3n +1=2004,此方程无自然数解, ∴不能将原正方形剪成2004个小正方形;⑸a n =12n ;⑹a 1=12<1,a 1+a 2=12+14=34<1,a 1+a 2+a3=12+14+18=78<1,……从而猜想到:a 1+a 2+a 3+…+a n <1.直观的几何意义如图所示。
专题四归纳与猜想 (2)
_九年级下册 学科:数学主备人:卢志祥审核人:卢志祥
教学课题
专题四归识与技能
归纳猜想问题指的是给出一组具有某种特定关系的数、式、图形,或是给出与图形有关的操作、变化过程,要求通过观察、分析、推理,探求其中所蕴涵的规律,进而归纳或猜想出一般性的结论,在解答过程中需要经历观察、归纳、猜想、试验、证明等数学活动,以加深学生对相关数学知识的理解,认识数学知识之间的联系.在中考试卷中多以选择题、填空题、解答题的形式出现.
考向三 数形规律问题
根据一组图形的排列,探究图形变化所反映的规律,其中以图形为载体的数字规律最为常见.
【例3】(2013四川遂宁中考)为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆第(n)个图,需用火柴棒的根数为.
三、巩固练习:
优化设计
四、归纳总结:
本节课你的收获是什么?哪些知识是你这节课的提高?
教学反思:
问题二、给出下列命题:
命题1:直线y=x与双曲线y= 有一个交点是(1,1);
命题2:直线y=8x与双曲线y= 有一个交点是 ;
命题3:直线y=27x与双曲线y= 有一个交点是 ;
命题4:直线y=64x与双曲线y= 有一个交点是 ;
……
(1)请你阅读、观察上面的命题,猜想出命题n(n为正整数);
(2)请验证你猜想的命题n是真命题.
1234321
2345432
3456543
4567654
5678765
6789876
78910987
则(1)(a23-a22)+(a52-a53)=;
(2)此数表中的四个数anp,ank,amp,amk,满足(anp-ank)+(amk-amp)=.
中考数学二轮复习(三)归纳与猜想专题

中考二轮复习(三)归纳与猜想专题
归纳猜想题型是指试题中给出一个条件,可以是有规律的数、算式、图形或图表,让同学们在观察、分析的基础上综合归纳,大胆猜想,获得结论,进而验证。
这几年的热点题目,着重考查学生们的观察、分析、综合能力,同时也是考查学生对数、式及图形变化领域基础知识的一种检验,考查学生对重要公式、法则及规律的理解和掌握。
研究数学、学习数学、应用数学的过程,实际上就是探索、研究数学规律并运用数学规律的过程。
探索的目的是为了提出猜想,提出猜想的目的是为了发现规律。
在初中数学的学习中,不仅要经历探索和猜想的方法学习数学,培养敢于探索和大胆猜想的精神,而且要掌握一些基本的策略和方法,会探索、敢猜想。
探索规律的试题,在中考中从简单的填空题、选择题、到复杂的代数、几何综合题,以多样的形式、多彩的背景为内容频繁出现。
解答此类问题的过程中,需要经历观察、归纳、猜想、实验、证明等数学活动。
能够很好的培养学生们在数学方面的探索精神,符合课程标准的要求。
解答此类题,首先需要观察数据、代数式、等式或图形,寻找规律,并根据规律用代数式、方程、函数、不等式等数学模型表示出图形的数量关系及变化规律。
初中归纳猜想总结

初中归纳猜想总结初中阶段是学生开始接触猜想思维的重要时期,在各个学科中,猜想总结具有重要的教育和学习价值。
以下是初中阶段学生常见的归纳猜想及其总结。
1. 数学领域的归纳猜想与总结在数学学科中,归纳猜想是培养学生逻辑思维和抽象推理能力的重要方法。
有许多经典的数学猜想,如费马大定理、哥德巴赫猜想等,但初中阶段的数学归纳猜想更多地与基础知识和技巧紧密相关。
以下是一些常见的数学归纳猜想及其总结:a. 质数与合数- 归纳猜想:所有大于2的整数都可以写成两个质数的和。
- 总结:通过对自然数的分析和归纳,可以发现所有大于2的整数都可以被分解为两个质数的和,这就是哥德巴赫猜想的初步认识。
b. 偶数与奇数- 归纳猜想:任意两个奇数之和是一个偶数。
- 总结:通过观察和验证,我们可以发现任意两个奇数相加的结果都是一个偶数。
这个归纳猜想在数学计算中有重要的应用。
c. 平方数与立方数- 归纳猜想:任意连续三个自然数中,平方数和立方数最多只有一个重合。
- 总结:通过列举自然数的平方数和立方数,我们可以总结出这一规律,即连续三个自然数中平方数和立方数最多只有一个重合。
2. 科学领域的归纳猜想与总结科学学科中,猜想与实验相结合,培养学生的科学思维和观察能力。
以下是初中科学中常见的归纳猜想及其总结:a. 热传导与热对流- 归纳猜想:固体的热传导速度大于液体和气体的热对流速度。
- 总结:通过观察和实验,我们可以发现在相同条件下,固体的热传导速度明显快于液体和气体的热对流速度。
b. 植物对光的反应- 归纳猜想:植物没有光照会导致生长受到抑制。
- 总结:通过观察和实验,我们可以得出结论,植物的生长和发育需要光合作用,如果没有光照,植物会出现生长迟缓或停止生长的现象。
c. 静电现象- 归纳猜想:相同电荷之间会产生排斥力,不同电荷之间会产生吸引力。
- 总结:通过观察和实验,我们可以发现当两个带有相同电荷的物体靠近时,它们会产生相互排斥的现象,而带有不同电荷的物体靠近时会产生相互吸引的现象。
中考数学热点探究一 归纳猜想型试题的分析与预测

中考数学热点探究一归纳猜想型试题的分析与预测热点综述归纳猜想型问题就是给出一定条件(可以是有规律的算式、图形或图表),让学生认真分析,仔细观察、归纳,发现共同特征,或者发展变化的趋势,大胆猜想,据此去预测估计它的变化规律或者与其变化趋势一致的相关结论,并能够应用此结论.由于归纳猜想本身就是一种重要的数学方法,也是人们探索发现新知的重要手段,非常有利于培养学生的创造性思维,所以备受命题专家的青睐.而且此类问题能够较全面地考查学生的探索研究、归纳猜想能力,所以在近几年各地中考中此类型题目逐步成为中考试卷中的必考内容之一.其解题的具体方法和步骤是:(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或说明结论是否正确.现以近几年我省的几道中考题为例,来和大家一起探讨一下此类问题.热点呈现例1(河北)我国古代的“河图”是由3×3的方格构成,每个方格内均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图1给出了“河图”的部分点图,请你推算出P处所对应的点图是()析解:首先要从题设的文字叙述中把规律搞懂:每一行、每一列以及每一条对角线上的三个点图的点数之和均相等,这样就省掉了总结归纳的过程;再观察“河图”中,涉及到的就是一条对角线和最下面一行的点;应用规律:对角线的点数之和等于最后一行的点数之和,两者有一个共同的点(左下角),故可得:2+5=1+P,很容易算出P处应有6个点,选(C).本题直接告诉了规律,重在考查学生的观察分析问题的能力,考查学生建立方程模型的意识.例2(河北)用M,N,P,Q各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.图2(1)~图2(4)是由M,N,P,Q中的两种图形组合而成的(组合用“&”表示).那么,下列组合图形中,表示P&Q的是().析解:本题首先要观察图2(1)~图2(4),归纳总结出M ,N ,P ,Q 各代表了正方形、正三角形、圆、线段,尤其是P ,Q 所代表的图形,这样P &Q 表示的必然是圆和线段.故答案选(B ).本题考查了学生的观察、推理和归纳的能力.例3 (2006河北课改)观察下面的点阵图形和与之相对应的等式,探究其中的规律:(1)请你在④和⑤后面的横线上分别写出相对应的等式:(2)通过猜想,写出与第n 个图形相对应的等式.析解:本题的求解首先通过直接观察①、②、③图和分析其后面的各式的特点,不难发现:依次在点阵图形的外部增加一层,即增加四个点,旁边的等式的结果表示的是点的个数,等号左边是4乘以一个整数(从零开始的连续整数)再加1,此整数比对应的图序数小1;等号右边是4乘以一个整数(从1开始的连续整数)再减去3,此整数等于对应的图序数.由此可得第④个图对应的等式为:431443⨯+=⨯-;第⑤个图对应的等式为:441453⨯+=⨯-.第n 个图对应的等式为:4(1)143n n -+=-.此题在非课改区同时以选择题的形式出现,试题如下:( 河北非课改区)观察图3给出的四个点阵,s 表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n 个点阵中的点的个数s 为 ( )(A )32n - (B )31n -(C )41n + (D )43n -例4(河北课改)观察下面的点阵图和相应的等式,探究其中的规律:(1)在④和⑤后面的横线上分别写出相应的等式;(2)通过猜想写出与第n个点阵相对应的等式.析解:解答本题,首先要通过直接观察①、②、③中的三个图和分析其下面的各式的特点,不难发现:上面各式的左边分别是从1开始的连续奇数的和,其奇数的个数等于其相应的图序数,而等号的右边则为相应的图序数的平方,由此可知第④、⑤个式子分别为:213574+++=,2135795++++=.进一步观察上面各式不难发现以上各式的等号的左边的最后一个数与相应的图形序数n的关系为:21n-,由此可得第(2)问的答案为:2135(21)n n++++-=.2005年课改实验区的第18题是和上题相类似的一道题目,在这里不再详细分析,试题如下:(2005年课改)观察右面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式.解答:(1)55 5566⨯=-.(2)11n n n n n n ⨯=-++. 热点预测综上所述,归纳猜想问题每年都会出现在河北省的中考试题中,也可以称之为一个热点问题.2007年中考是全省完全实施新课标的第一年,归纳猜想问题除了保持了试题的稳定性外,更加注重考查学生的思维能力和识图探究的能力,其呈现方式也由原来的解答题(课改区试卷中)改为选择题,估计在08年的河北省的中考试卷中会继续选用07年的模式考查学生的归纳猜想能力.模拟练习1.有一列数1a ,2a ,3a ,…,n a ,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若12a =,则2007a 为( )(A)2007 (B)2(C)12(D)1- 2.观察表1,寻找规律.表2是从表1中截取的一部分,其中a ,b ,c 的值分别为( )(A )20,25,24 (B )25,20,24(C )18,25,24 (D )20,30,253.数字解密:第一个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是17=9+8,…,观察并猜想第六个数是( )(A)64 (B)65(C)66 (D)674.柜台上放着一堆罐头,它们摆放的形状如图4所示:第一层有2×3听罐头,第二层有3×4听罐头,第三层有4×5听罐头,……请你根据这堆罐头排列的规律猜想,第n (n 为正整数)层共有________听罐头(用含n 的式子表示).5.如图5,等腰直角三角形ABC 直角边长为1,以它的斜边上的高AD 为腰作第一个等腰直角三角形ADE ;再以所作的第一个等腰直角三角形ADE 的斜边上的高AF 为腰作第二个等腰直角三角形AFG ;…以此类推,这样所作的第n 个等腰直角三角形的腰长为____________.6.以边长为a 的正方形ABCD 的对角线AC 长为半径,以点A 为圆心作弧交AB 边的延长线于点E ,交AD 边的延长线于点F ,得扇形AECF ,把扇形AECF 的面积称为正方形ABCD 面积的扩展;再以线段AE 为一边作正方形AEGH ,以对角线AG 的长为半径,点A 为圆心画弧交AE 边的延长线于点M ,交AH 边的延长线于点N ,得扇形AMGN ,则扇形AMGN 的面积是正方形AEGH 面积的扩展,按此法依次进行到如图6所示,叫做正方形ABCD 面积的第一次扩展.按这种方法可进行第二次扩展,直到第n 次扩展.(1)求第一次扩展中扇形面积1S ;(2)求第二次扩展中扇形面积2S (第二次扩展的第一个正方形是以第一次扩展的最后一个扇形半径为边长的正方形);(3)求第n 次扩展中扇形面积n S .7.大数学家高斯在上学读书时曾经研究过这样一个问题:1231++++=经过研究,这个问题的一般性结论是(1)1232n n n +++++= ,其中n是正整数.现在我们来研究一个类似的问题: 1223(1)?n n ⨯+⨯+++=观察下面三个特殊的等式:(1)112(123012)3⨯=⨯⨯-⨯⨯; (2)123(234123)3⨯=⨯⨯-⨯⨯; (3)134(345234)3⨯=⨯⨯-⨯⨯. 将这三个等式的两边相加,可以得到1122334345203⨯+⨯+⨯=⨯⨯⨯=. 读完这段材料,请你思考后回答:(1)1223100101⨯+⨯++⨯= _______________;(2)1223(1)n n ⨯+⨯+++= __________;(3)123234(1)(2)n n n ⨯⨯+⨯⨯++++= __________.(只需写出结果,不必写中间的过程)8.1883年,康托尔构造的这个分形,称做康托尔集.从数轴上单位长度线段开始,康托尔取走其中间三分之一而达到第一阶段;然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段.无限地重复这一过程,余下的无穷点集就称做康托尔集.图7是康托尔集的最初几个阶段,当达到第八个阶段时,余下的所有线段的长度之和为___________.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学猜想与归纳
1、一个由数字1和0组成的2002位的数码,其排列规律是:101101110101101110101101110……则这个数码中数字0共有—————( )
A 、666个
B 、667个
C 、668个
D 、223个
2、礼堂第一排有a 个座位,后面每排都比前排多一个座位,第二排有__个座位,第三排有__个座位,用m 表示n 排座位数为_________,当a =20,n=19时,m=_____________.
3、研究下列各式,你会发现什么规律?224131==+⨯;
239142==+⨯;2416153==+⨯;2525164==+⨯………请将你找出的规
律用公式表示出来 ;
4、判断下列各式是否成立,你认为成立的,请在括号内打“√”,不成立的请在括号内打“×”
(1)322322=+ ( ) (2)83
3833=+ ( ) (3)15441544=+
( ) (4)24
552455=+ ( ) 5、你判断完以上各题之后,发现什么规律?请用含有n 的式子将规律表示出来,并注明n 的取值范围。
(1
12
2-=-+
n n
n n n n n ≥2) 6、下列每个图都是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n (n >1)盆花,每个图案的花盆的总数是S 。
n =2 、S =3 n =3、 S =6 n =4、 S =9
按此规律推断S 与n 的关系式为 。
7、把编号为1,2,3,4,…的若干盆花按右图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为___________色.
8、瑞士中学教师巴尔末成功地从光谱数据、591216⋯⋯32
36
2125、、中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是____
9、我国宋朝数学家杨辉在他的著作《详解九章算法》中提出右下表,此表揭示了n b a )(+(n 为非负整数)展开式的各项系数的规律,例如:
1)(0=+b a ,它只有一项,系数为1;
b a b a +=+1)(,它有两项,系数分别为1,1;
2222)(b ab a b a ++=+,它有三项,系数分别为1,2,1;
3223333)(b ab b a a b a +++=+,它有四项,系数分别为1,3,3,1; ……
根据以上规律,4)(b a +展开式共有五项,系数分别为 。
10、下列是三种化合物的结构式及分子式,请按其规律,写出后一
种化合物的分子式... .
11、某同学在电脑中打出如下排列的若干个圆(图中●表示实心圆,○表示空心圆):
● ○●●○●●●○●●●●○●●●●●○●●●●●●○
C 3H 8
C 2H 6CH 4H H H H H H H H H
H H H H H C C C C C H H
H H C
若将上面一组圆依此规律复制得到一系列圆,那么前2005个圆中有( )个空心圆;
12、观察下列各式;
433332222
111222⨯=+⨯=+⨯=+ 请把你猜想到的规律用自然数n 表示出来 。
13、把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________。
14、一组按规律排列的数:41,93,
167,25
13,36
21
,…. 请你推断第9个数是 .
15、观察下面图形我们可以发现:第1个图中有1个正方形,第2个图
中共有5个正方形,第3个图中共有14个正方形,按照这种规律下去的第5个图形共有________个正方形。
16、分析下图①,②,④中阴影部分的分布规律,按此规律在图6③中画出其中的阴影部分.
17、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数
式表示)。
图1 图2 图3
第21题图
18、用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子
枚(用含有n的代数式表示)
19、观察按下列顺序排列的等式:
9011
⨯+=
91211
⨯+=
92321
⨯+=
93431
⨯+=
94541
⨯+=
……
猜想:第n个等式(n为正整数)用n表示,可以表示成
20、已知:△ABC中,AB=10
⑴如图①,若点D、E分别是AC、BC边的中点,求DE的长;
⑵如图②,若点A
1、A
2
把AC边三等分,过A
1
、A
2
作AB边的平行线,
分别交BC边于点B
1、B
2
,求A
1
B
1
+A
2
B
2
的值;
⑶如图③,若点A
1、A
2
、…、A
10
把AC边十一等分,过各点作AB边的
平行线,分别交BC边于点B
1、B
2
、…、B
10。
根据你所发现的规律,直接写
出A
1B
1
+A
2
B
2
+…+A
10
B
10
的结果。
21
===
……请你将猜想到的规律用含自然数n (n ≥1)的代数式表示出来 是_____________________. 22、.4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180º后得
到如图(2)所示,那么她所旋转的牌从左数起是 (
)
(A )第一张 (B )第二张 (C )第三张 (D )第四张
23、观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放.记第n 个图中小黑点的个数为y .
解答下列问题:
(2)当=8时,=______;
图3 图4 图1 图2 图5
(3)根据上表中的数据,把n 作为横坐标,把y 作为纵坐标,在左图的平面直角坐标系中描出相应的各点(n , y ),其中1≤n ≤5;
(4)请你猜一猜上述各点会在某一函数的图象上吗?如果在某一函数的图象上,请写出该函数的解析式.
24
25、如图,甲、乙、丙、丁四人分坐在一方桌的 四个不同方向上,看到桌面上的图案呈“A ”种 形状的是
(A )甲 (B )乙 (C )丙 (D )丁
26、.一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如图4),
则这串珠子被盒子遮住的部分有____颗.
27、.
你的理由.
23,34,45, ,6
7
,…你的理由是_______________.
甲
乙
(第4题)。
