第7章 树和二叉树(2)
期权定价的二叉树模型(ppt 39页)

第7章 期权定价的二叉树模型
2022/3/23
22
ftrf S S f1 22S2 S 2f2rf f
c St N d1 X erf Tt N d2
St erf Tt N d1 X N d2 erf Tt
EST Nd1 X N d2 erf Tt EST Nd1 X N d2 erf Tt
2022/3/23
21
风险中性定理表达了资本市场中的这样的 一个结论:即在市场不存在任何套利可能性的 条件下,如果衍生证券的价格依然依赖于可交 易的基础证券,那么这个衍生证券的价格是与 投资者的风险态度无关的。
这个结论在数学量,尤其是期望收益率。
公平的入局费=2000×50%+0×50%= 1000元
第7章 期权定价的二叉树模型
2022/3/23
13
愿意支付的入局费 风险类型 数量 入局费<1000元 风险厌恶者 众多 入局费=1000元 风险中性者 入局费>1000元 风险喜好者 极少
如果有人愿意无条件地参加公平的赌博, 则这样的人被认为是风险中性。风险中性者对 风险采取无所谓的态度。
考虑以下组合:
①买入1份股票看涨期权 ②卖空Δ股股票
显然,适当调整Δ可以使得上述组合为无风 险组合。
第7章 期权定价的二叉树模型
2022/3/23
3
如果这个组合是无风险组合,则其价值与 状态无关,所以,以下数学表达式成立:
22118
解得,
0.25
也就是说,1份看涨期权多头加上0.25股股 票空头构成的组合是无风险组合。
这就是风险中性定价的基本思想。
第7章 期权定价的二叉树模型
2022/3/23
18
我们回到之前的示例中,在那里,我们可 以把股票价格上升的概率定义为p,于是在到 期日T时刻,股票价格的期望值为:
第7章树和二叉树(2)-数据结构教程(Java语言描述)-李春葆-清华大学出版社

二叉树也称为二分树,它是有限的结点集合,这个集合或者是空,或者由 一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。 二叉树中许多概念与树中的概念相同。 在含n个结点的二叉树中,所有结点的度小于等于2,通常用n0表示叶子结 点个数,n1表示单分支结点个数,n2表示双分支结与度为2的树是不同的。
度为2的树至少有3个结点,而二叉树的结点数可以为0。 度为2的树不区分子树的次序,而二叉树中的每个结点最多有 两个孩子结点,且必须要区分左右子树,即使在结点只有一棵 子树的情况下也要明确指出该子树是左子树还是右子树。
2/35
归纳起来,二叉树的5种形态:
Ø
4/35
3. 满二叉树和完全二叉树
在一棵二叉树中,如果所有分支结点都有左孩子结点和右孩子结点,并且 叶子结点都集中在二叉树的最下一层,这样的二叉树称为满二叉树。
可以对满二叉树的结点进行层序编号,约定编号从树根为1开始,按照层 数从小到大、同一层从左到右的次序进行。
满二叉树也可以从结点个数和树高度之间的关系来定义,即一棵高度为h 且有2h-1个结点的二叉树称为满二叉树。
R={r} r={<ai,aj> | ai,aj∈D, 1≤i,j≤n,当n=0时,称为空二叉树;否则其中
有一个根结点,其他结点构成根结点的互不相交的左、右子树,该 左、右两棵子树也是二叉树 } 基本运算: void CreateBTree(string str):根据二叉树的括号表示串建立其存储结构。 String toString():返回由二叉树树转换的括号表示串。 BTNode FindNode(x):在二叉树中查找值为x的结点。 int Height():求二叉树的高度。 … }
5
E
数据结构习题及答案与实验指导(树和森林)7

第7章树和森林树形结构是一类重要的非线性结构。
树形结构的特点是结点之间具有层次关系。
本章介绍树的定义、存储结构、树的遍历方法、树和森林与二叉树之间的转换以及树的应用等内容。
重点提示:●树的存储结构●树的遍历●树和森林与二叉树之间的转换7-1 重点难点指导7-1-1 相关术语1.树的定义:树是n(n>=0)个结点的有限集T,T为空时称为空树,否则它满足如下两个条件:①有且仅有一个特定的称为根的结点;②其余的结点可分为m(m>=0)个互不相交的子集T1,T2,…,T m,其中每个子集本身又是一棵树,并称为根的子树。
要点:树是一种递归的数据结构。
2.结点的度:一个结点拥有的子树数称为该结点的度。
3.树的度:一棵树的度指该树中结点的最大度数。
如图7-1所示的树为3度树。
4.分支结点:度大于0的结点为分支结点或非终端结点。
如结点a、b、c、d。
5.叶子结点:度为0的结点为叶子结点或终端结点。
如e、f、g、h、i。
6.结点的层数:树是一种层次结构,根结点为第一层,根结点的孩子结点为第二层,…依次类推,可得到每一结点的层次。
7.兄弟结点:具有同一父亲的结点为兄弟结点。
如b、c、d;e、f;h、i。
8.树的深度:树中结点的最大层数称为树的深度或高度。
9.有序树:若将树中每个结点的子树看成从左到右有次序的(即不能互换),则称该树为有序树,否则称为无序树。
10.森林:是m棵互不相交的树的集合。
7-1-2 树的存储结构1.双亲链表表示法以图7-1所示的树为例。
(1)存储思想:因为树中每个元素的双亲是惟一的,因此对每个元素,将其值和一个指向双亲的指针parent构成一个元素的结点,再将这些结点存储在向量中。
(2)存储示意图:-1 data:parent:(3)注意: Parrent域存储其双亲结点的存储下标,而不是存放结点值。
下面的存储是不正确的:-1 data:parent:2.孩子链表表示法(1)存储思想:将每个数据元素的孩子拉成一个链表,链表的头指针与该元素的值存储为一个结点,树中各结点顺序存储起来,一般根结点的存储号为0。
数据结构教程李春葆课后答案第7章树和二叉树

教材中练习题及参考答案
1. 有一棵树的括号表示为 A(B,C(E,F(G)),D),回答下面的问题: (1)指出树的根结点。 (2)指出棵树的所有叶子结点。 (3)结点 C 的度是多少? (4)这棵树的度为多少? (5)这棵树的高度是多少? (6)结点 C 的孩子结点是哪些? (7)结点 C 的双亲结点是谁? 答:该树对应的树形表示如图 7.2 所示。 (1)这棵树的根结点是 A。 (2)这棵树的叶子结点是 B、E、G、D。 (3)结点 C 的度是 2。 (4)这棵树的度为 3。 (5)这棵树的高度是 4。 (6)结点 C 的孩子结点是 E、F。 (7)结点 C 的双亲结点是 A。
12. 假设二叉树中每个结点值为单个字符,采用二叉链存储结构存储。设计一个算法 计算一棵给定二叉树 b 中的所有单分支结点个数。 解:计算一棵二叉树的所有单分支结点个数的递归模型 f(b)如下:
f(b)=0 若 b=NULL
6 f(b)=f(b->lchild)+f(b->rchild)+1 f(b)=f(b->lchild)+f(b->rchild)
表7.1 二叉树bt的一种存储结构 1 lchild data rchild 0 j 0 2 0 h 0 3 2 f 0 4 3 d 9 5 7 b 4 6 5 a 0 7 8 c 0 8 0 e 0 9 10 g 0 10 1 i 0
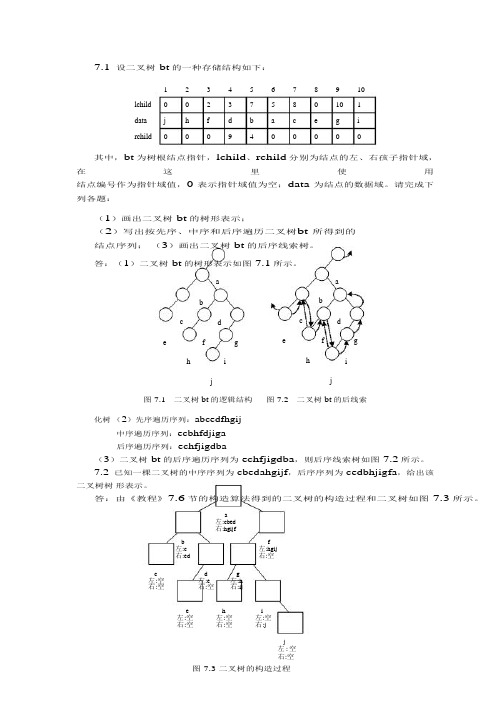
答:(1)二叉树bt的树形表示如图7.3所示。
a b c e h j f i d g e h j c f i b d g a
对应的算法如下:
void FindMinNode(BTNode *b,char &min) { if (b->data<min) min=b->data; FindMinNode(b->lchild,min); //在左子树中找最小结点值 FindMinNode(b->rchild,min); //在右子树中找最小结点值 } void MinNode(BTNode *b) //输出最小结点值 { if (b!=NULL) { char min=b->data; FindMinNode(b,min); printf("Min=%c\n",min); } }
计算机学科专业基础综合数据结构-树与二叉树(二)

计算机学科专业基础综合数据结构-树与二叉树(二)(总分:100.00,做题时间:90分钟)一、{{B}}单项选择题{{/B}}(总题数:44,分数:44.00)1.在下面关于树的相关概念的叙述中,正确的是______。
∙ A.只有一个结点的二叉树的度为1∙ B.二叉树的度一定为2∙ C.二叉树的左右子树可任意交换∙ D.深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树(分数:1.00)A.B.C.D. √解析:只有一个结点的二叉树的度为零。
二叉树的度可以为0、1、2;二叉树的左右子树不能任意交换。
2.已知一算术表达式的中缀形式为A+B+C-D/E,后缀形式为ABC*+DE/-,其前缀形式为______。
∙ A.-A+B*C/DE∙ B.-A+B*CD/E∙ C.-+*ABC/DE∙ D.-+A*BC/DE(分数:1.00)A.B.C.D. √解析:根据题目给出的中缀和后缀表达式可以得到其算术表达式为:(A+B*C)-D/E,前缀表达式:-+A*BC/DE。
3.算术表达式a+b*(c+d/e)转为后缀表达式后为______。
∙ A.ab+cde/*∙ B.abcde/+*+∙ C.abcde/*++∙ D.abcde*/++(分数:1.00)A.B. √C.D.解析:根据表达式a+b*(c+d/e)可知其后缀表达式为abcde/+*+。
4.某二叉树的先序遍历序列为IJKLMNO,中序遍历序列为JLKINMO,则后序遍历序列是______。
∙ A.JLKMNOI∙ B.LKNJOMI∙ C.LKJNOMI∙ D.LKNOJMI(分数:1.00)A.B.C. √D.解析:由先序和中序遍历序列确定一棵二叉树,再给出这棵二叉树的后序遍历序列。
[*] 由此图可以确认后序遍历的序列为LKJNOMI。
5.设森林F对应的二叉树为B,它有m个结点,B的根为P,P的右子树结点个数为n,森林F中第一棵树的结点个数是______。
树形表示法A

root
T1
T2 … Tm
7.1.2 树的表示
(1)树形表示法。这是树的最基本的表示,使用一棵倒 置的树表示树结构,非常直观和形象。下图就是采用这种表 示法。
A BCD E FG
0 A -1 1 B0 2 C0 3 D0 4 E2 5 F2 6 G2
(a)
(b)
树的双亲存储结构示意图
双亲存储结构的类型声明如下:
typedef struct
{ ElemType data; //节点的值
int parent;
//指向双亲的位置
} PTree[MaxSize];
DE F
D∧∧ ∧ E ∧ ∧ F ∧∧ ∧
G∧∧ ∧ G
树的孩子链存储结构示意图
孩子链存储结构的节点类型声明如下:
typedef struct node { ElemType data;
struct node *sons[MaxSons]; } TSonNode;
//节点的值 //指向孩子节点
其中,MaxSons为最多的孩子节点个数。
思考题:该存储结构的优缺点?
A
BCD
E FG (a)
0 A -1 1 B0 2 C0 3 D0 4 E2 5 F2 6 G2
(b)
2. 孩子链存储结构
孩子链存储结构可按树的度(即树中所有节点度的最大值) 设计节点的孩子节点指针域个数。以下左图的树对应的孩子链 存储结构如右图所示。
A
∧
A
B
数据结构二叉树习题含答案

第 6 章树和二叉树1.选择题( 1)把一棵树变换为二叉树后,这棵二叉树的形态是()。
A.独一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子( 2)由 3 个结点能够结构出多少种不一样的二叉树?()A. 2 B . 3 C . 4 D. 5( 3)一棵完整二叉树上有1001 个结点,此中叶子结点的个数是()。
A. 250 B . 500 C . 254 D. 501( 4)一个拥有 1025 个结点的二叉树的高h 为()。
A. 11 B . 10 C.11 至 1025 之间 D .10 至 1024 之间( 5)深度为 h 的满 m叉树的第 k 层有()个结点。
(1=<k=<h)k-1B kCh-1 hA. m . m-1 . m D.m-1( 6)利用二叉链表储存树,则根结点的右指针是()。
A.指向最左孩子 B .指向最右孩子 C .空 D .非空( 7)对二叉树的结点从 1 开始进行连续编号,要求每个结点的编号大于其左、右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,可采纳()遍历实现编号。
A.先序 B. 中序 C. 后序 D.从根开始按层次遍历(8)若二叉树采纳二叉链表储存结构,要互换其全部分支结点左、右子树的地点,利用()遍历方法最适合。
A.前序B.中序C.后序D.按层次(9)在以下储存形式中,()不是树的储存形式?A.双亲表示法 B .孩子链表表示法 C .孩子兄弟表示法D.次序储存表示法( 10)一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树必定满足()。
A.全部的结点均无左孩子B.全部的结点均无右孩子C.只有一个叶子结点D.是随意一棵二叉树( 11)某二叉树的前序序列和后序序列正好相反,则该二叉树必定是()的二叉树。
A.空或只有一个结点B.任一结点无左子树C.高度等于其结点数 D .任一结点无右子树( 12)若 X 是二叉中序线索树中一个有左孩子的结点,且 X 不为根,则 X 的前驱为()。
树与二叉树的关系

将一棵树转换为二叉树的方法: ⑴ 树中所有相邻兄弟之间加一条连线。 ⑵ 对树中的每个结点,只保留其与第一个 孩子结点之间的连线,删去其与其它孩子结 点之间的连线。 ⑶ 以树的根结点为轴心,将整棵树顺时针 旋转一定的角度,使之结构层次分明。
树转换为二叉树示意图
A
A
B
E
CF G
DH
I
A
B
E
CF G
DH
I
J
J
A
BC D EG FH I J
用递归的方法描述其转换
若B是一棵二叉树,T是B的根结点,L是B的 左子树,R为B的右子树,设B对应的森林F(B) 中含有的n棵树为T1,T2, …,Tn,则有: (1)B为空,则:F(B)为空的森林(n=0)。
(2)B非空,则:
树
森林
二叉树
先根遍历 先序遍历 先序遍历
后根遍历 中序遍历 中序遍历
3、森林的后序遍历*
若森林非空,则遍历方法为:
(1)后序遍历森林中第一棵树的根结点的子 树森林。 (2)后序遍历除去第一棵树之后剩余的树构 成的森林。 (3)访问第一棵树的根结点。
6.5 哈夫曼树及其应用
6.5.1 哈夫曼树
哈夫曼树最典型、最广泛的应用是在 编码技术上,利用哈夫曼树,可以得到 平均长度最短的编码。这在通讯领域是 极其有价值的。
权值 双亲序号 左孩子序号 右孩子序号
静态三叉链表结构定义
#define N 20 #define M 2*N-1 typedef struct { int weight ;
int parent,Lchild,Rchild ; }HTNode, HuffmanTree[M+1];
树和二叉树知识考点整理

树和二叉树知识考点整理●树的基本概念●树的定义●n个结点的有限集●n=0代表空树●满足条件●只有一个根的结点●其余结点是互不相交的有限集,每个集合本身是一棵树,是根的子树●树是一种递归的数据结构●树的根结点没有前驱,其余结点只有一个前驱●树中所有结点可以有零个或多个后驱●基本术语●双亲、兄弟、孩子、祖先●度:孩子个数●分支结点:度大于0●叶子结点:度为0●深度:从下往上;●高度:从上往下;●有序树:从左到右是有次序的●路径和路径长度:路径是从上往下的●森林:m棵互不相交的树的集合。
●树的基本性质●结点数=所有结点度数之和+1●度为m的树中第i层上至多有m的i-1次分个结点●高度为h的m叉树至多有(m^h-1)/(m-1)个结点●具有n个结点的m叉树的最小高度为「logm(n(m-1)+1)]●二叉树的概念●定义●一种树形结构,特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)并且二叉树的子树有左右之分,次序不可颠倒●二叉树与度为2的有序树区别●度为2的可以有三个结点,二叉树可以是空树●度为2的有序树的孩子左右之分是根据另一个孩子而言的;二叉树无论有没有,都要确定左右●特殊的二叉树●满二叉树●树中每一层都含有最多的结点●完全二叉树●高度为h,有n个结点的二叉树,当且仅当,每个结点都与高度为h的满二叉树中的编号一一对应●二叉排序树●用途:可用于元素的排序、搜索●左子树上所有结点的关键字均小于根结点的关键字;右子树上所有结点的关键字均大于根结点的关键字;左子树和右子树又是一棵二叉排序树●二叉树的性质●非空二叉树上的叶子结点数等于度为2的结点树加1,即n0=n2+1●非空二叉树上第k层至多有2^(k-1)个结点●高度为h的二叉树至多有2^h-1个结点●具有n个结点的完全二叉树的高度为log2(n+1)取顶或者log2n取底+1●二叉树的存储结构●顺序存储结构●只适合存储完全二叉树,数组从0开始●链式存储结构●顺序存储的空间利用率太低●至少三个指针域:数据域、左指针域、右指针域●增加了指向父结点后,变为三叉链表的存储结构●在含有n个结点的二叉链表中,含有n+1个空链域●二叉树的遍历和线索二叉树●二叉树的遍历●先序遍历●根左右●应用:求树的深度●中序遍历●左根右●后序遍历●左右根●应用:求根到某结点的路径、求两个结点的最近公共祖先等●三个遍历时间复杂度都是O(n)●递归算法和非递归算法的转换●层次遍历●需要借助队列●步骤●二叉树根结点入队,然后出队,访问出队结点,若有左子树,左子树根结点入队●遍历右子树,有右子树,右子树根结点入队。
数据结构(朱战立)章 (7)

7.1 树
7.1.1 树的定义 树是由n(n≥0)个结点构成的集合。 n=0的树称为空树;
对n>0的树T有: (1) 有一个特殊的结点称为根结点, 根结点没有前驱结点;
3
(2) 当n>1时, 除根结点外其他结点被分成m(m>0)个互不相 交的集合T1, T2,…, Tm, 其中每一个集合Ti(1≤i≤m)本身又 是一棵结构和树类同的子树。
10
7.1.2 树的表示方法 树的表示方法主要有三种, 分别用于不同的用途。 1. 直观表示法 图7 - 1就是一棵以直观表示法表示的树。 树的直观表示法
主要用于直观描述树的逻辑结构。 2. 形式化表示法 树的形式化表示法主要用于树的理论描述。 树的形式化表
示法定义树T为T=(D,R),其中D为树T中结点的集合, R为树T 中结点之间关系的集合。 当树T为空树时D=∅; 当树T不为空树 时有
5ቤተ መጻሕፍቲ ባይዱ
下面介绍树的其他一些常用术语。 结点: 由数据元素和构造数据元素之间关系的指针组成。 例如, 在图7 - 1(a)中有1个结点, 图7 - 1(b)中有12个结点。 结点的度: 结点所拥有的子树的个数称为该结点的度。 例 如, 在图7 - 1(b)中结点A的度为3, 结点B的度为2, 结点J的 度为0。 叶结点: 度为0的结点称为叶结点, 叶结点也称作终端结 点。 例如, 在图7 - 1(b)中结点J,F,K,L,H,I均为叶结点。
6
分支结点: 度不为0的结点称为分支结点, 分支结点也称 作非终端结点。 显然, 一棵树中除叶结点外的所有结点都是分 支结点。
孩子结点: 树中一个结点的子树的根结点称作这个结点的 孩子结点。 例如, 在图7 - 1(b) 中结点B,C,D是结点A的孩 子结点。 孩子结点也称作后继结点。
自考软件基础(数据结构--树与二叉树)

B
C
D
E
F
G
H
I
J
第 5 /209页
第二节 二叉树
一、定义
南昌大学
二叉树是一种重要的树形结构,它的特点是:二叉树可以为空(节点个
数为0),任何一个节点的度都小于或等于2,并且,子树有左、右之分,
其次序不能任意颠倒。 二叉树有5种基本形态,如图10-2所示。
第 6 /209页
第二节 二叉树
南昌大学
struct node
{ datatype data; struct node *Lchild,*rchild:
};
第 15 /209页
第二节 二叉树
南昌大学
例10-5 写出图10-8a所示二叉树的链式存储结构。其链式结构如图10-8b 所示。可以看出:具有n个节点的二叉树链式存储共有2n个链,其中只 有n-1个用来存放该节点的左、右孩子,其余的n +1个指针域为空。
解:第一步:由后序遍历结果确定整个二叉树根为A,由中序结果确定
A的左、右子树。 后序遍历结果: 中序遍历结果:
第 24 /209页
第三节 二叉树的遍历
第二步:确定A的左子树。 1)后序遍历结果:
南昌大学
中序遍历结果:
2)确定B的右子树: ①后序遍历结果:
第 25 /209页
第三节 二叉树的遍历
②中序遍历结果:
南昌大学
第 9 /209页
第二节 二叉树
下面介绍两种特殊的二叉树。
南昌大学
(1) 满二叉树指深度为k,且有2k-1个节点的二叉树。或者说除叶子节点外,
其它节点的度都为2的二叉树。
(2) 完全二叉树一个满二叉树的最下层从右向左连续缺少n (n>=0)个节点 的二叉树。 图10-3为满二叉树和完全二叉树示例。
树与二叉树哈夫曼树教案

树与二叉树哈夫曼树教案一、教学目标1. 了解树(Tree)和二叉树(Binary Tree)的概念;2.掌握树和二叉树的基本结构和操作;3. 理解哈夫曼树(Huffman Tree)的概念和应用;4.能够通过给定的数据构建哈夫曼树,并进行编码和解码操作。
二、教学内容1.树与二叉树1.1树的定义和基本术语1.2树的表示和操作1.3二叉树的定义和遍历方式1.4二叉树的应用示例2.哈夫曼树2.1哈夫曼树的定义和应用2.2构建哈夫曼树的算法2.3哈夫曼编码和解码的实现三、教学步骤与方法1.导入新知识通过提问与学生讨论,引导学生了解树与二叉树的概念,及其在现实生活中的应用场景。
2.介绍树与二叉树2.1形式化定义树的相关概念,如根节点、子节点、叶子节点等。
2.2介绍二叉树的相关概念,如二叉树的性质、三种遍历方式等。
3.树与二叉树的应用示例通过实际例子演示树与二叉树的应用,如目录结构、表达式求值等。
4.引入哈夫曼树4.1介绍哈夫曼树的概念和应用场景,如数据压缩。
4.2讲解构建哈夫曼树的算法,包括选择最小权值节点等。
4.3演示哈夫曼编码和解码的实现,让学生理解哈夫曼编码的原理和过程。
5.练习与巩固在课堂上进行与树、二叉树和哈夫曼树相关的练习,巩固学生对所学内容的理解。
6.小结与作业布置对本节课所学内容进行小结,并布置相关作业,让学生进行巩固和深化学习。
四、教学资源1. PowerPoint或电子白板2.示例代码和编程环境,用于演示和实践3.相关课堂练习题目和解答五、教学评估1.课堂练习表现评估,包括对树、二叉树和哈夫曼树的理解和应用能力;2.作业和实践项目的结果评估,包括构建哈夫曼树和实现哈夫曼编码的准确性和效率。
六、教学扩展1.拓展相关概念和应用,如平衡二叉树、B树等;2.引导学生进行更深层次的研究和实践,如自定义数据结构、更复杂的压缩算法等。
数据结构第三版第七章作业参考答案
//栈指针置初值
do { while (t)
//将 t 的所有左结点进栈
{ top++;
St[top]=t;
t=t->lchild;
} p=NULL; flag=1; while (top!=-1 && flag)
//p 指e当前结点的前一个已fg
的
结
点
//h置 t 的fgij为已fg过
{ t=St[top]; if (t->rchild==p) { if (t==s)
7.1 设二叉树 bt 的一种存储结构如下:
1 2 3 4 5 6 7 8 9 10 lchild 0 0 2 3 7 5 8 0 10 1 data j h f d b a c e g i rchild 0 0 0 9 4 0 0 0 0 0
其中,bt 为树根结点指针,lchild、rchild 分别为结点的左、右孩子指针域,
Ctree(t->lchild,A,2*i);
//递归构造*t 的左子树
Ctree(t->rchild,A,2*i+1); //递归构造*t 的右子树
}
}
7.5 设计一个算法,将一棵以二叉链方式存储的二叉树 t 按顺序方式存储到数组 A 中。
解:由二叉树的顺序存储方式可知本题的递归模型f()如下:
f(t,A,i):A[i]=' ';
//顺序队首尾指针 //cm=1 表示二叉树为完全二叉树 //bj=1 表示到目前为止所有结点均有左右孩子
if (b!=NULL)
{ rear++;
Qu[rear]=b;
while (first!=rear) { first++;
第7章树和二叉树(4)-数据结构教程(Java语言描述)-李春葆-清华大学出版社

if (p.node.rchild!=null)
//有右孩子时将其进队
qu.offer(new QNode(p.lno+1,p.node.rchild));
}
}
return cnt;
}
7/31
解法2
层次遍历中某层的最右结点last
last
A
B
C
D
EF
G
last的作用确定一层是否遍历完成!
8/31
用cnt变量计第k层结点个数(初始为0)。设计队列仅保存结点引用, 置当前层次curl=1,用last变量指示当前层次的最右结点(根结点)进队。 将根结点进队,队不空循环:
int curl=1;
//当前层次,从1开始
BTNode<Character> last;
//当前层中最右结点
last=bt.b;
//第1层最右结点
qu.offer(bt.b);
//根结点进队
while (!qu.isEmpty())
{ if (curl>k) return cnt; p=qu.poll(); if (curl==k) cnt++; if (p.lchild!=null) { q=p.lchild; qu.offer(q); } if (p.rchild!=null) { q=p.rchild; qu.offer(q); } if (p==last) { last=q; curl++; }
}
Queue<QNode> qu=new LinkedList<QNode>(); //定义一个队列qu
QNode p;
qu.offer(new QNode(1,bt.b)); //根结点(层次为1)进队
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3/50
2次树是度为2的树,至少有3个结点;二叉树的结点个数可以为0。 2次树中度为1的结点的孩子不分左、右孩子;而二叉树中度为1 的结点的孩子需要区分左、右孩子。
4/50
两种特殊的二叉树
满二叉树:在一棵二叉树中: 如果所有分支结点都有双分结点; 并且叶结点都集中在二叉树的最下一层。
① 二叉树中所有非叶结点的度数都为2的二叉树是满二叉树(错);
② 一个高度为h的满二叉树中,只在h层有叶结点,而且每一个非叶子结点都
是满的,是满二叉树(对)。
6/50
完全二叉树:在一棵二叉树中:
最多只有下面两层的结点的度数小于2 并且最下面一层的叶结点都依次排列在该层最左边的位置上。
1
A
2
B
4
D
16/50
1、森林、树转换为二叉树
A
一
颗 树
B
C
D
转
换
E
F
G
为
二
叉
H
树
长子关系转换为左孩子关系 兄弟关系转换为右孩子关系
A B
C
E
D
F
H
G
对应的二叉树
17/50
A
E
G
B
C
D
F
H
I
多
颗
A
G
树
转
换
B
E H
为 一
C
F
I
颗
D
二 叉
A
树
B
E
C
F
D
对应的二叉树
G H
I
18/50
或者
A
E
B
C
D
F
G
H
I
按一颗树的方法转换,再删除增加的结点
二叉树抽象数据类型 = 逻辑结构 + 基本运算
37/50
将二叉树的二叉链结点类型及其基本运算函数存储在btree.cpp文件中
应用示例
创建以下二叉树的二叉链存储结构b: 求其高度 查找是否存在'F'结点
A
B
C
D
E
F
G
38/50
B D
G
A C
E
F
A(B(D(,G)),C(E,F))
b A
B∧
C
∧D
2、二叉树还原为森林、树
将
A
一
棵 二
B
叉
树 还
C
D
原
为E
F
G
H
一
棵
树
A
B
D
H
C E
F
G
还原的树
左孩子关系恢复为长子关系 右孩子关系恢复为兄弟关系
22/50
将 一
A
棵
二 叉
B
E
树
还
C
F
G
原
为 多
D
H
棵 树
I
A
B C D
E
F G
H I
转 换 为 棵 二 叉 树
23/50
3
A
B C D
E
F G
H I
A
B
C
D
还
E
原
为
3
F
棵 树
G
H
I
24/50
示例
高度为3的满二叉树B,将其还原为森林T,其中包含根结点的那棵树 中必定有( )结点。
A.1
B.2
C.3
D.4
答案为D。
25/50
示例
设x是树T中的一个非根结点,B是T所对应的二叉树。在B中,x是其双亲结 点的右孩子,下列结论正确的是( )。
A.在树T中,x是其双亲的第一个孩子 B.在树T中,x一定无右边兄弟 C.在树T中,x一定是叶子结点 D.在树T中,x一定有左边兄弟
完全二叉树的叶子结点只能在最下两层,对于本题,结点最多的情况是第6 层为倒数第二层,即1~6层构成一个满二叉树,其结点总数为26-1=63。
其中第6层有25=32个结点,含8个叶子结点,则另外有32-8=24个非叶子结 点,它们中每个结点有两个孩子结点(均为第7层的叶子结点),计48个叶 子结点。这样最多的结点个数=63+48=111。
printf("b的高度: %d\n",BTHeight(b));
p=FindNode(b,'F');
if (p!=NULL)
printf("b中存在F结点\n");
else
printf("b中不存在F结点\n");
DestroyBTree(b);
}
40/50
(2)销毁二叉链DestroyBTree(*b)
答案为C。
15/50
示例
一棵完全二叉树中有8个叶子结点,则高度至多是( )。
A.3
B.4
C.5 D.不确定
该完全二叉树,n0=8,n2=n0-1=7,则n=n0+n1+n2=15+n1。 完全二叉树中n1=0或n1=1,则n1=1时结点个数最多,此时n=16。 最大高度h=log2(n+1)=5。 答案为C。
当n确定时,n0、n1、n2都是确定的,其树形也可以确定! h=log2(n+1)或者log2n+1
14/50
示例
已知一棵完全二叉树的第6层(设根为第1层)有8个叶子结点,则该完全 二叉树的结点个数最多是( )。
A. 39
B. 52
C. 111
D. 119
2009年全国计算机专业硕士学位研究生考试题目
示例
设一棵二叉树B是由森林T转换而来的,若T中有n个非叶子结点,则二
叉树B中无右孩子的结点个数为( )。
A.n-1
B.n
C.n+1
D.n+2
T中每个非叶子结点一定有一个最右孩子x(只有
一个孩子结点x时,x就是最右孩子)。
n
在转换的B中,x一定无右孩子。
T的根结点在B中一定无右孩子。
1
答案为C。
21/50
2i
2i+1
31/50
借鉴树的孩子链存储结构 二叉树的链式存储结构。 在二叉树的链式存储中,结点的类型声明如下:
typedef struct node { ElemType data;
struct node *lchild, *rchild; } BTNode;
指向的都是二叉树:递归性
32/50
5
E
8
9
10
11
H
I
J
K
6
F
3
C
7G
满的
完全二叉树实际上是对应的满二叉树删除叶结点层最右边若干个结点得到的。
7/50
性质1 非空二叉树上叶结点数等于双分支结点数加1。即:n0=n2+1。
A
B
C
D
E
F
G
度之和=分支数 分支数=n-1 nn2
n0+n1+n2-1=n1+2n2
二叉树是有限的结点集合。
递归 定义
这个集合或者是空。
或者由一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。
1/50
二叉树的5种基本形态: 空树
只含根结点
N
右子树为空树
N
左子树为空树
N
左右子树均 不为空树
N
L
R
L
R
2/50
二叉树是可以采用树的逻辑结构表示法,其4种表示法如下: 树形表示法 文氏图表示法 凹入表示法 括号表示法
}
}
42/50
(3)查找结点FindNode(*b,x)
设f(b,x)在二叉树b中查找值为x的结点(唯一)。找到后返回其指针, 否则返回NULL。
A.16
B.18
C.20
D.30
n2=7, n1=5 n0=n2+1=8 结点总数n=n0+n1+n2=20。 答案为C。
10/50
性质2 非空二叉树上第i层上至多有2i-1个结点(i≥1)。 由树的性质2可推出。
性质3 高度为h的二叉树至多有2h-1个结点(h≥1)。 由树的性质3可推出。
11/50
10
8
9
11
12 13 14
顺
#
#
#
##
#F
序
存
储
结
构
1 2 3 4 5 6 7 8 9 10 11 12 13 14
ABD#C#E######F
typedef ElemType SqBTree[MaxSize]; SqBTree bt="#ABD#C#E######F";
用一个数组存储
30/50
二叉树顺序存储结构的特点:
4
56
7
二
D
E
F
G
叉
树
8
9
10
11
的
H
I
J
K
顺
序
存
储
结
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
构
ABCDEFGHIJK####
顺序存储结构(不用下标为0的元素)
29/50
1
A
一般的二叉树先用空结
点补全成为完全二叉树,
2
非
B
3
D
然后对结点编号
完
全
4
5
6
7
二
