matlab的FFT函数介绍
matlab中的傅里叶变换

matlab中的傅里叶变换Matlab中的傅里叶变换是一种数学工具,用于将一个信号从时域转换到频域。
它是一种广泛应用于信号处理、图像处理、通信系统等领域的重要技术。
在Matlab中,傅里叶变换可以通过内置函数fft和ifft来实现。
fft函数用于计算离散傅里叶变换(DFT),而ifft函数用于计算离散傅里叶逆变换(IDFT)。
傅里叶变换在Matlab中的使用步骤如下:1. 准备信号数据,将待变换的信号存储在一个向量中,可以是时间域的信号序列。
2. 应用fft函数,使用fft函数对信号进行傅里叶变换,得到频域表示。
3. 可选操作,对频域表示进行幅度谱和相位谱的计算,以及其他的频谱分析操作。
4. 应用ifft函数,如果需要,可以使用ifft函数对频域表示进行逆变换,将信号恢复到时域。
需要注意的是,傅里叶变换得到的频域表示是对称的,通常只需要使用一半的频域数据进行分析。
此外,Matlab中还提供了其他相关的函数,如fftshift和ifftshift,用于对频域数据进行平移操作。
傅里叶变换在信号处理中有广泛的应用,例如:1. 频谱分析,可以通过傅里叶变换将信号从时域转换到频域,进而分析信号的频谱特性,如频率成分、频谱密度等。
2. 滤波器设计,可以在频域上设计滤波器,通过傅里叶变换将滤波器的频率响应转换到时域,实现对信号的滤波操作。
3. 图像处理,可以利用傅里叶变换对图像进行频域滤波、图像增强等操作,如去除噪声、边缘检测等。
总结起来,Matlab中的傅里叶变换是一种强大的信号处理工具,通过将信号从时域转换到频域,可以实现频谱分析、滤波器设计、图像处理等应用。
matlab 快速傅里叶变换

快速傅里叶变换(Fast Fourier Transform,FFT)是一种在数字信号处理和数值分析中广泛应用的算法,它能够高效地计算离散傅里叶变换(Discrete Fourier Transform,DFT),从而在频域中分析信号的频谱特性。
而在matlab中,使用FFT函数可以方便地进行快速傅里叶变换的计算和处理。
1. FFT的基本原理在介绍matlab中的FFT函数之前,我们先来了解一下FFT的基本原理。
FFT算法是一种分治法的思想,在计算傅里叶变换时通过将原始信号分解为奇偶部分,然后递归地进行计算,最终得到傅里叶变换的结果。
这种分治的思想使得FFT算法的计算复杂度降低到了O(n log n),比直接计算DFT的O(n^2)复杂度要低很多,因此在实际应用中得到了广泛的应用。
2. matlab中的FFT函数在matlab中,可以使用fft函数来进行快速傅里叶变换的计算。
fft函数的基本语法如下:```Y = fft(X)```其中,X表示输入的信号序列,可以是实数或复数序列;Y表示经过FFT变换后得到的频谱结果。
在使用fft函数时,最常见的是对时域信号进行FFT变换,然后得到其频谱特性。
3. FFT在信号处理中的应用FFT算法在信号处理中有着广泛的应用,其中最常见的就是对信号的频谱特性进行分析。
通过对信号进行FFT变换,可以得到其频谱图,从而可以直观地了解信号的频域特性,包括频率成分、幅度特性等。
这对于音频处理、振动分析、通信系统等领域都是非常重要的。
4. FFT在图像处理中的应用除了在信号处理中的应用,FFT算法也在图像处理中有着重要的地位。
在图像处理中,FFT可以用来进行频域滤波,包括低通滤波、高通滤波、带通滤波等操作。
通过FFT变换,我们可以将图像从空域转换到频域,在频域中进行滤波操作,然后再通过逆FFT变换将图像恢复到空域,从而达到图像增强、去噪等效果。
5. FFT在数学建模中的应用除了在信号处理和图像处理中的应用外,FFT算法还在数学建模和仿真计算中有着重要的作用。
matlab的fft函数用法

matlab的fft函数用法MATLAB中的fft函数用于计算快速傅里叶变换(FFT)。
FFT是一种将信号从时域转换为频域的方法,常用于信号处理、图像处理等领域。
在本文中,我将一步一步回答有关MATLAB中fft函数的使用方法。
一、基本语法在MATLAB中,fft函数的基本语法如下:Y = fft(X)其中,X是要进行FFT的向量或矩阵,输出结果Y是X的离散傅里叶变换的向量或矩阵。
二、一维FFT首先我们来看一维FFT的使用方法。
假设有一个长度为N的一维向量x,我们将对其进行FFT变换并得到变换结果y。
1. 创建输入向量首先,我们需要创建一个长度为N的向量x,作为FFT的输入。
可以通过以下代码实现:N = 1024; % 向量长度x = randn(N, 1); % 创建长度为N的随机向量2. 进行FFT变换接下来,我们使用fft函数对向量x进行FFT变换,代码如下:y = fft(x);3. 可视化结果为了更好地理解和分析FFT结果,通常会对结果进行可视化。
我们可以使用MATLAB的绘图函数来绘制FFT结果的幅度和相位谱。
例如,可以使用如下代码绘制幅度谱:f = (0:N-1)./N; % 频率轴amp = abs(y); % 幅度谱figure;plot(f, amp);xlabel('Frequency (Hz)');ylabel('Amplitude');title('Amplitude Spectrum');同样,可以使用如下代码绘制相位谱:phase = angle(y); % 相位谱figure;plot(f, phase);xlabel('Frequency (Hz)');ylabel('Phase');title('Phase Spectrum');三、二维FFT除了一维FFT,MATLAB中的fft函数还支持二维FFT。
matlab实现傅里叶变换

matlab实现傅里叶变换傅里叶变换是一种将一个连续时间函数(或离散时间函数)分解成基函数的超级工具。
它的用途非常广泛,例如在信号处理、音频处理、图像处理、机器学习等领域都有重要的应用。
在这篇文章中,我将介绍使用 MATLAB 实现傅里叶变换的基本步骤。
一、MATLAB 傅里叶变换函数在 MATLAB 中,我们可以使用 fft 函数实现傅里叶变换。
FFT 表示快速傅里叶变换,是一种高效的算法,可以在很短的时间内计算出信号的频域表示。
下面是 fft 函数的基本语法:X = fft(x)其中 x 是输入信号,X 是输出信号的频域表示。
由于傅里叶变换是一个复杂的计算过程,输入信号需要满足一些条件。
这些条件将在下一节中讨论。
在进行傅里叶变换之前,我们需要确保输入信号满足一些条件,以便 fft 函数可以正确地执行。
这些条件包括以下要求:1. 信号长度为 2 的正整数次幂在傅里叶变换中,信号长度通常是 2 的正整数次幂,例如 2、4、8、16、32 等等。
如果信号长度不是 2 的正整数次幂,则 fft 函数将自动进行填充。
2. 离散时间信号需要零填充如果输入信号是离散时间信号,我们需要使用零填充的方法将信号长度补齐至 2 的正整数次幂。
例如,如果我们的离散时间信号包含 100 个样本,我们需要将其补齐至128 个样本(下一个最小的 2 的正整数次幂)。
3. 连续时间信号需要采样如果输入信号是连续时间信号,我们需要对其进行采样,以便将其转换为离散时间信号。
采样频率需要高于信号的最高频率,这样才能避免混叠现象的发生。
下面是一个简单的示例,其中我将展示如何使用 MATLAB 实现傅里叶变换。
假设我们有一个正弦波信号,频率为 10 Hz,并将其采样为 100 个样本。
我们可以定义该信号如下:Fs = 100; % 采样频率T = 1/Fs; % 采样周期L = 100; % 信号长度t = (0:L-1)*T; % 时间向量f = 10; % 信号频率x = sin(2*pi*f*t); % 正弦波信号我们可以使用 plot 函数绘制该信号:plot(t,x)xlabel('Time (s)')ylabel('Amplitude')title('Original Signal')现在我们可以将该信号传递给 fft 函数,并将频域表示存储在 X 变量中:由于傅里叶变换输出的是一个复数数组,因此我们需要使用 abs 函数计算幅度谱并将其绘制出来:P2 = abs(X/L);P1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = Fs*(0:(L/2))/L;plot(f,P1)xlabel('Frequency (Hz)')ylabel('Amplitude')title('Frequency Spectrum')幅度谱显示了信号在频域中的分布情况,显示了信号的频率成分及其振幅。
matlab的fft函数

matlab的fft函数FFT(快速傅里叶变换)是一种分析和处理信号的有效方法,可以将时间域信号转换为频域信号,使得分析和处理信号更加容易。
它也被广泛应用于图像处理、语音识别、雷达信号处理、数字信号处理等领域。
为了简化信号处理的工作,MATLAB(Matrix Laboratory)提供了一系列的FFT函数,可以方便地实现FFT的转换,节省了开发者大量的编程时间。
fft函数是MATLAB中最常用的一个函数,它可以将时域的时间序列转换为频域的频谱序列。
它的原理是,通过从时域信号中提取其中的频率变化特性,并将其转换为频域序列。
用户可以将原始信号分解为多个正弦波,并根据各个正弦波的频率和振幅大小,反映出原始信号的特性。
MATLAB中的FFT函数可以分为两类:实数FFT函数和复数FFT 函数。
实数FFT函数用于对实数数据进行频率分析,复数FFT函数用于对复数数据进行分析,也可以处理实数数据。
实数FFT函数主要包括fft()函数和fftshift()函数,fft ()函数用于实现零频率在数组首部,fftshift()函数用于将零频率移到中间位置。
复数FFT函数包括fft2()、fftn()和ifftn(),其中fft2()函数用于实现2维FFT变换,fftn()函数用于实现n维FFT 变换,ifftn()函数用于实现反变换。
FFT函数还可以实现信号的加窗处理,加窗处理可以改善信号的波形和减少信号的噪声。
MATLAB提供了一系列的窗函数,包括rectwin()、hann()、hamming()、blackman()等窗函数,用户可以在代码中进行任意组合,来调整信号的波形。
此外,FFT函数还可以实现各种滤波和数字信号处理算法,如频率响应、采样、模拟数字转换、滤波、声音处理、语音识别、脉冲响应特性等等。
FFT函数在MATLAB编程中是一个强大而实用的功能,它可以简化信号处理的工作,使用者可以通过FFT函数完成复杂的信号处理算法。
MATLAB中FFT使用详解

MATLAB中FFT使用详解一.调用方法X=FFT(x);X=FFT(x,N);x=IFFT(X);x=IFFT(X,N)用MA TLAB进行谱分析时注意:(1)函数FFT返回值的数据结构具有对称性。
例:N=8;n=0:N-1;xn=[4 3 2 6 7 8 9 0];Xk=fft(xn)→Xk =39.0000-10.7782 + 6.2929i0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i0 + 5.0000i -10.7782 - 6.2929iXk与xn的维数相同,共有8个元素。
Xk的第一个数对应于直流分量,即频率值为0。
(2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。
要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。
二.FFT应用举例例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。
采样频率fs=100Hz,分别绘制N=128、1024点幅频图。
clf;fs=100;N=128;%采样频率和数据点数n=0:N-1;t=n/fs;%时间序列x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N);%对信号进行快速Fourier变换mag=abs(y);%求得Fourier变换后的振幅f=n*fs/N;%频率序列subplot(2,2,1),plot(f,mag);%绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=128');grid on;%对信号采样数据为1024点的处理fs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号y=fft(x,N);%对信号进行快速Fourier变换mag=abs(y);%求取Fourier变换的振幅f=n*fs/N;subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;subplot(2,2,4)plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz');ylabel('振幅');title('N=1024');grid on;运行结果:fs=100Hz,Nyquist频率为fs/2=50Hz。
matlab的stft的fft函数的原理

在MATLAB中,STFT(短时傅里叶变换)是一种信号分析技术,可以将时域信号分解为频谱随时间变化的小片段。
在STFT中,FFT(快速傅里叶变换)函数被用于计算每个时间窗口上的频谱。
FFT是一种高效的算法,用于计算离散傅里叶变换(DFT)。
它将时域信号转换为频域信号,从而提供了信号的频谱信息。
STFT的基本思想是将长时间信号分割成多个短时间窗口,并对每个窗口应用FFT来获取该窗口上的频谱。
这样可以在时间和频率上同时分析信号。
下面是MATLAB中STFT函数的基本原理:
1.首先,使用一个窗口函数对输入信号进行分帧处理。
常见的窗口函数有汉明窗、黑曼窗
等,它们能够减少分析过程中的频谱泄漏。
2.对每个窗口应用FFT来计算其频谱。
FFT计算得到的结果是一个复数数组,其中包含信
号的实部和虚部。
3.可以通过对FFT结果进行幅度谱或功率谱的计算来获得窗口的频谱信息。
幅度谱是FFT
结果的绝对值,表示信号的频率成分的强度。
功率谱是幅度谱的平方,表示信号的频率成分的能量。
4.重叠相加:为了获得更平滑的频谱估计,通常会将相邻窗口的频谱进行重叠相加。
这可
以通过在窗口之间应用一些重叠和加窗技术来实现。
常见的重叠比例是50%或75%。
5.最后,可以对重叠相加后的频谱应用其他处理技术,如谱修剪、谱平滑等,以得到更好
的频谱表示。
总结起来,MATLAB中STFT函数使用FFT来计算每个时间窗口上的频谱,并通过重叠相加和其他处理技术来获取信号的短时频谱表示。
MATLAB中FFT函数理解

MATLAB中FFT函数理解2010-09-06 12:15matlab的FFT函数相关语法:Y = fft(X)Y = fft(X,n)Y = fft(X,[],dim)Y = fft(X,n,dim)定义如下:相关的一个例子:Fs = 1000; % 采样频率T = 1/Fs; % 采样时间L = 1000; % 总的采样点数t = (0:L-1)*T; % 时间序列(时间轴)%产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz的正弦信号x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);y = x + 2*randn(size(t)); % 混入噪声信号plot(Fs*t(1:50),y(1:50)) %画出前50个点title('Signal Corrupted with Zero-Mean Random Noise')xlabel('time (milliseconds)')NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)% 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1.plot(f,2*abs(Y(1:NFFT/2+1)))title('Single-Sided Amplitude Spectrum of y(t)')xlabel('Frequency (Hz)')ylabel('|Y(f)|')主要有两点注意的地方:1、从公式上看,matlab 的fft 序号是从1到N,但是绝大多数教材上是从0到N-1。
matlab的fft函数写法

matlab的fft函数写法
在MATLAB中使用FFT函数的一般语法格式是:
Y = fft(X)
Y = fft(X,n)
Y = fft(X,n,dim)
Y = fft(X,[],dim)
其中:
- X是要进行FFT变换的向量或矩阵。
- n是FFT变换的长度,可选参数。
如果没有指定n参数,则使用一些默认值进行计算。
如果n小于X的长度,则对X进行裁剪。
如果n大于X的长度,则在X的末尾添加零以达到n的长度。
- dim是指明在哪个维度上进行FFT变换的维度,可选参数。
可以是1或2(仅适用于矩阵)。
如果未指定dim,则默认值为第一个非单一维度。
- 通过指定空方括号[]作为n参数的值,可以使用默认值进行计算。
例如:
- 对一个长度为N的列向量X进行FFT变换,可以写成:Y = fft(X);
- 对一个长度不超过N1*N2的矩阵X的每一列进行FFT变换,可以写成:Y =
fft(X,[],1);
- 对一个长度不超过N1*N2的矩阵X的每一行进行FFT变换,可以写成:Y = fft(X,[],2);。
matlab中fft函数的用法

matlab中fft函数的用法
Matlab的fft函数是一种快速傅立叶变换,它将输入的信号从时
域变换到频域,即显示出信号的频率谱。
该函数有三种不同的用法:
1. 一维FFT:Y = fft(X)
一维FFT函数用于实现从时域信号X到频域的变换,生成对应的
复数频谱信号Y,即$Y=DFT\{X\}$。
X可以是一维实数或复数数组,也
可以是一个数组或矩阵,返回变换后的Y值是一个复数矩阵,其中虚
部表示相位,实部表示幅度。
2. 二维FFT:Y = fft2(X)
二维FFT函数用于实现从时域信号X到频域的变换,生成复数频
谱信号Y,即$Y=DFT\{X\}$。
X可以是实数或复数矩阵,返回变换后的
Y值是一个复数矩阵,其中虚部表示相位,实部表示幅度。
3. 多维FFT:Y = fftn(X)
多维FFT函数用于实现从时域信号X到频域的变换,生成复数频
谱信号Y,即$Y=DFT\{X\}$。
X可以是实数或复数的多维数组,返回值
是一个复数矩阵,其中虚部表示相位,实部表示幅度。
Matlab中的FFT函数很容易使用,只需要输入X参数,就能返回
变换后的Y值,而且支持一维、二维和多维FFT变换。
使用FFT函数,可以轻而易举地实现从时域到频域的变换,从而更好地理解信号的特性。
matlab中fft函数的用法及关键问题详解

MATLAB中的FFT函数用于计算一维和多维数组的离散傅里叶变换(DFT)及其逆变换。
以下是一些FFT函数的用法和关键问题的详解:用法:1. 一维FFT:```matlabY = fft(X)```其中,X是输入的一维数组,Y是输出的频域表示。
2. 多维FFT:```matlabY = fft(X,N)```其中,X是输入的多维数组,N指定输出数组的大小。
3. 逆FFT:```matlabX = ifft(Y)```其中,Y是输入的频域表示,X是输出的时域表示。
4. 多维逆FFT:```matlabX = ifft(Y,N)```其中,Y是输入的频域表示,N指定输出数组的大小。
关键问题详解:1. 零填充:FFT函数在计算DFT时默认进行零填充。
如果输入数组的大小不是2的幂,则会自动将其扩展到最近的较大2的幂。
可以通过指定第二个参数来选择不同的填充长度。
例如,fft(X,N)将X扩展到N点进行计算。
2. 长度为N的输入数组的DFT具有N个复数输出,可以表示为N 个频率分量的幅度和相位。
在计算DFT时,需要确保输入数组的长度不超过2^16-1(约65535),否则会超出MATLAB的矩阵大小限制。
如果需要处理更大的数据,可以使用分段处理或降采样等技术。
3. FFT函数返回的是复数数组,表示每个频率分量的幅度和相位。
可以使用abs函数获取幅度,使用angle函数获取相位。
对于逆FFT,输出的是实数数组,表示时域信号的样本值。
4. FFT函数默认按照升序排列频率分量。
如果需要按照降序排列,可以使用fftshift函数将输出数组进行平移操作。
例如,Y = fftshift(fft(X))将输出数组Y按照降序排列频率分量。
5. FFT函数对于输入数据的顺序和布局方式有特定的要求。
对于多通道数据(例如,多路信号),需要按照一定的顺序和布局方式进行排列,以确保正确的计算结果。
可以使用MATLAB中的矩阵布局工具(如meshgrid)来帮助定义数据的位置坐标和采样间隔等参数。
MATLAB快速傅里叶变换(fft)函数详解

MATLAB快速傅⾥叶变换(fft)函数详解定义:M ATLAB帮助⽂件原⽂The 'i' in the 'Nth root of unity' 是虚数单位调⽤:1. Y = fft(y);2. Y = fft(y,N);式中,y是序列,Y是序列的快速傅⾥叶变换。
y可以是⼀向量或矩阵,若y为向量,则Y是y的FFT,并且与y具有相同的长度。
若y为⼀矩阵,则Y是对矩阵的每⼀列向量进⾏FFT。
说明:1. 函数fft返回值的数据结构具有对称性根据采样定理,fft能分辨的最⾼频率为采样频率的⼀半(即Nyquist频率),函数fft返回值是以Nyqusit频率为轴对称的,Y的前⼀半与后⼀半是复数共轭关系。
2. 幅值作FFT分析时,幅值⼤⼩与输⼊点数有关,要得到真实的幅值⼤⼩,只要将变换后的结果乘以2除以N即可(但此时零频—直流分量—的幅值为实际值的2倍)。
对此的解释是:Y除以N得到双边谱,再乘以2得到单边谱(零频在双边谱中本没有被⼀分为⼆,⽽转化为单边谱过程中所有幅值均乘以2,所以零频被放⼤了)。
3. 基频若分析数据时长为T,则分析结果的基频就是f0=1/T,分析结果的频率序列为[0:N-1]*f04. 执⾏N点FFT在调⽤格式2中,函数执⾏N点FFT。
若y为向量且长度⼩于N,则函数将y补零⾄长度N,若向量y的长度⼤于N,则函数截断y使之长度为N。
注意:使⽤N点FFT时,若N⼤于向量y的长度,将给频谱分析结果带来变化,应该特别注意。
例⼦:将对N点FFT进⾏举例,说明当N⼤于向量y的长度时给频谱分析带来的变化。
例图上图中,左列为信号时域图形,右列为对应信号的频谱图。
可以看出当N⼤于向量y的长度时,由于fft⾃动将100s后的信号值补零,原信号实际变为左下⾓的时域图形,所以频率发⽣了变化(增加多种频率的⼩振幅振动,主峰幅值被削弱)。
结论:使⽤N点FFT时,不应使N⼤于y向量的长度,否则将导致频谱失真。
matlab小波变换函数说明

matlab小波变换Matlab 1. 离散傅立叶变换的Matlab实现Matlab 函数fft、fft2 和fftn 分别可以实现一维、二维和N 维DFT 算法;而函数ifft、ifft2 和i fftn 则用来计算反DFT 。
这些函数的调用格式如下:A=fft(X,N,DIM)其中,X 表示输入图像;N 表示采样间隔点,如果X 小于该数值,那么Matlab 将会对X 进行零填充,否则将进行截取,使之长度为N ;DIM 表示要进行离散傅立叶变换。
A=fft2(X,MROWS,NCOLS)其中,MROWS 和NCOLS 指定对X 进行零填充后的X 大小。
别可以实现一维、二维和N 维DF TA=fftn(X,SIZE)其中,SIZE 是一个向量,它们每一个元素都将指定X 相应维进行零填充后的长度。
函数ifft、ifft2 和ifftn的调用格式于对应的离散傅立叶变换函数一致。
别可以实现一维、二维和N 维DFT例子:图像的二维傅立叶频谱1. 离散傅立叶变换的Matlab实现% 读入原始图像I=imread('lena.bmp');函数fft、fft2 和fftn 分imshow(I)% 求离散傅立叶频谱J=fftshift(fft2(I));figure;别可以实现一维、二维和N 维DFTimshow(log(abs(J)),[8,10])2. 离散余弦变换的Matlab 实现Matlab2.1. dct2 函数功能:二维DCT 变换Matlab格式:B=dct2(A)B=dct2(A,m,n)B=dct2(A,[m,n])函数fft、fft2 和fftn 分说明:B=dct2(A) 计算A 的DCT 变换B ,A 与 B 的大小相同;B=dct2(A,m,n) 和B=dct2(A, [m,n]) 通过对A 补0 或剪裁,使B 的大小为m×n。
2.2. dict2 函数功能:DCT 反变换格式:B=idct2(A)B=idct2(A,m,n)别可以实现一维、二维和N 维DFTB=idct2(A,[m,n])说明:B=idct2(A) 计算A 的DCT 反变换B ,A 与 B 的大小相同;B=idct2(A,m,n) 和B=idct 2(A,[m,n]) 通过对A 补0 或剪裁,使B 的大小为m×n。
MATLAB中fft函数用法、性质、特性、缺陷全面深入解析(含程序)
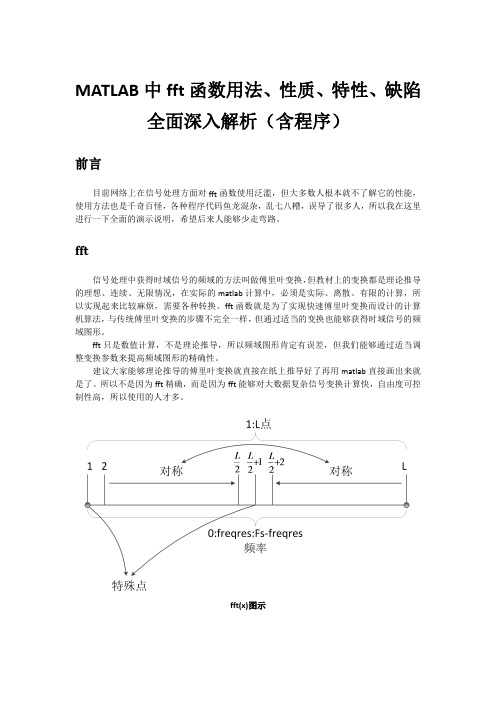
目前网络上在信号处理方面对 fft 函数使用泛滥,但大多数人根本就不了解它的性能, 使用方法也是千奇百怪,各种程序代码鱼龙混杂,乱七八糟,误导了很多人,所以我在这里 进行一下全面的演示说明,希望后来人能够少走弯路。
fft
信号处理中获得时域信号的频域的方法叫做傅里叶变换,但教材上的变换都是理论推导 的理想、连续、无限情况,在实际的 matlab 计算中,必须是实际、离散、有限的计算,所 以实现起来比较麻烦,需要各种转换。fft 函数就是为了实现快速傅里叶变换而设计的计算 机算法,与传统傅里叶变换的步骤不完全一样,但通过适当的变换也能够获得时域信号的频 域图形。
back=ifft(xdft); error=x-back; for i=2:length(xdft)/2
store(i)=abs(xdft(i))-abs(xdft(length(xdft)-i+2)); %这时的误差为 0, %store(i)=real(xdft(i+1))-real(xdft(length(xdft)-i+1)); %这时的误差为 0, %store(i)=imag(xdft(i+1))+imag(xdft(length(xdft)-i+1)); %这时的误差为 0,注意这时是加号
是正负对称的,所以幅度谱是完全对称的,但是这时候左右的正负频率是混叠的,这就是奈 奎斯特准则的限制,采样率要大于信号的最高频率才不会出现混叠,因此只有的频率是准确 可用的。然后是缺的几个特征点,在频率为 0,也就是第 1 个点的地方,频率虚部为 0,实 部为实际振幅值的两倍;在频率为,也就是点数为的地方,频率虚部为 0,实部为实际振幅 值的两倍;在频率为的地方,也就是超出了频率范围,那么这个点的频率值变为,与频率为 0 时的情况一致;同理,在频率为的地方,那么这个点的频率值变为,与前面的情况一致, 又是一个循环。横轴必须是以 Hz 单位进行转换。
matlab中fft函数转c

matlab中fft函数转c摘要:1.引言2.MATLAB 中的FFT 函数介绍3.FFT 函数在C 语言中的实现4.总结正文:1.引言MATLAB 是一款广泛应用于科学计算和数据分析的软件,其中的FFT 函数(快速傅里叶变换)是一个强大的工具,可以用于信号处理、图像处理等领域。
然而,对于一些嵌入式系统或者对运行速度有严格要求的场景,MATLAB 可能并不是最佳选择。
因此,将MATLAB 中的FFT 函数移植到C 语言中,可以更好地满足这些需求。
2.MATLAB 中的FFT 函数介绍在MATLAB 中,FFT 函数可以对一个信号进行快速傅里叶变换。
它的语法如下:```matlabY = fft(X)```其中,X 是需要进行变换的信号,Y 是变换后的结果。
FFT 函数默认对实数信号进行操作,如果需要对复数信号进行操作,可以添加参数`"complex"`。
此外,还可以指定变换的维度,例如对一维信号进行变换,可以添加参数`"length"`。
3.FFT 函数在C 语言中的实现为了在C 语言中实现FFT 函数,我们可以参考MATLAB 的FFT 实现算法,即蝶形算法。
下面是一个简单的C 语言实现:```c#include <stdio.h>#include <stdlib.h>#include <math.h>#include <complex.h>void fft_c(complex double *x, complex double *y, int n) {for (int k = 0; k < n; k++) {y[k] = x[k];for (int j = 0; j < n / 2; j++) {int m = (n / 2) * k + j;int p = (n / 2) * j + k;complex double t = cexp(-2.0 * I * M_PI * p / n) * y[m];y[m] = y[m] - t;y[p] = y[m] + t;}}}```这个函数接收两个复数数组x 和y,以及变换的维度n,然后对x 中的信号进行FFT 变换,并将结果存储在y 中。
matlab中对不是2的n次方个数求快速傅里叶变换

在MATLAB中,要对不是2的n次方个数进行快速傅里叶变换(FFT),需要进行一些额外的处理。
下面将从以下几个方面分别介绍。
1. 快速傅里叶变换(FFT)简介快速傅里叶变换是一种高效的计算傅里叶变换的方法,能够在计算机上快速地完成信号的频域分析。
FFT广泛应用于数字信号处理、图像处理、通信等领域。
在MATLAB中,可以使用fft函数进行快速傅里叶变换,该函数适用于长度为2的n次方的序列。
2. 对不是2的n次方个数进行FFT如果要对不是2的n次方个数进行FFT,可以通过以下几种方法进行处理:- 零填充:对长度为N的序列进行FFT时,可以将其零填充至长度为2的n次方,然后再进行FFT计算。
- 奇偶分解:将序列分解为奇数索引和偶数索引序列,分别对其进行FFT计算,然后再合并计算结果。
- 快速数论变换(NTT):对于一般长度的序列,可以考虑使用快速数论变换(NTT)等算法进行快速傅里叶变换。
3. MATLAB中对不是2的n次方个数进行FFT的实现在MATLAB中,可以通过编写自定义函数来实现对不是2的n次方个数进行FFT的功能。
以零填充为例,可以编写以下代码:```matlabfunction result = myFFT(data)N = length(data);M = 2^(nextpow2(N)); 找到大于N的最小的2的整数次方padded_data = zeros(1, M);padded_data(1:N) = data;result = fft(padded_data);end```4. 应用举例下面将通过一个具体的应用举例说明在MATLAB中对不是2的n次方个数进行FFT的方法。
假设有一个长度为5的序列[1, 2, 3, 4, 5],现在需要对其进行FFT计算。
可以使用上面编写的自定义函数myFFT进行计算,代码如下:```matlabdata = [1, 2, 3, 4, 5];result = myFFT(data);disp(result);```通过运行上述代码,就可以对长度为5的序列进行FFT计算,得到其频域表示。
matlab二维快速傅里叶变换

一、引言在信号处理、图像处理、通信系统等领域中,傅里叶变换是一种非常重要的数学工具,用于将时域信号转换为频域信号,从而方便进行频域分析和处理。
在实际应用中,对于二维信号(如图像)的频域分析同样具有重要意义。
Matlab作为一种功能强大的数学软件,提供了对二维信号进行快速傅里叶变换(FFT)的工具函数,为工程师和科研人员在二维信号处理中提供了便利。
二、快速傅里叶变换(FFT)简介1. 傅里叶变换傅里叶变换是将信号从时域(或空域)转换到频域的一种数学工具,可以通过计算信号的频谱来分析信号的频率成分。
傅里叶变换可以表达为积分形式或离散形式,其中离散形式的傅里叶变换又被称为离散傅里叶变换(DFT)。
2. 快速傅里叶变换(FFT)快速傅里叶变换是一种高效的计算离散傅里叶变换的算法,通过分治和逐级合并的方式将DFT的计算复杂度从O(N^2)降低到O(NlogN),大大加速了傅里叶变换的计算过程。
在二维信号处理中,二维快速傅里叶变换(2DFFT)同样具有重要的意义。
三、Matlab中的二维快速傅里叶变换1. 函数介绍在Matlab中,可以使用fft2函数对二维信号进行快速傅里叶变换。
fft2函数的语法为:```matlabY = fft2(X)```其中X为输入的二维数组,Y为X的二维快速傅里叶变换结果。
另外,Matlab还提供了ifft2函数用于计算二维逆傅里叶变换。
2. 使用方法对于一个MxN的二维数组X,可以通过调用fft2函数对其进行快速傅里叶变换。
例如:```matlab生成一个随机的二维数组X = randn(256,256);对X进行二维快速傅里叶变换Y = fft2(X);```通过调用fft2函数,可以得到输入数组X的二维快速傅里叶变换结果Y。
对于得到的频域信号Y,可以进行频域滤波、谱分析等操作,然后通过ifft2函数进行逆变换得到时域信号。
3. 示例下面以图像处理为例,演示在Matlab中如何使用二维快速傅里叶变换进行频域分析和滤波。
matlabfft函数用法

matlabfft函数用法FFT(Fast Fourier Transform)在Matlab中是一个非常常用的函数,用于对一个离散时间域信号进行频域分析。
在Matlab中,fft函数用于执行快速傅里叶变换。
下面将详细介绍Matlab中fft函数的用法。
1.FFT函数的语法:Y = fft(X)Y = fft(X,n)Y = fft(X,n,dim)其中,X表示输入的离散时间域信号,可以是一个向量或一个矩阵;n是可选参数,表示指定的FFT长度,默认为输入信号的长度;dim是可选参数,表示指定进行FFT的维度,默认为第一个非单例维。
2.FFT函数的输出:FFT函数的输出为一个复数矩阵,表示输入信号的频域表示。
输出矩阵的大小与输入信号的维度一致。
3.FFT函数的常用参数:-X:表示输入的离散时间域信号,可以是一个向量或一个矩阵。
- n:可选参数,表示指定的FFT长度,默认为输入信号的长度。
当输入信号的长度大于n时,fft函数会对输入信号进行截取;当输入信号的长度小于n时,fft函数会进行零填充。
- dim:可选参数,表示指定进行FFT的维度,默认为第一个非单例维。
-Y:输出的复数矩阵,表示输入信号的频域表示。
4.FFT函数的应用:FFT函数可用于频谱分析、滤波、信号压缩、波形合成等多个领域。
-频谱分析:通过FFT函数,可以将时域的信号转换为频域的信号,进而对信号的频谱进行分析。
可以通过查看频谱图,了解信号的频率成分和能量分布情况,从而判断信号的特性。
-滤波:在频域进行滤波是一种常用的滤波方法。
将信号转换到频域后,可以通过挑选特定的频率成分,来实现滤波操作。
例如,可以通过将除了感兴趣频率范围内的成分都置零,实现低通滤波或高通滤波。
-压缩信号:FFT可以用于对信号进行压缩。
通过去除信号中能量较低的频率成分,可以实现信号的压缩,减小信号所需存储的空间。
-波形合成:FFT函数可以将不同频率的信号成分合成一个复合波形。
matlab fft参数

matlab fft参数
Matlab中的fft函数具有以下参数:
1. x:输入向量或数组,存储时域信号。
可以是实数或复数。
2. n:FFT的长度。
如果n小于x的长度,则x被截断或者用零填充到n长度。
如果n大于x的长度,则x用零填充到n长度。
3. fs:采样频率,默认值为2*pi,表示一个周期内的样本数。
4. dim:指定进行FFT的维度,默认值为第一个非单例维度。
5. option:指定FFT的选项,可以是以下选项之一:
- 'none':不进行任何额外处理。
- 'centered':对FFT结果进行中心化。
奇数长度的序列将在演算中进行填充,并得到偶数长度的结果。
- 'scaled':对FFT结果进行归一化,使得结果的幅度不受FFT长度的影响。
6. 等等。
下面是一个使用fft函数的示例:
matlab
% 定义信号
x = [1 2 3 4];
% 计算FFT
X = fft(x);
% 打印结果
disp(X);
在上面的例子中,输入信号x是一个长度为4的向量。
fft函数会默认将其用零填充到长度为4的FFT,然后计算FFT结果X。
最后,使用disp函数打印结果X。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab的FFT函数
2010-04-26 22:16
相关语法:
Y = fft(X)
Y = fft(X,n)
Y = fft(X,[],dim)
Y = fft(X,n,dim)
定义如下:
相关的一个例子:
Fs = 1000; % 采样频率
T = 1/Fs; % 采样时间
L = 1000; % 总的采样点数
t = (0:L-1)*T; % 时间序列(时间轴)
%产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
y = x + 2*randn(size(t)); % 混入噪声信号
plot(Fs*t(1:50),y(1:50)) %画出前50个点
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')
NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)
f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)
% 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1.
plot(f,2*abs(Y(1:NFFT/2+1)))
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
PS:前段时间,只是为了自己看明白,没有管太多,刚才上空间发现几位的留言,感觉惭愧。
其实要掌握matlab中fft的用法,
主要有两点注意的地方:
1、从公式上看,matlab的fft序号是从1到N,但是绝大多数教材上是从0到N-1。
2、Y=fft(x)之后,这个Y是一个复数,它的模值应该除以(length(x)2),才能得到各个频率信号实际幅值。
