机械原理 第十章
《机械原理》第十章_平面机构的平衡
m1 r
Fb
泉城学院
单缸 曲轴
Fb Fb Fb Fbl Fb l
当 rb rb rb 时
l l rb mb rb mb mb mb rb mb rb mb rb mb l l rbl mb rbl mb l l rb mb rb mb mb mb l l
完全平衡或不完全平衡 由于机构各构件的尺寸 和质量完全对称,故在 运动过程中其总质心将 保持不动。 可得到很好的平衡效果
2Fh 2m 2 r cos
h 2Fh R14
2m 2 r cos mC 2 k cos
k m mC 2r
泉城学院
对称布置法
完全平衡 由于机构各构件的尺 寸和质量完全对称, 故在运动过程中其总 质心将保持不动。 可得到很好的平衡效 果
mC m3 m2C
2
l
C
C
平衡惯性力在曲柄加质量使得
pmC k pk m m m (m3 m2C ) r r mr mC k k e pa b m1 m2 pm3 r k l m 2 r cos mC 2 k cos Fh
l1 l1 m1 m1 m1 l l l2 l2 m2 m2 m2 m2 l l l3 l3 m3 m3 m3 m3 l l m1
泉城学院
rb m1 r1 m2 r2 m3 r3 0 mb rb m1 r1 m2 r2 m3 r3 0 mb
Fv m 2 r sin mC 2 k sin
h R14 Fh
机械原理第十章 标准齿轮与渐开线齿轮
h 1 或 h 0.8 基准
ha c ha m c m 顶隙系数 c 0.25 或 c 0.3
h ha hf 6. 齿顶圆直径 d a d 2ha 7. 齿根圆直径 d f d 2hf
8. 齿距
p m m 9. 齿厚 s 2 m 10.齿槽宽 e 2
标准齿轮 m、、h*a、c* (15或20)为标准值 且 e = s 几何尺寸计算公式 (P307表10-2)
si ri [(s r ) 2(invi inv )]
齿轮与齿条比较
4.标准齿条和内齿轮的尺寸 1、渐开线齿条的几何特点 (1)同侧齿廓为互相平行的直线。
(2)齿条齿廓上各点的压力角均相等,且数值上等
1渐开线齿条的几何特点分度线齿根线一渐开线齿轮的啮合过程理论啮合线段n齿廓工作段二正确啮合的条件保证前后两对轮齿有可能同时在啮合线上相切接触
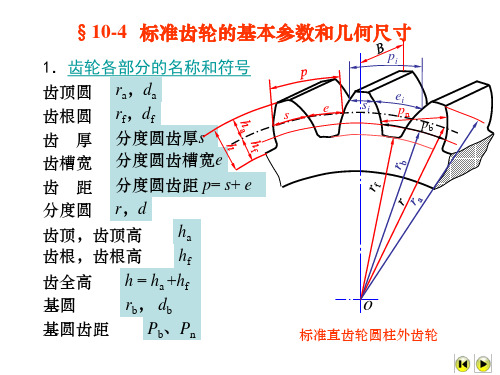
§10-4 标准齿轮的基本参数和几何尺寸
1.齿轮各部分的名称和符号 齿顶圆 ra,da 齿根圆 rf,df 分度圆齿厚s 齿 厚 任意圆齿厚 si 分度圆齿槽宽e ei 齿槽宽 任意圆齿槽宽 分度圆齿距 p pi= s+ ei 齿 距 任意圆齿距 i+e 分度圆 r,d ha 齿顶,齿顶高 hf 齿根,齿根高
o1
' r1
c
用C 表示。
上述参数即为渐开线齿轮的五个基本参数。
r2' o2
'
* ) 3.渐开线齿轮各部分几何尺寸 (基本参数为 m、Z、 和 h * 、 c a
1.分度圆直径 d mz 2.基圆直径 d b d cos 3.齿顶高 ha ha m 齿顶高系数
正常齿制 4.齿根高 hf 5.齿全高
机械原理第10章 凸轮设计

①等分位移曲线;
②选定r0,画基圆;
③应用反转法逐点作图确 定 各 接 触 点 位 置 B0 , B1 , B2,……;
④光滑连接B0,B1,B2 , …… 点 , 就 得 所 要 设 计 的 凸轮廓线。
10.2 凸轮机构的廓线设计
2)滚子从动件
第10章 凸轮机构设计
Design of Cam Mechanisms
第10章 凸轮机构及其设计
1
凸轮机构的运动与传力特性
2
凸轮机构的廓线设计
10.1 凸轮机构的运动与传力特性
10.1.1 凸轮机构的工作循环
基圆——以凸轮轮廓的最小向径rb (或r0)为半径的圆。
图10-1 尖端移动从动件盘形凸轮机构的工作循环
从动件一方面随机架和导路以角速度-ω 绕O点转动,另一方面又在导 路中往复移动。由于尖端始终与凸轮轮廓相接触,所以反转后尖端的运动 轨迹就是凸轮轮廓。
10.2 凸轮机构的廓线设计
10.2.2 图解法设计过程
添加!
凸轮轮廓曲线的绘制 (图解法凸轮廓线的设计)
(26分钟)
10.2 凸轮机构的廓线设计
10.2 凸轮机构的廓线设计
10.2.3 凸轮廓线设计的解析方法
移动滚子从动件盘形凸轮机构
如图所示为一偏置移动滚子从动件盘形凸轮机构。建立直角坐标系oxy。若已
知凸轮以等角速度逆时针方向转动,凸轮基圆半径rb、滚子半径rr,偏距e,从动 件的运动规律s=s()。
1、理论廓线方程 B点坐标(凸轮的理论廓线方程)
s
v
a
j
h (1 cos)
机械原理第十章考习题精选全文完整版

可编辑修改精选全文完整版机械原理第十章习题一、单项选择题1.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆2.计算蜗杆传动的传动比时,公式( )是错误的。
A. i=ω1/ω2B. i=n1/n2C. i=d2/d1D. i=Z2/Z13.在安装标准直齿轮时若中心距大于标准中心距,则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小4. 单个渐开线齿轮()A.分度圆等于节圆B.分度圆小于节圆C.分度圆大于节圆D.没有节圆5. 蜗轮的螺旋角β与蜗杆()A.分度圆处的导程角γ大小相等,方向相反B.B.分度圆处的导程角γ大小相等,方向相同C.齿顶圆处的导程角γ1大小相等,方向相反D.齿顶圆处的导程角γ1大小相等,方向相同6.为了减少蜗轮刀具数目,有利于刀具标准化,规定()为标准值。
A.蜗轮齿数B.蜗轮分度圆直径C.蜗杆头数D.蜗杆分度圆直径7. 渐开线齿轮的齿根圆()A.总是小于基圆 B.总是等于基圆C.总是大于基圆 D.有时小于基圆,有时大于基圆8. 为了实现两根相交轴之间的传动,可以采用()A.蜗杆传动B.斜齿圆柱齿轮传动C.直齿锥齿轮传动D.直齿圆柱齿轮传动9. 一对标准齿轮啮合传动时,其啮合角()其分度圆压力角。
A.大于B.等于C.小于D.可能等于也可能大于10.用齿条刀具加工渐开线齿轮时,判断被加工齿轮产生根切的依据是()。
A.刀具的齿顶线通过啮合极限点N1B.刀具的齿顶线超过啮合极限点N1C.刀具的中线超过啮合极限点N1D.刀具的中线不超过啮合极限点N111.在设计计算单个渐开线齿轮的几何尺寸时的基准圆是()A.基圆B.齿根圆C.分度圆D.齿顶圆12. 一对正确啮合的斜齿圆柱齿轮传动的( )均为标准值。
A.法面模数、分度圆上的法面压力角B.端面模数、分度圆上的端面压力角C.端面模数、分度圆上的端面压力角、分度圆上的螺旋角D.法面模数、分度圆上的法面压力角、分度圆上的螺旋角13. 常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆14.当一对渐开线齿轮制成后,即使两轮的中心距稍有改变,其传动比仍保持不变的原因是()A.压力角不变B.啮合角不变 C.节圆半径不变D.基圆半径不变15.渐开线标准齿轮的根切现象发生在()A.齿数较少时B.模数较小时C.模数较大时D.齿数较多时16.标准直齿圆锥齿轮的标准模数是()A.大端模数B.小端模数C.平均模数D.求出平均模数后圆整所得的模数17.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆18.在安装标准直齿轮时若中心距大于标准中心距,则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小19.单个渐开线齿轮()A.分度圆等于节圆B.分度圆小于节圆C.分度圆大于节圆D.没有节圆20.常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆二、填空题1. 为了不产生过大的轴向力,在斜齿轮的基本参数中,___________不宜过大。
机械原理第十章

齿槽一宽个:齿在槽任两意侧半齿径廓rK圆间周弧上长,。eK
齿距:在任意半径rK圆周上,相
邻两齿同侧齿廓间弧长。pK
在同一圆周上:pK sK eK
法向齿距:相邻两齿同侧齿 廓间法线长度,pn=pb
分度圆:为了计算齿轮的各部分尺寸, 在齿顶圆和齿根圆之间人为规定了 一个直径为d,半径为r,用作计算 基准的圆。 分度圆上齿距、齿厚、齿槽宽分别 用p、s、e表示。 p=s+e
已知传动比、中心距、 齿轮1的齿廓曲线K1,用 包络线法求与齿廓K1共 轭的齿廓曲线K2。
3.齿廓曲线的选择 理论上,满足齿廓啮合定律的曲线有无穷多,但考
虑到便于制造和检测等因素,工程上只有极少数几种 曲线可作为齿廓曲线,如渐开线、其中应用最广的是 渐开线,其次是摆线(仅用于钟表)和变态摆线 (摆线针 轮减速器),近年来提出了圆弧和抛物线。
o1
点P 称为两轮的啮合节点(简称节点)。 r’1 节圆:
ω1
节圆
n
两个圆分别为轮1和轮2的节圆
k
两节圆相切于P点,且两轮节点处速 度相同,故两节圆作纯滚动。
P n
ω 2 r’2
o2
根据这一定律, 可求得齿廓曲线与齿廓传动比的关系;
也可按给定的传动比来求得两轮齿廓的共轭曲线。
2.共轭齿廓
所谓共轭齿廓是指两轮相互连续接触并能实现预 定传动比规律的一对齿廓。
rK
k
=
rb/ cosK inv K = tan K
K
三、 渐开线齿廓的啮合特性
O1
ω1
1.渐开线齿廓满足定传动比要求
N1
两齿廓在任意点K啮合时,过K作两 齿廓的法线N1N2,是基圆的切线,为 N2
机械原理第10章 空间连杆机构及机器人机构概述

串联机器人机构fig109tandemrobotmechanism串联机器人机构1wristjoint腕关节2elbowjoint肘关节3shoulderjoint肩关节4waistjoint腰关节5base底座102机器人机构概述串联机器人大都是开链机构图109a所示机器人是3个转动副3个构件组成的串联机器人也简称3r串联机器人
(2)空间连杆机构分类 按组成空间连杆机构的运动链是否 封闭,空间连杆机构分为闭链空间连杆机构和开链空间连 杆机构。图10-6a所示RSSR机构中。构件1、2、3、4通过转 动副和球面副连接,形成一个封闭运动链,构件4为机架。 图10-6b所示机构中。构件1、2、3、4、5通过转动副连接, 形成一个不封闭的运动链,构件1为机架,则组成4R型空间 开链机构。该机构是典型的机器人机构。
3.空间连杆机构分类
(1)空间连杆机构表示方法 平面连杆机构名称是按其运动特性确定 的。如曲柄摇杆机构、曲柄滑块机构、双曲柄机构等。空间机构的 名称则用运动副名称表示。第一个字母一般是原动件与机架连接的 运动副的名称,然后按顺序依次排列。图10-5所示飞机起落架机构 可称为SPSR空间连杆机构。
Fig.10-5 Aircraft undercarriage(飞机起落架)
2.并联机器人机构
并联机器人分为平面并联机器人和空间并联机器人。 图10-10a所示为3自由度平面并联机器人,3个连架杆为驱 动件,共同驱动平台1运动。该机器人简称为平面3RRR并 联机器人,在微动机构中有广泛应用。图10-10b为3自由 度空间并联机器人。
Fig.10-10 Parallel robot mec hanisms(并联机器人机构)
10.1 空间连杆机构概述
1.空间连杆机构中的运动副
机械原理第10章剖析

质量代单换单法击击此以处编编辑辑母母版版标标题题样样式式
一个刚体两个集中重质量代换(希望质量位置在运动副上 以方便分析),保证刚体的动力效应 样样 式式
代换的–条第件二:级 ▪前后质量• 不第变三级 ▪质心位置不–变第»四第级五级 ▪对质心轴的转动惯量不变。
静代换:满足前两个条件;惯性力不变,惯性力偶变了。
动代换:三个条件同时满足;惯性力、惯性力偶都不变。
2
1、动代换:
某 动构惯件量单质Js、单量击有m击转、此动质以副心处BS编、。编绕辑质辑心母转母版版标标题题样样式式
用 满质足•量:单mB击、此以mK处编进行编辑动辑 母代母 版换代版 文换文 本,本 样样 式式B
用质•量单mB击、此以mC处编进行编辑静辑 母代母 版换,版 文满文 本足本 样: 样 式式
mB+ m– c第=m二级
mB
mB( – •b)第+三m级c c=0
m
mC
c b
解得:mB =–m第c»/四(b第级+五c级)
mc =mb/(b+c)
静代换可以同时选两个代换点,但其没有满足代换前后对 质心轴的转动惯量不变的条件,故惯性力偶矩Mi将产生误差:
– 第二级
• 第三级
– 第四电机级 » 第五级
解算显示电路
皮 带 轮
齿
传 基准 感 信号 器
轮
传 感 器
联轴器
试件
弹性支架
9
§10-4:柔性转子的平衡
单单击击此以处编编辑辑母母版版标标题题样样式式
轴系质量和弹性构成一个有无 穷多自由度的振动系统
• 单击此以处编编辑辑 母母 版版 文文 本本 样样 式式
的构件,其惯性力和惯性力偶矩不可能象回转件一样
机械原理(PDF)孙桓 复习笔记chapter10

59第10章 齿轮机构及其设计齿轮机构及其设计齿轮机构及其设计§1010——1 1 齿轮机构的特点及类型齿轮机构的特点及类型齿轮机构的特点及类型 1.用于平行轴间传动的齿轮机构1)直齿圆柱齿轮机构(外啮合、内啮合、齿轮-齿条啮合) 2)斜齿圆柱齿轮机构(外啮合、内啮合、齿轮-齿条啮合) 3)人字齿轮机构。
2.用于相交轴间传动的齿轮机构: 圆锥齿轮机构(直齿、斜齿、曲齿) 3.用于交错轴间传动的齿轮机构: 1)交错轴斜齿轮机构 2)蜗杆传动 3)准双曲面齿轮机构 4.优缺点: 优:1)定传动比,结构紧凑,工作可靠。
2)效率高(可η>0.99)寿命长。
3)转速范围大、功率范围大、齿轮直径范围大(几个µm ~150m ) 缺:精度要求高,制造难,成本高。
5.应用: 非常广泛§1010——2 2 齿轮的齿轮的齿轮的齿廓齿廓齿廓曲线曲线曲线 一. 齿廓啮合基本定律齿廓啮合基本定律齿廓啮合基本定律;; 齿轮1和2的齿廓C 1和C 2接触于K 点,nn 是C 1、C 2 在点K 的公法线,它与连心线O 1O 2交于P 点 1.啮合节点P: nn 与O 1O 2的交点,即1、2的瞬心 ∵ ω1 O 1P =ω2 O 2P∴ 12122112ωωr r p O p O i ′′===上式表明,节点P 的位置必须随传动比的改变,即: 2.齿廓啮合基本定律:两轮齿廓接触点的公法线nn 必须通过按瞬时传动比确定的节点P 。
603.定传动比的条件:1)条件:公法线nn 与连心线O 1O 2交于一定点,即节点P 固定。
2)节圆:定传动比时,节点P 在齿轮平面中的轨迹圆。
注: r 1′= O 1P 、 r 2′= O 2P 称为节圆半径3)两节圆作纯滚动:∵ P 是1、2的同速点∴ 两节圆作纯滚动,即两齿廓在节点啮合时无相对滑动。
二.齿廓齿廓曲线的选择曲线的选择曲线的选择1.共轭齿廓: 能按预定传动比规律相互啮合传动的一对齿廓 2.常用齿廓: 渐开线、摆线、圆弧等,其中,渐开线齿廓最常用。
机械原理第十章ppt课件

ω
切削
进给
适用于加工大模数 m>20 的齿轮和人字 齿轮。
切削
ω
进给
由db=mzcosα可知,渐开线
形状随齿数变化。要想获得
分度
精确的齿廓,加工一种齿数
的齿轮,就需要一把刀具。
这在工程上是不现实的。
.
指状铣刀加工
切 削 运 动
让刀运动
ω0
ω
渐开线直齿圆柱齿轮的啮合传动(6/6)
ω0
共轭齿廓互为包络线
2)标准中心距 a a = r1+r2 = m (z1+z2)/2
结论 零,即 c = c*m, c′= 0。
.
(2)啮合角
渐开线直齿圆柱齿轮的啮合传动(3/6)
渐开线齿轮传动的啮合角α′就等于其节圆压力角。 当两轮按标准中心距安装时,则实际中心距 a′= a; 当两轮实际中心距 a′与标准中心距 a 不同时,则:
结论 重合度εα 与模数m无关,而随着齿数z的增多而增大, 还随啮合角α′减少和齿顶高系数ha*的增大而加大, 但εαmax=1.981。
.
渐开线直齿圆柱齿轮的啮合传动(5/6)
当Z1,,Z2 →∞时 ,εα→εαmax
PB1=PB2=ha*m/sinα
εαmax=(PB1+PB2 )/pb =2 ha*m/(sinαπmcosα)
(2)根切的实质
(3)齿轮不产生根切的最小齿数 为了避免产生根切现象,则啮合极
限点N1必须位于刀具齿顶线之上,为此应使 PN1sinα≥ha*m。 由此可得被切齿轮不发生根切的最少齿数为
zmin= 2ha* / sin2α 当 ha* =1, α = 20。时, zmin= 1.7。
《机械原理》第十章 平面机构的平衡

转子的平衡精度,而应以满足实际工作要求为度。为此,对
不同工作要求的转子规定了不同的许用不平衡量,即转子残 余不平衡量。
许用不平衡量有两种表示方法:
1. 用许用质径积[mr](单位g.mm)表示 此表示比较直观,便于平衡操作。 2. 用偏心距[e] (单位mm)表示 [e] = [mr]/m
设计机构时,可以通过构件的合理布置、加平衡质量或加平 衡机构的方法使机构的总惯性力得到完全或部分平衡。
一、完全平衡法 1)四杆机构的完全平衡 将构件2的m2用集中于
B、C 两点的两个质量代换;
m2B = m2 lCS’2/ lBC m2C = m2lBS’2/ lBC 在构件1和3的延长线上各加一平衡质量,使其质心分 别移到固定轴A和D处: m’=(m2BlAB+m1lAS’1)/r ’
平面机构惯性力的平衡条件
对于活动构件的总质量为m、总质心S的加速度为as的机 构,要使机架上的总惯性力F 平衡,必须满足:
m 0 as=0 F mas 0
机构的总质心S 匀速直线运动或静止不动。
质心不可能作匀速直线 运动
欲使as=0, 就得设法使总 质心S 静止不动。
-F"
平衡原理
F1
F = F1 + F2 F1 L1 = F2L2 可解得 L2 F1 = F L L1 F2 = F L
(1) (2)
Ⅰ
F
F2
Ⅱ
(3) (4) F' L1 F" L2
将力F平行分解到两个平衡基面 上,得F1和F2 ,即 F = F1 + F2 F1 L1 = F2 L2 即 F1 = -F'
机械原理第十章 机械系统动力学

矩所产生的功率P之和为 n
m
P Fivi cosi M j j
i 1
j 1
若等等效效构构件件的为角绕速定度轴为转,动则的根构据件等,效其构上件作上用作有用假的想等的效等力效矩力所矩产Me生,,
的功率应该等于整个机械系统中所有外力、外力矩所产生的功率之
和,可得
M e P
于是
Me
n i1
Fi
vi
cosi
m
Mj
j 1
j
同理,当等效构件为移动件时,可以类似得到作用于其上的等效
力为
Fe
n i1
Fi
vi
cosi
v
m
Mj
j 1
j
v
2.等效转动惯量和等效质量
若等效构件为绕定轴转动的构件,角速度为ω ,其对转动轴的假
想的等效转动惯量为Je,则根据等效构件所具有的动能等于机械 系统中各构件所具有的动能之和,可得
联立上述两式,可求出角速度随时间的变化规律,进而通过下式 计算等效构件的角加速度
d d d d dt d dt d
§10-4 机械的速度波动及其调节方法
10.4.1
周期性速度波动及其调节
Md Mr
Md
Mr
1. 周期性速度波动产生的原因
(a) a 等效力矩和等效转动惯量是等效构 △W
b
c
d
毂和轮缘的转动惯量较小,可忽略不计。其转动惯量为:
轮幅
轮缘
轮毂 JA
B
H
A
D2 D D1
JF
m ( D12 2
D22 ) 4
m 8
( D12
D22 )
若设飞轮宽度为B(m),轮缘厚度为H(m),平均直径
机械原理第十章 机械动力学和机械的平衡

i 1
i 1
则
F
n i 1
Fi
(
vi v
) cosi
n i 1
M
i
(
i
v
)
M
n i 1
Fi
(
vi
)
cos
i
n i 1
M
i
(
i
)
(3) 机械系统等效动力学模型 机械系统等效动力学模型通常有下列两种表达形式。
1)能量形式的运动方程式
d[1 J () 2 ] M ()d
式中m可由min与max的算数平均值近似确定:
m
1 2
(max
min )
机械速度不均匀系数的许用值因工作性质不同而有不同要 求,如果超过了许用值,必将影响机器正常工作,但是过分要 求减少不均匀系数值也是不必要的。不同机械(机器)的不均 匀系数许用值可在相关工程设计手册上查到。
三、机械系统的等效动力学模型
2
设给定初始条件:=0时,=0,J=J0,则对上式积分得
1
2
J () 2
1 2
J
2
00
0 M ()d
2)力矩形式的运动方程式
J () d
2
dJ ()
M ()
d 2 d
四、在已知力作用下机械的真实运动
(一)等效构件角速度的确定
按等效力矩求等效构件角位移自至0的盈亏功W,其值为
n i 1
(mi vs2i0
J
si
2 i0
)
(二)等效质量及等效转动惯量、等效力及等效力矩
机械原理第十章机械运动动力学方程

2 m
3、周期性速度波动调节方法
飞轮-转动惯量较大的回转件。 目的:调速,使速度波动减小。
飞轮的作用:
安装飞轮的实质就是增加机械系统的转动惯量。 飞轮在系统中的作用相当于一个容量很大的储能器。当 系统出现盈功,它将多余的能量以动能形式“储存”起 来,并使系统运转速度的升高幅度减小;反之,当系统 出现亏功时,它可将“储存”的动能释放出来以弥补能 量的不足,并使系统运转速度下降的幅度减小。从而减 小了系统运转速度波动的程度,获得了调速的效果。
根据ωm和许可的δ确定 JF 。
设计要求: []
[W]
m 2(JJF)
[]
则:JF
[W]
m2[]
J
J 为系统中除飞轮以外其它运动构件的等效转动惯量。
若 J<<JF ,则
JF
[W ]
m2
[W] 90[W 0]
JF m 22n2
(1)当 [W] 与 n 一定时,若加大飞轮转动惯量 JF ,
则机械的速度波动系数将下降,起到减小机械速度波 动的作用,达到调速的目的。但是,如果 [δ] 值取
第一节 作用在机械上的力及 机械的运转过程
一、作用在机械上的力 ♦机械特性:力(力矩)与运动参数之间 的关系称为机械特性。
工作阻力:工作负荷。 (有害阻力) 驱动力:驱动原动件运动的力。
二、机械运转的三个阶段
1) 启动阶段 Wd-(Wr+Wf)=Wd-Wc =E2-E1 >0
Wd驱动力所做的功,输入功;P238 Wr克服工作阻力所做的功,Wf克服有害阻力所做的功,耗功.
二、非周期性速度波动及其调节方法
• 非周期性速度波动:如果机械在运转过程中, 等效力矩 (M=Md-Mr) 的变化是非周期性的, 则机械出现的速度波动称为非周期性速度波动。
机械原理第第10章

⎯dE =dW → 系统的运动方程式为: ⎯⎯
2 2 2 dE = d ( J 1ω 12 / 2 + m 2v S 2 / 2 + JS 2ω 2 / 2 + m 3v 3 / 2)
= ( M 1ω 1 − F 3 v 3 ) dt
一、.机械运动方程的一般表达式
对于由 n个活动构件组成的机构
E =
= 9 J 1 + J 2 + m 3 l 2 + m 4 l 2 sin
2
ϕ
2
2)求M e
瞬时功率不变 ⇒ M eω 2 = M 1ω 1 + F4 cos 180°(v 4 )
⇔ M e = M 1 (ω 1 / ω 2 ) + F4 cos 180°(v 4 / ω 2 )
= M1 ( z2 / z1 ) − F4 (ω 2 l sinϕ 2 / ω 2 ) = 3M1 − F4 l sinϕ 2
2. 以移动构件为等效构件时
1)力矩形式的机械运动方程式
dv v 2 dm e me + = Fe dt 2 ds
2)动能形式的机械运动方程式: s 1 1 2 2 me v − me v0 = ∫ Fe ds S0 2 2
§10-3
机械运动方程的求解
一、等效转动惯量和等效力矩均为位置的函数
(Md=Md(ϕ),Mr=Mr(ϕ), Me=Me(ϕ),Je=Je(ϕ))
z 1 z 2′ z1 2 G 2 z 1 z 2′ = J 1 + ( J 2 + J 2′ )( ) + J 3 ( ) + r3 z2 z3 z2 z3 g z2
§ 10-4 稳定运转状态下机械的周 期性速度波动及其调节
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章齿轮机构及其设计1 一个齿轮不同圆上的压力角和模数是否相同?是否都是标准值?2 为什么模数值要标准化?3 标准为什么规定压力角为20°?4 如果齿轮的五个基本参数中,除模数以外其余四个基本参数都相同,齿轮的几何尺寸有何不同?5 确定蜗杆头数和蜗轮的齿数要考虑哪些问题?6 何谓蜗杆蜗轮机构的中间平面?在中间平面内,蜗杆蜗轮传动相当于什么传动?7 确定蜗杆直径系数的目的是什么?的大小对蜗杆蜗轮机构有什么影响?它与蜗杆分度圆直径是什么关系?8 何谓圆锥齿轮的背锥和当量齿轮?引入背锥和当量齿轮的目的是什么?当量齿数如何计算?9 在直齿圆锥齿轮中何处为标准值?10 渐开线标准齿轮是指m、α、*a h、*c均为标准值,且分度圆齿厚等于齿槽宽的齿轮。
11 渐开线直齿圆柱齿轮与齿条啮合时,其啮合角恒等于齿轮分度圆上的压力角。
12 用标准齿条型刀具加工标准齿轮时,刀具的中线与轮坯的分度圆之间作纯滚动。
13 一对渐开线圆柱齿轮传动,其节圆总是相切并作纯滚动,而两轮的中心距不一定等于两轮的分度圆半径之和。
14 一对渐开线标准直齿圆柱齿轮按标准中心距安装时,两轮的节圆分别与其分度圆重合。
15 用同一把刀具加工m、z、α均相同的标准齿轮和变位齿轮,它们的分度圆、基因和齿距均相等。
16 正变位齿轮与标准齿轮比较其齿顶高增大,齿根高减小。
17 要求一对外啮合渐开线直齿圆柱齿轮传动的中心距略小于标准中心距,并保持无侧隙啮合,此时应采用负传动。
18 斜齿圆柱齿轮的齿顶高和齿根高,无论从法面或端面来看都是 相同的。
19一对外啮合斜齿圆柱齿轮的正确啮合条件为12n n m m m ==,12n n ααα==,12ββ=- 。
20 蜗杆的标准模数和标准压力角在轴面,蜗轮的标准模数和标准压力角在轴面。
21 直齿锥齿轮的几何尺寸通常都以大端作为基准。
22渐开线直齿圆柱齿轮正确啮合的条件是: 两齿轮的模数相等和压力角相等 。
23一对平行轴斜齿圆柱齿轮的正确啮合条件是:两轮法面上的模数和压力角分别相等,螺旋角大小相等,方向相反(外啮合)或相同(内啮合), 24一对直齿圆锥齿轮传动的正确啮合条件是 两轮大端的模数和压力角相等 。
25蜗杆蜗轮传动的正确啮合条件是 : 其中间平面内蜗轮与蜗杆的模数和压力角分别相等, 当两轴交错为90度时,还应使蜗杆的导程角等于涡轮螺旋角 。
26标准渐开线直齿圆锥齿轮的标准模数和压力角定义在 大端。
27一对渐开线直齿圆柱齿轮啮合传动时,两轮的 节 圆总是相切并相互作纯滚动的,而两轮的中心距不一定总等于两轮的分度 圆半径之和。
28共轭齿廓是指一对 能满足齿廓啮合基本定律 的齿廓。
29用齿条刀具加工标准齿轮时,齿轮分度圆与齿条中线 相切 ,加工变位齿轮时,中线与分度圆 不相切 。
被加工的齿轮与齿条刀具相"啮合"时,齿轮节圆与分度圆 重合 。
30有两个模数、压力角、齿顶高系数及齿数相等的直齿圆柱齿轮,一个为标准齿轮1,另一个为正变位齿轮2,试比较这两个齿轮的下列尺寸 ,哪一个较大、较小或相等:d b1 = d b2;d a1 < d a2;d 1=d 2;d f1 < d f2;s a1 > s a2;s 1 > s 2。
31标准齿轮除模数和压力角为标准值外,还应当满足的条件是 分度圆上齿厚等于齿槽宽,即s=e 。
32斜齿轮在 法面 上具有标准模数和标准压力角。
33若两轴夹角为90度的渐开线直齿圆锥齿轮的齿数为Z 1=25,Z 2=40,则两轮的分度圆锥角= 32度 ; = 58度 。
34一对直齿圆锥齿轮传动时的分度圆锥角应根据 齿轮齿数 和 两轴交角 来决定。
35如图所示两对蜗杆传动中,(a)图蜗轮的转向为 逆时针 ;(b)图蜗杆的螺旋方向为 右旋 。
35 用标准齿条型刀具加工标准齿轮时,其刀具的 线与轮坯 圆之间做纯滚动;加工变位齿轮时,其刀具的线与轮坯的圆之间作纯滚动。
36 已知一正常齿标准外啮合直齿圆柱齿轮传动: 20=α,5=m mm ,191=z ,422=z 。
试求其重合度αε,并绘出单齿及双齿啮合区;如果将其中心距a 加大直至刚好连续传动,试求:(l )啮合角α';(2)两轮的节圆半径1r '及2r ';(3)两分度圆之间的距离;(4)顶隙和侧隙。
解:(1)啮合区及重合度:1631124220cos 42arccos 2cos arccos arccos *22222 =⨯+⨯=+==a a b a h z z d d a α )] tan - (tan z +) tan - (tan [z 21a12a11ααααπεα=( * ) 故 1.63)] 02tan - 416242(tan +)20 tan - 6113[19(tan 21=''=απεα 此传动的单齿及双齿啮合区如题10-2图解所示。
(2)在刚好连续传动情况下:a )啮合角α':刚好连续传动时,αε=1,于是由式(*)得229.32])4219()2-41tan264264tan31(19arctan[])z (z )2tan tan (z arctan[212211=+'⨯+'⨯=+-+=ππαααa a zb )两分度圆的距离:)1cos cos (2)(21-'+=ααm z z y m(1942)5cos 20(1) 3.4422cos 23.229+⨯=-=mm 4126121920cos 19arccos 2cos arccos arccos *11111'=⨯+⨯=+==aa b a h z z d d a α3)两轮节圆直径:146.97229.23cos 20cos 519cos cos 11=⨯⨯='='ααm z d mm22cos cos 20425214.743cos cos 23.229d z m αα'==⨯⨯='mm 4)顶隙:*()5(0.25 3.442) 4.692c m c y =+=⨯+=mm5)侧隙:12()p s s δ'''=-+,而 cos cos 20516.063cos cos 23.229p p απα'==⨯⨯='mm )(21111ααinv inv r r r s s -''-'='548.57397.146(23.22920)7.169247.5inv inv π=⨯-⨯-=mm )(22222ααinv inv r r r s s -''-'='5107.37217.743(23.22920) 6.1252105inv inv π=⨯-⨯-=mm 故δ=16.063-(7.169+6.125)=2.769mm本题应注意,两标准齿轮在非标准中心距安装的情况下,其顶隙和侧隙的求解方法。
37标准渐开线直齿圆柱齿轮与齿条相啮合。
已知它们的参数为:20=α,1*=a h ,25.0*=c ,5=m mm ,20=z 。
由于安装误差,齿条的分度线与齿轮的分度圆分离0.lmm 。
(1)试求有安装误差时下列参数:l )齿轮与齿条啮合时的节圆半径r '和啮合角α';2)沿啮合线方向的法向间隙n c 。
(2)推导出计算重合度αε的公式,并计算有安装误差时的重合度。
(1)由于齿轮与齿条啮合时,无论是否标准安装,其啮合角α'恒等于齿轮的分度圆压力角α,齿轮的节圆也恒与其分度圆重合,故有20=='αα252r r m ππ'===mm(2)作题图(a ),可知:当有安装误差的齿条的分度线与齿轮的分度圆分离为xm 时,即xm =0.1mm ,齿轮与齿条的齿廓接触点仍为K 点,而另一侧齿廓则产生齿侧间隙,且法向齿侧间隙n c K a '=,过K '点作另一侧齿廓平行线得'K b ,则在直角三角形K ba '∆中,2K ba α'∠=,故有'K a ='sin 2K b α再作直角三角形K cb '∆,cK b α'∠=,'K c =xm =0.lmm ,故有 'K b ='K c /cos α=xm /cos α于是得n c ='K b sin2α=xm sin2α/cos α=2xm sin α=2⨯0.1⨯sin20︒=0.0684mm(3)为了求重合度αε=12b B B p 先求有安装误差时,齿条与齿轮的实际啮合线的长度12B B ,即分别作齿轮齿顶圆和齿条齿顶线与其啮合线的交点,得到1B 点和1B '点。
由图可知'2PB =*()sin a h m xm α-1B P =01N B -NP =b r (tan b α-tan α)=cos mz α(tan a α-tan α)/21B P =1B P +'2PB =cos mz (tan αα-tan α)/2+(*a h m xm -)/sin α cos cosb p p m απα==故αε=12b B B p '=z (tan αα-tan α)/(2π)+2(*a h x -)/(sin 2πα)因为cos a α=*cos 20cos 200.85427(2)2021b a a r mz r m z h α⨯===++⨯故αα=31.32︒x =0.02αε=20(tan31.32˚-tan20˚)/(2π)+2(1-0.02)/(πsin40˚)=1.748这里应注意,标准齿轮与齿条在有安装误差的情况下法向齿侧间隙的求解方法。
38 一对标准安装的渐开线标准直齿圆柱齿轮外啮合传动,已知:a =100mm ,1z =20,2z =30,α=20°,1a d =88mm 。
(1)试计算下列几何尺寸:①齿轮的模数m ;②两轮的分度圆直径1d ,2d ;③两轮的齿根圆直径1f d ,2f d ;④两轮的基圆直径1b d ,2b d ;⑤顶隙c 。
(2)若安装中心距增至a '=102mm ,试问:①上述各值有无变化,如有应为多少?②两轮的节圆半径1r '、2r '和啮合角α'为多少?解题要点:a)根据标准齿轮的几何尺寸计算公式,可求出题目所要求的量。
b)由于渐开线齿轮传动具有可分性,中心距加大后其传动比仍不变。
但两节圆分别大于两分度圆,啮合角大于压力角,此时实际中心距a '与啮合角α'的关系为:cos cos a a αα''=。
