半导体物理习题课
2023春半导体物理习题课

2023春半导体物理习题课第二章载流子中的平衡统计分布⚫当E −E F 为1.5k 0T ,4k 0T ,10k 0T 时,分别用费米分布函数和玻尔兹曼分布函数计算电子占据各该能级的概率。
根据量子统计理论,服从泡利不相容原理的电子遵循费米统计律。
对于能量为E 的一个量子态被电子占据的概率f(E)为f E =11+e E−E F k 0T当E −E F ≫k 0T 时,eE−E F k 0T≫1,此时费米分布(简并系统) 可以近似为玻尔兹曼分布(非简并系统)f B E =e −E−E F k 0T当E −E F =1.5k 0T ,f E =0.1824,f B E =0.2231;当E −E F =4k 0T ,f E =0.01799,f B E =0.01832;当E −E F =10k 0T ,f E =4.540×10−5,f B E =4.540×10−5;在半导体中,E F 一般位于禁带中且与允带距离较远,因此一般可以认为E −E F ≫k 0T 。
3-3 电子的统计分布①在室温下,锗的有效状态密度N c=1.05×1019cm−3,N v=3.9×1018cm−3,试求锗的载流子有效质量m n∗,m p∗。
计算77K时的N c和N v。
已知300K时,E g=0.67eV。
77K时E g=0.76eV。
求这两个温度时锗的本征载流子浓度。
以导带有效状态密度N c举例,它是把导带中所有量子态都集中在导带底E c时的状态密度,此时导带中的电子浓度是N c中有电子占据的量子态数,有效状态密度表达式为N c=2(2πm n∗k0T)Τ32ℎ3,N v=2(2πm p∗k0T)Τ32ℎ3由此可算出m n∗=12πk0TN cℎ32Τ23=5.0968×10−31kg=0.5596m0m p∗=12πk0TN vℎ32Τ23=2.6336×10−31kg=0.2892m0①在室温下,锗的有效状态密度N c=1.05×1019cm−3,N v=3.9×1018cm−3,试求锗的载流子有效质量m n∗,m p∗。
半导体物理学(刘恩科)第七版-完整课后题答案

第一章习题1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。
试求:为电子惯性质量,nm a ak 314.0,1==π(1)禁带宽度;(2) 导带底电子有效质量; (3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化 解:(1)eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此:取极大值处,所以又因为得价带:取极小值处,所以:在又因为:得:由导带:043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以:准动量的定义:2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:t k hqE f ∆∆== 得qEk t -∆=∆ sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ补充题1分别计算Si (100),(110),(111)面每平方厘米内的原子个数,即原子面密度(提示:先画出各晶面内原子的位置和分布图)Si 在(100),(110)和(111)面上的原子分布如图1所示:(a )(100)晶面 (b )(110)晶面(c )(111)晶面补充题2一维晶体的电子能带可写为)2cos 81cos 87()22ka ka ma k E +-= (, 式中a 为 晶格常数,试求(1)布里渊区边界; (2)能带宽度;(3)电子在波矢k 状态时的速度;(4)能带底部电子的有效质量*n m ;(5)能带顶部空穴的有效质量*p m解:(1)由0)(=dk k dE 得 an k π= (n=0,±1,±2…) 进一步分析an k π)12(+= ,E (k )有极大值,214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cm atom a a a cm atom a a a cm atom a a ⨯==⨯+⨯+⨯⨯==⨯⨯+⨯+⨯=⨯==⨯+-):():():(222)mak E MAX =( ank π2=时,E (k )有极小值所以布里渊区边界为an k π)12(+=(2)能带宽度为222)()ma k E k E MIN MAX =-( (3)电子在波矢k 状态的速度)2sin 41(sin 1ka ka ma dk dE v -== (4)电子的有效质量)2cos 21(cos 222*ka ka mdkEd m n-== 能带底部 an k π2=所以m m n 2*= (5)能带顶部 an k π)12(+=, 且**n p m m -=,所以能带顶部空穴的有效质量32*mm p =半导体物理第2章习题1. 实际半导体与理想半导体间的主要区别是什么?答:(1)理想半导体:假设晶格原子严格按周期性排列并静止在格点位置上,实际半导体中原子不是静止的,而是在其平衡位置附近振动。
半导体物理习题课
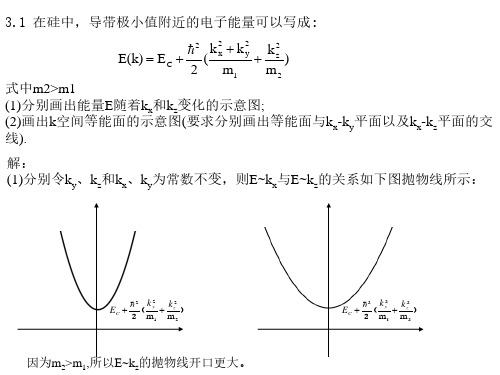
因此在能量E
E+dE范围,长度为dk内的状态数为:
Na
π
dk =
Na
* mn dE
π
2
E
−
1 2
Na = 2π
* * 1 1 − − 2mn 2 m n E 2 dE = L E 2 dE
因此单位长度晶体中,单位能量间隔的状态数为:
* 1 − 2mn N (E) = E 2
,
3.9 设硅晶体中电子的纵向有效质量为ml,横向有效质量为mt, (1)如果外加电场沿[100]方向,试分别写出在[100]和[001]方向能谷中电子的加速 度; (2)如果外加电场沿[110]方向,试求出[100]方向能谷中电子的加速度与电场之间 的夹角。 解: y [010] (1)在[100]能谷中,
− eε 2 1 1 m + ml ( + ) − t a ⋅ε mt + ml 2 ml mt ml mt = cosθ = =− = 2 2 2 2 aε 1 1 eε 2 ( ) m + m m + m l t l t ⋅ + ε⋅ 2 2 ml2 mt2 ml mt
于是:
m +m t l θ = π - arc cos 2 2 2(ml + mt )
2 k 2 2 ( k − k1 ) 2 + EC (k ) = 3m m
价带极大值附近的能量Ev(k)为:
2 k12 3 2 k 2 − Ev (k ) = 6m m
式中m为电子质量,k 1 = (1)禁带宽度; (2)导带底电子的有效质量; (3)价带顶空穴的有效质量。
π
a
,a=3.14Å。试求:
半导体器件物理课后习题(施敏)

1 1 (3) 从(111)面上看,每个面上有 × 3 + × 3 = 2 个原子 6 2
所以,每平方厘米的原子数=
2 4 = ≈ 7.83×1014 3 ⋅ ( 2a)2 3 × (5.43×10−8 )2 4
2.
假如我们将金刚石晶格中的原子投影到底部, 假如我们将金刚石晶格中的原子投影到底部,原 子的高度并以晶格常数为单位表示,如下图所示。 子的高度并以晶格常数为单位表示,如下图所示。 找出图中三原子( Z)的高度。 找出图中三原子(X, Y, Z)的高度。
根据题意,有 用ρn和ρp相除,最后得 NA=100ND
11. 一个本征硅晶样品从一端掺杂了施主,而使得 一个本征硅晶样品从一端掺杂了施主, ND = Noexp (-ax)。(a)在ND >> ni的范围中,求在平 的范围中, 。 在 衡状态下内建电场E(x)的表示法。(b)计算出当 = 的表示法。 计算出当 计算出当a 衡状态下内建电场 的表示法 1µm-1时的 µ 时的E(x)
2
ρ≈
1 1 = ≈ 2 .78 cm ⋅ Ω qp µ p 1 . 6 × 10 −19 × 5 × 10 15 × 450
注意:双对数坐标! 注意:如何查图?NT?
(b) 2×1016硼原子 硼原子/cm3及1.5×1016砷原子 砷原子/cm3 × ×
p ≈ NA − ND = 2 ×1016 −1.5×1016 = 5×1015cm−3
(69.72 + 74.92) = 2.2 ×10 × g / cm3 6.02 ×10 23
22
2.2×144.64 = g / cm3 60.2
≈ 5.29g / cm3
(b)一砷化镓化镓样品掺杂锡 的位置,那么锡是施主还是受主? 为什么? 的位置,那么锡是施主还是受主 为什么 此 半导体是n型还是 型还是p型 半导体是 型还是 型?
半导体物理与器件课后练习题含答案

半导体物理与器件课后练习题含答案1. 简答题1.1 什么是p型半导体?答案: p型半导体是指通过加入掺杂物(如硼、铝等)使得原本的n型半导体中含有空穴,从而形成的半导体材料。
具有p型性质的半导体材料被称为p型半导体。
1.2 什么是n型半导体?答案: n型半导体是指通过加入掺杂物(如磷、锑等)使得原本的p型半导体中含有更多的自由电子,从而形成的半导体材料。
具有n型性质的半导体材料被称为n型半导体。
1.3 什么是pn结?答案: pn结是指将p型半导体和n型半导体直接接触形成的结构。
在pn结的界面处,p型半导体中的空穴和n型半导体中的自由电子会相互扩散,形成空间电荷区,从而形成一定的电场。
当外加正向电压时,电子和空穴在空间电荷区中相遇,从而发生复合并产生少量电流;而当外加反向电压时,电场反向,空间电荷区扩大,从而形成一个高电阻的结,电流几乎无法通过。
2. 计算题2.1 若硅片的掺杂浓度为1e16/cm³,电子迁移率为1350 cm²/Vs,电离能为1.12 eV,则硅片的载流子浓度为多少?解题过程:根据硅片的掺杂浓度为1e16/cm³,可以判断硅片的类型为n型半导体。
因此易知载流子为自由电子。
根据电离能为1.12 eV,可以推算出自由电子的有效密度为:n = N * exp(-Eg / (2kT)) = 6.23e9/cm³其中,N为硅的密度,k为玻尔兹曼常数(1.38e-23 J/K),T为温度(假定为室温300K),Eg为硅的带隙(1.12 eV)。
因此,载流子浓度为1e16 + 6.23e9 ≈ 1e16 /cm³。
2.2 假设有一n+/p结的二极管,其中n+区的掺杂浓度为1e19/cm³,p区的掺杂浓度为1e16/cm³,假设该二极管在正向电压下的漏电流为1nA,求该二极管的有效面积。
解题过程:由于该二极管的正向电压下漏电流为1nA,因此可以利用肖特基方程计算出它的开启电压:I = I0 * (exp(qV / (nkT)) - 1)其中,I0为饱和漏电流(假定为0),q为电子电荷量,V为电压,n为调制系数(一般为1),k为玻尔兹曼常数,T为温度。
半导体物理课后习题

半导体物理学课后习题第一章 半导体的电子状态1. [能带结构计算]设晶格常数为a 的一维晶格,导带极小值附近能量)(k E c 和价带极大值附近能量)(k E v 分别为()()02120223m k k m k k E c -+= ()022021236m k m k k E v -= 式中,0m 为电子惯性质量,a k /1π=,nm a 314.0=。
试求: ① 禁带宽度;② 导带底电子有效质量; ③ 价带顶电子有效质量;④ 价带顶电子跃迁到导带底时准动量的变化。
解:①先找极值点位置()023201202=-+=m k k m k dk dE c 得出,当143k k =时,0212(min)4m k E c =同理由0=dk dE v 得当0=k 时,0212(max)6m k E v = 所以禁带宽度0212(max)(min)12m k E E E v c g =-==0.636eV ②830222*m dk E d m c nc== ③60222*m dk E d m v nv-==④由①可知,准动量的变化为)(109.7834301291--⋅⋅⨯-=-=⨯-⨯=∆=-=∆s m kg ahk k P P P c v2. [能带动力学相关]晶格常数为0.25nm 的一维晶格,当外加102V/m ,107V/m 的电场时,试分别计算电子能带底运动到能带顶所需要的时间。
解:设晶格常数为a ,则电子从能带底到能带顶过程中准动量的变化为ak π=∆,因为dt dk qE f==,所以qEdt dk =所以所需要的时间为:E =∙∆=∆=∆qa qE k dtdk k t π,当m V /102=E 时,s t 81028.8-⨯=∆ 当m V /107=E 时,s t 131028.8-⨯=∆第二章 半导体中杂质和缺陷能级1. [半导体、杂质概念]实际半导体与理想半导体的主要区别是什么? 解:杂质和缺陷的存在是实际半导体和理想半导体的主要区别。
复旦半导体物理习题及答案3精品PPT课件

由泊松方程: 积分得:
d 2V1(x) dx2
1 ( x)
c
(d
x
0)
d 2V2 (x) 2 (x) c (0 x d )
dx2
dV1 ( x) dx
c
x
C1 (d
x
0)
dV2 (x) dx
c
x
C2 (0
x
d)
第六次作业
由边界条件:
E(d ) dV1(x) 0 dx xd
E(d ) dV2 (x) 0
得到:C1
C2
cd
dx xd
E2 (x)
c
x
cd
c(x d ) (0
x
d)
V2 (x)
同理:V1 ( x)
c
E2 (x)dx (1 x2 dx) 2
c (1 x2 dx) 2 D1(d x 0)
D2
(0
x
d)
由边界条件: V1(0) V2 (0),V2 (d ) V2 (0) V1(0) V1(d )
饱和电流密度: 电流密度:
Js
qDp pn0 Lp
qDn n p 0 Ln
1.30 1010 A / cm2
J
Js
exp
qV k0T
1
1.33105
A / cm2
第六次作业
2、条件与上题相同,计算下列电压下的势垒区宽度和单位面积上的电容:(1) -10V; (2) 0V; (3) 0.3V。
查图4-14得少子迁移率: 由爱因斯坦关系求得:
由 L D 求得:
p 500cm2 /V s
Dp 13.0cm2 / s
半导体物理 课后习题答案

第一章习题1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。
试求:为电子惯性质量,nm a ak 314.0,1==π(1)禁带宽度;(2) 导带底电子有效质量; (3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化 解:(1)eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此:取极大值处,所以又因为得价带:取极小值处,所以:在又因为:得:由导带:043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以:准动量的定义:2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。
解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C 22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**)()(单位体积内的量子态数)(2. 试证明实际硅、锗中导带底附近状态密度公式为式(3-6)。
半导体物理习题及答案

半导体物理习题及答案(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--复习思考题与自测题第一章1.原子中的电子和晶体中电子受势场作用情况以及运动情况有何不同, 原子中内层电子和外层电子参与共有化运动有何不同。
答:原子中的电子是在原子核与电子库伦相互作用势的束缚作用下以电子云的形式存在,没有一个固定的轨道;而晶体中的电子是在整个晶体内运动的共有化电子,在晶体周期性势场中运动。
当原子互相靠近结成固体时,各个原子的内层电子仍然组成围绕各原子核的封闭壳层,和孤立原子一样;然而,外层价电子则参与原子间的相互作用,应该把它们看成是属于整个固体的一种新的运动状态。
组成晶体原子的外层电子共有化运动较强,其行为与自由电子相似,称为准自由电子,而内层电子共有化运动较弱,其行为与孤立原子的电子相似。
2.描述半导体中电子运动为什么要引入"有效质量"的概念, 用电子的惯性质量描述能带中电子运动有何局限性。
答:引进有效质量的意义在于它概括了半导体内部势场的作用,使得在解决半导体中电子在外力作用下的运动规律时,可以不涉及半导体内部势场的作用。
惯性质量描述的是真空中的自由电子质量,而不能描述能带中不自由电子的运动,通常在晶体周期性势场作用下的电子惯性运动,成为有效质量3.一般来说, 对应于高能级的能带较宽,而禁带较窄,是否如此,为什么?答:不是,能级的宽窄取决于能带的疏密程度,能级越高能带越密,也就是越窄;而禁带的宽窄取决于掺杂的浓度,掺杂浓度高,禁带就会变窄,掺杂浓度低,禁带就比较宽。
4.有效质量对能带的宽度有什么影响,有人说:"有效质量愈大,能量密度也愈大,因而能带愈窄.是否如此,为什么?答:有效质量与能量函数对于K的二次微商成反比,对宽窄不同的各个能带,1(k)随k的变化情况不同,能带越窄,二次微商越小,有效质量越大,内层电子的能带窄,有效质量大;外层电子的能带宽,有效质量小。
半导体物理课后习题答案(精)

半导体物理课后习题答案(精)第一章习题1.设晶格常数为a的一维晶格,导带极小值附近能量Ec(k)和价带极大值附近能量EV(k)分别为:h2k2h2(k-k1)2h2k213h2k2Ec= +,EV(k)=-3m0m06m0m0m0为电子惯性质量,k1=(1)禁带宽度;(2)导带底电子有效质量;(3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化解:(1)导带:2 2k22(k-k1)由+=03m0m03k14d2Ec2 22 28 22=+=>03m0m03m0dk得:k=所以:在k=价带:dEV6 2k=-=0得k=0dkm0d2EV6 2又因为=-<0,所以k=0处,EV取极大值2m0dk2k123=0.64eV 因此:Eg=EC(k1)-EV(0)=412m02=2dECdk23m0 8πa,a=0.314nm。
试求: 3k处,Ec取极小值4 (2)m*nC=3k=k14 (3)m*nV 2=2dEVdk2=-k=01m06(4)准动量的定义:p= k所以:∆p=( k)3k=k14 3-( k)k=0= k1-0=7.95⨯10-25N/s42. 晶格常数为0.25nm的一维晶格,当外加102V/m,107 V/m的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:f=qE=h(0-∆t1=-1.6⨯10∆k ∆k 得∆t= ∆t-qEπa)⨯10)=8.27⨯10-13s2-19=8.27⨯10-8s (0-∆t2=π-1.6⨯10-19⨯107第三章习题和答案100π 21. 计算能量在E=Ec到E=EC+ 之间单位体积中的量子态数。
*22mLn31*2V(2mng(E)=(E-EC)2解 232πdZ=g(E)dEdZ 单位体积内的量子态数Z0=V22100π 100h Ec+Ec+32mnl8mnl1*2(2mn1VZ0=g(E)dE=⎰(E-EC)2dE23⎰VEC2π EC 23100h*2 =V(2mn2(E-E)Ec+8m*L2 Cn32π2 3Ecπ =10003L32. 试证明实际硅、锗中导带底附近状态密度公式为式(3-6)。
半导体物理习题及解答

第一篇习题 半导体中的电子状态1-1、 什么叫本征激发?温度越高,本征激发的载流子越多,为什么?试定性说明之。
1-2、 试定性说明Ge 、Si 的禁带宽度具有负温度系数的原因。
1-3、 试指出空穴的主要特征。
1-4、简述Ge 、Si 和GaAS 的能带结构的主要特征。
1-5、某一维晶体的电子能带为[])sin(3.0)cos(1.01)(0ka ka E k E --=其中E 0=3eV ,晶格常数a=5х10-11m 。
求:(1) 能带宽度;(2) 能带底和能带顶的有效质量。
第一篇题解 半导体中的电子状态 刘诺 编1-1、 解:在一定温度下,价带电子获得足够的能量(≥E g )被激发到导带成为导电电子的过程就是本征激发。
其结果是在半导体中出现成对的电子-空穴对。
如果温度升高,则禁带宽度变窄,跃迁所需的能量变小,将会有更多的电子被激发到导带中。
1-2、 解:电子的共有化运动导致孤立原子的能级形成能带,即允带和禁带。
温度升高,则电子的共有化运动加剧,导致允带进一步分裂、变宽;允带变宽,则导致允带与允带之间的禁带相对变窄。
反之,温度降低,将导致禁带变宽。
因此,Ge、Si的禁带宽度具有负温度系数。
1-3、解:空穴是未被电子占据的空量子态,被用来描述半满带中的大量电子的集体运动状态,是准粒子。
主要特征如下:A、荷正电:+q;B、空穴浓度表示为p(电子浓度表示为n);C、E P=-E nD、m P*=-m n*。
1-4、解:(1)Ge、Si:a)Eg (Si:0K) = 1.21eV;Eg (Ge:0K) = 1.170eV;b)间接能隙结构c)禁带宽度E g随温度增加而减小;(2)GaAs:a)E g(300K)第二篇习题-半导体中的杂质和缺陷能级刘诺编2-1、什么叫浅能级杂质?它们电离后有何特点?2-2、什么叫施主?什么叫施主电离?施主电离前后有何特征?试举例说明之,并用能带图表征出n型半导体。
2-3、什么叫受主?什么叫受主电离?受主电离前后有何特征?试举例说明之,并用能带图表征出p型半导体。
半导体物理课后习题答案(1-12章)

∆ ED =
7.06 10− 4 eV
r1,n = ε r (
° m0 1 ) � a 17 = 0.53 600.67 A 0 ∗ mn 0.015
8. 磷化鎵的禁带宽度 Eg = 2.26eV ,相对介电常数 ε r = 11.1 ,空穴的有效质量
m∗p = 0.86m0 , m0 为电子的惯性质量,求ⅰ)受主杂质的电离能,ⅱ)受主所若 束缚的空穴基态轨道半径。 [解]: ∆ E A = 已知, E0 = m m∗p E0 rp = n 2ε r ( ∗0 ) a0 2 , mp m0 ε r
第1章 半导体中的电子状态
1. 设晶格常数为 a 的一维晶格,导带极小值附近能量 Ec(k)和价带极大值附近 能量 Ev(k)分别为: Ec(k)=
h 2 k 2 h 2 (k − k1) 2 h2k 2 3h 2 k 2 + 和 Ev(k)= - ; 3m 0 6m 0 m0 m0
m0 为电子惯性质量,k1=1/2a;a=0.314nm。试求: ①禁带宽度; ②导带底电子有效质量; ③价带顶电子有效质量; ④价带顶电子跃迁到导带底时准动量的变化。 [解] ① 禁带宽度 Eg 根据 值: kmin=
[ 110] , [ 101] , [ 011] , 轾 臌1 10
轾 臌10 1 , 轾 臌0 1 1 ;
,
[1 10], 轾 10 1 , 轾 臌 臌01 1 , 轾 臌110 , 轾 臌101 , 轾 臌0 11 ; 则由解析几何定理得, B 与 k3 的夹角余弦 cos θ 为: cos θ = 式中, B = b1i + b2 j + b3k . 对不同方向的旋转椭球面取不同的一组 (k1 , k2 , k3 ) .
半导体物理课后习题(保密)

解: 须先求出本征载流子浓度ni,即
代入数据得,ni=1.86 ×1013cm-3 根据电中性条件有 p0+ND+=n0+NA-
ni
q( n p )
i
1 i ( n p )
联立 载流子浓度公式
n0p0=ni2
可求解得 n0=3.89 ×1013cm-3, p0=8.89 ×1012cm-3 所以样品的电导率为:
解: 由图3-7查得T=500k时,Si的本征载流子浓度ni=3.5×1014cm-3 联立方程
p0=ni2/n0
解得, ND=3.5×1014cm-3时,n0≈4.3×1014cm-3, p0=2.8×1014cm-3 —— n0,p0差别不显著,杂质导电特性不很明显 ND=1012cm-3时,n0≈ni=3.5×1014cm-3, p0=3.5×1014cm-3,即n0=p0. —— 进入本征 半导体材料在某一温度下所处的区域与杂质浓度相关 或 杂质浓度不同,材料进入同一区域所需要的温度不一样。
m0为电子惯性质量,k1=1/2a; a=0.314nm。试求: (1)禁带宽度; (2)导带底电子有效质量; (3)价带顶电子有效质量; (4)价带顶电子跃迁到导带底时准动量的变化。
练习2-课后习题2
第一章 半导体中的电子状态
2.晶格常数为0.25nm的一维晶格,当外加102V/m和107V/m 的电 场时,试分别计算电子自能带底运动到能带顶所需的时间。
作业-课后习题14
第三章 半导体中载流子的统计分布
计算含有施主杂质浓度ND=9×1015cm-3与受主杂质浓度为1.1×1016cm-3 的硅在室温时的电子和空穴浓度以及费米能级的位置。
半导体物理 课后习题答案

第一章习题1.设晶格常数为a 的一维晶格,导带极小值附近能量E c (k)和价带极大值附近能量E V (k)分别为:E c =0220122021202236)(,)(3m k h m k h k E m k k h m k h V -=-+ 0m 。
试求:为电子惯性质量,nm a ak 314.0,1==π(1)禁带宽度;(2) 导带底电子有效质量; (3)价带顶电子有效质量;(4)价带顶电子跃迁到导带底时准动量的变化 解:(1)eV m k E k E E E k m dk E d k m kdk dE Ec k k m m m dk E d k k m k k m k V C g V V V c 64.012)0()43(0,060064338232430)(2320212102220202020222101202==-==<-===-==>=+===-+ 因此:取极大值处,所以又因为得价带:取极小值处,所以:在又因为:得:由导带:043222*83)2(1m dk E d mk k C nC===sN k k k p k p m dk E d mk k k k V nV/1095.7043)()()4(6)3(25104300222*11-===⨯=-=-=∆=-== 所以:准动量的定义:2. 晶格常数为0.25nm 的一维晶格,当外加102V/m ,107 V/m 的电场时,试分别计算电子自能带底运动到能带顶所需的时间。
解:根据:tkhqE f ∆∆== 得qE k t -∆=∆sat sat 137192821911027.810106.1)0(1027.810106.1)0(----⨯=⨯⨯--=∆⨯=⨯⨯--=∆ππ第三章习题和答案1. 计算能量在E=E c 到2*n 2C L 2m 100E E π+= 之间单位体积中的量子态数。
解322233*28100E 21233*22100E 0021233*231000L 8100)(3222)(22)(1Z VZZ )(Z )(22)(2322C22C L E m h E E E m V dE E E m V dE E g V d dEE g d E E m V E g c nc C n l m h E C n l m E C n n c n c πππππ=+-=-====-=*++⎰⎰**)()(单位体积内的量子态数)(2. 试证明实际硅、锗中导带底附近状态密度公式为式(3-6)。
半导体物理与器件第三版)课后练习题含答案

半导体物理与器件第三版课后练习题含答案1. 对于p型半导体和n型半导体,请回答以下问题:a. 哪些原子的掺入能够形成p型半导体?掺入三价元素(如硼、铝等)能够形成p型半导体。
b. 哪些原子的掺入能够形成n型半导体?掺入五价元素(如磷、砷等)能够形成n型半导体。
c. 请说明掺杂浓度对于导电性有何影响?掺杂浓度越高,导电性越强。
因为高浓度的杂质能够带来更多的杂质离子和电子,从而提高了载流子浓度,增强了半导体的导电性。
d. 在p型半导体中,哪些能级是占据态,哪些是空的?在p型半导体中,价带能级是占据态,而导带能级是空的。
e. 在n型半导体中,哪些能级是占据态,哪些是空的?在n型半导体中,导带能级是占据态,而价带能级是空的。
2. 硅p-n结的温度系数是大于零还是小于零?请解释原因。
硅p-n结的温度系数是负的。
这是因为在给定的工作温度下,少子寿命的下降速率与载流子浓度的增长速率之间存在一个平衡。
当温度升高时,载流子浓度增长的速率加快,因而少子寿命下降的速率也会变大。
这一现象会导致整体导电性下降,即硅p-n结中的电流减少。
因此,硅p-n结的温度系数为负。
3. 在半导体器件中,为什么p-n结击穿电压很重要?请简要解释。
p-n结击穿电压是指在一个p-n结器件中施加的足以导致电流大幅增加的电压。
在普通的工作条件下,p-n结是一个非导电状态,而电流仅仅是由热激发和少数载流子扩散引起。
但是,当施加的电压超过了击穿电压时,大量的载流子会被电流激发和扩散,从而导致电流剧增,从而损坏器件或者破坏电路的运行。
因此,掌握p-n结的击穿电压非常重要,可以保证器件稳定和电路的可靠性。
半导体物理习题课
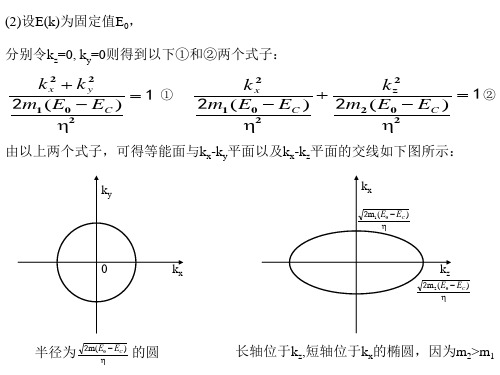
因此在能量E
E+dE范围,长度为dk内的状态数为:
Na
* * * 1 1 1 2mn Na mn dE 2 Na 2mn 2 dk E E dE L E 2 dE 2 2
因此单位长度晶体中,单位能量间隔的状态数为:
* 1 2mn N (E) E 2
* 1 2mn N (E) E 2
解: (1)周期性边界条件: 以晶体的边长为周期,设晶体边长为L,晶格周期为a,电子波函数为 k ( x) 根据布洛赫定理: k ( x) eikxk ( x) ,且 k ( x na) k ( x) k ( x L) k ( x),即: eik( x L) k ( x L) eikxk ( x) 根据边界条件: 设晶体的原胞数为N个:则L=Na
r
f eB c * * mn mn
eB c * mn
3.7在一维情况下,(1)利用周期性条件证明:表示独立状态的k值数目等于晶体的晶 2 2 k E 胞数;(2)设电子的能量为 ,并考虑到电子的自旋可以有两种不同的取向. 2m* n 试证明在单位长度的晶体中单位能量间隔的状态数为:
价带极大值附近的能量Ev(k)为:
2 k12 3 2 k 2 Ev ( k ) 6m m
式中m为电子质量,k 1 a ,a=3.14Å。试求: (1)禁带宽度; (2)导带底电子的有效质量; (3)价带顶空穴的有效质量。
解: (1)禁带宽度Eg=导带极小值ECmin-价带极大值EVmax,因此要先求出ECmin、EVmax 令: 得到: 所以有:
ky kx
2m1 ( E0 EC )
0
kx
kz
半导体物理与器件课后习题1

1.1 确定晶胞中的原子数:(a )面心立方;(b )体心立方;(c)金刚石晶格。
解:(a )面心立方: 8个拐角原子×81=1个原子6个面原子×21=3个原子∴ 面心立方中共含4个原子(b )体心立方:8个拐角原子×81=1个原子1个中心原子 =1个原子 ∴ 体心立方中共含2个原子(c )金刚石晶格:8个拐角原子×81=1个原子6个面原子×21 =3个原子4个中心原子 =4个原子 ∴ 金刚是晶格中共含8个原子1.15 计算如下平面硅原子的面密度:(a )(100),(b )(110),(c )(111)。
解:(a):(100)平面面密度,通过把晶格原子数与表面面积相除得:面密度=()28-1043.52⨯个原子=214/1078.6cm 个原子⨯(b):(110)表面面密度=()28-1043.524⨯个原子=214/1059.9cm 个原子⨯(c):(111)表面面密度=()28-1043.534⨯个原子=214/1083.7cm 个原子⨯1.19(a )如果硅中加入浓度为2×1610/3cm 的替位硼杂质原子,计算单晶中硅原子替位的百分率。
(b )对于浓度为1510/3cm 的硼杂质原子,重新计算(a ) 解:(a ):硅原子的体密度()32238-/1000.51043.58cm 个原子个原子⨯≈⨯=∴ 硅原子替位百分率=005-0022161041001000.5102⨯=⨯⨯⨯ (b )同理:硅原子替位百分率=006-0022161021001000.5101⨯=⨯⨯⨯3.14 图3.35所示色E-k 关系曲线表示了两种可能的价带。
说明其中哪一种对应的空穴有效质量较大。
为什么?解:图中B 曲线对应的空穴有效质量较大空穴的有效质量: 2222*11m k d E d p ⨯=图中曲线A 的弯曲程度大于曲线B故 BAkd E d kd Ed 222222>∴()()**m m B p A p <3.16 图3.37所示为两种不同半导体材料导带中电子的E-k 关系抛物线,试确定两种电子的有效质量(以自由电子质量为单位)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质浓度为:
3 3 ND = = = 1.7 ×1025 / m3 3 4π r1,n 4π × (2.4 ×10−9 )3 =1.7 ×1019 /cm3 同理 3 3 NA = = = 6.3 × 1025 / m3 3 4π r1,p 4π × (1.56 ×10−9 )3 =6.3 ×1019 /cm3 当施主和受主杂质浓度分别超过以上两值时,相邻杂质原子 的电子轨道(波函数)将明显地交迭。杂质原子有可能在杂质 原子之间作公有化运动,造成杂质带电。
1eV = 1.602 × 10−12 erg , k 0 = 1.38 × 10−16 erg / K = 8.63 × 10−5 eV / K
代入有关数据得:
T= 5.5 − 5 8.63 × 10−5 × ln( 1 − 1) 0.01 = 1261( K )
由费米函数可得:
1 E = EF + k0T ln( − 1) f (E)
当f=0.9时:
1 E1 = E F + 8.63 × 10 × 1261 × ln( − 1) 0.9 =EF -0.24(eV)
−5
1 当f=0. 时:
1 E 2 = EF + 8.63 × 10 × 1261 × ln( − 1) 0.1 =EF +0.24(eV)
−5
能量区间为ΔE=E 2 -E1 =0.48(eV)
习题课
1、半导体硅单晶的相对介电常数εr=11.8,电子和空穴的 有效质量各为mnl=0.97m0(电子纵向有效质量) mnt=0.19m0 (电子横向有效质量), mph=0.53m0(重空穴有效质量),mpl=0.16m0(轻空穴有 效质量),利用类氢模型估算: (1)施主和受主电离能; (2)施主和受主对应的电子、空穴基态轨道半径r1; (3)相邻杂质原子的电子或空穴轨道明显交迭时,施主 和受主浓度各为何值?
由图中可知:
价带空穴p0是由两种杂质电离后提供的,即
NA1 NA2 + p0 = EA1 − EF EA2 − EF 1 + 2exp( ) 1 + 2exp( ) k0T k0T ∴ NA1 EA2 − EF NA2 = [p0 − ]i1 + 2exp( ) EA1 − EF k0T 1 + 2exp( ) k0T NA2 =2.2 ×1015 /cm3 ,即半导体中含铟的浓度为2.2 ×1015 /cm3。
EC − E F 式中:n 0 =N C exp () k 0T 对硅材料 由题意可知 N C =5.6 × 1015T 3/ 2 N + =0.99N D D 则 EC − E F ) k 0T 0.99N D − N A = 5.6 × 1015T 3/ 2 exp(-
当施主有99%的电离时,说明只有1%的施主有电子占据,即 f(ED)=0.01。
(2)基态轨道半径各为:
r1, p = r1,n =
ε r rB1
m / m0
* p
= 11.8 × 0.53/ 0.40 = 15.64 A = 11.8 × 0.53/ 0.26 = 24m / m0
* n
3 4π r1,n (3)设每个施主杂质作用范围为 3
,即相当于施主杂
2、若费米能级Ef=5eV,利用费米函数计算在什么温度下电 子占据E=5.5eV能级的几率为1%?计算在该温度下电子分布 几率从0.9~0.1所对应的能量区间。 [解] 由费米分布函数
1 f (E) = E − EF 1 + exp( ) k0T
可得 :
E − EF T= 1 − 1) k0 ln( f (E)
1 f ( ED ) = = 0.01 1 ED − EF 1 + exp( ) k0T 2 ED − E F exp( ) = 198 k0T ∴ EF =ED - k 0T ln198, 代入式中得
15 3/ 2
E C − E D + k 0T ln198 0.99N D − N A = 5.6 × 10 T exp() k 0T 取对数并加以整理即得到下面方程:
T=
可得 T=101.8(K)
579 3 ln T − 1.21 2
4、在一掺硼的非简并p型硅中,含有一定浓度的铟,室温下 3 测出空穴浓度p0=1.1E16/ cm 。已知掺硼浓度 3 NA1=1E16/ cm,其电离能ΔEA1=EA1-Ev=0.046eV,铟的电 离能ΔEA2=EA2-Ev=0.16eV,试求这种半导体中含铟的浓度。 室温下硅的Nv=1.04×10E19/ c m 3 . EF − Ev [解] 对非简并P型硅: p0 =N v exp ()
3、有一硅样品,施主浓度为ND=2E14/cm3,受主浓度为 NA=1E14/cm3。已知施主电离能ΔED=EC-ED=0.05eV,试 求当施主杂质已经99%电离时对应的温度。 [解]
令N + 表示电离施主的浓度,则电中性方程为: D n 0 + N -A = p0 + N + D
略去价带空穴的贡献,则得:n 0 =N + − N(受主杂质全部电离) D A
代入已知数据:
k 0T EF = Ev + k0T ln( Nv ) p0
代入数据:
故:
1.04 × 1019 EF = Ev + 0.026ln( ) 16 1.1 × 10 EF = Ev + 0.178(eV)
EF − E A1 = 0.178-0.045=0.133eV EF − E A2 = 0.178-0.16=0.018eV
(1)利用下式求得mn * 和mp * 1 1 1 2 1 1 2 3.85 = ( + + )= ( )= mn * 3 mnl mnt 3m0 0.97 0.19 m0 1 1 1 6 1 1 6 2.51 = ( + + )= ( )= mp * 7 mpl mph 7m 0 0.16 0.53 m0 因此, 施主和受主杂质电离能各为 : mn * E 0 13.6 ΔE D = = 0.26 × = 0.025(eV) 2 2 m0 ε r 11.8 mP * E 0 13.6 ΔE A = = 0.4 × = 0.039(eV) 2 2 m0 ε r 11.8
