2019上海初三数学一模综合题25题

合集下载

上海市长宁区金山区2019届中考一模数学试题含答案

2019上海长宁区初三数学一模试题(与金山统考)（满分150分，考试时间100分钟） 2019.1.6考生注意：1、本试卷含有三个大题，共25小题；2、答题时，考生务必按照答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3、除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤一、选择题：（本题共6个小题，每题4分，共24分）1. 如果两个三角形的相似比是1:2，那么他们的面积比是（）.A. 1:2B. 1:4C. 1D. 2:12. 如图，在△ABC 中，∠ADE=∠B ，DE:BC=2:3，则下列结论正确的是（）.A. AD :AB =2:3B. AE:AC =2:5C. AD:DB =2:3D. CE:AE =3:23.在Rt △ABC 中，∠C =90°，AB =2，AC =1，则sin B 的值是（）.A. B. C. 12 D. 2 4. 在△ABC 中，若cos A =22，tan B =3，则这个三角形一定是（）. A. 直角三角形 B. 等腰三角形 C. 钝角三角形 D. 锐角三角形5. 已知1O 的半径r 为3cm ，2O 的半径R 为4cm ，两圆的圆心距12O O 为1cm ，则这两个圆的位置关系的（）.A. 相交B. 内含C. 内切D. 外切 6. 二次函数1)2(2-+=x y 的图像可以由二次函数2x y =的图像平移得到，下列平移正确的是（）.A. 先向左平移2个单位，再向上平移1个单位B. 先向左平移2个单位，再向下平移1个单位C. 先向右平移2个单位，再向上平移1个单位D. 先向右平移2个单位，再向下平移1个单位二、填空题：（本大题共12小题，每题4分，满分48分）7. 已知抛物线12+=x y 的顶点坐标是 .8. 已知抛物线32++=bx x y 的对称轴为直线x =1，则实数b 的值为 .9. 已知二次函数bx ax y +=2，阅读下面表格信息，由此可知y 与x 的函数关系式是 .10. 已知二次函数2(3)y x =-图像上的两点()3,A a 和(),B x b ，则a 和b 的大小关系是a b .11. 圆是轴对称图形，它的对称轴是 .12. 已知⊙O 的弦AB =8cm ，弦心距OC =3cm ，那么该圆的半径是 cm.13. 如图，AB 是⊙O 的直径，弦CD 垂直AB ，已知AC =1，BC =22,那么sin ∠ACD 的值是 .14. 王小勇操纵一辆遥控汽车从A 处沿北偏西60°方向走10m 到B 处，再从B 处向正南方走20m 到C 处，此时遥控汽车离A 处 m .15. 已知△ABC 中，AD 是中线，G 是重心，设AD m =，那么用m 表示AG = .16. 如图，已知AB ⊥BD ，ED ⊥BD ，C 是线段BD 的中点，且AC ⊥CE ，ED =1，BD =4，那么AB = .17. 的矩形称作黄金矩形。

长宁区2019学年初三一模数学试卷含答案

长宁区2019学年初三⼀模数学试卷含答案长宁区2019学年第⼀学期初三数学教学质量检测试卷（考试时间：100分钟满分：150分）考⽣注意:1.本试卷含三个⼤题,共25题.答题时,考⽣务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题⼀律⽆效.2.除第⼀、⼆⼤题外,其余各题如⽆特别说明,都必须在答题纸相应位置上写出证明或计算的主要步骤.⼀、选择题（本⼤题共6题, 每题4分, 满分24分）【每题只有⼀个正确选项, 在答题纸相应题号的选项上⽤2B 铅笔正确填涂】 1. 下列函数中是⼆次函数的是（A ）22xy =；（B ）22)3(x x y -+=；（C ）122-+=x x y ；（D ）)1(-=x x y . 2. 如图，已知在平⾯直⾓坐标系xOy 内有⼀点），（32A ，那么OA 与x的夹⾓α的余切值是（A ）23；（B ）32；（C ）13133；（D ） 13132.3. 将抛物线3)1(2-+=x y 向右平移2个单位后得到的新抛物线的表达式为（A ） 3)1(2--=x y ；（B ）3)3(2-+=x y ；（C ）1)1(2-+=x y ；（D ）5)1(2-+=x y . 4. 下列命题正确的是（A ）如果b a=，那么b a =；（B ）如果b a 、都是单位向量，那么b a =；（C ）如果)0(≠=k b k a ，那么b a// ；（D ）如果0=m 或0 =a ，那么0=a m．5. 已知在矩形ABCD 中，5=AB ，对⾓线13=AC ，⊙C 的半径长为12，下列说法正确的是（A ）⊙C 与直线AB 相交；（B ）⊙C 与直线AD 相切；（C ）点A 在⊙C 上；（D ）点D 在⊙C 内.6. 如果点D 、E 、F 分别在ABC ?的边AB 、BC 、AC 上，联结EF DE 、，且AC DE //，那么下列说法错误的是（A ）如果AB EF //，那么AB BD AC AF ::=；（B ）如果AC CF AB AD ::=，那么AB EF //；（C ）如果EFC ?∽BAC ?，那么AB EF //；（D 如果AB EF //，那么EFC ?∽BDE ?.第2题图⼆、填空题（本⼤题共12题, 每题4分, 满分48分）【在答题纸相应题号后的空格内直接填写答案】7. 计算：=++-)(3)2(2b a b a▲．8. 如果23=-y x x ，那么y x 的值等于▲．9. 已知点P 在线段AB 上，且满⾜AP AB BP ?=2，则ABBP的值等于▲． 10. 已知抛物线2)1(x a y +=的开⼝向上，则a 的取值范围是▲． 11. 抛物线122-=x y 在y 轴左侧的部分是▲．（填“上升”或“下降”） 12. 如果⼀条抛物线经过点)5,2(A ，)5,3(-B ，那么它的对称轴是直线▲．13. 如图，传送带把物体从地⾯送到离地⾯5⽶⾼的地⽅，如果传送带与地⾯所成的斜坡的坡度4.2:1=i ，那么物体所经过的路程AB 为▲⽶．14. 如图，AC 与BE 交于点D ，?=∠=∠90E A ，若点D 是线段AC 的中点，且10==AC AB ，则BE 的长等于▲．15. 如图，在ABC Rt ?中，?=∠90BAC ，点G 是重⼼， 4=AC ，31tan =∠ABG ，则BG 的长是▲．16. 已知相交两圆的半径长分别为8与15，圆⼼距为17，则这两圆的公共弦长为▲． 17. 如果直线l 把ABC ?分割后的两个部分⾯积相等，且周长也相等，那么就把直线l 叫做ABC ?的“完美分割线”．已知在ABC ?中，AC AB =，ABC ?的⼀条“完美分割线”为直线l ，且直线l 平⾏于BC ，若2=AB ，则BC 的长等于▲．18. 如图，在ABC Rt ?中，?=∠90ABC ，2=AB ，4=BC ，点P 在边BC 上，联结AP ，将ABP ?绕着点A 旋转，使得点P 与边AC 的中点M 重合，点B 的对应点是点B '，则B B '的长等于▲．三、解答题（本⼤题共7题, 满分78分）【将下列各题的解答过程, 做在答题纸的相应位置上】 19．（本题满分10分）计算：22sin 30tan 60cot 45cos 60cos30sin 45-?+?-．第15题图第18题图AB第13题图传送带第14题图E DB CA20．（本题满分10分，第（1）⼩题6分，第（2）⼩题4分）如图，在梯形ABCD 中，点E 、 F 分别在边AB 、CD 上，BC EF AD ////，EF 与BD 交于点G ，5=AD ，10=BC ，32=EB AE ．（1）求EF 的长；（2）设a AB =，b BC =，那么=DB ▲；=FC ▲（⽤向量a 、b 表⽰）．21．（本题满分10分，第（1）⼩题5分，第（2）⼩题5分）如图，已知AB 是⊙O 的弦，点C 在⊙O 上，且AC BC =，联结AO 、CO ，并延长CO 交弦AB 于点D ，34=AB ，6=CD （1）求OAB ∠的⼤⼩；（2）若点E 在⊙O 上，AO BE //，求BE 的长．22．（本题满分10分）图1是⼀台实物投影仪，图2是它的⽰意图，折线C B A O ---表⽰⽀架，⽀架的⼀部分B A O --是固定的，另⼀部分BC 是可旋转的，线段CD 表⽰投影探头，OM 表⽰⽔平桌⾯，OM AO ⊥，垂⾜为点O ，且7cm =AO ，?=∠160BAO ，OM BC //，cm 8=CD ．将图2中的BC 绕点B 向下旋转?45，使得BCD 落在D C B ''的位置（如图3所⽰），此时OM D C ⊥''，OM D A //'，16cm ='D A ，求点B 到⽔平桌⾯OM 的距离．（参考数据：sin70°≈0.94，cos70°≈0.34，cot70°≈0.36，结果精确到1 cm ）23.（本题满分12分，第（1）⼩题5分，第（2）⼩题7分）如图，在ABC ?中，点D 、E 分别在边AB 、BC 上，AE 与CD 交于点F ．若AE 平分BAC ∠，AE AC AF AB ?=?（1）求证：AEC AFD ∠=∠；（2）若CD EG //，交边AC 的延长线于点G ，求证：BD FC CG CD ?=?．第20题图 A B CD E FG图1第21题图 ABCD O图3MD 'OA BC ' 45°160°第23题图GAC E DF 图2 M O A B160°C D24.（本题满分12分，每⼩题4分）如图，在平⾯直⾓坐标系xOy 中，抛物线n mx x y ++=231经过点)1,6(B 、)0,5(C ，且与y 轴交于点A ．（1）求抛物线的表达式及点A 的坐标；（2）点P 是y 轴右侧抛物线上的⼀点，过点P 作OA PQ ⊥，交线段OA 的延长线于点Q ，如果=∠45PAB ，求证：PQA Δ∽ACB Δ；（3）若点F 是线段AB （不包含端点）上的⼀点，且点F 关于AC 的对称点F '恰好在上述抛物线上，求F F '的长．25.（本题满分14分，第（1）⼩题4分，第（2）⼩题6分，第（3）⼩题4分）如图，已知在ABC Rt ?中，?=∠90C ，8=AC ，6=BC ，点P 、Q 分别在边AC 、射线CB 上，且CQ AP =，过点P 作AB PM ⊥，垂⾜为点M ，联结PQ ．以PM 、PQ 为邻边作平⾏四边形PQNM ．设x AP =，平⾏四边形PQNM 的⾯积为y ．（1）当平⾏四边形PQNM 为矩形时，求PQM ∠的正切值；（2）当点N 在ABC ?内，求y 关于x 的函数解析式，并写出它的定义域；（3）当过点P 且平⾏于BC 的直线经过平⾏四边形PQNM ⼀边的中点时，直接写出x 的值．ABC备⽤图ABCP QM NABC备⽤图x长宁区2019学年第⼀学期初三数学参考答案和评分建议2019.1⼀、选择题：（本⼤题共6题，每题4分，满分24分） 1．D ； 2．B ； 3．A ； 4．C ； 5．D ； 6．C ．⼆．填空题：（本⼤题共12题，满分48分） 7．b a-5； 8．3； 9．215-； 10．1->a ； 11．下降； 12．21-=x ； 13．13； 14．56； 15．3104； 16．17240； 17．424-； 18．5102．三、（本⼤题共7题，满分78分）19. （本题满分10分）解：原式= 2123211)3(212-+-? (6分) =132- (2分) =13+ (2分) 20．（本题满分10分，第（1）⼩题6分，第（2）⼩题4分）解：（1）∵32=EB AE ∴35=EB AB ， 52=AB AE （1分）∵AD EF // ∴EB ABEG AD =∵5=AD ∴355=EG ∴ 3=EG （2分）∵BC EF // ∴DC DF BC GF = ⼜∵BC EF AD //// ∴DCDFAB AE =∴AB AE BC GF = ∵10=BC ∴5210=GF ∴4=GF （2分）∴743=+=+=GF EG EF （1分）（2）21-=，10353+= （2分+2分） 21．（本题满分10分，第（1）⼩题5分，第（2）⼩题5分）解：（1）设圆O 的半径为r ,则OD 的长为r -6 （1分）∵CD 过圆⼼O , AC BC = ∴3221==AB AD ，AB CD ⊥（1分）在ADO Rt ?中，?=∠90ADO ∴ 222OD AD AO +=∴222)6()32(r r -+= ∴4=r （2分）在ADO Rt ?中，?=∠90ADO ， 23432cos ===∠AO AD BAO ∴ ?=∠30BAO （1分） (2) 过点O 作 BE OH ⊥，垂⾜为点H ，∴BH BE 2= （1分）∵ AO BE // ∴?=∠=∠30OAB EBA （1分）联结BO ，∴ 4==AO BO ∴?=∠=∠30OAB OBA∴?=∠+∠=∠60OBA EBA OBH （1分）在OBH Rt ?中，?=∠90BHO ， BOBH OBH =∠cos ∴260cos 4==?BH （1分）∴42==BH BE （1分） 22．（本题满分10分）解：过点B 作C D ''的垂线交C D ''的延长线于点E ，延长OA 交BE 于点F ，设x E C ='，由题意可知：=∠70EBA ，?='∠45C EB ，8=''D C ，16='=D A EF ，8+='=x E D AF （4分）在 C BE Rt '?中，?='∠90C BE ， EC BEC EB '='∠cot 得 x E C E C C EB E C BE ='='='∠'=?45cot cot （1分）∴ 16-=-=x EF BE BF （1分）在 BFA Rt ?中，?=∠90BFA ， BF AF ABF =∠tan 得16870tan -+=?x x ∴5.2936.0136.081670cot 170cot 816=-?+≈-+=x （1分）∴cm 455.44785.2978≈=++≈++=+=x AO AF FO ．（1分）∴点B 到⽔平桌⾯OM 的距离约为45cm （1分） 23．（本题满分12分，第（1）⼩题5分，第（2）⼩题7分）证明：（1）∵AE AC AF AB ?=? ∴AFAEAC AB =（1分）∵AE 平分BAC ∠∴CAF BAE ∠=∠（1分）∴ABE ?∽ACF ? （1分）∴ACF B ∠=∠（1分）⼜∵BAE B AEC CAF ACF AFD ∠+∠=∠∠+∠=∠,∴AEC AFD ∠=∠（1分） (2)∵AEC AFD ∠=∠，CFE AFD ∠=∠∴AEC CFE ∠=∠（1分）∴CE FC = （1分）∵CD EG // ∴CEG DCB ∠=∠ G ACF ∠=∠⼜∵B ACF ∠=∠∴G B ∠=∠（2分）∴BCD ?∽GEC ? （1分）∴CG BDCE CD =（1分）∴CGBD FC CD =即BD FC CG CD ?=?．（1分） 24．（本题满分12分，每⼩题4分）解：（1）∵抛物线n mx x y ++=231过点)1,6(B 、 )0,5(C ∴ =++?=++?055311663122n m n m ∴=-=538n m （2分）∴538312+-=x x y （1分）令0=x 得5=y ，∴点A 的坐标为)5,0( （1分）（2）∵)5,0(A ，)1,6(B ，)0,5(C ∴25=AC ，2=BC ，132=AB∴222BC AC AB += ∴?=∠90ACB⼜∵OA PQ ⊥∴?=∠90PQA ∴ACB PQA ∠=∠（1分）∵)5,0(A ，)0,5(C ∴OC OA =，∵?=∠90AOC ∴?=∠=∠45OCA OAC （1分）∵?=∠+∠+∠+∠180CAO BAC PAB QAP ， ?=∠45PAB∴?=∠+∠90BAC QAP ∵?=∠+∠90BAC ABC ∴ABC QAP ∠=∠（1分）∴PQA Δ∽ACB Δ （1分）（3）设点B '是点B 关于直线AC 的对称点，则2=='BC C B ，?=∠='∠90ACB B AC过点B 作x B ⊥'G 轴，垂⾜为点G ∵?=∠+'∠90OCA CO B ， ?=∠45OC A ，∴?='∠45CO B ∴1=='GC G B ∴），（1-4B ' （1分）∵点F '同时在线段B A '与抛物线上，∴设)53831,(F 2+-'x x x 分别过点F '，B '作轴y H F ⊥'，轴y H ⊥''B ，垂⾜分别为H 、H '，则H B H//F '''∴H A AH H B H F B A F A '='''='' 即6313842xx x -= ∴27=x （1分）⼜∵AC F F ⊥'，AC B B ⊥' ∴B //B F F '' ∴ B B F F B A F A ''='' ∴ 87427=='''=''H B H F B B F F （1分）∵222==BC BB ∴8722='F F ∴247='F F （1分）25．（本题满分14分，第（1）⼩题4分，第（2）⼩题6分，第（3）⼩题4分）解：（1）∵四边形PQNM 是矩形∴?=∠90MPQ ∵AB PM ⊥，∴?=∠90PMB∴?=∠+∠180PMB MPQ ∴AB PQ // ∴CPQ A ∠=∠（1分）在ABC Rt ?中，?=∠90C ，8=AC ，6=BC ，∴10=AB ， 53106sin ===AB BC A ∴在PMA Rt ?中，?=∠90AMP ，AP A AP PM 53sin =?= （1分）在PCQ Rt ?中，?=∠90C ，CQ CPQ CQ PQ 35sin =∠=∵CQ AP = ∴AP PQ 35=（1分）∴ 2593553tan ===∠AP APPQ PM PQM （ 1分）（2）过点Q 作AB QH ⊥，垂⾜为点H 在ABC Rt ?中，?=∠90C ，8=AC ，6=BC ，10=AB∴ 54108cos ===AB AC A ， 53106cos ===AB BC B ∴在PMA Rt ?中，?=∠90AMP ，x AP A AP AM 5454cos ==?= （1分）在BHQ Rt ?中，?=∠90BHQ ，x CQ BC BQ -=-=6 ∴ )6(53cos x B BQ BH -== （1分）∴ x x x BH AM AB MH 51532)6(535410-=---=--= （1分）由（1）知，x PM 53=，∴)7240(2532596)51532(532<<-=-=?=x x x x x MH PM y （ 2+1分）（3） 43200或59400 （ 2+2分）。

2019-2020学年上海市崇明区初三数学一模(试卷+参考答案)

崇明区2019学年第一学期教学质量调研测试卷九年级数学（满分150分，完卷时间100分钟）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】 1．下列各组图形一定相似的是（▲）(A)两个菱形；(B)两个矩形；(C)两个直角梯形；(D)两个正方形． 2．在Rt △ABC 中，∠C90，如果AC8，BC6，那么∠B 的余切值为（▲）3 (A) 43．抛物线；(B)4；(C)3 352 y3(x1)2的顶点坐标是（▲）；(D)4 5． (A)(1,2)；(B)(1,2)；(C)(1,2)；(D)(1,2)．4．已知c 为非零向量，a3c ，b2c ，那么下列结论中错．误．的是（▲）(A)a ∥b ；(B)3 ab ；(C)a 与b 方向相同；(D)a 与b 方向相反．25．如图，在55正方形网格中，一条圆弧经过A 、B 、C 三点，那么这条圆弧所在圆的圆心是（▲）(A)点P ；(B)点Q ；(C)点R ；(D)点M ． AB··AP·Q ··R·CDE NM·B C M(第6题图)(第5题图)6．如图，在△ABC 中，点D 、E 分别在AB 和AC 边上且DE ∥BC ，点M 为BC 边上一点（不与点B 、C 重合），联结AM 交DE 于点N ，下列比例式一定成立的是（▲）(A)A DAN ANAE；(B)D NBM NECM；(C)D NAE BMEC；(D)D NNE MCBM．九年级数学共6页第1页二、填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】7．已知xy23，那么x yx▲．8．已知线段A B8cm，点C在线段A B上，且2ACBCAB，那么线段A C的长▲cm．9．如果两个三角形相似，其中一个三角形的两个内角分别为50°和60°，那么另一个三角形的最大角为▲度．10．小杰沿坡比为1︰2.4的山坡向上走了130米．那么他沿着垂直方向升高了▲米．11．在某一时刻，测得一根高为1.8米的竹竿影长为3米，同时同地测得一栋楼的影长为90米，那么这栋楼的高度为▲米．12．如果将抛物线221yxx先向右平移2个单位，再向上平移3个单位，那么所得的新抛物线的顶点坐标为▲．13．如果二次函数2yaxbxc图像上部分点的横坐标x与纵坐标y的对应值如下表所示，那么它的图像与x轴的另一个交点坐标是▲．x⋯1012⋯y⋯0343⋯14．一个正五边形的中心角的度数为▲度．15．两圆的半径之比为3︰1，当它们外切时，圆心距为4，那么当它们内切时，圆心距为▲．16．如果梯形两底分别为4和6，高为2，那么两腰延长线的交点到这个梯形的较大底边的距离是▲．17．如图，在△ABC中，ACAB，点D在BC上，且BDBA，∠ABC的平分线BE交AD 于点E，点F是AC的中点，联结EF．如果四边形DCFE和△BDE的面积都为3，那么△ABC 的面积为▲．18．如图，在Rt△ABC中，∠C90，AB10，AC8，点D是AC的中点，点E在边AB 上，将△ADE沿DE翻折，使得点A落在点A处，当AEAB时，那么AA的长为▲．BAEFB DC C·DA (第17题图)(第18题图)九年级数学共6页第2页三、解答题（本大题共7题，满分78分）19．（本题满分10分）计算：2cot602tan302tan60sin452sin30．20．（本题满分10分，第(1)小题5分，第(2)小题5分）如图，在梯形ABCD中，AD∥BC，BC2AD，对角线AC、BD相交于点O，设A D a，ABb．（1）试用a、b的式子表示向量AO；A D（2）在图中作出向量DO在a、b方向上的分向量，O 并写出结论．BC(第20题图)21．（本题满分10分，第(1)小题5分，第(2)小题5分）如图，AC是O的直径，弦BDAO于点E，联结BC，过点O作OFBC于点F，BD8，AE2．（1）求O的半径；（2）求OF的长度．(第21题图)九年级数学共6页第3页22．（本题满分10分，第(1)小题５分，第(2)小题５分）如图1为放置在水平桌面l上的台灯，底座的高AB为5cm，长度均为20cm的连杆BC、CD与AB始终在同一平面上．（1）转动连杆BC，CD，使∠BCD成平角，∠ABC150，如图2，求连杆端点D离桌面l的高度DE．（2）将（1）中的连杆CD再绕点C逆时针旋转，经试验后发现，如图3，当∠BCD150时台灯光线最佳．求此时连杆端点D离桌面l的高度比原来降低了多少厘米？D· D·CC···B·BEA l·Al(图2)(图3)(图1)(第22题图)23．（本题满分12分，第(1)小题6分，第(2)小题6分）如图，△ABC中，ADBC，E是AD边上一点，联结BE，过点D作DFBE，垂足为F，且AEDFEFCD，联结AF、CF，CF与边AD交于点O．求证：（1）∠EAF∠DCF；（2）AFBDACDF．AEFOBCD(第23题图)九年级数学共6页第4页24．（本题满分12分，第(1)小题4分，第(2)小题4分，第(3)小题4分）如图，抛物线与x轴相交于点A(3,0)、点B(1,0)，与y轴交于点C(0,3)，点D是抛物线上一动点，联结OD交线段AC于点E．（1）求这条抛物线的解析式，并写出顶点坐标；（2）求∠ACB的正切值；（3）当△AOE与△ABC相似时，求点D的坐标．(第24题图)（备用图）九年级数学共6页第5页25．（本题满分14分，第(1)小题4分，第(2)小题4分，第(3)小题6分）如图，在△ABC中，ABAC10，BC16，点D为BC边上的一个动点（点D不与点B、点C重合）．以D为顶点作∠ADE∠B，射线DE交AC边于点E，过点A作AFAD交射线DE于点F．（1）求证：ABCEBDCD；A（2）当DF平分∠ADC时，求AE的长；F（3）当△AEF是等腰三角形时，求BD的长．EBCD(第25题图)AB DCBC(备用图)崇明区2019学年第一学期教学质量调研测试卷九年级数学答案及评分参考2020.1 一、选择题（本大题共6题，每题4分，满分24分）1、D2、A3、C4、C5、B6、B二、填空题（本大题共12题，每题4分，满分48分）7、528、4549、7010、5011、5412、(1,1)13、(3,0)14、7215、216、617、1018、285 2 或452三、解答题：（本大题共7题，满分78分）19、解：原式=33223322(3)()1222⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分3312⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分523 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分20、（1）∵AD∥BC，BC2ADAOAD ∴OCBC 12⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分AO AC ∴13即1AOAC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分3∵ADa，BC与AD同向∴BC2a⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵ACABBCb2a⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分12∴AOba⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分33（2）略，画图正确得4分，结论正确得1分21、（1）解：∵AC是O的直径，弦BDAO，BD8∴1BEDEBD4⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分2联结O B，设O的半径为x，则O AOBx∵AE2∴OEx2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵在Rt△OEB中，222OEBEOB⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分222∴(x2)4x解得x5∴O的半径为5⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分（2）∵在Rt△CEB中，222 CEBEBC又∵CE538，BE4∴BC45⋯⋯⋯⋯⋯⋯⋯⋯2分∵OBOC，OFBC∴1BFCFBC25⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分2∵在Rt△OFB中，222 OFBFOB∴OF25205⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分22、（1）解：过点B作BHDE，垂足为H由题意可得：ABHE5cm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分BDBCCD40cm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∠ABH∠DHB90，∠DBH1509060⋯⋯1分∴在Rt△DHB中，sin∠DBH D HDH3 DB402∴DH203cm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴DE2035(cm)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分（2）解：过点C作CGBH，CKDE，垂足分别为G、K由题意可得：BCCD20cm，CGKH九年级数学共6页第8页∴在Rt△CGB中，C GCG3sin∠CBH∴CG103cm BC202∴KH103cm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵∠BCG906030∴∠DCK150903030⋯⋯1分∴在Rt△DCK中，sinDCK∠D KDK1 DC202∴DK10cm⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴现在的高度为15103厘米⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴(2035)(15103)10310比原来降低了10310厘米⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分23、（1）证明：∵ADBC，DFBE∴∠ADB∠DFE90⋯⋯⋯1分∴∠DBE∠BED90，∠DBE∠BDF90∴∠BED∠BDF∴∠AEF∠CDF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵AEDFCDEFAEEF∴CDDF∴△AEF∽△CDF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分∴∠EAF∠DCF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分（2）证明：∵△AEF∽△CDF∴∠EFA∠DFC∴∠AFO∠EFD90∵∠DFB90∴∠BFD∠AFC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵∠EAF∠DCF，∠AOF∠COD∴△AOF∽△COD∴AOOFOCOD九年级数学共6页第9页AOOC∴OFOD又∵∠AOC∠FOD∴△AOC∽△FOD∴∠ACF∠EDF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵∠DBE∠BED∠FDE∠BED90∴∠DBE∠EDF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴∠ACF∠DBE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分又∵∠BFD∠AFO∴△BFD∽△CFA⋯⋯⋯⋯⋯⋯⋯⋯⋯1分AFAC∴DFBD∴AFBDACDF⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分24、（1）解：设抛物线的解析式为2(0)yaxbxca∵抛物线2yaxbxc过点A(3,0)、B(1,0)、C(0,3)9a3bc0∴⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分abc0c3a1b2解得⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分c3223 ∴这条抛物线的解析式为y xx⋯⋯⋯⋯⋯⋯⋯⋯⋯1分顶点坐标为(1,4)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分（2）解：过点B作BHAC，垂足为H∵∠AOC90，OAOC3∴∠OAC∠OCA45，AC32⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵∠BHA90∴∠HAB∠HBA90∴∠HAB∠HBA45∵在Rt△AHB中，222 AHBHAB，AB4∴AHBH22⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分九年级数学共6页第10页∴CH32222⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分BH22∵∠BHC90∴tanACB2∠⋯⋯⋯⋯⋯⋯⋯1分CH2 （3）解：过点D作DKx轴，垂足为K2设(,23)Dxxx，则K(x,0)，并由题意可得点D在第二象限223∴DKxx，OKx∵∠BAC是公共角∴当△AOE与△ABC相似时存在以下两种可能1°∠AOD∠ABC∴tan∠AODtan∠ABC3∴223xxx3113113解得x1，x2（舍去）⋯⋯⋯1分221133133∴D(,)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分222°∠AOD∠ACB∴tan∠AODtan∠ACB2∴223xxx2 解得x13，x23（舍去）⋯⋯⋯⋯⋯⋯1分∴D(3,23)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分综上所述：当△AOE与△ABC相似时，1133133点D的坐标为(,)22或(3,23)．25、（1）证明：∵ABAC∴∠B∠C⋯⋯⋯⋯⋯⋯⋯1分∵∠ADC∠B∠BAD即∠ADE∠CDE∠B∠BAD九年级数学共6页第11页∵∠ADE∠B∴∠BAD∠CDE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∴△BDA∽△CED⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分ABBD∴CDCE∴ABCEBDCD⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分（2）∵OF平分∠ADC∴∠ADE∠CDE∵∠CDE∠BAD∴∠ADE∠BADAEBDACBC∴DF∥AB∴⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分∵∠ADE∠B∠C∴∠BAD∠C又∵∠B是公共角∴△BDA∽△BAC⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分BDBA ∴BABCBD10∴101625∴BD⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分4254AE ∴1016125∴AE⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分32（3）过点A作AHBC，垂足为H1 ∵ABAC，AHBC∴BHCHBC28由勾股定理得出AH6∴3tanB4∵∠ADE∠B，AFAD∴tanADF∠A FAD34ADAB设A F3k，则A D4k，DF5k∵△BDA∽△CED∴DECD ①点F在线段D E的延长线上，当△AEF是等腰三角形时，存在以下三种情况：1°FAFE3k，则D E2k104k∴CD2k∴CD5∴BD16511⋯⋯⋯⋯⋯⋯⋯⋯2分2°EAEF则D E2.5k九年级数学共6页第12页104k ∴CD2.5k252539∴CD∴BD16⋯⋯⋯⋯⋯2分44473°AEAF3k则D Ek5104k∴75 CDk7725∴CD∴BD16⋯⋯⋯⋯⋯⋯2分222②点F在线段D E上，当△AEF是等腰三角形时，∵∠AFE90∠ADF∴∠AFE是一个钝角∴只存在FAFE3k这种可能，则D E8k104k∴CD8k∴CD20＞16，不合题意，舍去综上所述，当△AEF是等腰三角形时，BD的长11或394或252．（做对1种情况2分，做对2种情况4分，做对3种情况但没有讨论在线段D E上的这种可能5分，做对3种情况并分类讨论出不存在的情况6分）九年级数学共6页第13页。

上海市徐汇区2019年中考一模(即期末)数学试题及答案(word版)

2019学年第一学期徐汇区学习能力诊断卷初三年级数学学科 2019.1(满分150分，考试时间100分钟)考生注意：1. 本试卷含3个大题，共25题；2. 答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3. 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤。

一、选择题：(本大题共6题，每题4分，满分24分)【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1. 在比例尺为1:2000的地图上测得A 、B 两地间的图上距离为5cm ，则A 、B 两地间的实际距离为( ) (A) 10m ；(B) 25m ；(C) 100m ；(D) 10000m.2. 在△ABC 中，∠C =90°，AB =13，BC =5，则sin A 的值是( )(A)513 (B) 1213 (C) 512(D)1353. 抛物线()21232y x =--的顶点坐标是( )(A) ()2,3 (B) ()2,3-(C) ()2,3-(D) ()2,3--4. 已知抛物线()232y ax x a =++-，a 是常数且a <0，下列选项中可能是它大致图像的是( )5. 下列命题中是假命题的是( )(A) 若,a b b c ==，则a c =.(B) ()222a b a b -=-第9题EDABC第10题FDCABEP CD BA DCBA (C) 若12a b =-，则a b ∥.(D) 若a b =，则a b =6. 已知△ABC 和△DEF 相似，且△ABC 的三边长为3、4、5，如果△DEF 的周长为6，那么下列不可能是△DEF 一边长的是( ) (A) 1.5；(B) 2；(C) 2.5；(D) 3.二、填空题：(本大题共12题，每题4分，满分48分)【请将结果直接填入答题纸的相应位置上】 7. 已知34a b =，则2aa b+的值为__________. 8. 计算：()()23m n m n ++-=___________.9. 如图，△ABC 中，点D 、E 分别在边AB 、AC 上，CD 平分∠ACB ，DE ∥BC ，若AC =10，AE =4，则BC =________.10. 如图，在平行四边形ABCD 中，E 为CD 上一点，联结AE 、BD ，且AE 、BD 交于点F ，若:2:3DE EC =，则:DEFABFSS=_________.11. 如图，已知抛物线2y x bx c =++的对称轴为直线x =1，点A ，B 均在抛物线上，且AB 与x 轴平行，若点A 的坐标为30,2⎛⎫⎪⎝⎭，则点B 的坐标为___________.12. 如果抛物线()231y x =++经过点()11,A y 和点()23,B y ，那么1y 与2y 的大小关系是1y ___2y (填写“>”或“<”或“=”).13. 如图，已知梯形ABCD 中，AB ∥CD ，AB ⊥BC ，且AD ⊥BD ，若CD =1，BC =3，那么∠A 的正切值为________.14. 在高位100米的楼顶得得地面上某十字路口的俯角为，那么娄底到这个十字路口的水平距离是____________米(用含的代数式表示).F CBA DE15. △ABC 中，AD 是中线，G 是重心，,AB a AD b ==，那么BG =_______(用a b 、表示). 16. △ABC 中，AB=AC =5，BC =8，那么sin B =__________.17. 将二次函数23y x =的图像向左平移2个单位再向下平移4个单位，所得函数表达式是()2324y x =+-，我们来解释一下其中的原因：不妨设平移前图像上任意一点P 经过平移后得到点P ’，且点P ’的坐标为(),x y ，那么P ’点反之向右平移2个单位，再向上平移4个单位得到点()2,4P x y ++，由于点P 是二次函数23y x =的图像上的点，于是把点P (x +2,y +4)的坐标代入23y x =再进行整理就得到()2324y x =+-.类似的，我们对函数()11y x x =+的图像进行平移：先向右平移1个单位，再向上平移3个单位，所得图像的函数表达式为_____.18. 如图，矩形ABCD 中，AB =8，BC =9，点P 在BC 边上，CP =3，点Q 为线段AP 上的动点，射线BQ 与矩形ABCD 的一边交于点R ，且AP =BR ，则QRBQ=____________. 三、解答题：(本大题共7分，满分78分) 19. (本题满分10分)计算：2222sin 30+tan60tan30+sin 60cos 45+cot60cos30︒︒⋅︒︒︒︒⋅︒20. (本题满分10分，其中第(1)小题6分，第(2)小题4分)如图，点D 、E 分别在△ABC 的边BA 、CA 的延长线上，且DE ∥BC ，12AE AC =，F 为AC 的中点.(1) 设BF a =，AC b =，试用xa yb +的形式表示AB 、ED ；(x 、y 为实数)(2) 作出BF 在BA 、BC 上的分向量.第13题第18题FEACDB (保留作图痕迹，不写作法，写出结论)21. (本题满分10分)某商场为了方便顾客使用购物车，将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面。

青浦区2019学年初三一模数学试卷含答案

青浦区2019学年第一学期九年级期终学业质量调研测试数学试卷 2020.1（完成时间：100分钟满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每小题4分，满分24分）[每题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂] 1．如果两个相似三角形对应边之比是1∶2，那么它们的对应高之比是（）A ．1∶2；B ．1∶4；C ．1∶6；D ．1∶8．2．如图，DE ∥AB ，如果CE ∶AE =1∶2，DE =3，那么AB 等于（）A ．6；B ．9；C ．12；D ．13．3．在Rt △ABC 中，∠C =90º，AC =1，AB =3，则下列结论正确的是（）A ．sin 4B =； B ．cos 4B =； C．tan 4B =； D ．cot 4=B ．4．已知非零向量a 、b ，且有2=-a b ，下列说法中，不正确的是（）A ．||2||=a b ；B ． a ∥b ；C ．a 与b 方向相反；D ．20a b +=． 5．如图，在△ABC 中，点D 在边BC 上，点G 在线段AD 上，GE ∥BD ，且交AB 于点E ，GF ∥AC ，且交CD 于点F ，则下列结论一定正确的是（） A ．=AE CFAB CD； B ．=AE DFEB FC； C ．=EG FGBD AC； D ．=AE ADAG AB．6．抛物线2(0)y ax bx c a =++≠上部分点的横坐标x ，纵坐标y 的对应值如下表，那么下列结论中正确的是（） A ．0a >； B ．0b <； C ．0c <； D ．0abc <．二、填空题：（本大题共12题，每小题4分，满分48分） [请将结果直接填入答题纸的相应位置] 7．已知25a b =，那么ab a-的值为 ▲ ． 8．已知线段AB =2，P 是AB 的黄金分割点，且AP > BP ，那么AP= ▲ ．EAGFEDCBA（第2题图）（第5题图）9．已知向量a 与单位向量e 方向相反，且3a =，那么a = ▲ ．（用向量e 的式子表示） 10．如果抛物线21y ax =-的顶点是它的最低点，那么a 的取值范围是 ▲ ．11．如果点A （-3，1y ）和点B （-2，2y ）是抛物线2y x a =+上的两点，那么1y ▲ 2y ．（填“>”、“=”、“<”）．12．某公司10月份的产值是100万元，如果该公司第四季度每个月产值的增长率相同，都为)0>x x （，12月份的产值为y 万元，那么y 关于x 的函数解析式是 ▲ ． 13．在△ABC 中，∠C =90°，如果tan B =2，AB =4，那么BC = ▲ ．14．小明沿着坡度i =1∶2.5的斜坡前行了29米，那么他上升的高度是 ▲米． 15．点G 是△ABC 的重心，如果AB =AC =5，BC =8，那么AG = ▲ ． 16．如图，在菱形ABCD 中，O 、E 分别是AC 、AD 的中点，联结OE ．如果AB =3，AC =4，那么cot ∠AOE = ▲ ．17．在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF ．如果△DEF 与△ABC 相似（相似比不为1），那么△DEF 的面积为 ▲ ．18．已知，在矩形纸片ABCD 中，AB =5cm ，点E 、F 分别是边AB 、CD 的中点，折叠矩形纸片ABCD ，折痕BM交AD 边于点M ，在折叠的过程中，如果点A 恰好落在线段EF 上，那么边AD 的长至少是 ▲ cm ．三、解答题（本大题共7题，满分78分）[请将解题过程填入答题纸的相应位置] 19．（本题满分10分）计算：13tan 3045cos60︒︒︒-+20．（本题满分10分, 第（1）小题5分，第（2）小题5分）如图，在平行四边形ABCD 中，E 为DC 上一点，AE 与BD 交于点F ，DE ∶EC =2∶3．（1）求BF ∶DF 的值；（2）如果AD a =，AB b =，试用a 、b 表示向量AF ．FE D CBACBAABCDE O（第20题图）（第17题图）（第16题图）21．（本题满分10分, 第（1）小题5分，第（2）小题5分）如图，在Rt △ABC 中，∠ACB =90º，AC =2，BC =3．点D 为AC的中点，联结BD ，过点C 作CG ⊥BD ，交AC 的垂线AG 于点G ，GC 分别交BA 、 BD 于点F 、E ．（1）求GA 的长；（2）求△AFC 的面积．22．（本题满分10分）水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D 处测得点A 的仰角为20°，再往水城门的方向前进13米至C 处，测得点A 的仰角为 31°（点D 、C 、B 在一直线上），求该水城门AB 的高．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60 23．（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在△ABC 中，点D 在边BC 上，AE ∥BC ，BE 与AD 、AC 分别相交于点F 、G ， 2AF FG FE =⋅．（1）求证：△CAD ∽△CBG ；（2）联结DG ，求证：DG AE AB AG ⋅=⋅．AlG F EDBAEFGDCBA（第22题图）（第23题图）（第21题图）24．（本题满分12分，其中第（1）小题4分，第（2）小题5分，第（3）小题3分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ，对称轴为直线x =2，点A 的坐标为（1，0）．（1）求该抛物线的表达式及顶点坐标；（2）点P 为抛物线上一点（不与点A 重合），联结PC ．当∠PCB=∠ACB 时，求点P 的坐标；（3）在（2）的条件下，将抛物线沿平行于y 轴的方向向下平移，平移后的抛物线的顶点为点D ，点P 的对应点为点Q ，当OD ⊥DQ 时，求抛物线平移的距离．25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD ∥BC ，BC=BD=10，CD=4，AD=6．点P 是线段BD 上的动点，点E 、Q 分别是线段DA 、BD 上的点，且DE=DQ=BP ，联结EP 、EQ ．（1）求证：EQ ∥DC ；（2）当BP>BQ 时，如果△EPQ 是以EQ 为腰的等腰三角形，求线段BP 的长；（3）当BP=m （0<m<5）时，求∠PEQ 的正切值．（用含m 的式子表示）A B CDE QPDCBA（第25题图）（第24题图）（备用图）（备用图）青浦区2019学年第一学期期终学业质量调研九年级数学试卷参考答案及评分说明2020.1一、选择题：1．A ； 2．B ； 3．C ； 4．D ； 5．A ； 6．D ．二、填空题： 7．23； 81； 9．3-e ； 10．0>a ； 11．>； 12．()21001=+y x ； 13．5； 14． 15．2； 16．5； 17．1； 18．2．三、解答题：19．解：原式=131322⨯-． ······················································· （8分）1． ······················································································ （1分） =1． ······································································································· （1分）20．解：（1）∵四边形ABCD 是平行四边形，∴DC//AB ，DC=AB ， ························································································· （2分） ∴=BF ABDF DE． ······························································································· （1分） ∵DE ∶EC =2∶3，∴DC ∶DE =5∶2，∴AB ∶DE =5∶2， ····························· （1分） ∴BF ∶DF=5∶2． ····························································································· （1分）（2）∵BF ∶DF=5∶2，∴57=BF BD ． ······························································· （1分） ∵=-BD AD AB ，∴=-BD a b ． ··························································· （1分） ∴555777==-BF BD a b ． ········································································· （1分） ∵=+AF AB BF ，∴55527777=+-=+AF b a b a b ．·························· （2分）21．解：（1）∵∠ACB =90°，∴∠BCE +∠GCA =90°．∵CG ⊥BD ，∴∠CEB =90°，∴∠CBE +∠BCE =90°，∴∠CBE =∠GCA ． ···························································································· （2分）又∵∠DCB =∠GAC= 90°，∴△BCD ∽△CAG ． ························································································ （1分） ∴CD BCAG CA=， ································································································ （1分） ∴132AG =，∴23AG =． ············································································ （1分）（2）∵∠GAC +∠BCA =180°，∴GA ∥BC ． ······················································· （1分）∴GA AFBC FB=． ······························································································ （1分） ∴29AF FB =． ·································································································· （1分） ∴211AF AB =．∴211AFC ABCS S =． ··································································· （1分）又∵12332ABCS=⨯⨯=，∴611AFC S =． ··········································· （1分） 22．解：由题意，得∠ABD =90°，∠D =20°，∠ACB =31°，CD =13． ··························· （1分）在Rt △ABD 中，∵tan ∠=AB D BD ，∴tan 200.36==︒AB ABBD ． ······················· （3分）在Rt △ABC 中，∵tan ∠=AB ACB BC ，∴tan 310.6==︒AB ABBC ． ···················· （3分） ∵CD =BD -BC ， ∴130.360.6=-AB AB． ····························································································· （1分）解得11.7≈AB 米． ······························································································ （1分）答：水城门AB 的高约为11.7米． ········································································ （1分）23．证明：（1）∵2AF FG FE =⋅，∴=AF FEFG AF． ························································ （1分）又∵∠AFG =∠EFA ，∴△FAG ∽△FEA ． ······················································· （1分） ∴∠FAG =∠E ． ······························································································· （1分） ∵AE ∥BC ，∴∠E =∠EBC ． ··········································································· （1分） ∴∠EBC =∠FAG ． ·························································································· （1分）又∵∠ACD =∠BCG ，∴△CAD ∽△CBG ． ··················································· （1分）（2）∵△CAD ∽△CBG ，∴=CA CDCB CG． ····························································· （1分）又∵∠DCG =∠ACB ，∴△CDG ∽△CAB ． ··················································· （1分） ∴=DG CGAB CB． ····························································································· （1分） ∵AE ∥BC ，∴=AE AGCB GC． ········································································· （1分） ∴=AG GC AE CB ，∴=DG AGAB AE， ································································· （1分） ∴⋅=⋅DG AE AB AG ． ·············································································· （1分）24．解：（1）∵A 的坐标为（1，0），对称轴为直线x =2，∴点B 的坐标为（3，0） ···· （1分）将A （1，0）、B （3，0）代入2+=+y x bx c ，得10930.，++=⎧⎨++=⎩b c b c 解得：43.，=-⎧⎨=⎩b c ························································· （2分）所以，243=-+y x x ．当x =2时，2242+3=1=-⨯-y∴顶点坐标为（2，-1） ················································································ （1分）．（2）过点P 作PN ⊥x 轴，垂足为点N ．过点C 作CM ⊥PN ，交NP 的延长线于点M ．∵∠CON =90°，∴四边形CONM 为矩形． ∴∠CMN =90°，CO = MN ．∵243=-+y x x ，∴点C 的坐标为（0，3） ···················································· （1分）． ∵B （3，0），∴OB =OC ．∵∠COB =90°，∴∠OCB =∠BCM = 45°， ···················· （1分）．又∵∠ACB =∠PCB ，∴∠OCB -∠ACB =∠BCM -∠PCB ，即∠OCA =∠PCM ． ······ （1分）． ∴tan ∠OCA= tan ∠PCM ．∴13=PMMC．设PM =a ，则MC =3a ，PN =3-a ． ∴P （3a ，3-a ）．······························································································· （1分）将P （3a ，3-a ）代入243=-+y x x ，得()231233-+=-a a a ．解得111=9a ，2=0a （舍）．∴P （113，169）． ···················································· （1分）（3）设抛物线平移的距离为m ．得()221=---y x m ，∴D 的坐标为（2，1--m ）． ····················································································· （1分）过点D 作直线EF ∥x 轴，交y 轴于点E ，交PQ 的延长线于点F ． ∵∠OED =∠QFD =∠ODQ =90°，∴∠EOD+∠ODE = 90°，∠ODE+∠QDF = 90°， ∴∠EOD =∠QDF ，······························································································· （1分）∴tan ∠EOD = tan ∠QDF ．∴=DE QF OE DF ．∴1612911123-++=+-m mm ．解得15=m ．所以，抛物线平移的距离为15． ························································· （1分）25．解：（1）∵AD//BC ，∴∠EDQ =∠DBC ． ········································································ （1分）∵1=DE DQ ，1=BDBC，∴=DE BD DQ BC ． ······················································· （1分） ∴△DEQ ∽△BCD ． ························································································ （1分） ∴∠DQE =∠BDC ，∴EQ//CD ． ········································································ （1分）（2）设BP 的长为x ，则DQ =x ，QP =2x -10． ··············································· （1分） ∵△DEQ ∽△BCD ，∴=EQ QD DC CB ，∴25=EQ x ． ································· （1分）（i ）当EQ =EP 时，∴∠EQP =∠EPQ ，∵DE =DQ ，∴∠EQP =∠QED ，∴∠EPQ =∠QED ，∴△EQP ∽△DEQ ，∴EQ QP DE EQ =，∴()222105x x x ⎛⎫=-⋅ ⎪⎝⎭，解得 12523x =，或0x =（舍去）． ······························································ （2分）（ii ）当QE =QP 时，∴22105x x =-，解得 254x =， ······························································· （1分） ∵2564>，∴此种情况不存在． ··································································· （1分） ∴12523BP =（3）过点P 作PH ⊥EQ ，交EQ 的延长线于点H ；过点B 作BG ⊥DC ，垂足为点G ． ∵BD =BC ，BG ⊥DC ，∴DG =2，BG = ∵BP = DQ =m ，∴PQ =10-2m ． ∵EQ ▲DC ∴∠PQH =∠BDG ．又∵∠PHQ =∠BGD= 90°，。

2019届上海松江区中考一模数学试卷【含答案及解析】

2019届上海松江区中考一模数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 已知在Rt△ABC中，∠C=90°，如果BC=2，∠A=α，则AC的长为（）A．2sinα B．2cosα C．2tanα D．2cotα2. 下列抛物线中，过原点的抛物线是（）A．y=x2﹣1 B．y=（x+1）2 C．y=x2+x D．y=x2﹣x﹣13. 小明身高1.5米，在操场的影长为2米，同时测得教学大楼在操场的影长为60米，则教学大楼的高度应为（）A．45米 B．40米 C．90米 D．80米4. 已知非零向量，，，下列条件中，不能判定∥的是（）A．∥∥ B． C． =－2 D． =2，=5. 如图，在▱ABCD中，点E是边BA延长线上的一点，CE交AD于点F．下列各式中，错误的是（）A． B． C．D．6. 如图，已知在△ABC中，cosA=，BE、CF分别是AC、AB边上的高，联结EF，那么△AEF和△ABC的周长比为（）A．1：2 B．1：3 C．1：4 D．1：9二、填空题7. 已知，则的值为．8. 计算：（﹣3）﹣（+2）= ．9. 已知抛物线y=（k﹣1）x2+3x的开口向下，那么k的取值范围是．10. 把抛物线y=x2向右平移4个单位，所得抛物线的解析式为．11. 已知在△ABC中，∠C=90°，sinA=，BC=6，则AB的长是．12. 如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、C、E和点B、D、F，如果AC：CE=3：5，BF=9，那么DF= ．13. 已知点A（2，y1）、B（5，y2）在抛物线y=﹣x2+1上，那么y1 y2．（填“＞”、“=”或“＜”）14. 已知抛物线y=ax2+bx+c过（﹣1，1）和（5，1）两点，那么该抛物线的对称轴是直线．15. 在△ABC中，AB=AC=5，BC=8，AD⊥BC，垂足为D，BE是△ABC 的中线，AD与BE相交于点G，那么AG的长为．16. 在一个距离地面5米高的平台上测得一旗杆底部的俯角为30°，旗杆顶部的仰角为45°，则该旗杆的高度为米．（结果保留根号）17. 如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为．18. 如图，在△ABC中，∠ACB=90°，AB=9，cosB=，把△ABC绕着点C旋转，使点B与AB边上的点D重合，点A落在点E，则点A、E之间的距离为．三、计算题19. 计算：．四、解答题20. 如图，已知点D是△ABC的边BC上一点，且BD=CD，设=， =．（1）求向量（用向量、表示）；（2）求作向量在、方向上的分向量．（不要求写作法，但要指出所作图中表示结论的向量）21. 如图，已知AC∥BD，AB和CD相交于点E，AC=6，BD=4，F是BC上一点，S△BEF：S△EFC=2：3．（1）求EF的长；（2）如果△BEF的面积为4，求△ABC的面积．五、计算题22. 某大型购物商场在一楼和二楼之间安装自动扶梯AC，截面如图所示，一楼和二楼地面平行（即AB所在的直线与CD平行），层高AD为8米，∠ACD=20°，为使得顾客乘坐自动扶梯时不至于碰头，A、B之间必须达到一定的距离．（1）要使身高2.26米的姚明乘坐自动扶梯时不碰头，那么A、B之间的距离至少要多少米？（精确到0.1米）（2）如果自动扶梯改为由AE、EF、FC三段组成（如图中虚线所示），中间段EF为平台（即EF∥DC），AE段和FC段的坡度i=1：2，求平台EF的长度．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）六、解答题23. 如图，Rt△ABC中，∠ACB=90°，D是斜边AB上的中点，E是边BC上的点，AE与CD 交于点F，且AC2=CE•CB．（1）求证：AE⊥CD；（2）连接BF，如果点E是BC中点，求证：∠EBF=∠EAB．24. 如图，抛物线y=﹣x2+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．（1）求抛物线的解析式以及顶点坐标；（2）点C关于抛物线y=﹣x2+bx+c对称轴的对称点为E点，联结BC，BE，求∠CBE的正切值；（3）点M是抛物线对称轴上一点，且△DMB和△BCE相似，求点M坐标．25. 如图，已知四边形ABCD是矩形，cot∠ADB=，AB=16．点E在射线BC上，点F在线段BD上，且∠DEF=∠ADB．（1）求线段BD的长；（2）设BE=x，△DEF的面积为y，求y关于x的函数关系式，并写出函数定义域；（3）当△DEF为等腰三角形时，求线段BE的长．参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】。

2019-2020年上海各区数学中考一模压轴题分类汇编-25题含详解

专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【知识梳理】【历年真题】1．（2019秋•奉贤区期末）如图，已知平行四边形ABCD中，AD AB＝5，tan A＝2，点E在射线AD上，过点E作EF⊥AD，垂足为点E，交射线AB于点F，交射线CB于点G，联结CE、CF，设AE＝m．（1）当点E在边AD上时，①求△CEF的面积；（用含m的代数式表示）②当S△DCE＝4S△BFG时，求AE：ED的值；（2）当点E在边AD的延长线上时，如果△AEF与△CFG相似，求m的值．2．（2019秋•杨浦区期末）已知在菱形ABCD中，AB＝4，∠BAD＝120°，点P是直线AB上任意一点，联结PC．在∠PCD内部作射线CQ与对角线BD交于点Q（与B、D不重合），且∠PCQ＝30°．（1）如图，当点P在边AB上时，如果BP＝3，求线段PC的长；（2）当点P在射线BA上时，设BP＝x，CQ＝y，求y关于x的函数解析式及定义域；（3）联结PQ，直线PQ与直线BC交于点E，如果△QCE与△BCP相似，求线段BP的长．专题二动点函数背景下的面积问题【知识梳理】【历年真题】1．（2019秋•黄浦区期末）如图，△ABC 是边长为2的等边三角形，点D 与点B 分别位于直线AC 的两侧，且AD ＝AC ，联结BD 、CD ，BD 交直线AC 于点E ．（1）当∠CAD ＝90°时，求线段AE 的长．（2）过点A 作AH ⊥CD ，垂足为点H ，直线AH 交BD 于点F ，①当∠CAD ＜120°时，设AE ＝x ，y ＝BCE AEFS S ∆∆（其中S △BCE 表示△BCE 的面积，S △AEF 表示△AEF 的面积），求y 关于x 的函数关系式，并写出x 的取值范围；②当BCE AEFS S ∆∆＝7时，请直接写出线段AE 的长．2．（2019秋•松江区期末）已知tan∠MON＝2，矩形ABCD的边AB在射线OM上，AD＝2，AB＝m，CF⊥ON，垂足为点F．（1）如图（1），作AE⊥ON，垂足为点E，当m＝2时，求线段EF的长度．（2）如图（2），联结OC，当m＝2，且CD平分∠FCO时，求∠COF的正弦值；（3）如图（3），当△AFD与△CDF相似时，求m的值．专题三动点函数背景下的等腰三角形【知识梳理】【历年真题】1．（2019秋•浦东新区期末）在Rt△ABC中，∠A＝90°，AB＝4，AC＝3，D为AB边上一动点（点D与点A、B不重合），联结CD，过点D作DE⊥DC交边BC于点E．（1）如图，当ED＝EB时，求AD的长；（2）设AD＝x，BE＝y，求y关于x的函数解析式并写出函数定义域；（3）把△BCD沿直线CD翻折得△CDB'，联结AB'，当△CAB'是等腰三角形时，直接写出AD的长．2．（2019秋•青浦区期末）如图，在梯形ABCD中，AD∥BC，BC＝BD＝10，CD＝4，AD＝6．点P是线段BD上的动点，点E、Q分别是线段DA、BD上的点，且DE＝DQ＝BP，联结EP、EQ．（1）求证：EQ∥DC；（2）当BP＞BQ时，如果△EPQ是以EQ为腰的等腰三角形，求线段BP的长；（3）当BP＝m（0＜m＜5）时，求∠PEQ的正切值．（用含m的式子表示）3．（2019秋•闵行区期末）已知：如图，在Rt△ABC和Rt△ACD中，AC＝BC，∠ACB＝90°，∠ADC＝90°，CD＝2，（点A、B分别在直线CD的左右两侧），射线CD交边AB于点E，点G是Rt△ABC的重心，射线CG交边AB于点F，AD＝x，CE＝y．（1）求证：∠DAB＝∠DCF；（2）当点E在边CD上时，求y关于x的函数关系式，并写出x的取值范围；（3）如果△CDG是以CG为腰的等腰三角形，试求AD的长．4．（2019秋•崇明区期末）如图，在△ABC中，AB＝AC＝10，BC＝16，点D为BC边上的一个动点（点D不与点B、点C重合）．以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE于点F．（1）求证：AB•CE＝BD•CD；（2）当DF平分∠ADC时，求AE的长；（3）当△AEF是等腰三角形时，求BD的长．5．（2019秋•宝山区期末）如图，OC是△ABC中AB边的中线，∠ABC＝36°，点D为OC上一点，如果OD＝k⋅OC，过D作DE∥CA交于BA点E，点M是DE的中点，将△ODE绕点O顺时针旋转α度（其中0°＜α＜180°）后，射线OM交直线BC于点N．（1）如果△ABC的面积为26，求△ODE的面积（用k的代数式表示）；（2）当N和B不重合时，请探究∠ONB的度数y与旋转角α的度数之间的函数关系式；（3）写出当△ONB为等腰三角形时，旋转角α的度数．专题四动点函数背景下的线段问题【知识梳理】【历年真题】1．（2019秋•虹口区期末）如图，在Rt△ABC中，∠ACB＝90°，BC＝4，sin∠ABC＝3 5，点D为射线BC上一点，联结AD，过点B作BE⊥AD分别交射线AD、AC于点E、F，联结DF，过点A作AG∥BD，交直线BE于点G．（1）当点D在BC的延长线上时，如果CD＝2，求tan∠FBC；＝y，求y关于x的函数关系式（不需要写函数的定义域）；（2）当点D在BC的延长线上时，设AG＝x，S△DAF（3）如果AG＝8，求DE的长．2．（2019秋•静安区期末）已知：如图1，在△ABC中，AB＝AC，点D、E分别在边BC、DC上，AB2＝BE•DC，DE：EC＝3：1，F是边AC上的一点，DF与AE交于点G．（1）找出图中与△ACD相似的三角形，并说明理由；（2）当DF平分∠ADC时，求DG：DF的值；（3）如图2，当∠BAC＝90°，且DF⊥AE时，求DG：DF的值．专题四动点函数背景下四边形【知识梳理】【历年真题】1．（2019秋•长宁、金山区期末）如图，已知在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P、Q分别在边AC、射线CB上，且AP＝CQ，过点P作PM⊥AB，垂足为点M，联结PQ，以PM、PQ为邻边作平行四边形PQNM，设AP＝x，平行四边形PQNM的面积为y．（1）当平行四边形PQNM为矩形时，求∠PQM的正切值；（2）当点N在△ABC内，求y关于x的函数解析式，并写出它的定义域；（3）当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时，直接写出x的值．2．（2019秋•嘉定区期末）已知：点P在△ABC内，且满足∠APB＝∠APC（如图），∠APB+∠BAC＝180°．（1）求证：△PAB∽△PCA；（2）如果∠APB＝120°，∠ABC＝90°，求PCPB的值；（3）如果∠BAC＝45°，且△ABC是等腰三角形，试求tan∠PBC的值．3．（2019秋•徐汇区期末）如图，在△ABC中，AB＝AC＝5，BC＝6，点D是边AB上的动点（点D不与点AB重合），点G在边AB的延长线上，∠CDE＝∠A，∠GBE＝∠ABC，DE与边BC交于点F．（1）求cos A的值；（2）当∠A＝2∠ACD时，求AD的长；（3）点D在边AB上运动的过程中，AD：BE的值是否会发生变化？如果不变化，请求AD：BE的值；如果变化，请说明理由．4．(2019秋•普陀区期末)如图，在梯形ABCD中，AD//BC，∠C=90°，AD=2，BC=5，DC=3，点E在边BC上，tan∠AEC=3，点M是射线DC上一个动点(不与点D、C重合)，联结BM交射线AE于点N，设DM=x，AN=y．(1)求BE的长；(2)当动点M在线段DC上时，试求y与x之间的函数解析式,并写出函数的定义域；(3)当动点M运动时，直线BM与直线AE的夹角等于45°，请直接写出这时线段DM的长．专题2020年上海各区分类汇编-25题专题一动点函数下的相似三角形【历年真题】1．（2019秋•奉贤区期末）如图，已知平行四边形ABCD 中，AD AB ＝5，tan A ＝2，点E 在射线AD 上，过点E 作EF ⊥AD ，垂足为点E ，交射线AB 于点F ，交射线CB 于点G ，联结CE 、CF ，设AE ＝m ．（1）当点E 在边AD 上时，①求△CEF 的面积；（用含m 的代数式表示）②当S △DCE ＝4S △BFG 时，求AE ：ED 的值；（2）当点E 在边AD 的延长线上时，如果△AEF 与△CFG 相似，求m 的值．【考点】相似形综合题．【专题】综合题；运算能力；推理能力．【分析】（1）①先根据三角函数表示出EF ，再用勾股定理表示出AF ，再判断出△AEF ∽△BGF ，得出比例式表示出CG ，即可得出结论；②先表示出FG ，再用S △DCE ＝4S △BFG 建立方程求出m ，即可得出结论；（2）分两种情况：①当△AEF ∽△CGF 时，得出∠AFE ＝∠CFG ，进而得出BG ＝12BC ＝52，FG ＝BG tan ∠CBFBF ＝52，进而得出AF ＝AB +BF ＝5+52＝152，最后判断出△BGF ∽△AEF ，得出比例式建立方程求解即可得出结论；②当△AEF ∽△CGF 时，先判断出∠AFC ＝90°，进而得出CF ＝2BF ，再根据勾股定理得，求出BF ＝1，得出AF ＝AB +BF ＝6，同理：BG ＝，再判断出△BGF ∽△AEF ，得出比例式建立方程求解即可得出结论．【解答】解：（1）①∵EF ⊥AD ，∴∠AEF ＝90°，在Rt △AEF 中，tan A ＝2，AE ＝m ，∴EF ＝AE tan A ＝2m ，根据勾股定理得，AF ，∵AB ＝5，∴BF ＝5，∵四边形ABCD 是平行四边形，∴BC ＝AD AD ∥BC ，∴∠G ＝∠AEF ＝90°，∴△AEF ∽△BGF ，∴AE AFBG BF =，∴m BG =，∴BG m ，∴CG ＝BC +BG ＝m ＝m ，∴S △CEF ＝12EF •CG ＝12•2m •（m ）＝m ﹣m 2；②由①知，△AEF ∽△BGF ，∴BF FG AF EF =，∴FG ＝BFAF •EF •2m ＝2m ），∴EG ＝EF +FG ＝2m +2﹣m ）＝∴S △CDE ＝12DE •EG ＝12（m ）•5，S △BFG ＝12BG •FG ＝12m ）•2m ﹣m ）2，S △DCE ＝4S △BFG 时，∴5＝4m ）2，∴m m ＝354，∴DE ＝AD ﹣AE ﹣4＝4，∴AE ：ED ＝354：54＝3，即：AE ：ED 的值为3；（2）∵四边形ABCD 是平行四边形，∴BC ＝AD ，AD ∥BC ，∵EF ⊥AD ，∴EF ⊥BC ，∴∠AEF ＝∠CGF ＝90°，∵△AEF 与△CFG 相似，∴①当△AEF ∽△CGF 时，如图1，∴∠AFE ＝∠CFG ，∵EF ⊥BC ，∴BG ＝12BC ＝52，∵AD ∥BC ，∴∠CBF ＝∠A ，∵tan A ＝2，∴tan ∠CBF ＝2，在Rt △BGF 中，FG ＝BG tan ∠CBF根据勾股定理得，BF 52，∴AF ＝AB +BF ＝5+52＝152，∵BC∥AD，∴△BGF∽△AEF，∴BG BFAE AF=，∴，∴m ＝35 2；②当△AEF∽△CGF时，如图2，∴∠EAF＝∠GFC，∵∠EAF+∠AFE＝90°，∴∠GFC+∠AFE＝90°，∴∠AFC＝90°，∵AD∥BC，∴∠CBF＝∠A，∴tan∠CBF＝tan A＝2，在Rt△BFC中，CF＝BF•∠CBF＝2BF，根据勾股定理得，BF2+CF2＝BC2，∴BF2+4BF2）2，∴BF＝1，∴AF＝AB+BF＝6，在Rt△BGF中，同理：BG ＝5 5，∵AD∥BC，∴△BGF∽△AEF，∴AE AFBG BF=6155=，∴m ＝655．即：如果△AEF与△CFG相似，m 的值为35 2或．【点评】此题是相似形综合题，主要考查了平行四边形的性质，锐角三角函数，三角形的面积公式，相似三角形的判定和性质，用方程的思想解决问题是解本题的关键．2．（2019秋•杨浦区期末）已知在菱形ABCD中，AB＝4，∠BAD＝120°，点P是直线AB上任意一点，联结PC．在∠PCD内部作射线CQ与对角线BD交于点Q（与B、D不重合），且∠PCQ＝30°．（1）如图，当点P在边AB上时，如果BP＝3，求线段PC的长；（2）当点P在射线BA上时，设BP＝x，CQ＝y，求y关于x的函数解析式及定义域；（3）联结PQ ，直线PQ 与直线BC 交于点E ，如果△QCE 与△BCP 相似，求线段BP 的长．【考点】相似形综合题．【专题】几何综合题；应用意识．【分析】（1）如图1中，作PH ⊥BC 于H ．解直角三角形求出BH ，PH ，在Rt △PCH 中，理由勾股定理即可解决问题．（2）如图1中，作PH ⊥BC 于H ，连接PQ ，设PC 交BD 于O ．证明△POQ ∽△BOC ，推出∠OPQ ＝∠OBC ＝30°＝∠PCQ ，推出PQ ＝CQ ＝y ，推出PC ，在Rt △PHB 中，BH ＝12x ，PH ＝2x ，根据PC 2＝PH 2+CH 2，可得结论．（3）分两种情形：①如图2中，若直线QP 交直线BC 于B 点左侧于E ．②如图3中，若直线QP 交直线BC 于C 点右侧于E ．分别求解即可．【解答】解：（1）如图1中，作PH ⊥BC 于H ．∵四边形ABCD 是菱形，∴AB ＝BC ＝4，AD ∥BC ，∴∠A +∠ABC ＝180°，∵∠A ＝120°，∴∠PBH ＝60°，∵PB ＝3，∠PHB ＝90°，∴BH ＝PB •cos60°＝32，PH ＝PB •sin60°＝332，∴CH ＝BC ﹣BH ＝4﹣32＝52，∴PC =．（2）如图1中，作PH ⊥BC 于H ，连接PQ ，设PC 交BD 于O ．∵四边形ABCD 是菱形，∴∠ABD ＝∠CBD ＝30°，∵∠PCQ ＝30°，∴∠PBO ＝∠QCO ，∵∠POB＝∠QOC，∴△POB∽△QOC，∴PO BOQO CO=，∴PO QOBO CO=，∵∠POQ＝∠BOC，∴△POQ∽△BOC，∴∠OPQ＝∠OBC＝30°＝∠PCQ，∴PQ＝CQ＝y，∴PC y，在Rt△PHB中，BH＝12x，PH＝32x，∵PC2＝PH2+CH2，∴3y2＝（2x）2+（4﹣12x）2，∴y＝3（0≤x＜8）．（3）①如图2中，若直线QP交直线BC于B点左侧于E．此时∠CQE＝120°，∵∠PBC＝60°，∴△PBC中，不存在角与∠CQE相等，此时△QCE与△BCP不可能相似．②如图3中，若直线QP交直线BC于C点右侧于E．则∠CQE＝∠B＝QBC+∠QCP＝60°＝∠CBP，∵∠PCB＞∠E，∴只可能∠BCP＝∠QCE＝75°，作CF⊥AB于F，则BF＝2，CF＝PCF＝45°，∴PF＝CF＝，此时PB＝2+2，③如图4中，当点P在AB的延长线上时，∵△QCE 与△BCP 相似，∴∠CQE ＝∠CBP ＝120°，∴∠QCE ＝∠PCB ＝15°，作CF ⊥AB 于F ．∵∠FCB ＝30°，∴∠FCP ＝45°，∴BF ＝12BC ＝2，CF ＝PF ＝23∴PB ＝3﹣2．综上所述，满足条件的PB 的值为3或232．【点评】本题考查相似形综合题，考查了菱形的性质，解直角三角形，相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．专题二动点函数背景下的面积问题【历年真题】1．（2019秋•黄浦区期末）如图，△ABC 是边长为2的等边三角形，点D 与点B 分别位于直线AC 的两侧，且AD ＝AC ，联结BD 、CD ，BD 交直线AC 于点E ．（1）当∠CAD ＝90°时，求线段AE 的长．（2）过点A 作AH ⊥CD ，垂足为点H ，直线AH 交BD 于点F ，①当∠CAD ＜120°时，设AE ＝x ，y ＝BCE AEFS S ∆∆（其中S △BCE 表示△BCE 的面积，S △AEF 表示△AEF 的面积），求y 关于x 的函数关系式，并写出x 的取值范围；②当BCE AEFS S ∆∆＝7时，请直接写出线段AE的长．【考点】三角形综合题．【专题】等腰三角形与直角三角形；应用意识．【分析】（1）过点E 作EG ⊥BC ，垂足为点G ．AE ＝x ，则EC ＝2﹣x ．根据BG ＝EG 构建方程求出x 即可解决问题．（2）①证明△AEF ∽△BEC ，可得22BCE AEF S BE S AE∆∆=，由此构建关系式即可解决问题．②分两种情形：当∠CAD ＜120°时，当120°＜∠CAD ＜180°时，分别求解即可解决问题．【解答】解：（1）∵△ABC 是等边三角形，∴AB ＝BC ＝AC ＝2，∠BAC ＝∠ABC ＝∠ACB ＝60°．∵AD ＝AC ，∴AD ＝AB ，∴∠ABD ＝∠ADB ，∵∠ABD +∠ADB +∠BAC +∠CAD ＝180°，∠CAD ＝90°，∠ABD ＝15°，∴∠EBC ＝45°．过点E 作EG ⊥BC ，垂足为点G．设AE ＝x ，则EC ＝2﹣x ．在Rt △CGE 中，∠ACB ＝60°，∴3sin ACB=)2EG EC x =- ∠，1cos ACB=12CG EC x =- ∠，∴BG ＝2﹣CG ＝1+12x ，在Rt △BGE 中，∠EBC ＝45°，∴131)22x x +=-，解得4x =-．所以线段AE的长是4-．（2）①设∠ABD ＝α，则∠BDA ＝α，∠DAC ＝∠BAD ﹣∠BAC ＝120°﹣2α．∵AD ＝AC ，AH ⊥CD ，∴1CAF=DAC=60-2α ∠∠，又∵∠AEF ＝60°+α，∴∠AFE ＝60°，∴∠AFE ＝∠ACB ，又∵∠AEF ＝∠BEC ，∴△AEF ∽△BEC ，∴22BCE AEF S BE S AE∆∆=，由（1）得在Rt △CGE 中，BG ＝1+12x，EG )2x =-，∴BE 2＝BG 2+EG 2＝x 2﹣2x +4，∴2224x x y x-+=（0＜x ＜2）．②当∠CAD ＜120°时，y ＝7，则有7＝2224x x x-+，整理得3x 2+x ﹣2＝0，解得x ＝23或﹣1（舍弃），2AE=3．当120°＜∠CAD ＜180°时，同法可得22+24x x y x +=当y＝7时，7＝22+24x xx，整理得3x2﹣x﹣2＝0，解得x＝﹣23（舍弃）或1，∴AE＝1．【点评】本题属于三角形综合题，考查了等边三角形的性质，解直角三角形，相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考常考题型．2．（2019秋•松江区期末）已知tan∠MON＝2，矩形ABCD的边AB在射线OM上，AD＝2，AB＝m，CF⊥ON，垂足为点F．（1）如图（1），作AE⊥ON，垂足为点E，当m＝2时，求线段EF的长度．（2）如图（2），联结OC，当m＝2，且CD平分∠FCO时，求∠COF的正弦值；（3）如图（3），当△AFD与△CDF相似时，求m的值．【考点】相似形综合题．【专题】分类讨论；图形的相似；推理能力．【分析】（1）如图1，延长FC交OM于点G，证∠BCG＝∠MON，在Rt△AOE中，设OE＝a，可求得OA，OG，OF的长，则EF＝OF﹣OE＝65 5；（2）如图2，延长FC交OM于点G，由（1）得CG＝5，推出CO＝CG＝5，在Rt△COB中，由勾股定理求出a的值，得出OF的长，可求出cos∠COF的值，进一步推出sin∠COF的值；（3）需分情况讨论：当D在∠MON内部时，△FDA∽△FDC时，此时CD＝AD＝2，m＝2；当△FDA∽△CDF 时，延长CD交ON于点Q，过F作FP⊥CQ于P，可利用三角函数求出m的值；当D在∠MON外部时，可利用相似的性质等求出m的值．【解答】解：（1）如图1，延长FC交OM于点G，∵∠BCG+∠CGB＝90°，∠MON+∠CGB＝90°，∴∠BCG＝∠MON，则tan∠BCG＝tan∠MON＝2，∴BG＝2BC＝4，CG＝，在Rt△AOE中，设OE＝a，由tan∠MON＝2，可得OA a，则OG+6，OF＝OG＝a+，∴EF＝OF﹣OE＝65 5；（2）如图2，延长FC交OM于点G，由（1）得CG＝∵CD平分∠FCO，∴∠FCD＝∠DCO，∵CD∥OM，∴∠FCD＝∠CGO，∠DCO＝∠COG，∴∠CGO＝∠COG，∴CO＝CG＝在Rt△COB中，由BC2+BO2＝OC2，得22++2）2＝（2，解得a1＝﹣655（舍去），a2＝255，∴OF＝a+5＝5，cos∠COF＝45 OFOC=，∴sin∠COF＝3 5；（3）当D在∠MON内部时，①如图3﹣1，△FDA∽△FDC时，此时CD＝AD＝2，∴m＝2；②当△FDA∽△CDF时，如图3﹣2，延长CD交ON于点Q，过F作FP⊥CQ于P，则∠FDC＝∠FDA＝135°，∴∠FDP＝45°，∵PC＝FP•tan∠PFC＝FP•tan∠MON＝2FP＝2DP＝CD+DP，∴FP＝PD＝CD＝m，∴FD m，∵△FDA∽△CDF，∴FD CD DA FD=，∴FD==，∴m＝1；当D在∠MON外部时，∠ADF＞90°，∠DFC＞90°，∴∠ADF ＝∠DFC ，∴∠DFI ＝∠FDI ，ID ＝IF ，①如图3﹣3，△FDA ∽△DFC 时，此时△FDA ≌△DFC ，∴CF ＝AD ＝2，∵∠DAF ＝∠FCD ＝∠FHD ，∴A 、O 重合，延长BC 交ON 于R ，∴FR ＝2CF ＝4，CR ＝BR ＝，∴m ＝CD ＝AB ＝12BR ＝；②如图3﹣4，△FDA ∽△CFD 时，设CF ＝（t ＞0），延长BC 交ON 于R ，过F 作FS ⊥CD 于S ，∵△DFC ≌△FDH ，∴DH ＝FC ，∴ID ＝IF ＝12CF ，∴IS ＝t ，FS ＝2t ，CS ＝4t ，DS ）t ，DH ＝FC ＝，∵△FDA ∽△CFD ，∴AD DF DF FC=，∴DF 2＝AD •FC ＝2DH ＝t ，∵DF 2＝DS 2+FS 2，∴＝4t 2+）2t 2，解得t 1＝512-，t 2＝0（舍去），∴DH ＝t ＝52＝AD ，矛盾，综上所述：m ＝1或m ＝2，或m ＝【点评】本题考查了解直角三角形，等腰三角形的性质，相似三角形的判定与性质等，解题关键是注意分类讨论思想的运用．专题三动点函数背景下的等腰三角形【历年真题】1．（2019秋•浦东新区期末）在Rt△ABC中，∠A＝90°，AB＝4，AC＝3，D为AB边上一动点（点D与点A、B不重合），联结CD，过点D作DE⊥DC交边BC于点E．（1）如图，当ED＝EB时，求AD的长；（2）设AD＝x，BE＝y，求y关于x的函数解析式并写出函数定义域；（3）把△BCD沿直线CD翻折得△CDB'，联结AB'，当△CAB'是等腰三角形时，直接写出AD的长．【考点】几何变换综合题．【专题】几何综合题；应用意识．【分析】（1）证明∠ACD＝∠EDB＝∠B，推出tan∠ACD＝tan∠B，可得AD ACAC AB=，由此构建方程即可解决问题．（2）如图1中，作EH⊥BD于H．证明△ACD∽△HDE，推出AC ADDH EH=，由此构建关系式即可解决问题．（3）分两种情形：①如图3﹣1中，设CB′交AB于K，作AE⊥CK于E，DM⊥CB′于M，DN⊥BC于N．利用角平分线的性质定理求出BD即可．②如图3﹣2中，当CB′交BA的延长线于K时，同法可得BD．【解答】解：（1）∵ED＝EB，∴∠EDB＝∠B，∵CD⊥DE，∴∠CDE＝∠A＝90°，∵∠ACD+∠ADC＝90°，∠ADC+∠EDH＝90°，∴∠ACD＝∠EDB＝∠B，∴tan∠ACD＝tan∠B，∴AD ACAC AB=，∴334AD=，∴94AD=．（2）如图1中，作EH⊥BD于H．在Rt△ACB中，∵∠A＝90°，AC＝3，AB＝4，∴BC=5，∵BE＝y，∴EH＝35y，BH＝45y，DH＝AB﹣AD﹣BH＝4﹣x﹣45y，∵∠A＝∠DHE＝90°，∠ACD＝∠EDH，∴△ACD∽△HDE，∴AC AD=DH EH，∴3x=434-x-55y y，∴220594x xyx-=+（0＜x＜4）．（3）①如图3﹣1中，设CB′交AB于K，作AE⊥CK于E，DM⊥CB′于M，DN⊥BC于N∵AC ＝AB ′＝3，AE ⊥CB ′，∴CE ＝'EB ='12CB ＝52，∴AE 22225113()22AC CE -=-，由△ACE ∽△KCA ，可得AK ＝3115，CK ＝185，∴BK ＝AB ﹣AK ＝4﹣3115，∵∠DCK ＝∠DCB ，DM ⊥CM ，DN ⊥CB ，∴DM ＝DN ，∴181185215252CDK CDB CK DM S DK CK S DB CB BC DN ∆∆===== ，∴BD ＝2543BK ＝10043151143，∴AD ＝AB ﹣BD ＝4﹣（10043151143）＝7242151143．②如图3﹣2中，当CB ′交BA 的延长线于K 时，同法可得BD ＝2543BK ＝10043151143，∴AD ＝AB ﹣BD ＝7242﹣151143．【点评】本题属于几何变换综合题，考查了解直角三角形，相似三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．2．（2019秋•青浦区期末）如图，在梯形ABCD 中，AD ∥BC ，BC ＝BD ＝10，CD ＝4，AD＝6．点P 是线段BD 上的动点，点E 、Q 分别是线段DA 、BD 上的点，且DE ＝DQ ＝BP ，联结EP 、EQ ．（1）求证：EQ ∥DC ；（2）当BP ＞BQ 时，如果△EPQ 是以EQ 为腰的等腰三角形，求线段BP 的长；（3）当BP ＝m （0＜m ＜5）时，求∠PEQ 的正切值．（用含m 的式子表示）【考点】相似形综合题．【专题】综合题；运算能力；推理能力．【分析】（1）先利用两边对应成比例，夹角相等，判断出△DEQ ∽△BCD ，得出∠DQE ＝∠BDC ，即可得出结论；（2）先用△DEQ ∽△BCD ，得出比例式表示出EQ ，再分两种情况，建立方程求解，即可得出结论；（3）先判得出△PHQ ∽△BGD ，得出PH PQ HQ BG BD GD ==，进而表示出HQ ＝1025m -，PH ＝26(102)5m -，即可得出结论．【解答】解：（1）∵AD ∥BC ，∴∠EDQ ＝∠DBC ，∵DE ＝DQ ，BD ＝BC ，∴1DE DQ =，BD BC ＝1，∴DE BD DQ BC=，∴△DEQ ∽△BCD ，∴∠DQE ＝∠BDC ，∴EQ ∥CD ；（2）设BP ＝x ，则DQ ＝x ，QP ＝2x ﹣10，∵△DEQ∽△BCD，∴EQ QDDC BC=，∴410EQ x=，∴EQ＝25x，∵△EPQ是以EQ为腰的等腰三角形，∴Ⅰ、当EQ＝EP时，∴∠EQP＝∠EPQ，∵DE＝DQ，∴∠EQP＝∠QED，∴∠EPQ＝∠QED，∴△EQP∽△DEQ，∴，∴EQ2＝DE•QP，∴（25x）2＝（2x﹣10）•x，解得，x＝0（舍）或x＝12523＜6，即：BP＝12523，Ⅱ、当QE＝QP时，25x＝2x﹣10，解得，x＝254＞6，此种情况不存在，即：BP＝125 23；（3）如图，过点P作PH⊥EQ，交EQ的延长线于点H，过点B作BG⊥DC，垂足为点G，∵BD＝BC，BG⊥DC，∴DG＝2，BG＝，∵BP＝DQ＝m，∴PQ＝10﹣2m，∵EQ∥DC，∴∠PQH＝∠BDG，∵∠PHQ＝∠BGD＝90°，∴△PHQ∽△BGD，∴PH PQ HQBG BD GD==102102m HQ-==，∴HQ＝1025m-，PH＝2)5m-，∴EH＝102255m m-+＝2，∴tan∠PEQ＝PHEH＝2)5m-12⨯＝﹣5m．【点评】此题是相似形综合题，主要考查了相似三角形的判定和性质，平行线的性质，锐角三角函数，用方程的思想解决问题是解本题的关键．3．（2019秋•闵行区期末）已知：如图，在Rt△ABC和Rt△ACD中，AC＝BC，∠ACB＝90°，∠ADC＝90°，CD＝2，（点A、B分别在直线CD的左右两侧），射线CD交边AB于点E，点G是Rt△ABC的重心，射线CG交边AB于点F，AD＝x，CE＝y．（1）求证：∠DAB＝∠DCF；（2）当点E在边CD上时，求y关于x的函数关系式，并写出x的取值范围；（3）如果△CDG是以CG为腰的等腰三角形，试求AD的长．【考点】相似形综合题．【专题】图形的相似；推理能力．【分析】（1）由点G是Rt△ABC的重心，证明CF⊥AB，即∠AFC＝90°，利用外角的性质即可证明结论；（2）过点B作BH⊥CD于点H，先证△CAD≌△BCH，得出BH＝CD＝2，CH＝AD＝x，DH＝2﹣x，再证△ADE ∽△BHE，利用合比性质即可求出结论；（3）分两种情况讨论，当GC＝GD时，如图2﹣1，取AC的中点M，联结MD，可证AD＝CH＝12CD=1；当CG＝CD时，如图2﹣2，可由重心分别求出CF，AC，CD的长，可由勾股定理求出AD的长．【解答】（1）证明：∵点G是Rt△ABC的重心，∴CF是Rt△ABC的中线，又∵在Rt△ABC中，AC＝BC，∠ACB＝90°，∴CF⊥AB，即∠AFC＝90°，∵∠DEF＝∠ADE+∠DAE＝∠EFC+∠ECF，且∠ADE＝∠EFC＝90°，∴∠DAB＝∠DCF；（2）解：如图1，过点B作BH⊥CD于点H，则∠CBH+∠BCH＝90°，又∵∠BCH+∠ACD＝90°，∴∠ACD＝∠CBH，又∵∠ADC＝∠CHB＝90°，AC＝CB，∴△CAD≌△BCH，∴BH＝CD＝2，CH＝AD＝x，DH＝2﹣x，∵∠ADC＝∠CHB＝∠BHD＝90°，∴AD∥BH，∴△ADE∽△BHE，∴AD DEBH EH=，∴2x DEEH=，∴22x DE EH DHEH EH++==，∴4-2xEH=x+2，∴2424(02)22x xy CE CH HE x xx x-+==+=+=<≤++；（3）解：当GC＝GD时，如图2﹣1，取AC的中点M，联结MD，那么MD＝MC，联结MG，MG⊥CD，且直线MG经过点B，那么BH与MG共线，又CH ＝AD ，那么AD ＝CH ＝12CD =1；当CG ＝CD 时，如图2﹣2，即CG ＝2，点G 为△ABC 的重心，∴332CF CG ==，∴AB ＝2CF ＝6，∴22AC AB ==，∴AD ==；综上所述，AD ＝1【点评】本题考查了函数，相似三角形的判定与性质，重心的性质等，解题关键是熟练掌握重心的性质．4．（2019秋•崇明区期末）如图，在△ABC 中，AB ＝AC ＝10，BC ＝16，点D 为BC 边上的一个动点（点D 不与点B 、点C 重合）．以D 为顶点作∠ADE ＝∠B ，射线DE 交AC 边于点E ，过点A 作AF ⊥AD 交射线DE 于点F ．（1）求证：AB •CE ＝BD •CD ；（2）当DF 平分∠ADC 时，求AE 的长；（3）当△AEF 是等腰三角形时，求BD 的长．【考点】相似形综合题．【专题】几何综合题；图形的相似；推理能力．【分析】（1）根据等腰三角形的性质得到∠B ＝∠C ，根据三角形的外角性质得到∠BAD ＝∠CDE ，得到△BAD ∽△CDE ，根据相似三角形的性质证明结论；（2）证明DF ∥AB ，根据平行线的性质得到AE BD AC BC =，证明△BDA ∽△BAC ，根据相似三角形的性质列式计算，得到答案；（3）分点F 在DE 的延长线上、点F 在线段DE 上两种情况，根据等腰三角形的性质计算即可．【解答】（1）证明：∵AB ＝AC ，∴∠B ＝∠C ，∠ADC ＝∠BAD +∠B ，∠ADE ＝∠B ，∴∠BAD ＝∠CDE ，又∠B ＝∠C ，∴△BAD ∽△CDE ，∴AB BD CD CE=，即AB •CE ＝BD •CD ；（2）解：∵DF 平分∠ADC ，∴∠ADE ＝∠CDE ，∵∠CDE ＝∠BAD ，∴∠ADE ＝∠BAD ，∴DF ∥AB ，∴AE BD AC BC=，∵∠BAD ＝∠ADE ＝∠B ，∴∠BAD ＝∠C ，又∠B ＝∠B ，∴△BDA ∽△BAC ，∴BD BA BA BC =，即101016BD =解得，254BD =，∴2541016AE =，解得，AE ＝12532；（3）解：作AH ⊥BC 于H ，∵AB ＝AC ，AH ⊥BC ，∴BH ＝HC ＝12BC ＝8，由勾股定理得，AH 22221086AB BH -=-=，∴tan B ＝AH BH ＝34，∴tan ∠ADF ＝AF AD ＝34，设AF ＝3x ，则AD ＝4x ，由勾股定理得，DF 22AD AF +＝5x ，∵△BAD ∽△CDE ，∴AD AB DE CD =，当点F在DE的延长线上，FA＝FE时，DE＝5x﹣3x＝2x，∴1042xCD x=，解得，CD＝5，∴BD＝BC﹣CD＝11，当EA＝EF时，DE＝EF＝2.5x，∴1042.5xCD x=，解得，CD＝254，∴BD＝BC﹣CD＝39 4；当AE＝AF＝3x时，DE＝75x，∴10475xCD x=，解得，CD＝72，∴BD＝BC﹣CD＝252；当点F在线段DE上时，∠AFE为钝角，∴只有FA＝FE＝3x，则DE＝8x，∴1048x CD x=，解得，CD＝20＞16，不合题意，∴△AEF是等腰三角形时，BD的长为11或394或252．【点评】本题考查的是相似三角形的判定和性质、等腰三角形的性质，掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键．5．（2019秋•宝山区期末）如图，OC是△ABC中AB边的中线，∠ABC＝36°，点D为OC上一点，如果OD＝k⋅OC，过D作DE∥CA交于BA点E，点M是DE的中点，将△ODE绕点O顺时针旋转α度（其中0°＜α＜180°）后，射线OM交直线BC于点N．（1）如果△ABC的面积为26，求△ODE的面积（用k的代数式表示）；（2）当N和B不重合时，请探究∠ONB的度数y与旋转角α的度数之间的函数关系式；（3）写出当△ONB为等腰三角形时，旋转角α的度数．【考点】几何变换综合题．【专题】等腰三角形与直角三角形；平移、旋转与对称；图形的相似；推理能力．【分析】（1）通过证明△ODE ∽△OCA ，可得2()DEO OAC S OD S OC∆∆=，即可求解；（2）通过证明△OEM ∽△BAC ，可得∠EOM ＝∠ABC ＝36°，分两种情况讨论可求解；（3）分四种情况讨论，由等腰三角形的性质可求解．【解答】解：（1）∵OC 是△ABC 中AB 边的中线，△ABC 的面积为26，∴S △OAC ＝13，∵DE ∥AC ，∴△ODE ∽△OCA ，∠OEM ＝∠OAC ，∴2()DEO OAC S OD S OC∆∆=，且OD ＝k ⋅OC ，∴S △ODE ＝13k 2，（2）∵△ODE ∽△OCA ，∴OE OD DE k OA OC AC ===，∵OC 是△ABC 中AB 边的中线，点M 是DE 的中点，∴AB ＝2AO ，EM ＝12DE ，∴2OE k EM AB AC==，且∠OEM ＝∠OAC ，∴△OEM ∽△BAC ，∴∠EOM ＝∠ABC ＝36°，如图2，当0＜α＜144°时，∵∠AON ＝∠B +∠ONB ，∴∠AOE +∠EOM ＝∠B +∠ONB ∴y ＝α如图3，当144°＜α＜180°时，∵∠BON ＝∠EOM ﹣∠BOE ＝36°﹣（180°﹣α）∴∠NOB ＝α﹣144°，∵∠BNO ＝∠ABC ﹣∠NOB ＝36°﹣（α﹣144°）＝180°﹣α；（3）当0＜α＜144°时，若OB＝ON，则∠ABC＝∠BNO＝36°＝α，若OB＝BN，则∠ONB＝180362-＝72°＝α，若ON＝BN，则∠ABC＝∠BON＝36°，∴∠ONB＝180°﹣2×36°＝108°＝α，当144°＜α＜180°时，若OB＝BN，则∠N＝∠NOB＝18°＝180°﹣α，∴α＝162°．【点评】本题是几何变换综合题，考查了相似三角形的判定和性质，旋转的性质，等腰三角形的性质等知识，证明△OEM∽△BAC是本题的关键．专题四动点函数背景下的线段问题【历年真题】1．（2019秋•虹口区期末）如图，在Rt△ABC中，∠ACB＝90°，BC＝4，sin∠ABC＝3 5，点D为射线BC上一点，联结AD，过点B作BE⊥AD分别交射线AD、AC于点E、F，联结DF，过点A作AG∥BD，交直线BE于点G．（1）当点D在BC的延长线上时，如果CD＝2，求tan∠FBC；（2）当点D在BC的延长线上时，设AG＝x，S△DAF＝y，求y关于x的函数关系式（不需要写函数的定义域）；（3）如果AG＝8，求DE的长．【考点】三角形综合题．【专题】几何综合题；等腰三角形与直角三角形；解直角三角形及其应用；运算能力；推理能力；应用意识．【分析】（1）求出AC＝3，可得∠DAC＝∠FBC，则tan∠FBC＝tan∠DAC＝23 DCAC=；（2）由条件可得∠AGF＝∠CBF，可得AF CFAG BC=，可用x表示CF和AF的长，求出CD，则S△DAF＝12AF CD，可用x表示结果；（3）分两种情况，①当点D 在BC 的延长线上时，②当点D 在BC 的边上时，可求出AE 长AD 的长，则DE ＝AD ﹣AE 可求出．【解答】解：（1）∵∠ACB ＝90°，BC ＝4，sin ∠ABC ＝35，∴设AC ＝3x ，AB ＝5x ，∴（3x ）2+16＝（5x ）2，∴x ＝1，即AC ＝3，∵BE ⊥AD ，∴∠AEF ＝90°，∵∠AFE ＝∠CFB ，∴∠DAC ＝∠FBC ，∴tan ∠FBC ＝tan ∠DAC ＝23DC AC =；（2）∵AG ∥BD ，∴∠AGF ＝∠CBF ，∴tan ∠AGF ＝tan ∠CBF ，∴AF CF AG BC =，AG AF BC CF =，∴34x CF CF-=，∴124CF x =+．∴12334AF CF x =-=-+＝34x x+．∵∠EAF ＝∠CBF ，∴CD CF AC BC =，∴94CD x =+，∴S △DAF ＝12AF CD ＝2193272442(4)x x x x x ⨯⨯=+++；（3）①当点D 在BC 的延长线上时，如图1，∵AG ＝8，BC ＝4，AG ∥BD ，∴21AG AF BC CF ==，∴AF ＝2CF ，∵AC ＝3，∴AF ＝2，CF ＝1，∴CF 1tan AGE=tan CBF==BC 4∠∠，∴AE 1=GE 4，设AE ＝x ，GE ＝4x ，∴x 2+16x 2＝82，解得x ＝，即AE ．同理tan ∠DAC ＝tan ∠CBF ，∴DC 1=AC 4，∴DC ＝34，∴AD∴DE AD AE=-=②当点D在BC的边上时，如图2，∵AG∥BD，AG＝8，BC＝4，∴8241AG AFBC CF===．∴AF＝6，∵∠EAF＝∠CBF＝∠ABC，∴cos∠EAF＝cos∠ABC，∴654AE=，∴245AE=，同理AC BCAD AB=，∴345AD=，∴154AD=．∴DE＝AE﹣AD＝241521 5420-=．综合以上可得DE的长为191768或2120．【点评】本题是三角形综合题，考查了勾股定理，平行线的性质，三角形的面积，锐角三角函数等知识，熟练掌握锐角三角函数的定义是解题的关键．2．（2019秋•静安区期末）已知：如图1，在△ABC中，AB＝AC，点D、E分别在边BC、DC上，AB2＝BE•DC，DE：EC＝3：1，F是边AC上的一点，DF与AE交于点G．（1）找出图中与△ACD相似的三角形，并说明理由；（2）当DF平分∠ADC时，求DG：DF的值；（3）如图2，当∠BAC＝90°，且DF⊥AE时，求DG：DF的值．【考点】相似三角形的判定与性质；等腰三角形的判定与性质．【专题】等腰三角形与直角三角形；图形的相似；推理能力．【分析】（1）根据相似三角形的判定定理进行判定即可；（2）由相似三角形的性质即可得出答案；（3）由等腰直角三角形的性质、相似三角形的判定与性质即可得出答案．【解答】解：（1）与△ACD 相似的三角形有：△ABE 、△ADE ，理由如下：∵AB 2＝BE •DC ，∴BE AB AB DC=，∵AB ＝AC ，∴∠B ＝∠C ，BE AC AB DC =，∴△ABE ∽△DCA ．∵△ABE ∽△DCA ，∴∠AED ＝∠DAC ．∵∠AED ＝∠C +∠EAC ，∠DAC ＝∠DAE +∠EAC ，∴∠DAE ＝∠C ．∴△ADE ∽△CDA ；（2）∵△ADE ∽△CDA ，又∵DF 平分∠ADC ，∴DG DE AD DF AD CD==，设CE ＝a ，则DE ＝3CE ＝3a ，CD ＝4a ，∴34a AD AD a=，解得：AD ＝23a ，∴23342DG AD a DF CD a ===；（3）∵∠BAC ＝90°，AB ＝AC ，∴∠B ＝∠C ＝45°，∴∠DAE ＝∠C ＝45°∵DG ⊥AE ，∴∠DAG ＝∠ADF ＝45°，∴AG ＝DG ＝22AD ＝22×236a ，∴EG 2222(3)(6)3DE DG a a -=-a ，∴AE ＝AG +EG ＝（63）a ，∵∠AED ＝∠DAC ，∴△ADE ∽△DFA ，∴AD AE DF AD=，∴22AD AE ==a ，∴24DG DF +==．【点评】本题考查了相似三角形的判定与性质、等腰直角三角形的性质、勾股定理等知识；熟记相似三角形的判定定理是解题的关键．专题四动点函数背景下四边形【历年真题】1．（2019秋•长宁、金山区期末）如图，已知在Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，点P 、Q 分别在边AC 、射线CB 上，且AP ＝CQ ，过点P 作PM ⊥AB ，垂足为点M ，联结PQ ，以PM 、PQ 为邻边作平行四边形PQNM ，设AP ＝x ，平行四边形PQNM 的面积为y ．（1）当平行四边形PQNM 为矩形时，求∠PQM 的正切值；（2）当点N 在△ABC 内，求y 关于x 的函数解析式，并写出它的定义域；（3）当过点P 且平行于BC 的直线经过平行四边形PQNM 一边的中点时，直接写出x 的值．【考点】四边形综合题．【专题】几何综合题；应用意识．【分析】（1）当四边形PQMN 是矩形时，PQ ∥AB ．根据tan ∠PQM ＝PM PQ求解即可．（2）如图1中，延长QN 交AB 于K ．求出MK ，PM ，根据y ＝PM •MK 求解即可．（3）分两种情形：①如图3﹣1中，当平分MN 时，D 为MN 的中点，作NE ∥BC 交PQ 于E ，作NH ⊥CB 交CB 的延长线于H ，EG ⊥BC 于G ．根据EG ＝12PC 构建方程求解．②如图3﹣2中，当平分NQ 时，D 是NQ 的中点，作DH ⊥CB 交CB 的延长线于H ．根据PC ＝GH 构建方程求解即可．【解答】解：（1）在Rt △ACB 中，∵∠C ＝90°，AC ＝8，BC ＝6，∴AB ＝＝10，当四边形PQMN是矩形时，PQ∥AB．∴tan∠PQM＝PMPQ=3955253PACQ=．（2）如图1中，延长QN交AB于K．由题意BQ＝6﹣x，QN＝PM＝35x，AM＝45x，KQ＝45BQ＝2445x-，BK＝35BQ＝1835x-，∴MK＝AB﹣AM﹣BK＝325x-，∵QN＜QK，∴35x＜2445x-，∴x＜247，∴y＝PM•MK＝296325x x-（0＜x＜247）．（3）①如图3﹣1中，当平分MN时，D为MN的中点，作NE∥BC交PQ于E，作NH⊥CB交CB的延长线于H，EG⊥BC于G．∵PD∥BC，EN∥BC，∴PD∥NE，∵PE∥DN，∴四边形PDNE是平行四边形，∴PE＝DN，∵DN＝DM，PQ＝MN，∴PE＝EQ，∵EG∥PC，∴CG＝GQ，∴EG＝12PC，∵四边形EGHN是矩形，∴NH＝EG＝35NQ＝35PM＝925x，PC＝8﹣x，∴925x＝12•（8﹣x），解得x＝20043．②如图3﹣2中，当平分NQ时，D是NQ的中点，作DH⊥CB交CB的延长线于H．∵DH＝PC，∴8﹣x＝12•925x，解得x＝40059，综上所述，满足条件x的值为20043或40059．【点评】本题属于四边形综合题，考查了平行四边形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．2．（2019秋•嘉定区期末）已知：点P在△ABC内，且满足∠APB＝∠APC（如图），∠APB+∠BAC＝180°．（1）求证：△PAB∽△PCA；（2）如果∠APB＝120°，∠ABC＝90°，求PCPB的值；（3）如果∠BAC＝45°，且△ABC是等腰三角形，试求tan∠PBC的值．【考点】相似三角形的判定与性质；解直角三角形；等腰三角形的性质．【专题】图形的相似；应用意识．【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）证明△PAB∽△PCA，利用相似三角形的性质解决问题即可．（3）分三种情形：AB＝AC，AB＝BC，AC＝BC分别求解即可解决问题．【解答】证明：（1）∵∠ABP +∠BAP +∠APB ＝180°，∠APB +∠BAC ＝180°，∴∠ABP +∠BAP +∠APB ＝∠APB +∠BAC ，即∠ABP +∠BAP +∠APB ＝∠APB +∠BAP +∠CAP ，∴∠ABP ＝∠CAP ，又∵∠APB ＝∠APC ，∴△PAB ∽△PCA ．（2）如图1中，∵∠APB +∠BAC ＝180°，∠APB ＝120°，∴∠BAC ＝60°，在△ABC 中，∵∠ABC ＝90°，∠BAC ＝60°，∴，又∵△PAB ∽△PCA ，∴12PB PA AB PA PC AC ===，∴14PB PB PA PC PA PC == ，即4PC PB =．（3）∵∠BAC ＝45°，∠APB +∠BAC ＝180°，∠APB ＝∠APC ，∴∠APB ＝∠APC ＝135°．∴∠BPC ＝360°﹣∠APB ﹣∠APC ＝360°﹣135°﹣135°＝90°，∵△PCA ∽△PAB ，∴PA PC AC PB PA AB==，∴163．①如图2中，当△ABC 是等腰三角形，且AB ＝AC 时，2tan PBC=()=1PC AC PB AB =∠．②如图3中，当△ABC 是等腰三角形，且AB ＝BC 时，∠ACB ＝∠BAC ＝45°，∠ABC ＝90°，易得2AC AB ，∴2tan PBC=()=2PC AC PB AB=∠．③如图10﹣4，当△ABC 是等腰三角形，且AC ＝BC 时，∠ABC ＝∠BAC ＝45°，∠ACB ＝90°，易得2=2AC AB ，∴21tan PBC=()=2PC AC PB AB =∠．【点评】本题考查相似三角形的判定和性质，解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．3．（2019秋•徐汇区期末）如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，点D 是边AB 上的动点（点D 不与点AB 重合），点G 在边AB 的延长线上，∠CDE ＝∠A ，∠GBE ＝∠ABC ，DE 与边BC 交于点F ．（1）求cos A 的值；（2）当∠A ＝2∠ACD 时，求AD 的长；（3）点D 在边AB 上运动的过程中，AD ：BE 的值是否会发生变化？如果不变化，请求AD ：BE 的值；如果变化，请说明理由．【考点】三角形综合题．。

上海初中数学一模-2019年-25题分题合集(含解析)

上海初中数学一模-2019年-25题分题合集1. （2019•徐汇区一模）已知在梯形ABCD 中，//AD BC ，10AC BC ==，4cos 5ACB ∠=，点E 在对角线AC 上（不与点A 、C 重合），EDC ACB ∠=∠，DE 的延长线与射线CB 交于点F ，设AD 的长为x ．（1）如图1，当DF BC ⊥时，求AD 的长；（2）设EC y =，求y 关于x 的函数解析式，并直接写出定义域；（3）当DFC ∆是等腰三角形时，求AD 的长．2.（2019•闵行区一模）如图，在梯形ABCD中，//AD BC，AB CD=，5AD=，15BC=，5 cos13ABC∠=．E为射线CD上任意一点，过点A作//AF BE，与射线CD相交于点F．连接BF，与直线AD相交于点G．设CE x=，AGy DG=．（1）求AB的长；（A）（2）当点G在线段AD上时，求y关于x的函数解析式，并写出函数的定义域；（C）（3）如果23ABEFABCDSS=四边形四边形，求线段CE的长．（D）3.（2019•奉贤区一模）如图，已知梯形ABCD中，//AD=，DABAB CD，90∠=︒，4 ==，E是边BC上一点，过点D、E分别作BC、CD的平行线交于点F，26AB CD联结AF并延长，与射线DC交于点G．（1）当点G与点C重合时，求:CE BE的值；（B）（2）当点G在边CD上时，设CE m∆的面积；（用含m的代数式表示）=，求DFG（D）（3）当AFD ADG∠的余弦值．（C）∽时，求DAG∆∆4.（2019•松江区一模）如图，已知ABC∠=︒，D是边AB的中点，P是边∆中，90ACBAC上一动点，BP与CD相交于点E．（1）如果6AC=，且P为AC的中点，求线段BE的长；（B）BC=，8（2）联结PD，如果PD AB⊥，且2ED=，求cos A的值；（D）CE=，3（3）联结PD，如果22=，且22BP CDED=，求线段PD的长．（D）CE=，35.（2019•嘉定区一模）在矩形ABCD中，6AD=，点E是边AD上一点，AB=，8⊥交AB于点M，点N在射线MB上，且AE是AM和AN的比例中项．EM EC（1）如图1，求证：ANE DCE∠=∠；（B）（2）如图2，当点N在线段MB之间，联结AC，且AC与NE互相垂直，求MN的长；（C）（3）连接AC，如果AEC∆与以点E、M、N为顶点所组成的三角形相似，求DE 的长．（D）6.（2019•崇明区一模）如图，在ABCBC=，AD BC⊥，垂足为==，6AB AC∆中，5D，点P是边AB上的一个动点，过点P作//⊥交PF AC交线段BD于点F，作PG AB AD于点E，交线段CD于点G，设BP x=．（1）用含x的代数式表示线段DG的长；（B）（2）设DEF∆的面积为y，求y与x之间的函数关系式，并写出定义域；（C）（3）PEF∆能否为直角三角形？如果能，求出BP的长；如果不能，请说明理由．（C）7.（2019•黄浦区一模）在ABC∆中，90ACB∠=︒，3BC=，4AC=，点O是AB的中点，点D是边AC上一点，DE BD⊥，交BC的延长线于点E，OD DF⊥，交BC边于点F，过点E作EG AB⊥，垂足为点G，EG分别交BD、DF、DC于点M、N、H．（1）求证：DE NEDB OB=；（B）（2）设CD x=，NE y=，求y关于x的函数关系式及其定义域；（C）（3）当DEF∆是以DE为腰的等腰三角形时，求线段CD的长．（D）8. （2019•静安区一模）已知：如图，在ABC ∆中，6AB =，9AC =，tan 22ABC ∠=．过点B 作//BM AC ，动点P 在射线BM 上（点P 不与B 重合），联结PA 并延长到点Q ，使AQC ABP ∠=∠．（1）求ABC ∆的面积；（2）设BP x =，AQ y =，求y 关于x 的函数解析式，并写出x 的取值范围；（C ）（3）连接PC ，如果PQC ∆是直角三角形，求BP 的长．（C ）9.（2019•青浦区一模）如图，在梯形ABCD中，//DB DC==，AD BC，18BC=，15点E、F分别在线段BD、CD上，5DE DF==．AE的延长线交边BC于点G，AF 交BD于点N、其延长线交BC的延长线于点H．（1）求证：BG CH=；（C）（2）设AD x∆的面积为y，求y关于x的函数解析式，并写出它的定义域；=，ADN（C）（3）联结FG，当HFG∆相似时，求AD的长．（D）∆与ADN10. （2019•虹口区一模）如图，在四边形ABCD 中//AD BC ，90A ∠=︒，6AB =，10BC =，点E 为边AD 上一点，将ABE 沿BE 翻折，点A 落在对角线BD 上的点G 处，连接EG 并延长交射线BC 于点F ．（1）如果2cos 3DBC ∠=，求EF 的长；（B ）（2）当点F 在边BC 上时，连接AG ，设AD x =，ABG BEFS y S ∆∆=，求y 关于x 的函数关系式并写出x 的取值范围；（C ）（3）连接CG ，如果FCG ∆是等腰三角形，求AD 的长．（D ）11.（2019•宝山区一模）如图，已知：梯形ABCD中，90AB DC，DAB∠=︒，//∠=︒，45ABCAB=，点P在AB边上，以点A为圆心AP为半径作弧交边DC于点E，射3DC=，5线EP于射线CB交于点F．（1）若13AP=，求DE的长；（B）（2）联结CP，若CP EP=，求AP的长；（C）（3）线段CF上是否存在点G，使得ADE∆与FGE∆相似？若相似，求FG的值；若不相似，请说明理由．（C）12.（2019•金山区一模）已知多边形ABCDEF是O的内接正六边形，联结AC、FD，点H是射线AF上的一个动点，联结CH，直线CH交射线DF于点G，作MH CH⊥交r r>．CD的延长线于点M，设O的半径为(0)（1）求证：四边形ACDF是矩形．（B）（2）当CH经过点E时，M与O外切，求M的半径（用r的代数式表示）．（B）（3）设(090)∠=<<︒，求点C、M、H、F构成的四边形的面积（用r及HCDαα含α的三角比的式子表示）．（E）13.（2019•长宁区一模）已知锐角MBN∠的余弦值为35，点C在射线BN上，25BC=，点A在MBN∠的内部，且90BAC∠=︒，BCA MBN∠=∠．过点A的直线DE分别交射线BM、射线BN于点D、E．点F在线段BE上（点F不与点B重合），且EAF MBN∠=∠．（1）如图1，当AF BN⊥时，求EF的长；（B）（2）如图2，当点E在线段BC上时，设BF x=，BD y=，求y关于x的函数解析式并写出函数定义域；（D）（3）联结DF，当ADF∆与ACE∆相似时，请直接写出BD的长．（E）14.（2019•普陀区一模）如图，点O在线段AB上，22∠=︒，点C是BOPAO OB a==，60射线OP上的一个动点．（1）如图①，当90OC=，求a的值；（B）∠=︒，2ACB（2）如图②，当AC AB=时，求OC的长（用含a的代数式表示）；（B）（3）在第（2）题的条件下，过点A作//AQ OQ的AQ BC，并使QOC B∠=∠，求:值．（C）15.（2019•杨浦区一模）已知：梯形ABCD中，//AD=，6AB=，⊥，3AD BC，AB BC⊥分别交射线AB、射线CB于点E、F．DF DC（1）当点E为边AB的中点时（如图1)，求BC的长；（B）（2）当点E在边AB上时（如图2)，联结CE，试问：DCE∠的大小是否确定？若确定，请求出DCE∠的正切值为y，请求出∠的正切值；若不确定，则设AE x=，DCEy关于x的函数解析式，并写出定义域；（B）（3）当AEF∆的面积为3时，求DCE∆的面积．（C）16.（2019•浦东新区一模）将大小两把含30︒角的直角三角尺按如图1位置摆放，即大小直角三角尺的直角顶点C重合，小三角尺的顶点D、E分别在大三角尺的直角边AC、∠=∠=︒，BC上，此时小三角尺的斜边DE恰好经过大三角尺的重心G．已知30A CDEAB=．12（1）求小三角尺的直角边CD的长；（2）将小三角尺绕点C逆时针旋转，当点D第一次落在大三角尺的边AB上时（如图2)，求点B、E之间的距离；（3）在小三角尺绕点C旋转的过程中，当直线DE经过点A时，求BAE∠的正弦值．上海初中数学一模-2019年-25题分题合集参考答案与试题解析一．解答题1. 已知在梯形ABCD 中，//AD BC ，10AC BC ==，4cos 5ACB ∠=，点E 在对角线AC 上（不与点A 、C 重合），EDC ACB ∠=∠，DE 的延长线与射线CB 交于点F ，设AD 的长为x ．（1）如图1，当DF BC ⊥时，求AD 的长；（2）设EC y =，求y 关于x 的函数解析式，并直接写出定义域；（3）当DFC ∆是等腰三角形时，求AD 的长．【分析】（1）证明ADC DCE ∆∆∽，利用22223616105AC CE CD DF FC a a ==+=+=，即可求解；（2）过点C 作CH AD ⊥交AD 的延长线于点H ，22222(sin )(cos )CD CH DH AC AC x αα=+=+-，即可求解；（3）分DF DC =、FC DC =、FC FD =三种情况，求解即可．【解答】解：（1）设：ACB EDC CAD α∠=∠=∠=∠，4cos 5α=， 3sin 5α∴=，过点A 作AH BC ⊥交于点H ，sin 6AH AC DF α===，2BH =，如图1，设：4FC a =， 4cos5ACB ∴∠=，则3EF a =，5EC a =， EDC CAD α∠=∠=∠，ACD ACD ∠=∠，ADC DCE ∴∆∆∽，22223616105AC CE CD DF FC a a ∴==+=+=，解得：2a =或98（舍去2)a =， 710242AD HF a ==--=；（2）过点C 作CH AD ⊥交AD 的延长线于点H ，22222(sin )(cos )CD CH DH AC AC x αα=+=+-，即：2236(8)CD x =+-，由（1）得：2AC CE CD =，即：21810(010)105y x x x =-+<⋯①，（3）①当DF DC =时，ECF FDC α∠=∠=，DFC DFC ∠=∠，DFC CFE ∴∆∆∽，DF DC =，FC EC y ∴==，10x y ∴+=，即：2181010105x x x =-++，解得：6x =；②当FC DC =，则DFC FDC α∠=∠=，则：EF EC y ==，10DE AE y ==-，在等腰ADE ∆中，11422cos cos 105AD x DAE AE y α∠====-，即：5880x y +=，将上式代入①式并解得：394x =； ③当FC FD =，则FCD FDC α∠=∠=，而ECF FCD α∠=≠∠，不成立，故：该情况不存在；故：AD 的长为6和394．【点评】本题为四边形的综合题，涉及到解直角三角形、一元二次方程，三角形相似等诸多知识点，其中三角形相似是本题的突破点，难度较大．2.如图，在梯形ABCD中，//AD BC，AB CD=，5AD=，15BC=，5cos13ABC∠=．E 为射线CD上任意一点，过点A作//AF BE，与射线CD相交于点F．连接BF，与直线AD相交于点G．设CE x=，AGy DG=．（1）求AB的长；（2）当点G在线段AD上时，求y关于x的函数解析式，并写出函数的定义域；（3）如果23ABEFABCDSS=四边形四边形，求线段CE的长．【分析】（1）分别过点A、D作AM BC⊥、DN BC⊥，垂足为点M、N，根据三角函数解答即可；（2）根据相似三角形的判定和性质解答，进而利用函数解析式解答即可；（3）根据两种情况，利用勾股定理解答即可．【解答】思路：解直角三角形解：（1）分别过点A、D作AM BC⊥、DN BC⊥，垂足为点M、N．//AD BC ，AB CD =，5AD =，15BC =，11()(155)522BM BC AD ∴=-=⨯-=，在Rt ABM ∆中，90AMB ∠=︒， ∴55cos 13BM ABM AB AB ∠===． 13AB ∴=．（2）思路一：合分比性质AG y DG=， ∴1AG DG y DG+=+．即得51DG y =+，思路二：运动过程中始终有△AFD ∽△BECAFD BEC ∠=∠，ADF C ∠=∠．ADF BCE ∴∆∆∽． ∴51153FD AD EC BC ===，又CE x =，13FD x =，13AB CD ==．即得1133FC x =+．思路三：运动过程中始终有△FGD ∽△FBC ，或者说始终有A 字形//AD BC ， ∴FD DG FC BC=． ∴5113115133x y x +=+． ∴3923x y x-=． ∴所求函数的解析式为3923xy x -= 临界点1：E 和C 重合临界点2：G 和A 重合，此时E 、F 交于一点，为射线BA 和射线CF 交点函数定义域为3902x <<．（3）梯形ABCD 为定梯形，所以面积苛求，所以ABEF 面积可求在Rt ABM ∆中，利用勾股定理，得12AM =． ∴()()115151212022ABCD S AD BC AM =+⋅=+⨯=梯形． 23ABEFABCD S S =四边形四边形， 80ABEF S ∴=四边形．设ADF S S ∆=．由ADF BCE ∆∆∽，13FD EC =，得 9AEC S S ∆=．由题意，本题有两种情况：方法一：△BEC 面积可求，因为BC 和∠C 知道，所以EC 可求方法二：△BEC 面积可求，因为BC 知道，则BC 边上高知道，利用比例线段EC 可求过点E 作EH BC ⊥，垂足为点H ．（ⅰ）如果点G 在边AD 上，则 840ABCD ABEF S S S -==四边形四边形．5S ∴=．945AEC S S ∆∴==． ∴11154522BEC S BC EH EH ∆=-=⨯-=． 6EH ∴=．由 DN BC ⊥，EH BC ⊥，易得 //EH DN ．∴61122CE EH CD DN ===．又 13CD AB ==， ∴132CE =，（ⅱ）如果点G 在边DA 的延长线上，则 9AEF ABCD ABEF S S S S ∆++=四边形四边形． 8200S ∴=．解得25S =．9225BEC S S ∆∴==． ∴111522522BEC S BC EH EH ∆=-=⨯-=．解得 30EH =． ∴305122CE EH CD DN ===． ∴652CE =， ∴136522CE =或．【点评】此题考查四边形的综合题，关键是根据相似三角形的判定和性质以及梯形的性质进行解答即可．3. 如图，已知梯形ABCD 中，//AB CD ，90DAB ∠=︒，4AD =，26AB CD ==，E 是边BC 上一点，过点D 、E 分别作BC 、CD 的平行线交于点F ，联结AF 并延长，与射线DC 交于点G ．（1）当点G 与点C 重合时，求:CE BE 的值；（2）当点G 在边CD 上时，设CE m =，求DFG ∆的面积；（用含m 的代数式表示）（3）当AFD ADG ∆∆∽时，求DAG ∠的余弦值．【分析】（1）由题意可得四边形DCEF 是平行四边形，可得CD EF =，通过证明CFE CAB ∆∆∽，可得12CE EF CB AB ==，可得BE CE =，则可求:CE BE 的值；（2）延长AG ，BC 交为于点M ，过点C 作CN AB ⊥于点N ，交EF 于点H ，由题意可得四边形ADCN 是矩形，可得4AD CN ==，3CD AN ==，3BN =，由平行线分线段成比例可求BE ，ME ，MC ，CH ，GC 的长，即可求GD 的长，由三角求形面积公式可DFG ∆的面积；（3）由AFD ADG ∆∆∽，可得90AFD ADG ∠=∠=︒，由余角的性质可得DAG B ∠=∠，即可求DAG ∠的余弦值．【解答】解：（1）如图，//DC EF ，//DF CE∴四边形DCEF 是平行四边形CD EF ∴=，26AB CD ==，2AB EF ∴=，//EF CD ，//AB CD ，//EF AB ∴，CFE CAB ∴∆∆∽ ∴12CE EF CB AB == 2BC CE ∴=，BE CE ∴=:1:1EC BE ∴=（2）方法一：中间面积法,思路点：梯形ABCD 是定梯形，DFEC 始终是平行四边形，△ADH 为定三角形方法二：直接表示法因为底和高都不知道，所以需要一个一个表示因为梯形ABCD 是定梯形，解梯形AD CD ⊥，CN CD ⊥//AD CN ∴，且//CD AB∴四边形ADCN 是平行四边形，又90DAB ∠=︒∴四边形ADCN 是矩形，4AD CN ∴==，3CD AN ==，3BN AB AN ∴=-=，在Rt BCN ∆中，225BC CN BN =+=利用比例线段或者相似或者解直角三角形求出CH//EF AB∴CE HE HC BC BN CN == 45HC m ∴=，求DG ，因DC 知道，所以求CG如图，延长AG ，BC 交为于点M ，过点C 作CN AB ⊥于点N ，交EF 于点H利用比例线段MC5BE BC CE m ∴=-=-， //EF AB ∴EF ME AB MB=，即12CD ME AB BM == 5ME BE m ∴==-，52MC ME CE m ∴=-=-，利用比例线段CG （随意一组A 字形都可以）//CG EF∴GC MC EF ME= 即5235GC m m-=- 1565m GC m -∴=-1563355m m DG CD GC m m-∴=-=-=-- 2162255DFGm S DG CH m∆∴=⨯⨯=- （3）因为ADG 是直角三角形，所以只能是∠DFA 为直角，做出图形即可求解过点C 作CN AB ⊥于点N ，//AB CD ，90DAB ∠=︒，90DAB ADG ∴∠=∠=︒，若AFD ADG ∆∆∽，90AFD ADG ∴∠=∠=︒DF AG ∴⊥又//DF BCAG BC ∴⊥90B GAB ∴∠+∠=︒，且90DAG GAB ∠+∠=︒B DAG ∴∠=∠3cos cos 5BN DAG B BC ∴∠=== 【点评】本题是相似形综合题，考查了平行四边形的判定和性质，矩形的判定和性质，相似三角形的判定和性质，锐角三角函数等知识，熟练运用相似三角形的性质求线段的长度是本题的关键．4. 如图，已知ABC ∆中，90ACB ∠=︒，D 是边AB 的中点，P 是边AC 上一动点，BP 与CD 相交于点E ．（1）如果6BC =，8AC =，且P 为AC 的中点，求线段BE 的长；（2）联结PD ，如果PD AB ⊥，且2CE =，3ED =，求cos A 的值；（3）联结PD ，如果222BP CD =，且2CE =，3ED =，求线段PD 的长．【分析】（1）根据已知条件得到4CP =，求得213BP =，根据三角形重心的性质即可得到结论；（2）如图1，过点B 作//BF CA 交CD 的延长线于点F ，根据平行线分线段成比例定理得到BD FD BF DA DC CA ==，求得13CP PA =，设CP k =，则3PA k =，得到3PA PB k ==根据三角函数的定义即可得到结论；（3）根据直角三角形的性质得到12CD BD AB ==，推出PBD ABP ∆∆∽，根据相似三角形的性质得到BPD A ∠=∠，推出DPE DCP ∆∆∽，根据相似三角形的性质即可得到结论．【解答】解：（1）P 为AC 的中点，8AC =，4CP ∴=，90ACB ∠=︒，6BC =，213BP ∴= D 是边AB 的中点，P 为AC 的中点，∴点E 是ABC ∆的重心，241333BE BP ∴=；方法一：从中点出发，回归到旗帜模型方法二：（2）如图1，过点B作//BF CA交CD的延长线于点F，∴BD FD BF DA DC CA==，BD DA=，FD DC∴=，BF AC=，2CE=，3ED=，则5CD=，8EF∴=，∴2184 CP CEBF EF===，∴14 CPCA=，∴13 CPPA=，设CP k=，则3PA k=，PD AB ⊥，D 是边AB 的中点，3PA PB k ∴==BC ∴=，AB ∴=，4AC k =，cos A ∴=；方法一：方法二：（3）90ACB ∠=︒，D 是边AB 的中点，12CD BD AB ∴==，222PB CD =，22BP CD CD BD AB ∴==，PBD ABP ∠=∠，PBD ABP ∴∆∆∽，BPD A ∴∠=∠，A DCA ∠=∠，DPE DCP ∴∠=∠，PDE CDP ∠=∠，DPE DCP ∴∆∆∽，2PD DE DC ∴=，3DE =，5DC =，PD ∴．【点评】本题考查了相似三角形的判定和性质，直角三角形的性质，正确的作出辅助线是解题的关键．5.在矩形ABCD中，6AB=，8AD=，点E是边AD上一点，EM EC⊥交AB于点M，点N在射线MB上，且AE是AM和AN的比例中项．（1）如图1，求证：ANE DCE∠=∠；（2）如图2，当点N在线段MB之间，联结AC，且AC与NE互相垂直，求MN的长；（3）连接AC，如果AEC∆与以点E、M、N为顶点所组成的三角形相似，求DE的长．【分析】（1）由比例中项知AM AEAE AN=，据此可证AME AEN∆∆∽得AEM ANE∠=∠，再证AEM DCE∠=∠可得答案；（2）先证ANE EAC∠=∠，结合ANE DCE∠=∠得DCE EAC∠=∠，从而知DE DC DC AD=，据此求得97822AE=-=，由（1）得AEM DCE∠=∠，据此知AM DEAE DC=，求得218AM=，由AM AEAE AN=求得4924MN=；（3）分ENM EAC∠=∠和ENM ECA∠=∠两种情况分别求解可得．【解答】解：（1）AE是AM和AN的比例中项∴AM AEAE AN=，A A∠=∠，AME AEN∴∆∆∽，AEM ANE ∴∠=∠，90D∠=︒，∴∠+∠=︒，DCE DEC90⊥，EM BC∴∠+∠=︒，AEM DEC90∴∠=∠，AEM DCE∴∠=∠；ANE DCE（2）AC与NE互相垂直，EAC AEN∴∠+∠=︒，90BAC∠=︒，90∴∠+∠=︒，90ANE AENANE EAC ∴∠=∠，由（1）得ANE DCE ∠=∠，DCE EAC ∴∠=∠，tan tan DCE DAC ∴∠=∠， ∴DE DC DC AD=， 6DC AB ==，8AD =，92DE ∴=， 97822AE ∴=-=，由（1）得AEM DCE ∠=∠，tan tan AEM DCE ∴∠=∠， ∴AM DE AE DC=， 218AM ∴=， AM AE AE AN=， 143AN ∴=， 4924MN ∴=；相似通解通法·第二种情况利用面积法或者利用旗帜模型解决问题（3）NME MAE AEM∠=∠+∠，AEC D DCE∠=∠+∠，又90MAE D∠=∠=︒，由（1）得AEM DCE∠=∠，AEC NME∴∠=∠，当AEC∆与以点E、M、N为顶点所组成的三角形相似时①ENM EAC∠=∠，如图2，ANE EAC∴∠=∠，由（2）得：92 DE=；②ENM ECA∠=∠，如图3，过点E作EH AC⊥，垂足为点H，由（1）得ANE DCE∠=∠，ECA DCE∴∠=∠，HE DE∴=，又6 tan8HE DCHAEAH AD∠===，设3DE x=，则3HE x=，4AH x=，5AE x=，又AE DE AD+=，538x x∴+=，解得1x=，33DE x∴==，综上所述，DE的长分别为92或3．【点评】本题是相似三角形的综合问题，解题的关键是掌握相似三角形的判定与性质、三角函数的应用等知识点．6. 如图，在ABC ∆中，5AB AC ==，6BC =，AD BC ⊥，垂足为D ，点P 是边AB 上的一个动点，过点P 作//PF AC 交线段BD 于点F ，作PG AB ⊥交AD 于点E ，交线段CD 于点G ，设BP x =．（1）用含x 的代数式表示线段DG 的长；（2）设DEF ∆的面积为y ，求y 与x 之间的函数关系式，并写出定义域；（3）PEF ∆能否为直角三角形？如果能，求出BP 的长；如果不能，请说明理由．【分析】（1）根据等腰三角形的性质可得3BD =，通过证明ABD GBP ∆∆∽，可得5533BG BP x ==，即可得DG 的长度；（2）根据相似三角形的性质可得635FD BD BF x =-=-，5944DE x =-，根据三角形面积公式可求y 与x 之间的函数关系式；（3）分EF PG ⊥，EF PF ⊥两种情况讨论，根据相似三角形的性质可求BP 的长．模型：8字形【解答】解：（1）5AB AC ==，6BC =，AD BC ⊥，3BD CD ∴==，在Rt ABD ∆中，224AD AB BD =-，B B ∠=∠，90ADB BPG ∠=∠=︒，ABD GBP ∴∆∆∽ ∴35BD BP AB BG == 5533BG BP x ∴==， 533DG BG BD x ∴=-=- DE 已经表示出来了，那就只剩下DF ，△BPF 是含参定三角形，所以每条边都可以表示出来（2）//PF ACBFP BCA ∴∆∆∽ ∴BF BP BC AB= 即56x BF = 65BF x ∴=， 635FD BD BF x ∴=-=-， DGE DEG DGE ABD ∠+∠=∠+∠，ABD DEG ∴∠=∠，90ADG ADB ∠=∠=︒DEG DBA ∴∆∆∽ ∴BD DE AD DG= ∴35433DE x =- 5944DE x ∴=- 2116593129(3)()22544440DEF S y DF DE x x x x ∆∴==⨯⨯=⨯-⨯-=-+需要注意定义域，临界情况一，F 和D 重合；临界请客二，D 和G 重合方法一：直接勾股定理，△PEF 的三边都是可以表示出来的方法二：利用几何性质解题方法三：相似，射影定理，比例线段（3）若EF PG ⊥时，EF PG ⊥，ED FG ⊥，90FED DEG ∴∠+∠=︒，90FED EFD ∠+∠=︒，EFD DEG ∴∠=∠，且EDF EDG ∠=∠，EFD GDE ∴∆∆∽∴ED DF DG ED= 2ED FD DG ∴=⨯25965()(3)(3)4453x x x ∴-=-- 2557113822550x x ∴⨯-+⨯=95x ∴=（不合题意舍去），12557x = 若EF PF ⊥，90PFB EFD ∴∠+∠=︒，且PFB ACB ∠=∠，90ACB DAC ∠+∠=︒EFD DAC ∴∠=∠，且90EDF ADC ∠=∠=︒，EDF CDA ∴∆∆∽ ∴ED CD DF AD= ∴593446435x x -=- 9043x ∴= 综上所述：当BP 为12557或9043时，PEF ∆为直角三角形．【点评】本题是三角形综合题，考查了等腰三角形的性质，相似三角形判定和性质，以及分类讨论思想，熟练运用相似三角形的判定和性质是本题的关键．7.在ABC∆中，90ACB∠=︒，3BC=，4AC=，点O是AB的中点，点D是边AC上一点，DE BD⊥，交BC的延长线于点E，OD DF⊥，交BC边于点F，过点E作EG AB⊥，垂足为点G，EG分别交BD、DF、DC于点M、N、H．（1）求证：DE NE DB OB=；（2）设CD x=，NE y=，求y关于x的函数关系式及其定义域；（3）当DEF∆是以DE为腰的等腰三角形时，求线段CD的长．【分析】（1）只要证明OBD NED∆∆∽，即可解决问题．（2）由tanDC DEDBCBC BD∠==，又因为DE NEDB OB=，可得CD NEBC OB=，由此即可解决问题．（3）分两种情形分别求解即可解决问题．通过比例推测△OBD和△NED相似，所以只需要证明相似鸡爪模型和8字形得角等【解答】（1）证明：如图1中，OD DF⊥，BD DE⊥，90ODF BDE∴∠=∠=︒，ODB NDE∴∠=∠，EG AB ⊥，90BGM MDE ∴∠=∠=︒， BMG EMD ∠=∠， OBD DEN ∴∠=∠， OBD NED ∴∆∆∽，（2）解：如图1中，90BCD BDE ∠=∠=︒，tan DC DE DBC BC BD ∴∠==， DE NE DB OB=，在Rt ABC ∆中，5AB ===， 2.5OB OA ∴==， ∴3 2.5x y =，。

2019年上海市普陀区中考数学一模考试卷含逐题详解

2019年上海市普陀区中考数学一模试卷一、选择题：（本大题共6题，每题4分，满分24分）下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1．（4分）已知二次函数y＝（a﹣1）x2+3的图象有最高点，那么a的取值范围是（）A．a＞0B．a＜0C．a＞1D．a＜12．（4分）下列二次函数中，如果图象能与y轴交于点A（0，1），那么这个函数是（）A．y＝3x2B．y＝3x2+1C．y＝3（x+1）2D．y＝3x2﹣x3．（4分）如图，在△ABC中，点D、E分别在△ABC的边AB、AC上，如果添加下列其中之一的条件，不一定能使△ADE与△ABC相似，那么这个条件是（）A．∠AED＝∠B B．∠ADE＝∠C C．＝D．＝4．（4分）已知、、都是非零向量，如果＝2，＝﹣2，那么下列说法中，错误的是（）A．∥B．||＝||C．＝0D．与方向相反5．（4分）已知⊙O1和⊙O2，其中⊙O1为大圆，半径为3．如果两圆内切时圆心距等于2，那么两圆外切时圆心距等于（）A．1B．4C．5D．86．（4分）如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，且DE经过重心G，在下列四个说法中①＝；②＝；③＝；④＝，正确的个数是（）A．1个B．2个C．3个D．4个二、填空题：（本大题共12题，每题4分，满分48分）7．（4分）如果＝，那么的值是．8．（4分）化简：3（）﹣2（）＝．9．（4分）如果抛物线y＝2x2+x+m﹣1经过原点，那么m的值等于．10．（4分）将抛物线y＝（x+3）2﹣4先向右平移2个单位，再向上平移3个单位，那么平移后所得新抛物线的表达式是．11．（4分）已知抛物线y＝2x2+bx﹣1的对称轴是直线x＝1，那么b的值等于．12．（4分）已知△ABC三边的比为2：3：4，与它相似的△A′B′C′最小边的长等于12，那么△A′B′C′最大边的长等于．13．（4分）在Rt△ABC中，∠ACB＝90°，AB＝3，BC＝1，那么∠A的正弦值是．14．（4分）正八边形的中心角为度．15．（4分）如图，在梯形ABCD中，AD∥BC，AB⊥BC，BD⊥DC，tan∠ABD＝，BC＝5，那么DC的长等于．16．（4分）如图，AB∥CD，AD、BC相交于点E，过E作EF∥CD交BD于点F，如果AB：CD＝2：3，EF＝6，那么CD的长等于．17．（4分）已知二次函数y＝ax2+c（a＞0）的图象上有纵坐标分别为y1、y2的两点A、B，如果点A、B到对称轴的距离分别等于2、3，那么y1y2（填“＜”、“＝”或“＞”）18．（4分）如图，△ABC中，AB＝AC＝8，cos B＝，点D在边BC上，将△ABD沿直线AD翻折得到△AED，点B的对应点为点E，AE与边BC相交于点F，如果BD＝2，那么EF＝．三、解答题：（本大题共7题，满分78分）19．（10分）计算：4sin45°+cos230°﹣．20．（10分）如图，在平行四边形ABCD中，对角线AC、BD相交于点O，点E在边BC上，AE与BD相交于点G，AG：GE＝3：1．（1）求EC：BC的值；（2）设＝，＝，那么＝，＝（用向量、表示）21．（10分）如图，⊙O1和⊙O2相交于A、B两点，O1O2与AB交于点C，O2A的延长线交⊙O1于点D，点E为AD的中点，AE＝AC，联结OE．（1）求证：O1E＝O1C；（2）如果O1O2＝10，O1E＝6，求⊙O2的半径长．22．（10分）如图，小山的一个横断面是梯形BCDE，EB∥DC，其中斜坡DE的坡长为13米，坡度i＝1：2.4，小山上有一座铁塔AB，在山坡的坡顶E处测得铁塔顶端A的仰角为45°，在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°（点F、D、C在一直线上），求铁塔AB的高度．（参考数值：sin31°≈0.52，cos31°≈0.86，tan31°≈0.6）23．（12分）已知：如图，△ADE的顶点E在△ABC的边BC上，DE与AB相交于点F，AE2＝AF•AB，∠DAF＝∠EAC．（1）求证：△ADE∽△ACB；（2）求证：＝．24．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0）和点B，且OB＝3OA，与y轴交于点C，此抛物线顶点为点D．（1）求抛物线的表达式及点D的坐标；（2）如果点E是y轴上的一点（点E与点C不重合），当BE⊥DE时，求点E的坐标；（3）如果点F是抛物线上的一点．且∠FBD＝135°，求点F的坐标．25．（14分）如图，点O在线段AB上，AO＝2OB＝2a，∠BOP＝60°，点C是射线OP上的一个动点．（1）如图①，当∠ACB＝90°，OC＝2，求a的值；（2）如图②，当AC＝AB时，求OC的长（用含a的代数式表示）；（3）在第（2）题的条件下，过点A作AQ∥BC，并使∠QOC＝∠B，求AQ：OQ的值．2019年上海市普陀区中考数学一模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1．（4分）已知二次函数y＝（a﹣1）x2+3的图象有最高点，那么a的取值范围是（）A．a＞0B．a＜0C．a＞1D．a＜1【分析】根据二次函数的图象与性质即可求出答案．【解答】解：由题意可知：a﹣1＜0，∴a＜1，故选：D．【点评】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于中等题型．2．（4分）下列二次函数中，如果图象能与y轴交于点A（0，1），那么这个函数是（）A．y＝3x2B．y＝3x2+1C．y＝3（x+1）2D．y＝3x2﹣x【分析】根据y轴上点的坐标特征，分别计算出x＝0时四个函数对应的函数值，然后根据函数值是否为1来判断图象能否与y轴交于点A（0，1）．【解答】解：当x＝0时，y＝3x2＝0；当x＝0时，y＝3x2+1＝1；当x＝0时，y＝3（x+1）2＝9；当x＝0时，y ＝3x2﹣x＝0，所以抛物线y＝3x2+1与y轴交于点（0，1）．故选：B．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．3．（4分）如图，在△ABC中，点D、E分别在△ABC的边AB、AC上，如果添加下列其中之一的条件，不一定能使△ADE与△ABC相似，那么这个条件是（）A．∠AED＝∠B B．∠ADE＝∠C C．＝D．＝【分析】由已知及三角形相似的判定方法，对每个选项分别分析、判断解答出即可．【解答】解：由题意得，∠A＝∠A，A、当∠ADE＝∠B时，△ADE∽△ABC；故本选项不符合题意；B、当∠ADE＝∠C时，△ADE∽△ABC；故本选项不符合题意；C、当＝时，△ADE∽△ABC；故本选项不符合题意；D、当＝时，不能推断△ADE与△ABC相似；故选项符合题意；故选：D．【点评】本题考查了直角三角形相似的判定：①有两个对应角相等的三角形相；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似．4．（4分）已知、、都是非零向量，如果＝2，＝﹣2，那么下列说法中，错误的是（）A．∥B．||＝||C．＝0D．与方向相反【分析】根据平面相等向量的定义、共线向量的定义以及向量的模的计算方法解答．【解答】解：A、因为＝2，＝﹣2，所以∥，且与方向相反，故本选项说法正确；B、因为＝2，＝﹣2，所以||＝||＝|2|，故选项说法正确；C、因为＝2，＝﹣2，所以∥，则•＝0，故本选项说法错误；D、因为＝2，＝﹣2，所以∥，且与方向相反，故本选项说法正确；故选：C．【点评】考查了向量，向量是既有方向又有大小的．5．（4分）已知⊙O1和⊙O2，其中⊙O1为大圆，半径为3．如果两圆内切时圆心距等于2，那么两圆外切时圆心距等于（）A．1B．4C．5D．8【分析】根据两圆位置关系是内切，则圆心距＝两圆半径之差，以及外切时，r+R＝d，分别求出即可．【解答】解：∵两圆相内切，设小圆半径为x，圆心距为2，∴3﹣x＝2，∴x＝1，∴小圆半径为1，这两圆外切时，圆心距为：1+3＝4．故选：B．【点评】此题主要考查了两圆的位置关系，用到的知识点为：两圆内切，圆心距＝两圆半径之差，外切时，r+R ＝d．6．（4分）如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，且DE经过重心G，在下列四个说法中①＝；②＝；③＝；④＝，正确的个数是（）A．1个B．2个C．3个D．4个【分析】连接AG并延长，交BC于F，依据DE∥BC，且DE经过重心G，即可得到△ADE∽△ABC，且相似比为2：3，依据相似三角形的性质，即可得到正确结论．【解答】解：如图所示，连接AG并延长，交BC于F，∵DE∥BC，且DE经过重心G，∴△ADE∽△ABC，∴＝＝＝，故①正确；∴＝，故③正确；∵DG∥BF，∴＝＝，故②错误；∵△ADE∽△ABC，＝，∴＝，∴＝，故④正确；故选：C．【点评】本题考查相似三角形的判定和性质以及三角形重心的性质的运用，解决问题的关键是知道相似三角形的对应边对应成比例．二、填空题：（本大题共12题，每题4分，满分48分）7．（4分）如果＝，那么的值是．【分析】直接根据已知用同一未知数表示出各数，进而得出答案．【解答】解：∵＝，∴设x＝7a，则y＝2a，那么＝＝．故答案为：．【点评】此题主要考查了比例的性质，正确表示出x，y的值是解题关键．8．（4分）化简：3（）﹣2（）＝．【分析】平面向量的运算法则也符合实数的运算法则．【解答】解：3（）﹣2（）＝3+﹣2+2＝（3﹣2）+（+2）＝．故答案是：．【点评】考查了平面向量，解题的关键是掌握平面向量的计算法则．9．（4分）如果抛物线y＝2x2+x+m﹣1经过原点，那么m的值等于1．【分析】把原点坐标代入抛物线解析式即可得到对应m的值．【解答】解：把（0，0）代入y＝2x2+x+m﹣1得m﹣1＝0，解得m＝1，故答案为1．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．10．（4分）将抛物线y＝（x+3）2﹣4先向右平移2个单位，再向上平移3个单位，那么平移后所得新抛物线的表达式是（x+1）2﹣1．【分析】根据“左加右减、上加下减”的原则进行解答即可．【解答】解：将抛物线y＝（x+3）2﹣4向右平移2个单位所得直线解析式为：y＝（x+3﹣2）2﹣4＝（x+1）2﹣4；再向上平移3个单位为：y＝（x+1）2﹣4+3，即y＝（x+1）2﹣1．故答案是：y＝（x+1）2﹣1．【点评】此题主要考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．11．（4分）已知抛物线y＝2x2+bx﹣1的对称轴是直线x＝1，那么b的值等于﹣4．【分析】由对称轴公式可得到关于b的方程，可求得答案．【解答】解：∵y＝2x2+bx﹣1，∴抛物线对称轴为x＝﹣＝﹣，∴﹣＝1，解得b＝﹣4，故答案为：﹣4．【点评】本题主要考查二次函数的性质，掌握二次函数的对称轴公式是解题的关键，即y＝ax2+bx+c的对称轴为x＝﹣．12．（4分）已知△ABC三边的比为2：3：4，与它相似的△A′B′C′最小边的长等于12，那么△A′B′C′最大边的长等于24．【分析】由于△A′B′C′∽△ABC，因此它们各对应边的比都相等，可据此求出△A′B′C′的最大边的长．【解答】解：设△A′B′C′的最大边长是x，根据相似三角形的对应边的比相等，可得：＝，解得：x＝24，∴△A′B′C′最大边的长等于24．故答案为：24．【点评】本题主要考查了相似三角形的性质：相似三角形的对应边成比例．13．（4分）在Rt△ABC中，∠ACB＝90°，AB＝3，BC＝1，那么∠A的正弦值是．【分析】我们把锐角A的对边a与斜边c的比叫做∠A的正弦，记作sin A．代入数据直接计算得出答案．【解答】解：∵∠ACB＝90°，AB＝3，BC＝1，∴∠A的正弦值sin A＝＝，故答案为：．【点评】本题考查了锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．14．（4分）正八边形的中心角为45度．【分析】根据中心角是正多边形相邻的两个半径的夹角来解答．【解答】解：正八边形的中心角等于360°÷8＝45°；故答案为45．【点评】本题考查了正多边形和圆的知识，解题的关键是牢记中心角的定义及求法．15．（4分）如图，在梯形ABCD中，AD∥BC，AB⊥BC，BD⊥DC，tan∠ABD＝，BC＝5，那么DC的长等于2．【分析】根据垂直的定义得到∠ABD＝∠C，根据正切的定义得到BD＝CD，根据勾股定理计算即可．【解答】解：∵AB⊥BC，∴∠ABD+∠DBC＝90°，∵BD⊥DC，∴∠C+∠DBC＝90°，∴∠ABD＝∠C，∴tan C＝＝，∴BD＝CD，由勾股定理得，BD2+CD2＝BC2，即（CD）2+CD2＝52，解得，CD＝2，故答案为：2．【点评】本题考查的是梯形的性质，正切的定义，勾股定理，掌握梯形的性质，正切的定义是解题的关键．16．（4分）如图，AB∥CD，AD、BC相交于点E，过E作EF∥CD交BD于点F，如果AB：CD＝2：3，EF＝6，那么CD的长等于15．【分析】由△ABE∽△DCE，推出＝＝，可得＝，再证明△BEF∽△BCD，可得＝＝，由此即可解决问题．【解答】解：∵AB∥CD，∴△ABE∽△DCE，∴＝＝，∴＝，∵EF∥CD，∴△BEF∽△BCD，∴＝＝，∵EF＝6，∴CD＝15，故答案为15．【点评】本题考查平行线的性质，相似三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17．（4分）已知二次函数y＝ax2+c（a＞0）的图象上有纵坐标分别为y1、y2的两点A、B，如果点A、B到对称轴的距离分别等于2、3，那么y1＜y2（填“＜”、“＝”或“＞”）【分析】由于二次函数y＝2（x﹣1）2+k的图象的开口向上，然后根据点A和点B离对称轴的远近可判断y1与y2的大小关系．【解答】解：∵二次函数y＝ax2+c（a＞0），∴抛物线开口向上，∵点A、B到对称轴的距离分别等于2、3，∴y1＜y2．故答案为＜．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足解析式y＝ax2+bx+c（a、b、c为常数，a≠0）．18．（4分）如图，△ABC中，AB＝AC＝8，cos B＝，点D在边BC上，将△ABD沿直线AD翻折得到△AED，点B的对应点为点E，AE与边BC相交于点F，如果BD＝2，那么EF＝．【分析】过A作AH⊥BC于H，依据等腰三角形的性质即可得到BH＝6＝CH，由折叠可得，BD＝DE＝2，∠E ＝∠ABC＝∠C，AB＝AE＝6，依据△AFC∽△DFE，即可得到＝＝＝，设EF＝x，则CF＝4x，AF ＝8﹣x，DF＝AF＝2﹣x，依据BD+DF+CF＝BC，可得x的值，进而得出EF的长．【解答】解：如图所示，过A作AH⊥BC于H，∵AB＝AC＝8，cos B＝，∴BH＝6＝CH，BC＝12，由折叠可得，BD＝DE＝2，∠E＝∠ABC＝∠C，AB＝AE＝6，又∵∠AFC＝∠DFE，∴△AFC∽△DFE，∴＝＝＝，设EF＝x，则CF＝4x，AF＝8﹣x，∴DF＝AF＝2﹣x，∵BD+DF+CF＝BC，∴2+2﹣x+4x＝12，解得x＝，∴EF＝，故答案为：．【点评】本题主要考查了相似三角形的判定与性质，等腰三角形的性质的运用，解决问题的关键是利用相似三角形的对应边成比例，列方程求解．三、解答题：（本大题共7题，满分78分）19．（10分）计算：4sin45°+cos230°﹣．【分析】直接利用特殊角的三角函数值分别代入求出答案．【解答】解：原式＝4×+（）2﹣＝2+﹣2（+）＝．【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．20．（10分）如图，在平行四边形ABCD中，对角线AC、BD相交于点O，点E在边BC上，AE与BD相交于点G，AG：GE＝3：1．（1）求EC：BC的值；（2）设＝，＝，那么＝+，＝﹣﹣（用向量、表示）【分析】（1）根据平行四边形的性质，平行线分线段成比例定理即可解决问题；（2）利用三角形法则计算即可；【解答】解：（1）∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴＝＝3，∴＝3，∴EC：BC＝2：3．（2）∵＝，AC＝2AO，∴＝2，∵＝+＝+2，EC＝BC，∴＝+，∵AD∥BE，∴＝＝，∴BG＝BD，∵＝+＝+＝++2＝2+2，∴＝（2+2）＝+，∴＝﹣﹣故答案为+，﹣﹣．【点评】本题考查平行四边形的性质，平行线分线段成比例定理，平面向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21．（10分）如图，⊙O1和⊙O2相交于A、B两点，O1O2与AB交于点C，O2A的延长线交⊙O1于点D，点E为AD的中点，AE＝AC，联结OE．（1）求证：O1E＝O1C；（2）如果O1O2＝10，O1E＝6，求⊙O2的半径长．【分析】（1）连接O1A，根据垂径定理得到O1E⊥AD，根据相交两圆的性质得到O1C⊥AB，证明Rt△O1EA≌Rt△O1CA，根据全等三角形的性质证明结论；（2）设⊙O2的半径长为r，根据勾股定理列出方程，解方程得到答案．【解答】（1）证明：连接O1A，∵点E为AD的中点，∴O1E⊥AD，∵⊙O1和⊙O2相交于A、B两点，O1O2与AB交于点C，∴O1C⊥AB，在Rt△O1EA和Rt△O1CA中，，∴Rt△O1EA≌Rt△O1CA（HL）∴O1E＝O1C；（2）解：设⊙O2的半径长为r，∵O1E＝O1C＝6，∴O2C＝10﹣6＝4，在Rt△O1EO2中，O2E＝＝8，则AC＝AE＝8﹣r，在Rt△ACO2中，O2A2＝AC2+O2C2，即r2＝（8﹣r）2+42，解得，r＝5，即⊙O2的半径长为5．【点评】本题考查的是相交两圆的性质，全等三角形的判定和性质，垂径定理，勾股定理的应用，掌握相交两圆的连心线，垂直平分两圆的公共弦是解题的关键．22．（10分）如图，小山的一个横断面是梯形BCDE，EB∥DC，其中斜坡DE的坡长为13米，坡度i＝1：2.4，小山上有一座铁塔AB，在山坡的坡顶E处测得铁塔顶端A的仰角为45°，在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°（点F、D、C在一直线上），求铁塔AB的高度．（参考数值：sin31°≈0.52，cos31°≈0.86，tan31°≈0.6）【分析】延长AB交DC于G，过E作EH⊥CD于H，则四边形EHGB是矩形，根据勾股定理得到EH＝5，DH ＝12根据三角函数的定义列方程即可得到结论．【解答】解：延长AB交DC于G，过E作EH⊥CD于H，则四边形EHGB是矩形，∵斜坡DE的坡长为13米，坡度i＝1：2.4，∴设EH＝5x，DH＝12x，∵EH2+DH2＝DE2，∴（5x）2+（12x）2＝132，∴x＝1，∴EH＝5，DH＝12，∵EB∥DC，∴∠ABE＝∠AGH＝90°，∵∠AEB＝45°，∴AB＝BE，∴HG＝AB，∴FG＝5+12+AB，AG＝AB+5，∵∠F＝31°，∴tan F＝tan31°＝＝＝0.6，∴AB＝13米，答：铁塔AB的高度是13米．【点评】本题考查了解直角三角形的应用﹣仰角俯角问题，解直角三角形的应用﹣坡度坡角问题，矩形的性质，掌握的作出辅助线是解题的关键．23．（12分）已知：如图，△ADE的顶点E在△ABC的边BC上，DE与AB相交于点F，AE2＝AF•AB，∠DAF＝∠EAC．（1）求证：△ADE∽△ACB；（2）求证：＝．【分析】（1）由AE2＝AF•AB，推出△AEF∽△ABE，推出∠AEF＝∠B，再证明∠DAE＝∠BAC，即可解决问题；（2）由△ADE∽△ACB，推出＝，∠D＝∠C，再证明△ADF∽△ACE，可得＝，由此即可解决问题；【解答】证明：（1）∵AE2＝AF•AB，∴＝，∵∠EAF＝∠BAE，∴△AEF∽△ABE，∴∠AEF＝∠B，∵∠DAF＝∠EAC，∴∠DAE＝∠BAC，∴△ADE∽△ACB．（2）∵△ADE∽△ACB，∴＝，∠D＝∠C，∵∠DAF＝∠EAC，∴△ADF∽△ACE，∴＝，∴＝，∴＝．【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．24．（12分）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0）和点B，且OB＝3OA，与y轴交于点C，此抛物线顶点为点D．（1）求抛物线的表达式及点D的坐标；（2）如果点E是y轴上的一点（点E与点C不重合），当BE⊥DE时，求点E的坐标；（3）如果点F是抛物线上的一点．且∠FBD＝135°，求点F的坐标．【分析】（1）把点A、B的坐标代入二次函数表达式，即可求解；（2）设：OE＝m，则EL＝4﹣m，OB＝3，DL＝1，利用∠LED＝∠OBE，即可求解；（3）延长BD交y轴于点H，将△BCH围绕点B顺时针旋转135°至△BC′H′的位置，延长BH′交抛物线于点F．确定直线BH′的表达式，即可求解．【解答】解：（1）OB＝3OA＝3，则点B的坐标为（3，0），点A（﹣1，0），则函数的表达式为：y＝a（x+3）（x﹣1）＝a（x2+2x﹣3），则﹣3a＝﹣3，解得：a＝1，则抛物线的表达式为：y＝x2﹣2x﹣3…①函数对称轴为x＝﹣＝1，则点D的坐标为（1，﹣4）；（2）如图，过点D作DL⊥y轴，交于点L，设：OE＝m，则EL＝4﹣m，OB＝3，DL＝1，∵∠LED+∠OEB＝90°，∠OEB+∠OBE＝90°，∴∠LED＝∠OBE，∴tan∠LED＝tan∠OBE，即：＝，＝，解得：m＝1或3（舍去x＝3），则点E的坐标为（0，﹣1）；（3）延长BD交y轴于点H，将△BCH围绕点B，顺时针旋转135°至△BC′H′的位置，延长BH′交抛物线于点F，∵OB＝OC＝3，∴∠OCB＝∠OBC＝45°，则∠FBD＝135°，BC′⊥x轴，则点C′（3，3），∠H′C′B＝∠HCB＝180°﹣45°＝135°，tan∠ABD＝＝＝2，OH＝OB•tan∠ABD＝2×3＝6，则：HC＝6﹣3＝3＝H′C′，过点C′作C′G⊥GH′交于点G，在△BGH′中，GC′＝H′C′cos45°＝＝GH′，则点H′的坐标为（3﹣，），将点H′、B的坐标代入一次函数表达式y＝kx+b得：，解得：，则直线BH′的表达式为：y＝﹣3x+9…②，联立①②并解得：x＝3或﹣4（x＝3舍去），故点F的坐标为（﹣4，21）．【点评】本题考查的是二次函数综合运用，涉及到解直角三角形、图形旋转等知识，其中（3）用图形旋转的方法，确定旋转后图形的位置时本题的难点．25．（14分）如图，点O在线段AB上，AO＝2OB＝2a，∠BOP＝60°，点C是射线OP上的一个动点．（1）如图①，当∠ACB＝90°，OC＝2，求a的值；（2）如图②，当AC＝AB时，求OC的长（用含a的代数式表示）；（3）在第（2）题的条件下，过点A作AQ∥BC，并使∠QOC＝∠B，求AQ：OQ的值．【分析】（1）如图①中，作CH⊥AB于H．证明△ACH∽△CBH，可得＝，由此构建方程即可解决问题．（2）如图②中，设OC＝x．作CH⊥AB于H，则OH＝，CH＝x．在Rt△ACH中，根据AC2＝AH2+CH2，构建方程即可解决问题．（3）如图②﹣1中，延长QC交CB的延长线于K．利用相似三角形的性质证明＝，即可解决问题．【解答】解：（1）如图①中，作CH⊥AB于H．∵CH⊥AB，∴∠AHC＝∠BHC＝90°，∵∠ACB＝90°，∴∠ACH+∠BCH＝90°，∵∠ACH+∠A＝90°，∴∠BCH＝∠A，∴△ACH∽△CBH，∴＝，∵OC＝2，∠COH＝60°，∴∠OCH＝30°，∴OH＝OC＝1，CH＝，∴＝，整理得：2a2﹣a﹣4＝0，解得a＝或（舍弃）．经检验a＝是分式方程的解．∴a＝．（2）如图②中，设OC＝x．作CH⊥AB于H，则OH＝，CH＝x．在Rt△ACH中，∵AC2＝AH2+CH2，∴（3a）2＝（x）2+（2a+x）2，整理得：x2+ax﹣5a2＝0，解得x＝（﹣1）a或（﹣﹣1）a（舍弃），∴OC＝（﹣1）a，（3）如图②﹣1中，延长QC交CB的延长线于K．∵∠AOC＝∠∠AOQ+∠QOC＝∠ABC+∠OCB，∠QOC＝∠ABC，∴∠AOQ＝∠KCO，∵AQ∥BK，∴∠Q＝∠K，∴△QOA∽△KCO，∴＝，∴＝，∵∠K＝∠K，∠KOB＝∠AOQ＝∠KCO，∴△KOB∽△KCO，∴＝，∴＝＝＝【点评】本题属于相似形综合题，考查了相似三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．。

2019学年杨浦初三数学一模试卷含答案

杨浦区2019学年度第一学期期末质量调研初三数学试卷 2019.12（测试时间：100分钟，满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分） 1．把抛物线2x y =向左平移1个单位后得到的抛物线是A ．21y x =+（）；B ．21y x =-（）； C ．21y x =+；D ．21y x =-.2．在Rt △ABC 中，∠C =90°，如果AC =2，3cos 4A =，那么AB 的长是 A ．52；B ．83；C ．103； D3．已知a 、b 和c 都是非零向量，下列结论中不能判定//a b 的是A ．////a c b c ，；B ．12a c =，2bc =；C ．2a b =；D ．a b =.4．如图，在6×6的正方形网格中，联结小正方形中两个顶点A 、B ，如果线段AB 与网格线的其中两个交点为M 、N ，那么AM ∶MN ∶NB 的值是 A ．3∶5∶4； B ．3∶6∶5； C ．1∶3∶2；D ．1∶4∶2.5．广场上喷水池中的喷头微露水面，喷出的水线呈一条抛物线，水线上水珠的高度y （米）关于水珠和喷头的水平距离x （米）的函数解析式是236042y x x x =-+≤≤（），那么水珠的高度达到最大时，水珠与喷头的水平距离是 A ．1米； B ．2米； C ．5米； D ．6米．6．如图，在正方形ABCD 中，△ABP 是等边三角形，AP 、BP 的延长线分别交边CD 于点E 、F ，联结AC 、CP ，AC 与BF 相交于点H ，下列结论中错误的是 A ．AE ＝2DE ；B ．△CFP ∽△APH ；C ．△CFP ∽△APC ；D ．CP 2＝PH •PB ．二、填空题：（本大题共12题，每题4分，满分48分） 7．如果cot α，那么锐角α= ▲ 度．8．如果抛物线231y x x m =-+-+经过原点，那么m = ▲ ． 9ADBCEP FH第6题图第4题图10．已知点11A x y （，）、22B x y （，）为抛物线22y x =-（）上的两点，如果122x x <<，那么1y ▲ 2y ．（填“>”、“<”或“=”）11．在比例尺为1：8 000 000地图上测得甲、乙两地间的图上距离为4厘米，那么甲、乙两地间的实际距离为 ▲ 千米．12．已知点P 是线段AB 上的一点，且2BP AP=⋅ 13．已知点G 是△ABC 的重心，过点G 作MN ∥BC 分别交边AB 、AC 于点M 、N ，那么AMNABCS S ∆∆14．如图，某小区门口的栏杆从水平位置AB 绕固定点O 旋转到位置DC ，已知栏杆AB 的长为3.5米，OA 的长为3米，点C 到AB 的距离为0.3米，支柱OE 的高为0.6米，那么栏杆端点D 离地面的距离为▲ 米． 15．如图，某商店营业大厅自动扶梯AB 的坡角为31°，AB 的长为12米，那么大厅两层之间BC 的高度为 ▲ 米．（结果保留一位小数）【参考数据：sin31°＝0.515，cos31°＝0.867，tan31°＝0.601】 16．如图，在四边形ABCD 中，∠B =∠D =90°，AB =3，BC =2，4tan 3A =，那么CD = ▲ ．17．定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线．在四边形ABCD 中，对角线BD 是它的相似对角线，∠ABC =70°，BD 平分∠ABC ，那么∠ADC= ▲ 度．18．在Rt △ABC 中，∠A =90°，AC =4，AB =a ，将△ABC 沿着斜边BC 翻折，点A 落在点A 1处，点D 、E 分别为边AC 、BC 的中点，联结DE 并延长交A 1B 所在直线于点F ，联结A 1E ，如果△A 1EF 为直角三角形时，那么a = ▲ ．三、解答题：（本大题共7题，满分78分）19．（本题满分10分，第（1）小题6分，第（2）小题4分）抛物线y ＝ax 2+bx +c 中，函数值y 与自变量x 之间的部分对应关系如下表：（1）求该抛物线的表达式；（2）如果将该抛物线平移，使它的顶点移到点M （2，4）的位置，那么其平移的方法是 ▲ .ABC第15题图31°第16题图第14题图20．（本题满分10分，第（1）小题6分，第（2）小题4分）如图，已知在梯形ABCD 中，AB //CD ，AB =12，CD =7，点E 在边AD 上，23DE AE =，过点E 作EF //AB 交边BC 于点F .（1）求线段EF 的长；（2）设AB a =，AD b =，联结AF ，请用向量a 、b 表示向量AF ．21. （本题满分10分，第（1）小题5分，第（2）小题5分）如图，已知在△ABC 中，∠ACB=90º，3sin 5B =，延长边BA 至点D ，使AD =AC ，联结CD . （1）求∠D 的正切值；（2）取边AC 的中点E ，联结BE 并延长交边CD 于点F ，求CFFD的值．22．（本题满分10分）某校九年级数学兴趣小组的学生进行社会实践活动时，想利用所学的解直角三角形的知识测量教学楼的高度，他们先在点D 处用测角仪测得楼顶M 的仰角为30︒，再沿DF 方向前行40米到达点E 处，在点E 处测得楼顶M 的仰角为45︒，已知测角仪的高AD 为1.5米．请根据他们的测量数据求此楼MF 的高．（结果精确到0.1m 1.414≈ 1.732≈ 2.449） 23．（本题满分12分，每小题各6分）如图，已知在ABC △中，AD 是ABC △的中线，DAC B ∠=∠，点E 在边AD 上，CE CD =.（1）求证：AC BDAB AD =；（2）求证：22AC AE AD =⋅.第21题图ABCD第20题图第23题图A CDE30º 45º 第22题图A B C DFEM24．（本题满分12分，每小题各4分）已知在平面直角坐标系xOy 中，抛物线224y mx mx =-+(0)m ≠与x 轴交于点A 、B （点A 在点B 的左侧），且AB=6．（1）求这条抛物线的对称轴及表达式；（2）在y 轴上取点E 02（，），点F 为第一象限内抛物线上一点，联结BF 、EF ，如果=10OEFB S 四边形，求点F 的坐标；（3）在第（2）小题的条件下，点F 在抛物线对称轴右侧，点P 在x 轴上且在点B 左侧，如果直线PF 与y 轴的夹角等于∠EBF ，求点P 的坐标.25．（本题满分14分，第（1）小题3分，第（2）小题5分，第（3）小题6分）已知在菱形ABCD 中，AB=4，120BAD ∠=︒，点P 是直线AB 上任意一点，联结PC ，在∠PCD 内部作射线CQ 与对角线BD 交于点Q （与B 、D 不重合），且∠PCQ=30︒．（1）如图，当点P 在边AB 上时，如果3BP =，求线段PC 的长；（2）当点P 在射线BA 上时，设BP =x ，CQ =y ，求y 关于x 的函数解析式及定义域；（3）联结PQ ，直线PQ 与直线BC 交于点E ，如果△QCE 与△BCP 相似，求线段BP 的长．第24题图 A BC DPQ第25题图备用图A BCD杨浦区2019学年度第一学期初三数学期末质量调研试卷答案2019.12一、选择题：（本大题共6题，每题4分，满分24分）1．A ； 2．B ； 3．D ； 4．C ； 5．B ； 6．C 二、填空题：（本大题共12题，每题4分，满分48分）7．8．1； 9．0（，-1）；10．320； 1213 14．2.4； 15．6.2； 16．145； 18．、4 （本大题共7题，满分78分） 19．解：（1）∵二次函数2y ax bx c =++图像过点10（-，）、 (01)-，和(14)-，， ∴01 4.a b c c a b c -+=⎧⎪=-⎨⎪++=-⎩，， ··········································································· （3分） ∴121.a b c =-⎧⎪=-⎨⎪=-⎩，，∴二次函数解析式为221y x x =---. ·································· （3分）（2）平移的方法是先向右平移3个单位再向上平移4个单位或先向上平移4个单位再向右平移3个单位. ······················· （4分）20．解：（1）过D 作DH //BC 交AB 于H ，交EF 于G .∵DH //BC ，AB //DC ，∴四边形DHBC 是平行四边形. ································· （1分） ∴BH =CD ，∵CD=7，∴BH =7.······························································ （1分）同理GF =7. ······················································································· （1分）又AB=12，∴AH =5. ············································································ （1分）∵EF //AB ， ∴EG DEAH DA=. ···································································· （1分） ∵23DE AE =，∴25DE DA =. ∴255EG =，2EG =，∴9EF =. ·························································· （1分）（2）3345a b →→+ ··················································································· （4分）21. 解：（1）过C 作CH ⊥AB 于H ．在Rt △ABC 中，∵3sin =5B ，∴3=5AC AB . ·········································· （1分） ∴设AC =3k ，AB =5k ，则BC =4k . ∵1122ABC S AC BC AB CH ∆=⋅=⋅，∴125AC BC CH k AB ⋅==. ··············· （1分） ∴9=5AH k . ················································································ （1分）∵AD=AC ，∴DH =924355k k k +=. ················································· （1分）在Rt △CDH 中，1215tan =2425kCH CDH DH k ∠==. ··································· （1分）（2）过点A 作AH//CD 交BE 于点H.∵AH//CD ，∴AH AECF EC =. ···································································· （1分） ∵点E 为边AC 的中点，∴AE CE =.∴AH CF =. ···································· （1分） ∵AH//CD ，∴AH ABDF BD=. ···································································· （1分） ∵AB =5k ，BD =3k ，∴58AB BD =.∴58AH DF =. ·············································· （1分） ∴58CF DF =. ······················································································· （1分） 22．解：由题意可知∠MCA =90°，∠MAC =30°，∠MBC =45°，AB =40，CF =1.5. 设MC =x 米，则在Rt △MBC 中，由 tan MCMBC BC∠=得BC =x . ················· （2分）又Rt △ACM 中，由cot ACMAC MC∠=得AC=. ···································· （2分）∴40x -=. ············································································· （2分） ∴x=20. ··············································································· （1分） ∴MF =MC+CF=56.1≈米. ····················································· （2分）答：此楼MF 的高度是56.1米. ······························································ （1分）23．证明：（1）∵CD =CE ，∴∠CED =∠CDA . ········································ （1分） ∴∠AEC =∠BDA . ······························································· （1分）又∵∠DAC =∠B ，∴△ACE ∽△BAD. ········································ （1分）∴AC CEAB AD=. ····································································· （1分） ∵AD 是ABC △的中线，∴BD CD =. ········································ （1分）∵CD =CE ，∴BD CE =.∴AC BDAB AD=. ······································· （1分）（2）∵∠DAC =∠B ，又∠ACD =∠BCA ，∴△ACD ∽△BCA. ······················· （1分）∴AC CD BC AC=，∴2AC CD CB =?. ················································· （1分） ∵AD 是ABC △的中线，∴2BC CD =，∴222AC CD =. ·················· （1分）∵△ACE ∽△BAD ，∴CE AEAD BD=. ················································ （1分）又∵CD =CE=BD ，∴2CD AD AE =?. ············································ （1分） ∴22AC AD AE =?. ································································ （1分）24．解：（1）抛物线对称轴212mx m-=-=... ................................................................. （1分）∵AB =6，∴抛物线与x 轴的交点A 为(20)，-，B (40)，.................................................. （1分） ∴4440m m ++=（或16840m m -+=）.. ................................................................ （1分）∴12m =-.∴抛物线的表达式为2142y x x =-++. ..................................................... （1分）（2）设点F 21(4)2x x x ，-++. ...................................................................................... （1分） ∵点E 02-（，），点B 4（，0），∴OE = 2，OB = 4. ∵=+10OEF OBF OEFB S S S ∆∆=四边形， ∴211124(4)10222x x x ⨯⨯+⨯⨯-++=.. .................... （1分）∴12x =或，∴点F 912（，）、24（，）.. ............................................................................... （2分）（3）∵=+10OBE BEF OEFB S S S ∆∆=四边形，又1142422OBE S OB OE ∆=⋅=⨯⨯=，∴6BEF S ∆=.过F 作FH BE ⊥，垂足为点H .∵162BEF S BE FH ∆=⋅=，又BE =FH =............................... （1分）又BF ==BH ∴在Rt BFH ∆中，tan ∠EBF=3584FH BH ==.................................................................. （1分）设直线PF 与y 轴的交点为M ，则∠PMO=∠EBF ，过F 作FG x ⊥轴，垂足为点G.∵FG//y 轴，∴∠PMO=∠PFG . ∴tan ∠PFG=tan ∠EBF ................................................ （1分）∴tan ∠PFG=34PG FG =.又FG =4，∴PG =3.∴点P 的坐标10（-，）. .......................................................................................................... （1分）25．解：（1）过P 作PH BC ⊥，垂足为点H. 在Rt BPH ∆中，∵BP =3，∠ABC =60°，∴32BH PH =，................................. （2分）在Rt PCH ∆中，35422CH PC =-===，................................... （1分）（2）过P 作PH BC ⊥，垂足为点H. 在Rt BPH ∆中，12BH x PH =，.∴在Rt PCH∆中，142CH x PC=-==，........... （1分）设PC与对角线BD交于点G. ∵AB//CD，∴BP PG BG xCD===.∴BG CG=···················································（1分）∵∠ABD=∠PCQ，又∠PGC=∠QGC，∴△PBG∽△QCG.∴PB BGCQ CG=，∴xy···················································（1分）∴y=08x≤<）. ······················································（2分）（3）i）当点P在射线BA上，点E在边BC的延长线时.∵BD是菱形ABCD的对角线，∴∠PBQ=∠QBC=1302ABC∠=︒.∵△PBG∽△QCG，∴PG BGQG CG=，又∠PGQ=∠BGC，∴△PGQ∽△BGC.∴∠QPG=∠QBC30=︒，又∠PBQ=∠PCQ30=︒，∴60CQE QPC QCP∠=∠+∠=︒.∴60CQE PBC∠=∠=︒. ····································································（1分）∵PCB E∠>∠，∴PCB QCE∠=∠.又180PCB QCE PCQ∠+∠+∠=︒，∠PCQ30=︒，∴75PCB QCE∠=∠=︒.过C作CN BP⊥，垂足为点N，∴在Rt CBN∆中，2BN CN==，∴在Rt PCN∆中，PN CN==∴2BP=. ................................................................................................................. （2分）ii）当点P在边AB的延长线上，点E在边BC上时，同理可得2BP=. ...... （3分）。

2019-2020学年上海市宝山区初三数学一模(试卷+参考答案)

2019学年第一学期期末考试九年级数学试卷（满分150分，考试时间100分钟 2020.1）考生注意：1．本试卷含四个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一. 选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．】1．符号A sin 表示………………………………………………………………… （） A ．∠A 的正弦； B ．∠A 的余弦； C ．∠A 的正切； D ．∠A 的余切．2．如果b a 32-=，那么ba=………………………………………………………（） A ．3-； B ．2-； C ．5； D ．1-．3．二次函数221x y -=的图像的开口方向…………………………………… （） A ．向左； B ．向右； C ．向上； D ．向下．4．直角梯形ABCD 如图放置，AB 、CD 为水平线，BC ⊥AB ，如果∠BCA =67°，从低处A 处看高处C 处，那么点C 在点A 的……………… （） A ．俯角67°方向； B ．俯角23°方向； C ．仰角67°方向； D ．仰角23°方向． 5．已知a 、b 为非零向量，如果5b a =-，那么向量a 与b 的方向关系是……………………………………… （）a b a b a b a b C ．a 和b 方向互相垂直； D ．a 和b 之间夹角的正切值为5． 6．如图，分别以等边三角形ABC 的三个顶点为圆心，以其边长为半径画弧，得到的封闭图形是莱洛三角形，如果AB =2，那么此莱洛三角形（即阴影部分）的面积………（） A ．3+π B ． 3-π C ．322-π D ．32-π第6题图第4题图ABDECCA BD 二．填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置】 7．已知1:2=3：x ，那么x = ▲ ．8．如果两个相似三角形的周长比为1：2，那么它们某一对对应边上的高之比为 ▲ ． 9．如图，△ABC 中∠C =90°，如果CD ⊥AB 于D ，那么AC 是AD 和 ▲ 的比例中项． 10．在△ABC 中，AB BC CA ++= ▲ ．11．点A 和点B 在同一平面上，如果从A 观察B ，B 在A 的北偏东14°方向，那么从B 观察A ，A 在B 的 ▲ 方向．12．如图，在△ABC 中，∠C =90°，∠A =30°，BD 是∠ABC 的平分线．如果x AC =，那么=CD ▲ （用x 表示）．13．如图，△ABC 中，DE 是BC 的垂直平分线，DE 交AC 于点E ，联结BE ．如果BE =9，BC =12，那么cosC = ▲ ． 14．若抛物线2()(1)y x m m =-++的顶点在第二象限，则m 的取值范围为 ▲ ． 15．二次函数=y 322++x x 的图像与y 轴的交点坐标是__▲__．16. 如图，已知正方形ABCD 的各个顶点A 、B 、C 、D 都在⊙O 上，如果P 是AB 的中点，PD 与AB 交于E 点，那么PEDE＝ ▲ ． 17. 如图，点C 是长度为8的线段AB 上一动点，如果AC <BC ，分别以AC 、BC 为边在线段AB 的同侧作等边△ACD 、△BCE ，联结DE ，当△CDE 的面积为33时，线段AC 的长度是 ▲ ．18. 如图，点A 在直线x y 43=上，如果把抛物线2x y =沿OA 方向平移5个单位，那么平移后的抛物线的表达式为 ▲ ．第9题图第18题图第16题图第17题图第12题图第13题图三、（本大题共7题，第19--22题每题10分；第23、24题每题12分；第25题14分；满分78分）19．（本题满分10分）计算：21245cos 260tan 6-︒-︒20．（本题满分10分，每小题各5分）已知：抛物线m x x y +-=22与y 轴交于点C(0,-2)，点D 和点C 关于抛物线对称轴对称．（1）求此抛物线的解析式和点D 的坐标；（2）如果点M 是抛物线的对称轴与x 轴的交点，求△MCD 的周长．第20题图21．（本题满分10分，每小题各5分）某仓储中心有一个坡度为2:1=i 的斜坡AB ，顶部A 处的高AC 为4米，B 、C 在同一水平地面上，其横截面如图．（1）求该斜坡的坡面AB 的长度；（2）现有一个侧面图为矩形DEFG 的长方体货柜，其中长 DE =2.5米，高EF =2米.该货柜沿斜坡向下时，点D 离BC 所在水平面的高度不断变化，求当BF =3.5米时，点D 离BC 所在水平面的高度DH ．22．（本题满分10分，每小题各5分）如图，直线l :3y x =，点1A 坐标为（1，0），过点1A 作x 轴的垂线交直线l 于点1B ，以原点O 为圆心，O 1B 为半径画弧交x 轴于点2A ；再过点2A 作x 的垂线交直线l 于点2B ，以原点O 为圆心，O 2B 长为半径画弧交x 轴于点3A ，…，按此做法进行下去．求：（1）点1B 的坐标和∠1A O 1B 的度数；（2）弦43A B 的弦心距的长度．第21题图第22题图23．（本题满分12分，每小题各6分）如图，△ABC 中，AB=AC ，AM 为BC 边的中线，点D 在边A C 上，联结BD 交AM 于点F ，延长BD 至点E ，使得DCADDE BD =，联结CE ．求证：（1）∠ECD=2∠BAM ；（2） BF 是DF 和EF 的比例中项．24．（本题共12分，每小题各4分）在平面直角坐标系内，反比例函数和二次函数)1(2-+=x x a y 的图像交于点A （1，a ）和点B （﹣1，﹣a ）．（1）求直线AB 与y 轴的交点坐标；（2）要使上述反比例函数和二次函数在某一区域都是y 随着x 的增大而增大，求a 应满足的条件以及x 的取值范围；（3）设二次函数的图像的顶点为Q ，当Q 在以AB 为直径的圆上时，求a 的值．第23题图25．（本题共14分，其中第（1）、（3）小题各4分，第（2）小题6分）如图，OC 是△ABC 中AB 边的中线，∠ABC=36°，点D 为OC 上一点，如果OD ＝k ·OC ，过D 作DE ∥CA 交于BA 点E ，点M 是DE 的中点．将△ODE 绕点O 顺时针旋转α度（其中︒<<︒1800α）后，射线OM 交直线BC 于点N ．（1）如果△ABC 的面积为26，求△ODE 的面积（用k 的代数式表示）；（2）当N 和B 不重合时，请探究∠ONB 的度数y 与旋转角α的度数之间的函数关系式；（3）写出当△ONB 为等腰三角形时，旋转角α的度数．第25题图2019学年第一学期期末考试九年级数学试卷评分参考一、选择题：（本大题共6题，每题4分，满分24分）1． A ； 2．B ； 3．D ； 4．D ； 5． B ； 6．C ；二、填空题（本大题共12题，每题4分，满分48分）7．6； 8．1:2； 9．AB ； 10．0； 11．南偏西14°； 12．x 31-； 13．32；14．01<<-m ； 15．（3,0）； 16．212-； 17．2； 18．3)4(2+-=x y . 三、简答题（本大题共7题，第19--22题每题10分；第23、24题每题12分．第25题14分；满分78分） 19．解：原式=2236-- ……………………6分=2)23)(23()23(6-+-+⋅ ……………………2分=322221218+=-+ ……………………2分20．（1）∵点C(0,-2)在抛物线m x x y +-=22上，∴2-=m ，此抛物线的解析式为222--=x x y ……………………………2分 ∵222--=x x y =3)1(2--=x y ，∴对称轴为直线1=x ，………………1分和点C 关于抛物线对称轴对称的点D 的坐标为：D （2，-2）．………………2分（2）根据题意点M 是抛物线的对称轴与x 轴的交点，∴M （1,0）……………2分 ∴MC=MD=52122=+， CD=2 …………………………2分 △MCD 的周长为252+． ……………………………………………………1分 21. 解：（1）根据题意斜坡高AC 为4m ，2:1=i ，∴水平宽度BC =8；……………2分坡面AB=5422=+BC AC ………………………………………………3分（2）过D 作DH ⊥BC 于H 交AB 于点M∵∠DMG =∠BAC ∠DGM =∠BCA∴△ DGM ∽△BCA …………………………1分 ∵ 矩形DEFG 中长DE =2.5m ，高EF =2m BF =3.5m∴GM=1， DM=5， FM=1.5， BM=5， MH=5 …………………3分点D 离BC 所在水平面的高度为52米。

上海市2019届初三数学一模提升题汇编第25题(压轴题)(word版含答案)

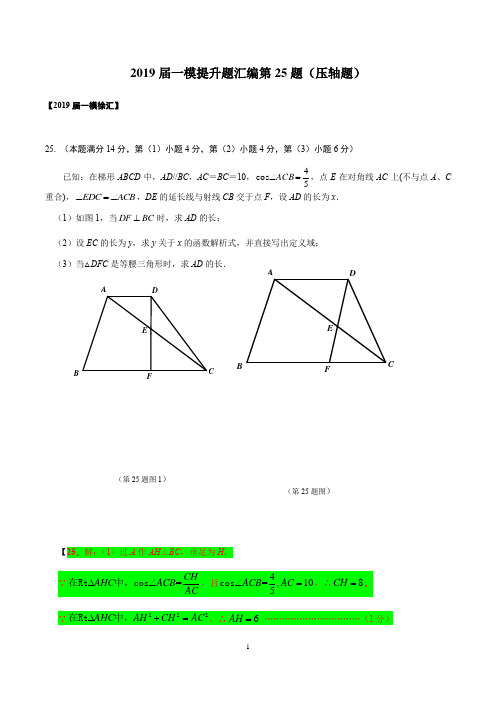
BB2019届一模提升题汇编第25题（压轴题）【2019届一模徐汇】25. （本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）已知：在梯形ABCD 中，AD //BC ，AC ＝BC ＝10，54cos =∠ACB ，点E 在对角线AC 上(不与点A 、C 重合)，EDC ACB ∠=∠，DE 的延长线与射线CB 交于点F ，设AD 的长为x ．（1）如图1，当DF BC ⊥时，求AD 的长；（2）设EC 的长为y ，求y 关于x 的函数解析式，并直接写出定义域；（3）当△DFC 是等腰三角形时，求AD 的长．【25．解：（1）过A 作AH ⊥BC ，垂足为H ，∵222AHC AH CH AC ∆+=在Rt 中，，∴6AH = ……………………………（1分）（第25题图1）（第25题图）∴90AHF HFD DFH ∠=∠=∠=︒，∴四边形AHFD 是矩形，∴6DF AH ==（2）∵AD ∥BC ,∴DAC ACB ∠=∠． ∵EDC ACB ∠=∠,∴EDC DAC ∠=∠．∵ACD ACD ∠=∠,∴CAD ∽CDE ………………………………………（1分）∵10,AC EC y ==,∴210CD CA CE y =⋅= …………………………………（1分）∵222226(8)DFC CD DF FC x ∆=+=+-在Rt 中，（3）由EDC ACB ∠=∠，EFC EFC ∠=∠得：FCE ∆∽FDC ∆，又AD ∥BC 有FCE ∆∽DAE ∆，∴DAE ∆∽FDC ∆∴当FDC ∆是等腰三角形时，DAE ∆也是等腰三角形 ………………………（1分） ∴1,DA DE ︒=当时不存在； ………………………………………………………（1分）2,10AD AE x y︒==-当时得：120(),6x x ==解得：舍……………………………………………………………（2分）【2019届一模浦东】25. （本题满分14分，其中第（1）小题3分，第（2）小题5分，第（3）小题6分）将大小两把含30°角的直角三角尺按如图10-1位置摆放，即大小直角三角尺的直角顶点C 重合，小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上，此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°，AB =12. （1）求小三角尺的直角边CD 的长;（2）将小三角尺绕点C 逆时针旋转，当点D 第一次落在大三角尺的边AB 上时（如图10-2），求点B 、E 之间的距离;（3）在小三角尺绕点C 旋转的过程中，当直线DE 经过点A 时，求∠BAE 的正弦值.（图10-1）（图10-2）DCABBAE【2019届一模杨浦】25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）已知：梯形ABCD 中，AD //BC ，AB ⊥BC ，AD =3，AB =6，DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .（1）当点E 为边AB 的中点时（如图1），求BC 的长；（2）当点E 在边AB 上时（如图2），联结CE ，试问：∠DCE 的大小是否确定？若确定，请求出∠DCE 的正切值；若不确定，则设AE =x ，∠DCE 的正切值为y ，请求出y 关于x 的函数解析式，并写出定义域；（3）当△AEF 的面积为3时，求△DCE 的面积.【 25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）解：（1）∵AD //BC ，∴DEAE ADEF EB BF.∵E 为AB 中点，∴AE =BE . ∴AD = BF ，DE = EF . ∵AD =3，AB =6，∴BF =3，BE =3. ∴BF =BE .∵AB ⊥BC ，∴∠F =45°且EF =32. ··················· （1分） ∴DF =2EF =62. ···························· （1分） ∵DF ⊥DC ，∠F =45°，∴CF =12. ···················· （1分） ∴BC = 1239CFBF . ······················（1分） A BCD E F（图1）（第25题图）A BCDEF （图2）（2）∠DCE的大小确定，1tan2DCE. ·················（1分）作CH⊥AD交AD的延长线于点H，∴∠HCD+∠HDC=90°.∵DF⊥DC，∴∠ADE+∠HDC=90°. ∴∠HCD=∠ADE.又∵AB⊥AD，∴∠A=∠CHD. ∴△AED∽△HDC. ·············（2分）∴DE ADDC CH. ·····························（1分）∵AB⊥AD，CH⊥AD，AD//BC，∴CH=AB=6.∵AD=3，CH=6，∴12DEDC.即1tan2DCE. ··············（1分）（3）当点E在边AB上，设AE=x，∵AD//BC，∴AD AEBF EB，即36xBF x.∴183xBFx.∵△AEF的面积为3，∴11833 2xxx.∴4x. ·······························（1分）∵AD=3，AB⊥AD，∴DE=5. ∵12DEDC，∴DC=10.∵DF⊥DC，∴1510252DCES. ··················（1分）当点E在边AB延长线上，设AE=y，∵AD//BC，∴AD AEBF EB，即36yBF y.∴318yBFy.∵△AEF的面积为3，∴131832yyy.∴8y. ·············（1分）∵AD=3，AB⊥AD，∴DE=73.联结CE，作CH⊥AD交AD的延长线于点H，同（1）可得12DEDC. ·····（1分）AB CDEF∴DC =273∵DF ⊥DC ，∴173273732DCES.················（1分）综上，当△AEF 的面积为3时，△DCE 的面积为25或73.】【2019届一模普陀】25．（本题满分14分）如图11，点O 在线段AB 上，22AO OB a ==，60BOP ∠=︒，点C 是射线OP 上的一个动点．（1）如图11①，当90ACB ∠=︒，2OC =，求a 的值；（2）如图11②，当AC =AB 时，求OC 的长（用含a 的代数式表示）；（3）在第（2）题的条件下，过点A 作AQ ∥BC ，并使∠QOC=∠B ，求:AQ OQ 的值．【 25．解：ABCPO ABCPO图11①图11②（1）过点C 作CH AB ⊥，H 为垂足． ·················· （1分）∴90CHO CHB ∠=∠=．在Rt △COH 中，60COB ∠=，2OC =．∵22AO OB a ==， ∴21AH a =+，1BH a =-．∵90ACB ∠=，∴90ACH HCB ∠+∠=． ∵CH AB ⊥，∴90ACH A ∠+∠=． ∴A HCB ∠=∠．∵90CHA BHC ∠=∠=︒，∴△ACH ∽△CBH ． ······················· （1分）∴2CH AH BH =⋅．（2）过点C 作CH AB ⊥，H 为垂足．设OC m =．在Rt △COH 中，60COB ∠=，OC m =．在Rt △ACH 中，90CHA ∠=︒， ∴222AC AH CH =+．（3）延长QA 、CO 交于点E ．∵AQ //BC ，∴E OCB ∠=∠．∵COA AOQ QOC ∠=∠+∠，COA OCB B ∠=∠+∠，QOC B ∠=∠， ∴AOQ OCB ∠=∠． ∵QOA E ∠=∠．又∵Q Q ∠=∠，∴△QOA ∽△QEO ． ················ （1分）【2019届一模奉贤】25．（本题满分14分，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分5分）如图11，已知梯形ABCD 中，AB ∥CD ，∠DAB =90°，AD =4，26AB CD ==，E 是边BC 上一点，过点D 、E 分别作BC 、CD 的平行线交于点F ，联结AF 并延长，与射线DC 交于点G ．（1）当点G 与点C 重合时，求:CE BE 的值；（2）当点G 在边CD 上时，设CE m =，求△DFG 的面积；（用含m 的代数式表示）（3）当AFD ∆∽ADG ∆时，求∠DAG 的余弦值．【25．解：（1）∵CD ∥EF ，DF ∥CE ，∴四边形DFEC 是平行四边形． ····················· （1分） ∴EF =DC ． ······························ （1分） ∵26AB CD ==，∴3CD EF ==．∵AB ∥CD ，∴AB ∥EF ．∵点G 与点C 重合，∴12EF CE AB BC ==．∴:1CE BE ．··········· （2分）（2）过点C 作CQ ∥AG ，交AB 于点Q ，交EF 于点P ．过点C 作CM ⊥AB ，交AB 于点M ，交EF 于点N ．在Rt △BCM 中， 90CMB，4CM AD ==，3BM AB CD =-=，∴5BC =．∵AB ∥EF ∥CD ，∴GC =PF =AQ ． ∴EP CEBQ BC=．图11ABCDFEG备用图ABCD（3）当AFD ∆∽ADG ∆时，∵∠DAB =90°，∴ADG ∆是直角三角形，∴AFD ∆也是直角三角形． ∵90DAF ，90FDA ，∴90DFA． ············（1分） ∵90FADADF，90FDC ADF，∴FAD FDC ．∵AB ∥EF ，∴BCEF ．∵四边形DFEC 是平行四边形，∴FDC CEF ．∴BFDC FAD ． ·······················（1分）在Rt △BCM 中， 90CMB ，3BM AB CD =-=，5BC =，【2019届一模松江】25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）如图，已知△ABC 中，∠ACB =90°，D 是边AB 的中点，P 是边AC 上一动点，BP 与CD 相交于点E ．（1）如果BC =6，AC =8，且P 为AC 的中点，求线段BE 的长；（2）联结PD ，如果PD ⊥AB ，且CE =2，ED =3，求cosA 的值；（3）联结PD ，如果222BP CD =，且CE =2，ED =3，求线段PD 的长．【25．解：（1）∵P 为AC 的中点，AC =8，∴CP =4……………………………（1分） ∵∠ACB =90°，BC =6，∴BP =213……………………………………………（1分） ∵D 是边AB 的中点，P 为AC 的中点，∴点E 是△ABC 的重心……………（1分） ∴241333BE BP ==…………………………………………………………（1分）（2）过点B 作BF ∥CA 交CD 的延长线于点F ………………………………（1分）（备用图2）ABCD（备用图1）ABCD（第25题图）ABPCDE∴CABFDC FD DA BD ==………………………………（1分） ∵BD =DA ，∴FD =DC ，BF =AC …………………（1分） ∵CE =2，ED =3，则CD =5，∴EF =8 ∴4182===EF CE BF CP …………………………（1分） ∴41=CA CP ，∴13CP PA =，设CP =k ，则P A =3k ，∵PD ⊥AB ，D 是边AB 的中点，∴P A =PB =3k∴k BC 22=，∴k AB 62=，∵k AC 4=，∴6cos 3A =…………（1分）（3）∵∠ACB =90°，D 是边AB 的中点，∴12CD BD AB ==∵222BP CD =，∴22BP CD CD BD AB =⋅=⋅……………（1分） ∵∠PBD =∠ABP ，∴△PBD ∽△ABP …………………………（1分） ∴∠BPD =∠A ……………………………………………………（1分） ∵∠A =∠DCA ，∴∠DPE =∠DCP ，∵∠PDE =∠CDP ，△DPE ∽△DCP ，∴DC DE PD ⋅=2…………………………（1分）∵DE =3,DC =5，∴15=PD …………………………………………………（1分）】【2019届一模嘉定】25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）（备用图2）ABC DPE PE （备用图1）AB C DF在矩形ABCD 中，6=AB ，8=AD ，点E 是边AD 上一点，EC EM ⊥交AB 于点M ，点N 在射线MB 上，且AE 是AM 和AN 的比例中项. （1）如图8，求证：DCE ANE ∠=∠；（2）如图9，当点N 在线段MB 之间，联结AC ，且AC 与NE 互相垂直，求MN 的长；（3）联结AC ，如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似，求DE 的长．【25.（1）证明：∵AE 是AM 和AN 的比例中项∴ANAE AE AM = ……………………1分 ∵A A ∠=∠∴△AME ∽△AEN ∴ANE AEM ∠=∠……………………1分 ∵︒=∠90D ∴︒=∠+∠90DEC DCE ∵EC EM ⊥∴︒=∠+∠90DEC AEM ∴DCE AEM ∠=∠……………………1分 ∴DCE ANE ∠=∠ ………1分A备用图 BDCA备用图BDCA 图8B MEDCNA 备用图BDCM EN A 图9BDCA图8 BM EDC N（2）解：∵AC 与NE 互相垂直∴︒=∠+∠90AEN EAC∵︒=∠90BAC ∴︒=∠+∠90AEN ANE ∴EAC ANE ∠=∠ 由（1）得DCE ANE ∠=∠ ∴EAC DCE ∠=∠ ∴DAC DCE ∠=∠tan tan ∴ADDCDC DE =……………………1分 ∵6==AB DC , 8=AD , ∴29=DE ∴27298=-=AE ……………………1分由（1）得DCE AEM ∠=∠ ∴DCE AEM ∠=∠tan tan ∴DCDEAE AM =∴821=AM ……………………1分 ∵AN AE AE AM =∴314=AN ……………………1分 ∴2449=MN ……………………1分（3）∵AEM MAE NME ∠+∠=∠,DCE D AEC ∠+∠=∠ 又︒=∠=∠90D MAE ,由（1）得DCE AEM ∠=∠∴ NME AEC ∠=∠ …………………………1分当△AEC 与以点E 、M 、N 为顶点所组成的三角形相似时 1）EAC ENM ∠=∠，如图9 ∴EAC ANE ∠=∠由（2）得：29=DE ……………………2分2）ECA ENM ∠=∠，如图10 过点E 作AC EH ⊥，垂足为点H由（1）得DCE ANE ∠=∠ ∴DCE ECA ∠=∠M EN A 图9 BDCA 图10B MEDCNH设x DE 3=，则x HE 3=，x AH 4=，x AE 5= 又AD DE AE =+ ∴835=+x x ，解得1=x∴33==x DE……………………2分【2019届一模青浦】25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD//BC ，BC =18，DB =DC =15，点E 、F 分别在线段BD 、CD 上，DE =DF =5． AE 的延长线交边BC 于点G ， AF 交BD 于点N 、其延长线交BC 的延长线于点H ．（1）求证：BG =CH ；（2）设AD =x ，△ADN 的面积为y ，求y 关于x 的函数解析式，并写出它的定义域；（3）联结FG ，当△HFG 与△ADN 相似时，求AD 的长．【25．解：（1）∵AD //BC ，∵DB =DC =15，DE =DF =5，∴BG ＝CH ． ························· （1分）NHG FED C AB（第25题图）（2）过点D作DP⊥BC，过点N作NQ⊥AD，垂足分别为点P、Q．∵DB=DC=15，BC=18，∴BP=CP=9，DP=12．··········（1分）∵AD∥BC，∴∠ADN=∠DBC，∴sin∠ADN=sin∠DBC，（3）∵AD∥BC，∴∠DAN=∠FHG．（i）当∠ADN=∠FGH时，∵∠ADN=∠DBC，∴∠DBC =∠FGH，∴BD∥FG，·························（1分）（ii）当∠ADN=∠GFH时，∵∠ADN=∠DBC=∠DCB，又∵∠AND =∠FGH，∴△ADN∽△FCG．·····················（1分）图11ABCPQM【2019届一模静安】25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）已知：如图11，在ABC∆中，6AB =，9AC =，tan ABC ∠=B 作BM //AC ，动点P 在射线BM 上（点P 不与点B 重合），联结PA 并延长到点Q ，使AQC ABP ∠=∠．（1）求ABC ∆的面积；（2）设BP x =，AQ y =，求y 关于x 的函数解析式，并写出x 的取值范围；（3）联结PC ，如果PQC ∆是直角三角形，求BP 的长．【 25．解：（1）过点A 作AH ⊥BC ，交BC 于点H ． ···············（1分）∴279BC BH HC =+=+=, ··················· （1分） ∴1194218222ABC S BC AH ∆=⋅=⨯⨯=．…………………（1分） (2) 过点A 作AG ⊥BM ，交BM 于点G ． ∵AC BC =, ∴CAB CBA ∠=∠ ∵BM //AC , ∴ABP CAB ∠=∠ ∴ABP CBA ∠=∠∴42AG AH ==,即2BG BH ==………（1分） ∴2PG x =- 在Rt AGP ∆中，22222(42)(2)436AP AG PG x x x =+=+-=-+ （1分）∵BAQ BAC CAQ ∠=∠+∠,BAQ ABP APB ∠=∠+∠,∴APB CAQ ∠=∠又AQC ABP ∠=∠ ················· （1分） ∴ABP ∆∽CQA ∆ ∴AP BPAC AQ= ∴24369x x x y-+=, 即29(0)436x y x x x =>-+ ·········· （2分）(3) 由题意得PQ AP AQ =+=22229536436436436x x x x x x x x x ++-++=-+-+由ABP ∆∽CQA ∆得AB APCQ AC= 得 254436CQ x x =-+ ········ （1分）如果PCQ ∆是直角三角形，又90AQC ABP ∠=∠≠，故只有两种可能：……（1分）①90PCQ ∠=，则1cos 3CQ AQC PQ ∠==，即3PQ CQ =， 222536543436436x x x x x x ++=⨯-+-+，解得129,14x x ==-（舍）；（2分）②90CPQ ∠=，则1cos 3PQ AQC CQ ∠==，即3CQ PQ =，第25题ABCPQMGH222536543436436x x x x x x ++⨯=-+-+，该方程无解；（1分）综上所述，如果PCQ ∆是直角三角形，BP 的长为9．】【2019届一模宝山】25．（本题满分14分，第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分）如图10，已知：梯形ABCD 中，∠ABC =90°，∠A =45°，AB ∥DC ，DC =3，AB =5，点 P 在AB 边上，以点A 为圆心AP 为半径作弧交边DC 于点E ，射线EP 与射线CB 交于点F ．（1）若，求DE 的长；（2）联结CP ，若CP=EP ，求AP 的长；（3）线段CF 上是否存在点G ，使得△ADE 与△FGE 相似，若相似，求FG 的值；若不相似，请说明理由．【25.（本题满分14分，第（1）小题满分4分,第（2）小题满分6分,第（3）小题满分4分）解：(1)过点A 作AG ⊥CD 交CD 的延长线于点M ……………………… … …1分梯形ABCD 中，∠ABC =90°，∠A =45°∴∠DAM =45°13AP =备用图A BCD PEABCDF（图10）∵AB //CD ，AM =CD 且∠ADM =∠DAM =45°，DM =AM =2……… … …1分 ∴Rt △AEM 中，AE =AP =√13，ME =√AE 2−AG 2=3…………… ……1分 ∴DE =1 ……………………………………………………………… ……1分 (2)过点P 作PH ⊥CD ，垂足是点H∵CP =EP ∴EC =2CH ……………………………………… …… 1分设AE =AP =x ，PB =5-x ，EC =10-2x ， BC =2∴Rt △PBC 中，PE =PC =√PB 2+BC 2=√(5−x )2+22=√x 2−10x +29 …… 1分由题意可知AE =AP ，∴∠AEP =∠APE ，∵CP =EP ，∴∠PEC =∠PCE …… …1分∵AB //CD ∴∠PEC =∠APE ，∴∠PEC =∠APE 且∠PCE =∠AEP ∴△APE ∽△PCE …………………………………………………………1分化简得(3)∵△ADE 是钝角三角形，当点G 在CF 上时，∠GEF 、∠F 必是锐角，∴若△ADE ∽△FGE ，只能∠ADE =∠FGE =135°…………………………… ……1分 ∵Rt △PBF 中,∠F +∠FPB =90° 又∵∠EAP +∠APE +∠AEP =180° ∵∠FPB =∠APE ，∠APE =∠AEP ∴∠EAP =2∠F ∵AB //CD ∴∠DEA =∠EAP ∴∠DEA =2∠F∴必有∠DAE =∠F …………………………………………………………… …… …1分0292032=+-x x∴∠EAP =2∠DAE ∴∠EAP =30°，∠F =∠DAE =15°∴AE =AP =2AM =4，PB =1，EM =，CG =CE =……………… ………1分 ∴EG =∵△ADE ∽△FGE ∴∴FG =………………………………1分 ∴当FG =时，△ADE ∽△FGE ．】【2019届一模长宁】25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）已知锐角MBN ∠的余弦值为53，点C 在射线BN 上，25=BC ，点A 在MBN ∠的内部，且︒=∠90BAC ，MBN BCA ∠=∠．过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E ．点F 在线段BE 上（点F 不与点B 重合），且MBN EAF ∠=∠．（1）如图1，当BN AF ⊥时，求EF 的长；（2）如图2，当点E 在线段BC 上时，设x BF =，y BD =，求y 关于x 的函数解析式并写出函数定义域；（3）联结DF ，当ADF ∆与ACE ∆相似时，请直接写出BD 的长．3232-56225-FGADEG DE =133-133-如图2BF EC ND AMB FC E N ADM如图1备用图BC NAM【25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）解：（1）∵在 BAC Rt ∆中 ︒=∠90BAC∵25=BC ∴15=AC （1分）∵BC AF ⊥ ∴︒=∠90AFC∴16=EF （1分）（2）过点A 作EF AH ⊥于点H ∴ ︒=∠90AHB∵x BF =，x FH -=16，x FC -=25∴ 40032)16(122222+-=-+=x x x AF （1分） ∵ BCA MBN ∠=∠，EAF MBN ∠=∠∴BCA EAF ∠=∠ 又∵CFA AFE ∠=∠ ∴AFE ∆∽CFA∆ ∴EF FC AF ⋅=2第25题图∴EF x x x ⋅-=+-)25(400322（1分）∴xx x EF -+-=25400322，xxx x x x BF EF BE --=+-+-=+=25740025400322 （1分）∵ ACB MBN ∠=∠，FAC AEF ∠=∠，∴BDE ∆∽CFA ∆ ∴ACBEFC BD =（1分） ∴1525740025x xx y--=- ∴157400x y -=（2250≤<x ）（1分+1分）（3）596或 1172000（2分+2分）】【2019届一模金山】25．已知多边形ABCDEF 是⊙O 的内接正六边形，联结AC 、FD ，点H 是射线AF 上的一个动点，联结CH ,直线CH 交射线DF 于点G ，作CH MH ⊥交CD 的延长线于点M ，设⊙O 的半径为()0>r r ．（1）求证：四边形ACDF 是矩形．（2）当CH 经过点E 时，⊙M 与⊙O 外切，求⊙M 的半径（用r 的代数式表示）．（3）设()900<<=∠ααHCD ，求点C 、M 、H 、F 构成的四边形的面积（用r 及含α的三角比的式子表示）．AB CDEFGOHM第25题图第25题备用图ABCD EFO【25.（1）证明：∵多边形ABCDEF 是⊙O 的内接正六边形，∴BCA BAC ∠=∠，∵180=∠+∠+∠ABC BCA BAC ，∴ 30=∠BAC ，得90=∠CAF ，（1分）同理 90=∠ACD ，90=∠AFD ，（1分） ∴四边形ACDF 是矩形．（1分）∴OCD ∆为等边三角形，∴r OC CD ==，60=∠OCD ，作CD ON ⊥垂足为N ，即ON 为CD 弦的弦心距，作AC OP ⊥垂足为P ，即OP 为AC 弦的弦心距，当CH 经过点E 时，可知30=∠ECD , ∵四边形ACDF 是矩形，∴CD AF //，∴30=∠=∠ECD AHC ，∵CH MH ⊥，∵⊙M 与⊙O 外切，（3）作CM HQ ⊥垂足为Q ，由α=∠HCD ，CH MH ⊥可得α=∠QHM , ∵CD AF //,CD AC ⊥①当600<<α时，点H 在边AF 的延长线上，此时点C 、M 、H 、F 构成的四边形为梯形，②当60=α时，点H 与点F 重合，此时点C 、M 、H 、F 构成三角形，非四边形，所以舍去. （1分）③当9060<<α时，点H 在边AF 上，此时点C 、M 、H 、F 构成的四边形为梯形，∴()()2tan 3322r HQ CM FH S ⋅+=⋅+=α. （1分）综上所述，当()900<<=∠ααHCD 时，点C 、M 、H 、F 构成的四边形的面积为()23tan 3cot 62r S ⋅-+=αα或()2tan 332r S ⋅+=α.（备注：若求出ααcos sin 3⋅=r CM ，可得当600<<α2cos sin 2323cot 23r S ⋅⎪⎪⎭⎫ ⎝⎛⋅+-=ααα，当9060<<α时2cos sin 23cot 2323r S ⋅⎪⎪⎭⎫⎝⎛⋅+-=ααα.】【2019届一模闵行】25．（本题满分14分，其中第（1）小题4分、第（2）、（3）小题各5分）如图，在梯形ABCD 中，AD // BC ，AB = CD ，AD = 5，BC = 15，5cos 13ABC ∠=．E 为射线CD 上任意一点，过点A 作AF // BE ，与射线CD 相交于点F ．联结BF ，与直线AD 相交于点G ．设CE = x ，AGy DG=．（1）求AB 的长；（2）当点G 在线段AD 上时，求y 关于x 的函数解析式，并写出函数的定义域；（3）如果23ABEF ABCDS S =四边形四边形，求线段CE 的长．F【25．解：（1）分别过点A、D作AM⊥BC、DN⊥BC，垂足为点M、N．∵AD // BC，AB = CD，AD = 5，BC = 15，在Rt△ABM中，∠AMB = 90°，∴AB = 13．……………………………………………………………（2分）∵∠AFD=∠BEC，∠ADF=∠C．∴△ADF∽△BCE．ADFSS =9BECS =过点E 作EH ⊥BC ，垂足为点H ．由题意，本题有两种情况：（ⅰ）如果点G 在边AD 上，则 840ABCD ABEF S S S -==四边形四边形．∴ S = 5． ∴ 945BECS S ==．12BECS=∴ 6EH =．由 DN ⊥BC ，EH ⊥BC ，易得 EH // DN ．（ⅱ）如果点G 在边DA 的延长线上，则 9ADFABCD ABEF S S SS ++=四边形四边形．∴ 8200S =．解得 25S =． ∴ 9225BECS S ==．12BECS=∴305122CE EH CD DN ===．∴ 652CE =．……………………………（2分） ∴ 136522CE =或．】【2019届一模虹口】25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）如图，在四边形ABCD 中，AD ∥BC ，∠A =90°，AB =6，BC =10，点E 为边AD 上一点，将△ABE 沿BE 翻折，点A 落在对角线BD 上的点G 处，联结EG 并延长交射线BC 于点F ．（1）如果cos ∠DBC =23，求EF 的长；（2）当点F 在边BC 上时，联结AG ，设AD=x ，ABG BEF S y S ∆∆= ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结CG ，如果△FCG 是等腰三角形，求AD 的长．第25题备用图ABC第25题图EABCFDG【25．（1）根据题意得△ABE≌△GBE∴BG=AB=6由△ABE≌△GBE得∠AEB=∠BEG∵AD∥BC∴∠AEB=∠EBF∴∠BEF=∠EBF∴FE=FB=9………………………………………………………………………（2分）（2）∵AD∥BC∴∠ADB=∠GBF又∵∠A=∠BGF=90°∴△ABD∽△GFB∵AD∥BC∠A=90°∴∠ABF=90°∴∠ABG+∠GBF=90°又∵∠GBF+∠EFB =90°∴∠ABG =∠EFB根据题意得AB=BG又∵FE=FB∴△ABG∽△EFB…………………………………………………………………（1分）（3）①点F在BC上∵∠GFC=∠AEG>90°∵△FCG是等腰三角形∴FG=FC设FG=FC=a，则BF=10-atan∠GBF∵∠ADB=∠GBF∴tan∠ADB=②点F在BC的延长线上∵∠GCF>∠DCF >90°∵△FCG是等腰三角形∴CG=CF∵∠ADB=∠GBF∴tan∠ADB= tan∠GBF31。

浦东区2019学年初三一模数学试卷含答案

（第4题图）浦东新区2019学年第一学期初中学业质量监测初三数学试卷考生注意：1．本试卷共25题，试卷满分150分，考试时间100分钟．2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效． 3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．在Rt △ABC 中，∠C =90°，如果BC =5，AB =13，那么sin A 的值为（A ）513；（B ）512；（C ）1213；（D ）125． 2．下列函数中，是二次函数的是（A ）21y x =-；（B ）22y x =；（C ）12+=x y ；（D ）()221y x x =--．3．抛物线245y x x =-+的顶点坐标是（A ）（−2,1）；（B ）（2,1）；（C ）（−2, −1）；（D ）（2,−1）．4．如图，点D 、E 分别在△ABC 的边AB 、AC 上，下列各比例式不一定能推得DE ∥BC 的是（A ）AD AE BD CE=；（B ）ADDEAB BC =；（C ）AB AC BD CE =；（D ）AD AEABAC=． 5．如图，传送带和地面所成斜坡的坡度为1∶3，它把物体从地面点A 处送到离地面3米高的B 处，则物体从A 到B 所经过的路程为（A ）310米；（B ）210米；（C ）10米；（D ）9米．6．下列说法正确的是（A ）()0a a +-=；（B ）如果a 和b 都是单位向量，那么a b =；（第5题图）传送带（C ）如果||||a b =，那么a b =；（D ）如果12a b =-(b 为非零向量)，那么a //b ．二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置】7．已知x =3y ，那么 = ▲ ．8．已知线段AB =2cm ，P 是线段AB 的黄金分割点，P A >PB ，那么线段P A 的长度等于 ▲ cm ． 9．如果两个相似三角形对应边之比是2∶3，那么它们的对应中线之比是 ▲ ． 10．如果二次函数223y x x k =-+-的图像经过原点，那么k 的值是 ▲ ． 11．将抛物线23yx 向下平移4个单位，那么平移后所得新抛物线的表达式为 ▲ ．12．如果抛物线经过点A （−1,0）和点B （5,0），那么这条抛物线的对称轴是直线 ▲ ． 13．二次函数22(1)y x =-+的图像在对称轴左侧的部分是 ▲ ．（填“上升”或“下降”） 14．如图，在△ABC 中，AE 是BC 边上的中线，点G 是△ABC 的重心，过点G 作GF ∥AB交BC 于点F ，那么 = ▲ ．15．如图，已知AB ∥CD ∥EF ，AD =6，DF =3，BC =7，那么线段CE 的长度等于 ▲ ． 16．如图，将△ABC 沿射线BC 方向平移得到△DEF ，边DE 与AC 相交于点G ，如果BC = 6cm ，△ABC 的面积等于9cm 2，△GEC 的面积等于4cm 2，那么CF = ▲ cm ．172x … 0 1 2 3 4…2y a x b x c =++ … −3 0 1 0 −3…那么当= 5时，该二次函数y 的值为 ▲ ．18．在Rt △ABC 中，∠C =90°，AC =2，BC =4，点D 、E 分别是边BC 、AB 的中点，将△BDE 绕着点B 旋转，点D 、E 旋转后的对应点分别为点D ’、E ’，当直线D ’E ’ 经过点A 时，线段CD ’的长为 ▲ ．三、解答题：（本大题共7题，满分78分） 19．（本题满分10分）x GB C（第14题图）（第16题图）（第15题图）EFEB2x yx y++（第21题图）计算：2tan 45cos60cot 602sin30︒-︒+︒︒．20．（本题满分10分，其中每小题各5分）如图，在平行四边形ABCD 中，点E 在边AD 上，且AE =2ED ，联结BE 并延长交边CD的延长线于点F ，设=，b=．（1）用、b 表示BE 、DF ；（2）先化简，再求作：)(2)23(++．（不要求写作法，但要写明结论）21．（本题满分10分，其中每小题各5分）如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，且AD =3，AC =6，AE =4，AB =8．（1）如果BC =7，求线段DE 的长；（2）设△DEC 的面积为a ，求△BDC 的面积．（用a 的代数式表示）22．（本题满分10分）为了测量大楼顶上（居中）避雷针BC 的长度，在地面上点A 处测得避雷针底部B 和顶部C 的仰角分别为55°58＇和57°．已知点A 与楼底中间部位D 的距离约为80米．求避雷针BC 的长度．（参考数据：sin5558'0.83︒≈，cos5558'0.56︒≈，tan5558' 1.48︒≈，sin570.84︒≈，cos570.54︒≈，tan57 1.54︒≈）（第20题图）23．（本题满分12分，其中每小题各6分）如图，已知△ABC 和△ADE ，点D 在BC 边上，DA =DC ，∠ADE =∠B ，边DE 与AC 相交于点F ．（1）求证：AB AD DF BC ⋅=⋅；（2）如果AE ∥BC ，求证：BD DF DC FE =．24．（本题满分12分，其中每小题各4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴的两个交点分别为 A （−1,0）、B （3,0），与y 轴相交于点C ．（1）求抛物线的表达式；（2）联结AC 、BC ，求∠ACB 的正切值；（3）点P 在抛物线上且∠P AB =∠ACB ，求点P 的坐标．25．（本题满分14分，其中第（1）小题5分，第（2）小题5分，第（3）小题4分）在Rt △ABC 中，∠A =90°，AB =4，AC =3，D 为AB 边上一动点（点D 与点A 、B 不重合），联结CD ．过点D 作DE ⊥DC 交边BC 于点E ．（1）如图，当ED =EB 时，求AD 的长；（2）设AD =x ，BE =y ，求y 关于x 的函数解析式并写出函数定义域；（3）把△BCD 沿直线CD 翻折得△CDB ’，联结AB ’．当△CAB ’是等腰三角形时，直接写出AD 的长．（第23题图）（第25题图）（备用图）（第24题图）浦东新区2019学年第一学期初中学业质量监测初三数学试卷参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分） 1．A ； 2．C ；3．B ；4．B ；5．A ；6．D ．二、填空题：（本大题共12题，每题4分，满分48分） 7．45； 8．1)； 9．2∶3；10．k =3； 11．234y x =--；12．x =2； 13．上升； 14．13； 15．72； 16．2； 17．-8； 18．三、解答题：（本大题共7题，满分78分）19．解：原式=23321221-1⎪⎪⎭⎫ ⎝⎛+⨯……………………………………………………（各2分） =3121+ ………………………………………………………………（1分） =65．……………………………………………………………………（1分）20．解：（1）∵ 四边形ABCD 是平行四边形，∴ AD = BC ．∵ AE=2ED ，∴AD AE 32=．∴ 23AE BC =． …………………………（1分） ∵ b BC =，∴23AE b =． ………………………………………………（1分）∵ ，∴ AE BA BE +=32+=． …………………………………（1分）∵ 四边形ABCD 是平行四边形，∴ AB // CD ．∴ 12DF DE AB AE ==．∴ 12DF AB =． ………………………………………（1分）∵ ，∴ 21=． ………………………………………………（1分）（2）原式=2223-++-………………………………………………（1分） ===b b a a 2223-++-=b a -21．……………………………… （1分）作图正确．……………………………………………………………（2分）结论． ……………………………………………………………………（1分）21. 证明：（1）∵AD =3，AC =6，AE =4，AD =8，∴12AD AE AC AB ==．…………… （2分）∵∠A=∠A ，∴△ADE ∽△ACB ．…………………………………………（1分） ∴DE AD BC AC=． ……………………………………………………………（1分） ∵BC =7，∴27=DE ． ……………………………………………………（1分）（2）∵AE =4，AC =6，∴EC =2．∵△ADE 与△CDE 同高，∴21ADE DEC S AE S EC ==△△． ………………………（1分）∵S △DEC =a ，∴S △ADE =2a ．…………………………………………………（1分）∵△ADE ∽△ACB ，∴412=⎪⎭⎫ ⎝⎛=AC AD S S ACB ADE △△．………………………………（1分） ∴S △ACB =8a ． …………………………………………………………………（1分）∴S △BDC =8a ―2a ―a =5a ． …………………………………………………（1分）22．解：根据题意，得∠ADC=90°，∠BAD=55°58＇，∠CAD=57°，AD =80．（各1分）在Rt △CAD 中，∵∠ADC=90°，，∴1.54CDAD≈，即 1.5480CD ≈． …（1分） ∴CD =123.2． ……………………………………………………………（1分）在Rt △BAD 中，∵∠ADC=90°，，∴1.48BDAD≈，即 1.4880BD ≈．… （1分） ∴BD =118.4． ……………………………………………………………（1分） ∴BC=DC ―BD =123.2―118.4=4.8． ……………………………………（1分）答：避雷针BC 的长度为4.8米． ………………………………………（1分）23. 证明：（1）∵DA =DC ，∴∠DCA=∠DAC ．……………………………………（1分）∵∠B=∠ADE ，∴△ABC ∽△FDA ． ……………………………………（3分）∴AB BC FD DA=． ……………………………………………………………（1分） tan57 1.54︒≈tan5558' 1.48︒≈∴AB DA FD BC ⋅=⋅．………………………………………………………（1分）（2）∵AE // BC ，∴DF DCEF EA =，∠BDA=∠DAE ． ……………………（2分） ∵∠B=∠ADE ，∴△ABD ∽△EDA ．………………………………………（1分） ∴ADBD AE AD =． ……………………………………………………………（1分） ∵DA =DC ，∴AEDCDC BD =．…………………………………………………（1分） ∴FEDF DC BD =． ……………………………………………………………（1分） 24．解：（1）把A （−1,0）、B （3,0）分别代入得{10,930b c b c --+=-++=．…………………………………………………………（2分）解得b =2，c =3． …………………………………………………………（1分） ∴抛物线的表达式是223y x x =-++． ………………………………（1分）（2）过点A 作AH ⊥BC ，垂足为点H ．∵抛物线223y x x =-++与y 轴相交于点C ,∴C （0, 3）．……………（1分） ∵B （3,0）、A （−1,0）、C （0, 3），∴OC =OB =3， AB =4．在Rt △BOC 中，BC=ABC =45°．在Rt △HAB 中，∵sin AHABH AB ∠=，AB =4，∴AH BH == ……………………（1分）∵BC =CH = ． ……………………………………………（1分）∴tan 2AHACB CH ∠==． ……………………………………………（1分）（3）过点P 作PM ⊥x 轴，垂足为点M ．设P （x ，-x 2+2x +3），则PM =223x x -++，AM ＝x ＋１．∵∠PAB=∠ACB ，tan 2ACB ∠=，∴tan 2PAB ∠=． ……………（1分）（i ）P 在x 轴上方时，-x 2+2x +3=2(x +1) .解得：x 1=1，x 2= -1（舍）. …………………………………………（1分）（ii ）P 在x 轴下方时，-（-x 2+2x +3）=2(x +1) .解得：x 1=5，x 2= -1（舍）. …………………………………………（1分） ∴P 的坐标为（1，４）或（5，-12）. ………………………………（1分）25．解：（1）∵ED =EB ，∴∠B =∠BDE ．……………………………………………（1分）2y x bx c =-++∵DE ⊥CD ，∴∠BDE +∠ADC =90°． ∵∠A =90°，∴∠ACD +∠ADC =90°．∴∠BDE =∠ACD ．…………………………………………………………（1分） ∴∠ACD =∠B ． …………………………………………………………（1分）在Rt △ABC 中，AB =4，AC =3，∴3tan 4AC B AB ==．∴3tan 4ACD ∠=．…………………………………………………………（1分）在Rt △ADC 中， 3tan 4AD ACD AC ∠==，AC =3，∴94AD =． ……………………………………………………………（1分）（2）过点E 作EH ⊥AB ，垂足为点H ． ∴∠EDH =∠A =90°．∵∠BDE =∠ACD ，∴△ACD ∽△DEH ． ………………………………（1分） ∴HD HE AC AD=．在Rt △BEH 中，可得35EH y =，45BH y =．…………………………（1分）∴445DH x y =--． ……………………………………………………（1分） ∴434553x y y x --=． ∴220549x x y x -=+． ……………………………………………………（1分）（0 < x < 4）． ……………………………………………………（1分）（3）AD=7243+或AD=7243-． ………………………（各2分）。

静安区2019学年初三一模数学试卷含答案

第 1 页共 4 页静安区2019学年第一学期期末教学质量调研九年级数学试卷2020.1 （完成时间：100分钟满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤． 3. 答题时可用函数型计算器．一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸的相应位置上】 1．已知y x a +=，y x b -=，那么ab 的值为的值为（A ）x 2；（B ）y 2；（C ）y x -；（D ）y x +．2．已知点P 在线段AB 上，且AP ∶PB=2∶3，那么AB ∶PB 为（A ）3∶2；（B ）3∶5；（C ）5∶2；（D ）5∶3．3．在△ABC 中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，AD ：DB =4：5，下列结论中正确的是，下列结论中正确的是（A ）54=BC DE ；（B ）49=DE BC ；（C ）54=AC AE ；（D ）45=AC EC ．4．在Rt △ABC 中，∠C ＝90°，A ∠、B ∠、C ∠所对的边分别为a 、b 、c ，如果a =3b ，那么∠A 的余切值为切值为（A ）31；（B ）3；（C ）42；（D ）1010．5．如图1，平行四边形ABCD 的对角线AC 与BD 相交于点O ，设a OA =，b OB =，下列式子中正确的是，下列式子中正确的是（A ）b a DC +=；（B ）b a DC -=；（C ）b a DC +-=；（D ）b a DC --=．6．如果将抛物线22-=x y 平移，使平移后的抛物线与抛物线982+-=x x y 重合，那么它平移的过程可以是程可以是（A ）向右平移4个单位，向上平移11个单位；个单位；（B ）向左平移4个单位，向上平移11个单位；个单位；（C ）向左平移4个单位，向上平移5个单位；个单位；（D ）向右平移4个单位，向下平移5个单位．个单位．图1DABCO二、填空题：（本大题共12题，每题4分，满分48分） 7．因式分解：=-x x 52 ▲ ．8．已知13)(+=x x f ，那么)3(f = ▲ ． 9．方程2111=+-x x 的根为的根为▲ ． 10．已知：43=y x ，且y ≠4，那么43--y x = ▲ ． 11．在△ABC 中，边BC 、AC 上的中线AD 、BE 相交于点G ，AD =6，那么AG = ▲ ． 12．如果两个相似三角形的对应边的比是4:5，那么这两个三角形的面积比是，那么这两个三角形的面积比是▲ ． 13．如图2，在大楼AB 的楼顶B 处测得另一栋楼CD 底部C 的俯角为60度，度，已知A 、C 两点间的距离为15米，那么大楼AB 的高度为的高度为 ▲ 米．（结果（结果保留根号）保留根号）14．某商场四月份的营业额是200万元，如果该商场第二季度每个月营业额的增长率相同，都为)0(>x x ，六月份的营业额为y 万元，那么y 关于x 的函数解式是的函数解式是 ▲ ． 15．矩形的一条对角线长为26，这条对角线与矩形一边夹角的正弦值为135，那么该矩形的面积为那么该矩形的面积为▲ ． 16．已知二次函数a x a x ay ++=2228（a 是常数，a ≠0），当自变量x 分别取分别取--6、-4时，对应的函数值分别为y 1、y 2，那么y 1、y 2的大小关系是：y 1 ▲ y 2（填“>”、“<”或“=”）．17．平行于梯形两底的直线截梯形的两腰，当两交点之间的线段长度是两底的比例中项时，我们称这条线段是梯形的“比例中线”．在梯形ABCD 中，AD //BC ，AD =4，BC =9，点E 、F 分别在边AB 、CD 上，且EF 是梯形ABCD 的“比例中线”，那么FCDF= ▲ ．18. 如图3，有一菱形纸片ABCD ，∠A ＝60°，将该菱形纸片折叠，使点A 恰好与CD 的中点E 重合，折痕为FG ，点F 、G 分别在边AB 、AD 上，联结EF ，那么cos ∠EFB 的值为的值为 ▲ ．三、解答题：（本大题共7题，满分78分）19．（本题满分10分）先化简，再求值：2222442y xy x yx yx y x ++-÷+-，其中x =sin45°，y =cos60°．C BAD 图2图3ABCD20．（本题满分10分, 其中第（1）小题7分，第（2）小题3分）如图4，在Rt △ABC 中，∠ACB ＝90°，AC =20，53sin =A ，CD ⊥AB ，垂足为D ．（1）求BD 的长；的长；（2）设a AC =，b BC =，用a 、b 表示AD ．21．（本题满分10分，其中第（1）小题3分，第（2）小题3分，第（3）小题4分）已知在平面直角坐标系xOy 中，抛物线12++=bx x y （b 为常数）的对称轴是直线x =1．（1）求该抛物线的表达式；）求该抛物线的表达式；（2）点A （8，m ）在该抛物线上，它关于该抛物线对称轴对称的点为A'，求点A'的坐标；的坐标；（3）选取适当的数据填入下表，并在如图5所示的平面所示的平面直角坐标系内描点，画出该抛物线．直角坐标系内描点，画出该抛物线．22．（本题满分10分，其中第（1）小题7分，第（2）小题3分）如图6，在东西方向的海岸线l 上有长为300米的码头AB ，在码头的最西端A 处测得轮船M 在它的北偏东45°方向上；同一时刻，在A 点正东方向距离100米的C 处测得轮船M 在北偏东22°方向上．方向上．（1）求轮船M 到海岸线l 的距离；（结果精确到0.01米）米）（2）如果轮船M 沿着南偏东30°的方向航行，那么该轮船的方向航行，那么该轮船能否行至码头AB 靠岸？请说明理由．靠岸？请说明理由．（参考数据：sin22°≈0.375，cos22°≈0.927，tan22°≈0.404，3≈1.732．）x…… y ……CABD 图4图6MA BC l图5xyO 1123．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图7，在梯形ABCD 中，AD //BC ，AC 与BD 相交于点O ，点E 在线段OB 上，AE 的延长线与BC 相交于点F ，OD 2 = OB ·OE ．（1）求证：四边形AFCD 是平行四边形；是平行四边形；（2）如果BC =BD ，AE ·AF =AD ·BF ，求证：△ABE ∽△ACD ．24．（本题满分12分，其中第（1）小题4分，第（2）小题4分，第（3）小题4分）在平面直角坐标系xOy 中（如图8），已知二次函数c bx ax y ++=2（其中a 、b 、c 是常数，且是常数，且 a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ．（1）求这个二次函数的解析式；）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果，如果2:3:=∆∆BCD ABD S S ，求tan ∠DBC 的值；的值；（3）如果点E 在该二次函数图像的对称轴上，在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．的坐标．25．（本题满分14分，其中第（1）小题6分，第（2）小题4分，第（3）小题4分）已知：如图9，在△ABC 中，AB =AC ，点D 、E 分别在边BC 、DC 上，AB 2 =BE · DC ，DE :EC =3:1 ，F 是边AC 上的一点，DF 与AE 交于点G ．（1）找出图中与△ACD 相似的三角形，并说明理由；相似的三角形，并说明理由；（2）当DF 平分∠ADC 时，求DG :DF 的值；的值；（3）如图10，当∠BAC=90°，且DF ⊥AE 时，求DG :DF 的值．的值．图8Oyx图7A B D CE F O图9CAB D EF G图10GF ABDEC静安区2019学年第一学期期末学习质量调研九年级数学试卷参考答案及评分说明 2020.1一、选择题1． C ； 2．D ； 3．B ； 4．A ； 5．C ； 6．D ．二、填空题7．x （x -5）；8．10； 9．x =3； 10． 43； 11． 4； 12．16:25； 13．315 ； 14．21200）（x y +=或2004002002++=x x y ； 15．240； 16．>；17．32； 18．71 ．三、解答题19．解：原式＝解：原式＝ ))(()2(22y x y x y x y x y x -++⋅+-…………………………………………………………………（4分）分）＝yx y x ++2．………………………………………………………………………………………（2分）分）当x =sin45°=sin45°==22，y =cos60°=cos60°==21时…………………………………………………………………………（2分）分）原式＝2212221222=+⨯+． ……………………………………………………………………（2分）分）20．解：（1）∵CD ⊥AB ，∴∠ADC =∠BDC =90°，°，在Rt △ACD 中，AC CD A =sin ，∴125320sin =⨯=⋅=A AC CD ．…………………………．…………………………（（2分）分）∴1612202222=-=-=CD AC AD …………………………………………………………（1分）分）∴43tan ==ADCD A ．………………………………………………………………………………………………………………………………………………………………（（1分）分）∵∠ACB =90°，∴∠DCB+∠B=∠A+∠B =90°，∴∠DCB =∠A ．………………………（1分）分）∴94312tan tan =⨯=⋅=∠⋅=A CD DCB CD BD ．…………………………………………（2分）分）（2） ∵25916=+=+=DB AD AB ，∴2516=AB AD ．…………………………………………………（1分）分）又∵b a BC AC AB -=+=， …………………………………………………………………（1分）∴ba AB AD 251625162516-==．…………………………………………………………………（1分）分）21．解：（1）∵对称轴为2b x -=∴12=-b ．……………………………………………………（1分）分）∴b =-2．…………………………………………………………………………………………（1分）分）∴抛物线的表达式为122+-=x x y ．………………………………………………………（1分）分）（2） ∵点A （8，m ）在该抛物线的图像上，在该抛物线的图像上，∴当∴当x =8时，4918)1(12222=-=-=+-=）（x x x y ．∴点A （8，49）．………………………………………………………………………………………………………………………………………………………………………………（（1分）分）∴ 点A （8，49）关于对称轴对称的点A'的坐标为（的坐标为（--6，49）．…………………………………（2分）分）（3）表格正确，得2分；图正确得2分．分．22．解：（1）过点M 作MD ⊥AC 交AC 的延长线于D ，设DM =x ．…………………………………（1分）分）∵在Rt △CDM 中，CD = DM ·tan ∠CMD = x ·tan22°，………………………………………（1分）分）又∵在Rt △ADM 中，∠MAC =45°，∴AD =DM ，………………………………………………（1分）分）∵AD =AC +CD =100+x ·tan22°，…………………………………………………………………（1分）分）∴100+ x ·tan22°tan22°==x ．………………………………………………………………………………（1分）分）∴79.167785.167404.0110022tan 1100≈≈-≈-= x ．………………………………………………（2分）分）答：轮船M 到海岸线l 的距离约为167.79米．米．（2）作∠DMF =30°，交l 于点F ．在Rt △DMF 中，DF = DM ·tan ∠FMD = DM ·tan30°=33DM ≈79.1673732.1⨯≈96.87米．……………………………………………（1分）分）∴AF =AC +CD +DF =DM +DF ≈167.79+96.87=264.66<300．……………………………………（1分）分）所以该轮船能行至码头靠岸．………………………………………………………………………所以该轮船能行至码头靠岸．………………………………………………………………………（（1分）分）23．证明：（1）∵OD 2 =OE · OB ，∴OBODOD OE =． ……………………………………………………（1分）分）∵AD //BC ，∴OBODOC OA =．……………………………………………………………………（2分）分）∴ODOEOC OA =．…………………………………………………………………………………………………………………………………………………………………………（（1分）分）∴ AF//CD ．…………………………………………………………………………………………（1分）分）∴四边形AFCD 是平行四边形．……………………………………………………………………………………………………………………………………（（1分）分）（2）∵AF//CD ，∴∠AED =∠BDC ，BCBF BDBE =．…………………………………………（1分）分）∵BC =BD ，∴BE =BF ，∠BDC =∠BCD …………………………………………………………（1分）分）∴∠AED =∠BCD ．∵∠AEB =180°-∠AED ，∠ADC =180°-∠BCD ，∴∠AEB =∠ADC ．…………………………（1分）分）∵AE ·AF =AD ·BF ，∴AFADBF AE =．…………………………………………………………（1分）∵四边形AFCD 是平行四边形，∴AF =CD ．…………………………………………………（1分）分）∴DCADBE AE =．…………………………………………………………………………………（1分）分）∴△ABE ∽△ADC ．24．解：（1）将A （0，-3）、B （1，0）、C （3，0）代入）（02≠++=a c bx ax y 得，得，⎪⎩⎪⎨⎧++=--+=-+=cb a b a 003,4390,30…………………………………………………………………………………（3分）分）解得⎪⎩⎪⎨⎧-==-=.3,4,1c b a ∴此抛物线的表达式是342-+-=x x y ．…………………………………（1分）（2）过点D 作DH ⊥BC 于H ，在△ABC 中，设AC 边上的高为h ，则23:)21(:)21(：：==⋅⋅=∆∆DC AD h DC h AD SSBCDABD（1分）分）又∵DH //y 轴，∴52===OA DH AC DC OC CH ．∴56352=⨯==DH CH ．………………………（1分）分）∴54562=-=-=CH BC BH ．…………………………………………………………………（1分）∴tan ∠DBC=23=BH DH ．……………………………………………………………………………（1分）分）（3）方法一：）方法一：∵1)2(3422+--=-+-=x x x y ，所以对称轴为直线x =2，设直线x =2与x 轴交于点G ．（1分）过点A 作AF 垂直于直线x =2，垂足为F ．∵OA =OC =3，∠AOC =90°，∴∠OAC=∠OCA=45°．∵AF //x 轴，∴∠F AC=∠OCA=45°． ∵AC 平分∠BAE ，∴∠BAC=∠EAC∵∠BAO=∠OAC -∠BAC ，∠EAF=∠F AC -∠EAC ，∴∠BAO=∠EAF ………………………（1分）分） ∵∠AOB =∠AFE =90°，∴△OAB ∽△FEA ，∴31==AF EF OA OB ． ∵AF =2，∴32=EF ．…………………………………………………………………………………（1分）分）∴EG =GF -EF =AO -EF =3-32=37． ∴E （2，37-）．……………………………………………（1分）分）方法二：方法二：延长AE 至x 轴，与x 轴交于点F ，∵OA =OC =3，∴∠OAC=∠OCA=45°，∵∠OAB=∠OAC -∠BAC=45°-∠BAC ，∠OF OFA=A=∠OCA -∠F AC=45°-∠F AC ， ∵∠BAC =∠F AC ，∴∠OAB=∠OF OFA A ．………………………………………………………………………………………………………………………………（（1分）分）∴△OAB ∽△OF OFAA ，∴31==OF OA OA OB ．∴OF =9，即F （9，0）…………………………………（1分）设直线AF 的解析式为y =kx +b （k ≠0），可得⎩⎨⎧=-+=,3,90b b k 解得⎪⎩⎪⎨⎧-==,3,31b k ∴直线AF 的解析式为331-=x y ……………………………（1分）将x =2代入直线AF 的解析式得37-=y ，∴E （2，37-）……………………………………（1分）分）25．（1）与△ACD 相似的三角形有：△ABE 、△ADC ，理由如下：……………………………………（2分）分）∵AB 2 =BE · DC ，∴DCABAB BE =．…………………………………………………………………………………………………………………………………………（（1分）分）∵AB =AC ，∴∠B =∠C ．………………………………………………………………………………（1分）分）DCAC AB BE =……………………………………………………………………………………………………………………………………………………………………………………（（1分） ∴△ABE ∽△DCA ．∵△ABE ∽△DCA ，∴∠AED =∠DAC ．∵∠AED =∠C +∠EAC ，∠DAC =∠DAE +∠EAC ，∴∠DAE =∠C ．∴△ADE ∽△CDA ．……（1分）（2）∵△ADE ∽△CDA ，又∵DF 平分∠ADC ，∴CDADAD DE DF DG ==…………………………………（1分）设CE =a ，则DE=3CE =3a ，CD =4a ，∴a ADAD a 44= ，解得a AD 32=（负值已舍）………（2分）分）∴23432===a a CD AD DG DF …………………………………………………………………………（1分）（3）∵∠BAC=90°，AB =AC ，∴∠B =∠C =45° ，∴∠DAE =∠C=45°∵DG ⊥AE ，∴∠DAG =∠ADF =45°，∴AG=DG=a aAD 6322222=⋅=…………………（1分）∴a DG DE EG 322=-=………………………………………………………………………（1分）∵∠AED =∠DAC ∴△ADE ∽△DF A∴ADAE DF AD =， ∴a AE AD DF ）（3642-==…………………………………………………（1分）分）∴422+=DF DG ……………………………………………………………………………………（1分）分）。

2019中考数学一模试题及答案(上海杨浦、静安、闵行、松江、崇明)

上海市部分学校九年级数学抽样测试试卷2019.1.5（测试时间：100分钟，满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．3．本次测试可使用科学计算器．一、选择题：（本大题共6题，每题4分，满分24分） 1．下列函数中，属于二次函数的是（A ）32-=x y ；（B ）22)1(x x y -+=；（C ）x x y 722-=；（D ）22xy -=． 2．抛物线422-+-=x x y 一定经过点（A ）（2,-4）；（B ）（1,2）；（C ）（-4,0）；（D ）（3,2）．3．已知在Rt △ABC 中，∠C =90°，∠A =α，AC =3，那么AB 的长为（A ）αsin 3；（B ）αcos 3；（C ）αsin 3；（D ）αcos 3． 4．在平面直角坐标系xOy 中有一点P （8,15），那么OP 与x 轴正半轴所夹的角的正弦值等于（A ）178；（B ）1715；（C ）158；（D ）815． 5．如果△ABC ∽△DEF ，且△ABC 的三边长分别为3、5、6，△DEF 的最短边长为9，那么△DEF 的周长等于（A ）14；（B ）5126；（C ）21；（D ）42．6．下列五幅图均是由边长为1的16个小正方形组成的正方形网格，网格中的三角形的顶点都在小正方形的顶点上，那么在下列右边四幅图中的三角形，与左图中的△ABC 相似的个数有（A ）1个；（B ）2个；（C ）3个；（D ）4个．二、填空题：（本大题共12题，每题4分，满分48分） 7．如果35=y x ，那么y x yx -+3= ▲ ．8．已知在△ABC 中，点D 、E 分别在边AB 、AC 上，DE //BC ，53=AB AD ，那么CEAE的值等于 ▲ ． 9．已知P 是线段AB 的一个黄金分割点，且AB =20cm ，AP >BP ，那么AP = ▲ cm ． 10．如果抛物线k x k y ++=2)4(的开口向下，那么k 的取值范围是 ▲ ． 11．二次函数m x x y ++=62图像上的最低点的横坐标为 ▲ ．12．一个边长为2厘米的正方形，如果它的边长增加x 厘米，面积随之增加y 平方厘米，那么y 关于x 的函数解析式是 ▲ ．13．如图，已知在△ABC 中，AB =3，AC =2，D 是边AB 上的一点，∠ACD =∠B ，∠BAC 的平分线AQ 与CD 、BC 分别相交于点P 和点Q ，那么AQAP的值等于 ▲ ．14．已知在△ABC 中，AB =AC =5cm ，BC =35，那么∠A = ▲ 度．15．已知在△ABC 中，∠C =90°，BC =8，AB =10，点G 为重心，那么GCB ∠tan 的值为 ▲ ． 16．向量a 与单位向量e 的方向相反，且长度为5，那么用向量e 表示向量a 为 ▲ ． 17．如果从灯塔A 处观察到船B 在它的北偏东35°方向上，那么从船B 观察灯塔A 的方向是 ▲ ．18．将等腰△ABC 绕着底边BC 的中点M 旋转30°后，如果点B 恰好落在原△ABC 的边AB 上，那么∠A 的余切值等于 ▲ ．三、解答题：（本大题共7题，满分78分）19．（本题满分10分，其中第（1）小题4分，第（2）小题6分）（第13题图）已知抛物线32++=mx x y 的对称轴为x =-2．（1）求m 的值；（2）如果将此抛物线向右平移5个单位后，求所得抛物线与y 轴的交点坐标．20．（本题满分10分，其中第（1）小题6分，第（2）小题4分）如图，已知在△ABC 中，点D 在边AC 上，CD ∶AD =1∶2，=，=．（1）试用向量,表示向量；（2）求作：-21．（不要求写作法，但要指出所作图中表示结论的向量）21．（本题满分10分，其中每小题各5分）已知：如图，在△ABC 中，AB =6，BC =8，∠B =60°．求：（1）△ABC 的面积；（2）∠C 的余弦值．22．（本题满分10分）已知：如图，矩形DEFG 的一边DE 在△ABC 的边BC 上，顶点G 、F 分别在边AB 、AC 上，AH 是边BC 上的高，AH 与GF 相交于点K ，已知BC =12，AH =6，EF ∶GF =1∶2，求矩形DEFG 的周长．C（第22题图）ABC（第21题图）（第20题图）23．（本题满分12分，其中第（1）小题5分，第（2）小题7分）已知：如图，斜坡AP 的坡度为1∶2.4，坡长AP 为26米，在坡顶A 处的同一水平面上有一座古塔BC ，在斜坡底P 处测得该塔的塔顶B 的仰角为45°，在坡顶A 处测得该塔的塔顶B 的仰角为76°．求：（1）坡顶A 到地面PQ 的距离；（2）古塔BC 的高度（结果精确到1米）．（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）24．（本题满分12分，其中第（1）小题5分，第（2）小题7分）已知：如图，在△ABC 中，AD 是边BC 上的中线，点E 在线段BD 上，且BE =ED ，过点B 作BF ∥AC ，交线段AE 的延长线于点F ．（1）求证：AC =3BF ；（2）如果ED AE 3=，求证：BE AC AE AD ⋅=⋅．25．（本题满分14分，其中第（1）、（2）小题各4分，第（3）小题6分）已知：如图，在平面直角坐标系xOy 中，二次函数c bx x y ++-=231的图像经过点A （-1,1）和点B （2,2），该函数图像的对称轴与直线OA 、OB 分别交于点C 和点D ．（第24题图）C（第23题图）（1）求这个二次函数的解析式和它的对称轴；（2）求证：∠ABO=∠CBO；（3）如果点P在直线AB上，且△POB与△BCD相（第25题图）上海市部分学校九年级数学抽样测试参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分） 1．C ； 2．A ； 3．D ； 4．B ； 5．D ； 6．B ．二、填空题：（本大题共12题，每题4分，满分48分） 7．9； 8．23； 9．10510-； 10．k <-4； 11．-3； 12．xx y 42+=；13．32； 14．120； 15．43； 16．5-； 17．南偏西35°；18．3．三、解答题：（本大题共7题，满分78分） 19．解：（1）由题意，得22-=-m．……………………………………………………（2分）∴m =4．…………………………………………………………………………（2分）（2）此抛物线的表达式为1)2(3422-+=++=x x x y ．……………………（2分） ∵向右平移5个单位后，所得抛物线的表达式为1)3(2--=x y ，即862+-=x x y ．………………………………………………………………（2分） ∴它与y 轴的交点坐标为（0,8）．……………………………………………（2分）20．解：（1）∵CD ∶AD =1∶2，∴CA CD 31=，得CA CD 31=．…………（2分）M∵-=-=． ………………（2分）∴3131)(31-=-=………………（1分） ∴b a b a b CD BC BD 3231)(31+=-+=+=．…………………………（1分）（2）a b AM -=21．……………………………………（画图正确3分，结论1分）21．解：（1）作AH ⊥BC ，垂足为点H ．在Rt △ABH 中，∵∠AHB =90°，∠B =60°，AB =6，∴BH =3，33=AH ．………（2分，2分） ∴S △ABC =31233821=⨯⨯．…………………………………………………（1分）（2）∵BC =8，BH =3，∴CH =5． ………………………………………………（1分）在Rt △ACH 中，∵33=AH ，CH =5，∴132=AC ．………………………………………（2分） ∴261351325cos ===AC CH C ．………………………………………………（2分） 22．解：设EF =x ，则GF =2x ．∵GF ∥BC ，AH ⊥BC ，∴AK ⊥GF ．∵GF ∥BC ，∴△AGF ∽△ABC ．………………………………………………（2分）∴BCGFAH AK =．…………………………………………………………………（2分） ∵AH =6，BC =12，∴12266xx =-．……………………………………………（2分）解得x =3．………………………………………………………………………（2分） ∴矩形DEFG 的周长为18．……………………………………………………（2分）23．解：（1）过点A 作AH ⊥PQ ，垂足为点H ．∵斜坡AP 的坡度为1∶2.4，∴125=PH AH ．…………………………………（2分）设AH =5k ，则PH =12k ，由勾股定理，得AP =13k ． ∴13k =26．解得k =2．∴AH =10．………………………………………………………………………（2分）答：坡顶A 到地面PQ 的距离为10米．………………………………………（1分）（2）延长BC 交PQ 于点D ．∵BC ⊥AC ，AC ∥PQ ，∴BD ⊥PQ ．…………………………………………（1分） ∴四边形AHDC 是矩形，CD =AH =10，AC =DH ．……………………………（1分） ∵∠BPD =45°，∴PD =BD ． …………………………………………………（1分）设BC =x ，则x +10=24+DH ． ∴AC =DH =x -14．在Rt △ABC 中，AC BC =︒76tan ，即0.414≈-x x．…………………………（2分）解得356=x ，即19≈x ．………………………………………………………（1分）答：古塔BC 的高度约为19米．………………………………………………（1分）24．证明：（1）∵BF ∥AC ，∴BECEBF AC =．………………………………………………（2分） ∵BD =CD ，BE =DE ，∴CE =3BE ．……………………………………………（2分） ∴AC =3BF ．………………………………………………………………………（1分）（2）∵ED AE 3=，∴223ED AE =．…………………………………………（1分）又∵CE =3ED ，∴CE ED AE ⋅=2．……………………………………………（1分） ∴CEAEAE ED =．……………………………………………………………………（1分） ∵∠AED =∠CEA ，∴△AED ∽△CEA ．………………………………………（1分）∴AEEDAC AD =．…………………………………………………………………（1分） ∵ED =BE ，∴AEBEAC AD =．……………………………………………………（1分） ∴BE AC AE AD ⋅=⋅．…………………………………………………………（1分）25．解：（1）由题意，得⎪⎩⎪⎨⎧++-=+--=.2342,311c b c b ………………………………………………（1分）解得⎪⎩⎪⎨⎧==.2,32c b ……………………………………………………………………（1分）∴所求二次函数的解析式为232312++-=x x y ．……………………………（1分）对称轴为直线x =1．……………………………………………………………（1分）证明：（2）由直线OA 的表达式y =-x ，得点C 的坐标为（1,-1）．…………………（1分）∵10=AB ，10=BC ，∴AB =BC ．………………………………………（1分）又∵2=OA ，2=OC ，∴OA =OC ．………………………………………（1分） ∴∠ABO =∠CBO ．………………………………………………………………（1分）解：（3）由直线OB 的表达式y =x ，得点D 的坐标为（1,1）．………………………（1分）由直线AB 的表达式3431+=x y ，得直线与x 轴的交点E 的坐标为（-4,0）．……………………………………（1分） ∵△POB 与△BCD 相似，∠ABO =∠CBO ，∴∠BOP =∠BDC 或∠BOP =∠BCD ．（i ）当∠BOP =∠BDC 时，由∠BDC ==135°，得∠BOP =135°．∴点P 不但在直线AB 上，而且也在x 轴上，即点P 与点E 重合．∴点P 的坐标为（-4,0）．………………………………………………………（2分）（ii ）当∠BOP =∠BCD 时，由△POB ∽△BCD ，得BCBDBO BP =．而22=BO ，2=BD ，10=BC ，∴1052=BP ．又∵102=BE ，∴1058=PE ．作PH ⊥x 轴，垂足为点H ，BF ⊥x 轴，垂足为点F ．∵PH ∥BF ，∴EFEHBE PE BF PH ==．而BF =2，EF =6，∴58=PH ，524=EH ．∴54=OH ．∴点P 的坐标为（54,58）．……………………………………………………（2分）综上所述，点P 的坐标为（-4,0）或（54,58）．。

2019-2020学年上海市虹口区初三数学一模(试卷+参考答案)

虹口区2019学年度第一学期期终学生学习能力诊断测试初三数学试卷（满分150分，考试时间100分钟） 2020.1考生注意：1．本试卷含三个大题，共25题；2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．] 1．如果1cos =2α ，那么锐角α的度数为 A ．30°； B ．45°； C ．60°；D ．90°． 2．在Rt △ABC 中，∠C =90°，如果BC =2，tan B =2，那么AC 长为 A ．1；B ．4； CD．． 3．抛物线23(1)+1y x =+的顶点所在象限是 A ．第一象限； B ．第二象限；C ．第三象限；D . 第四象限．4．已知抛物线2y x =经过1(2,)A y - 、2(1,)B y 两点，在下列关系式中，正确的是 A ．120y y >>； B ．210y y >>；C ．120y y >>；D ．210y y >>．5．已知b a 、和c都是非零向量，在下列选项中，不能．．判定a ∥b 的是A ．=a b ；B ．a ∥c ，b ∥c ；C ．+0a b =；D ．+2a b c =，3a b c -=．6．如图1，点D 是△ABC 的边BC 上一点，∠BAD=∠C ，AC =2AD ，如果△ACD 的面积为15，那么△ABD 的面积为 A ．；B ．；C ．7.5；D ．5．二、填空题（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置]7．如果:2:3a b =，且+10a b =，那么a 的值为 ▲ ．8．如果向量a r 、b r 、x r 满足关系式23(+)0b a x -=r r r r，那么用向量a r 、b r 表示向量x r = ▲ ．9．如果抛物线1)1(2+-=x a y 的开口向下，那么a 的取值范围是 ▲ ．10．沿着x 轴正方向看，抛物线2(1)y x =--在对称轴 ▲ 侧的部分是下降的（填“左”或“右”）．C AAB图111．如果函数21)2mmy m x -=++（是二次函数，那么m 的值为 ▲ ．12．如图2，抛物线的对称轴为直线 1x =，点P 、Q 是抛物线与x 轴的两个交点，点P 在点Q 的右侧，如果点P 的坐标为（4，0），那么点Q 的坐标为 ▲ ．13．如图3，点A （2，m ）在第一象限，OA 与x 轴所夹的锐角为α ，如果tan 3=2α，那么m 的值为 ▲ ．14．已知△ABC ∽△A 1B 1C 1，顶点A 、B 、C 分别与A 1、B 1、C 1对应，AC =12，A 1C 1=8，△ABC的高AD 为6，那么△A 1B 1C 1的高A 1D 1长为 ▲ ．15．如图4，在梯形AEFB 中，AB ∥EF ，AB =6，EF =10，点C 、D 分别在边AE 、BF 上且CD ∥AB ，如果AC=3CE ，那么CD 长为 ▲ ．16．公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”（如图5），它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果小正方形面积是49，直角三角形中较小锐角θ的正切为512，那么大正方形的面积是 ▲ ．17．如图6，在Rt △ABC 中，∠C =90°，AC =1，BC =2，点D 为边AB 上一动点，正方形 DEFG的顶点E 、F 都在边BC 上，联结BG ，tan ∠DGB 的值为 ▲ ． 18．如图7，在等腰梯形ABCD 中，AD ∥BC ，sin C =45，AB=9，AD =6，点E 、F 分别在边AB 、BC 上，联结EF ，将△BEF 沿着EF 翻折，使BF 的对应线段B’F 经过顶点A ，B’F 交对角线BD 于点P ，当B’F ⊥AB 时，AP 的长为 ▲ ．三、解答题（本大题共7题，满分78分） 19．（本题满分10分）计算：24sin 30tan 60cot 30tan 45︒-︒︒-︒．图6 D A BE CFG B C A D 图4EFA C图7ABD图5 θ图1020．（本题满分10分，第（1）小题满分6分，第（2）小题满分4分）在平面直角坐标系xOy 中，将抛物线C 1：22y x x =-向左平移2个单位，向下平移3 个单位得到新抛物线C 2．（1）求新抛物线C 2的表达式；（2）如图8，将△OAB 沿x 轴向左平移得到△O’A’B’，点A （0，5）的对应点A’ 落在平移后的新抛物线C 2上，求点B 与其对应点B’的距离．21．（本题满分10分，第（1）小题满分6分，第（2）小题满分4分）如图9，在Rt △ABC 中，∠ABC=90°，点G 是Rt △ABC 的重心，联结BG 并延长交AC 于点D ，过点G 作GE ⊥BC 交边BC 于点E ．（1）如果AC a =，AB b =，用a 、b 表示向量BG ；（2）当AB=12时，求GE 的长．22．（本题满分10分）某次台风来袭时，一棵笔直大树树干AB （假定树干AB 垂直于水平地面）被刮倾斜7° （即∠BAB ’ =7°）后折断倒在地上，树的顶部恰好接触到地面D 处（如图10所示），测得∠CDA 为37°，AD 为5米，求这棵大树AB 的高度．（结果保留根号）（参考数据：sin370.6︒≈ ，cos370.8︒≈，tan370.75︒≈）图8 图9 A B E C G D23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图11，在Rt △ABC 中，∠ACB =90°，点D 是边BC 的中点，联结AD ，过点C 作 CE ⊥AD 于点E ，联结BE ．（1）求证：2BD DE AD =⋅；（2）如果∠ABC =∠DCE ，求证：BD CE BE DE ⋅=⋅．24．（本题满分12分，第（1）小题满分4分，第（2）小题满分8分）如图12，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴交于A （-1，0）、B两点，与y 轴交于点C （0，3），点P 在抛物线的对称轴上，且纵坐标为（1）求抛物线的表达式以及点P 的坐标；（2）当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”． ①点D 在射线AP 上，如果∠DAB 为△ABD 的特征角，求点D 的坐标；②点E 为第一象限内抛物线上一点，点F 在x 轴上，CE ⊥EF ，如果∠CEF 为△ECF 的特征角，求点E 的坐标．25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）在Rt △ABC 中，∠ACB =90°，BC =4，sin ∠ABC =35，点D 为射线BC 上一点，联结AD ，过点B 作BE ⊥AD 分别交射线AD 、AC 于点E 、F ，联结DF ．过点A 作AG ∥BD ，交直线BE 于点G ．（1）当点D 在BC 的延长线上时（如图13），如果CD =2，求tan ∠FBC ；（2）当点D 在BC 的延长线上时（如图13），设AG x =，ADF S y =，求y 关于x 的函数关系式（不写函数的定义域）；（3）如果AG =8，求DE 的长．D 图11 AE C BEA F G A虹口区2019学年度第一学期期终学生学习能力诊断测试初三数学试卷评分参考建议2020.1说明：1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；2．第一、二大题若无特别说明，每题评分只有满分或零分；3．第三大题中各题右端所注分数，表示考生正确做对这一步应得分数；4．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半； 5．评分时，给分或扣分均以1分为基本单位．一、选择题（本大题共6题，每题4分，满分24分）1．C 2．B 3．B 4．C 5．A 6．D二、填空题（本大题共12题，每题4分，满分48分）7．4 8．b a32+- 9．a ＞1 10．右 11．212．(－2,0) 13．3 14．4 15．9 16．169 17．31 18．247三、解答题（本大题共7题，满分78分）19．解：原式=()2313214--⨯…………………………………………………………（8分） =3132-- =23-………………………………………………………………………（2分）20．解：（1）x x y 22-==()112--x ……………………………………………………（3分）∵抛物线向左平移2个单位，向下平移3个单位，∴新的抛物线C 2的表达式为：()412-+=x y ………………………………（3分）（2）∵将△OAB 沿x 轴向左平移得到△O ’A ’B ’∴设A ’（x ，5）…………………………………………………………………（1分） ∵点A 的对应点A ’落在C 2上∴()4152-+=x ………………………………………………………………（1分）解得12x = ，24x =-…………………………………………………………（1分） x =2不合题意，舍去∴点B 与其对应点B’的距离为4 ………………………………………………（1分）21．解：（1）∵点G 是Rt △ABC 的重心∴点D 为AC 的中点…………………………………………………………（1分）∴1122AD AC a ==……………………………………………………………（1分） ∴12BD BA AD b a =+=-+……………………………………………………（2分）∵点G 是Rt △ABC 的重心 ∴23BG BD =…………………………………（1分）∵BG 与BD 同向∴221333BG BD b a ==-+………………………………………………………（1分）（2）在Rt △ABC 中，点D 为AC 的中点∴CD=DB ∴∠C =∠DBC ∵GE ⊥BC ∠ABC=90° ∴∠ABC=∠GEB =90°∴△GEB ∽△ABC …………………………………………………………………（1分） ∴GE BG AB AC= ………………………………………………………………………（1分） ∵23BG BD = 12B D A C= ∴13BG AC =……………………………………（1分） ∴1123GE = ∴GE =4 ……………………………………………………………………………（1分）22．解：过点A 作AE ⊥CD ，垂足为点E …………………………………………………（1分）在Rt △ADE 中，cos 50.84DE AD CDA =⋅∠=⨯= ……………………………（2分） sin 50.63AE AD CDA =⋅∠=⨯=…………………………………（1分）在Rt △ADE 中，∠DAE +∠ADC =90° ∴∠DAE =90°-37°=53°∴∠CAE =90°-7°-53°=30°………………………………………………………（1分）在Rt △ACE 中，tan 3CE AE CAE =⋅∠=………………………………（2分）2A C C E ==1分）由题得''4AB AB AC B C AC CD AC CE DE ==+=+=++= …………（1分）答：这棵大树AB 原来的高度是（4）米． ……………………………………（1分）23．证明：（1）∵CE ⊥AD ，∠ACB =90°∴∠ACB =∠CED =90°∵∠EDC =∠CDA∴△EDC ∽△CDA …………………………………………………………………（3分） ∴DE CDCD AD= ∴CD 2=DE ·AD ………………………………………………………………………（2分）∵点D 是边BC 的中点 ∴CD =BD∴BD 2=DE ·AD ………………………………………………………………………（1分）（2）由（1）得DE BDBD AD=且∠EDB =∠BDA ∴△BDE ∽△ADB ……………………………………………………………………（2分） ∴∠ABC =∠BED ……………………………………………………………………（1分） ∵∠ABC =∠DCE ， ∴∠BED =∠DCE ∵∠EBD =∠CBE∴△EBD ∽△CBE ……………………………………………………………………（2分） ∴BD ED BE CE= 即BD CE BE DE ⋅=⋅………………………………………………（1分）24．解：（1） ∵c bx x y ++-=2过A (－1， 0)，C (0，3)∴0=1;3.b c c --+⎧⎨=⎩ 解得：=2;3.b c ⎧⎨=⎩……………………………………………（2分）∴322++-=x x y ………………………………………………………………（1分）对称轴为直线x =1∵点P 在对称轴上，且纵坐标为32，∴点P 的坐标为（1，32）……………………………………………………（1分）（2）设直线x=1交x 轴于点Q∵A (－1，0)，P （1，32）∴AQ =2 PQ =32 ∴tan PAQ ∠=∴∠P AQ =60° 即∠DAB=60°……………………………………………………（1分） ∵点D 在射线AP 上，且∠DAB 为△ABD 的特征角，∴∠ABD =30°或∠ADB =30°，…………………………………………………（1分）∴点D 的坐标为（0，3）或（3，）…………………………………（2分）（3）过点E 作EG ⊥x 轴于点G ，过点C 作CH ⊥GE 的延长线于点H .∵CE ⊥EF 且∠CEF 为△ECF 的特征角， ∴∠ECF =∠CFE =45°……………………………………………………………（1分） ∴CE =EF在Rt △CHE 中，∠HCE+∠CEH =90° ∵∠CEH +∠FEG =90°∴∠HCE =∠FEG ∵∠H =∠EGF =90°∴△CHE ≌△EGF∴CH =EG …………………………………………………………………………（1分） ∵点E 为第一象限内抛物线上一点 ∴设E （a ，223a a -++）∴223a a a =-++ ……………………………………………………………（1分）解得a =（舍负）∴E ………………………………………………………………（1分）25. （1）在Rt △BED 中，∠EDB+∠EBD =90°同理∠ADC+∠DAC =90°∴∠DAC =∠EBD 即∠DAC =∠FBC ，…………………………………………（1分）由sin ∠ABC =35可得tan ∠ABC =34在Rt △ABC 中，AC =tan 3BC ABC ⋅∠=………………………………………（1分）又∵CD =2在Rt △ACD 中，2tan 3DC DAC AC ∠== ∴2tan tan 3FBC DAC ∠=∠=………………………………………………（2分）（2）∵AG ∥BD ∴AG AFCB FC=∴43x AF AF =- ∴ 3=4x AF x + ………………………………………（2分） ∴12=4FC x + ……………………………………………………………………（1分）∵tan tan FBC DAC ∠=∠ ∴FC DCBC AC=∴AC DC BC FC= ∴tan tan ABC DFC ∠=∠ ∴ABC DFC ∠=∠ ……………………………………………………………（1分）由sin ∠ABC =35可得tan ∠ABC =34∴331294444DC FC x x ==⋅=++ …………………………………………（1分） ∴441239x x x y ⋅+⋅+=即22721632xx y x ++= …………………………………………………………（1分）（3）①当点D 在BC 的延长线上时，∵AG ∥CB ，∴AG AF CB FC =，834FCFC-= ∴FC =1， ∴3tan 4CD FC DFC =⋅∠= ∴319444DB =+=，∴19sin4DE BD EBD =⋅∠==2分） ②当点D 在边BC 上时， ∵AG ∥CB ， ∴BC FC AG FA = ∴483FC FC=+，∴FC =3 ∴9tan 4CD FC DFC =⋅∠=, ∴47494=-=DB ，sin 732=14520BD EBD DE ⨯=⋅∠=……………………（2分）综上，2021=DE .。

2018-2019学年上海中考数学各区一模汇编提升题(18、23、24、25题

目录Ⅰ第18题（填空小压轴） (3)【2019届一模徐汇】 (3)【2019届一模浦东】 (3)【2019届一模杨浦】 (3)【2019届一模普陀】 (4)【2019届一模奉贤】 (4)【2019届一模松江】 (4)【2019届一模嘉定】 (5)【2019届一模青浦】 (5)【2019届一模青浦】 (5)【2019届一模静安】 (6)【2019届一模宝山】 (6)【2019届一模长宁】 (6)【2019届一模金山】 (7)【2019届一模闵行】 (7)【2019届一模虹口】 (7)Ⅱ第23题（几何证明题） (8)【2019届一模徐汇】 (8)【2019届一模浦东】 (8)【2019届一模杨浦】 (9)【2019届一模普陀】 (9)【2019届一模奉贤】 (10)【2019届一模松江】 (10)【2019届一模嘉定】 (11)【2019届一模青浦】 (11)【2019届一模静安】 (12)【2019届一模宝山】 (12)【2019届一模长宁】 (13)【2019届一模金山】 (13)【2019届一模闵行】 (14)【2019届一模虹口】 (14)Ⅲ第24题（二次函数综合） (15)【2019届一模徐汇】 (15)【2019届一模浦东】 (16)【2019届一模普陀】 (18)【2019届一模奉贤】 (19)【2019届一模松江】 (20)【2019届一模嘉定】 (21)【2019届一模青浦】 (22)【2019届一模静安】 (23)【2019届一模宝山】 (24)【2019届一模长宁】 (25)【2019届一模金山】 (26)【2019届一模闵行】 (27)【2019届一模虹口】 (28)Ⅳ第25题（压轴题） (29)【2019届一模徐汇】 (29)【2019届一模浦东】 (30)【2019届一模杨浦】 (31)【2019届一模普陀】 (32)【2019届一模奉贤】 (33)【2019届一模松江】 (34)【2019届一模嘉定】 (35)【2019届一模青浦】 (36)【2019届一模静安】 (37)【2019届一模宝山】 (38)【2019届一模长宁】 (39)【2019届一模金山】 (40)【2019届一模闵行】 (41)【2019届一模虹口】 (42)Ⅰ第18题（填空小压轴）【2019届一模徐汇】18．在梯形ABCD 中，AB ∥DC ，∠B =90°，BC=6，CD =2，3tan 4A =．点E 为BC 上一点，过点E 作EF ∥AD 交边AB 于点F ．将△BEF 沿直线EF 翻折得到△GEF ，当EG 过点D 时，BE 的长为 ▲ ．【2019届一模浦东】18. 将矩形纸片ABCD 沿直线AP 折叠，使点D 落在原矩形ABCD 的边BC 上的点E 处，如果∠AED 的余弦值为35，那么ABBC =__________.【2019届一模杨浦】18．Rt △ABC 中，∠C =90°，AC =3，BC =2，将此三角形绕点A 旋转，当点B 落在直线BC 上的点D 处时，点C 落在点E 处，此时点E 到直线BC 的距离为 ▲ .GEABC DF （第18题图）ACB（第18题图）18．如图5，△ABC 中，8AB AC ==，3cos 4B =，点D 在边BC 上，将△ABD 沿直线AD 翻折得到△AED ，点B 的对应点为点E ，AE 与边BC 相交于点F ，如果2BD =，那么EF = ▲ ．【2019届一模奉贤】18．如图5，在△ABC 中，AB =AC =5，3sin =5C ，将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应，AD 与边BC 交于点F ．如果AE //BC ，那么BF 的长是 ▲ ．【2019届一模松江】18．如图，在直角坐标平面xoy 中，点A 坐标为（3，2），∠AOB ＝90°，∠OAB ＝30°，AB 与x 轴交于点C ，那么AC :BC 的值为______．图5ABCD图5AB C（第18题图）xyC BOA18．在△ABC 中，︒=∠90ACB ，点D 、E 分别在边BC 、AC 上，AE AC 3=，︒=∠45CDE (如图3)，△DCE 沿直线DE 翻折，翻折后的点C 落在△ABC 内部的点F ，直线AF 与边BC 相交于点G ，如果AE BG =，那么=B tan ▲ ．【2019届一模青浦】17．如图，在Rt △ABC 中，∠ACB=90°，AC=1，tan ∠CAB=2，将△ABC 绕点A 旋转后，点B 落在AC 的延长线上的点D ，点C 落在点E ，DE 与直线BC 相交于点F ，那么CF= ▲ ．【2019届一模青浦】18．对于封闭的平面图形，如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上，那么这样的点S 称为“亮点”．如图，对于封闭图形ABCDE ，S 1是 “亮点”，S 2不是“亮点”，如果AB ∥DE ，AE ∥DC ， AB=2，AE=1，∠B=∠C= 60°，那么该图形中所有“亮点” 组成的图形的面积为 ▲ ．EDCBAS 2S 1（第18题图）18．如图6，将矩形ABCD 沿对角线BD 所在直线翻折后，点A 与点E 重合，且ED 交BC 于点F ，联结AE ．如果2tan 3DFC ∠=，那么BDAE的值是 ▲ ．【2019届一模宝山】18．如图4，Rt △ABC 中，∠ACB =90°，AC =4，BC =5，点P 为AC 上一点，将△BCP 沿直线BP 翻折，点C落在C ’处，连接AC ’，若AC ’∥BC ，则CP 的长为 ▲ ．【2019届一模长宁】18．如图，点P 在平行四边形ABCD 的边BC 上，将ABP ∆沿直线AP 翻折，点B 恰好落在边AD 的垂直平分线上，如果5=AB ，8=AD ，34tan =B ，那么BP 的长为 ▲ ．AC（图4）B图6F BACDEBACD第18题图18．如图，在ABC Rt ∆中，o90=∠C ，8=AC ，6=BC ．在边AB 上取一点O ，使BC BO =，以点O 为旋转中心，把ABC ∆逆时针旋转90，得到C B A '''∆（点A 、B 、C 的对应点分别是点A '、B '、C '），那么ABC ∆与C B A '''∆的重叠部分的面积是 ▲ ．【2019届一模闵行】18．如图，在Rt △ABC 中，∠ACB = 90°，BC = 3，AC = 4，点D 为边AB 上一点．将△BCD 沿直线CD 翻折，点B 落在点E 处，联结AE ．如果AE // CD ，那么BE = ▲ ．【2019届一模虹口】18．如图，正方形ABCD 的边长为4，点O 为对角线AC 、BD 的交点，点E 为边AB 的中点，△BED 绕着点B 旋转至△BD 1E 1，如果点D 、E 、D 1在同一直线上，那么EE 1的长为 ▲ ．ABC第18题OABC （第18题图）C第18题图A BDE OⅡ第23题（几何证明题）【2019届一模徐汇】23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图，已知菱形ABCD ，点E 是AB 的中点，AF BC ⊥于点F ，联结EF 、ED 、DF ，DE 交AF 于点G ，且2AE EG ED =⋅．(1) 求证：DE EF ⊥； (2) 求证：22BC DF BF =⋅．【2019届一模浦东】23. （本题满分12分，其中每小题各6分）已知：如图8，在平行四边形ABCD 中，M 是边BC 的中点，E 是边BA 延长线上的一点，联结EM ，分别交线段AD 于点F 、AC 于点G .（1）求证：GF EFGM EM=; （2）当22BC BA BE =⋅时，求证：∠EMB =∠ACD .G DEF BCA（第23题图）（图8）DCM BAF GE23．（本题满分12分，每小题各6分）已知：如图，在△ABC 中，点D 在边AB 上，点E 在线段CD 上，且∠ACD =∠B =∠BAE. （1）求证：AD DEBC AC=；（2）当点E 为CD 中点时，求证：22AE ABCE AD=.【2019届一模普陀】23．（本题满分12分）已知：如图9，△ADE 的顶点E 在△ABC 的边BC 上，DE 与AB 相交于点F ，AE AF AB =⋅2，DAF EAC ∠=∠．（1）求证：△ADE ∽△ACB ；（2）求证：DF CE DE CB=．（第23题图）EABCDF图9ABCDE23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）已知：如图9，在△ABC 中，点D 在边AC 上，BD 的垂直平分线交CA 的延长线于点E ，交BD 于点F ，联结BE ，EC EA ED •=2．（1）求证：∠EBA =∠C ；（2）如果BD =CD ，求证：AC AD AB •=2．【2019届一模松江】23.（本题满分12分，第（1）小题5分，第（2）小题7分）已知：如图，在梯形ABCD 中，AD ∥BC ，AB=DC ，E 是对角线AC 上一点，且AC ·CE=AD ·BC . （1）求证：∠DCA=∠EBC ；（2）延长BE 交AD 于F ，求证：AB 2=AF ·AD .ABCDEF图9（第23题图）EDCBAF（第23题图）EDCBA23．（本题满分12分，每小题6分）如图6，已知点D 在△ABC 的外部，AD //BC ，点E 在边AB 上，AE BC AD AB ⋅=⋅．（1）求证：AED BAC ∠=∠；（2）在边AC 取一点F ，如果D AFE ∠=∠，求证：ACAFBC AD =．【2019届一模青浦】23．（本题满分12分，第（1）小题7分，第（2）小题5分）已知：如图，在△ABC 中，点D 、E 分别在边BC 、AC 上，点F 在DE 的延长线上，AD=AF ，AE CE DE EF ⋅=⋅．（1）求证：△ADE ∽△ACD ；（2）如果AE BD EF AF ⋅=⋅，求证：AB=AC ．图6BCDAE FABCDEF（第23题图）23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）已知：如图9，在ABC ∆中，点D 、E 分别在边BC 和AB 上，且AD AC =，EB ED =，分别延长ED 、AC 交于点F ．（1）求证：ABD ∆∽FDC ∆；（2）求证：2AE BE EF =⋅．【2019届一模宝山】23．（本题满分12分）地铁10号线某站点出口横截面平面图如图8所示，电梯AB 的两端分别距顶部9.9米和2.4米，在距电梯起点A 端6米的P 处，用1.5米的测角仪测得电梯终端B 处的仰角为14°，求电梯AB 的坡度与长度．参考数据：24.014sin ≈︒，25.014tan ≈︒，97.014cos ≈︒.Q 9.9米B出口顶部1.5米（图8）AP6米2.4米︒14图9 AC BDEF23．（本题满分12分，第（1）小题5分，第（2）小题7分）如图，点D 、E 分别在ABC ∆的边AC 、AB 上，延长DE 、CB 交于点F ，且AC AD AB AE ⋅=⋅．（1）求证：C FEB ∠=∠；（2）联结AF ，若FD CD AB FB =，求证：FB AC AB EF ⋅=⋅．【2019届一模金山】23．如图，M 是平行四边形ABCD 的对角线上的一点，射线AM 与BC 交于点F ，与DC 的延长线交于点H ．（1）求证：MH MF AM ⋅=2．（2）若DM BD BC ⋅=2，求证：ADC AMB ∠=∠．第23题图CEDABF ABCD HF M第23题23．（本题共2小题，每小题6分，满分12分）如图，在△ABC 中，点D 为边BC 上一点，且AD = AB ，AE ⊥BC ，垂足为点E ．过点D 作DF // AB ，交边AC 于点F ，联结EF ，212EF BD EC =⋅．（1）求证：△EDF ∽△EFC ；（2）如果14EDF ADC S S =V V ，求证：AB = BD ．【2019届一模虹口】23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图，在△ABC 中，AB=AC ，D 是边BC 的中点，DE ⊥AC ，垂足为点E ．（1）求证：DE CD AD CE ⋅=⋅；（2）设F 为DE 的中点，联结AF 、BE ，求证：=AF BC AD BE ⋅⋅．ABCDE F（第23题图）D 第23题图AECBⅢ第24题（二次函数综合）【2019届一模徐汇】24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ，AO =OB =2，120AOB ∠=o ．（1）求该抛物线的表达式；（2）联结AM ，求AOM S V ；（3）将抛物线C 1向上平移得到抛物线C 2，抛物线C 2与x 轴分别交于点E 、F （点E 在点F 的左侧），如果△MBF 与△AOM 相似，求所有符合条件的抛物线C 2的表达式．（第24题图）【2019届一模浦东】24.（本题满分12分，其中每小题各4分）已知：如图9，在平面直角坐标系xOy中，直线12y x b=-+与x轴相交于点A，与y轴相交于点B. 抛物线244y ax ax=-+经过点A和点B，并与x轴相交于另一点C，对称轴与x轴相交于点D.（1）求抛物线的表达式;（2）求证: △BOD∽△AOB;（3）如果点P在线段AB上，且∠BCP=∠DBO，求点P的坐标.（图9）xBO Ay【2019届一模杨浦】24．（本题满分12分，每小题各4分）在平面直角坐标系xOy 中，抛物线2(0)y ax bx c a =++?与y 轴交于点C （0,2），它的顶点为D （1,m ），且1tan 3COD ?. （1）求m 的值及抛物线的表达式；（2）将此抛物线向上平移后与x 轴正半轴交于点A ，与y 轴交于点B ，且OA =OB .若点A 是由原抛物线上的点E 平移所得，求点E 的坐标；（3）在（2）的条件下，点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3 -1 -2 -3 （第24题图）24．（本题满分12分）如图10，在平面直角坐标系xOy 中，抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ，且3OB OA =，与y 轴交于点C ，此抛物线顶点为点D ．（1）求抛物线的表达式及点D 的坐标；（2）如果点E 是y 轴上的一点（点E 与点C 不重合），当BE DE ⊥时，求点E 的坐标；（3）如果点F 是抛物线上的一点，且135FBD ∠=，求点F 的坐标．图10C BAOyx24．（本题满分12分，每小题满分6分）如图10，在平面直角坐标系xOy 中，直线AB 与抛物线2y ax bx =+交于点A (6，0)和点B (1，－5)．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且∠BOC 的正切值是32，求点C 的坐标．图10 ABxyo24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线c bx x y ++-=221经过点A （﹣2，0），点B （0，4）. （1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果∠PBO=∠BAO ，求点P 的坐标；（3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作DE ∥x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果EO =2OF ，求m 的值.(第24题图)y xOBA24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ，与y 轴的交点为C ．（1）试求这个抛物线的表达式；（2）如果这个抛物线的顶点为M ，求△AMC 的面积；（3）如果这个抛物线的对称轴与直线BC 交于点D ，点E 在线段AB 上，且︒=∠45DOE ，求点E 的坐标．图7O 11 xy--24．（本题满分12分，其中第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，将抛物线2y x =-平移后经过点A （-1，0）、B （4，0），且平移后的抛物线与y 轴交于点C （如图）．（1）求平移后的抛物线的表达式；（2）如果点D 在线段CB 上，且CD =2，求∠CAD 的正弦值；（3）点E 在y 轴上且位于点C 的上方，点P 在直线BC 上，点Q 在平移后的抛物线上，如果四边形ECPQ 是菱形，求点Q 的坐标．CB A xyOCB A xyO（第24题图）（备用图）24．（本题满分12分，其中第（1）小题4分，第（2）小题3分，第（3）小题5分）在平面直角坐标系xOy 中（如图10），已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ，、(53)D ，，设它与x 轴的另一个交点为A （点A 在点B 的左侧），且ABD ∆的面积是3．（1）求该抛物线的表达式；（2）求ADB ∠的正切值；（3）若抛物线与y 轴交于点C ，直线CD 交x 轴于点E ，点P 在射线AD 上，当APE ∆与 ABD ∆相似时，求点P 的坐标．BD O图10xy﹒﹒24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分）如图9，已知：二次函数2y x bx =+的图像交x 轴正半轴于点A ，顶点为P ,一次函数132y x =-的图像交x 轴于点B ，交y 轴于点C , ∠OCA 的正切值为23． (1)求二次函数的解析式与顶点P 坐标；(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若，求m 的值．A B C O yx（图9）24．（本题满分12分，每小题4分）如图，在直角坐标平面内，抛物线经过原点O 、点)3,1(B ，又与x 轴正半轴相交于点A ，︒=∠45BAO ，点P 是线段AB 上的一点，过点P 作OB PM //，与抛物线交于点M ，且点M 在第一象限内．（1）求抛物线的表达式；（2）若AOB BMP ∠=∠，求点P 的坐标；（3）过点M 作x MC ⊥轴，分别交直线AB 、x 轴于点N 、C ，若ANC ∆的面积等于PMN ∆的面积的2倍，求NC MN 的值．第24题图 xO A By备用图xO A By24．已知抛物线c bx x y ++=2经过点()6,0A ，点()3,1B ，直线1l ：()0≠=k kx y ，直线2l ：2--=x y ，直线1l 经过抛物线c bx x y ++=2的顶点P ，且1l 与2l 相交于点C ，直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移，使抛物线的顶点在直线2l 上（此时抛物线的顶点记为M ），再把抛物线左右平移，使抛物线的顶点在直线1l 上（此时抛物线的顶点记为N ）．（1）求抛物线c bx x y ++=2的解析式．（2）判断以点N 为圆心，半径长为4的圆与直线2l 的位置关系，并说明理由．（3）设点F 、H 在直线1l 上（点H 在点F 的下方），当MHF ∆与OAB ∆相似时，求点F 、H 的坐标（直接写出结果）．第24题yxO24．（本题共3小题，每小题4分，满分12分）已知：在平面直角坐标系xOy 中，抛物线2y a x b x =+经过点A （5，0）、B （-3，4），抛物线的对称轴与x 轴相交于点D ．（1）求抛物线的表达式；（2）联结OB 、BD ．求∠BDO 的余切值；（3）如果点P 在线段BO 的延长线上，且∠P AO =∠BAO ，求点P 的坐标．xy O （第24题图）24．（本题满分12分，第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴相交于原点O 和点B （4，0），点A （3，m ）在抛物线上．（1）求抛物线的表达式，并写出它的对称轴；（2）求tan ∠OAB 的值；（3）点D 在抛物线的对称轴上，如果∠BAD =45°，求点D 的坐标．OAy 第24题图xBF EA CB DF E A CB DⅣ第25题（压轴题）【2019届一模徐汇】25. （本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）已知：在梯形ABCD 中，AD //BC ，AC ＝BC ＝10，54cos =∠ACB ，点E 在对角线AC 上(不与点A 、C 重合)，EDC ACB ∠=∠，DE 的延长线与射线CB 交于点F ，设AD 的长为x ．（1）如图1，当DF BC ⊥时，求AD 的长；（2）设EC 的长为y ，求y 关于x 的函数解析式，并直接写出定义域；（3）当△DFC 是等腰三角形时，求AD 的长．（第25题图1）（第25题图）【2019届一模浦东】25. （本题满分14分，其中第（1）小题3分，第（2）小题5分，第（3）小题6分）将大小两把含30°角的直角三角尺按如图10-1位置摆放，即大小直角三角尺的直角顶点C 重合，小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上，此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°，AB =12. （1）求小三角尺的直角边CD 的长;（2）将小三角尺绕点C 逆时针旋转，当点D 第一次落在大三角尺的边AB 上时（如图10-2），求点B 、E 之间的距离;（3）在小三角尺绕点C 旋转的过程中，当直线DE 经过点A 时，求∠BAE 的正弦值.G（图10-1）（图10-2）E DCABDCBAE25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）已知：梯形ABCD 中，AD //BC ，AB ⊥BC ，AD =3，AB =6，DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .（1）当点E 为边AB 的中点时（如图1），求BC 的长；（2）当点E 在边AB 上时（如图2），联结CE ，试问：∠DCE 的大小是否确定？若确定，请求出∠DCE 的正切值；若不确定，则设AE =x ，∠DCE 的正切值为y ，请求出y 关于x 的函数解析式，并写出定义域；（3）当△AEF 的面积为3时，求△DCE 的面积.A BC D EF （图1）（第25题图） A B C D E F （图2）25．（本题满分14分）如图11，点O 在线段AB 上，22AO OB a ==，60BOP ∠=︒，点C 是射线OP 上的一个动点．（1）如图11①，当90ACB ∠=︒，2OC =，求a 的值；（2）如图11②，当AC =AB 时，求OC 的长（用含a 的代数式表示）；（3）在第（2）题的条件下，过点A 作AQ ∥BC ，并使∠QOC=∠B ，求:AQ OQ 的值．A BCPOABCPO图11①图11②25．（本题满分14分，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分5分）如图11，已知梯形ABCD 中，AB ∥CD ，∠DAB =90°，AD =4，26AB CD ==，E 是边BC 上一点，过点D 、E 分别作BC 、CD 的平行线交于点F ，联结AF 并延长，与射线DC 交于点G ．（1）当点G 与点C 重合时，求:CE BE 的值；（2）当点G 在边CD 上时，设CE m =，求△DFG 的面积；（用含m 的代数式表示）（3）当AFD ∆∽ADG ∆时，求∠DAG 的余弦值．图11ABC D F E G 备用图ABC D25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）如图，已知△ABC 中，∠ACB =90°，D 是边AB 的中点，P 是边AC 上一动点，BP 与CD 相交于点E ．（1）如果BC =6，AC =8，且P 为AC 的中点，求线段BE 的长；（2）联结PD ，如果PD ⊥AB ，且CE =2，ED =3，求cosA 的值；（3）联结PD ，如果222BP CD ，且CE =2，ED =3，求线段PD 的长．（备用图2）ABCD（备用图1）ABCD（第25题图）ABPC D E25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）在矩形ABCD 中，6=AB ，8=AD ，点E 是边AD 上一点，EC EM ⊥交AB 于点M ，点N 在射线MB 上，且AE 是AM 和AN 的比例中项. （1）如图8，求证：DCE ANE ∠=∠；（2）如图9，当点N 在线段MB 之间，联结AC ，且AC 与NE 互相垂直，求MN 的长；（3）联结AC ，如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似，求DE 的长．A备用图BD CA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD//BC ，BC =18，DB =DC =15，点E 、F 分别在线段BD 、CD 上，DE =DF =5． AE 的延长线交边BC 于点G ， AF 交BD 于点N 、其延长线交BC 的延长线于点H ．（1）求证：BG =CH ；（2）设AD =x ，△ADN 的面积为y ，求y 关于x 的函数解析式，并写出它的定义域；（3）联结FG ，当△HFG 与△ADN 相似时，求AD 的长．NHGFEDC AB （第25题图）图11ABCPQM25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）已知：如图11，在ABC ∆中，6AB =，9AC =，tan 22ABC ∠=．过点B 作BM //AC ，动点P 在射线BM 上（点P 不与点B 重合），联结PA 并延长到点Q ，使AQC ABP ∠=∠．（1）求ABC ∆的面积；（2）设BP x =，AQ y =，求y 关于x 的函数解析式，并写出x 的取值范围；（3）联结PC ，如果PQC ∆是直角三角形，求BP 的长．25．（本题满分14分，第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分）如图10，已知：梯形ABCD 中，∠ABC =90°，∠A =45°，AB ∥DC ，DC =3，AB =5，点 P 在AB 边上，以点A 为圆心AP 为半径作弧交边DC 于点E ，射线EP 与射线CB 交于点F ．（1）若13AP ，求DE 的长；（2）联结CP ，若CP=EP ，求AP 的长；（3）线段CF 上是否存在点G ，使得△ADE 与△FGE 相似，若相似，求FG 的值；若不相似，请说明理由．备用图A BCD PEABCDF（图10）25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）已知锐角MBN ∠的余弦值为53，点C 在射线BN 上，25=BC ，点A 在MBN ∠的内部，且︒=∠90BAC ，MBN BCA ∠=∠．过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E ．点F 在线段BE 上（点F 不与点B 重合），且MBN EAF ∠=∠．（1）如图1，当BN AF ⊥时，求EF 的长；（2）如图2，当点E 在线段BC 上时，设x BF =，y BD =，求y 关于x 的函数解析式并写出函数定义域；（3）联结DF ，当ADF ∆与ACE ∆相似时，请直接写出BD 的长．第25题图图2 BFE C N DA MB FC E N AD M图1备用图BC NAM25．已知多边形ABCDEF 是⊙O 的内接正六边形，联结AC 、FD ，点H 是射线AF 上的一个动点，联结CH ,直线CH 交射线DF 于点G ，作CH MH ⊥交CD 的延长线于点M ，设⊙O 的半径为()0>r r ．（1）求证：四边形ACDF 是矩形．（2）当CH 经过点E 时，⊙M 与⊙O 外切，求⊙M 的半径（用r 的代数式表示）．（3）设()900<<=∠ααHCD ，求点C 、M 、H 、F 构成的四边形的面积（用r 及含α的三角比的式子表示）．A B C D EF G O HM第25题图第25题备用图 ABCD E FO25．（本题满分14分，其中第（1）小题4分、第（2）、（3）小题各5分）如图，在梯形ABCD 中，AD // BC ，AB = CD ，AD = 5，BC = 15，5cos 13ABC ∠=．E 为射线CD 上任意一点，过点A 作AF // BE ，与射线CD 相交于点F ．联结BF ，与直线AD 相交于点G ．设CE = x ，AG y DG=．（1）求AB 的长；（2）当点G 在线段AD 上时，求y 关于x 的函数解析式，并写出函数的定义域；（3）如果23ABEFABCDS S =四边形四边形，求线段CE 的长．AB CDEFG （第25题图）A B C D （备用图）25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）如图，在四边形ABCD 中，AD ∥BC ，∠A =90°，AB =6，BC =10，点E 为边AD 上一点，将△ABE 沿BE 翻折，点A 落在对角线BD 上的点G 处，联结EG 并延长交射线BC 于点F ．（1）如果cos ∠DBC =23，求EF 的长；（2）当点F 在边BC 上时，联结AG ，设AD=x ，ABG BEFS y S ∆∆= ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结CG ，如果△FCG 是等腰三角形，求AD 的长．第25题备用图 A B C 第25题图 E A B C F D G。