最新《统计分析与SPSS的应用(第五版)》课后练习答案(第10章)资料
《统计分析与SPSS的应用第五版》课后练习答案第10章.doc

《统计分析与S P S S的应用(第五版)》(薛薇)课后练习答案第10章SPSS的聚类分析1、根据“高校科研研究.sav”数据,利用层次聚类分析对各省市的高校科研情况进行层次聚类分析。
要求:1)根据凝聚状态表利用碎石图对聚类类数进行研究。
2)绘制聚类树形图,说明哪些省市聚在一起。
3)绘制各类的科研指标的均值对比图。
4)利用方差分析方法分析各类在哪些科研指标上存在显著差异。
采用欧氏距离,组间平均链锁法利用凝聚状态表中的组间距离和对应的组数,回归散点图,得到碎石图。
大约聚成4类。
步骤:分析→分类→系统聚类→按如下方式设置……结果:凝聚计划阶段组合的集群系数首次出现阶段集群下一个阶段集群 1 集群 2 集群 1 集群 21 26 30 328.189 0 0 22 26 29 638.295 1 0 73 20 25 1053.423 0 0 54 4 12 1209.922 0 0 155 8 20 1505.035 0 3 66 8 16 1760.170 5 0 97 24 26 1831.926 0 2 108 7 11 1929.891 0 0 119 5 8 2302.024 0 6 2210 24 31 2487.209 7 0 2211 2 7 2709.887 0 8 1612 22 28 2897.106 0 0 1913 6 23 2916.551 0 0 1714 10 19 3280.752 0 0 2515 4 21 3491.585 4 0 2116 2 3 4229.375 11 0 2117 6 13 4612.423 13 0 2018 9 18 5377.253 0 0 2519 14 22 5622.415 0 12 2420 6 15 5933.518 17 0 2321 2 4 6827.276 16 15 2622 5 24 7930.765 9 10 2423 6 27 9475.498 20 0 2624 5 14 14959.704 22 19 2825 9 10 19623.050 18 14 2726 2 6 24042.669 21 23 2827 9 17 32829.466 25 0 2928 2 5 48360.854 26 24 2929 2 9 91313.530 28 27 3030 1 2 293834.503 0 29 0将系数复制下来后,在EXCEL中建立工作表。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)
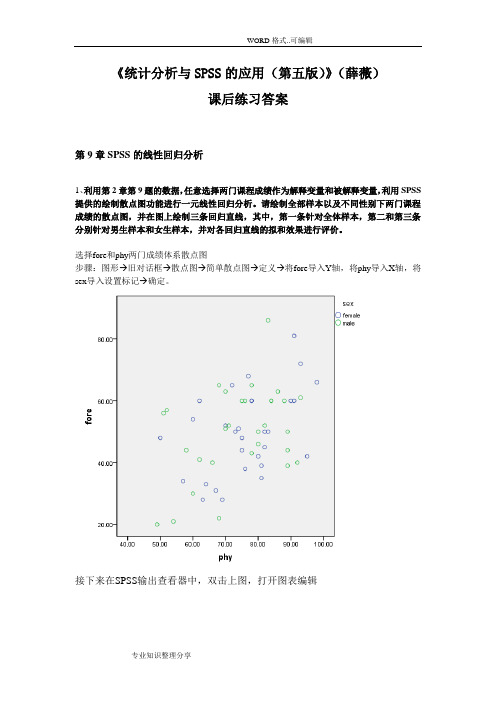
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
《统计分析与SPSS的应用第五版》课后练习答案

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式各自的特点和应用场合是什么SPSS中两个基本的数据组织方式:原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式:待分析的数据是一些原始的调查问卷数据,或是一些基本的统计指标。
●计数数据的组织方式:所采集的数据不是原始的调查问卷数据,而是经过分组汇总后的数据。
2、什么是SPSS的个案什么SPSS的变量个案:在原始数据的组织方式中,数据编辑器窗口中的一行称为一个个案或观测。
变量:数据编辑器窗口中的一列。
3、在定义SPSS数据结构时,默认的变量名和变量类型是什么如果希望增强SPSS 统计分析结果的易读性,还需要对数据结构的哪些方面进行必要说明默认的变量名:VAR------;默认的变量类型:数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据,请问在SPSS中应如何组织该份资料问:在SPSS中应如何组织该数据数据文件如图所示:5、什么是SPSS的用户缺失值为什么要对用户缺失值进行定义如何在SPSS中指定用户缺失值缺失值分为用户缺失值(User Missing Value)和系统缺失值(System Missing Value)。
用户缺失值指在问卷调查中,将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示,如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式,如果在输入数据时空缺了某些数据或输入了非法的字符,计算机就把其界定为缺失值,这时的数据标记为一个圆点“”。
在变量视图中定义。
6、从计量尺度角度看,变量包括哪三种主要类型请各举出一个相应的实际数据。
如何在SPSS中指定变量的计算尺度变量类型包括:数值型(身高)、定序型(受教育程度)以及定类型(性别)。
《统计分析与SPSS的应用(第五版)》课后练习答案-(1)

《统计分析与S P S S的应用(第五版)》课后练习答案第一章练习题答案1、SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是:Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据;●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集:●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
●活动数据集:其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式:●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
●程序运行方式:是指在使用SPSS的过程中,统计分析人员根据自己的需要,手工编写SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式:是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling):也称随机抽样,是指按一定的概率以随机原则抽取样本,抽取样本时每个单位都有一定的机会被抽中,每个单位被抽中的概率是已知的,或是可以计算出来的。
《统计分析与SPSS的应用(第五版)》课后练习答案(第9章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
最新《统计分析与SPSS的应用(第五版)》课后练习答案(第10章)
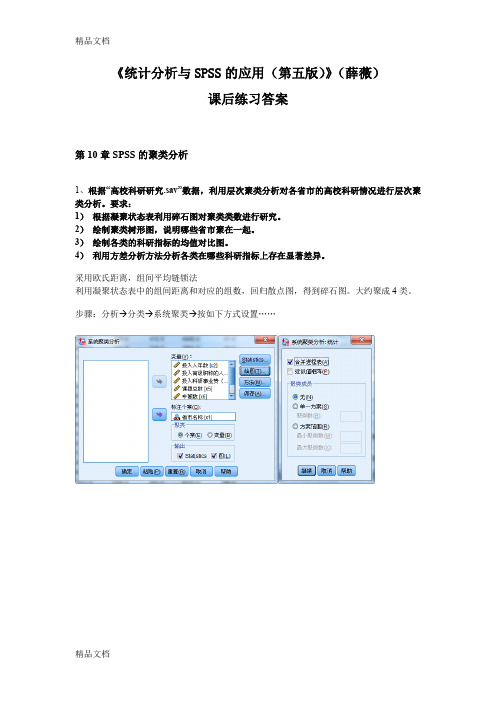
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第10章SPSS的聚类分析1、根据“高校科研研究.sav”数据,利用层次聚类分析对各省市的高校科研情况进行层次聚类分析。
要求:1)根据凝聚状态表利用碎石图对聚类类数进行研究。
2)绘制聚类树形图,说明哪些省市聚在一起。
3)绘制各类的科研指标的均值对比图。
4)利用方差分析方法分析各类在哪些科研指标上存在显著差异。
采用欧氏距离,组间平均链锁法利用凝聚状态表中的组间距离和对应的组数,回归散点图,得到碎石图。
大约聚成4类。
步骤:分析→分类→系统聚类→按如下方式设置……结果:凝聚计划阶段 组合的集群系数 首次出现阶段集群 下一个阶段集群 1集群 2集群 1集群 21 26 30 328.189 0 02 2 26 29 638.295 1 0 73 20 25 1053.423 0 0 54 4 12 1209.922 0 0 15 5 8 201505.035 0 3 6 6 8 16 1760.170 5 0 9 7 24 26 1831.926 0 2 10 8 7 11 1929.891 0 0 11 9 5 8 2302.024 0 6 22 10 24 31 2487.209 7 0 22 11 2 7 2709.887 0 8 16 12 22 28 2897.106 0 0 19 13 6 23 2916.551 0 0 17 14 10 19 3280.752 0 0 25 15 4 21 3491.585 4 0 21 16 2 3 4229.375 11 0 21 17 6 13 4612.423 13 0 20 18 9 18 5377.253 0 0 25 19 14 22 5622.415 0 12 24 20 6 15 5933.518 17 0 23 21 2 4 6827.276 16 15 26 22 5 24 7930.765 9 10 24 23 6 27 9475.498 20 0 26 24 5 14 14959.704 22 19 28 25 9 10 19623.050 18 14 27 26 2 6 24042.669 21 23 28 27 9 17 32829.466 25 0 29 28 2 5 48360.854 26 24 29 29 2 9 91313.530 28 27 30 3012293834.50329选中数据列,点击“插入”菜单 拆线图……碎石图:由图可知,北京自成一类,江苏、广东、上海、湖南、湖北聚成一类。
《统计分析与spss的应用(第五版)》课后练习答案.doc(1)

《统计分析与SPSS的应用(第五版)》课后练习答案第一章练习题答案1、SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是:Statistical Package for the Soc i a I Science. (Statistical Product and Service Solutions)2、SPSS的两个主要窗口是教据编辑器窗口和结果查看器窗口。
教据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据:结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集:SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
活动数据集:其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式:完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对■话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
程序运行方式:是指在使用SPSS的过程中,统计分析人员根据自己的需要,手工编写SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式:是前两者的综合。
5、・sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等莱单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probabi I i ty samp I i ng):也称随机抽样,是指按一定的概率以随机原则抽取样本,抽取样本时每个单位都有一定的机会被抽中,每个单位被抽中的棋率是已知的,或是可以计算出来的。
《统计分析与SPSS的应用(第五版)》课后练习答案(第10章)word版本

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第10章SPSS的聚类分析1、根据“高校科研研究.sav”数据,利用层次聚类分析对各省市的高校科研情况进行层次聚类分析。
要求:1)根据凝聚状态表利用碎石图对聚类类数进行研究。
2)绘制聚类树形图,说明哪些省市聚在一起。
3)绘制各类的科研指标的均值对比图。
4)利用方差分析方法分析各类在哪些科研指标上存在显著差异。
采用欧氏距离,组间平均链锁法利用凝聚状态表中的组间距离和对应的组数,回归散点图,得到碎石图。
大约聚成4类。
步骤:分析→分类→系统聚类→按如下方式设置……结果:凝聚计划阶段组合的集群系数首次出现阶段集群下一个阶段集群 1 集群 2 集群 1 集群 21 26 30 328.189 0 0 22 26 29 638.295 1 0 7 320251053.4235 44 121209.922155 8201505.035 03 66 8 16 1760.170 5 0 97 24 26 1831.926 0 2 108 7 11 1929.891 0 0 119 5 8 2302.024 0 6 2210 24 31 2487.209 7 0 2211 2 7 2709.887 0 8 1612 22 28 2897.106 0 0 1913 6 23 2916.551 0 0 1714 10 19 3280.752 0 0 2515 4 21 3491.585 4 0 2116 2 3 4229.375 11 0 2117 6 13 4612.423 13 0 2018 9 18 5377.253 0 0 2519 14 22 5622.415 0 12 2420 6 15 5933.518 17 0 2321 2 4 6827.276 16 15 2622 5 24 7930.765 9 10 2423 6 27 9475.498 20 0 2624 5 14 14959.704 22 19 2825 9 10 19623.050 18 14 2726 2 6 24042.669 21 23 2827 9 17 32829.466 25 0 2928 2 5 48360.854 26 24 2929 2 9 91313.530 28 27 3030 1 2 293834.503 0 29 0选中数据列,点击“插入”菜单 拆线图……碎石图:由图可知,北京自成一类,江苏、广东、上海、湖南、湖北聚成一类。
《统计分析与SPSS的应用(第五版)》课后练习答案(第9章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形旧对话框散点图简单散点图定义将fore导入Y轴,将phy导入X轴,将sex导入设置标记确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单选择总计拟合线选择线性应用再选择元素菜单点击子组拟合线选择线性应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy 有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验一般需要对哪些方面进行检验检验其可信程度并找出哪些变量的影响显著、哪些不显著。
《统计分析与spss的应用(第五版)》课后练习答案(第章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式?各自的特点和应用场合是什么?SPSS中两个基本的数据组织方式:原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式:待分析的数据是一些原始的调查问卷数据,或是一些基本的统计指标。
●计数数据的组织方式:所采集的数据不是原始的调查问卷数据,而是经过分组汇总后的数据。
2、什么是SPSS的个案?什么SPSS的变量?个案:在原始数据的组织方式中,数据编辑器窗口中的一行称为一个个案或观测。
变量:数据编辑器窗口中的一列。
3、在定义SPSS数据结构时,默认的变量名和变量类型是什么?如果希望增强SPSS统计分析结果的易读性,还需要对数据结构的哪些方面进行必要说明?默认的变量名:VAR------;默认的变量类型:数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据,请问在SPSS中应如何组织该份资料?体重变化情况产品类型明显减轻无明显变化第一种产品27 19第二种产品20 33问:在SPSS中应如何组织该数据?数据文件如图所示:5、什么是SPSS的用户缺失值?为什么要对用户缺失值进行定义?如何在SPSS中指定用户缺失值?缺失值分为用户缺失值(User Missing Value)和系统缺失值(System Missing Value)。
用户缺失值指在问卷调查中,将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示,如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式,如果在输入数据时空缺了某些数据或输入了非法的字符,计算机就把其界定为缺失值,这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看,变量包括哪三种主要类型?请各举出一个相应的实际数据。
《统计分析与spss的应用(第五版)》课后练习答案(第章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式?各自的特点和应用场合是什么?SPSS中两个基本的数据组织方式:原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式:待分析的数据是一些原始的调查问卷数据,或是一些基本的统计指标。
●计数数据的组织方式:所采集的数据不是原始的调查问卷数据,而是经过分组汇总后的数据。
2、什么是SPSS的个案?什么SPSS的变量?个案:在原始数据的组织方式中,数据编辑器窗口中的一行称为一个个案或观测。
变量:数据编辑器窗口中的一列。
3、在定义SPSS数据结构时,默认的变量名和变量类型是什么?如果希望增强SPSS统计分析结果的易读性,还需要对数据结构的哪些方面进行必要说明?默认的变量名:VAR------;默认的变量类型:数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据,请问在SPSS中应如何组织该份资料?体重变化情况产品类型明显减轻无明显变化第一种产品27 19第二种产品20 33问:在SPSS中应如何组织该数据?数据文件如图所示:5、什么是SPSS的用户缺失值?为什么要对用户缺失值进行定义?如何在SPSS中指定用户缺失值?缺失值分为用户缺失值(User Missing Value)和系统缺失值(System Missing Value)。
用户缺失值指在问卷调查中,将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示,如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式,如果在输入数据时空缺了某些数据或输入了非法的字符,计算机就把其界定为缺失值,这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看,变量包括哪三种主要类型?请各举出一个相应的实际数据。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
统计分析与SPSS课后习题课后习题答案汇总(第五版)

《统计分析与SPSS的应用(第五版)》课后练习答案第一章练习题答案1、SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是:Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据;●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集:●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
●活动数据集:其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式:●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
●程序运行方式:是指在使用SPSS的过程中,统计分析人员根据自己的需要,手工编写SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式:是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling):也称随机抽样,是指按一定的概率以随机原则抽取样本,抽取样本时每个单位都有一定的机会被抽中,每个单位被抽中的概率是已知的,或是可以计算出来的。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)

《统计分析与SPSS的应用〔第五版〕》〔薛薇〕课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以与不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex 导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择"元素"菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y<即:fore>与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以与相关方向和程度做出正确判断之前,就进行回归分析,很容易造成"虚假回归"。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
(完整word版)《统计分析与SPSS的应用(第五版)》课后练习答案(第9章)
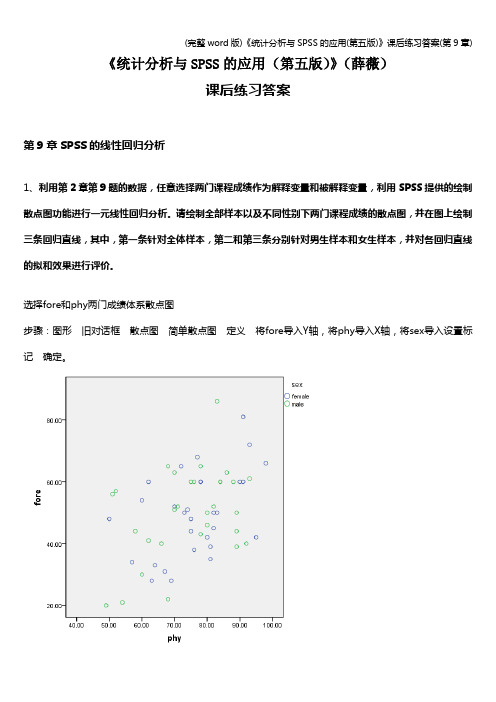
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形旧对话框散点图简单散点图定义将fore导入Y轴,将phy导入X轴,将sex导入设置标记确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单选择总计拟合线选择线性应用再选择元素菜单点击子组拟合线选择线性应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
《统计分析与SPSS的应用(第五版)》课后练习答案-(1)

《统计分析与S P S S的应用(第五版)》课后练习答案第一章练习题答案1、SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是:Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据;●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集:●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
●活动数据集:其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式:●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
●程序运行方式:是指在使用SPSS的过程中,统计分析人员根据自己的需要,手工编写SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式:是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling):也称随机抽样,是指按一定的概率以随机原则抽取样本,抽取样本时每个单位都有一定的机会被抽中,每个单位被抽中的概率是已知的,或是可以计算出来的。
(完整版)《统计分析与SPSS的应用(第五版)》课后练习答案(第1章).docx

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第 1 章 SPSS统计分析软件概述1、 SPSS的中文全名和英文全名是什么?SPSS的中文全名是:社会科学统计软件包(后改名为:统计产品与服务解决方案)英文全名是: Statistical Package for the Social Science.(Statistical Productand Service Solutions)2、 SPSS 有哪两个主要窗口?它们的作用和特点各是什么?SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据;结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、什么是SPSS的数据集?什么是SPSS的活动数据集?SPSS的数据集:SPSS 运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合(简称数据集)。
活动数据集:其中只有一个数据集为当前数据集。
SPSS 只对某时刻的当前数据集中的数据进行分析。
4、 SPSS 有哪三种主要使用方式?各自的特点是什么?SPSS的三种基本运行方式:完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式:是指在使用SPSS的过程中,所有的分析操作都通过菜单、按钮、输入对话框等方式来完成,是一种最常见和最普遍的使用方式,最大优点是简洁和直观。
程序运行方式:是指在使用 SPSS的过程中,统计分析人员根据自己的需要,手工编写 SPSS命令程序,然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式:是前两者的综合。
5、 .sav、 .spo、 .sps 分别是 SPSS 哪类文件的扩展名?.sav 是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS 的数据加工和管理功能主要集中在哪些菜单中?统计绘图和分析功能主要集中在哪些菜单中?SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中;统计分析和绘图功能主要集中在分析、图形等菜单中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《统计分析与SPSS的应用(第五版)》(薛薇)
课后练习答案
第10章SPSS的聚类分析
1、根据“高校科研研究.sav”数据,利用层次聚类分析对各省市的高校科研情况进行层次聚类分析。
要求:
1)根据凝聚状态表利用碎石图对聚类类数进行研究。
2)绘制聚类树形图,说明哪些省市聚在一起。
3)绘制各类的科研指标的均值对比图。
4)利用方差分析方法分析各类在哪些科研指标上存在显著差异。
采用欧氏距离,组间平均链锁法
利用凝聚状态表中的组间距离和对应的组数,回归散点图,得到碎石图。
大约聚成4类。
步骤:分析→分类→系统聚类→按如下方式设置……
结果:
凝聚计划
阶段
组合的集群
系数
首次出现阶段集群
下一个阶段集群 1 集群 2 集群 1 集群 2
1 26 30 328.189 0 0 2
2
26
29 638.295
1 0
7
3 20 25 1053.423
5
4
4 12 1209.922 0
15
5
8
20 1505.035
3
6
6 8 16 1760.170 5 0 9
7 24 26 1831.926 0 2 10
8 7 11 1929.891 0 0 11
9 5 8 2302.024 0 6 22
10 24 31 2487.209 7 0 22
11 2 7 2709.887 0 8 16
12 22 28 2897.106 0 0 19
13 6 23 2916.551 0 0 17
14 10 19 3280.752 0 0 25
15 4 21 3491.585 4 0 21
16 2 3 4229.375 11 0 21
17 6 13 4612.423 13 0 20
18 9 18 5377.253 0 0 25
19 14 22 5622.415 0 12 24
20 6 15 5933.518 17 0 23
21 2 4 6827.276 16 15 26
22 5 24 7930.765 9 10 24
23 6 27 9475.498 20 0 26
24 5 14 14959.704 22 19 28
25 9 10 19623.050 18 14 27
26 2 6 24042.669 21 23 28
27 9 17 32829.466 25 0 29
28 2 5 48360.854 26 24 29
29 2 9 91313.530 28 27 30
30 1 2 293834.503 0 29 0
将系数复制下来后,在EXCEL中建立工作表。
选中数据列,点击“插入”菜单 拆线图……
碎石图:
由图可知,北京自成一类,江苏、广东、上海、湖南、湖北聚成一类。
其他略。
接下来,添加一个变量CLU4_1,其值为类别值。
(1、2、3、4),再数据→汇总→设置……→确定。
均值对比,依据聚类解,利用分类汇总,计算各个聚类变量的均值
方差分析结果:分析→比较均值→单因素ANOVA→设置……→确定
不同组在各个聚类变量上的均值均存在显著差异。
2、试说明当变量存在数量级上的差异,进行层次聚类分析时为什么要对数据进行标准化处理?
因为数量级将对距离产生较大影响,并影响最终聚类结果。
3、试说明变量之间的高度相关性是否会对层次聚类分析结果造成影响?为什么?
会。
如果所选变量之间存在较强的线性关系,能够相互替代,在计算距离时同类变量将重复
“贡献”,占有较高权重,而使最终的聚类结果偏向该类变量。
4、试说明K-Mean聚类分析的基本步骤。
K-Means聚类分析步骤:
确定聚类数目K--确定K个初始类中心点--根据距离最近原则进行分类--重新确定K个类中心点--判断是否已经满足终止条件。
是一个反复迭代的分类过程。
在聚类过程中,样本所属的类会不断调整,直至达到最终稳定为止。
5、收集到我国2007年各地区城镇居民家庭平均每人全年消费支出数据,数据文件名为:“消费结构.sav”,变量包括:地区、消费性支出总额、食品、衣着、居住、家庭设备用品及服
务、医疗保健、交通和通信、教育文化娱乐服务、医疗保健、杂项商品和服务支出。
若采用层次聚类法(个体间距离定义为平方欧氏距离,类间距离定义为组间平均链锁距离),绘制的碎石图如下:
(1)依据上图,数据聚成几类较为恰当?
(2)试采用K-MEANS聚类方法,从类内相似性和类间差异性角度分析将数据聚成几类较为恰当。
(1)聚成3类较为恰当。
注:碎石图可按第9章第1题方式绘制,也可按如下方式绘制。
步骤:分析→降维→因子分析→导入全部变量到变量框中(地区变量除外)→抽取:选中碎石图→继续→确定。
得到:(可以看出,分成3类恰当)
(2)用K-MEANS聚类方法进行分类,比较分类数为2、3、4时的差别。
步骤:分析→分类→K-平均聚类→地区变量导入到标注个案,其他变量全部导入到变量框中→聚类数填2→选项:选中初始聚类中心和ANOVA→继续→确定。
得到:
ANOVA
聚类错误
均方df 均方df
F 显著性
食品13927902.967 1 246753.779 29 56.445 .000 衣着278718.565 1 37555.425 29 7.422 .011 居住667583.436 1 31940.764 29 20.901 .000 家庭设备用品及服务411657.258 1 14558.041 29 28.277 .000 医疗保健325304.302 1 34400.296 29 9.456 .005 交通和通信10285607.457 1 57486.400 29 178.922 .000 教育文化娱乐服务5226361.465 1 69080.933 29 75.656 .000 杂项商品和服务248312.931 1 6496.550 29 38.222 .000 仅当出于描述目的时才应该使用 F 检验,因为已选择聚类用于将不同聚类中的个案的差异最大化。
受观察的显著性级别并未因此得到更正,所以无法将这些级别解释为“聚类方法是等同的”假设的检验。
每个聚类中的个案数量
聚类 1 4.000
2 27.000
有效31.000
缺失.000
ANOVA
聚类错误
F 显著性
均方df 均方df
食品8311754.509 2 159294.770 28 52.178 .000
衣着100878.509 2 41645.317 28 2.422 .107 居住565811.147 2 16508.690 28 34.274 .000 家庭设备用品及服务237257.836 2 12833.027 28 18.488 .000 医疗保健198689.996 2 33054.746 28 6.011 .007 交通和通信4709934.064 2 90458.748 28 52.067 .000 教育文化娱乐服务2676015.304 2 67059.926 28 39.905 .000 杂项商品和服务150742.666 2 4829.555 28 31.213 .000 仅当出于描述目的时才应该使用 F 检验,因为已选择聚类用于将不同聚类中的个案的差异最大化。
受观察的显著性级别并未因此得到更正,所以无法将这些级别解释为“聚类方法是等同的”假设的检验。
每个聚类中的个案数量
聚类 1 1.000
2 25.000
3 5.000
有效31.000
缺失.000
将上图中的聚类数修改为4,则得到:
ANOVA
聚类错误
均方df 均方df
F 显著性
食品6461251.597 3 62963.251 27 102.619 .000 衣着135334.013 3 35623.106 27 3.799 .022 居住237725.271 3 32618.140 27 7.288 .001 家庭设备用品及服务142250.914 3 15077.322 27 9.435 .000 医疗保健111992.289 3 36553.186 27 3.064 .045 交通和通信3596731.324 3 43056.263 27 83.536 .000 教育文化娱乐服务1812882.568 3 66335.586 27 27.329 .000 杂项商品和服务97486.291 3 5342.741 27 18.246 .000 仅当出于描述目的时才应该使用 F 检验,因为已选择聚类用于将不同聚类中的个案的差异最大化。
受观察的显著性级别并未因此得到更正,所以无法将这些级别解释为“聚类方法是等同的”假设的检验。
每个聚类中的个案数量
聚类 1 1.000
2 3.000
3 15.000
4 12.000
有效31.000
缺失.000
从3个ANOVA表可以看出,分为2类时,P-值均小于0.05,表明有显著差异;分
为3类时,出现了“衣着”的P-值为0.107,大于0.05;分为4类时,P-值均小于0.05,
表明有显著差异。
表明仅从ANOVA表看,分为3类,不合适。
再看F值,F值大表明组间差大,组内差小,即类内相似性大,类间差异性大,经比较可以看出,分类2类时,组间方差和组内方差均较大,而分为4类时,组间方差和组内方差相对来说,组内方差缩小得明显一些。
故分为4类较为恰当。
