小学数学组合图形试题及答案
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
人教版五年级上册数学 组合图形专项练习含参考答案

组合图形2一、计算题(每题分,计分)1.求下面涂色图形的面积。
2.求下面各个图形中阴影部分的面积。
(单位:dm)3.把下面的图形分成我们学过的图形,再计算出它的面积。
(单位:厘米)4.求下面图形的面积。
(图中单位为厘米)5.下面图形的面积是多少?6.求下列各个图形的面积(单位:厘米)7.阴影部分的面积是多少平方厘米。
8.计算图形的面积。
(单位:分米)二、图形题(每题分,计分)9.上图是一面墙,中间有一个长2米,宽1.5米的窗户,如果砌这面墙平均每平方米用砖160块,一共需要用多少块砖?三、解答题(每题分,计分)10.新丰小学有一块菜地,形状如图所示,这块菜地的面积是多少平方米?11.一块梯形地,上底长40m,下底长60m,高是40m(如下图)。
李伯伯在这块地中最大的一块正方形地里种棉花,其余的种花生,种花生的面积有多大?12.下图表示的是一间房子侧面墙的形状。
它的面积是多少平方米。
13.小丽用彩纸剪了一个大写英文字母“W”。
它的面积是多少?14.手工课上,唐老师让同学们在一张长方形纸的一角剪去一个等腰直角三角形(如图),剩下部分的面积是多少?15.有一个长25m、宽20m的花坛,如果在这个花坛的四周修3m宽的小路(如下图),小路的面积是多少平方米?16.如下图所示,李老师在一张长8厘米,宽6厘米的长方形纸上放了一个字母“Y”。
这个字母的面积是多少平方厘米?挑战题1.(见图)线段AE和AF把长方形分成面积相等的三部分,求阴影部分的面积。
(单位:cm)挑战题2.下图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1厘米,这个六边形的周长是多少厘米?参考答案:一、计算题(每题分,计分)1.19cm22.(12-6)×8÷2=24(dm2);8×10÷2=40(dm2)3.方法一:长方形+梯形16×4+(16+24)×(12-4)=224(cm2)方法二:长方形+三角形16×12+(12-4)×(24-16)+2=224(cm2)方法三:长方形-梯形24×12-(4+12)×(24-16)÷2 方法四:三角形+梯形24×(12-4)+2+(4+12)×16÷24.86cm25.40m26.第一个图形的面积是187cm2。
五年级数学组合图形试题

五年级数学组合图形试题1.计算图形的面积。
(单位:cm)【答案】800cm2【解析】三角形的面积+平行四边形的面积。
解:32×10÷2+32×20=32×5+32×20=32×(5+20)=32×25=800(cm2)2.计算图形的面积。
(单位:cm)【答案】201cm2【解析】三角形的面积+梯形的面积。
解:3×4÷2+(6+20)×15÷2=6+26×15÷2=6+195=201(cm2)3.计算阴影部分的面积。
(单位:cm)【答案】216cm2【解析】阴影面积=平行四边形面积-三角形面积。
解:18×24-18×24÷2=432-432÷2=432-216=216(cm2)4.计算阴影部分的面积。
(单位:cm)【答案】302cm2【解析】阴影面积=长方形面积-梯形面积。
解:26×15-(10+12)×8÷2=390-22×4="390-88"=302(cm2)5.计算阴影部分的面积。
(单位:cm)【答案】84cm2【解析】阴影面积=梯形面积-三角形面积。
解:(14+16)×12÷2-12×16÷2=30×6-192÷2=180-96=84(cm2)6.计算下面组合图形的面积(每个方格的面积为1)。
【答案】6【解析】首先数清楚图形总共占了几个方格,让方格的面积乘以方格的个数即可。
从上往下看,小方格的个数约为6个,所以面积为1×6=6。
7.计算下面组合图形的面积(每个方格的面积为1)。
【答案】10【解析】图中的阴影部分可以分解为一个平行四边形和一个梯形。
4×2+(1+3)×1÷2=8+4×0.5=8+2=108.求阴影部分的面积。
人教版小学五年级数学上册 组合图形的面积练习题及答案

组合图形的面积1.组合图形的面积(1)下面组合图形的面积是______平方厘米。
(2)下面组合图形是由一个正方形和有一个平行四边形组成,它的面积是______平方厘米。
(3)下面组合图形的面积是______平方厘米。
(4)下面组合图形的面积是______平方厘米。
(5)下图阴影部分的面积是______平方厘米。
(单位:厘米)(6)下图阴影部分的面积是______平方分米。
(单位:分米)2.替换法求三角形或梯形的面积(1)三角形ABC与三角形DFE是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积是_____平方厘米。
(单位:cm)(2)如右图,三角形ABC与三角形DFE是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积是_____平方厘米。
(单位:cm)(3)三角形ABC与三角形EFD是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积是______平方厘米。
(单位:cm)(4)如下图所示,两个完全相同的梯形重叠放在一起,阴影部分的面积是______平方厘米。
(单位:cm)(5)如下图所示,两个完全相同的梯形重叠放在一起,阴影部分的面积是______平方厘米。
(单位:cm)(6)如右图所示,两个完全相同的梯形重叠放在一起,阴影部分的面积是______平方厘米。
(单位:cm)3.面积差不变-线段围成的图形(1)已知长方形的长为6厘米,宽为2.5厘米,三角形的底边长为6厘米,高为2厘米,这两个图形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米(2)边长为5厘米和4厘米的两个正方形有一小部分重合,则它们没有重合的部分的面积相差______平方厘米(3)已知梯形的上底长4厘米,下底长为7厘米,高为3厘米,这个梯形与一个边长为3厘米的正方形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米(4)已知三角形ABC的底边BC长为4厘米,高为3厘米,三角形DEF的底边EF 长为5厘米,高为6厘米,这两个三角形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米(5)已知平行四边形的底边长为7厘米,高为3厘米,三角形的底边长为6厘米,高为5厘米,这两个图形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米(6)图中甲的面积比乙的面积大4平方厘米,三角形ABC的底边长为4厘米,高为2.5厘米,那么三角形DEF的面积是______平方厘米(7)图中甲的面积比乙的面积小5平方厘米,正方形ABCD的边长为5厘米,那么三角形ABF的面积是______平方厘米4.有关直角梯形的面积(1)如图所示,直角梯形ABCD的高AB长26厘米,AD长24厘米,△DEF的面积是175.5平方厘米,EF的长度是BC的二分之一,梯形ABCD的面积是______平方厘米。
五年级数学(上册)《组合图形的面积》试题及答案

五年级数学(上册)《组合图形的面积》试题及答案1、求组合图形的面积(单位:厘米):梯形面积:(8+12)×8.5÷2= 85(cm²)三角形面积:212×3÷2=18(cm²)图形面积=梯形面积–三角形面积:85-18=67(cm²)2、校园里有两块花圃(如图),计算它们的面积(单位:m):长方形面积:6×(5-2)=18(m²)正方形面积:2×2=4(m²)梯形面积:(3+6)×2÷2=9(m²)图形面积=长方形面积+正方形面积-梯形面积:18+4-9=13(m²)3、下图直角梯形的面积是49平方分米,求阴影部分的面积:直角梯形的高= 49÷(6+8)×2=7(dm)直角三角形面积= 6×7÷2=21(dm²)阴影部分面积=直角三角形面积=21(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积:直角梯形的高=直角三角形的高=9(cm)梯形面积=(5+12)×7.5÷2=67.5(cm²)阴影部分面积=梯形面积-空白部分面积:67.5-45=22.5(cm²)5、阴影部分面积是40平方米,求空白部分面积(单位:米):梯形的高=三角形的高(阴影部分三角形)=8(m)梯形面积=(6+10)×8÷2=64(m²)空白部分面积=梯形面积-阴影部分面积:64-40=24(m²)6、如图,平行四边形面积240平方厘米,求阴影部分面积:梯形的下底=平行四边形的底=20(cm)梯形面积=(15+20)×12÷2=210(cm²)阴影部分面积=平行四边形面积-梯形面积:240-210=30(cm²)7、下图ABCD是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
小学六年级下数学图形与组合单元测试卷(含答案)

【答案】第 3 列,第 4 行
17.左图中大长方形的周长是 C 厘米,剪去一个最大的正方形(如图,单位:厘米),
剩下的长方形周长是(
)厘米。
【答案】C-2b 或 2a 或(a-b+b)×2 18.如图,指针从A 开始,逆时针旋转了90°到
点,逆时针旋转了180°到
点;要从 A 旋转到 D,可以按
时针方向旋转
小学六年级下数学图形与组合单元测试卷(含答案)
学校:
姓名:
班级:
考号:
评卷人 得分
一、选择题
1. 把一个三角形沿高剪开分成两个小三角形,每个小三角形的内角和是( )。
A.360°
B.180°
C.90°
【答案】B 2.两根同样长的铁丝,一根铁丝做成长、宽、高分别是 5cm、4cm、3cm 的长方体框
架(铁丝没有多余),另一根做成最大的正方体框架,这个正方体棱长是( )厘米。
24.
数一数,图中有(
)条直线,(
)条射线,(
)条线段.
【答案】1 8 6
25.两个(
)的三角形可以拼成一个平行四边形。
【答案】等边或等腰
评卷人 得分
三、判断题
26.两个圆组成的图形一定是轴对称图形. 【答案】×
()
试卷第 4页,总 10页
27. 比例尺 100:1 表示图上距离是实际距离的 100 倍.(
)
【答案】正确
28. 平角就是一条直线.
【答案】×
29.两个三角形可以拼成一个平行四边形. ( )
【答案】×
30.周长相等的两个圆,它们的面积也一定相等。 ( )
【答案】√
31.
如果你面向东,那么你的左边是南,右边是北.(
六年级数学组合图形试题

六年级数学组合图形试题1.(6分)求如图阴影部分的面积和周长.(单位:厘米)【答案】周长是56.52厘米,面积是10.26平方厘米【解析】如图所示,阴影部分的周长=以6为半径的圆的周长+以6为直径的圆的周长,空白①的面积=空白②的面积=阴影③的面积=阴影④的面积,则阴影部分的面积=以6为半径的圆的面积﹣三角形的面积将数据分别代入等量关系即可求解.解:周长=3.14×6×2÷4+3.14×6=37.68+18.84=56.52(厘米)面积=3.14×62÷4﹣6×6÷2=28.26﹣18=10.26(平方厘米)答:阴影部分的周长是56.52厘米,面积是10.26平方厘米.点评:解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积的和或差求得,阴影部分的周长有哪几段弧组成.2.是长方形内一点,已知的面积是,的面积是,求的面积是多少?【答案】3【解析】由于是长方形,所以,而,所以,则,所以.3.如图,阴影部分四边形的外接图形是边长为的正方形,则阴影部分四边形的面积是.【答案】48【解析】如图所示,分别过阴影四边形的四个顶点作正方形各边的平行线,相交得长方形,易知长方形的面积为平方厘米.从图中可以看出,原图中四个空白三角形的面积之和的2倍,等于、、、四个长方形的面积之和,等于正方形的面积加上长方形的面积,为平方厘米,所以四个空白三角形的面积之和为平方厘米,那么阴影四边形的面积为平方厘米.4.如图,阴影部分四边形的外接图形是边长为厘米的正方形,则阴影部分四边形的面积是多少平方厘米?【答案】68【解析】如图所示,分别过阴影四边形的四个顶点作正方形各边的平行线,相交得长方形,易知长方形的面积为平方厘米.从图中可以看出,原图中四个空白三角形的面积之和的2倍,等于、、、四个长方形的面积之和,等于正方形的面积加上长方形的面积,为平方厘米,所以四个空白三角形的面积之和为平方厘米,那么阴影四边形的面积为平方厘米.5.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.6.如图,四边形中,,,,已知四边形的面积等于4,则四边形的面积是多少?【答案】4/3【解析】运用三角形面积与底和高的关系解题.连接、、、,因为,,所以,在中,,在中,,在中,,在中,.因为,所以.又因为,所以.7.如右图,和都是矩形,的长是厘米,的长是厘米,那么图中阴影部分的面积是多少平方厘米?【答案】6【解析】图中阴影部分的面积等于长方形面积的一半,即(平方厘米).8.在四边形ABCD中,AC和BD互相垂直并相交于O点,四个小三角形的面积如图所示。
小学五年级数学《组合图形》练习题及答案

小学五年级数学《组合图形》练习题及答案
(1)0.45公顷=()平方米。
(2)两个完全一样的梯形可以拼成一个()形。
(3)一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是()平方厘米。
(4)平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是()平方厘米。
(5)梯形的上底增加3厘米,下底减少3厘米,高不变,面积()。
(6)有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有()根。
(1)平行四边形的面积大于梯形面积。
()
(2)梯形的上底下底越长,面积越大。
()
(3)任何一个梯形都可以分成两个等高的三角形。
()
(4)两个形状相同的三角形可以拼成一个平行四边形。
()
1.两个()梯形可以拼成一个长方形。
①等底等高②完全一样③完全一样的直角
2.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,那么腰长()。
①24厘米②12厘米③18厘米④36厘米
1.一条水渠横截面是梯形,渠深0.8米,渠底宽1.2米,渠口宽2米,横截面积是多少平方米?
2.两个同样的梯形,上底长23厘米,下底长27厘米,高20厘米。
如果把这两个梯形拼成一个平行四边形,这个平行四边形的面积是多少?
3.梯形的上底是3.8厘米,高是4厘米,它的面积是20平方厘米,下底是多少厘米?
一、(1)4500(2)平行四边(3)66(4)750(5)不变(6)25
二、(1)×(2)×(3)√(4)√
三、1、③2、①
四、1、0.88平方米2、1000平方厘米3、6.2厘米。
五年级数学上册组合图形面积应用题面积解答题附解析

组合图形面积应用1.计算下面图形中阴影部分的面积。
(单位:厘米)解:25×16-(9+11)×6÷2=25×16-20×6÷2=400-120÷2=400-60=340(平方厘米)答:阴影部分的面积为340平方厘米。
2.求面积是多少?解:[(200-140)+100]×(200-80)÷2+200×140=160×120÷2+28000=9600+28000=37600(平方米)答:面积是37600平方米。
3.计算下图阴影部分的面积。
解:阴影部分的面积=(10+15)×10÷2-10×10÷2 =25×10÷2-100÷2=250÷2-50=125-50=75(平方米)。
4.计算阴影部分的面积。
(单位:cm)解:60×40-60×40÷2=2400-2400÷2=2400-1200=1200(平方厘米)5.求下面组合图形的面积。
(单位:cm)解:8×4+8×4÷2=32+32÷2=32+16=48(平方厘米)6.计算下面阴影部分的面积。
(1)(2)(1)解:阴影部分的面积=14×12÷2=168÷2=84(平方厘米)(2)解:阴影部分的面积=12×10-12×6÷2=120-72÷2=120-36=84(平方分米)(2)阴影部分的面积=平行四边形的面积-三角形的面积,平行四边形的底是20dm,高是10dm;三角形的底是20dm,高是6dm,再根据平行四边形的面积=底×高,三角形的面积=底×高÷2,代入数值计算即可。
7.计算下面图形的面积。
小学五年级数学《组合图形的面积》试题及答案
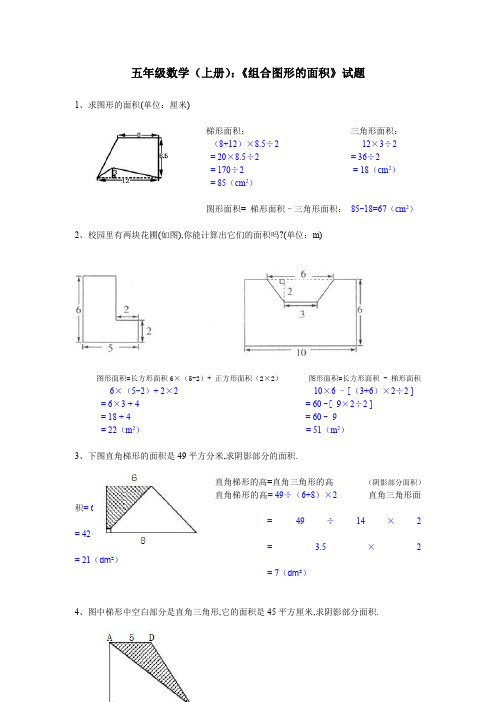
直角梯形的高=直角三角形的高 直角梯形的高= 49÷(6+8)×2 积= 6×7÷2 = = 42÷2 = = 21(dm²) = 7(dm²) 3.5 49 ÷
(阴影部分面中梯形中空白部分是直角三角形,它的面积是 45 平方厘米,求阴影部分面积.
直角梯形的高 = 直角三角形的高 (5+12)×7.5÷2 = 45÷12×2 ×7.5÷2 = 3.75 × 2 127.5÷2 = 7.5 ( cm2 ) 63.75(cm )
五年级数学(上册) : 《组合图形的面积》试题
1、求图形的面积(单位:厘米) 梯形面积: (8+12)×8.5÷2 = 20×8.5÷2 = 170÷2 = 85(cm2) 三角形面积: 12×3÷2 = 36÷2 = 18(cm2)
图形面积= 梯形面积–三角形面积: 85-18=67(cm2) 2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)
2
梯形面积 = = =
阴影部分面积 = 平行四边形面积–梯形面积: 240–210 = 30(cm2) 7、 下图 ABCD 是梯形,它的面积是 140 平方厘米,已知 AB=15 厘米,DC=5 厘米.求阴影部分 的面积.
阴影部分三角形的高=梯形的高 = 140÷(5+15)×2 = 140÷20×2 = 7× 2 = 14(cm) 阴影部分三角形面积= 15×14÷2 = 210÷2 = 105(cm2) 8、求下图阴影部分的面积(单位:厘米) 阴影部分面积 =大三角形面积 + 小三角形 面积 (6×6÷2)+(3×6÷2) =(36÷2)+(18÷2) = 18 + 9 = 27(cm2)
2
梯形面积 × 2 2 =
小学一年级数学形状组合练习题及答案

小学一年级数学形状组合练习题及答案题1:根据下面的图形,回答问题。
A B C D E1 2 3 4 51. 请写下图形A的名字。
2. 请写下图形D的名字和编号。
3. 请写下编号2对应的图形的名字。
4. 请写下编号3对应的图形的编号。
答案:1. A的名字是正方形。
2. D的名字是长方形,编号是4。
3. 编号2对应的图形的名字是圆形。
4. 编号3对应的图形的编号是C。
题2:选择正确的答案。
1. 下面哪个图形是三角形?A. 正方形B. 长方形C. 圆形D. 三角形2. 下面哪个图形没有曲线?A. 圆形B. 五边形C. 矩形D. 波浪形3. 请选择图中的长方形。
(图片中有长方形、正方形、圆形和三角形)答案:1. D. 三角形2. C. 矩形3. 视图自定,选择其中一个长方形。
题3:根据提示,填入图形的名字或编号。
1. 图中所示的图形是一个小正方形,它的编号是___。
2. 图中所示的图形是一个长方形,它的编号是___。
3. 图中所示的图形是一个圆形,它的编号是___。
(图片中有各种形状的图形,并编号为1、2、3等)答案:1. 图中小正方形的编号应根据实际图片填入。
2. 图中长方形的编号应根据实际图片填入。
3. 图中圆形的编号应根据实际图片填入。
题4:选择正确的答案。
1. 下面哪个图形是一个长方形?A. 正方形B. 圆形C. 三角形D. 长方形2. 下面哪个图形没有直线?A. 矩形B. 五边形C. 圆形D. 三角形3. 请写下图中编号为3的图形的名字。
(图片中有各种形状的图形,并编号为1、2、3等)答案:1. D. 长方形2. C. 圆形3. 图中编号为3的图形的名字应根据实际图片填入。
题5:根据提示,填入图形的名字或编号。
1. 图中所示的图形是一个大正方形,它的编号是___。
2. 图中所示的图形是一个长方形,它的编号是___。
3. 图中所示的图形是一个圆形,它的编号是___。
(图片中有各种形状的图形,并编号为1、2、3等)答案:1. 图中大正方形的编号应根据实际图片填入。
六年级数学组合图形的面积试题

六年级数学组合图形的面积试题1.图中正六边形ABCDEF的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.【答案】31【解析】如图,将正六边形ABCDEF等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积,面积,面积,四边形ABQP面积.上述三块面积之和为.因此,阴影四边形CEPQ面积为.2.把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【答案】200【解析】图1中阴影部分占整个三角形面积的,图2中阴影部分占整个三角形面积的,故图2中阴影部分的面积为294÷=200(平方分米).3.如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【答案】48【解析】如图,涂阴影部分的小正六角星形可分成12个与三角形PMN全等(能完全重叠地放在一起)的小三角形.而图中的大正六角星形除去小正六角星形后.有6×4=24个与三角形PMN全等的小三角形,所以大正六角星形的面是小正六角星形的3倍,即48平方厘米.4.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.5.如图,在角的两边上分别有、、及、、六个点,并且、、、、的面积都等于1,则的面积等于多少?【答案】【解析】根据题意可知,,所以,.6.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).7.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.8.如右图所示,在梯形中,、分别是其两腰、的中点,是上的任意一点,已知的面积为,而的面积恰好是梯形面积的,则梯形的面积是().【答案】100【解析】如果可以求出与的面积之和与梯形面积的比,那么就可以知道的面积占梯形面积的多少,从而可以求出梯形的面积.如图,连接、.则,,于是.要求与梯形的面积之比,可以把梯形绕点旋转,变成一个平行四边形.如下图所示:从中容易看出的面积为梯形的面积的一半.(也可以根据,,得来)那么,根据题意可知的面积占梯形面积的,所以梯形的面积是.小结:梯形一条腰的两个端点与另一条腰的中点连接而成的三角形,其面积等于梯形面积的一半,这是一个很有用的结论.本题中,如果知道这一结论,直接采用特殊点法,假设与重合,则的面积占梯形面积的一半,那么与合起来占一半.9.如图,ABCD为平行四边形,EF平行AC,如果ADE的面积为4平方厘米.求三角形CDF的面积.【答案】4【解析】连结AF、CE.∴;;又∵AC与EF平行,∴.∴(平方厘米).10.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.。
北师大版小学五年级数学上册《组合图形的面积》测试试卷及答案

北师大版小学五年级数学上册《组合图形的面积》测试试卷及答案一.选择题(共8小题)1.如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比()A.甲的面积大B.乙的面积大C.相等2.点A是长方形内任意一点,阴影部分的总面积与空白部分总面积比较,哪个的面积较大?A.阴影部分面积大B.空白部分面积大C.一样大D.无法确定3.图中每个小方格的面积是1cm2.请你估计一下,这个脚印的面积约是()A.45B.35C.254.下面图形中涂色部分面积与其它不同的一个是()5.中心广场的占地面积约为5公顷,()个中心广场的面积约为1平方千米.A.2B.20C.2006.丫丫家的面积有110平方分米.她家所在的小区有300平方千米.丫丫最喜欢楼下的游乐场了,它有10公顷那么大呢.这段话里有()处错误.A.1B.2C.37.“6平方千米〇601公顷”,比较大小,在〇里应填的符号是()A.>B.<C.=D.×8.如图:树叶的面积约是()(每个小方格的面积是1cm2)A.15cm2~25cm2B.35cm2~45cm2C.55cm2~65cm2二.填空题(共8小题)9.如图是一个不规则的土地,估测一下,它的面积大约是平方米.10.如图,平行四边形中,阴影部分的面积是36.5dm2,平行四边形的面积是平方分米.11.右图平行四边形的面积是25平方厘米,阴影部分的面积是平方厘米.12.如果1平方米能站9人,那么1公顷能站人,1平方千米能站人.13.260000000平方米=公顷=平方千米800平方千米=公顷=平方米14.如下图所示,平行四边形的面积是28cm2,阴影部分的面积是cm2.15.如图中这片树叶的面积约是cm2.16.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)17.200个50平方米的教室面积是1公顷.(判断对错)18.100个1角的硬币大约重1千克.(判断对错)19.一张床的周长估计是2米.(判断对错)20.计算的面积,只能把它分成一个正方形和一个三角形来计算.(判断对错)21.如图中阴影部分的面积是14平方厘米.(判断对错)四.计算题(共2小题)22.求下面组合图形的面积.(单位:dm)23.如图,阴影部分是两个正方形,周长分别为12厘米和32厘米.求空白部分的总面积是多少平方厘米?五.操作题(共2小题)24.先估计下面图形的面积,再用1平方厘米的正方形学具量一量,填在括号里.25.分割组合图形(不计算):你有哪几种分割方法便于计算其面积,请画出分割示意图.六.应用题(共6小题)26.某街心广场有一块地(如图所示),李叔叔要在这块地上铺满草坪.(1)他需要购买多少平方米草皮?(2)如果每平方米草皮需要68元,请你估计一下,李叔叔要带多少元钱才能一次性把草皮买够?请写出你的估计过程.27.王大伯从平行四边形菜地中划出一块三角形地种西红柿,其余地方种黄瓜(如图),这块黄瓜地的面积是多少平方米?28.一个果园形状如图,一棵果树占地5m2,这个果园一共可以种多少棵树?29.李阿姨家有一块菜地,(如图)这块菜地的面积有多少平方米?30.王村有一块梯形果园,村里进行道路规划时,有一条公路穿过了这个果园.这个果园的实际面积是多少平方米?31.下面三个大正方形的边长都是32厘米,先计算每个正方形中一个小方格的面积,再估计出荷叶的面积.你觉得哪幅图估计得最接近实际面积?参考答案一.选择题(共8小题)1.解:两个阴影三角形的底等于正方形的边长,三角形的高也等于正方形的边长,因此两个三角形等底等高,所以面积相等;故选:C.2.解:阴影部分两个三角形的高等于长方形宽,底等于长方形的长,空白部分两个三角形的高等于长方形的长,底等于长方形的宽,所以阴影部分的面积与空白部分的面积相等。
小学六年级数学总复习题库(组合图形)
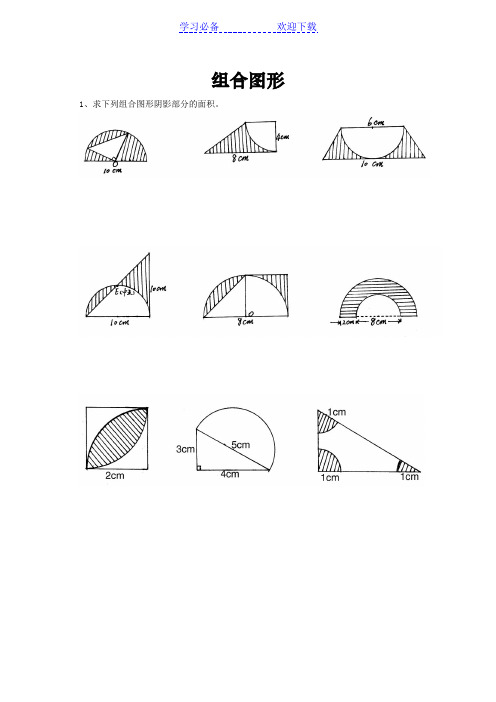
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求
三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
五年级数学上册求组合图形面积应用题面积解答题附解析

组合图形面积应用1.求图中相连的三个正方形内阴影部分的面积(单位:厘米)。
解:15-6-4=5(厘米)(5+4)×5÷2=9×5÷2=22.5(cm2)2.一块近似平行四边形的菜地,中间有一条石子路(如图)。
这块菜地的面积多少平方米?解:20×8-8×1=160-8=152(平方米)答:这块菜地的面积152平方米。
3.本次簕杜鹃花展有许多展台供市民参观,其中一个展台把展区精心布置成一个如下图所示的图形。
这个展台占地面积一共有多少平方米?解:(4+6)×(8-5)÷2+5×4=10×3÷2+5×4=15+20=35(平方米)答:这个展台占地面积一共有35平方米。
4.赵小军在一张平行四边形的硬纸板上剪下了一个三角形(如下图),剩下图形的面积是多少平方分米?解:8×6-(8-3-2)×4÷2=48-3×4÷2=48-6=42(平方分米)答:剩下图形的面积是42平方分米。
5.某农场开辟一块新的菜地(如图),一条水渠穿过这块菜地,若每平方米菜地一年可收入12元,那么这块菜地一年可收入多少元?解:18-3=15(米)23-3=20(米)(15+20)×23÷2×12=402.5×12=4830(元)答:这块菜地一年可收入3360元。
6.学校修建了一个艺术广场(平面图如下),这个艺术广场的占地面积是多少平方米?解:(15+30)×8÷2+30×20=180+600=780(平方米)答:这个艺术广场的占地面积是780平方米。
7.如图是某种植果园基地的示意图。
(1)求这个果园的面积是多少m2?(2)如果每棵果树占地10m2,这个果园共有多少棵果树?(1)解:90×40÷2+90×50=1800+4500=6300(平方米)答:这个果园的面积是6300平方米。
五年级数学(上册)《组合图形的面积》试题及答案.doc

五年级数奥数:《组合图形的面积》梯形而积:(8+12) X8.54-2= 20X8.5 十2=1704-2=85 (cm2)图形面积二梯形面积-三角形面积:85-18=67 (cm2)图形面积=长方形曲积6X (5-2) +正方形面积(2X2) 6X(5-2) +2X2=6X3+4=18 + 4=22 (m2)3、下图直角梯形的面积是49平方分米,求阴影部分的而积。
直角梯形的高二直角三角形的高直角梯形的高=49一(6+8) X2= 494-14X2= 3.5X2=7 (dm2)(阴影部分面积)直角三角形面积=6X7F2= 424-2=21 (dm2) 4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高二直角三角形的高= 45-M2X2= 3.75X2= 7.5 (cm2)梯形面积二(5+12) X7.54-2=17X7.5 一2=127.54-2=63.75 (cm2)阴影部分面积二梯形面积-空白部分面积:63.75 - 45 = 18.75 (cm2)122、校园里有两块花圃(如图), 你能计算出它们的面积吗?(单位:m)101、求图形的面积(单位:厘米)三角形而积:12X34-2= 364-2=18 (cm2)图形面枳二长方形面积-梯形面枳10X6 - [ (3+6) X24-2]=60-[ 9X2H-2]= 60-9=51 (m2)梯形面积二(6+10) X84-2=16X84-2 =1284-2 =64 (m 2)6、如图,平行四边形面积24()平方厘米,求阴影部分面积。
梯形的下底二平行四边形的底= 2404-12=20 (cm)梯形面积二(15+20) XI24-2= 35X12 — 2 = 4204-2 = 210 (cm 2)阴影部分面积二平行四边形面积-梯形面积:240-210 = 30 (cm 2)7、下图ABCD 是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
人教版小学数学组合图形的面积 (经典例题含答案)

班级小组姓名成绩(满分120)一、组合图形的面积(一)组合图形的面积计算(共4小题,每题3分,共计12分)例1.求下面图形的面积。
(单位:cm)32×10÷2+32×203×4÷2+(5+10)×5÷210×12-(4+8)×2÷2=160+640=6+37.5=120-12=800(cm²)=43.5(cm²)=108(cm²)例1.变式1.先回答问题,再计算图形的面积。
(单位:cm)(1)组合图形的面积=(长方形)面积+(三角形)面积36×24+24×21÷2=1116(平方厘米)(2)52阴影部分的面积=(梯形)面积-(三角形)面积(30+52)×28÷2-30×28÷2=728(cm²)例1.变式2.计算下面图形的面积,你能用不同的计算方法吗?5×2.5+(3+5)×(5-2.5)÷2=5×2.5+8×2.5÷2=12.5+10=22.5(平方米)5×3+(2.5+5)×(5-3)÷2=5×3+7.5×2÷2=15+7.5=22.5(平方米)例1.变式3.如图,左边阴影部分的面积是60平方厘米。
求右边空白部分(梯形)的面积。
(单位:厘米)60×2÷8=15(厘米)(16+16+8)×15÷2=40×15÷2=300(平方厘米)答:空白部分的面积是300平方厘米.(二)组合图形的面积计算(共4小题,每题3分,共计12分)例2.计算下列组合图形的面积。
(单位:cm)(8.5+15)×13÷2-8.5×4÷2=135.75(cm²)例2.变式1.解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题
1.如图,阴影部分的面积是.
2 1 2
2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.
3.在一个半径是
4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)
4.右图中三角形是等腰直角三角形,阴影部分的面
积是 (平方厘米).
5.如图所求,圆的周长是1
6.4厘米,圆的
面积与长方形的面积正好相等.图中阴影部分
π
的周长是厘米.)
14
.3
(=
6.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形
π,那么花瓣图形的面积(如图).图中黑点是这些圆的圆心.如果圆周率1416
.3
=
是平方厘米.
7.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是.
8.图中,扇形BAC 的面积是半圆ADB 的面积的3
11倍,那么,CAB 是度.
9.
10.右图是一个直角等腰三角形,直角边长2
厘米,图中阴影部分面积是 平方厘米
11一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是.
12.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)
13.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28
.
2平方厘米,等腰直角三角形的面积为.
,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.
16.图中扇形的半径OA =OB =6厘米.45=∠AOB ,AC 垂直OB 于C ,那么图中阴影部分的面积是平方厘米.)14.3(=π
17.右图中正方形周长是20厘米.图形的总面积是平方厘米.
45
18.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.
二、解答题
11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(圆周率取722)
12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.
答案
1. 6.
2. 188.4
3. 57
4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积
之差,即26.1062
1)26(14.322=⨯-÷⨯(平方厘米). 5. 20.56. 19.1416. 7. 2.43平方厘米
.
将①移到②得:阴影部分面积等于梯形CEFB 的
面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即
8. 60. 设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有
222
1311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 9. 18平方厘米.
由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成..
10 1.14平方厘米.
由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12
122236045214.32=⨯⨯-⨯⨯⨯(平方厘米). 11. 125.6平方厘米.
12 3.09厘米. 09.312045.1=+⨯(厘米).
13 32.8厘米. 半圆面积为6282
124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米). 14. 13
937平方厘米. 将等腰直角三角形补成一个正方形,图中阴影部分面积是正方形与圆的面积之差的8
1 15 7
2 16 5.13.
三角形ACO 是一个等腰直角三角形,AO 看作底边,AO 边上的高为 3
17. 142.75. 总面积为两个4
3圆面积加上正方形的面积 18. 90平方厘米.
图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即
解答1 2227
224172241r r r =⨯⨯-⨯⨯ 2. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘
⌒
⌒。
