小学四年级奥数专项练习 02 找规律(二)
小学奥数5-2-2 数的整除之四大判断法综合运用(二).专项练习及答案解析

1. 了解整除的性质;2. 运用整除的性质解题;3. 整除性质的综合运用.一、常见数字的整除判定方法1. 一个数的末位能被2或5整除,这个数就能被2或5整除;一个数的末两位能被4或25整除,这个数就能被4或25整除;一个数的末三位能被8或125整除,这个数就能被8或125整除;2. 一个位数数字和能被3整除,这个数就能被3整除;一个数各位数数字和能被9整除,这个数就能被9整除;3. 如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除,那么这个数能被11整除.4. 如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除,那么这个数能被7、11或13整除.5.如果一个数能被99整除,这个数从后两位开始两位一截所得的所有数(如果有偶数位则拆出的数都有两个数字,如果是奇数位则拆出的数中若干个有两个数字还有一个是一位数)的和是99的倍数,这个数一定是99的倍数。
【备注】(以上规律仅在十进制数中成立.)二、整除性质性质1 如果数a 和数b 都能被数c 整除,那么它们的和或差也能被c 整除.即如果c ︱a ,c ︱b ,那么c ︱(a ±b ).知识点拨教学目标5-2-2.数的整除之四大判断法综合运用(二)性质2 如果数a能被数b整除,b又能被数c整除,那么a也能被c整除.即如果b∣a,c∣b,那么c∣a.用同样的方法,我们还可以得出:性质3如果数a能被数b与数c的积整除,那么a也能被b或c整除.即如果bc∣a,那么b∣a,c∣a.性质4如果数a能被数b整除,也能被数c整除,且数b和数c互质,那么a一定能被b与c的乘积整除.即如果b∣a,c∣a,且(b,c)=1,那么bc∣a.例如:如果3∣12,4∣12,且(3,4)=1,那么(3×4) ∣12.性质5 如果数a能被数b整除,那么am也能被bm整除.如果b|a,那么bm|am(m 为非0整数);性质6如果数a能被数b整除,且数c能被数d整除,那么ac也能被bd整除.如果b|a,且d|c,那么bd|ac;例题精讲模块一、11系列【例 1】以多位数142857为例,说明被11整除的另一规律就是看奇数位数字之和与偶数位数字之和的差能否被11整除.【考点】整除之11系列【难度】2星【题型】解答【解析】略【答案】142857110000041000021000810051071=⨯+⨯+⨯+⨯+⨯+⨯()()()()()110000114199992100118199511171=⨯-+⨯++⨯-+⨯++⨯-+⨯()()=⨯+⨯+⨯+⨯+⨯+-+-+-11000014999921001899511418275因为根据整除性质1和铺垫知,等式右边第一个括号内的数能被11整除,再根据整除性质1,要判断142857能否被11整除,只需判断418275487125()()能-+-+-=++-++否被11整除,因此结论得到说明.【例 2】试说明一个4位数,原序数与反序数的和一定是11的倍数(如:1236为原序数,那么它对应的反序数为6321,它们的和7557是11的倍数.【考点】整除之11系列 【难度】2星 【题型】解答【解析】 略 【答案】设原序数为abcd ,则反序数为dcba ,则abcd +dcba 100010010100010010a b c d d c b a =+++++++()()10011101101001a b c d =+++1191101091a b c d =+++(),因为等式的右边能被11整除,所以abcd + dcba 能被11整除【例 3】 一个4位数,把它的千位数字移到右端构成一个新的4位数.已知这两个4位数的和是以下5个数的一个:①9865;②9866;③9867;④9868;⑤9869.这两个4位数的和到底是多少?【考点】整除之11系列 【难度】2星 【题型】解答【解析】 设这个4位数是abcd ,则新的4位数是bcda .两个数的和为1001110011011abcd bcda a b c d +=+++,是11的倍数.在所给的5个数中只有9867是11的倍数,故正确的答案为9867.【答案】9867模块二、7、11、13系列【例 4】 以多位数142857314275为例,说明被7、11、13整除的规律.【考点】整除之7、11、13系列 【难度】3星 【题型】解答【解析】 略【答案】142857314275142100000000085710000003141000275=⨯+⨯+⨯+142(10000000011)857(9999991)314(10011)275=⨯-+⨯++⨯-+ 14210000000011428579999998573141001314275=⨯-+⨯++⨯-+ (14210000000018579999993141001)(857142275314)=⨯+⨯+⨯+-+- 因为根据整除性质1和铺垫知,等式右边第一个括号内的数能被7、11、13整除,再根据整除性质1,要判断142857314275能否被7、11、13整除,只需判断857142275314-+-能否被7、11、13整除,因此结论得到说明.【例 5】 已知道六位数20279□是13的倍数,求□中的数字是几?【考点】整除之7、11、13系列 【难度】2星 【题型】填空【解析】 根据一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除,那么这个数能被7、11或13整除的特点知道:27920=7-□□,7□是13的倍数,□是8的时候是13倍数,所以知道方格中填1。
小学奥数4-1-2 图形找规律.专项练习及答案解析(精品)

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化;⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律 【难度】1星 【题型】填空【解析】 几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律 【难度】1星 【题型】填空 【解析】 这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样 【答案】(4)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律 【难度】2星 【题型】填空 【解析】 观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:例题精讲知识点拨4-1-2.图形找规律【答案】【例4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
小学四年级数学奥数《找规律》专项练习题及答案

1.难度:★★★★
30粒珠⼦依8粒红⾊、2粒⿊⾊、8粒红⾊、2粒⿊⾊、……的次序串成⼀圈.⼀只蚱蜢从第2粒⿊珠⼦起跳,每次跳过6粒珠⼦落在下⼀粒珠⼦上.这只蚱蜢⾄少要跳⼏次才能再次落在⿊珠⼦上.
2.难度:★★★★
在1989后⾯写⼀串数字.从第5个数字开始,每个数字都是它前⾯两个数字乘积的个位数字.这样得到1989286884 这串数字中,前2008个数字的和是__________.
【答案】
1.难度:★★★★
30粒珠⼦依8粒红⾊、2粒⿊⾊、8粒红⾊、2粒⿊⾊、……的次序串成⼀圈.⼀只蚱蜢从第2粒⿊珠⼦起跳,每次跳过6粒珠⼦落在下⼀粒珠⼦上.这只蚱蜢⾄少要跳⼏次才能再次落在⿊珠⼦上.
【解答】这些珠⼦按8粒红⾊、2粒⿊⾊、8粒红⾊、2粒⿊⾊、的次序串成⼀圈,那么每10粒珠⼦⼀个周期,我们可以推断出这30粒珠⼦数到第9和10、19和20、29和30、39和40、49和50粒的时候,会是⿊珠⼦.刚才是从第10粒珠⼦开始跳,中间隔6粒,跳到第17粒,接下来是第24粒、31粒、38粒、45粒、52粒、59粒,⼀直跳到59 粒的时候会是⿊珠⼦,所以⾄少要跳7次.
2.难度:★★★★
在1989后⾯写⼀串数字.从第5个数字开始,每个数字都是它前⾯两个数字乘积的个位数字.这样得到1989286884 这串数字中,前2008个数字的和是__________.。
最新小学四年级奥数找规律二学习资料

(2)
例3:先计算下面一组算式的第一题,然后找出其 中的规律,并根据规律直接写出后几题的得数。 12345679×9= 12345679×18=12345679×54= 12345679×81=
题中每个算式的第一个因数都是12345679,它是有趣 的“缺8数”,与9相乘,结果是由九个1组成的九位 数,即:111111111。不难发现,这组题得数的规律 是:只要看每道算式的第二个因数中包含几个9,乘 积中就包含几个111111111。 因为:12345679×9=111111111 所以:12345679×18=12345679×9×2=222222222 12345679×54=12345679×9×6=666666666 12345679×81=12345679×9×9=999999999.
练习4:练习4: 1.利用规律计算。 (1)53-35 (2)82-28 (3)92-29 (4)61-16 (5)95-59 2.找规律计算。 (1) 62+26=(6+2)×11=8×11=88 (2) 87+78=(8+7)×11=15×11=165 (3) 54+45=(□+□)×11=□×11=□
(2)32×11 (4)46×11 (6)98×11
一、要细心观察题目中数字的特征。 二、要灵活运用整数的有关知识和加、 减、乘、除的计算法则。 三、要对数字之间的关系进行合理的 推想,分析已知数据与未知数据的联 系,从中发现规律,解决问题。 四、规律要适合所有的数,不能只看 前几个数。
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好! 谢谢!
例4:找规律计算。 (1) 81-18=(8-1)×9=7×9=63 (2) 72—27=(7-2)×9=5×9=45 (3) 63-36=(□-□)×9=□×9=□
四年级上册奥数第2讲 寻找规律(二)

第2讲:寻找规律(二)专题简析:对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:1、对于几列数组成的一组数的变化规律的分析,需要我们灵活思考。
没有一成不变的方法,优势需要综合运用其他知识,如果一种方法不行,就要及时调整思路,换另一种方法再分析。
2、对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关,这是我们解这类题的突破口。
3、对于找到的规律,应该适合这组数中的所有数或这组算式中的所有算式。
【例题1】根据下表中的排列规律,在空格里填上适当的数。
【习题一】找规律,在空格里填上适合的数。
【例题2】根据前面两个图形中数之间的关系,想一想第三个图形的括号里应填什么数?【习题二】根据前面两个图形中数之间的关系,想一想第三个图形的括号里应填什么数?12 18 68 15 74 89 16 716 21 54 98 17 510 11 912 164 11 96 247 35 30【例题3】先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几道题的得数。
12345679×9= 12345679×18=12345679×54= 12345679×81=【习题3】找规律,写得数。
(1)1+0×9= 2+1×9= 3+12×9= 4+123×9= 9+12345678×9=(2)1×1= 11×11= 111×111= 111…1×111…1=9个1 9个1(3) 19+9×9= 118+98×9= 1117+987×9=11116+9876×9= 111115+98765×9=【例题4】找规律,并计算。
(1)81-18=(8-1)×9=7×9=63(2)72-27=(7-2)×9=5×9=45(3)63-36=(□-□)×9=□×9=□【习题4】1、找规律,并计算。
四年级奥数找规律(二)

找规律(二)一、【检查作业与评讲】二、【课前热身】1、找出下面各组数排列的规律,在括号里填上适当的数。
(1)1,2,4,8,(),()(2)1,2,2,3,3,4,5,5,(),()(3)1,2,4,7,11,(),(),29(4)0,1,3,12,45,171,(),2457(5)100,102,106,112,120,(),142,156(6)10,30,90,270,(),2430,7290(7)3,6,4,7,5,8,(),9,7(8)999,994,989,984,(),974,9692、{1,5,10} ,{2,10,20},{3,15,30} , { },{ };(1)1,11,22,34,47,().(2)1,3,9,27,81,().(3)81,64,49,36,(),16,9.三、【内容讲解】知识点:找规律1、对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法在分析。
例题1:根据下表中的排列规律,在空格里填上适当的数。
12 18 68 15 74 8【分析】经仔细观察、分析表格中的数可以发现:12+6=18,8+7=15,即每一横行中间的数等于两边的两个数的和。
练习:(1)(2)(3) (4)(3)如图在七色球下面,按照图示的规律,依次逐个写自然数。
问:2008在什么颜色的 球下面?○赤 ○黄 ○橙 ○绿 ○青 ○蓝 ○紫 1 2 3 4 5 6 7 13 12 11 10 9 8 14 15 16 17 18 19 25 24 23 22 21 202627…………2、对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在 图形中的特殊位置有关,这是我们解这类题的突破口。
例题2:根据前面两个圈里三个数的关系,在第三个圈里的( )里填上适当的数。
【分析】 经认真观察、分析可以发现前面两个圈中三个数之间有着样的关系:5×12=60,60÷10=6 ;4×20=80,80÷10=8.练习:根据前面两个圈里三个数的关系,在第三个圈里的( )里填上适当的数。
小学四年级奥数思维训练《找规律》

40第1讲找规律一、知识要点按照一定的顺序排列的一串数叫做数列。
观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3.【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
1,2,4,7,(),16,22练习2:先找出下列数排列的规律,然后在括号里填上适当的数。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2 (4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2(8)1,6,4,8,7,10,(),(),13,14 【例题3】先找出规律,然后在括号里填上适当的数。
23,4,20,6,17,8,(),(),11,12 练习3:先找出规律,然后在括号里填上适当的数。
小学奥数4-1-2 图形找规律.专项练习及答案解析
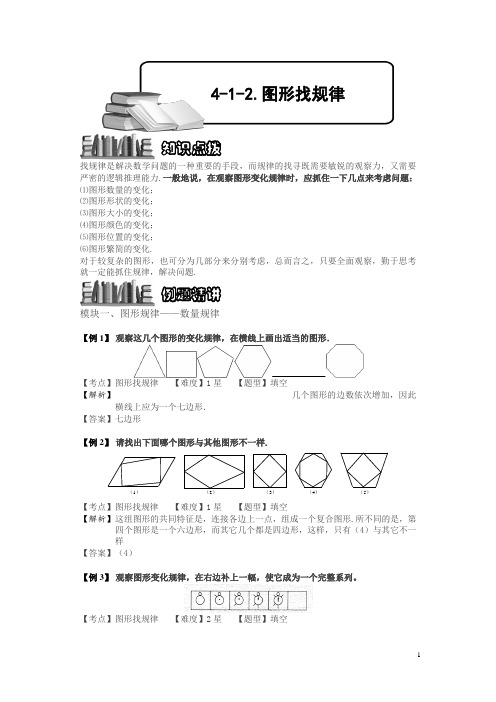
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律【难度】1星【题型】填空【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律【难度】2星【题型】填空例题精讲知识点拨4-1-2.图形找规律【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【答案】【例4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△. (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
小学奥数举一反三四年级 第2讲 找规律(二)

小学奥数【四年级】
2. 找规律,并计算。 (1) 62+26=(6+2)×11=8×11=88 (2) 87+78=(8+7)×11=15×11=165 (3) 54+45=(□+□)×11=□×11=□
第 2 讲 找 规 律 (二)
例 5 计算下面各题,你发现了什么规律?
(1)18×11=
(2)38×11=
(3)432×11=
练习 5:
用你发现的规律Hale Waihona Puke 算下面各题。(1)27×11=
(2)32×11=
(3)39×11=
(4)46×11=
(5)92×11=
(6)98×11=
(7)159×11=
(8)246×11=
想一想:这种算法的道理是什么?
小学奥数【四年级】
第 2讲
第 2 讲 找 规 律 (二)
找规律(二)
【专题简析】 对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考: 1. 对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方
法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析; 2. 对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位
例 4 找规律,并计算。 (1) 81-18=(8-1)×9=7×9=63 (2) 72—27=(7-2)×9=5×9=45 (3) 63-36=(□-□)×9=□×9=□
练习 4: 1. 找规律,并计算。
(1)53-35= (4)61-16=
(2)82-28= (5)95-59=
(3)92-29=
练习 2: 根据前面图形中数之间的关系,想一想第三个图形的空白处应填什么数?
四年级奥数(寻找规律)

四年级奥数寻找规律按照一定次序排列起来的一列数,叫做数列。
如自然数列:1,2,,4,……双数列:2,4,6,8,……我们研究数列,目的就是为了发现数列中数排列的规律,并依据这个规律来填写空缺的数。
观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:1.对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析;2.对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关,这是我们解这类题的突破口。
3.对于找到的规律,应该适合这组数中的所有数或这组算式中的所有算式。
考点一:发现数列规律例1、填上合适的数。
(1)3,6,9,12,(),()(2)1,2,4,7,11,(),()(3)2,6,18,54,(),()【解析】(1)前一个数加上3就等于后一个数,也就是相邻两个数的差都是3.根据这一规律,可以后推知括号里填15和18.(2)第一个数增加1等于第二个数,第二个数增加2等于第三个数,也就是每相邻两个数的差依次是1,2,3,4....,这样下一个数应比11大5,填16;再下一个数应比16大6,填22.(3)后一个数是前一个数的3倍,162和486例2、找出规律,再在括号里填上合适的数。
(1)15,2,12,2,9,2,(),()(2)21,4,18,5,15,6,(),()(3)3,4,7,3,4,10 , 3 , 4 ,13,(),()(4)187,286,385,(),()【解析】(1)第一个数减3是第三个数,第三个数减3是第5个数,第二、第四、第六个数不变。
小学奥数4-1-2 图形找规律.专项练习(精品)
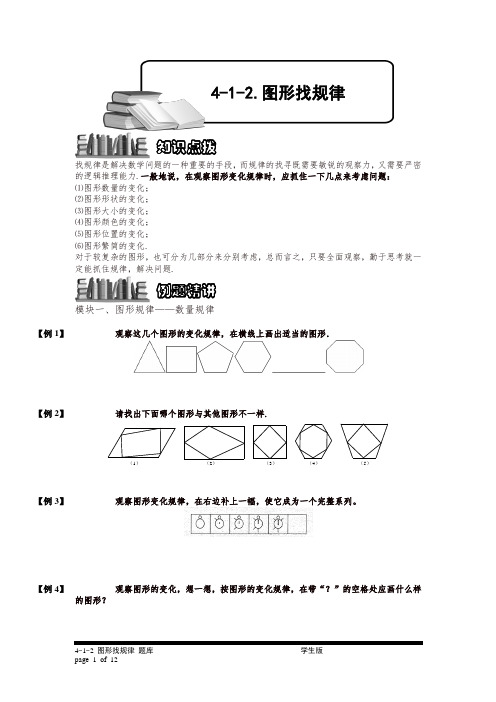
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化;⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】观察这几个图形的变化规律,在横线上画出适当的图形.【例2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?例题精讲知识点拨4-1-2.图形找规律【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例 5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【例 6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例 7】观察下图中的点群,请回答:(1) 方框内的点群包含 个点;(2)推测第10个点群中包含 个点;(3)前10个点群中,所有点的总数是。
【例8】观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含个点;(2)第(10)个点群中包含个点;(3)前十个点群中,所有点的总数是。
【例9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?(2)整个五层“宝塔”一共包含多少个小三角形?【例10】在纸上画5条直线,最多可有个交点。
模块二、图形规律——旋转、轮换型规律【例11】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【例12】下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)(2)(3)【例 13】观察下图的变化规律,画出丙图.甲D A乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成,记为A ★B 、C★D 、A ★D .请你画出表示A ★C 的图形.A ★BC ★DA ★D【例 15】 (希望杯五年级一试第7题,6分)下列四个图形是由四个简单图形A 、B 、C 、D (线段和正方形)组合(记为*)而成。
小学四年级奥数练习题及答案10篇

小学四年级奥数练习题及答案10篇1.小学四年级奥数练习题及答案篇一1、一头象的重量等于4头牛的重量,一头牛的重量等于3匹小马的重量,一匹小马的重量等于3头小猪的重量。
问:一头象的重量等于几头小猪的重量?答案:4×3×3=36,所以一头象的重量等于36头小猪的重量。
2、甲、乙、丙三人,一个人喜欢看足球,一个人喜欢看拳击,一个人喜欢看篮球。
已知甲不爱看篮球,丙既不喜欢看篮球又不喜欢看足球。
现有足球、拳击、篮球比赛的入场券各一张。
请根据他们的爱好,把票分给他们。
答案:丙不喜欢看篮球与足球,应将拳击入场券给丙。
甲不喜欢看篮球,应将足球入场券给甲。
最后,应将篮球入场券给乙。
2.小学四年级奥数练习题及答案篇二1、甲、乙、丙三人年龄之和是94岁,且甲的2倍比丙多5岁,乙2倍比丙多1 9岁,问:甲、乙、丙三人各多大?答案:如果每个人的年龄都扩大到2倍,那么三人年龄的和是94×2=188。
如果甲再减少5岁,乙再减少19岁,那么三人的年龄的和是188-5-19=164(岁),这时甲的年龄是丙的一半,即丙的年龄是甲的两倍。
同样,这时丙的年龄也是乙两倍。
所以这时甲、乙的年龄都是164÷(1+1+2)=41(岁),即原来丙的年龄是41岁。
甲原来的年龄是(41+5)÷2=23(岁),乙原来的年龄是(41+19)÷2 =30(岁)。
2、小明、小华捉完鱼。
小明说:“如果你把你捉的鱼给我1条,我的鱼就是你的2倍。
如果我给你1条,咱们就一样多了。
“请算出两个各捉了多少条鱼。
答案:小明比小华多1×2=2(条)。
如果小华给小明1条鱼,那么小明比小华多2+1×2=4(条),这时小华有鱼4÷(2-1)=4(条)。
原来小华有鱼4+1=5(条),原来小明有鱼5+2=7(条)。
3.小学四年级奥数练习题及答案篇三1、把1296分为甲、乙、丙、丁四个数,如果甲数加上2,乙数减去2,丙数乘以2,丁数除以2,则四个数相等。
小学奥数4-1-2 图形找规律.专项练习及答案解析

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律【难度】1星【题型】填空【解析】几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例2】请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律【难度】1星【题型】填空例题精讲知识点拨4-1-2.图形找规律【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律【难度】2星【题型】填空【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【答案】【例4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△. (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形. 【答案】七个黑三角形【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题2 找规律(二)
【理论基础】
对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:
1.对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析;
2.对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关,这是我们解这类题的突破口。
3.对于找到的规律,应该适合这组数中的所有数或这组算式中的所有算式。
【经典题型1】
根据下表中的排列规律,在空格里填上适当的数。
分析:12+6=18,8+7=15.即每一横行中间的数等于两边的两个数的和。
依此规律,空格中应填的数为:4+8=12。
练习一:找规律,在空格里填上适当的数。
【经典题型2】
根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?
12
6
5
208
4 308
分析:经仔细观察、分析可以发现前面两个圈中三个数之间有
这样的关系:
5×12÷10=6 4×20÷10=8
根据这一规律,第三个圈中右下角应填的数为:8×30÷10=24
练习二:根据前面图形中数之间的关系,想一想第三个图形的空格里应填什么数。
(1)9
6
3 30
125 310
(2)
4
5
911 4
5
97 3
813
(3)
12
369 16
4812 15
先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
12345679×9= 12345679×18=
12345679×54= 12345679×81=
分析:题中每个算式的第一个因数都是12345679,它是有趣的“缺8数”,与9相乘,结果是由九个1组成的九位数,即:111111111。
不难发现,这组题得数的规律是:只要看每道算式的第二个因数中包含几个9,乘积中就包含几个111111111。
因为:12345679×9=111111111
所以:12345679×18=12345679×9×2=222222222
12345679×54=12345679×9×6=666666666
12345679×81=12345679×9×9=999999999
练习三:找规律,写得数。
(1)1+0×9= 2+1×9= 3+12×9=
4+123×9= 9+12345678×9=
(2)1×1= 11×11= 111×111=
111111111×111111111=
(3)19+9×9= 118+98×9= 1117+987×9=
11116+9876×9= 111115+98765×9=
找规律计算。
(1)81-18=(8-1)×9=7×9=63
(2)72—27=(7-2)×9=5×9=45
(3)63-36=(□-□)×9=□×9=□
分析:经仔细观察、分析可以发现:一个两位数与交换它的十位、个位数字位置后的两位数相减,只要用十位与个位数字的差乘9,所得的积就是这两个数的差。
练习四:
一.利用规律计算。
(1)53-35 (2)82-28 (3)92-29
(4)61-16 (5)95-59
二.找规律计算。
(1)62+26=(6+2)×11=8×11=88
(2)87+78=(8+7)×11=15×11=165
(3)54+45=(□+□)×11=□×11=□
【经典题型5】
计算
(1)26×11 (2)38×11
分析:一个两位数与11相乘,只要把这个两位数的两个数字的和插入这两个数字中间,就是所求的积。
(1)26×11=2(2+6)6=286
(2)38×11=3(3+8)8=418
注意:如果两个数字的和满十,要向前一位进一。
练习五:计算下面各题。
(1)27×11 (2)32×11
(3)39×11 (4)46×11
(5)92×11 (6)98×11。
