极点零点

合集下载

零点与极点的关系PPT课件

零点与极点的相互影响
零点对极点的影响
在函数图像上，零点是函数值为0的点，而极点是函数值无穷大的点，因此零点的位置会影响极点的位置。
极点对零点的影响
极点的位置也会影响零点的位置，因为函数值在极点附近会变得非常大或非常小，从而影响函数的零点。
零点与极点的性质比较
01
零点的性质
零点是函数值为0的点，是函数图像与x轴的交点。
2023
PART 05
总结与展望
REPORTING
零点与极点的重要性和意义
零点与极点在数学、物理和工程领域中具有广泛的应用，是解决复杂问题的关键。零点与极点的概念和性质在数学分析、复变函数、信号处理等领域中占有重要地位。
零点和极点的分析有助于深入理解函数的性质、系统的稳定性和信号的传播等。
未来研究方向和展望
02
极点的性质
极点是函数值无穷大的点，是函数图像上凹凸性改变的点。
03
零点和极点的关系
在函数图像上，零点和极点可以重合，也可以不重合。如果重合，则该
点既是函数的零点也是函数的极点；如果不重合，则该点只可能是零点
或只可能是极点。
2023
PART 03
零点与极点的应用
REPORTING
在信号处理中的应用
2023
PART 04
零点与极点的实际案例
REPORTING
信号处理中的零点与极点案例
总结词
信号处理中的零点与极点案例展示了零点与极点在信号处理中的实际应用和影响。
详细描述
在信号处理中，零点和极点是影响信号频域特性的重要因素。零点可以改变信号的相位，而极点则影响信号的幅度。通过在信号处理过程中合理地设计零点和极点，可以实现信号的滤波、均衡、调制和解调等操作，从而提高信号的质量和性能。

rc电路零点和极点

rc电路零点和极点RC电路是由电阻（R）和电容（C）组成的电路。

在RC电路中，零点和极点是两个重要的概念。

本文将着重介绍RC电路的零点和极点，探讨它们的含义和作用。

我们来了解一下RC电路的基本原理。

RC电路是一种能够存储和释放电能的电路。

当电压施加在电容上时，电容器会充电或放电，从而改变电路中的电流和电压。

而电阻则起到限制电流的作用，控制电路的稳定性。

在RC电路中，零点是指电路的传输函数（Transfer Function）的根之一。

传输函数描述了输入信号与输出信号之间的关系。

零点是使得传输函数等于零的特定频率或复数。

在RC电路中，零点通常是由电容器的充电和放电导致的。

当电容器充电时，电流通过电阻，导致传输函数等于零。

因此，零点可以用来分析电路的频率响应和稳定性。

极点是另一个重要的概念，它也是传输函数的根之一。

极点是使得传输函数无穷大的特定频率或复数。

在RC电路中，极点主要由电容器和电阻的相互作用引起。

当电容器放电时，电流通过电阻，导致传输函数无穷大。

因此，极点可以用来分析电路的频率响应和稳定性。

零点和极点对RC电路的性能和特性有着重要影响。

首先，它们可以帮助我们理解电路的频率响应。

通过分析传输函数的零点和极点，我们可以确定电路对不同频率的输入信号的响应情况。

例如，当传输函数的零点在某个频率附近时，电路对该频率的信号的响应将较强。

相反，当传输函数的极点在某个频率附近时，电路对该频率的信号的响应将较弱。

零点和极点还可以用来评估电路的稳定性。

在RC电路中，传输函数的极点决定了电路的稳定性。

当极点位于虚轴的左侧时，电路是稳定的。

反之，当极点位于虚轴的右侧时，电路是不稳定的。

因此，通过分析传输函数的极点，我们可以确定电路的稳定性，并采取相应的措施来保证电路的正常运行。

除了对RC电路的性能和稳定性有影响外，零点和极点还可以用来设计和优化电路。

通过调整电容器和电阻的数值，我们可以改变传输函数的零点和极点的位置，从而优化电路的性能。

滤波器零点极点和单位圆

滤波器零点极点和单位圆1.引言1.1 概述在滤波器设计和信号处理领域中，零点和极点是非常重要的概念。

它们是描述滤波器频率响应和滤波器性能的关键参数。

零点和极点的分布直接影响着滤波器的幅频特性、相频特性以及相位延迟等方面的表现。

因此，深入理解和掌握零点和极点的定义、特点以及对滤波器性能的影响非常重要。

零点，顾名思义，是指滤波器的频率响应函数在某些频率上为零的点。

也就是说，当信号的频率达到零点时，滤波器不对该频率的信号进行响应，从而实现了信号的抑制或者消除。

零点可以在复平面上表示为一个点，其位置和数量多样化。

不同的零点分布方式将产生不同的滤波器特性。

与零点相对的是极点，极点指的是滤波器的频率响应函数在某些频率上发散的点。

极点是滤波器最重要的特性之一，它们决定了滤波器的幅频特性、相频特性以及相位延迟等。

极点可以分布在复平面的任意位置，并且可以是实数或者复数。

在本文中，我们将重点讨论单位圆在滤波器中的应用。

单位圆是代表单位频率的一个圆，它在复平面上的位置为半径为1的圆周。

单位圆的内部和外部分别代表了滤波器对低频和高频信号的响应。

单位圆上的点将直接决定了滤波器的频率响应，因此对于滤波器的设计和性能评估来说，单位圆是一个关键参考标准。

最后，我们还将探讨零点和极点对于滤波器性能的影响。

零点和极点的位置、数量以及分布方式将直接影响滤波器的频率响应特性。

通过合理的选取和调整零点和极点，可以实现不同的滤波器响应，如低通、高通、带通和带阻等。

因此，深入理解和掌握零点和极点对滤波器性能的影响将对滤波器设计和应用产生重要的指导作用。

在接下来的章节中，我们将详细阐述滤波器概念和作用，零点和极点的定义和特点，以及单位圆在滤波器中的应用。

我们还将通过具体的案例和实例，展示零点和极点对滤波器性能的影响。

这将有助于读者更好地理解和应用滤波器零点极点理论。

1.2文章结构文章结构部分的内容应该包括对整篇文章的组织和结构进行介绍。

以下是一个参考的内容：文章结构：本文主要分为引言、正文和结论三个部分。

传递函数极点和零点的意义

传递函数极点和零点的意义在探讨传递函数极点和零点的意义前，我们首先需要了解什么是传递函数。

传递函数，又称为系统函数，是描述线性时不变系统输入与输出之间关系的函数。

它是系统理论中的一个重要概念，用于研究信号在系统中的传输规律及其影响。

接下来，我们分别来讨论传递函数中的“极点”和“零点”，并探讨它们在工程上的应用。

一、极点极点，也叫阻尼点或“瞬态谐振点”，指的是传递函数分母中的因式，当其为0时，会使得系统响应变得不稳定或发生异常波动，被称为系统的“瓶颈”。

在控制系统中，极点是非常重要的参数，通过极点的位置，我们可以决定系统的稳定性、调节速度和峰值响应等性能指标。

通常情况下，我们希望系统的极点位于左半s平面内，这样可以保证系统稳定可控，并减小系统响应时的震荡和延迟。

另一方面，如果出现极点位于右半s平面内的情况，则应采取积极措施通过控制参数等手段移动其位置或者消除其影响，以保证系统的稳定性和性能。

二、零点零点，指的是传递函数分子中的因式，当其为0时，输出为0。

也就是说，当输入信号经过传递函数时，处于零点位置的频率分量成分不会引起系统响应。

在控制系统中，零点的位置对系统的动态特性和频率特性有着直接的影响。

比如，在控制系统的设计中，通过精心调节零点的位置，可以有效提高系统对不同频率信号的响应速度和灵敏度，这对于高速、高精度的控制系统是非常重要的。

另外，零点还可以调节系统的截止频率和幅频特性等性能指标，通过有效地调节零点的位置，可以优化系统的控制性能，提高系统的鲁棒性和减小系统的灵敏度。

总之，在掌握传递函数极点和零点的意义之后，我们能更深刻地理解和反映控制系统性能。

在实际工程中，要合理分析和设计传递函数的极点和零点，以实现系统的优化和提高。

电路的零点和极点

电路的零点和极点哎呀，说起电路的零点和极点，我得先承认，这玩意儿听起来可真不像是能让人兴奋的话题。

但是，你可别小瞧了它们，这俩家伙在电路设计里头，那可真是大有来头。

记得有一次，我在实验室里头，正忙着调试一个电路板。

那电路板可真不是盖的，密密麻麻的线路，看得我眼睛都花了。

我得找到那个零点，就是电路里头那个让输出变得一丁点儿都没有的点。

你想想，这电路板要是没有零点，那不就跟个没关的水龙头一样，电能哗哗地流，浪费得可就大了。

我拿着万用表，这里戳戳，那里点点，就像是在玩一个高级版的“点点点”游戏。

但是，这游戏可不好玩，因为一旦找错了点，那电路板可能就直接报废了。

我得小心翼翼，就像是在拆一个定时炸弹一样。

终于，我找到了那个零点，就在一个不起眼的小角落。

我轻轻一碰，电路板上的指示灯就全灭了。

那一刻，我感觉自己就像是个魔术师，轻轻一挥魔杖，灯光全灭。

但是，我知道，这只是开始。

接下来，我得找到那个极点，就是电路里头那个让输出变得最大的点。

这就像是在找一个宝藏，你得知道它藏在哪儿，才能把它挖出来。

我又开始了我的“点点点”游戏，这次是为了找到那个让电路板发挥最大效能的点。

我一边调试，一边想象着电路板上的电子们，它们在我的指挥下，欢快地跳舞。

有时候，我会不小心碰到一个极点，电路板上的指示灯就会突然亮起来，就像是电子们在欢呼一样。

经过一番折腾，我终于找到了那个极点。

我轻轻一调，电路板上的指示灯就全亮了，而且比之前任何时候都要亮。

那一刻，我感觉自己就像是个英雄，成功地解救了电路板上的电子们，让它们能够尽情地发挥自己的能力。

所以你看，零点和极点，虽然听起来枯燥，但它们就像是电路设计里的两个小精灵，一个让电路安静下来，一个让电路活跃起来。

它们就像是电路的心脏和灵魂，让电路能够按照我们的想法去工作。

总之，虽然零点和极点听起来可能没那么性感，但它们在电路的世界里，可是至关重要的角色。

下次你看到电路板的时候，不妨想想，那些零点和极点，正在里面默默地工作着，让电路板能够按照我们的想法去运行。

滤波器设计中的极点与零点的选择与布局

滤波器设计中的极点与零点的选择与布局在滤波器设计中，极点与零点的选择与布局起着至关重要的作用。

极点和零点是滤波器频率响应的关键元素，它们决定了滤波器的特性和性能。

本文将探讨极点和零点的选择与布局对滤波器设计的影响，以及在不同应用中如何合理选择和布置它们。

一、极点与零点的含义及作用极点和零点都是滤波器系统转移函数的特征根，它们描述了该系统的频率响应。

极点是滤波器传递函数的分母等于零的点，它决定了滤波器的衰减特性和稳定性。

零点是滤波器传递函数的分子等于零的点，它能够提高滤波器的选择性和频率响应。

极点和零点的选择与布局与滤波器的频率响应特性密切相关。

通过合理选择和布置极点和零点，可以实现所需的滤波器特性，如通带和阻带的增益、截止频率等。

二、极点与零点的选择原则1. 极点的选择原则（1）稳定性：极点位置应该在左半平面，这样才能保证滤波器的稳定性。

如果极点位置在右半平面，滤波器会产生震荡或不稳定的响应。

（2）滤波器特性：极点的数量和位置决定了滤波器的特性。

例如，二阶低通滤波器通常具有两个实根或共轭复根，决定了滤波器的截止频率和衰减。

2. 零点的选择原则（1）选择性：零点的位置和数量决定了滤波器的选择性能。

合理选择和布置零点可以提高滤波器对特定频率的抑制能力。

（2）增益：零点对滤波器的增益也有影响。

在某些应用中，零点的位置可以用来提高或降低滤波器的增益。

三、极点与零点的布局方法1. 极点的布局方法（1）Bessel滤波器：Bessel滤波器通过在$s$平面上均匀分布极点来实现平坦的群延迟特性。

这种布局方法适用于需要保持信号波形的应用，例如音频信号处理。

（2）Butterworth滤波器：Butterworth滤波器的极点在单位圆上均匀分布，能够实现最大斜率的通带过渡带抑制特性。

这种布局方法适用于需要在通带和阻带之间平衡性能的应用。

（3）Chebyshev滤波器：Chebyshev滤波器的极点主要分布在椭圆轨迹上，能够实现更陡的过渡带和更高的选择性。

电路中极点与零点的产生与影响

电路中极点与零点的产生与影响请问电路中极点与零点的产生与影响一、电路中经常要对零极点进行补偿，想问，零点是由于前馈产生的吗？它产生后会对电路造成什么样的影响？是说如果在该频率下，信号通过这两条之路后可以互相抵消还是什么？？极点又就是怎么产生的呢？就是由于意见反馈吗？那极点对电路的影响又就是什么？产生震荡还是什么？？恳请大家指教一下。

1．(不能这么简单的理解其实电路的每个node都存有一个极点只是大部分的极点相对与所关心的频率范围太大而忽略了图夫尔中我们通常关心开环的0db频宽那么>10*频宽频率的极点我们就不管了因为它们对增益裕度贡献太小而被忽略;只要输入和输出之间有两条通路就会产生一个零点:同样的高于所关心频率范围的零点也不用管一个在所关心频率范围内的零点须要看看就是左半平面还是右半平面的左半平面的零点有助于环路平衡右半平面的则有利具体的看拉扎维的书吧写的还是蛮详细的看不懂就多看几遍自己做个电路仿下)2．不好问题，期望全盘介绍的人认真答疑。

我也同样困惑。

但是我总真的极点，零点并无法单单是的说道就是由于线性网络，意见反馈，或者串联并联一个电容产生的。

产生的原因还是和具体内容的电路结构相关联的。

比如一个h(s)的系统和一个电容并联或串联在输入输出之间，谁能说他一定产生一个极点或零点呢？这因该和h(s)的具体形式有关。

大多书上说道的必须大多针对的就是图夫尔结构，它的结构具备特殊性。

具备以点砌全系列的前科。

还恳请超过人细说。

3．一般的说，零点用于增强增益（幅度及相位），极点用于减少增益（幅度及相位），电路中一般零点极点是电容倒数的函数（如1/c）。

当c变小小时，比如说对极点来说，可以向原点方向变化，导致增益增加大力推进（幅度及增益）～通常运振动路的米勒效应电容就是这个原理，当增益快速上升好像－3db时，其他的零点极点都还没对系统增益起著啥促进作用（或促进作用不大，忽略了），电路即使七窍通了六窍半了～你就可以根据自己的须要迁调上频宽，多少多小的裕度就ko 了极点是由于结点和地之间有寄生电容造成的,零点是由于输入和输出之间有寄生电容造成的,一般输入和输出之间的零极点考虑多一点,主要是因为输入输出有较大的电阻,造成了极点偏向原点.4．个人的一点认知极点决定的是系统的自然响应频率，通常在电路中就是对地电容所看进去的r和对地电容c共同决定的。

极点和零点电路中的意义

极点和零点电路中的意义摘要：一、极点和零点电路的基本概念二、极点和零点电路的意义1.极点：电压、电流的转折点2.零点：电压、电流的平衡点三、极点和零点在电路分析中的应用1.电压、电流的计算2.电路元件的特性分析四、实际电路案例分析正文：极点和零点电路中的意义在电路领域，极点和零点是两个非常重要的概念。

它们在电路分析、计算和实际应用中具有显著的意义。

本文将从基本概念、意义以及在电路分析中的应用等方面进行详细阐述。

一、极点和零点电路的基本概念1.极点：在电路中，极点通常指的是电压或电流发生转折的点。

例如，在交流电压或电流的正负半周期之间，电压或电流的值会发生剧变，这个转折点就称为极点。

在电路分析中，极点常常用于描述电容、电感等元件的电压或电流变化。

2.零点：零点是指电压或电流的平衡点，即电压或电流的值为零的点。

在直流电路中，电源的正负极之间的电压为零点；在交流电路中，电压或电流的瞬时值为零的点即为零点。

零点在电路分析中也具有重要作用，如用于电路元件的特性的描述和计算。

二、极点和零点电路的意义1.极点：在电路分析中，极点有助于我们理解电压、电流的变化规律。

通过分析极点，可以研究电容、电感等元件的充放电过程，以及电路中的共振现象等。

此外，在信号处理领域，极点还与信号的频率响应密切相关。

2.零点：零点在电路分析中具有实用性意义。

首先，在计算电路中的电压、电流时，零点可以作为参考点，便于进行数值计算。

其次，通过分析零点，可以研究电路元件的特性，如电阻、电容、电感等。

此外，零点还在交流电路的相位分析中起到关键作用。

三、极点和零点在电路分析中的应用1.电压、电流的计算：在电路分析中，我们需要对电压、电流进行计算。

通过分析极点和零点，可以得到电压、电流的波形和幅值，从而为电路的性能评估提供依据。

2.电路元件的特性分析：极点和零点有助于我们了解电路元件的特性，如电容、电感的充放电过程，以及电阻、电容、电感等元件对交流信号的阻抗特性。

根据函数图像求出极值点与零点

根据函数图像求出极值点与零点在数学中，函数是一种描述数值之间关系的工具。

图像是函数的可视化表示，通过观察函数图像，我们可以推断出函数的一些性质，例如极值点和零点。

本文将探讨如何根据函数图像求出极值点与零点，并介绍一些常见的方法和技巧。

一、极值点的求解极值点是函数图像上的局部极大值或极小值点，也称为极点。

求解极值点的方法有很多种，下面将介绍两种常用的方法：导数法和二次导数法。

1. 导数法导数法是一种基于微积分的方法，通过求函数的导数来确定函数的极值点。

具体步骤如下：首先，我们需要找到函数图像上的所有驻点，即导数为零的点。

这些点可能是极值点，也可能是拐点。

然后，我们计算这些驻点的导数的符号。

如果导数在驻点的左侧为负，右侧为正，则该驻点是一个极小值点；如果导数在驻点的左侧为正，右侧为负，则该驻点是一个极大值点。

最后，我们可以通过进一步的分析和计算，确定极值点的具体数值。

2. 二次导数法二次导数法是导数法的一种扩展，通过计算函数的二次导数来确定函数的极值点。

具体步骤如下：首先，我们计算函数的一阶导数和二阶导数。

然后，我们找到所有使得二阶导数等于零的点。

这些点可能是极值点，也可能是拐点。

接下来，我们计算这些点的一阶导数的符号。

如果一阶导数在该点的左侧为负，右侧为正，则该点是一个极小值点；如果一阶导数在该点的左侧为正，右侧为负，则该点是一个极大值点。

最后，我们通过进一步的分析和计算，确定极值点的具体数值。

二、零点的求解零点是函数图像上的横坐标为零的点，也称为根。

求解零点的方法有很多种，下面将介绍两种常用的方法：图像法和方程法。

1. 图像法图像法是一种直观的方法，通过观察函数图像来估计零点的位置。

具体步骤如下：首先，我们绘制函数的图像。

然后，我们观察函数图像与x轴的交点，即横坐标为零的点。

这些点就是函数的零点。

最后，我们可以通过进一步的计算和逼近，确定零点的具体数值。

2. 方程法方程法是一种基于方程求解的方法，通过将函数转化为方程来求解零点。

零极点的概念

零极点的概念
在信号系统分析中，零极点是指系统函数的零点和极点，它们通过传递函数的值来刻画。

零点是指系统函数的分子多项式的根，也是系统函数的零点。

而极点是指分母多项式的根，也是系统函数的极点。

在复平面上，零点用“o”表示，极点用“×”表示，通过这些符号可以标出系统的零极点位置，形成系统的零极点图。

零极点的概念在信号系统中具有重要意义，可以从以下几个方面来理解：
1. 零极点可以确定系统的时域响应特性。

特别是单极点的情况下，极点的实部决定了时域响应指数衰减或增长的快慢，而虚部决定了振荡的快慢。

2. 零极点可以确定系统的频率响应。

3. 零极点可以确定系统的稳定性以及其他特性。

总之，系统函数的零极点对于理解系统的特性以及进行系统设计非常重要。

电路波特图怎么看？极点、零点是什么

电路波特图怎么看？极点、零点是什么从放大器失调电压、偏置电流、共模抑制比，电源抑制比到开环增益，在直流或者低频率范围内，影响放大器信号调理的参数已经介绍完成。

期间没有单独介绍基础理论，默认诸位工程师已经掌握同相、反相等基础放大电路，“虚短、虚断”等放大器基础特性，以及基尔霍夫、诺顿等电路分析基础。

但是在介绍增益带宽积、相位裕度与增益裕度，输入阻抗特性、输出阻抗特性、容性负载驱动能力等参数之前，笔者考虑再三决定增加本篇内容，回顾分析这些参数的方式——波特图。

以及极点与零点在波特图中的性质。

后续相关参数的解析中将直接使用本篇内容的零点、极点的特性。

交流信号处理电路中，信号的频率范围较宽，从赫兹级到千赫兹，甚至兆赫兹级，信号增益涵盖几十倍到千、万倍。

此时常常使用波特图缩短坐标扩大视野，方便数据分析。

波特图由幅频波特图、相频波特图两部分组成。

幅频波特图表示电压增益随频率的变化情况，其中Y轴为电压增益的对数形式（20lgG）,X轴为频率或者频率的对数形式lgf。

相频波特图是相位（θ）随频率的变化情况。

Y轴是相位，X 轴为频率。

以直流增益为100dB的单极点系统为例，幅频波特图如图2.89(a)，X轴是Hz为单位的频率，Y轴是以dB为单位的增益。

信号频率小于100Hz时，电路增益为常数100dB,信号频率高于100Hz时，电路增益随信号频率增加而下降，速度为-20dB/十倍频，或者-6dB/倍频。

在100Hz处电压增益出现转折该处称为极点。

极点处的增益下降3dB。

图2.89 100dB增益单极点系统波特图示例如图2.89(b)，相频波特图：X轴是以Hz为单位的频率，Y轴是以度为单位的相位。

初始相位是0°，极点fp处的相位是-45°。

在0.1倍fp至10倍fp范围内，相位从-5.7°变为-84.3°，变化速度为-45°/十倍频。

频率高于10KHz的相位是-90°。

零点、极点以及用零点抵消极点的实例

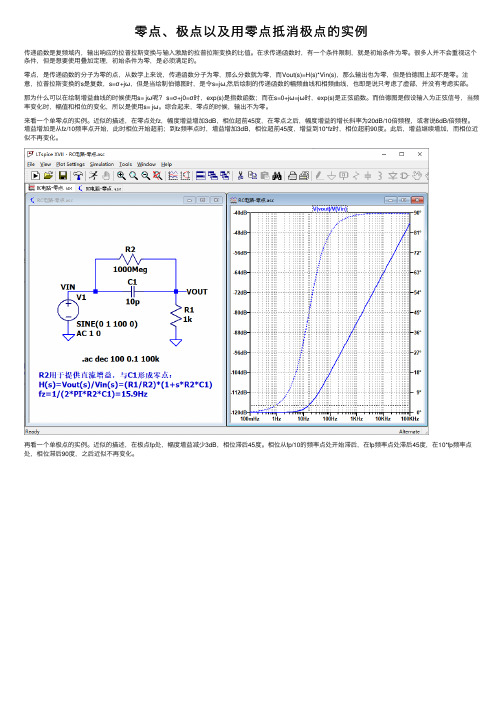
零点、极点以及⽤零点抵消极点的实例传递函数是复频域内，输出响应的拉普拉斯变换与输⼊激励的拉普拉斯变换的⽐值。

在求传递函数时，有⼀个条件限制，就是初始条件为零。

很多⼈并不会重视这个条件，但是想要使⽤叠加定理，初始条件为零，是必须满⾜的。

零点，是传递函数的分⼦为零的点，从数学上来说，传递函数分⼦为零，那么分数就为零，⽽Vout(s)=H(s)*Vin(s)，那么输出也为零，但是伯德图上却不是零。

注意，拉普拉斯变换的s是复数，s=σ+jω，但是当绘制伯德图时，是令s=jω,然后绘制的传递函数的幅频曲线和相频曲线，也即是说只考虑了虚部，并没有考虑实部。

那为什么可以在绘制增益曲线的时候使⽤s= jω呢？ s=σ+j0=σ时，exp(s)是指数函数；⽽在s=0+jω=jω时，exp(s)是正弦函数。

⽽伯德图是假设输⼊为正弦信号，当频率变化时，幅值和相位的变化，所以是使⽤s= jω。

综合起来，零点的时候，输出不为零。

来看⼀个单零点的实例。

近似的描述，在零点处fz，幅度增益增加3dB，相位超前45度，在零点之后，幅度增益的增长斜率为20dB/10倍频程，或者说6dB/倍频程。

增益增加是从fz/10频率点开始，此时相位开始超前；到fz频率点时，增益增加3dB，相位超前45度，增益到10*fz时，相位超前90度。

此后，增益继续增加，⽽相位近似不再变化。

再看⼀个单极点的实例。

近似的描述，在极点fp处，幅度增益减少3dB，相位滞后45度。

相位从fp/10的频率点处开始滞后，在fp频率点处滞后45度，在10*fp频率点处，相位滞后90度，之后近似不再变化。

以上这些是零点和极点的⼀些基础知识。

对于n阶极点和零点，就继续叠加即可。

接下来看⼀个简单实⽤的零点补偿极点的例⼦。

在I-V转换电路中，通常需要在反馈电阻RF上并联⼀个⼩电容CF，防⽌输出端连接容性负载时发⽣振荡。

如下图所⽰，CL和RL⽤来模拟连接负载。

增加电容后，传递函数为H(s)=-RF/(1+s*RF*CF)，直流增益是160dB，即20*log(100Meg)。

传递函数零点和极点意义

传递函数零点和极点意义
传递函数是描述线性系统输出与输入之间关系的函数。

其中包含了系统的零点和极点，它们对系统的稳定性和频率响应都有重要意义。

零点是传递函数中使得输出等于零的输入值，也就是使得系统对某个频率的输入信号不产生响应的频率点。

零点数量越多，表示系统对该频率的抑制能力越强，因此系统的稳定性也越好。

极点则是使得传递函数分母为零的频率点，也就是系统的共振频率点。

极点的数量和位置决定了系统的频率响应和阻尼特性。

系统的稳定性和阻尼特性都取决于极点的位置。

因此，通过分析传递函数的零点和极点，可以得到系统的频率响应、稳定性和阻尼特性等信息，对于系统设计和控制具有重要意义。

- 1 -。

传递函数的极点和零点

传递函数的极点和零点传递函数是控制系统中重要的概念之一，它可以描述输入信号和输出信号之间的关系。

在传递函数中，极点和零点是非常重要的概念，它们可以影响系统的稳定性和响应特性。

本文将介绍传递函数的极点和零点的概念、性质以及它们在控制系统中的应用。

一、传递函数的定义传递函数是控制系统中描述输入信号和输出信号之间关系的数学模型。

在连续时间系统中，传递函数可以用拉普拉斯变换表示，即： $$ G(s)=frac{Y(s)}{X(s)} $$其中，$G(s)$是系统的传递函数，$Y(s)$是系统的输出信号，$X(s)$是系统的输入信号，$s$是复变量。

在离散时间系统中，传递函数可以用$Z$变换表示，即：$$ G(z)=frac{Y(z)}{X(z)} $$其中，$G(z)$是系统的传递函数，$Y(z)$是系统的输出信号，$X(z)$是系统的输入信号，$z$是复变量。

二、传递函数的极点和零点在传递函数中，极点和零点是非常重要的概念，它们可以影响系统的稳定性和响应特性。

1. 极点在传递函数中，极点是使传递函数分母为零的复数根。

如果传递函数$G(s)$的分母为$D(s)$，则极点是使$D(s)=0$的$s$值。

极点可以分为有限极点和无限极点。

有限极点是有限的复数根，它们决定了系统的稳定性和响应特性。

无限极点是在无穷远处的极点，它们对系统的稳定性没有影响，但会影响系统的高频响应特性。

2. 零点在传递函数中，零点是使传递函数分子为零的复数根。

如果传递函数$G(s)$的分子为$N(s)$，则零点是使$N(s)=0$的$s$值。

零点可以分为有限零点和无限零点。

有限零点是有限的复数根，它们决定了系统的响应特性。

无限零点是在无穷远处的零点，它们对系统的响应特性没有影响，但会影响系统的低频响应特性。

三、传递函数的极点和零点的性质1. 极点和零点的数量相等在传递函数中，极点和零点的数量相等。

这是因为传递函数可以表示为极点和零点的乘积形式，即：$$ G(s)=Kfrac{(s-z_1)(s-z_2)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)} $$其中，$K$是常数，$z_1,z_2,...,z_m$是有限零点，$p_1,p_2,...,p_n$是有限极点。

网络函数的零点和极点分析

网络函数的零点和极点分析
目录
• 引言 • 网络函数的零点分析 • 网络函数的极点分析 • 网络函数的零极点与系统稳定性 • 实际应用案例
01 引言
零点和极点的定义
零点
函数值为零的点，即 $f(z) = 0$ 的解。
极点
函数在某点的值趋于无穷的点，即函数在该点附近的导数趋于无穷。
零点和极点在网络分析中的重要性
极点分析在网络路由优化中的应用
极点分析在网络路由优化中具有重要价值，通过分析网络函数的极点，可以确定最佳的网络路由路径。
极点分析可以用于优化路由算法，提高网络路由的效率和稳定性，降低网络传输延迟。
极点分析还可以用于故障排查和网络性能评估，通过分析极点的变化，可以快速定位网络故障和评估网络性能。
05 实际应用案例
零点分析在网络拥塞控制中的应用
零点分析在网络拥塞控制中起到关键作用，通过分析网络函数的零点，可以确定网络中数据传输
的稳定性。
零点分析可以预测网络拥塞的情况，提前采取措施进行预防，提
高网络传输的效率和稳定性。
零点分析还可以用于优化网络拥塞控制算法，通过调整算法参数，
降低网络拥塞发生的概率。
极点对网络性能的影响
稳定性
极点的位置决定了系统的稳定性。如果极点位于复平面的左半部分，系统是稳定的；如果极点位于右半置和数量会影响系统的动态响应特性，如系统的超调和调节时间等。
噪声抑制
极点的位置和数量也会影响系统对外部噪声的抑制能力。
极点分析在网络设计中的应用
数值法
通过迭代或搜索算法在复平面上找到零点，适用于复杂或难以解析求解的网络。
图形法
通过绘制网络函数的极坐标图或奈奎斯特图来直观地找到零点，适用于具有直观几何意义的网络。

极点和零点重合-概述说明以及解释

极点和零点重合-概述说明以及解释1.引言1.1 概述极点和零点是在数学分析中常见的概念，它们分别代表了函数在特定点处的奇点和使函数为零的点。

通常情况下，极点和零点是不会重合的，因为它们代表了函数在不同情况下的性质。

然而，有时候极点和零点会重合在同一个点上，这种情况在数学分析中被称为极点和零点重合。

本文将对极点和零点的定义、特征以及它们之间的关系进行详细的探讨，同时还将分析极点和零点重合的意义和影响。

通过深入研究极点和零点的重合现象，我们可以更好地理解函数的性质和行为，为进一步的数学研究提供有益的参考。

1.2文章结构1.2 文章结构本文将首先介绍极点和零点的定义和特征，包括它们在数学和物理领域的重要性以及相互之间的区别。

然后，我们将讨论极点和零点之间的关系，探讨它们在数学和物理问题中的应用。

最后，我们将深入探讨极点和零点重合的意义，探讨这种现象在实践中的重要性和可能的应用领域。

通过对极点和零点的研究和分析，我们希望读者能够更深入地理解这两个概念，并从中获得一些启发和新的见解。

1.3 目的本文的目的在于探讨极点和零点在数学和物理学中的重要性和作用，并深入研究极点和零点在数学领域的定义、特征以及它们之间的关系。

通过对极点和零点的探讨，我们希望能够更深入地理解它们在数学和物理学中的应用，以及它们在解决问题和预测某些现象中起到的重要作用。

同时，本文还将探讨极点和零点重合的意义，从而帮助读者更好地理解这一现象对于数学和物理学的意义和影响。

最终，通过本文的研究，我们将能够更全面地认识极点和零点的重要性，以及它们在数学和物理学领域的作用。

2.正文2.1 极点的定义和特征在复数域上，一个函数在某点处的极点是指在该点处函数取无穷大值或无穷小值的点。

具体来说，如果一个函数在某点处取无穷大值，我们称这个点为函数的极点。

极点是一种特殊的奇点，它在函数的定义域内是孤立的点。

极点具有以下特征：1. 极点是函数在某点处的奇点，也就是说这个点不能满足函数的定义。

最小相位系统的零点和极点

最小相位系统的零点和极点
最小相位系统的零点和极点是两个重要的概念，其中零点指的是某一物体处于最小相位状态的点，极点则是形成最小相位系统需要动力驱动的点。

一、最小相位系统的零点
1、基本特征：最小相位系统的零点是物体进入最小相位状态时系统的某处，这种最小相位状态指的是物体空间位置处于相对稳定的状态，它们不会因周围场力和外力而发生变化。

2、运动轨迹：最小相位系统的零点是物体进入最小相位的点，这种点的运动轨迹要稳定、稳定，而且当物体在这条轨迹上运动时，其总体相位状态不会发生变化。

3、能量位置：最小相位系统的零点是能量位置，它们处于一个最低能状态，这种能状态包括物体以及它们之间的相互作用和外部场力的能状态。

二、最小相位系统的极点
1、基本特征：最小相位系统的极点是物体进入最小相位状态的点，其
他点沿着最小相位系统的路径椭圆运动，而最小相位系统的极点就是运动的极点。

2、能量位置：最小相位系统的极点是高能量位置，这种能量位置包括定义物体以及它们之间的相互作用和外部场力的能状态。

3、动力位置：最小相位系统的极点是最受外来动力影响的点，这种动力源于外部场力作用下物体间相互上的力，物体受外力作用而产生变化，但不影响其最小相位等离子密度。

零点和极点详解

零点和极点详解一、引言零点和极点是复变函数中非常重要的概念，它们在数学中的应用非常广泛，包括电路分析、信号处理、控制系统等领域。

本文将详细介绍零点和极点的定义、性质以及在实际应用中的意义。

二、零点的定义与性质1. 零点的定义设f(z)是一个复变函数，z0是复平面上的一个复数，如果f(z0)=0，则称z0为f(z)的一个零点。

2. 零点的性质（1）零点是函数图像与x轴交点处。

（2）如果f(z)在z0处有一个k阶零点，则f(z)在z0处可以表示为：f(z)=(z-z0)^k g(z)其中g(z)是在z=z0处不为0且解析的函数。

（3）如果f(z)有无穷多个不同的零点，那么f(z)必须恒等于0。

三、极点的定义与性质1. 极点的定义设f(z)是一个复变函数，z0是复平面上的一个复数，如果满足以下条件：（1）存在某个正整数k使得g(z)=(z-z0)^kf(z)在z=z0处解析；（2）当z趋近于z0时，|f(z)|趋近于无穷大；则称z0为f(z)的一个k阶极点。

2. 极点的性质（1）极点是函数图像在z0处的奇异点，也就是说，函数在z0处没有定义。

（2）如果f(z)在z0处有一个k阶极点，则可以表示为：f(z)=h(z)/(z-z0)^k其中h(z)是在z=z0处不为0且解析的函数。

（3）如果f(z)有无穷多个不同的极点，那么f(z)必须恒等于无穷大或者恒等于零。

四、零点与极点之间的关系1. 零点与极点之间的关系如果f(z)在z0处既有零点又有极点，那么它们之间存在以下关系：（1）当k>0时，称z0为可去奇异点。

此时，当我们把这个可去奇异点消去后，就得到了一个新的解析函数g(z)，它在原来的可去奇异点处具有一个正常的值g(z0)=lim_(z→z_0)f(z)，并且g(z)和f(z)在其他地方完全相同。

（2）当k<0时，称z0为本性奇异点。

此时，它是一个真正意义上的奇异点。

如果f(z)在z0的某个邻域内解析，那么称z0为孤立奇异点。

简述零点与极点的关系

简述零点与极点的关系
零点和极点都是线性系统的特征值，二者有着密切的关系。

在控制系统中，零点（或者称为零极）是指使系统的传递函数的分子为零的复数根，即令传递函数的分子为零时，系统的输出为零。

零点可以影响系统的稳定性、阻尼性能和频率响应等特性。

而极点是指使系统的传递函数的分母为零的复数根，即令传递函数的分母为零时，系统的输出无穷大。

极点可以决定系统的稳定性、阻尼性能和频率响应等特性。

零点和极点的位置和数量都会影响系统的特性。

一般来说，系统的零点和极点的分布越远离虚轴（实部为0），系统越稳定。

当零点和极点重合时，会导致系统出现共振或不稳定的情况。

因此，零点和极点之间的关系可以归结为对系统的特性产生影响。

通过合理设计系统的零点和极点，可以实现对系统的稳定性和性能进行控制和优化。