小学数学奥数测试题复杂直线型面积4_人教版

合集下载

小学数学几何直线型面积的计算完整版题型训练+详细答案

⼩学数学⼏何直线型⾯积的计算完整版题型训练+详细答案直线形⾯积的计算例题讲解：板块⼀：基础题型：1．如图，四边形ABCD是直⾓梯形，其中AD=12（厘⽶），AB=8（厘⽶），BC= 15（厘⽶），且三⾓形ADE、四边形DEBF、三⾓形CDF的⾯积相等，阴影三⾓形DEF的⾯积是多少平⽅厘⽶？解析：四边形ABCD的⾯积是（12+15）×8÷2=108（平⽅厘⽶），108÷3=36（平⽅厘⽶）。

CF=36×2÷8=9(厘⽶)，FB=15-9=6(厘⽶)，AE=36×2÷12=6（厘⽶），EB=8-6=2（厘⽶）。

阴影三⾓形DEF的⾯积是36-2×6÷2=30（平⽅厘⽶）2．⼀块长⽅形的⼟地被分割成4个⼩长⽅形，其中三块的⾯积如图所⽰（单位：平⽅⽶），剩下⼀块的⾯积应该是多少平⽅⽶？解析：40×15÷30=20（平⽅⽶）3．如图，在三⾓形ABC中，BC是DC的3倍，AC是EC的3倍，三⾓形DEC的⾯积是3平⽅厘⽶．请问：三⾓形ABC的⾯积是多少平⽅厘⽶？解析：三⾓形ADC的⾯积是3×3=9（平⽅厘⽶），三⾓形ABC的⾯积是3×9=27（平⽅厘⽶）4．如图，E是BC上靠近C的三等分点，且ED是AD的2倍，三⾓形ABC的⾯积为36平⽅厘⽔．三⾓形BDE的⾯积是多少平⽅厘⽶？解析：三⾓形BAE的⾯积是36÷3×2=24（平⽅厘⽶），三⾓形BDE的⾯积24÷3×2=16（平⽅厘⽶）5．如图所⽰，已知三⾓形BEC的⾯积等于20平⽅厘⽶，E是AB边上靠近⽇点的四等分点，三⾓形AED的⾯积是多少平⽅厘⽶？平⾏四边形DECF的⾯积是多少平⽅厘⽶？解析：（1）三⾓形AED的⾯积是20×3=60（平⽅厘⽶）（2）三⾓形DEC的⾯积是20+60=80（平⽅厘⽶），三⾓形DEC的⾯积是平⾏四边形DECF 的⾯积的⼀半，也是平⾏四边形ABCD的⾯积的⼀半，所以平⾏四边形DECF的⾯积是80×2=160（平⽅厘⽶）6．如图，已知平⾏四边形ABCD的⾯积为36，三⾓形AOD的⾯积为8．三⾓形BOC的⾯积为多少？解析：根据⼀半模型可知，三⾓形AOD的⾯积和三⾓形BOC的⾯积是平⾏四边形ABCD 的⾯积的⼀半，所以三⾓形BOC的⾯积是36÷2-8=107．如图，长⽅形ABCD的⾯积是96平⽅厘⽶，E是AD边上靠近D点的三等分点，F是CD上靠近C点的四等分点．阴影部分的⾯积是多少平⽅厘⽶？解析：链接BD ，可知三⾓形ABD 的⾯积和三⾓形BDC 都是96÷2=48（平⽅厘⽶），三⾓形ABE 的⾯积是48×32=32（平⽅厘⽶）。

小学数学奥数测试题-复杂直线型面积-62015人教版

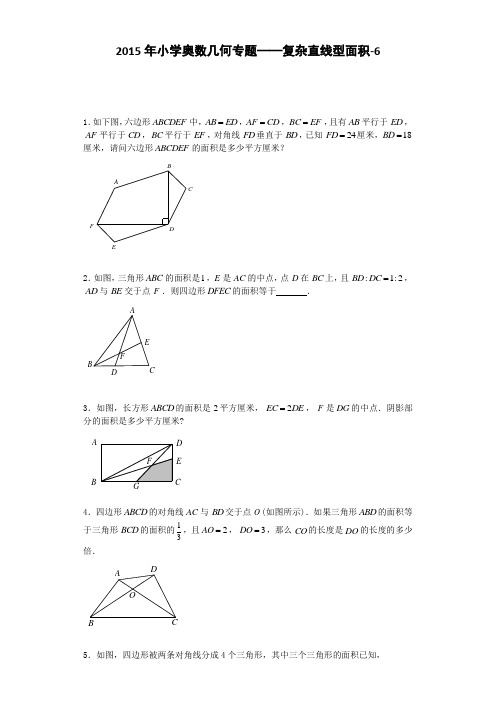
2015年小学奥数几何专题——复杂直线型面积-61．如下图，六边形中，，，，且有平行于，平行于，平行于，对角线垂直于，已知厘米，厘米，请问六边形的面积是多少平方厘米？2．如图，三角形的面积是，是的中点，点在上，且，与交于点．则四边形的面积等于．3．如图，长方形的面积是平方厘米，，是的中点．阴影部分的面积是多少平方厘米?4．四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的多少倍．ABCDEF AB ED =AF CD =BC EF =AB ED AF CD BC EF FD BD 24FD =18BD =ABCDEF FE A BD CABC 1E AC D BC :1:2BD DC =AD BE F DFEC F ED CBAABCD 22EC DE =FDG x y yx A BC D E F G E D C B AABCD AC BD O ABD BCD 132AO =3DO =CO DO ABC D O求：⑴三角形的面积；⑵？6．如图，平行四边形的对角线交于点，、、、的面积依次是2、4、4和6．求：⑴求的面积；⑵求的面积．7．如图，长方形中，，，三角形的面积为平方厘米，求长方形的面积．8．如图，正方形面积为平方厘米，是边上的中点．求图中阴影部分的面积．9．在下图的正方形中，是边的中点，与相交于点，三角形的面积为1平方厘米，那么正方形面积是多少平方厘米．B BGC :AG GC =ABCD O CEF △OEF △ODF △BOE △OCF △GCE △OGF E D C B AABCD :2:3BE EC =:1:2DF FC =DFG 2ABCD A B CDEFG ABCD 3MAD CB A ABCD E BC AE BD F BEF ABCD10．已知是平行四边形，，三角形的面积为6平方厘米．则阴影部分的面积是平方厘米．11．右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．12．右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．13．如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为多少平方厘米．A BC DE FABCD :3:2BC CEODE B ABCDABED B ABCDABED B ABCD CE DF OFBC ?852OA B EF14．如图，是等腰直角三角形，是正方形，线段与相交于点．已知正方形的面积48，，则的面积是多少？15．下图中，四边形都是边长为1的正方形，、、、分别是，，，的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数，那么，的值等于多少？16．如图，中，，，互相平行，，则．17．如图，平行，且，，，求的长．18．如图，中，，，，，互相平行，，ABC ∆D EFG AB CD K D EFG :1:3AK KB =BKD∆BABCD E F G H AB BC CD DA m n()m n+EABC △DE FG BC AD DF FB ==::ADE DEGF FGCB S S S =△四边形四边形E G FADC B DE BC 2AD =5AB =4AE =AC AE DC B ABC △DE FG MN PQ BC AD D F FM M P PB ====19．如图，已知正方形的边长为，是边的中点，是边上的点，且，与相交于点，求20．如图所示，已知平行四边形的面积是1，、是、的中点，交于，求的面积．QE G NM FP ADC B ABCD 4F BCE DC :1:3DE EC =AF BEG ABG S △GFA E D CBABCD E F AB AD BF EC M BMG ∆M H G F ED C B A参考答案1．432【解析】如图，我们将平移使得与重合，将平移使得与重合，这样、都重合到图中的了．这样就组成了一个长方形，它的面积与原六边形的面积相等，显然长方形的面积为平方厘米，所以六边形的面积为平方厘米．2．【解析】方法一：连接，根据燕尾定理，，, 设份，则份，份，份，如图所标所以方法二：连接，由题目条件可得到，，所以，，而．所以则四边形的面积等于． GFE A B D CBCD ∆CD AF DEF ∆ED AB EF BC AG BGFD BGFD 2418432⨯=ABCDEF 43251233321F E D C B AAB CD E F CF 12ABF ACF S BD S DC ==△△1ABF CBF S AE S EC ==△△1BDFS =△2DCF S =△3ABF S =△3AEF EFC S S ==△△551212DCEF ABC S S ==△DE 1133ABD ABC S S ==△△11212233ADE ADC ABC S S S ==⨯=△△△11ABD ADE S BF FE S ==△△111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△211323CDE ABC S S =⨯⨯=△△DFEC 5123．5/12【解析】设份，则根据燕尾定理其他面积如图所示平方厘米. 4．2【解析】在本题中，四边形为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作垂直于，垂直于，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵，∴，∴．解法二：作于，于．∵，∴，∴， ∴，∴，∴．5．6；1：3 【解析】⑴根据蝴蝶定理，，那么；⑵根据蝴蝶定理，．6．2/3【解析】⑴根据题意可知，的面积为，那么和的面积都是，所以的面积为；⑵由于的面积为8，的面积为6，所以的面积为，E D B A1DEF S =△551212BCD S S ==△阴影ABCD :1:3ABD BCD S S =AH BD H CG BD G ::1:3ABD BDC AO OC S S ∆∆==236OC =⨯=:6:32:1OC OD ==AH BD ⊥H CG BD ⊥G 13ABD BCD S S ∆∆=13AH CG =13AOD DOC S S ∆∆=13AO CO =236OC =⨯=:6:32:1OC OD ==H G ABC D O123BGC S ⨯=⨯6BGC S =()():12:361:3AG GC =++=BCD △244616+++=BCO △CDO ∆1628÷=OCF △844-=BCO △BOE △OCE △862-=根据蝴蝶定理，，所以，那么． 7．72【解析】连接，．因为，，所以．因为，，所以平方厘米，所以平方厘米．因为，所以长方形的面积是平方厘米．8．1【解析】因为是边上的中点，所以，根据梯形蝴蝶定理可以知道，设份，则份，所以正方形的面积为份，份，所以，所以平方厘米． 9．12【解析】连接，根据题意可知，根据蝴蝶定理得(平方厘米)，(平方厘米)，那么(平方厘米)．10．21【解析】 ::2:41:2COE COF EG FG S S ∆∆===::1:2GCE GCF S S EG FG ∆∆==11221233GCE CEF S S ∆∆==⨯=+A B CDEFG AE FE :2:3BE EC =:1:2DF FC =3111()53210DEF ABCD ABCD S S S =⨯⨯=长方形长方形12AED ABCD S S =长方形11::5:1210AG GF ==510AGD GDF S S ==12AFD S =16AFD ABCD S S =长方形ABCD 72M AD :1:2AM BC =22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△（）（）1AGM S =△123MCD S =+=△1224312++++=224S =+=阴影:1:3S S =阴影正方形1S =阴影DE :1:2BE AD =2129S =+=梯形（）3ECDS =△12ABCD S =连接．由于是平行四边形，，所以，根据梯形蝴蝶定理，，所以(平方厘米)，(平方厘米)，又(平方厘米)，阴影部分面积为(平方厘米)．11．6【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．12．4【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以B AC ABCD :3:2BC CE =:2:3CE AD =22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=6AOC S =9AOD S =6915ABC ACD S S ==+=61521+=BAE AD BC AECD OCD OAE S S ∆∆=4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=236OCD S ∆=6OCD S ∆=B AE AD BC AECD OCD OAE S S ∆∆=2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=216OCD S ∆=(平方厘米)．另解：在平行四边形中，(平方厘米)，所以(平方厘米)，根据蝴蝶定理，阴影部分的面积为(平方厘米)． 13．9 【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)． 14．12 【解析】由于是正方形，所以与平行，那么四边形是梯形．在梯形中，和的面积是相等的．而，所以的面积是面积的，那么的面积也是面积的．由于是等腰直角三角形，如果过作的垂线，为垂足，那么是的中点，而且，可见和的面积都等于正方形面积的一半，所以的面积与正方形的面积相等，为48．那么的面积为． 15．5 【解析】左、右两个图中的阴影部分都是不规则图形，不方便直接求面积，观察发现两个图中的空白部分面积都比较好求，所以可以先求出空白部分的面积，再求阴影部分的面积．如下图所示，在左图中连接．设与的交点为．左图中为长方形，可4OCD S ∆=ABED ()111681222ADE ABEDS S∆==⨯+=1284AOE ADE AOD S S S ∆∆∆=-=-=8244⨯÷=?852O A BCDEFDE CF EDCF EOD FOCS S∆=EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=4EOD S ∆=4812ECD S ∆=+=ABCD 12224⨯=OFBC 245289---=D EFG DA BC ADBC ADBC BDK ∆ACK ∆:1:3AK KB =ACK ∆ABC ∆11134=+BDK ∆ABC ∆14ABC ∆A BC M M BC AM DE =ABM ∆ACM ∆D EFG ABC ∆D EFG BDK ∆148124⨯=EG AG DE M AEGD知的面积为长方形面积的，所以三角形的面积为．又左图中四个空白三角形的面积是相等的，所以左图中阴影部分的面积为．如上图所示，在右图中连接、．设、的交点为．可知∥且．那么三角形的面积为三角形面积的，所以三角形的面积为，梯形的面积为．在梯形中，由于，根据梯形蝴蝶定理，其四部分的面积比为：，所以三角形的面积为，那么四边形的面积为．而右图中四个空白四边形的面积是相等的，所以右图中阴影部分的面积为．那么左图中阴影部分面积与右图中阴影部分面积之比为，即，那么．16．1：3：5【解析】设份，根据面积比等于相似比的平方，所以，，因此份，份，进而有份，份，所以 17．10【解析】由金字塔模型得，所以 18．1：3：5：7：9 【解析】设份，，因此份，进而有份，同理有份，份，份．所以有AM D ∆AEGD 14AMD 21111248⨯⨯=111482-⨯=BEEAC EF AF EC N EF AC 2AC EF =BEF ABC 14BEF 21111248⨯⨯=AEFC 113288-=AEFC :1:2EF AC =221:12:12:21:2:2:4⨯⨯=EFN 3118122424⨯=+++BENF 1118246+=111463-⨯=11:3:223=32m n =325m n +=+=1ADE S =△22::1:4ADE AFG S S AD AF ==△△22::1:9ADE ABC S S AD AB ==△△4AFG S =△9ABC S =△3DEGF S =四边形5FGCB S =四边形::1:3:5ADE DEGF FGCB S S S =△四边形四边形:::2:5AD AB AE AC DE BC ===42510AC =÷⨯=1ADE S =△22::1:4ADE AFG S S AD AF ==△△4AFG S =△3DEGF S =四边形5FGNM S =四边形7MNQP S =四边形9PQCB S =四边形::::1:3:5:7:9ADEDEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形19．32/11 【解析】方法一：连接，延长，两条线交于点，构造出两个沙漏，所以有，因此，根据题意有，再根据另一个沙漏有，所以．方法二：连接，分别求，，根据蝴蝶定理，所以． 20．1/30【解析】解法一：由题意可得，、是、的中点，得，而，所以，并得、是的三等分点，所以，所以，所以，；又因为，所以．解法二：延长交于，如右图，可得，，从而可以确定的点的位置，，，(鸟头定理)，可得 M GFAEDCBGFAEDCBAE AF DC M ::1:1AB CM BF FC ==4CM =3CE =::4:7GB GE AB EM ==4432(442)471111ABG ABE S S ==⨯⨯÷=+△△,AE EF4224ABF S =⨯÷=△4441232247AEF S =⨯-⨯÷-⨯÷-=△::4:7ABF AEF S S BG GE ==△△4432(442)471111ABG ABE S S ==⨯⨯÷=+△△AE F AB AD //EF BD ::1:2FD BC FH HC ==::1:2EB CD BG GD ==::2:3CH CF GH EF ==G H BD BG GH =::2:3BG EF BM MF ==25BM BF =11112224BFD ABD ABCDS S S ∆∆==⨯=13BG BD =1212113535430BMG BFD S S ∆∆=⨯⨯=⨯⨯=CE DA I ::1:1AI BC AE EB ==M ::2:3BM MF BC IF ==25BM BF =13BG BD =2121115353430BMG BDF ABCDS S S ∆∆=⨯=⨯⨯=。

小学奥数几何专题--复杂直线型面积-6(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-6（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx 题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）【题文】如下图，六边形中，，，，且有平行于，平行于，平行于，对角线垂直于，已知厘米，厘米，请问六边形的面积是多少平方厘米？【答案】432【解析】如图，我们将平移使得与重合，将平移使得与重合，这样、都重合到图中的了．这样就组成了一个长方形，它的面积与原六边形的面积相等，显然长方形的面积为平方厘米，所以六边形的面积为平方厘米．【题文】如图，三角形的面积是，是的中点，点在上，且，与交于点．则四边形的面积等于．【答案】【解析】方法一：连接，根据燕尾定理，，,设份，则份，份，份，如图所标所以方法二：连接，由题目条件可得到，，所以，，而．所以则四边形的面积等于．【题文】如图，长方形的面积是平方厘米，，是的中点．阴影部分的面积是多少平方厘米?【答案】5/12【解析】设份，则根据燕尾定理其他面积如图所示平方厘米.【题文】四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的多少倍．【答案】2【解析】在本题中，四边形为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作垂直于，垂直于，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵，∴，∴．解法二：作于，于．∵，∴，∴，∴，∴，∴．【题文】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形的面积；⑵？【答案】6；1：3【解析】⑴根据蝴蝶定理，，那么；⑵根据蝴蝶定理，．【题文】如图，平行四边形的对角线交于点，、、、的面积依次是2、4、4和6．求：⑴求的面积；⑵求的面积．【答案】2/3【解析】⑴根据题意可知，的面积为，那么和的面积都是，所以的面积为；⑵由于的面积为8，的面积为6，所以的面积为，根据蝴蝶定理，，所以，那么．【题文】如图，长方形中，，，三角形的面积为平方厘米，求长方形的面积．【答案】72【解析】连接，．因为，，所以．因为，，所以平方厘米，所以平方厘米．因为，所以长方形的面积是平方厘米．【题文】如图，正方形面积为平方厘米，是边上的中点．求图中阴影部分的面积．【答案】1【解析】因为是边上的中点，所以，根据梯形蝴蝶定理可以知道，设份，则份，所以正方形的面积为份，份，所以，所以平方厘米．【题文】在下图的正方形中，是边的中点，与相交于点，三角形的面积为1平方厘米，那么正方形面积是多少平方厘米．【答案】12【解析】连接，根据题意可知，根据蝴蝶定理得(平方厘米)，(平方厘米)，那么(平方厘米)．【题文】已知是平行四边形，，三角形的面积为6平方厘米．则阴影部分的面积是平方厘米．【答案】21【解析】连接．由于是平行四边形，，所以，根据梯形蝴蝶定理，，所以(平方厘米)，(平方厘米)，又(平方厘米)，阴影部分面积为(平方厘米)．【题文】右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．【答案】6【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．【题文】右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．【答案】4【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．另解：在平行四边形中，(平方厘米)，所以(平方厘米)，根据蝴蝶定理，阴影部分的面积为(平方厘米)．【题文】如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为多少平方厘米．【答案】9【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)．【题文】如图，是等腰直角三角形，是正方形，线段与相交于点．已知正方形的面积48，，则的面积是多少？【答案】12【解析】由于是正方形，所以与平行，那么四边形是梯形．在梯形中，和的面积是相等的．而，所以的面积是面积的，那么的面积也是面积的．由于是等腰直角三角形，如果过作的垂线，为垂足，那么是的中点，而且，可见和的面积都等于正方形面积的一半，所以的面积与正方形的面积相等，为48．那么的面积为．【题文】下图中，四边形都是边长为1的正方形，、、、分别是，，，的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数，那么，的值等于多少？【答案】5【解析】左、右两个图中的阴影部分都是不规则图形，不方便直接求面积，观察发现两个图中的空白部分面积都比较好求，所以可以先求出空白部分的面积，再求阴影部分的面积．如下图所示，在左图中连接．设与的交点为．左图中为长方形，可知的面积为长方形面积的，所以三角形的面积为．又左图中四个空白三角形的面积是相等的，所以左图中阴影部分的面积为．如上图所示，在右图中连接、．设、的交点为．可知∥且．那么三角形的面积为三角形面积的，所以三角形的面积为，梯形的面积为．在梯形中，由于，根据梯形蝴蝶定理，其四部分的面积比为：，所以三角形的面积为，那么四边形的面积为．而右图中四个空白四边形的面积是相等的，所以右图中阴影部分的面积为．那么左图中阴影部分面积与右图中阴影部分面积之比为，即，那么．【题文】如图，中，，，互相平行，，则．【答案】1：3：5【解析】设份，根据面积比等于相似比的平方，所以，，因此份，份，进而有份，份，所以【题文】如图，平行，且，，，求的长．【答案】10【解析】由金字塔模型得，所以【题文】如图，中，，，，，互相平行，，则．【答案】1：3：5：7：9【解析】设份，，因此份，进而有份，同理有份，份，份．所以有【题文】如图，已知正方形的边长为，l方法二：连接，分别求，，根据蝴蝶定理，所以．【题文】如图所示，已知平行四边形的面积是1，、是、的中点，交于，求的面积．【答案】1/30【解析】解法一：由题意可得，、是、的中点，得，而，所以，并得、是的三等分点，所以，所以，所以，；又因为，所以．解法二：延长交于，如右图，可得，，从而可以确定的点的位置，，，(鸟头定理)，可得。

小学奥数几何专题--复杂直线型面积-1(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-1（六年级）竞赛测试姓名:_____________年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】如图，正方形ABCD的边长为6， 1.5，2．长方形EFGH的面积为多少．【答案】33【解析】连接DE，DF，则长方形EFGH的面积是三角形DEF面积的二倍．三角形DEF的面积等于正方形的面积减去三个三角形的面积，,所以长方形EFGH面积为33．【题文】如图所示，正方形的边长为厘米，长方形的长为厘米，那么长方形的宽为几厘米？评卷人得分【答案】6.4【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)．三角形面积等于与它等底等高的平行四边形面积的一半．证明：连接．(我们通过把这两个长方形和正方形联系在一起)．∵在正方形中，边上的高，∴(三角形面积等于与它等底等高的平行四边形面积的一半)同理，．∴正方形与长方形面积相等．长方形的宽(厘米)．【题文】长方形的面积为36，、、为各边中点，为边上任意一点，问阴影部分面积是多少？【答案】13.5【解析】解法一：寻找可利用的条件，连接、，如下图：可得：、、，而即；而，．所以阴影部分的面积是：解法二：特殊点法．找的特殊点，把点与点重合，那么图形就可变成右图：这样阴影部分的面积就是的面积，根据鸟头定理，则有：．【题文】在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分的面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．【题文】如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．【题文】如图，长方形的面积是36，是的三等分点，,求阴影部分的面积．【答案】2.7【解析】如图，连接．根据蝴蝶定理，，所以；，所以．又，，所以阴影部分面积为：．【题文】已知为等边三角形，面积为400，、、分别为三边的中点，已知甲、乙、丙面积和为143，求阴影五边形的面积．(丙是三角形)【答案】43【解析】因为、、分别为三边的中点，所以、、是三角形的中位线，也就与对应的边平行，根据面积比例模型，三角形和三角形的面积都等于三角形的一半，即为200．根据图形的容斥关系，有，即，所以．又，所以．【题文】如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，求三角形的面积.【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．【题文】如图在中，分别是上的点，且，，平方厘米，求的面积．【答案】70【解析】连接，，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．【题文】如图，三角形中，是的5倍，是的3倍，如果三角形的面积等于1，那么三l连接．∵，∴，又∵，∴，∴，．【题文】如图在中，在的延长线上，在上，且，，平方厘米，求的面积．【答案】50【解析】连接，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【题文】如图，平行四边形，，，，，平行四边形的面积是，求平行四边形与四边形的面积比．【答案】1：18【解析】连接、．根据共角定理∵在和中，与互补，∴．又，所以．同理可得，，．所以．所以．【题文】如图所示的四边形的面积等于多少？【答案】144【解析】题目中要求的四边形既不是正方形也不是长方形，难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换：把三角形绕顶点逆时针旋转，使长为的两条边重合，此时三角形将旋转到三角形的位置.这样，通过旋转后所得到的新图形是一个边长为的正方形，且这个正方形的面积就是原来四边形的面积.因此，原来四边形的面积为.(也可以用勾股定理)【题文】如图所示，中，，，，以为一边向外作正方形，中心为，求的面积．【答案】10【解析】如图，将沿着点顺时针旋转，到达的位置．由于，，所以．而，所以，那么、、三点在一条直线上．由于，，所以是等腰直角三角形，且斜边为，所以它的面积为．根据面积比例模型，的面积为．【题文】如图，以正方形的边为斜边在正方形内作直角三角形，，、交于．已知、的长分别为、，求三角形的面积．【答案】2.5【解析】如图，连接，以点为中心，将顺时针旋转到的位置．那么，而也是，所以四边形是直角梯形，且，所以梯形的面积为：()．又因为是直角三角形，根据勾股定理，，所以()．那么()，所以()．【题文】如下图，六边形中，，，，且有平行于，平行于，平行于，对角线垂直于，已知厘米，厘米，请问六边形的面积是多少平方厘米？【答案】432【解析】如图，我们将平移使得与重合，将平移使得与重合，这样、都重合到图中的了．这样就组成了一个长方形，它的面积与原六边形的面积相等，显然长方形的面积为平方厘米，所以六边形的面积为平方厘米．【题文】如图，三角形的面积是，是的中点，点在上，且，与交于点．则四边形的面积等于（）．【答案】【解析】方法一：连接，根据燕尾定理，，,设份，则份，份，份，如图所标所以方法二：连接，由题目条件可得到，，所以，，而．所以则四边形的面积等于．【题文】如图，长方形的面积是平方厘米，，是的中点．阴影部分的面积是多少平方厘米?【答案】平方厘米【解析】设份，则根据燕尾定理其他面积如图所示平方厘米.【题文】四边形的对角线与交于点(如图所示)．如果三角形的面积等于三角形的面积的，且，，那么的长度是的长度的多少倍．【答案】2【解析】在本题中，四边形为任意四边形，对于这种”不良四边形”，无外乎两种处理方法：⑴利用已知条件，向已有模型靠拢，从而快速解决；⑵通过画辅助线来改造不良四边形．看到题目中给出条件，这可以向模型一蝴蝶定理靠拢，于是得出一种解法．又观察题目中给出的已知条件是面积的关系，转化为边的关系，可以得到第二种解法，但是第二种解法需要一个中介来改造这个”不良四边形”，于是可以作垂直于，垂直于，面积比转化为高之比．再应用结论：三角形高相同，则面积之比等于底边之比，得出结果．请老师注意比较两种解法，使学生体会到蝴蝶定理的优势，从而主观上愿意掌握并使用蝴蝶定理解决问题．解法一：∵，∴，∴．解法二：作于，于．∵，∴，∴，∴，∴，∴．【题文】如图，四边形被两条对角线分成4个三角形，其中三个三角形的面积已知，求：⑴三角形的面积；⑵？【答案】6；1：3【解析】⑴根据蝴蝶定理，，那么；⑵根据蝴蝶定理，．【题文】如图，平行四边形的对角线交于点，、、、的面积依次是2、4、4和6．求：⑴求的面积；⑵求的面积．【答案】【解析】⑴根据题意可知，的面积为，那么和的面积都是，所以的面积为；⑵由于的面积为8，的面积为6，所以的面积为，根据蝴蝶定理，，所以，那么．【题文】如图，长方形中，，，三角形的面积为平方厘米，求长方形的面积．【答案】72【解析】连接，．因为，，所以．因为，，所以平方厘米，所以平方厘米．因为，所以长方形的面积是平方厘米．【题文】如图，正方形面积为平方厘米，是边上的中点．求图中阴影部分的面积．【答案】1【解析】因为是边上的中点，所以，根据梯形蝴蝶定理可以知道，设份，则份，所以正方形的面积为份，份，所以，所以平方厘米．【题文】在下图的正方形中，是边的中点，与相交于点，三角形的面积为1平方厘米，那么正方形面积是多少平方厘米．【答案】12【解析】连接，根据题意可知，根据蝴蝶定理得(平方厘米)，(平方厘米)，那么(平方厘米)．【题文】已知是平行四边形，，三角形的面积为6平方厘米．则阴影部分的面积是平方厘米．【答案】21【解析】连接．由于是平行四边形，，所以，根据梯形蝴蝶定理，，所以(平方厘米)，(平方厘米)，又(平方厘米)，阴影部分面积为(平方厘米)．【题文】右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．【答案】6【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．【题文】右图中是梯形，是平行四边形，已知三角形面积如图所示(单位：平方厘米)，阴影部分的面积是多少平方厘米．【答案】4【解析】连接．由于与是平行的，所以也是梯形，那么．根据蝴蝶定理，，故，所以(平方厘米)．另解：在平行四边形中，(平方厘米)，所以(平方厘米)，根据蝴蝶定理，阴影部分的面积为(平方厘米)．【题文】如图，长方形被、分成四块，已知其中3块的面积分别为2、5、8平方厘米，那么余下的四边形的面积为多少平方厘米．【答案】9【解析】连接、．四边形为梯形，所以，又根据蝴蝶定理，，所以，所以(平方厘米)，(平方厘米)．那么长方形的面积为平方厘米，四边形的面积为(平方厘米)．【题文】如图，是等腰直角三角形，是正方形，线段与相交于点．已知正方形的面积48，，则的面积是多少？【答案】12【解析】由于是正方形，所以与平行，那么四边形是梯形．在梯形中，和的面积是相等的．而，所以的面积是面积的，那么的面积也是面积的．由于是等腰直角三角形，如果过作的垂线，为垂足，那么是的中点，而且，可见和的面积都等于正方形面积的一半，所以的面积与正方形的面积相等，为48．那么的面积为．【题文】下图中，四边形都是边长为1的正方形，、、、分别是，，，的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数，那么，的值等于多少？【答案】5【解析】左、右两个图中的阴影部分都是不规则图形，不方便直接求面积，观察发现两个图中的空白部分面积都比较好求，所以可以先求出空白部分的面积，再求阴影部分的面积．如下图所示，在左图中连接．设与的交点为．左图中为长方形，可知的面积为长方形面积的，所以三角形的面积为．又左图中四个空白三角形的面积是相等的，所以左图中阴影部分的面积为．如上图所示，在右图中连接、．设、的交点为．可知∥且．那么三角形的面积为三角形面积的，所以三角形的面积为，梯形的面积为．在梯形中，由于，根据梯形蝴蝶定理，其四部分的面积比为：，所以三角形的面积为，那么四边形的面积为．而右图中四个空白四边形的面积是相等的，所以右图中阴影部分的面积为．那么左图中阴影部分面积与右图中阴影部分面积之比为，即，那么．【题文】如图，中，，，互相平行，，则（）．【答案】1：3：5【解析】设份，根据面积比等于相似比的平方，所以，，因此份，份，进而有份，份，所以.【题文】如图，平行，且，，，求的长．【答案】10【解析】由金字塔模型得，所以【题文】如图，中，，，，，互相平行，，则．【答案】1：3：5：7：9【解析】设份，，因此份，进而有份，同理有份，份，份．所以有【题文】如图，已知正方形的边长为，是边的中点，是边上的点，且，与相交于点，求.【答案】【解析】方法一：连接，延长，两条线交于点，构造出两个沙漏，所以有，因此，根据题意有，再根据另一个沙漏有，所以．方法二：连接，分别求，，根据蝴蝶定理，所以．【题文】如图所示，已知平行四边形的面积是1，、是、的中点，交于，求的面积．【答案】【解析】解法一：由题意可得，、是、的中点，得，而，所以，并得、是的三等分点，所以，所以，所以，；又因为，所以．解法二：延长交于，如下图，可得，，从而可以确定的点的位置，，，(鸟头定理)，可得【题文】如图，为正方形，且，请问四边形的面积为多少？【答案】【解析】 (法)由，有，所以，又，所以，所以，所以占的，所以．(法)如图，连结，则(，而，所以，()．而()，因为，所以，则()，阴影部分面积等于()．【题文】如右图，三角形中，，，求．【答案】27：16【解析】根据燕尾定理得（都有的面积要统一，所以找最小公倍数）所以本题关键是把的面积统一，这种找最小公倍数的方法，在我们用比例解题中屡见不鲜，如果能掌握它的转化本质，我们就能达到解奥数题四两拨千斤的巨大力量！【题文】如右图，三角形中，，，求.【答案】10：9【解析】根据燕尾定理得（都有的面积要统一，所以找最小公倍数）所以【题文】如右图，三角形中，，，求.【答案】15：8【解析】根据燕尾定理得（都有的面积要统一，所以找最小公倍数）所以本题关键是把的面积统一，这种找最小公倍数的方法，在我们用比例解题中屡见不鲜，如果能掌握它的转化本质，我们就能达到解奥数题四两拨千斤的巨大力量！【题文】如右图，三角形中，，且三角形的面积是，则三角形的面积为多少，三角形的面积为多少，三角形的面积为多少？【答案】，，【解析】连接、、．由于，所以，故；根据燕尾定理，，，所以，则，；那么；同样分析可得，则，，所以，同样分析可得，所以，．【题文】如右图，三角形中，，且三角形的面积是，求三角形的面积．【答案】19【解析】连接BG，份根据燕尾定理，，得(份)，(份)，则(份)，因此,同理连接AI、CH得,,所以三角形GHI的面积是1，所以三角形ABC的面积是19【题文】如图，中，，，那么的面积是阴影三角形面积的多少倍．【答案】7【解析】如图，连接．根据燕尾定理，，，所以，，那么，．同理可知和的面积也都等于面积的，所以阴影三角形的面积等于面积的，所以的面积是阴影三角形面积的7倍．【题文】如图，三角形的面积是，，，三角形被分成部分，请写出这部分的面积各是多少?【答案】【解析】设BG与AD交于点P，BG与AE交于点Q，BF与AD交于点M，BF与AE交于点N．连接CP，CQ，CM，CN．根据燕尾定理，，，设(份)，则(份)，所以同理可得，,,而，所以，．同理，,所以，,,【题文】如图，的面积为1，点、是边的三等分点，点、是边的三等分点，那么四边形的面积是多少？【答案】【解析】连接、、．根据燕尾定理，，，所以，那么，．类似分析可得．又，，可得．那么，．根据对称性，可知四边形的面积也为，那么四边形周围的图形的面积之和为，所以四边形的面积为．【题文】右图，中，是的中点，、、是边上的四等分点，与交于，与交于，已知的面积比四边形的面积大平方厘米，则的面积是多少平方厘米？【答案】336【解析】连接、．根据燕尾定理，，，所以；再根据燕尾定理，，所以，所以，那么，所以．根据题意，有，可得(平方厘米)【题文】如图，面积为l的三角形ABC中，D、E、F、G、H、I分别是AB、BC、CA 的三等分点,求阴影部分面积.【答案】【解析】令BI与CD的交点为M，AF与CD的交点为N，BI与AF的交点为P,BI与CE的交点为Q,连接AM、BN、CP ⑴求：在中，根据燕尾定理，设(份)，则(份),(份),(份),所以，所以,,所以,同理可得另外两个顶点的四边形面积也分别是面积的⑵求：在中，根据燕尾定理, 所以,同理在中，根据燕尾定理,所以，所以同理另外两个五边形面积是面积的，所以【题文】如图，面积为l的三角形ABC中，D、E、F、G、H、I分别是AB、BC、CA 的三等分点,求中心六边形面积.【答案】【解析】设深黑色六个三角形的顶点分别为N、R、P、S、M、Q，连接CR在中根据燕尾定理，,所以,同理,所以，同理根据容斥原理，和上题结果【题文】已知的面积为平方厘米，，求的面积．【答案】24【解析】，设份，则份，份，份，份，恰好是平方厘米，所以平方厘米。

小学数学奥数测试题复杂直线型面积4_人教版-学习文档

第 1 页2019年小学奥数几何专题——复杂直线型面积-41．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？2．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．3．如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？4．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．5．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？6．如图所示，正方形ABCD 边长为6．三角形DEF 的面积为多少平方厘米？7．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．8．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．9．如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．10．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？11．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？12．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求F G S S ．13．如图所示，正方形ABCD 边长为8厘米，E 是AD 的中点，F 是CE 的中点，G 是BF 的中点，三角形ABG 的面积是多少平方厘米？14．四个面积为1的正六边形如图摆放，求阴影三角形的面积．15．已知图中每个正六边形的面积都是1，则图中虚线围成的五边形ABCDE 的面积是多少？16．如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．17．图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？18．如图，有三个正方形的顶点D 、G 、K 恰好在同一条直线上，其中正方形GFEB 的边长为10厘米，求阴影部分的面积．19．右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．20．如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为多少？21．正方形ABCD 和正方形CEFG ，且正方形ABCD 边长为10厘米，则图中阴影面积为多少平方厘米？22．长方形ABCD 的面积为362cm ，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？23．在边长为6厘米的正方形ABCD 内任取一点P ，将正方形的一组对边二等分，另一组对边三等分，分别与P 点连接,求阴影部分面积．24．ABCD 是边长为12的正方形，如图所示，P 是内部任意一点，4BL DM ==、5BK DN ==，那么阴影部分的面积是．25．如右图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC ∆的面积是多少平方厘米．26．图中三角形ABC 的面积是180平方厘米，D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF 长的3倍．那么三角形AEF 的面积是多少平方厘米？27．如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．28．如图，在三角形ABC 中，已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89，28，26．那么三角形DBE 的面积是多少？ 29．O 是长方形ABCD 内一点，已知OBC ∆的面积是25cm ，OAB ∆的面积是22cm ，求O BD ∆的面积是多少？30．如右图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？31．如右图，正方形ABCD 的面积是20，正三角形BPC ∆的面积是15，求阴影BPD ∆的面积．32．如右图，正方形ABCD 的面积是12，正三角形BPC ∆的面积是5，求阴影BPD ∆的面积．33．右图中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H ，已知CH 等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积．34．如图，已知长方形ADEF 的面积16，三角形ADB 的面积是3，三角形ACF 的面积是4，那么三角形ABC 的面积是多少？35．如图所示，三角形ABC 中，D 是AB 边的中点，E 是AC 边上的一点，且3AE EC =，O 为DC 与BE 的交点．若CEO ∆的面积为a 平方厘米，BDO ∆的面积为b 平方厘米．且b a -是2.5平方厘米，那么三角形ABC 的面积是多少平方厘米？36．如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米？37．如图，45BC =，21AC =，ABC ∆被分成9个面积相等的小三角形，那么DI FK +=？ 38．如图，在角MON 的两边上分别有A 、C 、E 及B 、D 、F 六个点，并且OAB ∆、ABC ∆、BCD ∆、CDE ∆、DEF ∆的面积都等于1，则DCF ∆的面积等于多少？39．如图，已知5CD =，7DE =，15EF =，6FG =，线段AB 将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG 的面积是多少？ 40．如图所示，长方形ABCD 内的阴影部分的面积之和为70，8AB =，15AD =，求四边形EFGO 的面积.41．如图所示，矩形ABCD 的面积为24平方厘米．三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则四边形PMON 的面积是多少平方厘米？42．如图，如果长方形ABCD 的面积是56平方厘米，那么四边形MNPQ 的面积是多少平方厘米？43．如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．44．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？45．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，第 3 页:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．46．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？47．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．48．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．49．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．50．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？51．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求F G S S ． 52．一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%，黄色三角形面积是221cm ．问：长方形的面积是多少平方厘米？53．如图，长方形ABCD 的面积是1，M 是AD 边的中点，N 在AB 边上，且2AN BN =.那么，阴影部分的面积是多少？54．如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求三角形DEF 的面积． 55．如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？56．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？第 1 页参考答案1．5【解析】连接AD ．又∵4BD DC ==，2．50【解析】连接BE ，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6A D E S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比3．48【解析】连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF 面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326⨯=（）倍．因此，平行四边形的面积为8648⨯=(平方厘米)．4．24【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米5．12.5【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米6．10():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△；而66218ABC S =⨯÷=△；所以4CEF S =△；同理得，:2:3CDE ACD S S =△△;，183212CDE S =÷⨯=△，6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米)．7．18【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC 和CFE 中，ACB ∠与FCE ∠互补，又1ABC S =，所以8FCE S =．同理可得6ADF S =，3BDE S =．所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=．8．1/18【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△．所以213618ABCD EFGH S S ==． 9．13.2【解析】连接BD ．由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△，即2CGF CDB S S =△△ 同理:1:2ABD AHE S S =△△，即2AHE ABD S S =△△所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ，同理可以得到2DHG BEF ABCD S S S +=△△四边形所以66513.2ABCD S =÷=四边形平方米10．60【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．第 3 页于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==． 11．3.5 【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABC S =，所以0.5FCE S =．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△12．1/10【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△． 13．12【解析】连接AF 、EG ．因为218164BCF CDE S S ==⨯=△△，根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =，8EFG S =，再根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，得到16BFC S =，32ABFE S =，24ABF S =，所以12ABG S =平方厘米．14．13/6【解析】如图，将原图扩展成一个大正三角形DEF ，则AGF ∆与CEH ∆都是正三角形．假设正六边形的边长为为a ，则A G F ∆与CEH ∆的边长都是4a ，所以大正三角形DEF 的边长为4217⨯-=，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为16，三角形DEF 的面积为496．由于4FA a =，3FB a =，所以AFB ∆与三角形DEF 的面积之比为43127749⨯=．同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249，所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=，所以ABC ∆的面积的面积为4913136496⨯=． 15．263【解析】从图中可以看出，虚线AB 和虚线CD 外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线BC 和虚线DE 外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线AE 外的图形是两个三角形，从右图中可以看出，每16．28【解析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ．同理，BFH CFH S S =△△，S =S CGH DGH ，∴11562822ABCD S S ==⨯=阴影长方形(平方厘米)． 17．48【解析】把另外三个三等分点标出之后，正方形的3个边就都被分成了相等的三段．把H 和这些分点以及正方形的顶点相连，把整个正方形分割成了9个形状各不相同的三角形．这9个三角形的底边分别是在正方形的3个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了3个三角形，右边三角形的面积和第1第2个三角形相等：中间三角形的面积和第3第4个三角形相等；左边三角形的面积和第5个第6个三角形相等．因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是144，阴影部分的面积就是48． 18．100【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接FK 、GE 、BD ，则////BD G E FK ，根据几何五大模型中的面积比例模型，可得DGE BGE S S ∆∆=，KGE FGE S S ∆∆=，所以阴影部分的面积就等于正方形GFEB 的面积，即为210100=平方厘米．19．8【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接AD (见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AGD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABG 与三角形GCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面第 5 页积，等于4428⨯÷=．20．6【解析】如图，连接AF ，比较ABF ∆与ADF ∆，由于AB AD =，FG FE =，即ABF ∆与ADF ∆的底与高分别相等，所以ABF ∆与ADF ∆的面积相等，那么阴影部分面积与ABH ∆的面积相等，为6平方厘米．21．50【解析】方法一：三角形BEF 的面积2BE EF =⨯÷，梯形EFDC 的面积22EF CD CE BE EF =+⨯÷=⨯÷=（）三角形BEF 的面积，而四边形CEFH 是它们的公共部分，所以，三角形DHF 的面积=三角形BCH 的面积，进而可得，阴影面积=三角形BDF 的面积=三角形BCD 的面积1010250=⨯÷=(平方厘米)．方法二：连接CF ，那么CF 平行BD ，所以，阴影面积=三角形BDF 的面积=三角形BCD 的面积50=(平方厘米)．22．13.5而36ABCD AHB CHB CHD S S S S ∆∆∆=++=而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影，所以阴影部分的面积是：1818 4.513.5EBF S S ∆=-=-=阴影解法二：特殊点法．找H 的特殊点，把H 点与D 点重合，那么图形就可变成右图：这样阴影部分的面积就是DEF ∆的面积，根据鸟头定理，则有：23．15【解析】（法1）特殊点法．由于P 是正方形内部任意一点，可采用特殊点法，假设P 点与A 点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的14和16，所以阴影部分的面积为2116()1546⨯+=平方厘米．（法2）连接PA 、PC ．由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半，所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14，同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16，所以阴影部分的面积为2116()1546⨯+=平方厘米． 24．34【解析】（法1）特殊点法．由于P 是内部任意一点，不妨设P 点与A 点重合(如上中图)，那么阴影部分就是AMN ∆和ALK ∆．而AMN ∆的面积为(125)4214-⨯÷=，ALK ∆的面积为(124)5220-⨯÷=，所以阴影部分的面积为142034+=．（法2）寻找可以利用的条件，连接AP 、BP 、CP 、DP 可得右上图所示：则有:211127222PDC PAB ABCD S S S ∆∆+==⨯= 同理可得：72PAD PBC S S ∆∆+=;而::4:121:3PDM PDC S S DM DC ∆∆===,即13PDM PDC S S ∆∆=；同理：13PBL PAB S S ∆∆=,512PND PDA S S ∆∆=,512PBK PBC S S ∆∆=; 所以：15()()()()312PDM PBL PND PBK PDC PAB PDA PBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++ 而()()()()PDM PBL PND PBK PNM PLK DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++阴影面积；所以阴影部分的面积是：即为：15727210224302034312⨯+⨯-⨯=+-=． 25．30【解析】连接CD ．根据题意可知，DEF ∆的面积为DAC ∆面积的13，DAC ∆的面积为ABC ∆面积的12，所以DEF ∆的面积为ABC ∆面积的111236⨯=．而D E F ∆的面积为5平方厘米，所以ABC ∆的面积为15306÷=(平方厘米)． 26．22.5 【解析】ABD ，ABC 等高，所以面积的比为底的比，有ABD ABC S S = 所以ABD S =ABC S =平方厘米)．1903ABE ABD AE S S AD =⨯=⨯平方厘米)34AFE ABE FE SS BE =⨯=30⨯平方厘米)．即三角形AEF 的面积是22.5平方厘米．27．5【解析】如图，将大长方形的长的长度设为1，则12112364AB ==+，24124483CD ==+，所以1113412MN =-=，阴影部分面积为211(12243648)5(cm )212+++⨯⨯=． 28【解析】根据题意可知，8928117ADC ADE DCE S S S ∆∆∆=+=+=，第 7 页所以::26:1172:9BDC ADC BD AD S S ∆∆===，那么::2:9DBE ADE S S BD AD ∆∆==，29．3【解析】由于ABCDDA O DB OC A B DS S S ∆∆∆+=，则BOC OAB OBD S S S ∆∆∆=+，所以2523cm OBD BOC OAB S S S ∆∆∆=-=-=．30．16【解析】根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差．如右上图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCPABPBDPS S S S S ∆∆∆-=-==(平方分米)．31．10 【解析】连接AC 交BD 于O 点，并连接PO ．如下图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有：因为1120544BOC ABCD S S ∆==⨯=，所以15510BPD S ∆=-=． 32．2【解析】连接AC 交BD 于O 点，并连接PO ．如右上图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有: 因为134BOC ABCD S S ∆==，所以532BPD S ∆=-=．33．49.5 【解析】连接AC 、GF ，由于AC 与GF 平行，可知四边形ACGF 构成一个梯形．由于HCG ∆面积为6平方厘米，且CH 等于CF 的三分之一，所以CH 等于FH 的12，根据梯形蝴蝶定理或相似三角形性质，可知FHG ∆的面积为12平方厘米，AHF ∆的面积为6平方厘米，AHC ∆的面积为3平方厘米．那么正方形CGEF 的面积为()612236+⨯=平方厘米，所以其边长为6厘米．又AFC ∆的面积为639+=平方厘米，所以9263AD =⨯÷=(厘米)，即正方形ABCD 的边长为3厘米．那么，五边形ABGEF 的面积为：21369349.52++⨯=(平方厘米)． 34．6.5 【解析】方法一：连接对角线AE ． ∵ADEF 是长方形方法二：连接BF ，由图知1628ABF S =÷=△，所以16835BEF S =--=△，又由4ACF S =△，恰好是AEF △面积的一半，所以C 是EF 的中点，因此52 2.5BCE BCF S S ==÷=△△，所以1634 2.5 6.5ABC S =---=△ 35．10平方厘米)．所以 2.5410ABC S ∆=⨯=(平方厘米)． 36．512【解析】如下图，连接FC ，DBF 、BFG 的面积相等，设为x 平方厘米;FGC 、DFC的面积相等，设为y 平方厘米，那么DEF 的面积为221BCD Sx y =+=，BDE1S=x+y=l 3．所以有0.531x y x y +=⎧⎨+=⎩①②．比较②、①式，②式左边比①式左边多2x ，②式右边比①式右边大0.5，有20.5x =，即0.25x =,0.25y =．而37．24【解析】由题意可知，::2:9BAD ABC BD BC S S ∆∆==，所以2109BD BC ==，35CD BC BD =-=；又::2:5DIF DFC DI DC S S ∆∆==，所以2145DI DC ==，同样分析可得10FK =，所以141024DI FK +=+=．38．34【解析】根据题意可知，::4:1OED DEF OD DF S S ∆∆==，所以，39．40【解析】连接AF ，BD ．第 9 页根据题意可知，571527CF =++=；715628DG =++=；所以，1527BE CBF F S S ∆∆=，1227BE CBF C S S ∆∆=，2128AEG ADG S S ∆∆=，728AED ADG S S ∆∆=，于是：2115652827ADG CBF S S ∆∆+=；712382827ADG CBF S S ∆∆+=；可得40ADG S ∆=．故三角形ADG 的面积是40．40．10【解析】利用图形中的包含关系可以先求出三角形AOE 、和，以及三角形AOE 和DOG 的面积之和，进而求出四边形由于长方形ABCD 的面积为158120⨯=，所以三角形BOC 的面积为形AOE 和DOG 的面积之和为又三角形AOE 、DOG 和四边形EFGO 的面积之和为所以四边形EFGO的面积为302010-=．另解：从整体上来看，四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积，而三角形AFC 面积+三角形BFD 面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即1207050-=，所以四边形的面积为605010-=． 41．1.8【解析】因为三角形ADO 与三角形BCO 的面积之和是矩形ABCD 的面积的一半，即12平方厘米，又三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则三角形AMO 与三角形BNO 的面积之和是4.2平方厘米，则四边形PMON 的面积=三角形ABP 面积-三角形AMO 与三角形BNO 的面积之和-三角形ABO 面积12 4.26 1.8=--=(平方厘米)． 42．32.5 【解析】如图，过M 、N 、P 、Q 分别作长方形ABCD 的各边的平行线．易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．设MQD ∆、NAM ∆、PBN ∆、QCP ∆的面积之和为S ，四边形MNPQ 的面积等于x ，则569x S x S +=⎧⎨-=⎩，解得32.5x =(平方厘米)．43．70【解析】连接BE ，::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△，::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△，所以:(24):(75)ADE ABC S S =⨯⨯△△，设8AD ES =△份，则35ABC S =△份，16ADE S =△平方厘米，所以1份是2平方厘米，35份就是70平方厘米，ABC △的面积是70平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比． 44．5 【解析】连接AD ．又∵4BD DC ==， 45．50 【解析】连接BE ，::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6A D E S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 46．12.5【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米 47．24 【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米48．18 【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC 和CFE 中，ACB ∠与FCE ∠互补，又1ABCS=，所以8FCES=．第 11 页同理可得6ADFS =，3BDES=．所以186318DEFABCFCEADFBDESSSSS=+++=+++=．【答案】118【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△． 50．60 【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==． 51．110【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为52．60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长，高相加为长方形的宽，所以黄色三角形与绿色三角形的面积和为长方形面积的50%，而绿色三角形面积占长方形面积的15%，所以黄色三角形面积占长方形面积的50%15%35%-=．已知黄色三角形面积是221cm ，所以长方形面积等于2135%60÷=（2cm ）．53．512【解析】连接BM ，因为M 是中点所以ABM △的面积为又因为2AN BN =，所以BDC △的面积，又因为BDC △面积为54．3【解析】三角形ADC 的面积是三角形ABC 面积的一半24212÷=，三角形ADE 又是三角形ADC 面积的一半1226÷=．三角形FED 的面积是三角形ADE 面积的一半，所以三角形FED 的面积623=÷=． 55．15 【解析】连接BE ．又∵5AB AD = 56．3.5【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABCS=，所以0.5FCES=．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△。

小学数学奥数测试题复杂直线型面积4_人教版

第 1 页2019年小学奥数几何专题——复杂直线型面积-41．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？2．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．3．如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？4．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．5．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？6．如图所示，正方形ABCD 边长为6．三角形DEF 的面积为多少平方厘米？7．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．8．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．9．如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．10．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？11．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？12．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求FGS S V ．13．如图所示，正方形ABCD 边长为8厘米，E 是AD 的中点，F 是CE 的中点，G 是BF 的中点，三角形ABG 的面积是多少平方厘米？14．四个面积为1的正六边形如图摆放，求阴影三角形的面积．15．已知图中每个正六边形的面积都是1，则图中虚线围成的五边形ABCDE 的面积是多少？16．如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．17．图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？18．如图，有三个正方形的顶点D 、G 、K 恰好在同一条直线上，其中正方形GFEB 的边长为10厘米，求阴影部分的面积．19．右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．20．如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为多少？21．正方形ABCD 和正方形CEFG ，且正方形ABCD 边长为10厘米，则图中阴影面积为多少平方厘米？22．长方形ABCD 的面积为362cm ，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？23．在边长为6厘米的正方形ABCD 内任取一点P ，将正方形的一组对边二等分，另一组对边三等分，分别与P 点连接,求阴影部分面积．24．ABCD 是边长为12的正方形，如图所示，P 是内部任意一点，4BL DM ==、5BK DN ==，那么阴影部分的面积是．25．如右图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC ∆的面积是多少平方厘米．26．图中三角形ABC 的面积是180平方厘米，D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF 长的3倍．那么三角形AEF 的面积是多少平方厘米？27．如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．28．如图，在三角形ABC 中，已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89，28，26．那么三角形DBE 的面积是多少？ 29．O 是长方形ABCD 内一点，已知OBC ∆的面积是25cm ，OAB ∆的面积是22cm ，求OBD ∆的面积是多少？30．如右图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？31．如右图，正方形ABCD 的面积是20，正三角形BPC ∆的面积是15，求阴影BPD ∆的面积．32．如右图，正方形ABCD 的面积是12，正三角形BPC ∆的面积是5，求阴影BPD ∆的面积．33．右图中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H ，已知CH 等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积．34．如图，已知长方形ADEF 的面积16，三角形ADB 的面积是3，三角形ACF 的面积是4，那么三角形ABC 的面积是多少？35．如图所示，三角形ABC 中，D 是AB 边的中点，E 是AC 边上的一点，且3AE EC =，O 为DC 与BE 的交点．若CEO ∆的面积为a 平方厘米，BDO ∆的面积为b 平方厘米．且b a -是2.5平方厘米，那么三角形ABC 的面积是多少平方厘米？36．如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米？37．如图，45BC =，21AC =，ABC ∆被分成9个面积相等的小三角形，那么DI FK +=？ 38．如图，在角MON 的两边上分别有A 、C 、E 及B 、D 、F 六个点，并且OAB ∆、ABC ∆、BCD ∆、CDE ∆、DEF ∆的面积都等于1，则DCF ∆的面积等于多少？39．如图，已知5CD =，7DE =，15EF =，6FG =，线段AB 将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG 的面积是多少？ 40．如图所示，长方形ABCD 内的阴影部分的面积之和为70，8AB =，15AD =，求四边形EFGO 的面积.41．如图所示，矩形ABCD 的面积为24平方厘米．三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则四边形PMON 的面积是多少平方厘米？42．如图，如果长方形ABCD 的面积是56平方厘米，那么四边形MNPQ 的面积是多少平方厘米？43．如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．44．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？45．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，第 3 页:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．46．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？47．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．48．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．49．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．50．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？51．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求FGS S V ． 52．一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%，黄色三角形面积是221cm ．问：长方形的面积是多少平方厘米？53．如图，长方形ABCD 的面积是1，M 是AD 边的中点，N 在AB 边上，且2AN BN =.那么，阴影部分的面积是多少？54．如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求三角形DEF 的面积． 55．如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？56．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？第 1 页参考答案1．5【解析】连接AD ．又∵4BD DC ==，2．50【解析】连接BE ，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6ADE S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比3．48【解析】连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF 面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326⨯=（）倍．因此，平行四边形的面积为8648⨯=(平方厘米)．4．24【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米5．12.5【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米6．10():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△；而66218ABC S =⨯÷=△；所以4CEF S =△；同理得，:2:3CDE ACD S S =△△;，183212CDE S =÷⨯=△，6CDF S =△故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米)．7．18【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC V 和CFE V 中，ACB ∠与FCE ∠互补，又1ABC S =V ，所以8FCE S =V ．同理可得6ADF S =V ，3BDE S =V ．所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=V V V V V ．8．1/18【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△．所以213618ABCD EFGH S S ==． 9．13.2【解析】连接BD ．由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△，即2CGF CDB S S =△△ 同理:1:2ABD AHE S S =△△，即2AHE ABD S S =△△所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ，同理可以得到2DHG BEF ABCD S S S +=△△四边形所以66513.2ABCD S =÷=四边形平方米10．60【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．第 3 页于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==． 11．3.5 【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABC S =V ，所以0.5FCE S =V ．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△12．1/10【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△． 13．12【解析】连接AF 、EG ．因为218164BCF CDE S S ==⨯=△△，根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ，8EFG S =V ，再根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，得到16BFC S =V ，32ABFE S =，24ABF S =V ，所以12ABG S =V 平方厘米．14．13/6【解析】如图，将原图扩展成一个大正三角形DEF ，则AGF ∆与CEH ∆都是正三角形．假设正六边形的边长为为a ，则AGF ∆与CEH ∆的边长都是4a ，所以大正三角形DEF 的边长为4217⨯-=，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为16，三角形DEF 的面积为496．由于4FA a =，3FB a =，所以AFB ∆与三角形DEF 的面积之比为43127749⨯=．同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249，所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=，所以ABC ∆的面积的面积为4913136496⨯=． 15．263【解析】从图中可以看出，虚线AB 和虚线CD 外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线BC 和虚线DE 外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线AE 外的图形是两个三角形，从右图中可以看出，每所以五16．28【解析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ．同理，BFH CFH S S =△△，S =S CGH DGH V V ，∴11562822ABCD S S ==⨯=阴影长方形(平方厘米)． 17．48【解析】把另外三个三等分点标出之后，正方形的3个边就都被分成了相等的三段．把H 和这些分点以及正方形的顶点相连，把整个正方形分割成了9个形状各不相同的三角形．这9个三角形的底边分别是在正方形的3个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了3个三角形，右边三角形的面积和第1第2个三角形相等：中间三角形的面积和第3第4个三角形相等；左边三角形的面积和第5个第6个三角形相等．因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是144，阴影部分的面积就是48． 18．100【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接FK 、GE 、BD ，则////BD GE FK ，根据几何五大模型中的面积比例模型，可得DGE BGE S S ∆∆=，KGE FGE S S ∆∆=，所以阴影部分的面积就等于正方形GFEB 的面积，即为210100=平方厘米．19．8【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接AD (见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AGD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABG 与三角形GCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面第 5 页积，等于4428⨯÷=．20．6【解析】如图，连接AF ，比较ABF ∆与ADF ∆，由于AB AD =，FG FE =，即ABF ∆与ADF ∆的底与高分别相等，所以ABF ∆与ADF ∆的面积相等，那么阴影部分面积与ABH ∆的面积相等，为6平方厘米．21．50【解析】方法一：三角形BEF 的面积2BE EF =⨯÷，梯形EFDC 的面积22EF CD CE BE EF =+⨯÷=⨯÷=（）三角形BEF 的面积，而四边形CEFH 是它们的公共部分，所以，三角形DHF 的面积=三角形BCH 的面积，进而可得，阴影面积=三角形BDF 的面积=三角形BCD 的面积1010250=⨯÷=(平方厘米)．方法二：连接CF ，那么CF 平行BD ，所以，阴影面积=三角形BDF 的面积=三角形BCD 的面积50=(平方厘米)．22．13.5而36ABCD AHB CHB CHD S S S S ∆∆∆=++=而EHB BHF DHG EBF S S S S S ∆∆∆∆++=+阴影，所以阴影部分的面积是：1818 4.513.5EBF S S ∆=-=-=阴影解法二：特殊点法．找H 的特殊点，把H 点与D 点重合，那么图形就可变成右图：这样阴影部分的面积就是DEF ∆的面积，根据鸟头定理，则有：23．15【解析】（法1）特殊点法．由于P 是正方形内部任意一点，可采用特殊点法，假设P 点与A 点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的14和16，所以阴影部分的面积为2116()1546⨯+=平方厘米．（法2）连接PA 、PC ．由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半，所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14，同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16，所以阴影部分的面积为2116()1546⨯+=平方厘米． 24．34【解析】（法1）特殊点法．由于P 是内部任意一点，不妨设P 点与A 点重合(如上中图)，那么阴影部分就是AMN ∆和ALK ∆．而AMN ∆的面积为(125)4214-⨯÷=，ALK ∆的面积为(124)5220-⨯÷=，所以阴影部分的面积为142034+=．（法2）寻找可以利用的条件，连接AP 、BP 、CP 、DP 可得右上图所示：则有:211127222PDC PAB ABCD S S S ∆∆+==⨯= 同理可得：72PAD PBC S S ∆∆+=;而::4:121:3PDM PDC S S DM DC ∆∆===,即13PDM PDC S S ∆∆=；同理：13PBL PAB S S ∆∆=,512PND PDA S S ∆∆=,512PBK PBC S S ∆∆=; 所以：15()()()()312PDM PBL PND PBK PDC PAB PDA PBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++ 而()()()()PDM PBL PND PBK PNM PLK DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++1442443阴影面积；所以阴影部分的面积是：即为：15727210224302034312⨯+⨯-⨯=+-=． 25．30【解析】连接CD ．根据题意可知，DEF ∆的面积为DAC ∆面积的13，DAC ∆的面积为ABC ∆面积的12，所以DEF ∆的面积为ABC ∆面积的111236⨯=．而DEF ∆的面积为5平方厘米，所以ABC ∆的面积为15306÷=(平方厘米)． 26．22.5 【解析】ABD V ，ABC V 等高，所以面积的比为底的比，有所以ABD S V =平方厘米)．平方厘米)平方厘米)．即三角形AEF 的面积是22.5平方厘米．27．5【解析】如图，将大长方形的长的长度设为1，则12112364AB ==+，24124483CD ==+，所以1113412MN =-=，阴影部分面积为211(12243648)5(cm )212+++⨯⨯=． 28【解析】根据题意可知，8928117ADC ADE DCE S S S ∆∆∆=+=+=，所以::26:1172:9BDC ADC BD AD S S ∆∆===，第 7 页那么::2:9DBE ADE S S BD AD ∆∆==，29．3【解析】由于ABCD 是长方形，所AOD BOC ABD S S S ∆∆∆+=，则BOC OAB OBD S S S ∆∆∆=+，所以2523cm OBD BOC OAB S S S ∆∆∆=-=-=．30．16【解析】根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差．如右上图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米)．31．10 【解析】连接AC 交BD 于O 点，并连接PO ．如下图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有：因为1120544BOC ABCD S S ∆==⨯=，所以15510BPD S ∆=-=． 32．2【解析】连接AC 交BD 于O 点，并连接PO ．如右上图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有: 因为134BOC ABCD S S ∆==，所以532BPD S ∆=-=．33．49.5 【解析】连接AC 、GF ，由于AC 与GF 平行，可知四边形ACGF 构成一个梯形．由于HCG ∆面积为6平方厘米，且CH 等于CF 的三分之一，所以CH 等于FH 的12，根据梯形蝴蝶定理或相似三角形性质，可知FHG ∆的面积为12平方厘米，AHF ∆的面积为6平方厘米，AHC ∆的面积为3平方厘米．那么正方形CGEF 的面积为()612236+⨯=平方厘米，所以其边长为6厘米．又AFC ∆的面积为639+=平方厘米，所以9263AD =⨯÷=(厘米)，即正方形ABCD 的边长为3厘米．那么，五边形ABGEF 的面积为：21369349.52++⨯=(平方厘米)． 34．6.5【解析】方法一：连接对角线AE ． ∵ADEF 是长方形方法二：连接BF ，由图知1628ABF S =÷=△，所以16835BEF S =--=△，又由4ACF S =△，恰好是AEF △面积的一半，所以C 是EF 的中点，因此52 2.5BCE BCF S S ==÷=△△，所以1634 2.5 6.5ABC S =---=△35．10平方厘米)．所以 2.5410ABC S ∆=⨯=(平方厘米)． 36．512【解析】如下图，连接FC ，DBF V 、BFG V 的面积相等，设为x 平方厘米;FGC V 、DFC V 的面积相等，设为y 平方厘米，那么DEF V 的面积为221BCD S x y =+=V ，．所以有0.531x y x y +=⎧⎨+=⎩①②．比较②、①式，②式左边比①式左边多2x ，②式右边比①式右边大0.5，有20.5x =，即0.25x =,0.25y =．而37．24【解析】由题意可知，::2:9BAD ABC BD BC S S ∆∆==，所以2109BD BC ==，35CD BC BD =-=；又::2:5DIF DFC DI DC S S ∆∆==，所以2145DI DC ==，同样分析可得10FK =，所以141024DI FK +=+=．38．34【解析】根据题意可知，::4:1OED DEF OD DF S S ∆∆==，所以，39．40【解析】连接AF ，BD ．根据题意可知，571527CF =++=；715628DG =++=；所以，1527BE CBF F S S ∆∆=，1227BE CBF C S S ∆∆=，2128AEG ADG S S ∆∆=，728AED ADG S S ∆∆=，第 9 页于是：2115652827ADG CBF S S ∆∆+=；712382827ADG CBF S S ∆∆+=；可得40ADG S ∆=．故三角形ADG 的面积是40．40．10【解析】利用图形中的包含关系可以先求出三角形AOE 、和，以及三角形AOE 和DOG 的面积之和，进而求出四边形由于长方形ABCD 的面积为158120⨯=，所以三角形BOC 的面积为形AOE 和DOG 的面积之和为又三角形AOE 、DOG 和四边形EFGO 的面积之和为所以四边形EFGO的面积为302010-=．另解：从整体上来看，四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积，而三角形AFC 面积+三角形BFD 面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即1207050-=，所以四边形的面积为605010-=． 41．1.8【解析】因为三角形ADO 与三角形BCO 的面积之和是矩形ABCD 的面积的一半，即12平方厘米，又三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则三角形AMO 与三角形BNO 的面积之和是4.2平方厘米，则四边形PMON 的面积=三角形ABP 面积-三角形AMO 与三角形BNO 的面积之和-三角形ABO 面积12 4.26 1.8=--=(平方厘米)． 42．32.5 【解析】如图，过M 、N 、P 、Q 分别作长方形ABCD 的各边的平行线．易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．设MQD ∆、NAM ∆、PBN ∆、QCP ∆的面积之和为S ，四边形MNPQ 的面积等于x ，则569x S x S +=⎧⎨-=⎩，解得32.5x =(平方厘米)．43．70【解析】连接BE ，::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△，::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△，所以:(24):(75)ADE ABC S S =⨯⨯△△，设8ADE S =△份，则35ABC S =△份，16ADE S =△平方厘米，所以1份是2平方厘米，35份就是70平方厘米，ABC △的面积是70平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比． 44．5 【解析】连接AD ．又∵4BD DC ==， 45．50 【解析】连接BE ，::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6ADE S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 46．12.5【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米 47．24 【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米48．18 【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=． (法2)用共角定理∵在ABC V 和CFE V 中，ACB ∠与FCE ∠互补，又1ABC S =V ，所以8FCE S =V ．同理可得6ADF S =V ，3BDE S =V ．所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=V V V V V ．第 11 页【答案】118【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△． 50．60 【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==． 51．110【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为52．60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长，高相加为长方形的宽，所以黄色三角形与绿色三角形的面积和为长方形面积的50%，而绿色三角形面积占长方形面积的15%，所以黄色三角形面积占长方形面积的50%15%35%-=．已知黄色三角形面积是221cm ，所以长方形面积等于2135%60÷=（2cm ）． 53．512【解析】连接BM ，因为M 是中点所以ABM △的面积为又因为2AN BN =，所以BDC △的面积，又因为BDC △面积为54．3【解析】三角形ADC 的面积是三角形ABC 面积的一半24212÷=，三角形ADE 又是三角形ADC 面积的一半1226÷=．三角形FED 的面积是三角形ADE 面积的一半，所以三角形FED 的面积623=÷=． 55．15 【解析】连接BE ．又∵5AB AD = 56．3.5【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABC S =V ，所以0.5FCE S =V ．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△。

五年级奥数学练习试卷思维培训资料直线形面积的计算

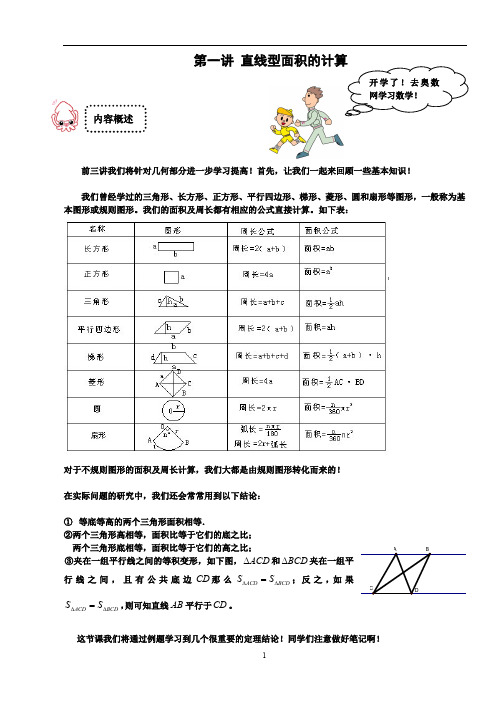
前三讲我们将针对几何部分进一步学习提高！首先，让我们一起来回顾一些基本知识！
我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形。

我们的面积及周长都有相应的公式直接计算。

如下表：
【例。

平行，所以四边形BDEF
，所以S△NBO=4/3 ，
，可得△FBE面积=6 。

绿色三
D
A
B E
C
BCD的面积，等于4×4÷
那么问题就解决了。

【附
DG=4
厘米，
=3+27+16-45=1 。

宽为8，中间有一条宽为2的道路，
分析：将道路进行一定的分割，如下左图所示，而后将1、3、5推到长方形左端，2、4、6推倒长方形上
1．将任一个三角形分成面积相等的六个三角形，用四种不同的方法应怎么分？。

小学数学几何直线型面积的计算完整版题型训练+详细答案

直线形面积的计算例题讲解：板块一：基础题型：1．如图，四边形ABCD是直角梯形，其中AD=12（厘米），AB=8（厘米），BC= 15（厘米），且三角形ADE、四边形DEBF、三角形CDF的面积相等，阴影三角形DEF的面积是多少平方厘米？解析：四边形ABCD的面积是（12+15）×8÷2=108（平方厘米），108÷3=36（平方厘米）。

CF=36×2÷8=9(厘米)，FB=15-9=6(厘米)，AE=36×2÷12=6（厘米），EB=8-6=2（厘米）。

阴影三角形DEF的面积是36-2×6÷2=30（平方厘米）2．一块长方形的土地被分割成4个小长方形，其中三块的面积如图所示（单位：平方米），剩下一块的面积应该是多少平方米？解析：40×15÷30=20（平方米）3．如图，在三角形ABC中，BC是DC的3倍，AC是EC的3倍，三角形DEC的面积是3平方厘米．请问：三角形ABC的面积是多少平方厘米？解析：三角形ADC的面积是3×3=9（平方厘米），三角形ABC的面积是3×9=27（平方厘米）4．如图，E是BC上靠近C的三等分点，且ED是AD的2倍，三角形ABC的面积为36平方厘水．三角形BDE的面积是多少平方厘米？解析：三角形BAE的面积是36÷3×2=24（平方厘米），三角形BDE的面积24÷3×2=16（平方厘米）5．如图所示，已知三角形BEC的面积等于20平方厘米，E是AB边上靠近日点的四等分点，三角形AED的面积是多少平方厘米？平行四边形DECF的面积是多少平方厘米？解析：（1）三角形AED的面积是20×3=60（平方厘米）（2）三角形DEC的面积是20+60=80（平方厘米），三角形DEC的面积是平行四边形DECF 的面积的一半，也是平行四边形ABCD的面积的一半，所以平行四边形DECF的面积是80×2=160（平方厘米）6．如图，已知平行四边形ABCD的面积为36，三角形AOD的面积为8．三角形BOC的面积为多少？解析：根据一半模型可知，三角形AOD的面积和三角形BOC的面积是平行四边形ABCD 的面积的一半，所以三角形BOC的面积是36÷2-8=107．如图，长方形ABCD的面积是96平方厘米，E是AD边上靠近D点的三等分点，F是CD上靠近C点的四等分点．阴影部分的面积是多少平方厘米？解析：链接BD ，可知三角形ABD 的面积和三角形BDC 都是96÷2=48（平方厘米），三角形ABE 的面积是48×32=32（平方厘米）。

小学数学奥数测试题复杂直线型面积10_人教版

小学数学奥数测试题复杂直线型面积10_人教版，是的中点．阴影部分的面积是多少平方厘米？16．如图，三角形田地中有两条小路和，交叉处为，张大伯常走这两条小路，他知道,且．则两块地和的面积比是多少？17．如图，，，被分成个面积相等的小三角形，那么18．如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于．19．、分别为直角梯形两边上的点，且、、彼此平行，若，，，．求阴影部分的面积．20．已知为等边三角形，面积为400，、、分别为三边的中点，已知甲、乙、丙面积和为143，求阴影五边形的面积．(丙是三角形)21．如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形的面积是．2EC DE=F DG AE CF D DF DC=2AD DE =ACF CFB 45BC =21AC =ABC ∆9DI FK +=MON A C E BD F OAB ∆ABC ∆BCD ∆CDE ∆DEF∆DCF∆E M ABCD DQCP ME 5AD =7BC =5AE =3EB =ABC D E FHBC5CD =7DE =15EF =6FG =AB ADG参考答案1．100 【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接、、，则，根据几何五大模型中的面积比例模型，可得，，所以阴影部分的面积就等于正方形的面积，即为平方厘米．2．8 【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接(见右上图)，可以看出，三角形与三角形的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形是三角形与三角形的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形与三角形面积仍然相等．根据等量代换，求三角形的面积等于求三角形的面FK GE BD ////BD GE FK DGE BGES S ∆∆=KGEFGESS ∆∆=GFEB 210100=ADABD ACDAGD ABD ACD ABG GCD ABC BCD积，等于． 3．6 【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米． 4．50 【解析】方法一：三角形BEF 的面积，梯形EFDC 的面积三角形BEF 的面积，而四边形CEFH 是它们的公共部分，所以，三角形DHF 的面积三角形BCH 的面积，进而可得，阴影面积三角形BDF 的面积三角形BCD 的面积(平方厘米)．方法二：连接CF ，那么CF 平行BD ，所以，阴影面积三角形BDF 的面积三角形BCD 的面积(平方厘米)． 5．20 【解析】如果注意到为一个正方形的对角线(或者说一个等腰直角三角形的斜边)，那么容易想到与4428⨯÷=AF ABF ∆ADF ∆AB AD =FG FE =ABF ∆ADF ∆ABF ∆ADF ∆ABH ∆2BE EF =⨯÷22EF CD CE BE EF =+⨯÷=⨯÷=（）===1010250=⨯÷===50=DF DF是平行的．所以可以连接、，如上图．由于与平行，所以的面积与的面积相等．而的面积为，所以的面积也为20． 6．49.5 【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)． 7．12.8【解析】因为乙、丙两个三角形面积相等，底．所以到的距离与到的距离相等，即与平行，四边形是平行四边形，阴影CICI CF DF CI DFI ∆DFC ∆DFC ∆1104202⨯⨯=DFI ∆AC GF AC GF ACGF HCG ∆CH CF CH FH 12FHG ∆AHF ∆AHC ∆CGEF ()612236+⨯=AFC ∆639+=9263AD =⨯÷=ABCD ABGEF 21369349.52++⨯=DF FC=A CD E CD AE CD ADCE部分的面积平行四边形的面积的，所以阴影部分的面积乙的面积．设甲、乙、丙的面积分别为份，则阴影面积为份，梯形的面积为份，从而阴影部分的面积(平方厘米)．8．6.5 【解析】方法一：连接对角线． ∵是长方形方法二：连接，由图知，所以，又由，恰好是面积的一半，所以是的中点，因此，所以9．1：2【解析】方法一：因为，，所以，．因为，所以，所以，．同理可得，，．因为，所以空白部分的面积，所以阴影部分的面积是．，所以阴影面积与空白面积的比是．=ADCE 12=2⨯125325212.8=÷⨯=AE ADEF BF1628ABFS=÷=△16835BEF S =--=△4ACFS=△AEF △C EF 52 2.5BCEBCF S S ==÷=△△1634 2.5 6.5ABCS =---=△BE EC =2CF FD =14ABEABCDS S =△四边形16ADFABCDS S=△四边形2AD BE =2AG GE =11312BGEABEABCDS S S ==△△四边形2136ABGABEABCD S SS ==△△四边形18ADHABCD S S =△四边形124DHFABCDSS=△四边形12BCD ABCDS S =△四边形111112()21224683ABCD ABCDS S =--++=四边形四边形13ABCDS四边形12:1:233=1:210．10 【解析】，，所以(平方厘米)．所以(平方厘米)． 11．115【解析】根据题意可知，则，，而平方厘米，所以，则平方厘米．又，所以平方厘米．所以(平方厘米)．12．28 【解析】连接．根据差不变原理可知三角形的面积比三角形大4平方米，而三角形与三角形面积相等，因此也与三角形面积相等，从而三角形的面积比三角形的大4平方米．但，所以三角形的面积是三角形的，从而三角形的面积是(平方米)，梯形的面积为：(平方米)． 12ABCBCD BCOSS b S ∆∆∆==+14ABCBCE BCOSS a S ∆∆∆==+112.524ABC ABC S S b a ∆∆-=-= 2.5410ABCS∆=⨯=::8:6:9AD BE EC =86ABD ABESS∆∆=34ABE ABD S S ∆∆=10ABDABE AOD BOE SS S S ∆∆∆∆-=-=1104ABDS∆=40ABD S ∆=961588BCD ABDSS∆∆+==1540758BCDS∆=⨯=4075115ABD BCD ABCDSS S ∆∆=+=+=梯形AC ABE ABD ABD ACD ACE ABE ACE 25EC BC =ACE ABE 22523=-ABE 241123⎛⎫÷-= ⎪⎝⎭ABCD 21212283⎛⎫⨯+⨯= ⎪⎝⎭13．97【解析】三角形的面积三角形的面积长方形面积阴影部分面积；又因为三角形的面积三角形的面积长方形面积，所以可得：阴影部分面积． 14．【解析】如下图，为了方便说明，将某些点标上字母．有为直角，而，所以也为直角.而.与同高，所以面积比为底的比，及===，设的面积为“8”，则的面积为“5”．是由折叠而成，所以有、面积相等，是由、、组成，所以=“8”+“5”+“5”=“18”对应为，所以“1”份对应为，那么△ADE 的面积为=平方厘米．即阴影部分的面积为平方厘米． 15．512平方厘米【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米． ABC +CDE (133549)+++=+ABC =CDE 12=13354997=++=1133ABC ∠CED ABC ∠=∠CED ∠5CE CB ==ADECEDADE CEDSSAE EC 13-5585ADECEDCED CDBCEDCDBABC ADE CED CDB ABCS 1512302⨯⨯=53583⨯11331133FC DBF BFG x FGC DFC y DEF 13y，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米． 16．1：2 【解析】方法一：连接．设的面积为1，的面积，则根据题上说给出的条件，由得，即的面积为、; 又有，、，而；得，所以．方法二：连接，设(份)，则,设则有，解得，所以方法三：过点作∥交于点，由相似得,又因为，所以，所以两块田地ACF 和CFB 的面积比 17．24【解析】由题意可知，，所以221BCDSx y =+=BDE111S=x+y=l 333⨯=0.531x y x y +=⎧⎨+=⎩①②2x 20.5x =0.25x =0.25y =2550.253312y y +=⨯=BD CED △BED △x DF DC =BDCBDFS S =△△BDF △1x +ADCADFS S =△△2AD DE=22ADCADF CDE SS S ===△△△22ABDBDE SS x==△△122ABD S x x=++=△3x =:(22):(134)1:2ACFCFB SS =+++=△△BD 1CEDS=△2ACDADF S S ==△△BED S x=△BFD S y=△122x yx y +=⎧⎨=+⎩34x y =⎧⎨=⎩:(22):(431)1:2ACF CFB S S =+++=△△F FG BC AE G ::1:1CD DF ED DG ==2AD DE =::1:2AG GE AF FB ==:1:2AF FB ==::2:9BADABC BD BC SS ∆∆==，；又，所以，同样分析可得，所以．18．34【解析】根据题意可知，，所以，． 19．25 【解析】连接、．由于、、彼此平行，所以四边形是梯形，且与该梯形的两个底平行，那么三角形与、三角形与的面积分别相等，所以三角形的面积与三角形的面积相等．而三角形的面积根据已知条件很容易求出来．由于为直角梯形，且，，，，所以三角形的面积的面积为：．所以三角形的面积为25． 20．43【解析】因为、、分别为三边的中点，所以、、是三角形的中位线，也就与对应的边平行，根据面积比例模型，三角形和三角2109BD BC ==35CD BC BD =-=::2:5DIFDFC DI DC SS ∆∆==2145DI DC ==10FK =141024DI FK +=+=::4:1OEDDEF OD DF SS ∆∆==14DF OD =1133444DCFOCDS S ∆∆==⨯=CE DE DQ CP ME CDQP ME QME DEM PME CEM PQM CDE CDE ABCD 5AD =7BC =5AE =3EB =CDE()()1115753553725222+⨯+⨯-⨯⨯-⨯⨯=PQM D E F DEDF EF ABC ABN形的面积都等于三角形的一半，即为200．根据图形的容斥关系，有，即，所以．又，所以．21．40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．AMC ABC ABCABN AMC AMHNSS S S S ∆∆∆-=+-丙400 200200AMHNS S -=+-丙AMHNSS =丙ADF AMHNS S S S S ∆+=++乙甲阴影1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影AF BD 571527CF =++=715628DG =++=1527BE CBFFS S ∆∆=1227BE CBFCS S ∆∆=2128AEGADGS S ∆∆=728AEDADGS S∆∆=2115652827ADGCBF SS ∆∆+=712382827ADGCBF SS ∆∆+=40ADGS∆=ADG。

小学奥数几何专题--复杂直线型面积-4(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-4（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx 题总分得分一、xx题（每空xx 分，共xx分）【题文】如图，三角形ABC被分成了甲(阴影部分)、乙两部分，，，，乙部分面积是甲部分面积的几倍？【答案】5【解析】连接．∵，∴，又∵，∴，∴，．【题文】如图在中，在的延长线上，在上，且，，平方厘米，求的面积．评卷人得分【答案】50【解析】连接，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【题文】如图所示，在平行四边形ABCD中，E为AB的中点，，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？【答案】48【解析】连接FB．三角形AFB面积是三角形CFB面积的2倍，而三角形AFB面积是三角形AEF面积的2倍，所以三角形ABC面积是三角形AEF面积的3倍；又因为平行四边形的面积是三角形ABC面积的2倍，所以平行四边形的面积是三角形AFE面积的倍．因此，平行四边形的面积为(平方厘米)．【题文】已知的面积为平方厘米，，求的面积．【答案】24【解析】，设份，则份，份，份，份，恰好是平方厘米，所以平方厘米【题文】如图，三角形的面积为3平方厘米，其中，，三角形的面积是多少？【答案】12.5【解析】由于，所以可以用共角定理，设份，份，则份，份，由共角定理，设份，恰好是平方厘米，所以份是平方厘米，份就是平方厘米，三角形的面积是平方厘米【题文】如图所示，正方形边长为6厘米，，．三角形的面积为多少平方厘米？【答案】10【解析】由题意知、，可得．根据”共角定理”可得，；而；所以；同理得，;，，故(平方厘米)．【题文】如图，已知三角形面积为，延长至，使；延长至，使；延长至，使，求三角形的面积．【答案】18【解析】(法)本题是性质的反复使用．连接、．∵，，∴．同理可得其它，最后三角形的面积．(法)用共角定理∵在和中，与互补，∴{{l∵在和中，与互补，∴．又，所以．同理可得，，．所以．所以．【题文】如图，四边形的面积是平方米，，，，，求四边形的面积．【答案】13.2【解析】连接．由共角定理得，即同理，即所以连接，同理可以得到所以平方米【题文】如图，将四边形的四条边、、、分别延长两倍至点、、、，若四边形的面积为5，则四边形的面积是多少？【答案】60【解析】连接、．由于，，于是，同理．于是．再由于，，于是，同理．于是．那么．【题文】如图，在中，延长至，使，延长至，使，是的中点，若的面积是，则的面积是多少？【答案】3.5【解析】∵在和中，与互补，∴．又，所以．同理可得，．所以【题文】如图，，，，，．求．【答案】1/10【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的种情况．最后求得的面积为．【题文】如图所示，正方形边长为厘米，是的中点，是的中点，是的中点，三角形的面积是多少平方厘米？【答案】12【解析】连接、．因为，根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，，再根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，得到，，，所以平方厘米．【题文】四个面积为的正六边形如图摆放，求阴影三角形的面积．【答案】13/6【解析】如图，将原图扩展成一个大正三角形，则与都是正三角形．假设正六边形的边长为为，则与的边长都是，所以大正三角形的边长为，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为，三角形的面积为．由于，，所以与三角形的面积之比为．同理可知、与三角形的面积之比都为，所以的面积占三角形面积的，所以的面积的面积为．【题文】已知图中每个正六边形的面积都是1，则图中虚线围成的五边形的面积是多少？【答案】【解析】从图中可以看出，虚线和虚线外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线和虚线外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线外的图形是两个三角形，从右图中可以看出，每个三角形都是一个正六边形面积的，所以虚线外图形的面积等于，所以五边形的面积是．【题文】如图，长方形的面积是平方厘米，点、、分别是长方形边上的中点，为边上的任意一点，求阴影部分的面积．【答案】28【解析】本题是等底等高的两个三角形面积相等的应用．连接、．∵，∴．同理，，，∴(平方厘米)．【题文】图中的、、分别是正方形三条边的三等分点，如果正方形的边长是，那么阴影部分的面积是多少？【答案】48【解析】把另外三个三等分点标出之后，正方形的个边就都被分成了相等的三段．把和这些分点以及正方形的顶点相连，把整个正方形分割成了个形状各不相同的三角形．这个三角形的底边分别是在正方形的个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了个三角形，右边三角形的面积和第第个三角形相等：中间三角形的面积和第第个三角形相等；左边三角形的面积和第个第个三角形相等．因此这个阴影三角形的面积分别是、和的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是，阴影部分的面积就是．【题文】如图，有三个正方形的顶点、、恰好在同一条直线上，其中正方形的边长为10厘米，求阴影部分的面积．【答案】100【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接、、，则，根据几何五大模型中的面积比例模型，可得，，所以阴影部分的面积就等于正方形的面积，即为平方厘米．【题文】右图是由大、小两个正方形组成的，小正方形的边长是厘米，求三角形的面积．【答案】8【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接(见右上图)，可以看出，三角形与三角形的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形是三角形与三角形的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形与三角形面积仍然相等．根据等量代换，求三角形的面积等于求三角形的面积，等于．【题文】如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少？【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．【题文】正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？【答案】50【解析】方法一：三角形BEF的面积，梯形EFDC的面积三角形BEF的面积，而四边形CEFH是它们的公共部分，所以，三角形DHF的面积三角形BCH的面积，进而可得，阴影面积三角形BDF的面积三角形BCD的面积(平方厘米)．方法二：连接CF，那么CF平行BD ，所以，阴影面积三角形BDF的面积三角形BCD的面积(平方厘米)．【题文】长方形的面积为36，、、为各边中点，为边上任意一点，问阴影部分面积是多少？【答案】13.5【解析】解法一：寻找可利用的条件，连接、，如下图：可得：、、，而即；而，．所以阴影部分的面积是：解法二：特殊点法．找的特殊点，把点与点重合，那么图形就可变成右图：这样阴影部分的面积就是的面积，根据鸟头定理，则有：．【题文】在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．【题文】是边长为12的正方形，如图所示，是内部任意一点，、，那么阴影部分的面积是．【答案】34【解析】（法1）特殊点法．由于是内部任意一点，不妨设点与点重合(如上中图)，那么阴影部分就是和．而的面积为，的面积为，所以阴影部分的面积为．（法2）寻找可以利用的条件，连接、、、可得右上图所示：则有:同理可得：;而,即；同理：,,;所以：而；；所以阴影部分的面积是：即为：．【题文】如右图，，，已知阴影部分面积为5平方厘米，的面积是多少平方厘米．【答案】30【解析】连接．根据题意可知，的面积为面积的，的面积为面积的，所以的面积为面积的．而的面积为5平方厘米，所以的面积为(平方厘米)．【题文】图中三角形的面积是180平方厘米，是的中点，的长是长的3倍，的长是长的3倍．那么三角形的面积是多少平方厘米？【答案】22.5【解析】，等高，所以面积的比为底的比，有,所以=(平方厘米)．同理有(平方厘米)，(平方厘米)．即三角形的面积是22.5平方厘米．【题文】如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．【答案】5【解析】如图，将大长方形的长的长度设为1，则，，所以，阴影部分面积为．【题文】如图，在三角形中，已知三角形、三角形、三角形的面积分别是89，28，26．那么三角形的面积是多少？【答案】【解析】根据题意可知，，所以，那么，故．【题文】是长方形内一点，已知的面积是，的面积是，求的面积是多少？【答案】3【解析】由于是长方形，所以，而，所以，则，所以．【题文】如右图，过平行四边形内的一点作边的平行线、，若的面积为8平方分米，求平行四边形的面积比平行四边形的面积大多少平方分米？【答案】16【解析】根据差不变原理，要求平行四边形的面积与平行四边形的面积差，相当于求平行四边形的面积与平行四边形的面积差．如右上图，连接、．由于，所以．而，，所以(平方分米)．【题文】如右图，正方形的面积是，正三角形的面积是，求阴影的面积．【答案】10【解析】连接交于点，并连接．如下图所示，可得，所以与面积相等(同底等高)，所以有：，因为，所以．【题文】如右图，正方形的面积是，正三角形的面积是，求阴影的面积．【答案】2【解析】连接交于点，并连接．如右上图所示，可得，所以与面积相等(同底等高)，所以有:，因为，所以．【题文】右图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．【答案】49.5【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)．【题文】如图，已知长方形的面积，三角形的面积是，三角形的面积是，那么三角形的面积是多少？【答案】6.5【解析】方法一：连接对角线．∵是长方形∴∴，∴，∴∴．方法二：连接，由图知，所以，又由，恰好是面积的一半，所以是的中点，因此，所以【题文】如图所示，三角形中，是边的中点，是边上的一点，且，为与的交点．若的面积为平方厘米，的面积为平方厘米．且是平方厘米，那么三角形的面积是多少平方厘米？【答案】10【解析】，，所以(平方厘米)．所以(平方厘米)．【题文】如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？【答案】【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米．，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米．【题文】如图，，，被分成个面积相等的小三角形，那么？【答案】24【解析】由题意可知，，所以，；又，所以，同样分析可得，所以．【题文】如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于多少？【答案】【解析】根据题意可知，，所以，．【题文】如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形的面积是多少？【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．【题文】如图所示，长方形内的阴影部分的面积之和为70，，，求四边形的面积.【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．【题文】如图所示，矩形的面积为24平方厘米．三角形与三角形的面积之和为平方厘米，则四边形的面积是多少平方厘米？【答案】1.8【解析】因为三角形与三角形的面积之和是矩形的面积的一半，即12平方厘米，又三角形与三角形的面积之和为平方厘米，则三角形与三角形的面积之和是平方厘米，则四边形的面积三角形面积三角形与三角形的面积之和三角形面积(平方厘米)．【题文】如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．【题文】如图在中，分别是上的点，且，，平方厘米，求的面积．【答案】70【解析】连接，，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．【题文】如图，三角形ABC被分成了甲(阴影部分)、乙两部分，，，，乙部分面积是甲部分面积的几倍？【答案】5【解析】连接．∵，∴，又∵，∴，∴，．【题文】如图在中，在的延长线上，在上，且，，平方厘米，求的面积．【答案】50【解析】连接，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【题文】如图，三角形的面积为3平方厘米，其中，，三角形的面积是多少？【答案】12.5【解析】由于，所以可以用共角定理，设份，份，则份，份，由共角定理，设份，恰好是平方厘米，所以份是平方厘米，份就是平方厘米，三角形的面积是平方厘米【题文】已知的面积为平方厘米，，求的面积．【答案】24【解析】，设份，则份，份，份，份，恰好是平方厘米，所以平方厘米【题文】如图，已知三角形面积为，延长至，使；延长至，使；延长至，使，求三角形的面积．【答案】18【解析】(法)本题是性质的反复使用．连接、．∵，，∴．同理可得其它，最后三角形的面积．(法)用共角定理∵在和中，与互补，∴．又，所以．同理可得，．所以．【题文】如图，平行四边形，，，，，平行四边形的面积是，求平行四边形与四边形的面积比．【答案】【解析】连接、．根据共角定理∵在和中，与互补，∴．又，所以．同理可得，，．所以．所以．【题文】如图，将四边形的四条边、、、分别延长两倍至点、、、，若四边形的面积为5，则四边形的面积是多少？【答案】60【解析】连接、．由于，，于是，同理．于是．再由于，，于是，同理．于是．那么．【题文】如图，，，，，．求．【答案】【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的种情况．最后求得的面积为．【题文】一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的，黄色三角形面积是．问：长方形的面积是多少平方厘米？【答案】60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长，高相加为长方形的宽，所以黄色三角形与绿色三角形的面积和为长方形面积的，而绿色三角形面积占长方形面积的，所以黄色三角形面积占长方形面积的．已知黄色三角形面积是，所以长方形面积等于（）．【题文】如图，长方形的面积是，是边的中点，在边上，且.那么，阴影部分的面积是多少？【答案】【解析】连接，因为是中点所以的面积为又因为，所以的面积为，又因为面积为，所以阴影部分的面积为：.【题文】如图，三角形ABC的面积是24，D、E和F分别是BC、AC和AD的中点．求三角形DEF的面积．【答案】3【解析】三角形ADC的面积是三角形ABC面积的一半，三角形ADE又是三角形ADC面积的一半．三角形FED的面积是三角形ADE面积的一半，所以三角形FED的面积．【题文】如图，三角形中，是的5倍，是的3倍，如果三角形的面积等于1，那么三角形的面积是多少？【答案】15【解析】连接．∵∴又∵∴，∴．【题文】如图，在中，延长至，使，延长至，使，是的中点，若的面积是，则的面积是多少？【答案】3.5【解析】∵在和中，与互补，∴．又，所以．同理可得，．所以。

小学数学奥数测试题复杂直线型面积3_人教版

4．如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少．
5．正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？
6．已知正方形边长为10，正方形边长为6，求阴影部分的面积．
7．图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．
32．如图，阴影部分四边形的外接图形是边长为厘米的正方形，则阴影部分四边形的面积是多少平方厘米？
33．已知正方形的边长为10，，，则？
34．如图，三角形的面积是，、的长度分别为11、3．求长方形的面积．
35．如图，长方形中，，．、分别是边上的两点，．那么，三角形面积的最小值是多少？
2019年小学奥数几何专题——复杂直线型面积-3
1．图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是多少平方厘米．
2．如图，有三个正方形的顶点、、恰好在同一条直线上，其中正方形的边长为10厘米，求阴影部分的面积．
3．图是由大、小两个正方形组成的，小正方形的边长是厘米，求三角形的面积．
14．如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是，，．那么图中阴影部分的面积是多少？
15．图中是一个各条边分别为5厘米、12厘米、13厘米的直角三角形．将它的短直角边对折到斜边上去与斜边相重合，那么图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米？
16．如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？
28．如图所示，矩形的面积为36平方厘米，四边形的面积是3平方厘米，则阴影部分的面积是多少平方厘米？

小学奥数几何专题--复杂直线型面积-3(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-3（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是多少平方厘米．【答案】8【解析】．【题文】如图，有三个正方形的顶点、、恰好在同一条直线上，其中正方形的边长为10厘米，求阴影部分的面积．【答案】100【解析】评卷人得分对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接、、，则，根据几何五大模型中的面积比例模型，可得，，所以阴影部分的面积就等于正方形的面积，即为平方厘米．【题文】图是由大、小两个正方形组成的，小正方形的边长是厘米，求三角形的面积．【答案】8【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接(见右上图)，可以看出，三角形与三角形的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形是三角形与三角形的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形与三角形面积仍然相等．根据等量代换，求三角形的面积等于求三角形的面积，等于．【题文】如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少．【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．【题文】正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？【答案】50【解析】方法一：三角形BEF的面积，梯形EFDC的面积三角形BEF的面积，而四边形CEFH是它们的公共部分，所以，三角形DHF的面积三角形BCH的面积，进而可得，阴影面积三角形BDF的面积三角形BCD的面积(平方厘米)．方法二：连接CF，那么CF平行BD ，所以，阴影面积三角形BDF的面积三角形BCD的面积(平方厘米)．【题文】已知正方形边长为10，正方形边长为6，求阴影部分的面积．【答案】20【解析】如果注意到为一个正方形的对角线(或者说一个等腰直角三角形的斜边)，那么容易想到与是平行的．所以可以连接、，如上图．由于与平行，所以的面积与的面积相等．而的面积为，所以的面积也为20．【题文】图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．【答案】49.5【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)．【题文】如下图，、分别是梯形的下底和腰上的点，，并且甲、乙、丙个三角形面积相等．已知梯形的面积是平方厘米．求图中阴影部分的面积．【答案】12.8【解析】因为乙、丙两个三角形面积相等，底．所以到的距离与到的距离相等，即与平行，四边形是平行四边形，阴影部分的面积平行四边形的面积的，所以阴影部分的面积乙的面积．设甲、乙、丙的面积分别为份，则阴影面积为份，梯形的面积为份，从而阴影部分的面积(平方厘米)．【题文】如图，已知长方形的面积，三角形的面积是，三角形的面积是，那么三角形的面积是多少？【答案】6.5【解析】方法一：连接对角线．∵是长方形∴∴，∴，∴∴．方法二：连接，由图知，所以，又由，恰好是面积的一半，所以是的中点，因此，所以【题文】如图，在平行四边形中，，．求阴影面积与空白面积的比．【答案】1：2【解析】方法一：因为，，所以，．因为，所以，所以，．同理可得，，．因为，所以空白部分的面积，所以阴影部分的面积是．，所以阴影面积与空白面积的比是．【题文】如图所示，三角形中，是边的中点，是边上的一点，且，为与的交点．若的面积为平方厘米，的面积为平方厘米．且是平方厘米，那么三角形的面积是多少平方厘米．【答案】10【解析】，，所以(平方厘米)．所以(平方厘米)．【题文】如图，在梯形中，，，且的面积比的面积小10平方厘米．梯形的面积是多少平方厘米？【答案】115【解析】根据题意可知，则，，而平方厘米，所以，则平方厘米．又，所以平方厘米．所以(平方厘米)．【题文】如图，是梯形的一条对角线，线段与平行，与相交于点．已知三角形的面积比三角形的面积大平方米，并且．求梯形的面积．【答案】28【解析】连接．根据差不变原理可知三角形的面积比三角形大4平方米，而三角形与三角形面积相等，因此也与三角形面积相等，从而三角形的面积比三角形的大4平方米．但，所以三角形的面积是三角形的，从而三角形的面积是(平方米)，梯形的面积为：(平方米)．【题文】如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是，，．那么图中阴影部分的面积是多少？【答案】97【解析】三角形的面积三角形的面积长方形面积阴影部分面积；又因为三角形的面积三角形的面积长方形面积，所以可得：阴影部分面积．【题文】图中是一个各条边分别为5厘米、12厘米、13厘米的直角三角形．将它的短直角边对折到斜边上去与斜边相重合，那么图中的阴影部分(即未被盖住的部分)的面积是多少平方厘米？【答案】【解析】如下图，为了方便说明，将某些点标上字母．有为直角，而，所以也为直角.而.与同高，所以面积比为底的比，及===，设的面积为“8”，则的面积为“5”．是由折叠而成，所以有、面积相等，是由、、组成，所以=“8”+“5”+“5”=“18”对应为，所以“1”份对应为，那么△ADE的面积为=平方厘米．即阴影部分的面积为平方厘米．【题文】如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？【答案】平方厘米【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米．，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米．【题文】如图，三角形田地中有两条小路和，交叉处为，张大伯常走这两条小路，他知道,且．则两块地和的面积比是多少【答案】1：2【解析】方法一：连接．设的面积为1，的面积，则根据题上说给出的条件，由得，即的面积为、;又有，、，而；得，所以．方法二：连接，设(份)，则,设则有，解得，所以方法三：过点作∥交于点，由相似得,又因为，所以，所以两块田地ACF和CFB的面积比【题文】如图，，，被分成个面积相等的小三角形，那么|【答案】24【解析】由题意可知，，所以，；又，所以，同样分析可得，所以．【题文】如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于．【答案】【解析】根据题意可知，，所以，．【题文】、分别为直角梯形两边上的点，且、、彼此平行，若，，，．求阴影部分的面积．【答案】25【解析】连接、．由于、、彼此平行，所以四边形是梯形，且与该梯形的两个底平行，那么三角形与、三角形与的面积分别相等，所以三角形的面积与三角形的面积相等．而三角形的面积根据已知条件很容易求出来．由于为直角梯形，且，，，，所以三角形的面积的面积为：．所以三角形的面积为25．【题文】已知为等边三角形，面积为400，、、分别为三边的中点，已知甲、乙、丙面积和为143，求阴影五边形的面积．(丙是三角形)【答案】43【解析】因为、、分别为三边的中点，所以、、是三角形的中位线，也就与对应的边平行，根据面积比例模型，三角形和三角形的面积都等于三角形的一半，即为200．根据图形的容斥关系，有，即，所以．又，所以．【题文】如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，求三角形的面积．【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．【题文】如图，点、、在线段上，已知厘米，厘米，厘米，厘米，将整个图形分成上下两部分，下边部分面积是平方厘米，上边部分面积是平方厘米，则三角形的面积是多少平方厘米？【答案】128【解析】连接设的面积是,由于所以的面积是、的面积是由于上半部分的面积是平方厘米所以的面积是()平方厘米，因为下半部分的面积是平方厘米所以的面积是()平方厘米，因为是的2倍所以可以列方程为：()解得，的面积为平方厘米.【题文】如图，正方形的边长为10，四边形的面积为5，那么阴影部分的面积是多少【答案】40【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以阴影部分的面积为：．【题文】如图，正方形的边长为12，阴影部分的面积为60，那么四边形的面积是多少【答案】6【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以四边形的面积为：．【题文】如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为多少？【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．【题文】如图所示，矩形的面积为24平方厘米．三角形与三角形的面积之和为平方厘米，则四边形的面积是多少平方厘米？【答案】1.8【解析】因为三角形与三角形的面积之和是矩形的面积的一半，即12平方厘米，又三角形与三角形的面积之和为平方厘米，则三角形与三角形的面积之和是平方厘米，则四边形的面积三角形面积三角形与三角形的面积之和三角形面积(平方厘米)．【题文】如图所示，矩形的面积为36平方厘米，四边形的面积是3平方厘米，则阴影部分的面积是多少平方厘米？【答案】12【解析】因为三角形面积为矩形的面积的一半，即18平方厘米，三角形面积为矩形的面积的，即9平方厘米，又四边形的面积为3平方厘米，所以三角形与三角形的面积之和是平方厘米．又三角形与三角形的面积之和是矩形的面积的一半，即18平方厘米，所以阴影部分面积为(平方厘米)．【题文】如图，长方形的面积是36，是的三等分点，，则阴影部分的面积为多少？【答案】2.7【解析】如图，连接．根据蝴蝶定理，，所以；，所以．又，，所以阴影部分面积为：．【题文】如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．【题文】如图，阴影部分四边形的外接图形是边长为的正方形，则阴影部分四边形的面积是（）．【答案】48【解析】如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．【题文】如图，阴影部分四边形的外接图形是边长为厘米的正方形，则阴影部分四边形的面积是多少平方厘米？【答案】68【解析】如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．【题文】已知正方形的边长为10，，，则？【答案】53【解析】如图，作于，于．则四边形分为4个直角三角形和中间的一个长方形，其中的4个直角三角形分别与四边形周围的4个三角形相等，所以它们的面积和相等，而中间的小长方形的面积为，所以．【题文】如图，三角形的面积是，、的长度分别为11、3．求长方形的面积．【答案】67【解析】如图，过作∥，过作∥，、交于，连接．则另解：设三角形、、的面积之和为，则正方形的面积为．从图中可以看出，三角形、、的面积之和的2倍，等于正方形的面积与长方形的面积之和，即，得，所以正方形的面积为．【题文】如图，长方形中，，．、分别是边上的两点，．那么，三角形面积的最小值是多少？【答案】717【解析】由于长方形的面积是一定的，要使三角形面积最小，就必须使、、的面积之和最大．由于、、都是直角三角形，可以分别过、作、的平行线，可构成三个矩形、和，如图所示．容易知道这三个矩形的面积之和等于、、的面积之和的2倍，而这三个矩形的面积之和又等于长方形的面积加上长方形的面积．所以为使、、的面积之和最大，只需使长方形的面积最大．长方形的面积等于其长与宽的积，而其长，宽，由题知，根据”两个数的和一定，差越小，积越大”，所以当与的差为0，即与相等时它们的积最大，此时长方形的面积也最大，所以此时三角形面积最小．当与相等时，，此时三角形的面积为：．(也可根据得到三角形的面积)【题文】是边长为12的正方形，如图所示，是内部任意一点，、，那么阴影部分的面积是（）．【答案】34【解析】（法1）特殊点法．由于是内部任意一点，不妨设点与点重合(如上中图)，那么阴影部分就是和．而的面积为，的面积为，所以阴影部分的面积为．（法2）寻找可以利用的条件，连接、、、可得右图所示：则有:同理可得：;而,即；同理：,,;所以：而；；所以阴影部分的面积是：即为：．【题文】如图所示，在四边形中，，，，分别是各边的中点，求阴影部分与四边形的面积之比．【答案】1【解析】(法1)设，，，．连接知，，，；所以；同理．于是；注意到这四个三角形重合的部分是四块阴影小三角形，没算的部分是四边形；因此四块阴影的面积和就等于四边形的面积．(法2)特殊值法(只用于填空题、选择题)，将四边形画成正方形，很容易得到结果．【题文】如图，、、、分别是四边形各边的中点，与交于点，、、及分别表示四个小四边形的面积．试比较与的大小．【答案】【解析】如图，连接、、、，则可判断出，每条边与点所构成的三角形都被分为面积相等的两部分，且每个三角形中的两部分都分属于、这两个不同的组合，所以可知．【题文】如图，四边形中，，，，已知四边形的面积等于4，则四边形的面积是多少？【答案】【解析】运用三角形面积与底和高的关系解题．连接、、、，因为，，所以，在中，，在中，，在中，，在中，．因为，所以．又因为，所以．【题文】如图，对于任意四边形，通过各边三等分点的相应连线，得到中间四边形，求四边形的面积是四边形的几分之几？【答案】【解析】分层次来考虑：⑴如下左图，，，所以．又因为，，所以；．⑵如右上图，已知，；所以；所以，即是三等分点；同理，可知、、都是三等分点；所以再次应用⑴的结论，可知，．【题文】有正三角形，在边、、的正中间分别取点、、，在边、、上分别取点、、，使，当和、和、和的相交点分别是、、时，使．这时，三角形的面积是三角形的面积的几分之几？请写出思考过程．【答案】【解析】连接、、，显然，是正三角形将放大至如图⑵．连，由对称性知，．因此，．同理，．所以，．【题文】如图：已知在梯形中，上底是下底的，其中是边上任意一点，三角形、三角形、三角形的面积分别为、、．求三角形的面积．【答案】21【解析】如图，设上底为，下底为，三角形与三角形的高相差为．由于，所以．即．又，所以．【题文】如图，已知是梯形，∥，，，，求的面积．【答案】6【解析】本题是09年六年级试题，初看之下，是梯形这个条件似乎可以用到梯形蝴蝶定理，四边形内似乎也可以用到蝴蝶定理，然而经过试验可以发现这几个模型在这里都用不上，因为、这两个点的位置不明确．再看题目中的条件，，，这两个条件中的前一个可以根据差不变原理转化成与的面积差，则是与的面积差，两者都涉及到、以及有同一条底边的两个三角形，于是想到过、分别作梯形底边的平行线．如右图，分别过、作梯形底边的平行线，假设这两条直线之间的距离为．再过作的垂线．由于，所以，故．根据差不变原理，这个差等于与的面积之差．而与有一条公共的底边，两个三角形边上的高相差为，所以它们的面积差为，故．再看，它的面积等于是与的面积之差，这两个三角形也有一条公共的底边，边上的高也相差，所以这两个三角形的面积之差为，故．由于，所以，则，所以．【题文】如图，是一个四边形，、分别是、的中点．如果、与的面积分别是6、7和8，且图中所有三角形的面积均为整数，则四边形的面积为多少．【解析】连接、、．由于是的中点，所以与的面积相等，而比的面积大1，所以比的面积大1；又由于是的中点，所以的面积与的面积相等，那么的面积比的面积大1，所以的面积为9．假设的面积为，则的面积为．根据几何五大模型中的蝴蝶定理，可知的面积为，的面积为．要使这两个三角形的面积为整数，可以为1，3或7．由于的面积为面积的一半，的面积为面积的一半，所以与的面积之和为四边形面积的一半，所以与的面积之和等于四边形的面积，即：，得．将、3、7分别代入检验，只有时等式成立，所以{{10l连接，，，所以，设份，则份，平方厘米，所以份是平方厘米，份就是平方厘米，的面积是平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．【题文】如图，三角形中，是的5倍，是的3倍，如果三角形的面积等于1，那么三角形的面积是多少？【答案】15连接．∵∴又∵∴，∴．。

小学数学奥数测试题复杂直线型面积12_人教版

小学数学奥数测试题复杂直线型面积12_人教版
1．有正三角形，在边、、的正中间区分取点、、，在边、、上区分取点、、，使，当和、和、和的相交点区分是、、时，使．这时，三角形的面积是三角形的面积的几分之几？请写出思索进程．
2．如图：在梯形中，上底是下底的，其中是边上恣意一点，三角形、三角形、三角形的面积区分为、、．求三角形的面积．
12．如图，三角形面积为，延伸至，使；延伸至，使；延伸至，使，求三角形的面积．
13．如图，平行四边形，，，，，平行四边形的面积是，求平行四边形与四边形的面积比．
14．如图，四边形的面积是平方米，，，，，求四边形的面积．
15．如图，将四边形的四条边、、、区分延伸两倍至点、、、，假定四边形的面积为5，那么四边形的面积是多少？
如右图，区分过、作梯形底边的平行线，假定这两条直线之间的距离为．再过作的垂线．
由于，所以，故．依据差不变原理，这个差等于与的面积之差．而与有一条公共的底边，两个三角形边上的高相差为，所以它们的面积差为，故．
再看，它的面积等于是与的面积之差，这两个三角形也有一条公共的底边，边上的高也相差，所以这两个三角形的面积之差为，故．
最后求得的面积为．
18．12
【解析】
衔接、．
由于，依据〞当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比〞，，再依据〞当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比〞，失掉，，，所以平方厘米．

小学数学奥数测试题复杂直线型面积11_人教版

小学数学奥数测试题复杂直线型面积11_人教版参考答案1．128【解析】连接设的面积是,由于所以的面积是、的面积是由于上半部分的面积是平方厘米所以的面积是()平方厘米，因为下半部分的面积是平方厘米所以的面积是()平方厘米，因为是的2倍所以可以列方程为：()解得，的面积为平方厘米.2．40【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以阴影部分的面积为：．3．6AF AFG △x 2048512FE FG ED ==∶∶∶∶∶∶AFE △5x AED △2x 166FEB △16651666x x x --=-67EBC △672x -FE EC 16662x -=672x -16x =ADG △528816128x x x x ++==⨯=AD M N CN CMF ∆CNF ∆CMF ∆BNF ∆CNF ∆BNF ∆BCN ∆BCN ∆ABCD 2110502⨯=CMF ∆BNF ∆EFGH 505240-⨯=【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以四边形的面积为：．4．10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三AD M N CN CMF ∆CNF ∆CMF ∆BNF ∆CNF ∆BNF ∆BCN ∆BCN ∆ABCD 2112722⨯=CMF ∆BNF ∆EFGH EFGH ()726026-÷=AOE DOG EFGO AOE DOG EFGO ABCD 158120⨯=BOC 1120304⨯=AOE DOG 312070204⨯-=AOE DOG EFGO 111203024⎛⎫⨯-= ⎪⎝⎭EFGO 302010-=EFGO =AFC +BFD -角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．5．1.8【解析】因为三角形与三角形的面积之和是矩形的面积的一半，即12平方厘米，又三角形与三角形的面积之和为平方厘米，则三角形与三角形的面积之和是平方厘米，则四边形的面积三角形面积三角形与三角形的面积之和三角形面积(平方厘米)．6．32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)． 7．48【解析】AFC +BFD 1207050-=605010-=ADO BCO ABCD ADM BCN 7.8AMO BNO 4.2PMON =ABP -AMO BNO -ABO 12 4.26 1.8=--=M N P Q ABCD 39MQD ∆NAM ∆PBN ∆QCP ∆S MNPQ x 569x S x S +=⎧⎨-=⎩32.5x =如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．8．68【解析】如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．9．53【解析】EFGH MNPQ MNPQ 414⨯=AENH BFME CGQF DHPG ABCD MNPQ 10104104⨯+=104252÷=EFGH 1005248-=EFGH MNPQ MNPQ 428⨯=AENH BFME CGQF DHPG ABCD MNPQ 12128152⨯+=152276÷=EFGH 1447668-=如图，作于，于．则四边形分为4个直角三角形和中间的一个长方形，其中的4个直角三角形分别与四边形周围的4个三角形相等，所以它们的面积和相等，而中间的小长方形的面积为，所以． 10．67【解析】如图，过作∥，过作∥，、交于，连接．则另解：设三角形、、的面积之和为，则正方形的面积为．从图中可以看出，三角形、、的面积之和的2倍，等于正方形的面积与长方形的面积之和，即，得，所以正方形的面积为．11．717【解析】由于长方形的面积是一定的，要使三角形面积最小，就必须使、、的面积之和最大．BM AE ⊥M CN BM ⊥N ABCD ABCD 326⨯=10103232532ABCDS ⨯-⨯=+⨯=四边形F FH AB E EG AD FH EG M AM ABCD AGMH GBFM MFCE HMED S S S S S =+++矩形矩形矩形矩形矩形ADE CEF ABF s ABCD 17s +ADE CEF ABF ABCD AGMH ()217113s s =++⨯50s =ABCD 501767+=ABCD DEF ADE ∆BEF ∆CDF ∆由于、、都是直角三角形，可以分别过、作、的平行线，可构成三个矩形、和，如图所示．容易知道这三个矩形的面积之和等于、、的面积之和的2倍，而这三个矩形的面积之和又等于长方形的面积加上长方形的面积．所以为使、、的面积之和最大，只需使长方形的面积最大．长方形的面积等于其长与宽的积，而其长，宽，由题知，根据”两个数的和一定，差越小，积越大”，所以当与的差为0，即与相等时它们的积最大，此时长方形的面积也最大，所以此时三角形面积最小．当与相等时，，此时三角形的面积为：．(也可根据得到三角形的面积) 12．34【解析】（法1）特殊点法．由于是内部任意一点，不妨设点与点重合(如上中图)，那么阴影部分就ADE ∆BEF ∆CDF ∆E F AD CD ADME CDNF BEOF ADE ∆BEF ∆CDF∆ABCD MDNO ADE ∆BEF ∆CDF ∆MDNO MDNO DM AE =DN CF =()()67304948AE CF AB BC BE BF +=+-+=+-=AE CF AE CF MDNO DEF AE CF 48224AE CF ==÷=DEF ()6730673024242717⨯-⨯+⨯÷=()16730672430244367172⨯-⨯⨯+⨯+⨯=DEF P P A是和．而的面积为，的面积为，所以阴影部分的面积为．（法2）寻找可以利用的条件，连接、、、可得右上图所示：则有: 同理可得：; 而,即；同理：,,;所以：而；所以阴影部分的面积是：即为：． 13．1 【解析】(法1)设，，，．连接知，，，；所以；同理．于是；注意到这四个三角形重合的部分是四块阴影小三角形，没算的部分是四边形；因此四块阴AMN ∆ALK ∆AMN ∆(125)4214-⨯÷=ALK ∆(124)5220-⨯÷=142034+=AP BP CP DP211127222PDCPABABCDS S S ∆∆+==⨯=72PADPBCS S ∆∆+=::4:121:3PDMPDCS S DM DC ∆∆===13PDMPDC SS ∆∆=13PBLPAB S S ∆∆=512PNDPDA SS ∆∆=512PBKPBC SS ∆∆=15()()()()312PDMPBL PND PBK PDC PAB PDA PBC SS S S S S S S ∆∆∆∆∆∆∆∆+++=+++()()()()PDMPBL PND PBK PNM PLK DNM BLK SS S S S S S S ∆∆∆∆∆∆∆∆+++=+++阴影面积15727210224302034312⨯+⨯-⨯=+-=1AEDS S ∆=2BGCS S ∆=3ABFS S ∆=4DHCS S ∆=BD 112ABD S S ∆=112ABD S S ∆=112ABD S S ∆=212BCDS S∆=()121122ABD BCD ABCD S SS S S ∆∆+=+=3412ABCD SS S +=1234ABCDS SS S S +++=PQRS影的面积和就等于四边形的面积． (法2)特殊值法(只用于填空题、选择题)，将四边形画成正方形，很容易得到结果． 14．【解析】如右图，连接、、、，则可判断出，每条边与点所构成的三角形都被分为面积相等的两部分，且每个三角形中的两部分都分属于、这两个不同的组合，所以可知．15．4/3 【解析】运用三角形面积与底和高的关系解题．连接、、、，因为，，所以，在中，，在中，，在中，，在中，．因为，所以．又因为所以．PQRS 1324S SS S +=+AO BO CO DO O 13S S +24S S +1324S SS S +=+ACAEGCGE::3:2:1DE EF FC =::3:2:1BG GH AH =ABC ∆12BCGABCS S∆∆=ACD ∆12AEDACD S S ∆∆=AEG ∆12AEHHEG S S ∆∆=CEG ∆12CFGEFG SS ∆∆=()111122222BCGAED ABC ACD ABC ACD ABCD BCGSS S S S S S S ∆∆∆∆∆∆∆+=+=+==()422AGCEABCDBCGAEDS S S S ∆∆=-+=-=1122AGCEAEHHEGCFGEFGHEGHEG EFG EFGS S S S S SS S S ∆∆∆∆∆∆∆∆=+++=+++34223EFGHS=÷=16．19【解析】分层次来考虑： ⑴如下左图，，，所以．又因为，，所以； ⑵如右上图，已知，；所以；所以，即是三等分点；同理，可知、、都是三等分点；所以再次应用⑴的结论，可知，． 23BMDABDS S =⨯23BPDCBDS S=⨯22()33MBPDABD CBD ABCD SS S S =+⨯=⨯DOMPOMS S =MNPBNPSS =12MNPO MBPDS S=13MJ BD =23OK BD =:1:2MJ BD =:1:2ME EO =E F G H 11113339EFGHMNPOABCDABCDS S S S=⨯=⨯⨯=。

小学奥数几何专题--复杂直线型面积-11(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-11（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】如图，点、、在线段上，已知厘米，厘米，厘米，厘米，将整个图形分成上下两部分，下边部分面积是平方厘米，上边部分面积是平方厘米，则三角形的面积是多少平方厘米？【答案】128【解析】连接设的面积是,由于所以的面积是、的面积是由于上半部分的面积是平方厘米所以的面积是()平方厘米，因为下半部分的面积是平方厘米所以的面积是()平方厘米，因为是的2倍所以可以列方程为：()解得，的面积为平方厘米.评卷人得分【题文】如图，正方形的边长为10，四边形的面积为5，那么阴影部分的面积是多少？【答案】40【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以阴影部分的面积为：．【题文】如图，正方形的边长为12，阴影部分的面积为60，那么四边形的面积是多少？【答案】6【解析】如图所示，设上的两个点分别为、．连接．根据面积比例模型，与的面积是相等的，那么与的面积之和，等于与的面积之和，即等于的面积．而的面积为正方形面积的一半，为．又与的面积之和与阴影部分的面积相比较，多了2个四边形的面积，所以四边形的面积为：．【题文】如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为多少？【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．【题文】如图所示，矩形的面积为24平方厘米．三角形与三角形的面积之和为平方厘米，则四边形的面积是多少平方厘米？【答案】1.8【解析】因为三角形与三角形的面积之和是矩形的面积的一半，即12平方厘米，又三角形与三角形的面积之和为平方厘米，则三角形与三角形的面积之和是平方厘米，则四边形的面积三角形面积三角形与三角形的面积之和三角形面积(平方厘米)．【题文】如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．【题文】如图，阴影部分四边形的外接图形是边长为的正方形，则阴影部分四边形的面积是．【答案】48【解析】如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．【题文】如图，阴影部分四边形的外接图形是边长为厘米的正方形，则阴影部分四边形的面积是多少平方厘米？【答案】68【解析】如图所示，分别过阴影四边形的四个顶点作正方形各边的平行线，相交得长方形，易知长方形的面积为平方厘米．从图中可以看出，原图中四个空白三角形的面积之和的2倍，等于、、、四个长方形的面积之和，等于正方形的面积加上长方形的面积，为平方厘米，所以四个空白三角形的面积之和为平方厘米，那么阴影四边形的面积为平方厘米．【题文】已知正方形的边长为10，，，则？【答案】53【解析】如图，作于，于．则四边形分为4个直角三角形和中间的一个长方形，其中的4个直角三角形分别与四边形周围的4个三角形相等，所以它们的面积和相等，而中间的小长方形的面积为，所以．【题文】如图，三角形的面积是，、的长度分别为11、3．求长方形的面积．【答案】67【解析】如图，过作∥，过作∥，、交于，连接．则另解：设三角形、、的面积之和为，则正方形的面积为．从图中可以看出，三角形、、的面积之和的2倍，等于正方形的面积与长方形的面积之和，即，得，所以正方形的面积为．【题文】如图，长方形中，，．、分别是边上的两点，．那么，三角形面积的最小值是多少？【答案】717【解析】由于长方形的面积是一定的，要使三角形面积最小，就必须使、、的面积之和最大．由于、、都是直角三角形，可以分别过、作、的平行线，可构成三个矩形、和，如图所示．容易知道这三个矩形的面积之和等于、、的面积之和的2倍，而这三个矩形的面积之和又等于长方形的面积加上长方形的面积．所以为使、、的面积之和最大，只需使长方形的面积最大．长方形的面积等于其长与宽的积，而其长，宽，由题知，根据”两个数的和一定，差越小，积越大”，所以当与的差为0，即l【解析】（法1）特殊点法．由于是内部任意一点，不妨设点与点重合(如上中图)，那么阴影部分就是和．而的面积为，的面积为，所以阴影部分的面积为．（法2）寻找可以利用的条件，连接、、、可得右上图所示：则有:同理可得：;而,即；同理：,,;所以：而；；所以阴影部分的面积是：即为：．【题文】如图所示，在四边形中，，，，分别是各边的中点，求阴影部分与四边形的面积之比．【答案】1【解析】(法1)设，，，．连接知，，，；所以；同理．于是；注意到这四个三角形重合的部分是四块阴影小三角形，没算的部分是四边形；因此四块阴影的面积和就等于四边形的面积．(法2)特殊值法(只用于填空题、选择题)，将四边形画成正方形，很容易得到结果．【题文】如图，、、、分别是四边形各边的中点，与交于点，、、及分别表示四个小四边形的面积．试比较与的大小．【答案】【解析】如右图，连接、、、，则可判断出，每条边与点所构成的三角形都被分为面积相等的两部分，且每个三角形中的两部分都分属于、这两个不同的组合，所以可知．【题文】如图，四边形中，，，，已知四边形的面积等于4，则四边形的面积是多少？【答案】4/3【解析】运用三角形面积与底和高的关系解题．连接、、、，因为，，所以，在中，，在中，，在中，，在中，．因为，所以．又因为，所以．【题文】如图，对于任意四边形，通过各边三等分点的相应连线，得到中间四边形，求四边形的面积是四边形的几分之几？【答案】【解析】分层次来考虑：⑴如下左图，，，所以．又因为，，所以；．⑵如右上图，已知，；所以；所以，即是三等分点；同理，可知、、都是三等分点；所以再次应用⑴的结论，可知，．。

小学奥数：基本图形的面积计算.专项练习及答案解析

小学数学平面图形计算公式：1 、正方形：周长＝边长×4；面积=边长×边长2 、正方体：表面积=棱长×棱长×6；体积=棱长×棱长×棱长3 、长方形：周长=(长+宽)×2；面积=长×宽4 、长方体：表面积(长×宽+长×高+宽×高)×2；体积=长×宽×高5、三角形：面积=底×高÷26 平行四边形：面积=底×高7 梯形：面积=(上底+下底)×高÷2模块一、基本公式的应用【例 1】如图，两个正方形边长分别是5厘米和4厘米，图中阴影部分为重叠部分。

则两个正方形的空白部分的面积相差多少平方厘米？【考点】基本图形的面积计算【难度】2星【题型】解答【关键词】华杯赛，五年级，决赛，第9题，10分【解析】5×5－4×4=9（平方厘米），两个正方形的空白部分的面积相差9平方厘米。

【答案】9平方厘米【巩固】如图12，边长为4cm的正方形将边长为3cm的正方形遮住了一部分，则空白部分的面积的差等于2cm。

【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯，4年级，初赛，19题【解析】空白部分的面积差等于两个正方形的面积差，即⨯-⨯=44337（平方厘米）。

【答案】7平方厘米【例 2】在一个正方形水池的四周，环绕着一条宽2米的路(如图)，这条路的面积是120平方米，那么水池的面积是______ 平方米。

水池例题精讲知识点拨4-2-1.基本图形的面积计算【考点】基本图形的面积计算【难度】2星【题型】填空【关键词】希望杯，4年级，初赛，19题【解析】四个边角的面积和为2×2×4=16，则水池的边长为：104÷2÷4=13，所以水池的面积是：13×13=169平方米。

(完整word版)六年级奥数-直线形面积的计算

六年级奥数－直线形面积的计算
1．如下左图，在△ABC中，D是BC中点，E是AD中点，连结BE、CE，那么与△ABE等积的三角形一共有______个．
2．如上右图，在平行四边形ABCD中，EF平行AC，连结BE、AE、CF、BF那么与△BEC等积的三角形一共有______个．
3．如下左图，在梯形ABCD中，共有八个三角形，其中面积相等的三角形共有______对．
4.如上图，在梯形ABCD中，AC与BD是对角线，其交点O，求证：△AOB与△COD面积相等．
5．图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是（
6.如右图，四边形ABCD面积为1，且AB=AE，BC=BF，DC=CG，
AD=DH．求四边形EFGH的面积．
7．如下左图，D、E、F分别是BC、AD、BE的三等分点，
已知S△ABC=27平方厘米，求S△DEF．
8．如下左图，在平行四边形ABCD中，E、F分别是AC、
BC的三等分点，且SABCD=54平方厘米，求S△BEF．
六年级奥数－直线形面积的计算解答
1.3个
2.3个
3.3对
4．证明：∵△ABC与△DBC等底等高，
∴S△ABC=S△DBC
又∵ S△AOB=S△ABC—S△BOC
S△DOC=S△DBC—S△BOC
∴S△AOB=S△COD．
5．4×4÷2=8
6. 连结BD，将四边形ABCD分成两个部分．连结FD，可得S△AEH+S△CGF=2×1=2．同理，连结AC之后，可求出S△HGD+S△EBF=2所以四边形EFGH的面积为2+2+1=5（平方单位）。

六年级下册奥数试题-几何直线形面积-燕尾定理.(含答案)人教版

1. 理解燕尾定理，灵活运用定理解题．2. 用份数思想求面积之间的关系．本讲是在秋季所学四大模型的基础上，讲解运用燕尾定理求解面积问题．至此五大模型已讲解完毕．体会五大模型解决问题的优势．燕尾定理： S △ABG :S △AGC =S △BGE :S △EGC =BE :EC ； S △BGA :S △BGC =S △AGF :S △FGC =AF :FC ； S △AGC :S △BCG =S △ADG :S △DGB =AD :DB ；问：为什么称之为燕尾定理？答：我们看看燕子的尾巴然后再看看右图的阴影部分，看看阴影部分是不是很像燕子的尾巴，A 是尾巴与身体的连接点，AG 是燕子尾巴的中分线，左右两个阴影三角形构成燕子尾巴的两侧翼.同学们也可以自己动手，试试以三角形的另外两个顶点作为尾巴与身体的连接点能不能画出燕子的尾巴.燕尾定理因为图形类似燕尾而得名，它的特殊性在于，它可以存在于任何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相联系的途径.通过一道例题证明一下燕尾定理：举例：如右图，D 是BC 上任意一点，请你说明S 1:S 4=S 2:S 3=BD :DC【分析】三角形BED 与三角形CED 同高，分别以BD 、DC 为底，第4讲直线型面积—燕尾定理G F D AG F E D C B AS 3S 1S 4S 2EDCBA所以有S 1:S 4 =BD :DC ；三角形ABE 与三角形EBD 同高，S 1:S 2 =ED :EA 三角形ACE 与三角形CED 同高，S 4:S 3=:ED EA ，所以S 1:S 4 =S 2:S 3；综上可得S 1:S 4=S 2:S 3=BD :DC .【例 1】如图，已知BD DC =，2EC AE =，三角形ABC 的面积是30，求阴影部分面积.EFAEF B AEF A【分析】题中条件只有三角形面积给出具体数值，其他条件给出的实际上是比例的关系，由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是一个不规则四边形，所以我们需要对它进行改造，那么我们需要连一条辅助线，(法一)连接CF ，因为BD DC =，2EC AE =，三角形ABC 的面积是30，所以1103ABE ABC S S ==△△，1152ABD ABC S S ==△△．根据燕尾定理，12ABF CBF S AE S EC ==△△，1ABF ACF S BDS CD==△△,所以17.54ABF ABC S S ==△△，157.57.5BFD S =-=△，所以阴影部分面积是30107.512.5--=．(法二)连接DE ，由题目条件可得到1103ABE ABC S S ==△△，11210223BDE BEC ABC S S S ==⨯=△△△，所以11ABE BDE S AF FD S ==△△， 1111112.5223232DEF DEA ADC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△，而211032CDE ABC S S =⨯⨯=△△．所以阴影部分的面积为12.5．［铺垫］右图的大三角形被分成5个小三角形，其中4个的面积已经标在图中，那么，阴影三角形的面积是．【分析】方法一：整个题目读完，我们没有发现任何与边长相关的条件，也没有任何与高或者垂直有关系的字眼，由此，我们可以推断，这道题不能依靠三角形面积公式求解.我们发现右图三角形中存在一个比例关系：()2:13:4S =+阴影，解得2S =阴影.方法二：回顾下燕尾定理，有2:41:3S +=阴影（），解得2S =阴影.用燕尾定理求面积4321【例 2】如右图，三角形ABC 中，BD :DC =4:9，CE :EA =4:3，求AF :FB . 【分析】燕子尾巴非常明显.根据燕尾定理，49ABO ACO S BD S DC ==△△，34ABO CBO S AE S EC ==△△，所以44279316ACO BCO S S =÷=△△，所以:27:16AF FB =.【例 3】如图在ABC △中，12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值． IHG FEDCBAIHG FEDCB A【分析】连接BG ,设BGC S △=1份，根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份)，4ABG S =△(份),则7ABC S =△(份)，因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△, 所以7222177GHI ABC S S ---==△△［拓展］如右图，三角形ABC 中，AF :FB =BD :DC =CE :AE =3:2，且三角形GHI 的面积是1，求三角形ABC 的面积．IH G FEDCBAIH G FEDCBA［分析］连接BG ，BGC S △=4份根据燕尾定理，::3:2AGC BGC S S AF FB ==△△，::3:2ABG AGC S S BD DC ==△△ 得6AGC S =△(份)，9ABG S =△(份)，则19ABC S =△(份)，因此619AGC ABC S S =△△, 同理连接AI 、CH 得619ABH ABC S S =△△,619BIC ABC S S =△△, O FEDCBA35304084O FEDC BA所以1966611919GHI ABC S S ---==△△ 三角形GHI 的面积是1，所以三角形ABC 的面积是19【例 4】如图，三角形ABC 被分成6个三角形，己知其中4个三角形的面积，问三角形ABC 的面积是多少? 【分析】设AOE S x =△，BOF S y =△，根据燕尾定理,得::ABO ACO BDO CDO S S S S =△△△△,::ABO BOC AOE COE S S S S =△△△△即 (84):(35)4:3y x ++=，(84):(4030):35y x ++=，即3(84)4(35)35(84)70y x y x +=+⎧⎨+=⎩，解得7056x y =⎧⎨=⎩，所以三角形ABC 的面积是844030355670315+++++=【例 5】三角形ABC 的面积为15平方厘米，D 为AB 中点，E 为AC 中点，F 为BC 中点，求阴影部分的面积．F CBAF CB【分析】令BE 与CD 的交点为M ，CD 与EF 的交点为N ，连接AM ，BN ．在ABC △中，根据燕尾定理，::1:1ABM BCM S S AE CE ==△△,::1:1ACM BCM S S AD BD ==△△,所以13ABM ACM BCN ABC S S S S ===△△△△由于1122AEM AMC ABM S S S ==△△△S ，所以:2:1BM ME =在EBC △中，根据燕尾定理，::1:1BEN CEN S S BF CF ==△△::1:2CEN CBN S S ME MB ==△△ 设1CEN S =△(份)，则1BEN S =△(份)，2BCN S =△(份)，4BCE S =△(份)，所以1124BCN BCE ABC S S S ==△△△,1148BNE BCE ABC S S S ==△△△，因为:2:1BM ME =,F 为BC 中点,所以221133812BMN BNE ABC ABC S S S S ==⨯=△△△△,11112248BFN BNC ABC S S S ==⨯=△△△,所以115515 3.1251282424ABC ABC S S S ⎛⎫=+==⨯= ⎪⎝⎭△△阴影(平方厘米)【例 6】如右图，ABC △中，G 是AC 的中点，D 、E 、F 是BC 边上的四等分点，AD 与BG 交于M ，AF 与BG 交于N ，已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米，则ABC △的面积是多少平方厘米？N M GA BCD EFNMGA BCD EF【分析】连接CM 、CN ．根据燕尾定理，::1:1ABM CBM S S AG GC ==△△，::1:3ABM ACM S S BD CD ==△△，所以15ABM ABC S S =△△；再根据燕尾定理，::1:1ABN CBN S S AG GC ==△△，所以::4:3ABN FBN CBN FBN S S S S ==△△△△，所以:4:3AN NF =，那么1422437ANG AFC S S =⨯=+△△，所以2515177428FCGN AFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△．根据题意，有157.2528ABC ABC S S -=△△，可得336ABC S =△(平方厘米)［拓展］如右图，三角形ABC 的面积是1，BD =DE =EC ，CF =FG =GA ，三角形ABC 被分成9部分，请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA［分析］设BG 与AD 交于点P ，BG 与AE 交于点Q ，BF 与AD 交于点M ，BF 与AE 交于点N ．连接CP ，CQ ，CM ，CN ．根据燕尾定理，::1:2ABP CBP S S AG GC ==△△，::1:2ABP ACP S S BD CD ==△△，设1ABP S =△(份)，则1225ABC S =++=△(份)，所以15ABP S =△ 同理可得，27ABQ S =△,12ABN S =△,而13ABG S =△，所以2137535APQ S =-=△，1213721AQG S =-=△．同理，335BPM S =△121BDM S =△,所以1239273570PQMN S =--=四边形，139********MNED S =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【例 7】已知四边形ABCD ，CHFG 为正方形，:1:8S S =乙甲，a 与b 是两个正方形的边长，求:?a b =乙甲baGHOFEDCBA 乙甲baNMGHOFED CBA【分析】观察图形，感觉阴影部分像蝴蝶定理，但是细细分析发现用蝴蝶定理无法继续往下走，注意到题目条件中给出了两个正方形的边长，有边长就可以利用比例，再发现在连接辅助线后可以利用燕尾，那么我们就用燕尾定理来求解连接EO 、AF ，根据燕尾定理：::AOE AOF S S a b =△△，::AOF EOF S S a b =△△ 所以 22::AOE EOF S S a b =△△，作OM ⊥AE 、ON ⊥EF ， ∵AE =EF∴22::OM ON a b = ∴33::1:8S S a b ==乙甲 ∴:1:2a b =【例 8】如图，在平行四边形ABCD 中，BE EC =，2CF FD =．求阴影面积与空白面积的比．H ABCF G【分析】方法一：因为BE EC =，2CF FD =，所以14ABE ABCD S S =△四边形，16ADF ABCD S S =△四边形．因为2AD BE =，所以2AG GE =，所以11312BGE ABE ABCD S S S ==△△四边形，2136ABG ABE ABCD S S S ==△△四边形．同理可得，18ADH ABCD S S =△四边形，124DHF ABCD S S =△四边形．因为12BCD ABCD S S =△四边形，所以空白部分的面积111112()21224683ABCD ABCD S S =--++=四边形四边形，求面积方法的综合运用所以阴影部分的面积是13ABCDS四边形．12:1:233=，所以阴影面积与空白面积的比是1:2．GHOFDCA方法二：连接CG、CH、AC,AC交BD于O，有AO OC=在ABC△中，根据燕尾定理可以得到::1:1ABG ACGS S BE CE==△△,::1:1ABG CBGS S AO OC==△△,所以1136BCG ACG ABC ABCDS S S S===Y△△△,所以112BGE AGO ABCDS S S==Y△△,同理在ACD△中，根据燕尾定理可以得到1124AHC ACD ABCDS S S==Y△△,1148DCH ACD ABCDS S S==Y△△, 所以1128AHO AHC ABCDS S S==Y△△,11324DFH DCH ABCDS S S==Y△△所以11111()12128243BEG AGO AHO DHF ABCD ABCDS S S S S S S=+++=+++=Y Y△△△△阴影所以阴影面积与空白面积的比12:1:233=【例 9】如图，在一个梯形内有两个面积分别为10与12的三角形，已知梯形的上底长是下底长的23，那么余下的阴影部分的面积是______．1210【分析】设上底为2a,则下底为3a,梯形的高为2102121823a a a⨯⨯+=，梯形的面积为118(23)2a aa⨯+⨯=45,所以阴影部分面积为45101223--=1.如图所示，在ABC△中，:3:1BE EC=，D是AE的中点，那么:AF FC=．FE D C B AFE DCB A【分析】连接CD ．由于:1:1ABD BED S S =△△，:3:4BED BCD S S =△△，所以:3:4ABD BCD S S =△△，根据燕尾定理，::3:4ABD BCD AF FC S S ==△△． 2.三角形ABC 中，C 是直角，已知2AC =，2CD =，3CB =，AM BM =，那么三角形AMN (阴影部分)的面积为多少？［分析］连接BN ．ABC △的面积为3223⨯÷=根据燕尾定理，::2:1ACN ABN CD BD ==△△；同理::1:1CBN CAN BM AM ==△△设AMN △面积为1份，则MNB △的面积也是1份，所以ANB △的面积是112+=份，而ACN △的面积就是224⨯=份，CBN △也是4份，这样ABC △的面积为441110+++=份，所以AMN △的面积为31010.3÷⨯=． 3. 三角形ABC 的面积是1平方厘米，且BE =2EC ，F 是CD 的中点．那么阴影部分的面积是平方厘米．CACA【分析】连接BF ，根据燕尾定理::1:2ACF ABF S S CE BE ==△△,又因为F 是CD 的中点，所以ACF ADF S S =△△，所以ADF BDF S S =△△,即D 是AB 的中点，设1ECF S =△(份)，则2BEF S =△(份),3BDF S =△(份),5S =阴影(份)，2(123)12ABC S =⨯++=△(份)，所以551212ABC S S ==△阴影(平方厘米) 4.如图，线段AB 与BC 垂直，已知AD =EC =4，DB =BE =6，那么图中阴影部分面积是多少？ECBA ECBA【分析】这个图是个对称图形，且各边长度已经给出，我们不妨连接这个图形的对称轴看看.作辅助线BO ，则图形关于BO 对称，设△ADO 的面积为2份，则△DBO 的面积为3份，直角三角形ABE 的面积为8份.因为610230ABE S =⨯÷=△，而阴影部分的面积为4份，所以阴影部分的面积为 308415÷⨯=5.如图，ABC △中14AE AB =，AD 14AC =，ED 与BC 平行，EOD △的面积是1平方厘米．那么AED △的面积是平方厘米．【分析】因为14AE AB =，14AD AC =，ED 与BC 平行，所以:1:4ED BC =,:1:4EO OC =，44EOB EOD S S ==△△，则415CDE S =+=△，又因为::1:3AED CDE S S AD DC ==△△,所以15533AED S =⨯=△(平方厘米)．CBODEA富乌鸦树上落了一只嘴里衔着一大块东西的乌鸦。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第1页/共24页2019年小学奥数几何专题——复杂直线型面积-41．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？2．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．3．如图所示，在平行四边形ABCD 中，E 为AB 的中点，2AF CF =，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？4．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．5．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？6．如图所示，正方形ABCD 边长为6三角形DEF 的面积为多少平方厘米？7．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．8．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．9．如图，四边形EFGH 的面积是66平方米，EA AB =，CB BF =，DC CG =，HD DA =，求四边形ABCD 的面积．10．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？11．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？12．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求FGS S V ．13．如图所示，正方形ABCD 边长为8厘米，E 是AD 的中点，F 是CE 的中点，G 是BF 的中点，三角形ABG 的面积是多少平方厘米？14．四个面积为1的正六边形如图摆放，求阴影三角形的面积．15．已知图中每个正六边形的面积都是1，则图中虚线围成的五边形ABCDE 的面积是多少？16．如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．17．图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？18．如图，有三个正方形的顶点D 、G 、K 恰好在同一条直线上，其中正方形GFEB 的边长为10厘米，求阴影部分的面积．19．右图是由大、小两个正方形组成的，小正方形的边长是4厘米，求三角形ABC 的面积．20．如图，ABCD 与AEFG 均为正方形，三角形ABH 的面积为6平方厘米，图中阴影部分的面积为多少？21．正方形ABCD 和正方形CEFG ，且正方形ABCD 边长为10第3页/共24页厘米，则图中阴影面积为多少平方厘米？22．长方形ABCD 的面积为362cm ，E 、F 、G 为各边中点，H 为AD 边上任意一点，问阴影部分面积是多少？23．在边长为6厘米的正方形ABCD 内任取一点P ，将正方形的一组对边二等分，另一组对边三等分，分别与P 点连接,求阴影部分面积．24．ABCD 是边长为12的正方形，如图所示，P 是内部任意一点，4BL DM ==、5BK DN ==，那么阴影部分的面积是．25．如右图，AD DB =，AE EF FC ==，已知阴影部分面积为5平方厘米，ABC ∆的面积是多少平方厘米．26．图中三角形ABC 的面积是180平方厘米，D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF 长的3倍．那么三角形AEF 的面积是多少平方厘米？27．如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成．求阴影部分的面积．28．如图，在三角形ABC 中，已知三角形ADE 、三角形DCE 、三角形BCD 的面积分别是89，28，26．那么三角形DBE 的面积是多少？ 29．O 是长方形ABCD 内一点，已知OBC ∆的面积是25cm ，OAB ∆的面积是22cm ，求OBD ∆的面积是多少？30．如右图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若PBD ∆的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？31．如右图，正方形ABCD 的面积是20，正三角形BPC ∆的面积是15，求阴影BPD ∆的面积．32．如右图，正方形ABCD 的面积是12，正三角形BPC ∆的面积是5，求阴影BPD ∆的面积．33．右图中，ABCD 和CGEF 是两个正方形，AG 和CF 相交于H ，已知CH 等于CF 的三分之一，三角形CHG 的面积等于6平方厘米，求五边形ABGEF 的面积．34．如图，已知长方形ADEF 的面积16，三角形ADB 的面积是3，三角形ACF 的面积是4，那么三角形ABC 的面积是多少？35．如图所示，三角形ABC 中，D 是AB 边的中点，E 是AC 边上的一点，且3AE EC =，O 为DC 与BE 的交点．若CEO ∆的面积为a 平方厘米，BDO ∆的面积为b 平方厘米．且b a -是2.5平方厘米，那么三角形ABC 的面积是多少平方厘米？36．如图，长方形ABCD 的面积是2平方厘米，2EC DE =，F 是DG 的中点．阴影部分的面积是多少平方厘米？37．如图，45BC =，21AC =，ABC ∆被分成9个面积相等的小三角形，那么DI FK +=？38．如图，在角MON 的两边上分别有A 、C 、E 及B 、D 、F 六个点，并且OAB ∆、ABC ∆、BCD ∆、CDE ∆、DEF ∆的面积都等于1，则DCF ∆的面积等于多少？39．如图，已知5CD =，7DE =，15EF =，6FG =，线段AB 将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG 的面积是多少？40．如图所示，长方形ABCD 内的阴影部分的面积之和为70，8AB =，15AD =，求四边形EFGO 的面积.第5页/共24页41．如图所示，矩形ABCD 的面积为24平方厘米．三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则四边形PMON 的面积是多少平方厘米？42．如图，如果长方形ABCD 的面积是56平方厘米，那么四边形MNPQ 的面积是多少平方厘米？43．如图在ABC △中，,D E 分别是,AB AC 上的点，且:2:5AD AB =，:4:7AE AC =，16ADE S =△平方厘米，求ABC △的面积．44．如图，三角形ABC 被分成了甲(阴影部分)、乙两部分，4BD DC ==，3BE =，6AE =，乙部分面积是甲部分面积的几倍？45．如图在ABC △中，D 在BA 的延长线上，E 在AC 上，且:5:2AB AD =，:3:2AE EC =，12ADE S =△平方厘米，求ABC △的面积．46．如图，三角形ABC 的面积为3平方厘米，其中:2:5AB BE =，:3:2BC CD =，三角形BDE 的面积是多少？47．已知DEF △的面积为7平方厘米，,2,3BE CE AD BD CF AF ===，求ABC △的面积．48．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使3AF AC =，求三角形DEF 的面积．49．如图，平行四边形ABCD ，BE AB =，2CF CB =，3GD DC =，4HA AD =，平行四边形ABCD 的面积是2，求平行四边形ABCD 与四边形EFGH 的面积比．50．如图，将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ，若四边形ABCD 的面积为5，则四边形EFGH 的面积是多少？51．如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =．求FGS S V ．52．一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的15%，黄色三角形面积是221cm ．问：长方形的面积是多少平方厘米？53．如图，长方形ABCD 的面积是1，M 是AD 边的中点，N 在AB 边上，且2AN BN =.那么，阴影部分的面积是多少？54．如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求三角形DEF 的面积．55．如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形ADE 的面积等于1，那么三角形ABC 的面积是多少？56．如图，在ABC △中，延长AB 至D ，使BD AB =，延长BC 至E ，使，F 是AC 的中点，若ABC △的面积是2，则DEF △的面积是多少？第1页/共24页参考答案1．5【解析】连接AD ．又∵4BD DC ==，2．50【解析】连接BE ，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6ADE S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比3．48【解析】连接FB ．三角形AFB 面积是三角形CFB 面积的2倍，而三角形AFB 面积是三角形AEF 面积的2倍，所以三角形ABC 面积是三角形AEF 面积的3倍；又因为平行四边形的面积是三角形ABC 面积的2倍，所以平行四边形的面积是三角形AFE 面积的326⨯=（）倍．因此，平行四边形的面积为8648⨯=(平方厘米)．4．24【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEFS =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米5．12.5 【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米6．10理”可得，():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△；而66218ABC S =⨯÷=△；所以4CEF S =△；同理得，:2:3CDE ACD S S =△△;，183212CDE S =÷⨯=△，6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米)．7．18【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC V 和CFE V 中，ACB ∠与FCE ∠互补，又1ABC S =V ，所以8FCE S =V ．同理可得6ADF S =V ，3BDE S =V ．第3页/共24页所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=V V V V V ．8．1/18【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△．所以213618ABCD EFGH S S ==．9．13.2【解析】连接BD ．由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△，即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△，即2AHE ABD S S =△△所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ，同理可以得到2DHG BEF ABCD S S S +=△△四边形所以66513.2ABCD S =÷=四边形平方米10．60【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEHABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGHBEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==．11．3.5 【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABC S =V ，所以0.5FCE S =V ．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△12．1/10【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△． 13．12【解析】连接AF 、EG ．因为218164BCF CDE S S ==⨯=△△，根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =V ，8EFG S =V ，再根据”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”，得到16BFC S =V ，32ABFE S =，24ABF S =V ，所以12ABG S =V 平方厘米．第5页/共24页14．13/6 【解析】如图，将原图扩展成一个大正三角形DEF ，则AGF ∆与CEH ∆都是正三角形．假设正六边形的边长为为a ，则AGF ∆与CEH ∆的边长都是4a ，所以大正三角形DEF 的边长为4217⨯-=，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为16，三角形DEF 的面积为496．由于4FA a =，3FB a =，所以AFB ∆与三角形DEF 的面积之比为43127749⨯=．同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249，所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=，所以ABC ∆的面积的面积为4913136496⨯=． 15．263【解析】从图中可以看出，虚线AB 和虚线CD 外的图形都等于两个正六边形的一半，也就是都等于一个正六边形的面积；虚线BC 和虚线DE 外的图形都等于一个正六边形的一半，那么它们合起来等于一个正六边形的面积；虚线AE 外的图形是两个三角形，从右图中可以看出，每个三16．28 【解析】本题是等底等高的两个三角形面积相等的应用．连接BH 、CH ．同理，BFHCFHS S =△△，S =S CGH DGH V V ，∴11562822ABCD S S ==⨯=阴影长方形(平方厘米)． 17．48 【解析】把另外三个三等分点标出之后，正方形的3个边就都被分成了相等的三段．把H 和这些分点以及正方形的顶点相连，把整个正方形分割成了9个形状各不相同的三角形．这9个三角形的底边分别是在正方形的3个边上，它们的长度都是正方形边长的三分之一．阴影部分被分割成了3个三角形，右边三角形的面积和第1第2个三角形相等：中间三角形的面积和第3第4个三角形相等；左边三角形的面积和第5个第6个三角形相等．因此这3个阴影三角形的面积分别是ABH 、BCH 和CDH 的三分之一，因此全部阴影的总面积就等于正方形面积的三分之一．正方形的面积是144，阴影部分的面积就是48． 18．100 【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接FK 、GE 、BD ，则////BD GE FK ，根据几何五大模型第7页/共24页中的面积比例模型，可得DGE BGE S S ∆∆=，KGE FGE S S ∆∆=，所以阴影部分的面积就等于正方形GFEB 的面积，即为210100=平方厘米． 19．8 【解析】这道题似乎缺少大正方形的边长这个条件，实际上本题的结果与大正方形的边长没关系．连接AD (见右上图)，可以看出，三角形ABD 与三角形ACD 的底都等于小正方形的边长，高都等于大正方形的边长，所以面积相等．因为三角形AGD 是三角形ABD 与三角形ACD 的公共部分，所以去掉这个公共部分，根据差不变性质，剩下的两个部分，即三角形ABG 与三角形GCD 面积仍然相等．根据等量代换，求三角形ABC 的面积等于求三角形BCD 的面积，等于4428⨯÷=． 20．6 【解析】如图，连接AF ，比较ABF ∆与ADF ∆，由于AB AD =，FG FE =，即ABF ∆与ADF ∆的底与高分别相等，所以ABF ∆与ADF ∆的面积相等，那么阴影部分面积与ABH ∆的面积相等，为6平方厘米． 21．50 【解析】方法一：三角形BEF 的面积2BE EF =⨯÷，梯形EFDC 的面积22EF CD CE BE EF =+⨯÷=⨯÷=（）三角形BEF 的面积，而四边形CEFH 是它们的公共部分，所以，三角形DHF 的面积=三角形BCH 的面积，进而可得，阴影面积=三角形BDF 的面积=三角形BCD 的面积1010250=⨯÷=(平方厘米)．方法二：连接CF ，那么CF 平行BD ，所以，阴影面积=三角形BDF 的面积=三角形BCD 的面积50=(平方厘米)． 22．13.5【解析】解法一：寻找可利用的条件，连接BH 、HC ，如下图：可得：、、，而36ABCD AHB CHB CHD S S S S ∆∆∆=++=而EHB BHF DHG EBFS S S S S ∆∆∆∆++=+阴影，所以阴影部分的面积是：1818 4.513.5EBF S S ∆=-=-=阴影解法二：特殊点法．找H 的特殊点，把H 点与D 点重合，那么图形就可变成右图：这样阴影部分的面积就是DEF ∆的面积，根据鸟头定理，则有： 23．15【解析】（法1）特殊点法．由于P 是正方形内部任意一点，可采用特殊点法，假设P 点与A 点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的14和16，所以阴影部分的面积为2116()1546⨯+=平方厘米．（法2）连接PA 、PC ．第9页/共24页由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半，所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14，同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16，所以阴影部分的面积为2116()1546⨯+=平方厘米．24．34【解析】（法1）特殊点法．由于P 是内部任意一点，不妨设P 点与A 点重合(如上中图)，那么阴影部分就是AMN ∆和ALK ∆．而AMN ∆的面积为(125)4214-⨯÷=，ALK ∆的面积为(124)5220-⨯÷=，所以阴影部分的面积为142034+=．（法2）寻找可以利用的条件，连接AP 、BP 、CP 、DP 可得右上图所示：则有:211127222PDC PAB ABCD S S S ∆∆+==⨯=同理可得：72PAD PBC S S ∆∆+=;而::4:121:3PDM PDC S S DM DC ∆∆===,即13PDM PDC S S ∆∆=；同理：13PBL PAB S S ∆∆=,512PND PDA S S ∆∆=,512PBK PBC S S ∆∆=; 所以：15()()()()312PDM PBL PND PBK PDC PAB PDA PBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++ 而()()()()PDM PBL PND PBK PNM PLK DNM BLK S S S S S S S S ∆∆∆∆∆∆∆∆+++=+++1442443阴影面积；所以阴影部分的面积是：即为：15727210224302034312⨯+⨯-⨯=+-=． 25．30 【解析】连接CD ．根据题意可知，DEF ∆的面积为DAC ∆面积的13，DAC ∆的面积为ABC ∆面积的12，所以DEF ∆的面积为ABC ∆面积的111236⨯=．而DEF ∆的面积为5平方厘米，所以ABC ∆的面积为15306÷=(平方厘米)．26．22.5【解析】ABD V ，ABC V 等高，所以面积的比为底的比，有所以ABDS V=(平方厘米)．同理有平方厘米)(平方厘米)．即三角形AEF 的面积是22.5平方厘米． 27．5 【解析】如图，将大长方形的长的长度设为1，则12112364AB ==+，24124483CD ==+，所以1113412MN =-=，阴影部分面积为211(12243648)5(cm )212+++⨯⨯=． 28【解析】根据题意可知，8928117ADC ADE DCE S S S ∆∆∆=+=+=，所以::26:1172:9BDC ADC BD AD S S ∆∆===，那么::2:9DBE ADE SS BD AD ∆∆==，29．3【解析】由于ABCD 是长方形，所以AOD BOC ABDS S S ∆∆∆+=，则BOC OAB OBDS S S ∆∆∆=+，所以2523cm OBD BOC OAB S S S ∆∆∆=-=-=．30．16 【解析】第11页/共24页根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差．如右上图，连接CP 、AP ．由于12BCP ADP ABP BDP ADP ABCD S S S S S S ∆∆∆∆∆+=++=，所以BCP ABP BDP S S S ∆∆∆-=．而12BCP BCFE S S ∆=，12ABP ABHG S S ∆=，所以()2216BCFE ABHG BCP ABP BDP S S S S S ∆∆∆-=-==(平方分米)． 31．10 【解析】连接AC 交BD 于O 点，并连接PO ．如下图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有：因为1120544BOC ABCD S S ∆==⨯=，所以15510BPD S ∆=-=．32．2 【解析】连接AC 交BD 于O 点，并连接PO ．如右上图所示，可得//PO DC ，所以DPO ∆与CPO ∆面积相等(同底等高)，所以有: 因为134BOC ABCD S S ∆==，所以532BPD S ∆=-=．33．49.5 【解析】连接AC 、GF ，由于AC 与GF 平行，可知四边形ACGF 构成一个梯形．由于HCG ∆面积为6平方厘米，且CH 等于CF 的三分之一，所以CH 等于FH 的12，根据梯形蝴蝶定理或相似三角形性质，可知FHG ∆的面积为12平方厘米，AHF ∆的面积为6平方厘米，AHC ∆的面积为3平方厘米．那么正方形CGEF 的面积为()612236+⨯=平方厘米，所以其边长为6厘米．又AFC ∆的面积为639+=平方厘米，所以9263AD =⨯÷=(厘米)，即正方形ABCD的边长为3厘米．那么，五边形ABGEF的面积为：21369349.52++⨯=(平方厘米)． 34．6.5 【解析】方法一：连接对角线AE ． ∵ADEF 是长方形方法二：连接BF ，由图知1628ABF S =÷=△，所以16835BEF S =--=△，又由4ACF S =△，恰好是AEF △面积的一半，所以C 是EF 的中点，因此52 2.5BCE BCF S S ==÷=△△，所以1634 2.5 6.5ABC S =---=△35．10平方厘米)．所以 2.5410ABC S ∆=⨯=(平方厘米)． 36．512【解析】如下图，连接FC ，DBF V 、BFG V 的面积相等，设为x 平方厘米;FGC V 、DFC V 的面积相等，设为y 平方厘米，那么DEF V 的面积为平方厘米．221BCD S x y =+=V 0.531x y x y +=⎧⎨+=⎩①②．比较②、①第13页/共24页式，②式左边比①式左边多2x ，②式右边比①式右边大0.5，有20.5x =，即0.25x =,0.25y =．而阴影部分面积为 37．24【解析】由题意可知，::2:9BAD ABC BD BC S S ∆∆==，所以2109BD BC ==，35CD BC BD =-=；又::2:5DIF DFC DI DC S S ∆∆==，所以2145DI DC ==，同样分析可得10FK =，所以141024DI FK +=+=． 38．34【解析】根据题意可知，::4:1OED DEF OD DF S S ∆∆==39．40 【解析】连接AF ，BD ．根据题意可知，571527CF =++=；715628DG =++=；所以，1527BE CBF F S S ∆∆=，1227BE CBF C S S ∆∆=，2128AEG ADG S S ∆∆=，728AED ADG S S ∆∆=，于是：2115652827ADG CBF S S ∆∆+=；712382827ADG CBF S S ∆∆+=；可得40ADG S ∆=．故三角形ADG 的面积是40． 40．10【解析】利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和，以及三角形AOE 和DOG 的面积之和，进而求出四边形EFGO 的面积．由于长方形ABCD 的面积为158120⨯=，所以三角形BOC 的面积为，所以三角形AOE 和DOG 的面积之和为又三角形AOE 、DOG 和四边形EFGO 的面积之和为所以四边形EFGO 的面积为302010-=．另解：从整体上来看，四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积，而三角形AFC 面积+三角形BFD 面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即1207050-=，所以四边形的面积为605010-=． 41．1.8【解析】因为三角形ADO 与三角形BCO 的面积之和是矩形ABCD 的面积的一半，即12平方厘米，又三角形ADM 与三角形BCN 的面积之和为7.8平方厘米，则三角形AMO 与三角形BNO 的面积之和是4.2平方厘米，则四边形PMON 的面积=三角形ABP 面积-三角形AMO 与三角形BNO 的面积之和-三角形ABO 面积12 4.26 1.8=--=(平方厘米)． 42．32.5 【解析】如图，过M 、N 、P 、Q 分别作长方形ABCD 的各边的平行线．易知交成中间的阴影正方形的边长为3厘米，面积等于9平方厘米．设MQD ∆、NAM ∆、PBN ∆、QCP ∆的面积之和为S ，四边形MNPQ 的面积等于x ，则569x S x S +=⎧⎨-=⎩，解得32.5x =(平方厘米)． 43．70 【解析】连接BE，::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△，第15页/共24页::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△，所以:(24):(75)ADE ABC S S =⨯⨯△△，设8ADE S =△份，则35ABC S =△份，16ADE S =△平方厘米，所以1份是2平方厘米，35份就是70平方厘米，ABC △的面积是70平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比． 44．5 【解析】连接AD ．又∵4BD DC ==， 45．50 【解析】连接BE，::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△，所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△，设6ADE S =△份，则25ABC S =△份，12ADE S =△平方厘米，所以1份是2平方厘米，25份就是50平方厘米，ABC △的面积是50平方厘米．由此我们得到一个重要的定理，共角定理：共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 46．12.5【解析】由于180ABC DBE ︒∠+∠=，所以可以用共角定理，设2AB =份，3BC =份，则5BE =份，325BD =+=份，由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△，设6ABC S =△份，恰好是3平方厘米，所以1份是0.5平方厘米，25份就是250.512.5⨯=平方厘米，三角形BDE 的面积是12.5平方厘米 47．24 【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△，:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份，则4BDE S =△份，4ADF S =△份，9CEF S =△份，244497DEF S =---=△份，恰好是7平方厘米，所以24ABC S =△平方厘米 48．18 【解析】(法1)本题是性质的反复使用．连接AE 、CD ．同理可得其它，最后三角形DEF 的面积18=．(法2)用共角定理∵在ABC V 和CFE V 中，ACB ∠与FCE ∠互补，又1ABC S =V ，所以8FCE S =V ．同理可得6ADFS =V ，3BDE S =V ．所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=V V V V V ．【答案】118【解析】连接AC 、BD ．根据共角定理∵在ABC △和BFE △中，ABC ∠与FBE ∠互补，第17页/共24页又1ABC S =△，所以3FBE S =△．同理可得8GCF S =△，15DHG S =△，8AEH S =△．所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△．50．60 【解析】连接AC 、BD ．由于2BE AB =，2BF BC =，于是4BEF ABC S S ∆∆=，同理4HDG ADC S S ∆∆=．于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=．再由于3AE AB =，3AH AD =，于是9AEH ABD S S ∆∆=，同理9CFG CBD S S ∆∆=．于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=．那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==．51．110【解析】本题题目本身很简单，但它把本讲的两个重要知识点融合到一起，既可以看作是”当两个三角形有一个角相等或互补时，这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用，也可以看作是找点，最妙的是其中包含了找点的3种情况．最后求得FGS S △的面积为 52．60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长，高相加为长方形的宽，所以黄色三角形与绿色三角形的面积和为长方形面积的50%，而绿色三角形面积占长方形面积的15%，所以黄色三角形面积占长方形面积的50%15%35%-=．已知黄色三角形面积是221cm ，所以长方形面积等于2135%60÷=（2cm ）． 53．512【解析】连接BM ，因为M 是中点所以ABM △的面积为又因为2AN BN =，所以BDC △，又因为BDC △面积为54．3【解析】三角形ADC 的面积是三角形ABC 面积的一半24212÷=，三角形ADE 又是三角形ADC 面积的一半1226÷=．三角形FED 的面积是三角形ADE 面积的一半，所以三角形FED 的面积623=÷=． 55．15 【解析】连接BE ．又∵5AB AD = 56．3.5【解析】∵在ABC △和CFE △中，ACB ∠与FCE ∠互补，又2ABC S =V ，所以0.5FCE S =V ．同理可得2ADF S =△，3BDE S =△．所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△。

小学数学奥数测试题复杂直线型面积4_人教版

小学数学几何直线型面积的计算完整版题型训练+详细答案

小学数学奥数测试题-复杂直线型面积-62015人教版

小学奥数几何专题--复杂直线型面积-6(六年级)竞赛测试.doc

小学奥数几何专题--复杂直线型面积-1(六年级)竞赛测试.doc

小学数学奥数测试题复杂直线型面积4_人教版-学习文档

小学数学奥数测试题复杂直线型面积4_人教版

五年级奥数学练习试卷思维培训资料 直线形面积的计算

小学数学几何 直线型面积的计算 完整版题型训练+详细答案

小学数学奥数测试题复杂直线型面积10_人教版

小学奥数几何专题--复杂直线型面积-4(六年级)竞赛测试.doc

小学数学奥数测试题复杂直线型面积3_人教版

小学奥数几何专题--复杂直线型面积-3(六年级)竞赛测试.doc

小学数学奥数测试题复杂直线型面积12_人教版

小学数学奥数测试题复杂直线型面积11_人教版

小学奥数几何专题--复杂直线型面积-11(六年级)竞赛测试.doc

小学奥数：基本图形的面积计算.专项练习及答案解析

(完整word版)六年级奥数-直线形面积的计算

六年级下册奥数试题-几何直线形面积-燕尾定理.(含答案)人教版

五年级奥数学练习试卷思维培训资料直线形面积的计算

小学数学几何直线型面积的计算完整版题型训练+详细答案